1 Introduction

The cavity-optomechanics—cavity mediated interaction between mechanical resonators and light via radiation pressure—has been the subject of many stunning investigations over the last two decades [1,2,3]. It has been proven to be the best tool to manipulate mechanical effects of light to govern new physics. The recent studies on the optomechanical systems coupled with other physical objects, like Bose–Einstein condensate (BEC), have attracted the growing interests of researcher both in theory and experiment [4,5,6,7,8,9]. The most interesting example of such systems is an optomechanical cavity with one mechanical oscillator (or moving-end mirror) and the ultracold atoms or BEC trapped inside the cavity. Furthermore, benefiting from the development of optical microcavity technology, the mechanical resonator with a smaller mass can be used to magnify the optomechanical effect in such systems [10,11,12]. Thus, the construction of such hybrid optomechanical systems provides the opportunity to explore new quantum phenomena, for instance, dynamical phase transitions to optomechanical superradiance [13], cooling the atoms to ground state [14,15,16,17,18,19], developing optomechanical crystals [20,21,22] as well as realizing non-Hermitian system [23, 24].

Bender and Boettcher demonstrated that a non-Hermitian system can possess a real energy spectrum when the parity-time (PT) symmetry condition is satisfied in 1998 [25]. These systems demand a complex potential V(x) characterized by \( V(x)=V^*(-x) \), in which the real part of the potential should be even, and the imaginary part should be odd to realize PT symmetry. Very recently, there are various non-Hermitian studies based on quantum optomechanical systems, such as optomechanically induced transparency (OMIT) [26,27,28,29,30,31], optomechanically induced light squeezing [32], PT symmetry breaking enhanced cavity optomechanical magnetometry [33] and optomechanical crystal cavities [34]. Further, cavity-optomechanics has proven to be a suitable tool to study non-Hermitian physics [35, 36], especially regarding the behavior of PT symmetry [37,38,39,40]. Although, there has been sufficient work done in this direction, exploring non-Hermitian physics in a single optomechanical cavity is still desirable, and we intend to do so by manipulating excited state dissipation in BEC-optomechanics in our work.

The subject of stability (or instabilities) of light in cavity quantum electrodynamics (QED) is very crucial in order to study and implement quantum optical devices. Optical bistability (multistability) gives the behavior as a discontinuous transition between high and low transmission of two (or more) stable states [41, 42], where the system can be described linearly, and instability implies that driven far from the thermodynamic equilibrium of the system means towards high-order nonlinearities like chaos [43]. The interaction between cavity mode and atoms excites different population densities of the cavity photons corresponding to these stable and unstable states [44]. Although, there has been a lot of work done on optical bistability in cavity QED, but it is worthwhile to see such optical effects in an engineered non-Hermitian cavity-atom system.

In this paper, we investigate optical multistable dynamics in a non-Hermitian optomechanical system containing BEC and driven by a single mode pump laser. In order to make our system non-Hermitian, we consider the dissipation of the excited state as a gain for the ground state, by not using the adiabatic elimination of excited state decay. After governing the steady-state dynamics of our system, we find that non-Hermicity has a profound effect on steady-state cavity photon number. It is interesting to note that at low pump powers, the cavity photon number shows optical bistable behavior and at high pump power, it illustrates, so-called, optical biunstability. In particular, we illustrate that the angle of phase shift \( \phi \) on an optical lattice has a very strong effect on steady-state dynamics, especially at high pump power regions. Further, we illustrate the effects of non-Hermicity on the effective steady-state potential of the system as a function of cavity photon number.

This paper starts by introducing our mode and calculation in Sect. 2. Section 3 shows the multistability of steady-state cavity photon number under the negative and positive value of phase shift as \( \cos 2\phi \). Finally, Sect. 4 summarizes and prospect our work.

2 The model

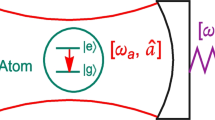
The model is composed of \(^{87}\)Rb BEC trapped inside a high quality factor optical cavity shown as Fig. 1 [45]. A single-mode pump laser with frequency \( \omega _p \) drives the cavity and generates a strong intracavity field with coupling strength \(\eta =\sqrt{P\times \kappa /\hbar \omega _p}\). The total Hamiltonian of the system can be divided into two parts,

$$\begin{aligned} \hat{H}=\hat{H}_a+\hat{H}_c, \end{aligned}$$
(1)

where \( \hat{H}_a \) describes BEC and its optomechanical interactions with cavity, while \( \hat{H}_c \) corresponds to the intracavity optical field and its coupling with external pump field.

Fig. 1
figure 1

Schematic illustration of Bose–Einstein condensate trapped inside a Fabry–P\(\acute{e}\)rot cavity. An external pump laser \(\eta \) with frequency \(\omega _p\) drives the cavity. The cavity mode oscillates at frequency is \(\omega _c\) with coupling with two level atoms having ground state \(|g\rangle \) and excited state \( |e\rangle \), respectively

Full size image

The atomic mode (or BEC) have ground state \(|g\rangle \) and excited state \(|e\rangle \) with transitional frequency \(\omega _0\). We use \(\hat{\Psi }_g^\dagger (\hat{\Psi }_g) \) and \( \hat{\Psi }_e^\dagger (\hat{\Psi }_e)\) to represent creation (annihilation) operator of ground and excited state, respectively. The Hamiltonian of two-level atoms in optical lattice \(\hat{H}_a\) is given by [40],

$$\begin{aligned} \begin{aligned} \hat{H}_a=&\int \sum _{i=g,e}\hat{\Psi }_i^\dagger (x)\big (-\dfrac{\hbar ^2 \bigtriangledown ^2}{2m}+U(x)\big ) \hat{\Psi }_i(x) +\hbar \omega _0 \hat{\Psi }_e^\dagger (x)\hat{\Psi }_e(x)\\&-\big (\textbf{d}\cdot \textbf{E}(x,t)\hat{\Psi }_g^\dagger (x) \hat{\Psi }_e(x)\hat{a}^\dagger + H.c.\big )\\&+\frac{u}{2}\hat{\Psi }_g^\dagger (x)\hat{\Psi }_g^\dagger (x) \hat{\Psi }_g(x)\hat{\Psi }_g(x) dx, \end{aligned} \end{aligned}$$
(2)

where m is the atomic mass and \( U(x)=\hbar V_0 \hat{a}^\dagger \hat{a}\cos ^2(kx) \) corresponds to the optical lattice formed by the intracavity mode [46,47,48], \( V_0 \) is the optical lattice depth and \( k=\omega _c/c \) is the wave number. \( \textbf{E}(x,t)=\textbf{E}_0\cos (kx+\phi ) \) is the electric field with \( E_0 \) being the electric component of cavity field along with \(\phi \) as a scattering phase shift. \( \textbf{d}=\left\langle {e}\right| \hat{\textbf{d}}\left| {g}\right\rangle \) corresponds to the electric dipole moment, and u is the interatomic interaction coefficient. We consider that the excited state has dissipation larger than the spontaneous emission rate and thus, this dissipation acts as a contribution to the mechanics of the ground state. In other words, we consider the decay of the excited state as a gain for the ground state, by ignoring the adiabatic elimination of the excited state. This gain later makes our system non-Hermitian, which is the main topic of the work. To include such dissipation, one can adopt the Heisenberg equation approach for excited state under rotating wave approximation (RWA) given as,

$$\begin{aligned} \dot{\hat{\Psi }}_e(x) = i \delta \hat{\Psi }_e(x)+i\dfrac{\mathbf {d\cdot E(x,t)}}{\hbar }\hat{\Psi }_g(x)\hat{a}-\dfrac{\Gamma }{2}\hat{\Psi }_e(x), \end{aligned}$$
(3)

here \( \delta =\omega _c-\omega _0 \) is the detuning between cavity field and atoms. The decay of the excited state to the ground state is indicated with \( \Gamma \). While using a near-resonant light pump, we suppose \( \delta \ll \Gamma \). Under these conditions, the above equation will read as,

$$\begin{aligned} \hat{\Psi }_e(x)\approx i\dfrac{2\mathbf {d\cdot E(x,t)}}{\Gamma \hbar }\hat{\Psi }_g(x)\hat{a}. \end{aligned}$$
(4)

We assume that the atomic densities are low enough that one can neglect the two body interactions. By considering the relation excited state \( \hat{\Psi }_e(x) \) with ground state \( \hat{\Psi }_g(x) \) in Eq. (2), one can rewrite the Hamiltonian for atoms (or BEC) in optical lattice \( \hat{H}_a \) as,

$$\begin{aligned} \hat{H}_a= \int dx \hat{\Psi }_g^\dagger (x)\big (-\dfrac{\hbar ^2 \bigtriangledown ^2}{2m}+U(x)-i\dfrac{2|\mathbf {d\cdot E(x,t)}|^2}{\hbar \Gamma }\hat{a}^\dagger \hat{a}\big )\hat{\Psi }_g(x). \end{aligned}$$
(5)

Here it should be noted that we have omitted the subscription g from the ground state in order to make things simpler. Now one can note that the Hamiltonian is now in non-Hermitian form because the intracavity effective optical potential for atoms appears to be complex. Further, the PT symmetry can be achieved or tuned by adjusting phase shift \( \phi \) in the effective optical lattice [40], as can be noted in V(x) below,

$$\begin{aligned} V(x)=\hbar V_0\hat{a}^\dagger \hat{a}\big (\cos ^2(kx)-i\gamma \cos ^2(kx+\phi )\big ), \end{aligned}$$
(6)

here \(i2|\mathbf {d\cdot E(x,t)}|^2/\hbar \Gamma =i\gamma \cos ^2(kx+\phi )\) with effective non-Hermitian parameter \( \gamma =2|\textbf{d} \cdot \textbf{E}_0(x)|^2/\hbar V_0\Gamma \). After that, one can rewrite the effective Hamiltonian for the atoms inside the cavity \( \hat{H}_a \) as,

$$\begin{aligned} \hat{H}_a= \int dx \hat{\Psi }_g^\dagger (x)\big (-\dfrac{\hbar ^2 \bigtriangledown ^2}{2m}+V(x)\big )\hat{\Psi }_g(x). \end{aligned}$$
(7)

To study the interaction between BEC and cavity field, it is necessary to know the expression of the bosonic operator \( \hat{\Psi }_g \). The inter-cavity field couples with different momentum modes at \( \pm 2l\hbar k \) of the BEC, where l is an integer and k is the wave number of the cavity field. The experiment shows that when the photon number is not large, the BEC and cavity field interaction will significantly engender with those momenta 0 and \( \pm 2\hbar k \) while neglecting higher order modes we could expend the bosonic operator \( \hat{\Psi }_g \) in k-space as [49]

$$\begin{aligned} \hat{\Psi }_g(x)=[\hat{c}_0+\sqrt{2}\cos (2kx)\hat{c}_2]/\sqrt{L}, \end{aligned}$$
(8)

where \( \hat{c}_0 \) and \( \hat{c}_2 \) are zero momentum and side-mode components for bosonic annihilation operator for atoms respectively and satisfy \( |\hat{c}_0|^2+|\hat{c}_2|^2=N \), L is cavity length, with this expansion we have

$$\begin{aligned} \begin{aligned} \hat{H}'_a=&\hbar V_0\hat{a}^\dagger \hat{a}(\frac{1}{2}(\hat{c}_0^\dagger \hat{c}_0+\hat{c}_2^\dagger \hat{c}_2)(1-i\gamma )\\&+\frac{\sqrt{2}}{4}(\hat{c}_0^\dagger \hat{c}_2+\hat{c}_2^\dagger \hat{c}_0)(1-i\gamma \cos 2\phi ))\\&+4\omega _r\hat{c}_2^\dagger \hat{c}_2. \end{aligned} \end{aligned}$$
(9)

First term describes the potential energy and the second term describes the optical coupling between the zero momentum and side-mode of the BEC, the last term is the energy of side-mode with frequency \( 4\omega _r=2k^2\hbar ^2/m \), we suggest the atom number is less with \( \hat{c}_0^\dagger \hat{c}_0\simeq N \), which means side-mode atoms occupy only a few parts if condensate, treating the condensate with “c”approach via \( \hat{c}_0 \) and \( \hat{c}_2 \rightarrow \sqrt{N}\) then Eq. (9) could be reduced as

$$\begin{aligned} \begin{aligned} \hat{H}'_a=&\frac{1}{2}\hbar V_0 N\hat{a}^\dagger \hat{a}(1-i\gamma )+\dfrac{1}{2}\hbar \sqrt{N}V_0\hat{a}^\dagger \hat{a}\hat{q}(1-i\gamma \cos 2\phi )\\&+4\omega _r(\hat{p}^2+\hat{q}^2), \end{aligned} \end{aligned}$$
(10)

here \(\hat{q}=(\hat{c}_2^\dagger +\hat{c}_2)/\sqrt{2}\) and \( \hat{p}=i(\hat{c}_2^\dagger -\hat{c}_2)/\sqrt{2} \) are position operator and momentum operator of side-mode satisfying the canonical commutation relation \( [\hat{q},\hat{p}=i] \), the behavior of side-mode BEC is effectively as movable mirror.

Fig. 2
figure 2

Bistable dynamics of the cavity field as a function of the normalized pump intensity \( \eta ^2/\kappa ^2 \). a–c show the steady-state result with the phase shift \( \cos 2\phi \) take value of 1,0,\(-1\), respectively. The relation between the steady-state of cavity photon number and the atoms will have two roots illustrated by the blue and red curve in a and c. In a and c show the local enlarged of lower bistability when the pump intensity is small. Here, other used parameters are \(\omega _r=0.1\) and \( \gamma /\gamma _{sm}=0.08 \). The coupling of cavity and atoms \( g/\omega _r=4 \), the effective cavity-pump detuning \(\Delta /\kappa =-5.1\) and the decay of the side-mode atoms are \(\gamma _{sm}/\kappa =0.001\)

Full size image

The Hamiltonian for intra-cavity field \( \hat{H}_c \) can be expressed as [1]

$$\begin{aligned} \hat{H}_c= -\hbar \Delta _c\hat{a}^\dagger \hat{a}-i\hbar \eta (\hat{a}-\hat{a}^\dagger ), \end{aligned}$$
(11)

where, \( \Delta _c=\omega _p-\omega _c \) is the cavity-pump detuning, \( \hat{a} \) and \( \hat{a}^\dagger \) correspond to the photonic annihilation and creation operators for the optical cavity field with frequency \( \omega _c \) and canonical relation \( [\hat{a},\hat{a}^\dagger ]=1 \). The second term describes the external pumping of the cavity mode with the amplitude of the coupling field \(\eta \).

As an open system, we have to consider effects of dissipation on the optical field, the decay of exited state of atoms, and the damping of the side-mode atoms, we incorporate standard quantum noise operators by deriving quantum Langevin equations in non-Hermitian system. It must be stressed that the non-Hermitian quantum Langevin equation runs differently from Hermitian case [50,51,52], In general the non-Hermitian quantum Langevin equation is given by \( \dot{\hat{O}}=-i/\hbar (\hat{H}\hat{O}-\hat{O}\hat{H}^\dagger )-\kappa \hat{O}+\hat{N}\) here \(\hat{O}\) is the generic operator of the system and \(\kappa \) is the corresponding decay rate, \(\hat{N}\) is the noise operator. Now the coupled non-Hermitian quantum Langevin equations are given by

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}\hat{a}}{{\text {d}}t}=&(i\Delta -ig\hat{q}-(\sqrt{N}g\gamma +g\gamma \cos 2\phi \hat{q})(2\hat{a}^\dagger \hat{a}+1)-\kappa )\hat{a}\\&+\eta +\sqrt{2\kappa }\hat{a}_{in},\\ \dfrac{{\text {d}}\hat{a}^\dagger }{{\text {d}}t}=&\hat{a}^\dagger (-i\Delta +ig\hat{q}-(\sqrt{N}g\gamma +g\gamma \cos 2\phi \hat{q})(2\hat{a}^\dagger \hat{a}+1)-\kappa )\\&\eta +\sqrt{2\kappa }\hat{a}_{in},\\ \dfrac{{\text {d}}\hat{q}}{{\text {d}}t}=&4\omega _r\hat{p}-\gamma _{sm}\hat{q}+\hat{f}_{1M},\\ \dfrac{{\text {d}}\hat{p}}{{\text {d}}t}=&-4\omega _r\hat{q}-g\hat{a}^\dagger \hat{a}-g\hat{a}^\dagger \hat{a}\gamma \cos 2\phi (\hat{q}\hat{p}+\hat{p}\hat{q})\\&-\gamma _{sm}\hat{p}+\hat{f}_{2M}, \end{aligned} \end{aligned}$$
(12)

where \( \Delta =\Delta _c-NV_0/2 \) is the effective detuning of the system, \( g=\sqrt{N}V_0/2 \) is the coupling of cavity field and side-mode atoms. \( \hat{a}_{in} \) is the Markovian input noise of the optical cavity field, the damping of atoms is described by \( \gamma _{sm} \) which is caused by the couples of the \( \pm 2\hbar k \)-momentum side-mode to the others, \( \hat{f}_1 \) as well as \( \hat{f}_2 \) are the associated noise operator, assumed to be Markovian. The side-mode atoms are driven by the radiation pressure of the cavity field, which deeply depends on the position of the oscillator. When the system is at the same input pump power one can reach to three or more different stable states, this hysteresis-like phenomenon is called multistability [52]. By treating the positions and momenta as classical variables we could generate the classical dynamics of the cavity field and side-mode atoms. By setting its time derivative to zero in Eq. (12) we could gain the steady-state dynamic of \(|\alpha _s|^2\) and \( q_s \) in the non-Hermitian situation are

$$\begin{aligned}{} & {} |\alpha _s|^2 =\dfrac{\eta ^2}{\big (g\gamma (2|a_s|^2+1)(\sqrt{N}+\cos 2\phi q_s)+\kappa ^2\big )+(\Delta -gq_s)^2}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} g|\alpha _s|^2\big (1+\dfrac{2\gamma \cos 2\phi \gamma _{sm}}{4\omega _r}q_s^2\big )+4\omega _r\big (1+(\frac{\gamma _{sm}}{4\omega _r})^2\big )q_s=0, \end{aligned}$$
(14)

where \( \alpha \) is the classical limit of \( \hat{a} \). In the non-Hermitian case, the steady-state dynamic of side-mode atoms is quite different from the Hermitian case that we are familiar with.

3 Multistability of steady-state cavity photon number

It has been confirmed in previous studies that the photon in a single optomechanics system can, with the help of cavity mediated radiation-pressure, exhibit optical bistability [48, 52]. In our model, in the absence of dissipation from excited state, the optomechanics system will follow conventional Hermitian condition and show bistable behavior, as studied in previous cases. However, the situation starts to change when we incorporate dissipation of the excited state to the ground state of atoms, resulting in completely altered steady-state behavior of intracavity photon number \(|\alpha _s|^2\).

To make our work experimentally feasible, we chose a particular set of parameters for calculations which adopted from experimental setups as discussed in refs [5, 49, 53,54,55]. We consider \( N=2.3\times 10^4 \,\, ^{87}\)Rb atoms trapped inside Fabry–P\(\acute{e}\)rot cavity with length \( L=1.25\times 10^{-4}\) m, driven by single mode pump field with power \( P=0.0164\) mW and wavelength \( \lambda _p=780\) nm. The intra-cavity optical mode oscillates with frequency \( \omega _c=15.3\times 2\pi \times 10^{14}\) Hz, where cavity decay rate is \( \kappa \approx 1.3\times 2\pi \) kHz. The intra-cavity potential depth \( V_0=3.9\times 2\pi \) MHz and effective detuning \(\Delta =0.52\times 2\pi \) MHz. Intra-cavity field produces recoil of \( \omega _r=3.8\times 2\pi \) kHz in atomic mode trapped inside cavity with damping rate \( \gamma _{sm}=0.21\times 2\pi \) kHz.

In this section, we focus on non-Hermicity-induced multistability, which is characterized by the decay of the excited state \( \gamma \). The steady-state relationship between photon number and atomic side-mode is given by Eq. (14), which will give us two roots when \( \cos 2\phi \ne 0 \). In the case of no phase shift in optical lattice \( \cos 2\phi =1 \), as shown in Fig. 2a, the two roots of Eq. (14) result in two red and blue curves forming an “\(\Omega \)” shape with respect to external pump laser power. The cavity photon first shows two stable and one unstable state at lower input powers and photon number states, while two unstable and one stable states at higher input power and photon number state, unlike previous studies on steady-state behavior of cavity photons. The reason behind is the dissipation of excited states that are appeared to be contributing to cavity photon number and resulting in another reverse biunstable state to the smaller bistable state occurring at lower input powers, as illustrated by the inset of Fig. 2a. In other words, at higher input power, the excited state dissipation occupies and saturates to higher values of photonic population. Further, unlike the hermitian case, with the increasing input pump strength the cavity photon number will not grow endlessly, the non-Hermitian effects under zero phase will limit the maximum number of photons in the cavity.

The value of phase shift \( \phi \) illustrates a deep influence on the stable-state of cavity-atom system. We note that the cavity optical potential satisfies the PT symmetry when the phase shift \( \phi =k\pi \) because the intracavity potential satisfy the relation \( V(x)=V^*(-x) \) while treating \( i\gamma \hbar V_0\hat{a}^\dagger \hat{a}/2 \) in Eq. (9) as global imaginary constant [56]. But we will not discuss the behavior of PT symmetry here in this work. We choose another two representative values of \( \phi \), with respect to the steady-state photon behavior, and discuss them in the following. When we consider \( \cos 2\phi =0 \), the stable state relation in Eq. (14) between photon number and atoms becomes much more simple and exhibits optical bistability, as shown in Fig. 2b, which is similar to the conventional bistable behavior of cavity photon number in any previous optomechanical system. It means that transitional phase of intracavity lattice provides an opportunity to convert (or revert) photon multistable state to conventional bistable state. Further, when we choose \( \cos 2\phi =-1 \), the photonic number again converts to multistability and unstability, as illustrated in Fig. 2c, similar to the first case. However, in this case, the photon number of the cavity exhibits one root (blue curve) at the low power pumping (see inset figure of Fig. 2c), but the other counterpart (root) occurs at so high values that it is not possible to visualize in the domain of possible pumping powers, as illustrated by the red cure in Fig. 2c. In this way, it appears to have conventional bistable behavior but in fact it is not. It means that, at this particular phase, the other part of the root which incorporates the dissipation of excited states moves to so higher powers that its contribution can be ignored.

Thus, from these results one can conclude that the excited state-induced dissipation appears in the form of gain for cavity field but gain unconventionally contributes to two unstable states and one stable state, crucially depending upon the lattice phase. At \( \cos 2\phi =0 \), contribution is appeared to be zero while at \( \cos 2\phi \ne 0 \), the contribution of \(\gamma \) appear in biunstable states at higher photon numbers and at higher input pump field powers. It is known that photons in the optical cavity exhibit bistability under hermitian conditions, similar to the blue curve in Fig. 2a. But the non-Hermitian effects appear to be playing major role in the high input pump powers. In our model, cavity mode acts as a lossy part while dissipation from excited state of two-level BEC acts as gain to the system, making a scenario to achieve non-Hermatianality. As mentioned previously, non-Hermitian parameter is defined over the dissipation of excited states, so its values will indeed affect a lot the photonic steady-state number states in cavity. Therefore, it is important to see the effects of \(\gamma \) on the steady-state cavity photon number, as illustrated in Fig. 3.

Fig. 3
figure 3

The steady-state cavity photon number \(|\alpha _s|^2\) as a function of normalized pump intensity \( \eta ^2/\kappa ^2 \) under different values of non-Hermitian strength \( \gamma \) which depict by black, blue, and red curves. a–c show the steady-state result when the phase shift \( \cos 2\phi \) takes value of 1,0,\(-1\) respectively. The coupling between cavity and atoms in all figures and subfigures is \( g/\omega _r=4 \). The other parameters are same as used in the calculation of Fig. 2

Full size image

From the previous discussion, we came to know that non-Hermicity yields in multistable “\(\Omega \)” type spectrum depending upon the phase of the lattice. In this section, we will see the effects of non-Hermitian parameter \(\gamma \) on the steady-state spectrum of cavity photon numbers, as we illustrated in Fig. 3. If we increase the non-Hermitian strength \( \gamma /\gamma _{sm} \) from 3 to 6 while keeping \( \cos 2\phi =1 \) constant, as shown in Fig. 3a, then the larger decay of the excited state will result in the smaller maximum number of steady-state cavity photons. However, at higher values of \(\gamma \), there should be increased steady-state photon number, because dissipation from excited state is acting as gain to the cavity field. Here the reason is phase shift \(\phi \) of the lattice. At \( \cos 2\phi =1 \), the excited state dissipation is though resulting in additional biunstable state but the higher values of \(\gamma \) are appeared to be scattering out more photons from the cavity field resulting in decrease in steady-state cavity photon number.

But if we choose different phase, like \( \cos 2\phi = -1 \) Fig., then the increase in \(\gamma \) will act in the form of addition to the effective steady-state photon number, as illustrated in Fig. 3c. The reason of this is same that now excited state dissipation is more align to the cavity mode and contributing in a gain to the cavity field. It is very important because, in this case, one can achieve high-order optomechanical interactions with relatively stronger cavity field. However, in the case of \( \cos 2\phi =0 \), the conventional bistable response will remain the same (because at this phase excited state dissipation is not align at all so that they can act as a gain). But the increase in \(\gamma \) will again scatter out the photons from cavity mode yielding in lesser steady-state photon number states, as shown in Fig. 3b. Thus, by modifying \(\gamma \), one not only can get opportunity to control the excited state mediated gain but, in combination with lattice phase, it also provides more precise controllability.

Fig. 4
figure 4

The steady-state cavity photon number \(|\alpha _s|^2\) as a function of normalized pump-cavity detuning \( \Delta /\kappa \) and normalized pump laser intensity \( \eta ^2/\kappa ^2 \) under the different values of non-Hermitian strength \( \gamma \) when \( \cos 2\phi =1 \) and at cavity-atom coupling \( g/\omega _r \)=4. a–d correspond to \( \gamma /\gamma _{sm}=3,4,5,6 \) respectively. While the other parameters used are same as in the calculations of Fig. 2

Full size image

In order to further enhance of understanding of steady-state response of inter-cavity photon number, we investigate the intracavity photon number as a function of effective cavity detuning \( \Delta \) and input pump laser intensity \( \eta \), as illustrated in Fig. 4. As displayed in Fig. 4 which shows the optical behavior of the cavity with different values of non-Hermitian strength, here we consider the zero phase shift case while \( \cos 2\phi =1 \). The tide structure indicates that the steady-state photon has bistability, and the bistability caused by non-Hermicity has a shape of horizontal section, it once again proves that the steady-state photon number has a limit under the non-Hermitian cavity-atoms interaction. We could see from Fig. 4 the steady-state cavity photon number consists of two parts; the main part represents root-1 and the tilted part represents root-2. The maximum number of intracavity photons is determined by root-1 and then depends on the value of root-2 along with the increase of \( \gamma /\gamma _{sm} \) from 3 to 6. But it should be noted here that we just study here the influence of excited state dissipation on steady-state values of photons at \( \cos 2\phi =1 \), where, as discussed previously, increase in \(\gamma \) is appeared to be decreasing the collective number of steady-state photons. However, at other phases (especially at \( \cos 2\phi =-1 \)), the results could be different. It is obvious because, as we already know, at other phase like \( \cos 2\phi =-1 \) excited state dissipation will scatter into the cavity mode resulting in increase in cavity photon number.

Fig. 5
figure 5

The effective potential \( V_s \) as a function of steady-state cavity photon number \(|\alpha _s|^2\). a and b show the potential under different value of non-Hermitian strength \( \gamma \) and cavity-atoms coupling g, respectively. In a the cavity-atoms coupling is \( g/\omega _r=1 \) and in b the non-Hermitian strength \( \gamma /\gamma _{sm}=6 \). Here we use blue and red curve to represent distinct root of Eq. (14), furthermore, we use solid, dashed and dotdashed line to depict various values of non-Hermitian strength \( \gamma /\gamma _{sm} \) in a and cavity-atoms coupling \( g/\omega _r \) in b. The other parameters used in the calculation are same as in Fig. 2

Full size image

In order to further broaden our understanding of the steady-state dynamics of the cavity-atom system containing non-Hermitian effects, we derive the effective steady-state potential of the cavity-atom system as a function of the steady-state cavity photon number. By assuming that the time scales short enough that atomic mechanical damping can be ignored, one can govern the equations of dynamics or motion for atomic mode inside the cavity, reading as,

$$\begin{aligned} \begin{aligned} \dfrac{{\text {d}}^2\hat{q}}{{\text {d}}t^2}=&-8\omega _r\gamma _{sm}\hat{p}+\gamma _{sm}^2\hat{q}-(4\omega _r)^2\hat{q}-4\omega _rg\hat{a}^\dagger \hat{a}\\&-4\omega _rg\hat{a}^\dagger \hat{a}\gamma \cos 2\phi (\hat{p}\hat{q}+\hat{q}\hat{p}), \end{aligned} \end{aligned}$$
(15)

from the equation of motion, the steady-state effective potential \( V_s \) can be easily derived as the function of steady-state cavity photon number \(|\alpha _s|^2\),

$$\begin{aligned} \begin{aligned} V_s = -(\gamma _{sm}^2+(4\omega _r)^2)q_s-4\omega _rg|\alpha _s|^2\left( {1+\frac{\gamma \cos 2\phi }{2\omega _r}q_s}\right) . \end{aligned} \end{aligned}$$
(16)

Here, we illustrate the effects of non-Hermitian parameter \(\gamma \) and cavity-atom coupling g on the steady-state effective potential while keeping the dissipation phase of excited state to the lattice same, i.e. \( \cos 2\phi =1 \), as illustrated in Fig. 5. It can be seen that the maximum number of steady-state photons are trapped (or occurs) during the particular interval of steady-state potential, i.e., \(0\le V_s \le 175\) approximately. It could be because of the proportionality of \(V_s\) with the steady-state position quadrature \(q_s\), which is consequently modifying the cavity mode strength. However, the particular photon number crucially depends on the system parametric configuration. One can further note that when we increase the value of normalized \(\gamma \), the maximum limit on steady-state cavity photon number, over the \(V_S\) interval, is appeared to be decreasing, as can be seen in Fig. 5a. The reason behind this is the same that at particular phase \( \cos 2\phi =1 \), an increase in excited state dissipation will be out-off phase with lattice and will scatter out more photons from the cavity field resulting in decrease in steady-state photon number. Moreover, if we change the atom-cavity coupling g in a similar configuration, the steady-state photon number will also show similar behavior, as can be seen in Fig. 5b. It is obvious and has been studied in multiple investigations in literature [2, 6,7,8,9]. The reason is that at stronger atom-cavity couplings, more photons will be bound to the interactions resulting in lesser steady-state photon number (and vise-versa) power, but crucially depending upon the phase of the lattice.

4 Conclusion

In conclusion, we first engineer non-Hermicity in a single optical cavity containing BEC, by incorporating mechanical dissipation of the excited state as gain to the system (or ground state). The non-Hermicity is achieved by considering dissipation of the excited state occurring at phase shift \(\phi \) with cavity lattice formed by the externally driving single pump laser. After that, by computing the steady-state behavior of the system via the Heisenberg picture, we study the occurrence of stability and instability in cavity photon number. We find that the steady-state cavity photon number crucially depends on the phase shift of the intracavity lattice. When \( \cos 2\phi =1 \), then the cavity photon number shows “\(\Omega \)” type shape containing a conventional bistable behavior at lower input powers, while a biunstable behavior at higher input powers occurs at higher photon number states. However, at \( \cos 2\phi =0 \), cavity photon number simply shows a conventional bistable behavior similar to the previous investigations. Further, at \( \cos 2\phi =-1 \), the photon number again illustrates “\(\Omega \)” type behavior but this time the second root occurs at so high values of input power that it can be ignored.

Furthermore, we illustrate the effects of the non-Hermitian parameter \(\gamma \) on cavity photon number for all cases of phase shift. We find that \(\gamma \) has appeared to be suppressing the steady-state values of cavity photon number in the cases. Especially, in the case of \( \cos 2\phi =-1 \), where it has appeared to further by shifting secondary roots to higher values, which resulted in only one root with bistable behavior. We also illustrate the effects of the non-Hermitian parameter \(\gamma \) on the effective potential of the system as a function of steady-state photon number. We show that \(\gamma \) as well as g are not only limiting the maximum steady-state photon to a particular interval of effective potential, but, with their increasing strengths, are also suppressing maximum values of steady-state photons as well. Our work provides a fundamental understanding of a non-hermitian optomechanics system mediated by ultra-cold atoms, which could act as a platform to explore further non-Hermicity, including PT symmetry behavior, and its effects on quantum nonlinear optics, which is also the topic of our future research.