1 Introduction

Dark energy and any studies about dark universe are important in theoretical physics and cosmology. In order to understand nature of dark universe one can investigate time-dependent density of dark energy [1]. There are several models to describe dark energy [2–16]. We are interested to the cases of Chaplygin gas (CG) as a model for dark energy [17–24], which is extended to generalized Chaplygin gas (GCG) for observational agreements [25–29]. Also, it is possible to extend GCG to the modified Chaplygin gas (MCG) [30], or modified cosmic Chaplygin gas (MCCG) [31]. Moreover, we know that the bulk viscosity plays an important role in cosmology [32–34]. The idea that Chaplygin gas may has viscosity first proposed by Ref. [35] and then developed by Refs. [36–41]. In Refs. [31, 36] we studied viscous modified cosmic Chaplygin gas and viscous modified Chaplygin gas, and calculated time-dependent energy density. In Ref. [38] we studied viscous Chaplygin gas in non-flat FRW universe. In these works we considered special case of α=0.5, so extension of viscous generalized Chaplygin gas for arbitrary α performed in Ref. [39]. In all cases the viscous parameter considered as a constant. In Ref. [42] it is pointed that the viscous coefficient may be considered proportional to powers of density (ζ∝ρ n). So, in this work we study effect of non-constant bulk viscosity on generalized Chaplygin gas.

2 Viscous Generalized Chaplygin Gas Cosmology

The generalized Chaplygin gas which unified dark energy and dark matter described by the following equation of state,

$$ p=-\frac{A}{\rho^{\alpha}}, $$
(1)

where A is a positive constant and 0<α≤1, so α=1 gives Chaplygin gas equation of state. As we know the Friedmann-Robertson-Walker (FRW) universe is described by the following metric,

$$ ds^2=-dt^2+a(t)^2\bigl(dr^2+r^{2}d\Omega^{2}\bigr), $$
(2)

where dΩ2=dθ 2+sin2 θdϕ 2, and a(t) represents the scale factor. We assume that the universe is filled with the generalized Chaplygin gas with equation of state (1) and neglect contribution of other components. Also,

$$ \bar{p}=p-3\zeta(\rho) H, $$
(3)

is the total pressure which involves the proper pressure p, given by equation of state (1), bulk viscosity coefficient ζ(ρ) and Hubble expansion parameter \(H=\dot{a}/a\). Also conservation equation is given by,

$$ \dot{\rho}+3H(\bar{p}+\rho)=0. $$
(4)

Now, one can obtain the following field equations,

$$ H^{2}=\frac{\rho}{3}, $$
(5)

and

$$ \dot{H}+H^{2}=-\frac{\rho}{6}-\frac{\bar{p}}{2}, $$
(6)

where dot denotes derivative with respect to cosmic time t. By using the equation of state (1) and total pressure in the energy-momentum conservation formula (4) one can obtain the following differential equation,

$$ \dot{\rho}+3H \left(\rho-\frac{A}{\rho^{\alpha}}-3\zeta(\rho) H\right)=0. $$
(7)

Main goal of this paper is considering ρ-dependent viscous coefficient instead of constant one. If we assume ζ(ρ)=0, then the energy density is obtained as the following,

$$ \rho=\left[A+\frac{C}{a^{3(1+\alpha)}}\right]^{\frac{1}{1+\alpha}}, $$
(8)

where C is an integration constant.

3 ρ-Dependent Bulk Viscosity

It is interesting to choose the bulk viscous coefficient as the following ρ-dependent expression,

$$ \zeta(\rho)=\zeta_{0}\rho^{n}, $$
(9)

where ζ 0 is a constant. In that case Eq. (7) may be written as the following,

$$ \dot{\rho}+\sqrt{3}\sqrt{\rho} \left(\rho-\frac{A}{\rho^{\alpha}}\right)-3\zeta_{0}\rho^{n+1}=0. $$
(10)

Our main goal is solving Eq. (10) to obtain time-dependent density. Then, we are able to discuss evolution of scale factor and Hubble expansion parameter.

Special case of \(n=-\alpha-\frac{1}{2}\) yields to the following expression in terms of the hypergeometric function,

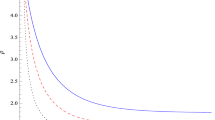
$$ t=\frac{2\sqrt{3}}{3}\rho^{-\frac{1}{2}} {_{2}F_{1}}\left(1, \frac{1}{2(1+\alpha)}; 1+\frac{1}{2(1+\alpha)}; f(\rho; \alpha, A, \zeta_{0})\right). $$
(11)

In Fig. 1 we show behavior of energy density in terms of time for n=−0.6, n=−1 and n=−1.4. This case corresponds to negative n which may be unphysical, because we expect that increasing density, increased viscosity. But for the negative n we find that increasing density decreased viscosity. Therefore, we will consider another special cases with positive n.

Fig. 1
figure 1

Time-dependent dark energy density for \(n=-\alpha-\frac{1}{2}\) with α=0.1 (dotted line), α=0.5 (solid line), α=0.9 (dashed line)

Full size image

In Fig. 2 we draw behavior of energy density in terms of time for α=0.5 and some positive value of n. We find that n≤0.2 is essential condition to avoid singularity.

Fig. 2
figure 2

Time-dependent dark energy density with α=0.5 for n=0 (dotted line), n=0.2 (solid line), n=0.1 (dashed line)

Full size image

Now, instead of equation of state (1) we used the following equation of state includes viscous coefficient,

$$ \bar{p}\rightarrow p=-\frac{A}{\rho^{\alpha}}-\sqrt{3}\zeta_{0}\rho^{n+\frac{1}{2}}. $$
(12)

If \(\zeta_{0}=-\frac{\sqrt{3}}{3}\gamma\) and n=0.5 then,

$$ p=\gamma\varrho-\frac{A}{\rho^{\alpha}}, $$
(13)

where γ is a positive constant, which is equation of state of modified Chaplygin gas. It means that viscous generalized Chaplygin gas may serves as modified Chaplygin gas. Therefore we can write scale factor dependent energy density as the following,

$$ \rho=\left[\frac{A}{1-\sqrt{3}\zeta_{0}}+\frac{C}{a^{3(1+\alpha)(1-\sqrt{3}\zeta_{0})}}\right]^{\frac{1}{1+\alpha}}, $$
(14)

where C is an integration constant and may be choose as the following,

$$ C=-\frac{A}{1-\sqrt{3}\zeta_{0}}\frac{a(0)^{3(1+\alpha)(1-\sqrt{3}\zeta_{0})}}{\sqrt{3}\zeta_{0}}. $$
(15)

It is clear that large values of the scale factor (a≫a(0)) give the following expression,

$$ \rho\approx\left[\frac{A}{1-\sqrt{3}\zeta_{0}}\right]^{\frac{1}{1+\alpha}}, $$
(16)

which is corresponding to an empty universe.

4 Conclusion

In this paper we considered generalized Chaplygin gas which has viscosity. Indeed we considered non-constant viscosity proportional to ρ n. Special case of n=0 and α=0.5 yields to the results of Ref. [43] for k=0 (flat space). Two possibility of positive and negative n investigated by using plots of Figs. 1 and 2. We found special case with n=0.5 and \(\zeta_{0}=-\frac{\sqrt{3}}{3}\gamma\), changed equation of state of viscous generalized Chaplygin gas to modified Chaplygin gas. Therefore, analogous to modified Chaplygin gas we obtained energy density in terms of scale factor and saw that ζ 0=0 limit of Eq. (14) reduced to Eq. (8). Hence we expect that this model will be stable. However obtaining solution for arbitrary n left for future study. Also It is interesting to consider another dependents of viscosity such as ζ(t).