Viscous Extended Cosmic Chaplygin Gas with Varying Cosmological Constant in FRW Universe

Abstract

In this paper, we study the viscous extended cosmic Chaplygin gas whose equation of state reduces to extended Chaplygin gas in the limit $\omega \rightarrow 0$ with varying cosmological constant in flat FRW universe. In this framework, we assume the bulk viscosity $\zeta$ and cosmological constant $\Lambda$ as a linear combination of two terms, one is constant and other is a function of dark energy density $\rho$. We obtain generalized Friedmann equations due to bulk viscosity, cosmological constant and extended cosmic Chaplygin gas. We calculate the time-dependent dark energy density $\rho$ for various values of n and $\alpha = 1/2$ both analytically and numerically. We analyse the behaviour of scale factor, Hubble expansion parameter and deceleration parameter graphically and discuss the stability of the model by using square of speed of sound.

1 Introduction

The accelerated expansion of the universe may be described by dark energy which has negative pressure and positive energy density, which works against gravity (Padmanabhan 2003; Sahni and Starobinsky 2000). There are several phenomenological models of dark energy. One of them is called cosmological constant which is not a dynamical model and has especially simple pressure expansion $p = -\rho$. Some alternative models for dark energy are quintessence model (Ratra and Peebles 1988; Wetterich 1988; Liddle and Scherrer 1999; Guo et al. 2007; Khurshudyan et al. 2014; Dutta et al. 2009), phantom model (Caldwell 2002; Caldwell et al. 2003; Nojiri and Odintsov 2003; Onemli and Woodard 2004; Saridakis 2009a, b; Gupta et al. 2009) and holographic model (Li et al. 2006; Sadeghi et al. 2014a; Setare et al. 2007; Saridakis 2008). Combination of quintessence and phantom is known as quintom, which is another model for dark energy (Feng et al. 2005).

An interesting model to describe the dark energy is Chaplygin gas (CG) (Kamenshchik et al. 2001; Bento et al. 2002), which emerged initially in cosmology from string theory point of view (Barrow 1986, 1988) which are based on CG equation of state (EoS) and developed to the generalized Chaplygin gas (GCG) (Bilic et al. 2002). The GCG was extended to modified Chaplygin gas (MCG) by Debnath et al. (2004). Gonzalez-Diaz (2003) gave another extension for CG called generalized cosmic Chaplygin gas (GCCG). A further extension of CG model is called modified cosmic Chaplygin gas (MCCG) was proposed recently by Saadat and Pourhassan (2013b), Pourhassan (2013), Sadeghi et al. (2014b).

Saadat and Pourhassan (2013b) considered FRW bulk viscous cosmology with MCCG. They obtained generalized Friedmann equations and calculated time-dependent dark energy density. They discussed Hubble expansion parameter deceleration parameter and investigated the stability of the theory. Pourhassan (2013) studied viscous MCCG with arbitrary $\alpha$ and by using more powerful tools obtained exact solution of field equations and also investigated the effect of viscosity to the evolution of the universe. Sadeghi et al. (2014b) constructed MCCG in the presence of variable cosmological constant $\Lambda$ and space curvature. By using numerical analysis, they found special polynomial form for the density and fixed the constant parameter by using the observational data and stability condition.

Pourhassan and Kahya (2014) introduced extended Chaplygin gas (ECG) with EoS

$$\begin{aligned} p= \sum _{n} A_{n}\rho ^{n}-\frac{B}{\rho ^{\alpha }}, \end{aligned}$$

(1)

where $A_{n}$ and B are constants and $0< \alpha \le 1.$

Eq. (1) reduces to MCG for $n = 1$ with EoS $p = A\rho - \frac{B}{\rho ^{\alpha }}.$ Then for $A = 0$ yields to EoS $p = -\frac{B}{\rho ^{\alpha }}$ which corresponds to GCG. Hence we get the simplest case for $\alpha = 1$ with EoS $p = -\frac{B}{\rho }$ which is called CG.

In this work, they used numerical methods to investigate the behaviour of some cosmological parameters such as scale factor, Hubble expansion parameter, energy density and deceleration parameter in the framework of ECG EoS and investigated the stability of the theory using density perturbations.

Kahya and Pourhassan (2014) studied the ECG as a candidate of inflation and predicted the values of gas parameters for physically viable cosmological model. Kahya and Pourhassan (2015) considered ECG with $n = 2$ and obtained energy density in terms of scale factor and studied density perturbations in relativistic and Newtonian regime.

Remark 1

In recent years, viscous cosmological models has been quite popular. The idea that CG may have viscosity was first proposed by Zhai et al. (2006) and then developed by Amani and Pourhassan (2013), Saadat and Pourhassan (2013a, b), Saadat and Farahani (2013) and Xu et al. (2012). In another words, the presence of viscosity in the fluid introduces many interesting pictures in the dynamics of homogeneous cosmological models.

When one is considering the deviation from the thermal equilibrium to the first order in the cosmic fluid, it should be known that there are in principle two different viscosity coefficients namely the bulk viscosity $\zeta$ and the shear viscosity $\eta$. In the view of commonly accepted spatial isotropy of the universe, the shear viscosity is usually omitted (Brevik et al. 2017). The motivation of considering the linear combination of bulk viscosity is that by fluid mechanics we know that the transport/viscosity phenomenon is related by the velocity ${\dot{a}}$ which is related to the scalar expansion $\theta$. Hence, the linear combination of $\zeta _{0}$ and $\zeta _{1}$ is more physical which means that one or more of physical quantities move to infinity at finite time in future.

Nojiri and Odintsov (2005) came up with the idea that the viscous fluid can also be understood as a class of inhomogeneous fluid. Dou and Meng (2011) discussed unified model of dark matter and dark energy which assumes that the universe is filled with single non-perfect viscous fluid. The bulk viscosity contributes to the cosmic pressure and also plays an important role in accelerating the universe. They studied red shift-dependent model of the type $9\lambda =\lambda _{0}+\lambda _{1}(1+z)^{n}$ and effective equation of state model of the form $\zeta =\zeta _{0}+\zeta _{1}\frac{{\dot{a}}}{a}+\zeta _{1}\frac{\ddot{a}}{a}$. Further, they used SNe Ia data, CMB shift and BAO observations and observed that the viscosity model can be fitted very well.

Normann and Brevik (2017) analysed the characteristic properties of two different viscous cosmological models. One is a concrete component dark energy model where bulk viscosity $\zeta$ is associated with the fluid as a whole in the form of $\zeta (\rho )=\zeta _{0}(\frac{\rho }{\rho _{0}})^{\lambda }$ where $\rho$ is the dark energy density. Other one is a two-component model where $\zeta$ is associated with dark matter component $\rho _{{\mathrm{m}}}$ only and the dark energy component is considered inviscid. Further, they found that the two-component model is more favourable with the observations.

In this paper, we construct extended cosmic Chaplygin gas (ECCG) with following EoS

$$\begin{aligned} p= \sum _{n} A_{n}\rho ^{n}-\frac{1}{\rho ^{\alpha }}\left[ U+\left( \rho ^{1+\alpha }-U\right) ^{-\omega }\right] , \end{aligned}$$

(2)

where $U = \frac{B}{1+\omega }-1$ and the cosmic effect is represented by $\omega$.

In Eq. (2), if we set $\omega = 0$ we get the EoS for ECG Eq. (1).

Also, for $n = 1$, Eq. (2) reduces to

$$\begin{aligned} p= A\rho -\frac{1}{\rho ^{\alpha }}\left[ U+\left( \rho ^{1+\alpha }-U\right) ^{-\omega }\right] , \end{aligned}$$

which is the EoS for MCCG given by Saadat and Pourhassan (2013b).

The case of $A = 0$ gives EoS

$$\begin{aligned} p= -\frac{1}{\rho ^{\alpha }}\left[ U+\left( \rho ^{1+\alpha }-U\right) ^{-\omega }\right] , \end{aligned}$$

which corresponds to GCCG.

With the motivation of the work of Pourhassan (2013) and Pourhassan and Kahya (2014) in this paper, we construct ECCG and obtain time-dependent dark energy density by using the method given earlier by them analytically and numerically and investigate the effect of viscosity to the evolution of universe in the presence of varying cosmological constant. We also analysed the behaviour of scale factor, Hubble expansion parameter and deceleration parameter numerically by increasing the values of n. Further, we investigate the stability of the system by using square of speed of sound.

2 FRW Model and Friedmann Equations

We consider the FRW universe of the form

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a(t)^{2}\left( \frac{\mathrm{d}r^{2}}{1-kr^{2}}+r^{2}\mathrm{d}\Omega ^{2} \right) , \end{aligned}$$

(3)

where $\mathrm{d}\Omega ^{2}= \mathrm{d}\theta ^{2}+ \mathrm{sin}^{2}\theta \mathrm{d}\phi ^2$ and a(t) represents the scale factor. The constant k denotes the curvature of space $k = 0, 1, -1$ for flat, closed and open universe, respectively.

The Einstein’s field equations are

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R= T_{\mu \nu } + g_{\mu \nu } \Lambda , \end{aligned}$$

(4)

where $G_{\mu \nu }$ is the Einstein tensor, $R_{\mu \nu }$ is the Ricci tensor, R is the Ricci scalar.

We assume $c = 1$ and $8 \pi G = 1$.

The energy-momentum tensor $T_{\mu \nu }$ corresponding to the bulk viscous fluid is given by

$$\begin{aligned} T_{\mu \nu }=(\rho +p)u_{\mu }u_{\nu }+{\bar{p}}g_{\mu \nu }, \end{aligned}$$

(5)

where $\rho$ is energy density.

Also,

$$\begin{aligned} {\bar{p}}=p-3\zeta H, \end{aligned}$$

(6)

is the total pressure which involves the pressure p, which is given in Eq. (2), bulk viscosity $\zeta$ and Hubble parameter H.

The field equations (4) with the help of line element (3) with $k = 0$ are given by

$$\begin{aligned} 3\left( \frac{{\dot{a}}}{a}\right) ^{2}= \rho + \Lambda , \end{aligned}$$

(7)

and

$$\begin{aligned} \frac{2\ddot{a}}{a}+\left( \frac{{\dot{a}}}{a}\right) ^{2}=- {\bar{p}} + \Lambda , \end{aligned}$$

(8)

where dot ($\cdot$) denotes the derivative with respect to cosmic time t.

The first Friedmann equation is given by

$$\begin{aligned} H^{2} = \frac{\rho }{3} + \frac{\Lambda }{3}, \end{aligned}$$

(9)

and its conservation equation is given by

$$\begin{aligned} {\dot{\rho }}+3H(\rho +{\bar{p}})= -{\dot{\Lambda }}. \end{aligned}$$

(10)

We assume both bulk viscosity $\zeta$ and cosmological constant $\Lambda$ as the linear combination of two terms where one is constant and other is a function of $\rho$ of the form

$$\begin{aligned} \zeta = \zeta _{0}+\zeta _{1} \rho ^{1/2}, \end{aligned}$$

(11)

and

$$\begin{aligned} \Lambda = \Lambda _{0} + \Lambda _{1} \rho . \end{aligned}$$

(12)

Then Eq. (6) becomes

$$\begin{aligned} {\bar{p}}=p-3(\zeta _{0}+\zeta _{1}\rho ^{1/2}) H. \end{aligned}$$

(13)

With the help of $\zeta$ and $\Lambda$ from Eqs. (11) and (12), the conservation equation (10) becomes

$$\begin{aligned} (1+\Lambda _{1}){\dot{\rho }}+3H(\rho +p)-9(\zeta _{0}+\zeta _{1}\rho ^{1/2})H^{2}=0. \end{aligned}$$

(14)

We solve the above conservation equation with ECCG EoS for three different cases.

Case I$n = 2$ and $\alpha = 1/2$

In this case, ECCG EoS (2) reduces to

$$\begin{aligned} p= A_{1}\rho + A_{2}\rho ^{2}-\frac{1}{\sqrt{\rho }}\left[ U+\left( \rho ^{3/2}-U\right) ^{-\omega }\right] . \end{aligned}$$

(15)

By using above equation in conservation equation (14), we get

$$\begin{aligned} {\dot{\rho }}+f(\rho )=0, \end{aligned}$$

(16)

where

$$\begin{aligned} f(\rho ) = a_{1}\rho ^{3}+a_{2}\rho ^{2}-a_{3}\rho ^{3/2}+a_{4}\rho -a_{5}\rho ^{1/2}-a_{6}-a_{7}\rho ^{-1/2}, \end{aligned}$$

with

$$\begin{aligned} a_{1} = \sqrt{\frac{3}{\Lambda _{0}}}\frac{A_{2}}{2},\;\;a_{2} = \sqrt{3\Lambda _{0}}\left( \frac{1+A_{1}+\omega }{2\Lambda _{0}}+\frac{A_{2}}{1+\Lambda _{1}}\right) ,\end{aligned}$$

$$\begin{aligned}\;\;a_{3} = 3\zeta _{1},\;\;a_{4} = \frac{\sqrt{3\Lambda _{0}}(1+A_{1}+\omega )}{1+\Lambda _{1}}-3\zeta _{0},\end{aligned}$$

$$\begin{aligned}a_{5} = \sqrt{\frac{3}{\Lambda _{0}}} \frac{B}{2} + \frac{3\zeta _{1}\Lambda _{0}}{1+\Lambda _{1}},\;\;a_{6} = \frac{3\zeta _{0}\Lambda _{0}}{1+\Lambda _{1}}\end{aligned}$$

$$\begin{aligned}{\mathrm{and}}\;\;a_{7} = \frac{\sqrt{3\Lambda _{0}}B}{1+\Lambda _{1}}. \end{aligned}$$

After solving Eq. (16), we obtain the following integral

$$\begin{aligned} t = -\int \frac{\mathrm{d}\rho }{f(\rho )}+C, \end{aligned}$$

(17)

where C is the constant of integration.

Since it is very difficult to find the solution of the above integral equation. Therefore, to solve Eq. (17) we use the method given earlier by Pourhassan and Kahya (2014). It gives the following energy density

$$\begin{aligned} \rho = \left[ Y+C\;{\mathrm{exp}}\left( \frac{-t}{2Y^{2}}Q(Y)\right) \right] ^2, \end{aligned}$$

(18)

where $Q(Y) = 7a_{1}Y^6+5a_{2}Y^{4}-4a_{3}Y^{3}+3a_{4}Y^2-2a_{5}Y-a_{6}$ and Y is the root of the equation

$$\begin{aligned} a_{1}Y^7+a_{2}Y^{5}-a_{3}Y^{4}+a_{4}Y^3-a_{5}Y^2-a_{6}Y-a_{7} = 0. \end{aligned}$$

We have drawn the behaviour of dark energy density $\rho$ with respect to cosmic time t in Fig. 1. It is observed that the dark energy density $\rho$ is a decreasing function of time for $n = 2$.

Now, from Eqs. (2), (7), (8), (12) and (13) we get the second-order differential equation of scale factor for $n = 2$ and $\alpha = 1/2$ as

$$\begin{aligned}&\frac{2\ddot{a}}{a}+(1+3\mu _{0})\left( \frac{{\dot{a}}}{a}\right) ^{2}\nonumber \\&\qquad -3\frac{{\dot{a}}}{a}\left[ \zeta _{0}+\zeta _{1}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{1/2}\right] \nonumber \\&\qquad +A_{1}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) +A_{2}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{2}\nonumber \\&\qquad -B\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{-\alpha }-(1+\mu _{0})\Lambda _{0}=0, \end{aligned}$$

(19)

where $\mu _{0} = \frac{\omega -\Lambda _{1}}{1+\Lambda _{1}}.$

Also, with the help of Eq. (7) we can rewrite Eq. (8) as

$$\begin{aligned} 2{\dot{H}}+3H^2=-{\bar{p}}+\Lambda . \end{aligned}$$

(20)

By using Eqs. (2), (7), (12) and (13) in (20), we get the differential equation of Hubble parameter for $n = 2$ and $\alpha = 1/2$ as

$$\begin{aligned}&2{\dot{H}}+3(1+\mu _{0})H^2-3\left[ \zeta _{0}+\zeta _{1}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{1/2}\right] H\nonumber \\&\qquad +A_{1}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) +A_{2}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{2}\nonumber \\&\qquad -B\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{-\alpha }-(1+\mu _{0})\Lambda _{0}=0. \end{aligned}$$

(21)

We solved Eq. (19) numerically and obtained the general behaviour of scale factor a with respect to cosmic time t for $n = 2$ in Fig. 2. It is noted that as time increases scale factor increases at late time. Figures 3 and 4 show the short-term and long-term variation of scale factor. Also, Eq. (21) is solved graphically and Hubble parameter is drawn with respect to cosmic time t for $n = 2$ in Fig. 5. It can be seen that the Hubble parameter H decreases as time increases.

Case II: $n = 3$ and $\alpha = 1/2$

In this case, the EoS (2) for ECCG reduces to the following expression

$$\begin{aligned} p= A_{1}\rho + A_{2}\rho ^{2}+A_{3}\rho ^{3} -\frac{1}{\sqrt{\rho }}\left[ U+\left( \rho ^{3/2}-U\right) ^{-\omega }\right] . \end{aligned}$$

(22)

By using the above equation conservation equation (14) becomes

$$\begin{aligned} {\dot{\rho }} + g(\rho ) =0, \end{aligned}$$

(23)

where

$$\begin{aligned} g(\rho ) = b_{1}\rho ^{4}+(b_{2}-a_{1})\rho ^{3}+f(\rho ), \end{aligned}$$

with

$$\begin{aligned} b_{1} = \sqrt{\frac{3}{\Lambda _{0}}}\frac{A_{3}}{2}\;\;{\mathrm{and}} \;\;b_{2} = \sqrt{3\Lambda _{0}}\left( \frac{A_{3}}{1+\Lambda _{1}}+\frac{A_{2}}{2\Lambda _{0}}\right) . \end{aligned}$$

After solving Eq. (23), we obtain the following integral

$$\begin{aligned} t = -\int \frac{{\mathrm{d}}\rho }{g(\rho )}+C_{1}, \end{aligned}$$

(24)

where $C_{1}$ is the constant of integration.

Again, by using the method given earlier by Pourhassan and Kahya (2014) we get the following energy density

$$\begin{aligned} \rho = \left[ Z+C_{1}\;{\mathrm{exp}}\left( \frac{-t}{2Z^{2}}R(Z)\right) \right] ^2, \end{aligned}$$

(25)

where

$$\begin{aligned} R(Z) = 9b_{1}Z^8+7b_{2}Z^6+5a_{2}Z^{4}-4a_{3}Z^{3}+3a_{4}Z^2-2a_{5}Z-a_{6}, \end{aligned}$$

$C_{1}$ is the constant of integration and Z is the root of the equation

$$\begin{aligned} b_{1}Z^9+b_{2}Z^7+a_{2}Z^{5}-a_{3}Z^{4}+a_{4}Z^3-a_{5}Z^2-a_{6}Z-a_{7} = 0. \end{aligned}$$

The graphical representation of dark energy density $\rho$ with respect to cosmic time t for $n = 3$ is shown in Fig. 1. It is noted that as time increases dark energy density decreases.

Again, from Eqs. (2), (7), (8), (12) and (13) we get the second-order differential equation of scale factor for $n = 3$ and $\alpha = 1/2$ as

$$\begin{aligned}&\frac{2\ddot{a}}{a}+(1+3\mu _{0})\left( \frac{{\dot{a}}}{a}\right) ^{2}\nonumber \\&\qquad -3\frac{{\dot{a}}}{a}\left[ \zeta _{0}+\zeta _{1}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{1/2}\right] \nonumber \\&\qquad +A_{1}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) +A_{2}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{2}\nonumber \\&\qquad +A_{3}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{3}-B\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{-\alpha }\nonumber \\&\qquad -(1+\mu _{0})\Lambda _{0}=0. \end{aligned}$$

(26)

Also, by using Eqs. (2), (7), (12) and (13) in Eq. (20) we get the differential equation of Hubble parameter for $n = 3$ and $\alpha = 1/2$ as

$$\begin{aligned}&2{\dot{H}}+3(1+\mu _{0})H^2-3\left[ \zeta _{0}+\zeta _{1}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{1/2}\right] H\nonumber \\&\qquad +A_{1}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) +A_{2}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{2}\nonumber \\&\qquad +A_{3}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{3}-B\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{-\alpha }\nonumber \\&\qquad -(1+\mu _{0})\Lambda _{0}=0. \end{aligned}$$

(27)

We solved Eq. (26) numerically for $n = 3$ and obtained the behaviour of scale factor a with respect to cosmic time t in Fig. 2. It can be seen that as time increases scale factor is constant initially and increases afterwards. The short-term and long-term variation of scale factor is shown in Figs. 3 and 4, respectively. After solving Eq. (27) graphical plot of Hubble parameter with respect to cosmic time t is given in Fig. 5 for $n = 3$. It is observed that as time increases Hubble parameter H decreases.

Case III: $n = arbitrary$ and $\alpha = 1/2$

The ECCG EoS (2) becomes

$$\begin{aligned} p= A_{1}\rho + A_{2}\rho ^{2}+\cdots +A_{n}\rho ^{n} -\frac{1}{\sqrt{\rho }}\left[ U+\left( \rho ^{3/2}-U\right) ^{-\omega }\right] . \end{aligned}$$

(28)

Therefore, the conservation equation becomes

$$\begin{aligned} {\dot{\rho }} + h(\rho ) =0, \end{aligned}$$

(29)

where

$h(\rho ) = c_{n}\rho ^{n+1}+c_{n-1}\rho ^{n}+\cdots +c_{1}\rho ^{2}-a_{3}\rho ^{4}+a_{4}\rho ^3-a_{5}\rho ^2-a_{6}\rho -a_{7},$

with

$$\begin{aligned} c_{n} = \sqrt{\frac{3}{\Lambda _{0}}}\frac{A_{n}}{2},\;\;\;c_{n-1} = \sqrt{3\Lambda _{0}}\left( \frac{A_{n}}{1+\Lambda _{1}}+\frac{A_{n-1}}{2\Lambda _{0}}\right) ,\end{aligned}$$

$$\begin{aligned}c_{n-2} = \sqrt{3\Lambda _{0}}\left( \frac{A_{n-1}}{1+\Lambda _{1}}+\frac{A_{n-2}}{2\Lambda _{0}}\right) ,\;\;\ldots ,\\ c_{1} = \sqrt{3\Lambda _{0}}\left( \frac{A_{3}}{1+\Lambda _{1}}+\frac{A_{2}}{2\Lambda _{0}}\right) . \end{aligned}$$

Upon solving, we obtain the following integral

$$\begin{aligned} t = -\int \frac{{\mathrm{d}}\rho }{h(\rho )}+C_{2}, \end{aligned}$$

(30)

where $C_{2}$ is the constant of integration.

By using similar procedure, we get the expression for density as

$$\begin{aligned} \rho = \left[ X+C_{2}\;{\mathrm{exp}}\left( \frac{-t}{2X^{2}}T(X)\right) \right] ^2, \end{aligned}$$

(31)

where

$$\begin{aligned} T(X) = \sum _{n} (2n+3)c_{n}X^{2n+2}-4a_{3}X^{3}+a_{4}X^{2}-2a_{5}X-a_{6}, \end{aligned}$$

X is the root of the equation

$$\begin{aligned} \sum _{n} c_{n}X^{2n+3} -a_{3}X^{4}+a_{4}X^{3}-a_{5}X^{2}-a_{6}X-a_{7} = 0. \end{aligned}$$

From the above equation, we have drawn the behaviour of dark energy density $\rho$ for $n = 1$ along with graph for $n = 2$ and $n = 3$ with respect to cosmic time t in Fig. 1. It is observed that the dark energy density decreases as time increases for various value of n and approaches to an infinitesimal constant at late times. It is also noted that the dark energy density decreases as n increases from 1 to 3. We can also find the dark energy density $\rho$ for $n = 4$ from Eq. (31) and plot the same.

By using the previous method differential equation of scale factor and Hubble parameter for arbitrary n and $\alpha = 1/2$, respectively, is obtained as

$$\begin{aligned}&\frac{2\ddot{a}}{a}+(1+3\mu _{0})\left( \frac{{\dot{a}}}{a}\right) ^{2}-3\frac{{\dot{a}}}{a}\left[ \zeta _{0}+\zeta _{1}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{1/2}\right] \nonumber \\&\qquad +\sum _{n} A_{n}\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{n} -B\left( \frac{3\left( \left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{\Lambda _{0}}{3}\right) }{\left( 1+\Lambda _{1}\right) }\right) ^{-\alpha }\nonumber \\&\qquad -(1+\mu _{0})\Lambda _{0}=0 \end{aligned}$$

(32)

and

$$\begin{aligned}&2{\dot{H}}+3(1+\mu _{0})H^2-3\left[ \zeta _{0}+\zeta _{1}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{1/2}\right] H\nonumber \\&\qquad +\sum _{n} A_{n}\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{n}-B\left( \frac{3(H^2 - \frac{\Lambda _{0}}{3})}{(1+\Lambda _{1})}\right) ^{-\alpha }\nonumber \\&\qquad -(1+\mu _{0})\Lambda _{0}=0. \end{aligned}$$

(33)

We solved Eq. (32) numerically and obtained the behaviour of scale factor a with respect to cosmic time t in Fig. 2. We fix all the other parameters and we took the values of n as 1, 2, 3 to find that as n increases value of scale factor decreases. Figure 3 shows the short-term variation of scale factor. Here also increasing n decreases the value of scale factor. Behaviour of scale factor at later stage is shown in Fig. 4. It is observed that increasing $\alpha$ decreases the value of scale factor. Also, we solved Eq. (33) graphically and drawn Hubble parameter with respect to cosmic time t for $n = 2$ and 3 along with $n = 1$ by fixing all the other parameters in Fig. 5. It can be seen that as n increases the value of Hubble parameter H decreases. Similarly, we can also find the differential equation of scale factor and Hubble parameter for $n = 4$ and plot the same from Eqs. (32) and (33).

Remark 2

We can also write Eq. (29) in terms of scale factor as

$$\begin{aligned} \frac{H{\mathrm{d}}\rho }{h(\rho )}=\frac{-{\mathrm{d}}a}{a}. \end{aligned}$$

(34)

With the help of Eqs. (9) and (12) above equation after integration becomes

$$\begin{aligned} \rho = \left[ K+C_{0}\;a^{\left( \frac{-1}{2K^{2}(1+mK^{2})}\sqrt{\frac{3}{\Lambda _{0}}}F(K)\right) }\right] ^2, \end{aligned}$$

(35)

where

$$\begin{aligned} F(K)&= \sum _{n} (2n+3)c_{n}K^{2(n+1)}+5a_{2}K^{4}\\&\quad -4a_{3}K^{3}+3a_{4}K^{2}-2a_{5}K-a_{6}, \end{aligned}$$

$m = \frac{1+\Lambda _{1}}{2\Lambda _{0}}$ and K is the root of the equation

$$\begin{aligned} \sum _{n} c_{n}K^{2n+3}+a_{2}K^{5}-a_{3}K^{4}+a_{4}K^{3}-a_{5}K^{2}-a_{6}K-a_{7} = 0. \end{aligned}$$

Putting the above value of $\rho$ in the field equation (7), one can obtain

$$\begin{aligned} H^{2}= d_{1}+d_{0}(1+d_{2}a^{-d_{3}})^{2}, \end{aligned}$$

(36)

where $d_{1}$ is the constant related to $\Lambda$. $d_{0}$, $d_{2}$ and $d_{3}$ are constants related to K, $ci's$ and $ai's$.

We can write the above equation of H in terms of red shift as

$$\begin{aligned} H= \left[ \left( d_{1}+d_{0}(1+d_{2}(1+z)^{d_{3}})^{2}\right) \right] ^{1/2}. \end{aligned}$$

(37)

Remark 3

In Fig. 6, we have drawn the Hubble parameter in terms of red shift and compared our numerical results with observational data (Thakur et al. 2009). We can see that our model is in agreement with the observational data. It can also be observed that the current value of Hubble parameter $H\;\approx \;70$ is confirmed. Pourhassan (2013), Kahya and Pourhassan (2014) and Pourhassan (2016) have earlier obtained similar kind of behaviour of Hubble parameter.

Fig. 1

Plot of the density $(\rho )$ versus time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1, \Lambda _{0} = \Lambda _{1} = 1$, $n = 1$ (solid line), $n = 2$ (dashed line) and $n = 3$ (dotted line)

Fig. 2

Plot of the scale factor (a) versus time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 1$ (solid line), $n = 2$ (dashed line) and $n = 3$ (dotted line)

Fig. 3

Plot of the scale factor (a) versus time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 1$ (solid line), $n = 2$ (dashed line) and $n = 3$ (dotted line)

Fig. 4

Plot of the scale factor (a) versus time (t) with $A_{1} = A_{2} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 2$, $\alpha = 0.1$ (solid line), $\alpha = 0.5$ (dashed line) and $\alpha = 0.9$ (dotted line)

Fig. 5

Plot of the Hubble parameter (H) versus time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 1$ (solid line), $n = 2$ (dashed line) and $n = 3$ (dotted line)

Fig. 6

Plot of the Hubble parameter (H) versus red shift (z) with $d_{1} = 1/3, d_{2} = 0.5$, $d_{3} = 1.5$ (solid), $d_{3} = 1.6$ (dotted), $d_{3} = 1.7$ (dashed), $d_{3} = 1.8$ (dashdotted) and $d_{3} = 1.9$ (long dashed); dots denotes observational data

3 Deceleration Parameter

In the previous section, we discussed the scale factor and Hubble parameter numerically. However, the analytical behaviour of these parameters is not quite clear so in this section we deal with another parameter of cosmology called deceleration parameter which is important from theoretical and observational point of view. It characterizes the accelerating $(q < 0)$ or decelerating $(q > 0)$ nature of the Universe and is given by

$$\begin{aligned} q = -\left( \frac{{\dot{a}}}{a}\right) ^{-2}\frac{\ddot{a}}{a}=-1-\frac{{\dot{H}}}{H^2}. \end{aligned}$$

(38)

By using Eqs. (2), (7), (12) and (13) in (38)

$$\begin{aligned} q&= \frac{1}{2}+\frac{1}{S(\rho )}\left( \sum _{n} A_{n}\rho ^{n}+\omega \rho -\frac{B}{\rho ^{\alpha }}\right) -\left( \zeta _{0}+\zeta _{1}\rho ^{1/2}\right) \nonumber \\&\times \left( \frac{3}{S(\rho )}\right) ^{1/2}-\left( \frac{\Lambda _{0}+\Lambda _{1}\rho }{S(\rho )}\right) , \end{aligned}$$

(39)

where $S(\rho ) = \frac{2}{3}(\Lambda _{0}+\rho (1+\Lambda _{1})).$

At early stage of the universe, the density is very high hence we set $B = 0$. So, the deceleration parameter may be reduced to

$$\begin{aligned}&q \approx \frac{1}{2}+\frac{1}{S(\rho )}\left( \sum _{n} A_{n}\rho ^{n}+\omega \rho \right) -\left( \zeta _{0}+\zeta _{1}\rho ^{1/2}\right) \nonumber \\&\quad \times \left( \frac{3}{S(\rho )}\right) ^{1/2}-\left( \frac{\Lambda _{0}+\Lambda _{1}\rho }{S(\rho )}\right) . \end{aligned}$$

(40)

At late time, there is low energy density so after ignoring the high energy terms and viscosity the behaviour of deceleration parameter may be described as

$$\begin{aligned}&q \approx \frac{1}{2}+ \frac{1}{S(\rho )}\left( \omega \rho -\frac{B}{\rho ^{\alpha }}\right) -\left( \zeta _{0}+\zeta _{1}\rho ^{1/2}\right) \left( \frac{3}{P(\rho )}\right) ^{1/2}\nonumber \\&\quad -\left( \frac{\Lambda _{0}+\Lambda _{1}\rho }{S(\rho )}\right) . \end{aligned}$$

(41)

Remark 4

Numerically, we have drawn deceleration parameter in terms of $\rho$ in Fig. 7. It is noted that as n increases value of q also increases. For extended Chaplygin gas, Pourhassan and Kahya (2014) obtained the identical behaviour of deceleration parameter with increasing energy density.

We have also drawn deceleration parameter q in terms of cosmic time t. It is observed from Fig. 8 that for $n = 1,$$q = -1$ which is in agreement with $\Lambda$CDM model. Further, from Fig. 9 it is seen that for $n = 2$ and $n = 3$, $q\rightarrow -1$. Also, it can be seen that for increasing n, q is decreasing. It clearly shows the transition of the universe from deceleration to acceleration at late time epoch. The similar kind of behaviour of deceleration parameter with respect to cosmic time t have been earlier obtained by Naji (2014).

Remark 5

In the following part, we obtain the deceleration parameter in terms of red shift.

We differentiate Eq. (36) and obtain

$$\begin{aligned} {\dot{H}} = \frac{a}{2}\frac{{\mathrm{d}}}{{\mathrm{d}}a}(d_{1}+d_{0}(1+d_{2}a^{-d_{3}})^{2}), \end{aligned}$$

(42)

which can be simply written as

$$\begin{aligned} {\dot{H}}= -\gamma a^{-d_{3}}(1+d_{2}a^{-d_{3}}), \end{aligned}$$

(43)

where $\gamma$ is some constant.

After using Eqs. (36) and (43), we get the deceleration parameter in terms of red shift as

$$\begin{aligned} q=-1-\frac{{\dot{H}}}{H^2}= -1+\frac{\gamma (1+z)^{d_{3}}(1+d_{2}(1+z)^{d_{3}})}{d_{1}+(1+d_{2}(1+z)^{d_{3}})^2}. \end{aligned}$$

(44)

Remark 6

We have given the plot of deceleration parameter in terms of red shift in Fig. 10. The transition from decelerated $q < 1/2$ to accelerated $q < 0$ universe is realized when q crosses zero, which means that the universe passes from matter dominated era to dark energy-dominated era where $(\rho _{{\mathrm{DE}}} \approx \rho _{{\mathrm{matter}}})$. It is interesting to note that the crossing happens and the acceleration expansion begins at $z\approx 0.5$ which is consistent with the observational data. It can also be said that for $d_{3} = 1.7$ the plot of q(z) fits well for spatially flat universe given by Li et al. (2011). The identical behaviour of deceleration parameter has been discussed earlier by Akarsu and Dereli (2012) and Aberkane et al. (2017).

From Figs. 6 and 10, it can be said that we can always choose the appropriate values of $d_{2}$ and $d_{3}$ to have a model which is in accordance with the experimental data.

Fig. 7

Plot of the deceleration parameter (q) versus energy density $(\rho )$ with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 1$ (solid line), $n = 2$ (dashed line) and $n = 3$ (dotted line)

Fig. 8

Plot of the deceleration parameter (q) versus cosmic time (t) with $A_{1} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1, \Lambda _{0} = \Lambda _{1} = 1, \omega = 0.5$, $n = 1$

Fig. 9

Plot of the deceleration parameter (q) versus cosmic time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 2$ (solid line) and $n = 3$ (dashed line)

Fig. 10

Plot of the deceleration parameter (q) versus red shift (z) with $d_{1} = 1/3, d_{2} = 0.5$, $d_{3} = 1.5$ (solid), $d_{3} = 1.6$ (dotted), $d_{3} = 1.7$ (dashed), $d_{3} = 1.8$ (dashdotted) and $d_{3} = 1.9$ (long dashed)

4 Stability

It is important to investigate the stability of the theory. There are several ways to investigate the same. Setare (2007) and Sadeghi et al. (2010) used the speed of sound in viscous fluid and studied the stability of the system. The square of sound speed is defined as

$$\begin{aligned} C_{s}^{2}= \frac{d{\bar{p}}}{d\rho }\ge 0. \end{aligned}$$

(45)

By using the ECCG Eq. (2) and the Friedmann Eq. (9) in Eq. (13), we get

$$\begin{aligned} {\bar{p}}&= \sum _{n} A_{n}\rho ^{n}- \frac{U}{\rho ^{\alpha }}- \frac{\left( \rho ^{1+\alpha }-U\right) ^{-\omega }}{\rho ^{\alpha }}\nonumber \\&\qquad - \sqrt{3}(\zeta _{0}+\zeta _{1}\rho ^{1/2})(\rho (1+\Lambda _{1})+\Lambda _{0})^{\frac{1}{2}}. \end{aligned}$$

(46)

For Case I, i.e. $n = 2$ and $\alpha = 1/2$ above equation becomes

$$\begin{aligned} {\bar{p}}&= A_{2}\rho ^{2}-\left( \sqrt{\frac{3}{\Lambda _{0}}}\frac{(1+\Lambda _{1})\zeta _{1}}{2}\right) \rho ^{3/2}\nonumber \\&+\left( A_{1}+\omega -\sqrt{\frac{3}{\Lambda _{0}}}\frac{(1+\Lambda _{1})\zeta _{0}}{2}\right) \rho -B\rho ^{-\frac{1}{2}}\nonumber \\&-\sqrt{3\Lambda _{0}}(\zeta _{0}+\zeta _{1}\rho ^{1/2}). \end{aligned}$$

(47)

The expression for square of speed of sound is

$$\begin{aligned} C_{s}^{2}&\,\equiv \frac{{\mathrm{d}}{\bar{p}}}{{\mathrm{d}}\rho } = 2A_{2}\rho -\left( \sqrt{\frac{3}{\Lambda _{0}}}\frac{3(1+\Lambda _{1})\zeta _{1}}{4}\right) \rho ^{1/2}\nonumber \\&\quad -\frac{\sqrt{3\Lambda _{0}}}{2}\zeta _{1} \rho ^{-1/2}+ \frac{1}{2}B\rho ^{-\frac{3}{2}}+A_{1}\nonumber \\&\quad + \omega - \sqrt{\frac{3}{\Lambda _{0}}}\frac{(1+\Lambda _{1})\zeta _{0}}{2} \ge 0, \end{aligned}$$

(48)

where $\rho$ is given in Eq. (18).

Similarly, for the case II, i.e. $n = 3$ and $\alpha = 1/2$ expression for square of speed of sound is of the form

$$\begin{aligned} C_{s}^{2}&\,\equiv \frac{{{\rm d}}{\bar{p}}}{{{\rm d}}\rho } = 3A_{3}\rho ^{2}+2A_{2}\rho -\left( \sqrt{\frac{3}{\Lambda _{0}}}\frac{3(1+\Lambda _{1})\zeta _{1}}{4}\right) \rho ^{1/2}\nonumber \\&\quad -\frac{\sqrt{3\Lambda _{0}}}{2}\zeta _{1} \rho ^{-1/2}+ \frac{1}{2}B\rho ^{-\frac{3}{2}}+A_{1} \nonumber \\&\quad + \omega - \sqrt{\frac{3}{\Lambda _{0}}}\frac{(1+\Lambda _{1})\zeta _{0}}{2} \ge 0, \end{aligned}$$

(49)

where $\rho$ is given in Eq. (25).

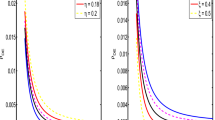
The graphical representation of $C_{s}^{2}$ is given in Fig. 11. It is observed that for $n = 2$ and $n = 3$ the speed of sound is decreasing in early universe and then it is constant at late time but for $n = 1$ speed of sound increases in early universe and then it is constant in late universe as shown in Fig. 12. Hence, we found that for $\omega = 0.5$ the theory is completely stable and there is no region of instability.

Fig. 11

Plot of square of speed of sound $(C_{s}^{2})$ versus time (t) with $A_{1} = A_{2} = A_{3} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$, $n = 2$ (solid line) and $n = 3$ (dashed line)

Fig. 12

Plot of square of speed of sound $(C_{s}^{2})$ versus time (t) with $A_{1} = 1/3, B = 3.4$, $\zeta _{0} = \zeta _{1} = 0.1,$$\Lambda _{0} = \Lambda _{1} = 1$, $\omega = 0.5$ and $n = 1$

5 Conclusion

In this paper, we have studied the ECCG with varying cosmological constant in flat FRW bulk viscous cosmology. We discussed the evolution of CG from its simplest form to ECCG with their corresponding EoS. Then, we introduced viscosity and cosmological constant as the linear combination of two terms, one is constant and other is a function of dark energy density $\rho$. Further, we obtained modified Friedmann equation and conservation equation due to bulk viscosity, cosmological constant and ECCG.

We considered $n = 2, 3$ and arbitrary n with $\alpha = 1/2$ and solved the nonlinear differential equation for dark energy density analytically and numerically for all the three cases and obtained the time-dependent dark energy density $\rho$. We discussed the behaviour of dark energy density $\rho$ for $n = 1$, 2 and 3 in Fig. 1. It is seen that dark energy density $\rho$ is a decreasing function of time which agrees with the expansion of the universe. It begins with the positive value and recovers asymptotically to a constant value. Also, it is observed that the dark energy density decreases as n increases in the presence of cosmological constant.

Further we solved Eqs. (32), (33) and (35) numerically for $n = 1, 2$ and 3 and obtained the evolution of scale factor a, Hubble expansion parameter H and deceleration parameter q and found the effect of increasing n in these cosmological parameters. The graphical representation of scale factor a is shown in Fig. 2 and it is found that scale factor decreases with increasing value of n. The behaviour of scale factor in early and late universe is drawn in Figs. 3 and 4, respectively. It is noted that as $\alpha$ increases a decreases in later stage of the universe.

Remark 7

Also, the behaviour of Hubble parameter H is drawn in terms of cosmic time t and red shift z in Figs. 5 and 6, respectively. It is observed that as n increases Hubble parameter H decreases. It is also seen that our model is in agreement with the observational data.

Remark 8

We plot deceleration parameter in terms of $\rho$, cosmic time t$(n = 1\; {\rm and}\; n = 2, 3)$ and red shift z in Figs. 7, 8, 9 and 10, respectively. It is observed that $q \rightarrow -1$ which recovers the result of $\Lambda$CDM model indicating the acceleration of the universe. Also, it is noted that as n increases value of q decreases. Further, it can be seen that the acceleration expansion begins at $z\approx 0.5$ which is consistent with the observational data. From the graphs, it is clear that universe transits from matter dominated era to dark energy-dominated phase.

Finally, we investigated the stability of the theory by using square of speed of sound $(C_{{\mathrm{s}}}^{2})$. The graphical representation of $C_{{\mathrm{s}}}^{2}$ is shown in Fig. 11. From the figure, it can be inferred that for $n = 2$ and 3 the speed of sound decreases at early time and is constant at late time but for $n =1$ the speed of sound increases as shown in Fig. 12. It starts with a positive value and reaches a constant value at late time. Hence, for $\omega = 0.5$ the theory is completely stable.

For the future study, it is possible to discuss this work for the case of arbitrary $\alpha$ with non-flat universe where $k \ne 0$.