1 Introduction

Cosmological observations such as Supernova-like Cosmological Observations Ia(SNeIa), the cosmic microwave background radiation (CMBR), the baryon acoustic oscillation (BAO) surveys, the large scale structure, the weak lensing and X-ray [1,2,3,4,5,6,7,8,9,10,11,12,13] confirmed the accelerated expansion of Universe. The dark energy models can describe this accelerated expansion. One model usually proposed to describe this phenomenon of dark energy is the cosmological constant, so there are some alternative models such as quintessence model [14,15,16,17,18,19], phantom model [20,21,22,23,24,25,26], quintom model [27,28,29], and tachyonic models [30]. Holographic model of dark energy is another interesting description of the dark energy [31,32,33,34]. Another proposal model for explaining the current acceleration of the Universe which is confirmed by observational data is to modify the gravitational theory [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]. In this perspective, we can cite f(R) gravity, \(f(R, {\mathcal {G}})\) gravity, \(f(R, {\mathcal {T}})\) [50,51,52,53,54,55,56,57,58,59] gravity where R denotes the curvature scalar, \({\mathcal {T}}\) the trace of the energy–momentum tensor and G the Gauss–Bonnet invariant defined by \({\mathcal {G}} = R^{2}-4R_{\nu \mu }R^{\nu \mu }+R_{\nu \mu \lambda \sigma }R^{\nu \mu \lambda \sigma }\). Recently, [60] implemented a new form of modified gravity that takes into account both R, G and \({\mathcal {T}}\) so-called \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity. In this paper, the author has constructed the \(f(R, {\mathcal {T}})\) gravity of sitter as well as the expansion in power law and the future singularity of finite time. The energetic conditions of \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity were studied. Finally, the author studied the stability of the constructed models.

There is another research circuit with which dark matter and dark energy are supposed to be a single component, and the Universe is to consider it as a single component that acts as both dark energy and dark matter. One way to achieve the unification of dark energy and dark matter is by using the so-called Chaplygin gas [61, 66]. Note that the (CG) was not consistent with observational data of SNIa, BAO, CMB [30, 63]. Pure Chaplygin gas with an exotic equation of state is characterized by a negative pressure. In this work, we are interested in generalized Chaplygin gas [66] and modified Chaplygin Gas [67] which are characterized by precise equations of state. Also, note that the state equation of the modified Chaplygin gas is composed of two parts: The first part is characterized by the ordinary fluid, and the second part is connected to the pressure by a power of the inverse of energy density.

Other work is done on the Chaplygin gas. There is the paper of B. Pourhassan et al. [68] which studied FRW cosmology with the extended Chaplygin gas, and they are shown that for your model the density of energy remains positive during the accelerated expansion phase of the Universe. We also have the paper of Ali R. Amani [69] which studied interacting \(f(R, {\mathcal {T}})\) gravity with modified Chaplygin gas and who found a very good result. Moreover, the cosmological viscosity plays a very important role in the present acceleration of Universe. The CMBR observations indicate an isotropic Universe, leading to bulk viscosity where the shear viscosity is neglected [70]. The possibility of the viscosity of Chaplygin gas was emitted by Xiang-Hua Zhai et al. [71] where, for the first time, the generalized Chaplygin gas with bulk viscosity was studied. One year later, H. B. Benaoum is studying Modified Chaplygin Gas Cosmology with Bulk Viscosity [72]. Other work is done on the viscosity of Chaplygin gas. There is the paper of Baffou et al., which studied the interaction between the Chaplygin gas with the modified \(f(R, {\mathcal {T}})\) gravity in order to determine the evolution of the parameters of dark energy as a function of time [73]. We can also quote the work of H. Saadat et al. who studied Effect of Varying Bulk Viscosity on Generalized Chaplygin Gas and FRW bulk viscous cosmology with modified Chaplygin gas in flat space [74, 75].

The physical motivation of this article revolves around three fundamental points:

  1. 1.

    Firstly, the model of the modified extended theory of gravity called gravitation \(f(R, {\mathcal {G}}, {\mathcal {T}})\) used here has not yet been enough cosmologically studied, so it is a new model since it is set up by Ujjal Debnath in 2020.

  2. 2.

    Secondly, we want to make our scientific contribution to this model and want to prove that this model is able to interpret physical phenomena in addition to what is done in it.

  3. 3.

    In a third step, we checked the contribution of G the Gauss–Bonnet invariant, on the effects of shear and apparent fluid viscosities in the framework of the generalized and modified Chaplygin gas on \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity

The paper is organized as follows: In section 2, we have established the basic equations of the \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity. In Section 3, we introduce briefly viscous cosmology in \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity. In Section 4, we consider the interaction between the generalized Chaplygin gas and \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity and we studied the effects of shear and bulk viscosities fluid on the cosmological parameters, namely the density energy of dark energy for three interacting models in power law of scale factor. In Section 5, the same studies of section 4 are done only that this time we have considered the modified Chaplygin gas. The last sections are devoted, respectively, to the commentary on the curves and to the conclusion.

2 Presentation of model

Let’s consider the following action [60]

$$S =\frac{1}{2\kappa } \int f(R,{\mathcal {G}}, {\mathcal {T}})\sqrt{-g}\,d^4 x + S_{m} .$$
(1)

where \(f\left( R,{\mathcal {G}}, {\mathcal {T}} \right)\) is the arbitrary function of Ricci scalar R, Gauss–Bonnet invariant G and of the trace \({\mathcal {T}} = g^{\upmu \upnu }T_{\upmu \upnu }\) of the stress–energy tensor of the matter. Also \(S_{m}\) is the matter action, \(\kappa = 8 \pi G\). The stress–energy tensor of the matter is defined as

$$\begin{aligned} {} T_{\upmu \upnu } = -\frac{2}{\sqrt{-g}}\frac{\delta S_{m}}{\delta g^{\upmu \upnu }} = - \frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}L_{m})}{\delta g^{\upmu \upnu }} \end{aligned}$$
(2)

where \(L_{m}\) is matter Lagrangian. Assuming that \(L_{m}\) depends on \(g_{\upmu \upnu }\), then the stress–energy tensor takes the following form

$$\begin{aligned} {} T_{\upmu \upnu } = g_{\upmu \upnu }L_{m} - 2\frac{\partial L_{m}}{\partial g_{\upmu \upnu }} \end{aligned}$$
(3)

Variation of the action (1) with respect to the metric components \(g_{\upmu \upnu }\) gives the gravitational field equations

$$\begin{aligned} {}{} & {} \left( R_{\upmu \upnu } + g_{\upmu \upnu }\square - \nabla _{\mu }\nabla _{\nu }\right) f_{R} -\frac{1}{2}f g_{\upmu \upnu }\nonumber \\{} & {} \quad +\left( 2 R R_{\upmu \upnu }-4R^{\zeta }_{\mu }R_{\zeta \nu }- 4R_{\mu \zeta \eta \nu }R^{\zeta \eta }+2R_{\mu }^{\zeta \eta \lambda }R_{\nu \zeta \eta \lambda }\right) f_{G} \nonumber \\{} & {} \quad + \left( 2 R g_{\upmu \upnu }\square - 2\nabla _{\mu }\nabla _{\nu }-4 g_{\upmu \upnu }R^{\zeta \eta }\nabla _{\zeta }\nabla _{\eta } -4 R_{\upmu \upnu }\square \right. \nonumber \\{} & {} \quad \left. + 4 R^{\zeta }_{\mu }\nabla _{\nu }\nabla _{\zeta } +4R^{\zeta }_{\mu }\nabla _{\mu }\nabla _{\zeta }+4 R_{\mu \zeta \nu \eta }\nabla ^{\zeta }\nabla ^{\eta }\right) f_{G}\nonumber \\{} & {} = \kappa T_{\upmu \upnu } - \left( T_{\upmu \upnu } + \varTheta _{\upmu \upnu }\right) f_{{\mathcal {T}}} \end{aligned}$$
(4)

where \(f_{A}\) is the derivative with respect to A, \(\square = \nabla _{\mu }\nabla ^{\mu }\) is the d’Alembertian operator and

$$\begin{aligned} {} \varTheta _{\upmu \upnu } = -2T_{\upmu \upnu } + g_{\upmu \upnu }L_{m}-2g^{\alpha \beta }\frac{\partial ^{2}L_{m}}{\partial g^{\upmu \upnu }\partial g^{\alpha \beta }} \end{aligned}$$
(5)

We choose in this work the simple form \(f\left( R,{\mathcal {G}}, {\mathcal {T}}\right) = R + 2{\mathcal {G}} + 2{\tilde{f}}\left( {\mathcal {T}} \right)\). Equation (4) then becomes

$$\begin{aligned} {} R_{\upmu \upnu } + g_{\upmu \upnu }R= & {} \kappa T_{\upmu \upnu } - 2\left( T_{\upmu \upnu } + \varTheta _{\upmu \upnu }\right) {\tilde{f}}_{{\mathcal {T}}}\nonumber \\{} & {} +g_{\upmu \upnu }\left( \frac{{\mathcal {G}}}{2} +{\tilde{f}}({\mathcal {T}})\right) \end{aligned}$$
(6)

3 Viscous in \(f\left( R,{\mathcal {G}}, {\mathcal {T}} \right)\) gravity

Here, we investigated the cosmological implications of generalized and modified viscous Chaplygin gas. To do this, we used a spatially flat Friedmann–Robertson–Walker (FRW) background metric of the form

$$\begin{aligned} ds^{2}=- dt^{2} + a^{2}\left( t\right) \delta ^{ij} dx_{i} dx_{j} \end{aligned}$$
(7)

where t is the cosmic time, \(x^{i}\) are the comoving spatial coordinates, and a(t) is the scale factor.

We consider that the matter is the generalized and modified Chaplygin gas and is assumed of having shear and bulk viscosities. We neglect the contribution of other components. The energy–momentum tensor corresponding to the shear and bulk viscous fluid and generalized Chaplygin gas can therefore be written as [73, 76]

$$\begin{aligned} {} T_{\upmu \upnu }^{m} = (\rho + {\overline{p}})u_{\mu }u_{\nu } - {\overline{p}}g_{\upmu \upnu } \end{aligned}$$
(8)

where \(\rho\) and \({\overline{p}}\) are the energy density and the pressure of the matter and \(u_{\mu }\) is the four-velocity vector with normalization condition \(u_{\mu }u^{\mu }\) = 1. According to the assumption, the pressure \({\overline{p}}\) of the matter is decomposed as

$$\begin{aligned} {} {\overline{p}} = p - 3\xi H + 2\eta H \end{aligned}$$
(9)

where \(\xi\) and \(\eta\) are bulk and shear viscosity coefficients, respectively. \(\rho\) and p are, respectively, the energy density and pressure density of Chaplygin gas and \(H = \dot{a}/a\) is the Hubble parameter.

The Lagrangian density may be chosen as \(L_{m}= -{\overline{p}}\), and Eq. (5) is recast as

$$\begin{aligned} {} \varTheta _{\upmu \upnu } = -2T_{\upmu \upnu } - g_{\upmu \upnu } {\overline{p}} \end{aligned}$$
(10)

We consider the total energy density and the total pressure of the Universe as the combination of components of a generalized and modified Chaplygin gas and dark energy. Therefore, within Eqs. (7) and (8), we have, in Planckian units \(\kappa = 1\),

$$\begin{aligned} {} 3 H^{2}= & {} \rho - f({\mathcal {T}}) + (\rho +{\overline{p}}){\tilde{f}}_{{\mathcal {T}}}+ 12 H^{2}({\dot{H}}+H^{2}) \nonumber \\= & {} \rho +\rho _\textrm{DE} = \rho _\textrm{tot} \end{aligned}$$
(11)
$$\begin{aligned} {} -2{\dot{H}} - 3 H^{2}= & {} {\overline{p}} + f({\mathcal {T}}) - 12 H^{2}({\dot{H}}+H^{2}) \nonumber \\= & {} p + p_\textrm{DE} = p_\textrm{tot} \end{aligned}$$
(12)

4 Interacting \(f\left( R,{\mathcal {G}}, {\mathcal {T}} \right)\) with generalized viscous Chaplygin gas

The energy density of the generalized Chaplygin gas (GCG) behaves as a cold dark matter in the past and as a cosmological constant at present with the following equation of state,

$$\begin{aligned} {} p = -\frac{B}{\rho ^{\gamma }} \end{aligned}$$
(13)

where \(B > 0\). The case \(\gamma = 1\) corresponds to the original Chaplygin gas first introduced by Chaplygin [77]

The conservation equation of the total energy density

$$\begin{aligned} {} {\dot{\rho }}_\textrm{tot} + 3H\left( \rho _\textrm{tot} + p_\textrm{tot}\right) = 0 \end{aligned}$$
(14)

translates into two continuity equations for dark energy and GCG with an interaction term Q

$$\begin{aligned} {} {\dot{\rho }}_\textrm{DE} + 3H\left( \rho _\textrm{DE} + p_\textrm{DE}\right)= & {} -Q \end{aligned}$$
(15)
$$\begin{aligned} {} {\dot{\rho }} + 3H(\rho + p)= & {} Q \end{aligned}$$
(16)

Interaction term Q corresponds to energy between dark energy and generalized Chaplygin gas, which usually can take the following forms: \(Q = 3Hc\rho\) ; \(Q = 3Hc\rho _\textrm{DE}\) ; \(Q = 3Hc\rho _\textrm{tot}\) ; \(Q = \sigma {\dot{\rho }}\) ; \(Q = \sigma {\dot{\rho }}_\textrm{DE}\) ; \(Q = \sigma {\dot{\rho }}_\textrm{tot}\) with c and \(\sigma\) being coupling constants. These types of interactions are either positive or negative and cannot change sign. However, a variable sign interaction has been studied in [32]

$$\begin{aligned} {} Q = q(\sigma {\dot{\rho }} + 3Hc\rho ) \end{aligned}$$
(17)

with \(\sigma\) and c being coupling constants and q the deceleration parameter defined by

$$\begin{aligned} {} q = -1-\frac{{\dot{H}}}{H^{2}} \end{aligned}$$
(18)

The deceleration phase of the Universe corresponding to \(q > 0\) and the acceleration phase to \(q < 0\). Equation (17) can change sign according to the different phases of the evolution of the Universe. We choose in the present work three interaction forms of Q to describe the evolution of the cosmological parameters in the Universe dominated by generalized and modified Chaplygin gas and dark energy.

From (11) and (12), we infer dark energy density and pressure as

$$\begin{aligned} {} \rho _\textrm{DE}= & {} - {\tilde{f}}({\mathcal {T}})+\frac{{\mathcal {G}}}{2}+ (\rho +{\overline{p}}) f_{{\mathcal {T}}} \end{aligned}$$
(19)
$$\begin{aligned} {} p_\textrm{DE}= & {} - 3\xi H + 2\eta H + f({\mathcal {T}}) -\frac{{\mathcal {G}}}{2} \end{aligned}$$
(20)

Moreover, the equation-of-state parameter of dark energy, \(w_\textrm{DE}\), is defined as

$$\begin{aligned} {}{} & {} w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}} = \frac{- 6\xi H + 4\eta H + 2 f({\mathcal {T}}) - {\mathcal {G}}}{-2 f({\mathcal {T}})+{\mathcal {G}}+ 2(\rho +{\overline{p}})f_{{\mathcal {T}}}} \end{aligned}$$
(21)

Following the work ([73]), we choose

$$\begin{aligned} {} {\tilde{f}}({\mathcal {T}}) = {\mathcal {T}}^{\beta } \end{aligned}$$
(22)

with \(\beta\) being a constant and \({\mathcal {T}} = \rho -3{\overline{p}}\) the trace of energy–momentum tensor. Equations (19) and (20) read

$$\begin{aligned} {} \rho _\textrm{DE}= & {} \left[ \rho -3p +9\xi H -6\eta H \right] ^{\beta -1}\nonumber \\\times & {} \left[ (-1+2\beta )\rho +(3-2\beta )p \right. \nonumber \\{} & {} \left. +3\xi H(3+2\beta )+2\eta H(3-2\beta )\right] \nonumber \\{} & {} + 12 H^{2}\left( {\dot{H}}+H^{2}\right) \end{aligned}$$
(23)

and

$$\begin{aligned} {} p_\textrm{DE}= & {} - 3\xi H + 2\eta H + \left[ \rho -3p +9\xi H -6\eta H \right] ^{\beta }\nonumber \\{} & {} -12H^{2}({\dot{H}}+H^{2}) \end{aligned},$$
(24)

respectively.

We consider in the following the power-law mode of the scalar factor in terms of cosmic time ([73])

$$\begin{aligned} {} a \propto t^{n} \end{aligned}$$
(25)

to describe the evolution of cosmological parameters [73]. Recall that there are several expressions of a based on different periods of evolution of the Universe. We are interested here in the cosmological evolution of the dark energy density \(\rho _\textrm{DE}\) and pressure \(p_\textrm{DE}\).

4.1 Model \(Q = 3Hc\rho\)

In this case, the continuity equation of GCG reads

$$\begin{aligned} {\dot{\rho }}+3H\rho \left( 1-c\right) -\frac{3BH}{\rho ^{\gamma }} = 0 \end{aligned}$$
(26)

whose solution is given by

$$\begin{aligned} {} \rho = \left( \frac{B}{1-c}\right) ^{1/\left( 1+\gamma \right) }\bigg ( 1+A \,a^{-3\left( 1-c\right) \left( 1+\gamma \right) }\bigg ) ^{1/\left( 1+\gamma \right) } \end{aligned}$$
(27)

where A is a constant of integration. From (13), the pressure of generalized Chaplygin gas is given by

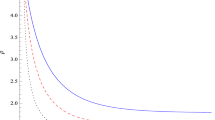
$$\begin{aligned} {} p = -\left( 1-c \right) \left( \frac{B}{1-c}\right) ^{1/\left( 1+\gamma \right) }\bigg ( 1+A \,a^{-3\left( 1-c\right) \left( 1+\gamma \right) }\bigg ) ^{-\gamma /\left( 1+\gamma \right) } \end{aligned}$$
(28)

In view of Eqs. (23)–(25), we can compute the expressions of \(\rho _\textrm{DE}\) and \(p_\textrm{DE}\) in terms of cosmic time t. Figures 1 and 2 present the evolution of dark energy and pressure densities and the equation-of-state parameter \(w_\textrm{DE}\) for the interaction model \(Q = 3Hc\rho\).

Fig. 1
figure 1

Plot of dark energy pressure with respect to cosmic time for the generalized Chaplygin gas for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(c = 0.5\), \(n = 1\) ; for the first panel we fix \(\xi = 0.2\) and vary \(\eta\) and for the second panel we fix \(\eta = 0.1\) and vary \(\xi\)

Full size image
Fig. 2
figure 2

Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy state equation \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the generalized Chaplygin gas for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(c = 0.5\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image

4.2 Model \(Q = q(\sigma {\dot{\rho }}+3cH\rho )\)

Using the interacting model Q, the continuity equation takes the following form

$$\begin{aligned} {} {\dot{\rho }}\left( 1+\sigma +\sigma \frac{{\dot{H}}}{H^{2}}\right) +3H\rho \left( 1+c+c\frac{{\dot{H}}}{H^{2}}\right) -\frac{3BH}{\rho ^{\gamma }} \end{aligned}$$
(29)

Using equation (25), equation (29) becomes

$$\begin{aligned} {} {\dot{\rho }}\left( 1+\sigma -\frac{\sigma }{n}\right) +\frac{3n}{t}\left( 1+c-\frac{c}{n}\right) \rho -\frac{3Bn}{t}\,\rho ^{-\gamma } = 0 \end{aligned}$$
(30)

After integrating, the general solution of this equation yields

$$\begin{aligned} {} \rho \left( t\right)= & {} \left( \frac{B n}{n + \left( n-1 \right) c } \right) ^{1/\left( 1+\gamma \right) }\nonumber \\{} & {} \bigg (1 + A\, t^{- 3n\left[ n+ \left( n-\gamma -1 \right) c \right] /\left[ n + \left( n-1 \right) \sigma \right] } \bigg )^{1/\left( 1+\gamma \right) } \end{aligned}$$
(31)

where A is a constant of integration. From the equation of state (13), we deduct for this interacting model type the pressure of the generalized Chaplygin gas as the following form

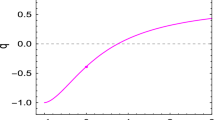
$$\begin{aligned} {} p\left( t\right) = -\left( 1 + \left( 1-\frac{1}{n} \right) c \right) \left( \frac{B n}{n + \left( n-1 \right) c } \right) ^{1/\left( 1+\gamma \right) }\nonumber \\ \times \left( 1 + A t^{- 3n\left[ n+ \left( n-\gamma -1 \right) c \right] /\left[ n + \left( n-1 \right) \sigma \right] } \right) ^{-\gamma /\left( 1+\gamma \right) } \end{aligned}$$
(32)

We shall get the time-dependent expressions of dark energy and pressure densities and dark energy equation-of-state parameter by substituting Eqs. (31) and (32) into (23)–(25). In Figs. 3 and 4, we visualize dark energy pressure and equation-of-state parameter, respectively.

Fig. 3
figure 3

Plot of dark energy pressure with respect to cosmic time for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(c = 0.5\), \(n = 1\), for the first panel we fix \(\xi = 0.6\) and vary \(\eta\) and second panel we fix \(\eta = 0.1\) and vary \(\xi\)

Full size image
Fig. 4
figure 4

Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy state equation \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the generalized Chaplygin gas for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(c = 0.5\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image

4.3 Model \(Q = 3Hb\rho _\textrm{tot}\)

Using the interacting model Q, the continuity equation takes the following form

$$\begin{aligned} {}{} & {} {\dot{\rho }} + \frac{3n\rho }{t}(1-b+\beta b)-\frac{3n\beta }{t\rho ^{\alpha }}(1-3b\beta )\nonumber \\{} & {} \quad -\frac{9n^{2}\beta b}{t^{2}}(2\eta - 3 \xi )+\frac{36n^{3}b}{t^{5}}(n^{2}-1) = 0 \end{aligned}$$
(33)

Since Eq. (33) is very difficult to solve analytically, we first solve it numerically to obtain the density of the generalized Chaplygin gas, and then, we use equations (19) and (20) to obtain the density of dark energy, pressure density and state equation of dark energy.

Fig. 5
figure 5

Plot of dark energy pressure with respect to cosmic time for \(B = 5\), \(\beta = 0.01\), \(\gamma = 0.1\), \(\sigma = 0.1\), \(n = 1\). For the first panel, we fix \(\xi = 0.2\) and vary \(\eta,\) and for the second panel, we fix \(\eta = 0.01\) and vary \(\xi\)

Full size image

5 Interacting \(f\left( R,{\mathcal {G}}, {\mathcal {T}}\right)\) with modified Chaplygin gas

A modification to the GCG results in the modified Chaplygin gas (MCG) with an equation of state given by

$$\begin{aligned} {} p = w \rho - \frac{B}{\rho ^{\gamma }}, \end{aligned}$$
(34)

where w, B and \(\gamma\) are constant parameters. When \(B = 0\), we recover the equation of state of perfect fluid, i.e., \(p = w\rho\). For \(w = 0\), it reduces to the generalized Chaplygin gas.

5.1 Model \(Q = 3Hc\rho\)

The continuity equation reads

$$\begin{aligned} {\dot{\rho }}+3H\rho (1+w-c)-\frac{3BH}{\rho ^{\gamma }} = 0. \end{aligned}$$
(35)

Using (25), the general solution of the energy density of modified Chaplygin gas is

$$\begin{aligned} {} \rho = \left( \frac{B}{1+w-c} \right) ^{1/\left( 1+\gamma \right) } \bigg ( 1+A\,t^{-3n(1+w-c)\left( 1+\gamma \right) }\bigg )^{1/\left( 1+\gamma \right) } \end{aligned}$$
(36)

where A is constant of integration. From 34, the pressure of the modified Chaplygin gas is as follows

$$\begin{aligned} {} p= & {} w\left( \frac{B}{1+w-c} \right) ^{1/\left( 1+\gamma \right) } \bigg ( 1+A\,t^{-3n(1+w-c)\left( 1+\gamma \right) }\bigg )^{1/\left( 1+\gamma \right) }\nonumber \\{} & {} \times \left[ 1- \left( \frac{1+w-c}{w} \right) \bigg ( 1+A t^{-3n(1+w-c)\left( 1+\gamma \right) }\bigg )^{-1}\right] \end{aligned}$$
(37)

Substituting Eqs. (22), (36), (37) into (23) and (24) gives \(\rho _\textrm{DE}\) and \(\rho _\textrm{DE}\).

The following figures present the numerical analysis of the dark energy, pressure density and equation of state of dark energy for the interaction model \(Q = 3Hc\rho\) with the modified Chaplygin gas.

Fig. 6
figure 6

Plot of dark energy density with respect to cosmic time for modified Chaplygin gas for \(B = 2\), \(A = 1\), \(\beta = 0.1\), \(\gamma = 01\), \(c = 02\), \(m = 0.5\), \(w = 01\). For the first panel. we set \(\xi = 0.3\) and vary \(\eta,\) and in the second panel, we set \(\eta = 0.02\) and vary \(\xi\)

Full size image
Fig. 7
figure 7

Plot of dark energy density with respect to cosmic time for modified Chaplygin gas for \(B = 3\), \(A = 0.2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(c = 0.1\), \(n = 1\), \(w = 1\). For the first panel, we fix \(\xi = 0.6\) and vary \(\eta,\) and for the second panel, we set \(\eta = 0.01\) and vary \(\xi\)

Full size image
Fig. 8
figure 8

Plot of dark energy density with respect to cosmic time for modified Chaplygin gas for \(B = 3\), \(\beta = 0.01\), \(\sigma = 0.1\) , \(n = 1\), \(w = 1\). For the first panel, we fix \(\xi = 0.8\) and vary \(\eta,\) and for the second panel, we fix \(\eta = 0.3\) and vary \(\xi\)

Full size image
Fig. 9
figure 9

Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy state equation \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the generalized Chaplygin gas for \(B = 5\), \(\beta = 0.1\), \(\gamma = 0.1\), \(\sigma = 0.5\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image
Fig. 10
figure 10

Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy state equation \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the modified Chaplygin gas for \(B = 5\), \(\beta = 0.1\), \(\gamma = 0.1\), \(w = 01\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image

5.2 Model \(Q = q(\sigma {\dot{\rho }}+3cH\rho )\)

Using (25), the continuity equation can be written in the form

$$\begin{aligned} {} {\dot{\rho }}(1+\sigma -\frac{\sigma }{n})+3\frac{n}{t}\rho (1+w+c-\frac{c}{n})-\frac{3Bn}{t\rho ^{\gamma }} = 0 \end{aligned}$$
(38)

After integrating, the general solution of this equation yields

$$\begin{aligned} {} \rho= & {} \left( \frac{B n}{ \left( 1+w+c\right) n-c }\right) ^{1/\left( 1+\gamma \right) }\nonumber \\{} & {} \left( 1+A t^{-3n\left[ \left( 1+w+c \right) n-c \right] /\left[ n+\left( n-1 \right) \sigma \right] } \right) ^{1/\left( 1+\gamma \right) } \end{aligned}$$
(39)

and

$$\begin{aligned} {} p= & {} w \left( \frac{B n}{ \left( 1+w+c\right) n-c }\right) ^{1/\left( 1+\gamma \right) }\nonumber \\{} & {} \left( 1+A\,t^{-3n\left[ \left( 1+w+c \right) n-c \right] /\left[ n+\left( n-1 \right) \sigma \right] } \right) ^{1/\left( 1+\gamma \right) }\nonumber \\\times & {} \left[ 1-\left( \frac{ \left( 1+w+c\right) n-c }{w n} \right) \right. \nonumber \\{} & {} \left. \left( 1+A\,t^{-3n\left[ \left( 1+w+c \right) n-c \right] /\left[ n+\left( n-1 \right) \sigma \right) } \right) ^{-1} \right] \end{aligned}$$
(40)

where A is a constant of integration.

The following figures present the numerical analysis of the dark energy, pressure density and equation of state of dark energy for the interaction model \(Q = q(\sigma {\dot{\rho }}+3cH\rho )\) with the modified Chaplygin gas.

Fig. 11
figure 11

Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy state equation \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the modified Chaplygin gas for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(w = 01\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image

5.3 Model \(Q = 3Hb\rho _\textrm{tot}\)

Using the interacting model Q, the continuity equation takes the following form

$$\begin{aligned} {}{} & {} {\dot{\rho }} + \frac{3n\rho }{t}\left( 1+A(1+3\beta b)-b(1-\beta )\right) \nonumber \\{} & {} \quad -\frac{3n B}{t\rho ^{\alpha }}(1-3b\beta )-\frac{9n^{2}\beta b}{t^{2}}(2\eta - 3 \xi )\nonumber \\{} & {} \quad -\frac{36n^{3}b}{t^{5}}(n^{2}-1) = 0 \end{aligned}$$
(41)

Since equation (41) is very difficult to solve analytically, we first solve it numerically to obtain the density of the modified Chaplygin gas, and then, we use equations (19) and (20) to obtain the density of dark energy, pressure density and state equation of dark energy.

Fig. 12
figure 12

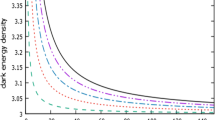
Plot of dark energy pressure \(p_\textrm{DE}\) and dark energy equation of state \(w_\textrm{DE} = \frac{p_\textrm{DE}}{\rho _\textrm{DE}}\) versus cosmic time for the modified Chaplygin gas for \(B = 5\), \(A = 2\), \(\beta = 0.1\), \(\gamma = 0.1\), \(\sigma = 0.1\), \(w = 01\), \(\xi = 0.15\), \(\eta = 0.025\)

Full size image

6 Discussion

From Figs. 1, 3, 5 and then 6, 7, 8 showing the compote of the energy density as a function of time, respectively, for the generalized Chaplygin gas and the modified Chaplygin gas, we can say that the behavior of the cosmological parameters obtained is in conformity with the observational data because in all studied cases, the figures show clearly that the dark energy density falls with expansion. Additionally, Figs. 2, 4, 9, 10, 11 and 12 reveal that during its evolution, the Universe can cross the following evolutions phantom era (\(\omega _\textrm{DE} < -1\)), the quintessence evolution (\(-1<\omega _\textrm{DE}<-1/3\)) and the constant cosmology (\(\omega _\textrm{DE}=-1\)). Pendent that the other evolution phases are located on very little duration, these graphs show that the dark energy parameter stretches forward to \(-1\) characterizing the constant cosmology or the \(\Lambda\)CDM era. We note that the viscosity parameters have a remarkable impact on the cosmological evolution of the Universe. Thus, we find that for the two Chaplygin gas models, as cosmic time evolves, the dark energy effects become very remarkable with bulk viscosity but decreases with shear viscosity. Such a behavior of energy density was found in ([73]) where the authors studied viscous generalized Chaplygin gas with gravity \(f(R, {\mathcal {T}})\). Our results lead to the conclusion that the combination of \(f(R, {\mathcal {G}}, {\mathcal {T}})\) gravity and Chaplygin gas models is a real alternative to General Relativity and scalar field to investigate the dark energy problem which is one of the most current tenacious enigmas in cosmology.

7 Conclusions

In this paper, we investigated the effect of generalized and modified viscous Chaplygin gas on the \(f(R,{\mathcal {G}},{\mathcal {T}})\) gravity. We assumed that the Universe is dominated by dark energy and dark matter (generalized and modified Chaplygin gas) in interaction with gravity. We obtained modified Friedmann equations resulting from this interaction, the energy and pressure density of generalized and modified Chaplygin gas, and we verified the effect of shear and bulk viscosities on dark energy density. It emerges from our study that the density of dark energy is increasing and decreasing, respectively, and that the density of pressure of the dark energy decreases when the Universe is in a phase of accelerated expansion. It was also emphasized that the Gauss–Bonnet invariant \({\mathcal {G}}\) has a remarkable impact on the shape of the curves obtained. In short, we can say that the viscosity parameters are very important in the realization of a coincidence of our data with the observational data.