On branched coverings of singular (G, X)-manifolds

Abstract

Branched coverings boast a rich history, ranging from the ramification of Riemann surfaces to the realization of 3-manifolds as coverings branched over knots and spanning both geometric topology and algebraic geometry. This work delves into branched coverings “à la Fox” of (G, X)-manifolds, encompassing three main avenues: Firstly, we introduce a comprehensive class of singular (G, X)-manifolds, elucidating elementary theory paired with illustrative examples to showcase its efficacy and universality. Secondly, building on Montesinos’ work, we revisit and augment the prevailing knowledge, formulating a Galois theory tailored for such branched coverings. This includes a detailed portrayal of the fiber above branching points. Lastly, we identify local attributes that guarantee the existence of developing maps for singular (G, X)-manifolds within the branched coverings framework. Notably, we pinpoint conditions that ensure the existence of developing maps for these singular manifolds. This research proves especially pertinent for non-metric singular (G, X)-manifolds like those of Lorentzian or projective nature, as discussed by Barbot, Bonsante, Suhyoung Choi, Danciger, Seppi, Schlenker, and the author, among others. While examples are sprinkled throughout, a standout application presented is a uniformization theorem “à la Mess” for singular locally Minkowski manifolds exhibiting BTZ-like singularities.

1 Introduction

1.1 Some motivational examples

Consider ${\mathbb {H}}$ the hyperbolic plane and $\text {Isom}^+({\mathbb {H}})\simeq \text {O}_{0}(1,2; {\mathbb {R}})\simeq \text {PSL}(2;{\mathbb {R}})$¹ its group of direct isometries. The quotient of ${\mathbb {H}}$ by a geometrically finite discrete torsion-free subgroup of $\text {Isom}^+({\mathbb {H}})$, say $\varGamma$, gives a locally hyperbolic manifold, a ${\mathbb {H}}$-manifold, say $\varSigma :=\varGamma \backslash {\mathbb {H}}$. Such a $\varSigma$ admits a developing map ${\mathcal {D}}:{\widetilde{\varSigma }}\rightarrow {\mathbb {H}}$ and a holonomy homomorphism $\rho :\pi _1(\varSigma )\rightarrow \text {Isom}^+({\mathbb {H}})$ where ${\widetilde{\varSigma }}$ is the universal covering of $\varSigma$ and $\pi _1(\varSigma )$ its fundamental group. If, furthermore, the holonomies of the ends of $\varSigma$ are parabolic, then one can associate to each end an ideal point “at infinity”, effectively compactifying $\varSigma$ to some ${{\overline{\varSigma }}}$ (which is the Freudenthal compactification [23] of $\varSigma$). The geometric model $(\text {Isom}^+({\mathbb {H}}),{\mathbb {H}})$ is an instance of a geometric structure in the sense of Ehresmann [24], popularised by Thurston [48] and others [2, 12, 13, 25, 29, 40, 43] ie a couple (G, X) where X is a locally path-connected Hausdorff topological space and G is a group acting analytically on X by homeomorphisms. Here “analytically” means that for all $g,h\in G$, if the restrictions to any nontrivial open subset ${\mathcal {U}}$ of g and h agree, then $g=h$. A (G, X)-manifold is then a second countable Hausdorff topological space M endowed with an atlas whose change of charts lies in G. The existence of a developing map from the universal covering of such a manifold M to the model space X and of a holonomy from its fundamental group to the model group G is a general property as long as the universal covering exists.²

The manipulation of such points “at infinity” (or even irrational conical singularities), though legal and quite simple in this specific context, requires some additional care in the general setting of (G, X)-manifolds especially if one considers nonmetric analytical structures such as conformal structures, Lorentzian structures or affine structures ie, $(\text {Aff}({\mathbb {R}}^n),{\mathbb {R}}^n)$-structures. Compactifications and completions are not (G, X)-manifolds anymore but rather “singular” (G, X)-manifolds. The notion of singularity is not a unified concept: singularities are usually described in a specific context, making clear what those singularities entail. Most “singularities” arise either via

• completion or compactification procedures as presented above (see also [17, 20]);

• quotienting a regular (G, X)-manifold by a discrete group acting properly discontinuously by automorphisms [34];

• gluings of simplices of the model space X (when it makes sense) [8, 26],

• suspensions such as presented in [5, 47].

In all instances, the regular locus is open and dense. Additional properties are, however, required for any weak form of analyticity to hold. In fact, consider $X={\mathbb {R}}^2$ and G either $\text {Isom}({\mathbb {E}}^2) \simeq \text {O}_2({\mathbb {R}}) \ltimes {\mathbb {R}}^2$ or $\text {Aff}({\mathbb {R}}^2)\simeq \text {GL}_2({\mathbb {R}})\ltimes {\mathbb {R}}^2$ acting as usual on ${\mathbb {R}}^2$; then consider the manifold $M = {\mathbb {R}}^2$ together with the (G, X)-structure induced by the atlas composed of a unique chart $\text {Id}: {\mathbb {R}}^2{\setminus } S \rightarrow {\mathbb {R}}^2{\setminus } S$ for some subset S. If S is a singleton, using the metric, it is easy to check that one can extend uniquely the flat metric structure to the whole ${\mathbb {R}}^2$. The same statement is true in the affine case. However, if S is a line segment, say $S=\{0\}\times [-1,1]$, the uniqueness of the atlas extension can be proved only in the metric case, while in the affine case, uniqueness fails. More precisely, in the affine case, one can add any one of the charts

$$\begin{aligned} \displaystyle \varphi _{\lambda ,\mu }:\begin{array}{l|rcl} &{} \displaystyle {\mathbb {R}}\times ]-1,1[ &{} \longrightarrow &{} \displaystyle {\mathbb {R}}\times ]-1,1[ \\ &{} \displaystyle (x,y),x\le 0 &{} \longmapsto &{} \displaystyle (\lambda x,y) \\ &{} \displaystyle (x,y),x\ge 0 &{} \longmapsto &{} \displaystyle (\mu x,y)\end{array},\quad \lambda ,\mu >0. \end{aligned}$$

The new regular locus is then the complement of two points, and its holonomy is trivial if and only if $\lambda =\mu$. In any case, different extensions of the initial atlas give rise to inequivalent affine structures.³

1.2 Singular (G, X)-manifolds and branched coverings

We show that an efficient definition for singular (G, X)-manifold is that they have a (G, X)-atlas defined almost everywhere in the sense that its support is portly: open, dense and locally connected in the whole manifold.⁴ The complement of a portly subset is called skeletal. In Sect. 2, we write a primer on such singular (G, X)-manifolds, generalizing elementary results to this context, showing that this definition is satisfactory.

Beyond elementary analyticity statements, we would like a good notion of developing map, holonomy, and universal covering for singular (G, X)-manifolds. A natural first step in this direction is to consider, for some singular (G, X)-manifold M, the universal covering ${\widetilde{\text {Reg}}}(M)$ of its regular locus $\text {Reg}(M)$, which gives rise to a map ${\widetilde{\text {Reg}}}(M)\rightarrow M$, then try to complete ${\widetilde{\text {Reg}}}(M)$ in a natural way.

We argue that Fox has provided this natural way in the 1950s [27, 33] with the notions of spread, complete spread, and completion of spread and then extended to include branched coverings; we refer the interested reader to Montesinos [39] for an up to date review. We shall recall fundamental properties of coverings à la Fox as well as extend it in two directions. First, we define a Galois Theory of branched coverings with the important addition of a characterization of Galoisian universal branched coverings above given loci. In particular, we prove in Proposition 3.52 that for a Hausdorff, connected, locally path-connected topological space X, the universal covering branched above a skeletal locus S is Galoisian if and only if $X{\setminus } S$ is semi-locally simply connected in X in a sense we will define. Second, we give a path space description of the universal covering branched above a given locus akin to that of the universal unbranched covering; see Theorem 2. To this end, we introduce a notion of almost trivial loop. Most intermediary results and definitions presented are folkloric; however, to the author’s knowledge, most are not presented in the generality considered in the present work, and the notion of “semi-locally simply connected in” is new as well as the path description of the maximal branched covering.

Coming back to singular (G, X)-manifolds, we introduce the classes of tame singular (G, X)-manifolds and virtually tame singular (G, X)-manifolds that admit natural developing maps. We prove localization Theorems to ensure those global properties can be efficiently derived from local ones. See Theorems 4 and 5.

1.3 General references

We use freely standard notions from general topology (separation and countable basis hypotheses, compact-open topology), algebraic topology (first fundamental group, semi-local simple connectedness, Galois correspondence, etc.), group actions and category theory (categories, commutative diagrams, projective limits). We refer the reader uncomfortable with some of these notions to reference texts [14, 15, 32, 41, 46, 50]. Thurston’s book [48] contains many intuitions and constructions; however, the only reference textbook on the fundamentals of (G, X)-manifolds is Goldman’s book [30]. Benzecri thesis [7] as well as Ratcliff’s [43] and Bonahon’s [13] books which include some metric background in the (G, X)-manifold context and some elementary account of conical singularities. However, our assumptions may be slightly more general at times. We may also refer to the (yet unpublished) book of Choi [20]. Having a particular interest in Lorentzian manifolds, the author kindly asks the reader to pardon his tendency to draw nontrivial examples from those. The reader unfamiliar with the geometry of Lorentzian manifolds may find useful [3, 42].

2 Singular (G, X)-manifolds (I): bases and examples

We give ourselves some analytical structure (G, X), ie, a connected, locally connected, Hausdorff topological space X together with a faithful action of a group G by homeomorphisms such that for all $\phi _1,\phi _2\in G$ and all nontrivial open subset ${\mathcal {U}}\subset X$ if the actions of $\phi _1$ and $\phi _1$ agree on ${\mathcal {U}}$ they agree on X. A (G, X)-atlas on a topological space M is a family $({\mathcal {U}}_i,{\mathcal {V}}_i,\varphi _i)_{i\in I}$ where for all $i\in I$, ${\mathcal {U}}_i$ is an open subset of M, ${\mathcal {V}}_i$ is an open subset of X and $\varphi _i:{\mathcal {U}}_i\rightarrow {\mathcal {V}}_i$ an homeomorphism, with the property that for all $i,j\in I$ such that ${\mathcal {U}}_i\cap {\mathcal {U}}_j\ne \emptyset$ and for all connected component ${\mathcal {W}}$ of ${\mathcal {U}}_i\cap {\mathcal {U}}_j$, there exists a $\phi \in G$ such that $\phi \circ \varphi _{i|{\mathcal {W}}} = \varphi _{j|{\mathcal {W}}}$. By analyticity of (G, X), such a $\phi$ is unique. The support $\text {supp}({\mathcal {A}})$ of such an atlas ${\mathcal {A}}$ is defined as the union of the ${\mathcal {U}}_i$. A (G, X)-manifold is a second countable Hausdorff topological space M endowed with a (G, X)-atlas whose support is M.

The simplest example of singularities occurring in the literature of (G, X)-manifolds are conical singularities in homogeneous Riemannian manifolds.

Example 2.1

Let $\alpha >0$ and $n\ge 2$, define ${\mathbb {E}}_\alpha ^n = {\mathbb {R}}^{n-2}\times {\mathbb {R}}^2$ endowed with cylindrical coordinates $(z,r,\theta ) \in {\mathbb {R}}^{n-2}\times {\mathbb {R}}_+\times {\mathbb {R}}/{\mathbb {Z}}$ and the Riemannian metric ${{\textbf {g}}} = \text {d}z^2+\text {d}r^2 + \alpha r^2\text {d}\theta ^2$. This Riemannian metric is well-defined and locally Euclidean on the complement of the domain $\{r=0\}$. One can thus endow the domain $\{r>0\}$ with a $({\mathbb {E}}^n,{\mathbb {R}}^n \rtimes \text {SO}(n))$-structure. However, this geometric structure cannot be extended to the whole ${\mathbb {R}}^n$ except for $\alpha =2\pi$. An obstruction is given by the holonomy $\rho :\pi _1(\{r>0\})={\mathbb {Z}}\rightarrow {\mathbb {R}}^n\rtimes \text {SO}(n)$, indeed $\rho (1)$ is the rotation of angle $\alpha$ which is non trivial when $\alpha \notin 2\pi {\mathbb {N}}^*$.

In the previous example, manifolds with conical singularities have an underlying metric space structure that gives a natural notion of isomorphism class. In a way, the author feels that such an underlying structure distracts from the fact that the notion of isomorphism between singular (G, X)-manifolds does not depend on such metrics and is actually more general. Gluing projective polyhedra leads to “singular” projective manifolds, and it would feel “unnatural” to define isomorphism classes for such manifolds based upon some metric choice. As an illustration of the richness of nonmetric singularities and their usefulness, we wish to refer, for instance, to [5] for a fundamental study of conical $2+1$ Lorentzian singularities or [19, 22] for their role in geometric transitions.

The present section is devoted to the most basic definitions and properties of the notion of singular (G, X)-manifolds we introduce. It encompasses most singularities of the literature, and we show some elementary properties ensuring the theory of such manifolds works well.

2.1 Topological preliminaries

Recall that for X a topological space, a subset ${\mathcal {U}}\subset X$ is locally connected in X if for all open connected ${\mathcal {W}}\subset X$, the intersection ${\mathcal {W}}\cap {\mathcal {U}}$ is connected. Note in particular that if X is connected, then ${\mathcal {U}}$ is connected.

Definition 2.2

(Portly/skeletal subset) Let X be a Hausdorff locally connected topological space, a subset ${\mathcal {U}}$ of X is portly (in X) if ${\mathcal {U}}$ is open dense and locally connected in X. A subset $S\subset X$ is skeletal if its complement in X is portly.

Example 2.3

The following examples of S are skeletal in X.

• S finite and X a surface;

• S a tame knot in a 3-manifold X;

• S the k-skeleton of a pure n-dimensional simplicial complex X with $k\le n-2$;

• S a Cantor set wildly embedded into an n-manifold X.

Portly subsets have nice properties, the proof of which relies on usual connectedness and density arguments and are thus left to the reader, most can be found in [16, 27, 33, 37]. Consider a locally connected Hausdorff topological space X.

• finite intersections of portly subsets are portly;

• if ${\mathcal {U}}\subset {\mathcal {V}}$, ${\mathcal {U}}$ is portly in X and ${\mathcal {V}}$ is open, then ${\mathcal {V}}$ is portly (hence unions of portly subsets are portly);

• if ${\mathcal {U}}\subset {\mathcal {V}}$ and ${\mathcal {U}}$ is portly in X then ${\mathcal {U}}$ is portly in ${\mathcal {V}}$;

• if ${\mathcal {U}}$ is portly in ${\mathcal {V}}$ and ${\mathcal {V}}$ is portly in X then ${\mathcal {U}}$ is portly in X;

• locally portly subsets are portly (ie if $({\mathcal {U}}_i)_{i\in I}$ is a family of open subsets and for each $i\in I$, ${\mathcal {V}}_i\subset {\mathcal {U}}_i$ is a portly subset of ${\mathcal {U}}_i$, then $\bigcup _{i\in I}{\mathcal {V}}_i$ is portly in $\bigcup _{i\in I}{\mathcal {U}}_i$);

• if $X\xrightarrow {f} Y$ is a local homeomorphism and ${\mathcal {U}}\subset Y$ is portly in Y then $f^{-1}({\mathcal {U}})$ is portly in X.

• if $X\xrightarrow {f} Y$ is a continuous open surjective and ${\mathcal {U}}\subset X$ is portly in X then $f({\mathcal {U}})$ is portly in Y.

2.2 Almost everywhere (G, X)-atlases

The objects of this section are a.e. (G, X)-atlases, which are the first step toward (G, X)-structures defined almost everywhere.

Definition 2.4

An almost everywhere (G, X)-atlas on a topological space M is a (G, X)-atlas supported by some portly subset of M.

In order to avoid caveats, we need to build suitable maximality properties for such (G, X)-atlases. We can first extend the usual properties to this context. A (G, X)-atlas is complete if for all $({\mathcal {U}},{\mathcal {V}},\phi )\in {\mathcal {A}}$ and all ${\mathcal {U}}'\subset {\mathcal {U}}$ we have $({\mathcal {U}}',\phi ({\mathcal {U}}'),\phi _{|{\mathcal {U}}'}) \in {\mathcal {A}}$. We can complete any (G, X)-atlas by adding missing sub-charts; the completed atlas is still a (G, X)-atlas. In our context, a (G, X)-atlas ${\mathcal {A}}= ({\mathcal {U}}_i,{\mathcal {V}}_i,\phi _i)_{i\in I}$ is thinner than a (G, X)-atlas ${\mathcal {B}}= ({\mathcal {U}}_j',{\mathcal {V}}_j',\phi _j')_{j\in J}$ if the support of ${\mathcal {A}}$ is a subset of the support of ${\mathcal {B}}$ and for all $p\in \text {supp} {\mathcal {A}}$ and all $j\in J$ such that $p\in {\mathcal {U}}_j'$, there exists $g\in G$ and $i\in I$ such that $p\in {\mathcal {U}}_i\subset {\mathcal {U}}_j'$ and $\phi _{i} = g\circ \phi _{j|{\mathcal {U}}_i}'$. Notice that if such an ${\mathcal {A}}$ is thinner than such a ${\mathcal {B}}$, then the completion of ${\mathcal {A}}$ is still thinner than ${\mathcal {B}}$.

What we need and now provide is the flexibility to manipulate atlases that are defined up to some “negligible set” akin to the similar notion in measure theory.

Lemma 2.5

Let N be a locally connected topological space. Let $({\mathcal {B}}_k)_{k\in K}$ be a family of a.e. (G, X)-atlases on N. Assume for all $(k,k')\in K^2$, there exists an a.e. (G, X)-atlas ${\mathcal {A}}$ such that ${\mathcal {A}}$ is thinner than both ${\mathcal {B}}_{k}$ and ${\mathcal {B}}_{k'}$.

Then, the union $\bigcup _{k\in K} {\mathcal {B}}_k$ is an a.e. (G, X)-atlas.

Proof

Let $k,k'\in K$ and write ${\mathcal {B}}_k=({\mathcal {U}}_i,{\mathcal {V}}_i,\phi _i)_{i\in I(k)}$ and ${\mathcal {B}}_{k'}=({\mathcal {U}}_i,{\mathcal {V}}_i,\phi _i)_{i\in I(k')}$. Let $i\in I(k), j\in I(k')$ such that ${\mathcal {U}}_i\cap {\mathcal {U}}_j \ne \emptyset$ and let ${\widehat{{\mathcal {W}}}} \subset {\mathcal {U}}_i\cap {\mathcal {U}}_j$ be an open connected non empty subset. Let ${\mathcal {A}}$ be an a.e. (G, X)-atlas supported by some portly subset $M\subset N$ which is thinner that both ${\mathcal {B}}_{k}$ and ${\mathcal {B}}_{k'}$. Without loss of generality, we assume that ${\mathcal {A}}$ is complete.

• Consider $p\in {\widehat{{\mathcal {W}}}}\cap M$ and a chart $({\mathcal {U}},{\mathcal {V}},\phi )$ of ${\mathcal {A}}$ around p such that ${\mathcal {U}}\subset {\widehat{{\mathcal {W}}}}$. The existence of such a chart is guaranteed since ${\mathcal {A}}$ is complete and thinner than ${\mathcal {B}}_k$, ${\mathcal {B}}_{k'}$. Let ${\mathcal {W}}\subset {\mathcal {U}}$ be an open connected neighborhood of p. There exists unique $g,h\in G$ such that

  $$\begin{aligned} \phi _{|{\mathcal {W}}} =g\circ \phi _{i|{\mathcal {W}}} \quad \phi _{|{\mathcal {W}}} =h\circ \phi _{j|{\mathcal {W}}}, \end{aligned}$$

  hence

  $$\begin{aligned} \phi _{j|{\mathcal {W}}}=(h^{-1} g)\circ \phi _{i|{\mathcal {W}}}. \end{aligned}$$

  Define $g_{p,{\mathcal {U}},{\mathcal {W}}}:=h^{-1}g$ so that $\phi _{j|{\mathcal {W}}}= g_{p,{\mathcal {U}},{\mathcal {W}}}\circ \phi _{i|{\mathcal {W}}}$.

• We show that $g_{p,{\mathcal {U}},{\mathcal {W}}}$ depends neither on ${\mathcal {U}}$ nor on ${\mathcal {W}}$ nor on p.

  Fixing $p\in {\widehat{{\mathcal {W}}}}\cap M$, consider $({\mathcal {U}},{\mathcal {V}},\phi )$ and $({\mathcal {U}}',{\mathcal {V}}',\phi ')$ two charts of ${\mathcal {A}}$ on a neighborhood of p as well as ${\mathcal {W}}$ and ${\mathcal {W}}'$ two open connected neighborhoods of p in ${\mathcal {U}}$ and ${\mathcal {U}}'$ respectively. Since

  $$\begin{aligned} \forall x\in \phi _i({\mathcal {W}}\cap {\mathcal {W}}'),\quad g_{p,{\mathcal {U}},{\mathcal {W}}}(x)= \phi _j(\phi _i^{-1}(x))=g_{p,{\mathcal {U}}',{\mathcal {W}}'}(x) \end{aligned}$$

  we thus have $g_{p,{\mathcal {U}},{\mathcal {W}}}=g_{p,{\mathcal {U}}',{\mathcal {W}}'}$ so $g_p:=g_{p,{\mathcal {U}},{\mathcal {W}}}$ only depends on p. Furthermore, if $q\in {\mathcal {W}}$, we prove the same way that $g_{q,{\mathcal {U}},{\mathcal {W}}}=g_{p,{\mathcal {U}},{\mathcal {W}}}$. Finally, the map ${\mathcal {W}}\cap M\rightarrow G, p\mapsto g_p$ is locally constant. Since M is portly and since ${\widehat{{\mathcal {W}}}}$ is connected, the intersection ${\widehat{{\mathcal {W}}}} \cap M$ is connected and $p\mapsto g_p$ is constant on ${\widehat{{\mathcal {W}}}}\cap M$.

• We proved there exists $g\in G$ such that

  $$\begin{aligned} \forall x\in M\cap {\widehat{{\mathcal {W}}}}, \quad \phi _j(x)=g\circ \phi _i(x) \end{aligned}$$

  Since $\phi _i,\phi _j$ and g are continuous, X is Hausdorff and M is dense, the intersection ${\widehat{{\mathcal {W}}}}\cap M$ is then dense in ${\widehat{{\mathcal {W}}}}$ and

  $$\begin{aligned} \phi _{j|{\widehat{{\mathcal {W}}}}}=g\circ \phi _{i|{\widehat{{\mathcal {W}}}}}. \end{aligned}$$

Finally, ${\mathcal {B}}_k\cup {\mathcal {B}}_{k'}$ is an a.e. (G, X)-atlas, moreover $k,k'\in K$ are arbitrary thus $\bigcup _{k\in K} {\mathcal {B}}_k$ is an a.e. (G, X)-atlas. $\square$

Corollary 2.6

Let M be a locally connected Hausdorff topological space. Consider the set ${\mathcal {E}}$ of a.e. (G, X)-atlas ${\mathcal {A}}$ on M ordered by ${\mathcal {A}}\le {\mathcal {B}}$ if the completion of ${\mathcal {A}}$ is thinner than ${\mathcal {B}}$.

Then, for every ${\mathcal {A}} \in {\mathcal {E}}$ the maximum

$$\begin{aligned} \max \,({\mathcal {B}}~:~ {\mathcal {A}}\le {\mathcal {B}}\in {\mathcal {E}}\}) \end{aligned}$$

is well-defined.

Proof

By Lemma 2.5, this maximum is $\bigcup _{{\mathcal {B}}\ge {\mathcal {A}}}{\mathcal {B}}$. $\square$

2.3 Category of singular (G, X)-manifolds

Definition 2.7

An a.e. (G, X)-structure on a topological space M is an a.e. (G, X)-atlas on M which maximal in the sense of Corollary 2.6.

Definition 2.8

A singular (G, X)-manifold is a locally connected Hausdorff second countable topological space M endowed with an a.e. (G, X)-structure.

The support of its a.e. (G, X)-atlas is called its regular locus denoted $\text {Reg}(M)$, and the complement of $\text {Reg}(M)$ is called the singular locus denoted $\text {Sing}(M)$.

Definition 2.9

(a.e. (G, X)-morphism) Let M and N be two singular (G, X)-manifolds.

An a.e. morphism $\phi :M\rightarrow N$ is a continuous map such that there exists portly subsets ${\mathcal {U}}\subset \text {Reg}(M)$ and ${\mathcal {V}}\subset \text {Reg}(N)$ such that $\phi _{|{\mathcal {U}}}^{|{\mathcal {V}}}:{\mathcal {U}}\rightarrow {\mathcal {V}}$ is a (G, X)-morphism.

Remark 2.10

Composition of a.e. (G, X)-morphisms is an a.e. (G, X)-morphism. The category ${\textbf {SingGX}}$ of singular (G, X)-manifold, which morphisms are a.e. (G, X)-morphisms, is then well defined. Isomorphisms of singular (G, X)-manifolds are then maps that are both homeomorphisms and a.e. (G, X)-morphisms.

Remark 2.11

A.e. (G, X)-morphisms are analytical: if two are equal on an open set, they are equal everywhere.

Remark 2.12

Let $M\rightarrow N$ be a continuous map between singular (G, X)-manifolds. The following properties are equivalent.

• (i) f is an a.e. (G, X)-morphism;

• (ii) f is locally an a.e. (G, X)-morphism;

• (iii) $f_{|{\mathcal {U}}}$ is an a.e. (G, X)-morphism for some portly set ${\mathcal {U}}\subset M$.

Lemma 2.13

Let M and N be singular (G, X)-manifolds and let $f:M\rightarrow N$ an be a.e. (G, X)-morphism. Let ${\mathcal {E}}$ be the set of open subsets ${\mathcal {U}}\subset \text {Reg}(M)$ such that $f({\mathcal {U}})\subset \text {Reg}(N)$ and $f_{|{\mathcal {U}}}^{|\text {Reg}(N)}$ is a (G, X)-morphism.

Ordered by the inclusion, ${\mathcal {E}}$ has a maximum.

Proof

Let ${\mathcal {U}}_0:=\bigcup _{{\mathcal {U}}\in {\mathcal {E}}}{\mathcal {U}}$, the map $f_{|{\mathcal {U}}_0}^{|\text {Reg}(N)}$ is locally a (G, X)-morphism hence a (G, X)-morphism. Finally, ${\mathcal {U}}_0\in {\mathcal {E}}$ is certainly the maximum. $\square$

Definition 2.14

Let M and N be singular (G, X)-manifolds and let $f:M\rightarrow N$ an a.e. (G, X)-morphism. The maximal open subset of M on which f induces a (G, X)-morphism is the regular locus of f, which we denote by $\text {Reg}(f)$.

The following properties give characterizations of $\text {Reg}(f)$ in typical situations, limiting what can go wrong.

Lemma 2.15

Let M and N be singular (G, X)-manifolds and let $f:M\rightarrow N$ an a.e. (G, X)-morphism. Then,

$$\begin{aligned} \text {Reg}(f)=\text {Reg}(M)\cap f^{-1}(\text {Reg}(N)). \end{aligned}$$

Proof

The left-hand side is clearly included in the right-hand side. Via restrictions to charts, it suffices to prove the special case of $N=X$ hence $M=f^{-1}(\text {Reg}(N))$.

Let $x\in \text {Reg}(M)$ and let $({\mathcal {U}},{\mathcal {V}},\varphi )$ be a connected chart around x. The map $f\circ \varphi ^{-1}$ induces a (G, X)-morphisms from $\varphi ({\mathcal {U}}\cap \text {Reg}(f))$ to X. Since $\text {Reg}(f)$ is locally connected in M and ${\mathcal {U}}$ is connected, $\varphi ({\mathcal {U}}\cap \text {Reg}(f))$ is also connected and there exists a unique $g\in G$ such that

$$\begin{aligned} \forall y\in \varphi ({\mathcal {U}}\cap \text {Reg}(f)),\quad f\circ \varphi ^{-1}(y)=g(y). \end{aligned}$$

Since $\varphi :{\mathcal {U}}\rightarrow {\mathcal {V}}$ is a homeomorphism and ${\mathcal {U}}\cap \text {Reg}(f)$ is dense in ${\mathcal {U}}$, then $\varphi (\text {Reg}(f)\cap {\mathcal {U}})$ is dense in ${\mathcal {V}}$. Since $f\circ \varphi ^{-1}$ is continuous, we have

$$\begin{aligned} \forall y\in {\mathcal {U}},\quad f(y)=g\circ \varphi (y). \end{aligned}$$

Finally, f is a regular on ${\mathcal {U}}$. The result follows. $\square$

Lemma 2.16

Let $M\xrightarrow {f} N$ be a continuous map with M locally connected Hausdorff topological space and N a singular (G, X)-manifold.

If f is a.e. a local homeomorphism, there exists a unique a.e. (G, X)-structure on M such that f is an a.e. (G, X)-morphism.

Proof

Let ${\mathcal {O}}\subset M$ and ${\mathcal {P}}\subset \text {Reg}(N)$ both portly such that $f_{|{\mathcal {O}}}^{|{\mathcal {P}}}$ is a local homeomorphism.

By usual results, there exists a unique a.e. (G, X)-structure ${\mathcal {A}}$ supported on ${\mathcal {O}}$ such that $f_{|{\mathcal {O}}}^{|{\mathcal {P}}}$ is a (G, X)-morphism. Since ${\mathcal {O}}, {\mathcal {P}}$ are portly, we thus defined an a.e. (G, X)-structure on M such that f in an a.e. (G, X)-morphism.

Assume that M is endowed with an a.e. (G, X)-structure ${\mathcal {B}}$ supported on some portly subset ${\mathcal {O}}'\subset M$ such that $f_{|{\mathcal {O}}'}^{|{\mathcal {P}}}$ is a (G, X)-morphism. In particular $f_{|{\mathcal {O}}'\cap {\mathcal {O}}}^{|f({\mathcal {O}}'\cap {\mathcal {O}})}$ is a (G, X)-morphism, therefore the ${\mathcal {A}}_{|{\mathcal {O}}'\cap \mathcal O}={\mathcal {B}}_{|{\mathcal {O}}'\cap {\mathcal {O}}}$. By Corollary 2.6 and maximality ${\mathcal {A}}={\mathcal {B}}$ and ${\mathcal {O}}={\mathcal {O}}'$. $\square$

Definition 2.17

With the notations of Lemma 2.16, the unique a.e. (G, X)-structure $f^*{\mathcal {A}}$ on M is called the pullback by f of the a.e. (G, X)-structure ${\mathcal {A}}$ of N.

Corollary 2.18

Let $L\xrightarrow {f}M\xrightarrow {g} N$ be locally connected, Hausdorff topological space. And let ${\mathcal {A}}$ be an a.e. (G, X)-structure on N. Then $f^*g^*{\mathcal {A}}= (g\circ f)^*{\mathcal {A}}$.

Lemma 2.19

Let M and N be singular (G, X)-manifolds and let $f:M\rightarrow N$ an a.e. (G, X)-morphism. Then,

$$\begin{aligned} \text {Reg}(f)=\text {Reg}(M)\cap \{x\in M ~|~ f \text { is a local homeomorphism around }x\} \end{aligned}$$

Proof

By definition, $\text {Reg}(f)\subset \text {Reg}(M)$, furthermore a (G, X)-morphism is always a local homeomorphism; therefore, the left-hand side is included in the right-hand side. Furthermore, let ${\mathcal {A}},{\mathcal {B}}$ be the a.e. (G, X)-atlases of M, N respectively. Since f is a.e. a (G, X)-morphism, then it is a.e. a local homeomorphism; we may thus apply Lemma 2.16 to show that $f^*{\mathcal {B}}= {\mathcal {A}}$. In particular, if $f_{|{\mathcal {U}}}^{|{\mathcal {V}}}$ is an homeomorphism for some ${\mathcal {U}},{\mathcal {V}}$ then $\text {Reg}({\mathcal {U}}) = f^{-1}(\text {Reg}({\mathcal {V}}))\cap {\mathcal {U}}$ and $f:\text {Reg}({\mathcal {U}})\rightarrow \text {Reg}({\mathcal {V}})$ is a (G, X)-morphism. Therefore, if f is a local homemorphism around x and in $\text {Reg}(M)$ then $x\in \text {Reg}({\mathcal {U}})$ for a ${\mathcal {U}}$ such as above thus f is (G, X)-morphism around x and $x\in \text {Reg}(f)$. $\square$

Corollary 2.20

If an a.e. (G, X)-morphism is also a local homeomorphism, then it preserves both regular and singular loci.

Remark 2.21

As a consequence, an isomorphism $M\xrightarrow {f} N$ of singular (G, X)-manifolds is an isomorphism of almost everywhere (G, X)-atlas in the sense that given the maximal almost everywhere (G, X)-atlases ${\mathcal {A}}$ and ${\mathcal {B}}$ of M and N respectively, the pullback $f^*{\mathcal {B}}$ and ${\mathcal {A}}$ are equal. It is then an isomorphism in every natural way relative to singular (G, X)-manifolds.

2.4 Common construction of singular (G, X)-manifolds

From the literature, we can list common construction leading to “informal” singular (G, X)-manifolds:

• branched coverings;

• gluings of projective polyhedron; [1, 6, 10, 12, 17]

• a quotient of some (G, X)-manifold M by some discrete group $\varGamma$ acting via (G, X)-morphisms [34];

• suspensions [5, 47];

• completions [17]

Branched coverings will be studied more thoroughly in the following sections. When $X\subset \mathbb {R}P^n$ and $G\subset \text {PGL}(n+1; {\mathbb {R}})$, gluings of projective polyhedra via elements of G have a natural (G, X)-structure on the complement of the $(n-2)$-skeleton. The latter being skeletal, such gluings are singular (G, X)-manifolds with our definitions. This includes, in particular, most usual Lie group actions, such as semi-Riemannian isometry groups, as well as conformal and symplectic actions. We will not cover completions.

2.4.1 Quotients

The first example that comes to mind is the following.

Example 2.22

Consider $X=M = {\mathbb {E}}^n$ and $G=\text {Isom}^+({\mathbb {E}}^n)$ identifying ${\mathbb {E}}^n$ with ${\mathbb {R}}^n$ and $n\in {\mathbb {N}}_{\ge 2}$. The point-wise stabilizer of $S = {\mathbb {R}}^{n-2}\times \{(0,0)\}$ is isomorphic to $\textrm{SO}(2;{\mathbb {R}})$, we choose $\varGamma \subset \text {Stab}(S)$ a finite group of rotations of order p. The group $\varGamma$ acts freely on $M{\setminus } S$, which is portly; therefore, the quotient $\varGamma \backslash M$ has a natural singular (G, X)-structure. The metric on $\text {Reg}(\varGamma \backslash M)$ extends continuously to $\varGamma \backslash M$. As a metric space $\varGamma \backslash M$ is isomorphic to ${\mathbb {E}}^n_ {2\pi /p}$ described in Example 2.1.

Variations on this example can be done either by replacing X with another Riemannian spaceform such as ${\mathbb {H}}^n$ or ${\mathbb {S}}^n$. More generally, one can take a submodel of the projective model space: $X \subset {\mathbb {K}} P^n$ and $G \subset \text {PGL}(n;{\mathbb {K}})$ for ${\mathbb {K}} \in \{{\mathbb {R}},\mathbb C\}$ with G preserving X.

We can relate this example to a known⁵ result for regular (G, X)-manifolds.

Proposition 2.23

Let M be a (G, X)-manifold and let $\varGamma$ be a discrete group acting freely and properly discontinuously on M. Then, there exists a unique (G, X)-structure on $\varGamma \backslash M$ such that the natural projection $M\rightarrow \varGamma \backslash M$ is a (G, X)-morphism.

In the example above, the action is not free, and the singular locus of the quotient corresponds to the “non-free locus”: the projection of the set of points of nontrivial stabilizer. Nonetheless, we may extend the last Proposition to a.e. (G, X)-manifolds.

Proposition 2.24

Let M be a singular (G, X)-manifold, and let $\varGamma$ be a discrete group acting properly discontinuously on M by a.e. (G, X)-morphisms.

If there exists a portly $\varGamma$-invariant subset ${\mathcal {U}}$ on which $\varGamma$ acts freely then $\varGamma \backslash M$ has a unique a.e. (G, X)-structure such that the natural projection $M \rightarrow \varGamma \backslash M$ is an a.e. (G, X)-morphism.

Proof of Proposition 2.24

By assumption, the quotient $\varGamma \backslash M$ is Hausdorff. Furthermore, the projection $M \xrightarrow {\pi } \varGamma \backslash M$ is open; hence, as an open quotient of a locally connected and second countable space, $\varGamma \backslash M$ is locally connected and second countable. Let ${\mathcal {U}}\subset M$ be a portly $\varGamma$-invariant subset on which $\varGamma$ acts freely, since $\varGamma$ acts by a.e. (G, X)-morphisms, in particular $\varGamma$ preserves $\text {Reg}({\mathcal {U}})$. By Proposition 2.23, the quotient $\varGamma \backslash \text {Reg}({\mathcal {U}})$ admits a unique (G, X)-structure such that $\pi _{|\text {Reg}({\mathcal {U}})}^{|\varGamma \backslash \text {Reg}({\mathcal {U}})}$ is a (G, X)-morphism. Since $\pi$ is open and surjective, the image of a portly subset of M is a portly subset of $\varGamma \backslash M$; in particular, $\pi (\text {Reg}({\mathcal {U}}))$ is portly. Therefore, the (G, X)-structure on $\varGamma \backslash \text {Reg}({\mathcal {U}})$ induces an a.e. (G, X)-structure ${\mathcal {A}}$ on $\varGamma \backslash M$ for which $\pi$ is an a.e. (G, X)-morphism.

If $\varGamma \backslash M$ is endowed with some other a.e. (G, X)-structure ${\mathcal {B}}$ for which $\pi$ is an a.e. (G, X)-morphism then $\pi _{|{\mathcal {V}}}^{|\text {Reg}({\mathcal {B}})}$ is a (G, X)-morphism for some portly subset ${\mathcal {V}}\subset \text {Reg}(M)$ and thus $\pi _{|{\mathcal {U}}\cap {\mathcal {V}}}^{|\text {Reg}({\mathcal {B}})\cap \text {Reg}({\mathcal {A}})}$ is a (G, X)-morphism both for ${\mathcal {A}}$ and ${\mathcal {B}}$. In particular, on the portly subset $\pi ({\mathcal {U}}\cap {\mathcal {V}})\subset \text {supp}({\mathcal {A}})\cap \text {supp}({\mathcal {B}})$, the two (G, X)-structures agree. By Lemma 2.5 and maximality of ${\mathcal {A}}$ and ${\mathcal {B}}$, we conclude that ${\mathcal {A}}={\mathcal {B}}$. $\square$

Example 2.25

Consider ${\mathbb {D}}_{\infty }$ the topological space $\{(r,\theta )\in {\mathbb {R}}_{+}\times {\mathbb {R}}~|~ r>0 \text { or } \theta = 0\}$ endowed witht the topology generated by the usual one on ${\mathbb {R}}_+^*\times {\mathbb {R}}$ and open subsets $\{(r,\theta ) \in \mathbb D_{\infty } ~|~ r<r_0\}$ for $r_0>0$. We may refer to the space ${\mathbb {D}}_\infty$ as the “infinite angle disc.”

The infinite angle cylinder, the space ${\mathbb {C}}_\infty ^{(n)}:={\mathbb {D}}_\infty \times {\mathbb {R}}^n$, can be endowed with an a.e. affine structure for some choice $G\subset \text {Aff}({\mathbb {R}}^n)$ and $X\subset {\mathbb {R}}^n$ via pullback by a local homeomorphism ${\mathcal {D}}: \{r>0\}\rightarrow X$. We call this singular (G, X)-manifold ${{\widetilde{M}}}$ and naturally, $\text {Sing}({{\widetilde{M}}})\subset \{r=0\}$.

Take $\varGamma _\alpha ={\mathbb {Z}}$ acting on ${{\widetilde{M}}}$ via $k\cdot (r,\theta ,z)= (r,\theta +k\alpha ,z)$ for some $\alpha \in {\mathbb {R}}_+^*$, assume that $\varGamma _\alpha$ acts via a.e. (G, X)-morphisms, then $M:=\varGamma _\alpha \backslash {{\widetilde{M}}}$ is naturally a singular (G, X)-manifold homeomorphic to ${\mathbb {R}}^n$ endowed with cylindrical coordinates. Its singular locus is $\text {Sing}(M) = \{r=0\}$.

Consider the special case $X={{\mathbb {E}}}^{1,2}_{}$ eg ${\mathbb {R}}^3$ endowed with the bilinear form $Q(t,x,y)=x^2+y^2-t^2$ of signature (2, 1); with $G = \text {Isom}_0(X)$ the identity component of the affine isometry group. ${{\mathbb {E}}}^{1,2}_{}$ is the 3-dimensional Minkowski space and G the group of isometries preserving both orientation and time orientation (see Sects. 5.1 and 5.2 for more details). We can recover several instances of Lorentzian singularities [5, 11] for different choices of ${\mathcal {D}}$.

• ${\mathcal {D}}(r,\theta ,z) = (z+\sigma \theta /\alpha , r\cos (\theta /\alpha ),r\sin (\theta /\alpha ))$ then M is the so-called massive particle of mass $m=1-\alpha /2\pi$ and spin $\sigma$.

• Consider

  $$\begin{aligned} {\mathcal {D}}\left( r,\theta ,t\right) = P_\theta \cdot (x_0+rv + t u) \end{aligned}$$

  with $x_0\in X$ arbitrary, $(P_\theta )_{\theta \in {\mathbb {R}}}$ the 1-parameter family of parabolic isometries fixing point wise $x_0+{\mathbb {R}}u$ some future lightlike vector and $\langle v|u\rangle <0$. Then M is a so-called extreme BTZ whitehole that we shall focus on in Sect. 5. Choosing ${\mathcal {D}}'(r,\theta ,t) = {\mathcal {D}}(r,\theta ,-t)$ gives an extreme BTZ blackhole instead.

• Variations allow to construct so-called Misner particles, BTZ white/blackholes. It suffices to choose u spacelike instead and v spacelike or future/past timelike, respectively.

So-called tachyons (resp. photons) can be obtained as variations of the above example with a hyperbolic (resp. parabolic) action of $\varGamma ={\mathbb {Z}}$ on the coordinate $\theta$ with the identification ${\mathbb {D}}_\infty = {\mathbb {R}}_+^*\times \widetilde{{\mathbb {R}}{\mathbb {P}}^1} \cup \{(0,0)\}$.

All these examples can also be obtained via gluings of polyhedra.

Remark 2.26

The previous examples are instances of developing maps defined on the universal covering of some singular space branched over its singular locus. This is the archetype we will describe with more precisions in Sect. 4.

2.4.2 Suspensions

One can construct conical singularities (without spin) iteratively following a method of Thurston [47].

• 1. Let us say that any compact $({\mathbb {S}}^1,\text {SO}(2))$-manifold is regular, so there is no singular model to construct.

• 2. Assume you have constructed local models of singularities in $({\mathbb {S}}^n,\text {SO}(n+1))$-manifolds. A $({\mathbb {S}}^n,\text {SO}(n+1))$-manifold with conical singularities is then a metric space locally isometric to either of the local models.

• 3. You can then construct local model of singularity for $({\mathbb {S}}^{n+1},\text {SO}(n+2))$.

  • (a) Take a $({\mathbb {S}}^n,\text {SO}(n+1))$-manifold M with conical singularities and with M homeomorphic to ${\mathbb {S}}^n$, denote its Riemannian metric by ${{\textbf {g}}}$ which is defined on the complement of the singularities;

  • (b) Define the suspension of M by ${\widehat{M}} = (M\times {\mathbb {R}}_+)/\sim$ the set of $(\theta ,r)$ where $(\theta _1,0)\sim (\theta _2,0)$ for all $\theta _1,\theta _2\in M$;

  • (c) Endow ${\widehat{M}}$ with a Riemannian metric

    $$\begin{aligned} \widehat{{{\textbf {g}}}}(\theta ,r) = {\textbf {d r}}\otimes {\textbf {d r}}+ \sin (r)^2 {{\textbf {g}}}(\theta ) \end{aligned}$$

    which is “regular”, eg locally isometric to ${\mathbb {S}}^{n+1}$, on rays through “regular” points of M.

This way, we obtain usual conical singularities in dimension 2, then so-called “collisions” of conical lines in dimension 3, etc.

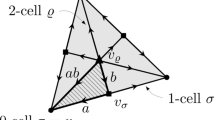
From $({\mathbb {S}}^{n-1},\text {SO}(n))$-manifolds with conical singularities one can construct conical local models for $({\mathbb {H}}^n,SO(n,1))$ and $({\mathbb {E}}^n, {\mathbb {R}}^n\times \text {SO}(n))$ replacing $\sin (r)^2$ by $\sinh ^2(r)$ and $r^2$ respectively in the formula for Riemannian metric of the suspension above. One can show that gluings of finitely many Spherical (or Euclidean or hyperbolic) polyhedra give rise to such singularities on the codimension $k\ge 2$ skeletons of the underlying simplicial complex.

We are led to the following definition.

Definition 2.27

(Topological suspension) Let $\varSigma$ be a topological space; the topological suspension of $\varSigma$ is

$$\begin{aligned} \text {susp}(\varSigma ):= (\varSigma \times {\mathbb {R}}_+)/{\sim } \end{aligned}$$

where $(\sigma ,r) \sim (\sigma ',r')$ if $r=r'=0$; endowed with the topology generated by the quotient topology on $\{r>0\}$ and the image of $\varSigma \times [0,\varepsilon [$ for $\varepsilon >0$. We also define $O:= \{r=0\}$.

Remark 2.28

One may check that the suspension preserves Hausdorff as well as the first and second countable properties.

Remark 2.29

The infinite angle disc ${\mathbb {D}}_\infty$ is the suspension of ${\mathbb {R}}$.

Counter-Example 2.30

The topology we chose is the same as the quotient topology if $\varSigma$ is compact; however, the suspension $\text {susp}({\mathbb {R}})$ endowed with the quotient topology is not first countable. Indeed, a basis of open neighborhoods of O is given by ${\mathcal {U}}_f:= \{(\theta ,r)~|~ r<f(\theta )\}$ for $f:{\mathbb {R}}\rightarrow {\mathbb {R}}_+^*$ continuous. For any sequence $(f_n)_{n\in {\mathbb {N}}}$ we may construct $g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ continuous and such that $\forall n\in {\mathbb {N}}, g(n):= \frac{1}{2}\min (f_k: k\le n )$. This way, which proves $({\mathcal {U}}_{f_n})_{n\in {\mathbb {N}}}$ is not a basis of neighborhoods of O.

Remark 2.31

The topological suspension is, in fact, a functor from the category of topological space to itself, as continuous maps can be extended radially in a natural way. Suspension preserves injectivity, surjectivity, and embeddings.

Geometrical suspension as above can be described abstractly as a lift of the topological suspension functor $\text {susp}$

where (G, X) and (H, Y) are analytical structures, and the vertical arrows are the forgetful functor. Thurston method provides a functors ${\textbf {Sing}}\varvec{{\mathbb {S}}}^n \rightarrow {\textbf {Sing}}\varvec{{\mathbb {S}}}^{n+1}$ and Bonsante, Barbot, Schlenker [5] generalized to a functor ${\textbf {Sing}}\varvec{\mathbb{H}\mathbb{S}}^2 \rightarrow {\textbf {Sing}}\varvec{{\mathbb {E}}}^{1,2}$ where $\mathbb{H}\mathbb{S}^2:=({{\mathbb {E}}}^{1,2}_{}{\setminus }\{O\})/{\mathbb {R}}_+^*$ is the space of rays from the origin in ${{\mathbb {E}}}^{1,2}_{}$ with automorphism group $G:=\text {SO}_0(1,2)$. For these suspensions, the image of regular (G, X)-manifolds are regular except possibly at O and are regular at O if and only if $\varSigma$ is homeomorphic to a sphere.⁶

To ensure that iterated suspensions described above are of this type, we need to prove the following.

Proposition 2.32

Let $\varSigma$ be a Hausdorff, connected, locally connected topological space and let ${\mathcal {U}}\subset \varSigma$ be a portly subset. Then $\text {susp}({\mathcal {U}}){\setminus } \{O\}$ is a portly subset of $\text {susp}(\varSigma )$.

Let us to recall a classical connectivity Lemma, the proof of which is omitted.

Lemma 2.33

Let M be a topological space and let $({\mathcal {U}}_i)_{i\in I}$ be a nonempty family of nonempty connected open subset. Define on I the equivalence relation $\sim$ generated by $i\sim j$ if ${\mathcal {U}}_i\cap {\mathcal {U}}_j \ne \emptyset$.

The $\bigcup _{i\in I} {\mathcal {U}}_i$ is connected if and only if $I/\sim$ is a singleton.

Proof of Proposition 2.32

Let $\pi : \varSigma \times {\mathbb {R}}_+ \rightarrow \text {susp}(\varSigma )$ be the natural projection and define ${\mathcal {V}}:= \text {susp}({\mathcal {U}}){\setminus }\{O\}$. We also introduce $\psi : \text {susp}(\varSigma ){\setminus } \{O\} \rightarrow \varSigma$ induced by the projection $\varSigma \times {\mathbb {R}}_+^* \rightarrow \varSigma$. Notice that $\pi _{|\varSigma \times {\mathbb {R}}_+^*}$ is an embedding, therefore ${\mathcal {V}}= \pi ({\mathcal {U}}\times {\mathbb {R}}_+^*)$ is open. Since ${\mathcal {U}}$ is dense in $\varSigma$ and since $\psi$ is open, then ${\mathcal {V}}= \psi ^{-1}({\mathcal {U}})$ is dense in $\text {susp}(\varSigma ){\setminus } \{O\}$. For any neighborhood ${\mathcal {W}}$ of $\{O\}$ and for all $\sigma \in \varSigma$, for r small enough $\pi (\sigma ,r)\in {\mathcal {W}}$; then O is also in the closure of ${\mathcal {V}}$ and ${\mathcal {V}}$ is dense in $\text {susp}(\varSigma )$.

Let ${\mathcal {W}}$ be a connected open subset of $\text {susp}(\varSigma )$.

• Assume that $O\notin {\mathcal {W}}$. We may write ${\mathcal {W}}= \bigcup _{i\in I} {\mathcal {W}}_i$ with ${\mathcal {W}}_i = \pi ({\widehat{{\mathcal {W}}}}_i\times ]r_i,r_i'[)$, $0<r_i<r_i'$ and ${\widehat{{\mathcal {W}}}}_i$ open subset of $\varSigma$. Since $\varSigma$ is locally connected, we assume without loss of generality that each ${\widehat{{\mathcal {W}}}}_i$ is connected. Denote by $\sim _1$ the equivalence relation defined in Lemma 2.33 for the family $({\mathcal {W}}_i)_{i\in I}$ so that $I/\sim _1$ is singleton.

  Then consider the family $({\mathcal {W}}_i\cap {\mathcal {V}})_{i\in I}$ and define $\sim _2$ the associated equivalence relation on I. On the one hand, if ${\mathcal {W}}_i \cap {\mathcal {W}}_j\ne \emptyset$ then by density of ${\mathcal {V}}$ we have $({\mathcal {W}}_i\cap {\mathcal {V}}) \cap ({\mathcal {W}}_j\cap {\mathcal {V}}) = ({\mathcal {W}}_i\cap {\mathcal {W}}_j)\cap {\mathcal {V}}\ne \emptyset$. Therefore, $\sim _1$ and $\sim _2$ are equal, so $I/\sim _2=I/ \sim _1$ is a singleton.

  Furthermore, ${\mathcal {W}}_i\cap {\mathcal {V}}= \pi (({\widehat{{\mathcal {W}}}}_i \cap {\mathcal {U}}) \times ]r_i,r_i'[)$; since ${\mathcal {W}}_i$ is connected and ${\mathcal {U}}$ portly, $\widehat{\mathcal {W}}_i\cap {\mathcal {U}}$ is connected and so is ${\mathcal {W}}_i\cap {\mathcal {V}}$. Again by Lemma 2.33, ${\mathcal {W}}\cap {\mathcal {V}}= \bigcup _{i\in I} ({\mathcal {W}}_i\cap {\mathcal {V}})$ is connected.

• Assume that $O\in {\mathcal {W}}$, to reduce to the previous case, it suffices to prove that ${\mathcal {W}}{\setminus } \{O\}$ is connected too. Consider ${\mathcal {O}} = \pi (\{(\sigma ,r) ~:~ \sigma \in \varSigma ,~ r\in [0,f(\sigma )[\})$ with $f(\sigma ):=\sup \{r^*>0 ~|~ \forall r<r^*,~\pi (\sigma ,r)\in {\mathcal {W}}\}$. Note that, since ${\mathcal {W}}$ is open, $\forall \sigma \in \varSigma ,~ (\sigma ,f(\sigma ))\notin {\mathcal {W}}$.

  Assume that f is not lower semi-continuous, then (since $\varSigma$ is first countable) there exists some $\sigma \in \varSigma$ and some sequence $\sigma _n\rightarrow \sigma$ such that $\ell :=\lim f(\sigma _n)<f(\sigma )$. The sequence $\pi (\sigma _n,f(\sigma _n))$ converges toward $(\sigma ,\ell ) \in {\mathcal {W}}$ but $\forall n\in {\mathbb {N}}, \pi (\sigma _n,f(\sigma _n)) \notin {\mathcal {W}}$. Contradiction, f is thus lower semi-continuous.

  We may thus construct some neighborhood ${\mathcal {W}}_O$ of O in ${\mathcal {W}}$ such that ${\mathcal {W}}_O = \bigcup _{i\in J} \pi ({\widehat{{\mathcal {W}}}}_j \times [0,r_j[)$ with ${\widehat{{\mathcal {W}}}}_j$ connected and open. We notice that $\bigcup _{k\in J} {\widehat{{\mathcal {W}}}}_j = \varSigma$ is connected, that the relation $\sim$ on j in Lemma 2.33 for the families $({\widehat{{\mathcal {W}}}}_j)_{j\in J}$, $({\mathcal {W}}_j)_{j\in J}$ and $({\mathcal {W}}_j{\setminus } \{O\})_{j\in J}$ are equal. Since every $\widehat{\mathcal {W}}_j, j\in J$ is connected, so are the ${\mathcal {W}}_j{\setminus } \{O\}$; we deduce that ${\mathcal {W}}_O{\setminus } \{O\}$ is connected.

  Write ${\mathcal {W}}{\setminus } \{O\} = \bigcup _{k\in K\cup \{O\}} ({\mathcal {W}}_k{\setminus } \{O\})$ with $({\mathcal {W}}_k)_{k\in K}$ the family of connected component of ${\mathcal {W}}{\setminus } \{O\}$, in particular $\forall k\in K, {\mathcal {W}}_k{\setminus } \{O\}={\mathcal {W}}_k$. Since ${\mathcal {W}}$ is connected, for all $k\in K$, we have $({\mathcal {W}}_k{\setminus } \{O\}) \cap ({\mathcal {W}}_O {\setminus } \{O\})={\mathcal {W}}_k\cap {\mathcal {W}}_O \ne \emptyset$. We may apply Lemma 2.33 again to conclude that ${\mathcal {W}}{\setminus } \{O\}$ is connected.

$\square$

Remark 2.34

The proof above works for the quotient topology.

3 Branched coverings à la Fox: spreads, paths and Galois

Although some of the results of this section may be proven with more generality, all topological spaces are Hausdorff, locally path-connected, and first countable unless explicitly stated otherwise.

In this section, we recall fundamentals on spreads and branched coverings with some enrichments. Considering those will be needed later on, we prefer to lay out a solid foundation and provide most of the proofs. Some results presented in Sects. 3.1 and 3.2, though not found in the literature by the author, are probably “folkloric”. Our presentation is in part redundant with [36,37,38,39], but our different purposes lead to divergences. For instance, to our knowledge, Lemma 3.23 and Proposition 3.24 are new.

To the author’s knowledge, the path representation of maximal branched coverings⁷ presented in Sect. 3.3 as well as the topological characterization of Galoisian maximal branched coverings presented in Sect. 3.4 are both new. The former is a natural extension of the usual description of the universal covering as a space of paths to branched coverings. The critical point is the introduction of the adequate homotopy equivalence relation: almost-homotopic loops. An extension of the classical semi-local simple connectedness notion based on almost-homotopy equivalence is then introduced and shown to characterize branching locus giving rise to Galoisian coverings, which is described in Sect. 3.4. Examples and counter-examples are given throughout the section.

3.1 Preliminaries on spreads

Definition 3.1

(Category of spreads) A spread $X\xrightarrow {p} Y$ is a continuous map such that the topology of X is generated by the connected components of the preimages of open subsets of Y.

We define the category of spreads ${\textbf {Spr}}$ whose objects are spreads and morphisms in $\text {Hom}(X\xrightarrow {p} Y, X'\xrightarrow {p'} Y')$ are couples of continuous functions (f, g) such that the following diagram commutes

Remark 3.2

Let $X\xrightarrow {p} Y$ be a spread, with ${\mathcal {U}},{\mathcal {V}}$ open of X and Y respectively such that $p({\mathcal {U}})\subset {\mathcal {V}}$, the (co)restriction $p_{|{\mathcal {U}}}^{|{\mathcal {V}}}$ is a spread.

Definition 3.3

Let $X\xrightarrow {p} Y$ be a continuous map, the ordinary locus $\text {Ord}_p(Y)$ of Y is the set of point $y\in Y$ for which there exists an open neighborhood ${\mathcal {U}}$ evenly covered by p ie, such that p maps each connected component of $p^{-1}({\mathcal {U}})$ homeomorphically onto ${\mathcal {U}}$. The ordinary locus $\text {Ord}_p(X)$ of X is the preimage of the ordinary locus of Y.

We will write $\text {Ord}$ instead of $\text {Ord}_p$ when there is no ambiguity.

Remark 3.4

The ordinary loci are open but may not be connected. The only obstruction for the restriction $\text {Ord}(X)\rightarrow \text {Ord}(Y)$ to be a covering is the connectedness of $\text {Ord}(X)$.

Remark 3.5

Let $X\xrightarrow {p}Y$ be a surjective continuous map. Then

$$\begin{aligned} p(X{\setminus } \text {Ord}(X)) = Y{\setminus } \text {Ord}(Y). \end{aligned}$$

Lemma 3.6

Let $X\xrightarrow {p} Y$ be a continuous map inducing a covering $X_1\rightarrow Y_1$ for some $X_1\subset X$ and $Y_1\subset Y$ with $X_1$ portly and $Y_1$ open.

Then $Y_1\subset \text {Ord}(Y)$, $X_1 \subset \text {Ord}(X)$ and $p^{-1}(Y_1)=X_1$.

Proof

Let $y\in Y_1$ and let ${\mathcal {U}}\subset Y_1$ be an open neighborhood of y evenly covered by $p_{|X_1}^{|Y_1}$ ie

$$\begin{aligned} p^{-1}({\mathcal {U}})\cap X_1 = \left( p_{|X_1}^{|Y_1}\right) ^{-1}({\mathcal {U}})=\bigsqcup _{i\in I} {\mathcal {V}}_i \end{aligned}$$

with ${\mathcal {V}}_i$ open connected and $p_{|{\mathcal {V}}_i}^{|{\mathcal {U}}_i}$ homeomorphisms for all $i\in I$.

Assume by contradiction there exists some $x\in p^{-1}({\mathcal {U}}){\setminus } X_1$, consider some connected open subset ${\mathcal {V}}$ such that $x\in {\mathcal {V}}\subset p^{-1}({\mathcal {U}})$. Since $X_1$ is portly, ${\mathcal {V}}\cap X_1$ is connected and dense in ${\mathcal {V}}$, thus ${\mathcal {V}}\cap X_1 \subset {\mathcal {V}}_i$ for some $i\in I$ and $x\in \overline{{\mathcal {V}}_i}$. Let $x':= (p_{|{\mathcal {V}}_i}^{|{\mathcal {U}}})^{-1}\circ p(x)$ and let ${\mathcal {W}},{\mathcal {W}}'$ disjoint open neighborhoods of x and $x'$ respectively with ${\mathcal {W}}'\subset {\mathcal {V}}_i$. Since $p(x) \in p({\mathcal {W}}')$ which is open, there exists some open neighborhood ${\mathcal {W}}''\subset {\mathcal {W}}$ of x such that $p({\mathcal {W}}'')\subset p({\mathcal {W}}')$. Therefore, $\emptyset \ne p({\mathcal {W}}''\cap {\mathcal {V}}_i) \subset p({\mathcal {W}}')=p({\mathcal {W}}'\cap {\mathcal {V}}_i)$. This contradicts injectivity on $p_{|{\mathcal {V}}_i}$, hence $p^{-1}({\mathcal {U}})\subset X_1$ and ${\mathcal {U}}$ is evenly covered by p. In particular, $p^{-1}(Y_1) = X_1$.

Therefore, $Y_1\subset \text {Ord}(Y)$ and $\text {Ord}(X) = p^{-1}(\text {Ord}(Y)) \supset p^{-1}(Y_1) = X_1$ $\square$

Though not the core of the present work, for pedagogical purposes, we provide counter-examples to Lemma 3.6 we feel help understand some caveats when dealing with spreads.

Counter-Example 3.7

The conclusion of Lemma 3.6 fails if $Y_1$ is not open.

Consider $X = {\mathbb {R}}\times \{0\}$ and $Y = {\mathbb {R}}^2$ with p the inclusion map. p is a continuous map (it is even a spread) and induces a covering $X\rightarrow X \subset Y$ but $\text {Ord}(Y)=\emptyset$.

Counter-Example 3.8

The conclusion of Lemma 3.6 fails if $X_1$ is not portly.

• If $X_1$ is not open, then take $x \in X_1{\setminus } Int(X_1)$, for a neighborhood ${\mathcal {V}}$ of x small enough, the set ${\mathcal {V}}\cap X_1$ is mapped homeomorphically to some open neighborhood ${\mathcal {U}}$ of p(x). For ${\mathcal {V}}$ small enough, $p({\mathcal {V}})\subset {\mathcal {U}}$ thus $p({\mathcal {V}}{\setminus } X_1) \cap p({\mathcal {V}}\cap X_1)\ne \emptyset$. In other words, p is not injective in any neighborhood of x. In particular, $p(x)\notin \text {Ord}(Y)$ and $x\notin \text {Ord}(X)$.

• Take $X\subset Y={\mathbb {R}}^2$ with the Euclidean norm, $X=\{x~|~\Vert x\Vert \ge 1\} \cup \{\lambda x ~|~ \lambda \in ]0,1], \Vert x\Vert =1, x\in {\mathbb {Q}}^2\}$. Endow Y with its usual topology but X with the coarsest topology making the natural injection $X\rightarrow Y$ a spread: the subset $\{\lambda x ~|~ \lambda \in ]0,1[, \Vert x\Vert =1, x\in {\mathbb {Q}}^2\}$ is homeomorphic to $\coprod _{i\in {\mathbb {N}}} ]0,1[$. Define piecewise $p(x) = \frac{x}{\Vert x\Vert ^2}$ if $\Vert x\Vert \le 1$ and $p(x) = x$ if $\Vert x\Vert >1$. Take $X_1=\{x~|~\Vert x\Vert >1\}=Y_1$. Notice that $X_1\xrightarrow {p} Y_1$ is a homeomorphism, hence a covering, X is Hausdorff, second countable and locally path-connected, $X\xrightarrow {p}Y$ is a spread, $Y_1$ is open, and $X_1$ is open locally connected in X. However, $\text {Ord}(Y)=\emptyset$ since for every open neighborhood ${\mathcal {U}}$ of some $y\in p(X)$, the preimage $p^{-1}({\mathcal {U}})$ contains points x with $\Vert x\Vert <1$ but p is not a local homeomorphism around such a point.

Lemma 3.9

Let $X_i\xrightarrow {p_i} Y_i$ be spreads for $i\in \{1,2\}$ and let (f, g) be a spread isomorphism from $X_1\rightarrow Y_1$ to $X_2\rightarrow Y_2$. Then $g(\text {Ord}(X_1)) = \text {Ord}(X_2)$ and $f(\text {Ord}(Y_1)) = \text {Ord}(Y_2)$.

Proof

Let ${\mathcal {U}}$ be an open connected neighborhood of $p_1(x)$ evenly covered by $p_1$, let $({\hat{{\mathcal {U}}}}_i)_{i\in I}$ the connected components of $p_1^{-1}({\mathcal {U}})$ and define ${\mathcal {V}}:=f({\mathcal {U}})$ and ${\hat{{\mathcal {V}}}}_i:= g(\hat{\mathcal {U}}_i)$ for $i\in I$. Since f and g are bijective and $f\circ p_1=p_2\circ g$, we have

$$\begin{aligned} p_2^{-1}({\mathcal {V}})=g\circ p_1^{-1}\circ f^{-1}({\mathcal {V}}) = g\circ p_1^{-1}({\mathcal {U}}) = \bigsqcup _{i\in I} {\hat{{\mathcal {V}}}}_i \end{aligned}$$

and each ${\hat{{\mathcal {V}}}}_i$ is both open and connected.

Furthermore, $p_{2|{\hat{{\mathcal {V}}}}_i}^{|{\mathcal {V}}}\circ g^{|{\hat{{\mathcal {V}}}}_i}_{|{\hat{{\mathcal {U}}}}_i} = f_{|{\mathcal {U}}}^{|{\mathcal {V}}}\circ p_{1| {\hat{{\mathcal {U}}}}_i}^{|{\mathcal {U}}}$ for all $i\in I$ and $g^{|{\hat{{\mathcal {V}}}}_i}_{|{\hat{{\mathcal {U}}}}_i}$ as well as $f_{|{\mathcal {U}}}^{|{\mathcal {V}}}\circ p_{1| {\hat{{\mathcal {U}}}}_i}^{|{\mathcal {U}}}$ are homeomosphims; therefore, for all $i\in I$, $p_{2|{\hat{{\mathcal {V}}}}_i}^{|{\mathcal {V}}}$ is an homeomorphism. Finally, ${\mathcal {V}}$ is evenly covered by $p_2$. The result follows. $\square$

Definition 3.10

(Complete spread, spread completion) Let $X\xrightarrow {p} Y$ be a spread. For $y\in \overline{p(X)}$, consider the set $X_y$ of maps

$$\begin{aligned} \chi : \{{\mathcal {U}}\subset Y ~ \text { open and connected neighborhood of }y\} \rightarrow \{{\mathcal {V}}\subset X ~ \text {open connected}\} \end{aligned}$$

increasing for the inclusion and such that $\chi ({\mathcal {U}})$ is a connected component of $p^{-1}({\mathcal {U}})$ for all ${\mathcal {U}}$. The spread $X\xrightarrow {p} Y$ is complete if for all $y\in \overline{p(X)}$ and all $\chi \in X_y$, the intersection of $\chi ({\mathcal {U}})$ for ${\mathcal {U}}$ going through all open, connected neighborhood of y is nonempty.

A completion of a spread $X\xrightarrow {p} Y$ is a spread $X'\xrightarrow {p'} Y$ together with a spread morphism $(Id_Y,\iota )$

such that $\iota$ is an embedding, $X'$ is complete and the image of $\iota$ is portly.

Recall that a functor T is fully faithful if the induced function $\text {Hom}(X, Y) \rightarrow \text {Hom}(T(X), T(Y))$ is bijective.

Theorem 1

[27, 36] Every spread admits a unique completion up to isomorphism; furthermore, the completion of spread is a fully faithful functor from ${\textbf {Spr}}$ to itself.

Let $X\xrightarrow {p} Y$ be a spread and let $b\in Y$. Let $\varvec{{\mathcal {U}}}$ be a connected neighborhood basis of b. For ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$, let $X_{\mathcal {U}}$ be the space of connected components of $p^{-1}({\mathcal {U}})$ endowed with the discrete topology. Define bonding maps $X_{\mathcal {U}}\xrightarrow {\pi _{{\mathcal {U}}{\mathcal {V}}}} X_{\mathcal {V}}$ by setting for ${\mathcal {U}}\subset {\mathcal {V}}$ the image $\pi _{{\mathcal {U}}{\mathcal {V}}}({\widehat{{\mathcal {U}}}})$ of $\widehat{\mathcal {U}}\in X_{\mathcal {U}}$ to be the unique ${\widehat{{\mathcal {V}}}}\in X_{\mathcal {V}}$ such that ${\widehat{{\mathcal {U}}}} \subset {\widehat{{\mathcal {V}}}}$. For $x\in p^{-1}(b)$ and ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$, denote by $x_{\mathcal {U}}$ the connected component of x in $p^{-1}({\mathcal {U}})$. We have a natural continuous map

$$\begin{aligned} \displaystyle \begin{array}{l|rcl} &{} \displaystyle p^{-1}(b) &{} \longrightarrow &{} \displaystyle \varprojlim _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}}X_{\mathcal {U}} \\ &{} \displaystyle x &{} \longmapsto &{} \displaystyle (x_{\mathcal {U}})_{u\in \varvec{{\mathcal {U}}}} \end{array}. \end{aligned}$$

Proposition 3.11

[36] Let $X\xrightarrow {p} Y$ be a spread and let $b\in Y$. Let $\varvec{{\mathcal {U}}}$ be a connected neighborhood basis of b.

Then, the natural map $p^{-1}(b) \rightarrow \varprojlim _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}}X_{\mathcal {U}}$ is injective and open. Furthermore, it is a homeomorphism if and only if the spread $X\xrightarrow {p}Y$ is complete.

Proof

Denote by $\phi$ the natural map $p^{-1}(b) \xrightarrow {\phi }\varprojlim X_{\mathcal {U}}$. For every $x\in p^{-1}(b)$, since p is a spread, a neighborhood basis of x is given by the connected components of x in each $p^{-1}({\mathcal {U}})$ for ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$. If two elements $x_1,x_2 \in X$ have the same image by $\phi$ then $x_1,x_2 \in \phi (x_1)_{\mathcal {U}}$ for all ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$. Hence, $x_1,x_2$ have a common neighborhood basis. The space X so $x_1=x_2$; we deduce that $\phi$ is injective.

Notice that for all ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$ and all ${\mathcal {V}}\in X_{\mathcal {U}}$,

$$\begin{aligned} \phi ({\mathcal {V}}\cap p^{-1}(b)) = \pi _{\mathcal {U}}^{-1}({\mathcal {V}}) \end{aligned}$$

with $\pi _{\mathcal {U}}$ the natural map $\varprojlim _{{\mathcal {W}}\in \varvec{{\mathcal {U}}}} X_{\mathcal {W}}\xrightarrow {~~~} X_{\mathcal {U}}$. On the one hand, such $\pi _{\mathcal {U}}^{-1}({\mathcal {V}})$ form a basis of the topology of $\varprojlim X_{\mathcal {U}}$. On the other hand, since p is a spread, such ${\mathcal {V}}\cap p^{-1}({\mathcal {V}})$ form a basis for the topology of $p^{-1}(b)$. Therefore, $\phi$ is open.

Let $\hat{\varvec{{\mathcal {U}}}}=\left( {\hat{{\mathcal {U}}}}\right) _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}} \in \varprojlim _{i\in I}X_i$. The intersection $\bigcap _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}}{\hat{{\mathcal {U}}}}$ contains at most a point $x \in p^{-1}(b)$ and for such an x, we have $\phi (x)=\hat{\varvec{{\mathcal {U}}}}$. Reciprocally, if $\hat{\varvec{{\mathcal {U}}}} \in \phi (p^{-1}(b))$ then $\phi ^{-1}(\hat{\varvec{{\mathcal {U}}}}) \in \bigcap _{{\hat{{\mathcal {U}}}}\in \hat{\varvec{{\mathcal {U}}}}}{\hat{{\mathcal {U}}}}$.

Therefore, $\phi$ is surjective if and only if $\forall \hat{\varvec{{\mathcal {U}}}}\in \varprojlim X_{\mathcal {U}}, ~ \bigcap _{{\hat{{\mathcal {U}}}}\in \hat{\varvec{{\mathcal {U}}}}}{\hat{{\mathcal {U}}}} \ne \emptyset$. Which is merely a pedantic way to write that the spread $X\xrightarrow {p}Y$ is complete. $\square$

Corollary 3.12

[36] Let $X\xrightarrow {p} Y$ be a spread, then the fibers of p are totally discontinuous.

3.2 Primer on branched coverings

The object of this section is to recall fundamentals on branched coverings from definition to path-lifting characterization, essential properties, and composition. We end this section with the existence and uniqueness of universal branched covering with constrained branching locus. This will be the basis for further analysis.

As before, unless explicitly stated otherwise, all topological spaces are Hausdorff, locally path-connected and first countable. In the present section, as well as the following, we will make intensive use of the following Lemmata, which, for brevity’s sake, we will not refer to systematically.

Lemma 3.13

Let X be a connected first countable, locally path-connected, Hausdorff topological space and let ${\mathcal {U}}\subset X$ be a portly subset. For all $a\in {\mathcal {U}}$ and all $b\in X$, there exists a path $\gamma : [0,1]\rightarrow X$ from a to b such that $\gamma ([0,1[)\subset {\mathcal {U}}$.

Proof

Let $(a,b) \in {\mathcal {U}}\times X$ and let $({\mathcal {V}}_n)_{n\in {\mathbb {N}}}$ be a decreasing base of open connected neighborhood of b. Since ${\mathcal {U}}$ is portly, in particular ${\mathcal {U}}$ is dense and there exists a sequence $(b_n)_{n\in {\mathbb {N}}}$ such that $\forall n\in {\mathbb {N}}, b_n \in {\mathcal {V}}_n\cap {\mathcal {U}}$. Since ${\mathcal {U}}$ is portly and X is connected, then ${\mathcal {U}}$ is connected, and we can choose a path $\gamma _0$ in ${\mathcal {U}}$ from a to $b_0$. Then for $n\in {\mathbb {N}}$, $b_n$ and $b_{n+1}$ are both in ${\mathcal {U}}\cap {\mathcal {V}}_n$ and since ${\mathcal {U}}$ is portly and ${\mathcal {V}}_n$ open connected, ${\mathcal {U}}\cap {\mathcal {V}}_n$ is open connected (hence path-connected) and we can choose a path $\gamma _{n+1}$ in ${\mathcal {U}}\cap {\mathcal {V}}_n$ from $b_n$ to $b_{n+1}$. The concatenation of the sequence of path $(\gamma _n)_{n\in {\mathbb {N}}}$ is a path $\gamma :[0,1[\rightarrow {\mathcal {U}}$ such that $\lim _{1^-}\gamma = b$. The result follows. $\square$

Lemma 3.14

Let X be a connected first countable, locally path-connected Hausdorff topological space and let $X_1$ a subset containing a portly subset. Then, $X_1$ is first countable, locally path connect and Hausdorff.

Proof

To begin with, $X_1$ inherits Hausdorff and first countable properties from X as any subspace. It remains to show local path-connectedness. Take ${\mathcal {U}}\subset X_1$, some portly subset of X. Let $x\in X_1$ and let ${\mathcal {V}}_1$ be an open neighborhood of x in $X_1$. Choose some connected open ${\mathcal {V}}$ of X such that $x\in {\mathcal {V}}_2:={\mathcal {V}}\cap X_1 \subset {\mathcal {V}}_1$. It suffices to show that ${\mathcal {V}}_2$ is path-connected, so we choose some $a,b\in {\mathcal {V}}_2$. Since ${\mathcal {U}}$ is portly in X, the intersection ${\mathcal {U}}\cap {\mathcal {V}}$ is portly in ${\mathcal {V}}$. Take any $c\in {\mathcal {U}}\cap {\mathcal {V}}$ and apply Lemma 3.13 to construct paths $\gamma _1$ from c to a and $\gamma _2$ from c to b such that $\gamma _{i}([0,1[)\subset {\mathcal {U}}\cap {\mathcal {V}}\subset {\mathcal {V}}_2$ for $i\in \{1,2\}$. Concatenating the reverse of the former with the latter, we obtain a path from a to b contained in ${\mathcal {V}}_2$. $\square$

Definition 3.15

(Branched covering) A branched covering is a complete surjective spread $X\rightarrow Y$, with X and Y connected, whose ordinary locii in X and Y are portly subsets of X and Y respectively. We call Y the base space, X the total space, and the inverse image of a point a of Y is called the fiber above a.

We say that $X\rightarrow Y$ is branched over $Y{\setminus } \text {Ord}(Y)$. The latter is the branching locus of $X\rightarrow Y$, and for $S\subset Y$, we say that $X\rightarrow Y$ is possibly branched over S if S contains its branching locus.

Remark 3.16

The branching loci of a branched covering are skeletal and thus closed with an empty interior.

Remark 3.17

The ordinary part $\text {Ord}(X)\rightarrow \text {Ord}(Y)$ of a branched covering $X\rightarrow Y$ is a covering. Indeed, X is open connected and $\text {Ord}(X)$ is portly so $\text {Ord}(X)=\text {Ord}(X)\cap X$ is connected.

Lemma 3.18

If $X\xrightarrow {p} Y$ is a branched covering, then the preimage of a portly subset of Y is portly in X.

Proof

Let ${\mathcal {U}}$ be a portly subset of Y. The map $\text {Ord}_p(X) \xrightarrow {p} \text {Ord}_p(Y)$ is a local homeomorphism and $\text {Ord}_p(Y)$ is portly in Y thus $p^{-1}(Y\cap \text {Ord}_p(Y))$ is portly in $\text {Ord}_p(X)$. Since $\text {Ord}_p(X)$ is portly in X, then $p^{-1}(Y\cap \text {Ord}_p(Y))$ is portly in X. The subset $p^{-1}(Y)\subset X$ is open and contains a portly subset of X; it is thus also portly. $\square$

We begin with a branched covering version of the lifting property for complete spreads (“Corollary of the extension Theorem” in Fox [27]).

Lemma 3.19

Let $X\xrightarrow {p} Y$ be a spread with X connected, which induces a covering $X_1\rightarrow Y_1$ for some $X_1$ and $Y_1$ portly subsets of X and Y respectively. Then the following are equivalent:

• (i) $X\rightarrow Y$ is a branched covering;

• (ii) $X\rightarrow Y$ is a complete spread

• (iii) for every Hausdorff locally connected topological space Q and every homotopy $H:Q\times [0,1]\rightarrow Y$ such that $H(Q\times [0,1[)\subset Y_1$, every partial lift ${\hat{H}}: Q \times [0,1[ \rightarrow X_1$ of H extends continuously to some lift $Q \times [0,1] \rightarrow X$ of H;

• (iv) for every path $\gamma :[0,1]\rightarrow Y$ such that $\gamma ([0,1[) \subset Y_1$, every partial lift ${\hat{\gamma }}: [0,1[ \rightarrow X_1$ extends continuously to some lift $[0,1] \rightarrow X$ of $\gamma$.

Proof

To begin with, by Lemma 3.6 we have $X_1\subset \text {Ord}(X)$ and $Y_1\subset \text {Ord}(Y)$ so both $\text {Ord}(X)$ and $\text {Ord}(Y)$ are portly.

One has $(i)\Rightarrow (ii)$ by definition, $(ii)\Rightarrow (iii)$ is a direct consequence of the corollary of Fox mentioned above, and $(iii)\Rightarrow (iv)$ is trivial (it suffices to take Q a singleton). Assume (iv) and consider some $y_0 \in Y_1$. Since $Y_1$ is portly in Y, for every $y\in Y$ by Lemma 3.13 there exists a path $\gamma :y_0\rightsquigarrow y$ such that $\gamma ([0,1[)\subset Y_1$. Since $X_1\rightarrow Y_1$ is a covering, $\gamma _{|[0,1[}$ lifts to some ${\hat{\gamma }}:[0,1[\rightarrow X_1$. By assumption, ${\hat{\gamma }}$ admits a limit x at 1 and by continuity, $p(x)=y$. Therefore, p is surjective. Consider ${\overline{X}} \rightarrow Y$ the completion of $X\rightarrow Y$; without loss of generality, we may assume that $X\subset {\overline{X}}$ and also denote by p the map ${\overline{X}}\rightarrow Y$. Notice that since $X_1$ is portly in X and X is portly in ${\overline{X}}$, then $X_1$ is portly in ${\overline{X}}$. Let $x \in {\overline{X}}$ and let ${\hat{y}}_0$ be some lift of $y_0$ in $X_1$. Let ${\hat{\gamma }}$ be some path from ${\hat{y}}_0$ to x in ${\overline{X}}$ such that ${\hat{\gamma }}([0,1[)\subset X_1$. Since ${\hat{\gamma }}_{|[0,1[}$ is a lift in $X_1$ of the path $p\circ {\hat{\gamma }}_{|[0,1[} \subset Y_1$, assuming (iv) we deduce that ${\hat{\gamma }}_{|[0,1[}$ has limit at 1 in X. Therefore $x = {\hat{\gamma }}(1)= \lim _{1^-} {\hat{\gamma }}_{|[0,1[} \in X$. Finally, ${\overline{X}}\subset X$ hence ${\overline{X}} = X$ and $X\rightarrow Y$ is complete. $\square$

Lemma 3.20

[36] Let $X\xrightarrow {p} Y$ be a branched covering, let ${\mathcal {U}}$ be some open connected subset of Y and let ${\mathcal {V}}$ be a connected component of $p^{-1}({\mathcal {U}})$. Then ${\mathcal {V}}\xrightarrow {p} {\mathcal {U}}$ is a branched covering.

Proof

To begin with, sing ${\mathcal {U}},{\mathcal {V}}$ are open, the restriction $p_{|{\mathcal {U}}}^{|{\mathcal {V}}}$ is a spread. Since $\text {Ord}(X)$ is dense, we can choose some ${\hat{x}}\in \text {Ord}(X)\cap {\mathcal {V}}$; define $x:=p({\hat{x}})$. Since Y is locally pathwise connected and since $\text {Ord}(Y)$ is portly, then $\text {Ord}(Y)\cap {\mathcal {U}}$ is path-connected. We then can and do consider a path $\gamma :[0,1]\rightarrow \text {Ord}(Y)\cap {\mathcal {U}}$ from x to some $y\in \text {Ord}(Y)\cap {\mathcal {U}}$. Consider the unique lift ${\hat{\gamma }}$ of $\gamma$ in $\text {Ord}(X)$ such that ${\hat{\gamma }}(0)={\hat{x}}$. On the one hand, ${\hat{\gamma }}([0,1])\subset p^{-1}({\mathcal {U}})$; on the other end, ${\hat{\gamma }}([0,1])$ is connected. Therefore, ${\hat{\gamma }}$ is actually a path in ${\mathcal {V}}$ and $\gamma ([0,1])\subset p({\mathcal {V}})$. The path $\gamma$ is arbitrary, so $p(\text {Ord}(X)\cap {\mathcal {V}})=\text {Ord}(Y)\cap {\mathcal {U}}$ and

$$\begin{aligned} \text {Ord}(X)\cap {\mathcal {V}}\xrightarrow { ~~p~~} \text {Ord}(Y)\cap {\mathcal {U}}\end{aligned}$$

is a covering.

Since $X\xrightarrow {p} Y$ is a branched covering, it satisfies item (iv) of Lemma 3.19. Since X, Y are locally path-connected, this item is clearly satisfied by ${\mathcal {V}}\xrightarrow {p}{\mathcal {U}}$. Finally, ${\mathcal {V}}\rightarrow {\mathcal {U}}$ is a branched covering $\square$

Corollary 3.21

Let $X\xrightarrow {p} Y$ be a branched covering. Then p is open, furthermore for every connected open ${\mathcal {U}}\subset Y$ and every connected component ${\mathcal {V}}$ of $p^{-1}({\mathcal {U}})$ the map ${\mathcal {V}}\xrightarrow {p} {\mathcal {U}}$ is surjective.

Proof

Surjectivity is part of the definition of branched coverings and thus follows from Lemma 3.20. For all such ${\mathcal {U}},{\mathcal {V}}$ we thus have $p({\mathcal {V}})={\mathcal {U}}$. Since p is a spread, such ${\mathcal {V}}$ is a basis of the topology of X; hence p is open. $\square$

Corollary 3.22

Let $X\xrightarrow {p} Y$ be a branched covering, let ${\mathcal {U}}$ be some portly subset of Y then $p^{-1}({\mathcal {U}})\xrightarrow {p}{\mathcal {U}}$ is a branched covering.

Proof

From Lemma. 3.18 the subset $p^{-1}({\mathcal {U}})$ is portly in X and since X is connected so is $p^{-1}({\mathcal {U}})$. The result then follows from Lemma 3.20. $\square$

Lemma 3.23

Let $X\xrightarrow {p} Y$ be a branched covering, let $Y_1\subset Y$ containing a portly subset of Y then $p^{-1}(Y_1)\xrightarrow {~p~}Y_1$ is a branched covering.

Proof

Denote $X_1:=p^{-1}(Y_1)$ and $q:= p_{|X_1}^{|Y_1}$. Take some ${\mathcal {U}}\subset Y_1$ portly in Y.

• By Lemma 3.18, the subset ${\widehat{{\mathcal {U}}}}:=p^{-1}({\mathcal {U}})\subset X_1$ is portly in X.

• By Lemma 3.14, $X_1,Y_1$ are first countable, Hausdorff, locally path-connected.

• Let ${\mathcal {V}}$ an open subset of $X_1$ and $x\in {\mathcal {V}}$. Consider ${\mathcal {V}}_1$ open subset of X such that ${\mathcal {V}}={\mathcal {V}}_1\cap X_1$. Since p is a spread, there exists some open subset ${\mathcal {U}}_1\subset Y$ and some connected component ${\mathcal {W}}_1$ of $p^{-1}({\mathcal {U}}_1)$ such that $x\in {\mathcal {W}}_1 \subset {\mathcal {V}}_1$. Since ${\widehat{{\mathcal {U}}}}\subset X_1$ is portly in X, the subset ${\mathcal {W}}_1\cap {\widehat{{\mathcal {U}}}}$ is connected and dense in ${\mathcal {W}}_1\cap X_1$. It follows that ${\mathcal {W}}_2:={\mathcal {W}}_1\cap X_1$ is connected and thus a connected component of $q^{-1}({\mathcal {U}}_1\cap Y_1)$. Moreover, ${\mathcal {W}}_2$ is open in $X_1$ and $x\in {\mathcal {W}}_2\subset {\mathcal {V}}$. Therefore, $X_1 \xrightarrow {q} Y_1$ is a spread.

• Define $r:=p_{|{\widehat{{\mathcal {U}}}}}^{|{\mathcal {U}}}$. By Corollary 3.22, ${\widehat{{\mathcal {U}}}}\xrightarrow {r}{\mathcal {U}}$ is a branched covering, in particular $\text {Ord}_{r}(\widehat{\mathcal {U}})\xrightarrow {p} \text {Ord}_r({\mathcal {U}})$ is a covering. Furthermore $\text {Ord}_r({\widehat{{\mathcal {U}}}})$ is portly in ${\widehat{{\mathcal {U}}}}$ which is portly in $X_1$, so $\text {Ord}_r({\widehat{{\mathcal {U}}}})$ is portly in $X_1$. The same way, $\text {Ord}_r({\mathcal {U}})$ is portly in $Y_1$.

• Let $\gamma : [0,1] \rightarrow Y_1$ such that $\gamma ([0,1[) \subset \text {Ord}_r({\mathcal {U}})$ and let ${\hat{\gamma }}: [0,1[\rightarrow \text {Ord}_r({\mathcal {U}})$ be a lift of $\gamma$. Since $X\xrightarrow {p} Y$ is a branched covering, ${\hat{\gamma }}$ extends continuously at 1 and

  $$\begin{aligned} p\circ {\hat{\gamma }}(1)=\lim _{1^-}p\circ {\hat{\gamma }} =\lim _{1^-}\gamma =\gamma (1)\in Y_1. \end{aligned}$$

  Consequently, ${\hat{\gamma }}(1)\in p^{-1}(Y_1)=X_1$.

We checked the assumptions of Lemma 3.19 as well as point (iv) of the equivalence. We thus conclude that $X_1\xrightarrow {q} Y_1$ is a branched covering. $\square$

Proposition 3.24

Let $X\xrightarrow {p} Y \xrightarrow {q} Z$ be two branched coverings. Then the following are equivalent:

• (i) $X\xrightarrow {q\circ p} Z$ is a branched covering,

• (ii) $q(Y{\setminus } \text {Ord}_p(Y))$ is skeletal in Z.

Proof

To begin with, the composition of spread is a spread, so $q\circ p$ is a spread.

• $\underline{(i)\Rightarrow (ii)}$. Let ${\mathcal {U}}\subset \text {Ord}_{q\circ p}(Z)$ be a connected open evenly covered subset and define

  $$\begin{aligned} (q\circ p)^{-1}({\mathcal {U}}) = \bigsqcup _{i\in I} {\hat{{\mathcal {U}}}}_i; \quad \forall i\in I,\quad {\mathcal {V}}_i:= p({\hat{{\mathcal {U}}}}_i) \end{aligned}$$

  respectively the connected component decomposition of the preimage of ${\mathcal {U}}$ and their image by p. For all $i\in I$, on the one hand ${\mathcal {V}}_i$ is open connected by Corollary 3.21, on the other hand $(q\circ p)_{|{\hat{{\mathcal {U}}}}_i}^{|{\mathcal {U}}}$ is injective, furthermore q is open and $q({\mathcal {V}}_i) = {\mathcal {U}}$. Therefore, $q_{|{\mathcal {V}}_i}^{|{\mathcal {U}}}$ is bijective open thus an homeomorphism.

  Denote by ${\hat{{\mathcal {V}}}}_i$ the connected component of $q^{-1}({\mathcal {U}})$ containing ${\mathcal {V}}_i$. If ${\mathcal {V}}_i\ne {\hat{{\mathcal {V}}}}_i$ we may find some $j\in I$ such that $\hat{\mathcal {V}}_i = {\hat{{\mathcal {V}}}}_j$ and such that ${\mathcal {V}}_i\cap {\mathcal {V}}_j \ne \emptyset$; as well as some $y\in ({{\overline{{\mathcal {V}}}}}_i{\setminus } {\mathcal {V}}_i) \cap {\mathcal {V}}_j$. An argumentation like the one of Lemma 3.6 yields a contradiction showing that in fact $\forall i\in I, {\mathcal {V}}_i = {\hat{{\mathcal {V}}}}_i$. We conclude that $q^{-1}({\mathcal {U}})\xrightarrow {q} {\mathcal {U}}$ and for all $i\in I$, $p^{-1}({\mathcal {V}}_i)\xrightarrow {p} {\mathcal {V}}_i$ are coverings; with the preimages being a disjoint union of connected components among the ${\mathcal {V}}_i$ and ${\hat{{\mathcal {U}}}}_i$ respectively. As a consequence

  $$\begin{aligned} \text {Ord}_{q\circ p}(X)\xrightarrow {p} p(\text {Ord}_{q\circ p}(X))=q^{-1}(\text {Ord}_{q\circ p}(Z)) \xrightarrow {q} \text {Ord}_{q\circ p}(Z) \end{aligned}$$

  is a composition of coverings. Therefore:

  $$\begin{aligned} q(Y{\setminus } \text {Ord}_p(Y)) \subset q(Y{\setminus } q^{-1}(\text {Ord}_{q\circ p}(Z))) = Z{\setminus } \text {Ord}_{q\circ p}(Z) \end{aligned}$$

  The latter is skeletal; thus, so is the former.

• $\underline{(ii)\Rightarrow (i)}$. Consider $Y_0:=\text {Ord}_p(Y)\cap \text {Ord}_q(Y)$, and consider $Z_1:= Z{\setminus } q(Y{\setminus } Y_0)$. We note that

  $$\begin{aligned} Z_1= Z{\setminus } (q(Y{\setminus } \text {Ord}_p(Y)) \cup q(Y{\setminus } \text {Ord}_q(Y)) = \text {Ord}_q(Z) {\setminus } q(Y{\setminus } \text {Ord}_p(Y)) \end{aligned}$$

  Since $\text {Ord}_q(Z)$ is portly and $q(Y{\setminus } \text {Ord}_p(Y))$ is skeletal, $Z_1$ is portly. Since q is a covering, it is a surjective local homeomorphism, so $Y_1:=q^{-1}(Z_1)$ is portly in Y. Furthermore, $Y_1\subset Y_0$. Since $r:=q_{|\text {Ord}_q(Y)}^{|\text {Ord}_q(Z)}$ is a covering, then its (co)restriction is also $q_{|Y_1}^{|Z_1} = r_{|r^{-1}(Z_1)}^{|Z_1}$ is a covering. The same way, $p_{|X_1}^{|Y_1}$ is a covering with $X_1:= \left( p^{|\text {Ord}_p(Y)}_{|\text {Ord}_p(X)}\right) ^{-1}(Y_1)$ and $X_1$ is portly. Therefore, $(q\circ p)_{|X_1}^{|Z_1}$ is a composition of covering hence a covering.

  Applying Lemma 3.19, we see that item (iv) is stable by composition of branched coverings. Therefore, $q\circ p$ is a branched covering.

$\square$

Lemma 3.25

Let $X\xrightarrow {p} Y$ be a branched covering and ${\mathcal {U}}\subset Y$ some portly subset. The spread $X\rightarrow Y$ is isomorphic to the completion of $p^{-1}({\mathcal {U}})\rightarrow Y$.

Proof

$X\rightarrow Y$ is a completion of the spread $p^{-1}({\mathcal {U}})\rightarrow Y$ which is unique up to isomorphism by Theorem 1. $\square$

Recall that a connected, locally path-connected Hausdorff topological space X is semi-locally simply connected if every $x\in X$ admits a neighborhood ${\mathcal {U}}$ such that every loop $\gamma$ in X of base point x is trivial in X. By standard results [15], it is a necessary and sufficient condition for such a topological space X to admit a universal covering.

Proposition 3.26

Let Y be a connected, locally path-connected, Hausdorff topological space. Let S be a skeletal subset of Y.

If $Y{\setminus } S$ is semi-locally simply connected, then there exists a covering ${{\widetilde{Y}}}^S$ of Y possibly branched over S, which is maximal among such branched coverings. Furthermore, ${{\widetilde{Y}}}^S$ is unique up to isomorphism and universal in the sense that for any covering $X\xrightarrow {p} Y$ possibly branched over S, there exists a covering ${{\widetilde{Y}}}^S\rightarrow X$ possibly branched over $p^{-1}(S)$.

Remark 3.27

One could sum up the proof below by saying Fox’s completion induces a category equivalence between the category of covering of $Y{\setminus } S$ and the category of covering of Y possibly branched over S.

Proof

Assume $Y{\setminus } S$ is semi-locally simply connected. Then define ${{\widetilde{Y}}}^S$ the completion of spread $\widetilde{Y{\setminus } S} \rightarrow Y$ with $\widetilde{Y{\setminus } S}$ the universal covering of $Y{\setminus } S$. For any branched covering $X\xrightarrow {p}Y$ possibly branched over S, since $Y{\setminus } S\subset \text {Ord}(Y)$ is portly, $p^{-1}(Y{\setminus } S)$ is portly (hence connected) and $p^{-1}(Y{\setminus } S) \rightarrow Y{\setminus } S$ is a covering. Hence, there exists a covering morphism $\widetilde{Y{\setminus } S} \rightarrow p^{-1}(Y{\setminus } S)$. Since the completion of $p^{-1}(Y{\setminus } S) \rightarrow Y$ and $\widetilde{Y{\setminus } S}\rightarrow Y$ are respectively X and $\widetilde{Y}^S$, by Theorem 1 we obtain a morphism of branched covering ${{\widetilde{Y}}}^S \rightarrow X$, which is itself a branched covering, and its ordinary locus in X contains $p^{-1}(Y{\setminus } S)$. Finally, ${{\widetilde{Y}}}^S \rightarrow X$ is possibly branched over $p^{-1}(S)$.

If $X\rightarrow Y$ is a maximal covering possibly branched over S, then the induced covering $p^{-1}(Y{\setminus } S)\rightarrow Y{\setminus } S$ is maximal among covering of $Y{\setminus } S$ hence its universal covering. Therefore, X is isomorphic to $\widetilde{Y}^S$. $\square$

Remark 3.28

Considering the maximal covering ${{\widetilde{Y}}}^S$ of some Y possibly branched over some subset S, there is an ambiguity: the branching locus of ${{\widetilde{Y}}}^S$ might be smaller than S. One can consider the example where $Y={\mathbb {S}}^2$ the 2-dimensional sphere and S is a singleton; since the complement of a point is simply connected, the maximal covering of ${\mathbb {S}}^2$ possibly branched above S is trivial and the branching locus is empty.

Example 3.29

To illustrate Proposition 3.24, follows an instance of a composition of branched coverings that fails to be a covering.

Taking notions from Example 2.25, Consider $Z={\mathbb {D}}$, $Y={\mathbb {D}}_\infty$ with $Y\xrightarrow {q} Z$ the quotient map which is a branched covering. Consider $Y_0 = \{(r,\theta ) ~|~ \theta \in ]0,1[\}$ and choose $(r_n,\theta _n)_{n\in {\mathbb {Z}}}$ a countable dense family in $Y_0$. Consider $S:= (r_n,\theta _n+n)_{n\in {\mathbb {Z}}}$. We see that S is skeletal and that $Y{\setminus } S$ is semi-locally simply connected. We thus consider $X:= {{\widetilde{Y}}}^{S} \xrightarrow {p} Y$ the maximal covering possibly branched over S.

Notice that $q(Y{\setminus } \text {Ord}_p(Y)) = q(S)$ is dense in Z and hence not skeletal; therefore, the composition $q\circ p$ is not a branched covering.

3.3 Paths and maximal branched covering

The abstract description of Fox’s completion of a spread, though very general, may benefit from a path point of view. This section is devoted to a path description of the maximal covering possibly branched above some locus akin to the path description (as a set of homotopy classes of paths) of the universal covering of a Hausdorff, connected, locally path-connected, semi-locally simply connected topological space.

To begin with, we introduce some notations as well as a refinement of the homotopy equivalence relation so that we can keep track of the branched locus of a branched covering. Considering some connected Hausdorff, locally path-connected topological space X, some connected open subset ${\mathcal {U}}$ and some $x,y\in {{\overline{{\mathcal {U}}}}}$ we denote by $\varOmega _X(x,y,{\mathcal {U}})$ the set of path $\gamma :[0,1]\rightarrow X$ such that $\gamma (0)=x$,$\gamma (1)=y$ and $\gamma (]0,1[)\subset {\mathcal {U}}$. The index X is dropped whenever clear from the context. This set will always be endowed with its compact-open topology and two paths $\gamma _1,\gamma _2$ of $\varOmega (x,y,{\mathcal {U}})$ are homotopic with respect to ${\mathcal {U}}$ if they are in the same connected component of $\varOmega (x,y,{\mathcal {U}})$ or, equivalently, if there exists a homotopy $H:[0,1]^2\rightarrow X$ with fixed ends such that $H(0,\cdot )=\gamma _1$, $H(1,\cdot )=\gamma _2$ and such that $H([0,1]\times ]0,1[)\subset {\mathcal {U}}$. The composition of paths is denoted $*$ so that $\gamma _1*\gamma _2$ represents any parameterization of the concatenation of $\gamma _1$ then $\gamma _2$. We also use the notation ${\gamma }^{-1}:t\mapsto \gamma (1-t)$.

The homotopic relation is not suitable for our purpose as this section, as well as the following, will make clear; we thus introduce a weaker equivalence relation.

Definition 3.30

(Almost trivial loop) Let X be a Hausdorff, locally path-connected topological space, let ${\mathcal {U}}\subset X$ be an open subset and let $x\in {{\overline{{\mathcal {U}}}}}$.

A loop $\gamma \in \varOmega (x,x,{\mathcal {U}})$ is almost trivial with respect to ${\mathcal {U}}$ if its connected component in $\varOmega (x,x,{\mathcal {U}})$ intersects $\varOmega (x,x,{\mathcal {V}}\cap {\mathcal {U}})$ for all neighborhood ${\mathcal {V}}$ of x.

Example 3.31

Consider $Y = {\mathbb {R}}^3$ with carthesian coordinates x, y, z and its usual Euclidean distance; let $S_1= \{y=z=0\}$ and

$$\begin{aligned} S_2=\{y=\sin (1/x):~ x\in {\mathbb {R}}^*\}\cup \{x=z=0, |y|\le 1 \}; \end{aligned}$$

denote $O=(0,0,0)$ the origin. We make the following claims.

• The fundamental group of $Y{\setminus } S_i$ is isomorphic to ${\mathbb {Z}}$ for both $i=1$ and $i=2$. The isomorphism is given by “the number of turns” around $S_i$.

• Every loop $\gamma \in \varOmega (O,O,Y{\setminus } S_1)$ is homotopically trivial hence almost trivial.

• Every loop $\gamma \in \varOmega (O,O,Y{\setminus } S_2)$ is almost trivial.

• There exists non homotopically trivial loops $\gamma \in \varOmega (O,O,Y{\setminus } S_2)$.

Proof

The first two claims are left to the reader. Let us prove the last two.

• Consider any ball $B=B(O,r)$ centered at O, we may choose some $t_1,t_2$ such that $\gamma ([0,t_1]),\gamma ([t_2,1]) \subset B$. By compactness $\gamma ([t_1,t_2])$ there exists $\varepsilon \in [0,r[$ such that $\gamma _{|[t_1,t_2]}$ stays at distance at least $2\varepsilon$ of $S_2$. Since $Y{\setminus } \overline{B}(S_2,\varepsilon )$ is homeomorphic to $Y{\setminus } S_1$, we see that $\gamma ([t_1,t_2])$ is homotopic in $Y{\setminus } S_2$ with fixed extreminites to a path in $B{\setminus } B(S_2,\varepsilon )$. Finally, $\gamma$ is homotopic in $\varOmega (O,O,Y{\setminus } S_2)$ to a path in $\varOmega (O,O,B{\setminus } S_2)$.

• Consider some $\gamma \in \varOmega (O,O,Y{\setminus } S_2)$ such that

  $$\begin{aligned} \forall t< 1/4,\quad \gamma (t) = (0,0,t),\quad \gamma (1-t) = (0,0,-t) \end{aligned}$$

  and assume by contradiction that $\gamma$ is homotopically trivial. Let H be a homotopy from $\gamma$ to O in $\varOmega (O,O,Y{\setminus } S_2)$ and let $c: [0,1]^2 \rightarrow [0,1]^2$ such that for all s, $c(s,\cdot )$ is piecewise affine with

  $$\begin{aligned} c(s,0)= (0,0)&\quad&c(s,1/5)= (0,1/2-s/2) \\ c(s,2/5)= (s,1/2-s/2)&\quad&c(s,3/5)= (s,1/2+s/2) \\ c(s,4/5)= (0,1/2+s/2 )&\quad&c(s,1)= (0,1). \end{aligned}$$

  We see that $H'=H\circ c$ is still a homotopy from $\gamma$ to O in $\varOmega (O,O,Y{\setminus } S_2)$ with the additional property that

  $$\begin{aligned}{} & {} \forall s \in [0,1],\quad \exists ! \lambda _s>0,\quad \forall t<1/5, \\{} & {} \quad H'(s,t) = (0,\lambda _s t,0)\quad H'(s,1-t) = (0,-\lambda _s t,0). \end{aligned}$$

  Denoting $H''(s,t) = H'(s,\frac{3t + 1}{5})$ and I(X, Y) the mod 2 intersection numbers of X and Y [31], this property implies that

  $$\begin{aligned} \forall s \in [0,1], \quad I(H''(s,\cdot ),\{z=0\}) = 1. \end{aligned}$$

  Let ${\mathcal {U}}=B(O,1/2)$ be the ball of center 0 and radius 1/2 and let $\eta >0$ such that for $s>1-\eta$, $H''(s,\cdot )\subset {\mathcal {U}}$. We notice that ${\mathcal {U}}\cap \{z=0\}{\setminus } S_2$ is disconnected, we denote by ${{\textbf {C}}}$ the set of its connected components (which are all closed submanifolds of dimension 2 of $\{z=0\}{\setminus } S_2$) and define

  $$\begin{aligned} \displaystyle f:\begin{array}{l|rcl} &{} \displaystyle {{\textbf {C}}} &{} \longrightarrow &{} \displaystyle {\mathbb {Z}}/2{\mathbb {Z}} \\ &{} \displaystyle C &{} \longmapsto &{} \displaystyle I(H''(s,\cdot ),C) \end{array} \end{aligned}$$

  which is well defined and does not depend on $s>1-\eta$ since the intersection number is a homotopic invariant and has finite support by compactness of $H''(s,[0,1])\cap \{z=0\}$. On the one hand,

  $$\begin{aligned} \sum _{C\in {{\textbf {C}}}} f(C) = I(H(s,\cdot ),\{z=0\})=1. \end{aligned}$$

  On the other hand, $\forall C\in {{\textbf {C}}}, O \notin {\overline{C}}$ thus for all $C\in {{{\textbf {C}}}}$, there exists $\omega >0$ such that for all $s>1-\omega$, we have $H(s,\cdot )\cap C = \emptyset$. In other word, $\forall C\in {{\textbf {C}}}, f(C)=0$. Contradiction.

$\square$

Definition 3.32

(Almost homotopic paths) Let X be a Hausdorff, locally path-connected topological space, let ${\mathcal {U}}\subset X$ be an open subset, and let $(x,y)\in {\mathcal {U}}\times {{\overline{{\mathcal {U}}}}}$.

Two paths $\gamma _1,\gamma _2 \in \varOmega (x,y,{\mathcal {U}})$ are almost homotopic with respect to ${\mathcal {U}}$ if the loop $(\gamma _2)^{-1}*\gamma _1$ is almost trivial with respect to ${\mathcal {U}}$.

Remark 3.33

Implicitely, two almost homotopic paths $\gamma _1,\gamma _2$ always satisfy $\gamma _1(1)=\gamma _2(1)$ and $\gamma _1(0)=\gamma _2(0)$.

Lemma 3.34

Let X be a Hausdorff, first countable, connected, locally path-connected topological space, let ${\mathcal {U}}\subset X$ be an open subset, and let $x \in {{\overline{{\mathcal {U}}}}}$.

For $\gamma \in \varOmega (x,x,{\mathcal {U}})$, the following are equivalent:

• (i) $\gamma$ is almost trivial with respect to ${\mathcal {U}}$;

• (ii) for all open neighborhood ${\mathcal {V}}$ of x and for all $t_0,t_1\in ]0,1[$ such that $t_0<t_1$ and $\gamma ([0,t_0]\cup [t_1,1])\subset {\mathcal {V}}$, there exists a path $\omega : \gamma (t_0)\rightsquigarrow \gamma (t_1)$ in ${\mathcal {V}}\cap {\mathcal {U}}$ such that $\gamma$ is homotopic to $\gamma _{|[0,t_0]}*\omega *\gamma _{|[t_1,t_0]}$ in $\varOmega (x,x,{\mathcal {U}})$.

Proof

(ii) trivially implies (i), we thus assume that $\gamma$ is almost trivial with respect to ${\mathcal {U}}$. Let ${\mathcal {V}}$ be an open neighborhood of x and let $t_0<t_1$ such that $\gamma ([0,t_0]\cup [t_1,1])\subset {\mathcal {V}}$. Let $H:[0,1]\times [0,1]\rightarrow X$ be a homotopy from $\gamma$ to some path $\gamma _0\in \varOmega (x,x,{\mathcal {V}})$ such that $\forall s\in [0,1], H(s,\cdot )\in \varOmega (x,x,{\mathcal {U}})$. Consider the following closed connected subset B of the boundary of $[0,1]\times [0,1]$:

$$\begin{aligned} B:= \{0\}\times [0,t_0]\ \cup \ [0,1]\times \{0\}\ \cup \ \{1\}\times [0,1]\ \cup \ [0,1]\times \{1\}\ \cup \ \{0\}\times [t_1,1]. \end{aligned}$$

Since $H(B)\subset {\mathcal {V}}$, there exists a connected open neighborhood ${\mathcal {W}}$ of B in $[0,1]\times [0,1]$ such that $H({\mathcal {W}})\subset {\mathcal {V}}$. Take some path $\eta :[t_0,t_1]\rightarrow {\mathcal {W}}$ such that $\eta (t_0)=(0,t_0)$, $\eta (t_1)=(0,t_1)$ and $\eta (]t_0,t_1[)\subset ]0,1[\times ]0,1[$ and define $\omega :=H\circ \eta$. With $\eta (\cdot )=(\eta _1(\cdot ),\eta _2(\cdot ))$, the homotopy

$$\begin{aligned} \displaystyle J:\begin{array}{l|rcl} &{} \displaystyle [0,1]\times [0,1] &{} \longrightarrow &{} \displaystyle X \\ &{} \displaystyle s\in [0,1],t\in [0,t_0] &{} \longmapsto &{} \displaystyle H(0,t)\\ &{} \displaystyle s\in [0,1], t\in [t_0,t_1] &{} \longmapsto &{} \displaystyle H\left( s\cdot \eta _1(t),(1-s)t+s\cdot \eta _2(t)\right) \\ &{} \displaystyle s\in [0,1],t\in [t_1,1] &{} \longmapsto &{} \displaystyle H(0,t)\end{array} \end{aligned}$$

is such that $J(0,\cdot )=\gamma$ and $J(1,\cdot )=\gamma _{|[0,t_0]}*\omega *\gamma _{|[t_1,t_0]}$, moreover for all $s\in [0,1]$, we have $J(s,\cdot )\in \varOmega (x,x,{\mathcal {U}})$. The result follows. $\square$

Lemma 3.35

Let X be a Hausdorff, first countable, connected, locally path-connected topological space, let ${\mathcal {U}}\subset X$ be an open subset, and let $(x,y)\in {\mathcal {U}}\times {{\overline{{\mathcal {U}}}}}$.

Then, the “almost homotopic” relation is an equivalence relation in $\varOmega (x,y,{\mathcal {U}})$.

Proof

The relation is clearly reflexive and symmetric; we shall then prove that it is also transitive. Let $\gamma _1, \gamma _2,\gamma _3 \in \varOmega (x,y,{\mathcal {U}})$ such that $\gamma _1,\gamma _2$ are almost homotopic with respect to ${\mathcal {U}}$ and such that $\gamma _2,\gamma _3$ are almost homotopic with respect to ${\mathcal {U}}$. Let ${\mathcal {V}}$ be an open neighborhood of x and let $t \in ]0,1[^3$ such that $\forall i\in \{1,2,3\},\ \gamma _i([t_i,1])\subset {\mathcal {V}}$. By Lemma 3.34, there exists a path $\omega _{1}$ (resp. $\omega _2$) in ${\mathcal {V}}\cap {\mathcal {U}}$ from $\gamma _1(t_1)$ to $\gamma _2(t_2)$ (resp. from $\gamma _2(t_2)$ to $\gamma _3(t_3)$) such that $\gamma _1^{-1}*\gamma _2$ is homotopic to $(\gamma _{1|[t_1,1]})^{-1} *\omega _1*\gamma _{2|[t_2,1]}$ (resp. such that $\gamma _2^{-1}*\gamma _1$ is homotopic to $(\gamma _{2|[t_2,1]})^{-1}*\omega _2*\gamma _{3|[t_3,1]}$ ). Then $(\gamma _{1|[0,t_1]})^{-1}*\gamma _{2|[0,t_2]}*\omega _1^{-1}$ is homotopically trivial and the loop $\gamma _{1}^{-1}*\gamma _3$ is homotopic to

$$\begin{aligned} (\gamma _{1|[t_1,1]})^{-1}*\left( (\gamma _{1|[0,t_1]})^{-1}*\gamma _{2|[0,t_2]}*\omega _1^{-1}\right) *\omega _1*(\gamma _{2|[0,t_2]})^{-1}*\gamma _3 \end{aligned}$$

which is thus homotopic to $(\gamma _{1|[t_1,1]})^{-1}*\omega _1*(\gamma _{2|[0,t_2[})^{-1}*\gamma _3$. The same way, the loop $(\gamma _{2|[0,t_1]})^{-1}*\gamma _{3|[0,t_3]}*\omega _2^{-1}$ is homotopically trivial and $\gamma _{1}^{-1}*\gamma _3$ is then homotopic to $(\gamma _{1|[t_0,1]})^{-1}*\omega _1*\omega _3*\gamma _{3|[t_3,1]} \in \varOmega (x,x,{\mathcal {V}}\cap {\mathcal {U}})$. Finally, $\gamma _{1}^{-1}*\gamma _3$ is almost trivial with respect to ${\mathcal {U}}$ and $\gamma _1$ is almost homotopic to $\gamma _3$. $\square$

Lemma 3.36

Let ${{\widetilde{Y}}}^S\xrightarrow {p} Y$ be a maximal covering possibly branched above some S, let $(x,y)\in (Y{\setminus } S)\times Y$ and let ${\hat{x}} \in p^{-1}(x)$. Let $\gamma _1, \gamma _2\in \varOmega (x,y,Y{\setminus } S)$ and let ${\hat{\gamma }}_1,{\hat{\gamma }}_2$ be the respective lifts of $\gamma _1$ and $\gamma _2$ such that $\hat{\gamma }_1(0)={\hat{\gamma }}_2(0)={\hat{x}}$.

Then, ${\hat{\gamma }}_1(1)={\hat{\gamma }}_2(1)$ if and only if $\gamma _1$ and $\gamma _2$ are almost homotopic.

Proof

Assume $\gamma _1$ and $\gamma _2$ are almost homotopic. For ${\mathcal {U}}$ some standard neighborhood of ${\hat{\gamma }}_1(1)$. By Corollary 3.21, $p({\mathcal {U}})$ is a connected open neighborhood of y, and since $\gamma _1$ and $\gamma _2$ are almost homotopic, $\gamma _1$ is homotopic to a path $\gamma _1'$ of the form $\gamma _{2|[0,t_2]}*\omega *\gamma _{1|[t_1,1]}$ with $t_1\in ]0,1[$ such that $\gamma _i([t_i,1])\subset p({\mathcal {U}})$ for $i\in \{1,2\}$ and $\omega \in \varOmega (\gamma _2(t_2),\gamma _1(t_1),Y{\setminus } S)$. Since $\gamma _1$ and $\gamma _1'$ are homotopic and $p^{-1}(y)$ is totally disconnected, then $\gamma _1(1)=\gamma _1'(1)$. Since $\omega *\gamma _{1|[t_1,1]}\subset p({\mathcal {U}})$, the lift $\eta$ of $\omega *\gamma _{1|[t_1,1]}$ such that $\eta (0)=\gamma _2(t_2)$ stays in ${{\overline{{\mathcal {U}}}}}$. In particular ${\hat{\gamma }}_1(1)=\eta (1)\in {{\overline{{\mathcal {U}}}}}$. Therefore, ${\hat{\gamma }}_1(1)$ is in the closure of all neighborhood of ${\hat{\gamma }}_2(1)$, since ${{\widetilde{Y}}}^S$ is Hausdorff we conclude that ${\hat{\gamma }}_1(1)={\hat{\gamma }}_2(1)$.

Assume ${\hat{\gamma }}_1(1)={\hat{\gamma }}_2(1)$. Let ${\mathcal {U}}\subset \widetilde{Y}^S$ be some standard neighborhood of ${\hat{\gamma }}_1(1)$, let $t_1,t_2\in ]0,1[$ such that ${\hat{\gamma }}_i([t_i,1])\subset {\mathcal {U}}$ for $i\in \{1,2\}$ and let $\omega \in \varOmega ({\hat{\gamma }}_1(t_1),{\hat{\gamma }}_2(t_2),{\mathcal {U}}\cap p^{-1}(Y{\setminus } S))$. Since $p^{-1}(Y{\setminus } S)$ is simply connected, the loop ${\hat{\gamma }}_{1|[0,t_1]} *\omega * ({\hat{\gamma }}_{2|[0,t_2]})^{-1}$ is homotopically trivial. Therefore, ${\hat{\gamma }}_2$ is homotopic to ${\hat{\gamma }}_{1|[0,t_1]}*\omega *{\hat{\gamma }}_{2|[t_2,1]}$, hence $\gamma _2$ is homotopic to $\gamma _{1|[0,t_1]}*(p\circ \omega )*\gamma _{2|[t_2,1]}$. Finally, the loop $(\gamma _1)^{-1}*\gamma _2$ is homotopic to $(\gamma _1)^{-1}*\gamma _{1|[0,t_1]}*(p\circ \omega )*\gamma _{2|[t_2,1]}$ which is homotopic to $(\gamma _{1|[t_1,1]})^{-1}*(p\circ \omega )*\gamma _{2|[t_2,1]} \subset {\mathcal {U}}$. The loop $(\gamma _1)^{-1}*\gamma _2$ is thus almost trivial and $\gamma _1$ is almost homotopic to $\gamma _2$. $\square$

Theorem 2

Let Y be a first countable connected locally path-connected Hausdorff topological space and let $S\subset Y$ be a skeletal subset. Let $y_0\in Y{\setminus } S$ and let $\varOmega :=\bigcup _{x\in Y}\varOmega (y_0,x,Y{\setminus } S)$. Define X as the set of almost homotopy classes of $\varOmega$ with respect to $Y{\setminus } S$ and define the map $\varphi :\varOmega \rightarrow Y, \gamma \mapsto \gamma (1)$.

Then, $\varphi$ induces a branched covering $X \xrightarrow {~~{{\overline{\varphi }}}~~ } Y$ isomorphic to ${{\widetilde{Y}}}^S \xrightarrow {~~p~~} Y$.

Proof

Let ${\hat{y}}_0$ be some lift of $y_0$ in ${{\widetilde{Y}}}^S$. Consider the function $\psi : \varOmega \rightarrow {{\widetilde{Y}}}^S$ which associate to $\gamma \in \varOmega$ the point ${\hat{\gamma }}(1)$ where ${\hat{\gamma }}$ is the unique lift of $\gamma$ in ${{\widetilde{Y}}}^S$ such that ${\hat{\gamma }}(0)={\hat{y}}_0$. By Lemma 3.36, $\psi$ induces an injective function ${{\overline{\psi }}}:X\rightarrow {{\widetilde{Y}}}^S$, the following diagram commutes

and it suffices to prove that ${{\overline{\psi }}}$ is an homeomorphism.

• Since ${{\widetilde{Y}}}^S$ is first countable and $p^{-1}(Y{\setminus } S)$ is portly, for all $x\in {{\widetilde{Y}}}^S$ there exists a path ${\hat{\gamma }}\in \varOmega ({\hat{y}}_0,x,p^{-1}(Y{\setminus } S))$ and, for such a path, $\psi (p\circ {\hat{\gamma }})={\hat{\gamma }}(1)=x$. The map $\psi$ is thus surjective, hence bijective.

• Let ${\mathcal {U}}$ be a neighborhood of some $x\in {{\widetilde{Y}}}^S$, since p is a spread and by Corollary 3.21 without loss of generality, we may assume ${\mathcal {U}}$ is a connected component of $p^{-1}(p({\mathcal {U}}))$ and consider some $\gamma \in \varOmega$ such that $\psi (\gamma )=x$. Recall that $p({\mathcal {U}})$ is also open.

  Take some $t_0\in ]0,1[$ such that $\gamma ([t_0,1])\subset p({\mathcal {U}})$. Since $Y{\setminus } S$ is semi-locally simply connected, for all $t\in [0,t_0]$ there exists some path-connected open neighborhood ${\mathcal {V}}\subset Y{\setminus } S$ of $\gamma (t)$ such that all loop in ${\mathcal {V}}$ are homotopically trivial in $Y{\setminus } S$. By compactness, we can choose finitely many such neighborhoods $({\mathcal {V}}_i)_{i\in [\![1,n ]\!]}$ as well as an increasing sequence $\alpha \in [0,t_0]^{[\![0,n]\!]}$ such that: $\alpha _0=0, \alpha _n=t_0$ and $\forall i\in [\![1,n]\!],\ \gamma ([\alpha _{i-1},\alpha _i]) \subset {\mathcal {V}}_i$. Define ${\mathcal {V}}_{n+1}:={\mathcal {U}}$ and ${\mathcal {W}}_i$ the connected component of $\gamma (\alpha _i)$ in ${\mathcal {V}}_i\cap {\mathcal {V}}_{i+1}$ for $i\in [\![1,n]\!]$ and define

  $$\begin{aligned} {\mathcal {O}}:= \left\{ \eta \in \varOmega ~\left| ~\begin{array}{l} \forall i\in [\![1,n]\!], \eta ([\alpha _{i-1},\alpha _i])\subset {\mathcal {V}}_i) \\ \forall i\in [\![1,n]\!],\ \eta (\alpha _i)\in {\mathcal {W}}_i \\ \eta ([t_0,1])\subset p({\mathcal {U}}) \end{array} \right. \right\} . \end{aligned}$$

  ${\mathcal {O}}$ is an open neighborhood of $\gamma$ for the compact-open topology of $\varOmega$. Let $\eta \in {\mathcal {O}}$, forall $i\in [\![1,n]\!]$, choose a path $\omega _i \in \varOmega (\gamma (\alpha _i),\eta (\alpha _i),{\mathcal {W}}_i)$. We also define $\omega _0$ as the constant path at $y_0$. We notice that for all $i\in [\![1,n,]\!]$, the loop $\gamma _{|[\alpha _{i-1},\alpha _i]}*\omega _i*(\eta _{|[\alpha _{i-1},\alpha _i]})^{-1}*\omega _{i-1}$ is homotopically trivial. Therefore, $\eta$ is homotopic to the loop $\eta ':=\gamma _{|[0,t_0]}*\omega _n*\eta _{|[t_0,1]}$. Consider the lifts ${\hat{\gamma }}$ and ${\hat{\eta }}'$ of $\gamma$ and $\eta '$ respectively, both starting at ${\hat{y}}_0$. They are equal on $[0,t_0]$; since $\gamma$ and $\eta$ both stay in $p({\mathcal {U}})$, the paths ${\hat{\gamma }}$ and ${\hat{\eta }}'$ stay in the same connected component of $p^{-1}(p({\mathcal {U}}))$, hence they both stay in ${\mathcal {U}}$. We then deduce that $\psi (\eta )={\hat{\eta }}'(1)\in {\mathcal {U}}$ thus $\psi ({\mathcal {O}})\subset {\mathcal {U}}$. Finally, $\psi$ is continuous, and so is ${{\overline{\psi }}}$.

• Let ${\mathcal {U}}\subset Y$ open and $K\subset [0,1]$ compact, define ${\mathcal {O}}:= \{ \gamma \in \varOmega ~|~ \gamma (K)\subset {\mathcal {U}}\}$. Four cases can occur:

  • 1. If $0\in K$ and $y_0 \notin {\mathcal {U}}$, then $\psi ({\mathcal {O}})= \emptyset$;

  • 2. If $0\notin K$ or $y_0 \in {\mathcal {U}}$;

    • (a) If $1 \notin K$, then $\psi ({\mathcal {O}})={{\widetilde{Y}}}^S$;

    • (b) If $1\in K\ne [0,1]$, then $\psi ({\mathcal {O}})= p^{-1}({\mathcal {U}})$;

    • (c) If $K = [0,1]$ then $\psi ({\mathcal {O}})$ is the connected component of ${\hat{y}}_0$ in $p^{-1}({\mathcal {U}})$.

  Case (1) is trivial. In case (2.a), consider $x\in \widetilde{Y}^S$, $\gamma \in \varOmega$ such that $\psi (\gamma )=x$. Take some $t_0\in ]0,1[$ such that $[t_0,1]\cap K = \emptyset$ and consider the path $\eta (t)=y_0$ if $t\le t_0$ and $\eta (t)=\gamma (\frac{t-t_0}{1-t_0})$ if $t\in [t_0,1]$. We indeed have $\psi (\eta )=\psi (\gamma )=x$. A similar argument shows case (2.b). Then, in case (2.c), we have $y_0\in {\mathcal {U}}$ and the connected component ${\hat{{\mathcal {U}}}}$ of ${\hat{y}}_0$ in $p^{-1}({\mathcal {U}})$ is path-connected. For $x\in {\hat{{\mathcal {U}}}}$, there thus exists some path ${\hat{\gamma }} \in \varOmega ({\hat{y}}_0,x,{\hat{{\mathcal {U}}}})$ and, for such a path, $\psi (p\circ \gamma )=x$. Furthermore $p\circ \gamma \subset {\mathcal {U}}$ thus $p\circ \gamma \in {\mathcal {O}}$. Therefore, ${\hat{{\mathcal {U}}}} \subset \psi ({\mathcal {O}})$. Certainly, $\psi ({\mathcal {O}})\subset p^{-1}({\mathcal {U}})$ and since ${\hat{\gamma }}$ is connected and ${\hat{\gamma }}(0)={\hat{y}}_0\in {\hat{{\mathcal {U}}}}$, then $\psi ({\mathcal {O}})\subset {\hat{{\mathcal {U}}}}$. Finally, $\psi ({\mathcal {O}})={\hat{{\mathcal {U}}}}$, the connected component of ${\hat{y}}_0$ in $p^{-1}({\mathcal {U}})$.

  We deduce from the previous analysis that $\psi$ is open; hence, ${{\overline{\psi }}}$ is open.

Together, the points above show that ${{\overline{\psi }}}$ is a homeomorphism. $\square$

We end this section with two corollaries of Proposition 3.11, the proofs of which are left to the reader, and two examples illustrating possible behaviors of the fiber above a branching point.

Definition 3.37

Let $X\xrightarrow {p} Y$ be a covering branched over $S\subset Y$. Given two paths $\gamma _1,\gamma _2$ with fixed start point $a\in Y{\setminus } S$ and free endpoint in an open connected subset ${\mathcal {U}}\subset Y{\setminus } S$; $\gamma _1$ and $\gamma _2$ are p-homotopic if their lifts, from the same start point, end in the same connected component of $p^{-1}({\mathcal {U}})$.

Proposition 3.38

Let $X\xrightarrow {p} Y$ be a covering branched over $S\subset Y$. Let $a\in Y{\setminus } S$ and let ${\mathcal {U}}\subset Y$ be open and connected. Define $\pi _1(a,p,{\mathcal {U}})$ the set of paths with fixed start at a and free end in ${\mathcal {U}}$ up to p-homotopy.

Then, for all $b\in Y$ and all connected neighborhood basis $\varvec{{\mathcal {U}}}$ of b we have

$$\begin{aligned} p^{-1}(b) \simeq \varprojlim _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}} \pi _1(a,p,{\mathcal {U}}) \end{aligned}$$

where the projective system is given by the natural maps $\pi _1(a,p,{\mathcal {U}})\rightarrow \pi _1(a,p,{\mathcal {V}})$ for ${\mathcal {U}}\subset {\mathcal {V}}$.

Proposition 3.39

Let Y be a first countable connected locally path-connected Hausdorff topological space and let $S\subset Y$ skeletal such that $Y{\setminus } S$ is semi-locally simply connected. Let $a\in Y{\setminus } S$ and let ${\mathcal {U}}\subset Y$ be open and connected. Denote ${{\widetilde{Y}}}^S\xrightarrow {p} Y$ the maximal cover of Y possibly branched over S. Define $\pi _1(a,{\mathcal {U}})$ the set of paths with fixed start at a and free end in ${\mathcal {U}}$ up to homotopy.

Then, for all $b\in Y$ and all connected neighborhood basis $\varvec{{\mathcal {U}}}$ of b we have

$$\begin{aligned} p^{-1}(b) \simeq \varprojlim _{{\mathcal {U}}\in \varvec{{\mathcal {U}}}} \pi _1(a,{\mathcal {U}}) \end{aligned}$$

where the projective system is given by the natural maps $\pi _1(a,{\mathcal {U}})\rightarrow \pi _1(a,{\mathcal {V}})$ for ${\mathcal {U}}\subset {\mathcal {V}}$.

Example 3.40

Consider $Y = {\mathbb {R}}^2$ and $S=\{(\frac{1}{n},0)~:~n\in {\mathbb {N}}^*\cup \{\infty \}\}$. The fiber above (0, 0) in ${{\widetilde{Y}}}^S$ is homeomorphic to ${\mathbb {Z}}^{\mathbb {N}}$ endowed with the weak topology; hence, it is not locally compact. This answers positively Problem 10.8 of [36].

Proof

Consider the neighborhood basis given by the discs $D_n$ centered at (0, 0) of radius $\frac{1}{n-1/2}$ for $n\in {\mathbb {N}}^*$. Let $a = (2,0)$ and $b:=(0,0)$, for $n\in {\mathbb {N}}^*$, the natural map $\pi _1(a,D_{n+1})\rightarrow \pi _1(a,D_{n})$ has an infinite fiber above every point. The result then follows from Proposition 3.39. $\square$

3.4 Galoisian branched coverings

The usual notion of Galoisian covering can be extended naturally to branched coverings via the group of automorphisms of a branched covering. Although, as we shall see, the completion of a Galoisian covering need not be Galoisian. The main result of this section is a topological criterion akin to semi-local simple connectedness, which ensures maximal branched coverings are Galoisian, see Proposition 3.52. It allows the state a Galoisian correspondence for branched covering stated in Theorem 3.

Definition 3.41

(Automorphisms of a spread) Let $X\xrightarrow {p} Y$ be a spread, an automorphisms of p is an homeomorphism $\varphi$ of X such that $p\circ \varphi = p$. Denote by $\varGamma (X/Y)$ the group of spread automorphisms of X above Y. We also denote by $\varGamma _x$ the stabilizer of x if $x\in X$ and by $\varGamma _{\mathcal {U}}$ the set-wise stabilizer of ${\mathcal {U}}$ if ${\mathcal {U}}$ is a subset of X.

Note that a spread automorphism is just an automorphism in the category ${\textbf {Spr}}$.

Definition 3.42

A branched covering $X\xrightarrow {p} Y$ is Galoisian if the group $\varGamma (X/Y)$ of automorphism of p acts transitively on the fibers of p. It is called quasi-Galoisian if p is the completion of a Galoisian covering.

Remark 3.43

If a branched covering $X\xrightarrow {p} Y$ is Galoisian then p induces an homeomorphism $\varGamma (X/Y)\backslash X \rightarrow Y$.

Lemma 3.44

Let $X\xrightarrow {p} Y$ be a branched covering, the group of automorphisms of p is exactly the group of automorphisms of the induced branched covering $p^{-1}({\mathcal {U}}) \rightarrow {\mathcal {U}}$ for any ${\mathcal {U}}$ portly in Y:

$$\begin{aligned} \varGamma (X/Y) = \varGamma (p^{-1}({\mathcal {U}})/{\mathcal {U}}). \end{aligned}$$

Proof

An automorphism $\phi$ of $X \rightarrow Y$ lifts the identity thus for any ${\mathcal {U}}$ subset of Y, the automorphism $\phi$ preserves $p^{-1}({\mathcal {U}})$. In particular, for any ${\mathcal {U}}$ portly subset of Y, such a $\phi$ induces an automorphism of $p^{-1}({\mathcal {U}}) \xrightarrow {~~~} {\mathcal {U}}$. Furthermore, with ${\mathcal {U}}$ portly in Y, by functoriality of the spread completion and since the completion of $p^{-1}({\mathcal {U}})\rightarrow Y$ is $X\rightarrow Y$, an automorphism of $p^{-1}({\mathcal {U}}) \xrightarrow {~~~} {\mathcal {U}}$ extends uniquely to a automorphism of $X \xrightarrow {~~~} Y$. Therefore, $\varGamma (X/Y) = \varGamma (p^{-1}({\mathcal {U}})/{\mathcal {U}}))$. $\square$

Corollary 3.45

Let $X\xrightarrow {p} Y$ be a branched covering, then

$$\begin{aligned} \varGamma (X/Y) = \varGamma (\text {Ord}(X)/\text {Ord}(Y)). \end{aligned}$$

The maximal covering branched over some locus need not be Galoisian. Indeed, one can consider $Y={\mathbb {R}}^2$ and $S:=\{(1/n,0):n\in {\mathbb {N}}^*\}\cup \{(0,0)\}$. On the one hand, the automorphisms group of $\widetilde{Y}^S$ is countable (it is the fundamental group of $Y{\setminus } S$, thus a free group generated by countably infinitely many generators). On the other hand, there are uncountably infinitely many homotopy classes in of path from (2, 0) to (0, 0) and none of these classes are equivalent in the sense of Theorem 2; hence the fibre above (0, 0) is uncountable. The action of $\varGamma (X/Y)$ is then not transitive on the fiber above 0, and ${{\widetilde{Y}}}^S \rightarrow Y$ is not Galoisian.

Definition 3.46

(semi-locally simple connectedness) Let X be a Hausdorff, connected, locally path-connected topological space. We say that an open subset ${\mathcal {U}}$ is semi-locally simply connected at $x \in {{\overline{{\mathcal {U}}}}}$ if there exists a connected open neighborhood ${\mathcal {V}}$ of x such that every loop $\gamma$ of $\varOmega (x,x,{\mathcal {V}}\cap {\mathcal {U}})$ seen as an element of $\varOmega (x,x,{\mathcal {U}})$ is almost trivial.

${\mathcal {U}}$ is then semi-locally simply connected in X if ${\mathcal {U}}$ is dense and semi-locally simply connected at every point of X

Remark 3.47

The definition of semi-locally simply connected is coherent with the usual definition of semi-locally simply connected. Indeed, a topological space X is semi-locally simply connected if and only if it is semi-locally simply connected in itself.

Remark 3.48

Using the same notations as in the definition above, there are generic situations in which dense open subsets are semi-locally simply connected at every point of the whole space.

• If X is a manifold and $X{\setminus } {\mathcal {U}}$ is a submanifold of codimension at least 2, more generally if X is a simplicial complex and $X{\setminus } {\mathcal {U}}$ is a union of facets (such that ${\mathcal {U}}$ is still dense and locally connected);

• or if X admits a basis of neighborhoods such that for each ${\mathcal {V}}$ of said basis, ${\mathcal {V}}\cap {\mathcal {U}}$ is semi-locally simply connected in ${\mathcal {V}}$;

then ${\mathcal {U}}$ is locally simply connected at every point of X.

Lemma 3.49

Let $X\xrightarrow {p} Y$ be a quasi-galoisian branched covering. Let $a\in Y$ and ${\hat{a}} \in p^{-1}(a)$, the orbit $\varGamma (X/Y){\hat{a}}$ is dense in $p^{-1}(a)$.

Proof

We use the same notation as in Proposition 3.11. Since the branched covering p is quasi-Galoisian, for every ${\mathcal {U}}\in \varvec{{\mathcal {U}}}$, $\varGamma (X/Y)$ acts transitively on $X_{\mathcal {U}}$. Furthermore, $\varGamma (X/Y)$ acts by homeomorphisms on X, hence preserves connected components; its action thus commutes with the bonding maps of the projective system $(X_{\mathcal {U}})_{{\mathcal {U}}\in \varvec{{\mathcal {U}}}}$. Finally, the action of $\varGamma (X/Y)$ on each $X_{\mathcal {U}}$ lifts to an action on $\varprojlim _{\mathcal {U}}X_{\mathcal {U}}$ whose orbits are dense. $\square$

Proposition 3.50

Let $X\xrightarrow {p} Y$ be a quasi-Galoisian branched covering possibly branched over $S\subset Y$.

For all $b\in Y$ and all connected neighborhood basis $({\mathcal {U}}_i)_{i\in I}$ of b we have

$$\begin{aligned} p^{-1}(b) \simeq \varprojlim _{i\in I} \varGamma (X/Y)/\varGamma _{{\hat{{\mathcal {U}}}}_i} \end{aligned}$$

where ${\hat{{\mathcal {U}}}}_i$ is the connected component of ${\hat{b}}$ in $p^{-1}({\mathcal {U}}_i)$ for $i\in I$.

Proof

Since $X\xrightarrow {p} Y$ is quasi-Galoisian, $\varGamma (X/Y)$ acts transitively on the connected components of $p^{-1}({\mathcal {U}})$ for every open ${\mathcal {U}}\subset Y$. The group $\varGamma _{\mathcal {V}}$ is by definition the stabilizer of ${\mathcal {V}}$ for ${\mathcal {V}}$ a connected of $p^{-1}({\mathcal {U}})$ for some open ${\mathcal {U}}\subset Y$. The discrete spaces $\varGamma (X/Y)/\varGamma _{{\hat{{\mathcal {U}}}}}$ and $X_{\mathcal {U}}$ are thus homeomorphic (using the same notations as Proposition 3.11). The result then follows from Proposition 3.11. $\square$

Lemma 3.51

Let $X\xrightarrow {p} Y$ be a quasi-Galoisian branched covering possibly branched over $S\subset Y$ and let $b\in Y$.

Assume that $\varGamma (X/Y)$ is countable, then the following are equivalent:

• (i) $p^{-1}(b)$ is discrete;

• (ii) $p^{-1}(b)$ is countable;

• (iii) $\varGamma (X/Y)$ acts transitively on $p^{-1}(b)$.

Proof

Consider a neighborhood basis $({\mathcal {U}}_n)_{n\in {\mathbb {N}}}$ of b in Y indexed over ${\mathbb {N}}$ such that ${\mathcal {U}}_n\subset {\mathcal {U}}_m$ whenever $n\ge m$. Denote by $X_n$ the discrete space of connected components of $p^{-1}({\mathcal {U}}_n)$ and $(p_{n,m})_{n\ge m}: X_n \rightarrow X_m$ the bonding maps which associated a connected component ${\mathcal {V}}$ of $p^{-1}({\mathcal {U}}_n)$ its connected component in $p^{-1}({\mathcal {U}}_m)$. For $n\in {\mathbb {N}}$, define $N_n:= \#p_{n+1,n}^{-1}(x)$ for some $x\in X_n$. Since the action of $\varGamma (X/Y)$ is transitively on each $X_n$ and commutes with the bonding maps, $N_n$ does not depend on the choice of x and $N_n\le \aleph _0$.

• If $N_n>1$ for infinitely many $n\in {\mathbb {N}}$, then the projective limit $\varprojlim _n X_n$ is uncountable, hence the action of $\varGamma (X/Y)$ is not transitive. Furthermore, a basis of the topology is given by the inverse image of subsets of the $X_n$ by the natural projection $p_m: \varprojlim _n X_n \rightarrow X_m$. None of these preimages is reduced to a point; hence, the topology of $\varprojlim _n X_n$ is not discrete.

• If $N_n> 1$ only for finitely many $n\in {\mathbb {N}}$, then the projective limit $\varprojlim _n X_n$ is stationnary. Then $\varprojlim _n X_n \simeq X_m$ for some $m\in {\mathbb {N}}$ big enough. In particular $\varprojlim _n X_n$ is discrete and, by Lemma 3.49, the action of $\varGamma (X/Y)$ on it is transitive, since $\varGamma (X/Y)$ is countable then so is $\varprojlim _n X_n$.

$\square$

Proposition 3.52

Let Y be a connected, locally path-connected, second countable, Hausdorff topological space and let $S\subset Y$ skeletal such that $Y{\setminus } S$ is semi-locally simply connected. Let $\widetilde{Y}^S\xrightarrow {p} Y$ be the maximal covering of Y possibly branched above S. The following are equivalent:

• (i) ${{\widetilde{Y}}}^S\xrightarrow {p} Y$ is Galoisian;

• (ii) $Y{\setminus } S$ is semi-locally simply connected in Y;

Proof

We write $\varGamma = \varGamma ({{\widetilde{Y}}}^S/Y)$ and $X = \widetilde{Y}^S$. By Lemma 3.51, we can replace (i) by the equivalent statement that the fibers of p are discrete.

• $(ii)\Rightarrow (i)$. Assume that $\text {Ord}(Y)$ is semi-locally simply connected at every point of Y and consider some $y\in Y$, we show that $p^{-1}(y)$ is discrete.

  If $y\in \text {Ord}(Y)$, it follows from the standard theory of (unbranched) covering; henceforth we assume $y\notin \text {Ord}(Y)$ and consider some connected open neighborhood ${\mathcal {U}}$ of y such that for every loop $\gamma \in \varOmega (y,\text {Ord}({\mathcal {U}}))$, the constant loop at y is in the adherence of the connected component of $\gamma$ in $\varOmega (y,\text {Ord}(Y))$. We choose a connected component ${\mathcal {V}}$ of $p^{-1}({\mathcal {U}})$ and consider $x_1,x_2 \in p^{-1}(y)\cap {\mathcal {V}}$. Consider a path ${\hat{\gamma }}\in \varOmega (x_1,x_2,\text {Ord}(X)\cap {\mathcal {V}})$. Such a path exists since ${\mathcal {V}}$ is connected and $\text {Ord}(X)$ portly; hence $\text {Ord}(X)\cap {\mathcal {V}}$ is open dense in ${\mathcal {V}}$ and path-connected.

  For any open neighborhood ${\mathcal {W}}$ of y, by hypothesis we can choose some $\gamma _1\in \varOmega (y,{\mathcal {W}})$ in the connected component of $\gamma _0=p\circ {\hat{\gamma }}$ in $\varOmega (y,\text {Ord}(Y)$. Let $H:[0,1]\times [0,1]\rightarrow Y$ be a homotopy from $\gamma _0$ to $\gamma _1$ in $\varOmega (y,\text {Ord}(Y))$ the ordinary part of H defined on $]0,1[\times [0,1]\rightarrow Y$ lifts to $\text {Ord}(X)$ and, by Lemma 3.19, this lift extends continuously to a lift ${{\widetilde{H}}}:[0,1]\times [0,1]\rightarrow X$ of H. Since the fibers of p are totally disconnected and $\forall s\in [0,1], H(0,s)=H(1,s)=y$, then ${{\widetilde{H}}}(0,\cdot )$ and $\widetilde{H}(1,\cdot )$ are constant. In particular, $x_1$ and $x_2$ are in the same connected component in $p^{-1}({\mathcal {W}})$. We deduce that $x_1=x_2$ by Proposition 3.11. Finally, ${\mathcal {V}}\cap p^{-1}(y)$ is a singleton.

• $(i)\Rightarrow (ii)$. Assume the fibers of p are discrete and consider some neighborhood ${\mathcal {V}}$ of some $x\in X$ such that ${\mathcal {V}}\cap p^{-1}(p(x))=\{x\}$; denote by ${\mathcal {U}}:=p({\mathcal {V}})$. Since p is a branched covering, by Corollary 3.21 we may choose ${\mathcal {V}}$ connected and such that ${\mathcal {V}}$ is a connected component of $p^{-1}({\mathcal {U}})$.

  Consider some path $\gamma \in \varOmega (y,{\mathcal {U}})$ and some lift ${\hat{\gamma }}: [0,1]\rightarrow {\mathcal {V}}$. Since $\gamma (0)=\gamma (1)=y$ both ${\hat{\gamma }}(0)$ and ${\hat{\gamma }}(1)$ are in $p^{-1}(y)\cap {\mathcal {V}}$ and are thus equal to x ie ${\hat{\gamma }} \in \varOmega (x,{\mathcal {V}})$.

  Let ${\mathcal {W}}$ be some neighborhood of y, choose some $t_0,t_1 \in ]0,1[$ such that $\gamma (]0,t_0])\subset {\mathcal {W}}$ and $\gamma ([t_1,1[)\subset {\mathcal {W}}$. The connected component ${\hat{{\mathcal {W}}}}$ of x in $p^{-1}({\mathcal {W}})$ contains both ${\hat{\gamma }}([t_1,1[)$ and ${\hat{\gamma }}(]0,t_0])$; moreover ${\hat{{\mathcal {W}}}}\cap \text {Ord}(X)$ is path-connected; there thus exists a path $\omega :{\hat{\gamma }}(t_1)\rightsquigarrow {\hat{\gamma }}(t_0)$ in ${\hat{{\mathcal {W}}}}$. Since $\text {Ord}(X)$ is the universal covering of $\text {Ord}(Y)$, it is simply connected and the loop $\gamma _{|[t_0,t_1]}* \omega$ is trivial. Therefore, ${\hat{\gamma }}$ is homotopic to ${\hat{\gamma }}_{[t_1,1]}* \omega ^{-1} * {\hat{\gamma }}_{[0,t_0]}$. Hence, ${\hat{\gamma }}$ is homotopic in $\varOmega (x,\text {Ord}(X))$ to a loop in $\varOmega (x,\text {Ord}({\hat{{\mathcal {W}}}})$. Finally, $\gamma$ is homotopic in $\varOmega (y,\text {Ord}(Y))$ to a loop in $\varOmega (x,\text {Ord}({\mathcal {W}}))$. The open subset ${\mathcal {W}}$ is arbitrary, then $\text {Ord}(Y)$ is semi-locally simply connected at y.

$\square$

The following Theorem is then a direct consequence of Propositions 3.52 and 3.26.

Theorem 3

(Galois correspondance) Let Y be a connected, locally path-connected Hausdorff topological space and let $S\subset Y$ skeletal. Assume $Y{\setminus } S$ is semi-locally simply connected in Y.

Then, the maximal covering ${{\widetilde{Y}}}^S$ possibly branched over S is Galoisian.

Furthermore, every covering X of Y possibly branched over S is isomorphic to the quotient of ${\widetilde{Y}}^S$ by a subgroup of $\varGamma ({\widetilde{Y}}^S/Y)$. Finally, this subgroup is normal if and only if X is Galoisian.

Example 3.53

In the following situations, $Y{\setminus } S$ is semi-locally simply connected in Y

• 1. Y is a n-manifold with $n\ge 2$ and S is a finite subset;

• 2. Y is a 3-manifold and S is a tame knot.

• 3. Y is a simplicial complex of dimension n and S is a $(n-2)$-skeleton.

Example 3.54

Consider $Y = {\mathbb {R}}^2$ and $S=\{(\frac{1}{n},0)~:~n\in {\mathbb {N}}^*\cup \{\infty \}\}$ and denote by $\varGamma$ the absolute Galois group $\varGamma ({{\widetilde{Y}}}^S/Y)$. We see that $Y{\setminus } S$ is not semi-locally simply connected in Y. Let $\varGamma _2:=\langle \varGamma [\gamma _n]^2\varGamma ~:~ n\in {\mathbb {N}}\rangle$ where $\gamma _n$ is a simple loop around (1/n, 0). Consider $Y_2$, the completion of the spread $\varGamma _2\backslash \text {Ord}({{\widetilde{Y}}}^S) \rightarrow Y$. The fiber above (0, 0) in $Y_2$ is a Cantor set. This answers positively Problem 10.7 of [36].

Example 3.55

If S is a wild Cantor [9] embedded into $Y = {\mathbb {S}}^3$, then $Y{\setminus } S$ is not semi-locally simply connected in Y.

4 Singular (G, X)-manifolds (II): tame and wild

In this section, we utilize elements laid out on branched coverings to construct singular equivalents to tools of the standard theory of (G, X)-manifolds. A fundamental property of regular (G, X)-manifolds is the developement Theorem: let M be a connected (G, X)-manifold and let ${{\widetilde{M}}}$ be its universal covering, there exists a couple $({\mathcal {D}},\rho )$ with $\rho : \pi _1(M)\rightarrow G$ and ${\mathcal {D}}:{{\widetilde{M}}}\rightarrow X$ a $\rho$-equivariant (G, X)-morphism; furthermore the couple is unique up to the action of G.

One of the goals is to allow for efficient proof of uniformization results. For instance, if ${\mathcal {D}}$ is injective ${{\widetilde{M}}}$ naturally identifies set-wise to a domain in X and we may identify set-wise M to $\rho \backslash {\mathcal {D}}({{\widetilde{M}}})$. As will become apparent in the examples given in the last section of the present work, topology is a core difficulty. We may define a developing map as merely an a.e. (G, X)-morphism from ${{\widetilde{M}}}$ to X; this leads to tamely singular (G, X)-manifolds.

Example 4.1

Let $n\in {\mathbb {N}}$ and $\theta \in {\mathbb {R}}_+^*{\setminus } \{2\pi \}$ and $M = {\mathbb {E}}^{n+2}_{\theta }$ so that $\text {Sing}(M) = \{r=0\}$ in cylindrical coordinates. We observe that $\widetilde{\mathbb E}^{n+2}_{\theta }:= {{\widetilde{M}}}^{\text {Sing}(M)}$ can be identified with $\text {susp}({\mathbb {R}})\times {\mathbb {R}}^{n}$. In cylindrical coordinates $(r,\theta ,z_1,\ldots ,z_{n}) \in {\mathbb {R}}_+\times {\mathbb {R}}\times {\mathbb {R}}^{n}$, the covering $\widetilde{{\mathbb {E}}}^{n+2}_{\theta }$ can be endowed with the singular Euclidean metric $\text {d}r^2 + r^2 \text {d}\theta ^2 + \sum _{i=1}^{n}\text {d}z_i^2$ and we can define the developing map

$$\begin{aligned} \displaystyle {\mathcal {D}}:\begin{array}{l|rcl} &{} \displaystyle \widetilde{{\mathbb {E}}}^{n+2}_{\theta } &{} \longrightarrow &{} \displaystyle {\mathbb {E}}^{n+2} \\ &{} \displaystyle (r,\theta ,z_1,\ldots ,z_{n}) &{} \longmapsto &{} \displaystyle (r\cos \theta ,r\sin (\theta ),z_1,\ldots ,z_n) \end{array}. \end{aligned}$$

However, the following example shows that many interesting examples are not tamely singular.

Example 4.2

Using notation from 2.25, the extreme BTZ-like whitehole model has a maximal branched covering but no developing map. Indeed, one can observe that the developing map

$$\begin{aligned} \displaystyle {\mathcal {D}}:\begin{array}{l|rcl} &{} \displaystyle \text {Reg}({\mathbb {C}}_\infty ^{(3)}) &{} \longrightarrow &{} \displaystyle {\mathbb {E}}^{1,2} \\ &{} \displaystyle \left( \tau ,{\mathfrak {r}},\frac{\theta }{2\pi }\right) &{} \longmapsto &{} \displaystyle \begin{pmatrix}t \\ x \\ y\end{pmatrix}=\begin{pmatrix} \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 \\ \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 -r \\ -{\mathfrak {r}}\theta \end{pmatrix} \end{array}. \end{aligned}$$

does not extends continuously at ${\mathfrak {r}}= 0$. For instance, the sequence $(\tau _n,{\mathfrak {r}}_n,\theta _n)_{{\mathbb {N}}^*}$ with

$$\begin{aligned} \forall n\in {\mathbb {N}}^*, \quad \tau _n=0,\quad {\mathfrak {r}}_n=\frac{1}{n},\quad \theta _n = n \end{aligned}$$

is such that $(\tau _n,{\mathfrak {r}}_n,\theta _n)\xrightarrow {n\rightarrow +\infty } (0,0,0)$ in ${\mathbb {C}}_\infty ^{(3)}$ but ${\mathcal {D}}(\tau _n,{\mathfrak {r}}_n,\theta _n)$ is unbounded.

Aiming at a uniformization for this last example leads to a notion of virtually tame singular (G, X)-manifolds by relaxing the continuity assumption on the developing map. In this context, we are able to construct uniformization results.

Of course, a natural definition of a developing map (even discontinuous) is not guaranteed in general, as the following example shows.

Example 4.3

Let $M = {\mathbb {S}}^2$ and $N\in M$ endowed with a singular $(\text {Isom}^+({\mathbb {E}}^2),{\mathbb {E}}^2)$-structure induced by a stereographic projection ${\mathbb {S}}^2{\setminus } \{N\} \rightarrow {\mathbb {E}}^2$. On the one hand, M is a singular Euclidean manifold with $\text {Sing}(M)=\{N\}$ and ${{\widetilde{M}}}^{\text {Sing}(M)} = M$. On the other hand, the developing map ${\mathcal {D}}:\text {Reg}(M)\rightarrow {\mathbb {E}}^2$ given by the stereographic projection cannot be extended continuously and no sequence $x_n\xrightarrow {n\rightarrow +\infty } N$ with $\forall n\in {\mathbb {N}}, x_n\in \text {Reg}(M)$ is such that $({\mathcal {D}}(x_n))_{n\in {\mathbb {N}}}$ converges.

The present section lays out distinctions between singularities in (G, X)-manifolds based on the existence or absence of developing maps. We thus introduce notions of tame and virtually tame singular (G, X)-manifolds; the section revolves around the localization of these notions. Localization achieved in Theorems 4 and 5.

In the whole section, we need a guarantee that we are allowed to consider the maximal covering possibly branched over any skeletal subset of any open subset. We thus make an extra assumption on X.

Definition 4.4

A topological space X is locally unloopable if it is locally path-connected and if for all $x\in X$ and all neighborhood ${\mathcal {U}}$ of x, there exists an open neighborhood ${\mathcal {V}}\subset {\mathcal {U}}$ of x which is semi-locally simply connected.

Lemma 4.5

Let (G, X) be an analytical structure with X locally unloopable. Then every connected singular (G, X)-manifold M admits a maximal covering possibly branched over some given skeletal subset S as long as $S\supset \text {Sing}(M)$.

Proof

Since $S\supset \text {Sing}(M)$, we have $M{\setminus } S = \text {Reg}(M){\setminus } S$. Since X is locally unloopable and since $\text {Reg}(M){\setminus } S$ is locally homeomorphic to X, in particular, $\text {Reg}(M){\setminus } S$ is locally unloopable. Since M is connected and $\text {Reg}(M){\setminus } S$ portly, then $\text {Reg}(M){\setminus } S$ is connected and thus unloopable. $\square$

In the whole section (G, X) is an analytical structure with X locally unloopable.

4.1 Ramified coverings, group actions

In this section, we prove natural technical properties one expects to hold for the theory to work smoothly.

Proposition 4.6

Let M be a singular (G, X)-manifold and let $N\xrightarrow {\pi } M$ be a branched covering.

N has a unique a.e. (G, X)-structure for which $\pi$ is an a.e. (G, X)-morphism. and $\text {Reg}(\pi )\supset \text {Reg}(N)\cap \text {Ord}(\pi )$.

Furthermore, the Galois group $\varGamma ({{\widetilde{M}}}^S/M)$ acts by a.e. (G, X)-morphisms.

Proof

By Lemma 2.16 there exists a unique a.e. (G, X)-structure on N such that $\pi$ is an a.e. (G, X)-morphism. Lemma 2.15 implies that

$$\begin{aligned} \text {Reg}(\pi )=\text {Reg}(N)\cap \{x ~|~ f \text { local homeo. at }x\}\supset \text {Reg}(N)\cap \text {Ord}(\pi ) \end{aligned}$$

The Galois group $\varGamma (N/M)$ acts by homeomorphisms on $\widetilde{M}^S$, and $\pi$ is an a.e. local homeomorphism. Denoting ${\mathcal {A}},{\mathcal {B}}$ the a.e. (G, X)-atlases of N, M respectively, we may thus apply Proposition 2.16

$$\begin{aligned} \gamma ^*{\mathcal {A}}= \gamma ^* \pi ^*{\mathcal {B}}=(\pi \circ \gamma )^*{\mathcal {B}}= \pi ^*{\mathcal {B}}= {\mathcal {A}}. \end{aligned}$$

In other words, $\gamma$ is an a.e. (G, X)-morphism. $\square$

Corollary 4.7

Let M be a singular (G, X)-manifold and let S be a skeletal subset of M containing $\text {Sing}(M)$. Then ${{\widetilde{M}}}^S$ admits a unique a.e. (G, X)-structure such that the natural projection ${{\widetilde{M}}}^S\rightarrow M$ is an a.e. (G, X)-morphism.

Furthermore, the Galois group $\varGamma ({{\widetilde{M}}}^S/M)$ acts by a.e. (G, X)-morphisms.

4.2 Developing map and tameness

In this section, M, N will denote connected singular (G, X)-manifolds. For brevity’s sake, whenever it makes sense, we will denote by ${{\widetilde{M}}}$ the maximal covering of M possibly branched over $\text {Sing}(M)$, which can also be denoted by $\widetilde{M}^{\text {Sing}(M)}$ in the notation of the previous section.

4.2.1 Developing maps

Definition 4.8

(developing map) Let $N\xrightarrow {p} M$ be a branched covering of singular (G, X)-manifold. A developing map ${\mathcal {D}}$ of $N\rightarrow M$ is any a.e. (G, X)-morphism $N \rightarrow X$.

We say that M admits a developing map if there exists a branched covering ${\widehat{M}} \rightarrow M$ possibly branched above $\text {Sing}(M)$ and a developing map of ${\widehat{M}} \rightarrow M$

For simplicity’s sake, whenever it makes sense, a developing map of ${{\widetilde{M}}}\rightarrow M$ is simply called a developing map of M.

Up to reduction to portly subset, the proofs of the following three Lemmas are identical to the usual proof in the regular context and are thus skipped.

Lemma 4.9

Let $N\xrightarrow {f_1,f_2} X$ be a.e. (G, X)-morphisms, then there exists a unique $g\in G$ such that $f_1=gf_2$.

Lemma 4.10

Let M be a singular (G, X)-manifold and $\varGamma$ be a group acting on N by a.e. (G, X)-morphisms.

For any a.e. (G, X)-morphism $M\xrightarrow {f} X$ there exists a unique morphism $\rho :\varGamma \rightarrow G$ such that f is $\rho$-equivariant.

Definition 4.11

Let $N\xrightarrow {p} M$ be a quasi-Galoisian branched covering of singular (G, X)-manifold admitting a developing map ${\mathcal {D}}$. The holonomy of $N\rightarrow M$ (associated to ${\mathcal {D}}$) is the morphism $\rho$ of Lemma 4.10.

Remark 4.12

A developing map ${\mathcal {D}}$ of a quasi-Galoisian covering $M\rightarrow N$ sends points to some fixed point of their stabilizer: ${\mathcal {D}}(x) \in \text {Fix}(\rho (\varGamma _x))$.

Remark 4.13

Let M be a singular (G, X)-manifold. The holonomy of $\widetilde{M} \rightarrow M$ is indeed the holonomy of $\text {Reg}(M)$ in the usual sense.

Lemma 4.14

Let $N\xrightarrow {p} M$ be a quasi-Galoisian branched covering of singular (G, X)-manifold. If it admits a couple $({\mathcal {D}},\rho )$ of developing map and holonomy, then all other such couples are obtained via conjugation, ie: if $({\mathcal {D}}',\rho ')$ is another couple developing map and holonomy, then there exists a unique $g\in G$ such that $({\mathcal {D}}',\rho ')= (g\circ {\mathcal {D}},\rho ^g)$ with $\rho ^g: \gamma \mapsto g\rho (\gamma )g^{-1}$.

Lemma 4.15

Let $M\xrightarrow {p} N$ be a quasi-Galoisian branched covering of singular (G, X)-manifolds. Then, the following are equivalent:

• (i) there exists an a.e. (G, X)-morphism $M\rightarrow X$ and the holonomy of $M\rightarrow N$ is trivial,

• (ii) there exists an a.e. (G, X)-morphism $N\rightarrow X$.

Proof

Assume (i) and consider some a.e. (G, X)-morphism $M\xrightarrow {{\mathcal {D}}} X$ as well as the equivalence relation $x\sim y$ if $p(x)=p(y)$ for $x,y\in M$. By Lemma 3.49, the action of $\varGamma (M/N)$ has a dense orbit in the fiber of p then the equivalence classes of $\sim$ are the closure of orbits of $\varGamma (M/N)$. Furthermore, since $\rho =1$ then ${\mathcal {D}}$ is constant on the orbit of $\varGamma (M/N)$ and continuous, hence constant on the equivalence classes of $\sim$. Therefore, ${\mathcal {D}}$ induces a continuous map $\sim \backslash M \rightarrow X$. Moreover, p induces a continuous map $\sim \backslash M \rightarrow N$ which is open by Corollary 3.21, injective by definition and surjective since p is surjective; hence $\sim \backslash M \rightarrow N$ is a homeomorphism. We thus constructed a continuous map ${{\overline{{\mathcal {D}}}}}:N \rightarrow X$. Notice that ${{\overline{{\mathcal {D}}}}}$ is a (G, X)-morphism on $\text {Ord}(N)$ by usual results on (G, X)-manifolds. Finally, ${\mathcal {D}}$ is an a.e. (G, X)-morphism.

Assume (ii) and consider some $N\xrightarrow {{{\overline{{\mathcal {D}}}}}} X$, the map $M \xrightarrow {{{\overline{{\mathcal {D}}}}} \circ p} X$ is thus an a.e. (G, X)-morphism and

$$\begin{aligned} \forall \gamma \in \varGamma (M/N),\quad {\mathcal {D}}\circ \gamma = {{\overline{{\mathcal {D}}}}}\circ p\circ \gamma = {{\overline{{\mathcal {D}}}}}\circ p = {\mathcal {D}}\end{aligned}$$

so $\rho = 1$ ie the holonomy of $M\rightarrow N$ is trivial. $\square$

Lemma 4.16

Let $f: M\rightarrow N$ be a morphism of singular (G, X)-manifolds, and let ${\hat{M}}$ and ${\hat{N}}$ be branched coverings of M and N respectively. If ${\hat{f}}:{\hat{M}} \rightarrow {\hat{N}}$ is a lift of f, then ${\hat{f}}$ is a morphism of singular (G, X)-manifolds.

Proof

One can restrict to portly subsets to reduce the Lemma to the case where M, N are regular, ${\hat{M}},{\hat{N}}$ are unbranched coverings, and f is a (G, X)-morphism. Standard results apply. $\square$

Proposition 4.17

Let M be a singular (G, X)-manifold. The following are equivalent:

• (i) there exists an a.e. (G, X)-morphism ${{\widetilde{M}}}\rightarrow X$,

• (ii) there exists a branched covering of $N\xrightarrow {p} M$ which admits a developing map.

Proof

Clearly, $(i)\Rightarrow (ii)$. Assume (ii) and consider some branched covering $N\xrightarrow {p}M$ and a developing map $N\xrightarrow {{\mathcal {D}}} X$. Denote by $S:=M{\setminus } \text {Ord}_p(M)$ and ${{\widetilde{S}}}$ the lift of S to ${{\widetilde{M}}}:=\widetilde{M}^{\text {Sing}(M)}$. Since $S\subset S\cup \text {Sing}(M)$, by Proposition 3.26, the map $N \xrightarrow {{\mathcal {D}}} X$ lifts to an a.e. (G, X)-morphism ${\widehat{M}}:= {{\widetilde{M}}}^{S\cup \text {Sing}(M)}\xrightarrow {~~{\widehat{{\mathcal {D}}}}~~} X$. The developing map of $\text {Reg}(M)$ is a (G, X)-morphism $\widetilde{\text {Reg}}(M)\xrightarrow {{\mathcal {D}}_0} X$ thus a (G, X)-morphism ${\widehat{M}}' \xrightarrow {{\widehat{{\mathcal {D}}}}_0} X$ were ${\widehat{M}}'$ is the universal covering of $\widetilde{\text {Reg}}(M){\setminus } \widetilde{S}$ which embeds naturally in ${\widehat{M}}$ since it is the universal covering of $\text {Reg}(M){\setminus } S$. By Lemma 4.15, the holonomy

$$\begin{aligned} \varGamma :=\varGamma ({\widehat{M}}'/{\widetilde{\text {Reg}}}(M)) = \varGamma ({\widehat{M}}/{{\widetilde{M}}}) \xrightarrow {~~~\rho ~~~} G \end{aligned}$$

of ${\widehat{M}}' \rightarrow \widetilde{\text {Reg}}(M)$ is trivial. Futhermore, there exists $g\in G$ such that $g\circ \widehat{\mathcal {D}}_{|{\widehat{M}}'} = {\widehat{{\mathcal {D}}}}_0$; therefore ${\widehat{{\mathcal {D}}}}_0$ extends continuously to ${\widehat{M}} \xrightarrow {{\widehat{{\mathcal {D}}}}_0} X$. Since the action of $\varGamma$ on ${\widehat{{\mathcal {D}}}}_{0|{\widehat{M}}'}$ is trivial and since ${\widehat{M}}'$ is dense in ${\widehat{M}}$, the action of $\varGamma$ on ${\widehat{{\mathcal {D}}}}_0$ is trivial. We can thus apply Lemma 4.15 again to obtain a continuous extension of ${\mathcal {D}}_0$ to ${{\widetilde{M}}}$. $\square$

4.2.2 Tame singularities

Following the discussion of the previous sections, we introduce the notion of time singular (G, X)-manifolds.

Definition 4.18

A singular (G, X)-manifold M is tame if it admits a developing map.

Since the notion of developing map is global, we need to localize tameness to ease the manipulation of this property.

Lemma 4.19

Let M, N be singular (G, X)-manifolds and let $M\rightarrow N$ be an a.e. (G, X)-morphism. If N is tame, then M is tame.

Proof

The morphism $M\rightarrow N$ lifts to a morphism $\widetilde{M}\rightarrow {{\widetilde{N}}}$. We can compose the latter by the developing map ${{\widetilde{N}}} \rightarrow X$ of N to obtain a developing map of M. $\square$

Corollary 4.20

A branched covering of a tame singular (G, X)-manifold is tame.

Corollary 4.21

Open subsets of tame singular (G, X)-manifolds are tame.

Theorem 4

Let M be a singular (G, X)-manifold the following are equivalent:

• 1. M is tamely singular

• 2. M locally tamely singular.

Proof

Denote by ${{\widetilde{M}}} \xrightarrow {p} M$ the maximal covering of M ramified above $\text {Sing}(M)$.

Assume M tamely singular, for any $x\in M$ and any neighborhood ${\mathcal {U}}$ of x, by local connectivity, there exists an connected open neighborhood ${\mathcal {V}}\subset {\mathcal {U}}$ of x. Take any connected component ${\mathcal {W}}$ of $p^{-1}({\mathcal {V}})$ so that ${\mathcal {W}}\rightarrow {\mathcal {V}}$ is a branched covering, by universality there exists a branched covering ${\widetilde{{\mathcal {V}}}}\xrightarrow {q} {\mathcal {W}}$. Take a developing map ${\mathcal {D}}$ of M, the map ${\mathcal {D}}_{|{\mathcal {W}}}\circ q$ is a developing map of ${\mathcal {V}}$ hence ${\mathcal {V}}$ is tamely singular.

Assume M locally tamely singular. Let ${{\widetilde{x}}}\in \widetilde{M}$ and let ${\mathcal {U}}$ be an open, connected neighborhood of $x:=p({{\widetilde{x}}})$ admitting a developing map. Define $\widetilde{\mathcal {U}}\xrightarrow {\pi } {\mathcal {U}}$ the natural branched covering. The natural injection ${\mathcal {U}}\xrightarrow {\iota } M$ lifts to an a.e. (G, X)-morphism ${\widetilde{{\mathcal {U}}}}\xrightarrow {{\widetilde{\iota }}} \widetilde{M}$. Let $\text {Reg}({{\widetilde{M}}}) \xrightarrow {{\mathcal {D}}_M} X$ be a (G, X)-morphism, the map $\text {Reg}({\widetilde{{\mathcal {U}}}}) \xrightarrow {{\mathcal {D}}_M\circ {\widetilde{\iota }}} X$ is a (G, X)-morphism and extends continuously to an a.e. (G, X)-morphism ${\widetilde{{\mathcal {U}}}}\xrightarrow {{\mathcal {D}}_{\mathcal {U}}} X$. Let ${\hat{{\mathcal {U}}}}$ be the connected component of ${\widetilde{\iota }} ({\widetilde{{\mathcal {U}}}})$ in $p^{-1}({\mathcal {U}})$; by Lemma 3.20, ${\widehat{{\mathcal {U}}}} \xrightarrow {p} {\mathcal {U}}$ is a branched covering, by Proposition 3.26 there thus exists a map ${\widetilde{{\mathcal {U}}}} \xrightarrow {\pi '} {\widehat{{\mathcal {U}}}}$ such that $p\circ \pi ' = \pi$. Since ${\widetilde{{\mathcal {U}}}}/{\widehat{{\mathcal {U}}}}$ is quasi-Galoisian, this map is unique up to the action of $\varGamma ({\widetilde{{\mathcal {U}}}}/{\widehat{{\mathcal {U}}}})$. Since $p \circ {\widetilde{\iota }} = \pi$, we conclude that $\pi ' = {\widetilde{\iota }} \circ \gamma$ for some $\gamma \in \varGamma ({{\widetilde{M}}}/{\widehat{M}})$. In particular, $\widetilde{\iota }^{|{\widehat{{\mathcal {U}}}}}$ is a branched covering.

Using the same argumentation as in the proof of Proposition 4.17, we show that ${\mathcal {D}}_{{\mathcal {U}}}$ descends to an a.e. (G, X)-morphism ${\widehat{{\mathcal {U}}}} \rightarrow X$ which extends continuously ${\mathcal {D}}_{M|{\widehat{{\mathcal {U}}}}}$. Finally, ${\mathcal {D}}_M$ extends continuously at ${{\widetilde{x}}}$ and, since ${{\widetilde{x}}}$ is arbitrary, to the whole ${{\widetilde{M}}}$. $\square$

The following remark, though trivial, is important.

Remark 4.22

Let M be a tamely singular (G, X)-manifold. If M admits an injective developing map $N\xrightarrow {{\mathcal {D}}}X$ for some branched covering N of M then M is isomorphic to $\varGamma (N/M)\backslash {\mathcal {D}}(N)$ where

• $\varGamma (N/M)$ acts on X via the holonomy of ${\mathcal {D}}$;

• ${\mathcal {D}}(N)$ is endowed with the topology making ${\mathcal {D}}$ an homeomorphism.

The specification of the topology is important as the developing map ${\mathcal {D}}$, though continuous, may not be open in neighborhoods of singular points.

Example 4.23

Take X the closed unit disc in ${\mathbb {R}}^2$ and identify the open disc with the pointcaré disc ${\mathbb {H}}$. Take G, the group of isometries of the Poincaré disc. Note that G acts by homeomorphisms on X. Consider M a genus g surface and $S\subset M$ a finite subset such that $2g-2+s>0$. Endow $M{\setminus } S$ with a finite volume complete hyperbolic metric. On the one hand, M is a tamely singular (G, X)-manifold with injective developing map $\widetilde{M} \xrightarrow {{\mathcal {D}}} X$. On the other hand, an open neighborhood ${\mathcal {U}}$ of a singular point x of ${{\widetilde{M}}}$ is homeomorphic to a domain $\{r<r_0\}$ in the “infinite angle disc” ${\mathbb {D}}_\infty$ introduced in Example 2.25. We may choose ${\mathcal {U}}$ so that ${\mathcal {D}}(U)$ is a horodisc centered at ${\mathcal {D}}(x)$. Such a domain is not open for the topology of X.

4.3 Singular models

In common settings, singularities are not arbitrary: they are assumed to be isomorphic to some model such as $(\mathbb E^2_{\theta })_{\theta >0}$ for singular locally Euclidean surfaces or $({\mathbb {E}}^{1,2}_\alpha )_{\alpha >0}$ for flat 3-spacetimes with massive particles.

4.3.1 Analytic family

Definition 4.24

Let M be a singular (G, X)-manifold. The automorphisms group of M denoted $\text {Aut}(M)$ is the group of isomorphisms of singular (G, X)-manifolds from M to itself.

Definition 4.25

A family $(X_\alpha )_{\alpha \in A}$ of singular (G, X)-manifolds each endowed with a non-empty subset $S_\alpha \subset \text {Sing}(X_\alpha )$ is an analytic family of model spaces if for all $\alpha _1,\alpha _2\in A$ and all a.e. (G, X)-isomorphism ${\mathcal {U}}_1\xrightarrow {\varphi } {\mathcal {U}}_2$ where ${\mathcal {U}}_1,{\mathcal {U}}_2$ are connected open subsets of $X_{\alpha _1}$ and $X_{\alpha _2}$ respectively we have:

$$\begin{aligned} {\mathcal {U}}_1\cap S_{\alpha _1}\ne \emptyset \Rightarrow \alpha _1=\alpha _2\quad \text {and}\quad \exists \phi \in \text {Aut}(X_{\alpha _1}), \varphi =\phi _{|{\mathcal {U}}_1}^{|{\mathcal {U}}_2}. \end{aligned}$$

Definition 4.26

($X_A$-atlas) Let $(X_\alpha )_{\alpha \in A}$ be an analytic family of model spaces and let M be a singular (G, X)-manifold.

For $\alpha \in A$, an $X_\alpha$-chart around $x\in \text {Sing}(M)$ is a triplet $({\mathcal {U}},{\mathcal {V}},\phi )$ with $x\in {\mathcal {U}}\subset M,\phi (x)\in S_\alpha , {\mathcal {V}}\subset X_\alpha$ open and connected; and ${\mathcal {U}}\xrightarrow {\phi } {\mathcal {V}}$ an isomorphism. If such a chart exists, we say that x has type $\alpha$.

An $X_A$-chart is an $X_\alpha$-chart for some $\alpha \in A$. An $X_A$-atlas is a collection of $X_A$-charts covering M.

Definition 4.27

Let $(X_\alpha )_{\alpha \in A}$ be an analytic family of model spaces and let M be a singular (G, X)-manifold.

A $X_A$-manifold is a singular (G, X)-manifold M admitting a $X_A$-atlas

Remark 4.28

A singular point $x\in \text {Sing}(M)$ of a $X_A$-manifold M has exactly one type. Indeed, let ${\mathcal {U}}_i\xrightarrow {\varphi _i} {\mathcal {V}}_i\subset X_{\alpha _i}$ be isomorphisms with ${\mathcal {U}}_i,{\mathcal {V}}_i$ open for $i\in \{1,2\}$ and with $x\in {\mathcal {U}}_1\cap {\mathcal {U}}_2$. Restricting $\varphi _1,\varphi _2$ if necessary, we may assume ${\mathcal {U}}_1={\mathcal {U}}_2$ connected so that ${\mathcal {V}}_1\xrightarrow {\varphi _2\circ \varphi _1^{-1}}{\mathcal {V}}_2$ is an isomorphism, Moreover, ${\mathcal {V}}_1$ contains the singular point $\varphi _1(x)\in S_{\alpha _1}$ so by analyticity $\alpha _1=\alpha _2$.

Remark 4.29

By Theorem 4, a $X_A$-manifold is tame if and only if all models are tame.

Example 4.30

It follows from Proposition 1.3 of [17] that the family $({{\mathbb {E}}}^{1,2}_{\theta })_{\theta \ge 0}$ is analytic.

Counter-Example 4.31

Start from $\varSigma$ a singular ${\mathbb {S}}^2$-manifold homeomorphic to a sphere with $s\ge 3$ conical singularities of respective angles $(\theta _i)_{i\in [\![1,s]\!]}$. We know from Troyanov [49] that one can construct such a surface for arbitrary $(\theta _i)_{i\in [\![1,s]\!]}$ as long as

$$\begin{aligned} 0<\sum _{i=1}^s( \theta _i -2\pi ) + 4\pi \le \min (4\pi , \theta _i: i\in [\![1,s]\!]). \end{aligned}$$

Apply the Thurston suspension method described in Sect. 2.4.2, the constructed manifold M is a singular $(\text {SO}(4),{\mathbb {S}}^3)$-manifold (we may either apply by Proposition 2.32 or check that directly). We call O its center.

An automorphism of M has to fix O since the singular locus is homeomorphic to a line except at O; furthermore, it preserves distances and geodesics. By considering the sphere of some radius $\varepsilon >0$ centered at O, we see that the natural map $\text {Aut}(\varSigma )\rightarrow \text {Aut}(M)$ is a group isomorphism. As a consequence, except for very particular $\varSigma$, $\text {Aut}(M)$ is trivial. For instance, if all the $\theta _i$ are different then $\text {Aut}(M)=\{Id\}$. These remarks hold for all neighborhoods of O.

For a generic $\varSigma$, since locally we may construct a rotation around any of the axes, and since those cannot be extended as an automorphism of M, we conclude that for $S\subset \text {Sing}(M)$, (M, S) is analytic if and only if $S=\{O\}$.

4.3.2 A motivational example: the BTZ model space

The BTZ model space ${{\mathbb {E}}}^{1,2}_{0}$ is defined as ${\mathbb {R}}^3$ endowed with the singular ${{\mathbb {E}}}^{1,2}_{}$-structure induced by the flat Lorentzian metric $\text {d}s^2=-2\text {d}\tau \text {d}{\mathfrak {r}}+\text {d}{\mathfrak {r}}^2+ r^2 \text {d}\theta$ in cylindrical coordinates. The singular locus of ${{\mathbb {E}}}^{1,2}_{0}$ is then $\text {Sing}({{\mathbb {E}}}^{1,2}_{0})=\{{\mathfrak {r}}=0\}$ and the regular locus is $\text {Reg}({\mathbb {E}}^{1,2}_0):= \{{\mathfrak {r}}>0\}$. Following example 2.25, from which we reuse notations, we denote the maximal covering of ${\mathbb {E}}^{1,2}_0$ possibly branched over $\text {Sing}({\mathbb {E}}^{1,2}_0)$ by ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$. Since ${\mathbb {E}}^{1,2}_0$ is simply ${\mathbb {R}}^3$ and $\text {Sing}({\mathbb {E}}^{1,2}_0)$ is a simply a line, ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ is homeomorphic to the maximal covering of ${\mathbb {R}}^3$ branched over a line denoted by ${\mathbb {C}}_\infty ^{(3)}$ and parameterize using cylindrical coordinates $(\tau ,{\mathfrak {r}},\theta )\in {\mathbb {R}}\times {\mathbb {R}}_+\times {\mathbb {R}}$. A natural candidate for a developing map is given by

$$\begin{aligned} \displaystyle {\mathcal {D}}:\begin{array}{l|rcl} &{} \displaystyle {{\widetilde{{\mathbb {E}}}}}^{1,2}_0 &{} \longrightarrow &{} \displaystyle {\mathbb {E}}^{1,2} \\ &{} \displaystyle \left( \tau ,{\mathfrak {r}},\frac{\theta }{2\pi }\right) &{} \longmapsto &{} \displaystyle \begin{pmatrix}t \\ x \\ y\end{pmatrix}=\begin{pmatrix} \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 \\ \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 -{\mathfrak {r}}\\ -{\mathfrak {r}}\theta \end{pmatrix} \\ &{} \displaystyle (\tau ,0,\cdot ) &{} \longmapsto &{} \displaystyle \begin{pmatrix}\tau \\ \tau \\ 0\end{pmatrix}\end{array} \end{aligned}$$

which can be checked to be a ${\mathbb {E}}^{1,2}$-morphism on $\text {Reg}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)=\{{\mathfrak {r}}>0\}$ but is discontinuous at every points of $\text {Sing}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)=\{{\mathfrak {r}}=0\}$. Furthermore, one may check that for all $x=(\tau ,0,0)\in \text {Sing}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)$ we have

$$\begin{aligned} \bigcap _{{\mathcal {U}}\ni x}\overline{{\mathcal {D}}(\text {Reg}({\mathcal {U}}))}=\{(\lambda ,\lambda ,0)~:~\lambda \ge \tau \} \end{aligned}$$

so that there is no way to extend ${\mathcal {D}}$ continusouly to $\{{\mathfrak {r}}=0\}$ keeping the standard topologies of ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ and ${{\mathbb {E}}}^{1,2}_{}$.

Consider the topology ${\mathcal {T}}$ of ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ generated by the standard topology ${\mathcal {T}}_0$ and the sets of the form

$$\begin{aligned} {\mathcal {U}}_\lambda = \left\{ (\tau ,{\mathfrak {r}},\theta )\in {{\widetilde{{\mathbb {E}}}}}^{1,2}_0~|~ {\mathfrak {r}}\theta ^2< \lambda \right\} ,\quad \lambda \in {\mathbb {R}}_+^*. \end{aligned}$$

Then ${\mathcal {D}}:({{\widetilde{{\mathbb {E}}}}}^{1,2}_0,{\mathcal {T}})\rightarrow {{\mathbb {E}}}^{1,2}_{}$ is continuous and element of $\text {Aut}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)$ are ${\mathcal {T}}$-continuous, furthermore the quotient topology induced on ${\mathbb {E}}^{1,2}_0$ is the usual topology. Finally, we note that $\text {Reg}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)$ is ${\mathcal {T}}$-portly.

4.3.3 Virtually tame models

Some model spaces of interest, such as the BTZ model space, are not tame but are almost tame in the sense that we may extend the developing map in a unique fashion, allowing us to construct a developing map on $X_A$-manifolds.

Definition 4.32

A singular (G, X)-manifold M is virtually tame if there exists a first countable locally path connected (strong) topology ${\mathcal {T}}$ on ${{\widetilde{M}}}$ thinner than the natural (weak) topology such that:

• (A) The quotient topology induced by ${\mathcal {T}}$ on M is the natural one.

• (B) the developing map ${\mathcal {D}}:\text {Reg}({{\widetilde{M}}})\rightarrow X$ admits a ${\mathcal {T}}$-continuous extension;

• (C) elements $\varGamma ({{\widetilde{M}}}/M)$ are ${\mathcal {T}}$-continuous;

• (D) the lift of $\text {Reg}(M)$ to ${{\widetilde{M}}}$ is ${\mathcal {T}}$-portly in ${{\widetilde{M}}}$.

We call such a ${\mathcal {T}}$ a tamifying topology.

Definition 4.33

A singular (G, X)-manifold M is locally Galoisian if for every ${\mathcal {U}}\subset {\mathcal {M}}$ open, $\text {Reg}({\mathcal {U}})$ is semi-locally simply connected in ${\mathcal {U}}$.

The goal of this section is to prove the following localization property.

Theorem 5

Let $(X_\alpha )_{\alpha \in A}$ be an analytical family of locally Galoisian model spaces. If for every $\alpha \in A$, there exists a tamifying topology ${\mathcal {T}}_\alpha$ such that the group $\text {Aut}(\widetilde{X}_\alpha )$ acts ${\mathcal {T}}_\alpha$-continuously, then every $X_A$-manifold is virtually tame.

To this end, we will need technical results on branched coverings involving two topologies on the same underlying space. In every instance, we shall refer to the strong and weak topologies, the former being the thinner of the two.

Definition 4.34

Let $(M,{\mathcal {T}}_M),(N,{\mathcal {T}}_N)$ be topological spaces and Let $M\xrightarrow {p} N$ be a continuous map. For any topology ${\mathcal {T}}$ on N define $p^*{\mathcal {T}}$ the topology of M generated by ${\mathcal {T}}_M$ and the ${\mathcal {T}}_M$-connected components of $p^{-1}({\mathcal {O}})$ for ${\mathcal {O}}\in {\mathcal {T}}$.

Lemma 4.35

Let M be a first countable, connected locally path connected Hausdorff topological space. Let $S\subset M$ be a skeletal subset such that $M{\setminus } S$ is semi-locally simply connected in M; consider a sub-covering $\widetilde{M}^S\xrightarrow {p}N\xrightarrow {q}M$.

Let ${\mathcal {T}}$ be a (strong) thinner first countable and locally path-connected topology on N for which elements of $\varGamma (N/M)$ are continuous. Consider the induced strong topology $p^*{\mathcal {T}}$ on ${{\widetilde{M}}}^S$. Assume, in addition, there exists some ${\mathcal {R}}\subset \text {Ord}_p(N)$ strongly portly in N on which strong and weak topologies agree.

Then, we have the following

• (a) ${{\widetilde{M}}}^S$ is strongly first countable connected locally path connected;

• (b) strong and weak topologies agree on $p^{-1}({\mathcal {R}})$;

• (c) $p^{-1}({\mathcal {R}})$ is strongly portly;

• (d) elements of $\varGamma ({{\widetilde{M}}}^S/M)$ are strongly continuous;

• (e) ${{\widetilde{M}}}^S\xrightarrow {p}N$ is a branched covering for the strong topologies.

Remark 4.36

Intuitively, if $(M,{\mathcal {T}}_M)\xrightarrow {p}(N,{\mathcal {T}}_N)$ is a spread and ${\mathcal {T}}$ is thinner than ${\mathcal {T}}_N$, then the strong topology $p^*{\mathcal {T}}$ is the coarsest topology on M such that $(M,p^*{\mathcal {T}})\xrightarrow {p}(N,{\mathcal {T}})$ is a spread. However, the definition does not guarantee that ${\mathcal {T}}_M$-connected components are $p^*{\mathcal {T}}$-connected components. Point (e) above is thus non-trivial.

Proof

To begin with, we define ${\widehat{{\mathcal {R}}}}:= p^{-1}({\mathcal {R}})$ and note that by definition of the ordinary loci, ${\widehat{{\mathcal {R}}}} \xrightarrow {p}{\mathcal {R}}$ is a covering for the weak topologies. Then, it is not difficult to see that $(p_{|{\widehat{{\mathcal {R}}}}}^{|{\mathcal {R}}})^*{\mathcal {T}}_{|{\mathcal {R}}} = (p^*{\mathcal {T}})_{|{\mathcal {R}}}$ so that point (b) is clear. We also note that it follows from the definitions that p is continuous for the strong topologies.

To show point (d), consider some $\gamma \in \varGamma (\widetilde{M}^S/M)$ and take some ${{\overline{\gamma }}}\in \varGamma (N/M)$ such that $p\circ \gamma = {{\overline{\gamma }}}\circ p$. For ${\widehat{{\mathcal {O}}}}$ a weak connected component of some $p^{-1}({\mathcal {O}})$ with ${\mathcal {O}}$ strong open, since $\gamma$ is a weak homemorphism $\gamma ^{-1}({\widehat{{\mathcal {O}}}})$ is a weak connected component of $(p\circ \gamma )^{-1}({\mathcal {O}})=(\overline{\gamma }\circ p )^{-1}({\mathcal {O}})$. Since ${{\overline{\gamma }}}$ is strongly continuous, ${{\overline{\gamma }}}^{-1}({\mathcal {O}})$ is strongly open so that ${\widehat{{\mathcal {O}}}}$ is strongly open since it is a weak connected component of $p^{-1}({{\overline{\gamma }}}^{-1}({\mathcal {O}}))$.

Claim: For all strong open ${\widehat{{\mathcal {O}}}}\subset {{\widetilde{M}}}^S$ that is a weak connected component $p^{-1}({\mathcal {O}})$ for some strong open ${\mathcal {O}}\subset N$ then ${\widehat{{\mathcal {O}}}}\cap \widehat{\mathcal {R}}\ne \emptyset$; Furthermore, for all ${\hat{y}}\in {{\widetilde{M}}}^S$ and for all strong neighborhood ${\widehat{O}}'\ni {\hat{y}}$, there exists ${\widehat{{\mathcal {O}}}}\ni {\hat{y}}$ such that ${\widehat{{\mathcal {O}}}}\subset {\widehat{{\mathcal {O}}}}'$ and such that for all ${\hat{x}}\in {\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$, there exists a a weakly continuous path ${\hat{\gamma }}: {\hat{x}}\rightsquigarrow {\hat{y}}$ with ${\hat{\gamma }}([0,1[)\subset {\widehat{{\mathcal {R}}}}\cap {\widehat{{\mathcal {O}}}}$. All such paths are strongly continuous. We may assume that ${\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$ is connected.

Indeed, take ${\widehat{{\mathcal {O}}}},{\mathcal {O}}$ as above and take ${\hat{y}}\in \widehat{\mathcal {O}}$ and $y=p({\hat{y}})$. Without loss of generality, we may assume ${\mathcal {O}}$ is strongly connected. Since N is strongly first countable connected locally path connected, since ${\mathcal {O}}$ is strongly connected and ${\mathcal {R}}$ strongly portly, ${\mathcal {O}}\cap {\mathcal {R}}\ne \emptyset$ so we may choose $x\in {\mathcal {O}}\cap {\mathcal {R}}\ne \emptyset$ and by Lemma 3.13 there exists a strongly continuous path $\gamma : x\rightsquigarrow y$ such that $\gamma ([0,1[)\subset {\mathcal {R}}$. By Proposition 3.52, ${{\widetilde{M}}}^S\rightarrow M$ is Galoisian and thus so is ${{\widetilde{M}}}^S\rightarrow N$. There thus exists some weakly continuous lift ${\hat{\gamma }}$ of $\gamma$ such that $\gamma (1)={\hat{y}}$. Therefore, ${\hat{y}}={\hat{\gamma }}(1)$ and $\gamma (0)$ are in the same weak connected component of $p^{-1}({\mathcal {O}})$ hence ${\hat{\gamma }}(0)\in {\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$ eg $\widehat{\mathcal {O}}\cap {\widehat{{\mathcal {R}}}}\ne \emptyset$.

Choose ${\hat{y}}\in {{\widetilde{M}}}^S$ and ${\widehat{{\mathcal {O}}}}'\ni {\hat{y}}$ and define $y:=p({\hat{y}})$, since ${{\widetilde{M}}}^S\rightarrow N$ is Galoisian, there exists some weak open neighborhood ${\mathcal {U}}\ni y$ such that the connected component of $p^{-1}({\mathcal {U}})$ has exactly one preimage of y in each weak connected componen. Hence, choosing ${\widehat{{\mathcal {O}}}}$ and ${\mathcal {O}}$ with the additional property that ${\mathcal {O}}\subset {\mathcal {U}}$ we have ${\widehat{{\mathcal {O}}}}\cap p^{-1}(y)=\{{\hat{y}}\}$. Then, for ${\hat{x}}\in {\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$ arbitrary and $x:=p({\hat{x}})$ we may consider the same $\gamma : x\rightsquigarrow y$ as before and then its weakly continuous lift ${\hat{\gamma }}$ such that $\hat{\gamma }(0)={\hat{x}}$. Therefore, ${\hat{\gamma }}(1)$ is in the same weak connected component of $p^{-1}({\mathcal {O}})$ as ${\hat{x}}$ so in ${\widehat{{\mathcal {O}}}}$ and thus ${\hat{\gamma }}(1)={\hat{y}}$. Since weak and strong topologies agree on ${\widehat{{\mathcal {R}}}}$, ${\hat{\gamma }}$ is strongly continuous on [0, 1[. Take any open ${\widehat{{\mathcal {O}}}}'\ni {\hat{y}}$ being a weak connected component of $p^{-1}({\mathcal {O}}')$ for some strong open ${\mathcal {O}}'$. Since $\gamma$ is strongly continuous, for some $\varepsilon >0$, we have $\gamma ([1-\varepsilon ,1])\subset {\mathcal {O}}'$ so that ${\hat{\gamma }}([1-\varepsilon ,1])\subset p^{-1}({\mathcal {O}}')$. Therefore for all $t\in [1-\varepsilon ,1[$, ${\hat{\gamma }}(t)$ and ${\hat{\gamma }}(1)={\hat{y}}$ are in the same weak connected component of $p^{-1}({\mathcal {O}}')$ thus ${\hat{\gamma }}([1-\varepsilon ,1])\subset \widehat{\mathcal {O}}'$. The path ${\hat{\gamma }}: {\hat{x}}\rightsquigarrow {\hat{y}}$ is thus strongly continuous.

Finally, if we consider in addition some ${\hat{z}}\in {\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$ and $z:= p({\hat{z}})$. Since $x,z \in {\mathcal {O}}\cap {\mathcal {R}}$ which is path connected, we may choose a path $\gamma :x \rightsquigarrow z$ which lifts to a path ${\hat{x}}\rightsquigarrow {\hat{z}}$ in ${\widehat{{\mathcal {R}}}} \cap {\widehat{{\mathcal {O}}}}$ hence ${\widehat{{\mathcal {O}}}} \cap {\widehat{{\mathcal {R}}}}$ is connected.

We now continue the proof of the Lemma.

• The first part of the claim shows that ${\widehat{R}}$ is strongly dense.

• Let ${\hat{y}}\in {{\widetilde{M}}}^S$ and $y=p({\hat{y}})$. Take a countable basis of neighborhood $({\mathcal {O}}_i)_{i\in I}$ of y. A basis of neighborhood of ${\hat{y}}$ is provided by weak connected components ${\widehat{{\mathcal {O}}}}_i$ of ${\hat{y}}$ in $p^{-1}({\mathcal {O}}_i)$ for $i \in I$. Hence, ${{\widetilde{M}}}^S$ is strongly first countable.

• Let ${\hat{y}}\in {{\widetilde{M}}}^S$ and $y=p({\hat{y}})$. Take ${\widehat{{\mathcal {O}}}}\ni {\hat{y}}$ such that the second part of the claim is satisfied (say for ${\widehat{{\mathcal {O}}}}'={{\widetilde{M}}}^S$). The statement implies that $\{{\hat{y}} \}\cup {\widehat{{\mathcal {O}}}}\cap {\widehat{{\mathcal {R}}}}$ is path connected. Take any ${\hat{z}}\in {\widehat{{\mathcal {O}}}}$ and choose $\widehat{O}_1\subset {\widehat{{\mathcal {O}}}}$ such that $\{{\hat{z}} \}\cup \widehat{\mathcal {O}}_1\cap {\widehat{{\mathcal {R}}}}$ is path connected. Since $\emptyset \ne {\widehat{{\mathcal {O}}}}_1\cap {\widehat{{\mathcal {R}}}}\subset \widehat{\mathcal {O}}\cap {\widehat{{\mathcal {R}}}}$ we may find a strongly continuous path $\hat{\gamma }$ from ${\hat{y}}$ to ${\hat{z}}$ via some arbitrary point ${\hat{x}}\in {\widehat{{\mathcal {O}}}}_1\cap {\widehat{{\mathcal {R}}}}$. Hence, ${{\widetilde{M}}}^S$ is strongly locally path connected.

• Since every point of ${{\widetilde{M}}}^S$ admits a strongly connected neighborhood, since ${\widehat{{\mathcal {R}}}}$ is weakly connected (thus strongly connected by point (b)) and ${\widehat{{\mathcal {R}}}}$ is strongly dense, ${{\widetilde{M}}}^S$ is strongly connected.

• ${\widehat{{\mathcal {R}}}}$ is strongly open as the only weak connected component of $p^{-1}({\mathcal {R}})$. It is also dense.

  Let ${\mathcal {W}}$ be a strongly connected open subset of $\widetilde{M}^S$, let ${\hat{x}},{\hat{y}}\in {\mathcal {W}}\cap {\widehat{{\mathcal {R}}}}$ and let $\hat{\gamma }_0:{\hat{x}}\rightsquigarrow {\hat{y}}$ be a strongly continuous path. For all $t\in [0,1]$, there exists a strong neighborhood ${\widehat{{\mathcal {O}}}}_t$ of ${\hat{\gamma }}(t)$ statisfying the second part of the claim (with ${\widehat{{\mathcal {O}}}}'={\mathcal {W}}$). Choose a family of such open sets, by the compactness of [0, 1] there exists sequences $t_0=0<t_1<\cdots <t_n=1$ and $\tau \in [0,1]^{[\![0,n-1]\!]}$ such that for all $i\in [\![0,n-1]\!]$, $\hat{\gamma }([t_i,t_{i+1}])\subset {\widehat{{\mathcal {O}}}}_{\tau _i}$. For each $i\in [\![1,n-1[\![$, we choose some ${\hat{x}}_i \in {\widehat{{\mathcal {O}}}}_{\tau _{i-1}}\cap {\widehat{{\mathcal {O}}}}_{\tau _i}\cap {\widehat{{\mathcal {R}}}}$ and define ${\hat{x}}_0={\hat{x}}$ and ${\hat{x}}_n={\hat{y}}$. We can construct a strongly continuous path ${\hat{\gamma }}':{\hat{x}}_0\rightsquigarrow {\hat{x}}_n$ by choosing for each $i\in [\![0, n-1]\!]$ a strongly continuous path ${\hat{x}}_i\rightsquigarrow {\hat{x}}_{i+1}$ taking its parameter in $[t_i,t_{i+1}]$ and its values in ${\widehat{{\mathcal {O}}}}_{\tau _i}\cap {\widehat{{\mathcal {R}}}}$. The path ${\hat{\gamma }}'$ takes its values in ${\mathcal {W}}\cap {\widehat{{\mathcal {R}}}}$ and joins ${\hat{x}}$ to ${\hat{y}}$, we conclude that ${\mathcal {W}}\cap {\widehat{{\mathcal {R}}}}$ is path connected.

  Finally, ${\widehat{{\mathcal {R}}}}$ is strongly portly.

• Consider the topology ${\mathcal {T}}'$ on ${{\widetilde{M}}}^S$ generated by strong connected components of preimage of strong open of N. Since for any strong open ${\mathcal {U}}$ the strong, connected components are included in a weak connected component, the topology ${\mathcal {T}}'$ is thinner than the strong topology on ${{\widetilde{M}}}^S$. On the other hand, the strong topology on ${{\widetilde{M}}}^S$ is locally connected, so any connected generator of ${\mathcal {T}}'$ is a strong open. We conclude that p is a spread for the strong topologies.

• Apply Lemma 3.19 with $X=\widetilde{M}^S, Y=N, X_1={\widehat{{\mathcal {R}}}}, Y_1={\mathcal {R}}$ for the strong topologies; to show that p is a branched covering for the strong topologies, it suffices to prove that for any path $\gamma : x\rightsquigarrow y$ such that $\gamma ([0,1[)\subset {\mathcal {R}}$, any partially lifts $\hat{\gamma }_{|[0,1[}$ extends strongly continuously at 1.

  Since p is a branched covering for the weak topologies, ${\hat{\gamma }}_{|[0,1[}$ admits a weak limit at 1, we denote $\hat{\gamma }$ its weak continuous extension so [0, 1]. The claim ensures that ${\hat{\gamma }}$ is actually strongly continuous. We conclude that p is a branched covering.

$\square$

Proof of Theorem 5

Assume that for every $\alpha \in A$, there exists a tamifying topology ${\mathcal {T}}_\alpha$ such that the group $\text {Aut}(\widetilde{X}_\alpha )$ acts ${\mathcal {T}}_\alpha$-continuously. Let M be a $X_A$-manifold. Denote by ${{\widetilde{M}}} \xrightarrow {p} M$ the maximal covering of M possibly branched over $\text {Sing}(M)$. For each $\alpha \in A$, we give ourselves a tamifying topology ${\mathcal {T}}_\alpha$ on $\widetilde{X}_\alpha$ and a ${\mathcal {T}}_\alpha$-continuous developing map ${\mathcal {D}}_\alpha$ given by hypothesis (b). We choose a developing map $\text {Reg}({{\widetilde{M}}})\xrightarrow {{\mathcal {D}}} X$.

Let $({\mathcal {U}},{\mathcal {V}},\phi )$ be a $X_A$-chart with ${\mathcal {V}}\subset X_\alpha$, let $\widetilde{X_\alpha } \xrightarrow {q} X_{\alpha }$ the maximal branched covering and let ${\widehat{{\mathcal {U}}}}$ be a connected component of $p^{-1}({\mathcal {U}})$. Take any connected component ${\widehat{{\mathcal {V}}}}$ of $q^{-1}({\mathcal {V}})$. By Lemma 3.20, ${\widehat{{\mathcal {U}}}}\xrightarrow {p} {\mathcal {U}}$ and ${\widehat{{\mathcal {V}}}}\xrightarrow {q}{\mathcal {V}}$ are branched coverings. Define ${\widetilde{{\mathcal {V}}}}\xrightarrow {r}\widehat{\mathcal {V}}$ and ${\widetilde{{\mathcal {U}}}} \xrightarrow {\ell } {\widehat{{\mathcal {U}}}}$ the natural maximal coverings and lift $\phi$ to an homemorphism $\widetilde{\mathcal {U}}\xrightarrow {{\widetilde{\phi }}}{\widetilde{{\mathcal {V}}}}$. Consider the topology $r^*{\mathcal {T}}_\alpha$ defined in Lemma 4.35 on $\widetilde{\mathcal {V}}$, we pull it back to ${\widetilde{{\mathcal {U}}}}$ by ${\widetilde{\phi }}$ to get $(r\circ {\widetilde{\phi }})^*{\mathcal {T}}_\alpha$ and then consider the quotient topology on ${\widehat{{\mathcal {U}}}}$. Using the universality of maximal branched covering, one may check this topology does not depend on $r,{\widetilde{\phi }}$ or $\ell$. We call ${\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}},\phi }$ the topology constructed this way on $p^{-1}({\mathcal {U}})$. We define the topology ${\mathcal {T}}$ on ${{\widetilde{M}}}$ generated by the topology of $\text {Reg}({{\widetilde{M}}})$ and the elements of ${\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}},\phi }$ on each for $({\mathcal {U}},{\mathcal {V}},\phi )$ going through all $X_A$-charts.

Since $X_\alpha$ is locally Galoisian, the branched coverings ${\widetilde{{\mathcal {V}}}}\rightarrow {\mathcal {V}}$, ${\widetilde{{\mathcal {V}}}}\rightarrow {\widehat{{\mathcal {V}}}}$, ${\widetilde{{\mathcal {U}}}}\rightarrow {\mathcal {U}}$, $\widetilde{\mathcal {U}}\rightarrow {\widehat{{\mathcal {U}}}}$ and ${{\widetilde{X}}}_\alpha \rightarrow X_\alpha$ are all Galoisian. Lemma 4.35 applies to ${\widetilde{{\mathcal {V}}}} \rightarrow {\widehat{{\mathcal {V}}}} \rightarrow {\mathcal {V}}$ taking ${\mathcal {R}}= {\widehat{{\mathcal {V}}}} \cap q^{-1}(\text {Reg}(X_\alpha ))$. Indeed, ${\mathcal {R}}$ is strongly portly in ${\widehat{{\mathcal {V}}}}$ by assumption (D) and since ${\widetilde{{\mathcal {V}}}}:= {\widetilde{{\mathcal {V}}}}^{\text {Sing}({\mathcal {V}})}$ we have

$$\begin{aligned} {\mathcal {R}}:={\widehat{{\mathcal {V}}}} \cap q^{-1}(\text {Reg}(X_\alpha ))= q^{-1}(\text {Reg}({\mathcal {V}}))\subset \text {Ord}_r(\widehat{\mathcal {V}}). \end{aligned}$$

• The topology ${\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}},\phi }$ on ${\widehat{{\mathcal {U}}}}$ does not depend on $({\mathcal {V}},\phi )$

  If we consider two $X_\alpha$-charts $({\mathcal {U}},{\mathcal {V}}_1,\phi _1)$ and $({\mathcal {U}},{\mathcal {V}}_2,\phi _2)$ then ${\mathcal {V}}_1\xrightarrow {\phi _1^{-1}\circ \phi _2} {\mathcal {V}}_2$ is an isomorphism. By analyticity, $\phi _1^{-1}\circ \phi _2$ is the restriction of an automorphism of $X_\alpha$ which lifts to an automorphism of ${{\widetilde{X}}}_\alpha$. Therefore, there exists $\psi \in \text {Aut}({{\widetilde{X}}}_\alpha )$ such that $\psi ({\widehat{{\mathcal {V}}}}_1)= {\widehat{{\mathcal {V}}}}_2$. By hypothesis, $\psi$ is ${\mathcal {T}}_\alpha$-continuous so $({\widehat{{\mathcal {V}}}}_1,{\mathcal {T}}_\alpha ) \simeq ({\widehat{{\mathcal {V}}}}_2,{\mathcal {T}}_\alpha )$ then ${\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}}_1,\phi _1}={\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}}_1,\phi _2}$.

• The strong topology on ${{\widetilde{M}}}$ is first countable and locally path connected:

  By Lemma 4.35, the strong topology on a given ${\widetilde{{\mathcal {U}}}}$ is first countable and locally path connected. Since ${\widetilde{{\mathcal {U}}}} \xrightarrow {\ell }{\widehat{{\mathcal {U}}}}$ is Galoisian, $\ell$ is open for the strong topologies, so the strong topology on ${\widehat{{\mathcal {U}}}}$ is first countable and locally path connected.

  • (A) The quotient topology induced by ${\mathcal {T}}_{\mathcal {U}}$ on ${\mathcal {U}}$ is by construction the pull back by $\phi$ of the quotient topology induced by $r^*{\mathcal {T}}_\alpha$ on ${\mathcal {V}}$. Since $\widetilde{\mathcal {V}}\xrightarrow {r} {\mathcal {V}}$ is a branched covering for the strong topology, the quotient topology of $r^*{\mathcal {T}}_\alpha$ on ${\widehat{{\mathcal {V}}}}$ is ${\mathcal {T}}_\alpha$ which induces the natural topology on ${\mathcal {V}}$.

    We deduce that the quotient topology induced by the strong topology on ${{\widetilde{M}}}$ is the natural topology M.

  • (B)

    • $\varGamma ({\widehat{{\mathcal {V}}}}/{\mathcal {V}})$ is the set of the restriction of the elements of $\varGamma ({{\widetilde{X}}}_\alpha /X_\alpha )$ stabilizing ${\widehat{{\mathcal {V}}}}$ setwise, these acts strongly continuously by hypothesis (C) on $X_\alpha$. By Lemma 4.35, the Galois group $\varGamma ({\widehat{{\mathcal {V}}}}/{\mathcal {V}})$ acts strongly continuously on ${\widetilde{{\mathcal {V}}}}$.

    • Denote ${\mathcal {D}}_{\mathcal {U}}:= {\mathcal {D}}_\alpha \circ r\circ {\widetilde{\phi }}$ which is strongly continuous and note that ${\mathcal {D}}_{{\mathcal {U}}|\text {Reg}({\widetilde{{\mathcal {U}}}})}$ is a (G, X)-morphism. The holonomy of ${\widetilde{{\mathcal {U}}}}\rightarrow {\widehat{{\mathcal {U}}}}$ is trivial hence for all $\gamma \in \varGamma (\widetilde{\mathcal {U}}/{\widehat{{\mathcal {U}}}})$, $({\mathcal {D}}_{\mathcal {U}}\circ \gamma )_{|\text {Reg}({\widetilde{{\mathcal {U}}}})} = {\mathcal {D}}_{{\mathcal {U}}|\text {Reg}({\widetilde{{\mathcal {U}}}})}$.

      By the previous point and strong density of $\text {Reg}(\widetilde{\mathcal {U}})$ we deduce that

      $$\begin{aligned} \forall \gamma \in \varGamma ({\widetilde{{\mathcal {U}}}}/ {\widehat{{\mathcal {U}}}}),\quad {\mathcal {D}}_{\mathcal {V}}\circ \gamma = {\mathcal {D}}_{{\mathcal {V}}}. \end{aligned}$$

    • Since ${\widetilde{{\mathcal {U}}}}\rightarrow {\widehat{{\mathcal {U}}}}$ is Galoisian, $\varGamma ({\widetilde{{\mathcal {U}}}}/{\widehat{{\mathcal {U}}}})$ acts transitively on the fibers of $\ell$. We can thus descend ${\mathcal {D}}_{{\mathcal {U}}}$ to an a.e. (G, X)-morphism ${\widehat{{\mathcal {U}}}}\xrightarrow {{\mathcal {D}}_{{\mathcal {U}},{\mathcal {V}},\phi }} X$ with ${\widehat{{\mathcal {U}}}}$ endowed with the strong topology.

      Since ${\mathcal {D}}_{|\text {Reg}({\widehat{{\mathcal {U}}}} )}=g{\mathcal {D}}_{{\mathcal {U}}|\text {Reg}({\widehat{{\mathcal {U}}}})}$ for some $g\in G$, the developing map ${\mathcal {D}}_{|\text {Reg}({\widehat{{\mathcal {U}}}})}$ extends to a strongly continuous map on ${\widehat{{\mathcal {U}}}}$. Finally, ${\mathcal {D}}_{|\text {Reg}({{\widetilde{M}}})}$ extends to an a.e. (G, X)-morphism for the strong topology on ${{\widetilde{M}}}$.

  • (C) Let $\gamma \in \varGamma ({{\widetilde{M}}}/M)$, for every $X_A$-chart $({\mathcal {U}},{\mathcal {V}},\phi )$, it sends connected component $\widehat{\mathcal {U}}$ of $p^{-1}({\mathcal {U}})$ to connected component so the local model of such a $p({\widehat{{\mathcal {U}}}})$ is the same as $p\circ \gamma (\widehat{\mathcal {U}})$. The topology ${\mathcal {T}}_{\mathcal {U}}$ on $\gamma ({\widehat{{\mathcal {U}}}})$ can then be constructed choosing the maximal branched covering $\widetilde{\mathcal {U}}\xrightarrow {\gamma \circ \ell } \gamma ({\widehat{{\mathcal {U}}}})$. As a consequence, the strong topology on $\gamma ({\widehat{{\mathcal {U}}}})$ is the image by $\gamma$ of the strong topology on ${\widehat{{\mathcal {U}}}}$. Therefore, $\gamma ^{-1}$ is strongly continuous. We deduce that $\varGamma ({{\widetilde{M}}}/M)$ acts strongly continuously on $\widetilde{M}$.

  • (D) Recall that we applied Lemma 4.35 with ${\mathcal {R}}=q^{-1}(\text {Reg}({\mathcal {V}}))$ so that

    $$\begin{aligned} r^{-1}({\mathcal {R}})\subset \text {Ord}_{q\circ r}({\widetilde{{\mathcal {V}}}})\cap \text {Reg}({\widetilde{{\mathcal {V}}}}) = \text {Ord}_{p\circ \ell \circ {\widetilde{\phi }}}({\widetilde{{\mathcal {V}}}})\cap \text {Reg}({\widetilde{{\mathcal {V}}}}) \end{aligned}$$

    and then its image by $\ell \circ {\widetilde{\phi }}$ is a subset of $p^{-1}(\text {Reg}({\mathcal {U}}))\subset {\widehat{{\mathcal {U}}}}$. Since $r^{-1}({\mathcal {R}})$ is strongly portly, its image by the strongly open surjective map $\ell \circ {\widetilde{\phi }}$ is also strongly portly.

    Since $p^{-1}(\text {Reg}({\mathcal {U}}))\cap {\widehat{{\mathcal {U}}}}$ is weakly open thus strongly open, and since it contains $\ell \circ \widetilde{\phi }(r^{-1}({\mathcal {R}}))$; then $p^{-1}(\text {Reg}({\mathcal {U}}))\cap {\widehat{{\mathcal {U}}}}$ is strongly portly in ${\widehat{{\mathcal {U}}}}$. Therefore, $p^{-1}(\text {Reg}( M))$ is locally strongly portly, hence strongly portly.

$\square$

Remark 4.37

Hypothesis (C) for the model spaces is necessary for the proof. Take $\theta \in {\mathbb {R}}_+{\setminus } \{0,2\pi \}$ and consider ${{\mathbb {E}}}^{1,2}_{\theta }$ as a singular model. We may choose as tamifying topology either the natural one or the tamifying topology ${\mathcal {T}}$ we defined on ${{\mathbb {E}}}^{1,2}_{0}$. Indeed, properties (A),(C) and (D) are purely topological and ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0\rightarrow {\mathbb {E}}^{1,2}_0$ is isomorphic to $\widetilde{\mathbb {E}}_\theta ^{1,2}\rightarrow {{\mathbb {E}}}^{1,2}_{\theta }$ in ${\textbf {Spr}}$. Property (B) is certainly satisfied since ${{\mathbb {E}}}^{1,2}_{\theta }$ is tame. We may thus construct a messed up tamifying topology on $\widetilde{\mathbb {E}}_\theta ^{1,2}$ by taking the topology ${\mathcal {T}}'$ generated by the natural one and the restriction of ${\mathcal {T}}$ to $\{t>0\}$. Since the Galois group acts by ’rotation’ around the ’axis’ $\{r=0\}$, it preserves ${\mathcal {T}}'$. However, the automorphism group also contains translations along the t-axis, which send points from $t<0$ to $t>0$.

The proof above thus fails at the first step since the induced topology ${\mathcal {T}}_{{\mathcal {U}},{\mathcal {V}},\phi }$ for $\text {Sing}({\mathcal {U}})\ne \emptyset$ depends on whether ${\mathcal {V}}\subset \{t>0\}$ or ${\mathcal {V}}\subset \{t>0\}$ or any other intermediary cases with $(0,0,0)\in {\mathcal {V}}$.

That being said, the author ignores whether one could remove this hypothesis by showing that from a given tamifying topology, the coarsest topology that makes the developing map and the automorphisms continuous would still satisfy (A) and (D).

Finally, the following remark, though trivial, is important.

Remark 4.38

Let M be a virtually tamely singular (G, X)-manifold. If M admits an injective developing map $N\xrightarrow {{\mathcal {D}}}X$ for some branched covering $N\rightarrow M$ possibly branched above $\text {Sing}(M)$ then M is isomorphic to $\varGamma (N/M)\backslash {\mathcal {D}}(N)$ where

• $\varGamma (N/M)$ acts on X via the holonomy of ${\mathcal {D}}$;

• N is endowed with the quotient of a tamifying topology ${\mathcal {T}}$;

• ${\mathcal {D}}(N)$ is endowed with the topology generated by that of X and the images by ${\mathcal {D}}$ of ${\mathcal {T}}$.

5 An application: uniformization of ${\mathbb {E}}^{1,2}_0$-manifolds

In this section, we present an ’application’ of the theory developed. Our aim is to present a uniformization result for ${\mathbb {E}}^{1,2}_0$-manifolds eg singular $(\text {Isom}({{\mathbb {E}}}^{1,2}_{}),{{\mathbb {E}}}^{1,2}_{})$-manifolds with singularities modeled on ${\mathbb {E}}^{1,2}_0$. Those manifolds are not tame, but we will show they are virtually tame. We can thus define $\varGamma ({{\widetilde{M}}}/M)$-equivariant developing maps on any ${\mathbb {E}}^{1,2}_0$-manifold, and we wish to apply Remark 4.38 to some reasonable class of ${\mathbb {E}}^{1,2}_0$-manifolds.

We begin with a short introduction to the geometry of Minkowski space is necessary.

5.1 Geometry of Minkowski space

We choose $X = {\mathbb {E}}^{1,2}$, the affine space ${\mathbb {R}}^3$ endowed with cartesian coordinates (t, x, y) and a quadratic form $Q(t,x,y)= -t^2+x^2+y^2$ of signature (1, 2); together with $G=\text {O}_{0}(1,2; {\mathbb {R}})\ltimes {\mathbb {R}}^3$, the identity component of its group of affine isometry. We will denote $({\mathbb {E}}^{1,2},\text {O}_{0}(1,2; {\mathbb {R}})\ltimes {\mathbb {R}}^3)$-manifolds by ${\mathbb {E}}^{1,2}$-manifolds for simplicity sake.

We choose the point $O=(0,0,0)\in {\mathbb {E}}^{1,2}$ and call it the origin of ${\mathbb {E}}^{1,2}$, we have a natural projection $\text {O}_{0}(1,2; {\mathbb {R}})\rtimes {\mathbb {R}}^3 \ltimes {\mathbb {E}}^{}\xrightarrow {L} \text {O}_{0}(1,2; {\mathbb {R}})$ we will refer to as linear part. $\text {O}_{0}(1,2; {\mathbb {R}})$ acts naturally on the paraboloid model of the hyperbolic plane ${\mathbb {H}}:= \{(t,x,y)\in {\mathbb {E}}^{1,2}~|~ t>0, ~~Q(t,x,y)=-1 \}$ and $\text {O}_{0}(1,2; {\mathbb {R}})\simeq \text {PSL}(2;{\mathbb {R}})$. We say that $\phi \in \text {O}_{0}(1,2; {\mathbb {R}})\ltimes {\mathbb {R}}^3$ is parabolic (resp. elliptic, resp. hyperbolic) if the action of its linear part $L(\phi )$ on ${\mathbb {H}}$ is parabolic (resp. elliptic, resp. hyperbolic). A useful characterization is that $\phi$ is

• parabolic if $\phi$ stabilizes set-wise exactly one lightlike line,

• elliptic if $\phi$ stabilizes set-wise exactly one timelike line,

• hyperbolic if $\phi$ stabilises set-wise two lightlike lines.

5.2 Causality of Minkowski space

Minkowski space ${\mathbb {E}}^{1,2}$ is naturally endowed with two partial order relations induced by strict orders defined as follows: for any $p:=(t,x,y), q:=(t',x',y')$ we say that $p<q$ (resp. $p\ll q$) if $Q(q-p)\le 0$ (resp. $Q(q-p)<0$) and $t'>t$. A non-trivial vector u is lightlike if $Q(u)=0$, causal if $Q(u)\le 0$, timelike if $Q(u)<0$ and spacelike if $Q(u)>0$. A line is lightlike (resp. spacelike, resp. timelike) if its direction is lightlike (resp. spacelike, resp. timelike). The relation < is the causal order, while $\ll$ is the chronological order. A curve is future causal (resp. chronological) if it is increasing of the order < (resp. $\ll$).

One can check that the group G acts by non-decreasing homeomorphisms for both orders, e.g.:

$$\begin{aligned}{} & {} \forall p,q \in {\mathbb {E}}^{1,2},\quad \forall \phi \in \text {O}_{0}(1,2; {\mathbb {R}}),\quad p< q \Rightarrow \phi p < \phi q.\\{} & {} \forall p,q \in {\mathbb {E}}^{1,2},\quad \forall \phi \in \text {O}_{0}(1,2; {\mathbb {R}}),\quad p\ll q \Rightarrow \phi p \ll \phi q. \end{aligned}$$

5.3 Locally Minkowski manifolds and Mess–Bonsante–Barbot theorem

Every ${\mathbb {E}}^{1,2}$ -manifold is naturally endowed with two sheaves of pre-order relations inherited from the order relations of ${\mathbb {E}}^{1,2}$. Future causal or chronological curves are curves that are locally increasing for respective pre-orders (or equivalently, that are increasing in charts).

Properties of these sheaves of pre-order provide a hierarchy of ${\mathbb {E}}^{1,2}$-manifolds [44]. Let M be a ${\mathbb {E}}^{1,2}$-manifold.

• M is causal if its induced pre-order $\le$ is an order.

• M is globally hyperbolic if there exists a surface $\varSigma \subset M$ such that every future causal curves intersect $\varSigma$ exactly once. Such a surface is called a Cauchy surface of M.

• M is globally hyperbolic Cauchy-compact if it admits a compact Cauchy-surface

• M is globally hyperbolic Cauchy-complete if it admits a smooth Cauchy-surface on which the semi-Riemannian metric of M induces a complete Riemannian metric.

Following notations of [42], for M a ${\mathbb {E}}^{1,2}$-manifold and $p\in M$, we denote

$$\begin{aligned} J^+(p):= & {} \{q\in M~|~ p\le q\} \quad J^-(p):= \{q\in M~|~ p\ge q\}\\ I^+(p):= & {} \{q\in M~|~ p\ll q\} \quad I^-(p):= \{q\in M~|~ p\gg q\}. \end{aligned}$$

A classical result of Geroch [28, 44] implies that a ${\mathbb {E}}^{1,2}$-manifolds M is globally hyperbolic if and only if M is causal and if $J^+(p)\cap J^-(q)$ is compact for all $p,q\in M$. Another classical result of Choquet-Bruhat and Geroch [18, 45] shows that any globally hyperbolic ${\mathbb {E}}^{1,2}$-manifolds M embeds naturally into a Cauchy-maximal globally hyperbolic extension. The precise definition of Cauchy-maximality is not relevant for the following except as a hypothesis; we therefore omit to develop it further.

Following the work of Mess [40], Bendetti and Bonsante [4, 12] and Barbot [2], a uniformization of globally hyperbolic Cauchy-maximal Cauchy-complete ${\mathbb {E}}^{1,2}$-manifolds is known. Let M be such a manifold of Cauchy surface $\varSigma$. For simplicity’s sake, we restrict ourselves to $\varSigma$ of finite type with genus g and s punctures such that $2g-2+s>0$. In this case, there exists a representation $\pi _1(\varSigma )\xrightarrow {~~\rho ~~} \text {O}_{0}(1,2; {\mathbb {R}})\ltimes {\mathbb {R}}^3$ whose linear part is discrete and faithful as well as a $\rho$-invariant convex domain $\varOmega \subset {\mathbb {E}}^{1,2}$ such that $M\simeq \rho \backslash \varOmega$ and ${{\widetilde{M}}} \simeq \varOmega$. Furthermore, up to reversing the causal order, there exists a $\rho$-invariant family $(\varDelta _i)_{i\in I}$ of lightlike lines such that

$$\begin{aligned} \varOmega = \bigcap _{i\in I} I^+(\varDelta _i). \end{aligned}$$

Note that for each $i\in I$, the set $I^+(\varDelta _i)$ is an open halfspace of ${\mathbb {E}}^{1,2}$.

5.4 Some complements on the BTZ model

Recall that we introduced the developing map

$$\begin{aligned} \displaystyle {\mathcal {D}}:\begin{array}{l|rcl} &{} \displaystyle {{\widetilde{{\mathbb {E}}}}}^{1,2}_0 &{} \longrightarrow &{} \displaystyle {\mathbb {E}}^{1,2} \\ &{} \displaystyle \left( \tau ,{\mathfrak {r}},\frac{\theta }{2\pi }\right) &{} \longmapsto &{} \displaystyle \begin{pmatrix}t \\ x \\ y\end{pmatrix}=\begin{pmatrix} \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 \\ \tau + \frac{1}{2}{\mathfrak {r}}\theta ^2 -{\mathfrak {r}}\\ -{\mathfrak {r}}\theta \end{pmatrix} \\ &{} \displaystyle (\tau ,0,\cdot ) &{} \longmapsto &{} \displaystyle \begin{pmatrix}\tau \\ \tau \\ 0\end{pmatrix}\end{array} \end{aligned}$$

is continuous for the topology ${\mathcal {T}}_{BTZ}$ generated by the natural topology of ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ and open sets of the form

$$\begin{aligned} {\mathcal {U}}_\lambda = \left\{ (\tau ,{\mathfrak {r}},\theta )\in {{\widetilde{{\mathbb {E}}}}}^{1,2}_0~|~ {\mathfrak {r}}\theta ^2< \lambda \right\} ,\quad \lambda \in {\mathbb {R}}_+^*. \end{aligned}$$

The image of this map is the causal future of a lightlike line $\varDelta$ ie ${\mathcal {D}}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)=J^+(\varDelta )$. More precisely, $\varDelta$ is the line directed by $\overrightarrow{u} = (1,1,0)$ through the origin of Minkowski space, ${\mathcal {D}}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)$ is then the union of $\varDelta$ with the open half space of ${{\mathbb {E}}}^{1,2}_{}$ above the plane directed by $\overrightarrow{u}^\perp$ through the origin. The Galois group $\varGamma :=\varGamma ({{\widetilde{{\mathbb {E}}}}}^{1,2}_0/{\mathbb {E}}^{1,2}_0)$ is isomorphic to ${\mathbb {Z}}$ and stabilizes point-wise the singular locus; taking $\gamma$ a generator of $\varGamma ({{\widetilde{{\mathbb {E}}}}}^{1,2}_0/{\mathbb {E}}^{1,2}_0)$, the holonomy $\rho$ sends $\gamma$ to $\phi :=\rho (\gamma )$ which thus stabilizes point-wise the image of $\text {Sing}({{\mathbb {E}}}^{1,2}_{0,\infty })$ ie $\varDelta$. Since $\varDelta$ is lightlike, $\phi$ is parabolic.

We did not quite prove that ${\mathbb {E}}^{1,2}_0$ is virtually tame, let us correct this.

Proposition 5.1

The ${\mathbb {E}}^{1,2}_0$ model space is virtually tame.

Proof

From the motivational example given in Sect. 4.3.2, the only missing property is that the induced quotient topology on ${\mathbb {E}}^{1,2}_0$ is indeed the natural one.

For any $\lambda >0$, the image of ${\mathcal {U}}_\lambda$ in ${\mathbb {E}}^{1,2}_0$ contains $\left\{ (\tau ,{\mathfrak {r}},\theta )~|~ {\mathfrak {r}}< \frac{\lambda }{4\pi ^2} \right\}$ and is thus open. Therefore, the quotient topology on ${\mathbb {E}}^{1,2}_0$ is the natural topology. $\square$

Proposition 5.2

All ${\mathbb {E}}^{1,2}_0$-manifolds are virtually tame.

Proof

By Proposition 5.1, the model space ${\mathbb {E}}^{1,2}_0$ is virtually tame. From the motivational example given in Sect. 4.3.2 we have that $\text {Aut}({{\widetilde{{\mathbb {E}}}}}^{1,2}_0)$ acts strongly continuously. Topologically, ${\mathbb {E}}^{1,2}_0$ is homeomorphic to ${\mathbb {R}}^{3}$ and $\text {Sing}({\mathbb {E}}^{1,2}_0)$ is a line. Therefore ${\mathbb {E}}^{1,2}_0$ is locally Galoisian. Theorem 5 thus applies. $\square$

We now identify the right topology to put on ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$. To begin with the holonomy is faithful and that ${\mathcal {D}}$ is injective, therefore the developing map induces a bijective map

$$\begin{aligned} {{\overline{{\mathcal {D}}}}}: {\mathbb {E}}^{1,2}_0\xrightarrow {} \varGamma \backslash J^+(\varDelta ). \end{aligned}$$

using the tamifying topology of ${\mathbb {E}}^{1,2}_0$ we deduce that ${{\overline{{\mathcal {D}}}}}$ is continuous.

However, the map ${{\overline{{\mathcal {D}}}}}$ is not open thus not a homeomorphism if the righthand side is endowed with the quotient topology of the usual topology of $J^+(\varDelta )$. Actually, $\varGamma \backslash J^+(\varDelta )$ is not even Hausdorff. The situation is very similar to that of cuspidal singularities viewed as point on the unit circle in the closure of the disc model of ${\mathbb {H}}$ embedded into ${\mathbb {R}}^2$. To see that, consider the sequence $(\tau _n,{\mathfrak {r}}_n,\theta _n)_{n\in {\mathbb {N}}}$ in ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ with $\tau _n=-1$, ${\mathfrak {r}}_n=1/n$ and $\theta _n=\sqrt{2n}$. Observe that ${\mathcal {D}}(\tau _n,{\mathfrak {r}}_n,\theta _n)\xrightarrow {n\rightarrow +\infty } (0,0,0)$ but that $(\tau _n,{\mathfrak {r}}_n,\theta _n) \xrightarrow {n\rightarrow +\infty } (-1,0,0)$. Furthermore, choose some sequence $(k_n)_{n\in {\mathbb {N}}}$ such that $\theta _n-k_n$ is bounded so that ${\mathcal {D}}(\tau _n,{\mathfrak {r}}_n,\theta _n-k_n)\xrightarrow {n\rightarrow +\infty } (-1,0,0)$. Since $(\tau _n,{\mathfrak {r}}_n,\theta _n)$ and $(\tau _n,{\mathfrak {r}}_n,\theta _n-k_n)$ are $\varGamma$-conjugate for all all $n\in {\mathbb {N}}$ they induce the same sequence in ${\mathbb {E}}^{1,2}_0$. Its image by ${{\overline{{\mathcal {D}}}}}$ thus has two distincts limits.

To force this map to be a homeomorphism, one has to add to the topology of $J^+(\varDelta )$ the image by ${\mathcal {D}}$ of neighborhood basis of points in $\{{\mathfrak {r}}=0\}\subset {{\widetilde{{\mathbb {E}}}}}^{1,2}_0$ which leads to the following definition.

Definition 5.3

(BTZ topology) Let $\varDelta$ be a lightlike line in ${{\mathbb {E}}}^{1,2}_{}$. The BTZ topology on $J^+(\varDelta )$ is the topology generated by the one induced by the natural topology of ${{\mathbb {E}}}^{1,2}_{}$ and open subsets of the form $I^+(p)\cup ]p,+\infty [$ for $p\in \varDelta$ where $]p,+\infty [$ denote the relatively open future half-ray from p.

With this definition we have the following.

Proposition 5.4

If $J^+(\varDelta )$ is endowed with the BTZ topology, then the map ${{\overline{{\mathcal {D}}}}}: {{\mathbb {E}}}^{1,2}_{0}\rightarrow \varGamma \backslash J^+(\varDelta )$ is an isomorphism of singular ${\mathbb {E}}^{1,2}$-manifold.

This last remark will be useful.

Remark 5.5

The tamifying topology ${\mathcal {T}}_{BTZ}$ is generated by ${\mathcal {T}}_{BTZ}$-open diamond eg the sets of the form $Int_{{\mathcal {T}}_{BTZ}}\left( J^{-}(p)\cap J^{+}(q)\right)$ for $p,q\in {{\widetilde{{\mathbb {E}}}}}^{1,2}_0$.

5.5 The maximal branched covering of ${{\mathbb {E}}}^{1,2}_{0}$-manifolds

Consider M a ${{\mathbb {E}}}^{1,2}_{0}$-manifold, ie a singular ${{\mathbb {E}}}^{1,2}_{}$-manifold whose singular locus is locally modelled on ${{\mathbb {E}}}^{1,2}_{0}$. As notice above, the ${\mathbb {E}}^{1,2}_0$ is locally Galoisian so ${{\widetilde{M}}}\rightarrow M$ is Galoisian. And by Proposition 5.2, M is virtually tame

We may add that the singular locus being a 1-submanifold of non trivial holonomy, ${{\widetilde{M}}}$ is exactly branched over $\text {Sing}(M)$. We summarize this as follow.

Proposition 5.6

Let M be a ${{\mathbb {E}}}^{1,2}_{0}$-manifold, then M admits a Galoisian maximal covering exactly branched above $\text {Sing}(M)$ and admits a developing map continuous for the tamifying topology ${\mathcal {T}}_{BTZ}$. Furthermore, ${{\widetilde{M}}}$ is a ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifold.

For simplicity sake, in the rest of the section, “Developing map” of some ${\mathbb {E}}^{1,2}_0$-manifold M will always refer to the one for the ${\mathcal {T}}_{BTZ}$-topology.

The goal of this section is to show, similarly to Cauchy-complete Cauchy-maximal ${{\mathbb {E}}}^{1,2}_{}$-manifolds, that Cauchy-complete Cauchy-maximal ${{\mathbb {E}}}^{1,2}_{0}$-manifolds can be realized as quotients of convex domains of Minkowski space.

Causal notions introduced in the Sect. 5.3 above extend naturally to ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifolds and ${\mathbb {E}}^{1,2}_0$-manifolds. Although, most of the proofs of elementary causal properties for Lorentzian manifold extend mutatis mutandis to such manifolds, a cautious reader will have to re-prove most properties from scratch. A proper framework for general topological spacetimes applying our manifolds of interests can be found in [16] and the author aims at publishing them.

Definition 5.7

A ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifold M is future distinguishing if the map $x\mapsto I^+(x)$ defined on M is injective.

Definition 5.8

A singular ${{\mathbb {E}}}^{1,2}_{}$-manifold M endowed with some causal pre-order $\le$ extending the one on $\text {Reg}(M)$ is causally connected if for all $x,y\in M$ such that $x\le y$, there exists a future causal path from x to y.

The proof of the following two Lemmas are omitted as they fall in the elementary causal property mentionned above and proving them (though logically necessary) is not particularly useful for our current exposition.

Lemma 5.9

Globally hyperbolic ${\mathbb {E}}^{1,2}_0$-manifolds and ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifolds are future distinguishing.

Lemma 5.10

${\mathbb {E}}^{1,2}_0$-manifolds and ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifolds are causally connected.

Lemma 5.11

Let M be a ${\mathbb {E}}^{1,2}_0$-manifold and let ${\mathcal {D}}:{{\widetilde{M}}}\rightarrow {{\mathbb {E}}}^{1,2}_{}$ be a developing map. Then ${\mathcal {D}}$ is increasing on M eg

$$\begin{aligned} \forall x,y\in M, \quad x<y \Rightarrow {\mathcal {D}}(x)<{\mathcal {D}}(y). \end{aligned}$$

Proof

The restriction of such a map to a chart neighborhood is the restriction of a developing map of the local model space. Since the developing maps of each model spaces are increasing, ${\mathcal {D}}$ is locally increasing. Furthermore, since M is connected, it is causally connected therefore ${\mathcal {D}}$ is increasing. $\square$

Definition 5.12

A ${\mathbb {E}}^{1,2}_0$-manifold M is future complete if for all $x\in \widetilde{M}$

$$\begin{aligned} {\mathcal {D}}(J^+(x)) = J^+({\mathcal {D}}(x))\quad \text {and}\quad {\mathcal {D}}(I^+(x)) = I^+({\mathcal {D}}(x)). \end{aligned}$$

Proposition 5.13

Globally hyperbolic Cauchy-complete ${\mathbb {E}}^{1,2}_0$-manifolds are future complete.

Proof

From Theorem 3 of [17] the regular par of M is globally hyperbolic and Cauchy-complete. Barbot uniformization Theorem [2] then implies future completeness of the regular part. Finally Lemma 2.4 of [17] implies that the singular locus contains full future BTZ rays. $\square$

Definition 5.14

A ${{\widetilde{{\mathbb {E}}}}}^{1,2}_0$-manifold M is future distinguishing if the map $x\mapsto I^+(x)$ defined on M is injective.

Lemma 5.15

Let M be a Globally hyperbolic ${\mathbb {E}}^{1,2}_0$-manifolds. Its maximal branched covering ${{\widetilde{M}}}$ is future distinguishing.

Although, one has to re-prove most causal properties from scratch, the proof of this Lemma it not different from the proof of the similar statement for Lorentzian manifolds.

Theorem 6

Let M be a globally hyperbolic Cauchy-complete Cauchy-maximal ${{\mathbb {E}}}^{1,2}_{0}$-manifold, let ${{\widetilde{M}}}$ its maximal covering branched over $\text {Sing}(M)$, of developing map and holonomy $({\mathcal {D}},\rho )$. We note $\varGamma :=\varGamma (\widetilde{M}/M)\simeq \pi _1(\text {Reg}(M))$ its Galois group. Then, up to time reversal of M:

• ${\mathcal {D}}$ is injective

• $\rho$ is faithful, discrete and torsion-free;

• there exists a $\varGamma$-invariant family of relatively open future complete lightlike rays $(\varDelta _i)_{i\in I}$ and a $\varGamma$-invariant family of lightlike planes $(\varPi _j)_{j\in J}$ such that

  $$\begin{aligned} {\mathcal {D}}({{\widetilde{M}}}) = \bigcap _{i\in I} J^+(\varDelta _i) \cup \bigcap _{j\in I} I^+(\varPi _j) \end{aligned}$$

• endowing ${\mathcal {D}}({{\widetilde{M}}})$ with the BTZ topology in the neighborhood of the lightlike rays $(\varDelta _i)_{i\in I}$, the developing map induces an isomorphism

  $$\begin{aligned} M\xrightarrow {~~{{\overline{{\mathcal {D}}}}}~~} \rho \backslash {\mathcal {D}}({{\widetilde{M}}} ) \end{aligned}$$

Proof

From Theorem 3 of [17], the regular part of M is globally hyperbolic, Cauchy-maximal and Cauchy-complete; therefore, by general result of Barbot [2], the restriction ${\mathcal {D}}_{|\text {Reg}({{\widetilde{M}}})}$ is injective, $\rho$ is faithful, discrete and without torsion and

$$\begin{aligned} \varOmega :={\mathcal {D}}(\text {Reg}({{\widetilde{M}}})) =\bigcap _{j\in I} I^+(\varPi _j) \end{aligned}$$

for some $\varGamma$-invariant family $(\varPi _j)_{j\in J}$ of lightlike planes. Furthermore, $\varGamma$ acts totally discontinuously and freely on $\varOmega$. Notice that $\varOmega$ is future complete ie for all $x\in \varOmega , J^+(x)\subset \varOmega$.

Note that from Lemma 5.11, ${\mathcal {D}}$ is increasing. Let $x\in \text {Sing}({{\widetilde{M}}})$, its stabilizer $\varGamma _x$ is isomorphic to ${\mathbb {Z}}$ and for $\gamma \in \varGamma _x{\setminus }\{1\}$, $\rho (\gamma )$ is parabolic. Therefore, the set of fix points of $\varGamma _x$ in ${{\mathbb {E}}}^{1,2}_{}$ is a lightlike line $\varDelta$. The restriction of ${\mathcal {D}}$ to the connected component $S_x$ of $\text {Sing}({{\widetilde{M}}})$ containing x is increasing with image $\varDelta _x:={\mathcal {D}}(S_x)\subset \varDelta$. Since $S_x$ is a totally ordered relatively open future half line, so is its image ${\mathcal {D}}(\varDelta _x)\subset \varDelta$.

Since $\varGamma$ does not act freely on $S_x$, it does not acts freely via $\rho$ on $\varDelta$, therefore $\varDelta$ does not intersects $\varOmega$. Since ${\mathcal {D}}$ is ${\mathcal {T}}_{BTZ}$-continuous ${\mathcal {D}}(\varDelta _x)$ lie in the closure of $\varOmega$ hence ${\mathcal {D}}(\varDelta _x)\subset \partial \varOmega$. Finally, since $J^+({\mathcal {D}}(\varDelta _x)) = I^+({\mathcal {D}}(\varDelta _x))\cup {\mathcal {D}}(\varDelta _x)$ and since M is future complete,

$$\begin{aligned} \varOmega \supset {\mathcal {D}}(I^+(S_x)) =I^+({\mathcal {D}}(S_x)) \end{aligned}$$

so ${\mathcal {D}}({{\widetilde{M}}})$ has the wanted form.

Let $x,y\in {{\widetilde{M}}}$ such that ${\mathcal {D}}(x)={\mathcal {D}}(y)$. Since M is future complete, we have

$$\begin{aligned} {\mathcal {D}}(I^+(x))=I^+({\mathcal {D}}(x))=I^+({\mathcal {D}}(y))={\mathcal {D}}(I^+(y))\subset \varOmega \end{aligned}$$

and since $I^+(x)$ and $I^+(y)$ are subsets of $\text {Reg}(M)$ and ${\mathcal {D}}_{|\text {Reg}(M)}^{|\varOmega }$ is a bijection we deduce that $I^+(x)=I^+(y)$. Since ${{\widetilde{M}}}$ is globally hyperbolic, it is future distinguishing and $x=y$. Finally, ${\mathcal {D}}:{{\widetilde{M}}} \rightarrow {{\mathbb {E}}}^{1,2}_{}$ is injective.

The map ${\mathcal {D}}_{|\text {Reg}({{\widetilde{M}}})}$ is open since it is a local homeomorphism. The image of a neighborhood basis of a singular point $x\in \text {Sing}({{\widetilde{M}}})$ is obtains by considering sets of the form $I_{p,q}:=\text {Int}(J^+(p)\cap J^-(q))$ with $p\in J^-(x)$ and $q\in I^+(x)$. By taking p, q sufficiently close to x, such a neighborhood can be chosen in a causally convex in M chart neighborhood ${\mathcal {U}}$ of x. This way $\text {Int}(J^+(p)\cap J^-(q)) = \text {Int}(J_{\mathcal {U}}^+(p)\cap J_{\mathcal {U}}^-(q))$ and the image by ${\mathcal {D}}$ of such a domain is the exactly $(I^+({\mathcal {D}}(p))\cup {\mathcal {D}}(]p,+\infty [)\cap I^-({\mathcal {D}}(q))$ with $]p,+\infty [$ the future half BTZ ray from p in ${{\widetilde{M}}}$. Therefore, the image of such ${\mathcal {D}}(I_{p,q})$ together with the topology induced by ${{\mathbb {E}}}^{1,2}_{}$ generates the BTZ topology on ${\mathcal {D}}({{\widetilde{M}}})$.

For the BTZ topology on ${\mathcal {D}}({{\widetilde{M}}})$, the map ${\mathcal {D}}: \widetilde{M} \rightarrow {\mathcal {D}}({{\widetilde{M}}})$ is then a $\varGamma$-invariant homeomorphism and induces a isomorphism of singular ${{\mathbb {E}}}^{1,2}_{}$-manifolds $\varGamma \backslash {{\widetilde{M}}}\simeq \rho \backslash {\mathcal {D}}({{\widetilde{M}}})$. Since ${{\widetilde{M}}} \rightarrow M$ is Galoisian, $M\simeq \varGamma \backslash {{\widetilde{M}}}$ and $M\simeq \rho \backslash {\mathcal {D}}({{\widetilde{M}}})$. $\square$