Homology theory formulas for generalized Riemann–Hurwitz and generalized monoidal transformations

Abstract

In the context of orientable circuits and subcomplexes of these as representing certain singular spaces, we consider characteristic class formulas generalizing those classical results as seen for the Riemann–Hurwitz formula for regulating the topology of branched covering maps and that for monoidal transformations which include the standard blowing-up process. Here the results are presented as cap product pairings, which will be elements of a suitable homology theory, rather than characteristic numbers as would be the case when taking Kronecker products once Poincaré duality is defined. We further consider possible applications and examples including branched covering maps, singular varieties involving virtual tangent bundles, the Chern–Schwartz–MacPherson class, the homology L-class, generalized signature, and the cohomology signature class.

1 Introduction

Given a topological group with an associated classifying space, we consider certain characteristic class expressions pertaining to a (virtual) bundle theory over spaces that are oriented circuits (viz. triangulated pseudomanifolds). The techniques follow from general topological constructions as presented in [13] (cf. [14, 15]) leading to formulas of a generalized Riemann–Hurwitz type, besides similar expressions that may regulate the topology of generalized monoidal transformations which include the standard blowing-up process.

The development of ideas in this present paper highlights a basic difference from [13,14,15], namely, that in contrast to using the usual Kronecker pairing in cohomology/homology that leads to actual characteristic numbers, we instead formulate the results applicable to a suitable homology theory over the circuits in question by taking cap product pairings, once fundamental classes are prescribed. This is a possible approach to a theory of ramified maps, or to a generalized blowing-up process in the presence of singular objects. When Poincaré duality is defined, it can be used to recover the numerical results via the Kronecker pairing in the usual way. Here we consider several instances to show how the general results may be applicable. To this extent, particular interest is when the circuits in question (e.g., branching sets) are stratified pseudomanifolds, or possibly singular complex projective varieties in which, for instance, Chern–Schwartz–MacPherson classes can be implemented, as well as the homology L-class, and the cohomology signature class in other cases.

We dedicate this paper to the memory of Professor Samuel Gitler–Hammer who was our co-author in [13]. Samuel was an exceptionally accomplished and gifted mathematician who greatly inspired many colleagues and students who were privileged to have worked with him. We can imagine that he would have been very interested in our current project with view to a renewed collaboration. Alas, for us, this will not be the case. His presence will be sadly missed by his family, and by the mathematical community at large.

2 The topological background

2.1 Adapted pairs

Definition 2.1

Following [13], let $\Lambda$ be a given (commutative) coefficient ring and $(\Xi , \Sigma )$ a pair of CW-complexes, with $\Xi$ of dimension n and $\Sigma$ a subcomplex of codimension $r \ge 2$, so that $H_q(\Xi , \Lambda ) = 0$ for $q > n$, and $H_q(\Sigma , \Lambda ) = 0$ for $q \ge n-1$. Then the pair $(\Xi , \Sigma )$ is called $(n, \Lambda )$-adapted if $H_n(\Xi , \Lambda ) \cong \Lambda$, and the following condition holds: there exists a neighborhood $B(\Sigma )$ of $\Sigma$, such that $\Sigma$ is a deformation retract of the interior $B^{0}(\Sigma )$ of $B(\Sigma )$, and the quotient map $p_n: C_n(\Xi ) \longrightarrow C_n(\Xi )/C_n(\Xi - B^{0}(\Sigma ))$ induces an isomorphism

$$\begin{aligned} p_{*}: H_n(\Xi ) \overset{\cong }{\longrightarrow } H_n(\Xi -B^{0}(\Sigma )). \end{aligned}$$

(2.1)

Having defined an adapted pair, we continue from [13] to form the subspace $\mathcal K$ of $\Xi \times I$, where

$$\begin{aligned} \mathcal K= (\Xi \times \partial I) \cup (\Xi -B^{0}(\Sigma )) \times I, \end{aligned}$$

(2.2)

together with the double $S(\Sigma ) \subset \mathcal K$, given by

$$\begin{aligned} S(\Sigma ) = (\partial B(\Sigma ) \times I) \cup (B(\Sigma ) \times \partial I). \end{aligned}$$

(2.3)

Now let

$$\begin{aligned} \mathcal K_1 = (\Xi \times \{0\}) \cup (\Xi -B^{0}(\Sigma )) \times \left[ 0, \frac{3}{4}\right] \end{aligned}$$

and

$$\begin{aligned} \mathcal K_2 = (\Xi \times \{1\}) \cup (\Xi -B^{0}(\Sigma )) \times \left[ \frac{1}{4}, 1\right] , \end{aligned}$$

and let $S(\Sigma )_i = S(\Sigma ) \cap \mathcal K_i$, for $i=1,2$.

By this construction, the spaces $\mathcal K_i$ are homotopically equivalent to $\Sigma$, and both the spaces $\mathcal K/\mathcal K_1$ and $S(\Sigma )/S(\Sigma )_1$ are homotopically equivalent to the generalized Thom space $\Xi /(\Xi - B^{0}(\Sigma ))$ (cf. [29]). It follows from the cofibration

$$\begin{aligned} S(\Sigma )_1 \longrightarrow S(\Sigma ) \longrightarrow S(\Sigma )/S(\Sigma )_1 \end{aligned}$$

(2.4)

and the above definition that

$$\begin{aligned} H_n(S(\Sigma )_1, \Lambda ) \cong H_n(S(\Sigma )/S(\Sigma )_1) \cong \Lambda . \end{aligned}$$

(2.5)

We assume there is a choice of generators for $H_n(\Xi , \Lambda )$ and $H_n(S(\Sigma ), \Lambda )$ giving (by definition) an orientation or a fundamental class $[\Xi ]$ of $\Xi$ and $[S(\Sigma )]$ of $S(\Sigma )$, respectively.

Remark 2.1

Observe that the conditions defining an $(n, \Lambda )$-adapted pair above are immediately satisfied when $\Xi$ is a closed (compact without boundary) connected orientable n-manifold, and $\Sigma$ is a closed connected and orientable submanifold of codimension $r \ge 2$, with $\Lambda$ any coefficient ring. This example also applies to topological, PL, as well as smooth (sub)manifolds, with $S(\Sigma )$ a corresponding normal sphere bundle (also closed, connected and orientable for $H_n(S(\Sigma ), \Lambda ) \cong \Lambda$, given the above topological type of $\Sigma$).

Let G be a topological group admitting a classifying space BG, and suppose $P \in H^*(BG, \Lambda )$ is a cohomology class. For a given vector bundle E of rank $\ell$ over $\Xi$, with structure group G, we have then a corresponding characteristic class $P = P_E \in H^*(BG, \Lambda )$, and an element $P(E) \in H^*(\Xi , \Lambda )$ defined by $P(E) = \Phi ^*_E(P)$, where $\Phi _E: \Xi \longrightarrow BG$ is the classifying map. Typically, $G = \mathcal U(\ell ), \mathrm{SO}(\ell )$ or $\mathrm{Sp}(\ell )$. Recall that $H^*(BG, \Lambda )$ is a polynomial ring in the Chern classes (for complex vector bundles, with $\Lambda = \mathbb {Z}$); in the Pontrjagin classes and Euler class (for real oriented vector bundles, with $\Lambda = \mathbb {Z}[ \frac{1}{2}]$); or the corresponding Pontrjagin classes (for symplectic vector bundles, with $\Lambda = \mathbb {Z}$), and in the Stiefel–Whitney classes (for real vector bundles, with $\Lambda = \mathbb {Z}_2$). We refer to [5, 8, 17] for the basic details.

2.2 Constructing the double $S(\Sigma )$

Starting from these axioms for an $(n, \Lambda )$-adapted pair above, the ‘double’ $S(\Sigma )$ of $\Sigma$ was constructed by general topological means in [13]. Here we will use a special, more geometric, case of this construction along the lines of [3, 20], which to some extent follows the approach given in [33].

We assume $\Xi$ to be a closed and connected orientable simple (finite) n-circuit (or a triangulated pseudomanifold in the sense of [16]; see also [9, 23]), and $\Sigma$ an arbitrary closed and connected subcomplex of (real) codimension $r \ge 2$, such that $(\Xi , \Sigma )$ satisfies the conditions of an $(n, \Lambda )$-adapted pair.

Here $B(\Sigma )$ is taken to be a closed tubular neighborhood of $\Sigma$. For $i=1,2$, let $B_i(\Sigma )$ be two distinct copies of $B(\Sigma )$, together with restriction maps

$$\begin{aligned} q_i: B_i(\Sigma ) \longrightarrow \Sigma . \end{aligned}$$

(2.6)

Identifying $B_1(\Sigma )$ and $B_2(\Sigma )$ along their common boundary $\partial B(\Sigma ) = \partial B_1(\Sigma ) = \partial B_2(\Sigma )$, the double $S(\Sigma )$ is formed by setting

$$\begin{aligned} S(\Sigma ) = B_1(\Sigma ) \cup _{\partial B(\Sigma )} B_2(\Sigma ), \end{aligned}$$

(2.7)

which leads to an r-sphere bundle

$$\begin{aligned} q: S(\Sigma ) \longrightarrow \Sigma , \end{aligned}$$

(2.8)

for which the fundamental class (or orientation) $[S(\Sigma )]$ is prescribed as the union of cycles

$$\begin{aligned}{}[S(\Sigma )] = [B_1(\Sigma )] \cup (-)[B_2(\Sigma )]. \end{aligned}$$

(2.9)

At this stage, it seems fitting for us to recall the general result of [13, Theorem 1.1] as it was expressed in terms of Kronecker pairings ($\langle ~,~\rangle$):

Theorem 2.1

Suppose $(\Xi , \Sigma )$ is an $(n, \Lambda )$-adapted pair and E, F are G-bundles over $\Xi$, such that on $\Xi - \Sigma$ there exists a homotopy

$$\begin{aligned} \theta : \Phi _E \vert _{\Xi - \Sigma } \sim \Phi _F \vert _{\Xi - \Sigma }. \end{aligned}$$

(2.10)

Then there exists a G-bundle $\xi _{\theta } \longrightarrow S(\Sigma )$ and orientations $[\Xi ]$ and $[S(\Sigma )]$, such that for any class $P \in H^n(BG,\Lambda )$, we have the following equality:

$$\begin{aligned} \langle P(E) - P(F), [\Xi ] \rangle = \langle P(\xi _{\theta }), [S(\Sigma )] \rangle . \end{aligned}$$

(2.11)

2.3 The clutching construction

Let E, F be G-bundles over $\Xi$. Specifically, we mean that $E,F \longrightarrow \Xi$ are vector bundles with structure group G. Since we are considering general characteristic classes, we could also take E, F to be locally free sheaves. Consider now a homomorphism $\psi : E \longrightarrow F$, such that

• (i) $\psi :E \vert _{\Xi - \Sigma } \overset{\cong }{\longrightarrow } F\vert _{\Xi - \Sigma }$, and

• (ii) $\psi \vert _{\Sigma }$ has constant rank.

The above data involving $\psi$ induces a ‘clutching function’ $\eta$ which is used to clutch E and F over the double $S(\Sigma )$ as outlined below. We refer to [3, 20, 33] for details of this construction. We have the following exact sequence of vector bundles on $\Sigma$:

$$\begin{aligned} 0 \longrightarrow K_1 \longrightarrow E\vert _{\Sigma } \overset{\psi }{\longrightarrow } F \vert _{\Sigma } \longrightarrow K_2 \longrightarrow 0, \end{aligned}$$

(2.12)

where $K_1 \cong \ker \psi$, and $K_2 \cong \mathrm{coker}~\psi$. Further, let

$$\begin{aligned} L := \psi (E\vert _{\Sigma }) \subset F\vert _{\Sigma }. \end{aligned}$$

(2.13)

In this construction the bundles E, F are pulled back to $S(\Sigma )$ via q, and the clutched bundle $\xi \longrightarrow S(\Sigma )$ is specified by

$$\begin{aligned} \xi = (E, \psi , F) \cong (q_1^*K_1, \eta , q_2^* K_2) \oplus q^*L . \end{aligned}$$

(2.14)

Letting $K= (q_1^*K_1, \eta , q_2^* K_2)$ we can express (2.14) as

$$\begin{aligned} \xi = K \oplus q^* L. \end{aligned}$$

(2.15)

Observe also, that by the above construction, we obtain isomorphisms

$$\begin{aligned} q_1^* i^* E \cong \xi \vert _{B_1(\Sigma )},\quad \text {and}\quad q_2^* i^* F \cong \xi \vert _{B_2(\Sigma )}, \end{aligned}$$

(2.16)

and

$$\begin{aligned} E \vert _{\Sigma } \cong K_1 \oplus L,\quad \text {and}\quad F \vert _{\Sigma } \cong K_2 \oplus L. \end{aligned}$$

(2.17)

For $x \in \Sigma$,

$$\begin{aligned} K_x = (q_1^* K_1\vert _{B_1(\Sigma )_x}, \eta _x, q_2^* K_2\vert _{B_2(\Sigma )_x}) \end{aligned}$$

(2.18)

is the vector bundle over $S(\Sigma )\vert _{x \in \Sigma }$ constructed via the transition function $\eta _x$, seen as the restriction of $\eta$ to $\partial B(\Sigma )_x$. That is, we have an isomorphism

$$\begin{aligned} \eta _x: q^*_1 K_1 \vert _{\partial B(\Sigma )_x} \overset{\cong }{\longrightarrow } q^*_2 K_2 \vert _{\partial B(\Sigma )_x}. \end{aligned}$$

(2.19)

Lemma 2.1

For $x,y \in \Sigma$ we have $K_x \cong K_y$, and $q_*(\Phi ^*_{K_x}(P) \cap [S(\Sigma )_x])$ is a constant multiple $k \mathbf {1}_{\Sigma }$ of the trivial class in $H^*(\Sigma )$, where $q_{*}$ denotes integration along the fiber (see (2.24) below).

Proof

Let c(x, y) is a curve in $\Sigma$ joining two points $x,y \in \Sigma$. Then the restrictions $K_1\vert _{c(x,y)}$, and $K_2\vert _{c(x,y)}$ are trivial. This leads to the following diagram in which the vertical maps are isomorphisms

(2.20)

and, modulo these isomorphisms, $\eta _x$ and $\eta _y$ are homotopic. Thus $K_x$ and $K_y$, regarded as bundles on $S^r \cong S(\Sigma )_x \cong S(\Sigma )_y$, are isomorphic. Since $\Sigma$ was taken to be connected, this implies that $q_*(\Phi ^*_{K_x}(P) \cap [S(\Sigma )_x])$ is independent of x, and thus is a constant multiple, $k \mathbf {1}_{\Sigma }$ of the trivial class in $H^*(\Sigma )$. $\square$

Theorem 2.2

Let K and L be as in (2.15), with $q: S(\Sigma ) \Sigma$ the r-sphere bundle in (2.8). With respect to the clutched bundle $\xi = (E, \psi , F)$ in (2.14) and the classifying map $\Phi$, suppose: (1) there exists a splitting $\Phi _{\xi }^*(P) = \Phi ^*_{K}(P) \cup \Phi ^*_{q^* L}(P)$, and (2) the cohomological degree of $P_K \le \mathrm{rank}(K) = r$. Then in $H_*(\Xi , \Lambda )$ we have the following formula

$$\begin{aligned} (P(E) - P(F)) \cap [\Xi ] = i_*(P(L) \cup k \mathbf {1}_{\Sigma } \cap [\Sigma ]), \end{aligned}$$

(2.21)

where k is a constant.

Proof

In view of (2.16), we have

$$\begin{aligned} (P(E) - P(F)) \cap [\Xi ] = i_*q_*(P(\xi ) \vert _{B_1(\Sigma )} \cap [B_1(\Sigma )] - P(\xi ) \vert _{B_2(\Sigma )} \cap [B_2(\Sigma )]). \end{aligned}$$

(2.22)

Recalling (2.9), we see that (2.22) equals

$$\begin{aligned} i_*q_*(P(\xi ) \vert _{B_1(\Sigma )} \cap [B_1(\Sigma )] + P(\xi ) \vert _{B_2(\Sigma )} \cap (-)[B_2(\Sigma )]) = i_*q_*(P(\xi ) \cap [S(\Sigma )]). \end{aligned}$$

(2.23)

Consider the Gysin sequence applied to $q: S(\Sigma ) \longrightarrow \Sigma$ (see e.g., [5, 17]). We have a long exact sequence:

$$\begin{aligned} \ldots H^i(S(\Sigma )) \overset{q_{*}}{\longrightarrow } H^{i-r}(\Sigma ) \overset{\cup e}{\longrightarrow } H^{i+1}(\Sigma ) \overset{q^*}{\longrightarrow } H^{i+1}(S(\Sigma )) \ldots \end{aligned}$$

(2.24)

With some abuse of notation $q_*$ in (2.24) above denotes integration along the fiber, and $\cup e$ denotes cup product with the Euler class. Let $\alpha \in \Phi ^*_L(P)$, and $\beta \in \Phi ^*_K(P)$. Then if $q_{*}$ and $q^{*}$ are the maps in (2.24), we have via fibre-integration along $S(\Sigma ) \vert _{x \in \Sigma }$, the equality $q_{*}(q^*(\alpha ) \cup \beta ) = \alpha \cup q_{*}(\beta )$. In view of (1) and (2) above, we have then

$$\begin{aligned} i_* q_*(P(\xi ) \cap [S(\Sigma )])&= i_* q_* (\Phi ^*_{\xi }(P) \cap [S(\Sigma )]) \nonumber \\&= i_* q_*((\Phi ^*_{q^*L}(P) \cup \Phi ^*_K(P)) \cap [S(\Sigma )])\nonumber \\&= i_*( q_*((\Phi ^*_{q^*L}(P) \cup \Phi ^*_K(P)) \cap [S(\Sigma )])). \end{aligned}$$

(2.25)

For $x \in \Sigma$, integration over the fiber of (2.25) yields

$$\begin{aligned}&i_*((\Phi ^*_L(P) \cap [\Sigma ]) \cup q_*(\Phi ^*_K(P) \cap [S(\Sigma )_x])) \nonumber \\&\quad = i_*((\Phi ^*_L(P) \cap [\Sigma ]) \cup q_*(\Phi ^*_{K_x}(P) \cap [S(\Sigma )_x])). \end{aligned}$$

(2.26)

Applying Lemma 2.1, we finally obtain

$$\begin{aligned} i_*(\Phi ^*_L(P) \cup k\mathbf {1}_{\Sigma } \cap [\Sigma ]) = i_*(P(L) \cup k \mathbf {1}_{\Sigma } \cap [\Sigma ]). \end{aligned}$$

(2.27)

$\square$

Remark 2.2

In applying this result to complex vector bundles (taking $\Lambda = \mathbb {Z}$), with P corresponding to the total (or top) Chern class $c_{*}$, for instance, (or $c_{top}$), we see that both assumptions (1) and (2) in Theorem 2.2 are satisfied (with r the rank of L as a complex vector bundle), so that $\Sigma$ is of real codimension 2r, with cohomological degree $c_{*} (L) \le 2r$. Likewise, if $\Phi ^* P(~)= e(~)$ is the Euler class of a real oriented vector bundle.

3 Examples and applications

3.1 A homology generalized Riemann–Hurwitz formula

In the following we will be considering situations of the following type. Let $f: (\Xi , \Sigma ) \longrightarrow (\Xi ', \Sigma ')$ be a simplicial map of $(n,\Lambda )$-adapted pairs such that

• (i) $f^{-1}(\Sigma ') = \Sigma$, and

• (ii) $f: \Xi - \Sigma \longrightarrow \Xi ' - \Sigma '$ is a homeomorphism,

(again, $\Sigma \subset \Xi$ and $\Sigma ' \subset \Xi '$ are taken to be subcomplexes of $\Xi$ and $\Xi '$ respectively). Consider then the diagram

(3.1)

Example 3.1

Let us first see how (2.21) looks when the adapted pairs $(\Xi , \Sigma )$ and $(\Xi ', \Sigma ')$ are smooth manifolds with $\dim _{\mathbb {R}} \Xi = \dim _{\mathbb {R}} \Xi '$, together with $E = T\Xi$, and $F = f^*T\Xi '$ (and thus $\mathrm{rank}_{\mathbb {R}} E = \mathrm{rank}_{\mathbb {R}} F$). Here we take the morphism $\psi$ of Sect. 2.3 to have constant rank equal to $\dim _{\mathbb {R}} \Sigma$, with an isomorphism

$$\begin{aligned} \psi : T\Sigma \vert _{\Sigma } \overset{\cong }{\longrightarrow } L = \psi (T\Sigma \vert _{\Sigma }). \end{aligned}$$

(3.2)

We then obtain from (2.21)

$$\begin{aligned} ((P(T\Xi ) - f^*P(T\Xi ')) \cap [\Xi ] = i_*((P(T\Sigma ) \cup k \mathbf {1}_{\Sigma } \cap [\Sigma ]) \in H_*(\Xi ). \end{aligned}$$

(3.3)

Riemann–Hurwitz type formulas in the smooth category expressed in terms of Kronecker pairings with fundamental classes involving Chern, Pontrjagin and Euler classes, for instance, have been obtained in [6, 13, 25, 31, 33].

Example 3.2

If, for instance, $\Xi$ and $\Xi '$ are compact complex manifolds with $\dim _{\mathbb {C}} \Xi = \dim _{\mathbb {C}} \Xi '=n$, and f is a holomorphic branched covering map with $\deg f = \ell$, having $\Sigma$ as the (complex) codimension $r=1$ branch set, then for top Chern classes one can derive the term (cf. [6, 31, 33]) $c_{n-1}(T \Sigma ) \cup k \mathbf {1} = (\ell -1) c_{n-1} (T \Sigma )$, and thus

$$\begin{aligned} (c_n(T\Xi ) - f^*c_n(T\Xi ')) \cap [\Xi ] = i_*((\ell -1) c_{n-1}(T\Sigma ) \cap [\Sigma ]). \end{aligned}$$

(3.4)

3.2 Virtual tangent bundles

When $\Xi$ is a smooth manifold (so the tangent bundle $T\Xi$ exists), then the cap product pairing leads to the characteristic homology class$P_*(\Xi ) = P(T\Xi ) \cap [\Xi ] \in H_*(\Xi , \Lambda )$. But here we are interested in knowing how much of the traditional theory carries through in the singular case. To this extent we follow, in part, the review article [30].

So to commence, let us take the category of (possibly singular) projective algebraic varieties. Let $\Xi$ be a singular variety. Then there is the problem of defining suitable characteristic classes. But suppose $\Xi$ is realized as a local complete intersection in a smooth variety M, so that the closed inclusion $\underline{j}: \Xi \longrightarrow M$ is a regular embedding. In this case, the normal cone$N_{\Xi }M \longrightarrow \Xi$ is a vector bundle over $\Xi$, and hence one can define the virtual tangent bundle of $\Xi$ by

$$\begin{aligned} T_{\mathrm{vir}}\Xi = [\underline{j}^* TM - N_{\Xi }M] \in K^0(\Xi ), \end{aligned}$$

(3.5)

which is independent of the embedding and thus produces a well-defined element in the Grothendieck group $K^0(\Xi )$ of vector bundles on $\Xi$ (see [11]).

In terms of the characteristic cohomology classes of vector bundles as we have already considered, an intrinsic homology class (independent of the embedding) applies relative to the virtual tangent bundle of $\Xi$, and is defined as

$$\begin{aligned} P_*^{\mathrm{vir}} (\Xi ) := P(T_{\mathrm{vir}}\Xi ) \cap [\Xi ] \in H_*(\Xi , \Lambda ). \end{aligned}$$

(3.6)

In this case, $[\Xi ] \in H_*(\Xi )$ can be taken as the fundamental class (or the class of the structure sheaf) of $\Xi$ in

$$\begin{aligned} H_*(\Xi ) = {\left\{ \begin{array}{ll} ~H^{\mathrm{BM}}_{2*} (\Xi ), &{}\text {the Borel--Moore homology in even degrees},\\ CH_*(\Xi ),&{}\text {the Chow group}, \\ G_0(\Xi ), &{}\text {the Grothendieck group of coherent sheaves}. \end{array}\right. } \end{aligned}$$

(3.7)

In terms of the Gysin homomorphism $\underline{j}^{!}: H_*(M) \longrightarrow H_{*-d}(\Xi )$ (where d is the embedding codimension), we also have, in relationship to characteristic classes, that

$$\begin{aligned} \underline{j}^{!}(P(M)) = \underline{j}^{!}(P(TM) \cap [M]) = P(N_{\Xi }M) \cap P_{*}^{\mathrm{vir}}(\Xi ). \end{aligned}$$

(3.8)

Example 3.3

If $\Xi$ and $\Xi '$ are singular varieties admitting closed regular embeddings as above, then Chern classes for virtual tangent bundles can be defined (see e.g., the lecture in [32]). In the case that $\Xi$ and $\Xi '$ are equidimensional, and $\Sigma$ a subvariety, each with fundamental classes defined, then from (3.2), we have

$$\begin{aligned} \psi : T_{\mathrm{vir}}\Sigma \vert _{\Sigma } \overset{\cong }{\longrightarrow } L = \psi (T_{\mathrm{vir}}\Sigma \vert _{\Sigma }). \end{aligned}$$

(3.9)

Given a rational map $f: \Xi \longrightarrow \Xi '$ in the setting of Sect. 3.1, and applying (2.21), we have for total Chern classes

$$\begin{aligned} (c(T_{\mathrm{vir}} \Xi ) - f^*c(T_{\mathrm{vir}} \Xi ')) \cap [\Xi ] = i_*(c(T_{\mathrm{vir}} \Sigma ) \cup k\mathbf {1}_{\Sigma } \cap [\Sigma ]). \end{aligned}$$

(3.10)

3.3 Stratified pseudomanifolds

To commence, we recall the definition as given in [10, 16].

Definition 3.1

An n-dimensional PL-stratified pseudomanifold$\mathcal S$ is a piecewise linear space (having a compatible family of triangulations) that also possesses a filtration by closed PL-subspaces

$$\begin{aligned} \mathcal S= \mathcal S^n \supset \mathcal S^{n-2} \supset \mathcal S^{n-3} \supset \cdots \supset \mathcal S^1 \supset \mathcal S^0 \supset \mathcal S^{-1} = \emptyset , \end{aligned}$$

(3.11)

forming a stratification that satisfies the following properties:

• 1. $\mathcal S- \mathcal S^{n-2}$ is dense in $\mathcal S$;

• 2. for each $k \ge 2$, $\mathcal S^{n-k} - \mathcal S^{n-k-1}$ is either empty or is an $(n-k)$-dimensional PL-manifold;

• 3. if $x \in \mathcal S^{n-k} - \mathcal S^{n-k-1}$, then x has a distinguished neighborhood that is PL-homeomorphic to $\mathbb {R}^{n-k} \times c\mathsf {L}$, where $c\mathsf {L}$ denotes the open cone on a compact $(k-1)$-dimensional manifold $\mathsf {L}$ whose stratification is compatible with that of $\mathcal S$.

A PL-stratified pseudomanifold $\mathcal S$ is oriented (or orientable) if $\mathcal S- \mathcal S^{n-2}$ has that same property. The sets $\mathcal S^i$ are called the skeleta (it can be verified from (2) above that each has dimension i as a PL-complex). The sets $\mathcal S_i = \mathcal S- \mathcal S^{i-1}$ are called the strata. In particular, $\mathcal S- \mathcal S^{n-2}$ are called regular strata, and the rest are called singular strata. The space $\mathsf {L}$ is called the link of x, or of the stratum containing x. We refer to [10, 16] for the additional topological characteristics of this sort of pseudomanifold.

3.4 Maps with branch-like singularities

In the context of Sects. 3.1 and 3.3, let $f: \Xi \longrightarrow \Xi '$ be a smooth map of compact oriented manifolds of equal dimension n, with degree $\deg f = \nu _f$. Let $\Sigma$ be a closed, connected PL-stratified pseudomanifold of codimension 2 in $\Xi$ such that $(\Xi , \Sigma )$ is a $(n, \Lambda )$-adapted pair. We say that f has branch-like singularities when the following holds. Let M be a closed oriented n-cycle in $\Xi$, such that each $B^{(\nu _i)}:= M \cap \mathcal S^i$ is a smooth connected oriented PL-submanifold of $\Sigma$ on which f has local degree $\nu _i = \vert \deg (f \vert B^{(\nu _i)}) \vert \le \nu _f$. Furthermore, M is assumed to have empty intersection with the singular strata of $\Sigma$. Note that this construction yields a nested sequence of the $B^{(\nu _i)}$ in accordance with the filtration in (3.11). Moreover, in this setting there is some scope in applying (2.21) and (3.3) to various characteristic classes. We will present such an application in Sect. 3.5 below.

3.5 Total Hirzebruch $\mathcal L$-polynomial and the signature

Let $f: \Xi \longrightarrow \Xi '$ be a smooth map of compact oriented manifolds of equal dimension 4n with f having branch-like singularities on $\Sigma$ as described above, such that $(\Xi , \Sigma )$ is a $(4n, \mathbb {Q})$-adapted pair. Recalling the above details, with M a closed oriented 4n-cycle in $\Xi$, it is possible to obtain from (2.21) and (3.3) several types of formulas in the Pontrjagin classes of the manifolds in question, whenever these classes can be defined.

Here we recall the total Hirzebruch $\mathcal L$-polynomial [17] on setting P( ) in (3.3) by $P(\Xi ) = \mathcal L\left( p_1(\Xi ), \ldots , p_n(\Xi )\right)$, where $p_i(\Xi )$ are the Pontrjagin classes of $\Xi$, etc., to obtain from (3.3):

$$\begin{aligned} (P(\Xi ) - f^*P(\Xi ')) \cap [\Xi ] = i_*\left( \sum _{\nu _i} P\left( B^{(\nu _i)}\right) \cup k \mathbf {1}_{B^{(\nu _i)}} \cap \left[ B^{(\nu _i)}\right] \right) . \end{aligned}$$

(3.12)

When Poincaré duality is defined, expressions such as (3.3) can be expressed in a numerical form via Kronecker pairings. Thus (3.12) becomes for the signature $\sigma$:

$$\begin{aligned} \sigma (\Xi ) - \nu _f \sigma (\Xi ') = k \sum _{\nu _i} \sigma \left( B^{(\nu _i)}\right) , \end{aligned}$$

(3.13)

where k is a suitable constant.

Note that given a smooth (or PL-locally flat) embedding $i: \Sigma \longrightarrow \Xi$, the codimension 2 stratified pseudomanifold $\Sigma$ here admits a homologyL-class in the sense of [7, 16] given by

$$\begin{aligned} L(\Sigma ) = [\Sigma ] \cap i^* \mathcal L\left( P(\Xi ) \cup (1 + \eta ^2)^{-1}\right) \in H_{2*} (\Sigma , \mathbb {Q}), \end{aligned}$$

(3.14)

where $P(\Xi ) \in H^*(\Xi )$ is the total Pontrjagin class of $\Xi$ and $\eta$ is the Poincaré dual of $i_*[\Sigma ]$ (see also Sect. 3.8). When Poincaré duality is defined, the latter transforms $L(\Sigma )$ to $\mathcal {L}$ as above.

Remark 3.1

Similar signature formulas have been obtained in [18, 34], and noting that the right-hand side of (3.12) is effectively a residual quantity, see also [25].

In the case of branched coverings of $S^4$ by 4-dimensional closed oriented PL-manifolds (reviewed in [19]), node singularities of the branching set are removable by suitable cobordisms [19]. Our approach is different since singularities in the strata are avoided by taking the appropriate intersection with the 4-cycle M to create the $B^{(\nu _i)}$, as described above.

3.6 Chern–Schwartz–MacPherson classes

Firstly, we recall the Chern–MacPherson transformation (over the field $\mathbb {C}$) [24]. To an extent we follow the exposition in [26]. For a quasi-projective variety X and proper morphisms this is a natural transformation, when X is smooth, from the constructible function functor to the Chow group functor

$$\begin{aligned} c_*: \mathcal F_*(X) \longrightarrow CH_*(X), \end{aligned}$$

(3.15)

satisfying the normalization property

$$\begin{aligned} c_*(\mathbb {I}_X) \longrightarrow c(TX) \cap [X] \in CH_*(X). \end{aligned}$$

(3.16)

On the other hand, if $\Sigma '$ is a possibly singular variety, then $c_*(\Sigma ') = c_*(\mathbb {I}_{\Sigma '})$ defines the Chern–Schwartz–MacPherson class of $\Sigma '$ in $CH_*(\Sigma ')$ [24].

There is a way this latter class can be realized as in [1]. Consider a closed embedding $j: \Sigma ' \longrightarrow X$, still assuming X is smooth. Resolving singularities, one obtains a birational map $f: \widetilde{X} \longrightarrow X$ such that $\widetilde{X}$ is smooth, with $\bar{\Sigma }' := f^{-1}(\Sigma )$. Furthermore, $\Sigma = \widetilde{X} - \Sigma '$ is a normal crossing divisor in X with smooth irreducible components $D_1, \ldots , D_k$. By induction on k, and properties of $c_*$, it is shown in [1] that

$$\begin{aligned} c_* \left( \mathbb {I}_{\Sigma '}\right) = f_*\left( \frac{c(T\widetilde{X})}{\Pi (1+D_i)} \cap [\widetilde{X}] \right) \in CH_*(X). \end{aligned}$$

(3.17)

In this last expression, the term $c(T\widetilde{X})/\Pi (1+D_i)$ is shown to equal the total Chern class $c(E^*)$ where $E = \Omega _{\widetilde{X}}^1(\log \Sigma )$ is a locally free sheaf of complex differential 1-forms with logarithmic poles along $\Sigma$ having $\mathrm{rank}_{\mathbb {C}} E = \dim _{\mathbb {C}} \widetilde{X}$.

Example 3.4

Within the setting of Sect. 3.1, we set $\Xi = \widetilde{X}$ and $\Xi ' = X$. We take $E = \Omega _{\widetilde{X}}^1(\log \Sigma )$, and set $F = f^*(TX)$. Again we have $L= \psi (E\vert _{\Sigma }) \subset F\vert _{\Sigma }$. Setting P as the total Chern class, and then applying the push-forward $f_*$ to (2.21), we have by [1, Theorem 1]:

$$\begin{aligned}&f_*\left( \left( c\left( \Omega _{\widetilde{X}}^1(\log \Sigma )\right) - f^*c(TX)\right) \cap [\widetilde{X}]\right) \nonumber \\&\quad = f_* i_* (c(L) \cup k \mathbf {1}_{\Sigma } \cap [\Sigma ]) \nonumber \\&\quad = - j_* c_{\mathrm{SM}} (\Sigma ') \in CH_*(X), \end{aligned}$$

(3.18)

which gives a further realization of the Chern–Schwartz–MacPherson class in the Chow group $CH_*(X)$.

3.7 Generalized monoidal tranformations for oriented circuits

We return now to the generalized set-up of Sect. 2.1 and Sect. 3.1 with regards a simplicial map $f: (\Xi , \Sigma ) \longrightarrow (\Xi ', \Sigma ')$ satisfying conditions (i) and (ii) in Sect. 3.1. The hypotheses outlined in Sect. 3.1, gave rise to the concept of a generalized monoidal transformation in [14]. So far, the development of ideas motivates the following proposition:

Proposition 3.1

Consider an $(n,\Lambda )$-adapted pair $(\Xi , \Sigma )$ as in Sect. 3.1 satisfying conditions (i) and (ii). Let the maps i, j in (3.1) be embeddings such that the Thom spaces $\mathcal T(\Sigma , \Xi ), \mathcal T(\Sigma ', \Xi ')$ of the normal bundles $\widehat{N}, N$, of i, j respectively, are defined. Then for suitable $P \in H^*(BG, \Lambda )$, we have

$$\begin{aligned} (P(\Xi ) - f^* P(\Xi ')) \cap [\Xi ] = \hat{t}^*(u \cdot a) \cap [\Xi ] \in H_*(\Xi ), \end{aligned}$$

(3.19)

where u is the Thom class of $\mathcal T(\Sigma , \Xi )$, $a \in H^*(\Sigma )$ is some suitable class, and $\hat{t}: \Xi \longrightarrow \mathcal T(\Sigma , \Xi )$ is the Thom–Pontrjagin map.

Proof

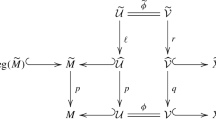
In view of the hypotheses on i, j, we have (following e.g., [12]) a natural commutative diagram

(3.20)

where $t, \hat{t}$ denote the Thom–Pontrjagin maps, together with excision relations:

$$\begin{aligned} \Xi&= (\Xi - \Sigma ) \cup \widehat{N}, ~ ~ ~ ~ (\Xi - \Sigma ) \cap \widehat{N} = \widehat{N} - \Sigma , \nonumber \\ \Xi '&= (\Xi ' - \Sigma ') \cup N, ~ ~ (\Xi ' - \Sigma ') \cap N = N - \Sigma '. \end{aligned}$$

(3.21)

Note that by excision, we have $H^*(\Xi , \Xi - \Sigma ) \cong H^*(\mathcal T(\Sigma , \Xi ))$. The proposition follows from the topological properties of $\mathcal T(\Sigma , \Xi )$ and the Thom class u of $\mathcal T(\Sigma , \Xi )$ relative to pullback via $\hat{t}$ in the far right square of (3.20). $\square$

In the case of the standard blowing-up process for non-singular varieties (see Sect. 3.9 below), the ‘suitable class’ $a \in H^*(\Sigma )$ was explicitly determined, as was the right-hand side of (3.19) in terms of total Chern classes in [12, Theorem (4.3)], as exhibited in (3.34) below (cf. [21, 22, 27]).

Remark 3.2

Once virtual tangent bundles are defined, then following (2.21) for connected n-circuits in the setting of Sect. 2.1, a generalized monoidal transformation satisfies

$$\begin{aligned} (P(T_{\mathrm{vir}} \Xi ) - P(f^*T_{\mathrm{vir}} \Xi ')) \cap [\Xi ] = i_*(P(T_{\mathrm{vir}} \Sigma ) \cup k \mathbf {1}_{\Sigma } \cap [\Sigma ]), \end{aligned}$$

(3.22)

for the appropriate $P \in H^*(BG, \Lambda )$.

3.8 Intersection cohomology signature

Following [30], in the compact case, we have a signature

$$\begin{aligned} \mathrm{sign}(\Xi ) = \deg (L_*(\Xi )), ~ \text {with}~ L_*: \Omega (\Xi ) \longrightarrow H_{2*}(\Xi , \mathbb {Q}), \end{aligned}$$

(3.23)

where the latter is the homologyL-class transformation of [7] (see also the review of related topics in [4]). Here $\Omega (\Xi )$ denotes the abelian group of corbordism classes of selfdual constructible complexes. From this it follows that $L_*(\Xi )= L_*([ \mathcal JC_{\Xi }])$ is the homologyL-class of [16] having a distinguished element $\mathbf {1}_{\Xi } = [\mathcal JC_{\Xi }]$ the class of their intersection homology complex. Thus $\mathrm{sign}(\Xi )$ is called the intersection cohomology signature of$\Xi$.

Proposition 3.2

If $f: (\Xi , \Sigma ) \longrightarrow (\Xi ', \Sigma ')$ in Sect. 3.1 is a map of compact spaces, then we have

$$\begin{aligned} f_*(L_*(\Xi ) - L_* (\Sigma )) = L(\Xi ') \in H_{2*}(\Xi ', \mathbb {Q}). \end{aligned}$$

(3.24)

In particular, on taking degrees we have the intersection cohomology signature relationship

$$\begin{aligned} \mathrm{sign}(\Xi )= \mathrm{sign}(\Xi ') + \mathrm{sign}(\Sigma ). \end{aligned}$$

(3.25)

Proof

Let $\mathcal U^0$ and $\mathcal V^0$ be open tubular neighborhoods of $\Sigma$ and $\Sigma '$, respectively, so that $\mathcal V^0 = f(\mathcal U^0)$, and let $V_1 = \Xi \times [0,1], V_2 = \Xi ' \times [0,1]$. Then set $S = V_1 \wedge V_2/ \sim$, where the identification ‘$\sim$’ is given by

$$\begin{aligned} (x,0) \in (\Xi ' \times \{0\}) - (\mathcal V^0 \times \{0\}) \sim (f(x), 1) \in (\Xi \times \{1\}) - (\mathcal U^0 \times \{1\}). \end{aligned}$$

(3.26)

Then, by smoothing the corners created by identification S is an oriented manifold whose oriented boundary is diffeomorphic to $\Xi ' + \Sigma - \Xi$, and $\Xi$ is oriented cobordant to $\Xi ' + \Sigma$ [14, Proposition (2.2)]. From this additivity property of cobordism invariants the first statement follows. The second statement then follows by taking degrees (cf. [14, Corollary (2.3)]). $\square$

Remark 3.3

In [14] the role of $\Sigma$ was there denoted by W, and it was aptly entitled a residual circuit.

3.9 The standard blowing-up process

In the following it will be useful to adapt (3.1) using more familiar information as follows. We set $\Sigma ' = Y$ and $\Xi ' = X$, and consider the inclusion $Y \subseteq X$ of non-singular (smooth) varieties. Let $\Xi = \widetilde{X}$ denote the blow-up of X along Y, with $\Sigma = \widetilde{Y}$:

(3.27)

We have then a biholomorphism $\hat{f}: \widetilde{X} - \widetilde{Y} \longrightarrow X - Y$. In this situation $\widetilde{Y} = \mathbb {P}(N_YX \oplus \mathbf {1})$ is the projectivized normal bundle of Y in X, that is a locally trivial bundle over Y with fiber $\mathbb {C}P^r$ ($r = \mathrm{codim}_{\mathbb {C}} Y$). Using [11, Theorem 15.4], we have

$$\begin{aligned} (c(T\widetilde{X}) - f^* c(TX)) \cap [\widetilde{X}]&= i_*(g^* c(TY) \cup \lambda \cap [\widetilde{Y} ]) \nonumber \\&= i_* (c(L) \cup k\mathbf {1}_{\widetilde{TY}} \cap [\widetilde{Y}]). \end{aligned}$$

(3.28)

Completely determining the right-hand side of (3.28) essentially leads to the Todd–Segre formula for Chern classes relative to the Chow ring of rational equivalence classes of cycles, as was first established by Porteous [27, 28]. Since then there have been several variations on this theme, exhibiting alternative proofs along with certain generalizations. We refer to, e.g., [2, 12, 21, 22] for the particular details, but for now, we briefly expose one common line of approach in terms of the geometry of projective bundles.

Suppose V is a rank r complex vector bundle, and consider the projective bundle $p: \mathbb {P}(V) \longrightarrow Y$. There is a short exact sequence

$$\begin{aligned} 0 \longrightarrow \mathcal L\longrightarrow p^*V \longrightarrow Q \longrightarrow 0, \end{aligned}$$

(3.29)

where $\mathcal L$ is the canonical line bundle and Q is the quotient bundle. We have then

$$\begin{aligned} T\mathbb {P}(V) = p^* TY \oplus B(T\mathbb {C}P^{r-1}), \end{aligned}$$

(3.30)

where $B(T\mathbb {C}P^{r-1})$ denote the bundle along the fibers in (3.29), which in this case is given by

$$\begin{aligned} B(T\mathbb {C}P^{r-1}) \cong \mathrm{Hom}(\mathcal L, Q) \cong \mathcal L^* \otimes Q, \end{aligned}$$

(3.31)

so that

$$\begin{aligned} T \mathbb {P}(V) = p^* TY \oplus \mathcal L^* \otimes Q. \end{aligned}$$

(3.32)

Applying these considerations to the short exact sequence

$$\begin{aligned} 0 \longrightarrow \widehat{N} \longrightarrow f^* N \longrightarrow Q \longrightarrow 0 \end{aligned}$$

(3.33)

leads, as in [12] (cf. [21, 22, 28]), to a realization of the right-hand side of (3.28) given by

$$\begin{aligned} (c(T\widetilde{X}) - f^* c(TX)) \cap [\widetilde{X}]&= i_*(g^* c(TY) \cup \lambda \cap [\widetilde{Y} ]) \nonumber \\&= t^*\big ( u(\hat{f}^* c(TY) \cup c(\widehat{N}) \cup B(\widehat{N}^*,Q)\big ) \cap [\widetilde{X}]. \end{aligned}$$

(3.34)