Finding disjoint surfaces in 3-manifolds

Abstract

Let M be a compact connected orientable 3-manifold, with non-empty boundary that contains no two-spheres. We investigate the existence of two properly embedded disjoint surfaces $S_{1}$ and $S_{2}$ such that $M - (S_{1} \cup S_{2})$ is connected. We show that there exist two such surfaces if and only if M is neither a $\mathbb Z _{2}$ homology solid torus nor a $\mathbb Z _{2}$ homology cobordism between two tori. In particular, the exterior of a link with at least three components always contains two such surfaces. The proof mainly uses techniques from the theory of groups, both discrete and profinite.

1 Introduction

In 3-manifold theory, properly embedded surfaces play a key role. It is particularly interesting when a compact 3-manifold $M$ contains two properly embedded disjoint surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected. It is this scenario that we will investigate in this paper. Our aim is to show that the 3-manifolds where this situation occurs are actually very plentiful. Moreover, we will see how algebraic methods can be profitably used to detect the existence of such a pair of surfaces. In particular, the infinite dihedral group $\mathbb{Z }_2 *\mathbb{Z }_2$ will play a central role. This is because a compact connected 3-manifold $M$ contains a pair of such surfaces if and only if $\pi _1(M)$ admits a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$ (see Theorem 3.1.)

Note that we do not require that $S_1$ and $S_2$ are two-sided. The existence of two disjoint properly embedded two-sided surfaces $S_1$ and $S_2$ in a 3-manifold $M$ with $M - (S_1 \cup S_2)$ connected appears to be a much more rare occurrence, and is equivalent to the existence of a surjective homomorphism $\pi _1(M) \rightarrow \mathbb{Z } *\mathbb{Z }$. (See [1] for example, where obstructions to the existence of such a homomorphism are given.)

The following is our main result.

Theorem 1.1

Let $M$ be a compact connected orientable 3-manifold, and suppose that $\partial M$ is non-empty and contains no 2-spheres. Then $M$ contains two properly embedded disjoint surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected if and only if $M$ is neither a $\mathbb{Z }_2$ homology solid torus nor a $\mathbb{Z }_2$ homology cobordism between two tori.

Corollary 1.2

Let $L$ be a link in $S^3$. Then the exterior $X$ of $L$ contains two properly embedded disjoint surfaces $S_1$ and $S_2$ such that $X - (S_1 \cup S_2)$ is connected if and only if one of the following holds:

• (i) $L$ has at least three components, or

• (ii) $L$ has two components, which have even linking number.

It is an interesting and not completely straightforward exercise to construct such surfaces in the exterior of the Whitehead link. We will do so explicitly in Sect. 4.

The case of two-component links was studied by Hillman in [3], where he stated Corollary 1.2 in this case. (It appears in the middle of the second full paragraph on p. 176 in [3].)

The plan of the paper is as follows. In Sect. 2, we prove the foundational result that the existence of a surjective homomorphism from a finitely generated group $G$ onto $\mathbb{Z }_2 *\mathbb{Z }_2$ is equivalent to the existence of an index two subgroup $K$ of $G$ with $b_1(K) > b_1(G)$. In Sect. 3, we first prove that, for a compact connected 3-manifold $M$, the existence of a surjective homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ is equivalent to the existence of two properly embedded disjoint surfaces as in the statement of Theorem 1.1. We then use these two facts to prove one direction of Theorem 1.1. The starting point is the well-known inequality $b_1(M) \ge b_1(\partial M)/2$ for any compact orientable 3-manifold $M$ (see Lemma 3.5 in [2] for example). Assuming that $M$ is a 3-manifold as in Theorem 1.1 which is neither a $\mathbb{Z }_2$ homology solid torus nor a $\mathbb{Z }_2$ homology cobordism between two tori, we find a double cover $\tilde{M}$ of $M$ such that $b_1(\partial \tilde{M}) > b_1(\partial M)$, and, after some work, we deduce that $b_1(\tilde{M}) > b_1(M)$. The results in Sect. 2 and earlier in Sect. 3 then give the required surfaces. The existence of these two surfaces is thereby proved, but the construction is group-theoretic and far from explicit. In Sect. 4, we give a more geometric way of finding these surfaces, which can be used easily in practice. We examine the case of the exterior of the Whitehead link, which is an instructive example. In Sect. 5, we introduce methods from profinite group theory. We show that the existence of a surjective homomorphism from a finitely generated group $G$ to $\mathbb{Z }_2 *\mathbb{Z }_2$ is detected by the pro-2 completion of $G$. These profinite techniques are used to prove the other direction of Theorem 1.1, which establishes that certain 3-manifolds as described in the theorem do not contain two disjoint properly embedded surfaces whose union is non-separating. In Sect. 6, we also use profinite group theory to control the $\mathbb{Z }_2$ homology classes of the surfaces for certain 3-manifolds. For example, we show that in the case where $M$ is a compact orientable 3-manifold that has the same $\mathbb{Z }_2$ homology as a handlebody (other than a solid torus), then $S_1$ and $S_2$ may be chosen to represent any pair of distinct non-trivial classes in $H_2(M, \partial M; \mathbb{Z }_2)$. The key input here is the fact that, in this case, $\pi _1(M)$ has the same pro-2 completion as a non-abelian free group. In Sect. 7, we pose some questions, which may stimulate further research in this area.

2 Surjections to the infinite dihedral group

We start with the following group-theoretic result.

Theorem 2.1

Let $G$ be a finitely generated group, and let $K$ be an index two subgroup. Then the following are equivalent:

• (i) There is a surjective homomorphism $\phi :G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ such that $K$ is the kernel of $\pi \phi$, where $\pi :\mathbb{Z }_2 *\mathbb{Z }_2 \rightarrow \mathbb{Z }_2$ is the homomorphism which is an isomorphism on each factor.

• (ii) $b_1(K) > b_1(G)$.

Note that this has the following immediate corollary.

Corollary 2.2

Let $G$ be a finitely generated group. Then the following are equivalent:

• (i) There is a surjective homomorphism $G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$.

• (ii) For some index two subgroup $K$ of $G, b_1(K) > b_1(G)$.

Proof of Theorem 2.1

(i) $\Rightarrow$ (ii). Suppose that there is a surjective homomorphism $\phi :G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ such that $K$ is the kernel of $\pi \phi$. We claim that $b_1(K) > b_1(G)$.

Now, the inclusion $i :K \rightarrow G$ induces a homomorphism $i^*:H^1(G; \mathbb{R }) \rightarrow H^1(K; \mathbb{R })$. This is clearly an injection. This is because $H^1(G; \mathbb{R })$ may be viewed as the set of homomorphisms $G \rightarrow \mathbb{R }$ and if a homomorphism $G \rightarrow \mathbb{R }$ is zero when restricted to $K$, then it is zero on all of $G$.

We will show that in fact this injection $i^*$ is not a surjection. This will prove that $b_1(K) > b_1(G)$ as required.

The kernel of the homomorphism $\pi$ is a subgroup $A$ of $\mathbb{Z }_2 *\mathbb{Z }_2$ that is infinite cyclic. Let $\psi$ be the composition $K \rightarrow A \rightarrow \mathbb{R }$, where the first map is the restriction of $\phi$ to $K$ and the second map is the standard inclusion of the infinite cyclic group into $\mathbb{R }$. We will show that $\psi$ is not in the image of $i^*$.

For suppose that $\psi$ is in this image. This means that $\psi$ extends to a homomorphism $\tilde{\psi }:G \rightarrow \mathbb{R }$. Let $a$ and $b$ be generators of the factors of $\mathbb{Z }_2 *\mathbb{Z }_2$. Let $g_a$ and $g_b$ be elements of $G$ that are sent by $\phi$ to these generators. Then $g_a g_b$ lies in $K$ and its image under $\psi$ is 1, say. On the other hand, $g_b g_a$ also lies in $K$ and its image under $\psi$ is $-1$, because $ab$ and $ba$ are inverses. But, because $\mathbb{R }$ is an abelian group, $\psi (g_a g_b) = \tilde{\psi }(g_a g_b) = \tilde{\psi }(g_b g_a) = \psi (g_b g_a)$, which is a contradiction.

(ii) $\Rightarrow$ (i). Let $K$ be an index two subgroup of $G$ with $b_1(K) > b_1(G)$. Let $V$ be the vector space $H^1(K; \mathbb{R })$. This acted on by $G/K = \mathbb{Z }_2$ via the conjugation action of $G$ on $K$. Let $\tau$ be the automorphism of $H^1(K; \mathbb{R })$ induced by the non-trivial element of $G/K$. Since $\tau$ is an involution, it gives rise to a decomposition $V = V_- \oplus V_+$, where $V_-$ and $V_+$ are the $-1$ and $+1$ eigenspaces of $\tau$.

We claim that the eigenspace $V_+$ consists of precisely the homomorphisms $K \rightarrow \mathbb{R }$ that extend to $G$. For suppose that a homomorphism $\psi :K \rightarrow \mathbb{R }$ extends to a homomorphism $\tilde{\psi }:G \rightarrow \mathbb{R }$. Let $g$ be an element of $G - K$. The image of $\psi$ under $\tau$ sends $k \in K$ to $\psi (g^{-1} k g) = \tilde{\psi }(g^{-1} k g) = \tilde{\psi }(k) = \psi (k)$. So, $\psi$ lies in $V_+$. Conversely, suppose that $\psi :K \rightarrow \mathbb{R }$ lies in $V_+$ and is therefore invariant under $\tau$. Then we extend $\psi$ to $\tilde{\psi }:G \rightarrow \mathbb{R }$ by defining

$$\begin{aligned} \tilde{\psi }(k)&= \psi (k) \\ \tilde{\psi }(gk)&= \psi (k) + (\psi (g^2))/2. \end{aligned}$$

Here, $g$ is a fixed element of $G - K$, and $k$ is an arbitrary element of $K$. It is easy to check that $\tilde{\psi }$ is a homomorphism, which clearly extends $\psi$. This proves the claim.

So, the dimension of $V_+$ is $b_1(G)$. Now, we are assuming that $b_1(K) > b_1(G)$, and so $V_-$ is therefore non-zero. We can view $H^1(K; \mathbb{Z })$ as a lattice in $H^1(K; \mathbb{R })$, consisting of those homomorphisms $K \rightarrow \mathbb{R }$ that have image in $\mathbb{Z }$. The action of $G/K$ on $H^1(K; \mathbb{R })$ leaves this lattice invariant as a set, simply because it sends a homomorphism $K \rightarrow \mathbb{Z }$ to another such homomorphism. Thus, we may find non-zero elements of $H^1(K; \mathbb{Z }) \cap V_-$, as follows. Take any element $\alpha$ of $H^1(K; \mathbb{Z })$ not in $V_+$, and consider $\alpha - \tau \alpha$, where $\tau \alpha$ is the image of $\alpha$ under the action of $\tau$. Thus, as we know that $H^1(K; \mathbb{Z }) \cap V_-$ is non-zero, we may find a primitive element $\psi$ in $H^1(K; \mathbb{Z }) \cap V_-$. This corresponds to a surjective homomorphism $\psi :K \rightarrow \mathbb{Z }$. We now use this to define a surjective homomorphism $\phi :G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$. Pick any element $g$ in $G - K$. Note that $g^2 \in K$ and that $\psi (g^2) = \psi (g^{-1} g^2 g) = - \psi (g^2)$, and hence $\psi (g^2) = 0$. Define a function

$$\begin{aligned}&G \mathop {\longrightarrow }\limits ^{\phi } \mathbb{Z }_2 *\mathbb{Z }_2 \\&k \mapsto (ab)^{\psi (k)}, \\&gk \mapsto a (ab)^{\psi (k)}. \end{aligned}$$

Here $k$ is an arbitrary element of $K$. This is easily checked to be a homomorphism. For example, suppose that $k_1, k_2 \in K$. We check that $\phi (k_1) \phi (g k_2) = \phi (k_1 g k_2)$:

$$\begin{aligned} \phi (k_1)\phi (gk_2)&= (ab)^{\psi (k_1)} a (ab)^{\psi (k_2)}\\ \phi (k_1 g k_2)&= \phi ( g (g^{-1} k_1 g) k_2) = a (ab)^{-\psi (k_1)} (ab)^{\psi (k_2)} = a (ba)^{\psi (k_1)} (ab)^{\psi (k_2)}. \end{aligned}$$

We also check that $\phi (g k_1) \phi (g k_2) = \phi (g k_1 g k_2)$:

$$\begin{aligned} \phi (gk_1)\phi (gk_2)&= a (ab)^{\psi (k_1)} a (ab)^{\psi (k_2)} = (ab)^{-\psi (k_1) + \psi (k_2)}\\ \phi (gk_1 g k_2)&= \phi (g^2 (g^{-1} k_1 g) k_2) = (ab)^{\psi (g^2)} (ab)^{-\psi (k_1)} (ab)^{\psi (k_2)}. \end{aligned}$$

This homomorphism $\phi$ is surjective. This can be seen as follows. Since $\psi$ is surjective, there is some $k \in K$ such that $\psi (k) = 1$. So, $\phi (gk) = aab = b$, and $\phi (kgk) = \phi (k) \phi (gk) = abb = a$.

Finally, note that $\mathrm{Ker}(\pi ) = A$ consists of precisely those elements of $\mathbb{Z }_2 *\mathbb{Z }_2$ of the form $(ab)^m$ for some $m \in \mathbb{Z }$. So, the kernel of $\pi \phi$ is exactly $K$, as required. This proves the theorem. $\square$

3 Constructing disjoint surfaces in 3-manifolds

The following is fairly well known. See, for example [4], where a related result is proved.

Theorem 3.1

Let $M$ be a compact connected 3-manifold. Then, the following are equivalent:

• (i) There is a surjective homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$.

• (ii) There are two disjoint properly embedded surfaces $S_1$ and $S_2$ in $M$ such that $M - (S_1 \cup S_2)$ is connected.

Proof

(ii) $\Rightarrow$ (i). Suppose that there are surfaces $S_1$ and $S_2$ as in (ii). We will use these to define a continuous map $f :M \rightarrow (\mathbb{R }P^3) \vee (\mathbb{R }P^3)$ such that $f_*:\pi _1(M) \rightarrow \pi _1((\mathbb{R }P^3) \vee (\mathbb{R }P^3)) = \mathbb{Z }_2 *\mathbb{Z }_2$ is surjective.

Let $N(S_1)$ and $N(S_2)$ be disjoint regular neighbourhoods of $S_1$ and $S_2$. Then $N(S_i)$ is an $I$-bundle over $S_i$ in which $S_i$ lies as a zero-section. We now define a map $f_i :N(S_i) \rightarrow \mathbb{R }P^3$.

Pick a cell structure on $S_i$. This lifts to a cell structure on $\tilde{S}_i = \mathrm{cl}(\partial N(S_i) - \partial M)$, which is the $(\partial I)$-bundle over $S_i$. This extends to a cell structure on $N(S_i)$, as follows. The fibre over each 0-cell of $S_i$ becomes a 1-cell of $N(S_i)$. The interior of each 1-cell of $S_i$ has inverse image in $N(S_i) - \tilde{S}_i$ that is an open disc, which we declare to be the interior of a 2-cell. Similarly, each 2-cell of $S_i$ induces a 3-cell of $N(S_i)$. We define $f_i$ one cell at a time, starting with the 0-cells, then the 1-cells and so on. Give $\mathbb{R }P^3$ the usual cell structure, with one 0-cell, one 1-cell, one 2-cell and one 3-cell. Now define $f_i$ on the 0-cells of $N(S_i)$, by sending them to the unique 0-cell of $\mathbb{R }P^3$. Map each 1-cell of $N(S_i)$ that misses $S_i$ also to the 0-cell of $\mathbb{R }P^3$. Send each 1-cell of $N(S_i)$ that intersects $S_i$ around the 1-cell of $\mathbb{R }P^3$ so that the interior of the cell is mapped in homeomorphically. There are two different ways of doing this. We pick one arbitrarily. The 2-cells of $N(S_i)$ come in two varieties. There are 2-cells that lie in $\tilde{S}_i$. We send these to the 0-cell of $\mathbb{R }P^3$. The 2-cells that are vertical in $N(S_i)$ we map to the 2-cell of $\mathbb{R }P^3$. This is possible because the boundary of each vertical 2-cell of $N(S_i)$ runs over two vertical 1-cells, and so its boundary has been mapped to a loop in $\mathbb{R }P^3$ that is homotopically trivial. Finally, the 3-cells of $N(S_i)$ may be mapped in because $\pi _2(\mathbb{R }P^3) = 0$.

Thus, we have defined a map $f_i :N(S_i) \rightarrow \mathbb{R }P^3$. Note that the image of $\tilde{S}_i$ is the 0-cell of $\mathbb{R }P^3$.

Now form the wedge $\mathbb{R }P^3 \vee \mathbb{R }P^3$ by gluing the two copies of $\mathbb{R }P^3$ along the 0-cells. We may define $f :M \rightarrow \mathbb{R }P^3 \vee \mathbb{R }P^3$ by sending points outside of $N(S_1) \cup N(S_2)$ to the basepoint of the wedge, and by mapping in $N(S_i)$ to the $i$th copy of $\mathbb{R }P^3$ using $f_i$.

We claim that $f_*:\pi _1(M) \rightarrow \pi _1((\mathbb{R }P^3) \vee (\mathbb{R }P^3))$ is a surjection. Give $M$ a basepoint that is disjoint from $N(S_1) \cup N(S_2)$. We just have to find based loops $\ell _1$ and $\ell _2$ in $M$ such that the image of $\ell _i$ is the generator for the $i$th factor of $\pi _1((\mathbb{R }P^3) \vee (\mathbb{R }P^3))$. Pick a path from the basepoint of $M$ to one of the 0-cells of $N(S_i)$, so that the interior of the path misses $N(S_1) \cup N(S_2)$. Then continue this path across the 1-cell that intersects $S_i$. Then run the path back to the basepoint of $M$, again with the interior of the path avoiding $N(S_1) \cup N(S_2)$. This is possible because we are assuming that $M - (S_1 \cup S_2)$ is connected. The result is a based loop $\ell _i$ with the required properties.

(i) $\Rightarrow$ (ii). Suppose that there is a surjective homomorphism $\phi :\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$.

Consider $\mathbb{R }P^2 \vee \mathbb{R }P^2$. Give each copy of $\mathbb{R }P^2$ the standard cell structure, and suppose that these two copies of $\mathbb{R }P^2$ are glued along their 0-cells. In the interior of each 1-cell, pick a point, and in each 2-cell, pick a properly embedded arc with endpoints equal to one of these points. Let $\alpha _1$ and $\alpha _2$ be the resulting disjoint simple closed curves in $\mathbb{R }P^2 \vee \mathbb{R }P^2$.

Pick a triangulation $T$ for $M$, and let $T^{(1)}$ and $T^{(2)}$ be its 1-skeleton and 2-skeleton. It is shown in the proof of Theorem 3.6 in [4] that $\phi$ is induced by a map $f :T^{(2)} \rightarrow \mathbb{R }P^2 \vee \mathbb{R }P^2$ with the following properties:

• (1) For $i = 1$ and $2, f^{-1}(\alpha _i)$ is disjoint from the 0-skeleton of $T$ and intersects the 1-skeleton in finitely many points. Moreover, $f^{-1}(\alpha _i)$ intersects each face of $T$ in a collection of properly embedded arcs, with boundary equal to $f^{-1}(\alpha _i) \cap T^{(1)}$. (In [4], this arrangement is called a regular mod 2 cocycle, where each interior vertex has valence 2. Note also the space referred to as $L(2)$ in [4] is just $\mathbb{R }P^2$.)

• (2) $f^{-1}(\alpha _1 \cup \alpha _2)$ is non-separating in $T^{(2)}$.

We now extend $f^{-1}(\alpha _1)$ and $f^{-1}(\alpha _2)$ to disjoint surfaces $S_1$ and $S_2$ properly embedded in $M$. For each tetrahedron $\Delta$ of $T, f^{-1}(\alpha _1)$ and $f^{-1}(\alpha _2)$ intersect this tetrahedron in a collection of simple closed curves in the boundary of $\Delta$. We attach a collection of disjoint discs properly embedded in $\Delta$ to these curves.

Note that $S_1 \cup S_2$ is non-separating. For consider two points in the complement of $S_1 \cup S_2$. We may find paths in $M - (S_1 \cup S_2)$ from these points to the 2-skeleton of $T$. Because $f^{-1}(\alpha _1 \cup \alpha _2)$ is non-separating in $T^{(2)}$, we may find a path joining these two points in the complement of $S_1 \cup S_2$. $\square$

Remark 3.2

Note that we can gain control over the mod 2 homology classes of the surfaces $S_1$ and $S_2$ in Theorem 3.1, in terms of the surjective homomorphism $\phi :\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$. We see from the construction that the composition of $\phi$ with projection $\mathbb{Z }_2 *\mathbb{Z }_2 \rightarrow \mathbb{Z }_2$ onto the $i$th factor is equal to the homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2$ that counts the mod 2 intersection number with $S_i$.

We can now prove one direction of Theorem 1.1. Suppose that $M$ is a compact connected orientable 3-manifold and that $\partial M$ is non-empty and contains no two-spheres. Suppose also that $M$ is neither a $\mathbb{Z }_2$ homology solid torus nor a $\mathbb{Z }_2$ homology cobordism between two tori. Then, we wish to show that $M$ contains two disjoint properly embedded surfaces $S_1$ and $S_2$ in $M$ such that $M - (S_1 \cup S_2)$ is connected. By Theorem 3.1, this is equivalent to $\pi _1(M)$ admitting a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$. By Corollary 2.2, this is equivalent to the existence of an index 2 subgroup $K$ of $\pi _1(M)$ such that $b_1(K) > b_1(M)$. To find such a subgroup, we use the following lemma.

Lemma 3.3

Let $M$ be a compact orientable 3-manifold, and let $\tilde{M}$ be a double cover of $M$ such that $\mathrm{genus}(\partial \tilde{M}) > \mathrm{genus}(\partial M)$. Then $b_1(\tilde{M}) > b_1(M)$.

Proof

Let $p :\tilde{M} \rightarrow M$ be the covering map. It is argued in the proof of Theorem 2.1 that $p^*:H^1(M; \mathbb{R }) \rightarrow H^1(\tilde{M}; \mathbb{R })$ is an injection. The same is true of $(p|\partial \tilde{M})^*:H^1(\partial M; \mathbb{R }) \rightarrow H^1(\partial \tilde{M} ; \mathbb{R })$. However, an alternative proof is required, because $\partial M$ may be disconnected and so an argument involving the fundamental group is not immediately appropriate. Instead, we consider the transfer homomorphism $t :H^1(\partial \tilde{M}; \mathbb{R }) \rightarrow H^1(\partial M; \mathbb{R })$. Recall that this is defined by sending a cocycle $c \in C^1(\partial \tilde{M}; \mathbb{R })$ to the cocycle $tc \in C^1(\partial M; \mathbb{R })$, where $tc(e) = c(\tilde{e}_1) + c(\tilde{e}_2)$. Here $e$ is an oriented edge in some cell structure on $\partial M$, and $e_1$ and $e_2$ are its inverse images in $\partial \tilde{M}$. It is well known that this gives a well-defined homomorphism $t :H^1(\partial \tilde{M}; \mathbb{R }) \rightarrow H^1(\partial M; \mathbb{R })$. It is clear the composition $t \circ (p|\partial \tilde{M})^*:H^1(\partial M; \mathbb{R }) \rightarrow H^1(\partial M; \mathbb{R })$ is the homomorphism that multiplies by 2. This is implies that $(p|\partial \tilde{M})^*$ is an injection, as required.

Now consider the commutative diagram

$$\begin{aligned} \begin{array}{ccc} H^1(M; \mathbb{R }) &{} {\mathop {\longrightarrow }\limits ^{p^*}}&{} H^1(\tilde{M}; \mathbb{R }) \\ \downarrow &{} \quad &{} \downarrow \\ H^1(\partial M; \mathbb{R }) &{} \mathop {\longrightarrow }\limits ^{(p|\partial \tilde{M})^*} &{} H^1(\partial \tilde{M}; \mathbb{R })\\ \end{array} \end{aligned}$$

where the vertical arrows are the homomorphisms induced by inclusion. It is a well-known consequence of Poincaré duality that, for the compact orientable 3-manifold $M$, the image of $H^1(M; \mathbb{R }) \rightarrow H^1(\partial M; \mathbb{R })$ has dimension equal to exactly half the dimension of $H^1(\partial M; \mathbb{R })$ (see the proof of Lemma 3.5 in [2] for example). A similar statement is true for $\tilde{M}$.

Suppose now that $b_1(\tilde{M}) \le b_1(M)$. Then $p^*:H^1(M; \mathbb{R }) \rightarrow H^1(\tilde{M}; \mathbb{R })$ is therefore an isomorphism. So,

$$\begin{aligned} \mathrm{Im}(H^1(\tilde{M}; \mathbb{R })&\rightarrow H^1(\partial \tilde{M};\mathbb{R })) \\ \quad =\mathrm{Im}(H^1(M; \mathbb{R })&\rightarrow H^1(\partial \tilde{M};\mathbb{R })) \\ \quad \cong \mathrm{Im}(H^1(M; \mathbb{R })&\rightarrow H^1(\partial M;\mathbb{R })). \end{aligned}$$

Hence, $b_1(\partial \tilde{M}) = b_1(\partial M)$. But this is equivalent to the statement that $\partial \tilde{M}$ and $\partial M$ have the same genus, which is contrary to hypothesis.$\square$

We now return to the proof of one direction of Theorem 1.1.

Case 1

$\partial M$ has a component which is not a torus.

Then, $\chi (\partial M) < 0$. Pick any double cover $\tilde{M} \rightarrow M$. Then, $\chi (\partial \tilde{M}) = 2 \chi (\partial M) < \chi (\partial M)$. Also, $|\partial \tilde{M}| \ge |\partial M|$. This implies that

$$\begin{aligned} {\mathrm{genus}}(\partial \tilde{M}) = {- \chi (\partial \tilde{M}) + 2 |\partial \tilde{M}| \over 2}> {- \chi (\partial M) + 2 |\partial M| \over 2} = {\mathrm{genus}}(\partial M), \end{aligned}$$

as required.

Case 2

$\partial M$ is at least three tori.

Then, $H^1(M; \mathbb{Z }_2)$ has rank at least three. Pick some torus $T$ in $\partial M$. Then the homomorphism $H^1(M; \mathbb{Z }_2) \rightarrow H^1(T; \mathbb{Z }_2)$ that is induced by inclusion has non-zero kernel. Pick some non-zero element in this kernel, and let $\tilde{M}$ be the corresponding double cover of $M$. Then, the inverse image of $T$ in $\tilde{M}$ is two copies of $T$. So, $\mathrm{genus}(\partial \tilde{M}) = |\partial \tilde{M}| > |\partial M| = \mathrm{genus}(\partial M)$, as required.

Case 3

$\partial M$ consists of two tori.

So, $H^1(M; \mathbb{Z }_2)$ has rank at least two. Now it cannot be the case that, for each torus $T$ in $\partial M, H^1(M; \mathbb{Z }_2) \rightarrow H^1(T; \mathbb{Z }_2)$ is an isomorphism. For this would imply that $M$ is a $\mathbb{Z }_2$ homology cobordism between the two components of $\partial M$, and this is contrary to assumption. So, for some component $T$ of $\partial M, H^1(M; \mathbb{Z }_2) \rightarrow H^1(T; \mathbb{Z }_2)$ is not an isomorphism, and is therefore not injective. As in Case 2, we consider a double cover $\tilde{M}$ of $M$ corresponding to a non-zero element in the kernel. This has $\mathrm{genus}(\partial \tilde{M}) > \mathrm{genus}(\partial M)$, as required.

Case 4

$\partial M$ is a single torus $T$.

Then, $H^1(M; \mathbb{Z }_2)$ has rank at least 1. In fact, it must have rank at least 2, since otherwise $M$ is a $\mathbb{Z }_2$ homology solid torus. But the image of $H^1(M; \mathbb{Z }_2) \rightarrow H^1(T; \mathbb{Z }_2)$ has rank one, and so again, there is a non-trivial element in its kernel. The argument then proceeds as in Cases 2 and 3. $\square$

4 Making the construction explicit

In the previous section, we completed the proof of one direction of Theorem 1.1, thereby establishing the existence of pairs of disjoint surfaces in many 3-manifolds whose union is non-separating. However, the proof is rather algebraic, and so it is hard to see how the surfaces arise explicitly. In this section, we will remedy this defect, by providing an alternative way of constructing these surfaces that is considerably more geometric.

A key part of the construction was to find a double cover $\tilde{M} \rightarrow M$ for which $b_1(\tilde{M}) > b_1(M)$. We saw in the proof of Theorem 2.1 that there is then a non-trivial primitive element $\alpha$ of $H^1(\tilde{M}; \mathbb{Z })$ that is in the $-1$ eigenspace of the action of the non-trivial covering transformation $\tau$.

We will show that the surfaces $S_1$ and $S_2$ required by Theorem 1.1 may be constructed as follows:

• 1. Find a compact, oriented, properly embedded, non-separating surface $S$ in $\tilde{M}$ that is dual to $\alpha$ and that is invariant under the covering transformation $\tau$, but for which $\tau$ reverses the orientation. We will prove below that such a surface $S$ always exists. Since $\tau$ reverses the orientation of $S$, its image in $M$ is unoriented and typically non-orientable. This image will be one of the surfaces, say $S_1$.

• 2. Cut $\tilde{M}$ along $S$ to give a compact orientable 3-manifold $M^{\prime }$. The involution $\tau$ restricts to $M^{\prime }$, and it swaps the two copies of $S$ in $\partial M^{\prime }$ (called $S_-$ and $S_+$, say). The next stage is to find a properly embedded surface $S^{\prime }$ in $M^{\prime }$ that is disjoint from $S_- \cup S_+$ and that is invariant under $\tau$. It must separate $M^{\prime }$ into two components, one containing $S_-$, the other containing $S_+$. Thus, $\tau$ swaps these two components. Again, the existence of such a surface will be established below. In practice, it is not hard to find. The image of $S^{\prime }$ in $M$ will be $S_2$.

Note that if these surfaces $S$ and $S^{\prime }$ exist, as claimed above, then their images $S_1$ and $S_2$ in $M$ have the required properties. Note that $S$ and $S^{\prime }$ are properly embedded and disjoint, by construction, and are the inverse images of $S_1$ and $S_2$. Hence, $S_1$ and $S_2$ are also properly embedded and disjoint. Also, $\tilde{M} - (S \cup S^{\prime })$ has two components that are swapped by $\tau$. So, $M - (S_1 \cup S_2)$ is connected, as required.

We now show that the surfaces $S$ and $S^{\prime }$ always exist. We know from Theorem 1.1 that $M$ contains properly embedded disjoint surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected. Also, from the proof of Theorem 1.1, $\tilde{M}$ is the double cover of $M$ corresponding to $[S_1] + [S_2] \in H_2(M, \partial M; \mathbb{Z }_2)$. This cover is constructed as follows. Let $\tilde{S}_1$ and $\tilde{S}_2$ be $\mathrm{cl}(\partial N(S_1) - \partial M)$ and $\mathrm{cl}(\partial N(S_2) - \partial M)$. These are (possibly disconnected) double covers of $S_1$ and $S_2$, respectively. Then $\tilde{M}$ is constructed by gluing together two copies of $\mathrm{cl}(M - N(S_1 \cup S_2))$, a copy of $\tilde{S}_1 \times [-1,1]$ and a copy of $\tilde{S}_2 \times [-1,1]$, as follows. We attach $\tilde{S}_1 \times \{1\}$ and $\tilde{S}_2 \times \{1\}$ to one copy of $\mathrm{cl}(M - N(S_1 \cup S_2))$, using the identity map. But we attach $\tilde{S}_1 \times \{ -1 \}$ to the other copy of $\mathrm{cl}(M - N(S_1 \cup S_2))$ via the covering involution on $\tilde{S}_1$. We attach $\tilde{S}_2 \times \{ -1\}$ in a similar way.

We take $S$ and $S^{\prime }$ to be the inverse image in $\tilde{M}$ of $S_1$ and $S_2$. These have the required properties. For example, $S$ is $\tilde{S}_1 \times \{ 0 \}$ which is transversely oriented in the product bundle $\tilde{S}_1 \times [-1,1]$. Hence it is oriented. Also, the covering transformation on $\tilde{M}$ reverses this transverse orientation, and hence reverses the orientation on $S$. Note that $S$ is an oriented surface, properly embedded and non-separating in $\tilde{M}$. Hence, it represents a non-trivial primitive element of $H^1(\tilde{M}; \mathbb{Z })$. Since $\tau$ preserves $S$ but reverses its orientation, this class is in the $-1$ eigenspace.

Thus, the existence of $S$ and $S^{\prime }$ is proved using the existence of $S_1$ and $S_2$. But in practice, it is easiest to find $S$ and $S^{\prime }$ first, and from these, construct $S_1$ and $S_2$.

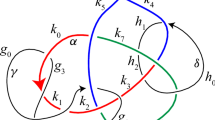
We give a concrete example. Let $M$ be the exterior of the Whitehead link $L_1 \cup L_2$, shown in the left in Fig. 1. Let $\tilde{M}$ be the double cover of $M$ that corresponds to the kernel of the homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2$ which counts linking number mod 2 with $L_2$. Since $L_2$ is unknotted, $\tilde{M}$ is the exterior of link in $S^3$ shown in the right of Fig. 1. The link has three components, whereas the Whitehead link has two, and so $b_1(\tilde{M}) > b_1(M)$. The surface $S$ shown in the right of Fig. 1 is non-separating, orientable and properly embedded in $\tilde{M}$. The covering involution $\tau$ of $\tilde{M}$ preserves $S$ but reverses its orientation. Thus, Step 1 above applies, and we may take $S_1$ to be the image of $S$ in $M$. This is shown in the left of Fig. 1.

Fig. 1

The surface $S_1$ in the exterior of the Whitehead link

The surface $S^{\prime }$ is not quite so easy to see. Let $D$ be the disc properly embedded in the exterior of $S_1$ shown in Fig. 2. Its inverse image in $\tilde{M}$ is two discs $\tilde{D}$ properly embedded in the exterior of $S$. Now $M^{\prime }$ (the exterior of $S$) is a sutured manifold because when $S$ is oriented, the two copies of $S$ in $\partial M^{\prime }$ naturally point into and out of $M^{\prime }$. Let $\gamma ^{\prime }$ be its sutures. The discs $\tilde{D}$ form product discs. We orient them in such a way that this orientation is reversed by the covering involution. Let $M_2^{\prime }$ be obtained by decomposing $M^{\prime }$ along $\tilde{D}$. This is homeomorphic to $T^2 \times [0,1]$. One component of its boundary, say $T^2 \times \{0 \}$, contains two sutures $\gamma _2^{\prime }$; the other has none. The covering involution $\tau$ restricts to an involution of $M_2^{\prime }$, which preserves the product structure on $T^2 \times [0,1]$ and preserves the sutures. However, it swaps the inward and outward-pointing parts of $\partial M_2^{\prime }$. Let $A^{\prime }$ be the vertical annuli $\gamma _2^{\prime } \times [0,1]$ in $T^2 \times [0,1]$. Now, inside $\partial M_2^{\prime }$ lies two copies of $\tilde{D}$, which therefore forms four discs. The sutures $\gamma _2^{\prime }$ run over each of these discs in a single arc.

Fig. 2

Discs in the exteriors of $S_1$ and $S$

When we reverse the sutured manifold decomposition, to form $M^{\prime }$ from $M_2^{\prime }$, we attach $\tilde{D} \times I$ to $M_2^{\prime }$. Inside each component of $\tilde{D} \times I$, we may insert a band of the form $[0,1] \times [0,1]$ where $[0,1] \times \{0, 1\}$ lies in $\gamma _2^{\prime }$ and $\{0,1\} \times [0,1]$ lies in $\gamma ^{\prime }$ (see Fig. 3). Attaching these two strips to $A^{\prime }$ forms the required surface $S^{\prime }$. It is properly embedded in $M^{\prime }$ and is disjoint from $S$. It is invariant under the action of $\tau$. Also, it separates $M^{\prime }$ into two components, which are swapped by $\tau$.

Fig. 3

One of the bands that are attached to $A^{\prime }$ to form $S^{\prime }$

Let $S_2$ be the image of $S^{\prime }$ in $M$. This can be seen as follows. The image of $\tilde{D}$ in the exterior of $S_1$ is the disc $D$. One cannot call it a product disc because the exterior of $S_1$ is not a sutured manifold. Nevertheless, one can cut the exterior of $S_1$ along $D$ to form a space $M_2$ which is also homeomorphic to $T^2 \times I$. This is the quotient of $M_2^{\prime }$ under $\tau$. The image of $\gamma _2^{\prime }$ is a single curve in $\partial M_2$. Let $A$ be the vertical annulus over this in $T^2 \times I$. This is properly embedded in $M_2$. Reconstruct the exterior of $S_1$ from $M_2$ by reattaching $D \times I$. Inside $D \times I$, we may find a band. Attaching this band to $A$ gives the surface $S_2$. It is a twice-punctured projective plane. It has two boundary components, one lying in $L_1$ and one lying in $L_2$. It is disjoint from $S_1$, and $S_1 \cup S_2$ is non-separating.

The surface $S_1$ is easy to see, but the difficulty in visualising $S_2$ perhaps arises from the fact that its boundary component on $L_2$ has slope $2/1$. Note that it is a spanning surface for $L_1 \cup L_2$. In fact, it is shown in Fig. 4, after an isotopy. This was constructed by retracting the annulus $A$ a little so that it lies in a small regular neighbourhood of $L_2$, and then attaching the band to form $S_2$.

Fig. 4

The surface $S_2$ in the exterior of the Whitehead link

5 Profinite methods

We still need to prove one direction of Theorem 1.1. We will show that if $M$ is a compact orientable 3-manifold that is either a $\mathbb{Z }_2$ homology solid torus or a $\mathbb{Z }_2$ homology cobordism between two tori, then it cannot support the surfaces $S_1$ and $S_2$ that are described in the theorem. In the course of this proof, we will introduce some techniques from the theory of pro-$p$ groups. These will turn out to have other uses. In particular, we will be able to use them to gain control of the $\mathbb{Z }_2$ homology classes of the surfaces $S_1$ and $S_2$ for certain 3-manifolds $M$.

Let $p$ be a prime. Recall that the pro-$p$ completion $\widehat{\Gamma }_{(p)}$ of a group $\Gamma$ is the inverse limit of all its finite quotients that are $p$-groups. More precisely, an element of $\widehat{\Gamma }_{(p)}$ is a choice, for each normal subgroup $N$ of $\Gamma$ with index a power of $p$, of an element $g_N$ of $\Gamma /N$, subject to the following compatibility condition. Whenever $N$ and $N^{\prime }$ are normal subgroups of $\Gamma$ with index that are powers of $p$, and satisfying $N \ge N^{\prime }$, then we insist that $g_{N^{\prime }}$ maps to $g_N$ under the quotient map $\Gamma /N^{\prime } \rightarrow \Gamma /N$.

The definition of $\widehat{\Gamma }_{(p)}$ is phrased in terms of normal subgroups of $\Gamma$ with index a power of $p$. However, $\widehat{\Gamma }_{(p)}$ contains information about a wider class of subgroups of $\Gamma$ which are defined as follows. We say that a subgroup $N$ of $\Gamma$ is co-$p$ if there is a sequence of finite index subgroups

$$\begin{aligned} \Gamma = N_0 \ge N_1 \ge \cdots \ge N_k = N \end{aligned}$$

such that each $N_i$ is normal in $N_{i-1}$ and has index a power of $p$. The terminology co-$p$ is not standard. The usual phrase is ‘subnormal with index a power of $p$’.

The following is a rapid consequence of the definition of $\widehat{\Gamma }_{(p)}$.

Proposition 5.1

Let $G$ and $\Gamma$ be finitely generated discrete groups, and let $p$ be a prime. Suppose that there is a group isomorphism $\phi :\widehat{G}_{(p)} \rightarrow \widehat{\Gamma }_{(p)}$ between their pro-$p$ completions. Then the following hold.

• (i) There is an induced bijection (also denoted $\phi$) between the set of co-$p$ subgroups of $G$ and the set of co-$p$ subgroups of $\Gamma$.

• (ii) For a co-$p$ subgroup $N$ of $G, [G:N] = [\Gamma : \phi (N)]$.

• (iii) If $N$ is any co-$p$ subgroup of $G$, then $N$ is normal in $G$ if and only if $\phi (N)$ is normal in $\Gamma$. In this case, $G/N$ is isomorphic to $\Gamma / \phi (N)$.

• (iv) If $N$ and $N^{\prime }$ are co-$p$ subgroups of $G$, then $N \subset N^{\prime }$ if and only if $\phi (N) \subset \phi (N^{\prime })$.

• (v) If $N$ is a co-$p$ subgroup of $G$, then $N$ and $\phi (N)$ have isomorphic pro-$p$ completions.

Thus, an isomorphism between $\widehat{G}_{(p)}$ and $\widehat{\Gamma }_{(p)}$ entails a strong correspondence between the co-$p$ subgroups of $G$ and the co-$p$ subgroups of $\Gamma$. Slightly surprisingly, $\widehat{\Gamma }_{(p)}$ also controls the first Betti number of $\Gamma$.

Proposition 5.2

Let $G$ and $\Gamma$ be finitely generated groups with isomorphic pro-$p$ completions for some prime $p$. Then $b_1(G) = b_1(\Gamma )$.

Proof

By (iii) of Proposition 5.1, there is a one-one correspondence between the quotients of $G$ that are abelian $p$-groups and the similar set of quotients of $\Gamma$. But $G$ surjects onto $(\mathbb{Z }/p^k \mathbb{Z })^l$ for all $k \in \mathbb{N }$ if and only if $l \le b_1(G)$. So, $b_1(G) = b_1(\Gamma )$. $\square$

These results imply that, for a finitely generated group $\Gamma$, the existence of a surjective homomorphism from $\Gamma$ onto the infinite dihedral group is determined by $\widehat{\Gamma }_{(2)}$.

Theorem 5.3

Let $G$ and $\Gamma$ be finitely presented groups with isomorphic pro-2 completions. Then $G$ admits a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$ if and only if $\Gamma$ does.

Proof

Suppose that $G$ admits a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$. Then, by Corollary 2.2, $G$ has an index two subgroup $G^{\prime }$ with $b_1(G^{\prime }) > b_1(G)$. Index 2 subgroups are normal and hence co-2. So, using Proposition 5.1, $G^{\prime }$ corresponds to a subgroup $\Gamma ^{\prime }$ of $\Gamma$ with index 2. Also by Proposition 5.1, $G^{\prime }$ and $\Gamma ^{\prime }$ have isomorphic pro-2 completions. So, by Proposition 5.2, $b_1(G^{\prime }) = b_1(\Gamma ^{\prime })$. Similarly, $b_1(G) = b_1(\Gamma )$, and hence $b_1(\Gamma ^{\prime }) > b_1(\Gamma )$. So, by Corollary 2.2, $\Gamma$ admits a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$. $\square$

The following result shows that the existence of an isomorphism between pro-$p$ completions is surprisingly common.

Theorem 5.4

Suppose that there is a homomorphism $\phi :G \rightarrow \Gamma$ between finitely presented groups that induces an isomorphism $H_1(G; \mathbb{Z }_p) \rightarrow H_1(\Gamma ; \mathbb{Z }_p)$ and a surjection $H_2(G ; \mathbb{Z }_p) \rightarrow H_2(\Gamma ; \mathbb{Z }_p)$. Then $\phi$ induces an isomorphism between the pro-$p$ completions of $G$ and $\Gamma$.

This is a fairly well known consequence of work of Stallings [6], and a proof can be found in [5] (see Theorem 2.12 of [5]).

Note that for any finite cell complex $M$, there is a surjective homomorphism $H_2(M; \mathbb{Z }_p) \rightarrow H_2(\pi _1(M); \mathbb{Z }_p)$. This is because $H_2(\pi _1(M); \mathbb{Z }_p)$ is the homology of an Eilenberg–Maclane space $K(\pi _1(M); 1)$, which can be obtained from $M$ by attaching cells in dimensions 3 and higher.

We are now in a position to prove the remaining direction of Theorem 1.1. Let $M$ be a compact orientable 3-manifold with non-empty boundary that contains no two-spheres.

Suppose first that $M$ is a $\mathbb{Z }_2$ homology solid torus. In other words, $H_1(M; \mathbb{Z }_2) = \mathbb{Z }_2$ and $H_2(M; \mathbb{Z }_2) = 0$. Let $\Gamma$ be $\pi _1(M)$. Then $H_1(\Gamma ; \mathbb{Z }_2) = \mathbb{Z }_2$ and $H_2(\Gamma ; \mathbb{Z }_2) = 0$. Let $\phi :\mathbb{Z } \rightarrow \Gamma$ be a homomorphism that sends a generator of $\mathbb{Z }$ to an element of $\Gamma$ that is non-trivial in $H_1(\Gamma ; \mathbb{Z }_2)$. Then $\phi$ induces isomorphisms on first and second homology with $\mathbb{Z }_2$ coefficients. Therefore, by Theorem 5.4 the pro-2 completions of $\mathbb{Z }$ and $\Gamma$ are isomorphic. Since there is no surjective homomorphism from $\mathbb{Z }$ to $\mathbb{Z }_2 *\mathbb{Z }_2$, the same is therefore true for $\Gamma$, by Theorem 5.3.

Now suppose that $M$ is a $\mathbb{Z }_2$ homology cobordism between two tori $T_1$ and $T_2$. Then, by assumption, $i_*:H_1(T_1; \mathbb{Z }_2) \rightarrow H_1(M; \mathbb{Z }_2)$ is an isomorphism, where $i :T_1 \rightarrow M$ is inclusion. We will also show that $i_*:H_2(T_1; \mathbb{Z }_2) \rightarrow H_2(M; \mathbb{Z }_2)$ is a surjection. Now there is an exact sequence

$$\begin{aligned} H_2(T_1; \mathbb{Z }_2) {\mathop {{}\rightarrow {}}\limits ^{i_*}} H_2(M; \mathbb{Z }_2) \rightarrow H_2(M,T_1; \mathbb{Z }_2) \end{aligned}$$

and so it suffices to show that $H_2(M,T_1; \mathbb{Z }_2)$ is trivial. But this is isomorphic to $H^1(M, T_2; \mathbb{Z }_2)$ by Poincaré duality. This fits into an exact sequence

$$\begin{aligned} H^0(M; \mathbb{Z }_2) {\mathop {{}\rightarrow {}}\limits ^{\cong }} H^0(T_2; \mathbb{Z }_2) \rightarrow H^1(M, T_2; \mathbb{Z }_2) \rightarrow H^1(M; \mathbb{Z }_2) {\mathop {{}\rightarrow {}}\limits ^{\cong }} H^1(T_2; \mathbb{Z }_2). \end{aligned}$$

So, $H^1(M, T_2; \mathbb{Z }_2)$ is trivial, and hence we have shown that $i_*:H_2(T_1; \mathbb{Z }_2) \rightarrow H_2(M; \mathbb{Z }_2)$ is a surjection. Now the torus is an Eilenberg–Maclane space and so $H_2(T_1; \mathbb{Z }_2) = H_2(\pi _1(T_1); \mathbb{Z }_2)$. Therefore, $i_*:H_2(\pi _1(T_1); \mathbb{Z }_2) \rightarrow H_2(\pi _1(M); \mathbb{Z }_2)$ is also a surjection.

Hence, using Theorem 5.4, $\pi _1(T_1)$ and $\pi _1(M)$ have isomorphic pro-2 completions. Now, $\pi _1(T_1) = \mathbb{Z } \times \mathbb{Z }$ clearly does not admit a surjective homomorphism onto $\mathbb{Z }_2 *\mathbb{Z }_2$. Hence, by Theorem 5.3, nor does $\pi _1(M)$.

This completes the proof of Theorem 1.1. $\square$

6 Controlling the homology classes of the surfaces

Given how common it is for a compact orientable 3-manifold $M$ to contain disjoint properly embedded surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected, it is natural to ask which pairs of classes in $H_2(M, \partial M; \mathbb{Z }_2)$ may be represented by such surfaces. In this section, we will address this question.

We start by observing that $[S_1]$ and $[S_2]$ must be non-trivial and distinct. This is because, when these surfaces exist, there is an associated surjective homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$. Composing this with the surjection onto the first and second factors, we obtain two homomorphisms $\phi _1$ and $\phi _2 :\pi _1(M) \rightarrow \mathbb{Z }_2$. These correspond to two classes $[\phi _1]$ and $[\phi _2]$ in $H^1(M; \mathbb{Z }_2)$ and the Poincaré duals of these classes are $[S_1]$ and $[S_2]$ in $H_2(M, \partial M; \mathbb{Z }_2)$. Hence, because $\phi _1$ and $\phi _2$ are distinct non-trivial homomorphisms to $\mathbb{Z }_2$, we deduce that $[S_1]$ and $[S_2]$ are distinct and non-trivial.

How much control do we have over $[S_1]$ and $[S_2]$, given the above restriction? Equivalently, how much control do we have over $\phi _1$ and $\phi _2$? By Theorem 2.1, the kernel of $(\phi _1 + \phi _2) :\pi _1(M) \rightarrow \mathbb{Z }_2$ is an index two subgroup $K$ of $\pi _1(M)$ such that $b_1(K) > b_1(M)$. Thus, we deduce the following from Theorems 2.1, 3.1 and Remark 3.2.

Proposition 6.1

Let $M$ be a compact connected orientable 3-manifold, and let $\alpha$ be a non-trivial class in $H^1(M ; \mathbb{Z }_2)$. Then, the following are equivalent:

• (i) There are disjoint properly embedded surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected, and such that $S_1 \cup S_2$ is dual to $\alpha$.

• (ii) The degree two cover $\tilde{M}$ of $M$ that corresponds to ${\mathrm{ker}}(\alpha :\pi _1(M) \rightarrow \mathbb{Z }_2)$ satisfies $b_1( \tilde{M}) > b_1(M)$.

This controls only the class $[S_1] + [S_2]$ in $H_2(M, \partial M; \mathbb{Z }_2)$. But nevertheless, it does constrain which classes can arise, as in the following theorem. The version of this for links of two-components was proved by Hillman (see Theorem 7.7 in [3]).

Theorem 6.2

Let $M$ be the exterior of a link $L$ in the three-sphere, and let $\alpha \in H^1(M ; \mathbb{Z }_2)$ count the linking number mod 2 with $L$. Then, the following are equivalent:

• (i) There are disjoint properly embedded surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected, and such that $S_1 \cup S_2$ is dual to $\alpha$.

• (ii) $\Delta _L(-1,-1, \ldots , -1) = 0$, where $\Delta _L(t_1, t_2, \ldots , t_n)$ is the Alexander polynomial of $L$.

• (iii) $L$ has a disconnected compact spanning surface, no component of which is closed.

Proof

(i) $\Leftrightarrow$ (ii): It is well known that the Alexander polynomial of a link $L$ encodes information about the homology of the finite abelian covers of its exterior. In particular, $\Delta _L(-1, \ldots , -1)$ equals the determinant of a square presentation matrix for $H_1(\widehat{M})$, where $\widehat{M}$ is the double cover of $S^3$ branched over $L$ (see p. 121 of [3] for example). Hence, $b_1(\widehat{M}) > 0$ if and only if $\Delta _L(-1, \ldots , -1) = 0$. An elementary calculation gives that $b_1(\widehat{M}) = b_1(\tilde{M}) - b_1(M)$, where $\tilde{M}$ is the double cover of $M$ dual to $\alpha$. Thus, applying Proposition 6.1 completes the proof.

(iii) $\Rightarrow$ (i): If $S$ is a compact spanning surface for $L$, then its restriction to $M$ is a properly embedded surface dual to $\alpha$. If $S$ is disconnected, then so too is the surface in $M$. If $S$ is a spanning surface with no closed components, the surface in $M$ is non-separating.

(i) $\Rightarrow$ (iii): Let $S_1$ and $S_2$ be disjoint, properly embedded surfaces in $M$ such that $S_1 \cup S_2$ is dual to $\alpha$, and such that $M - (S_1 \cup S_2)$ is connected. We will show how to modify $S_1$ and $S_2$, so that the number of components of $M - (S_1 \cup S_2)$ does not increase, and so that afterwards, $S_1 \cup S_2$ intersects each component of $\partial M$ in a single simple closed curve. These modifications will not change the homology classes of $S_1$ and $S_2$ and so each meridian of $L$ will still have non-empty intersection with $S_1 \cup S_2$. Also, $S_1$ and $S_2$ will remain non-empty, and each component of $S_1 \cup S_2$ will have non-empty boundary. Thus, we will be able to extend $S_1 \cup S_2$ into $N(L)$ to form a disconnected compact spanning surface for $L$ with no closed components.

We may first assume that $\partial S_1 \cup \partial S_2$ is a collection of essential simple closed curves on $\partial M$. For if some component of $\partial S_1 \cup \partial S_2$ is inessential, we may find one that bounds a disc with interior disjoint from $S_1 \cup S_2$. Attach this disc to $S_1 \cup S_2$ and push it a little into the interior of $M$ to make the surfaces properly embedded. This does not change the number of components of $M - (S_1 \cup S_2)$. It preserves the properties of these surfaces, but reduces the number of boundary components.

Thus, $\partial S_1 \cup \partial S_2$ divides each component of $\partial M$ into annuli. Consider a meridian $\mu$ for some component of $L$. This is a simple closed curve on a total component $T$ of $\partial M$. Arrange for $\mu$ to intersect $\partial S_1 \cup \partial S_2$ as few times as possible. The evaluation of $\mu$ under $\alpha$ is 1, and hence it intersects $\partial S_1 \cup \partial S_2$ an odd number of times. It cannot therefore meet $\partial S_1$, then $\partial S_2$, then $\partial S_1$, and so on in an alternating fashion. Thus, there are two successive intersections which both lie in $\partial S_1$, say. If these lie in distinct components of $\partial S_1$, then these two curves cobound an annulus in $T$. We attach this annulus to $S_1 \cup S_2$. This preserves the properties of $S_1 \cup S_2$ given in (i), but again reduces its number of boundary components. The only other possibility is that $\partial S_1 \cup \partial S_2$ intersects $T$ in a single simple closed curve. Modifying this curve by a mod 2 homology, we may assume that it intersects $\mu$ just once. Since this applies on every component of $\partial M$, we may extend $S_1 \cup S_2$ to the required spanning surface for $L$.

$\square$

In the case of the Whitehead link $L, \Delta _L(t_1, t_2) = (t_1-1)(t_2 - 1)$, and hence $\Delta _L(-1,-1) \not =0$. Therefore, although there exist two disjoint properly embedded surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected, there do not exist two such surfaces that together form a spanning surface for $L$.

We have already seen that the existence of a surjective homomorphism from a finitely generated group $G$ to $\mathbb{Z }_2 *\mathbb{Z }_2$ is controlled by the pro-2 completion of $G$. We may refine this further, as follows.

Let $G$ and $\Gamma$ be finitely generated groups. Suppose that their pro-2 completions are isomorphic. By Proposition 5.1, this sets up an isomorphism between $G/([G,G]G^2)$ and $\Gamma /([\Gamma ,\Gamma ]\Gamma ^2)$. This is because $G/([G,G]G^2)$ may be characterised as the quotient of $G$ that is an elementary abelian 2-group of maximal rank, and there is a similar characterisation of $\Gamma /([\Gamma ,\Gamma ]\Gamma ^2)$. This therefore gives a 1–1 correspondence between homomorphisms $G \rightarrow \mathbb{Z }_2$ and homomorphisms $\Gamma \rightarrow \mathbb{Z }_2$.

Proposition 6.3

Let $G$ and $\Gamma$ be finitely generated groups. Suppose that their pro-2 completions are isomorphic. Let $\phi _1$ and $\phi _2$ be non-trivial homomorphisms $G \rightarrow \mathbb{Z }_2$ and let $\phi _1^{\prime }$ and $\phi _2^{\prime }$ be the corresponding homomorphisms $\Gamma \rightarrow \mathbb{Z }_2$. Suppose that there is a surjective homomorphism $\phi :G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ such that the composition with projection onto the $i$th factor is $\phi _i$, for $i = 1$ and 2. Then there is a surjective homomorphism $\Gamma \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ such that the composition with projection onto the $i$th factor is $\phi _i^{\prime }$, for $i = 1$ and 2.

Proof

We define two subgroups of $G$. Let $G_2$ be the kernel of $G {\mathop {\rightarrow }\limits ^{\phi }} \mathbb{Z }_2 *\mathbb{Z }_2 {\mathop {\rightarrow }\limits ^{\pi }} \mathbb{Z }_2$, where $\pi$ sends the non-trivial element of each factor onto the non-trivial element of $\mathbb{Z }_2$. This is an index two normal subgroup of $G$. Let $G_4$ be the kernel of $G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2 \rightarrow \mathbb{Z }_2 \times \mathbb{Z }_2$, where again the first map is $\phi$, and the second map is abelianisation. This is an index four normal subgroup of $G$. It is equal to the elements of $G$ that have trivial images under both $\phi _1$ and $\phi _2$.

By Proposition 5.1, $G_2$ (respectively, $G_4)$ corresponds to an index 2 (respectively, 4) normal subgroup $\Gamma _2$ (respectively, $\Gamma _4$) of $\Gamma$. By Propositions 5.1 and 5.2, $b_1(G_2) = b_1(\Gamma _2)$, and therefore $H^1(G_2; \mathbb{Z })$ and $H^1(\Gamma _2; \mathbb{Z })$ are isomorphic. However, we wish to set up a slightly more precise correspondence between these two cohomology groups.

The group $G/G_2$ acts on $H^1(G_2; \mathbb{R })$ by conjugation. The non-trivial element of $G/G_2$ specifies an involution of $H^1(G_2; \mathbb{R })$, and hence $H^1(G_2; \mathbb{R })$ decomposes into a direct sum of $+1$ and $-1$ eigenspaces $H^1(G_2; \mathbb{R })^+$ and $H^1(G_2; \mathbb{R })^-$. Let $H^1(G_2; \mathbb{Z })^-$ be the intersection between $H^1(G_2; \mathbb{R })^-$ and the lattice $H^1(G_2; \mathbb{Z })$. Define $H^1(\Gamma _2; \mathbb{Z })^-$ similarly. Our goal is to find an isomorphism $H^1(G_2; \mathbb{Z })^- \rightarrow H^1(\Gamma _2; \mathbb{Z })^-$ such the following diagram commutes:

$$\begin{aligned} \begin{array}{ccc} H^1(G_2; \mathbb{Z })^- &{} \rightarrow &{}H^1(\Gamma _2; \mathbb{Z })^- \\ \downarrow &{}\quad &{} \downarrow \\ H^1(G_2; \mathbb{Z }_2) &{} \rightarrow &{}H^1(\Gamma _2; \mathbb{Z }_2)\\ \end{array} \end{aligned}$$

Here, the top horizontal arrow is the required isomorphism. The vertical arrows are the composition of inclusion into the full integral cohomology group, followed by reduction mod 2. The bottom horizontal arrow is the isomorphism that arises from the fact that the pro-2 completions of $G_2$ and $\Gamma _2$ are isomorphic. The point is that $\phi | G_2$ gives a primitive element of $H^1(G_2; \mathbb{Z })^-$, which we want to correspond to a primitive element of $H^1(\Gamma _2; \mathbb{Z })^-$. This then determines a surjective homomorphism $\phi ^{\prime } :\Gamma \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$. It is the commutativity of the above diagram that will ensure that the composition onto the first and second factors will be $\phi _1^{\prime }$ and $\phi _2^{\prime }$.

Let $k>1$ be a large enough integer so that $G_2$ does not surject onto $(\mathbb{Z }/2^k \mathbb{Z })^{b_1(G_2) + 1}$, and similarly for $\Gamma _2$. Let $\tilde{G}_2$ be the subgroup of $G_2$ generated by elements of $G_2$ that have finite order in $G_2 / [G_2,G_2]$, together with $2^k$th powers in $G_2$. This is a normal subgroup of $G_2$, such that $G_2 / \tilde{G}_2$ is isomorphic to $(\mathbb{Z }/2^k \mathbb{Z })^{b_1(G_2)}$. Then, using the isomorphism between pro-2 completions, $\tilde{G}_2$ corresponds to $\tilde{\Gamma }_2$, which is a normal subgroup of $\Gamma _2$ such that $\Gamma _2 / \tilde{\Gamma }_2$ is isomorphic to $(\mathbb{Z }/2^k \mathbb{Z })^{b_1(\Gamma _2)}$. Let $(G_2 / \tilde{G}_2)^*$ be the set of homomorphisms from $G_2$ to $\mathbb{Z }/2^k\mathbb{Z }$. This is also isomorphic to $(\mathbb{Z }/2^k \mathbb{Z })^{b_1(G_2)}$. Define $(\Gamma _2 / \tilde{\Gamma }_2)^*$ similarly.

Consider the groups $G/\tilde{G}_2$ and $\Gamma /\tilde{\Gamma }_2$. These are isomorphic. So, the conjugation action of $G/G_2$ on $(G_2 / \tilde{G}_2)^*$ is equivalent to the conjugation action of $\Gamma /\Gamma _2$ on $(\Gamma _2 / \tilde{\Gamma }_2)^*$. Let $(G_2 / \tilde{G}_2)^*_-$ be those elements of $(G_2 / \tilde{G}_2)^*$ that are sent to their inverses by this action. This is a subgroup of $(G_2 / \tilde{G}_2)^*$. Define $(\Gamma _2 / \tilde{\Gamma }_2)^*_-$ similarly. Then we have an isomorphism between $(G_2 / \tilde{G}_2)^*_-$ and $(\Gamma _2 / \tilde{\Gamma }_2)^*_-$. Now, $(G_2 / \tilde{G}_2)^*$ can be identified with the reduction mod $2^k$ of $H^1(G_2; \mathbb{Z })$. However, $(G_2 / \tilde{G}_2)^*_-$ is not necessarily the same as the reduction mod $2^k$ of $H^1(G_2; \mathbb{Z })^-$. This is because every element of $(G_2 / \tilde{G}_2)^*$ with order 2 is sent to its inverse under the conjugation action. Therefore, let $(G_2 / \tilde{G}_2)^*_0$ be the set of elements in $(G_2 / \tilde{G}_2)^*_-$ that are a multiple of an element of $(G_2 / \tilde{G}_2)^*_-$ which does not have order 2. This is the image of $H^1(G_2; \mathbb{Z })^-$ under the mod $2^k$ reduction map. Define $(\Gamma _2 / \tilde{\Gamma }_2)^*_0$ similarly. Then $(G_2 / \tilde{G}_2)^*_0$ and $(\Gamma _2 / \tilde{\Gamma }_2)^*_0$ are isomorphic. Pick a basis for $H^1(G_2;\mathbb{Z })^-$ that maps to a minimal generating set for $(G_2 / \tilde{G}_2)^*_0$. This is sent to a minimal generating set for $(\Gamma _2 / \tilde{\Gamma }_2)^*_0$. We may pick elements in $H^1(\Gamma _2;\mathbb{Z })^-$ in their inverse image which form a basis for $H^1(\Gamma _2;\mathbb{Z })^-$. Mapping the basis elements of $H^1(G_2;\mathbb{Z })^-$ to these basis elements of $H^1(\Gamma _2;\mathbb{Z })^-$ gives the required isomorphism between $H^1(G_2;\mathbb{Z })^-$ and $H^1(\Gamma _2;\mathbb{Z })^-$.

Using this isomorphism, $\phi |G_2 :G_2 \rightarrow \mathbb{Z }$ corresponds to a primitive element of $H^1(\Gamma _2; \mathbb{Z })^-$ and hence, as in the proof of Theorem 1.1, we obtain a surjective homomorphism $\phi ^{\prime } :\Gamma \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$.

We now show that the compositions of $\phi ^{\prime }$ with projections onto the first and second factors are $\phi _1^{\prime }$ and $\phi _2^{\prime }$.

Note that $G_4$ is the kernel of $G_2 \rightarrow \mathbb{Z } \rightarrow \mathbb{Z }_2$. Here, the first homomorphism is the restriction of $\phi$ to $G_2$ and the second is reduction mod 2. Consider $\Gamma _2 \rightarrow \mathbb{Z } \rightarrow \mathbb{Z }_2$, where the first homomorphism is the restriction of $\phi ^{\prime }$ to $\Gamma _2$ and the second is reduction mod 2. Due to the commutativity of the above diagram, the kernel of this is precisely $\Gamma _4$. Now, $\phi _1$ and $\phi _2$ can be characterised as the only non-trivial homomorphisms $G \rightarrow \mathbb{Z }_2$ that are non-trivial on $G_2$ but trivial on $G_4$. A similar statement holds for $\phi _1^{\prime }$ and $\phi _2^{\prime }$. So, $\phi _1$ and $\phi _2$ do indeed correspond to $\phi _1^{\prime }$ and $\phi _2^{\prime }$.

There is a minor complication. It may be the case that if we compose $\phi ^{\prime } :G \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ with projection onto the first (respectively, second) factor then we get $\phi _2^{\prime }$ (respectively, $\phi _1^{\prime }$). If this is the case, then redefine $\phi ^{\prime }$ by composing with the automorphism of $\mathbb{Z }_2 *\mathbb{Z }_2$ that swaps the factors. $\square$

We will now show that, in an important special case, there is a great deal of flexibility over the classes $[S_1]$ and $[S_2]$.

Theorem 6.4

Let $M$ be a compact orientable 3-manifold with the same $\mathbb{Z }_2$ homology as a handlebody. Then, given any two distinct non-zero classes $z_1$ and $z_2$ in $H_2(M, \partial M; \mathbb{Z }_2)$, there are disjoint properly embedded surfaces $S_1$ and $S_2$ in $M$, such that $M - (S_1 \cup S_2)$ is connected, and such that $z_i = [S_i]$.

Proof

Pick a basepoint for $M$, and pick based loops $\ell _1, \ldots , \ell _n$ such that $[\ell _1], \ldots , [\ell _n]$ form a basis for $H_1(M; \mathbb{Z }_2)$. We may choose these loops so that the mod 2 intersection numbers satisfy $[\ell _1]\cdot z_i = \delta _{1i}, [\ell _2]\cdot z_i = \delta _{2i}$ and $[\ell _j]\cdot z_i = 0$ for $j \ge 3$. Let $\phi _1^{\prime }$ and $\phi _2^{\prime } :\pi _1(M) \rightarrow \mathbb{Z }_2$ be the mod 2 intersection numbers with $z_1$ and $z_2$ respectively.

Let $F$ be the free group on $n$ generators. Let $\psi :F \rightarrow \pi _1(M)$ be the homomorphism that sends the $i$th free generator to $\ell _i$. Then, $\psi$ induces an isomorphism $H_1(F ; \mathbb{Z }_2) \rightarrow H_1(\pi _1(M); \mathbb{Z }_2)$ and, because $H_2(F; \mathbb{Z }_2)$ and $H_2(M; \mathbb{Z }_2)$ are trivial, $\psi$ induces an isomorphism $H_2(F ; \mathbb{Z }_2) \rightarrow H_2(\pi _1(M); \mathbb{Z }_2)$. Thus, by Theorem 5.4, $\psi$ induces an isomorphism between the pro-2 completions of $F$ and $\pi _1(M)$.

Now $F$ admits a surjective homomorphism $\phi :F \rightarrow \mathbb{Z _2} *\mathbb{Z }_2$ sending the first free generator to the non-trivial element in the first factor, the second free generator to the non-trivial element in the second factor, and the remaining free generators to the identity. Composing $\phi$ with projections onto the first and second factors gives homomorphisms $\phi _1, \phi _2 :F \rightarrow \mathbb{Z _2}$. These correspond to the homomorphisms $\phi _1^{\prime }$ and $\phi _2^{\prime }$. Using Proposition 6.3, there is a surjective homomorphism $\pi _1(M) \rightarrow \mathbb{Z }_2 *\mathbb{Z }_2$ such that its composition with projection onto the $i$th factor is $\phi _i^{\prime }$. Theorem 3.1 gives the required surfaces $S_1$ and $S_2$, and by Remark 3.2, $[S_1] = z_1$ and $[S_2] = z_2$. $\square$

A particularly interesting case is when $M$ is the exterior of a connected finite graph $X$ embedded in $S^3$. Then, as long as $b_1(X) > 1, M$ has the same $\mathbb{Z }_2$ homology as a handlebody other than a solid torus. We view it as quite striking that the conclusion of Theorem 6.4 applies in this level of generality.

7 Further questions and remarks

7.1 Making the surfaces essential

In 3-manifold theory, it is the surfaces that are essential that play a particularly important role. By definition, an orientable surface properly embedded in an orientable 3-manifold $M$ is essential if it is incompressible, boundary-incompressible and no component is boundary parallel. A non-orientable surface $S$ properly embedded in $M$ is essential if $\mathrm{cl}(\partial N(S) - \partial M)$ is essential. It is well known that this has an equivalent reformulation in terms of the way that $\pi _1(S)$ maps into $\pi _1(M)$. In particular, an essential surface is $\pi _1$-injective.

Question 7.1

Can one arrange for the surfaces $S_1$ and $S_2$ provided by Theorem 1.1 to be essential?

We do not have a definite answer. However, the following result establishes that one can ensure that the surfaces are incompressible. Recall that a (possibly non-orientable) surface $S$ properly embedded in $M$ is incompressible if, for any embedded disc $D$ in $M$ such that $D \cap S = \partial D$, the curve $\partial D$ bounds a disc in $S$.

Proposition 7.2

If a compact 3-manifold $M$ contains two disjoint, properly embedded surfaces $S_1$ and $S_2$ such that $M - (S_1 \cup S_2)$ is connected, then it contains two such surfaces that are, in addition, incompressible.

Proof

We may assume that $S_1$ and $S_2$ are both connected. Suppose that at least one is compressible. Then, their union is compressible, by a standard innermost curve argument. Let $D$ be a compression disc for $S_1 \cup S_2$. Suppose that its boundary lies in $S_1$, say. Compress $S_1$ along $D$, giving a surface $\overline{S}_1$. Suppose that $M - (\overline{S}_1 \cup S_2)$ is not connected. Now, $M - (\overline{S}_1 \cup S_2)$ is obtained from $M - (S_1 \cup S_2)$ by cutting along $D$ and then attaching a 2-handle. The latter operation does not change the number of components. So, we deduce that $D$ divides $M - (S_1 \cup S_2)$ into two components, $X$ and $Y$, say. One of these components, $X$ say, lies on the other side of $S_1$, near $\partial D$. Now, $\overline{S}_1$ must have two components. This is because, near $D$, one of the parts of $\overline{S}_1$ has $X$ on both sides, whereas the other has $X$ on one side and $Y$ on the other. Discard the latter component of $\overline{S}_1$, and let $S^{\prime }_1$ be the resulting surface. Then $M - (S_1^{\prime } \cup S_2)$ is connected. Hence, continuing in this fashion, we end up with two properly embedded, disjoint, incompressible surfaces $S^{\prime \prime }_1$ and $S^{\prime \prime }_2$ such that $M - (S^{\prime \prime }_1 \cup S^{\prime \prime }_2)$ is connected. $\square$

The difficulty in answering Question 7.1 in the affirmative is that if a non-orientable properly embedded surface fails to be essential, then there is no obvious modification that one can make to it which, in a suitable sense, simplifies it.

7.2 More than two surfaces

This paper has been devoted to the study of two disjoint surfaces properly embedded in a 3-manifold. It is natural to ask the following:

Question 7.3

Under what circumstances does a compact orientable 3-manifold $M$ contain disjoint properly embedded surfaces $S_1, \ldots , S_n$ such that $M - (S_1 \cup \cdots \cup S_n)$ is connected, for $n \ge 3$?

The methods in this paper do not obviously apply when $n \ge 3$. When $n = 2$, the group $\mathbb{Z }_2 *\mathbb{Z }_2$ plays the central role. This group is virtually abelian, and it is essentially for this reason that the existence of a surjection from a finitely generated group $G$ to $\mathbb{Z }_2 *\mathbb{Z }_2$ can be detected by the pro-2 completion $\hat{G}_{(2)}$. However, for $n \ge 3, *^n \mathbb{Z }_2$ is virtually free non-abelian, and so it seems unlikely that one can detect whether a group $G$ surjects onto $*^n \mathbb{Z }_2$ purely by examining $\hat{G}_{(2)}$. This probably implies that Question 7.3 has no straightforward answer.