Finding Non-orientable Surfaces in 3-Manifolds

Abstract

We investigate the complexity of finding an embedded non-orientable surface of Euler genus g in a triangulated 3-manifold. This problem occurs both as a natural question in low-dimensional topology, and as a first non-trivial instance of embeddability of complexes into 3-manifolds. We prove that the problem is NP-hard, thus adding to the relatively few hardness results that are currently known in 3-manifold topology. In addition, we show that the problem lies in NP when the Euler genus g is odd, and we give an explicit algorithm in this case.

1 Introduction

Since the foundational work of Haken [7] on unknot recognition, the past decades have witnessed a flurry of algorithms designed to solve decision problems in low-dimensional topology. Many of these results rely on the framework of normal surfaces, which provide a compact and algebraic way to analyze and enumerate the noteworthy surfaces embedded in a 3-manifold. In a nutshell, many low-dimensional problems can be seen as an instance of the following (intentionally vague) question, which encompasses the class of problems that normal surface theory has been designed to solve:

For example, for unknot recognition [10], one triangulates the complement of the knot and looks for a spanning disk that the knot bounds, while for knot genus [1], one looks for a Seifert surface of minimal genus instead. To solve 3-sphere recognition [34, 40], one looks for a maximal collection of stable and unstable spheres [8]. Prime decomposition [20] and JSJ decomposition [17, 18] work by finding embedded spheres or tori in a 3-manifold—note that these decompositions are the first steps to test homeomorphism of 3-manifolds [21], which is often considered a holy grail of computational 3-manifold theory. Other examples include the computation of Heegard genus (and Heegard splittings) [25, 26], determining whether a manifold is Haken [15] or the crosscap number of a knot [5].

In this work, we investigate one of the most natural instances of this generic problem: since every 3-manifold contains every orientable surface, these (at least without further restrictions) can be considered uninteresting, and therefore the first non-trivial question is the following:

This question is not just a toy problem for computational 3-manifold theory: non-orientable surfaces embedded in a 3-manifold provide structural informations about it. Following the foundational article of Bredon and Wood [3] classifying non-orientable surfaces in lens spaces and surfaces bundles, many works have been devoted to this study for specific 3-manifolds or specific surfaces (see for example [6, 14, 19, 24, 31,32,33]). Our work complements these by investigating the complexity of finding non-orientable surfaces in the most general setting.

Another motivation for studying this question comes from the higher dimensional analogues of graph embeddings. Graphs generalize naturally to simplicial complexes, and several recent efforts have been made to study higher dimensional versions of the classical notions of planar or surface-embedded graphs [27, 28, 41], see also Skopenkov [38] for some mathematical background. In particular, Matoušek, Sedgwick, Tancer and Wagner [27] recently showed that testing whether a given 2-complex embeds in $\mathbb {R}^3$ is decidable—the main algorithmic machinery underlying this result is yet another instance of the generic 3-manifold problem! In their paper, they ask what is the complexity of this problem for embeddings into other 3-manifolds (as opposed to $\mathbb {R}^3$), and since a non-orientable surface is a particular simple instance of a 2-complex, Non-Orientable Surface Embeddability is the first problem to investigate in this direction.

Our results Our first result is a proof of hardness.

Theorem 1.1

The problem Non-Orientable Surface Embeddability is NP-hard.

As an immediate corollary, it is thus NP-hard to decide, given a 2-complex K and a 3-manifold M, whether K embeds into M.¹ This might not come as a surprise: this is a higher-dimensional version of Graph Genus, which is already known to be NP-hard [39]. However, we would like to emphasize that non-orientable surfaces are among the simplest possible instances of 2-complexes, namely 2-manifolds, and by contrast deciding whether a 1-manifold, i.e., a circle graph, embeds on a surface is trivial. Furthermore, hardness results are well known to be elusive in 3-manifold topology, where iconic problems such as unknot recognition and 3-sphere recognition lie in NP $\cap$ co-NP [9, 10, 22, 36],² and nothing is known for most other problems, the notable exception being 3-Manifold Knot Genus [1] which is known to be NP-complete.³ Our result can be seen as a hint that many three-dimensional problems are hard when the description of a 3-manifold is part of the input.

The proof of Theorem 1.1 starts similarly to the aforementioned one for 3-Manifold Knot Genus by Agol, Hass and Thurston: the idea is to encode an instance of One-in-Three SAT within the embeddability of a non-orientable surface inside a 2-complex. This complex is then turned into a 3-manifold by a thickening step and a doubling step. A key argument in the proof of the reduction of Agol, Hass and Thurston revolves around computing a topological degree, which is trivial in the case of knot genus. It turns out that this computation still works but is significantly harder in our setting, and this is the main technical hurdle in our case, for which we need to introduce (co-)homological ingredients.

Our second result provides an algorithm for this problem, provided that g is odd, proving that it is also in NP.

Theorem 1.2

Let g be an odd positive integer and M a triangulation of a 3-manifold. The problem Odd Non-Orientable Surface Embeddability of testing whether M contains a non-orientable surface of Euler genus g is in NP.

Observing that in the reduction involved in the proof of Theorem 1.1, the non-orientable surface that we use has odd Euler genus, we immediately obtain as a corollary that Odd Non-Orientable Surface Embeddability is NP-complete.

As is the case with many problems in low-dimensional topology, proving membership in NP  is not as trivial as most computer scientists might be accustomed to. As an illustration, our techniques fail for even values of g, and in these cases the problem is not even known to be decidable. A particularity of our proof is to leverage simplifications  [4] of the crushing procedure of Jaco and Rubinstein [16] to reduce the problem to the case of an irreducible 3-manifold. Then our proof relies on normal surface theory.

2 Preliminaries

We only recall here the definitions of the basic objects which we investigate in this article. The technical tools used in the proofs will be introduced when needed, and in general we will assume that the reader is familiar with the basic concepts of algebraic topology, as explained for example in Hatcher [11].

A surface (resp. a surface with boundary) is a topological space which is locally homeomorphic to the plane (resp. locally homeomorphic to the plane or the half-plane). By the theorem of classification of surfaces, these are classified up to homeomorphism by their orientability and their genus (and the number of boundaries if there are any). Since we will deal frequently with non-orientable surfaces, when we use the word genus we actually mean Euler genus, sometimes also called non-orientable genus, which equals twice the usual genus for orientable surfaces. In particular, any surface with odd genus is non-orientable. The Euler characteristic of a surface equals 2 minus its Euler genus.

A 3-manifold (resp. a 3-manifold with boundary) is a topological space which is locally homeomorphic to $\mathbb {R}^3$ (resp. to $\mathbb {R}^3$ or the half-space $\mathbb {R}^3_{|x \ge 0}$). To be consistent with the literature in low-dimensional topology, we will describe 3-manifolds not with simplicial complexes, but with the looser concept of (generalized) $\textit{triangulations}$, which are defined as a collection of n abstract tetrahedra, all of whose 4n faces are glued together in pairs. In particular, we allow two faces of the same tetrahedron to be identified. Note that the underlying topological space may not be a 3-manifold, but if each vertex of the tetrahedra has a neighborhood homeomorphic to $\mathbb {R}^3$ and no edge is identified to itself in the reverse direction, we obtain a 3-manifold [30].

A simplicial complex K is a set of simplices such that any face from a simplex in K is also in K, and the intersection of two simplices $s_1$ and $s_2$ of K is either empty or a face of both $s_1$ and $s_2$. In this article, we will only deal with 2-dimensional simplicial complexes, which are simplicial complexes where the maximal dimension of the simplices is 2—these can be safely thought of as triangles glued together along their subfaces.

3 Hardness Result

In this section we prove the following theorem.

Theorem 1.1

The problem Non-Orientable Surface Embeddability is NP-hard.

Our reduction is inspired by the proof of Agol, Hass and Thurston [1] that Knot Genus in 3-manifolds is NP-hard. While the idea of the reduction is similar, the proof of its correctness is considerably more tricky. We use a reduction from the NP-complete [35] problem One-in-Three SAT, which we first recall. It is defined in terms of literals (Boolean variables or their negations) gathered in clauses consisting of three literals.

Starting from an instance I of One-in-Three SAT, we will build a non-orientable surface S and a 3-manifold M such that S embeds into M if and only if I is satisfiable.

3.1 The Gadget

Let I be an instance of One-in-Three SAT, consisting of a set $U=\{u_1, \ldots , u_n\}$ of variables and a set $C=\{c_1, \ldots , c_m\}$ of clauses. The surface S is taken to be the non-orientable surface of Euler genus $2m+2n+1$. The construction of M is more intricate, and follows somewhat the construction of the 3-manifold of Agol, Hass and Thurston, but with a Möbius band glued on the boundary. We build M in three steps.

• 1. We first build a 2-dimensional complex K.

• 2. We thicken K into a 3-manifold N with boundary.

• 3. We double N, that is, we glue two copies of N along their common boundary to obtain M.

We first describe how these spaces are defined topologically, and address in Lemma 3.1 the issue of computing an actual triangulation of M.

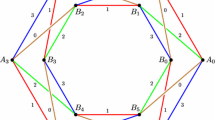
First step. The complex K is obtained in the following way. We start with a projective plane P with $n+m$ boundary curves, which we label by $u_1, \ldots , u_n$ and $c_1, \ldots , c_m$. Let us denote by $k_i$ the number of times that the variable $u_i$ appears in the collection of clauses C, and $\bar{k_i}$ the number of times that the negation of $u_i$ appears. Fix an orientation⁴ of the boundary curves as in Fig. 1. When gluing surfaces along curves, we will always use orientation-reversing homeomorphisms.

Fig. 1

The projective plane P with its $n+m$ boundary curves, and examples of surfaces $F_{u_1}$ and $F_{\bar{u_1}}$ glued to clauses containing $u_1$, respectively $\bar{u_1}$

For $i=1, \ldots , n$, let $F_{u_i}$ and $F_{\bar{u_i}}$ be genus one surfaces with $k_{i}+1$ and $\bar{k_i}+1$ boundaries. For each i, one boundary curve from the surface $F_{u_i}$ is identified to $u_i$. The remaining $k_i$ boundary components are identified with each of the curves $c_j$ such that $u_i$ appears in $c_j$. Similarly, $F_{\bar{u_i}}$ is attached to $u_i$ and to every curve $c_j$ for which $\bar{u_i}$ appears in $c_j$. In the end, three surfaces are attached along each $u_i$ ($F_{u_i}$, $F_{\bar{u_i}}$ and P), and four surfaces are attached along each $c_i$ (P and the surfaces corresponding to the three litterals in $c_i$). We call the curves $u_1 \ldots u_n, c_1 \ldots c_m$ the branching cycles of K, and we refer to Fig. 1 for an illustration.

Second step. A 3-manifold M is a thickening of a 2-dimensional complex K if there exists an embedding $f:K \rightarrow M$ such that M is a regular neighborhood of f(K). Intuitively, a thickening corresponds to the idea of growing a 3-dimensional neighborhood around a 2-complex, but some care is needed, as not every 2-complex is thickenable—see for example Skopenkov [37] for more details on this operation.

In our case though, the complex K is always thickenable, and the process is exactly the same as in the proof of Agol, Hass and Thurston. When K is locally a surface, the thickening just amounts to taking a product with a small interval (Fig. 2 (a)). Therefore, to define a thickening of K it suffices to describe how to thicken around its singular points, which by construction are the branching curves $u_1 \ldots u_n, c_1 \ldots c_m$. If $F_1, \ldots , F_k$ are the surfaces adjacent to a boundary curve, one can just pick a permutation of the surfaces around the curve and thicken the complex following this permutation, as in Fig. 2 (b).

This is akin to the fact that an embedding of a graph on a surface is described by a permutation of the edges around each vertex. Applying this construction for every boundary curve, we obtain a 3-manifold with boundary N since every point close to the branching circles has now a neighborhood locally homeomorphic to $\mathbb {R}^3$.

Fig. 2

(a) The thickening of a surface. (b.1) Four surfaces adjacent to a boundary curve. (b.2) A sectional drawing of these and (b.3) a sectional drawing of their thickening

Third step. In order to obtain a manifold without boundary, we double N, that is, we consider the disjoint union of two copies $N_1$ and $N_2$ of N, and glue them along the boundary $\partial N_1=\partial N_2$ with the identity homeomorphism.

The following lemma shows that this construction can be computed in polynomial time.

Lemma 3.1

A triangulation of the 3-manifold M can be computed in time polynomial in $|I|=n+m$, the complexity of the initial One-in-Three SAT instance I.

Proof

We first observe that the simplicial complex K can be computed in time polynomial in |I|: one can simply start with a big enough triangulation of the projective plane, remove disjoint triangles for the branching circles, and glue triangulations of the surfaces $F_{u_i}$ and $F_{\bar{u_i}}$ along these holes. The complexity of this construction is clearly linear in |I|.

The thickening step first involves replacing triangles of K by triangular prisms (see Fig. 2 (a)) and retriangulating them, which is done in linear time. Then, for every boundary curve, computing a triangulation of the thickening pictured in Fig. 2 (b) can be done in time linear in the number of adjacent surfaces, which is bounded by |I|.

Finally, the doubling just amounts to taking two triangulations of N and gluing them along their boundary. The complexity of this step is linear, and this concludes the proof. $\square$

Finally, let us fix some notation for the rest of the section. There is a natural projection $p:N \rightarrow K$ which corresponds to a deformation retraction of the thickening (since it is by definition a regular neighborhood). We define the continuous map $\tau :M \rightarrow N$ as being the identity on $N_1$ and sending every point of $N_2$ to its counterpart in $N_1$, and $\pi =p \circ \tau$.

3.2 Proof of the Reduction: The Easy Direction

To prove Theorem 1.1, there remains to show how to build an embedding of S into M from a satisfying assignment for I and vice-versa. The first direction is straightforward.

Proposition 3.2

If there is a truth assignment for I such that each clause in C has exactly one true literal, then S, the non-orientable surface of Euler genus $2m+2n+1$, embeds in M.

Proof

If there is a truth assignment for I such that each clause in C has exactly one true literal, we can embed S in K, and therefore in M, in the following way. Take the union of P and for every i, either $F_{u_i}$ if $u_i$ is true, or $F_{\bar{u_i}}$, if $u_i$ is false. Then exactly two boundary components are identified along each boundary component of P, so we obtain a surface $S'$. Since $S'$ contains P, it is non-orientable, and by construction $S'$ has Euler genus $2m+2n+1$. Thus we have found an embedding of S. $\square$

3.3 Proof of the Reduction: The Hard Direction

The other direction will occupy us for the rest of the section.

Proposition 3.3

If S embeds in M, then there is a truth assignment for I such that each clause in C has exactly one true literal.

Outline of the proof Proving this proposition is the main technical step of this section, and it requires some tools from algebraic topology. Therefore, we first provide some intuition as to how the proof goes.

The natural idea would be to try to do the reverse of Proposition 3.2, that is, starting from an embedding of S into K, to find the truth assignment by looking at which tube the embedding chooses at every branching circle $u_i$. The difficulty is that we do not start with an embedding into K, but only into M. Composing this embedding h with the map $\pi :M \rightarrow K$ leads to a continuous map $f:S \rightarrow K$, but f has no reason to be an embedding.

However, this approach can be salvaged. Following Agol, Hass and Thurston [1], we can still look at the topological degree mod 2 induced by the continuous map f at a point x in K, which roughly counts the parity of how many times f maps S to x. This number is constant where K is a surface, that is, outside of the branching circles $u_1, \ldots , u_n, c_1, \ldots , c_m$ of K, and the sum of the incoming degrees of the patches of K at a branching circle has to be 0: intuitively, every surface coming from one direction at a branching circle has to go somewhere. Therefore, if the degree of f in P is 1, exactly one of the surfaces $F_{u_i}$ or $F_{\bar{u_i}}$ also has degree 1. We can use it to define a truth assignment for the variable in U, choosing $u_i$ to be true if $F_{u_i}$ has degree 1, and false in the other case. Then, the sum of the degrees also has to be 0 at the circles corresponding to the clauses. Since P has degree 1, this means that either one or three of the incoming surfaces also has degree 1. We show that this number is always one, otherwise the surface S cannot have genus $2m+2n+1$. This will result from the fact that if we have a degree 1 map between two surfaces $S_1$ and $S_2$, then the genus of $S_2$ is not larger than the genus of $S_1$ (Lemma 3.6). This shows that every clause has exactly one true literal and concludes the proof.

This all hinges on the fact that the degree of f in P is one. This is where our proof diverges from the one of Agol, Hass and Thurston, as in their case this step is straightforward. Here, this will result from the non-orientability of S: morally, when embedding S into M and then mapping it into K, the only place where the non-orientability can go is P. To prove this fact formally is another matter and relies on three ingredients:

• 1. Since S is non-orientable and has odd genus, in the image of the embedding $h(S) \subseteq M$, there is a non-trivial homology cycle $h(\alpha )$, which has order 2 in the $\mathbb {Z}$-homology of M (Lemma 3.4).

• 2. The kernel of the map $\pi _{\#}:H_1(M) \rightarrow H_1(K)$ has no torsion (Lemma 3.5). In particular, $\pi \circ h(\alpha )=f(\alpha )$ is non-trivial in the $\mathbb {Z}$-homology of K. Intuitively, the reason is that the $\mathbb {Z}_2$-subgroup of $H_1(M)$ comes from P, which is preserved by $\pi$. To prove this formally, we split K and M at the “equator” and exploit the naturality of the Mayer–Vietoris sequence (Lemma 3.5).

• 3. Using cup-products, which provide an algebraic bridge between (co-)homology in dimensions 1 and 2, we leverage on this to prove that f has degree one on P.

Introductory lemmas. The notion of degree is conveniently expressed with the language of homology. In the following, we will rely extensively on the following notions: (relative) homology, Mayer–Vietoris sequence, cohomology, Kronecker pairing (which we denote with brackets), cup-products, and we will rely on Poincaré duality and the universal coefficient theorem. Alas, introducing (or even defining) these falls widely outside the scope of this paper, and we refer the reader to the textbook of Hatcher [11] to get acquainted with these concepts. For a map f, the induced maps in homology and cohomology are respectively denoted by $f_{\#}$ and $f^{\#}$.

Let us first prove the three aforementioned lemmas. The first one shows the non-triviality of maps from non-orientable surfaces of odd genus to 3-manifolds (see also Hempel [13, Lem. 5.1]). The second one shows that the map $\pi$ only kills torsion-free elements and the third one shows that degree 1 maps between surfaces can only reduce the genus. To streamline the notations, when no module is indicated, homology and cohomology are taken with $\mathbb {Z}$ coefficients.

Lemma 3.4

Let S be a non-orientable surface of odd genus, and $\alpha$ be a simple closed curve on S, inducing an element of order 2 in $H_1(S)$. Let $f:S\rightarrow M$ be an embedding of S into a 3-manifold M. Then $f(\alpha )$ is not null-homologous in $H_1(M)$.

Proof

We recall that a co-dimension 1 submanifold $M_1$ embedded in a manifold $M_2$ is two-sided if its normal bundle is trivial, otherwise it is one-sided. An embedded curve is orientation-preserving if it has an orientable neighborhood, otherwise it is orientation-reversing.

Since S has odd Euler characteristic, $\alpha$ is orientation-reversing on S. Now we distinguish two cases: either S is 2-sided in M, or it is 1-sided. In the first case, $f(\alpha )$ is orientation reversing in f(S), and therefore also in M. Therefore it is non-trivial in $\mathbb {Z}_2$ homology. In the second case, a small generic perturbation of $f(\alpha )$ makes it have a single intersection point with f(S). By Poincaré duality with $\mathbb {Z}_2$-coefficients, it is therefore non-trivial in $H_1(M, \mathbb {Z}_2)$. In both cases the result follows by the universal coefficient theorem. $\square$

Lemma 3.5

Let K, M and $\pi$ be as introduced in Sect. 3.1, then the kernel of the map $\pi _{\#}:H_1(M) \rightarrow H_1(K)$ has no torsion.

Fig. 3

Decomposing the complex K around the equator

Proof

Let $K_1$ and $K_2$ denote the lower and the upper hemispheres of K (see Fig. 3), $M_1$ and $M_2$ be the corresponding subspaces of M. By naturality of the Mayer–Vietoris sequence with reduced homology, we obtain the following commutative diagram, where the horizontal lines are exact.

We first remark that when applied to a surface, the process of thickening and doubling amounts to taking the product with $S^1$. Therefore, we know that $K_2$ is a Möbius band, $M_2$ is a Möbius band times a circle, $K_1 \cap K_2$ retracts to $S^1$ and $M_1 \cap M_2$ retracts to a torus T. Since $M_1 \cap M_2$ and $K_1 \cap K_2$ are connected, their reduced 0-homologies are zero, thus the maps $k_1-l_1$ and $k_2-l_2$ are surjective. Furthermore, $\pi _{2\#}$ is the projection of the $S^1$ fiber, ${{\mathrm{Im}}}(i_1)=\mathbb {Z}^2$, ${{\mathrm{Im}}}(j_1)=\mathbb {Z} \oplus 2\mathbb {Z}$, ${{\mathrm{Im}}}(i_2)=\mathbb {Z}$ and ${{\mathrm{Im}}}(j_2)=2 \mathbb {Z}$. Therefore, $k_1(H_1(M_1) \oplus H_1(M_2))$ contains no torsion, and the torsion subgroup of $H_1(M)$ comes from $-l_1(H_1(M_2))$. Similarly, the torsion subgroup of $H_1(K)$ comes from $-l_2(H_1(K_2))$. By commutativity of the diagram, $(k_2-l_2)\circ (\pi _{\#1},\pi _{2\#})=\pi _{\#} \circ (k_1-l_1)$ and thus their image contains the $\mathbb {Z}_2$ torsion subgroup of $H_1(K)$. Therefore, the kernel of the map $\pi _{\#}$ has no torsion and the claim is proved. $\square$

Lemma 3.6

Let $f:S_1 \rightarrow S_2$ be a continuous map of degree one mod 2 between two surfaces $S_1$ and $S_2$. Then the genus of $S_2$ is not larger than the genus of $S_1$.

Proof

Let us denote by $g_1$ the genus of $S_1$ and by $g_2$ the genus of $S_2$. Assume by contradiction that $g_2$ is larger than $g_1$. The map f induces a map on first cohomology groups $f^{\#}:H^1(S_2,\mathbb {Z}_2)=\mathbb {Z}_2^{g_2} \rightarrow H^1(S_1,\mathbb {Z}_2)=\mathbb {Z}_2^{g_1}$. Since $g_2$ is larger than $g_1$, by dimension this map has a non-trivial kernel. Pick an element a in this kernel, and an element $b\in H^1(S_2,\mathbb {Z}_2)$ such that $a \cup b$ generates $H^2(S_2,\mathbb {Z}_2)$ (which exists by Poincaré duality). Then $f^{\#}(a \cup b)=0$ by naturality of the cup product. But then, by naturality of the Kronecker pairing, we have

$$\begin{aligned} 0=\langle f^{\#}(a \cup b), [S_1] \rangle = \langle a \cup b, f_{\#}([S_1]) \rangle = \langle a \cup b, [S_2]\rangle = 1, \end{aligned}$$

and we have reached a contradiction. $\square$

Wrapping up the proof We can now proceed with the proof.

Proof of Proposition 3.3

Let us denote by h the embedding from S into M, and by $\alpha$ a simple cycle of order 2 (in homology over $\mathbb {Z}$) in S. By Lemma 3.4, $h(\alpha )$ is not null-homologous in M, and it has order 2 in $H_1(M)$. By Lemma 3.5, $\pi _{\#}:H_1(M) \rightarrow H_1(K)$ does not have $h(\alpha )$ in its kernel, therefore we obtain that $\pi \circ h(\alpha )=f(\alpha )$ is not null-homologous in K, and since $\alpha$ has order 2 in $H_1(S)$, it also has order 2 in $H_1(K)$.

But there is a unique homology class of order 2 in $H_1(K)$, which is induced by a simple cycle $\beta$ having order 2 in P. Therefore $h(\alpha )$ is homologous to $\beta$.

We now switch to $\mathbb {Z}_2$ coefficients, in order to use the 2-dimensional homology despite the non-orientability. Since $\mathbb {Z}_2$ is a field, homology and cohomology with $\mathbb {Z}_2$ coefficients are dual to each other so we can take a cohomology class b in $H^1(K, \mathbb {Z}_2)$ which evaluates to 1 on $[\beta ]$. The map $f^{\#} :H^1(K,\mathbb {Z}_2) \rightarrow H^1(S,\mathbb {Z}_2)$ maps b to a cohomology class $a \in H^1(S,\mathbb {Z}_2)$, and by naturality of the Kronecker pairing, we have

$$\begin{aligned} \langle a,[\alpha ] \rangle = \langle f^{\#}(b),[\alpha ]\rangle = \langle b,f_{\#}([\alpha ]) \rangle = \langle b,[\beta ] \rangle =1, \end{aligned}$$

where the brackets denote taking the representative in 1-dimensional homology with $\mathbb {Z}_2$ coefficients and the last equality follows from the definition of b. Now, denote by $(\alpha , \beta _1, \gamma _1, \beta _2, \gamma _2, \ldots , \beta _k, \gamma _k)$ a family of simple curves forming a basis of $H_1(S, \mathbb {Z}_2)$, such that each pair $(\beta _i,\gamma _i)$ intersects once and there are no other intersections. We have that a is the Poincaré dual of $\alpha + \sum _I \beta _i + \sum _J \gamma _j$, for some subsets $I,J \subseteq [k]$, and since $\langle a, [\alpha ] \rangle =1$, a quick computation in the ring $H^*(S,\mathbb {Z}_2)$ shows that $a \cup a=\xi$, where $\xi$ is the generator of $H^2(S, \mathbb {Z}_2)$.

Now, by naturality of the cup-product, we obtain $f^{\#}(b \cup b)=f^{\#}(b) \cup f^{\#}(b)=a \cup a=\xi$. Furthermore, once again by naturality of the Kronecker pairing, and writing [S] for the fundamental class mod 2 of S, we have

$$\begin{aligned} 1= \langle \xi , [S] \rangle = \langle f^{\#}(b \cup b), [S] \rangle = \langle b\cup b,f_{\#}([S])\rangle . \end{aligned}$$

(1)

Let us open a parenthesis and recall how the notion of degree of a continuous map can be extended when the target is not a manifold, applied to our specific case. The map f induces a mapping $f_{\#}$ in relative homology between $H_2(S,\emptyset ,\mathbb {Z}_2)$ and $H_2(K,B,\mathbb {Z}_2)$, where B is the set of branching circles of K. The group $H_2(K,B,\mathbb {Z}_2)$ is generated by the homology classes induced by the pieces $P, F_{u_i}$ and $F_{\bar{u_i}}$, and therefore the image of $f_{\#}(S)$ associates to each piece a 0 or 1 number, the topological degree mod 2 of f on this piece. An equivalent view of this number is the following. By standard transversality arguments, the map $f:S\rightarrow K$ can be homotoped so as to be a union of homeomorphisms of subsurfaces of S into one of the pieces $P, F_{u_i}, F_{\bar{u_i}}$ forming K. The parity of the number of subsurfaces of S mapped to a piece $P, F_{u_i}$ or $F_{\bar{u_i}}$ is also the topological degree mod 2 of the map f. This second point of view shows that the sum of the degrees of the pieces adjacent to a branching circle is 0, as S has no boundary.

Going back to the proof, we observe that, juggling between both interpretations of the degree, the geometric meaning of (1) is that f(S) covers the intersection point of two perturbated copies of $\beta$ an odd number of times, and as this intersection point is in P, the topological degree mod 2 of f on P is 1.

The sum of the incoming degrees of 2-dimensional patches along a boundary curve $u_i$ or $c_i$ in K is 0. Therefore, around every boundary curve $u_i$, this allows us to pick a truth assignment for $u_i$, depending on whether f has degree 1 on $F_{u_i}$ or $F_{\bar{u_i}}$. This will conclude the proof if we prove that this truth assignment $\varphi$ is valid for the 1-in-3 SAT instance I.

For every clause $c_i$, there are exactly four surfaces adjacent to the boundary curve $c_i$, one of these being P, and we denote the others by $F_1,F_2$ and $F_3$. Since f has degree 1 on P, it has degree 1 either on one of the other surfaces or on all three. If we are in the former case for every clause, this shows that all the clauses are satisfied exactly by one of its variables under the truth assignment $\varphi$, and we are done. Otherwise, for every clause where f has degree one on all three surfaces $F_1,F_2$ and $F_3$, pick arbitrarily one, say $F_1$, and consider the surface $S'$ obtained by gluing every such $F_1$ to P and every $F_2$ and $F_3$ together. We claim that this surface has genus strictly larger than $2n+2m+1$:

• The projective plane P contributes by 1.

• For every i, exactly one of the surfaces $F_{u_i}$ or $F_{\bar{u_i}}$ is chosen. Since they have (Euler) genus two, they contribute by 2.

• For every clause, the gluing of $F_1$ to P increases the genus by 2. We have already reached $2n+2m+1$.

• Every time we glue $F_2$ and $F_3$ together, we increase the genus yet again.

But by definition of $S'$, there is a degree one map from S to $S'$, which is impossible by Lemma 3.6. This concludes the proof. $\square$

The combination of Lemma 3.1 and Proposition 3.3 provides a polynomial reduction from 1-in-3 SAT to the problem of deciding the embeddability of a non-orientable surface into a 3-manifold, which concludes the proof of Theorem 1.1.

4 An Algorithm to Find Non-orientable Surfaces of Odd Euler Genus in 3-Manifolds

In this section we prove the following theorem.

Theorem 1.2

Let g be an odd positive integer and M a triangulation of a 3-manifold. The problem Odd Non-Orientable Surface Embeddability of testing whether M contains a non-orientable surface of Euler genus g is in NP.

We first observe that if a non-orientable surface S of genus g embeds in a 3-manifold M, then all the non-orientable surfaces of genus $g+2k$ for $k > 1$ also embed into M, since one can add orientable handles in a small neighborhood of S. Therefore, to prove Theorem 1.2 it is enough to find the non-orientable surface of minimal odd Euler genus which embeds into M, and this is what our algorithm will do.

Let us also note that if M is non-orientable, it contains a solid Klein bottle in the neighborhood of an orientation-reversing curve. Therefore it also contains every non-orientable surface of even genus, and the algorithm is trivial in this case. Thus, the only case not covered by our algorithm is the one of non-orientable surfaces of even Euler characteristic in orientable manifolds.

4.1 Background on Low-Dimensional Topology and Normal Surfaces

We introduce here quickly the tools we are using from 3-dimensional topology and normal surfaces, and refer to Hass, Lagarias and Pippenger [10] or Matveev [29] for more background.

A 3-manifold M is irreducible if every sphere embedded in M bounds a ball in M. The connected sum $M_1 \# M_2$ of two 3-manifolds $M_1$ and $M_2$ is obtained by removing a small ball from both $M_1$ and $M_2$ and gluing together the resulting boundary spheres. A 3-manifold is prime if it cannot be presented as a connected sum of more than one manifold, none of which is a sphere. It is well known [12, Prop. 1.4] that prime manifolds are irreducible, except for $S^2 \times S^1$ and the non-orientable bundle $S^2 \tilde{\times } S^1$.

Let S be a surface embedded in M. A compressing disk for S is an embedded disk $D \subset M$ whose interior is disjoint from S and whose boundary is a non-contractible loop in S. A surface is compressible if it has a compressing disk and incompressible if not. If a surface S is compressible, one can cut it along the boundary of a compressing disk and glue disks on the resulting boundaries, this is called a compression and this operation either reduces the genus of S by 2, or it disconnects S into two connected components $S_1$ and $S_2$, and the sum of the genus of $S_1$ and the genus of $S_2$ equals the genus of S.

To introduce normal surfaces, we denote by T a triangulation of a 3-manifold M. A normal isotopy is an ambient isotopy of M that fixes the 2-skeleton of T. A normal surface in T is a properly embedded surface in T that meets each tetrahedron in a (possibly empty) disjoint collection of normal disks, each of which is either a triangle (separating one vertex of the tetrahedron from the other three) or a quadrilateral (separating two vertices from the other two). In each tetrahedron, there are four possible types of triangles and three possible types of quadrilaterals, pictured in Fig. 4.

Fig. 4

The seven types of normal disks within a given tetrahedron: four triangles and three quadrilaterals

Normal surfaces are used to investigate combinatorially and computationally the surfaces embedded in a 3-manifold. In this endeavour, the first step is to prove that the surfaces we are interested in can be normalized, that is, represented by normal surfaces. The following theorem is due to Haken [7, Chap. 5], we refer to the book of Matveev for a proof.

Theorem 4.1

([29, Cor. 3.3.25]) Let M be an irreducible 3-manifold and S be an incompressible surface embedded in M. Then, if S is not a sphere, it is ambient isotopic to a normal surface.

For S a normal surface, denote by e(S) the edge degree of S, that is, the number of intersections of S with the 1-skeleton of the triangulation T. A normal surface is minimal if it has minimal edge degree over all the normal surfaces isotopic to it. Each embedded normal surface has associated normal coordinates: a vector in $\mathbb {Z}_{\ge 0}^{7t}$, where t is the number of tetrahedra in T, listing the number of triangles and quadrilaterals of each type in each tetrahedron. These coordinates provide an algebraic structure to normal surfaces: there is a one-to-one correspondence between normal surfaces up to normal isotopy and normal coordinates satisfying some constraints, called the matching equations and the quadrilateral constraints. In particular, one can add normal surfaces if they have no conflicting quadrilaterals by adding their normal coordinates, this is called a normal sum. One can verify easily that the Euler characteristic is additive under normal sum. Among normal surfaces, ones of particular interest are the fundamental normal surfaces, which are surfaces that cannot be written as a sum of other non-empty normal surfaces. Every normal surface can be decomposed as a sum of fundamental normal surfaces, and the following theorem provides tools to understand these.

Theorem 4.2

([29, Cor. 4.1.37], see also Jaco and Oertel [15]) Let a minimal connected normal surface S in an irreducible 3-manifold M be presented as a sum $S=\sum _{i=1}^nS_i$ of $n >1$ nonempty normal surfaces. If S is incompressible, so are the $S_i$. Moreover, no $S_i$ is a sphere or a projective plane.

4.2 Crushing

In order to rely on normal surface theory and apply the aforementioned theorems, we would like M to be irreducible. Therefore, the first step of the algorithm is to simplify the 3-manifold M so as to make it irreducible. In order to do this, we rely on the operation of crushing, which was introduced by Jaco and Rubinstein [16], and extended to the non-orientable case (as well as simplified) by Burton [4]. In particular, Burton proves the following theorem [4, Algorithm 7].

Theorem 4.3

Given a 3-manifold M, there is an algorithm which either decomposes M into a connected sum of prime manifolds, or else proves that M contains an embedded two-sided projective plane.

Furthermore, this algorithm is in NP  in the following sense: there exists a certificate of polynomial size (namely, the list of fundamental normal surfaces along which to crush) allowing to compute in polynomial time the triangulations of the summands or output that M contains an embedded two-sided projective plane.

If this algorithm outputs an embedded projective plane, we are done, since in this case our 3-manifold M contains every non-orientable surface of odd genus. If not, if we are provided the aforementioned certificate we can proceed separately on every summand, thanks to the following easy lemma.

Lemma 4.4

Let M be a connected sum of 3-manifolds $M_1, \ldots , M_k$. Then if a non-orientable surface S of odd genus g embeds into M, it also embeds into one of the $M_i$.

Proof

The 3-manifolds $M_i$ are obtained from M after a cut-and-paste procedure along 2-spheres, and let $S_i$ denote the surface S obtained in $M_i$ after this procedure. The surface S is the connected sum of the surfaces $S_i$, and since g is odd and the Euler characteristic is additive under connected sums, one of the $S_i$ has odd Euler characteristic. In particular it is non-orientable. By adding orientable handles to this $S_i$ inside $M_i$, one obtains a non-orientable surface of the same genus as S, and therefore an embedding of S. $\square$

If one of the summands is prime but not irreducible, then, as mentioned before, it is homeomorphic either to $S^2 \times S^1$ or the twisted bundle $S^2 \tilde{\times } S^1$. One of the features [4, Algorithm 7] of the crushing algorithm that we use is that the $S^2 \times S^1$ and $S^2 \tilde{\times } S^1$ summands in the prime decomposition are actually rebuilt afterwards based on the homology of the input 3-manifold. In particular, we know precisely if there are any and how many of them there are, without having to use some hypothetical recognition algorithm. Furthermore, the following lemma shows that these summands are uninteresting for our purpose.

Lemma 4.5

No non-orientable surface of odd genus embeds into $S^2 \times S^1$ or $S^2 \tilde{\times } S^1$.

Proof

By Lemma 3.4, if such an embedding existed, there would be an element of order 2 in $H_1(S^2 \times S^1)$ or $H_1(S^2 \tilde{\times } S^1)$, which is a contradiction since both of these groups are equal to $\mathbb {Z}$. $\square$

Therefore, the output of our algorithm is trivial for these summands, and in the rest of this section we assume that the manifold M is irreducible.

4.3 Fundamental Normal Surfaces

We now show that in order to find the non-orientable surface of minimal odd genus, it is enough to look at the fundamental normal surfaces.

Proposition 4.6

If a non-orientable surface of minimal odd genus embeds in an irreducible 3-manifold M, then it is witnessed by one of the fundamental normal surfaces. If none of the fundamental normal surfaces have odd genus, then no surface of odd genus embeds into M.

Before proving this proposition, let us show how it implies Theorem 1.2.

Proof of Theorem 1.2

By applying the crushing procedure and following Lemma 4.4 and the discussion in Sect. 4.2, one can assume that M is irreducible if one is given the certificate of Theorem 4.3. Then, by Proposition 4.6, the non-orientable surface of minimal odd genus, if it exists, appears among one of the fundamental normal surfaces. By a now standard argument of Hass, Lagarias and Pippenger [10, Lem. 6.1], the coordinates of fundamental normal surfaces can be described with a polynomial number of bits. Since there are 7t coordinates for a triangulation of size T, we can therefore use this as a second half $\mathcal {C}$ of an NP  certificate. In order to verify in polynomial time that $\mathcal {C}$ represents a non-orientable surface of Euler genus at most g, it is enough to:

• 1. Verify that it is a normal surface S, i.e., that is satisfies the matching equations and the quadrilateral constraints. This is easily done in polynomial time.

• 2. Verify that S is connected. This can be done in polynomial time using the orbit counting algorithm of Agol, Hass and Thurston [1, Sect. 4].

• 3. Verify that S is a non-orientable surface of Euler genus at most g. This can be done via its Euler characteristic: it is a linear form on the space of normal surfaces which can also be computed in polynomial time.

Thus, when provided with the two polynomial-sized certificates, one can verify in polynomial time that M contains a non-orientable surface of Euler genus at most g, which proves Theorem 1.2. $\square$

We now prove Proposition 4.6.

Proof of Proposition 4.6

Let S be a surface of minimal odd genus g embedded in M. We first claim that S is incompressible. Indeed, if it is not, let D be a compressing disk and $S \mid D$ be the surface obtained after the compression along D. Then either $S \mid D$ has genus $g-2$, or $S \mid D$ is disconnected and one of the components has odd genus less than g. In both cases, this contradicts the minimality of g.

The surface S being incompressible, then by Theorem 4.1, there exists a normal surface isotopic to it. Let us denote by $S'$ a normal surface of genus g and of minimal edge degree among all of those. If $S'$ is not fundamental, by Theorem 4.2, then it can be written as a sum of fundamental normal surfaces $S'=\sum _{i=1}^n S_i$ such that the $S_i$ are incompressible and none of them are spheres or projective planes. In particular, none of the surfaces $S_i$ have positive Euler characteristic. Since the Euler characteristic is additive on the space of normal coordinates, one of the surfaces $S_i$ has odd genus at most g. By minimality of g, this surface $S_i$ actually has genus g, and it has smaller edge degree by $S'$, which is a contradiction. Therefore $S'$ is fundamental, which concludes the proof. $\square$

Remark

The reason why the above proof fails in the case of even genus is that in general a non-orientable surface of genus g might be written as a normal sum of orientable surfaces. In our case, this issue is avoided by the fact that a surface of odd Euler genus is necessarily non-orientable. For even Euler genus, the first problem that we do not solve is the one of deciding whether a given 3-manifold contains a Klein bottle. For this specific case, we believe that the problem should be decidable, by computing a JSJ decomposition and identifying in the geometric pieces which ones contain Klein bottles: hyperbolic pieces do not, and one can detect which Seifert fibered spaces do just based on their invariants. However, this technique does not seem to apply to higher genera.