1 Introduction

Fiber-reinforced laminated composite structures are commonly used in various engineering applications due to their light weight, high strength, and corrosion resistance. However, their properties can be significantly influenced by exposure to moisture and temperature variations, also known as hygrothermal effects (Gürdal et al. 1999; Puck and Schürmann 2002). Hygrothermal effects can trigger premature failure mechanisms such as delamination, matrix cracking and fiber-matrix debonding, which can compromise the integrity and durability of composite structures over time (Papakonstantinou et al. 2001; Marlett et al. 2011; Jia et al. 2018; Qiao et al. 2019). Understanding how hygrothermal factors affect the mechanical properties of laminated composites is critical for mitigating damage and increasing the lifespan of composite structures, especially in marine environments (Graham-Jones and Summerscales 2015; Humeau et al. 2016; Davies 2016). Composite materials used in such environments are often exposed to water or high humidity levels. Moisture absorbed by the composite can promote the corrosion of any metallic components or fasteners embedded within the structure, leading to changes in mechanical and structural properties such as dimensional stability, mechanical strength, and durability (Poodts et al. 2015). Marine environments often involve significant temperature variations due to factors such as diurnal temperature changes, seasonal fluctuations, and exposure to direct sunlight (Graham-Jones and Summerscales 2015). These thermal cycling conditions can exacerbate the effects of moisture absorption by causing expansion and contraction of the material leading to mechanical stress variations and potential damage.

Despite several decades of research and development, there remains a significant demand for computational methods with high accuracy, efficiency, and robustness that can reliably model and predict damage in laminated composite structures. To this end, the advent of Isogeometric Analysis (IGA) Hughes et al. (2005); Cottrell et al. (2009) and the development of Kirchhoff–Love (KL) thin-shell formulations in the framework of IGA (Kiendl et al. 2009, 2010; Benson et al. 2011) are providing a pathway for higher-order accurate and smooth, yet efficient approximation of the stress fields that are favorable for modeling of damage and failure (Deng et al. 2015). For more recent developments in IGA-based KL shells that target the computational challenges such as finite deformation, plasticity, membrane-locking treatment, multi-patch coupling, explicit time integration and modeling of out-of-plane deformation, see (Kiendl et al. 2015; Breitenberger et al. 2015; Duong et al. 2017; Ambati et al. 2018; Guo et al. 2018; Schuß et al. 2019; Herrema et al. 2019; Leidinger et al. 2019; Casquero and Mathews 2023; Sauer et al. 2024; Taniguchi et al. 2022, 2024).

The first IGA-based multilayer formulation for KL shells was introduced in Bazilevs et al. (2018); Pigazzini et al. (2018), where the individual plies or lamina were governed by the KL shell theory and where the plies were connected through cohesive interfaces. Because the KL theory does not consider transverse-shear deformations, the resulting approach is free from transverse shear locking for the individual plies. The use of cohesive interfaces naturally enables modeling of delamination between the plies and recovers transverse-shear deformability at the laminate level. The formulation does not use rotational degrees-of-freedom, which makes it more efficient than traditional shell formulations. The resulting methodology was employed to simulate impact damage and delamination in laminated fiber-reinforced composite structures in Alaydin et al. (2022) where it was extensively validated using data from several impact tests. The IGA-based formulation was found to be more robust and effective for impact-damage modeling than the traditional low-order FEM approaches.

In the present work, we model damage and delamination in laminated fiber-reinforced polymer composite structures considering the effects of temperature and moisture. At the structural and constitutive-modeling levels we follow the comprehensive IGA KL shell framework developed in Alaydin et al. (2022), which includes continuum damage, plasticity and cohesive-interface models. To incorporate hygrothermal effects, we make the intralaminar and interlaminar material properties as functions of temperature and moisture content. The present approach uses dry, room-temperature material-model parameters as the baseline values and modifies them according to a scaling law, which is based on the Arrhenius equation and the material glass transition temperature, and which uses temperature and moisture content as input. We validate our computational framework using the experimental data found in the literature. The validation includes quantitative comparison of the failure strengths and qualitative comparison of the the failure modes.

2 Theoretical framework

2.1 3D continuum framework

We start with a weak form of the solid governing equations in 3D. Using the updated Lagrangian formulation (Belytschko et al. 2014), we look for the velocity \(v^{3D}_i\), such that for kinematically admissible virtual velocities or test functions \(\delta v_i^{3D}\),

$$\begin{aligned}{} & {} \int _{\Omega }\delta v_i^{3D}\rho \bigg (\frac{\partial v_i^{3D}}{\partial t}-f_i \bigg )~d\Omega + \int _\Omega \delta v^{3D}_{i,j} \sigma _{ij}~d\Omega \nonumber \\{} & {} \quad - \int _{\Gamma _h} \delta v^{3D} h_i~d\Gamma = 0. \end{aligned}$$
(1)

Here, \(\rho \) is the structure mass density in the current configuration \(\Omega \), \(\frac{\partial v_i^{3D}}{\partial t}\) is the acceleration, \(f_i\) is the body force per unit mass, \(h_i\) is the applied traction on the boundary \(\Gamma _h\), and \(\sigma _{ij}\) is the full 3D Cauchy stress. Index notation is employed in the above expression with indices \(i,j=1,\dots ,3\).

2.2 Reduction to a thin KL shell

Fig. 1
figure 1

3D KL shell domain

Full size image

We reduce the arbitrary 3D kinematics of a solid to that satisfying the assumptions commonly employed in thin shells. For this, we introduce the shell mid-surface \(\Gamma \). We assume that \(\Gamma \) may be parameterized using a pair of in-plane parametric coordinates \(\xi _1\) and \(\xi _2\). The through-thickness direction is then parameterized using \(\xi _3 \in [-1,+1]\). With these definitions, the full 3D position vector \(\textbf{x}^{3D}\) in the current configuration is given by

$$\begin{aligned} x_i^{3D} = x_i^{2D} + \frac{h}{2}\xi _3 n_i, \end{aligned}$$
(2)

where \(\textbf{x}^{2D}\) is the position vector of the shell mid-surface parameterized by \(\xi _1\) and \(\xi _2\) (here we suppress the dependence on \(\xi _1\) and \(\xi _2\) for brevity of notation), h is the local shell thickness, and \(\textbf{n}\) is the mid-surface normal vector. See Fig. 1 for an illustration. The mid-surface normal vector in Eq. (2) is computed directly as,

$$\begin{aligned} \textbf{n} = \frac{\frac{\partial \textbf{x}^{2D}}{\partial \xi _1} \times \frac{\partial \textbf{x}^{2D}}{\partial \xi _2} }{ \left\Vert \frac{\partial \textbf{x}^{2D}}{\partial \xi _1} \times \frac{\partial \textbf{x}^{2D}}{\partial \xi _2} \right\Vert }, \end{aligned}$$
(3)

making the 3D position vector \(\textbf{x}^{3D}\) a function of the mid-surface position vector \(\textbf{x}^{2D}\) and thickness only.

We now proceed to develop an expression for the full 3D strain rate tensor that is consistent with KL shell kinematics. First, we compute the full 3D velocity vector \(\textbf{v}^{3D}\) by taking a material time derivative of Eq. (2) as

$$\begin{aligned} v_i^{3D} = v_i^{2D} + \frac{h}{2}\xi _3 \bigg ( B^1_{ik}v^{2D}_{k,\xi _1} + B^2_{il}v^{2D}_{l,\xi _2} \bigg ). \end{aligned}$$
(4)

Here \(v_i^{2D}\) is the mid-surface velocity vector parameterized by \(\xi _1\) and \(\xi _2\), comma denotes partial differentiation and the auxiliary second-order tensors \(\textbf{B}^1\) and \(\textbf{B}^2\) are given by

$$\begin{aligned}{} & {} A_{ij} = \frac{\delta _{ij} -n_i n_j}{ \left\Vert \frac{\partial \textbf{x}^{2D}}{\partial \xi _1} \times \frac{\partial \textbf{x}^{2D}}{\partial \xi _2} \right\Vert },~ B^1_{ik} \nonumber \\{} & {} \quad = A_{ij}\epsilon _{jkl} x^{2D}_{l,\xi _2},~ B^2_{il} = A_{ij}\epsilon _{jkl} x^{2D}_{k,\xi _1}, \end{aligned}$$
(5)

where \(\delta _{ij}\) is the Kronecker delta and \(\epsilon _{ijk}\) is the Levi–Civita tensor. Taking the parametric derivatives of \(\textbf{v}^{3D}\) gives

$$\begin{aligned} \begin{aligned}&v^{3D}_{i,\xi _j}=v^{2D}_{i,\xi _j}+\frac{h}{2}\xi _3 \bigg (B^1_{ik,\xi _j}v^{2D}_{k,\xi _1} + B^1_{ik}v^{2D}_{k,\xi _1\xi _j} \\&+ B^1_{il,\xi _j}v^{2D}_{l,\xi _2} + B^1_{il}v^{2D}_{l,\xi _2\xi _j} \bigg ),~j=1,2~(\text {in-plane}),\\&v^{3D}_{i,\xi _j}=\frac{h}{2} \bigg (B^1_{ik}v^{2D}_{k,\xi _1} + B^1_{il}v^{2D}_{l,\xi _2} \bigg ),\\&j=3~(\text {through-thickness}), \end{aligned} \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{aligned}&B^1_{ik,\xi _j}= \epsilon _{pkl}\bigg (A_{ip,\xi _j} x^{2D}_{l,\xi _2} + A_{ip}x^{2D}_{l,\xi _2\xi _j} \bigg ),\\&B^2_{il,\xi _j}= \epsilon _{pkl}\bigg (A_{ip,\xi _j} x^{2D}_{k,\xi _2} + A_{ip}x^{2D}_{k,\xi _2\xi _j} \bigg ), \end{aligned} \end{aligned}$$
(7)

and where \(A_{ip,\xi _j}\) can be computed as

$$\begin{aligned}{} & {} A_{ip,\xi _j} = -\epsilon _{klm}\frac{A_{ik}n_p + A_{pk}n_i + A_{ip}n_k}{ \left\Vert \frac{\partial \textbf{x}^{2D}}{\partial \xi _1} \times \frac{\partial \textbf{x}^{2D}}{\partial \xi _2} \right\Vert } \nonumber \\{} & {} \quad \bigg (x^{2D}_{l,\xi _1\xi _j}x^{2D}_{m,\xi _2} +x^{2D}_{l,\xi _1}x^{2D}_{m,\xi _2\xi _j} \bigg ). \end{aligned}$$
(8)

The full 3D spatial velocity gradient \(\nabla \textbf{v}^{3D}\) can be expressed using the chain rule as

$$\begin{aligned}{}[\nabla \textbf{v}^{3D} _{ij} ]= v^{3D}_{i,j} = v^{3D}_{i,\xi _k} x^{3D^{-1}}_{j,\xi _k}, \end{aligned}$$
(9)

where the parametric derivatives of the position vector \(\textbf{x}^{3D}\) are given by

$$\begin{aligned} \begin{aligned}&x_{i,\xi _j}^{3D} = x_{i,\xi _j}^{2D}+ \frac{h}{2}\xi _3 \bigg (B^1_{ik}x^{2D}_{k,\xi _1\xi _j} + B^2_{i}x^{2D}_{l,\xi _1\xi _j} \bigg ),\\&j=1,2~(\text {in-plane}),\\&x_{i,\xi _j}^{3D} =\frac{h}{2} n_i ,~j=3~(\text {through-thickness}). \end{aligned} \end{aligned}$$
(10)

The full 3D strain-rate tensor, which is consistent with the kinematics of the KL shell, is obtained by symmetrizing the velocity gradient as \(\textbf{D} = \frac{1}{2}(\nabla \textbf{v}^{3D} + \nabla (\textbf{v}^{3D})^T )\).

The full 3D virtual velocity and its spatial gradient that are also consistent with the KL shell kinematics and that are employed in the weak form of the structure governing equations are now given by

$$\begin{aligned} \delta v_i^{3D} \approx \delta v_i^{2D} + \frac{h}{2}\xi _3 \bigg ( B^1_{ik}~\delta v^{2D}_{k,\xi _1} + B^2_{il}~\delta v^{2D}_{l,\xi _2} \bigg ) \end{aligned}$$
(11)

and

$$\begin{aligned} \delta v^{3D}_{i,j} \approx \delta v^{3D}_{i,\xi _k}~x^{3D^{-1}}_{j,\xi _k}, \end{aligned}$$
(12)

where

$$\begin{aligned} \begin{aligned}&\delta v^{3D}_{i,\xi _j} = \delta v^{2D}_{i,\xi _j}+\frac{h}{2}\xi _3 \bigg (B^1_{ik,\xi _j}~\delta v^{2D}_{k,\xi _1} \\&+ B^1_{ik}~\delta v^{2D}_{k,\xi _1\xi _j} + B^1_{il,\xi _j}~\delta v^{2D}_{l,\xi _2} + B^1_{il}~\delta v^{2D}_{l,\xi _2\xi _j} \bigg ),\\&j=1,2~(\text {in-plane}),\\&v^{3D}_{i,\xi _j}=\frac{h}{2} \bigg (B^1_{ik}~\delta v^{2D}_{k,\xi _1} + B^1_{il}~\delta v^{2D}_{l,\xi _2} \bigg ),\\&j=3~(\text {through-thickness}). \end{aligned} \end{aligned}$$
(13)

A multilayer shell is formulated by using the above governing equations for each ply (or ply group) of the laminate independently and by connecting the individual plies through cohesive interfaces, as described in the following sections. Here, the governing equations are discretized with NURBS-based IGA. The NURBS functions are used to construct a parameterization of the shell mid-surface in the current configuration as well as to approximate the shell mid-surface velocity. No rotational degrees of freedom are needed, which has efficiency benefits. The shell layers that are comprised of multiple NURBS patches are joined with \(C^0\)-continuity and make use of a penalty approach detailed in Alaydin et al. (2021) to handle the kinematic constraints at patch interfaces. Symmetry boundary conditions, where applicable, are also enforced via the penalty approach.

2.3 Intralaminar elasto-plastic damage model

Gradual failure of unidirectional fiber-reinforced composite materials is characterized by several phenomena, including fiber breaking/pullout, matrix cracking, and failure at the matrix-fiber interface. While these material failures occur at a microscopic scale, their effect on a meso- and macroscopic levels is commonly modeled using Continuum Damage Mechanics (CDM) Kachanov (1986); Matzenmiller et al. (1995); Salviato et al. (2016). In some cases, matrix plasticity plays an important role in the mechanical response (Tan and Sun 1985; Cairns 1991; Xue and Kirane 2022a, b) and may be included in the modeling. In what follows, we summarize the elements of our elasto-plastic damage modeling framework presented in detail in Alaydin et al. (2022), only emphasizing the parts that are directly affected by hygrothermal effects.

To introduce the CDM approach we adapt in this work, we first define the relationship between the effective and nominal Cauchy stress as

$$\begin{aligned} \tilde{\pmb {\sigma }} = \textbf{M}(\textbf{d})~\hat{\pmb {\sigma }} = \textbf{M}(\textbf{d})~\textbf{R}^T \pmb {\sigma } \textbf{R}, \end{aligned}$$
(14)

where \(\tilde{\pmb {\sigma }}\) is the effective Cauchy stress in principal material coordinates, \(\hat{\pmb {\sigma }}\) is the nominal Cauchy stress in principal material coordinates, \(\pmb {\sigma }\) is the nominal Cauchy stress in the fixed spatial coordinates, \(\textbf{R}\) is the corresponding rotation matrix, \(\textbf{d}\) is the vector of damage indices, and \(\textbf{M}(\textbf{d})\) is the damage operator defined in Voigt notation as

$$\begin{aligned} \textbf{M}(\textbf{d}) = \text {diag} \left[ \frac{1}{1-d_1} ; \frac{1}{1-d_2} ; 1;1;1;\frac{1}{1-d_6}\right] . \end{aligned}$$
(15)

Here \(d_1\), \(d_2\) and \(d_6\) are the scalar damage indices corresponding to the in-plane fiber, matrix and shear stress components, respectively, and with values ranging from 0 to 1 (i.e., from an undamaged to a fully damaged state). The rotation matrix \(\textbf{R}\) comes from a polar decomposition of the deformation gradient. It is initialized using principal material axes in the undeformed configuration and evolved in time using an algorithm detailed in Alaydin et al. (2022).

A hypoelastic–plastic constitutive law in rate form is employed, namely,

$$\begin{aligned} \dot{\tilde{\pmb {\sigma }}} = \textbf{C} \hat{\textbf{D}}^e, \end{aligned}$$
(16)

where \(\hat{\textbf{D}}^e\) is the elastic part of the co-rotational strain-rate tensor and \(\textbf{C} = \textbf{C}(E_1,E_2,G_{12},\nu _{12})\) is the elastic stiffness tensor describing a transversely isotropic material in an undamaged state. Here, \(E_1\) and \(E_2\) are the fiber and matrix elastic moduli, respectively, \(G_{12}\) is the shear modulus, and \(\nu _{12}\) is the Poisson’s ratio. Associative plasticity with a power-law isotropic hardening is employed. To model matrix plasticity, the yield surface uses a plastic potential that only depends on the matrix and shear stress components. A closest-point projection technique (Alaydin et al. 2022) is employed to update the stress. The stress update procedure outputs the end-of-step effective Cauchy stress, effective plastic strain (scalar), consistent tangent modulus, and accumulated elastic strain, all in co-rotational coordinates corresponding to the principal material directions. Both the effective Cauchy stress and accumulated elastic strain are employed in the damage evolution procedures described next.

2.3.1 Damage initiation

We employ the well-known Hashin criteria for damage initiation (Hashin and Rotem 1973; Hashin 1980), which consist of four primary damage modes and the associated failure functions, namely,

$$\begin{aligned} \begin{aligned}&F_{1T}= \bigg ( \frac{\tilde{\sigma }_{11}}{X_T} \bigg )^2 + \alpha \bigg ( \frac{\tilde{\sigma }_{12}}{S} \bigg )^2,~\tilde{\sigma }_{11} \ge 0\\&(\text {Tensile Fiber Failure}), \\&F_{1C}= \bigg ( \frac{\tilde{\sigma }_{11}}{X_C} \bigg )^2,~\tilde{\sigma }_{11}<0\\&(\text {Compressive Fiber Failure}), \\&F_{2T}= \bigg ( \frac{\tilde{\sigma }_{22}}{Y_T} \bigg )^2 + \bigg ( \frac{\tilde{\sigma }_{12}}{S} \bigg )^2,~\tilde{\sigma }_{22}\ge 0\\&(\text {Tensile Matrix Failure}), \\&F_{2C}= \bigg ( \frac{\tilde{\sigma }_{22}}{Y_C} \bigg )^2 + \bigg ( \frac{\tilde{\sigma }_{12}}{S} \bigg )^2,~\tilde{\sigma }_{22}<0\\&(\text {Compressive Matrix Failure}). \end{aligned} \end{aligned}$$
(17)

Here, the damage model parameters \(X_T\) and \(X_C\) are the fiber strengths in tension and compression, respectively, \(Y_T\) and \(Y_C\) are the matrix strengths in tension and compression, respectively, and S is the shear strength. While \(\alpha \) was set to zero in the original reference (Hashin and Rotem 1973), in the updated version (Hashin 1980) it was set to unity, which is what we do here. The functions \(F_{1T}-F_{2C}\) in Eq. (17) are monitored from the start of the computation, and, when they exceed unity, damage begins to evolve in the corresponding modes.

2.3.2 Damage evolution

For each of the four damage modes we define its’ equivalent displacements as

$$\begin{aligned} \begin{aligned}&\delta _{1T}=L_c \langle \hat{\epsilon }_{11}^e \rangle , \\&\delta _{1C}=L_c \langle -\hat{\epsilon }_{11}^e \rangle , \\&\delta _{2T}=L_c \sqrt{\langle \hat{\epsilon }_{22}^e \rangle ^2 + ( \hat{\epsilon }_{12}^e )^2 }, \\&\delta _{2C}=L_c \sqrt{\langle -\hat{\epsilon }_{22}^e \rangle ^2 + ( \hat{\epsilon }_{12}^e )^2 }, \end{aligned} \end{aligned}$$
(18)

and the corresponding stresses as

$$\begin{aligned} \begin{aligned}&\sigma _{1T} = \langle \tilde{\sigma }_{11} \rangle , \\&\sigma _{1C} = \langle -\tilde{\sigma }_{11} \rangle , \\&\sigma _{2T} = \frac{L_c \bigg (\langle \tilde{\sigma }_{22}\rangle \langle \hat{\epsilon }_{22}^e \rangle + \tilde{\sigma }_{12} \hat{\epsilon }_{12}^e \bigg )}{ \delta _{2T}}, \\&\sigma _{2C} = \frac{L_c \bigg (\langle -\tilde{\sigma }_{22}\rangle \langle -\hat{\epsilon }_{22}^e \rangle + \tilde{\sigma }_{12} \hat{\epsilon }_{12}^e \bigg )}{ \delta _{2T}}. \end{aligned} \end{aligned}$$
(19)

Here, the Macaulay bracket is given by \(\langle x \rangle = (x+|x|)/2\) and the characteristic length \(L_c\) is introduced to mitigate the dependence of the dissipated strain energy on the element size as suggested in Bažant and Oh (1983). We take \(L_c=c\sqrt{J}\), where J is the surface Jacobian determinant of the transformation between the element parent and physical domains and c is an \(\mathcal {O}(1)\) dimensionless constant. This smeared crack approach was shown to be effective in the context of multi-directional failure with finite strains in, e.g., Giffin and Zywicz (2023); Palizvan et al. (2020).

The equivalent displacement \(\delta _I^0\) and stress \(\sigma _I^0\) for each mode at the onset of damage are computed by

$$\begin{aligned} \begin{aligned}&\delta _I^0=\frac{\delta _I}{\sqrt{F_I}},\\&\sigma _I^0=\frac{\sigma _I}{\sqrt{F_I}}, \end{aligned} \end{aligned}$$
(20)

and the equivalent failure displacement \(\delta _I^f\) for each mode is computed from the mode fracture energy \(G_I\) and failure stress \(\sigma _I^0\) as

$$\begin{aligned} \delta _I^f = \frac{2G_I}{\sigma _I^0}. \end{aligned}$$
(21)

Here \(I \in \{1T, 1C, 2T, 2C\}\), and the above definition of failure displacement assumes that the damage law is approximated by a classical bi-linear function (i.e., linear-elastic response followed by linear softening). Assuming linear softening behavior, the current value of the damage variable for each mode may be obtained from the equivalent displacement for that mode as

$$\begin{aligned} d_I = \text {max} \bigg (d_I, \frac{\delta _I^f (\delta _I - \delta _I^0)}{\delta _I(\delta _I^f-\delta _I^0)} \bigg ), \end{aligned}$$
(22)

where the “max” function guarantees the irreversibility of damage growth. Viscous regularization (Lapczyk and Hurtado 2007) is employed to partially mitigate rapid damage growth and to improve nonlinear convergence. The indices \(d_1\), \(d_2\) and \(d_6\) in the damage operator \(\textbf{M}(\textbf{d})\) are computed from the damage variables \(d_I\) as

$$\begin{aligned} \begin{aligned}&d_1 = {\left\{ \begin{array}{ll} d_{1T} &{} \text {if}~\tilde{\sigma }_{11} \ge 0,\\ d_{1C} &{} \text {if}~\tilde{\sigma }_{11}< 0,\\ \end{array}\right. } \\&d_2 = {\left\{ \begin{array}{ll} d_{2T} &{} \text {if}~\tilde{\sigma }_{22} \ge 0,\\ d_{2C} &{} \text {if}~\tilde{\sigma }_{22} < 0,\\ \end{array}\right. },\\&d_6 = 1 - (1-d_{1T})(1-d_{1C})(1-d_{2T})(1-d_{2C}), \end{aligned} \end{aligned}$$
(23)

where, although not explicitly written, the irreversibility of damage growth is also enforced.

Remark From the standpoint of algorithmic implementation, the present approach may be though of as a plastic predictor - damage corrector method. Namely, at every nonlinear iteration the stress update due to plasticity occurs in the effective space, and the new effective stress is then used to evolve the damage indices. The updated damage state is then used to compute the nominal Cauchy stress, which, in turn, is employed in the computation of the nodal forces.

2.4 Delamination model

Here we summarize the ingredients of our delamination modeling approach presented in detail in Pigazzini et al. (2018), focusing on the parts that are directly affected by hygrothermal effects. The framework is based on a zero-thickness cohesive interface model to simulate the evolution of delamination between the adjacent laminate plies. The formulation was first introduced in the context of IGA-based KL shells in Pigazzini et al. (2018), Bazilevs et al. (2018) and later equipped with an improved technique to enforce the ply no-interpenetration condition in Alaydin et al. (2022).

Fig. 2
figure 2

Schematic representation of the cohesive interface

Full size image

To model delamination, the following cohesive-interface term is added to the weak form of the structural mechanics problem given by Eq. (1):

$$\begin{aligned} +\int _{\Gamma ^{coh}} \llbracket \delta \textbf{v}^{3D} \rrbracket \cdot \textbf{t}^{coh}~d\Gamma . \end{aligned}$$
(24)

were \(\Gamma ^{coh}\) is a collection of interfaces between the laminate plies, \(\textbf{t}^{coh}\) is a cohesive traction on \(\Gamma ^{coh}\), and \(\llbracket \delta \textbf{v}^{3D} \rrbracket \) denotes a “jump” or difference in the virtual velocity or test function across \(\Gamma ^{coh}\) given by

$$\begin{aligned} \begin{aligned} \llbracket \delta \textbf{v}^{3D} \rrbracket&= \bigg ( \delta \textbf{v}_{\Gamma _1}^{2D} + \frac{h_{\Gamma _1}}{2} ( \textbf{B}^1_{\Gamma _1}\delta \textbf{v}^{2D}_{1,\xi _1} + \textbf{B}^2_{\Gamma _1}\delta \textbf{v}^{2D}_{1,\xi _2} )\bigg ) \\&\quad - \bigg ( \delta \textbf{v}_{\Gamma _2}^{2D} + \frac{h_{\Gamma _2}}{2} ( \textbf{B}^1_{\Gamma _2}\delta \textbf{v}^{2D}_{2,\xi _1} + \textbf{B}^2_{\Gamma _2}\delta \textbf{v}^{2D}_{2,\xi _2} )\bigg ), \end{aligned} \end{aligned}$$
(25)

where the subscripts \(\Gamma _1\) and \(\Gamma _2\) refer to the quantities on the adjacent plies. The cohesive traction \(\textbf{t}^{coh}\) in Eq. (24) follows a relatively simple traction-separation law

$$\begin{aligned} \textbf{t}^{coh}{} & {} = (1-d^{coh})\left( K_n^{coh}\tilde{\textbf{n}}\otimes \tilde{\textbf{n}} + K_\tau ^{coh}(\textbf{I}-\tilde{\textbf{n}}\otimes \tilde{\textbf{n}}) \right) \nonumber \\{} & {} \quad \llbracket \textbf{x}^{3D} \rrbracket , \end{aligned}$$
(26)

where \(\llbracket \textbf{x}^{3D} \rrbracket \) is a separation between the adjacent plies given by

$$\begin{aligned}{} & {} \llbracket \textbf{x}^{3D} \rrbracket = \textbf{x}^{3D}_{\Gamma _1} - \textbf{x}^{3D}_{\Gamma _2} = \bigg (\textbf{x}_{\Gamma _1}^{2D}+\frac{h_{\Gamma _1}}{2} \textbf{n}_{\Gamma _1}\bigg ) \nonumber \\{} & {} \quad - \bigg (\textbf{x}_{\Gamma _2}^{2D}+\frac{h_{\Gamma _2}}{2} \textbf{n}_{\Gamma _1}\bigg ), \end{aligned}$$
(27)

\(d^{coh}\) is the cohesive damage variable, \(K_n^{coh}\) and \(K_\tau ^{coh}\) are the normal and tangential cohesive stiffness parameters, and \(\tilde{\textbf{n}}\) is the interface normal vector. Figure 2 illustrates the kinematic quantities employed in the formulation.

The cohesive damage variable \(d^{coh}\) evolves according to the Mixed-Mode Cohesive Model (MMCM) developed in Turon et al. (2006) Turon et al. (2010) Wu et al. (2016). For this, analogously to intralaminar damage, we first define the equivalent displacement jump at the onset of delamination and at complete failure as

$$\begin{aligned} \delta ^0_m = \sqrt{ (\delta ^0_n)^2 + \left( (\delta ^0_\tau )^2 - (\delta ^0_n)^2 \right) ~f(\beta ) } \end{aligned}$$
(28)

and

$$\begin{aligned} \delta ^f_m = \frac{\delta ^0_n \delta ^f_n + ( \delta ^0_\tau \delta ^f_\tau - \delta ^0_n \delta ^f_n)~f(\beta ) }{\delta ^0_m}, \end{aligned}$$
(29)

respectively. In Eq. (28),

$$\begin{aligned} \delta ^0_n = \frac{t_n}{K_n^{coh}} \end{aligned}$$
(30)

and

$$\begin{aligned} \delta ^0_\tau = \frac{t_\tau }{K_\tau ^{coh}} \end{aligned}$$
(31)

are the displacement-jump values where the delamination initiates under pure normal and tangential opening modes, respectively, with \(t_n\) and \(t_\tau \) denoting the corresponding cohesive-strength parameters. In Eq. (28),

$$\begin{aligned} \delta ^f_n = \frac{2 G_{cn}}{t_n} \end{aligned}$$
(32)

and

$$\begin{aligned} \delta ^f_\tau = \frac{2 G_{ct}}{t_\tau }, \end{aligned}$$
(33)

are the displacement-jump values corresponding to a complete failure of the interface under pure normal and tangential opening modes, respectively, with \(G_{cn}\) and \(G_{ct}\) denoting the corresponding fracture toughness parameters. The equivalent displacement jumps make use of an empirical function \(f(\beta )\) (see Pigazzini et al. (2018) for the expression employed), where \(\beta \) is a local, solution-dependent mode mixity ratio (Karnati and Shivakumar 2020) given by

$$\begin{aligned} \beta = {\left\{ \begin{array}{ll} \frac{\delta _\tau }{\delta _n+\delta _\tau }, &{} \text {if }~\bar{\delta } \le 0, \\ 1, &{} \text {if }~\bar{\delta } > 0, \end{array}\right. } \end{aligned}$$
(34)

where \(\bar{\delta }\) is the scalar-valued gap or normal separation between the plies with positive values corresponding to interface opening, and where \(\delta _n\) and \(\delta _\tau \) are the magnitudes of the normal and tangential components of \(\llbracket \textbf{x}^{3D} \rrbracket \), respectively.

Assuming linear softening, the cohesive damage variable is computed from

$$\begin{aligned} d^{coh} = \text {max} \bigg (d^{coh}, \frac{\delta _m^f (\delta _m - \delta _m^0)}{\delta _m(\delta _m^f-\delta _m^0)} \bigg ), \end{aligned}$$
(35)

where the current value of the mixed-mode displacement jump \(\delta _m\) is given by

$$\begin{aligned} \delta _m = {\left\{ \begin{array}{ll} \sqrt{(\delta _n)^2+(\delta _\tau )^2}, &{} \text {if }~\bar{\delta } \le 0, \\ \delta _\tau , &{} \text {if }~\bar{\delta } > 0. \end{array}\right. } \end{aligned}$$
(36)

Despite delamination growth happening under mixed-mode loading conditions, the modes are unified into a single damage variable \(d^{coh}\). Viscous regularization is also employed to evolve \(d^{coh}\).

Table 1 Scaling-law parameters and the corresponding coefficient of determination \(R^2\) for the target material IM7/8552. The scaling law parameters in Eq. (44) were obtained for each material property using a least-squares fitting procedure and the Levenberg–Marquardt algorithm. References in the last column point to the source of experimental data used in the fitting procedure.
Full size table
Fig. 3
figure 3

Scaling-law plots for the target material IM7/8552 mechanical properties

Full size image

3 Modeling of hygrothermal effects

The overall approach taken in this work is to leverage basic results in polymer physics and chemistry together with an existing set of experimental data to develop a scaling law that relates the intra- and interlaminar properties of a fiber-reinforced polymer composite material to the temperature and moisture content. This approach enables the modeling of damage and delamination of fiber-reinforced polymer composite structures using the methodology presented in the previous section under a variety of hygrothermal conditions. The proposed approach is a simple one-way dependence formulation where the mechanical response is sensitive to the hygrothermal conditions, but not vice versa. The two-way coupled models are more complex to formulate and discretize, and may be left for future work.

3.1 Summary of modeling parameters

In the previous sections we outlined the modeling framework and a set of material parameters whose specification is required to carry out meso- and macroscale simulations of damage and delamination in composite structures. These parameters are summarized as follows:

  • Lamina elastic properties:

    $$\begin{aligned} E_{1}, E_{2}, \nu _{12},~\text {and}~G_{12}. \end{aligned}$$
    (37)

  • Lamina damage properties:

    $$\begin{aligned} X_{T}, X_{C}, Y_{T}, Y_{C}, S, G_{1T}, G_{1C}, G_{2T},~\text {and}~G_{2C}. \end{aligned}$$
    (38)

  • Cohesive stiffness properties:

    $$\begin{aligned} K_{n}^{coh},~\text {and}~K_{\tau }^{coh}. \end{aligned}$$
    (39)

  • Cohesive damage properties:

    $$\begin{aligned} t_{n}, t_{\tau }, G_{cn},~\text {and}~G_{ct}. \end{aligned}$$
    (40)

In what follows, we develop a scaling law that defines the dependence of the above mechanical properties on the temperature and moisture content. In each case, the resulting scaling law is normalized by the reference value of a property taken at room-temperature, dry conditions.

3.2 Development of the scaling law

To arrive at the aforementioned scaling law for the material-property dependence on the temperature T and moisture content \(m_w\), we take T and \(m_w\) as state variables and use the Frenkel equation (Frenkel 1984), which was derived from the Arrhenius law and Boltzmann law for molecular bond breaking and formation:

$$\begin{aligned} A = A_{ref} \exp {\left( \frac{\Delta U}{R T} \right) }. \end{aligned}$$
(41)

Here, \(R=8.314\) J/(K\(\cdot \)mol) is the universal gas constant, \(A_{ref}\) is the reference value of property A at room-temperature dry conditions, and \(\Delta U\) is the activation energy of the bonds (i.e., energy needed to break the bonds, which is positive by convention). For a mixture of water and bulk polymer \(\Delta U\) can be written in terms of the constituents’ glass-transition temperature as in Sanditov et al. (2020), Gordon and Taylor (1952)

$$\begin{aligned} \Delta U = C T_{g,w} = C T_{g}\left( 1-\frac{m_w}{m_{w,max}}\right) , \end{aligned}$$
(42)

where \(T_{g,w}\) and \(T_{g}\) are the glass-transition temperatures of the polymer-water mixture and dry bulk polymer, respectively. The above equation implies that \(T_{g} = 0\) for \(m_w = m_{w,max}\), however, this is never achieved in reality because polymers break down before reaching this limit. The relationship between \(T_{g,w}\) and \(m_w\), however, was shown to be nonlinear in Arhant et al. (2016). To account for nonlinearity we propose to modify Eq. (42) by using a power-law dependence of the form

$$\begin{aligned} T_{g,w}= T_{g}\left[ 1 - \left( \frac{m_w}{m_{w,max}}\right) ^\alpha \right] . \end{aligned}$$
(43)

Combining Eqs. (41)–(43) yields the scaling law

$$\begin{aligned} A = A_{ref} \exp {\left\{ \frac{C T_{g}}{R T} \left[ 1 - \left( \frac{m_w}{m_{w,max}}\right) ^\alpha \right] \right\} }, \end{aligned}$$
(44)

where, given a set of experimental data, the parameters \(CT_{g}\) (taken as a product), \(\alpha \), and \(m_{w,max}\) are fitted for each material property separately.

Remark Several studies indicate that the relationship between \(T_{g,w}\) and \(m_w\) is universal among different polymeric adhesives (Mel 1997; Davison 2003; Chen 2015). As a result, we expect our scaling law to be broadly applicable. We also note that the scaling law for \(A/A_{ref}\) is unique for each polymer, which is consistent with the findings in Arhant et al. (2016).

3.3 Target material system

The material of interest in this work is a unidirectional carbon-epoxy composite IM7/8552. We apply the procedure described in the previous section to formulate the dependence of this composite’s mechanical properties on the temperature and moisture content. A summary of the results are provided in Table 1 and Fig. 3. Overall, the proposed scaling law captures the experimental trends well, perhaps with the exception of \(X_T\) and some cohesive-interface properties mainly due to large experimental data scatter.

Fig. 4
figure 4

Laminate shear stress–strain response and comparison with the experimentally measured in-plane shear strength

Full size image
Fig. 5
figure 5

Comparison of the numerically predicted and experimentally measured laminate in-plane shear modulus \(G_{12}\)

Full size image

While most of the properties are degrading with the increasing temperature and humidity, \(G_{cn}\) and \(G_{1T}\) appear to be insensitive to the increase in humidity. This seeming lack of sensitivity largely stems from parameter fitting using scarce data with relatively large error bars. As a result, no clear dependence on the moisture content could be extracted for \(G_{cn}\) and \(G_{1T}\). This ambiguity may also be explained by co-existence of two competing mechanisms: a simultaneous enhancement of polymer chain cohesion caused by the presence of an immediate hydrogen-bond network (Zhang et al. 2019; Choi et al. 2021) and the lubrication effect (Soler-Crespo et al. 2018). We note that other references (see, e.g., Plagianakos et al. (2020)) suggest that moisture tends to degrade interlaminar fracture toughness in a wide range of composite materials, including Graphite/Epoxy composites. However, as mentioned earlier, the experimental data for the IM7/8552 material is such that we are not able to clearly establish this dependence. Surprisingly though, \(G_{cn}\) and \(G_{1T}\) appear to be enhanced by the elevated temperature, which suggests that the thermal vibration monotonically increases cohesion between polymer chains and at the matrix-fiber interface.

Fig. 6
figure 6

In-plane shear test. Contours of matrix damage \(d_2\) on the top ply at failure. The predicted failure mode is consistent with the experimental observations form a similar in-plane shear test of an RTD specimen in Plappert et al. (2020) shown here for comparison.

Full size image
Fig. 7
figure 7

Problem configuration and boundary condition of the short beam shear test

Full size image

The following observations and assumptions were employed for the mechanical properties for which the experimental data was scarce or inconclusive:

  • The scaling law is only applicable to the matrix-direction elastic properties; the fiber-direction elastic properties are assumed to be insensitive to the ambient moisture and temperature conditions.

  • Plasticity-related parameters are assumed to be independent of the temperature and moisture content, mainly due to the scarcity of experiment data. The plasticity model parameters employed in the simulations are taken from Alaydin et al. (2022).

  • \(G_{1C}\) and \(G_{2C}\) follow the same scaling law as \(G_{1T}\) and \(G_{2T}\), respectively, as they share the same material.

  • Due to the scarcity of test data, \(K_{n}^{coh}\) and \(K_{\tau }^{coh}\) values are assumed to be insensitive to temperature and moisture content, and are set to be in a range defined in Bazilevs et al. (2018). We note that, a parametric study carried out in Bazilevs et al. (2018) suggests that cohesive stiffness can take on a range of values without significantly affecting the overall laminate mechanical response. Therefore, for simplicity, we eliminated the dependence of \(K^{coh}\) on temperature and moisture content.

4 Computational results

In this section, we compute three experimental test cases using the IM7/8552 carbon-epoxy composite laminates: (1) In-plane shear; (2) Short beam shear; and (3) Open-hole tension. Experimental data for these tests, which is used here for validation purposes, may be found in Marlett et al. (2011), Cole (2015). The computations are carried out using quadratic NURBS with \(C^1\)-continuity. Full three-point quadrature is employed in the surface directions and reduced two-point quadrature is used in the through-thickness direction. (See Hughes et al. 2010; Nagy and Benson 2015; Li et al. 2022; Li and Bazilevs 2023 for a discussion of reduced quadrature in IGA and related methods.) A fully implicit dynamic formulation is used in all cases, however, because the loading rate is relatively low, the structural response is essentially quasi-static. We employ the backward Euler time integration scheme with adaptive time stepping. We start the time integration scheme with an initial time step of 0.01 s. If convergence does not occur within a certain number of Newton–Raphson iterations (around 10 or so), the time step is halved. If convergence occurs in less than three Newton–Raphson iterations, the time step is increased by 10%. Otherwise, the time step size stays unchanged.

Fig. 8
figure 8

Short beam shear load–displacement response

Full size image
Fig. 9
figure 9

Contours of cohesive damage across the beam thickness. Also shown are the contours of shear strain \(\gamma _{13}\) captured using the DIC technique in the short beam shear experiments from Makeev et al. (2013). Note that the high shear strain regions captured by the DIC are coincident with the regions of cohesive damage predicted in the simulations.

Full size image

The following abbreviations are employed in the subsequent sections: CTD stands for Cold Temperature Dry and corresponds to \(T={-54}^\circ C\) and \(m_w=0\); RTD stands for Room Temperature Dry and corresponds to \(T={23}^\circ C\) and \(m_w=0\); ETD stands for Elevated Temperature Dry and corresponds to \(T={80}^\circ C\) and \(m_w=0\); and ETW stands for Elevated Temperature Wet and corresponds to \(T={121}^\circ C\) and \(m_w=0.9\%\). The lamina and cohesive material properties used in the computations follow the scaling law developed in Sect. 3.

Fig. 10
figure 10

RTD short bean shear load–displacement history overlaid with images of cohesive and fiber damage at different instances of loading

Full size image
Fig. 11
figure 11

CTD short bean shear load–displacement history overlaid with images of cohesive and fiber damage at different instances of loading

Full size image
Fig. 12
figure 12

ETW short bean shear load–displacement history overlaid with images of cohesive and fiber damage at different instances of loading

Full size image

4.1 In-plane shear

We simulate tensile tests performed on IM7/8552 laminates with a lamination sequence of \([\pm 45]_{3s}\). The structure is a plate with a problem domain size of \(75~\text {mm}\times 25~\text {mm}\times 1.1~\text {mm}\) in the length, width and thickness directions, respectively, with the latter consisting of 12 plies in total. There are 11 cohesive interfaces connecting the plies. The specimen undergoes unidirectional tensile loading in the length direction, with one side fixed and another subjected to a constant velocity of 1 mm/s. The computations are carried out using a uniform mesh of 1,200 NURBS elements per ply for RTD, ETD and ETW hygrothermal conditions.  The simulations are performed on a 2019 workstation with four Intel® Xeon(R) E-2224 CPUs and take around 10 h for each hygrothermal condition. The total number of time steps for the RTD, ETD and ETW cases is 209, 142 and 124, respectively.

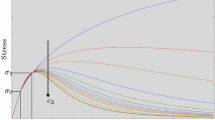
A comparison between the numerically predicted and experimentally measured laminate in-plane shear strength is presented in Fig. 4 showing the shear stress–strain response of the laminate. The experimentally determined shear stress is computed as \(\frac{F}{2bh}\) while the strain is given by \(\frac{d}{a}\). Here, F is the tensile force, d is the displacement, and a, b and h are the length, width and thickness of the specimen, respectively. The experimental data corresponds to a single value of the failure stress for each hygrothermal condition plotted using a dashed line in the figure. Very good comparison with the experimentally measured failure stress is attained in the three cases, with a maximum deviation of around \(5.8\%\) for the RTD case. A comparison of the predicted laminate-level \(G_{12}\) and its experimentally-measured counterpart is shown in Fig. 5, also exhibiting very good agreement. In the computations, the laminate-level \(G_{12}\) is computed from the equation \(G_{12} = \frac{aF}{bhd}\) evaluated at the initial strain of \(\frac{d}{a} = 0.001\).

Top-ply matrix damage distribution at failure (i.e., at an instant when the laminate in-plane shear stress drops to about 50% of the strength) is shown in Fig. 6. In the view shown, the bottom edge is fixed and the top edge is pulled upward. In all cases matrix damage initiates in an “X” shape pattern appearing 1/4 length away from the top and bottom edges and settles into a final “\(\backslash \)” or “/” shape failure pattern. No fiber failure or cohesive damage is present in this case. As both \(Y_{T}\) and \(E_{2}\) decrease with the temperature and moisture content, the structure becomes more compliant and damage pattern at failure tends to be less localized. As the temperature and moisture content increase, catastrophic failure is preceded by more extensive matrix damage. As indicated by the scaling parameters in Table 1, the ETW hygrothermal condition gives the lowest matrix fracture energies \(G_{2T}\) and \(G_{2C}\), which leads to the steepest load drop during softening and largest extent of damage at failure. The failure mode predicted in our simulations is consistent with experimental observations from similar in-plane shear test in Plappert et al. (2020) also shown in Fig. 6.

4.2 Short beam shear

We present a classical three-point bending test to validate the short beam shear strength prediction using experimental data from Marlett et al. (2011). The test setup and boundary conditions are shown in Fig. 7. We build a computational model of a 34-ply unidirectional IM7/8552 laminate \([0]_{34}\), where each ply has dimensions of \(28~\text {mm}\times 5~\text {mm}\times 0.184~\text {mm}\) in the length, width and thickness directions, respectively. The model also contains 33 cohesive interfaces connecting the plies. Despite the large number of plies in the structure, the problem NURBS mesh is comprized of only 1,224 elements because a single element is used to discretize the width direction, resulting in 36 elements per ply. The laminate is subjected to contact-driven boundary conditions as shown in Fig. 7. Two of the rollers are separated by a distance of 25 mm and fixed at the bottom, and the third roller pushes on the laminate from the top with a constant velocity of 1 mm/s. For details of the contact formulation employed, see Pigazzini et al. 2018, 2019; Bazilevs et al. 2018; Alaydin et al. 2022. The simulations are carried out in RTD, CTD and ETW conditions and the cohesive-interface stiffness values are set to \(K^{coh}_n = K^{coh}_{\tau } = 3.2 \times 10^5\) N/mm\(^3\). The computations are run on the same workstation as those in Sect. 4.1 and lasted around 10 h for each hygrothermal condition. The total number of time steps for the RTD, CTD and ETW cases is 1,498, 617 and 829, respectively.

Figure 8 plots the short beam shear stress given by \(F^{sbs}=0.75\times \frac{P}{bh}\) as a function of the top roller displacement \(d_p\) after the roller makes first contact with the top ply. Here, P, b and h are reaction force on the top roller, width of the specimen and total thickness of the specimen, respectively. The experimentally measured value of the peak \(F^{sbs}\) for each of the hygrothermal conditions is shown by dashed lines in Fig. 8. Relative error between the numerical predictions and experimental measurements in peak \(F^{sbs}\) is 4.7%, 1.4% and 8.1% for RTD, CTD and ETW, respectively.

Cohesive damage distribution for RTD, CTD and ETW at peak \(F^{sbs}\) is shown in Fig. 9. The structure is failing as a result of progressing sliding delaminations. No intralaminar damage is triggered in the structure at this stage of the loading. Cohesive damage contours are consistent among the three hygrothermal conditions and ETW gives the largest extent of the delamination zone due to the lowest cohesive shear strength \(t_{\tau }\) among the three cases. This failure mode is consistent with the experimental observations in Marlett et al. (2011) as well as with the Digital Image Correlation (DIC) measurements for the shear strain reported in Makeev et al. (2013) also shown in Fig. 9.

Reference (Marlett et al. 2011) also reported that short beam shear failure may occur in a combination of interlaminar shear and intralaminar fiber compression (Kumar 2021; Köllner et al. 2016; Kyriakides et al. 1995). The latter is attributed to a lower compressive strength in the fiber direction. To capture this failure mode, we first focus on the RTD case and continue loading the structure until complete failure. Figure 10 shows a longer load–displacement history overlaid with images of cohesive and fiber damage at different instances of loading. The structure is almost fully delaminated after the top roller displacement reaches \(d_p=0.40\) mm. Afterward, the load is transferred through normal contact in which the top lamina are subjected to compression. When the roller displacement reaches \(d_p=0.70\) mm, the load begins to drop again because fiber damage from compression starts to evolve in the top-most lamina. At \(d_p=0.73\) mm, fiber damage propagates to the second ply from the top, then to the third ply at \(d_p=0.77\) mm, fourth at \(d_p=0.82\) mm, and so on. At \(d_p=0.91\) mm, the fiber damage accumulation is almost sufficient to cause multi-lamina breaking, and the structure undergoes complete failure at \(d_p=1.20\) mm. A similar sequence of failures was reported in short beam shear experiments of \([0]^{\circ }\) laminates in Almeida et al. (2016).

For the CTD case, our scaling-law results plotted in Fig. 3 indicate that \(X_C\) is comparable to \(X_T\), which changes the failure mode to include both fiber tension and compression. As per Fig. 11, a complete cohesive failure occurs at \(d_p=0.5\) mm and the top four plies fail in compression, one after the other, at \(d_p=1.04, 1.07, 1.11\) and 1.13 mm, respectively. At the same time, the bottom-most ply fails in tension between \(d_p=1.04\) mm and \(d_p=1.13\) mm of roller displacement. A sudden load drop occurs around \(d_p=1.15\) mm, where both fiber compression damage at the top and fiber tension damage at the bottom propagate through several plies simultaneously. The remainder of the laminate fails catastrophically after \(d_p=1.19\) mm.

For the ETW case, \(G_{1C}\) is the highest among the hygrothermal cases considered. As the computational results indicate, this leads to higher structural tolerance against abrupt load drops caused by the fiber compressive failure. As per Figure  12, a complete cohesive failure occurs at \(d_p=0.30\) mm. Afterward, the top first, third, fifth and seventh plies fail in compression at \(d_p=0.70, 1.11, 1.21\) and 1.30 mm, respectively. The specimen is able to withstand fiber compression damage up to the fifth ply to give a secondary load peak after the earlier cohesive-interface failure. (Note that in the short beam shear experiments only the first load peak is reported.) An abrupt load drop caused by further fiber compression damage occurred at about \(d_p=1.38\) mm, and at \(d_p=1.46\) mm the structure experienced complete failure.

4.3 Open-hole tension

As the last example, we compute an open-hole tension test of an IM7/8552 laminate with a lamination sequence of \([\pm 45,0,\pm 45,90,\pm 45,\pm 45]_{s}\) at the RTD, CTD and ETW hygrothermal conditions. The computational model consists of 10 plies that comprise the top half of the laminate (i.e., \([\pm 45,0,\pm 45,90,\pm 45,\pm 45]\)), nine cohesive interfaces and symmetry boundary conditions along the thickness direction to account for the laminate mid-plane symmetry. Each ply is \(56~\text {mm}\times 36~\text {mm}\times 0.092~\text {mm}\) in the length, width and thickness directions, respectively, and uses a mesh of 2,808 NURBS elements. The hole diameter is 6 mm.

The laminate is fixed at the left edge and pulled at a constant velocity of 1 mm/s at the right edge. The problem configuration and mesh are shown in Fig. 13. The open-hole tension simulations were carried out on a 32-core cluster with 12th Gen Intel® Core™ i7-12,700 CPUs. Each hygrothermal condition computation lasted around four hours. The total number of time steps for RTD, CTD and ETW is 323, 374 and 322, respectively.

Figure 14 shows the stress–strain curves obtained in the computations. The stress is computed by dividing the reaction force by the laminate cross-section area in the reference configuration and the strain is computed by dividing the right-edge displacement by the length. The figure also presents a failure strength comparison between the numerically predicted and experimentally measured values. Relative errors between the numerical and experimental strengths for RTD, CTD and ETW are 10.9%, 10.2% and 4.0%, respectively.

The \(1^\textrm{st}\)-ply matrix damage, \(3^\textrm{rd}\)-ply fiber damage and cohesive damage at the interface between the \(3^\textrm{rd}\) and \(4^\textrm{th}\) plies at failure (i.e., when the stress drops to around 45% of the laminate strength) are shown in Fig. 15. The RTD and CTD cases give similar fiber and matrix damage patterns, yet the extent of CTD cohesive damage is smaller than that of RTD due to a higher cohesive strength. The ETW case gives a distinctive “Y” shape fracture pattern as well as the largest extent of matrix and cohesive damage due to the lowest matrix and cohesive strengths.

However, a lower \(G_{2T}\) leads to the eventual localization of damage into a major crack with a higher damage level. The failure pattern produced in the computations is typical of the laminates dominated by \(45^\circ \) plies and when little delamination is observed in the structural response.

The failure mode predicted in our simulations is consistent with experimental observations from a similar open-hole tension test in Laurin et al. (2016) also shown in Fig. 15.

Fig. 13
figure 13

Problem configuration and mesh of the open-hole tension test

Full size image

5 Conclusions

Fig. 14
figure 14

Laminate stress–strain response and comparison of the failure strength with the experimentally measured values plotted with dashed lines

Full size image
Fig. 15
figure 15

Distribution of matrix, fiber and cohesive damage at failure. Failure mode captured in the simulations closely matches that from an RTD open-hole tension experiment for a similar lay-up in Laurin et al. (2016) shown here for comparison.

Full size image

  • A scaling law based on the Arrhenius equation and glass transition temperature is developed to establish a dependence of the mechanical properties of polymer composites on the temperature and moisture content. The proposed scaling law captures the experimental trends well for a target material system of a unidirectional carbon-epoxy composite IM7/8552. We expect our scaling law to be broadly applicable because several studies indicate that the relationship between glass transition temperature and moisture content appears to be universal among different polymeric adhesives.

  • The scaling law is employed to parameterize the intra- and interlaminar elastic stiffness coefficients, strengths, and fracture energies of the target material system. This parameterization, in turn, enables meso- and macroscale simulations of damage and delamination in composite structures at different hygrothermal conditions in order to understand how these affect structural failure modes.

  • Using the IGA-based framework for multi-layer thin shells we carried out the simulations of three structural tests, mainly in an effort to validate both the IGA-based formulation and the proposed scaling law. The computational results showed very good agreement with the experimental data for the failure loads as well as for predicting the modes of failure under a variety of hygrothermal conditions.

  • For the short beam shear test of the RTD case we were able to capture a delicate transition from massive delamination to fiber failure in compression, where the latter starts at the top ply and propagates through the laminate one ply at a time, until finally resulting in a catastrophic multi-lamina breaking. In contrast to the RTD case, the CTD case, owing to comparable fiber strengths in tension and compression, showed simultaneous compressive fiber failure in the top plies and tensile fiber failure in the bottom plies. The ETW case showed a second force peak, which exceeded the first force peak in magnitude, and a greater tolerance against abrupt load drops due to fiber compressive failure owing to higher fracture energy in this mode. To the best of the authors’ knowledge, this work presents a first such set of simulations reported in the open literature.