1 Introduction

Interfacial fracture in multi-layer structures has been a critical reliability issue for thin film/substrate systems in electronic packages (Ho et al. 2004; Liu et al. 2007). Especially in chip-package systems, interfacial fractures along die and die-attach, die and epoxy molding compound interfaces are commonly observed after thermal processing (Zhang et al. 2008). These interfacial fractures normally grow under mixed-mode conditions due to differences in layer thicknesses, materials, residual stresses as well as the globally applied loading. To investigate these problems, linear elastic fracture mechanics was initially applied to reveal the correlation between mode-mix and interfacial toughness (Cao and Evans 1989; Chai and Liechti 1992; Wang and Suo 1990). However, limitations arise when analyzing interfacial cracks between purely elastic media without accounting for any interactions between the crack surfaces. Cohesive zone modeling, which does account for such interactions, was first proposed by (Barenblatt 1962; Dugdale 1960) and then adopted to model interfacial crack growth in the presence of cohesive interactions (Needleman 1987, 1990; Ungsuwarungsri and Knauss 1987). Cohesive zone modeling soon gained popularity not only for modeling interfacial delamination (Feraren and Jensen 2004; Li et al. 2005; Parmigiani and Thouless 2007; Valoroso and Champaney 2006), but also for other interface problems such as crack nucleation at bi-material corners (Mohammed and Liechti 2000), plastic dissipation in thin films (Shirani and Liechti 1998), and delamination of composites (Li and Thouless 2006; Moroni and Pirondi 2011; Sorensen and Jacobsen 2003). However, interfacial traction–separation relations must be specified and measured in order for the cohesive zone model to properly describe the fracture process and to make meaningful predictions.

To extract traction–separation relations, local measurements such as crack tip opening displacement (CTOD) and crack extension are typically required. Crack opening interferometry has been extensively used to provide crack tip measurements in multilayer systems (Chai and Liechti 1992; Gowrishankar et al. 2012; Liang and Liechti 1995; Liechti and Knauss 1982; Mello and Liechti 2006; Na et al. 2014; Swadener et al. 1999; Swadener and Liechti 1998) and in thin film blister tests (Cao et al. 2016; Liechti and Hanson 1988). The surface deflections of blistering films have also been measured with a view to extracting interactions between the films and substrates (Cao et al. 2015, 2014; Shirani and Liechti 1998; Xu and Liechti 2010). The application of crack opening interferometry relies on the transparency of at least one of the interacting materials. In this work, we exploit the transparency of silicon to infrared in an application of infra-red crack opening interferometry (IR-COI) for a silicon/epoxy system. However, this technique only provides crack opening displacements normal to the interface in the interior of the specimen; both the normal and tangential displacements were measured using digital image correlation (DIC).

Previously, double cantilever beam (DCB) specimens were used to extract the tensile traction–separation relation for a silicon/epoxy interface (Gowrishankar et al. 2012). For mixed-mode interfacial fracture, the topic of the present paper, the end-loaded split (ELS) specimen (Wang and Vu-Khanh 1996) was adopted with the modification that the epoxy thickness was varied to provide different mode-mixes while maintaining the same adherend thickness and materials. In order to extract traction–separation relations from experiments, the fracture resistance curves were obtained from measurements and a beam on elastic foundation model. By combining the ELS and DCB experiments, mixed-mode traction–separation relations were determined for phase angles ranging from \(-42^{\circ }\) to \(0^{\circ }\). Additional measurements would be necessary to further extend the reach of the model to mode-II dominant conditions.

The remainder of this paper is organized as follows. Section 2 describes the experiments, and Sect. 3 presents modeling and analyses, including a beam on elastic foundation model and a mixed-mode cohesive zone model for finite element simulations. Section 4 describes a procedure to determine the parameters in the traction–separation relations for the cohesive zone model. The results are further discussed in Sect. 5 before concluding in Sect. 6.

2 Experiments

In this section, we describe the specimen preparation, loading device and local displacement measurement techniques (IR-COI and DIC) that were used in the experiments.

Fig. 1
figure 1

a Schematics of the loading device and specimen for the end loaded split (ELS) experiments, with IR-COI measurement; b setup for DIC measurements

Full size image

2.1 Specimen preparation

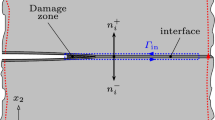
A schematic of the specimen geometry and apparatus is shown in Fig. 1. The specimen consists of two silicon strips joined by a layer of epoxy. The n-type Si(111) wafers supplied by WRS Materials were polished on both sides to facilitate the use of IR-COI. The wafers were 50 mm in diameter and nominally \(590\,\upmu \hbox {m}\) in thickness. An automatic dicer (Disco, model DAD 321) was used for cutting wafers into 50 by 5 mm (for top adherends) and 40 by 15 mm (for bottom adherends) strips, which were then cleaned individually by ultra-sonication in de-ionized water to remove any accumulated debris. The top adherend was coated with an Au/Pd thin film from one end of the strip to a length of about 25 mm. The metals were simultaneously sputtered on the silicon strip. The relatively low adhesion energy between the Au/Pd coating and the epoxy \(({\sim }0.07\hbox { J}/\hbox {m}^{2})\) allowed an initial crack to form with minimal damage to the silicon/epoxy interface.

The epoxy in the experiments was prepared by mixing the resin (modified bishpenol-A epoxy, Araldit\(^\circledR \) GY502) and hardener (polyamidoamine, Aradur\(^\circledR 955\)) in a ratio of 100:45 by weight. The epoxy mixture was then de-gassed in a vacuum chamber. To prepare the specimen, a silicon strip was placed on Teflon\(^\circledR \) tape with shims of different thickness to control the height of the epoxy layer. A bead of the degassed epoxy was dropped on the silicon surface and spread out with a spatula. Then the silicon strip coated with the Au/Pd thin film was pressed on the bead with a weight to spread the epoxy into a layer between the two silicon strips. The specimen was cured at \(65\,^{\circ }\hbox {C}\) for 3 hours and then allowed to cool to room temperature. For the DIC measurements (Fig. 1b), the lower adherend was diced to the same width as the top adherend so that the side faces of the specimen could be polished to have the required texture. Upon cooling of the specimen, a random pattern was generated in the region of interest by polishing of the side of the silicon strip with a high grit (\({>}{600})\) sand paper, which allowed image correlation software to match subsets of the images (Gowrishankar 2014). A total of 6 groups of specimens were prepared for both the IR-COI and DIC measurements. The epoxy thickness for these specimens varied between 5 and \(50\,\upmu \hbox {m}\), measured by calipers.

2.2 Load-displacement measurements

Once the specimen was prepared, it was mounted in the loading device as shown in Fig. 1. In the specimens that were used with IR-COI, the bottom silicon strip was wider than the top one so that it could be clamped along its length to a rigid base. The experiments with DIC required that the silicon strips had the same width, so, in this case, the bottom silicon strip was bonded to the rigid base using a cyanoacrylate adhesive. The loading device consists of a linear actuator coupled with a load cell connected to a loading head. The displacement-controlled loading protocol was prescribed at the lower surface of the end of the top silicon strip. The loading rate was set at \(0.1\, \upmu \hbox {m}/\hbox {s}\). Both the displacement and load measurements were taken simultaneously.

Fig. 2
figure 2

Load-displacement response for an ELS specimen with an epoxy thickness of \(8\, \upmu \hbox {m}\). The linear parts of the loading and unloading responses are compared to the beam-on-elastic foundation model (Eq. 1, dashed lines) to determine the initial and final crack lengths

Full size image

A typical load-displacement response under a loading-unloading cycle is shown in Fig. 2. The loading response started with a slightly nonlinear segment due to contact and formation of an initial crack by debonding of the part of the interface that was coated with the Au/Pd layer. The loading response then became linear until crack growth started along the silicon/epoxy interface. The crack growth led to the non-linear portion of the loading response as the slope decreased gradually with increasing crack length. The unloading response was largely linearly elastic, but with a smaller stiffness than the loading response, as expected for a longer crack. As discussed later, the load-displacement responses were used to determine the J-integral (essentially along a remote path) in order to construct fracture-resistance curves.

2.3 IR-COI measurements

The transparency of silicon to infra-red enabled the measurement of crack length and normal crack opening displacement (NCOD) by classical crack opening interferometry (Liechti 1993). This technique essentially uses the interference between the two rays reflected from the crack surfaces to determine the distance between them. The experiments were performed using an infrared microscope (Olympus BH2-UMA) that was fitted with an internal beam splitter and an IR filter (\(1040\pm 15\hbox {nm})\) to provide the normal incident beam. A digital camera (Lumenera Corporation, Infinity 3) with a resolution of \(1392\times 1040\) pixels captured the images. The images were then processed to determine the location of the crack front and the NCOD (Gowrishankar et al. 2012). Figure 3a shows a fringe pattern obtained by IR-COI and the variation of crack length with applied displacement. The procedure for measuring the crack length has been described in detail elsewhere (Gowrishankar et al. 2012). The crack front remained stationary until the applied displacement reached about 0.25 mm, after which the crack growth was observable by IR-COI. The corresponding NCOD profiles near the crack front at different applied displacements are shown in Fig. 3b. The location \(x=0\) was set at the location of the initial crack front as established by the initial intensity pattern. The resolution of the IR-COI technique implemented in this work was approximately 330 nm and 20 nm for measurements of crack length and NCOD, respectively.

Fig. 3
figure 3

Crack growth versus the applied displacement for the ELS specimen with an epoxy thickness of \(8\, \upmu \hbox {m}\): a crack extension obtained by local IR-COI measurements and global load-displacement responses with Eq. 2 from the beam on elastic foundation model; Inset shows a typical interferogram of the crack-front; b measured NCOD profiles at increasing applied displacements

Full size image

2.4 DIC measurements

DIC was implemented by analyzing images of areas of interest as time elapsed during experiment using the ARAMIS\(^\circledR \) correlation software. The images were taken with the help of a \(45^{\circ }\) prism mirror fixed to a groove parallel to the specimen (Fig. 1b). This allowed a surface of the specimen that was intersected by the crack front to be viewed during the experiment, thereby allowing both the normal and tangential displacements near the crack front to be obtained. The DIC technique essentially provides a full field measurement of the in-plane deformation, but two reference points were identified on the silicon strips at the same horizontal location as the crack front (Fig. 4a). The relative displacement between these two points, including both normal and tangential components with respect to the interface, were determined as the components of the crack tip opening displacements (CTOD) and recorded as a function of the applied displacement as shown in Fig. 4b. The resolution in the CTOD measurement was about 80 nm.

Fig. 4
figure 4

a Surface texture of an ELS specimen (\(50\, \upmu \hbox {m}\) epoxy thickness) for DIC measurements, with two reference points identified at the upper and lower sides of the initial crack front; b measured normal and tangential CTODs by DIC

Full size image

3 Modeling and analysis

To interpret the experimental data and then to predict mixed-mode interfacial fracture, a simple beam on elastic foundation (BEF) model was adopted first, followed by a mixed-mode cohesive zone model and finite element simulations in ABAQUS\(^\circledR \).

3.1 Beam on elastic foundation

Based on the loading condition, the ELS specimen can be considered approximately as a cantilever beam on an elastic foundation, with which the energy release rate (J-integral) can be calculated based on the global measurements of the applied load and displacement. A model based on an elastic foundation analysis was presented in a previous study (Gowrishankar et al. 2012), which yielded the force-displacement response at the loading point as

$$\begin{aligned} P\!=\!\frac{3E_{Si} I_{Si} \Delta }{a^{3}}\left( 1\!+\!\frac{3}{\lambda a}\!+\!\frac{3}{(\lambda a)^{2}}+\frac{3}{2(\lambda a)^{3}}\right) ^{-1}, \end{aligned}$$
(1)

where P is the applied force, \(\Delta \) is the displacement at the loading point, a is the crack length (measured from the loading point to the crack tip), \(E_{Si}\) is Young’s modulus of silicon, \(I_{Si} =\frac{1}{12}b_{Si} h_{Si}^{3}\), \(b_{Si}\) is the width of the silicon strip, \(h_{Si}\) is the thickness of the silicon strip, and \(\lambda =( \frac{6K_{0}}{E_{Si} h_{Si}^{3}} )^{1/4}\). The parameter \(K_{e}\) represents the stiffness of the elastic foundation, which may be approximated for the ELS specimen as \(K_{e} =\frac{E_{e}}{h_{e}}\) with \(E_{e}\) as the Young’s modulus of the epoxy and \(h_{e}\) as its thickness. The predicted load-displacement response by Eq. 1 compared well with the measurement (Fig. 2). The crack length can then be determined from the measurements of P and \(\Delta \) as

$$\begin{aligned} a_{eff} =\frac{1}{\lambda }\left[ \left( {3\lambda ^{3}E_{Si} I_{Si} \frac{\Delta }{P}-\frac{1}{2}} \right) ^{1/3}-1 \right] . \end{aligned}$$
(2)

The crack lengths thus obtained are shown in Fig. 3a, in excellent agreement with the crack lengths measured by IR-COI. In these calculations, \(E_{Si}\) and \(E_{e}\) were 165.5 and 2.03 GPa, respectively. The in-plane tensile modulus of the Si(111) strips was measured in three-point bending (Gowrishankar 2014). The beam thickness \(h_{Si}\) was 0.59 mm, and its width \(b_{Si}\) was 5 mm, while the epoxy thickness \(h_{e}\) was \(8\, \upmu \hbox {m}\).

The corresponding energy release rate or J-integral obtained from the BEF model (Gowrishankar et al. 2012) is

$$\begin{aligned} J(P,a)=\frac{6(Pa)^{2}}{E_{Si} b_{Si}^{2} h_{Si}^{3} }\left( {1+\frac{1}{\lambda a}} \right) ^{2}. \end{aligned}$$
(3)

With the effective crack length given in Eq. 2, the globally determined value of the J-integral can be obtained directly using the force and displacement data as

$$\begin{aligned} J( P, \Delta )=\frac{6P^{2}}{\lambda ^{2}E_{Si} b_{Si}^{2} h_{Si}^{3} }\left[ {\frac{\lambda ^{3}E_{Si} b_{Si} h_{Si}^{3}}{4}\left( {\frac{\Delta }{P}} \right) -\frac{1}{2}} \right] ^{2/3}. \end{aligned}$$
(4)

3.2 Fracture resistance curves

Fig. 5
figure 5

Fracture resistance curves for ELS specimens with different epoxy thicknesses

Full size image

Fracture resistance curves (Fig. 5) were critical to the extraction of the traction–separation relations. A resistance curve was generated for each epoxy thickness using the crack extension (\(\Delta a)\) obtained from the IR-COI measurements and the J-integral calculated by means of Eq. 4 and the measured load-displacement response. For each ELS specimen, the initial crack did not grow appreciably (\(\Delta a<0.2 \,\upmu \hbox {m}\)) until the J-integral reached a critical level (\(J_{0}\)). Subsequently, as the J-integral increased, the observable crack length increased. Eventually, the crack growth is expected to reach a steady state with a constant J-integral (\(J_{SS}\)) under the displacement-controlled loading condition. However, the experimental data did not always show clear evidence of the steady state, possibly due to the limitation placed by the field of view available to the IR-COI system. In such cases, the last data point on the resistance curve was taken as the closest approximation of the steady state. The amount of observable crack growth to reach the steady state is labeled as \(\Delta a_{ss}\), which corresponds to the steady-state damage zone size in the cohesive zone model as discussed later. Clearly, Fig. 5 shows that the resistance to fracture increased with decreasing epoxy thickness. However, since decreasing the adhesive layer thickness is usually expected to decrease the resistance to fracture (Chai 1988, 1990), the effect of fracture mode-mix on toughness for this epoxy (Chai and Liechti 1992) is considered in the next section as a potential contributing factor. In addition, the three quantities defined for each resistance curve, \(J_{0}\), \(J_{SS}\), and \(\Delta a_{ss}\), will be used to determine the key parameters of the traction–separation relations in the cohesive zone model.

3.3 Linearly elastic fracture analysis

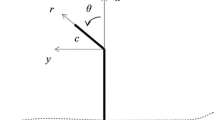
Based on linearly elastic fracture mechanics (LEFM) concepts for interface fracture (Hutchinson and Suo 1992; Rice 1988), the stresses on the interface directly ahead of the crack tip for an interfacial crack can be written in a complex form as

$$\begin{aligned} \sigma +i\tau =(K_{1} +iK_{2} )(2\pi r)^{-1/2}r^{i\varepsilon }, \end{aligned}$$
(5)

where \(\sigma \) and \(\tau \) are the normal and shear stresses, \(K=K_{1}+iK_{2}\) is the complex stress intensity factor, r is the distance to the crack tip, and \(\varepsilon =\frac{1}{2\pi }\ln \left( {\frac{1-\beta }{1+\beta }} \right) \) with Dundurs’ parameter \(\beta =\frac{1}{2}\frac{\mu _{1} (1-2\nu _{2} )-\mu _{2} (1-2\nu _{1} )}{\mu _{1} (1-\nu _{2} )+\mu _{2} (1-\nu _{1} )}\) (\(\mu \) for shear modulus and \(\nu \) for Poisson’s ratio). The ratio between the shear and normal stresses in Eq. 5 depends on r unless \(\varepsilon =0\) . Therefore, an arbitrary length scale (l) has to be used to define the phase angle of the fracture mode-mix as,

$$\begin{aligned} \psi _{K} =\tan ^{-1}\left( {\frac{\hbox {Im}\left( {Kl^{i\varepsilon }} \right) }{\hbox {Re}\left( {Kl^{i\varepsilon }} \right) }} \right) \end{aligned}$$
(6)

Using different length scales leads to a shift in the phase angle. In the present study, we take \(l=h_{e}\) for the ELS specimen and calculate the phase angle using a semi-analytical method and a plane strain finite element model of the ELS specimen.

The semi-analytical method recognizes that the ELS specimens in the present study are sandwich specimens where the complex stress intensity factor K of the interfacial crack depends on the elastic properties of the materials as well as the thickness of the sandwiched layer through (Suo and Hutchinson 1989)

$$\begin{aligned} K=h_{e}^{-i\varepsilon } \left( {\frac{1-\alpha }{1-\beta ^{2}}} \right) ^{1/2}(K_{I} +iK_{II} )e^{i\omega }, \end{aligned}$$
(7)

where \(K_{I}\) and \(K_{II}\) are the so-called global stress intensity factors associated with the reference homogeneous specimen (silicon strips joined without epoxy) but loaded in the same manner. The global stress intensity factors were obtained from tabulated values given in (Li et al. 2004) for a transversely loaded strip being separated from an infinitely thick substrate, which gives a global phase angle of the mode-mix, \(\psi _{K_{0}} =\tan ^{-1}\left( {K_{I} /K_{II} } \right) =-36^{\circ }\). The angle \(\omega \) depends on the elastic mismatch between silicon and epoxy, which is \(-8^{\circ }\) by numerical calculations as tabulated in (Suo and Hutchinson 1989). Then, by Eq. 6 with \(l=h_{e}\), the local phase angle of the mode-mix is \(-44^{\circ }\) for the ELS specimen. Note that this result represents the limiting case for an epoxy layer that is very small compared to the thickness of the silicon strip and other in-plane length scales (e.g., the crack length).

Fig. 6
figure 6

a Schematic of a plane strain finite element model for the ELS experiment; b mesh and normal stress contours near a crack tip in a linear elastic finite element mode; c mesh and normal stress contour near the initial crack tip in a nonlinear finite element model with surface-based cohesive interactions between silicon and epoxy

Full size image

In view of the assumptions in the semi-analytical method, a plane strain, linearly elastic finite element model (Fig. 6a) was also used to calculate the stress intensity factors and phase angles for the ELS specimens with a range of epoxy thicknesses. A stationary crack along the upper silicon/epoxy interface was assumed, and the interface ahead of the crack was perfectly bonded. A typical mesh near the crack tip, where the singular elements were used, is shown in Fig. 6b. The real and imaginary parts of the complex stress intensity factor at the crack tip were calculated and the corresponding phase angle of the mode-mix was obtained from Eq. 6. As shown later (Sect. 4.1), the phase angle depends on the epoxy thickness but approaches the asymptotic limit (\(-44^{\circ }\)) as the epoxy thickness decreases, thereby allowing the mode-mix in the experiments to be controlled by varying the epoxy thickness of the ELS specimens.

3.4 Mixed-mode cohesive zone analysis

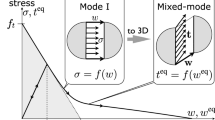
To simulate interfacial crack growth in the ELS specimens, a finite element model was constructed using the commercial package ABAQUS\(^\circledR \), where the silicon/epoxy interface was modeled by surface-based cohesive interactions with a mixed-mode traction–separation relation. At each point along the interface, the normal and shear tractions are related to the relative displacement across the interface through

$$\begin{aligned} \sigma _{n} (\delta _{n} , \delta _{t} )= & {} (1-D)K_{n} \delta _{n} \nonumber \\ \sigma _{t} (\delta _{n} , \delta _{t} )= & {} (1-D)K_{t} \delta _{t}, \end{aligned}$$
(8)

where \(D=f(\delta _{n} , \delta _{t})\) is a local damage parameter, generally a function of the interfacial separations in both the normal and tangential directions (\(\delta _{n}\) and \(\delta _{t})\). Prior to damage initiation, \(D=0\) and the normal and shear traction–separation relations are un-coupled and linearly elastic with respective stiffness, \(K_{n}\) and \(K_{t}\). The quadratic nominal stress criterion (QUADS) was used as the criterion for damage initiation:

$$\begin{aligned} \left( {\frac{\sigma _{n} }{\sigma _{n0} }} \right) ^{2}+\left( {\frac{\sigma _{t}}{\sigma _{t0} }} \right) ^{2}=1 \end{aligned}$$
(9)

where \(\sigma _{n0}\) and \(\sigma _{t0}\) are the strengths in the normal and shear directions, respectively. For the ELS specimens in the present study, it was found that damage initiation was primarily controlled by the normal traction (Gowrishankar 2014). This was accounted for here by setting \(\sigma _{t0}\) to be 1 GPa, much larger than \(\sigma _{n0}\), so that the second term in Eq. 9 was negligible. As a result, the critical normal traction for damage initiation is nearly independent of the mode-mix (i.e., \(\sigma _{n} \approx \sigma _{n0} )\), while the corresponding shear traction and the vectorial traction (\(\sigma =\sqrt{\sigma _{n}^{2} +\sigma _{t}^{2} })\) do depend on the mode-mix.

The mode-mix for the cohesive zone model can be defined locally based on the ratio between the displacement components or the traction components. When the same stiffness is used for the normal and shear components \(\left( K_{n} =K_{t} =K_{0} \right) \) in Eq. 8, the phase angle can be calculated from the ratio of the tractions or the displacements, i.e.

$$\begin{aligned} \psi =\tan ^{-1}\left( {\frac{\sigma _{t} }{\sigma _{n} }} \right) =\tan ^{-1}\left( {\frac{\delta _{t} }{\delta _{n}}} \right) \end{aligned}$$
(10)

It is noted that this definition of the phase angle may not result in the same phase angle at all locations within the cohesive zone depending on how damage evolves (Parmigiani and Thouless 2007). In all subsequent cohesive zone modeling, we take the phase angle at the initial crack tip before damage initiation as the mode-mix of each specimen. After damage initiation, the phase angle may change in general.

The mixed-mode traction–separation relation after damage initiation depends on the evolution of the damage parameter D in Eq. 8. Following the assumption that damage initiation is controlled by the normal traction, the critical displacements at the point of damage initiation are approximately, \(\delta _{n0} =\sigma _{n0} /K_{0}\) and \(\delta _{t0} =\delta _{n0} \tan \psi \). The corresponding vectorial displacement is \(\delta _0 =\sigma _0 /K_0 \) where \(\sigma _{0} =\sigma _{n0} / {\cos \psi } \) is the maximum vectorial traction. For a particular mode-mix, when the vectorial displacement \(\delta =\sqrt{\delta _{n}^{2} +\delta _{t}^{2} }>\delta _{0}\), the damage parameter evolves from 0 to 1 as a function of \(\delta \) . For this study, an exponential function was used for the damage evolution, which takes the form:

$$\begin{aligned} D\left( {\delta _{m} } \right) =1-\frac{\delta _{0} }{\delta _{m} }\left[ {1-\frac{1-\exp \left( {-\alpha \frac{\delta _{m} -\delta _{0} }{\delta _{f} -\delta _{0}}} \right) }{1-\exp \left( {-\alpha } \right) }} \right] \end{aligned}$$
(11)

where \(\delta _{m}\) is the maximum value of the vectorial displacement \(\delta \) that has been reached at any point throughout the loading history, \(\delta _{f}\) is the vectorial displacement when the interface is fully damaged \(( D=1 )\), and \(\alpha \) is a shape parameter for the exponential softening. As a result, if there is unloading and \(\delta \) decreases, \(\delta _{m}\) does not change and D remains a constant so that the traction decreases linearly with a reduced stiffness (Eq. 8). In other words, the damage is irrecoverable and there is no healing.

The J-integral on a contour enclosing the cohesive zone can be evaluated using the tractions and separations that are active there, so that (Rice 1968)

$$\begin{aligned} J(\delta _{n}^{*} , \delta _{t}^{*} )=\int _{0}^{{\delta _{n}^{*}} } {\sigma _{n} d\delta _{n} } +\int _{0}^{{\delta _{t}^{*}}} {\sigma _{t} d\delta _{t} } , \end{aligned}$$
(12)

where \(\delta _{n}^{*}\) and \(\delta _{t}^{*}\) are the normal and shear separations at the initial crack tip. The use of the same stiffness and damage parameter in the normal and tangential directions in Eq. 8 ensures that the vectorial traction \(( {\sigma =\sqrt{\sigma _{n}^{2} +\sigma _{t}^{2} }})\) is in the same direction as the vectorial displacement \(\delta \) so that this locally evaluated J-integral can be calculated by a single integral over the vectorial traction–separation relation \(\sigma ( \delta )\), namely

$$\begin{aligned} J(\delta ^{*})=\int _{0}^{{\delta ^{*}}} {\sigma d\delta } , \end{aligned}$$
(13)

where \(\delta ^{*}\) is the vectorial separation at the initial crack tip. With the damage evolution in Eq. 11, the mixed-mode fracture toughness can be obtained from the J-integral with \(\delta ^{*}=\delta _{f}\), i.e.

$$\begin{aligned} \Gamma (\psi )=\int _{0}^{{\delta _{f}}} {\sigma d\delta } . \end{aligned}$$
(14)

As shown in Fig. 7, the vectorial traction–separation relation consists of a linearly elastic part \(\left( {0<\delta <\delta _{0}} \right) \) followed by an exponentially softening regime \(\left( \delta _{0}<\delta \right. \left. <\delta _{f} \right) \). The two parts can be integrated separately to yield

$$\begin{aligned} \Gamma _{1} (\psi )=\int _{0}^{{\delta _{0}}} {\sigma d\delta } =\frac{1}{2}\sigma _{0} \delta _{0} \end{aligned}$$
(15)

and

$$\begin{aligned} \Gamma _2 (\psi )=\int _{{\delta _{0}}}^{{\delta _{f}}} {\sigma d\delta } =\sigma _{0} \left( {\delta _{f} -\delta _{0} } \right) \left( {\frac{1}{\alpha }-\frac{1}{e^{\alpha }-1}} \right) . \end{aligned}$$
(16)

As a result, \(\Gamma (\psi )=\Gamma _{1} (\psi )+\Gamma _{2} (\psi )\). This decomposition of the fracture toughness turned out to be useful for determining the traction–separation relation.

Fig. 7
figure 7

Schematic of a vectorial traction–separation relation

Full size image

In ABAQUS, the mixed-mode traction–separation relations can be specified in tabular form. First, a stiffness \(K_{0}\) is specified for the linear part of the traction–separation relation in both the normal and tangential directions. Next, for damage initiation, \(\sigma _{n0}\) and \(\sigma _{t0}\) in Eq. 9 are specified, which are independent of the mode-mix. In the present study, the values of \(K_{0}\) and \(\sigma _{n0}\) were extracted from experiments as discussed in Sect. 4, whereas \(\sigma _{t0}\) was set to be 1 GPa as noted before. The exponential damage evolution in Eq. 11 requires two parameters for each mode-mix, \(\delta _{f} -\delta _{0}\) and \(\alpha \), which can be tabulated with the corresponding energy ratio (\(m_{1}\)) for each mode-mix. By definition, the energy ratio is related to the phase angle of the mode-mix as

$$\begin{aligned} m_{1} =\frac{\int _{0}^{{\delta _{n}}} {\sigma _{n} d\delta _{n} }}{\int _{0}^{\delta } {\sigma d\delta } }=\left( {\cos \psi } \right) ^{2} \end{aligned}$$
(17)

In the cohesive zone modeling (CZM) of the ELS specimen, the silicon/epoxy interface was modeled by surface-based cohesive interactions with the mixed-mode traction–separation relation just described. An example of the mesh with some opening at the initial crack tip and the tractions due to the interactions within the cohesive zone is shown in Fig. 6c. The surface-based approach in ABAQUS differs slightly from the cohesive element approach. The latter treats the interface as a solid layer with an artificial thickness and implements the traction–separation relation as its constitutive behavior. However, it was found that using the cohesive elements did not correctly return the input tangential traction–separation relation under mixed-mode conditions. The likely cause of this issue is in the calculation of the shear strain for the cohesive element, which includes an additional term due to the gradient of normal separation, but is not part of the traction–separation relation. On the other hand, in the surface-based approach, the traction–separation relation is defined as a mechanical contact property between two surfaces and is implemented within the general contact pair framework in ABAQUS/Standard. This allows direct calculations of the interfacial separations as the relative displacements between the nodes on the slave surface and their corresponding projection points on the master surface in the normal and shear directions, without involving any strain or the thickness of the interface. It was found that the surface-based approach correctly reproduced the input mixed-mode traction–separation relations when the tractions and separations were tracked. The nonlinear finite element model with the cohesive surface interactions was then used in conjunction with the ELS experiments to determine the mixed-mode traction–separation relations for the silicon/epoxy interface.

4 Extraction of TSR parameters

The first step in establishing the key parameters in the mixed-mode traction–separation relations was to determine the variation of the phase angle of the mode-mix with epoxy thickness from the results of LEFM analyses and the cohesive zone modeling in comparison with the DIC measurements. Then the resistance curves for three of the ELS specimens shown in Fig. 5 were used to extract the parameters of the traction–separation relations that were associated with damage initiation and evolution for three different phase angles. The data for the other three specimens were used to validate the model in Sect. 5. Finally, the range of mode-mix phase angles accessible to this model was extended to pure mode I (\(\psi =0)\) by including data from DCB wedge tests of the same interface (Gowrishankar et al. 2012).

4.1 Mode-mix

Fig. 8
figure 8

Variation of mode-mix with epoxy thickness in the ELS specimens

Full size image

The phase angle of the mode-mix for the ELS specimen is determined from the LEFM analyses with \(l=h_{e}\) in Eq. 6 as shown in Fig. 8. The semi-analytical method predicts an asymptotic limit (\(-44^{\circ }\)) when the epoxy thickness is very small compared to other in-plane dimensions, as discussed in Sect. 3.3. The fact that this limit phase angle is independent of the epoxy thickness stems from Eq. 7 and the choice of the length scale \(l=h_{e}\) in Eq. 6, which cancel out the exponential terms in the length scale. On the other hand, the results from the linearly elastic, finite element analyses (Fig. 6b) exhibited a very clear dependence on the epoxy thickness with the phase angles ranging from \(-41^{\circ }\le \psi \le -25.5^{\circ }\), while respecting the analytical limit as the epoxy thickness tends to zero.

The results from cohesive zone modeling of the ELS specimens (Fig. 6c) with a traction–separation relation that was typical of those subsequently extracted from the experiments compare closely with the LEFM results for the phase angles. In this case, the phase angle was obtained by applying Eq. 10 to the displacements at the initial crack tip, which remained a constant for each ELS specimen up to the point of damage initiation. As a result, the pre-damage phase angle is nearly identical to the LEFM value. Thus, based on the cohesive zone modeling, the ELS experiments conducted in this study covered the range \(-42^{\circ }\le \psi \le -26^{\circ }\) by varying the epoxy thickness.

Following Eq. 10, the phase angle of the mode-mix could be determined by measurements of the normal and tangential CTODs, as shown in Fig. 4 by the DIC technique. The CTOD data (Fig. 4b) obtained from the DIC measurements was approximated by two linear fits for each displacement component. In each case, the lower slope was associated with the development of the cohesive zone, while the larger slope was associated with the passage of the traction-free portion of crack faces past the fiducial marks (Fig. 4a). The phase angles plotted in Fig. 8 were obtained from the ratio of the lower slopes from the normal and tangential displacement responses and in essence are an average of the elastic and softening behaviors in the cohesive zone. Apparently, these phase angles were considerably different from those obtained by the LEFM and cohesive zone modeling. As will be seen from later discussion of the finite element solutions, there is more structure to the CTOD data than the linear approximations being made at this stage, but the signal to noise ratio from the DIC measurements was not sufficient to resolve this structure. This may be due to the fact that the fiducial marks were in the silicon adherends, rather than on the crack faces. Since obtaining displacements near such discontinuities is difficult with DIC in general, future efforts at using DIC to determine phase angles should be directed at resolving these issues, most likely by making use of the full field nature of the DIC data.

4.2 Damage initiation

Fig. 9
figure 9

a Measured crack extension versus the applied displacement for a specimen with an epoxy thickness of \(50\, \upmu \hbox {m}\); b measured normal CTOD versus applied displacement; c fracture resistance curve; d early portion of the fracture resistance curve

Full size image
Table 1 Extracted parameters for the mixed-mode cohesive zone model
Full size table

The point of damage initiation in the cohesive zone model is assumed to coincide with the point of observable crack growth by IR-COI measurements in the ELS experiments. This is justified by noting that the normal crack opening is relatively small before damage initiation and thus may not be observable as the resolution in the normal crack opening displacements is 20 nm. Moreover, the resolution for the crack growth measurement was about 330 nm. As shown in Fig. 9a, the measured crack growth increased notably to about \(1\, \upmu \hbox {m}\) after an applied displacement, \(\Delta _{0}\), of about \(30\, \upmu \hbox {m}\), which was taken as the critical loading displacement for damage initiation. Meanwhile, the normal CTOD \(\delta _{n} ( \Delta _{0})\) at the same applied displacement was measured by IR-COI at about 20 nm (Fig. 9b). The corresponding J-integral as indicated in the resistance curve (Fig. 9c) is then taken to be identical to the elastic part of the fracture toughness in Eq. 15, namely, \(J_{0} =J\left( {\Delta _{0}} \right) =\Gamma _{1} =\frac{1}{2}\sigma _{0} \delta _{0}\). For a particular ELS specimen, the phase angle of the mode-mix was established in Fig. 8 and hence, \(\delta _{0} =\delta _{n} \left( {\Delta _{0} } \right) / {\cos \psi } \) and \(\sigma _{0} =2J_{0} /\delta _{0}\). The stiffness of the interaction is then obtained as \(K_{0} =\sigma _{0} /\delta _{0}\), and the maximum normal traction is \(\sigma _{n0} =K_{0} \delta _{n} \left( {\Delta _{0}} \right) \). Therefore, the stiffness \(K_{0}\) and the strength \(\sigma _{n0}\) can be extracted for each specimen by combining measurements of the crack extension and the normal CTOD. The results are listed in Table 1 for three of the six ELS specimens, while the data for the other three specimens will be used for validation (Sect. 5). We note that the extracted values for \(K_{0}\) and \(\sigma _{n0}\) varied slightly from specimen to specimen. In the mixed-mode cohesive zone model as described in Sect. 3.4, they are independent of mode-mix and should therefore be constant. As a result, the variations were considered to be data scatter, and the average values of \(K_{0}\) and \(\sigma _{n0}\) were taken as the parameters of the cohesive zone model in the subsequent analysis.

4.3 Damage evolution

The damage evolution for each mode-mix (Eq. 11) is governed by two additional parameters, \(\delta _{f}\) and \(\alpha \). Both parameters may be dependent on the mode-mix and specified as a tabulated input in ABAQUS. For each ELS specimen, the two parameters were extracted based on the resistance curve and the relation in Eq. 16. The steady-state J-integral of the resistance curve was taken as the mixed-mode fracture toughness, i.e., \(\Gamma \left( \psi \right) =J_{ss}\), and then, \(\Gamma _{2} ( \psi )=\Gamma ( \psi )-\Gamma _{1} ( \psi )\). Moreover, for a given mode-mix with corresponding values of \(\Gamma _{1} ( \psi )\) and \(\Gamma _{2} ( \psi )\), the crack growth required to reach the steady state (\(\Delta a_{ss} )\) depends on the index \(\alpha \), as shown in Fig. 10. It was found that \(\alpha =6\) yielded good agreement with the experiments for all the specimens in the present study. Once the value of \(\alpha \) was selected, the other parameter \(\delta _{f}\) was obtained by Eq. 16 via

$$\begin{aligned} \delta _{f} ( \psi )=\delta _{0} +\left( {\frac{J_{ss} -J_{0}}{K_{0} \delta _{0} }} \right) \frac{\alpha \left( {e^{\alpha }-1} \right) }{e^{\alpha }-1-\alpha }. \end{aligned}$$
(18)

To summarize the results, we have been able to extract the following parameters for the mixed-mode traction–separation relation (Table 1): stiffness \(K_{0}\), normal strength \(\sigma _{n0}\), \(\alpha \) and \(\delta _{f}\). In addition, we have assumed that the \(\sigma _{t0}\) was 1 GPa, much greater than \(\sigma _{n0}\). Among all these parameters, only \(\delta _{f}\) depended on the mode-mix and must be specified through the tabulated input option in ABAQUS (Table 2). Note that the values of \(\delta _{f}\) and \(\delta _{0}\) in Table 2 are slightly different from those first obtained in Table 1, since they were re-calculated from the average values of \(K_{0}\) and \(\sigma _{n0}\) along with the measured toughness \(\Gamma ( \psi )\) for each specimen.

Fig. 10
figure 10

a The amount of crack growth required to reach steady state for the ELS specimens. Measured values were compared with cohesive zone models with different values of the softening parameter \(\alpha \). b Comparison of the normalized values of the measured cohesive zone lengths with the normalized length scale parameter

Full size image
Table 2 Tabulated input for the mixed-mode traction–separation relations in ABAQUS
Full size table

Recall that the phase angle of the mode-mix as defined by Eq. 10 ranged from \(-42^{\circ }\) to \(-26^{\circ }\) for the ELS specimens used in the present study (Fig. 8). As a result, the extracted parameters are expected to be applicable only within the same range. In order to extend the range, we took advantage of the results from a previous study (Gowrishankar et al. 2012) where nominally mode-I DCB specimens (\(\psi =0)\) were used to determine the tensile traction–separation relation for the same silicon/epoxy interface. The stiffness was assumed to be \(2\hbox { GPa}/\upmu \hbox {m}\), slightly larger than the extracted value (\(1.33\hbox { GPa}/\upmu \hbox {m})\) in the present study. The maximum normal traction obtained from the DCB specimen was 18 MPa, much lower than the average value (37.3 MPa) from the ELS specimens. This discrepancy may be attributed to the different approaches that were used to determine the maximum traction. Nevertheless, based on the assumptions of the proposed mixed-mode cohesive zone model, we may use the same values, \(1.33\hbox { GPa}/\upmu \hbox {m}\) and 37.3 MPa, as the stiffness and strength under pure mode-I conditions. On the other hand, the mode-I fracture toughness of \(1.8\hbox { J}/\hbox {m}^{2}\) that was determined in the DCB experiment is not subject to any reinterpretation and was used to determine the corresponding \(\delta _{f}\) for mode I from Eq. 18. Thus for mode I, \(\delta _{0} =\sigma _{n0} /K_{0}\) was \(0.028\,\upmu \hbox {m}\), \(J_{0} =\frac{1}{2}\sigma _{n0} \delta _{0}\) was \(0.52\hbox { J}/\hbox {m}^{2}\), and \(\delta _{f}\) was \(0.236\,\upmu \hbox {m}\) with a toughness of \(1.8\hbox { J}/\hbox {m}^{2}\) and \(\alpha =6\) in Eq. 18. The inclusion of the mode-I parameters in Table 2 established \(-42^{\circ }\) to \(0^{\circ }\) as the range of mode-mix accessible to this model. Additional experiments would be necessary to further extend the range, especially for the cases close to pure mode-II \(\left( {\psi =90^{\circ }} \right) \).

5 Discussion

At this stage, we have obtained mixed-mode traction–separation relations for specimens whose epoxy thickness was 5, 9.3 and 50 \(\upmu \)m as embodied in the data supplied in Table 1. Although the parameters were extracted from measured crack extension and crack tip opening displacements as well as the resistance curve for each specimen, the average values of the extracted stiffness and normal strength were used for the final slate of parameters listed in Table 2. As a result, the model was first verified by conducting finite element analyses of the same specimens that were used to extract parameters and comparing the results with measurements of their load-displacement responses, normal crack tip opening displacements and the resistance curves. This was followed by applying the same model to the other ELS specimens with different mode-mixes for further validation.

Fig. 11
figure 11

Comparison of experimental and finite element analysis results for the ELS specimen with an epoxy thickness of \(50\, \upmu \hbox {m}\): a traction–separation relations; b load-displacement response; c normal CTOD versus applied displacement response; d fracture resistance curve

Full size image

First we compare the results (Fig. 11) for the ELS specimen with an epoxy thickness of \(50\, \upmu \hbox {m}\), which was one of the three specimens used for the parameter extraction. The traction–separation relation that results from the parameters given in Table 2 is shown for reference (Fig. 11a). The dominance of the normal component of the input traction–separation relation is clear at this mode-mix of \(-26^{\circ }\). The history of the vectorial tractions and separations at the initial crack tip from the finite element analysis was consistent with the input, despite the change of the phase angle during damage evolution. Note that the values of the output shear traction–separation relation were slightly higher than the ones that were input and vice versa for the normal traction–separation relations. However, these differences cancelled out for the vectorial traction–separation relation. The measured load-displacement response (Fig. 11b) and normal CTOD (Fig. 11c) were captured very well by the model. Note that both the IR-COI measurements and the finite element analysis were able to resolve the normal crack opening displacements sufficiently well to capture the passage of the elastic and softening portions of the cohesive interaction (Fig. 9b also), whereas the current implementation of DIC (Fig. 4b) was not. The fracture resistance curves are compared in Fig. 11d. Here, based on the traction distribution along the interface, the crack extension \(\Delta a\) obtained from the finite element model was the distance between the initial crack tip and the new crack tip defined at the location where the traction was equal to the strength \(\sigma _{0}\), or where the damage zone (\(0<D<1)\) and the elastic interaction zone (\(D=0)\) met. This definition is consistent with the assumption that \(J_{0} =\Gamma _{1}\), which was used in Sect. 4 for parameter extraction. Moreover, the J-integral that was used for extraction of the parameters of the traction–separation relation was based on the beam on elastic foundation (BEF) model, Eq. 4. When this equation was used with the load-displacement response obtained from the finite element analysis, the obtained resistance curve agrees closely with the data plotted in Fig. 11d. However, the BEF model is an approximation and does not account for the part of the cohesive zone where damage is evolving. Nonetheless, the contribution of this region to the J-integral can be obtained from the finite element analysis and Eqs. 12 or 13, giving a more accurate J-integral. Note that it is not accessible from the experiments without direct measurements of the tractions and the shear component of CTOD. As shown in Fig. 11d, the BEF approximation correctly predicts the initiation and steady-state values of the J-integral (\(J_{0}\) and \(J_{ss}\)), but underestimates the J-integral for the resistance curve in between.

The stage is now set to determine the traction–separation relations for the same silicon epoxy interface at any mode-mix between 0 and \(-42^{\circ }\) using the measured steady state toughness \(\Gamma \left( \psi \right) \) (Figs. 5, 12) and the input parameters listed in Table 2. The analytical procedure is described and then validated with finite element analyses in comparison with the data obtained from the three ELS specimens that were not used for parameter extraction.

Fig. 12
figure 12

Mixed-mode fracture toughness for silicon/epoxy and glass/epoxy interfaces (Chai and Liechti 1992)

Full size image

For cases with mode-mix not provided in the tabulated input (Table 2), the parameters of the traction–separation relations can be obtained by interpolation. Let \(m_{1}^{A}\) and \(m_{1}^{B}\) be two adjacent energy ratios in the tabulated input. For an energy ratio \(m_{1}\) in between these two values (\(m_{1}^{A}<m_{1}<m_{1}^{B} )\), the corresponding effective critical separation, \({\hat{\delta }}=\left( {\delta _f -\delta _0 } \right) \), is obtained by linear interpolation between the input values for \(m_{1}^{A}\) and \(m_{1}^{B}\). As a result, the effective critical separation is predicted as a function of mode-mix as

$$\begin{aligned} {\hat{\delta }}(\psi )={\hat{\delta }}_{B} +\left( {\hat{\delta }}_{A} -{\hat{\delta }}_{B} \right) \frac{\left( {\cos \psi } \right) ^{2}-\left( {\cos \psi _{B} } \right) ^{2}}{\left( {\cos \psi _{A} } \right) ^{2}-\left( {\cos \psi _{B} } \right) ^{2}} \end{aligned}$$
(19)

for \(\psi _{A}>\psi >\psi _{B}\). Correspondingly, the fracture toughness as a function of the phase angle is: \(\Gamma (\psi )=\Gamma _{1} (\psi )+\Gamma _{2} (\psi )\), where

$$\begin{aligned} \Gamma _{1} (\psi )=\frac{1}{2K_{0}}\left( {\frac{\sigma _{n0} }{\cos \psi }} \right) ^{2} \end{aligned}$$
(20)

and

$$\begin{aligned} \Gamma _{2} (\psi )=\frac{\sigma _{n0} {\hat{\delta }}\left( \psi \right) }{\cos \psi }\left( {\frac{1}{\alpha }-\frac{1}{e^{\alpha }-1}} \right) , \end{aligned}$$
(21)

using the same values of \(K_{0}\), \(\sigma _{n0}\) and \(\alpha \). The results of this process are shown as the interpolated variation of the toughness with mode-mix between \(-42^{\circ }\) and \(0^{\circ }\) (Fig. 12). The phase angles of the three ELS specimens not used for parameter extraction were \(-31^{\circ }\), \(-35^{\circ }\) and \(-38^{\circ }\), respectively, and the measured fracture toughness values are in close agreement with the interpolated values. With this interpolation procedure implemented in the finite element model, the same input parameters, including the tabulated data (Table 2) and the values of \(K_{0}\), \(\sigma _{n0}\), and \(\sigma _{t0}\) can be used in the finite element analyses for other experimental configurations. The results are compared with the measurements in Fig. 13 for an ELS specimen whose epoxy thickness was \(23.3\, \upmu \hbox {m}\,\left( {\psi =-31^{\circ }} \right) \). The normal and shear components of the interpolated traction–separation relation are shown first (Fig. 13a). The corresponding vectorial traction–separation relation is compared with the tractions and separations that were obtained from the output of the finite element analysis, once again establishing internal consistency of the model. The computed load-displacement and normal CTODs (Fig. 13b, c) were in excellent agreement with measurements. The resistance curve (Fig. 13d) with the J-integral computed from the beam on elastic foundation model tracked its measured counterpart well. The J-integral computed using the local tractions and separations at the crack tip rose more quickly to steady state as before. Similar levels of agreement were achieved for the other two ELS specimens. Therefore, it appears that a robust model of mixed-mode fracture between silicon and epoxy has been developed for phase angles between \(-42^{\circ }\) and \(0^{\circ }\). All that would be needed to extend the reach of the model would be a toughness measurement at a mode-mix outside this range. Although measurements of normal crack tip opening displacements would provide further validation, they are not required for extending the model. However, the present model is likely to run into trouble for mode-mixes that are close to pure shear, where damage initiation may not be controlled by the normal tractions as assumed in the present study and the shear strength, \(\sigma _{t0}\), in Eq. 9 has to be determined more accurately.

Fig. 13
figure 13

Comparison of experimental and results for the ELS specimen with an epoxy thickness of \(23.3\, \upmu \hbox {m}\): a traction–separation relations; b load-displacement response; c normal CTOD versus applied displacement response; d fracture resistance curve

Full size image

Note that the trend in interfacial toughness was quite similar for the silicon/epoxy interface being considered here and the glass/epoxy considered by (Swadener and Liechti 1998). The epoxy was nominally the same, although subtle differences in formulation may have crept in over time. The mode I toughness of both interfaces was the same (Fig. 12). However, the increase in toughness with increasing shear was higher for the silicon/epoxy interface. It is not clear at this time what caused this difference. The loading paths in the two experiments were different; the path was proportional in the current experiment, whereas it was sequential (tension + shear) in (Swadener and Liechti 1998).

The final point to be made in this discussion relates to the scale of the bridging provided by this silicon/epoxy interface. The data (Fig. 10a) for \(\Delta a_{ss}\), which corresponds to the length of the cohesive zone as a function of mode-mix, was normalized (Fig. 10b) by the thickness of the silicon strips and compared with the normalized fracture length scale \(\bar{{l}}=\frac{\bar{{E}}\Gamma }{\sigma _{0}^{2} h_{Si} }\) (Parmigiani and Thouless 2007). When the strength \(\sigma _{0}\), which was independent of the mode-mix and was obtained from the parameter extraction exercise and the measured values of the toughness \(\Gamma \) (Figs. 5, 12) were used in the expression, the normalized fracture length scale ranged (Fig. 10b) from about 0.7 to 2.7, while the normalized cohesive zone lengths represented by \(\Delta a_{ss}\) ranged from 2 to 2.8. The difference can be attributed to the fact that the fracture length scale parameter \(\bar{{l}}\) is useful for general scaling arguments, whereas \(\Delta a_{ss}\) is specific to the case at hand. It has been shown (Parmigiani and Thouless 2007) that, when the ratio of shear toughness is ten times that associated with tensile fracture, small scale bridging can be achieved for \(\bar{{l}}\) values of O(1). From Fig. 12, we expect a much larger ratio of toughness values and small scale bridging to occur for one to two lower orders of \(\bar{{l}}\). This means that large scale bridging was indeed in effect for the silicon/epoxy interface being considered here. This may further explain the discrepancy between the phase angles obtained from DIC (Fig. 8) and the values obtained from the LEFM analyses. Nonetheless, even under large scale bridging, the phase angles obtained from the linearly elastic portion of the traction–separation relations do still make close reference to values obtained from LEFM analyses. This is not surprising based on the results presented in Fig. 9b of Parmigiani and Thouless (2007), but it does provide a convenient and common point of reference for phase angles obtained from the two approaches.

6 Conclusions

This work builds on a previous characterization of the traction–separation relations of a silicon/epoxy interface that was separated under nominally mode I conditions (Gowrishankar et al. 2012). In the present work, mixed-mode conditions were provided by an end-loaded-split (ELS) configuration, where the epoxy was sandwiched between two silicon strips. The mode-mix provided by the ELS configuration was varied by varying the thickness of the epoxy layer. A series of experiments were conducted under displacement control. The normal crack opening displacements in the interior of the specimen were measured by infra-red crack opening interferometry. In some experiments, digital image correlation was used to measure the crack-tip displacements in both the normal and tangential directions. Finite element models were developed that accounted for the elastic behavior of the silicon and epoxy and the interactions between them using a damage-based cohesive zone model. The key parameters for the traction–separation relations were extracted from the measured resistance curves and normal crack opening displacements along with finite element solutions for a range of values of the softening parameter.

For the range of mode-mix considered here (\(-42^{\circ }\) to \(0^{\circ }\)), it was noted that, although the steady state toughness was a function of the mode-mix, the elastic behavior, normal and shear strengths and the softening parameter were not. The mixed-mode traction–separation relations from this model were validated by comparing to the ELS experiments using epoxy thickness values and associated phase angles that were not used for parameter extraction. The load-displacement responses, normal crack tip opening displacements and resistance curves were all captured very well. Interestingly, resistance curves based on J-integral calculations that also accounted for the damaging portion of the traction–separation relations had a different shape between \(J_{0}\) and \(J_{ss}\) than those that were only based on the elastic foundation analyses. This is to be expected, although the measurement-based parameter extraction was, and can only be, founded on the latter, and the J-integral obtained locally from the path surrounding the cohesive zone provides the actual resistance curve for the silicon/epoxy interface.