Mode-II interlaminar fracture of composite materials in the presence of randomly distributed defects

Abstract

The focus of the present paper is on the mode-II (shear mode) interlaminar fracture of laminated composite materials with randomly distributed defects such as those generated due to the manufacturing process. The study is conducted using cohesive-zone Finite Element (FE) models of the Interlaminar Shear (ILS) and the End Notch Flexure (ENF) geometries with explicit inclusion of defects on a representative interlaminar plane. The effective interlaminar shear strength and the effective mode-II fracture energy are obtained by comparing the FE analysis with explicit defects against corresponding homogeneous models. Based on the parametric FE results it was found that the effective ILS strength and the mode-II fracture energy are significantly affected by the defects present on the critical interlaminar fracture plane, and when the defects are small, they follow a linear scaling with the defect area fraction. Simulations with various defect sizes reveal that for defects larger than the size of the delamination process-zone, the concept of the effective ILS strength and effective mode-II fracture energy is not valid, and defects must be represented explicitly in the models.

1 Introduction

Processing induced defects, inherent in most materials, usually lead to a reduction in the performance of such materials. This is especially true for heterogeneous composite materials such as polymer matrix composites (PMCs) and ceramic matrix composites (CMCs) where defects, which form at multiple length scales due to inherent heterogeneity of the microstructure, can significantly reduce the elastic, damage, and fracture response of the material.

The effects of defects on the mechanical behavior of Polymer Matrix Composites (PMCs) have been studied extensively (see Talreja 2020 for an overview). Briefly, Huang and Talreja (2005) and Tavaf et al. (2019) studied the effects of defects on the elastic properties of unidirectional PMCs, and Dong and Gong (2018) studied the damage behavior in the presence of defects. In contrast to PMC materials, the processing methods used for CMCs may generate a higher percentage of defects. The reduction in the elastic properties of CMCs due to defects has been studied by analytical and/or numerical micromechanics approaches by a number of researchers including Goldberg et al. (2012), Gowayed et al. (2013), Nagaraja and Gururaja (2020), and Kumar (2021b).

In structural applications both PMCs and CMCs are typically used in a laminated form making them susceptible to interlaminar failure mode. This failure mode is induced due to high interlaminar tension and/or interlaminar shear stresses. High interlaminar stresses are often caused by geometry (e.g., complex part curvature), internal or external discontinuity such as ply-drops, cut-outs and notches, and/or loading conditions (e.g., transverse static and impact loads). Due to the lack of fibers in the through-thickness direction in unidirectional and two-dimensional (2D) woven composites, these materials have lower interlaminar properties compared to the in-plane properties. For the current generation of Polymer Impregnation and Pyrolysis (PIP)-based CMCs the interlaminar strength and toughness are quite low (see Kumar and Welsh 2012; Kumar 2013) compared to typical aerospace grade PMCs. This difference is commonly attributed to the higher amount of defects and/or weak fiber interphase coatings necessary for damage tolerance in CMCs. Thus, understanding how the interlaminar properties of CMCs are affected by the defects is important for successful design and insertion of these materials in gas turbines and other high-temperature applications.

The impact of processing induced voids on the interlaminar strength of polymer matrix composites has been studied by Gurdal et al. (1991) and Nikishkov et al. (2014). Ricotta et al. (2008) studied how the mode-I Strain Energy Release Rate (SERR) in PMCs is affected by defects, Chadegani and Batra (2011) studied the effects of voids and disbonds on the SERR in an adhesively bonded single lap joint, and de Moura et al. (2006) simulated the propagation of a delamination crack in a single-lap adhesive joint with defects. However, these studies focused on simplified defect structures (single or few voids), and, with the notable exception of de Moura et al. (2006), did not consider the effects of defects on the delamination propagation. In a recent work (Kumar 2021a), we studied the effects of multiple defects on the ILT strength and the mode-I delamination propagation. The reader is referred to this work for a more detailed discussion of the current state-of-the-art.

The present paper builds upon our previous work (Kumar 2021a) on mode-I fracture, utilizing similar modeling strategy to study the impact of multiple randomly distributed defects on the mode-II interlaminar fracture. The mode-I interlaminar properties (ILT strength and mode-I fracture energy) of PMCs and CMCs are typically lower than the corresponding mode-II fracture properties (ILS strength and mode-II fracture energy). However, despite this characteristic, under many common loading scenarios, delaminations in laminated composite materials tend to propagate under mode-II or mixed-mode conditions as they are constrained to remain on well-defined weak planes between the plies. This behavior is different from that observed in isotropic materials where, under mode-II or mixed-mode loading condition, the crack turns in such a way that mode-I condition prevails at the crack tip. Therefore, for a complete characterization both the mode-I and mode-II behaviors must be studied. The objective of the present paper is to study the role of defects on the mode-II delamination fracture in composite materials in order to: (1) determine the reduction in the ILS strength and the mode-II fracture toughness of the material and (2) to determine under what conditions, if any, we can define and use an effective ILS strength and an effective mode-II fracture energy in structural models, thereby, avoiding explicit modeling of the defects in the structural models. Similar to our previous work (Kumar 2021a), we use computational fracture mechanics for analysis and demonstrate the results using the properties representative of a PIP derived CMC material. However, it should be noted that the results are of general applicability and should apply to the mode-II interlaminar fracture in PMCs and bonded joints. We also note that defects in CMCs occur at multiple length-scales. However, our focus in the present paper is on defects at the ply-thickness length-scale. Lower length-scale defects are assumed to be implicitly modeled via elastic properties of the plies determined using an appropriate micromechanics method (see Kumar 2021b for one such method). Furthermore, as the focus of the present work is on the interlaminar strength and delamination crack propagation, we assume that the effects of the defects are felt only via their intersection on the plane of the crack propagation. Thus, it is implicitly assumed that the 3D aspect of these defects is accounted for via the homogenized elastic properties of the plies.

The organization of the paper is as follows: the FE modeling approach is described in Sect. 2. The results from the Finite Element Analysis (FEA) and parametric simulations are discussed in detail in Sect. 3. Here we also outline the procedure for deriving the effective strength and fracture properties. The conclusions derived from this study are summarized in the final Sect. 4.

2 Numerical models

Similar to our previous work (Kumar 2021a), we use FE models wherein the defect structures are explicitly represented in an idealized manner. Cohesive-zone FEA is used to model the delamination crack initiation and propagation. Corresponding models without any defects are also analyzed for comparison. Further details regarding the cohesive model used in the present work, including the formulation details, loading–unloading behavior, and meaning of the damage parameters to be discussed later, can be found in the users and theory manuals of Abaqus FE code (Abaqus 2018).

The numerical models and simulation results presented in this paper use the material properties representative of a CMC material. However, the approach and main conclusions are expected to apply to any layered composite such as PMCs and CMCs. The material properties and the [0/90]_4s layup considered are same as that used in our previous work (Kumar 2021a), as listed in Table 1 for completeness. It should be noted that the cohesive parameters listed in Table 1 are assumed to correspond to the pristine (no defects) case even though we fully realize that the experimental data is obtained from specimens with certain level of defects. Thus, the absolute values of the ILS strength and fracture energy reported in Sect. 3 for various defect levels should be interpreted relative to the defect area fraction in the test specimens. As the experimental data is taken from our prior work where the defects were not fully characterized, the exact defect area fraction corresponding to the experimental data in Table 1 is not known. However, the typical range of the defect area fraction in these composites is from 10–20%.

Table 1 S200H CMC material properties used in the FEA (Kumar 2021a)

2.1 FE model of ILS strength configuration

The ILS strength of composite materials can be determined experimentally using two methods standardized by the ASTM. The first method, recommended for PMCs, is the Short Beam Shear (SBS) test using the ASTM D2344/D2344M-16 (2016). On the other hand, for CMC materials ASTM C1292-16 (2016) recommends a Double Notch Shear (DNS) test method. However, researchers have also used the SBS method to determine the ILS strength of CMCs. In fact, unpublished FE calculations by the present author have shown that the Double Notch Shear (DNS) can yield artificially lower shear strength due to the effect of stress singularity at the tip of the two notches. On the other hand, the SBS configuration does not suffer from that limitation, and hence, can yield acceptable shear strength, provided the mode of failure is indeed the interlaminar shear mode, and not, for example, a bending failure or failure due to the stress concentration at the loading roller.

Instead of modeling any of the experimental configurations commonly used, in the present work, we adopt an idealized model where a simple shear loading is applied to a cuboidal domain representing the CMC material, as shown schematically in Fig. 1. The dimensions of the simulation domain are 25.4 mm × 25.4 mm × 5.4 mm. The thickness of 5.4 mm corresponds to a nominal thickness of a 16-ply S200H CMC. Without any loss of generality, we model the interlaminar fracture at the mid-plane of the specimen, and hence, the defects are also explicitly represented only on this plane. We only consider the simulation of the ILS stress component $\sigma_{13}$, which is representative of both the $\sigma_{13}$ and $\sigma_{23}$ cases. The boundary conditions simulating simple shear loading is indicated in this figure: the bottom face is constrained in all the three directions while the top face is constrained in $y -$ and $z -$ directions and displacement is specified in the $x -$ direction.

Fig. 1

FE model of the ILS strength geometry

A three-dimensional (3D) FE model of the ILS setup is shown in Fig. 1. As the fracture is considered only on the mid-plane of the domain, cohesive elements are embedded there. The remainder of the domain is modeled with continuum (brick) elements. The mesh was designed in such a way that the cohesive elements shared their nodes with the adjacent continuum elements at the mid-plane. As the in-plane dimensions of the cohesive elements and the continuum elements are same, a highly refined mesh was used wherein the element size was equal to the ply thickness of 0.34 mm. As will be discussed later, this consideration also sets the minimum size of the defects that can be simulated. As will be shown in Sect. 3, convergent solutions are obtained with this level of mesh refinement. The material properties assigned to the solid elements as well as the fracture properties assigned to the cohesive elements are listed in Table 1. It should be noted that the cohesive strength of the traction–separation law is taken to be equal to the experimentally determined interlaminar strength listed in Table 1. In order to model the fracture behavior correctly, the initial stiffness of the traction–separation response was set to 6895 GPa in both the modes, consistent with the recommendations in Turon et al. (2007). Furthermore, we use a power law (power = 1.0) to model the mixed mode behavior. All the analyses were conducted using Abaqus implicit FE software (Abaqus 2018).

2.2 FE model for mode-II delamination growth

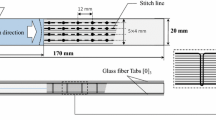
The propagation of the shear mode (or Mode-II) delamination in composite materials is characterized by the mode-II critical strain energy release rate or mode-II fracture energy. Experimentally this property is determined using an End Notch Flexure (ENF) test method using the procedure in ASTM standard D7905/7905 M (2019). Thus, we use a model of the ENF configuration to simulate mode-II delamination propagation with and without defects (Fig. 2). Similar to the ILS model we assume the delamination growth on a single plane spanning the pre-crack. In all the simulations, the specimen width (B) was taken to be 12.7 mm, which is typically used in the ENF experiments with CMC materials. Similarly, the beam span (L), the pre-crack length (a₀), and the beam thickness (h) used in the simulations are 101.6 mm, 25.4 mm, and 5.4 mm, respectively, typical of a 16-ply S200H CMC specimen. The support and the loading rollers are modeled as analytical rigid surfaces with a radius of 3.175 mm for both. All the degrees of freedom of the reference point associated with the support rollers are constrained. Similarly, all the degrees of freedom of the loading roller are constrained except for the $z -$ direction through which displacement is specified. We assume a frictionless contact interaction between the CMC beam and the rollers as well as between the crack faces as the effect of the friction on the delamination propagation is not expected to alter the conclusion.

Fig. 2

FE model of the ENF setup

The ENF specimen is modeled using 3D continuum elements with orthotropic elastic properties (see Table 1). The delamination initiation and growth are simulated using zero-thickness cohesive elements at the mid-plane. These cohesive elements share the nodes with the adjacent brick elements. The fracture properties assigned to the cohesive elements are same as that used for the ILS specimen (Table 1). Similar to the ILS geometry, a very fine uniform mesh with element size of 0.34 mm is used, which also dictates the lower bound of the defect size to be equal to the ply-thickness (see Sect. 2.1). As will be discussed in Sect. 3, a convergent solution is obtained with this level of mesh refinement.

2.3 Defect representation in the FE models

The approach for representing the defects in the FE models of the ILS and the ENF specimen is exactly the same as that discussed in Kumar (2021a) for the mode-I interlaminar fracture study. While the detailed discussion can be found in Kumar (2021a), we briefly summarize the approach for completeness. For the purposes of interlaminar fracture, we approximate the volumetric defects as 2D planar “disbonded” regions located on a single interlaminar plane, as shown in Fig. 3.

Fig. 3

Idealization of voids as planar defects on delamination propagation plane

As discussed in Kumar (2021a), defects on the delamination propagation or fracture plane are introduced by eliminating certain number of cohesive elements until a desired defect area fraction is achieved. Furthermore, a random process is used to decide which cohesive elements to remove. Clearly, this approach places a limit on the minimum defect size. However, no such limit is placed on the maximum size of the defects as removal of adjacent cohesive elements would lead to a larger defect size. Some representative defect structures generated using this procedure are shown in Fig. 4. It is interesting to note that this approach can generate realistic and complex defect structures (see, for example, Gowayed (2013) and Santhosh (2018) for representative defect structures in CMCs).

Fig. 4

Representative defect structures in a ILS and b ENF configurations

3 Results and discussion

The FE analysis of the ILS and the ENF configurations, with and without defects were conducted using the Abaqus implicit FE software (Abaqus 2018). The simulation results are discussed in the following.

3.1 Interlaminar shear strength

Analysis of the ILS strength configuration was conducted with various defect area fraction ranging from 10 to 80%. It should be noted that a typical range of defect area fraction in CMCs is 10–20%. Here a wider range of defect area fraction is considered to determine if percolation of defects at higher area fraction leads to a sudden drop in the strength. As the defects are generated randomly, we consider three realizations of defect structures for each defect area fraction case. Furthermore, we also simulate the case with no defects for comparison purposes.

From the simulations, the average interlaminar shear stress ($\overline{{\sigma_{13} }}$) vs. the applied displacement ($u_{1}$) plots are obtained. The average shear stress is obtained by dividing the total nodal reaction force in the x-direction from all the constrained nodes on the bottom ($z = 0$) plane of the model by the total area of the interlaminar fracture plane ($L^{2}$), see Fig. 1. The results are summarized in Fig. 5 where the responses with and without the defects are shown.

Fig. 5

Overall response of the ILS configuration with and without defects (A_f represents the defect area fraction)

In all the cases, the overall shear stress increases linearly until a peak is reached followed by a sudden reduction in the stress indicating a complete failure. In the models with defects a small nonlinearity is visible immediately before the peak stress, and furthermore, this nonlinearity is more pronounced when defects with higher area fraction are present. The effective ILS strength can be inferred from Fig. 5 as the peak interlaminar shear stress. It may be noted that for the defect-free case, the peak stress of 41.0 MPa (5958 psi) is ~ 7% lower than the ILS strength of 44.1 MPa (6400 psi) specified for the cohesive elements. This slight under-prediction, likely to be due to the free edge effects, does not affect the conclusion drawn in this work as the models with defects will also have the same effect, and furthermore, our interest is only in the relative difference in the ILS strength. It is also evident from Fig. 5 that the ILS strength reduces with the defect area fraction. Furthermore, the variation of the ILS strength with the area fraction of defects (Fig. 6) shows an approximately linear reduction in the strength. This linear scaling of the ILS strength ($S_{ILS}$) can be described by

$$ S_{ILS} = S_{ILS}^{0} \left( {1 - A_{f}^{d} } \right) $$

(1)

where $S_{ILS}^{0}$ is the ILS strength with no defects and $A_{f}^{d}$ is the area fraction of the defects intersecting with the fracture plane.

Fig. 6

Normalized ILS strength ($S_{ILS} /S_{ILS}^{0}$) from FEA for various defect area fraction [R1, R2, R3 indicate different realizations and linear-scaling refer to Eq. (1)]

While the FE models predict a slightly lower strength compared to the linear scaling, the difference is very small. Thus, the linear relationship of Eq. (1) can be considered as a good approximation. This observation is consistent with the linear reduction of the ILT strength with the defect area fraction presented in Kumar (2021a). As with the ILT strength (see Kumar 2021a) percolation of defects on the fracture plane does not lead to catastrophic drop in the ILS strength. It may also be noted from Fig. 6 that the scatter in the ILS strength between different realizations of the defect structures is very small.

In order to gain further insight into the interlaminar shear failure process, we examine the spatial variation of the interlaminar stress ($\sigma_{13}$) in Fig. 7. Here the contours of the interlaminar shear stress are shown in the cohesive elements corresponding to various points on the loading path (as shown in Fig. 5) for one specific simulation case (defect area fraction, ${\text{A}}_{{\text{f}}}^{{\text{d}}}$ = 0.2). It is clear that the interlaminar shear stress concentration develops in the vicinity of the defects very early in the loading process (stage (b) in Fig. 5 and Fig. 7). With further increase in the overall applied load the high stress region continues to increase in size (stages (c) through (e)). Finally, at the critical peak stress/load almost the entire fracture plane reaches the specified interlaminar shear strength for the cohesive elements. Beyond this point all the cohesive elements on the fracture plane fails suddenly, leading to a sudden drop of the average interlaminar stress from the maximum to zero. Thus, a gradual propagation and coalescence of few cracks from certain defects is not seen. This behavior may explain the linear reduction of the ILS strength with the defect area (or the remaining intact area) on the interlaminar fracture plane (Eq. 1). It should be noted that the nature of the failure at the critical fracture plane (instantaneous vs. gradual) may depend on the choice of the cohesive parameters. As discussed in the foregoing, in the present case of S200H CMC material, the cohesive parameters are such that an instantaneous interlaminar failure occurs under the ILS loading. Furthermore, this behavior is qualitatively similar to that observed in the mode-I ILT fracture studied in Kumar (2021a).

Fig. 7

Interlaminar shear stress ($\sigma_{13}$) in the cohesive elements for ILS geometry ($A_{f}^{d} = 0.2$) and labels (a)–(f) correspond to those in Fig. 5)

Similar to what was noted for the ILT strength variation with the defect area fraction in Kumar (2021a), the present result is also of practical importance. The ILS strength of specimens with defects can be estimated using the linear relationship of Eq. (1) in conjunction with an experimental determination of defect area fraction using, for example, X-ray CT-scan. In such an approach, the critical ply interface can be considered as the one with the highest defect area fraction.

3.2 Mode-II delamination propagation

The overall behavior of the ENF specimen can be gleaned from the force vs. displacement plot, where the force and the displacement correspond to the reaction force and the applied displacement, respectively, of the central loading roller. The force–displacement response of the ENF configuration with no defects is shown in Fig. 8. The FEA results are presented for two mesh sizes: a baseline mesh (Mesh 1) with an element size of 0.34 mm and a refined mesh (Mesh 2) with an element size of 0.17 mm. It is seen that the responses from the two meshes are very close, and hence, the baseline mesh is considered to give a converged solution. The force–displacement response, as obtained from the FEA, shows that the force increases linearly before reaching a maximum. After reaching the peak value, the load drops precipitously, reaches a local minimum point, and then increases again. From the simulation it is noted that the crack propagation starts at the peak load, grows suddenly to a certain length during the descending part of the load–displacement curve, followed by a gradual growth during which the load increases again. The slow-down of the delamination crack and the corresponding rise in the load is associated with the interaction of the delamination crack front with the compressive stress field of the central loading roller.

Fig. 8

Force–displacement curve of the ENF specimen without defects (Mesh 1—element size 0.34 mm; Mesh 2—element size 0.17 mm)

The response from the FEA can be compared against an analytical LEFM theory. This theory applied to the ENF geometry (Hashemi et al. 1990) gives the loading point displacement ($\delta$) and the corresponding force ($P$) during the delamination propagation via two parametric equations:

$$ G_{IIc} = \frac{{9P^{2} a^{2} }}{{16B^{2} E_{11} h^{3} }} $$

(2)

$$ \frac{\delta }{P} = \frac{{\left( {3a^{3} + 2L^{3} } \right)}}{{8Bh^{3} E_{11} }} $$

(3)

where $a$ is the crack length, $B$ is the specimen width, $G_{IIc}$ is the mode-II fracture energy, $E_{11}$ is the elastic modulus of the material, $L$ is the half span, and $h$ is the half thickness of the ENF specimen. The peak force ($P_{0}$) and corresponding displacement ($\delta_{0}$) can also be calculated using Eqs. (2) and (3) by using the pre-crack length ($a_{0}$). The response predicted from the FEA is compared against the analytical LEFM solution in Fig. 8. It is seen that the initial linear behavior and the peak load (associated with the onset of the delamination) from the two models agree well; small nonlinearity in the FEA is due to the development of the process-zone in the cohesive FE model. The analytical LEFM model also shows a sudden decrease in the force once the delamination starts to propagate in qualitative agreement with the FEA results. However, the curves differ in the decreasing portion of the load. In fact, the analytical LEFM shows a snap-back behavior with the displacement decreasing along with the load drop during the initial propagation phase. Clearly the FEA does not capture this snap-back behavior. In addition, the nature of the curve during the unstable propagation of the crack in the FEA model is also likely to be dependent on a small amount of damage stabilization used. We also note that the analytical LEFM model used in the present work cannot predict the load increase due to the interaction of the delamination crack with the loading roller, whereas that behavior is naturally captured in the FE model.

In any case, despite the differences between the overall load–displacement curves between the FE and the analytical models, there is an excellent agreement in the predicted peak load. Furthermore, as this peak load correspond to the onset of the delamination growth characterized by the mode-II fracture energy $G_{IIc}$, it can be used for comparing the FE models with defects against an equivalent homogenized analytical LEFM model, as will be discussed later.

We now consider the propagation of the mode-II delamination in the presence of the defects. For this study we take the specimen with the defect area fraction of 0.2 and generate three realizations of the defect structures, all with an element size of 0.34 mm, labeled as Mesh 1. The obtained force–displacement responses are plotted in Fig. 9. Also shown in this figure is the response with a refined mesh (Mesh 2; element length 0.17 mm). It is seen that the force–displacement response with defects is qualitatively similar to that without the defects (as seen in Fig. 8). The maximum force predicted by the finer mesh is slightly lower than that predicted by the baseline mesh; however, as the computational cost associated with the fine mesh is quite high, all the remaining simulations used the baseline Mesh 1 with element size of 0.34 mm. As all the defect cases will use the same baseline mesh, the slight over-prediction of the peak load compared to the refined mesh will not change the overall conclusion.

Fig. 9

Load–displacement curve of the ENF specimen ($A_{f}^{d} = 0.2$)

In order to quantify the effects of various defect area fractions on the delamination growth, a number of parametric simulations of the ENF specimen were conducted. As was noted for the ILS specimen (see Sect. 3.1), the defect area fraction was varied in the range 10% to 80%. Again, three realizations were considered for most cases; however, only a single realization was considered for higher defect area fraction cases to save on computational costs. The predicted load–displacement responses are shown in Fig. 10.

Fig. 10

Effect of defect area fraction on the load–displacement curves of the ENF specimen

It is observed that for all the cases the response is linear (with slight nonlinearity before the peak load) up to the maximum load. Thereafter, a sudden decrease in load occurs because of an unstable delamination growth. Once the delamination slows down due to the compressive stress field associated with the central loading roller, the force begins to increase again. It is also seen that the post-peak responses from different realizations are slightly different due to the variation in the defect structures amongst them. It is also interesting to note that, in contrast to the mode-I behavior discussed in Kumar (2021a), almost no local oscillations in the force–displacement response are seen. It was argued in Kumar (2021a) that the oscillatory response was due to the interaction of the mode-I delamination crack front with the defect structures. Clearly, the mode-II delamination crack in the ENF specimen also interacts with the distributed defects as it propagates. However, the absence of the small perturbations in the force–displacement response during the mode-II delamination growth in the ENF specimen is likely due to the unstable growth. Additionally, the lack of the oscillation during the post-peak load increase can be attributed to the strong effect of through-thickness compressive stress field induced by the central loading roller. As a final remark, we note that peak force decreases monotonically with the defect area fraction.

We now examine the propagation of the delamination front on the critical fracture plane where the defects are located. In Fig. 11 we depict various stages of the delamination propagation for one realization of the ENF specimen where the defect area fraction was 0.2. In this figure the crack front and the fracture process zone are identified via the cohesive damage parameter which ranges from 0.0 to 1.0, with a value of 1.0 leading to the deletion of the cohesive element and formation of a traction-free crack. The labels (a) – (h) indicated in Fig. 11 correspond to the points shown on the load–displacement curve in Fig. 9. It is seen that right up to the maximum load (stage (c)) there is no delamination growth from the pre-crack front. However, during this pre-peak regime, the cohesive elements ahead of the pre-crack develop some damage (i.e., softening) and the length of this process-zone increases from stage (b) to stage (c). The mild nonlinearity in the force–displacement response from stage (b) to (c) in Fig. 9 is due to the formation and increase of this damage zone. The onset of the delamination propagation occurs at stage (d) and continues while the force decreases (stages (d)–(f)). Note also that the growth of the delamination from stage (d) to (f) is rather sudden with a sharp drop in the load. Also note from Fig. 11 that at stage (f), which is very close to the minimum load point (see Fig. 9), the delamination front as well as its process zone are very close to the central loading roller. Further increase in the delamination length and the corresponding load increase (stages (f) – (h)) is associated with some interaction with the compressive stress field of the central loading roller. In fact, as seen in stage (h) of Fig. 11, the main delamination crack is arrested by the loading roller, and a new delamination crack has formed on the other side of the loading roller. Finally, we note that the overall delamination growth behavior with the defects is similar to that of the ENF specimen without any defects, the only difference is that the delamination crack front is jagged when the defects are present.

Fig. 11

Sequence of mode-II delamination propagation in the ENF specimen (Realization 1 with $A_{f}^{d} = 0.2$); cohesive damage parameter shown corresponding to the labels shown in Fig. 9

Similar to the mode-I delamination growth problem discussed in Kumar (2021a), we are interested in defining an effective mode-II fracture energy that can implicitly account for the effects of small manufacturing induced distributed defects. Following the same approach as in Kumar (2021a), we derive the effective mode-II fracture energy by matching the force–displacement response obtained from the FEA analysis of the ENF configuration with explicit defect structure against a corresponding homogeneous analytical LEFM model. Furthermore, as discussed earlier, due to the unstable nature of the delamination growth, we only compare the peak load, which, as we have seen, corresponds to the onset of the delamination growth. Thus, using the analytical LEFM model (Eqs. 2–3), we vary the fracture energy $G_{IIc}$ (all the remaining parameters including the pre-crack length are known from the geometry of the ENF specimen) to obtain a best-fit to the maximum force obtained from the FEA with explicit defects. The value of the $G_{IIc}$ that gives the best agreement of the peak force with the FEA results is taken as the effective mode-II fracture energy, $G_{IIc}^{eff}$, for that defect area fraction. All the results from this procedure are summarized in Fig. 12. The solid lines in this figure are the best fit analytical LEFM solution corresponding to the defect case modeled explicitly within FEA. The results show that a unique $G_{IIc}^{eff}$ can be defined, and it captures the effect of distributed defects on the mode-II fracture energy. Of course, the analytical model used here is unable to capture the response after the peak load due to the instability of the delamination growth and its further interaction with the loading roller, as discussed earlier. It may be noted that instead of using the analytical LEFM solution, one can compare the simulation results against an equivalent homogenized FE model to derive the effective $G_{IIc}$, albeit at a significantly more computational expense. As an illustration, such homogenized cohesive FE simulations were conducted for the defect area fraction of 0.2 and 0.4 using the effective $G_{IIc}$ obtained from the analytical LEFM (here it should be noted that mode-II cohesive strength is also scaled as per Eq. (1), and furthermore, both the mode-I cohesive strength and the mode-I fracture energy $G_{Ic}$ were similarly scaled, based on the conclusion reached in Kumar 2021a). The result from these simulations are also shown in Fig. 12, where it is seen that the cohesive-zone FEA with an effective mode-II fracture energy $G_{IIc}^{eff}$ is able to better match the entire load–displacement response of the FE models where defects are explicitly modeled. Of course, the homogeneous FE models can be further calibrated, as needed, to better match the results from the FEA models with defects. One may also note from Fig. 12 that larger defect area fraction leads to an increased nonlinearity in the force–displacement response prior to the peak load.

Fig. 12

Calculating effective G_IIc by comparing FEA results with explicit defects and analytical LEFM solution; results from homogenized cohesive FEA models with $A_{f}^{d}$ of 0.2 and 0.4 are also shown

The effective mode-II fracture energy, $G_{IIc}^{eff}$, derived using the procedure discussed above is summarized in Fig. 13. This plot shows that the effective mode-II fracture energy reduces in a more-or-less linear manner with the defect area fraction. Thus, similar to the ILS strength, $G_{IIc}^{eff}$ scales linearly with the intact area on the fracture plane. This scaling can be described by:

$$ G_{IIc}^{eff} = G_{IIc}^{0} \left( {1 - A_{f}^{d} } \right) $$

(4)

Fig. 13

Reduction in the normalized effective mode-II fracture energy ($G_{IIc}^{eff} /G_{IIc}^{0}$) with the area fraction of defects

In Fig. 13, this equation is plotted as a dashed line. It is seen that the linear scaling is able to capture the overall trend well. However, for larger defect area fraction the FEA results yield slightly lower value of the $G_{IIc}^{eff}$ compared to that obtained from the linear scaling relationship of Eq. (4).

The result that the $G_{IIc}^{eff}$ decreases linearly with the area fraction of defects is consistent with the mode-I delamination case reported in Kumar (2021a). The mode-II delamination crack front locally interacts with the same net area (total area minus defect area) of the interlaminar plane due to the uniformly distributed nature of the defect structure considered. Thus, on average the mode-II fracture energy scales with the intact area fraction ($1 - A_{f}^{d}$).

3.3 Effects of defect size

So far, we have not considered the effect of defect size explicitly. Recall from Sect. 2 that the defects were generated in such a manner that their minimum size was fixed by the underlying FE mesh (element size = 0.34 mm), but the maximum size was not specified. Thus, while coalescence of the individual defects led to an increase in the defect size, especially for higher defect area fractions, there was no control over the maximum defect size. We now turn our attention to a systematic study of the effects of defect size keeping the defect area fraction constant.

3.3.1 ILS strength

First, we study the effects of the defect size on the ILS strength. For this study we fix the area fraction of defects at 20% and vary the defect size (length of a square shaped defect). In addition to the defect size of 0.34 mm considered previously, we consider three additional sizes: 1.0 mm, 1.68 mm, and 4.36 mm. Note that while each individual defect is of square shape, a complex defect structure emerges due to the intersection of various defects (see Fig. 14). It should be noted that due to the sequential nature of the defect generation algorithm discussed in Sect. 2.3, it is not always possible to achieve the exact specified defect area fraction. In the ILS models, the average defect area fraction achieved was 0.181, 0.179, and 0.162 corresponding to the defect size of 1.0 mm, 1.68 mm, and 4.36 mm, respectively. Using the same procedure as discussed in Sect. 3.1, the mode-II fracture of the ILS geometry was simulated, and the corresponding ILS strength was derived from the peak load–displacement curves. These results are presented in Fig. 14 along with the associated defect geometry for one realization associated with each defect size. The average ILS strength from the three realizations is taken as the ensemble average. This figure also shows the ILS strength if it follows the linear scaling as specified by Eq. (1). Here it is important to note that the line specified by Eq. (1) is not horizontal (i.e., with a zero slope) as an exact defect area fraction of 0.2 is not realized in the simulations, but it decreases slightly with the defect size. In any case, it is clear from Fig. 14 that the ILS strength is sensitive to the size of the defect. Specifically, the ILS strength decreases with the size of the defect even when the area fraction of the defect is constant. Thus, larger defects are more detrimental to the ILS strength. This result is different from the conclusion reached in Kumar (2021a) where it was shown that the ILT strength was insensitive to the defect size. Furthermore, it is seen that the area-fraction-based scaling model is not accurate in predicting the ILS strength, especially for larger defect size. Specifically, the difference between the area fraction-based scaling and the ensemble average ILS strength from the explicit models is 3%, 6%, 7%, and 20% for 0.34 mm, 1.0 mm, 1.68 mm, and 4.36 mm defect sizes, respectively. It is also interesting on note that there is a considerable scatter in the predicted ILS strength for the largest defect size, while the scatter is significantly less for the three smaller defect sizes. Thus, depending on the desired accuracy (typically 10%), we can still model defects with size up to 1.68 mm using the effective strength model. On the other hand, larger defects would require an explicit representation in the structural models as the effective strength is unable to describe the ILS strength accurately.

Fig. 14

Variation of the ILS strength with defect size ($A_{f}^{d} \sim 0.2$)

In order to understand the reason for the size effect on the ILS strength, we examine the evolution of the delamination growth on the fracture plane of the ILS configuration. Figure 15 presents the contours of the cohesive damage parameter for one of the realizations of the ILS specimens with different defect sizes. Recall that the cohesive damage of 1.0 implies that the element has failed completely and is removed from the mesh. The top row in the figure shows the cohesive damage state at the peak applied load/stress, whereas the bottom row shows the damage state during the descending portion of the stress-displacement response. It is clear that the size and the distribution of the defects lead to differences in the pattern and distribution of the cohesive damage parameter. It is also seen that high cohesive damage region occurs in the regions where there are defect clusters. The propagation of the delamination proceeds from these higher damage region as shown by the second row. It is clear that the distribution of the cohesive damage becomes more non-uniform with an increase in the defect size. This non-uniformity leads to the differences in the critical load at which the catastrophic mode-II failure ensues, leading to an increased scatter as well as the size effect in the ILS strength as observed in Fig. 14.

Fig. 15

Nature of delamination evolution on the fracture plane of the ILS configuration with defects of various sizes ($A_{f}^{d} \sim 0.2$)

3.3.2 Mode-II delamination propagation

We now examine the defect size effect on the mode-II delamination propagation. The models of the mode-II delamination propagation discussed in Sect. 3.2 considered many distributed small defects. Furthermore, for smaller defect area fraction these defects are located farther apart without much overlap. We now study the effect of defect size keeping the defect area fraction constant. Our primary objective here is to determine whether the effective mode-II fracture energy is still a valid concept for larger defect size.

In order to conduct this study, we use a fixed defect area fraction of ${\text{A}}_{{\text{f}}}^{{\text{d}}} \sim 0.2$ and generate defects of various minimum sizes using a constrained version of the approach discussed Sect. 2.3. We consider four minimum defect sizes ($l_{d}$) of 0.34 mm, 1.0 mm, 1.67 mm, and 4.36 mm in the ENF configuration, as shown in the inset of Fig. 16. The force–displacement responses from the simulations are shown in Fig. 16 as well. It should be noted that for each defect size, two realizations (R1 and R2) of the defect structures were considered. For comparison, the response from the analytical LEFM model with the effective mode-II fracture toughness ($G_{IIc}^{eff}$) determined earlier for this defect area fraction case (see Fig. 12) is also shown.

Fig. 16

Load–displacement behavior of the ENF specimen ($A_{f}^{d} \sim 0.2$) with various sizes of defects

An interesting range of behavior is seen in the load–displacement response with various defect size. First, we note that for the defect size of 0.34 mm, 1.0 mm, and 1.68 mm the two realizations give fairly close responses. On the other hand, for the largest defect size of 4.36 mm, the force–displacement response displays a significant scatter in the peak force as well as in the overall shape of the curves. With the larger defect size, the number of defects generated on the fracture plane is small, and hence, the location of the defect structure with respect to the pre-crack front can be significantly different from one realization to another, thereby leading to a significantly different response for the two cases. Comparing the peak force, it appears that for the three smaller defect sizes, the peak load increases with the defect size. This counterintuitive behavior is likely to be due to the details of the defect structure in the process-zone of the pre-crack at the peak load. In any case, it should be noted that the difference in the peak force is small: the average peak force for 0.34 mm, 1.0 mm, and 1.68 mm defect sizes are, respectively, 436 N, 442 N and 459 N, a variation of ~ 5%. In addition, we note that the peak forces are within ~  ± 3% of the peak force predicted by the best fit analytical LEFM model. Thus, the effective mode-II fracture energy determined earlier (for the case with ${\text{A}}_{{\text{f}}}^{{\text{d}}} = 0.2$) can still be considered as a good approximation for the defect size of 1.0 mm and 1.68 mm. While the peak force predicted by the analytical LEFM model also seems to be close to the average peak force for the defect size of 4.36 mm, this outcome is fortuitous. For the largest defect size of 4.36 mm, the scatter in the peak force is quite large and the shape of the post-peak response of the two realizations are significantly different. The reason for the different behavior is, of course, the local defect structure close to the pre-crack. As seen from the inset in Fig. 16, which shows the defect structure for realization R1, a large defect intersects the pre crack front. On the other hand, it was verified that for the realization R2 of the same defect size, there was no intersection of any defect with the pre-crack front. This explains why realization R2 gives a higher peak force compared to realization R1. All these observations suggest that, for a large defect size, it may not be appropriate to model the delamination propagation behavior using the effective mode-II fracture energy.

We now examine the delamination propagation behavior as it traverses through the defects. This is shown in Fig. 17 where the cohesive damage parameter is plotted for two stages: (1) at the maximum load which corresponds to the onset of the propagation and (2) a state after some arbitrary amount of delamination propagation. This figure also shows the location of the pre-crack and the process zone of the delamination, which is determined by the cohesive elements with non-zero damage parameter.

Fig. 17

Evolution of mode-II delamination process zone in models with defects of various sizes ($A_{f}^{d} \sim 0.2$)

It is observed that the delamination front is more jagged when the defect size is larger. In fact, there is a considerable variation in the delamination length along the width of the specimen for the largest defect case due to the preferential location of all the defects on one edge of the specimen. Furthermore, it is seen that there are significantly lesser number of defects spanning the process zone of the delamination for the larger defect size. In fact, the size of the delamination process-zone is much smaller than the defect size for the largest defect case. This observation along with the previous result that the force–displacement response for the largest defect case cannot be adequately described by an effective mode-II fracture energy, $G_{IIc}^{eff}$, suggests that the ratio of the defect size and the fracture process-zone size must be considered. Thus, consistent with the work on mode-I delamination (Kumar 2021a), a practical guideline is as follows: if the defect size is greater than the size of the delamination process-zone, it is not appropriate to approximate them via a homogeneous effective fracture energy, and hence, they must be explicitly modeled. On the other hand, explicit modeling of defects is not necessary, and a homogeneous model with an effective mode-II fracture energy is appropriate, when the size of the defects is smaller than the delamination process zone size.

4 Conclusions

In the present paper we studied the mode-II interlaminar fracture of laminated composites in the presence of randomly distributed defects on the interlaminar fracture plane. The study was conducted using cohesive-zone FE models with defects modeled explicitly. Without any loss of generality, the 3D defects were idealized as planar 2D disbonds on the fracture plane. These disbonds or defects were generated by randomly eliminating cohesive elements from the mesh until a specific level of defect area is achieved.

From the FEA results of the ILS configuration it was found the interlaminar shear stress was amplified in the vicinity of the defects. However, this stress concentration did not result in a gradual onset and propagation of the fracture, which is consistent with what has been observed for mode-I fracture by Needleman (1990) and Kumar (2021a). As a result of this behavior the ILS strength was found to depend linearly on the intact (or equivalently the defect) area fraction on the critical interlaminar plane. A study of the effect of the defect size (for a fixed defect area fraction) revealed that the concept of the effective ILS strength is applicable for small defect sizes (up to 1.68 mm for defect area fraction of 0.2); however, it breaks down for larger defect sizes. Thus, large defects must be modeled explicitly rather than represented via an effective ILS strength property.

The mode-II delamination propagation behavior, studied using the ENF geometry, showed that defects can reduce the peak load corresponding to the onset of the delamination growth. Furthermore, it was shown that the onset of mode-II delamination growth in the presence of defects can be described using an effective mode-II fracture energy. This effective mode-II fracture energy was calculated by matching the response from the FEA where the defects are explicitly resolved with an equivalent homogeneous model, which can either be an analytical or numerical fracture model such as cohesive-zone models. Consistent with the mode-I behavior reported in Kumar (2021a), it was shown that when the defect size is small the effective mode-II fracture energy reduces linearly with the area fraction of the defects, though slightly more scatter was noted compared to the mode-I behavior in Kumar (2021a). Simulations of the ENF configuration with varying defect sizes at a fixed defect area fraction showed that that larger defects lead to a more jagged delamination front as well as increased oscillation in the force response in the post-peak regime. It was shown that defect size smaller than the delamination process zone size can still be homogenized and modeled via an effective mode-II fracture energy. On the other hand, when the defect size was greater than the size of the delamination process zone, the force–displacement response, including the peak force, showed a considerable scatter making the concept of effective mode-II fracture energy invalid.

The present paper quantifies the sensitivity of the mode-II interlaminar strength and fracture energy due to the distributed defects. In critical load-bearing applications, the effects of defects must be carefully accounted for in structural models. In this regard, based on the approach and results provided in this paper, appropriate decisions can be made whether to treat the effects of the defects in a homogenized manner or to model them explicitly.