Abstract
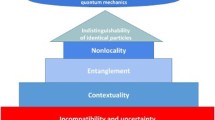
We present an information-theoretic interpretation of quantum formalism based on a Bayesian framework and devoid of any extra axiom or principle. Quantum information is construed as a technique for analyzing a logical system subject to classical constraints, based on a question-and-answer procedure. The problem is posed from a particular batch of queries while the constraints are represented by the truth table of a set of Boolean functions. The Bayesian inference technique consists in assigning a probability distribution within a real-valued probability space to the joint set of queries in order to satisfy the constraints. The initial query batch is not unique and alternative batches can be considered at will. They are enabled mechanically from the initial batch, quite simply by transcribing the probability space into an auxiliary Hilbert space. It turns out that this sole procedure leads to exactly rediscover the standard quantum information theory and thus provides an information-theoretic rationale to its technical rules. In this framework, the great challenges of quantum mechanics become simple platitudes: Why is the theory probabilistic? Why is the theory linear? Where does the Hilbert space come from? In addition, most of the paradoxes, such as uncertainty principle, entanglement, contextuality, nonsignaling correlation, measurement problem, etc., become straightforward features. In the end, our major conclusion is that quantum information is nothing but classical information processed by a mature form of Bayesian inference technique and, as such, consubstantial with Aristotelian logic.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Basically, data are stored in a definite register, but in 1948 Shannon [1] construed a sequence of symbols as a stochastic process, giving rise to information theory. He thus joined the core concepts of thermodynamics, revealed by the pioneering work of Lèo Szilard on Maxwell’s demon dating back to 1929 [2, 3], opening a new horizon sometimes viewed as the ultimate explanatory principle in physics [4, 5]. Nowadays, classical information theory focuses essentially on uncertain discrete variables. In 1957, Jaynes incorporated the Shannon’s concept of entropy in the Bayesian inference theory [6]. Later, contemplating quantum mechanical formalism, Jaynes noted in 1989 [7] that this formalism is strongly reminiscent of the Bayesian model. C. Rovelli considered in 1996 a reformulation of quantum mechanics in terms of information theory [8]. More explicitly, Caves et al. [9] proposed in 2002 in a seminal paper especially endorsed by Mermin [10], to understand quantum probability within a Bayesian framework. Fuchs coined the term “QBism” [11] for “Quantum Bayesianism” to describe this view.
1.1 Motivation
In this paper, we propose an explicit framework to implement the concept of “QBism”. We start from a logical system subject to logical constraints and regard calculation as a Bayesian estimation [12] of the variables involved. This means applying probability theory as an alternative tool to solve the problem, although the uncertainty about the solution sought has nothing to do with that of a conventional random issue. This nevertheless works because standard probability laws are just the extension of Aristotelian logic rules to cases where the variables are uncertain, as pointed out by Cox [13] and Jaynes [6]. Technically, this implies taking probabilities for the very unknowns of the problem instead of the variables themselves and next equating the calculation to a problem of inference.
Let us start with an informal draft of the model.
1.2 Quantum Information in a Nutshell
We consider quantum information as a technique for analyzing a logical system under constraints, represented by the truth table of a set of Boolean functions. As a result, the system behaves like a memory containing a maximum of (say) N bits of information. The issue is to extract this information. The classic solution would be to consider once and for all the relevant Boolean variables and to use a discrete algorithm to find their truth values.
By contrast, we consider the memory as whole and address all possible binary queries, introducing a question-and-answer procedure. The problem remains nevertheless initially posed from a particular batch of N dichotomous queries and therefore represented by a particular batch of N Boolean variables. Technically, they display a set, say \(\Omega\), of \(2 ^ N\) distinct classical states, \(\omega\). These classical states span a real-valued probability space, say \({\mathcal {P}}\), of dimension \(2 ^ N\) as
The Bayesian inference technique consists in estimating the probability \(\mathbb {P}(\omega )\) of the classical states to be valid, given the constraints regarded as prior information. This is achieved very simply, roughly by assigning a probability 1 to the Boolean constraints required to be valid and a probability 0 to the Boolean constraints required to be invalid. Then, we can calculate the probability \(\mathbb {P} (\omega )\) of the classical states \(\omega\) by solving a linear system in the probability space \({\mathcal {P}}\). As a result, the Bayesian expectation of any Boolean function and more generally of any linear combination of classical states, called observable, are immediately computed as a linear combination of classical state probabilities.
Even if we start from a particular batch of queries, this initial batch is by no means the only one and other batches can be addressed at will. They are necessary anyway to exhaust the set of all relevant observables because each particular observable calls for a specific batch of queries.
A major novelty of the model is that every new query batch can be enabled from the initial batch quite simply, by introducing an auxiliary Hilbert space, say \({\mathcal {H}}\), as
and then, transcribing the initial probability space \({\mathcal {P}}\) into \({\mathcal {H}}\). It turns out that each new basis in \({\mathcal {H}}\) defines by reverse transcription a new query batch in a new probability space \({\mathcal {P}}'\). Thus, it is easy to enable any query batch, merely by changing the basis in \(\mathcal {H}\).
For convenience, the memory is called Bayesian theater while the set of constraints is called Bayesian prior. In addition, a batch of N dichotomous queries is called an observation window and especially, the initial batch is called the source window. When the queries are independent, the window is called “principal”. Otherwise, the window is said to be “twisted”.
This construction completely rediscovers standard quantum information theory while completely ignoring this theory (with the exception of terminology, kept for clarity).
1.3 Main New Results
Listed below are the main new insights provided by the model in both quantum information and Bayesian inference theories. Some of these are very surprising because they are at odds with current beliefs.
1.3.1 Nature of Quantum Information
The major point is that quantum information is nothing but classical information processed by an elaborate Bayesian inference technique. It is the relevant tool for managing the responses to a set of binary queries. Its scope is therefore universal, well beyond physics.
1.3.2 Major Feature of Bayesian Representation
The Bayesian representation of a single Boolean variable is very different from its deterministic representation. The main reason is that in this latest case, its expression is determined in advance. By contrast, in the Bayesian representation, the Boolean variable has no reason to coincide with a specific query of the current window. As a result, it is generally represented by a set of \(2^N\) joint probabilities corresponding to the classical states generated by the N queries of the question-and-answer procedure.
1.3.3 Entanglement
Entanglement is in no way a characteristic of the system itself, but only expresses that the current binary queries are not mutually independent. In other words, entanglement is the aftermath of a twisted information window. Therefore, the concept of entanglement is not per se an intrinsic resource but a Bayesian artifact that expresses the non-independence of the current batch of variables. This seems surprising since it is often believed that entanglement is intrinsic and therefore cannot be changed by changing the observation window. But this is only true for local operations and classical communication (LOCC) and not in general. Among all observation windows, there is at least one optimal batch in which the queries are mutually independent. In this particular window, called “principal window” as opposed to “twisted window”, the problem is strictly classical.
1.3.4 Measurement
A measurement is defined naturally as the Bayesian estimate of an observable, which solves the so-called “measurement problem” as previously stated by Caves et al. [9]. Retrieving all the information stored in the memory usually requires several observation windows, but in return, this often generates some redundancy expressed by the uncertainty principle.
1.3.5 Uncertainty Principle
The iconic uncertainty principle expresses simply the obvious fact that it is impossible, by using two observation windows, to retrieve more information than is stored in the memory. Quantitatively, the uncertainty principle is expressed by standard entropic bounds, namely the Maassen and Uffink [14] and the more precise Frank and Lieb [15] inequalities. Now, the present model provides a concrete and intuitive basis for these relationships. They are by no means a mysterious property of the quantum world.
1.3.6 Observables
Observable are computed as linear combinations of classical state probabilities. The existence of non commutative observables is a trivial consequence of the fact that each particular observable calls for a specific batch of queries and therefore is defined with respect to a specific observation window, called its “proper window”.
1.3.7 Gauge Group
The gauge group is the symmetry group of the Hilbert space \({\mathcal {H}}\), expressing non-uniqueness of the transcription of the Bayesian probability state into \({\mathcal {H}}\). It turns out that this group is just another expression of the Bayesian prior, up to contextual parameters. In other words, symmetry of \({\mathcal {H}}\) is enough to describe the system. The model provides an explicit derivation of the gauge group as a combination of unitary and antiunitary operators. While antiunitary operators play an important but somewhat mysterious role in standard physics, they are now naturally introduced into the current model.
1.3.8 Window Contextuality
The window contextuality is the free choice of a particular batch of binary queries and gives rise to the famous “paradoxes”, like violation of Bell’s inequalities, perfectly rational in the present model. The model provides a concrete and intuitive basis for the contextually dependent aspects of quantum objects. Technically, the changes of binary queries, a priori complicated in the probability space \({\mathcal {P}}\), are simply expressed by unitary operators acting on the Hilbert space \({\mathcal {H}}\).
2 Background
This section introduces the memory accessible by a question-and-answer procedure and depicts its organization as a Kolmogorov probability space.
2.1 Classical Register
A classical register is a finite set \({\textsf{X}}\) capable of storing classical information. We will only deal with binary degrees of freedom.
Definition 1
(Discrete degree of freedom) A discrete degree of freedom is one dichotomic choice.
2.2 Boolean Algebra
First, we must assign a query to each degree of freedom. We identify the classical register with a binary Boolean algebra, still denoted by \({\textsf{X}}\), with a batch of N Boolean variables \({\textsf{X}}_i\), for \(i\in\left[[1,\;N\right]]\) taking value in \(\{0,1\}\). We adopt the symbol “1” for “valid” and “0” for “invalid”. We name complete assignment, x, a full assignment to the N variables and partial assignment an assignment to less than N variables. We note \(\overline{{\textsf{X}}}_i\) the negation of \({\textsf{X}}_i\). Finally, we call literal a variable or its negation. Obviously, this choice is a matter of gauge since we could rename \(\overline{{\textsf{X}}}_i= {\textsf{Y}}_i\) and \({\textsf{X}}_i= \overline{{\textsf{Y}}}_i\). Let us term “discrete Boolean gauge” this choice. This initial allocation is done once and for all and its simultaneous inversion for all variables is simply a change of terminology.
Definition 2
(Discrete Boolean gauge) The discrete Boolean gauge is the initial allocation of a Boolean variable or its negation to all N degrees of freedom.
Given two Boolean formulas \({\textsf{f}}_1\) and \({\textsf{f}}_2\), it is convenient to note \(({\textsf{f}}_1; {\textsf{f}}_2)\) (with a semicolon) the conjunction \({\textsf{f}}_1\wedge {\textsf{f}}_2\) and \(({\textsf{f}}_1, {\textsf{f}}_2)\) (with a comma) the disjunction \({\textsf{f}}_1\vee {\textsf{f}}_2\). We name partial requirement a partial register of literals, that is a conjunction of literals, e.g. \(({{\textsf{X}}}_i;\overline{{\textsf{X}}}_j;{{\textsf{X}}}_k)\) and complete requirement (or classical state), \(\omega\), a conjunction of N literals, e.g. \(\omega =({{\textsf{X}}}_1;\overline{{\textsf{X}}}_2;\dots ;{{\textsf{X}}}_N)\), which is satisfiable by a complete assignment \(x_\omega\), e.g. \(x_\omega =(1; 0;\dots ; 1)\). Clearly, there are \(2^N\) different complete assignments and therefore \(2^N\) complete requirements. In multivariate information analysis [16] these complete requirements are called atoms and the particular atom labelled \(\varpi _0=(0,0,\dots ,0)\) is referred to as the empty atom. Clearly, the fact that a particular atom is the empty atom depends on the discrete Boolean gauge, Definition (2). Throughout this paper, we will use indifferently the terms “complete requirement”, “classical state” or “atom”. Let \(\Omega {\mathop {=}\limits ^{{\mathrm{(def)}}}}\{ \omega \}\) denote the set of classical states.
On the other hand, with up to N variables, it is possible to construct \(2^{2^N}\) different Boolean formulas, \({\textsf{f}}:\Omega \rightarrow \{0,1\}\), described, e.g. as full disjunctive normal forms, i.e. reunion of complete requirements. Thus, any Boolean function can be described as a disjunction \((\omega _1,\omega _2,\dots ,\omega _\ell )\) of \(\ell \le 2^N\) classical states \(\omega _i\). In particular, the tautology \(I:\Omega \rightarrow \{1\}\) corresponds to the reunion of all \(2^N\) classical states.
2.3 Bayesian Algebra
We propose to treat any Boolean function as a random event and account for the constraints by a set of equations between the probabilities of the relevant requirements (partial or complete), as explained below in Sect. (3.1). For this, we use the Bayesian theory of inferences [6] and regard henceforth the Boolean variables \({\textsf{X}}_i\) as random variables taking values on the alphabet \(\{0,1\}\). We will name Bayesian algebra such a mathematical object composed of a classical Boolean algebra endowed with a Bayesian probability structure.
In general, the hypotheses are specified by a set of constraints. We regard these constraints as a Bayesian prior, that is an ensemble of definite conditions, say (\(\Lambda\)), e.g, a set of Boolean formulas compelled to be valid or invalid. We will see that it is convenient to consider more generally a linear combination of Boolean classical states in the probability space. Now, the probability of any event will be conditional on \(({\Lambda })\).
2.3.1 Kolmogorov Probability Space
The basic sample set is the ensemble \(\Omega = \{ \omega \}\) of all mutually exclusive \(2^N\) complete requirements, labelled by the \(2^N\) complete assignments \(x_\omega\). Since the cardinality of \(\Omega\) is finite, the power set \({\mathfrak {P}}(\Omega )\), of cardinality \(2^{2^N}\), is a sigma-algebra \({\mathcal {T}}\), pointwise identical to the ensemble of all Boolean functions. This means that any event is just a Boolean formula, that is a finite set of atoms. Next, we have to introduce an unknown probability measure \({\mathbb {P}}\) on \({\mathcal {T}}\) conditional on \(({\Lambda })\). Finally, the Kolmogorov probability space associated with the prior \((\Lambda )\) is \((\Omega , {\mathcal {T}}, {\mathbb {P}})\).
In general there is a number of probability distributions \({\mathbb {P}}\) compatible with a prior \((\Lambda )\). We will define later the selection of a single solution as the “source contextuality”.
2.3.2 Notation
Throughout this paper, we will specifically name \(unknowns\) the conditional probability of complete or partial requirements, not to be confused with the variables or Boolean functions subject to randomness. Except when mentioned otherwise, we will use a shorthand to describe the unknowns, namely \({\mathbb {P}}(i)\) for \({\mathbb {P}}({{\textsf{X}}_i}=1|\Lambda )\), \({\mathbb {P}}(-i)\) for \({\mathbb {P}}({{\textsf{X}}}_i=0|\Lambda )\), \({\mathbb {P}}(i;-j)\) for \({\mathbb {P}}({\textsf{X}}_i=1;{{\textsf{X}}}_j=0|\Lambda )\), etc. (for \(i,\;j\dots\in\left[[1,\;N\right]]\)). Similarly, we will use \({\mathbb {P}}(\omega )\) for \({\mathbb {P}}(\omega =1|\Lambda )\). We will often call partial probability an unknown like \({\mathbb {P}}(i;-j)\) with less than N literals and complete probability an unknown \({\mathbb {P}}(\omega )\) with N literals. An unknown labeled k without further detail will be denoted by \(p_k\), e.g. we may have \(p_k= {\mathbb {P}}(i;-j)\). An array of unknowns will be denoted by \(p=(p_k)\).
For clarity, we use most of the time the term “classical” in its usual acceptation, as opposed to “quantum”, although this term remains vague at this stage.
2.3.3 Observation Window
Up to Sect. (4.1), we ignore communication channels and only consider a single viewpoint. This means that we are given a classical register and investigate what we can infer from the known assumptions. All parameters, either input data in the prior \((\Lambda )\) or observable entries \((\textrm{q}_\omega )\), rely to a single batch of binary variables, what we call a single observation window. We will discuss later the possibility of reformulating the same problem by using other batches of queries, that is, in our terminology, other “observation windows”. This defines the concept of general system and requires the construction of transition mappings between successive windows: Eventually, the reunion of all windows within a global atlas, that we call a “Bayesian theater” will make use of a complex Hilbert space endowed with a density operator. We will refer to the initial static issue as the source observation window.
2.3.4 Universal Equations
Since the probability laws are just an extension of Aristotelian logic the following relations are universal:
etc. where \(i,j,k,\dots\) are signed integers and \(\vert i\vert,\vert j\vert,\vert k\vert,\dots\in\left[[1,\;N\right]]\) are distinct.
Note that accounting for Eqs. (2, 3, 4, etc.), Eq. (1) implies that
2.3.5 Bayesian LP System
To secure the unknowns to be indeed probabilities, the relevant universal equations must mandatory be added to the constraints. As a result, the LP problem considered in Sect. (3.1) below is specific, as opposed to a general LP system. Its solutions are indeed in the interval [0, 1] and its specific polytope will prove to be a simplex. It will be called “Bayesian LP system”.
3 Source Observation Window
This section poses the logical issue at hand. We start with a particular batch of queries, referred to as the “source window”. The problem is defined by a set of hypotheses to be satisfied. In the present Bayesian model, they are viewed as a prior, say \(({\Lambda })\). In principle, the prior is composed of Boolean formulas, that is events of the sigma-algebra \({\mathcal {T}}\), required to be valid or invalid. However, beyond Boolean formulas which can take only two values, it is convenient to use a more general concept, namely, “observables”.
Definition 3
(Observable) An observable Q is a real-valued function of the classical states on the register, defined as
We will denote the array \((\textrm{q}_\omega )\) by \(\textrm{q}\). Notice that while the set of Boolean functions \({\mathcal {T}}\) is closed under complement, unions and intersections, the set of observables is closed under linear combinations and is in fact nothing else than the dual of the probability space. This will be detailed in Sect. 3.2 below.
3.1 Linear Programming Problem
Bayesian inference of the variables consists in calculating their probability from the prior. To ensure that the solutions are indeed probabilities, we must first include in the prior the relevant universal equations, Eqs. (2, 3, 4, etc.). Next, we propose that the prior be simply incorporated by assigning a probability of 1 to logical functions required to be valid and a probability of 0 to logical functions required to be invalid. For instance, a partial requirement \(({{\textsf{X}}}_i;\overline{{\textsf{X}}}_j;{{\textsf{X}}}_k)\), compelled to be valid or invalid in the Boolean algebra, is trivially encoded as \({\mathbb {P}}(i;-j;k)=1\) or 0 respectively. A Boolean function defined as a disjunction of classical states \({\textsf{f}}=(\omega _1,\omega _2,\dots ,\omega _\ell )\) and required to be valid or invalid in the Boolean algebra, is encoded as \(\sum _i {\mathbb {P}}(\omega _i)=1\) or 0, because the classical states, \(\omega _i\), are disjoint, etc. In this way, any logical constraint is translated into a linear expression, that is to say, an observable.
Subsequently, the full prior, comprising both the specific equations and the relevant universal constraints is formulated as a linear programming (LP) problem in stack variables [17] within a convenient real-valued vector space.
Proposition 1
The Bayesian probability \(p_i\) are the solution of a LP system,
where \(p=(p_i)\) is a real-valued positive unknown vector, \(A=(\textrm{a}_{j,i})\) a real matrix and \(b=(b_j)\) a real vector, while \(p\ge 0\) stands for \(\forall i, p_i\ge 0\).
The number of unknowns \(p_i\), say n, is based on the particular formulation, that is the partial and complete probabilities explicitly involved. In explicit computation, it is crucial to have a minimum set of unknowns. On the contrary, for a theoretical discussion, it is necessary to take the full set of complete probabilities as unknowns, even if the number \(n=2^N\) is exponential in N. We will adopt this choice from Sect. (3.2). Let \(m>0\) denote the number of rows of the matrix, so that A is a \(m\times n\) matrix. We will assume that the non-independent rows have been eliminated and that m is also the rank of the system.
It remains to complete the computation by solving this LP problem, Eq. (7). A feasible solution is a numerical vector of unknowns, p, that satisfies the prior \((\Lambda )\), that is Eq. (7), and therefore defines a probability distribution \({\mathbb {P}}\) on the sample set \(\Omega\) and thus a probability measure on the sigma-algebra \({\mathcal {T}}\).
If the problem is inconsistent, the system is unfeasible. A priori, if the problem is well posed and admits a solution, one might expect that the system will provide a deterministic solution. In reality, most feasible LP problems do not accept deterministic solutions. This simply means that the initial batch variables are not mutually independent.
Proposition 2
When the LP problem accepts a deterministic solution, the binary variables \({\textsf{X}}_i\) of the source window are mutually independent.
Proof
A deterministic solution is trivially a separable joint probability which implies that the variables \({\textsf{X}}_i\) are mutually independent (see Sect. 3.5.1). \(\square\)
When the LP system is feasible but does not accept a deterministic solution, a deterministic solution exists nevertheless but in another window, namely a “principal window” defined in Sect. (5.2).
In general, the rank m of the matrix A is less than n and thus, there is a continuous set of solutions. This arises when for some reason the Bayesian prior \((\Lambda )\) is not specific enough. For example, in quantum mechanics, a set of data may be fundamentally out of control of the experimenter. Thus, the particular probability distribution to be used has to be fixed by an an exogenous choice. The system is said to be to context-dependent. Let us define precisely what we term “contextuality”.
Definition 4
(Contextuality) A system is context-dependent when the involved probability distribution depends on an exogenous choice.
Given that contextuality has also other causes in general systems (Sect. 4.1, below), we will refer to this property as the source contextuality.
Definition 5
(Source contextuality) Source contextuality expresses the possibility of choosing a particular feasible probability distribution among the solutions of the source LP problem.
A particular solution must be chosen by a selection rule. This rule will be said to fix a particular “context”. Thus, source contextuality is a piece of intrinsic information specified at the outset in addition to the Bayesian prior.
3.2 Real Probability Space \({\mathcal {P}}\)
We now assume that the unknowns \(p=(p_\omega )\) are specifically the \(2^N\) complete probabilities of the classical states, i.e. \(p_\omega = {\mathbb {P}}(\omega =1|\Lambda )\) with \(\omega \in \Omega\). This can easily be achieved by eliminating the partial probabilities using the universal equations, Eqs. (3, 4, ...). Then
We denote by \({\mathcal {P}}\) this real-valued vector space and \({\mathcal {P}}^*\) its dual space, both of dimension \(n=d= 2^N\). Clearly, from Definition (3), the dual space \({\mathcal {P}}^*\) is the space of the observables defined in the source window. As long as a single window is concerned, no metric is required. We will indifferently refer to \({\mathcal {P}}\) as the “real probability space” or the “LP space”.
Notation When there is no risk of confusion, we will use the same symbols \(\omega ,\omega ',\omega _i,\dots\) to designate either the classical states in \(\Omega\) or the different labels in \({\mathcal {P}}\) and \({\mathcal {P}}^*\).
-
We note \({\tilde{\omega }}\in {\mathcal {P}}\), with \(\omega \in \Omega\), the basis vectors in \({\mathcal {P}}\), i.e. \({\tilde{\omega }} =(p_{\omega '})\) with \(p_{\omega '}=\delta _{\omega '\omega }\). They describe deterministic probability distributions. The basis is denoted by \({\tilde{\Omega }}{\mathop {=}\limits ^{{\mathrm{(def)}}}}\{{\tilde{\omega }}\}\) or simply \(\Omega\) when no confusion can occur.
-
A covector in the dual space \({\mathcal {P}}^*\) is denoted \(\textrm{q} =(\textrm{q}_{ \omega })\) with \(\omega \in \Omega\). A covector defines an observable on the register, \(Q(\omega )=\textrm{q}_{ \omega }\).
-
A dual form \(({\mathcal {P}}^*,{\mathcal {P}})\rightarrow \mathbb {R}\) is denoted \(\langle \textrm{q} p \rangle\), where \(\textrm{q}\in {\mathcal {P}}^*\) and \(p\in {\mathcal {P}}\).
-
We will note \({\tilde{\omega }}^*\) the canonical basis covectors in \({\mathcal {P}}^*\) defined by.
-
An observable defined by a covector \(\textrm{q} =(\textrm{q}_{ \omega })\) with \(\textrm{q}_{ \omega } \ge 0\ (\forall \omega \in \Omega )\) is called non-negative.
-
A Boolean function \({\textsf{f}}\) defines an observable \(F(\omega )\), that is a non-negative dual form whose associated covector \(\textrm{f}=(\textrm{f}_\omega )\) is the indicator function of \({\textsf{f}}\) in \(\Omega\). In particular, a basis covector \({\tilde{\omega }}^*\) defines an observable \(F(\omega ')= \langle {\tilde{\omega }}^* {\tilde{\omega }}' \rangle\) that we will simply denote \({\tilde{\omega }}^*\) when no confusion can occur.
Expectation The value \(\langle Q \rangle\) of a dual form \(\langle \textrm{q} p \rangle\) with respect to the probability distribution \({\mathbb {P}}(\omega ) = p_\omega\), is trivially the expectation value of the observable \(Q(\omega )=\textrm{q}_\omega\).
Proposition (1) can be rewritten as
Theorem 1
(Bayesian formulation) Any LP system, Eq. (7), can be expressed as the following Bayesian problem,
where \(\ell\in\left[[1,\;m-1\right]]\). In addition, it is possible to assume that the expectation of the observables \(A_\ell\) is zero, that is \(b_\ell =0\).
Proof In Eq. (7), without loss in generality, assume that one row is the normalization constraint that is the tautology. We reserve the index \(\ell =0\) to this normalization equation, namely, \(A_0=I\), \(\textrm{a}_{0,\omega }=1, \forall \omega \in \Omega\) and \(b_0=1\). Clearly, each row, now labeled \(\ell\), defines a covector, \({\text{a}}_\ell=\sum_\omega{\text{a}}_{\ell,\omega}\widetilde\omega^\ast,\left(\ell\in\left[[1,\;m-1\right]]\right)\). It is a partial constraint expressed as the expectation of an observable \(A_\ell (\omega )=\textrm{a}_{\ell ,\omega }\). Indeed, \(\sum _\omega \textrm{a}_{\ell ,\omega } p_\omega =b_{\ell }\) means \(\langle A_\ell \rangle =b_\ell\).
Now, Eq. (7) can be reformulated as follows: Assign a probability distribution \({\mathbb {P}}\) on \(\Omega\), given that the expectation of m independent observables \(A_\ell\) are subject to \(\langle A_\ell \rangle = b_\ell\). Since normalization is implicit in probability theory, Eq. (7) can be expressed as Eq. (8). We can assume that \(b_\ell =0\) for \(\ell >0\) because otherwise, we can replace \(A_\ell\) by \(A_\ell -b_\ell A_0\). The converse is obvious. Now, the system, Eq. (8) depicts a standard Bayesian problem [6]. \(\Box\)
It is convenient to first address the simplest problem, in which the prior is reduced to the normalization equation.
3.2.1 Tautology
Irrespective of the current prior \((\Lambda )\), consider the following Bayesian LP system in the probability space \({\mathcal {P}}\),
Any solution \(p =(p_\omega )\) of this system describes a potential probability distribution \({\mathbb {P}}\) on \(\Omega\) and conversely any probability distribution is a solution of Eq. (9). The d classical deterministic states \(\omega \in \Omega\) label both the basis vector \({\tilde{\omega }}\in {\mathcal {P}}\) and the extreme points of a convex polytope, \({\mathcal {W}}_{\scriptscriptstyle I}\), of dimension \(d-1\) with d vertices, that is a \((d-1)\)-simplex, known as “probability simplex” or “Choquet simplex” in convex geometry. In the present context, we will call this polytope, \({\mathcal {W}}_{\scriptscriptstyle I}\), the d-dimensional tautological simplex.
Definition 6
(Tautological simplex \({\mathcal {W}}_{\scriptscriptstyle I}\)) The “tautological simplex” in the d-dimensional vector space \({\mathcal {P}}\) is the \((d-1)\)-simplex
Proposition 3
The entries \(p_{\omega }\) in Eq. (9) represent both the d components of p in \({\mathcal {P}}\) and the d barycentric coordinates of the point p on the tautological simplex \({\mathcal {W}}_{\scriptscriptstyle I}\). In other words, the distinction between barycentric and contravariant components vanishes on \({\mathcal {W}}_{\scriptscriptstyle I}\).
Proof
Since \(\sum _{\omega \in \Omega } p_\omega =1\), the two formulations mean \(p=\sum _\omega p_\omega \ {\tilde{\omega }}\). \(\square\)
Since \({\mathcal {W}}_{\scriptscriptstyle I}\) is a simplex, the barycentric coordinates are uniquely defined. The set of its extreme points \({\tilde{\Omega }}=\{{\tilde{\omega }}\}\) forms its Choquet boundary and describes the deterministic distributions.
Proposition 4
Any basis subspace of \({\mathcal {P}}\) is specified by a Boolean function compelled to be valid.
Proof
Any basis subspace is the direct sum of one-dimensional subspaces \({\mathcal {P}}_i\), each spanned by a basis vector \({\tilde{\omega }}_i\) so that the direct sum \({\mathcal {P}}_1\oplus {\mathcal {P}}_2\dots \oplus {\mathcal {P}}_\ell\) is specified by \({\textsf{f}}=(\omega _1,\omega _2,\dots ,\omega _\ell )=1\). \(\square\)
3.2.2 Current Bayesian LP System
Return now to the current Bayesian LP system, Eq. (8) associated with the prior \((\Lambda )\). Suppose that the system is feasible and consider the set of solutions. It is convenient to single out two subspaces containing these solutions, respectively the affine subspace and the effective probability space.
Definition 7
(Affine subspace \(P_{\scriptscriptstyle \Lambda }\)) The affine subspace \(P_{\scriptscriptstyle \Lambda }\) is the affine set of the solutions.
Definition 8
(Effective probability space \(\mathbb {W}_{d-m+1}\)) The effective probability space \(\mathbb {W}_{d-m+1}\) is the linear span of the solutions.
Specific polytope \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\)In fact, from standard LP theory, the locus of the solutions is a specific polytope \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\). Using Definition (6), we have from a simple inspection
In addition, for Bayesian LP systems, this polytope is compact and convex and will prove to be a simplex in \(\mathbb {W}_{d-m+1}\) with \(r = d-m+1\) vertices. Let \(\{w_\textrm{k}\}\) with \(k\in\left[[1,\;r\right]]\) denote its extreme points.
Definition 9
(Simplicial system) A simplicial system is a LP problem whose specific polytope is either an isolated point or a simplex.
Proposition 5
Any Bayesian LP system is simplicial.
Proof
Express the LP system in the effective probability space \(\mathbb {W}_{d-m+1}\). In this space, using the vertices \(\{w_\textrm{k}\}\) as basis vectors, the specific polytope is the tautological simplex. \(\square\)
Definition 10
(Specific simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\)) The solutions of the LP system, Eq. (7) are located on a simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\), called “specific simplex”, with \(r=d-m+1\) vertices.
3.2.3 Source Contextuality
In general, there are a number of solutions to the current Bayesian system Eq. (8) located on the specific simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\). The choice of a single solution, say \(w_{\scriptscriptstyle \Lambda }\in {\mathcal {W}}_{\scriptscriptstyle \Lambda }\), specifies the “source context”.
3.2.3.1 Default Context
Suppose first that there is no extra constraint, which we call the “default context”. The standard Bayesian solution is then the most likely distribution, determined by the maximum entropy principle [18], that is a generalization of the Laplace’s principle of indifference. This requires to consider a uniform probability density of dimension \(d-m\) over the affine subspace \(P_{\scriptscriptstyle \Lambda }\), normalized to unity on the convex hull of the specific polytope. The center of mass \({\tilde{c}}\) is the mean point with respect to this uniform hull density. The default context corresponds to \(w_{\scriptscriptstyle \Lambda } = {\tilde{c}}\). Equivalently, it is the barycenter of the vertices.
3.2.3.2 Other Contexts
Other context could be specified by assigning a non-uniform hull density over the specific polytope, but more simply, we will specify the context by means of a discrete probability distribution over the vertices of the specific simplex, which we will call the contextal probability distribution.
3.3 Representation of the Bayesian States
A Bayesian state is represented by a specific simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) and a contextual distribution.
3.3.1 Working Distribution, Contextual Distribution
Technically, we need only to specify the mean point \(w_{\scriptscriptstyle \Lambda }\) on the simplex with respect to the contextual distribution because the details can be derived from the framework. Let us name this mean point the “working distribution”.
Definition 11
(Working distribution) The working distribution \(w_{\scriptscriptstyle \Lambda }\in {\mathcal {W}}_{\scriptscriptstyle \Lambda }\) is the mean point with respect to an auxiliary probability distribution \(\Sigma _\mu\) on the vertices of the specific simplex.
Let \(r=d-m+1\), let \(w_i\) be the r vertices of the simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) and let \(\Sigma _\mu =\{\mu _i\}\) be the set of barycentric coordinates of \(w_{\scriptscriptstyle \Lambda }\in {\mathcal {W}}_{\scriptscriptstyle \Lambda }\) on the simplex, that is,
Therefore, \(w_{{\scriptscriptstyle \Lambda }}\) is well the center of mass of the vertices \(\{w_i\}\) weighted by \(\{\mu _i\}\).
Definition 12
(Contextual probability distribution) The contextual probability distribution \(\Sigma _\mu\) is the set of barycentric coordinates \(\{\mu _i\}\) specifying the working distribution in the simplex.
Let us compute its entropy.
Definition 13
(Working entropy) The working entropy \(\mathbb {H}(w_{\scriptscriptstyle \Lambda })\) is the Shannon entropy \(S_w\) of the working distribution \(w_{\scriptscriptstyle \Lambda }\).
The working entropy is rather a Bayesian parameter and has little to do with a real uncertainty. It will be identified later with the so-called “window entropy”, Definition (42). Indeed, we will show that the quantity \(N-\mathbb {H}(w_{\scriptscriptstyle \Lambda })\) represents the amount of information that can be extracted from the current observation window. By contrast, the “simplicial entropy” defined in the next section will directly represent a form of uncertainty.
3.3.2 Simplicial Quantum States
It turns out that a compact formulation of the Bayesian state, comprising the specific simplex and a contextual probability distribution, is the exact equivalent of the standard quantum state restricted to the source window. We propose to call it “a simplicial quantum state”.
Definition 14
(Simplicial quantum state) A simplicial quantum state is the pair \((\Sigma _\mu ,{\mathcal {W}}_{\scriptscriptstyle \Lambda })\) of a contextual probability distribution \(\Sigma _\mu =\{\mu _i\}\) and a specific simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\). The working distribution is the mean point \(w_{{\scriptscriptstyle \Lambda }} =\sum _{i=1}^{r}\mu _i w_i\) where \(r=d-m+1\). The simplicial quantum state will be designated indifferently by one of the pairs \((\Sigma _ \mu , {\mathcal {W}} _ {\scriptscriptstyle \Lambda })\) or \((w _ {\scriptscriptstyle \Lambda }, {\mathcal {W}} _ {\scriptscriptstyle \Lambda })\).
Let us compute the entropy of the contextual distribution.
Definition 15
(Simplicial entropy \(S_\mu\)) The simplicial entropy of a simplicial quantum state \((\Sigma _\mu ,{\mathcal {W}}_{\scriptscriptstyle \Lambda })\) is the Shannon entropy of the contextual distribution
We will use indifferently the terms “simplicial entropy” or “contextual entropy”.
To sum up, we encountered two forms of entropy, the working entropy \(\mathbb {H}(w_{\scriptscriptstyle \Lambda })\) on the sample set and the simplicial entropy \(\mathbb {H}(\Sigma _\mu )\) on the simplex. The two forms of entropy obviously differ in the source window, for instance the simplicial entropy of a pure state (defined just below) is zero, which is not the case in general for the working entropy. However, they will merge in a “principal window” (Proposition 28 below). At last, they are both bounded above by the storage capacity of the register, i.e. N bits.
The simplicial entropy is closely related to the von Neumann entropy of standard quantum information. It turns out that the von Neumann entropy is actually the lower bound of all simplicial entropies over all windows, defined in general systems, Sect. (5). This will lead to a more substantial interpretation of the von Neumann entropy in terms of information theory in Theorem (5) below.
3.3.3 Pure States
When the simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) is reduced to an isolated point, we have a pure state. This means that the rank m of the LP-system, Eq. (7) is equal to the dimension of the space, \(m=d\) and thus \(r=d-m+1=1\). There is a single feasible solution, \(w_{\scriptscriptstyle \Lambda }=(w_{{\scriptscriptstyle \Lambda },\omega })\) and the polytope \({\mathcal {W}}_{\scriptscriptstyle \Lambda }=\{{w}_{\scriptscriptstyle \Lambda }\}\subset {\mathcal {W}}_{\scriptscriptstyle I}\) is trivially identical to the working distribution. At last there is a single feasible probability distribution,
The simplicial entropy is zero. Finally, the expectation of any observable \(Q(\omega )=\textrm{q}_\omega\) reads trivially
Definition 16
(Pure and mixed simplicial quantum states) A simplicial quantum state is pure when the specific simplex is reduced to a single point. Otherwise, the state is mixed.
3.3.4 Mixed States
When the rank \(m>0\) is less than d the prior does not uniquely determine the solution of the system and therefore the working probability \(w_{\scriptscriptstyle \Lambda }\) is defined by the contextual distribution \(\Sigma _\mu\). In this case, from Definition (16) the simplicial state is termed “mixed”.
Let \(\mu _i\) be the simplicial coordinates of \(w_{\scriptscriptstyle \Lambda }\) in \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\). We have, using \(r = d-m+1\)
As a result, for any observable \(Q(\omega )=\textrm{q}_\omega\), we have
This equation is also valid for pure states, with \(m=d\), \(\mu _1=1\) and \(w_1=w_{\scriptscriptstyle \Lambda }\). Furthermore, when the contextual distribution is deterministic, that is when all \(\mu _i\) coefficients except one are zero, e.g. \(\mu _1=1\), the mixed state reduces to a pure state, e.g. \(w_{\scriptscriptstyle \Lambda }=w_1\).
3.4 Measurement with Respect to a Simplicial Quantum State
Let us now turn to the measurement of an observable of the source observation window with respect to a simplicial quantum state \((w_{\scriptscriptstyle \Lambda }, {\mathcal {W}}_{\scriptscriptstyle \Lambda })\). We simply identify the Bayesian measurement with the expectation value of the observable with respect to the working distribution.
3.4.1 Expectation of an Observable
Let \(\textrm{q}=(\textrm{q}_\omega )\) be a covector, corresponding to an observable Q.
Definition 17
(Quantum expectation \(\langle Q\rangle\)) The quantum expectation of an observable \(Q(\omega )=\textrm{q}_\omega\) is the expectation \(\langle Q\rangle =\langle \textrm{q} w_{\scriptscriptstyle \Lambda }\rangle\) with respect to the working distribution \(w_{\scriptscriptstyle \Lambda }\).
The expectation was previously computed in Eqs. (14, 16 ).
3.4.2 Projective Measurement
Let \(\Gamma =\{ \gamma \}\) denote a finite set. Define an ensemble of mutually disjoint Boolean functions \(\{{\textsf{f}}_\gamma , \gamma \in \Gamma \}\) such that the reunion of all \({\textsf{f}}_\gamma\) is the tautology. Equivalently, let \(\{\textrm{f}_\gamma =(\textrm{f}_{\gamma ,\omega }),\ \gamma \in \Gamma \}\) be the indicators \(F_\gamma\) of \({\textsf{f}}_\gamma\) in \({\mathcal {P}}^*\), such that \(\sum _{\gamma } \textrm{f}_{\gamma , \omega } =1\) for all \(\omega \in \Omega\), i.e. \(\sum _\gamma {F_\gamma }=I\).
A projective measurement is defined as
From Proposition (4), a projective measurement means expanding the working distribution \(w_{\scriptscriptstyle \Lambda }\) with respect to the set of subspaces defined by the Boolean functions \({\textsf{f}}_\gamma\). This is similar to a projective measurement in standard quantum information, but restricted to the source window. In particular, when \(\Gamma =\Omega\), \(\{{\textsf{f}}_\omega = {\tilde{\omega }}, \omega \in \Omega \}\), \(\textrm{p}(\omega )= {\mathbb {P}}(\omega )\).
3.4.3 General Measurement
Let \(\Gamma =\{ \gamma \}\) denote a finite set. Define an abstract resolution of the tautology in the source window, that is a set of non-negative forms in \({\mathcal {P}}^*\),{q\(_\gamma =(\textrm{q}_{\gamma , \omega })\)} (with \(\gamma \in \Gamma )\), such that \(\sum _{\gamma } \textrm{q}_{\gamma , \omega } =1\) for all \(\omega \in \Omega\), i.e. \(\sum _\gamma \textrm{q}_\gamma =I\). Since \(\textrm{q}_{\gamma , \omega }\) is not necessarily 0 or 1, \(\textrm{q}_\gamma\) is not necessarily associated with a Boolean function, but corresponds to a positive observable \(Q_\gamma\) and \(\sum _\gamma {Q_\gamma }=I\). A general measurement in the source window is defined by
This is similar to a particular positive-operator valued measure (POVM) in quantum information, when the involved observables commute.
3.5 Pair of Registers
The combination of two registers brings together most of the peculiarities of standard quantum information. This is the purpose of this section. Some developments are rather lengthy, but the results will be used later.
Consider a global classical register \({\textsf{X}}_c\) composed of two distinct subregisters \({\textsf{X}}_a\) and \({\textsf{X}}_b\). Let \((\Lambda _c)\) denote a global Bayesian prior. Let \(N_a\), \(N_b\) and \(N_c=N_a+N_b\) be the numbers of binary variables in \({\textsf{X}}_a\), \({\textsf{X}}_b\) and \({\textsf{X}}_c\) respectively. Let \({\mathcal {P}}_a\), \({\mathcal {P}}_b\) and \({\mathcal {P}}_c\) denote the probability spaces corresponding to \({\textsf{X}}_a\), \({\textsf{X}}_b\) and \({\textsf{X}}_c\) of dimension \(d_a=2^{N_a}\), \(d_b=2^{N_b}\) and \(d_c=2^{N_c}\) respectively. We have \({\mathcal {P}}_a \otimes {\mathcal {P}}_b={\mathcal {P}}_c\), \(N_a+N_b=N_c\) and \(d_a\times d_b=d_c\).
Notation The classical states, e.g. in \(\Omega _c\), are noted \(\omega_{c,i},\,i\in\left[[1,\;d_c\right]]\).
3.5.1 Separability and Entanglement of a Single Probability Distribution
Definition 18
(Separability, entanglement) A probability distribution, \({\mathbb {P}}_c(\omega _a;\omega _b)\) on a global register, \({\textsf{X}}_c =({\textsf{X}}_a,{\textsf{X}}_b\)), is separable with respect to a partition into the two distinct subregisters \({\textsf{X}}_a\) and \({\textsf{X}}_b\), if
Otherwise, the joint distribution is entangled.
On the other hand, the concept of marginal distribution is related to the joint distribution \({\mathbb {P}}_c(\omega _a;\omega _b)\) by the conditional probability \({\mathbb {P}}_c(\omega _a|\omega _b)\) thanks to Bayes’ law,
Define a particular separable probability distribution \({\mathbb {P}}_c'(\omega _c)\) still on \(\Omega _c\) as the product of the two marginal distributions \({\mathbb {P}}_a(\omega _a)\) and \({\mathbb {P}}_b(\omega _b)\), namely,
Define finally
Proposition 6
The global probability \({\mathbb {P}}_c\) is separable with respect to the partition (\({\textsf{X}}_a\), \({\textsf{X}}_b\)) if and only if its relative entropy with respect to the product \({\mathbb {P}}_c'(\omega _c)={\mathbb {P}}_a(\omega _a)\times {\mathbb {P}}_b(\omega _b)\) of the marginal distribution in \({\mathcal {P}}_a\) and \({\mathcal {P}}_b\) is zero, that is, \(S( {\mathbb {P}}_c \Vert {\mathbb {P}}_c')=0\).
Proof
We have \(S( {\mathbb {P}}_c \Vert {\mathbb {P}}_c')\ge 0\) because a relative entropy is non-negative. In addition, \(S( {\mathbb {P}}_c \Vert {\mathbb {P}}_c')\) is the minimum value over all possible relative entropies \(S( {\mathbb {P}}_c\Vert {\mathbb {P}}_c'')\) for all separable distributions \({\mathbb {P}}_c''(\omega _a;\omega _b) ={\mathbb {P}}_a''(\omega _a)\times {\mathbb {P}}_b''(\omega _b)\), since we have by expanding Eq. (19),
Therefore, \(0\le S( {\mathbb {P}}_c\ \Vert \ {\mathbb {P}}_a\times {\mathbb {P}}_b)\le S( {\mathbb {P}}_c\ \Vert \ {\mathbb {P}}_a''\times {\mathbb {P}}_b'')\). The minimum of \(S( {\mathbb {P}}_c\Vert {\mathbb {P}}_c'')\) is zero if \({\mathbb {P}}'_a={\mathbb {P}}_a\), \({\mathbb {P}}'_b={\mathbb {P}}_b\) and \({\mathbb {P}}_c={\mathbb {P}}_a\times {\mathbb {P}}_b\). \(\square\)
To sum up, we have the following result:
Proposition 7
A global probability distribution \(w_c\) governing a pair of distinct classical registers subject to a global prior is generally entangled with respect to the pair of registers. The amount of entanglement is characterized by the relative entropy between the global distribution and the product of its marginal distributions, Eq. (19). When the relative entropy is zero, the distribution \(w_c\) is separable and equal to the product of its marginals.
3.5.2 Partial Simplicial Quantum State
The restriction of a global LP system to a subregister will be termed “partial LP system”. In essence, the problem is to reconstruct the effective probability subspace in the subregister. Technically, the reduction is implemented with respect to the current working distribution at work in the global system, that is on the simplicial quantum state, but the reduced specific simplex is actually independent of the working distribution. We will use indifferently the terms “partial”, “reduced” and “marginal” when no confusion can occur.
While the concept of separable probability distribution is not ambiguous, the situation is more subtle for simplicial quantum state. For convenience, set the following definitions, where every vertex of the specific simplex is viewed as a single probability distribution.
Definition 19
(Separable simplex) A simplex is separable with respect to a partition between two subregisters if all of its vertices are separable. Otherwise, the simplex is twisted.
Definition 20
(Separable LP system) A LP system is separable with respect to a partition between two subregisters if its specific simplex is separable. Otherwise, the LP system is twisted.
Definition 21
(Separable simplicial quantum state) A simplicial quantum state \((w_c,{\mathcal {W}}_c)\) is separable with respect to a partition between two subregisters if its specific simplex \({\mathcal {W}}_c\) is separable, irrespective of the working distribution \(w_c\). Otherwise, the simplicial quantum state is twisted.
Definition 22
(Product state) A simplicial quantum state \((w_c,{\mathcal {W}}_c)\) is a product state with respect to a partition between two subregisters if it results merely from the simple concatenation of the two registers \({\textsf{X}}_a\) and \({\textsf{X}}_b\), meaning that the registers are defined independently, each subjected to its own constraint set.
Definition 23
(Completely divisible state) A simplicial quantum state \((w_c,{\mathcal {W}}_c)\) is completely divisible if it results from the concatenation of N independent 1-bit registers \({\textsf{X}}_i\), each subjected to its own constraint set.
3.5.2.1 Reduction of a Pure State
Assume first that the Bayesian system \((\Lambda _c)\) in \({\mathcal {P}}_c\) accepts a unique solution, i.e. depicts a pure state \(w_c=(w_{c,(\omega _a;\omega _b)})\). The rank of the LP system is \(m_c=d_c\). As a simplicial quantum state, its simplex is \(\{w_c\}\) and the state is noted \((w_c, \{w_c\})\) or just \(w_c\) for simplicity. The rank of the state is \(r_c=d_c-m_c+1=1\) and the effective probability space \(\mathbb {W}_c = \textrm{Span}(w_c)\) is of dimension 1.
Proposition 8
(Reduction of a pure simplicial quantum state) The restriction to \({\mathcal {P}}_a\) of a global pure state, \(w_c(\omega _c)={\mathbb {P}}_c(\omega _a;\omega _b)\in {\mathcal {P}}_c\), is a partial simplicial quantum state \((w_a, {\mathcal {W}}_a)\) whose specific simplex \({\mathcal {W}}_a\) is the convex hull of the points \({\tilde{v}}_{\omega _b}\in {\mathcal {P}}_a\)
Its rank \(r_a\) is thus the rank of the set of vectors \(\{{\tilde{v}}_{\omega _b}\}\) and the rank \(m_a\) of the associated LP system is \(m_a=d_a-r_a+1\). The working distribution \(w_a\) is the marginal in \({\mathcal {P}}_a\) of the probability distribution \(w_c\) in \({\mathcal {P}}_c\).
When the global pure state \(w_c\) is separable, \(r_a=1\) and the partial simplicial quantum state is also a pure state \((w_a, \{w_a\})\).
Proof
The restriction of the pure state \(w_c\in {\mathcal {P}}_c\) to \({\mathcal {P}}_a\) comprises by definition its marginal, \(w_a =(w_{a,\omega _a})\), as
where \({\mathbb {P}}_c(\omega _b){\mathop {=}\limits ^{{\mathrm{(def)}}}}\sum _{\omega _a\in \Omega _a} w_{c,(\omega _a;\omega _b)} =w_{b,\omega _b}= {\mathbb {P}}_b(\omega _b).\) Let \(v_{\omega _b,\omega _a} {\mathop {=}\limits ^{{\mathrm{(def)}}}}{\mathbb {P}}_c(\omega _a|\omega _b)\), that is
Construct the vector set \(\{{\tilde{v}}_{\omega _b}\,|\,\omega _b\in \Omega _b\}=\{(v_{\omega _b,\omega _a})\}\) in \({\mathcal {P}}_a\). Then, each vector \({\tilde{v}}_{\omega _b}\ne 0\) is a probability distribution in \({\mathcal {P}}_a\). Define \(\nu _{\omega _b} = {\mathbb {P}}_c(\omega _b)\) and let \(r_a\) denote the rank of \(\{{\tilde{v}}_{\omega _b}\}\). As a result, from Eq. (21), we have
In other words, the working distribution in \({\mathcal {P}}_a\) is determined by the barycentric coefficients \(\nu _{\omega _b} = {\mathbb {P}}_c(\omega _b)\). Since by hypothesis the outcomes \(\omega _b\) are no more involved in the partial states, the coefficients \(\nu _{\omega _b}\) are regarded henceforth as exogenous. As a result, the set of feasible solutions in \({\mathcal {P}}_a\) is the full polytope \(\textrm{conv}({\tilde{v}}_{\omega _b})\) and its extreme points \(\{w_{ai}\}\) are a subset of \(\{{\tilde{v}}_{\omega _b}\}\). This polytope is actually the tautological simplex \({\mathcal {W}}_{a}\) in the effective probability space \(\mathbb {W}_{a}=\textrm{Span}({\tilde{v}}_{\omega _b})\) with basis \(\{w_{ai}\}\) in \({\mathcal {P}}_a\). Thus, the pair of this simplex \({\mathcal {W}}_{a}\) and the initial marginal distribution \(w_a\), Eq. (21), defines a simplicial quantum state \((w_a, {\mathcal {W}}_{a})\) in the probability space \({\mathcal {P}}_a\). Since the global simplex \({\mathcal {W}}_{c}\) is reduced to a single point in isolation, there is only one choice for \(w_c\) and therefore there is a unique partial LP system.
When \(w_c\) is separable, \({\mathbb {P}}_c(\omega _a|\omega _b) = {\mathbb {P}}_c(\omega _a)\) irrespective of \(\omega _b\) and
so that the simplex \({\mathcal {W}}_{a}\) is reduced to the marginal distribution in isolation \(\{w_a\}\). \(\square\)
Proposition 9
A pure separable simplicial quantum state is a product state.
Proof
The two independent LP systems are trivially e.g. in \({\mathcal {P}}_a\), \(\langle {\tilde{\omega }}_a\rangle ={\mathbb {P}}_a(\omega _a)\) and in \({\mathcal {P}}_b\), \(\langle {\tilde{\omega }}_b\rangle ={\mathbb {P}}_b(\omega _b)\). The concatenation leads in \({\mathcal {P}}_c\) to \(\langle {\tilde{\omega }}_c\rangle ={\mathbb {P}}_c(\omega _c)\) with \(\omega _c=(\omega _a;\omega _b)\) so that \({\mathbb {P}}_c(\omega _c)={\mathbb {P}}_a(\omega _a)\times {\mathbb {P}}_b(\omega _c)\). \(\square\)
3.5.2.2 Construction of a global simplicial quantum state from a pair of reduced states
Given two arbitrary simplicial quantum states in \({\mathcal {P}}_a\) an \({\mathcal {P}}_b\), it is always possible to construct a compatible global state in \({\mathcal {P}}_c\).
Proposition 10
There is always a non-empty set of global simplicial quantum states compatible with an arbitrary pair of partial simplicial quantum states.
Proof
The set of compatible global simplicial quantum state contains the product state and is thus non-empty. \(\square\)
As a result, the restriction of a global simplicial quantum state to a subregister is always possible. Even if the global state \((w_c, {\mathcal {W}}_c)\) is pure, the partial states \((w_a, {\mathcal {W}}_a)\) and \((w_b, {\mathcal {W}}_b)\) are generally mixed, with the exception of separable pure states \((w_c, \{w_c\})\). The simplicial entropy of the subsystem can thus be greater than the entropy of the full system and therefore the simplicial entropy is not extensive. Again, this property is a simple consequence of the Bayesian method and corresponds to the partial trace in standard quantum information theory.
3.5.3 Local Consistency and Non-signaling Correlations
Consider two correlated subregisters \({\textsf{X}}_a\), \({\textsf{X}}_b\) and the partial sample sets \(\Omega _a\), \(\Omega _b\). The joint distribution \({\mathbb {P}}_c(\omega _c)\) is defined on the Cartesian product \(\Omega _c=(\Omega _a,\Omega _b)\). From the definition of a partial subsystem, a local observer has only access to the variables of one subsystem and can only take into account the corresponding marginal probabilities. In other words, each subsystem endowed with its marginal probability distribution is self-consistent and can be considered in isolation.
Proposition 11
The correlations between two partial subsystems subject to a global Bayesian prior are non-signaling.
Proof
From Proposition (10), whatever the second subsystem, the two partial subsystems are compatible. Therefore, any measurement in a subsystem is unable to provide information on the other subsystem. \(\square\)
The non-signaling property is less trivial when some input variables are implicit and considered as parameters. Then, for clarity, the actual variable set can be complemented so that the implicit variables become genuine variables as opposed to only parameters. Similarly, this is also an important feature of the partial trace in quantum information.
We first proved this conclusion in the context of the EPR paradox [19]. The expression “non-signaling correlations” was coined by Barrett et al [20] after a proposal by Popescu and Rohrlich to regard “nonlocality” as an axiom of quantum physics [21].
3.5.4 “Purification” of \((w_a, {\mathcal {W}}_a)\) into \({\mathcal {P}}_c\)
We saw that computing a partial LP system in a single observation window is similar to calculating the partial trace in quantum formalism. This suggests to consider the equivalent of a purification of the simplicial quantum state \((w_a, {\mathcal {W}}_a)\) in \({\mathcal {P}}_a\) with \(r_a>1\) vertices into a pure state \(w_c\) in \({\mathcal {P}}_c\). For convenience, we note “purification” (with quotes) this operation on the source probability space.
Consider the LP system of rank \(m_a\) in \({\mathcal {P}}_a\) with \(m_a=d_a-r_a+1\) extreme points, \(w_i\). It is possible to construct a “purification” of \((w_a, {\mathcal {W}}_a)\) in \({\mathcal {P}}_c\).
Proposition 12
(“Purification”) A simplicial quantum state \((w_a,{\mathcal {W}}_a)\) in a probability space \({\mathcal {P}}_a\) can be considered as the partial system of a pure state \(w_c\) in a probability space \({\mathcal {P}}_c={\mathcal {P}}_a\otimes {\mathcal {P}}_b\).
Proof
Start from
where \(\mu _i\) are the simplicial coordinates of \(w_a\). Define an auxiliary space \({\mathcal {P}}_b\) and suppose that \(d_b\ge r_a\). Construct an arbitrary set of \(r_a\) independent vectors \(v_i\) in the tautological simplex \({\mathcal {W}}_{I_b}\) in \({\mathcal {P}}_b\), i.e. \(v_i\in {\mathcal {W}}_{I_b}\subset {\mathcal {P}}_b\) for \(i\in\left[[1,\;r_a\right]]\). Construct a probability distribution \(w_{c}=(w_{c,\omega _c})=(w_{c,(\omega _a; \omega _b)})\in {\mathcal {P}}_c={\mathcal {P}}_a\otimes {\mathcal {P}}_b\) as
We have clearly,
so that \(w_c\) is indeed a probability distribution in \({\mathcal {P}}_c\) and from Eq. (24)
Then, \(w_a\in {\mathcal {P}}_a\) is effectively the marginal of \(w_c\in {\mathcal {P}}_c\). The “purification” is completed. \(\square\)
Depending upon the particular set of distributions \(\{v_i\}\) in \({\mathcal {P}}_b\) there is a number of possible solutions. For simplicity, it is possible to select \(v_i\) specifically among the basis vectors in \({\mathcal {P}}_b\). Label \(\omega _b\in\left[[1,\;d_b\right]]\) the basis vectors \({\tilde{\omega }}_b\) in \({\mathcal {P}}_b\). Consider the set of \(r_a\) basis vectors \({\tilde{\omega }}_b\in {\mathcal {P}}_b\) for \(\omega _b\in\left[[1,\;r_a\right]]\). For ease of exposition, rename \(\omega _b\) the dummy subscript i in Eq. (24). Rewrite \(w_a=\sum _{\omega _b=1}^{r_a}\mu _{\omega _b} w_{\omega _b}\) and set \(v_{\omega _b}={\tilde{\omega }}_b\in {\mathcal {P}}_b\) for \(\omega _b\in\left[[1,\;r_a\right]]\). Construct the specific probability distribution \(w_{c}=(w_{c,(\omega _a; \omega _b)})\in {\mathcal {P}}_c={\mathcal {P}}_a\otimes {\mathcal {P}}_b\) as
Partial systems and “purifications” in real probability spaces are formally equivalent to partial traces and purifications in Hilbert spaces.
4 Introducing an Auxiliary Hilbert Space
We constructed a Bayesian probability space, \({\mathcal {P}}\), based on an initial batch of N binary queries, constituting the source observation window. In this section, we address the issue of changing the observation window. This leads to the construction of an auxiliary Hilbert space.
4.1 Changing the Current Observation Window
Changing the observation window constitutes a form of contextuality that we will call “window contextuality”.
Definition 24
(Window contextuality) Window contextuality corresponds to the free choice of a particular batch of binary queries.
Obviously, there is a close connection between the current batch of queries and the current sample set \(\Omega\) of the Kolmogorov probability space.
Proposition 13
There is a one-to-one correspondence between the sample set \(\Omega\) defined in the current window and the current batch of binary queries.
Proof
By definition, the basic sample set \(\Omega\) is the ensemble \(\{ \omega \}\) of the \(2^N\) mutually exclusive classical states describing the joint probability distribution of all queries in the current window. \(\square\)
For simplicity, when no confusion can occur, we will name \(\Omega\) both the probability sample set and the corresponding query batch.
4.2 Introducing a Hermitian Metric
By hypothesis, all batches of queries concern the same logical system of total probability 1. Therefore, each observation window \(\Omega\) depicts a particular resolution of this total probability. Thus, irrespective of the current state, for any probability distribution \(p =(p_\omega )\), we have
Proposition 14
Any resolution of the tautology defines a particular observation window. Therefore, to change the observation window, it suffices to change the sample set \(\Omega\).
Proof
Any resolution of the tautology defines a sample set \(\Omega\) and thus, from Proposition (13), an observation window. Conversely, the sample set \(\Omega\) defines a unique set of queries, that is a unique observation window. \(\square\)
For convenience, let us use an equivalent formulation to Eq. (26), as
where \(\theta (\omega )\) is an arbitrary gauge parameter introduced for reasons which will appear later. The real valued probability space on the source window was defined as
Now, Eq. (27) suggests to introduce a Hermitian metric on a complex valued auxiliary space, namely, a finite dimensional Hilbert space \({\mathcal {H}}\) associated to the probability space \(\mathcal {P}\) and defined as
where \(|\omega \rangle\) represent the \(2^N\) basis vectors.
We now propose to transcribe the probability space \({\mathcal {P}}\) into \({\mathcal {H}}\), so as to keep in \({\mathcal {H}}\) the dual forms of \({\mathcal {P}}\). It turns out that this corresponds to the standard “Born rule”. Afterwards, we will specialize this transcription when \({\mathcal {P}}\) is endowed with a simplicial quantum state.
4.3 Born Rule
In the source window, the covectors, \(\textrm{q} = (\textrm{q}_\omega )\in {\mathcal {P}}^*\) are dual of the probability distributions \(p = (p_\omega )\in {\mathcal {P}}\). Irrespective of the current simplicial state, using a relevant transcription rule, it is possible to obtain a similar correspondence in the Hilbert space \({\mathcal {H}}\).
To this end, we propose to transcribe any specific probability vector p in \({\mathcal {P}}\) into a rank 1 projection operator \(\Pi\) acting on \({\mathcal {H}}\) as
Again \(\theta\) is a gauge parameter. From Eq. (26), \(\textrm{Tr}(\Pi ) =1\). We adopt the standard terminology of density operator to denote a Hermitian operator of unit trace. Let \(\textrm{D} ({\mathcal {H}})\) denote the set of density operators. Clearly, \(\Pi \in \textrm{D} ({\mathcal {H}})\).
Furthermore, we propose to transcribe any covector \(\textrm{q} \in {\mathcal {P}}^*\) into a Hermitian diagonal operators \({\textsf{Q}}\), as
where \(\textrm{Herm}({\mathcal {H}})\) is the set of Hermitian operators acting on \({\mathcal {H}}\).
Now, \(\textrm{D}({\mathcal {H}})\subset \textrm{Herm}({\mathcal {H}})\) while \(\textrm{Herm}({\mathcal {H}})\) is a vector space over \(\mathbb {R}\). Therefore, \(\textrm{Tr}({\textsf{Q}}\,\Pi )\) can be viewed as a dual form in \(\textrm{Herm}({\mathcal {H}})\). For ease of exposition, we will say that \(\textrm{Tr}({\textsf{Q}}\,\Pi )\) is a dual form in \({\mathcal {H}}\) while \(\langle \textrm{q}\,p\rangle\) is a dual form in \({\mathcal {P}}\).
Proposition 15
When using the transcription rules, Eqs. (28, 29) for vectors and covectors respectively, the dual forms in \({\mathcal {P}}\) are conserved in \({\mathcal {H}}\).
Proof
We have from a simple calculation,
\(\square\)
We propose to identify this result with the standard “Born rule”.
Definition 25
(Born rule) The Born rule expresses the conservation of the dual forms in the transcription \({\mathcal {P}}\rightarrow {\mathcal {H}}\), Eq. (30).
4.4 Transcription of the Current Probability Space Into the Hilbert Space
The above results, Sect. (4.2), are valid for any probability vector \(p\in {\mathcal {P}}\). We now specifically consider the current probability space endowed with a simplicial quantum states \((w _{\scriptscriptstyle \Lambda }, {\mathcal {W}} _{\scriptscriptstyle \Lambda })\). For clarity, we slightly change the terminology, i.e, p is now the working distribution \(w _{\scriptscriptstyle \Lambda }\) and the projector \(\Pi\) is a special case of density operator, say \(\rho _{\scriptscriptstyle \Lambda }\).
4.4.1 Transcription of Observables
The transcription of observables does not depend on the current state. Therefore we just have to repeat Eq. (29).
Definition 26
(Observables in the source window) In the source window the observables \(Q = (\textrm{q}_\omega )\in {\mathcal {P}}^*\) are transcribed into diagonal Hermitian operators acting on \({\mathcal {H}}\) as
Conversely, a diagonal Hermitian operator acting on \({\mathcal {H}}\) represents an observable. We will later change the basis in \({\mathcal {H}}\). As a result, irrespective of the basis, any Hermitian operator acting on \({\mathcal {H}}\) represents an observable. The operator \({\textsf{Q}}\) will remain Hermitian but obviously will no more remain diagonal.
Proposition 16
Observables are represented by Hermitian operators on the Hilbert space.
Proof
Any Hermitian operator is diagonal in some basis. \(\square\)
The fact that \({\textsf{Q}}\) is diagonal in the source window is expressed by saying that the source window is a “proper window” of the observable \({\textsf{Q}}\).
Definition 27
(Proper window of an observable) The proper window of an observable \({\textsf{Q}}\) on a Hilbert space \({\mathcal {H}}\) is an observation window in which the Hermitian operator \({\textsf{Q}}\) is diagonal.
Any observable is thus calculated in its proper window. So that all the observables can be calculated, all the observation windows must therefore be taken into account.
4.4.2 Transcription of a Pure State
Consider a pure simplicial state \(( w_{\scriptscriptstyle \Lambda },\{w_{\scriptscriptstyle \Lambda }\})\).
Proposition 17
It is possible to transcribe a pure simplicial quantum state \(( w_{\scriptscriptstyle \Lambda },\{w_{\scriptscriptstyle \Lambda }\})\) as a density matrix \(\rho _{\scriptscriptstyle \Lambda }=|a\rangle \langle a|\), with \(|a\rangle =\sum _{\omega \in \Omega } a_\omega |\omega \rangle\)
where \(\theta (\omega )\) is a gauge parameter (possibly 0).
Proof
This corresponds to Eq. (28). \(\square\)
In order to address mixed states, we find convenient to call “Gleason’s vector” the vector \(|a\rangle \in {\mathcal {H}}\).
Definition 28
(Gleason’s vector) A Gleason’s vector is any unit vector \(|a\rangle \in {\mathcal {H}}\) obtained by transcription of a pure state.
4.4.3 Transcription of a Mixed State
A mixed simplicial state, \((w_{\scriptscriptstyle \Lambda }, {\mathcal {W}} _{\scriptscriptstyle \Lambda })\) or equivalently \((\Sigma _\mu , {\mathcal {W}} _{\scriptscriptstyle \Lambda })\), is defined by a simplex \({\mathcal {W}} _{\scriptscriptstyle \Lambda }\) composed of \(r _{\scriptscriptstyle \Lambda }>1\) extreme points \(w_i\) in \({\mathcal {P}} _{\scriptscriptstyle \Lambda }\) and a set \(\Sigma _\mu =\{\mu _i\}\) of simplicial coordinates.
Proposition 18
A mixed simplicial quantum state \((\Sigma _\mu , {\mathcal {W}} _{\scriptscriptstyle \Lambda })\) can be transcribed as a density operator \(\rho _{\scriptscriptstyle \Lambda }\). Each extreme point \(w_i\) of the simplex is transcribed independently as a projector \(|a_i\rangle \langle a_i|\), where the vector \(|a_i\rangle\) is the Gleason’s vector of the pure state \(w_i\), while the simplicial coordinates \(\mu _i\) are conserved. Then
In general, the unit vectors \(|a_i\rangle\) are not orthogonal. An orthonormal array \(|e_i\rangle\) is easily obtained by diagonalizing the density operator \(\rho _{\scriptscriptstyle \Lambda }\) as,
Proof
The working distribution \(w _{\scriptscriptstyle \Lambda }\) can be viewed as a weighted combination of \(r _{\scriptscriptstyle \Lambda }>1\) auxiliary pure states of working distributions \(w_i\) in \({\mathcal {P}} _{\scriptscriptstyle \Lambda }\) for \(i\in\left[[1,\;r_{\scriptscriptstyle \Lambda }\right]]\). Since the weighting coefficients \(\mu _i\) are independent of the simplex itself, the mixed state must be transcribed for consistency as the same weighted combination of the r transcribed projectors \(|a_i\rangle \langle a_i|\) of the auxiliary pure states \(w_i\). From Eq. (32), we obtain Eq. (33) and next Eq. (34) conserving the same rank \({r _{{\scriptscriptstyle \Lambda }}}\). \(\square\)
Gauge selection can be derived for the gauge selection of a pure state. To this end, we can use the purification procedure defined in Sect. (3.5.4).
Proposition 19
The transcription of a mixed simplicial state can be implemented by (1) “purifying” this mixed state, (2) transcribing the simplicial pure state to obtained a standard quantum pure state and (3) tracing out this pure state.
Proof
We proceed in three steps. (1) “Purify” the simplicial quantum state \(\{ w _{\scriptscriptstyle \Lambda }, {\mathcal {W}} _{\scriptscriptstyle \Lambda } \}\) of rank \(r _{\scriptscriptstyle \Lambda }\) defined in the real probability space \({\mathcal {P}} _{\scriptscriptstyle \Lambda }\) into a pure state \(w_c\) living in an auxiliary space \({\mathcal {P}}_c={\mathcal {P}} _{\scriptscriptstyle \Lambda }\otimes {\mathcal {P}}_b\), as described in Sect. (3.5.4). (2) Transcribe the pure state \(w_c\) into a projection operator \(|c\rangle \langle c|\) defined in a Hilbert space \({\mathcal {H}}_c={\mathcal {H}} _{\scriptscriptstyle \Lambda }\otimes {\mathcal {H}}_b\). (3) Compute the partial trace over \({\mathcal {H}}_b\) of the projection operator \(|c\rangle \langle c|\) to obtain the relevant density operator \(\rho _{\scriptscriptstyle \Lambda }\) in \({\mathcal {H}} _{\scriptscriptstyle \Lambda }\). Step (1) has been defined in Sect. (3.5.2). Consider a real probability space \({\mathcal {P}}_b\) of dimension \(d_b\ge r _{\scriptscriptstyle \Lambda }\). Assume that \(d_b=r _{\scriptscriptstyle \Lambda }\) and select the set of \(r _{\scriptscriptstyle \Lambda }\) basis vectors in \({\mathcal {P}}_b\), as described by Eq. (25),
where we changed the dummy subscripts “i” into “\(\omega _b\)” for clarity.
Step (2) has been defined just above (Proposition 17). Let us denote \(|c\rangle\) the Gleason’s vector and \(c_{(\omega _{\scriptscriptstyle \Lambda };\omega _b)}\) its entries.
Step (3) is a standard operation in quantum information with a unique solution. Resuming the subscripts “\(\omega _b\)” into “i”, we obtain
We have recovered Eq. (33) as required. \(\square\)
Gauge Selection Any particular feasible Gleason’s vector \(|c\rangle\) constructed in Step (2) corresponds to a gauge selection, as described for pure states.
4.4.4 Transcription of Dual Forms
By construction, dual forms are conserved.
Theorem 2
Irrespective of the gauge, the expectation of an observable is
Proof
\(Q (w _{\scriptscriptstyle \Lambda }) = \sum _{\omega \in \Omega } \textrm{q}_\omega w _{\scriptscriptstyle \Lambda , \omega }\). Born’s rule applies. \(\square\)
5 General Systems
In this section and the followings, we will treat the auxiliary Hilbert space \({\mathcal {H}}\) as the standard Hilbert space of conventional quantum information theory. The difference is that every new basis of \({\mathcal {H}}\) defines a particular observation window \(\Omega _i\) and therefore a new probability space \({\mathcal {P}}_i\) (Fig. 1).
General system. The source window \(\Omega _0\) is associated with a probability space, \({\mathcal {P}}_0\) endowed with a simplicial quantum state, \((w_0, {\mathcal {W}}_0)\). The space \({\mathcal {P}}_0\) is transcribed into an auxiliary Hilbert space \({\mathcal {H}}\) with a basis also called \(\Omega _0\) and the simplicial quantum state, \((w_0, {\mathcal {W}}_0)\) is transcribed into a density operator \(\rho ^{(0)}\). When changing the basis in \({\mathcal {H}}\) from \(\Omega _0\rightarrow \Omega _i\), the window changes accordingly, the density operator expression changes from \(\rho ^{(0)}\) to \(\rho ^{(i)}\) and the new simplicial quantum state \((w_i, {\mathcal {W}}_i)\) is computed by reverse transcription \({\mathcal {H}}\rightarrow {\mathcal {P}}_i\)
In each observation window, the “factual” entity is the probability space while the Hilbert space is an auxiliary tool. Therefore, the ultimate justification for any rule in \({\mathcal {H}}\) must be found in the probability spaces \(\mathcal {P} _i\), obtained by reverse transcription. In particular, identical reverse transcriptions express an exact symmetry of \({\mathcal {H}}\).
Let us address the reverse transcription technique.
5.1 Reverse Transcription into a Source System
Reverse transcription is always possible, so any window can be considered a source window with the exception of a few exceptional windows which we will call “blind”.
5.1.1 Reverse Transcription of a Pure State
Let \(\rho _{\scriptscriptstyle \Lambda }= |e\rangle \langle e|\) denote a pure density matrix in \({\mathcal {H}}\). Construct a real probability space \({\mathcal {P}}\) of dimension \(d=2^N\). From Eq. (32), the working distribution is \(w_{\scriptscriptstyle \Lambda }= |e|^2\in {\mathcal {P}}\), i.e. \(w_{{\scriptscriptstyle \Lambda },\omega }= |e_\omega |^2\). The simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) is reduced to the isolated vertex \(\{w_{\scriptscriptstyle \Lambda }\}\).
Proposition 20
A density operator \(\rho _{\scriptscriptstyle \Lambda }= |e\rangle \langle e|\) of rank 1 is reverse-transcribed as a simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }=\{w_{\scriptscriptstyle \Lambda }\}\) composed of an isolated vertex \(w_{{\scriptscriptstyle \Lambda }}=(w_{{\scriptscriptstyle \Lambda },\omega })\) with \(w_{{\scriptscriptstyle \Lambda },\omega }= |e_\omega |^2\).
LP SystemThe vector \(w_{\scriptscriptstyle \Lambda }= {\mathbb {P}}(\omega )\) is trivially the solution of the Bayesian linear system \(p=|e|^2\) of rank \(m=d\) as
where \({\tilde{\omega }}^*\) is the indicator function corresponding to the classical state \(\omega\). The normalization of the probability distribution arises from the normalization of e.
5.1.2 Reverse Transcription of a Mixed State
We are going to propose two different techniques to reverse backwards mixed states: One using purification is rather opaque but always valid. The second generalizes the technique used for pure states but is not valid for “blind windows” defined just below.
Start from a density operator \(\rho _{\scriptscriptstyle \Lambda }\) of rank r acting on a standard Hilbert space \({\mathcal {H}}\) (Eq. 34) as
where the r vectors \(|e_i\rangle\) form an orthonormal array in \({\mathcal {H}}\). Construct a real probability space \({\mathcal {P}}\) of dimension \(d=2^N\) and let \({\mathcal {W}}_{\scriptscriptstyle I}\) be the tautological simplex in \({\mathcal {P}}\), Definition (6). Construct the vectors \(v_i= |e_i|^2=(v_{i,\omega })\in {\mathcal {W}}_{\scriptscriptstyle I}\) as \(v_{i,\omega } =|e_{i,\omega }|^2\) and \(w_{\scriptscriptstyle \Lambda }= \sum _{i=1}^r \lambda _i v_i\). Clearly, \(w_{\scriptscriptstyle \Lambda }\in {\mathcal {P}}\) is a probability distribution. The rank of the vectors \(\{ v_i\}\) is crucial.
5.1.2.1 Regular Versus Blind Windows
A “regular” window is a window in which transcription and reverse transcription are reversible. Thus, the rank is conserved by reverse transcription.
Definition 29
(Regular window, blind window) A window of rank r is “regular” when the r extreme orthonormal vectors \(|e_i\rangle\) in the Hilbert space are reverse transcribed as a system \(v_i = |e_i|^2\) of same rank r in the probability space. Otherwise, the window is called “blind”.
In particular, a pure window is trivially regular. It carries N information bits. By contrast, we will see that a blind window carries no information (see Sect. 7.5 below). As a result, a blind window is unable to serve as a “source window”.
5.1.2.2 Reverse Transcription By Purification of the Window
Let \({\mathcal {H}}_b\) be an auxiliary Hilbert space of dimension r. It is always possible to purify the mixed state into a Hilbert space \({\mathcal {H}}_c={\mathcal {H}}\otimes {\mathcal {H}}_b\) of dimension \(d\times r\), and next to reverse transcribe the pure state into a probability space \({\mathcal {P}}_c={\mathcal {P}}\otimes {\mathcal {P}}_b\) as in Sect. (5.1.1). The quantum state \((w_{\scriptscriptstyle \Lambda }, {\mathcal {W}}_{\scriptscriptstyle \Lambda })\) is then computed by applying Proposition (8).
Alternatively, it is possible to reverse transcribe a regular window by extending the method used in pure windows as follows.
5.1.2.3 Reverse Transcription of a Regular Window
Construct the r-dimensional subspace \(\mathbb {W}_r=\textrm{Span}_i(v_i)\subseteq {\mathcal {P}}\) and the tautological simplex \({\mathcal {W}}_{\scriptscriptstyle I}\) in \({\mathcal {P}}\). Identify \(\mathbb {W}_r\) with an effective probability space and define the polytope
The simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) admits r equivalent vertices, say \(w_j\). Since \(w_{\scriptscriptstyle \Lambda }\) is a probability distribution and \(w_{\scriptscriptstyle \Lambda }\in \mathbb {W}_r\), then \(w_{\scriptscriptstyle \Lambda }\in {\mathcal {W}}_{\scriptscriptstyle \Lambda }\) so that
for a specific set of simplicial coefficients \(\mu _j\). Finally, the reverse transcribed simplicial quantum state is \((w_{\scriptscriptstyle \Lambda }, {\mathcal {W}}_{\scriptscriptstyle \Lambda })\). From the demonstration in Sect. (4.4.3), this explicit method is consistent with the purification procedure and provides the same result.
Finally, we reach the final result,
Theorem 3
(Quantum state) A quantum state can be represented either by a standard density operator \(\rho _{\scriptscriptstyle \Lambda }\) in a Hilbert space \({\mathcal {H}}\) or by a simplicial quantum state, i.e. a working distribution \(w_{\scriptscriptstyle \Lambda }\) within a simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) in a real probability space \({\mathcal {P}}\). For a definite simplicial state (\(w_{\scriptscriptstyle \Lambda }, {\mathcal {W}}_{\scriptscriptstyle \Lambda }\)) in \({\mathcal {P}}\), the corresponding density operator \(\rho _{\scriptscriptstyle \Lambda }\) in \({\mathcal {H}}\) is defined up to a gauge selection.
5.1.3 Reverse Transcription of an Observable
We are given an observable \({\textsf{Q}}\), i.e. an Hermitian operator acting on a Hilbert space. Recall from Definition (3) that an observable is a real-valued function on a sample set \(\Omega\). Therefore, the observable can only be reverse transcribed in its proper window.
Theorem 4
Any observable represented by a Hermitian operator \({\textsf{Q}}\) acting on the Hilbert space \({\mathcal {H}}\) can be reversed transcribed in its proper window as a covector \(\textrm{q}_\omega\) in the probability space of \({\mathcal {P}}\).
Proof
Construct the probability space \({\mathcal {P}}\) of the \({\textsf{Q}}\) proper window. The entries of \(\textrm{q}\in {\mathcal {P}}^*\) are the eigenvalues of \({\textsf{Q}}\). \(\square\)
5.2 Principal Window
It is always possible to diagonalize the density matrix \(\rho _{\scriptscriptstyle \Lambda }\) in \({\mathcal {H}}\) by means of a unitary channel. This particular window is called “principal window” because it contains on its own all the Shannon information of the Bayesian theater, although in fact the principal basis is not unique when the eigenvalues are not all distinct.
Definition 30
(Principal window, twisted window) A principal window is an observation window in which the density operator is diagonal. Otherwise, the window is twisted.
Let \(|\omega _i\rangle\) be the d basis vectors of the Hilbert space \({\mathcal {H}}\) in a principal observation window. Let \(|e_i\rangle\) denote the eigenvectors normalized to unity and \(\lambda _i\) the eigenvalues of the density operator \(\rho _{\scriptscriptstyle \Lambda }\). Since \(\rho _{\scriptscriptstyle \Lambda }\) is diagonal, we have \(|e_i\rangle =|\omega _i\rangle\) up to arbitrary gauge phase factors. After reordering the basis vectors if necessary, we can assume that the eigenvalues \(\lambda _i\) are sorted in descending order. The density operator reads
Then, \(\sum _i\lambda _i=1\) and irrespective of the gauge factors
Proposition 21
In a principal window, the expression of the density operator \(\rho _{\scriptscriptstyle \Lambda }\) is independent of the gauge.
Proof
Gauge transformations just change the phases of the Gleason’s vector. Diagonal matrices are not affected. \(\square\)
The Hilbert space \({\mathcal {H}}\) is the direct sum of the eigensubspaces \({\textsf{h}}_k\) of the density operator \(\rho _{\scriptscriptstyle \Lambda }\) as \({\mathcal {H}}= \bigoplus _k {\textsf{h}}_k\). Let \({\textsf{A}}_k\) denote the orthogonal projector of \({\mathcal {H}}\) on \({\textsf{h}}_k\) and let \(n_e\) be the number of distinct values of multiplicity \(d_k\). Let \(\alpha _k\) be the common eigenvalues \(\lambda _i\) in \({\textsf{h}}_k\), ending with \(\alpha _{n_e}=0\), so that \(\sum _k n_k\alpha _k =1\). Then, irrespective of the gauge,
5.2.1 Reverse Transcription of a Principal Window
The reverse transcription of a principal window leads to a strictly conventional joint probability problem on the principal sample set \(\Omega\), with the distribution \(\mathbb {P}(\omega _i) = \lambda _i\). As a result, the principal window can immediately be interpreted in terms of standard probability distribution on the Boolean classical states.
Proposition 22
(Principal probability distribution) A principal window is always regular. Its reverse transcription into a probability space \({\mathcal {P}}\) leads to a simplicial quantum state \((w_{\scriptscriptstyle \Lambda }, {\mathcal {W}}_{\scriptscriptstyle \Lambda })\) describing a strictly classical distribution. The vertices \(w_i\) of the simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) are basic vectors in \({\mathcal {P}}\), i.e. deterministic states, \(w_i={\tilde{\omega }}_i\), \(\forall i\in\left[[1,\;r\right]]\) and the principal probability distribution is \(\mathbb {P}(\omega _i) = \lambda _i\), \(\forall i\in\left[[1,\;d\right]]\).
Proof
Construct a real-valued d-dimensional probability space \({\mathcal {P}}\) with basis \(\{{\tilde{\omega }}_i\}\). Let \(w_i={\tilde{\omega }}_i\in {\mathcal {P}}\) for \(i\in\left[[1,\;r\right]]\), so that the rank of the vector set \(\{w_i\}\) is r. Define \({\mathcal {W}}_{\scriptscriptstyle \Lambda }=\textrm{conv}(w_i)\) and \(w_{{\scriptscriptstyle \Lambda },\omega _i} = \lambda _i\), so that the working distribution is
By inspection, from Eq. (33), the direct transcription of the quantum state \((w_{{\scriptscriptstyle \Lambda }},{\mathcal {W}}_{\scriptscriptstyle \Lambda })\) is indeed the diagonal operator \(\rho _{\scriptscriptstyle \Lambda }\). In addition, the rank r of the density operator \(\rho _{\scriptscriptstyle \Lambda }\) is equal to the number of vertices of the simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\), which proves that the system is regular. \(\square\)
Proposition 23
(Independent binary variables) A principal window corresponds to a batch of N mutually independent Boolean variables.
Proof
In a principal window, all basic vectors of the probability space are deterministic solutions of the LP problem. Therefore, from Proposition (2) and Sect. 3.5.1, the binary variables are mutually independent. \(\square\)
From Eq. (37) any projector \({\textsf{A}}_k\) is a diagonal Hermitian operator with entries 0 or 1 and \(\textrm{Tr}( {\textsf{A}}_k)=d_k\). It also represents an observable whose reverse transcription is the indicator function of some Boolean function, say \(A_k\). For simplicity, we note \(A_k\) both the Boolean function itself in the Boolean algebra and its indicator function in \({\mathcal {P}}^*\).
The Principal Bayesian LP ProblemNow, we aim to recover the Bayesian system, that is the relevant LP problem in \({\mathcal {P}}\).
Proposition 24
When \(r<d\), the principal LP problem can be formulated as
When \(r=d\), the prior \((\Lambda )\) is reduced to the implicit normalization equation.
Proof
The r basis vectors \({\tilde{\omega }}_{i }\) span the effective probability space \(\mathbb {W}_r\subseteq {\mathcal {P}}\) and the specific simplex \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) is the tautological simplex \({\mathcal {W}}_{r}\) in \(\mathbb {W}_r\). The r vertices of the simplex in the probability space \({\mathcal {P}}\) are therefore the basic vectors \({\tilde{\omega }}_{i}\) for \(i\in\left[[1,\;r\right]]\). Complement the r basis vectors \({\tilde{\omega }}_{i }\) by \(d-r\) other basis vectors \({\tilde{\omega }}_{i'}\) in \({\mathcal {P}}\). In Eq. (38), \({\tilde{\omega }}_{i'}^*\) denote the \(d-r\) indicator functions corresponding to the classical states \(\omega _{i'}\). \(\square\)
As a result, the core of any Bayesian system is simply limited to its order r. Consequently, the main actual input is the contextual distribution.
The indicator function \({A}_{n_e}\in {\mathcal {P}}^*\) depicts the \(d_{n_e}=d-r\) vertices \({\tilde{\omega }}'_{i}\) of zero probability, \(\lambda _{n_e}=0\). Taking into account the other contextual multiplicities, let \({A}_k\in {\mathcal {P}}^*\) denote the indicator function of the union of all \(d_{k}\) vertices \({\tilde{\omega }}_{i}\) corresponding to the same probability \(\alpha _k\). Since the eigenvalues are sorted in descending order, \(A_k\) is the indicator function of a set of basic vectors with contiguous indexes, say \(k_1\) to \(k_2\), with \(d_k\) non zero entries, for instance, \(A_k\) may be the covector \((0,0,0,1,1,1,1, 0,0,0)\in {\mathcal {P}}^*\).
Now, for all \(k\in\left[[1,\;n_e\right]]\), the dual form \(\langle A_k\,p\rangle\) with \(p\in {\mathcal {P}}\) is \(\langle A_k\,p\rangle =\sum _{i=k_1}^{k_2} p_i\) while the expectation \(\langle A_k\,w_{\scriptscriptstyle \Lambda }\rangle\) is \(\langle A_k \rangle =d_k\alpha _k\). Clearly, the system is invariant under arbitrary permutation of the \(d_k\) indexes of same mixed probability \(\alpha _k\). This defines a contextual symmetry.
Definition 31
(Contextual symmetry) A contextual symmetry is a transformation of the sample set \(\Omega\) in a principal window, leaving invariant the mixed probability distribution.
Proposition 25
The contextual symmetry group is the direct product \(\textrm{S}_{d_{1}}\times \textrm{S}_{d_{2}}\times \dots \textrm{S}_{d_{n_e}}\) of the permutation symmetric groups of degree \(d_k\).
Proof
Any product of vertex permutations of same mixed probability \(\alpha _k\) is a contextual symmetry by definition. \(\square\)
Note that from Proposition (24), strictly speaking, the symmetry group does not depend on the context but on the core LP problem.
5.2.2 Fundamental Theorem
A principal window depicts a conventional probability problem, composed of d deterministic outcomes mutually exclusive, namely \(\omega _i\in \Omega\) with \(i\in\left[[1,\;d\right]]\), and a standard probability distribution, \(\Sigma _{\scriptscriptstyle \Lambda }=\{\lambda _i\}\), on the sample set \(\Omega\). Only \(r\le d\) probability masses \(\lambda _i\) are non-zero.
Theorem 5
(Fundamental theorem) Any density operator \(\rho _{\scriptscriptstyle \Lambda }\) of spectrum \(\Sigma _{\scriptscriptstyle \Lambda }=\{\lambda _i\}\) in a Hilbert space \({\mathcal {H}}\) is the image by a unitary channel of a strictly conventional probability problem consisting in drawing one object among d deterministic classical states \({\omega }_i\in \Omega\) with respect to the contextual probability distribution \(\Sigma _{\scriptscriptstyle \Lambda }\). The Shannon entropy of this conventional problem is the von Neumann entropy of the density operator on \({\mathcal {H}}\).
Proof
Just diagonalize the density operator. \(\square\)
In fact, much of this has been known since von Neumann [22] and the only novelty lies in the interpretation: Now, from Theorem (5), a Bayesian theater represents a quite classical logical system. In particular, entanglement is a property of the variable batch and not of the problem itself.
Proposition 26
A pure quantum state depicts a deterministic distribution expressed in the principal sample set.
Proof
By definition, a pure state is of rank 1 and thus deterministic in a principal window. \(\square\)
This can be expressed in striking form: With a relevant discrete Boolean gauge, a pure state represents just a reset register.
Proposition 27
It is always possible to choose a discrete Boolean gauge so that the deterministic distribution of a pure state coincides with the empty atom \(\varpi _0\), that is a reset register composed of N zeros, \((0,0,\dots ,0)\).
Proof
This is a consequence of the discrete Boolean gauge definition, Definition (2). For each variable required to be valid, just change its gauge so that the variable becomes required to be invalid. \(\square\)
5.2.3 Information Expressions
In a principal window, three probability distributions are identical: (1) the working distribution \(w_{\scriptscriptstyle \Lambda }\) in the sample set \(\Omega\), (2) the simplicial distribution \(\mu _i\) of the contextual distribution in \(\Sigma _\mu\) and (3) the distribution \(\lambda _i\) in the spectrum \(\Sigma _{\scriptscriptstyle \Lambda }\) of the density operator \(\rho _{\scriptscriptstyle \Lambda }\).
Entropy Let us recall the definition of the entropy of these different distributions in general.
Definition 32
(Forms of entropy)
-
The entropy of the working distribution \(w_{\scriptscriptstyle \Lambda }\) in a particular window is the working entropy \(S_w=\mathbb {H}(w)\).
-
The entropy of the contextual distribution in a particular window is the simplicial entropy \(S_\mu =\mathbb {H}(\Sigma _\mu )\). We will use interchangeably the terms “simplicial entropy” and “contextual entropy”.
-
The entropy of the Bayesian theater is the von Neumann entropy \(S_{\scriptscriptstyle \Lambda }=S(\rho _{\scriptscriptstyle \Lambda })=\mathbb {H}(\Sigma _{\scriptscriptstyle \Lambda })\). We will use interchangeably the terms “von Neumann entropy” and “mixed entropy”.
The von Neumann entropy \(S(\rho _{\scriptscriptstyle \Lambda })\) is invariant under a unitary channel and can be regarded as the global “theater entropy” while the window entropy \(S_w\) and the simplicial entropy \(S_\mu\) are window-dependent by definition.
Proposition 28
In a principal window, we have
Proof
By simple inspection, in a principal window, the three distributions are identical and therefore the entropies are identical as well. \(\square\)
By contrast, in a general window the three entropies are distinct.
Proposition 29
(Jaynes’ inequality) The von Neumann entropy \(S(\rho _{\scriptscriptstyle \Lambda })=\mathbb {H}(\Sigma _{\scriptscriptstyle \Lambda })\) is bounded above by the simplicial entropy in any window \(S_\mu =\mathbb {H}(\Sigma _\mu )\).
Proof
This inequality is due to Jaynes (Ref. [23], Appendix A). \(\square\)
Proposition 30
The von Neumann entropy is the lower bound of the simplicial entropy over all possible windows.
Proof
From Jaynes’ inequality, Proposition (29), \(S_{\scriptscriptstyle \Lambda }\le S_\mu\). From Proposition (28), the inequality is saturated in a principal window. \(\square\)
The upper bound of the simplicial entropy is trivially \(\log r\) when the working distribution coincides with the center of mass of the specific simplex.
At last, it is convenient to define also the overall information, or von Neumann negentropy, as \(\mathbb {I}(\rho _{\scriptscriptstyle \Lambda })=N-S(\rho _{\scriptscriptstyle \Lambda })\).
Definition 33
(von Neumann information) The von Neumann information, or von Neumann negentropy of a density operator \(\rho _{\scriptscriptstyle \Lambda }\) acting on a d-dimensional Hilbert space is \(\mathbb {I}(\rho _{\scriptscriptstyle \Lambda }]=N-S(\rho _{\scriptscriptstyle \Lambda })\), where \(d=2^N\) and \(S(\rho _{\scriptscriptstyle \Lambda })= -\textrm{Tr}(\rho _{\scriptscriptstyle \Lambda }\log _2\rho _{\scriptscriptstyle \Lambda })\).
Theorem 6
The information content of a N bit Bayesian theater endowed with density operator \(\rho _{\scriptscriptstyle \Lambda }\) is the von Neumann information \(N- S(\rho _{\scriptscriptstyle \Lambda })\)
Proof
By reverse transcription in the principal window, this corresponds to the probability distribution \(\{\lambda _i\}\). \(\square\)
6 Gauge Transcription Group
The gauge group stems from the transcription of a simplicial quantum state \((w, {\mathcal {W}})\) from the information domain \({\mathcal {P}}\) to a geometric domain, \({\mathcal {H}}\). This transcription is not uniquely defined, which generates the group, say \({\mathfrak {G}}\). In the present model, it is thus intrinsic.
By construction, it expresses the exact symmetry of the Hilbert space. Remarkably, it represents the Bayesian prior, except for its contextual distribution.
Since the probability distribution is conserved, from Wigner theorem, gauge operators are either unitary or antiunitary.
Choosing another transcription is called “changing the gauge”. This can be done either by using a new Hilbert space while keeping the same window (what is called “global gauge”), or by keeping the same Hilbert space but changing the window (which is called “local gauge”).
For simplicity, we will only detail the global gauge.
6.1 Global Gauge
Start from a given simplicial quantum state and consider its transcription into a Hilbert space. The transcription is performed from the source window which determines a particular gauge, say g, and requires a particular Hilbert space, \({\mathcal {H}}_{g}\). Actually, the particular source window itself is widely indifferent because it is straightforward to perform the transcription from any other regular window.
Proposition 31
For any gauge g, it is possible to construct a unique Hilbert space \({\mathcal {H}}_{g}\) irrespective of the regular source window used for the transcription.
Proof
Transcribe the simplicial quantum from a source window. This defines a gauge g and determines both a particular density operator and, by reverse transcription, a particular simplicial quantum state in every window (Fig. 1). Now just decide that some particular regular window is the new source window and that the corresponding density operator is precisely the result of the direct transcription with the same gauge referred to as g. \(\square\)
Definition 34
(Global gauge) A global gauge representation g is the specific transcription of the logical system into a specific Hilbert space \({\mathcal {H}}_g\).
6.2 Changing the Global Gauge
Consider a second gauge \(g'\) and therefore a new Hilbert space \({\mathcal {H}}_{g'}\). Let \(\rho _{g}\) and \(\rho _{g'}\) denote the density operators acting on \({\mathcal {H}}_{g}\) and \({\mathcal {H}}_{g'}\) respectively. First, make sure that as far as \(g'\ne g\), \({\mathcal {H}}_{g}\) and \({\mathcal {H}}_{g'}\) are distinct.
Proposition 32
When the gauge is global, distinct gauges require distinct Hilbert spaces.
Proof
From Proposition (21), irrespective of the gauge, the density operators are identical in a principal window. If the Hilbert spaces were the same for every gauge, the density operators would be also identical in every windows and the gauges would not be distinct. \(\square\)
Proposition 33
Any change from a gauge g to a gauge \(g'\) maps the eigensubspaces of \(\rho _g\) onto the eigensubspaces of \(\rho _{g'}\).
Proof
Since the expressions of the density operators are identical in the two principal windows, the eigensubspaces are globally invariant. \(\square\)
Let \(\Theta : {\mathcal {H}}_{g}\rightarrow {\mathcal {H}}_{g'}\) denote a gauge operator. For every window, the bases in the two Hilbert spaces are identical. As a result, when changing the source window, the expression of \(\Theta\) changes according to the transition matrix.
Proposition 34
Using another source window \(\Omega '\) obtained from the initial source window \(\Omega\) by a unitary transition matrix \({\textsf{U}}\in \textrm{U}(d)\), the gauge operator \(\Theta \in {\mathfrak {G}}\), whether unitary or antiunitary is expressed as
Proof
Since the gauge is global, the two bases \(\Omega\) and \(\Omega '\) are by hypothesis identical in the two distinct Hilbert spaces \({\mathcal {H}}_{g}\) and \({\mathcal {H}}_{g'}\). As a result, the transition unitary matrices \({\textsf{U}}\) are also identical. Let \(|\psi \rangle _g\) denote a current vector of the Hilbert space \({\mathcal {H}}_{g}\).

From simple inspection of the commutative diagram we have \(|\psi '_{g}\rangle =\textsf{U}|\psi _g\rangle\) and \(|\psi '_{g'}\rangle =\textsf{U}|\psi _{g'}\rangle\) so that, irrespective of \(|\psi _g\rangle\), \(|\psi '_{g'}\rangle =\Theta '\textsf{U}|\psi _g\rangle = \textsf{U}\Theta |\psi _g\rangle\) and thus \(\Theta ' = \textsf{U}\Theta \textsf{U}^{-1}\). \(\square\)
Since from Proposition (31) the source window is indifferent, it is convenient to select henceforth the source window as a principal window corresponding to a batch of mutually independent Boolean variables. The gauge operators \(\Theta\) can be unitary or antiunitary. Let us start by investigating the set of unitary operators, that is the unitary gauge group.
6.3 The Unitary Gauge Group \({\mathcal {G}}\)
Obviously, the unitary transformations of a global gauge into another global gauge form a unitary group.
Definition 35
(Unitary gauge group \({\mathcal {G}}\)) The unitary gauge group \({\mathcal {G}}\) is the unitary transformation group of the global gauges.
Proposition 35
The unitary group \({\mathcal {G}}\) is the group of unitary operators leaving invariant the eigensubspaces of the density operator expressed in any particular gauge.
Proof
From Proposition (21), the eigensubspaces of the density operator are invariant under every gauge transformation and conversely, any unitary transformation leaving invariant these eigensubspaces leaves invariant the density operator in any principal window and thus defines a gauge change. \(\square\)
Constructing the Unitary Gauge Group \({\mathcal {G}}\) We will hereafter regard the unitary gauge group \({\mathcal {G}}\) as realized by unitary matrices acting on the d-dimensional Hilbert space \({\mathcal {H}}_{g_0}\) for an arbitrary but fixed gauge \(g_0\) and expressed in a common principal basis, so that the group is isomorphic to a subgroup of the standard unitary matrix group \(\textrm{U}(d)\).
In the principal window, after reordering the basis vectors if necessary, suppose that the eigenvalues \(\lambda _i\) of the density operator \(\rho _{g_0}\) are sorted in descending order. Let \(|\omega _i\rangle \in {\mathcal {H}}_{g_0}\) for \(i\in\left[[1,\;d\right]]\) denote the basis vectors. The Hilbert space \({\mathcal {H}}_{g_0}\) is the direct sum of the eigensubspaces \({\textsf{h}}_k\) of the density operator \(\rho _{g_0}\) as \({\mathcal {H}}_{g_0}= \bigoplus _k {\textsf{h}}_k\). Let \({\textsf{A}}_k\) denote the orthogonal projectors \({\mathcal {H}}_{g_0}\rightarrow {\textsf{h}}_k\subseteq {\mathcal {H}}_{g_0}\) and let \(n_e\) be the number of distinct eigenvalues \(\alpha _k\) of multiplicity \(d_k\), including possibly zero. Then, from Eq. (37),
Proposition 36
The unitary gauge group \({\mathcal {G}}\) is a Lie group of dimension \(\sum _k d_k^2\) isomorphic to the direct product \(\textrm{U}(d_1)\times \textrm{U}(d_2)\times \textrm{U}(d_3)\dots \times \textrm{U}(d_{n_e})\), where \(\textrm{U}(d_k)\) are respectively the unitary groups acting on the \(d_k\)-dimensional eigensubspaces \({\textsf{h}}_k\) of the density operator.
Proof
By construction, the Hilbert space \({\mathcal {H}}_{g_0}\) is a linear representation of dimension d of the gauge group \({\mathcal {G}}\). On each subspace \({\textsf{h}}_k\) of dimension \(d_k\), (\(k\in\left[[1,\;n_e\right]]\)), \({\mathcal {G}}\) acts as the full unitary group \(\textrm{U}(d_k)\) so that any subspace \({\textsf{h}}_k\) is a linear representation of dimension \(d_k\). Finally \({\mathcal {H}}_g\) is a completely decomposable representation of \({\mathcal {G}}\). As a result, each subgroup \(\textrm{U}(d_k)\) is normal in \({\mathcal {G}}\) and \({\mathcal {G}}\) is the direct product \(\textrm{U}(d_1)\times \textrm{U}(d_2)\times \textrm{U}(d_3)\dots \times \textrm{U}(d_{n_e})\). The dimension of a unitary Lie group \(\textrm{U}(d_k)\) is \(d_k^2\), so that the dimension of the \(n_e\)-tuple is \(\sum _{k=1}^{n_e} d_k^2\). \(\square\)
Conversely, the set of eigensubspaces \(\{{\textsf{h}}_k\}\) determines the density operator, up to a possible rescaling of the mixed distribution \(\{\alpha _k\}\) leaving the multiplicities unchanged, allowing just a modification of the source contextuality. By contrast, a complete rescaling of the mixed distribution \(\{\lambda _i\}\) can e.g. increase the number of eigensubspaces, which would express a break of symmetry.
Proposition 37
There is a one-to-one correspondence between the unitary gauge subgroups \(\textrm{U}(d_k)\) and the intrinsic symmetry subgroups \(\textrm{S}_k\), Definition (31). Moreover, the intrinsic symmetry group is a discrete subgroup of the Lie gauge group.
Proof
The unitary gauge group and the intrinsic symmetry group are both determined by the same set \((d_k)\) of the \(n_e\) multiplicities. Moreover, from Proposition (25), the gauge group contains any permutation of the basis vectors in a principal window, leaving invariant the eigensubspaces, that is the intrinsic symmetry group. \(\square\)
Reversing the logic, the unitary gauge group \({\mathcal {G}}\) determines to some extent the density operator. In fact, the group of gauges does not specify the contextual distribution and is equivalent to simply giving the specific simplex, that is the LP system.
Theorem 7
(Correspondence between the unitary gauge group and the quantum state) The unitary gauge group \({\mathcal {G}}\) determines the quantum state up to a rescaling of the mixed distribution \(\{\alpha _k\}\). Conversely, the quantum state is specified by the set \(\{d_k, \alpha _k\}\) with \(\sum d_k=d\) and \(\sum d_k\alpha _k=1\) for \(k\in\left[[1,\;n_e\right]]\).
Proof
The gauge groups are direct products of subgroups \(\textrm{U}(d_k)\). Therefore the set \(\{d_k\}\) is completely determined by \({\mathcal {G}}\). The eigenvalues \(\{\alpha _k\}\) of the density operator can be arbitrary chosen provided they be positive, distinct and sum to 1 when accounting for the multiplicity. Therefore the quantum state is determined by the set \(\{d_k, \alpha _k\}, k\in\left[[1,\;n_e\right]]\). \(\square\)
6.4 Invariant Observables and Noether Constants
By definition, the eigenprojectors \({\textsf{A}}_k\) are invariant under the gauge group action. Consequently, their corresponding eigenvalues are the Noether constants of the gauge group.
Proposition 38
The eigenprojectors \({\textsf{A}}_k\) are invariant under the gauge group and commute with any group operator. They form a commutative POVM of mutually orthogonal observables. By reverse-transcription into any principal window, they are depicted by \(n_e\) indicator functions \(A_k\) corresponding to the union of the \(d_k\) classical states of same mixed probability \(\alpha _k\) so that \(\langle {A}_k\rangle =\langle {\textsf{A}}_k\rangle =d_k\alpha _k\).
Proof
By construction, the group operators leaves invariant the subspaces \({\textsf{h}}_k\). The projectors \({\textsf{A}}_k\) on \({\textsf{h}}_k\) commute with any group operator and therefore are invariant under the gauge group. They commute and have a common proper window, namely, any principal window. They sum to the identity, \(\sum_{k=1}^{n_e}A_k={\mathbb{1}}_d\). Therefore, they form a commutative POVM of orthogonal observables. In a principal window, they are reverse-transcribed as indicator functions \(A_k\). Finally \(\langle {A}_k\rangle =\langle {\textsf{A}}_k\rangle =d_k\alpha _k\). \(\square\)
Definition 36
(Invariant observables and Noether constants) The eigenprojectors \({\textsf{A}}_k\) constitute a set of invariant observables. The Noether constants \(\langle {\textsf{A}}_k\rangle =d_k\alpha _k\) are the expectation values of these observables.
Now it is possible to reformulate the correspondence between the gauge group and the quantum state, Theorem (7), in terms of these entities.
Theorem 8
The Bayesian theater is completely determined by the \(n_e\) invariant observables \({\textsf{A}}_k\) and the corresponding Noether constants, namely, the \(n_e\) expectations \(\langle {\textsf{A}}_k\rangle =d_k\alpha _k\).
The unitary gauge group \({\mathcal {G}}\) does not exhaust all gauge transformations because the antiunitary operators have been omitted. Let us now investigate these antiunitary gauge changes, obtained by complex conjugation \({\mathcal {H}}_{g}\rightarrow {\mathcal {H}}_{g^*}\)
6.5 The Conjugation Gauge Group \({\mathscr {C}}\)
The conjugation group arises from the transcription of a real-valued space into a complex-valued space. Then any transcription and its complex conjugate are equivalent. In other words, conjugation is a gauge transformation.
Let \({\textsf{K}}: z\mapsto z^*\) denote the standard complex conjugation in \(\mathbb {C}\). Consider the global conjugation gauge \({\mathcal {H}}_{g}\rightarrow {\mathcal {H}}_{g^*}\), obtained by changing each current vector, say \(|\psi _g\rangle\), into its complex conjugate \(|\psi _{g^*}\rangle =|\psi _{g}\rangle ^*\) in the source window. Let \({\mathbb{1}}_d\times\mathrm K\), or simply \({\textsf{K}}\) when no confusion can occur, denote the diagonal matrix \(\textrm{Diag}({\textsf{K}}, {\textsf{K}},\dots ,{\textsf{K}})\). Now from a theorem by E. Wigner [24], any antiunitary operator is of the form \({\textsf{U}}{\textsf{K}}\) where \({\textsf{U}}\) is unitary.
Proposition 39
In a principal window, any antiunitary gauge operator \(\Theta\) is the product \({\textsf{G}}{\textsf{K}}\) of a unitary gauge operator \({\textsf{G}}\in {\mathcal {G}}\) by the matrix \({\mathbb{1}}_d\times\mathrm K\).
Proof
Let \({\textsf{C}}\) denote a conjugation gauge operator. Then \({\textsf{C}}= {\textsf{G}}{\textsf{K}}\) where \({\textsf{G}}\) is unitary [24]. In a principal window the density operator \(\rho\) is real and invariant by any gauge operator. Therefore \({\textsf{G}}\) is a unitary gauge operator. \(\square\)
It is possible to select for definiteness the initial conjugation operator in the principal source window as \({\textsf{C}}=\mathbb {1}_d\times {\textsf{K}}\). Let us term this matrix “conjugation gauge operator”.
Definition 37
(Conjugation gauge operator \({\textsf{C}}\)) The conjugation operator \({\textsf{C}}\) is expressed in a principal source window \(\Omega\) by the matrix \(\mathbb {1}_d\times {\textsf{K}}\) so that in this window
Definition 38
(Conjugation gauge group \({\mathscr {C}}\)) The conjugation gauge group is the involutive group \({\mathscr {C}}=\{\mathbb {1}_d,{\textsf{C}} \}\)
Finally, the full gauge group \({\mathfrak {G}}\) is the semi-direct product of the discrete conjugation group \({\mathscr {C}}\) and the continuous unitary group \({\mathcal {G}}\).
Conjugation expresses exotic symmetry of the Hilbert space.
7 Measurement
In this section, we recover the concept of measurement of standard quantum information, notably by using observables or positive operator value measurements (POVM). From Theorem (6), a Bayesian theater in a state \(\rho\) contains \(N-S(\rho )\) information bits. The issue is to extract all or part of this information.
7.1 Observable Measurement
Let \(\rho\) denote the density operator and \({\textsf{Q}}\) an observable, that is a Hermitian operator acting on the Hilbert space. From the Born rule, regardless of the density matrix and whatever the observable, its expectation is
As such, this result does not directly provide strict information (i.e. in bits). To interpret it in terms of extracting information when possible, it is necessary to include the measurement in a positive operator value measurement (POVM), as discussed in the following sections.
7.2 POVM Measurement
The general measurement described in the source observation window, Sect. (3.4.3) can be equivalently reproduced in full generality in the Hilbert space. For commutative observables the measurement estimates the probability of outcomes collected from a unique viewpoint on the register. By contrast, for non commutative observables, the measurement estimates the probability of outcomes collected from different viewpoints.
Theorem 9
(General measurement) General POVMs can be performed regardless of the density matrix and whatever the positive observables.
Proof
Just use the Born’s rule. \(\square\)
Let \(\Gamma\) be a finite set. Consider a resolution of the identity in \({\mathcal {H}}\) described by a set of positive Hermitian operators \(\{{\textsf{Q}}_\gamma \}_{\gamma \in \Gamma }\), not necessarily commutative nor diagonal in the current window, such that
The expectation of \({\textsf{Q}}_\gamma\) is \(\langle {\textsf{Q}}_\gamma \rangle = \textrm{Tr}(\rho {\textsf{Q}}_\gamma )\le 1.\)
By linearity, we have
Therefore, the array \(\langle {\textsf{Q}}_\gamma \rangle\) is a probability distribution.
Definition 39
(POVM probability distribution) A POVM \(\{{\textsf{Q}}_\gamma \}_{\gamma \in \Gamma }\) defines a probability distribution \(\textrm{p}(\gamma ) {\mathop {=}\limits ^{{\mathrm{(def)}}}}\langle {\textsf{Q}}_\gamma \rangle\).
Let us address an information interpretation.
7.3 POVM Information Gain
From Theorem (6), a Bayesian theater in a state \(\rho\) contains \(N-S(\rho )\) information bits. The POVM \(\{{\textsf{Q}}_\gamma \}_{\gamma \in \Gamma }\) can be used to extract a fraction of this information. Practically, we will use the conventional relative entropy which depicts the gain of information between two states. The first state is the completely random distribution, \(\rho _\textrm{void}=(1/d)\times \mathbb {1}_d\), with \(d=2^N\), representing an absence of information. The corresponding POVM probability distribution \(\textrm{p}_\textrm{void}\) reads
where \(q_\gamma = \textrm{Tr}({\textsf{Q}}_\gamma )\). The second state is the current density operator \(\rho\). Now, the “POVM information gain” \(\mathbb {I}(\rho \Vert \Gamma )\) provided by the POVM (\(\Gamma\)) is the relative entropy \(\mathbb {H}(\textrm{p}\Vert \textrm{p}_\textrm{void})\).
Definition 40
(POVM information gain) The POVM information gain \(\mathbb {I}(\rho \Vert \Gamma )\) is the relative entropy \(\mathbb {H}(\textrm{p}\Vert \textrm{p}_\textrm{void})\),
If \(\rho =\rho _\textrm{void}\) then \(\textrm{p}=\textrm{p}_\textrm{void}\) and \(\mathbb {I}(\rho \Vert \Gamma )=\mathbb {H}(\textrm{p}_\textrm{void}\Vert \textrm{p}_\textrm{void})=0\). The information gain of a completely random state is well zero.
Proposition 40
The information gain \(\mathbb {I}(\rho \Vert \Gamma )\) is non-negative and less than the storage capacity N of the register and even of the total information \(N-S(\rho )\) currently stored in the Bayesian theater.
Proof
A relative entropy is non-negative, so that so is the information gain \(\mathbb {I}(\rho \Vert \Gamma )\). It is trivially less than the storage capacity N of the register and even of the total information \(N-S(\rho )\) currently stored in the Bayesian theater. Using Eq. (41) and \(d=2^N\)
\(\square\)
Information systems are generally characterized by their entropy, \(\mathbb {H}\), which corresponds to a lack of information. Therefore, the concept of information, \(\mathbb {I}\), defined in a Bayesian theater of N bits corresponds to an entropy of \(\mathbb {H} {\mathop {=}\limits ^{{\mathrm{(def)}}}}N-\mathbb {I}\). With this convention, \(\mathbb {I}(\rho \Vert \Gamma )\) corresponds to the entropy \(\mathbb {H}(\Gamma )\). From Eq. (43) we obtain
In general \(\mathbb {H}(\Gamma )\ne \mathbb {H}(p_\gamma )\) because \(q_\gamma =\textrm{Tr}({\textsf{Q}}_\gamma )\ne 1\).
Definition 41
(POVM entropy) The POVM entropy is the entropy \(\mathbb {H}(\Gamma ){\mathop {=}\limits ^{{\mathrm{(def)}}}}N-\mathbb {I}(\rho \Vert \Gamma )\) corresponding to the information gain \(\mathbb {I}(\rho \Vert \Gamma )\) that can be extracted by the POVM.
In particular, assume that the POVM corresponds to a von Neumann measurement in a particular window of sample set \(\Omega = \{\omega \}\) (see above Sect. 3.4.2). In the Hilbert space, let \(|\omega \rangle\) be the basis of this window. Then, \(\Gamma =\Omega\) and \({\textsf{Q}}_\omega = |\omega \rangle \langle \omega |\) so that \(q_\omega =1\) and \(\textrm{p}(\omega ) = \langle \omega | \rho |\omega \rangle\).
Definition 42
(Window entropy) The window entropy \(\mathbb {H}(\Omega )\) is the entropy \(N-\mathbb {I}(\rho \Vert \Omega )\) corresponding to the information that can be extracted by a von Neumann measurement in the window.
Proposition 41
The window entropy is the working entropy of the current window.
Proof
Proceed to the reverse transcription of the current window into its probability space. Let \(w_{\scriptscriptstyle \Lambda }\) denote the working distribution, Definition (13). By definition, \(\textrm{p}= w_{\scriptscriptstyle \Lambda }\). \(\square\)
In standard quantum information, a POVM is called “information-complete” when the operators \({\textsf{Q}}_\gamma\), \(\gamma \in \Gamma\) span the complete space \({\mathcal {L}}({\mathcal {H}})\). Indeed, such a measurement provides \(|\Gamma |\ge d^2-1\) coefficients \(\textrm{p}(\gamma )\) that allow the unique reconstruction of the density operator \(\rho\) and then the Bayesian probability distribution. This does not necessarily mean that the POVM entropy is equal to \(S(\rho )\) because this information is encoded in a particular way, which can cause a bias not taken into account in Eq. (43) and then a loss of information (or an increase of entropy).
In general, a particular measurement is not information-complete and therefore the determination of the density operator requires independent measurements from additional POVMs.
7.4 Independent POVMs
Suppose that a POVM \(\{{\textsf{Q}}_{\gamma }\}_{\gamma \in \Gamma }\), that we will refer to as (\(\Gamma\)), is information-incomplete and consider the possibility to complement this POVM by another POVM.
The set of density operators \(\textrm{D}({\mathcal {H}})\subset {\mathcal {L}}({\mathcal {H}})=\{\rho \}\) is a convex ensemble located in an affine subspace of real dimension \(d^2-1\). Motivated by Ref. [25], it is helpful to consider rather the set of traceless Hermitian operators, \(\{{{\textbf {e}}}\}\) defined as
because this ensemble generates a linear vector space \({\mathcal {E}}{\mathop {=}\limits ^{{\mathrm{(def)}}}}\textrm{Span}({{\textbf {e}}})\subset {\mathcal {L}}({\mathcal {H}})\) still of dimension \(d^2-1\). This mapping \(\textrm{D}({\mathcal {H}})\rightarrow {\mathcal {E}}\) can be extended to all operators of a POVM as follows. Consider the POVM \((\Gamma )\), \(\{{\textsf{Q}}_{\gamma }\}_{\gamma \in \Gamma }\) and define \({\textsf{Q}}_{\gamma }\mapsto {{\textbf {e}}}_\gamma\) as
The POVM is then characterized by
At last, define a Hermitian inner product in \({\mathcal {E}}\) as
Let \({\textsf{Q}}<\mathbb {1}_d\) be an additional Hermitian positive operator. Let \(q= \textrm{Tr}({\textsf{Q}})>0\), \({\textsf{E}}_{\scriptscriptstyle {\textrm{Q}}} = ({1}/{q}) {\textsf{Q}}\in \textrm{D}({\mathcal {H}})\) and \({{\textbf {e}}}_{\scriptscriptstyle {\textrm{Q}}}={\textsf{E}}_{\scriptscriptstyle {\textrm{Q}}}-({1}/{d})\mathbb {1}_d\in {\mathcal {E}}\). It turns out that \({\textsf{Q}}\) is independent of the POVM if and only if \({{\textbf {e}}}_{\scriptscriptstyle {\textrm{Q}}}\) is orthogonal to every \({{\textbf {e}}}_\gamma\). Indeed, assume that \({{\textbf {e}}}_{\scriptscriptstyle {\textrm{Q}}}\) is orthogonal to the subspace \(\textrm{Span}\{{{\textbf {e}}}_\gamma \}_{\gamma \in \Gamma }\subseteq {\mathcal {E}}\). We compute easily from Eqs. (46-48)
We have then
Conversely, if Eq. (49) holds, then \({{\textbf {e}}}_{\scriptscriptstyle {\textrm{Q}}}\) is orthogonal to every \({{\textbf {e}}}_\gamma\).
To check the independence of the additional operator \({\textsf{Q}}\), construct a second POVM with two operators, \(\{{\textsf{Q}}, \mathbb {1}_d-{\textsf{Q}}\}\). Assume that the system “lives” in the first POVM set, meaning that \(\rho =\rho _{\scriptscriptstyle {\Gamma }}\in \textrm{Span}(Q_\gamma )_{\gamma \in \Gamma }\). Then, from linearity, Eq. (49) and \(\textrm{Tr}(\rho _{\scriptscriptstyle {\Gamma }})=1\), the second measurement yields
exhibiting the effective density operator \(\rho _\textrm{void}=\mathbb {1}_d/d\) of a completely random system. Therefore \(\textrm{p}({\textsf{Q}})\) is totally independent of the density matrix \(\rho _{\scriptscriptstyle {\Gamma }}\in \textrm{Span}(Q_\gamma )_{\gamma \in \Gamma }\). Similarly, if the system lives in the second POVM set, \(\rho =\rho _{\scriptscriptstyle {\textrm{Q}}}\in \textrm{Span}(Q, \mathbb {1}_d-{\textsf{Q}})\) then the first POV-measurement yields
and again the coefficients \(\textrm{p}({\textsf{Q}}_\gamma )\) are totally independent of the density matrix \(\rho _{\scriptscriptstyle {\textrm{Q}}}\) We will refer to the two POVMs as mutually “independent”. More generally, consider two distinct POVMs, \(\{{\textsf{Q}}_{\gamma _1}\}_{\gamma _1\in \Gamma _1}\) and \(\{{\textsf{Q}}_{\gamma _2}\}_{\gamma _2\in \Gamma _2}\). For brevity, we say that a system defined by a density operator \(\rho \in {\mathcal {L}}({\mathcal {H}})\) “lives” in a POVM \(\{{\textsf{Q}}_{\gamma }\}_{\gamma \in \Gamma }\) when \(\rho \in \textrm{Span}\{{\textsf{Q}}_{\gamma }\}_{\gamma \in \Gamma }\).
Definition 43
(Independent POVMs) Two distinct POVMs, \(\{{\textsf{Q}}_{\gamma _1}\}_{\gamma _1\in \Gamma _1}\) and \(\{{\textsf{Q}}_{\gamma _2}\}_{\gamma _2\in \Gamma _2}\) are mutually independent if the measurement with one POVM when the system “lives” in the other POVM is identical to a measurement in a completely random state \(\rho _\textrm{void}=\mathbb {1}_d/d\).
Proposition 42
Two distinct POVMs, \(\{{\textsf{Q}}_{\gamma _1}\}_{\gamma _1\in \Gamma _1}\) and \(\{{\textsf{Q}}_{\gamma _2}\}_{\gamma _2\in \Gamma _2}\) are mutually independent if and only if
Proof
From Eq. (49) each \({{\textbf {e}}}_{\gamma _{i}}\) is orthogonal to every \({{\textbf {e}}}_{\gamma _{3-i}}\) (\(i=1,2\)). \(\square\)
Now, given that the two POVMs are independent, the information gains provided by the two measurements do not overlap. As a result the sum of the two information gains is still bounded by the total information, \(N-S(\rho )\), stored in the system.
Proposition 43
(POVM entropic inequality) Let \(\Gamma _1: \{{\textsf{Q}}_{\gamma _1}\}_{\gamma _1\in \Gamma _1}\) and \(\Gamma _2: \{{\textsf{Q}}_{\gamma _2}\}_{\gamma _2\in \Gamma _2}\) be two independent POVMs acting on a system in the state \(\rho\). Then
Proof
Proceed to the transformations \({{\textbf {e}}}=\rho -\mathbb {1}_d/d\), \(q_{\gamma _i}= \textrm{Tr}({\textsf{Q}}_{\gamma _i})\), \({\textsf{E}}_{\gamma _i} = ({1}/{q_{\gamma _i}}) {\textsf{Q}}_{\gamma _i}\in \textrm{D}({\mathcal {H}})\) and \({{\textbf {e}}}_{\gamma _i}={\textsf{E}}_{\gamma _i}-({1}/{d_{\gamma _i}})\mathbb {1}_d\in {\mathcal {E}}\), where \(i\in\left[[1,\;2\right]]\) and \(\gamma _i\in \Gamma _i\). Let \({\mathcal {E}}_i =\textrm{Span}_{\gamma _i\in \Gamma _i} ({{\textbf {e}}}_{\gamma _i})\). The space \({\mathcal {E}}\) splits into three mutually orthogonal subspaces, \({\mathcal {E}}={\mathcal {E}}_1\oplus {\mathcal {E}}_2\oplus {\mathcal {E}}_0\). As a result, we have a unique decomposition \({{\textbf {e}}} = {{\textbf {e}}}_1+{{\textbf {e}}}_2+{{\textbf {e}}}_0\). Define \(\rho _i ={{\textbf {e}}}_i +\mathbb {1}_d/d\). Then, still for \(i\in\left[[1,\;2\right]]\) and \(\forall \gamma _i\in \Gamma _i\) we obtain successively by a straightforward computation
so that \(\textrm{p}(\gamma _i)=\textrm{Tr}(\rho {\textsf{Q}}_{\gamma _i})\) depends only on \(\rho _i\). Therefore, the two information gains \(\mathbb {I}_1=\mathbb {I}(\rho \Vert \Gamma _1)\) and \(\mathbb {I}_2=\mathbb {I}(\rho \Vert \Gamma _2)\) are independent and the total information extracted by the two POVMs is the sum of the two information gains. This sum is trivially bounded by the storage capacity N of the register, and even by the actual information stored in the register \(N-S(\rho )\), i.e. \(\mathbb {I}_1+\mathbb {I}_2\le N-S(\rho )\le N\). In terms of entropy, \(\mathbb {H}(\Gamma _i)= N-\mathbb {I}_i\), we obtain Eq. (51). \(\square\)
To our knowledge, the POVM inequality, Eq. (51), is new but the concept of “unbiased POVM” was previously defined by Kalev and Gour [26]. In standard quantum information, the inequality is rather expressed for von Neumann measurements. Independent POVMs are then particularized by independent von Neumann measurements in the so called “mutually unbiased bases”.
7.5 Mutually Unbiased Bases (MUB)
Mutually unbiased bases, first introduced by J. Swinger in 1960 [27] are extensively used in standard quantum information [25]. Let us first define precisely a pair of mutually unbiased bases \(\Omega _1\) and \(\Omega _2\) in the present model. Each basis \(\Omega _i\), of basic vectors \(|\omega _i\rangle\), \((\omega _i\in \Omega _i)\), (\(i\in\left[[1,\;2\right]]\)), defines a von Neumann measurement i.e. a particular POVM, namely \(\{|\omega _i\rangle \langle \omega _i| \}_{\omega _i\in \Omega _i}\).
Definition 44
(Mutually unbiased bases (MUB) or mutually unbiased windows) A pair of bases are mutually unbiased when they determine two independent von Neumann measurements.
This definition is not standard. Let us recover the standard definition by the following proposition:
Proposition 44
(MUB) Two distinct windows of sample sets \(\Omega _1\) and \(\Omega _2\) and of basic vectors \(|\omega _1\rangle\), \((\omega _1\in \Omega _1)\) and \(|\omega _2\rangle\), \((\omega _2\in \Omega _2)\) are mutually unbiased if and only if
Proof
From Eq. (50) two von Neumann measurements are independent if and only if Eq. (52) holds. \(\square\)
Consider a pair of mutually unbiased bases, defining two independent von Neumann measurements. Then, Eq. (51) holds, with \(\Omega _i\) standing for \(\Gamma _i\), as
We recover the well known entropic relations of standard quantum information theory in the special case of independent windows. The first bound, \(N+S(\rho )\), corresponds to a special case of the Frank-Lieb’s inequality [15] and the second bound, N, to the less tight Massen-Uffink’s inequality [14]. Note the the present model provides an intuitive basis to these inequalities, usually regarded as somewhat technical and esoteric: Namely, whatever the measurement, it is impossible to recover more information than is stored in the memory. This is also the basis of the iconic uncertainty principle.
Finally, the totality of the information stored in the memory can be retrieved. Actually, this information is located in the principal window and is therefore perfectly classical.
8 Illustrative Example: One-Bit System
A one-bit system is a logical memory containing a maximum of one information bit. The issue is to extract this information.
There is not much to say about a classic one-bit system, it is a deterministic problem represented by a single Boolean variable, valid or invalid. Its entropy is zero and its Shannon information is therefore exactly 1 bit.
In contrast, a one-bit Bayesian system is a memory whose information content is specified by the state of the system. This state can be either a mixed state or a pure state, also called a qubit. It turns out that a qubit is actually a deterministic one-bit system, implemented by Bayesian inference.
8.1 Mixed One-Bit System
A mixed state corresponds to a one-bit memory without any particular constraint. The memory is investigated via a question-and-answer procedure. Let \({\textsf{X}} _1\) denote the Boolean variable representing the initial query. A remarkable property of the Bayesian representation is that this initial query only exposes one possible aspect of the system. At any rate, there are two classical states, namely, \(\omega _1 = \overline{\textsf{X}} _ 1\) and \(\omega _2 = {{\textsf{X}}} _ 1\), where \(\overline{{\textsf{X}}} _ 1\) is the negation of \({{\textsf{X}}} _ 1\). At this stage, there is no specific condition, so that the Bayesian prior information, say \((\Lambda )\), is initially void.
8.1.1 Source Observation Window
To address the Bayesian problem, we first construct a sample set \(\Omega =\{ \omega _1, \omega _2\}\) including the two initial classical states. Next, we build a real-valued probability space \({\mathcal {P}}{\mathop {=}\limits ^{{\mathrm{(def)}}}}\textrm{Span}(\omega _1,\omega _2)\), of dimension \(d=2^N=2\). This provides an initial view, called “source information window”.
Let \(p=(p_1,p_2)\in {\mathcal {P}}\). To secure \(p_1, p_2\) to be genuine probabilities, we have to introduce in the (initially void) prior \((\Lambda )\) the relevant universal equations, Eqs. (2, 3, 4, etc.), limited here to the sole normalization equation. Therefore, the prior information \((\Lambda )\) now reads \((\Lambda ): \ p_1+p_2 =1.\) We will interpret \(p_1\) and \(p_2\) as conditional probabilities given \((\Lambda )\). Using the convention of Sect. (2.3)
As a result, the unknowns \(p_1\) and \(p_2\) are the solutions of a LP system Eq. (7)
Each solution is a particular probability distribution \({\mathbb {P}}(\omega )\) on the sample set \(\Omega\). Actually, the normalization equation is implicit, so that the Bayesian formulation reduces to its simplest expression without any explicit constraint,
Let \({\tilde{\omega }}_1=(1,0)\) and \({\tilde{\omega }}_2=(0,1)\) denote the two deterministic solutions in \({\mathcal {P}}\). The LP system,

Equation (54), accepts not only the two classical deterministic distributions \({\tilde{\omega }}_1\) and \({\tilde{\omega }}_2\) but also a continuous set of solutions on their convex hull. The feasible solutions are located on a specific polytope \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\), that is the line segment \([{\tilde{\omega }}_1,{\tilde{\omega }}_2]\) identical to the so-called “tautological simplex” of one variable \({\mathcal {W}}_{\scriptscriptstyle I}\). The line itself is an affine 1-dimensional subspace \(P_{\scriptscriptstyle \Lambda }\). The simplex vertices are \(w_1={\tilde{\omega }}_1\) and \(w_2={\tilde{\omega }}_2\). Therefore, the system is simplicial (Definition 9) and \({\mathcal {W}}_{\scriptscriptstyle \Lambda }={\mathcal {W}}_{\scriptscriptstyle I}=\textrm{conv}({\tilde{\omega }}_1,{\tilde{\omega }}_2)\).
8.1.2 Simplicial Quantum State
The system, Eq. (54) defines a “mixed state” of rank \(r=2\) (i.e. with 2 vertices). The specific polytope \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\) is the tautological simplex. It is possible to single up a particular solution, \(w_{\scriptscriptstyle \Lambda }\), called “working distribution”, by assigning a weight to each vertex of the simplex that is a discrete contextual probability distribution. Define
so that \(w_{\scriptscriptstyle \Lambda } = \lambda _1{\tilde{\omega }}_1+\lambda _2{\tilde{\omega }}_2 \in {\mathcal {W}}_{\scriptscriptstyle \Lambda }\). By convention, when the contextual distribution is not explicit, the default working distribution \(w_{\scriptscriptstyle \Lambda }\) is the center of mass of the polytope, i.e. \({\tilde{c}} = (1/2)({\tilde{\omega }}_1+{\tilde{\omega }}_2)\).
The pair, \((w_{\scriptscriptstyle \Lambda },{\mathcal {W}}_{\scriptscriptstyle \Lambda })\), of a working distribution \(w_{\scriptscriptstyle \Lambda }\) and a specific simplex, \({\mathcal {W}}_{\scriptscriptstyle \Lambda }\), is termed “simplicial quantum state”.
8.1.3 Observable
In the source window, an observable is a function \(Q:\Omega \rightarrow \mathbb {R}\). Let \(Q(\omega )=\textrm{q}_\omega\). By definition, \(\textrm{q} = (\textrm{q}_1, \textrm{q}_2) \in {\mathcal {P}}^*\), where \({\mathcal {P}}^*\) is the dual of \({\mathcal {P}}\). The expectation of Q is defined with respect to the working distribution as
For instance, consider the particular observable \(S_Z(\omega )=\textrm{s}_\omega\) defined as
We have
8.1.4 Entropy and Information
The entropy of the state is \(\mathbb {H}(\Sigma _\lambda )= -\lambda _1 \log _2\lambda _1 -\lambda _2 \log _2\lambda _2\). This corresponds at the same time to the von Neumann entropy, the simplicial entropy and the working entropy and represents a Shannon information of \(I= 1- -\lambda _1 \log _2\lambda _1\). Actually since the window is principal, this information can be entirely extracted from the window.
8.1.5 Other Observation Windows
We started from a unique Boolean variable, \({\textsf{X}}_1\). Surprisingly enough, in a Bayesian framework, it is possible to pose the problem by using other alternatives than \({\textsf{X}}_1\) and \(\overline{{\textsf{X}}}_1\), that is to consider other observation windows. These new alternatives are necessary in order to compute the expectation value of every relevant observable.
To change the observation window, let us introduce a new tool, namely, an auxiliary Hilbert space.
8.1.6 Transcription into an Auxiliary Hilbert Space \({\mathcal {H}}\)
Indeed, to construct new observation windows, the fundamental novelty of quantum information is to transcribe the source window into an auxiliary Hilbert space \({\mathcal {H}}\) defined as the complex span of \((\omega _1, \omega _2)\). Let \((|1\rangle , |2\rangle )\) denote its basis vectors. Afterward, the new alternatives will be simply computed by changing this initial basis. The initial simplicial quantum state is transcribed as a standard density operator \(\rho _{\scriptscriptstyle \Lambda }=\lambda _1|1\rangle \langle 1| + \lambda _2|2\rangle \langle 2|\), or
The density operator is diagonal. As a result this source window is called principal.
Any observable in the source window \(Q:\Omega \rightarrow \mathbb {R}\) is transcribed as the following diagonal operator
For instance, the observable \(S_Z\) is transcribed as
where \(\sigma _3\) is a Pauli matrix. Its expectation is computed by the so-called “Born rule”, Eq. (35), as
8.1.7 Changing the Window
To obtain new windows, we simply have to change the basis in \({\mathcal {H}}\). It turns out that the new corresponding probability problem can be simply retrieved by reverse transcription in the new basis. In general, the new density operator is no longer diagonal in the new basis, so that the new observation window is not principal but twisted. Let \(|e_{i'}\rangle = (\alpha _{i',1}, \alpha _{i',2})^T\) for \(i'=1,2\) be the expression of its eigenvectors in the new basis. The new expression \(\rho '_{\scriptscriptstyle \Lambda }=\lambda _1|e_{1'}\rangle \langle e_{1'}| + \lambda _2|e_{2'}\rangle \langle e_{2'}|\) of the density operator is thus
and we have \(\textrm{Tr}(\rho '_{\scriptscriptstyle \Lambda })=\textrm{Tr}(\rho _{\scriptscriptstyle \Lambda })=w'_1+w'_2=1\). For example for \(|e_{1'}\rangle = (\cos \theta , \sin \theta )^T\) and \(|e_{2'}\rangle = (-\sin \theta , \cos \theta )^T\), we obtain
To reverse transcribe into a new real-valued probability space \({\mathcal {P}}'\), use the eigenvectors \(|e_{i'}\rangle \in {\mathcal {H}}\) to define the vectors \(v_i'=(|\alpha _{i',1}|^2, |\alpha _{i',2}|^2)^T\) in \({\mathcal {P}}'\). In the example, \(w'_1= \lambda _1\cos ^2\theta +\lambda _2\sin ^2\theta\), \(w'_2=\lambda _1\sin ^2\theta + \lambda _2\cos ^2\theta\), \(v_1'= (\cos ^2\theta , \sin ^2\theta )^T\) and \(v_2'=(\sin ^2\theta , \cos ^2\theta )^T\).
By exception, when \(v'_1=v'_2\), the new window is “blind” and \(w'_1=w'_2=1/2\). For example, this is obtained for \(\theta =\pi /4\), \(|e_{1'}\rangle = (1/\sqrt{2})(1, 1)\) and \(|e_{2'}\rangle = (1/\sqrt{2})(-1, 1)\).
Otherwise, the new simplex is the affine segment \([v'_1,v'_2]\) and the new working distribution is \(w'=(w'_1, w'_2)^T\). Finally, this defines a new sampling set \(\Omega '\). Although the system is basically classical, Bayesian inference leads to a twisted observation window because the basis vectors are correlated and no longer independent.
Obviously, the old observables \(\Omega \rightarrow \mathbb {R}\), represented by diagonal Hermitian operators in \({\mathcal {H}}\) will change accordingly but will no longer remain diagonal. Therefore, they cannot be reverse-transcribed in the new window because they are still defined on \(\Omega \ne \Omega '\). By contrast, the new window matches different observables, inaccessible from the old window, \(\Omega '\rightarrow \mathbb {R}\) which became diagonal in the new window. Nevertheless, all observables can always be computed in the Hilbert space from any observation window because each observable is expressed as an operator, whether diagonal or not, acting on the Hilbert space \({\mathcal {H}}\).
8.2 Qubit, Pure One-Bit State
We define a qubit as a pure state in a 1-bit LP system. As a result, a qubit represents a deterministic distribution. In a principal window, the qubit is simply a classical state!
Assume now that the source window is not necessarily principal. Define a covector \(\textrm{a}_\theta =(\textrm{a}_{\theta , \omega _1},\textrm{a}_{\theta , \omega _2})\) in \({\mathcal {P}}^*\) depending on a setting \(\theta\) associated with an observable, \(A_\theta\), so that \(A_\theta (p)=\textrm{a}_{\theta , \omega _1}\times p_1+\textrm{a}_{\theta , \omega _2}\times p_2\). Without loss in generality for feasible LP problems, we can choose the following formulation of \(\textrm{a}_\theta\)
The qubit is the unique solution of the Bayesian problem Eq. (8)
The rank of the LP system is \(m=d=2\) and the solution is \(w_\theta =(\cos ^2\theta /2,\sin ^2\theta /2)\). The quantum state \((w_\theta ,{\mathcal {W}}_\theta )\) is thus characterized by the isolated vertex \(w_\theta\) and \({\mathcal {W}}_\theta =\{w_\theta \}\).
8.2.1 Observable
Consider an observable \(Q(\omega )=\textrm{q}_{\omega }\) in the source window. The quantum expectation is defined as,
Specifically, the expectation of the observable \(S_Z=\sigma _3=(1,-1)\), Eq. (55), is \(\langle S_Z \rangle =\cos ^2\theta /2-\sin ^2\theta /2 = \cos \theta\).
8.2.2 Transcription into an Auxiliary Hilbert Space \({\mathcal {H}}\)
Different transcriptions depending on a gauge parameter are equivalent. Consider a gauge labelled \(\phi\). With this gauge, construct an auxiliary Hilbert space. The quantum state is transcribed as the rank 1 density operator \(\rho _{\theta ,\phi }=|a\rangle \langle a|\) with the Gleason’s vector \(|a\rangle\) (Definition 28),
as
The gauge parameter expresses an exact symmetry of the Hilbert space with respect to a rotation. There is also a antiunitary gauge generated by complex conjugation, that is simply here \(\phi \mapsto -\phi\). Note that the formulation is classical for \(\theta =0\).
8.2.3 Entropy and Information
The entropy of the Shannon distribution is zero. As a result, the Shannon information is 1 bit. The totality of this information is extracted by a measurement.
9 Discussion
The current model is of course expected to have repercussions in different fields, starting with physics, considered the science of observing the world based on reasoning [28].
9.1 Spin-off in Physics
Unquestionably, quantum information is the basis of quantum physic.
Actually, quantum physics identifies the universe with a Hilbert space. However, a major problem is that its state is usually represented by a wave vector, that is a pure state. In the present framework, a pure state describes an information register set to zero (with a particular Boolean gauge), so that the complexity of the world would be just an artifact only due to a sophisticated observation window. Therefore, paradoxically, for the universe to have a non-trivial content, a pure state is excluded and only a mixed state, that is a probabilistic mixture of pure states is acceptable.
But now we have to explain how standard physics can be so efficient despite problematic prerequisites. The solution could be that the behavior of the standard wave vector is actually a witness, characterizing the symmetry of the system, i.e. its gauge group. In turn, from proposition (8), this group itself characterizes the quantum state of the system. This ties in with Steven Weinberg’s deep intuition [29], namely “specifying Nature’s symmetry group may be all we need to say about the physical world”.
Another objection is that the present model only deals with logical concepts and can therefore provide only a bare landscape of the world, free from any specific ontological or “ontic” ingredient. Perhaps this is not so essential, especially since genuine ontological elements are undoubtedly unimaginable and therefore unfalsifiable, whereas the candidate “beables”, whether fire, aether, epicycles, points, vectors, strings or branes are highly problematic or at best purely phenomenological models. This suggests circumventing any specific ontology and adopt the concept “It from bit”, in agreement with the celebrated Wheeler’s doctrine. This means that abstract information is the ultimate ingredient while deliberately ignoring any ontological significance.
On these bases, let us outline a purely information model.
Towards new foundations of physics: The world could be reconstructed from a number of observations, expressed for convenience in terms of binary Boolean variables regarded as discrete degrees of freedom. From proposition (8), the state of the universe could be represented by a gauge group whose invariant observables express symmetry, thus joining Klein’s Erlangen program in mathematics [30] (see e.g. J.-B. Zuber [31]). This implies that the universe is described by a mixed state. Next, we would have to find the origin of most concepts in the corpus of information theory. For example, the concept of cosmic time could be related to the total entropy of the universe. Incidentally, the need for mixed states could solve some paradoxes, like the information loss in black holes. Finally, the method paves the way to a huge field of investigation obviously outside the scope of this article.
9.2 Beyond Physics
The Bayesian approach is likely to be powerful in all other area of reasoning.
The first application concerns Data Science. It provides an explanation of the speedup of both Bayesian computation and quantum computing. This explains especially the efficiency of neural networks which are implicit Bayesian calculations. This efficiency ultimately rests on the unique ability of real numbers to perform optimization unlike discrete implementations.
Beyond, this suggests that the Church-Turing principle may not be the end of the history and that Bayesian inference could be a more powerful tool than the Turing machine to conceive universal computation as previously suggested, but only for quantum computation, by Deutsch [32].
Bayesian inferences could even have spin-off in pure mathematics because the means of deducing mathematics from logic could include Bayesian inference and not only deduction. Leopold Kronecker is famous for having declared that “God made the integers, all else is the work of man.” [33] One step further, one could assert that “God made logical rules, all else is the work of man.” At last, more punctually, quantum information could explain the hitherto unknown link [34] between the theory of potential and probability [35].
More unexpected for quantum physicists, though suspected by David Bohm and Basil Hiley [36], other sciences including soft sciences already benefit from this approach. Applications have been described, e.g. in cognition and decision making [37,38,39], psychology [40, 41], social science [42] or grammatical language [43]. Beyond cognition, other emblematic examples could be found in biology, e.g. in both the immune system and immunotherapy and even in evolution theory.
10 Conclusion
Our goal was to propose an interpretation of quantum formalism. Although it is a long-standing issue, whose origins can be traced back to von Neumann [22], the foundations of quantum mechanics have remained elusive, giving rise to questioning and discomfort [44]. The probabilistic “Born interpretation” aroused the Einstein’s famous sentence, “I, at any rate, am convinced that He does not throw dice” [45]. Later, in a celebrated lecture [46], R. Feynman gave his equally famous verdict, “I think I can safely say that nobody understands quantum mechanics”. Let us finally quote the striking Jaynes’ opinion: “A standard of logic that would be considered a psychiatric disorder in other fields, is the accepted norm in quantum theory” [7].
To address this discomfort, countless approaches have been devised. Some authors tried to circumvent the conventional logic. Others attempted to reinterpret the experimental results. Finally, some simply denied the existence of a problem. In a tasty paper, updated in 2002 [47], Christopher Fuchs enumerated with humor a number of “religions”: “The Bohmians [48], the Consistent Historians [49], the Transactionalists [50], the Spontaneous Collapseans [51], the Einselectionists [52], the Contextual Objectivists [53], the outright Everettics [54, 55], and many more beyond that”. Recent approaches try to derive quantum logic from ad hoc information-theoretic extra principles assumed “reasonable” or, following Spekkens [56], propose frameworks claimed “operational” [57,58,59,60,61,62], based on the compatibility with specific information processing tasks. Epistemic approaches propose generalized probabilistic theories (GPT) comparing quantum and classical probabilities [63, 64]. Specifically, new frameworks aim to identify the additional axioms needed to derive the quantum formalism from probabilistic constraints, e.g, from “information causality” or from entropy [65, 66]. Another appealing approach inspired from thermodynamics is to use an entropic method of inference [67]. Eventually, a more direct way is to compare quantum states with Bayesian states of knowledge [68,69,70,71].
In the present paper, we abstain from introducing any extra axiom and we support the approaches based on Bayesian inference theory.
Although using quantum terminology when appropriate, we have basically dealt with classical information in a classical memory, but at the end, we obtain the exact apparatus of quantum information. This means that quantum information as such is nothing but information itself and therefore independent of any physical content. Our major conclusion, as sketched in Sect. (1.2), is somewhat baffling: Quantum information is simply classical information processed by Bayesian inference theory.
As far as quantum formalism itself is concerned, the current model is the first to logically deduce from information theory its fundamental characteristics, almost always posited from the outset as seemingly arbitrary postulates: Why is the theory probabilistic? Why is the theory linear? Where does the Hilbert space come from? Also, most of the emblematic paradoxes, such as entanglement, contextuality, nonsignaling correlation, measurement problem, no-cloning theorem etc., find a perfectly rational explanation. At last the controversial concept of Shannon information conveyed by a wave vector, or stored in the system is clarified.
Beyond physics, quantum information appears as a multipurpose technique for analyzing a system of logical constraints, in line with classical information. Whereas classical information is the universal tools of logic, quantum information in the universal tool of inference. This is perhaps the most important conclusion of this article.
References
Shannon, C. E.: A mathematical theory of communication, Bell System Technical Journal, 27 379–423 , 656–715. (1948), http://pespmc1.vub.ac.be/books/Shannon-TheoryComm.pdf
Szilard, L.: On the Decrease of Entropy in a Thermodynamic System by the Intervention of Intelligent Beings, Zeitschrift fuer Physik, 53 840–856, (1929). http://sns.ias.edu/~tlusty/courses/InfoInBioParis/Papers/Szilard1929.pdf
Brillouin, L.: Science and Information Theory, Academic Press, New-York, (1956). http://www.physics.mcgill.ca/~delrio/courses/phys559/lectures%20and%20notes/Brillouin-Information-Theory-Ch1-4.pdf
Wheeler, J.A.: Information, physics, quantum: the search for links. In: Zurek, W. (ed.) Complexity, entropy, and the physics of information, pp. 3–28. Addison-Wesley, Redwood City (1990)
Landauer, R.: The physical nature of information, Physics Letters A, 217 188–193, (1996). http://cqi.inf.usi.ch/qic/64_Landauer_The_physical_nature_of_information.pdf
Jaynes, E. T.: Probability Theory: the logic of science, Cambridge University Press, Cambridge, UK, (2003). http://omega.math.albany.edu:8008/JaynesBook.html
Jaynes, E. T.: Clearing up mysteries, in: J. Skilling (Ed.), Maximum entropy and Baysian methods, Kluwer, Dordrecht, (1989), pp. 1–29. http://bayes.wustl.edu/etj/articles/cmystery.pdf
Rovelli, C.: Relational quantum mechanics. Int. J. Theor. Phys. 35, 1637–1678 (1996). https://doi.org/10.1007/BF02302261
Caves, C.M., Fuchs, C.A., Schack, R.: Quantum probabilities as Bayesian probabilities. Phys. Rev. A 65(2), 22305 (2002). arXiv:quant-ph/0106133
Mermin, N. D.: Qbism puts the scientist back into science, Nature, 507 421–422, (2014). http://www.nature.com/polopoly_fs/1.14912!/menu/main/topColumns/topLeftColumn/pdf/507421a.pdf
Fuchs, C. A.: QBism, The Perimeter of Quantum Bayesianism (2010). arXiv:1003.5209
Boyd, S., Vandenberghe, L.: Convex optimization, Cambridge University Press, Cambridge, (2004). http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf
Cox, R. T.: Probability, frequency, and reasonable expectation, American Journal of Physics, 14 1–13, (1946). http://jimbeck.caltech.edu/summerlectures/references/ProbabilityFrequencyReasonableExpectation.pdf
Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103–1106 (1988)
Frank, R.L., Lieb, E.H.: Entropy and the uncertainty principle. Annales Henri Poincaré 13, 1711–1717 (2012). arXiv:1109.1209
Yeung, R.W.: Information theory and network coding. Springer-Verlag, New York (2008)
Murty, K.G.: Linear programming. Wiley, New York (1983)
Caticha, A.: Lectures on probability, entropy, and statistical physics, In: 28th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, (2008). arXiv:0808.0012
Feldmann, M.: New loophole for the Einstein-Podolsky-Rozen paradox. Found. Phys. Lett. 8(1), 41–53 (1995). https://doi.org/10.1007/BF02187530. arXiv:quant-ph/9904051
Barrett, J., Linden, N., Massar, S., Pironio, S., Popescu, S., Roberts, D.: Nonlocal correlations as an information-theoretic resource. Phys. Rev. A 71(2), 022101 (2005). arXiv:quant-ph/0404097
Popescu, S., Rohrlich, D.: Quantum nonlocality as an axiom. Found. Phys. 24, 379 (1994). arXiv:quant-ph/9508009
Birkhoff, G., von Neumann, J.: The logic of quantum mechanics, Annals of Mathematics, 37 823, (1936). http://www.jstor.org/stable/1968621
Jaynes, E. T.: Information theory and statistical mechanics. II, Phys. Rev. 108(2) 170–190, (1957). http://bayes.wustl.edu/etj/articles/theory.2.pdf
Wigner, E. P.: Normal form of antiunitary operators, J. Math. Phys. 1(5) 409–413, (1960). https://springerlink.bibliotecabuap.elogim.com/chapter/10.1007/978-3-662-02781-3_38
Durt, T., Englert, B.-G., Bengtsson, I., Zyczkowski, K.: On mutually unbiased bases. Int. J. Quantum Info. 8, 535–640 (2010). arXiv:1004.3348
Kalev, A., Gour, G.: Mutually unbiased measurements in finite dimensions, New Journal of Physics, 16(5), 053038 (2014). arXiv:1401.2706. http://stacks.iop.org/1367-2630/16/i=5/a=053038
Schwinger, J.: Unitary Operator Bases, Proc. Nat. Acad. Sci. USA. 46, 560 (1960). http://www.pubmedcentral.nih.gov/picrender.fcgi?artid=222876 &blobtype=pdf
Wiener, N.: The role of the observer, Philosophy of Science, 3(3), 307–319 (1936). http://www.jstor.org/stable/184668
Feynman, R., Weinberg, S.: Elementary particle physics and the laws of physics. Gen. Relativ. Gravitat. 33, 615–616 (1986)
Klein, F.: A comparative review of recent researches in geometry, Gesammelte mathematische Abhandlungen, 1, 460–497 (1931). arXiv:0807.3161. http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN243240503 &DMDID=dmdlog45
Zuber, J.-B.: Invariances in physics and group theory, In: Conference “Lie and Klein; the Erlangen program and its impact on mathematics and physics”, Strasbourg, Sept. 2012, (2013). arXiv:1307.3970
Deutsch, D.: Quantum theory, the Church-Turing principle and the universal quantum computer, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 400(1818), 97–117 (1985). https://people.eecs.berkeley.edu/~christos/classics/Deutsch_quantum_theory.pdf
Gray, J.: Plato’s Ghost: the modernist transformation of mathematics. Princeton University Press, Princeton (2008)
Bouleau, N.: La jonction entre la théorie du potentiel et les probabilités, Cahiers du séminaire d’histoire des mathématiques, 8, 43–66 (1987). http://www.numdam.org/article/CSHM_1987__8__43_0.pdf
Meyer, P.-A., Dellacherie, C.: Probabilité et potentiel, vol. 1 and 2, Hermann, Paris, 1975, (2008)
Hiley, B. J.: Process and the implicate order: their relevance to quantum theory and mind. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.357.4976 &rep=rep1 &type=pdf
Aerts, D., Gabora, L., Sozzo, S., Veloz, T.: Quantum structure in cognition: Fundamentals and applications, In: V. Privman, V. Ovchinnikov (Eds.), Proceedings of the Fifth International Conference on Quantum, Nano and Micro Technologies (ICQMN 2011), International Academy, Research and Industry Association, (2011), pp. 57–62. arXiv:1104.3344
Busemeyer, J.R., Bruza, P.D.: Quantum models of cognition and decision. Cambridge University Press, Cambridge (2012)
Bruza, P., Busemeyer, J., Gabora, L.: Introduction to the Special Issue on Quantum Cognition (2013). arXiv:1309.5673
Dzhafarov, E.N., Kujala, J.V.: Selectivity in probabilistic causality: where psychology runs into quantum physics. J. Math. Psychol. 56, 54–63 (2012). arXiv:1110.2388
Dzhafarov, E.N., Kujala, J.V.: Quantum entanglement and the issue of selective influences in psychology: an overview. Lecture Notes Comput. Sci. 7620, 184–195 (2012). arXiv:1209.0041
Haven, E., Khrennikov, A.: Quantum Soc. Sci. Cambridge University Press, Cambridge (2013)
Clark, S., Coecke, B., Grefenstette, E., Pulman, S., Sadrzadeh, M.: A quantum teleportation inspired algorithm produces sentence meaning from word meaning and grammatical structure (2013). arXiv:1305.0556
Ionicioiu, R.: Quantum mechanics: Knocking at the gates of mathematical foundations, In: I. Parvu, G. Sandu, I. Toader (Eds.), Romanian Studies in Philosophy of Science, Vol. 313 of Boston Studies in the Philosophy and History of Science, Springer, (2015). arXiv:1506.04511
Einstein, A., Born, M.: The Born-Einstein letters. Walker and Company, New-York (1971)
Feynman, R.: Lessons on Probability and Uncertainty in quantum mechanics, Cornell Messenger Lecture Archive, (2011)
Fuchs, C.A.: Quantum mechanics as quantum information (and only a little more). In: Khrennikov, A. (ed.) Quantum Theory: Reconsideration of Foundations, pp. 463–543. Växjö University Press, Växjö, Sweden (2002) . arXiv:quant-ph/0205039
Articles, In: J. T. Cushing, A. Fine, S. Goldstein (Eds.), Bohmian Mechanics and Quantum Theory: An Appraisal, Kluwer, Dordrecht, (1996)
Griffiths, R.B., Omnès, R.: Consistent histories and quantum measurements. Phys. Today 52(8), 26–31 (1999)
Cramer, J.G.: An overview of the transactional interpretation of quantum mechanics. Int. J. Theor. Phys. 27, 227–236 (1988)
Ghirardi, G. C., Pearle, P.: Dynamical reduction theories: Changing quantum theory so the statevector represents reality, In: M. F. A. Fine, L. Wessels (Eds.), Proceedings of the Biennial Meeting of the Philosophy of Science Association, Philosophy of Science Association, East Lansing, MI, (1990)
Zurek, W.H.: Decoherence, Einselection and the existential interpretation (The Rough Guide). Phil. Trans. R. Soc. Lond. A 356, 1793–1821 (1998). arXiv:quant-ph/9805065
Grangier, P.: Contextual objectivity: a realistic interpretation of quantum mechanics (2000). arXiv:quant-ph/0012122
Deutsch, D.: The fabric of reality: the science of parallel universes and its implications. Allen Lane, New York (1997)
Vaidman, L.: The many-worlds interpretation of quantum mechanics, In: E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy, Stanford University, Stanford, CA, (2002). http://plato.stanford.edu/entries/qm-manyworlds/
Spekkens, R.W.: Contextuality for preparations, transformations, and unsharp measurements. Phys. Rev. A 71, 052108 (2005). arXiv:quant-ph/0406166
Chiribella, G., D’Ariano, G.M., Perinotti, P.: Informational derivation of quantum theory. Phys. Rev. A 84(1), 012311 (2011). arXiv:1011.6451
Hardy, L.: Reconstructing quantum theory (2013). arXiv:1303.1538
Moeller, M. P., Masanes, L.: Information-theoretic postulates for quantum theory (2012). arXiv:1203.4516
Masanes, L., Mueller, M.P., Augusiak, R., Perez-Garcia, D.: A digital approach to quantum theory. Proc. Nat. Acad. Sci. USA 110(41), 16373 (2013). arXiv:1208.0493
Chiribella, G., D’Ariano, G. M., Perinotti, P.: Quantum from principles, In: R. Spekkens, G. Chiribella (Eds.), Quantum theory: informational foundations and foils, Springer Verlag, in press. arXiv:1506.00398
Oeckl, R.: A local and operational framework for the foundations of physics. arXiv:1610.09052
Pitowsky, I.: Quantum mechanics as a theory of probability (2005). arXiv:quant-ph/0510095
Janotta, P., Hinrichsen, H.: Generalized probability theories: what determines the structure of quantum theory? J. Phys. A Math. General 47(32), 323001 (2014). arXiv:1402.6562
Pawłowski, M., Paterek, T., Kaszlikowski, D., Scarani, V., Winter, A., Żukowski, M.: Information causality as a physical principle. Nature 461(7267), 1101–1104 (2009)
Barnum, H., Barrett, J., Clark, L.O., Leifer, M., Spekkens, R., Stepanik, N., Wilce, A., Wilke, R.: Entropy and information causality in general probabilistic theories. N. J. Phys. 12, 033024 (2010). arXiv:0909.5075
Caticha, A.: Entropic dynamics: mechanics without mechanism (2017). arXiv:1704.02663
Fuchs, C. A., Schack, R.: Quantum-Bayesian Coherence: The No-Nonsense Version (2013). arXiv:1301.3274
Leifer, M. S., Spekkens, R. W.: Formulating Quantum Theory as a Causally Neutral Theory of Bayesian Inference (2011). arXiv:1107.5849
De Raedt, H., Katsnelson, M. I., Michielsen, K.: Quantum theory as the most robust description of reproducible experiments (2013). arXiv:1303.4574
Fuchs, C.A., Mermin, N.D., Schack, R.: An introduction to QBism with an application to the locality of quantum mechanics. Am. J. Phys. 82, 749–754 (2014). arXiv:1311.5253
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Feldmann, M. Information-Theoretic Interpretation of Quantum Formalism. Found Phys 53, 58 (2023). https://doi.org/10.1007/s10701-023-00690-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10701-023-00690-1