Formal modelling of predator preferences using molecular gut-content analysis

Abstract

The literature on modelling a predator’s prey selection describes many intuitive indices, few of which have both reasonable statistical justification and tractable asymptotic properties. Here, we provide a simple model that meets both of these criteria, while extending previous work to include an array of data from multiple species and time points. Further, we apply the expectation–maximisation algorithm to compute estimates if exact counts of the number of prey species eaten in a particular time period are not observed. We conduct a simulation study to demonstrate the accuracy of our method, and illustrate the utility of the approach for field analysis of predation using a real data set, collected on wolf spiders using molecular gut-content analysis.

1 Introduction

The indices most commonly used to describe a predator’s food preferences, or selectivity, are relatively old (Ivlev 1964; Jacobs 1974; Chesson 1978; Strauss 1979; Vanderploeg and Scavia 1979; Chesson 1983), and yet many applied papers continue to use them. A quick search of papers published in 2014 returns hundreds of publications that cite these fundamental papers, a few being Clements et al. (2014), Hansen and Beauchamp (2014), Hellström et al. (2014), Lyngdoh et al. (2014), Madduppa et al. (2014). These indices, though intuitive, lack the statistical rigour of a full model, focus on a snapshot in time, and rarely allow more than one prey species to be considered (Lechowicz 1982). Other authors are using the Monte Carlo based method of Agustí et al. (2003) (see Davey et al. 2013; King et al. 2010), but this is also unable to take into account multiple prey species across multiple time points. We propose an intuitive statistical model to estimate and statistically test differences in a predator’s prey preferences across an array of time points and between multiple prey species.

A comprehensive overview by Lechowicz (1982), later summarised by Manly et al. (2002), details some of the benefits and faults of the most popular indices. According to these reviews, a majority of the indices give comparable results, save the linear index L by Strauss (1979), despite the fact that most of the methods differ by range and linearity of response. While Lechowicz recommends one index, $E^*$ by Vanderploeg and Scavia (1979) as the “single best” (Lechowicz 1982), albeit imperfect, index, Manly et al. (2002) instead take the approach of excluding the subset of indices which do not “estimate any biologically meaningful value” (Manly et al. 2002). Lechowicz (1982) recommends the index $E^*$, an element of the Manly et al. (2002) suggested indices, because the index value 0 denotes random feeding, the index has a range restricted to $[-1,1]$ (though $E^*=1$ is nigh impossible), and the index is based on the predator’s choice of prey as a function of both the availability of the prey as well as the number of available prey types (assumed known). The downside to this index is its lack of reasonable statistical properties (Lechowicz 1982), thus making the computation of standard errors and thus hypothesis testing difficult. This is, in fact, a common fault amongst most of the indices.

Manly et al. (2002) recognized the need for more formal statistical inference and proposed the use of generalised linear models (GLM). The well established literature on GLMs allows for formal hypothesis testing. Much of this work focuses on general resource selection and doesn’t directly address the problems of food selection. By combining the food selectivity literature with formal statistical modelling, our new method (1) focuses specifically on the problem of predators’ food selection, while maintaining the intuitiveness of the indices summarised by Lechowicz (1982) and Manly et al. (2002), (2) offers formal statistical justification, enabling proper inference and hypothesis testing similar to that of GLMs (Manly et al. 2002), (3) accommodates data collected from multiple prey species across multiple time points, (4) provides parameter estimates even when exact counts of prey species eaten are not fully observed, and (5) provides meaningful single number summaries of the predators’ food preferences.

Our model assumes that numbers of each prey species captured and the numbers consumed by an individual predator follow independent Poisson distributions with separate rates that might possibly vary between species and over time. Further, we are able to estimate the rates of interest even when exact counts of each prey species eaten within any given time period are not observed. When exact counts are unobserved, we instead rely on the researcher being able to detect prey DNA within the predator’s gut (Schmidt et al. 2014; Raso et al. 2014; Madduppa et al. 2014) and make a simple binary conclusion: this predator ate some of that prey species during this time period or did not.

This paper is organised as follows. Section 2 describes our statistical model, for both fully observed count data and for the non-observed count data for which we use the expectation–maximisation (EM) algorithm to estimate parameters of interest, and the statistical tests used to make statements about the parameters of interest. In Sect. 3, we offer a simulation study that demonstrates the accuracy of our methods. Section 4 provides a real data set, which investigates the eating preferences of wolf spiders (Araneae: Lycosidae), found in the Berea College Forest in Madison County, Kentucky, USA, to demonstrate how those interested in assessing trophic interactions with gut-content analyses could apply our methods. A brief discussion concludes the paper in Sect. 5. Alongside our model, we offer an R (Core Team R 2014) package named spiders that implements the methods discussed.

2 Methods

We assume that samples of both the predators and prey are captured from the study area on T occasions. Depending on the species involved and the design of the study the predators and prey may be sampled in the same way or using different methods. In the spider experiment described in Sect. 4, for example, prey are captured using pitfall traps that are dispersed throughout the study area whereas the predators (spiders) were captured by hand. Predators and prey species are collected and counted at each time period. We denote the number of predators and the number of traps in each time period $t \in \{1, \ldots , T\}$ by $J_t$ and $I_t$, respectively. Prey species will be indexed by $s \in \{1, \ldots , S \}$. Let $X_{jst}$ represent the number of prey species s that predator j ate during period t, where $j \in \{1, \ldots , J_t\}$. Let $Y_{ist}$ represent the number of prey species s found in trap i during period t, $i \in \{1, \ldots , I_t\}$.

The number of prey species s that predator j ate during period t is assumed to follow a Poisson distribution with rate parameter $\lambda _{st}$, $X_{jst} \mathop {\sim }\limits ^{{{\mathrm {iid}}}}\mathcal {P}(\lambda _{st})$. The parameter $\lambda _{st}$ represents the rate at which the predator ate prey species s during time period t. The number of prey species s found in trap i during period t is assumed to follow a Poisson distribution with rate parameter $\gamma _{st}$, $Y_{ist} \mathop {\sim }\limits ^{{{\mathrm {iid}}}}\mathcal {P}(\gamma _{st})$. The use of Poisson distributions makes the following implicit assumptions: 1) traps independently catch the prey species of interest, 2) predators eat independently of each other.

By modelling $\lambda _{st}, \gamma _{st}$ we are able to test claims about a predator’s eating preferences. Formal statistical statements about the relative magnitudes of the parameters $\varvec{\lambda } = (\lambda _{11}, \ldots , \lambda _{ST})^t$ and $\varvec{\gamma } = (\gamma _{11}, \ldots , \gamma _{ST})^t$ offer insights to the relative rates at which predators eat particular prey species. We consider four variations on the relative magnitude of $c_{st} = \lambda _{st}/\gamma _{st}$. These four hypotheses each allow $c_{st}$ to vary by time, prey species, both, or neither.

• 1. $c_{st} = c$

• 2. $c_{st} = c_s$

• 3. $c_{st} = c_t$

• 4. $c_{st} = c_{st}$

The first hypothesis states that the relative rates of sampling for the predator and the traps are the same for all species on all occasions. One imagines this is the case if the prey move randomly and the predator simply eats prey which comes within its reach, thus suggesting no selection for a particular prey item. The second hypothesis states that predators sample different prey species at different rates, but each rate is steady across time. This implies that the predator expresses preferences for one prey species over another, but is unresponsive to changes due to time. Conversely, the third hypothesis implies that each prey species is sampled similarly within each time period, while the rates across time are allowed to change. This would happen if the average amount of prey consumed by the predators changed over time while the relative rates of sampling remained the same, or if there were changes in the efficiency of the traps, or both. The final hypothesis assumes a predator’s selection varies by both time and prey species. This would make sense if environmental and biological variables, such as weather, prey availability, and/or palatability were affecting predators’ selection strategies.

Fig. 1

This hierarchy of hypotheses suggests the order in which the discussed models should be tested. One begins with the most complex models at the bottom and sequentially, following the arrows, tests simpler hypotheses using the formal test described in Sect. 2.3 until a final model is established

Because the four hypotheses are nested, a natural testing order is suggested in Fig. 1. For instance, suppose interest lies in the predator’s dietary preferences with respect to prey species $s_1$ and $s_2$ across three time periods. The hypothesis that the predator has the same preference for the two prey species can be tested with

$$\begin{aligned} H_0&: \lambda _t = c_t \gamma _t, \forall t \\ H_1&: \lambda _{st} = c_{st}\gamma _{st}. \end{aligned}$$

The alternative here allows for the predator’s preferences to vary independently for the two species and across the three time points. Similarly, the hypotheses

$$\begin{aligned} H_0&: \lambda _s = c_s \gamma _s, \forall s \\ H_1&: \lambda _{st} = c_{st}\gamma _{st} \end{aligned}$$

would test if the predator’s eating varies by prey species, but not by time, against the most parameter rich model $c_{st}$. The above two tests should be performed before any of the simpler models are tested.

2.1 Fully observed count data

The likelihood function that allows for estimation of these parameters is as follows. Since we assume $X_{jst}$ is independent of $Y_{ist}$ we can simply multiply the respective Poisson probability mass functions, and then form products over all s, t to obtain the likelihood

$$\begin{aligned} L( \varvec{\lambda }, \varvec{\gamma } | {\varvec{x}}, {\varvec{y}}) = \prod _{t = 1}^{T} \prod _{s=1}^S \left\{ \prod _{j=1}^{J_t} f_X(x_{jst}|\varvec{\lambda }) \prod _{i=1}^{I_t} f_Y(y_{ist} | \varvec{\gamma }) \right\} . \end{aligned}$$

(1)

Writing all four hypotheses as $\lambda _{st} = c_{st}\gamma _{st}$, we can, in the simplest cases, find analytic solutions for the maximum likelihood estimates (MLEs) of $c_{st}$, $\gamma _{st}$, and by invariance $\lambda _{st}$. Such solutions exist for the simplest model, $c_{st}=c$, provided that the data are balanced so that $J_t=J$ and $I_t=I$. The solutions are

$$\begin{aligned} \hat{c} = \frac{I \sum _{s,t} X_{\cdot st}}{J \sum _{s,t} Y_{\cdot st}} \quad \text { and } \quad \hat{\gamma }_{st} = \frac{X_{\cdot st} + Y_{\cdot st}}{I \left( \frac{\sum _{st} X_{\cdot st}}{\sum _{st} Y_{\cdot st}} + 1 \right) }, \end{aligned}$$

where $X_{\cdot st} = \sum _{j=1}^{J_t}X_{jst}$ and $Y_{\cdot st} = \sum _{i=1}^{I_t} Y_{ist}$.

In all other cases, analytic solutions are not readily available and instead we rely on the fact that the log-likelihood $l(\varvec{\lambda }, \varvec{\gamma }) = \log {L}$ is concave to maximise the likelihood numerically. To compute MLEs, we maximise the log-likelihood, using coordinate descent (Luo and Tseng 1992), by iteratively solving the likelihood equations (i.e. the equations obtained by setting the partial derivatives of the likelihood with respect to the parameters equal to zero). This yields the following equations for updating c in the models c, $c_t$, and $c_s$ respectively

$$\begin{aligned} \hat{c} = \frac{\sum _{s,t} X_{\cdot st}}{\sum _t J_t \sum _s \gamma _{st}}, \quad \hat{c}_t = \frac{\sum _s X_{\cdot st}}{J_t \sum _s \gamma _{st}}, \quad \hat{c}_s = \frac{\sum _{t}X_{\cdot st}}{\sum _t J_t \gamma _{st}}, \quad \text { and } \quad \hat{c}_{st} = \frac{X_{\cdot st}}{J_t \gamma _{st}}. \end{aligned}$$

The equation for updating $\hat{\gamma }_{st}$ is

$$\begin{aligned} \hat{\gamma }_{st} = \frac{X_{\cdot st} + Y_{\cdot st}}{J_t c_{st} + I_t}, \end{aligned}$$

where $c_{st}$ would be replaced by $c, c_t$, or $c_s$ depending on the chosen model.

2.2 Unobserved counts

In many applications, such as DNA-based gut-content analysis, it is not possible to count the number of individuals of each prey species that are in a predator’s gut. Instead, it is only possible to detect whether or not a predator consumed the prey species during a given time period, based on the rate at which prey DNA decays in the predator gut (Greenstone et al. 2013). In this case we can still make inference about the predators’ preferences for the different prey species by using an expectation–maximisation (EM) algorithm to compute MLEs.

We denote the binary random variable indicating whether the jth predator did in fact eat at least one individual of prey species s in time period t by $Z_{jst} = 1(X_{jst} > 0)$. Given the Poisson assumptions above, these variables are independent Bernoulli observations with success probability $p_{st} = P(Z_{jst}=1)= 1-\exp \{-\lambda _{st}\}$. Despite not observing $X_{jst}$, we can compute maximum likelihood estimates of the parameters $\varvec{\lambda }, \varvec{\gamma }$ through an EM algorithm using the complete data log-likelihood

$$\begin{aligned} l_{comp}(\varvec{\lambda }, \varvec{\gamma })= & {} \log f_{X,Y,Z}(\varvec{x}, \varvec{y}, \varvec{z}|\varvec{\lambda }, \varvec{\gamma })\\= & {} \sum _{s,t}^{S,T} \left[ \sum _{j=1}^{J_t} \log f_{X,Z}(x_{jst},z_{jst}|\varvec{\lambda }) + \sum _{i=1}^{I_t}\log f_Y(y_{ist}|\varvec{\gamma }) \right] . \end{aligned}$$

The mass function of $Y_{ist}$ is exactly as in Sect. 2.1 and so we focus on deriving the joint probability mass function of $X_{jst}$ and $Z_{jst}$. With the distribution of $Z_{jst}$ given above, we can compute $f_{X,Z}(x_{jst},z_{jst}|\varvec{\lambda })$ by noting that $X_{jst}=0$ with probability 1 if $Z_{jst}=0$, and that $[X_{jst}|Z_{jst}=0]$ has a truncated Poisson distribution with mass function

$$\begin{aligned} f_{X|Y,Z,\varvec{\lambda },\varvec{\gamma }}(x_{jst}|z_{jst}) = \frac{\exp {\{-\lambda _{st}\}} \lambda _{st}^{x_{jst}}}{(1 - \exp {\{-\lambda _{st}\}}) x_{jst}!}1(x_{jst} > 0) \end{aligned}$$

and expected value

$$\begin{aligned} {{\mathbb {E}}}_{X|Y,Z}X_{jst} = \frac{\lambda _{st} \exp {\{\lambda _{st} \}}}{\exp {\{ \lambda _{st} \}} - 1}. \end{aligned}$$

The joint probability mass function of $X_{jst}, Z_{jst}$ is then

$$\begin{aligned} f_{X,Z|\varvec{\lambda }}(x_{jst},z_{jst}) = \left\{ \begin{array}{lr} \exp {\{ -\lambda _{st} \}}, &{} x_{jst}=0\quad \text{ and }\quad z_{jst} = 0 \\ \frac{\exp {\{-\lambda _{st} \}} \lambda _{st}^{x_{jst}}}{x_{jst}!}, &{} x_{jst} > 0\quad \text{ and }\quad z_{jst} = 1 \\ 0 &{} \text{ otherwise } \end{array} \right. . \end{aligned}$$

EM algorithms work by iterating two steps, the E-step and M-step, until the optimum is reached (Dempster et al. 1977; McLachlan and Krishnan 2007). Let k index the iterations in this EM algorithm so that $\varvec{\lambda }^{(k)}$ and $\varvec{\gamma }^{(k)}$ denote the estimates computed on the kth M-step. The E-step consists of computing the expectation of $l_{comp}$ with respect to the conditional distribution of X given the current estimates of the parameters

$$\begin{aligned} Q^{(k)}(\varvec{\lambda },\varvec{\gamma }) = {{\mathbb {E}}}_{X|Y,Z,\varvec{\lambda }^{(k)}} l_{comp} \end{aligned}$$

in order to remove the unobserved data. The M-step then involves maximising $Q^{(k)}(\varvec{\lambda },\varvec{\gamma })$ with respect to the parameters in the model to obtain updated estimates of the parameters,

$$\begin{aligned} (\varvec{\lambda }^{(k+1)}, \varvec{\gamma }^{(k+1)}) = \mathop {\text {arg max}}\limits _{(\varvec{\lambda }, \varvec{\gamma })} Q^{(k)}(\varvec{\lambda }, \varvec{\gamma }). \end{aligned}$$

These steps are alternated until a convergence criterion monitoring subsequent differences in the parameter estimates/likelihood is met.

The calculation of $Q^{(k)}(\varvec{\lambda }, \varvec{\gamma })$ is not difficult and is given by:

$$\begin{aligned} Q^{(k)}(\varvec{\lambda }, \varvec{\gamma })= & {} {{\mathbb {E}}}\log {f_{X,Z|\varvec{\lambda }}(X,{\varvec{z}})} + \log {f_{Y|\varvec{\gamma }}({\varvec{y}})} \nonumber \\= & {} \sum _{s=1}^S \sum _{t=1}^T \sum _{j=1}^{J_t} {{\mathbb {E}}}\log {f_{X,Z|\varvec{\lambda }}(X_{jst},z_{jst})} + \sum _{s=1}^S \sum _{t=1}^T \sum _{i=1}^{I_t} \log {f_{Y|\varvec{\gamma }}(y_{ist})} \nonumber \\\propto & {} \sum _{s,t,j} \left( - \lambda _{st} + z_{jst} \log {\lambda _{st}} {{\mathbb {E}}}X_{jst} \right) + \sum _{s,t} \left( -I_t \gamma _{st} + Y_{\cdot st} \log {I_t \gamma _{st}} \right) \nonumber \\\propto & {} \sum _{s,t} \left( -J_t \lambda _{st} + z_{\cdot st} \log {\lambda _{st}} {{\mathbb {E}}}\left( X_{jst}|\lambda _{st}^{(k)},\gamma _{st}^{(k)}\right) \right) \nonumber \\&+ \sum _{s,t} \left( -I_t \gamma _{st} + Y_{\cdot st} \log {I_t \gamma _{st}} \right) . \end{aligned}$$

(2)

No analytic solution to the M-step exists, however, so we again chose to maximise Q with coordinate descent (Luo and Tseng 1992). In fact, as we only need to find parameters that increase the value of Q on each iteration, we forgo fully iterating the coordinate descent algorithm to find the maximum and instead perform just one step uphill within each EM iteration (Givens and Hoeting 2012). Since $Q^{(k)}$ is concave and smooth in the parameters $\varvec{\lambda }, \varvec{\gamma }$, we are able to use the convergence of parameter estimates, $||(\varvec{\lambda }^{(k)}, \varvec{\gamma }^{(k)}) - (\varvec{\lambda }^{(k+1)}, \varvec{\gamma }^{(k+1)})||_{\infty } < \tau$, for some $\tau >0$, as our stopping criterion.

As we show in our simulation study, this generalised EM algorithm accurately estimates the parameters when values of $\lambda _{st}$ are relatively small, such that zeros are prevalent in the data $Z_{jst}$. In contrast, if the predator consistently eats a given prey species, few to no zeros will show up in the observed data and ${{\mathbb {E}}}Z_{jst}$ is estimated to be nearly 1. The loss of information is best seen by attempting to solve for $\lambda _{st}$ in the equation $1 = {{\mathbb {E}}}Z_{jst} = 1 - \exp \{-\lambda _{st}\}$. As the proportion of ones in the observed data increases, we expect $\lambda _{st}$ to grow exponentially large. When no zeros are present in the data, so that only ones are observed, the likelihood can be made arbitrarily large by sending the parameter off to infinity.

2.3 Testing

The likelihood ratio test statistic is

$$\begin{aligned} \varLambda (X,Y):= -2 \log { \frac{ \sup _{\theta _0} L(\theta _0|X,Y)}{ \sup _{\theta _1} L(\theta _1|X,Y)} }, \end{aligned}$$

where $\theta _0, \theta _1$ represent the parameters estimated under the null and alternative hypotheses, respectively. It is well known that the asymptotic distribution of $\varLambda$ is a $\chi _{\rho }^2$ distribution with $\rho$ degrees of freedom (Wilks 1938). The degrees of freedom $\rho$ equal the number of free parameters available in the stated hypotheses under question. If we put the null hypothesis to be $H_0: \lambda _t = c_t \gamma _t$, for all t and contrast this against $H_1: \lambda _{st} = c_{st}\gamma _{st}$ then there are $\rho = 2(S \cdot T) - S \cdot T - T = S \cdot T - T$ degrees of freedom. When the observations $X_{jst}$ are not observed, we use $L_{obs}(\varvec{\lambda }, \varvec{\gamma }|Z,Y)$ as the likelihood in the calculation of $\varLambda$

$$\begin{aligned} L_{obs}(\varvec{\lambda }, \varvec{\gamma }|Z,Y) = \prod _{s,t}^{S,T} \left\{ \prod _{j=1}^{J_t}f_Z(z_{jst}|\varvec{\lambda }) \prod _{i=1}^{I_t}f_Y(y_{ist}|\varvec{\gamma }) \right\} . \end{aligned}$$

The level of significance $\alpha$ is used to reject the null hypothesis in favour of the alternative hypothesis if $\mathbb {P}(\chi ^2_{\rho } > \varLambda ) < \alpha$.

2.4 Linear transformations of $c_{st}$

After determining which model best fits the data, more detail may be extracted through specific hypothesis tests of the elements of $c_{st}$, or in vector notation as $\mathbf {c} \in \mathbb {R}^{S\cdot T}$. Let the elements of $\hat{\mathbf {c}}$ be the maximum likelihood estimates, $\hat{c}_{st}$, as found via the framework above. Since $\hat{\mathbf {c}}$ is asymptotically normally distributed, any linear combination of the elements is also asymptotically normally distributed. For instance, let a be a vector of the same dimension of $\hat{\mathbf {c}}$. Then $a^t\hat{\mathbf {c}}$ is asymptotically distributed as $\mathcal {N}(a^t\mathbf {c}, a^t\varSigma a)$, where $\varSigma$ is the covariance matrix of the asymptotic distribution of $\hat{\mathbf {c}}$. Tests of the form $H_0: a^t\mathbf {c} = \mu$ against any alternative of interest are then approximate Z-tests. Confidence intervals of any size are similarly, readily obtained. Suppose, for example, that the hypothesis $c_s$ is determined to best fit the data with s ranging $s = 1, 2, 3$. We can test to see whether or not the first two species are equally preferred under the null hypothesis $c_{1} = c_{2}$. This hypothesis is alternatively written in vector notation as $a^t\mathbf {c} = 0$, where $a = (1, -1, 0)^t$.

3 Simulation study

Our simulations assume two prey species and five time points, throughout. Of the hierarchy of hypotheses, we generate data under three models: $c, c_s, c_t$. Sample sizes for both prey species and predator gut count observations are randomly chosen from four overlapping levels: “small” sample sizes are randomly sampled numbers in [20, 50], “medium” [30, 75], “large” [50, 150], and “larger” [100, 200]. This is repeated for each level of sample size. We simulate 500 replicate data sets for each of the twelve scenarios above for both types of data, fully observed count data, $X_{jst}$, and for non-count data, when we observe only a binary response, $Z_{jst} = 1(X_{jst}>0)$. Each scenario is then fitted with the true model that generated the data. All simulations of non-count data use $\tau = 10^{-5}$ as the convergence tolerance. A subset of the examples are provided here; the interested reader is referred to the supplementary materials for the complete simulation results.

Fig. 2

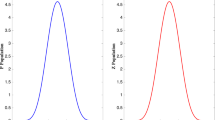
The density plot of all 500 estimates of fitting the true model to the data generated from models $c_s$ with the small sample size is shown. The ticks along the x-axis show the true parameter values associated with each density. Figures that also distinguish the densities by colour are available online

For all simulated data, the true parameter values for the rate at which prey species are encountered in the wild are fixed to be $\gamma _{st} = \pi \approx 3.14, \, \forall s,t$. The values of $\lambda _{st}$ are set with respect to each data generating model. For model $c_{st} = c$, where predator preferences don’t vary by either time or species, we put $\lambda _{st} = 2\pi , \forall s,t$. Under model $c_s$, the ratio of rates vary by species only, so we put $\lambda _{1t} = \sqrt{2}$ and $\lambda _{2t} = \pi$. Hence, $c_1 = \sqrt{2}/\pi \approx 0.45$ and $c_2 = 1$. For the last model, $c_t$, the ratio of rates vary by time t. Here, we put $\lambda _{st} = t$ for $t \in \{1, \ldots , 5 \}$.

We consider results when the correct model is fit to the simulated data. Figure 2 shows the density plot of the estimates of $c_s$ when fitting the true model to the fully observed count data generated under models $c_s$, while Fig. 3 shows the same for the estimates of c when data is generated under model c. The plots provide evaluations of parameter estimates under each scenario. For model $c_s$ in Fig. 2, the parameters $c_1 \approx 0.45$ and $c_2 = 1$ are on average, across all 500 simulations, estimated as $\hat{c}_1 = 0.45$ and $\hat{c}_2 = 1.00$, with sample standard deviations of $\text {SD}(\hat{c}_1) = 0.03$ and $\text {SD}(\hat{c}_2) = 0.06$. Figure 3 provides results for model $c_{st} = c$. Averaging across all 500 simulations, the parameter $c=2$ is estimated as $\hat{c} = 2.00$ with sample standard deviation $\text {SD}(\hat{c})=0.06$. This is further seen in Fig. 4, where box plots of the parameter estimates, centred at true parameter values, of the correct model fit to data generated from both $c_s$ and $c_t$ show empirically very little bias.

Fig. 3

The density plot of all 500 estimates of fitting the true model to the data generated from model c with the medium sample size is shown. A tick on the x-axis shows the true parameter value

Fig. 4

Shown are all 500 estimates, centred at the true parameter values, from fitting the true model to the data generated from models $c_s,c_t$ with sample sizes small and medium, respectively

We next generated data with unobserved counts. As noted above under certain circumstances our unobserved counts model accurately estimates the parameters of interest, and at other times can infinitely over-estimate parameters. To investigate this issue further, we consider the same scenarios mentioned above, but reduce all of the count data down to binary observations. For each scenario, we fit the unobserved counts model as if we knew the true underlying model that generated the observed data.

Figures 5 and 6 contain density plots of the estimates of $c_s, c_t$ for all 500 replications of the data generating models $c_s,c_t$ with the small and the larger sample sizes, respectively. When data are generated under the model $c_s$ and the true model is fit to the non-count data, we find even for the small sample size that point estimates are only very slightly biased. When parameter values are of sufficient size to make zeros in the simulated data less common, the estimates from fitting the correct model to the generated data are occasionally over-estimated. This effect is easily seen in Fig. 6 for the two greatest values of $c_t$ despite the increased sample size, but is also seen, less dramatically, in the density plot for the $c_s$ generated data. Figure 7 provides box plots of the parameter estimates, centred at true parameter values.

Fig. 5

The density plot of all 500 estimates of fitting the true model to the data generated from model $c_s$, when counts are not observed, is shown with the small sample size. The ticks along the x-axis show the true parameter values associated with each density. Figures that also distinguish the densities by colour are available online

The cluster of estimates for $c_5$ between 3.5 and 4.0 in Fig. 6 comes from data sets in which $Z_{js5}=1$ for all j, s. For the data shown in Fig. 6, this happened 73 times out of the 500 replicated data sets. As mentioned above, the estimate of $c_5$ is infinite in this case. However, this EM algorithm will always provide a finite estimate for all parameters when it terminates. In this case, we set $\tau =10^{-5}$ and this caused the algorithm to terminate with $\hat{c}_5$ between 3.5 and 4.0. To confirm that this is due to the arbitrary choice of $\tau$, we repeated the algorithm with smaller values of $\tau$ for several data sets. As expected, $\hat{c}_5$ increased without bound as we refit the model with increasingly small values of $\tau$. Thus, conditional on a mixture of 0s and 1s in the data the corresponding estimators appear to be unbiased, but when no 0s exist in the data the theoretical bias is infinite. In practice however we imagine that no 0s in the data seems an unlikely circumstance.

Fig. 6

The density plot of all 500 estimates of fitting the true model to the data generated from model $c_t$, when counts are not observed, is shown with the larger sample size. The ticks along the x-axis show the true parameter values associated with each density. Figures that also distinguish the densities by colour are available online

Fig. 7

Shown are all 500 estimates, centred at the true parameter values, from fitting the true model to the data generated from models $c_s,c_t$, when counts are not observed, with sample sizes small and larger, respectively

4 Application

To illustrate these methods, we analysed a data set collected to investigate the feeding preferences of two species of wolf spider, Schizocosa ocreata and Schizocosa stridulans (Araneae: Lycosidae). Every 6–12 days, 10–40 spiders were hand-collected between October 2011 and April 2013 within Berea College Forest in Madison County, Kentucky, USA. Spiders were removed from the leaf litter using an aspirator, placed in separate 1.5 mL microcentrifuge tubes filled with 95 % EtOH, and preserved at $-20\,^{\circ }\hbox {C}$ until DNA extraction. In parallel, we also surveyed availability of forest floor prey using pitfall traps $(n = 32)$. For the analysis, both species of Schizocosa were pooled and the number of spiders and prey were analysed by month. On average, 69 spiders, 111 Diptera, and 297 Collembola were caught in each time period. The range of the sample sizes across all 18 months was 11–181 for caught spiders, 7–322 for trapped Diptera, and 101–755 for trapped Collembola. Figure 8 plots the total number of each order that was caught during each time period while Fig. 9 shows the prey proportions in the sample spiders’ guts.

Fig. 8

For both Collembola (dashed) and Diptera (solid), the plot shows the number of the prey trapped in each time period. Figures that also distinguish the lines by colour are available online

Fig. 9

For both Collembola (dashed) and Diptera (solid), the plot shows the prey proportions in the sampled wolf spiders’ guts in each time period. Figures that also distinguish the lines by colour are available online

To determine whether spiders had consumed dipterans and/or collemblans, we conducted a molecular analysis of their gut-contents. First, DNA from spiders was extracted using Qiagen DNEasy$^{\circledR }$ Tissue Extraction Kit (Qiagen Inc., Chatsworth, California, USA) following the animal tissue protocol outlined by the manufacturer, with minor modifications. Whole bodies of the spiders were first crushed to release prey DNA from within their alimentary canal for extraction. The $200\,\upmu$L extractions were stored at $-20\,^{\circ }\hbox {C}$ until PCR. Second, order-specific primers from the literature were used to detect the DNA of Collembola and Diptera within the guts of the spiders. Primer pairs designed by Sint et al. (2012), targeting the 18S rDNA gene, were used to detect Collembola predation Table 1. A PCR cycling protocol for $12.5\,\upmu$L reactions containing $1\times$ Takara buffer (Takara Bio Inc., Shiga, Japan), 0.2 mM dNTPs, $0.2\,\upmu$M of each primer, 0.625 U Takara Ex TaqTM and $1.5\,\upmu$L of template DNA, using BioRad PTC-200 and C1000 thermal cyclers (Bio-Rad Laboratories, Hercules, California, USA), was optimised as follows: $95\,^{\circ }\hbox {C}$ for 1 min, followed by 35 cycles of $94\,^{\circ }\hbox {C}$ for 30 s, $61.2\,^{\circ }\hbox {C}$ for 90 s, and $72\,^{\circ }\hbox {C}$ for 60 s. Primer pairs designed by Eitzinger et al. (2014), targeting the 18S rDNA gene, were used to detect Diptera predation Table 1. PCR cycling protocol for $12.5\,\upmu$L reactions with Takara reagents (as above) and $2\,\upmu$L of template DNA was optimised as follows: $95\,^{\circ }\hbox {C}$ for 1 min, followed by 40 cycles of 94 for 45 s, $60\,^{\circ }\hbox {C}$ for 45 s, and $72\,^{\circ }\hbox {C}$ for 45 s. Both primer pairs were tested for cross-reactivity against a range of prey and predator species from the field site and in all cases, no amplification of DNA was observed, confirming suitable specificity of the primers for this study. Lastly, electrophoresis of $10\,\upmu$L of each PCR product was later conducted to determine success of DNA amplification using 2 % Seakem agarose (Lonza, Rockland, Maine, USA) stained with 1x GelRed™nucleic acid stain (Biotium, Hayward, California, USA). This procedure allowed us to determine a presence or an absence of Diptera and Collembola DNA within each spider.

Table 1 Targeted prey orders, primer names and sequences, size of amplicon, and source of design for the detection of prey taxa within the guts of Schizocosa spiders

Fig. 10

Point estimates (solid) and 95 % confidence intervals (dashed) as estimated from the model $c_{st}$ for Collembola. Figures that also distinguish the lines by colour are available online

These data provide an example of our hierarchy of hypotheses. From the bottom of the graph in Fig. 1, we tested the most parameter rich model $c_{st} = \lambda _{st}/\gamma _{st}$ against models $c_{s}, c_{t}$. In both cases, the more parameter rich model fits these data better than is expected by chance; $H_0: c_s$ versus $H_1: c_{st}$ gives p value $< 0.0001$ and $H_0: c_t$ versus $H_1: c_{st}$ gives p value $< 0.0001$. Model $c_{st}$ estimates 72 parameters in total; since, in this case, there are two prey of interest and 18 time periods, it takes 36 parameters to estimate each $c_{st}$ and $\gamma _{st}$. Figures 10 and 11 plot the point estimates and 95 % confidence intervals of $c_{st}$, for both prey across all time periods.

Fig. 11

Point estimates (solid) and 95 % confidence intervals (dashed) as estimated from the model $c_{st}$ for Diptera. Figures that also distinguish the lines by colour are available online

With point estimates of $c_{st}$ under the model $c_{st} = \lambda _{st}/\gamma _{st}$, we can test any number of linear contrasts. For instance, the hypotheses $c_{1t} = c_{2t}$, for $t \in \{1, \ldots , 18\}$ state that wolf spiders equally prefer the orders Diptera and Collembola at each of the 18 time points. Using a level of significance of 0.05, and after making a Bonferroni multiple comparisons adjustment, the data can not say that the two prey are differently preferred in October, November, and December of 2011 and for March and July of 2012. In all other time periods, the data suggest that Diptera and Collembola are unequally preferred by wolf spiders. Contrasts such as these allow molecular ecologists to identify in greater detail and formally test changes in prey preferences across time points and multiple species.

5 Discussion

The earliest estimators of predators’ dietary preferences, summarised by Lechowicz (1982) and Manly et al. (2002), produced one number summaries that rarely considered more than one prey species, did not take into account changes across time, and had minimal statistical justification. Instead, they were justified by arguing in favor of each index’s unique, and claimed “optimal,” properties. Further, these indices could not handle unobserved count data.

A more recent method for testing prey preferences was developed by Agustí et al. (2003). This method attempts to test the hypothesis that individuals are eating prey at random using a test based on Monte Carlo simulation (more specifically the bootstrap). Unfortunately, the method described does not attempt to model the distribution of the number of prey items eaten, as we have done, and therefore we provide a methodological advance on the approach described previously. The null hypothesis tested by Agustí et al. (2003) is that the proportion of prey species $j=1,\ldots ,J$ in the mesocosm, denoted $\pi _j$, is equal to the proportion of prey species j in the predator’s guts, denoted by $p_j$, at all of the sampling times. This is tested by repeatedly simulating the gut contents of spiders in each sample under this hypothesis and then comparing summary statistics computed from the observed data and the simulated data to generate a p value. The problem with this approach is that the relationship between $\pi _j$ and $p_j$ depends on the number of prey items eaten by each predator. If each predator had eaten exactly one prey item then the null hypothesis of Agustí et al. (2003) would be equivalent to random sampling of prey. However, the relationship between $\pi _j$ and $p_j$ is more complicated when predators can have more than one prey item in their gut. Given that a predator has m prey items in its gut, randomly sampled from the mesocosm, the marginal probability that at least one item from prey species j is present is $1-(1-\pi _j)^m$. The marginal probability that an individual has as least one item from prey species j in its gut is then $\sum _{m=1}^{\infty } (1-(1-\pi _j)^m)P(m)$, where P(m) is the probability that a predator has a total of m species in its gut. The presence of species in a predator’s gut contents also cannot be simulated without modeling the number of items in the gut for exactly the same reason. This demonstrates the importance of knowing the distribution of prey items in the gut in testing the hypothesis of random sampling. Monte Carlo simulation methods similar to this could be implemented using the output from our model, but these would be computationally intensive in comparison to the likelihood ratio tests which can be computed almost immediately.

Throughout this paper we assume the complete data were generated from underlying Poisson distributions. Though this assumption is not easily tested, and other factors affecting our model may distort our methods (e.g. sampling issues, environmental variables, differential decay rates), we do not believe a better assumption is readily available to handle all the cases we considered. The Poisson distribution provides reasonable biological interpretation to the available data, data obtained by ecologists interested in prey electivity. Alternatively, one could hypothesize a more complex distribution that similarly has good biological interpretation, say a distribution with more than one parameter. Such a distribution could theoretically perform better than our model when full count data are observed and the sampled data were not generated from a Poisson distribution—if the data were generated from a Poisson distribution then our likelihood ratio test ensures we are using the most powerful test available. However, when only unobserved count data is available, any distribution with more than one parameter is unidentifiable. The Poisson distribution on the other hand allowed us to use a relatively simple EM algorithm to estimate parameters of interest when only unobserved count data are available. Future development of our methods might consider more complex distributions to handle variables not presently considered in the case of fully observed count data.

Beyond the statistical assumptions, sampling of prey availability should be given careful attention. To survey prey of interest, we relied on pitfall trapping, which is a reasonable method to quantify potential prey encounters of sit-and-pursue predators, such as wolf spiders (Uetz et al. 1999). In general, however, human-made traps are liable to collect prey at rates unequal to that of the predator of interest. Confounded with researchers’ abilities to make sufficiently efficient traps are a host of environmental variables. Researchers should consider these potential sampling issues and attempt to determine, a priori, how well their traps will characterize prey availability according to the biology of their focal predator. If such issues are steady over time, then mathematically the parameter $c_{st} = \lambda _{st}/\gamma _{st}$ is directly affected. When human-made traps are relatively and consistently more efficient at catching prey than are the predators, $c_{st}$ will be relatively smaller. Conversely, when the traps are relatively and consistently less efficient, $c_{st}$ will be relatively larger. Unfortunately, these factors can be difficult to control, practically, or otherwise, and are to some degree unavoidable. Mark-recapture methods might be implemented to adjust for trap efficiency and estimate the true density of each prey species. However, recapture rates are likely to be low and this type of data is beyond what is regularly collected in these types of experiments.

If issues of trap efficiency or abundance are suspected to change across sampling times, we offer an alternative parameterization, details of which are found in “Appendix”. The ratio $c_{st} = \lambda _{st} / \gamma _{st}$ implicitly treats $\gamma _{st}$ as an index proportional to true abundance. This assumption is valid if the traps maintain efficiency across all occasions, but otherwise is incorrect. Rewriting $c_{st}$ as $k_{st}d_t$, such that $\sum _{s=1}^S k_{st} = 1$ for all t, allows for trap efficiency to vary across time. The parameter $d_t$ captures changes in the absolute relationship between $\lambda _{st}$ and $\gamma _{st}$ which may be due to actual changes in abundance or to changes in trap efficiency. $k_{st}$ then appropriately measures the ratio of consumption to encounter rates, taking into account changes in abundance or trap efficiency.

The methods we presented offer ecologists a formal statistical framework to model and test predator feeding preferences across an array of time points and prey species. Building from intuitive assumptions, we have developed methodologies for analyzing counts of prey items consumed and have extended these methods for analyzing simple presence/absence data. We have provided computationally efficient methods for fitting these models using the EM algorithm and developed powerful tests for a hierarchy of hypotheses based on the likelihood ratio. We are not aware of previous methods that have offered such abilities. These methods are available to researchers via the R package spiders which is available at http://cran.r-project.org/web/packages/spiders/index.html (Roualdes and Bonner 2014).

Appendix: Varying trap efficiency

When there is concern about trap efficiency varying across time, we recommend the following reparameterization of $c_{st} = \lambda _{st}/\gamma _{st}$. Let

$$\begin{aligned} k_{st}d_t = \frac{\lambda _{st}}{\gamma _{st}}, \end{aligned}$$

such that $\sum _{s=1}^S k_{st} = 1$, for all t. The parameter $d_t$ allows for changes in trap efficiency or in actual abundance over time. If such changes are believed to be present, this reparameterization allows for a more natural interpretation. The parameter $k_{st}$ models relative consumption to encounter rates, as expected.

Since this reparameterization amounts to a linear transformation of the parameters, the asymptotic distribution for $\hat{d}_t$ can be evaluated directly. Because of the constraint $\sum _{s=1}^S k_{st} = 1$, we find that $d_t = \sum _{s=1}^S c_{st}$ or written in matrix notation $\mathbf {d} = \mathbf {1}' \mathbf {c}$, where $\mathbf {d} \in \mathbb {R}^T$. The asymptotic distribution of $\hat{\mathbf {d}}$ follows immediately, $\hat{\mathbf {d}} \mathop {\sim }\limits ^{\cdot } \mathcal {N}(\mathbf {1}'\mathbf {d}, \mathbf {1}'\varSigma \mathbf {1})$, where $\varSigma$ is the covariance matrix of the asymptotic distribution of $\hat{\mathbf {c}}$.

More importantly, we can find the asymptotic distribution of $\hat{\mathbf {k}}_t = (k_{1t}, \ldots , k_{St})' \in \mathbb {R}^S$. We make use of the delta method (Serfling 2001). The asymptotic variance relies on the derivatives, $d k_{rt} / d c_{st}$. Let $c_{\cdot t} = \sum _{s=1}^S c_{st}$. Because $k_{st} = c_{st}/ c_{\cdot t}$, we can find the necessary derivatives in two cases

$$\begin{aligned} \frac{d k_{rt}}{d c_{st}} = {\left\{ \begin{array}{ll} \frac{-c_{rt}}{c_{\cdot t}^2}, &{} r \ne s \\ \frac{c_{\cdot t} - c_{st}}{c_{\cdot t}^2}, &{} r = s. \end{array}\right. } \end{aligned}$$

Thus, the asymptotic distribution of $\hat{\mathbf {k}}_{t}$ is $\mathcal {N}(\frac{c_{st}}{c_{\cdot t}}, (\frac{d \mathbf {k}_t}{d \mathbf {c}_t}) \varSigma (\frac{d \mathbf {k}_t}{d \mathbf {c}_t})')$.