Entering H$^{\infty }$-Optimal Control Robustness into a Macroeconomic LQ-Tracking Model

Abstract

This analysis explores robust designs for an applied macroeconomic discrete-time LQ tracking model with perfect state measurements. We develop a procedure that reframes the tracking problem as a regulator problem that is then used to simulate the deterministic, stochastic LQG, H-infinity, multiple-parameter minimax, and mixed stochastic/H-infinity control, for quarterly fiscal policy. We compare the results of the five different design structures within a closed-economy accelerator model using data for the United States for the period 1947–2012. When the consumption and investment tracking errors are more heavily emphasized, the H-infinity design renders the most aggressive fiscal policy, followed by the multiple-parameter minimax, mixed, LQG, and deterministic versions. When the control tracking errors are heavily weighted, the resulting fiscal policy is initially more aggressive under the multi-parameter specification than under the H-infinity and mixed designs. The results from both weighting schemes show that fiscal policy remains more aggressive under the robust designs than the deterministic model. The simulations show that the multi-parameter minimax and mixed designs provide a balancing compromise between the stochastic and robust methods when the worst-case concerns can be primarily limited to a subset of the state-space.

1 Introduction

Optimal control in applied macroeconomic analysis requires the modeling of equation parameters and disturbances in order to deal with uncertainty. Kendrick’s (1981) partial-adjustment, closed-economy macroeconomic accelerator model explores optimal control policies under multiplicative uncertainty by estimating stochastic equation parameters using adaptive control algorithms. Kendrick’s innovative analysis also explores additive uncertainty, which is the more commonly specified uncertainty that arises through the error terms in the system equations.

Most of the earlier control systems research focused on the linear-quadratic-Gaussian (LQG) approach, in which the disturbances were modeled as random Gaussian variables (Chow 1975; and Sage and White 1977), or on adaptive control, where the unknown disturbances are learned through complex feedback and feedforward loop algorithms (Kendrick 1981, 2005). The primary problem with these adaptive and LQG probabilistic approaches is that minimizing the expected value of a performance index leads to maximum system performance in the absence of misspecification, but it can lead to poor performance and instability if it is misspecified (Tornell 2000). This inadequacy creates a need for robust design considerations.

Robust control modeling explicitly accounts for imprecise system models or error models in order to synthesize a control policy that stabilizes a family of models (Bernhard 2002). H$^{\infty }$-optimal control was the primary subject of robust control research in the field of engineering in the 1980s and 1990s, and has been extensively applied in economics (Basar 1992; Hansen and Sargent 2008). Basar and Bernhard (1991) explore H$^{\infty }$-optimal control designs for continuous and discrete time systems with both perfect and imperfect information structures. Linear-quadratic (LQ) specifications in an H$^{\infty }$-optimal control model represent a minimax approach that seeks to achieve a robust design by minimizing a performance index under the worst possible disturbances, where the disturbances maximize that same performance index. Robust is defined as guaranteed performance for any disturbance sequence that satisfies the H$^{\infty }$-norm bound.

1.1 Purpose and Scope

The purpose of this paper is to integrate an H$^{\infty }$-optimal control design, a multiple-parameter minimax design, and a mixed stochastic/robust design into a macroeconomic accelerator model in order to compare the robust design policies with the deterministic and LQG stochastic policies. The paper builds upon Kendrick’s (1981) closed-economy LQ (Linear-Quadratic) tracking model that was applied to the US using quarterly data from 1947 to 1969 in order to evaluate optimal fiscal policy. Our analysis converts the LQ tracking problem to an LQ regulator design, and formulates the error structure of the model for five different cases: deterministic, LQG stochastic, H$^{\infty }$-optimal control, multiple-parameter minimax, and stochastic-H$^{\infty }$-mixed optimal control.

The H$^{\infty }$-optimal control, multiple-parameter minimax model, and mixed optimization models are specified as soft-constrained games. We develop a Matlab software program that allows the user to select the weighting parameters of the game to achieve disturbance attenuation. The empirical analysis re-estimates an expanded version of Kendrick’s (1981) model using quarterly data from 1947 to 2012. The estimated model shows fiscal crowding-in for consumption, and fiscal-crowding out for investment. Using an augmented performance index, we employ the estimated parameters to simulate the model and compare the trajectories of the deterministic, stochastic, robust, and mixed control designs. The results show that the multiple-parameter minimax and mixed designs can provide a balance between the LQG model’s potential failure due to worst-case scenario exposure, and the overly aggressive robust policy that operates under consistent extreme pessimism.

1.2 Contribution to Research on Robustness and Fiscal Policy

The most widely used approach to robustness in macroeconomics has been that of Hansen and Sargent (2007, 2008), which focuses on using entropy to measure model misspecification, imploring both state-space (time domain) and frequency domain methods. Svec (2012) and Karantounieas (2013) both employ the Hansen and Sargent robust control approach within the Lucas and Stokey (1983) complete markets economy without capital, where exogenous government spending is financed by labor income taxes. Svec (2012) studies how an altruistic government optimally sets labor taxes and one-period debt in an economy, where uncertain consumers believe that the true approximating probability model lies within a range on probabilities. The study finds that the political government that maximizes consumer welfare under consumers’ own subjective utility functions finances a smaller portion of a government spending shock from taxes than it would if consumers did not face model uncertainty. Karantounieas (2013) also explores optimal taxes when the government authorities trusts an exogenous government spending probability model, but the public has pessimistic expectations. The paternalistic planner will employ distortionary taxation by exploiting household mispricing and shifting household expectations, leading to higher tax rates during favorable shocks and lower tax rates for adverse shocks.

Carvalho (2005), Hansen et al. (1999), Hansen and Sargent (2008), Svec (2012), and Karantounieas (2013) are all representative agent models where robustness enters into government policy analyses through Ramsey consumer utility functions that depend on consumption and leisure. In contrast, our analysis calculates optimal robust government spending for unknown disturbances in aggregate consumption and investment where the government is minimizing a quadratic performance index function of the tracking errors. Hansen and Sargent (2008) explores robust control in the context of the LQ regulator, but does not consider the LQ tracking problem, nor the macroeconomic accelerator model. As far as we know, our analysis is the first application of the H$^{\infty }$-control, multi-parameter minimax, and stochastic-H$^{\infty }$-mixed control approaches to generate either optimal fiscal or monetary policy within the macroeconomic LQ-tracking problem.

Our empirical analysis confirms the usefulness of the accelerator model used in Kendrick (1981) and Kendrick and Shoukry (2013). The estimations in Kendrick (1981) experienced problems with the poor fit of some variables, and problems with coefficient signs that were opposite of theoretical expectations. The empirical results of our model show that the accelerator model achieves superior measurement and performance when constructed as a second-order difference equation system, which is consistent with the larger lag structure in Kendrick and Shoukry (2013). The fit of the model using a large data set aligns with the theoretical expectations of the consumption crowding-in effect and the investment crowding-out effect of government spending, and further establishes the accelerator model as being a fundamental tool for use in conducting policy analysis.

Kendrick and Amman (2010), and Kendrick and Shoukry (2013), demonstrate the benefits from employing a quarterly fiscal policy over an annual fiscal policy. They find that more frequent policy changes can respond more quickly to downturns, and achieve more stabilization while creating less additional public debt. The various designs considered in this paper provide a further rationale for the potential gains from quarterly fiscal policy, since the policymakers optimally employ more aggressive strategies that account for worst-case concerns. Kendrick and Amman (2010) consider the importance of both 1-period and 2-period lags in the control variable structure when evaluating quarterly policy, but do not consider the 2-period lags in the state variables, as we have done here. Kendrick and Amman (2006) discuss modeling stochastic systems with forward-looking variables, but our analysis does not employ forward-looking loops.

One limitation of robust control has been the model solution and computational difficulty. H$^{\infty }$-controls are determined for unstructured uncertainty sets with bounded perturbations with no particular form. Despite this difficulty, H$^{\infty }$-control rules are much better developed and much simpler than the control rules for the structured uncertainty modeled by the $\mu$-structured singular value as a measure of performance (Williams 2008). Dennis et al. (2009) use structural-form methods to solve robust control problems in order to avoid the onerous state-space methods used in Hansen and Sargent (2008). Our analysis develops an efficient method for obtaining the state-space representation of the robust LQ tracking accelerator model, and provides a computationally feasible framework for its solutions.

1.3 Policy Activism, and Issues in Robust Control

It should be clarified that robust control does not imply either more aggressive, or more dampened policy. Bernhard (2002) points out that robust control designs are not necessarily more cautious than designs that rely on an uncertain model. In some cases, including the simulations in this paper, the robust model may call for even greater control effort by the policymaker. For example, Dennis et al. (2009) explore robust monetary policy within a New Keynesian model, and find that central bank policy will become optimally more activist in order to curb the additional persistence of inflation that occurs in response to shocks. Onatski and Stock (2002) also find that monetary policy is generally more aggressive under robust specifications.

However, in contrast to critics of the worst-case design approaches, Barlevy (2011) argues that robust control strategies do not always respond more aggressively to incoming news than would optimal policies in models without uncertainty. The Brainard Principle holds when increased uncertainty or robust errors reduce the level of policy activism (Brainard 1967). Zakovic et al. (2007) examine a model of the euro area, and find that monetary policy rules under a minimax design approach do not lead to extreme activism, hence upholding the Brainard Principle.

The simulations in this paper explore the case where the state tracking errors are assigned a relatively large weight, and also the case where the control tracking errors are assigned a large weight. In both cases, our analyses found that fiscal policy was generally the most aggressive under the H$^{\infty }$-optimal control strategies with disturbance attenuation. When additional disturbance parameter weights are introduced for the multiple-parameter minimax approach, and when the mixed policy is employed, optimal fiscal policy becomes less aggressive than under the H$^{\infty }$-strategy, but is still more active than deterministic and LQG control policies. This is consistent with Bernhard (2002), Onatski and Stock (2002), and Dennis et al. (2009), which have found that the robust monetary trajectory was more aggressive than in the stochastic case. Our results are also consistent with Tornell (2000), which finds that H$^{\infty }$-derived stock market forecasts are more sensitive to news than are rational expectations forecasts. Tornell’s (2000) simulations demonstrate that when the degree of robustness increases, stock prices adjust more aggressively, and become more volatile relative to dividends.

The conclusions in our study do not align with those in Zakovic et al. (2007) and Barlevy (2011), which find that robust policy follows the Brainard Principle whereby it is more conservative. However, our analysis demonstrates that the primary concern is not simply whether or not the control is more aggressive under the robust design versus the deterministic design. Instead, the emphasis should be the selection from among a range of strategies which each lead to different control trajectories that provide a tradeoff between the degrees of freedom in the parameter selection, the level of robustness, and the balance between risk exposure and pessimism. Taken together, the conclusions from our accelerator model with two state equation disturbances show that the behavior of the system is likely to be complex and difficult to predict a priori; hence, there is a need for advanced simulation.

Robust modeling does have some considerable limitations. Diebold (2005) points out that most robust modeling in monetary policy may be naively complacent because the methods are aimed at dealing with models’ local deviations from certainty, when the problem may actually entail global deviations from uncertainty. Thus, when omitted variables render the model set too small, the minimax policy trajectory will be incompletely robustified. Another consideration in robust design is that the system must be formulated properly with an appropriately accurate model of the system; otherwise, optimizing the wrong controller makes performance worse instead of better.

2 Macroeconomic Model Derivation for Deterministic and LQG Optimal Control

This section develops a version of the Kendrick (1981) and Kendrick and Shoukry (2013) partial-adjustment, closed-economy macroeconomic accelerator model. Let the variables be defined as follows:

• $C_{k} =$ total personal consumption expenditures in period $k$, 2005 dollars

• $C_{k}^{*} =$ desired consumption, or target consumption, in period $k$

• $I_{k} =$ gross private domestic investment in period $k$, 2005 dollars

• $I_{k}^{*} =$ desired investment, or target investment, in period $k$

• $Y_{k} =$ gross domestic product in period $k$, 2005 dollars, minus net exports of goods and services, 2005 dollars, so that $Y_{k}$ = GDP – NX

• $G_{k-1} =$ government obligations in period $k$ – 1 that will result in total purchases of goods and services in period $k$, 2005 dollars

• $G_{k}^{*} =$ desired government obligations, or target obligations, in period $k$

The model is linear time-invariant (LTI), so that all of the coefficients in the linear equations are assumed to be constant over the entire time horizon. This allows for the use of standard techniques such as OLS (ordinary least squares) regression to estimate the equations. However, the optimal control solutions below will also work when the equations have time-variant coefficients, so the state-space notation reflects this.

The target consumption level is assumed to be a linear function of national output, as shown in Eq. (1). The level of consumption in period $k$ follows an accelerator framework, and is determined by the previous period’s consumption level plus a fraction of the difference between the current targeted level and the last period level, plus a fraction of the consumption level two periods earlier, as shown in Eq. (2).

$$\begin{aligned} C_{k}^{*}&= a+bY_{k}\end{aligned}$$

(1)

$$\begin{aligned} C_{k}&= C_{k-1} +\alpha _{1} (C_{k}^{*} -C_{k-1} )+\alpha _{2} C_{k-2} \end{aligned}$$

(2)

Equations (3) and (4) specify the investment functions. The targeted level of investment in Eq. (3) is a linear function of the difference between the current period investment and the investment level in the previous period, plus and adjustment for the level of government spending in the previous period. The fiscal effect on the target investment level can either be a positive crowding-in, or a negative crowding-out, depending on the coefficient signs. This is consistent with the empirical findings in Leeper et al. (2010), in which both the speed of the fiscal adjustment and the agents’ fiscal foresight have some impact on the policy effectiveness, where government investment with comparatively weak productivity can dictate a contractionary government investment policy in the long-run. The current level of investment in Eq. (4) follows its own accelerator function, which is driven by the target investment, and the levels of consumption and investment in the previous two periods.

$$\begin{aligned} I_{k}^{*}&= e_{\;1} +e_{\;2} (I_k -I_{k-1} )+e_{\;3} G_{k\;-\;1}\,\end{aligned}$$

(3)

$$\begin{aligned} I_{k}&= I_{k-1} +\theta _{1} (I_{k}^{*} -I_{k-1} )+\theta _{2} I_{k-2} +\theta _{3} (C_{k-1} -C_{k-2} ) \end{aligned}$$

(4)

Kendrick’s (1981) model does not include the two-period lagged variables in order to remain simple. Kendrick and Shoukry (2013) does use two-period lagged variables on a larger data set, and includes the interest rate. The empirical estimates using the revised data on our model, which are presented below, showed that the first-order difference equations contained a high degree of autocorrelation in the error terms, while the second-order difference equations were a better fit, and did not exhibit autocorrelated errors. In fact, the results show that the double-lag accelerator model produces statistically significant coefficients that are consistent with the theoretical predictions regarding their signs and magnitudes.

Equation (5) gives the national income identity, where the national output variable $Y$ represents real GDP minus net exports.

$$\begin{aligned} Y_{k} =C_{k} +I_{k} +G_{k-1} \end{aligned}$$

(5)

Substitute the national income identity in Eq. (5) into Eq. (1). Then substitute Eq. (1) into Eq. (2), and substitute Eq. (3) into Eq. (4). After rearranging and including the disturbance term variables $w_{1,k}$ and $w_{2,k}$, this yields Eqs. (6) and (7).

$$\begin{aligned} C_{k}&= \delta _{0} +\delta _{1} C_{k-1} +\delta _{2} I_{k-1} +\delta _{3} G_{k-1} +\delta _{4} C_{k-2} +\delta _{5} I_{k-2} +\delta _{6} w_{1,k}\end{aligned}$$

(6)

$$\begin{aligned} I_{k}&= \lambda _{0} +\lambda _{1} C_{k-1} +\lambda _{2} I_{k-1} +\lambda _{3} G_{k-1} +\lambda _{4} C_{k-2} +\lambda _{5} I_{k-2} +\lambda _{6} w_{2,k} \end{aligned}$$

(7)

where

$$\begin{aligned} z_{1}&= 1\;-\;\alpha _{1} b; \quad z_{2} =1\;-\;\theta _{1} e_{2} ; \quad \delta _{0} =\frac{\alpha _{1} a}{z_{1} }+\;\frac{\alpha _{1} b\;\theta _{1} e_{1} }{z_{1} \;z_{2} };\nonumber \\ \delta _{1}&= \frac{1\;-\;\alpha _{1} }{z_{1} }\;+\;\frac{\alpha _{1} b\;\theta _{3} }{z_{1} \;z_{2} }; \quad \delta _{2} =\frac{\alpha _{1} b\;(1\;-\;\theta _{1} -\;\theta _{1} e_{2} )}{z_{1} \;z_{2} }; \nonumber \\ \delta _{3}&= \frac{\alpha _{1} b}{z_{1} }\;\;+\frac{\alpha _{1} b\;\theta _{1} e_{3} }{z_{1} \;z_{2} };\nonumber \\ \delta _{4}&= \frac{\alpha _{2} }{z_{1} }\;-\;\;\frac{\alpha _{1} b\;\theta _{3} }{z_{1} \;z_{2} };\nonumber \\ \delta _{5}&= \frac{\alpha _{1} b\;\theta _{2} }{z_{1} \;z_{2} };\nonumber \\ \lambda _{0}&= \frac{\theta _{1} \;e_{1} }{z_{2} }; \quad \lambda _{1} =\frac{\theta _{3} }{z_{2} }; \quad \lambda _{2} =\frac{1\;-\;\theta _{1} -\;\theta _{1} \;e_{2} }{z_{2} };\nonumber \\ \lambda _{3}&= \frac{\theta _{1} e_{3} }{z_{2} }; \quad \lambda _{4} =\frac{-\;\theta _{3} }{z_{2} }; \quad \lambda _{5} =\frac{\theta _{2} }{z_{2} } \end{aligned}$$

(8)

The coefficients on the disturbance terms are $\delta _{6} =\lambda _{6} = 0$ in the deterministic model, and will be $\delta _{6} =\lambda _{6} = 1$ in the stochastic LQG model and all of the robust designs.

This LTI model in Eqs. (6) and (7) has the advantage of being derived from an accelerator framework, which has proven its utility over many decades, such as in Chow (1967), Kendrick (1981), and Kendrick and Shoukry (2013). Moreover, Eqs. (6) and (7) can be estimated and simulated without knowing the underlying parameters in Eqs. (1)–(4). Note that neither Kendrick (1981), Kendrick and Shoukry (2013), nor this analysis, suggests that this model should directly be applied as a complete econometric forecasting model. Rather, the model is useful for simulating the performance of various optimal control policy techniques, and then evaluating the effects that they would have if employed within a larger model, such as the 135-equation model in Taylor (1993). It also provides a framework to demonstrate exactly how to incorporate the deterministic, stochastic, and H$^{\infty }$-optimal control techniques within any given macroeconomic linear-quadratic (LQ) tracking model in order to construct and evaluate policy. For these objectives, this relatively simple model offers much insight.

We define the following LQ tracking problem. The objective is for the fiscal policymaker to choose the level of government purchases so that it will minimize the quadratic performance index given in Eq. (9) subject to the two linear state equations given by Eqs. (6) and (7). If the coefficients on the error terms in Eqs. (6) and (7) are set equal to zero, then the model becomes deterministic.

$$\begin{aligned} \mathop {\min }\limits _G J(G)&= \frac{1}{2}\left[ {q_{1,f} (C_{K+1} -C_{K+1}^{*} )^{2}+q_{2,f} (I_{K+1} -I_{K+1}^{*} )^{2}} \right] \nonumber \\&+\frac{1}{2}\sum _{k=1}^K {\left[ {q_{1,k} (C_{k} -C_{k}^{*} )^{2}+q_{2,k} (I_{k} -I_{k}^{*} )^{2}+R_{k} (G_{k} -G_{k}^{*} )^{2}} \right] }\nonumber \\&+\frac{1}{2}\sum _{k=1}^{K+1} {\left[ {q_{3,k} \left\{ {(G_{k} -G_{k-1})-(G_{k} -G_{k-1})^{*}} \right\} ^{2}} \right] } \end{aligned}$$

(9)

This LQ tracking problem has two state variables, consumption ($C$) and investment ($I$), and one control variable ($G$). The benefits and drawbacks of the symmetric quadratic performance index for economic and engineering applications need not be discussed here, since they are well known, and have been discussed in previous literature Kendrick (1981).

In Eq. (9), the policymaker is penalized for deviations of consumption, investment, and government spending from their target values. However, the last term in the tracking index in Eq. (9) offers a new contribution to the literature. The policymaker is also penalized for large changes in government spending between periods. This innovation to the model is an important pragmatic consideration because government policymakers will prefer more stable spending patterns in the ongoing budget appropriation process, and will not desire large fluctuations from the previous budget. This also reflects the fact that most new budgets are largely designed by adjusting the prevailing budget on a line-by-line basis. Our simulations also demonstrate the additional importance of this term when robust modeling designs are used.

The following procedure rewrites the above equations in a state-space form that transforms a Linear-Quadratic (LQ) tracking problem into a canonical LQ regulator problem to be employed in deterministic, stochastic LQG, and robust control. Transforming the tracking problem into a regulator problem requires increasing the number of state variables in order to incorporate the targets into the state-space. The tracking problem can be rewritten as an LQ regulator problem with eleven state variables, eleven state equations, and one control variable. Although this transformation creates a higher dimensional state-space, it greatly simplifies the subsequent solution procedures for the deterministic, stochastic, H$^{\infty }$- optimal control, multiple-parameter minimax, and mixed problems. This exploration of the latter two methods is a new contribution to the minimax literature.

There are two methods for handling the constant terms in Eqs.  (6) and (7) when writing the state-space system in a standard form. Kendrick and Amman (2006) use a vector of ones for the system, and then multiply this by a coefficient matrix that consists of the constants in each of the state equations. This leads to an extra additive matrix term in the system state equation. The present transformation uses another approach that avoids the use of the additional additive term in the linear matrix state equation. The tradeoff is that this will require an additional state variable. The constants can be effectively incorporated into the set of state variables as an additional state variable as follows. Rather than using a vector of ones, equation (10) defines a variable that is a sequence of recurring ones for all $k = 1,{\ldots }, K$.

$$\begin{aligned} c_{k+1} =1c_{k}; \quad c_{1} =1 \end{aligned}$$

(10)

Based on this equation and its initial value of 1, $c_{k} = 1$ for all $k = 1,{\ldots }, K$. This new state variable consisting of a sequence of ones serves as a placeholder in each state equation, where the coefficient of this $c_{k}$ variable in each individual equation is the constant. So, the constant terms in Eqs.  (6) and (7) become $\delta _{0} c_{k}$ and $\lambda _{0} c_{k}$, respectively, in the state space equations.

Although this analysis will only examine time invariant coefficients, note that the method used in Eq. (10) could be altered to include the time variant case. The variable $c_{k}$ will grow or shrink over time if the coefficient in Eq. (10) is greater than 1, or less than 1, respectively. In those cases, the constants in Eqs. (6) and (7) would thus grow or shrink over the time horizon.

The model allows for optimal consumption, investment, and government purchases to grow at quarterly target rates of $g_{C,k}$, $g_{I,k} , g_{G,k}$, respectively, that are specified by the fiscal policymaker, which results in an annual growth rate of (1 + $g_{i,k} )^{4}$ per year. The consumption, investment, and government purchases tracking equations can thus be written, respectively, as

$$\begin{aligned} C_{k+1}^{*} =(1 + g_{C,k} )C_{k}^{*}; \quad I_{k+1}^{*} =(1 + g_{I,k} )I_{k}^{*}; \quad G_{k+1}^{*} =(1 + g_{G,k} )G_{k}^{*} \end{aligned}$$

(11)

The state variables are defined as follows:

$$\begin{aligned} x_{1,k}&= C_{k} , \quad x_{2,k} = I_{k} , \quad x_{3,k} = c_{k} , \quad x_{4,k} = C_{k}^{*} , \quad x_{5,k} = I_{k}^{*} , x_{6,k} = G_{k}^{*}\nonumber \\ x_{7,k}&= G_{k-1} , \quad x_{8,k} = G_{k-1} -G_{k-2} , \quad x_{9,k} = (G_{k-1} -G_{k-2})^{*}\nonumber \\ x_{10,k}&= C_{k-1} , \quad x_{11,k} = \quad I_{k-1} \end{aligned}$$

(12)

Define the scalar control variable as difference between the actual and targeted level of government purchases so that

$$\begin{aligned} u_{k} =G_{k} -G_{k}^{*} \end{aligned}$$

(13)

Since the control variable, $u_{k}$, includes the negative of the targeted level of government purchases, $G_{k}^{*}$, this target variable will be added to the first state equation. The net of effect of adding and subtracting the same variable is 0, but this allows the problem to be written in standard LQ regulator format. Once the optimal control has been simulated to produce the values for $u_{k}$, the target level of government purchases, $G_{k}^{*}$, will have to be added to $u_{k}$ in order to recover the values for government purchases, $G_{k}$. The lagged actual value of government purchases, $G_{k\;-\;1}$, is recovered in the system output by the state variable $x_{7,k}$.

Expressions Eq. (10) through Eq. (13) can then be combined to write the new matrix state equation as

$$\begin{aligned} x_{k+1}&= A_{k} x_{k} +B_{k} u_{k} +D_{k} w_{k}; \quad u_{k} =G_{k} -G_{k}^{*}; \quad w_{k} =\left[ {{\begin{array}{l} {w_{1,k} } \\ {w_{2,k} } \\ \end{array} }} \right] ; \nonumber \\ x (1)&= x_{1} \end{aligned}$$

(14)

where the state-space is given by

$$\begin{aligned} x_{k}&= \left[ {{\begin{array}{c} {C_{k} } \\ {I_{k} } \\ {c_{k} } \\ {C_k^*} \\ {I_k^*} \\ {G_k^*} \\ {G_{k-1} } \\ {G_{k-1} -G_{k-2} } \\ {(G_{k-1} -G_{k-2} )*} \\ {C_{k-1} } \\ {I_{k-1} } \\ \end{array} }} \right] \quad x_{1} =\left[ {{\begin{array}{c} {x_{1,1} } \\ {x_{2,1} } \\ {x_{3,1} } \\ {x_{4,1} } \\ {x_{5,1} } \\ {x_{6,1} } \\ {x_{7,1} } \\ {x_{8,1} } \\ {x_{9,1} } \\ {x_{10,1} } \\ {x_{11,1} } \\ \end{array} }} \right] \quad B_{k} =\left[ {{\begin{array}{c} {\delta _{3} } \\ {\lambda _{3} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right] \quad D_{k} =\left[ {{\begin{array}{ll} {\delta _{6} }&{} 0 \\ 0&{} {\lambda _{6} } \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] \end{aligned}$$

(15)

$$\begin{aligned} A_{k}&= \left[ {{\begin{array}{llllllllllll} {\delta _{1} }&{}\quad {\delta _{2} }&{}\quad {\delta _{0} }&{}\quad 0&{} 0&{} {\delta _{3} }&{} 0&{} 0&{}\quad 0&{} \quad {\delta _{4} }&{} 0 \\ {\lambda _{1} }&{}\quad {\lambda _{2} }&{}\quad {\lambda _{0} }&{}\quad 0&{} 0&{} {\lambda _{3} }&{} 0&{} 0&{}\quad 0&{}\quad 0&{} {\lambda _{4} } \\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{} 0&{} 0&{} 0&{} 0&{} \quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1+ g_{C,k} &{} 0&{} 0&{} 0&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 1+ g_{I,k} &{} 0&{} 0&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} 1+ g_{G,k} &{} 0&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} 1&{} 0&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} 1&{} {-1}&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} {g_{G,k}}&{} 0&{} 0&{}\quad 0&{}\quad 0&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} 0&{} 0&{} 0&{}\quad 0&{}\quad 1&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{} 0&{} 0&{} 0&{} 0&{}\quad 0&{}\quad 0&{} 1 \\ \end{array} }} \right] \end{aligned}$$

(16)

First, consider the deterministic LQ regulator problem where $\delta _{6} =\lambda _{6}$ = 0. After rewriting expression Eq. (9) based on the state variable definitions in Eq. (10) through Eq. (16), the objective is to minimize the performance index

$$\begin{aligned} \mathop {\min }\limits _u J(u)=x_{K+1}^{T} Q_{f}\quad x_{K+1} +\sum _{k=1}^K {\left[ {x_k^{T} Q_{k} x_{k}+u_{k}^{T} R_{k} u_{k} } \right] } \end{aligned}$$

(17)

subject to equation Eq. (14), where the performance index weights are

$$\begin{aligned} Q_{k}&= \left[ {{\begin{array}{lllllllllll} {q_{1,k} }&{} \quad 0&{}\quad 0&{}\quad {-q_{1,k} }&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0 \\ 0&{}\quad {q_{2,k} }&{}\quad 0&{} \quad 0&{}\quad {-q_{2,k} }&{}\quad 0&{}\quad 0&{} \quad 0&{}\quad 0&{}\quad 0&{} \quad 0 \\ 0&{}\quad 0&{} \quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{}\quad 0 \\ {-q_{1,k} }&{}\quad 0&{}\quad 0&{}\quad {q_{1,k} }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{} {-q_{2,k} }&{}\quad 0&{}\quad 0&{}\quad {q_{2,k} }&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{}\quad 0 \\ 0&{}\quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{}\quad 0 \\ 0&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad {q_{3,k} }&{} \quad {-q_{3,k} }&{}\quad 0&{} \quad 0 \\ 0&{}\quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad {-q_{3,k} }&{}\quad {q_{3,k} }&{} \quad 0&{}\quad 0 \\ 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 \\ 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 \\ \end{array} }} \right] \end{aligned}$$

(18)

$$\begin{aligned} Q_{f}&= \left[ {{\begin{array}{lllllllllll} {q_{1,f} }&{}\quad 0&{}\quad 0&{} \quad {-q_{1,f} }&{}\quad 0&{} \quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{}\quad 0&{}\quad 0 \\ 0\quad &{} \quad {q_{2,f} }&{}\quad 0&{}\quad 0&{} \quad {-q_{2,f} }&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{}\quad 0 \\ {-q_{1,f} }&{}\quad 0&{} \quad 0&{} \quad {q_{1,f} }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{}\quad 0 \\ 0&{} \quad {-q_{2,f} }&{}\quad 0&{}\quad 0&{} \quad {q_{2,f} }&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{}\quad 0 \\ 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0 \\ 0&{}\quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{} \quad 0 \\ 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad {q_{3,K+1} }&{} \quad {-q_{3,K+1} }&{}\quad 0&{} \quad 0 \\ 0&{} \quad 0&{}\quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} {-q_{3,K+1} }&{}\quad {q_{3,K+1} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 \\ 0&{}\quad 0&{}\quad 0&{} \quad 0&{}\quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0&{}\quad 0 \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(19)

The solution to the LQ regulator problem is found by computing the recursive Eqs. (20) and (21) offline in retrograde time.

$$\begin{aligned} F_{k}&= \left( {B_{k}^{T} P_{k+1} B_{k} +R_{k} } \right) ^{-1}B_{k}^{T} P_{k+1} A_{k}\end{aligned}$$

(20)

$$\begin{aligned} P_{k}&= Q_{k} +A_{k}^{T} P_{k+1} \left( {A_{k} -B_{k} F_{k} } \right) ; \quad P_{k+1} =Q_{f} \end{aligned}$$

(21)

These recursive equations are much simpler to compute than the longer recursive equations employed by Kendrick (1981), Amman (1996), and Chow (1975) that arise when solving the LQ tracking problem. Using the values computed in (20) and Eq. (21), the unique optimal feedback control policy is computed in forward time by

$$\begin{aligned} u_{k}^{*} =-F_{k}\,\, x_{k} \end{aligned}$$

(22)

The optimal closed-loop state trajectory is given by

$$\begin{aligned} x_{k+1} =\left( {A_{k} -B_{k} F_{k} } \right) x_{k} +D_{k} w_{k}; \quad x (1) = x_{1} \end{aligned}$$

(23)

Since the constant ($c$) and the tracking variable trajectories for consumption ($C^{*}$), investment ($I^{*}$), and government obligations ($G^{*}$), are embedded within the state equations, they cannot be controlled. The controllability subspace for the above system has a dimension of two, which is the rank of the controllability matrix [$B {\vert } {AB} {\vert } A^{2}B {\vert } A^{3}B {\vert } A^{4}B {\vert } A^{5}B{\vert } A^{6}B{\vert } A^{7}B{\vert } A^{8}B A^{9}B{\vert } A^{10}B$]. Thus, consumption ($C$) and investment ($I$) can be tracked toward their targets. The control equations are the same for the deterministic and stochastic LQG form of the model; but, $\delta _{6} =\lambda _{6} = 0$ in the deterministic model, so that no disturbances are entering the system. The error coefficients are $\delta _{6} =\lambda _{6} = 1$ in the stochastic LQG model, where the each of the disturbances are independent and follow a Gaussian distribution with a mean of 0 and have a constant variance.

3 Robust Designs: H$^{\infty }$ -Optimal Control, Multiple-Parameter Minimax, and Mixed

The LQG only considers the average system performance when the disturbances follow a stochastic uncertainty. The robust designs account for the worst-case, which is generally not captured by the average performance of the LQG. Rustem and Howe (2002) summarize that even though optimal control under the average performance of the LQG is often adequate, most system failures occur only when the worst case is actually realized. However, if the policy design strictly follows the minimax strategy, then the inherent pessimism can cause a severe performance decline. The policy design therefore must account for both the expected performance and the worst-case design, and find a balance between the two approaches.

The next phase is to develop robust policy designs in order to assist in improved policy decisions. The worst-case methods here consider the discrete-time minimax controller design problem with perfect state measurements.

3.1 $H^{\infty }$ -Optimal Control

The H$^{\infty }$-optimal control problem is formulated in expression Eq. (24) as a soft-constrained LQ game. The controller $u$ is the minimizing player, and the disturbance term $w$, representing nature, is the maximizing player.

$$\begin{aligned} \mathop {\min }\limits _u \mathop {\max }\limits _w J_{\gamma } (u,w)=x_{K+1}^{T} Q_{k}\,\,\, x_{K+1} +\sum _{k=1}^K {\left[ {x_k^{T} Q_{k} x_{k} +u_{k}^{T} R_{k} u_{k} -r_{H} w_{k}^{T} w_{k} } \right] } \end{aligned}$$

(24)

subject to Eq. (14), where

$$\begin{aligned} r_{H}&= \gamma _H^{2} > 0; \quad R_{k} > 0; \quad Q_{f} , \quad Q_{k} \ge 0; \quad k = 1, 2,{\ldots }, K;\\ \dim (A_{k} )&= (n,n)=(11,11); \quad \dim (B_{k} )=(n,m)=(11,1); \\ \dim (D_{k} )&= (n,p)=(11,2)\\ \dim (Q_f )&= \dim (Q_{k} )=(n,n)=(11,11); \dim (R_{k} )=(m,m)=(1,1);\\ \dim (x_{k} )&= (n,1)=(11,1); \quad \dim (u_{k} )=(m,1)=(1,1);\\ \dim (w_{k} )&= (p,1)=(2,1) \end{aligned}$$

The simulations in this analysis assume that both players have access to closed-loop state information with memory, where $R_{k}$ is an identity matrix. Define the recursive matrix sequences $M_{k}$ and $\Lambda _{k}$, $k\in [1,K]$, where $\Lambda _{k}$ is invertible, by Eqs. (25) and (26):

$$\begin{aligned} M_{k}&= Q_{k} +A_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k}; \quad M_{k+1} =Q_{f}\end{aligned}$$

(25)

$$\begin{aligned} \Lambda _{k}&= I+\left( {B_{k} B_{k}^{T} -r_{H}^{-1} D_{k} D_{k}^{T} } \right) M_{k+1} \end{aligned}$$

(26)

Basar and Bernhard (1991) show that show that a unique (and global) feedback saddle-point solution exists if, and only if,

$$\begin{aligned} r_{H} I-D_{k}^{T} M_{k+1} D_{k} >0; \quad k = 1, 2,{\ldots }, K \end{aligned}$$

(27)

After computing Eqs. (25) and (26) offline, the solution trajectory ($x_k^{*} , u_k^{*},w_k^{*} )$ is given by Eqs. (28), (29), and (30). The unique saddle-point optimal control rule is

$$\begin{aligned} u_{k}^{*} =-B_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k} \end{aligned}$$

(28)

The unique saddle-point worst-case disturbance trajectory is

$$\begin{aligned} w_{k}^{*} =r_{H}^{-1} D_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k} \end{aligned}$$

(29)

and the state trajectory is given by

$$\begin{aligned} x_{k+1}^{*} =\Lambda _{k}^{-1} A_{k} x_{k}^{*}; \quad x_{1}^{*} =x_{1} \end{aligned}$$

(30)

The saddle-point value of the game is calculated by

$$\begin{aligned} J_\gamma ^{*} (u,w)=x_{1}^{T} M_{1} x_{1} \end{aligned}$$

(31)

If the matrix given by Eq. (27) has one or more negative eigenvalues, and is thus not positive definite, then the game does not have a saddle-point solution, and its upper value is unbounded (Basar and Bernhard 1991). Thus, we have written a Matlab program that will issue a warning to the user, and will cease calculation if Eq. (27) has any negative eigenvalues for any period.

3.2 Disturbance Attenuation

In the general minimax problem, the value of $r_{H} =\gamma _H^{2} > 0$ is a free scalar parameter than can be chosen by the policymaker, where larger values of $r_{H}$ correspond to larger penalties on the error terms. Choosing large values of $r_{H}$ will force the error terms to be very small. However, the objective of robust control is to stabilize the system under the worst-case design, which occurs when the magnitudes of the errors are the largest. This can be achieved by choosing very small values for $r_{H}$, which causes the errors to be as disruptive as possible under the game specification.

This process of choosing the value of $r_{H}$ so that the errors are creating their maximum disruption is called disturbance attenuation, which is discussed in Basar and Bernhard (1991) and Tornell (2000). To achieve disturbance attenuation, the value $\gamma _H^{*}$ must be chosen for $\gamma _{H}$, where $r_{H}^{*}=\gamma _H^{*2} > 0$, so that $\gamma _H^{*}$ is the infimum, i.e., the smallest value of $\gamma _{H}$ that still allows for a saddle-point solution of the game. Thus, it is important to note that under H$^{\infty }$-optimal control with disturbance attenuation, $r_{H}$ is not a free parameter. The value of $r_{H}^{*}$ must be chosen to be as small as possible.

Expressions Eqs. (25)–(27) show that $\gamma _{H}$ must be chosen to be large enough so that it will meet the conditions for the existence of a solution. Disturbance attenuation results from using the minimum for $\gamma _{H}$ that will satisfy these conditions. The Matlab program that the authors have created for the simulations below allows the user to decrease the value of $r_{H} =\gamma _H ^{2}$ until it is arbitrarily close to the infimum of the viable set that satisfies the saddle-point existence eigenvalue condition in Eq. (27). It should also be noted that if a solution exists, it is global, and not just local.

3.3 Multiple-Parameter Minimax Design

The H$^{\infty }$-optimal control design with disturbance attenuation computes a particular worst-case solution to the dynamic game. It generates the optimal control under the worst-case overall error structure as measured by the Euclidean norm of the disturbance vector $w$. Thus, the two disturbance variables $w_{1,k}$ and $w_{2,k}$ are equally weighted by the disturbance attenuation parameter, $r_{H}^{*} =\gamma _{H}^{*2}$.

The multiple-parameter minimax design reformulates the game so that a different weight is chosen for each of the two errors vectors $w_{1,k}$ and $w_{2,k}$. This requires modifying the soft-constrained game in Eq. (24) so that the disturbance vector is now weighted by a positive definite penalty matrix, $r_{M}$, rather than the original scalar $r_{H}$. The new minimax game is:

$$\begin{aligned} \mathop {\min }\limits _u \mathop {\max }\limits _w J_{\gamma } (u,w)=x_{K+1}^{T} Q_{k}\,\,\, x_{K+1} +\sum _{k=1}^K {\left[ {x_k^{T} Q_{k} x_{k} +u_{k}^{T} R_{k} u_{k} -w_{k}^{T} r_{M} w_{k} } \right] } \end{aligned}$$

(32)

subject to Eq. (14), where

$$\begin{aligned} r_{M} =\left[ {{\begin{array}{ll} {r_{1} }&{} 0 \\ 0&{} {r_{2} } \\ \end{array} }} \right] \quad r_{1} =\gamma _{1} ^{2}> 0; \quad r_{2} =\gamma _{2} ^{2}> 0 \end{aligned}$$

(33)

The saddle-point solution to this game is found by recursively computing Eqs. (25) and (34), where Eq. (34) is a modified version of Eq. (26).

$$\begin{aligned} \Lambda _{k} =I+\left( {B_{k} B_{k}^{T} -D_{k} r_{M}^{-1} D_{k}^{T} } \right) M_{k+1} \end{aligned}$$

(34)

The existence of a saddle-point solution requires that

$$\begin{aligned} r_{M} -D_{k}^{T} M_{k+1} D_{k} >0; \quad k = 1, 2,{\ldots }, K \end{aligned}$$

(35)

The optimal control and state trajectories are given by Eqs.  (28) and (30), respectively, and the optimal disturbance trajectory in Eq. (29) is now replaced by Eq. (36).

$$\begin{aligned} w_{k}^{*} =r_{M}^{-1} D_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k} \end{aligned}$$

(36)

In the 2-parameter minimax design, the policymaker can still achieve a robust design by choosing smaller values for the penalty weights $r_{1}$ and $r_{2}$. There is no H$^{\infty }$-optimal control disturbance attenuation value for the game in this case, since the smallest value of $r_{1}$ depends on the choice of $r_{2}$, and vice versa. Thus, there will always be a tradeoff in the robustness associated with each disturbance variable, where the designer chooses Pareto attenuation values of $r_{1 }$ and $r_{2}$. Pareto attenuation replaces H$^{\infty }$-disturbance attenuation, and requires the following. Given $r_{2}$, the policymaker must choose the smallest value of $r_{1}$ such that the existence condition in Eq. (35) is satisfied. If the user restricts the parameter choices so that $r_{1 }=r_{2}$, then the Pareto attenuation solution to the multiple-parameter minimax design will be identical to the disturbance attenuation solution to the H$^{\infty }$-optimal control design, where $r_{1}^{*}=r_{2}^{*} =r_{H}^{*}$.

One method of choosing these penalty weights is to set the DPR (disturbance penalty ratio), and then select the smallest set of penalty weights such that the saddle-point conditions in Eqs. (25), (34) and (35) are met. When there are $p$ disturbance terms, the DPR for each disturbance would be assigned relative to the weight on the most disruptive disturbance.

This is the method of selecting a set of Pareto attenuation parameters that is used in the simulations below. Since private domestic investment is the most volatile component of GDP, the disturbance penalty ratio is set at

$$\begin{aligned} DPR = \frac{r_{1} }{r_{2} } = 10 \end{aligned}$$

(37)

Recall that $r_{1}$ is the weight on the consumption disturbance, and $r_{2}$ is the weight on the investment disturbance. Larger values of the DPR mean that relatively higher weight is assigned to deviations in the consumption disturbances. In Eq. (37), the penalty weight for consumption disturbances is 10 times larger than the weight for investment disturbances. The resulting policy will generate investment disturbances, $w_{2,k}$, that have a larger magnitude than they would under the H$^{\infty }$-controller. Conversely, the consumption disturbances, $w_{1,k}$, will be smaller in magnitude than they would be under H$^{\infty }$-control.

Under the multi-parameter minimax design, the policymaker can freely choose the DPR ratios, as long as a solution to the game exists. Given a DPR, however, the disturbance attenuation problem requires that the smallest values for each of the disturbance penalty parameters be chosen in order for the optimal control to achieve maximum worst-case robustness. Once the DPR has been selected, $r_{1 }$and $r_{2}$ are not free parameters. We developed a Matlab program that allows the user to iteratively input parameter values that maintain the DPR until the smallest set of parameters that still satisfies the eigenvalue conditions Eqs. (25), (34) and (35) is found, provided that a solution exists.

3.4 Mixed Stochastic/H$^{\infty }$ - Optimal Control

In some cases, the policymaker may only be concerned with the robustness of a subset of the system equations that contain disturbances. For example, the unpredictable part of aggregate consumption may be considered to be well-modeled by the stochastic LQG specification, but the volatility of private investment might have an uncertain structure. This situation can be modeled by the mixed stochastic/H$^{\infty }$-optimal control specification. In the situation where there are two disturbances as described above, one of the disturbances, $w_{1,k}$, is modeled as a stochastic Gaussian variable, and the other disturbance, $w_{2,k}$, is modeled using the H$^{\infty }$-worst case design. This gives the user the option to focus on the robustness properties of just the equation with the error structure that is considered highly unstable.

The mixed stochastic/H$^{\infty }$-control can be designed by modifying the soft-constrained minimax game given by Eqs. (14) and (24) as follows. The state equation is now

$$\begin{aligned} x_{k+1} =A_{k} x_{k} +B_{k} u_{k} +D_{k} w_{2,k} +E_{k} w_{1,k}; \quad x (1) = x_{1} \end{aligned}$$

(38)

where the state-space disturbance coefficient matrices are redefined by

$$\begin{aligned} D_{k}&= \left[ {{\begin{array}{lllllllllll} 0&{} {\lambda _{6} }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T};\nonumber \\ E_{k}&= \left[ {{\begin{array}{lllllllllll} {\delta _{6} }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T}\end{aligned}$$

(39)

$$\begin{aligned} \mathop {\min }\limits _u \mathop {\max }\limits _w J_{\gamma } (u,w)&= x_{K+1}^{T} Q_{k} x_{K+1} +\sum _{k=1}^K {\left[ {x_k^{T} Q_{k} x_{k} +u_{k}^{T} R_{k} u_{k} -r_{MX} w_{2,k}^{2} } \right] }\qquad \quad \end{aligned}$$

(40)

The optimal closed-loop policy solution to the game in Eqs. (38)–(40) is given by Eqs. (41)–(45), provided that the existence condition in Eq. (43) is satisfied.

$$\begin{aligned}&M_{k} =Q_{k} +A_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} ; \quad M_{k+1} =Q_{f}\end{aligned}$$

(41)

$$\begin{aligned}&\Lambda _{k} =I+\left( {B_{k} B_{k}^{T} -r_{MX}^{-1} D_{k} D_{k}^{T} } \right) M_{k+1}\end{aligned}$$

(42)

$$\begin{aligned}&r_{MX} I-D_{k}^{T} M_{k+1} D_{k} >0; \quad k = 1, 2,{\ldots }, K\end{aligned}$$

(43)

$$\begin{aligned}&u_{k}^{*} =-B_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k}\end{aligned}$$

(44)

$$\begin{aligned}&w_{2,k}^{*} =r_{MX}^{-1} D_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k} \end{aligned}$$

(45)

In the mixed model expressed by Eqs. (38)–(45), the consumption disturbance term $w_{1,k}$ can be modeled under robust design, and the investment error $w_{2,k}$ can be modeled as a stochastic error. In that case, the $D_{k}$ and $E_{k}$ matrices in Eq. (38) would be switched, and Eqs.  (38)–(40) would be replaced by Eqs.  (46)–(48).

The state equation disturbance coefficient matrices are switched, so it becomes

$$\begin{aligned} x_{k+1} =A_{k} x_{k} +B_{k} u_{k} +D_{k} w_{1,k} +E_{k} w_{2,k} ; \quad x (1) = x_{1} \end{aligned}$$

(46)

The new disturbance coefficient matrices that model robust consumption disturbances are

$$\begin{aligned} D_{k}&= \left[ {{\begin{array}{lllllllllll} {\delta _{6} }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T};\nonumber \\ E_{k}&= \left[ {{\begin{array}{lllllllllll} 0&{} {\lambda _{6} }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T} \end{aligned}$$

(47)

The performance index game now has the disturbance penalty weight, $r_{MX}$, on the consumption disturbance $w_{1,k}$, rather than on the investment disturbance, $w_{2,k}$.

$$\begin{aligned} \mathop {\min }\limits _u \mathop {\max }\limits _w J_{\gamma } (u,w)=x_{K+1}^{T} Q_{k} x_{K+1} +\sum _{k=1}^K {\left[ {x_k^{T} Q_{k} x_{k} +u_{k}^{T} R_{k} u_{k} -r_{MX} w_{1,k}^{2} } \right] } \end{aligned}$$

(48)

The solution is given by Eqs. (41)–(44), where the optimal robust disturbance trajectory in (45) is replaced by Eq. (49), so that only the consumption errors are modeled under the worst-case design.

$$\begin{aligned} w_{1,k}^{*} =r_{MX}^{-1} D_{k}^{T} M_{k+1} \Lambda _{k}^{-1} A_{k} x_{k} \end{aligned}$$

(49)

Although we have explored the mixed design with robust consumption, as defined by Eqs. (46)–(49), the results are not reported here, due to length considerations. The mixed stochastic/H$^{\infty }$-control simulations below only examine the case given by Eq. (38)–(45), which models worst-case investment disturbances mixed with stochastic Gaussian consumption errors.

4 Estimation and Simulation

The model allows for optimal consumption, investment, and government purchases to grow at target rates that are specified by the policymaker. This particular set of simulations will follow Kendrick’s (1981) growth rate of $g_{C,k} =g_{I,k} = 0.75\,\%$ per quarter for consumption and investment. This results in an annual growth rate of about 3 % per year, which is consistent with the long-term growth rate for the US economy. Government purchases will be assumed to grow at a rate of $g_{G,k} = 0.5\,\%$ per quarter, which is an annualized rate of about 2 % per year. The consumption, investment, and government purchases tracking equations can thus be written, respectively, as

$$\begin{aligned} C_{k+1}^{*} =1.0075\,\,C_{k}^{*} \quad I_{k+1}^{*} =1.0075\,\,I_{k}^{*} \quad G_{k+1}^{*} =1.005\,\,G_{k}^{*} \end{aligned}$$

(50)

The following analysis estimates the accelerator model using U.S. Bureau of Economic Analysis (BEA) Real GDP component data in billions of chained 2005 dollars for the period 1947 quarter 1 to 2012 quarter 3. The estimates for Eqs. (6) and (7) are given below, with $t$-statistics in parentheses below the coefficients.

$$\begin{aligned} C_{k} =\mathop {-8.485}\limits _{(-1.02)} \mathop {{+1.29}}\limits _{{(21.7)}} C_{k-1} +\mathop {{0.234}}\limits _{{(5.4)}} I_{k-1} +\mathop {{0.039}}\limits _{{(2.4)}} \,\,G_{k-1} -\mathop {{0.307}}\limits _{{(-}{5.2)}} C_{k-2} -\mathop {{0.202}}\limits _{{(-}{4.7)}} I_{k-2} \end{aligned}$$

(51)

$R^{2} = .9999$; Durbin-Watson = 2.13; number of observations = 261

$$\begin{aligned} I_{k} =\mathop {{4.9}}\limits _{{(0.51)}} {+}\mathop {{0.83}}\limits _{{(12.1)}} C_{k-1} +\mathop {{1.12}}\limits _{{(22.5)}} I_{k-1} -\mathop {{0.041}}\limits _{{(- 2.2)}} { }G_{k-1} -\mathop {{0.804}}\limits _{{(-}{11.9)}} C_{k-2} -\mathop {{0.23}}\limits _{{(-}{4.6)}} I_{k-2} \end{aligned}$$

(52)

$R^{2} = 0.9988$; Durbin-Watson = 2.17; number of observations = 261

The fit of the above equations is excellent. All coefficients are statistically significant, and have the expected signs. We are not arguing that there could not have been one or more changes in the system coefficients over this long time span. Rather, the purpose is simply to evaluate the different control designs based on the approximated time-invariant coefficient system as measured above.

In Eq. (51), government purchases has the expected fiscal crowding-in effect on consumption, rather than the crowding-out effect that occurred in Kendrick’s (1981) original estimation. Equation (52) shows that consumption has a crowding-in effect investment, but government purchases has a fiscal crowding-out effect investment. The model thus has a unique set of internal dynamics. Expansionary fiscal policy increases consumption, but decreases investment. However, if fiscal policy is overly contractionary, then fall in consumption will in-turn create a negative impact on investment. Thus, the optimal tracking policies depend on the parameter values, and require simulation. The following analysis shows that this leads to a complex error interaction when constructing an optimal robust policy design.

Since the US was in a recessionary phase at the end of the data period, the simulations assume a recessionary gap, where consumption is initially 1 % below its target value, and investment is initially 3 % below its target. Since fiscal policy during the previous four years had reacted by being countercyclical and expansionary, the simulations assume that the initial current value of government spending is 0.74 % above its initial target value. The analysis compares two different overall policy approaches: heavily weighted tracking errors for the consumption and investment state variables, and a heavily weighted tracking error for the policy variable, government spending.

4.1 Heavy Weight on Tracking Errors for Consumption and Investment

The first set of simulations assigns weights for the final state tracking errors for consumption and investment that are 10 times the weight assigned to the government purchases policy tracking error. We set $q_{1,f} =q_{2,f} = 10$, and $q_{1,k} =q_{2,k} =q_{3,k} =R_{k} = 1$ for all $k = 1$, ..., $K$. Thus, the final state tracking error is also 10 times greater than the weight assigned to the state tracking errors for each period except for the terminal period. The use of parameters that are in multiples of 10 is consistent with Kendrick and Shoukry (2013).

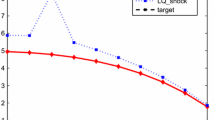
Figures 1, 2, 3, 4, 5 and Tables 1, 2, 3 show comparisons for the system trajectories under the five different error structures. The figures show the simulated trajectories for government purchases, consumption, investment, the consumption disturbance, and the investment disturbance, respectively. The disturbance terms are both zero for all periods under the deterministic design.

Fig. 1

Government purchases: heavy weight on the tracking errors for consumption and investment. $q_{1,\, f} = q_{2, f}=10; q_{1, \,k} = q_{2,\, k}=q_{3,\, k} = R_{k}=1; s_{w1}=27; s_{w2}=31; r_{H}=8,816.1; r_{1}=22,146; r_{2}=2,214.6; r_{MX}=1,483.4$

Fig. 2

Consumption: heavy weight on the tracking errors for consumption and investment. $q_{1,\,f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k}=q_{3,\, k} = R_{k}=1; s_{w1}=27; s_{w2}=31; r_{H}=8,816.1; r_{1}=22,146; r_{2}=2,214.6; r_{MX}=1,483.4$

Fig. 3

Investment: heavy weight on the tracking errors for consumption and investment. $q_{1,\, f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k}=q_{3,\, k} = R_{k}=1; s_{w1}=27; s_{w2}=31; r_{H}=8,816.1; r_{1}=22,146; r_{2}=2,214.6; r_{MX}=1,483.4$

Fig. 4

Consumption disturbance: heavy weight on tracking errors for consumption and investment. $q_{1,\, f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k}=q_{3,\, k} = R_{k}=1; s_{w1}=27; s_{w2}=31; r_{H}=8,816.1; r_{1}=22,146; r_{2}=2,214.6; r_{MX}=1,483.4$

Fig. 5

Investment disturbance: heavy weight on the tracking errors for consumption and investment. $q_{1,\, f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k}=q_{3,\, k} = R_{k}=1; s_{w1}=27; s_{w2}=31; r_{H}=8,816.1; r_{1}=22,146; r_{2}=2,214.6; r_{MX}=1,483.4$

For the LQG simulations, the two disturbance errors were randomly generated from a Gaussian distribution with a mean of 0. The standard deviation for the consumption disturbance $w_{1,k}$ and investment disturbance $w_{2,k}$ were taken from the regressions in Eqs. (51) and (52). They are respectively given by $s_{w1} = 27$ and $s_{w2} = 31$. The LQG optimal control model was simulated ten times, and then the average value of government purchases, consumption, investment, and the disturbances was plotted in the figures. Even when limiting the LQG model to 10 simulations, the average values for all of the variables are close to their values under the deterministic scenario. This masks some of the deviations that occur within each individual LQG simulation, but does show some volatility in the policy. As the number of simulations increases, the LQG trajectories become indistinguishable from the deterministic model trajectories.

The H$^{\infty }$-optimal disturbance attenuation parameter was iteratively calculated to be $r_{H}^{*} = 8,816.1$. This value is not a free-parameter. Given the performance index weights above, this is the smallest value that allows the system to have a saddle-point solution. With this value, the Euclidean norm of the system’s error vector is maximized, leading to the worst-case scenario for entire system.

The multiple-parameter (in this case, 2-parameter) minimax design assigned a disturbance parameter ratio of DPR = 10, as stated in Eq. (37). The Pareto attenuation weights for the 2-parameter minimax design for the consumption and investment errors were calculated to be $r_{1}^{*}= 22,146$ and $r_{2}^{*}= 2,214.6$, respectively. As explained above, these parameters were calibrated as follows. The model was iteratively solved for the smallest weights on the consumption and investment disturbances that were possible, while maintaining a ratio of DPR = 10 and still allowing for a solution to the minimax game. Note that the smaller of the 2-parameter minimax penalty weights will always be smaller than the H$^{\infty }$-optimal disturbance parameter $r_{H}^{*}$, and larger minimax parameter will be larger than the H$^{\infty }$-parameter, so that $r_{2}^{*}< r_{H}^{*} < r_{1}^{*}$.

For the mixed stochastic/H$^{\infty }$-optimal control specification, the simulations assume that the investment equation is most likely to experience a worst-case scenario. The H$^{\infty }$-optimal control single equation disturbance attenuation parameter value was found to be $r_{MX}^{*} = 1,483.4$, which was thus used as the weight on the investment error $w_{2,k}$ in the performance index. The consumption error $w_{1,k}$ was again assumed to follow a Gaussian distribution with a mean of 0 and standard deviation of $s_{w1} = 27$. In the mixed design, the single disturbance attenuation parameter will be smaller than the value under the 2-parameter minimax design. Thus, $r_{MX}^{*} < r_{2}^{*} < r_{H}^{*}$. This occurs because the mixed parameter model only considers the worst-case for the investment equation, hence the error can be made larger and still satisfy the eigenvalue condition. Note that as the disturbance parameter ratio $DPR \rightarrow \infty , r_{2}^{*} \rightarrow r_{MX}^{*}$. Hence, the 2-parameter minimax design becomes equivalent to the mixed design when no penalty weight is placed on the consumption disturbance. If DPR $=$ 1, $r_{1}^{*}=r_{1}^{*}=r_{H}^{*}$.

The data for all figures are in billions of constant dollars, so that each 1-point change represents $1 billion annualized. Figure 1 and appendix Table 1 show the trajectories for government purchases. Since the economy begins in a recession during quarter 1, the trajectories show that government spending is consistently above its target for all periods. The optimal policy is the most aggressive under H$^{\infty }$-optimal control. It is less aggressive under the 2-parameter minimax design where the investment error is assigned a higher penalty weight than consumption. The optimal mixed stochastic/H$^{\infty }$-optimal control policy trajectory is between the 2-parameter minimax design and the LQG design. This is occurring because the aggressive policy is only pessimistically countering one robust disturbance. However, the mixed policy thrust is still much closer to the other two robust policy trajectories than it is to the deterministic and stochastic policy trajectories.

The Brainard principle holds when the optimal policy action is less aggressive under the robust design than in the stochastic design. In this set of simulations, the Brainard principle clearly does not hold. There is some reduction in the control energy expenditure from utilizing the 2-parameter minimax and mixed designs, since policymaker is targeting the pessimism on just one variable, rather than two. So, the fiscal authorities achieve some cost savings over the H$^{\infty }$-strategy, which can be seen by converting the annualized data in the simulations to quarterly amounts. Employing the H$^{\infty }$-strategy over all 7 quarters requires government spending to become $276 billion greater than it would be under the LQG design, which yields an average cost savings of about $69 billion per quarter. The 2-parameter minimax design saves about $27.4 billion (about 1 %) over the horizon compared to the H$^{\infty }$-strategy, which is an average savings of $3.9 billion per quarter. The mixed design has a much greater total period savings of $21.1 billion (about 2.7 % of total spending), which saves about $6.2 billion per quarter compared to the H$^{\infty }$-strategy. Thus, the fiscal authorities can gain substantial cost savings from employing the 2-parameter minimax and mixed designs.

However, both the 2-parameter minimax and mixed designs strategies assume that investment is the more likely variable to encounter a worst-case scenario. If this is not case, and if consumption is also equally likely to obtain its worst-case, then the model is incompletely robustified and more exposed to severe shocks. Thus, the fiscal savings obtained from focusing the policymakers’ robustness concerns on investment performance must be evaluated based on the tradeoff from incurring the additional exposure to problems arising from downturns in the consumption component of the economy.

The consumption and investment trajectories in Figs. 2 and 3; and appendix Tables 2 and 3, show the extreme pessimism under the robust scenarios. Note that the initial condition on the state trajectories is assigned at period $k$ $=$  1, so that the policy impacts that occur in period 1 do not affect consumption and investment until period 2. Government spending in the last planning period $K$ $=$ 7 achieves its terminal manifestation on consumption and investment in period 8. Consumption is higher under H$^{\infty }$-optimal control than for the LQG and deterministic design in until period 5, when it begins to lag. Consumption is even higher under the 2-parameter minimax design, and does not fall below the deterministic and stochastic designs until after quarter 6. During quarters 1 through 6, consumption is largest under the mixed design, and it isn’t surpassed by the deterministic and LQG trajectories until after quarter 7.

The three robust designs have greater consumption values earlier in the planning horizon due to the more extreme government spending under the pessimistic safeguard stance. Consumption in the 2-parameter design has skewed it robustness toward investment, causing the consumption disturbances to be smaller in magnitude than they are for the H$^{\infty }$-design. As a result, consumption is consistently greater under the 2-parameter minimax design than it is under the H$^{\infty }$-design. The consumption disturbances are stochastic under the mixed design, since it limits the robust concern exclusively to the investment disturbance. So when comparing the mixed to the other two robust policies, the less aggressive government spending under the mixed policy is counteracted by a smaller overall negative impact arising through the disturbances.

During the first four periods, investment undershoots its trajectory the most under the mixed design, followed by the 2-parameter minimax, the H$^{\infty }$-optimal control policy, LQG, and deterministic. Since the 2-parameter minimax model has placed a much greater relative emphasis on investment robustness, the larger investment disturbances cause a more pessimistic path throughout the planning horizon than for investment in the H$^{\infty }$-design. Since the 2-parameter minimax and the H$^{\infty }$-designs still penalize both consumption and investment disturbances, the level of investment under the mixed design, which only designs the worst-case for the single investment equation, eventually surpasses them. This is partly due to the smaller crowding-out effect of less aggressive government spending under the mixed design, and partly due to the higher crowding-in effect of consumption over the planning horizon. The LQG investment path is consistently lower than the deterministic path due to the outcomes of the Gaussian errors in the reported simulations; however, this will not always be the case, since the stochastic disturbances will randomly move the path above and below the deterministic design. But, barring the case of prolonged repeated large random negative shocks, the LQG trajectory will generally be above the robust model trajectories.

Figures 4 and 5 show the disturbance errors for the stochastic and various robust cases. The average consumption and investment disturbances fluctuate around their mean of 0 for the LQG, as expected. This is also true for the consumption disturbance under the mixed design, since it is still assumed to be stochastic. Under the robust designs, the consumption disturbance initially has a large negative value, and the magnitude steadily decreases over the planning horizon.

The investment disturbance is assumed to be the primary worst-case concern. Since the 2-parameter minimax design allows for greater robustness in the investment equation, the investment disturbances $w_{2,k}$ have consistently greater (negative) magnitudes under the 2-parameter minimax model than they do under the H$^{\infty }$-design. This is due to the smaller penalty weight assigned to the investment disturbances in the 2-parameter minimax performance index. Conversely, the consumption disturbances have much greater magnitudes under the H$^{\infty }$-design since the 2-parameter minimax has assigned smaller penalty weights to the consumption disturbances. The investment disturbance trajectory under the mixed design consistently lies below the trajectories for the purely robust strategies in these simulations. This is expected since the penalty weight on the investment disturbance is the lowest under the mixed design.

4.2 Heavy Weight on the Control Tracking Errors for Government Purchases

The second set of simulations follow Kendrick (1981) by weighting the final period tracking errors of the state variables from their targets at 100 times more than the state tracking errors in any other period. We set $q_{1,f} =q_{2,f} = 1$, and $q_{1,k} =q_{2,k} = .01$ for all $k = 1$,..., $K$. The control tracking error is assigned a weight of $R_{k} = 1$, and the deviation of the change in government purchases from its targeted growth is given a weight of $q_{3,k} = 0.1$ for all $k = 1$,..., $K$. Under this scheme, the policy tracking error carries the same weight as the final consumption and investment tracking errors. The policy tracking error is assigned 10 times more weight than deviations from desired changes in the spending growth over the previous period, and 100 times more weight than state tracking errors in any period.

The H$^{\infty }$-optimal disturbance attenuation parameter was found at $r_{H}^{*} = 1,988.8$. The 2-parameter minimax design retained a disturbance parameter ratio of DPR = 10, as stated in the previous simulations. The Pareto attenuation weights were iteratively computed to be $r_{1}^{*}= 4,942$ and $r_{2}^{*}= 494.2$, respectively. The mixed disturbance attenuation parameter value was found to be $r_{MX}^{*} = 328.2$.

Figures 6, 7, 8, 9, 10 and appendix Tables 4, 5, 6 show comparisons for the system trajectories under the five different error structures. Figure 6 shows that government purchases decreases much faster and tracks its target more closely than in Fig. 1. In Fig. 6, the paths of government purchases under the H$^{\infty }$-structure and 2-parameter design are almost indistinguishable, but the differences can be seen in Table 4. In Table 4, the controller is slighter more aggressive under the 2-parameter design than under the H$^{\infty }$-structure until period 4, when the two become equal; after period 4, government spending is less aggressive in the 2-parameter design than under the H$^{\infty }$-design. This contrasts with Fig. 1, where the H$^{\infty }$-controller was the most aggressive throughout the entire planning horizon. The overall level spending across the horizon is about the same under these two designs, so there is no cost savings to the policymaker. The mixed trajectory for government purchases consistently lies below the 2-parameter and the H$^{\infty }$-control trajectories, as it did in Fig. 1. Thus, the mixed strategy still allows for a reduction in the control intensity over the two purely robust designs, which results in a total cost savings of about $131 billion (2.5 %), which is an average of about $33 billion per quarter.

Fig. 6

Government purchases: heavy weight on control tracking error. $q_{1,\, f} = q_{2,\, f} = R_{k}=1; q_{1,\, k} = q_{2,\, k} = 0.01; q_{3,\, k} = .1; s_{w1}=27; s_{w2}=31; r_{H}=1,988.8; r_{1}=4,942; r_{2}=494.2; r_{MX}=328.2$

Fig. 7

Consumption: heavy weight on control tracking error. $q_{1,\, f} = q_{2,\, f} = R_{k}=1; q_{1,\, k} = q_{2,\, k} = 0.01; q_{3,\, k} = .1; s_{w1}=27; s_{w2}=31; r_{H}=1,988.8; r_{1}=4,942; r_{2}=494.2; r_{MX}=328.2$

Fig. 8

Investment: heavy weight on control tracking error. $q_{1,\, f} = q_{2,\, f} = R_{k}=1; q_{1,\, k} = q_{2,\, k} = 0.01; q_{3, \,k} = .1; s_{w1}=27; s_{w2}=31; r_{H}=1,988.8; r_{1}=4,942; r_{2}=494.2; r_{MX}=328.2$

Fig. 9

Consumption disturbance: heavy weight on control tracking error. $q_{1,\,f} = q_{2,\, f} = R_{k}=1; q_{1,\, k} = q_{2,\, k} = 0.01; q_{3,\, k} = .1; s_{w1}=27; s_{w2}=31; r_{H}=1,988.8; r_{1}=4,942; r_{2}=494.2; r_{MX}=328.2$

Fig. 10

Investment disturbance: heavy weight on control tracking error. $q_{1,\, f} = q_{2,\, f} = R_{k}=1; q_{1,\, k} = q_{2,\, k} = 0.01; q_{3, k} = .1; s_{w1}=27; s_{w2}=31; r_{H}=1,988.8; r_{1}=4,942; r_{2}=494.2; r_{MX}=328.2$

The consumption and investment trajectories in Figs. 7 and 8; and Tables 5 and 6, continue to exhibit excess pessimism under the robust scenarios. Consumption declines over the entire planning horizon for all designs except for the LQG, which is only above the deterministic trajectory due the stochastic errors. Consumption is still the lowest under H$^{\infty }$-optimal control. Consumption is again lower under the multiple-parameter design that under the mixed structure, where consumption does not fall below the deterministic trajectory until after period 4. When the control tracking error is heavily weighted, the increased policy thrust under the purely robust designs it too small to increase consumption above the deterministic trajectory; thus, the resulting robust consumption paths are now lower in Fig. 7, which contrasts with their higher paths in Fig. 2.

Investment falls over the entire horizon for all error structures, with the exception of the LQG, where the average random error causes a slight increase investment toward the end of the horizon. In both Figs. 3 and 8, investment is lower under the 2-parameter minimax specification than under the H$^{\infty }$-design, due to the 2-parameter emphasis on the robustness in the investment equation. After period 5, the mixed design trajectory rises above the investment levels in the 2-parameter minimax and H$^{\infty }$-designs. As in the case where the state tracking errors were more heavily weighted, the more optimistic deterministic investment trajectory is above the purely robust path. Except for the case where unpredicted pessimism leads to a sequence of large negative random shocks in investment, the LQG investment trajectory will also lie predominantly above the robust model trajectory in this case as well.

Figures 9 and 10 display the disturbances. As in the case with larger weight on the state tracking errors, Fig. 9 shows that the consumption disturbances are larger in magnitude under H$^{\infty }$-control than in the 2-parameter minimax model. The consumption errors are random under the LQG and mixed designs. Since the 2-parameter minimax structure places all of the robustness concern on investment, it again produces the largest magnitude for the investment disturbance trajectory.

4.3 No Penalty for Deviations in the Control between Periods

In the previous simulations, the government was penalized for changing its spending above or below the stated quarterly target growth rate of $g_{G,k} = 0.5\,\%$ (which is about 2 % annualized growth) between periods. When the spending-change penalty parameter, $q_{3,k}$, is extremely large relative to the other performance index weights, then government spending will always increase in each quarter by $g_{G,k} = 0.5\,\%$, regardless of its initial value. Thus, the fiscal authorities will be forced to set the spending level in each new budget as a standard percentage above spending in the previous budget. This restricts the fiscal authorities’ ability to freely change government spending when attempting to track the policy and state variable targets.

The last set of simulations analyzes the case where the government is not penalized for changing its spending above or below the stated quarterly target growth rate of $g_{G,k} = 0.5\,\%$ between periods. This allows us to gauge the performance differential that results from including, versus omitting, the spending change penalty in the policy objective. In order to assess this, we reconsider the first case where there were heavy weights on the tracking errors for consumption and investment. Now, we alter this scenario and assign a zero weight for the policy deviations between periods, but retain all of the other weighting values. Thus, $q_{1,f} =q_{2,f} = 10$, $q_{1,k} =q_{2,k} =R_{k} = 1$, but $q_{3,k} = 0$ for all $k = 1$,..., $K$. Figures 11, 12, 13 and Tables 7, 8, 9 illustrate the system trajectories.

Fig. 11

Government purchases: heavy weight on the tracking errors for consumption and investment. $q_{1, \,f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k} = R_{k}=1; q_{3,\, k}=0; s_{w1}=27; s_{w2}=31; r_{H}=6,265.1; r_{1}=15,785; r_{2}=1,578.5; r_{MX}=1,060.0$

Fig. 12

Consumption: Heavy weight on the tracking errors for consumption and investment. $q_{1,\, f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k} = R_{k}=1; q_{3,\, k}=0; s_{w1}=27; s_{w2}=31; r_{H}=6,265.1; r_{1}=15,785; r_{2}=1,578.5; r_{MX}=1,060.0$

Fig. 13

Investment: heavy weight on the tracking errors for consumption and investment. $q_{1,\, f} = q_{2,\, f}=10; q_{1,\, k} = q_{2,\, k} = R_{k}=1; q_{3,\, k}=0; s_{w1}=27; s_{w2}=31; r_{H}=6,265.1; r_{1}=15,785; r_{2}=1,578.5; r_{MX}=1,060.0$

Government purchases is considerably more volatile when there is no penalty for excessive changes between periods. In period 1, government spending rises to approximately an annualized $4,000 billion in all three robust designs (H$^{\infty }$-control, 2-parameter minimax, and mixed), and reaches $3,463.6 billion in the deterministic and LQG designs. This is far greater than the period 1 levels when there is a penalty for excessive changes between periods, which resulted in period 1 spending of only $3,540 billion in the robust designs, and $3,170.8 billion under the deterministic and LQG structures. When there is no penalty for excessive changes between periods, the level of government spending continually falls across the planning horizon after period 1, and ends up at lower amounts in period 7 than in the case where there are penalties for excessive changes between periods.

Figures 12 and 13 show that consumption and investment end up closer to their final targets when government spending has the extra flexibility of being unhampered by penalties for changes between periods. However, this type of volatile budget policy would likely not be politically feasible, and would be difficult to implement in practice, for either annual or quarterly fiscal policy. The latter simulations in Figs. 11, 12, 13 would require the government to increase spending by around 40 % in the first policy quarter under the robust designs, and about 25 % under the LQG design, and then consistently lower spending by large increments thereafter. When budgetary changes between periods are penalized, the initial spending increase is half as much, at around 20 %, under the robust designs, and only about 11 % under the LQG design. This illustration confirms the merit of using a performance index penalty for excessive changes in the policy variable between periods, especially when robust designs are employed.

5 Conclusion

Once the model’s performance under the different error structures has been analyzed, the robust strategies offer several avenues for application. The fiscal authorities could implement the simulated H$^{\infty }$-optimal control or multi-parameter minimax strategy as the operating policy. However, strictly following a robust design can lead to an overly pessimistic control policy, since it only optimizes over the worst-case error scenarios (Rustem and Howe 2002). Alternatively, it could use the worst-case disturbances obtained in the simulations to determine the worst-case distribution for the error terms in the system equations (Basar and Bernhard 1991).

Policymakers could also construct control rules that use a weighted average of the trajectories from the H$^{\infty }$-optimal control, multi-parameter minimax, and/or mixed designs combined with the deterministic and LQG control specifications, to achieve a balanced policy that is less susceptible to instability issues than it would be without the attention to robustness. This latter approach is the most pragmatic. Several researchers, such as Kendrick (2005) and Zakovic et al. (2007), favor this approach to implementing robust designs. Rustem and Howe (2002) caution that minimax approaches and stochastic control are only risk management tools for coping with uncertainty, and hence they cannot be substituted for wisdom.

Finally, the fiscal authorities could use the mixed strategy that was obtained in this paper, if most of the robustness concerns are focused only on a subset of the system equations. Green and Limebeer (2012) emphasize that model reduction, whereby high-order systems are approximated by lower-order systems, serves as a key component that links control system design to plant modeling. Although our analysis only presented the mixed case where the H$^{\infty }$-strategy was modeled for the investment equation, it could have been designed where the robust concern was reduced to the consumption equation. The simulations showed the mixed strategy provides a reduction in the control effort over the designs where the entire system was modeled under the worst-case disturbance scenario.

Appendix

Tables 1, 2, 3 present the data graphed in Figs. 1, 2, 3, respectively, so that all of the data points can be compared with more detailed resolution. These data are in billions of constant dollars, so that a 1-point difference between data points represents $1 billion annualized. Consumption and investment are fixed at their initial values in period 1. Government purchases is fixed in period 0, and the first optimal policy action for government spending occurs in period 1. Deviations from targeted changes in government spending are penalized.

Table 1 Government purchases: heavy weight on tracking errors for consumption and investment

Table 2 Consumption: heavy weight on the tracking errors for consumption and investment

Table 3 Investment: heavy weight on the tracking errors for consumption and investment

Tables 4, 5, 6 present the data graphed in Figs. 6, 7, 8, 9, respectively. The trajectories for government purchases under the H$^{\infty }$-control and 2-parameter minimax designs appear close in Fig. 6, but the differences are easily seen in Table 4.

Table 4 Government purchases: heavy weight on control tracking error

Table 5 Consumption: heavy weight on control tracking error

Table 6 Investment: heavy weight on control tracking error

Tables 7, 8, 9 show the data graphed in Figs. 11, 12, 13, respectively, where the deviations from targeted changes in government spending are not penalized.

Table 7 Government purchases: heavy weight on tracking errors for consumption and investment no penalty for deviation from targeted change in government spending

Table 8 Consumption: heavy weight on the tracking errors for consumption and investment no penalty for deviation from targeted change in government spending

Table 9 Investment: heavy weight on the tracking errors for consumption and investment no penalty for deviation from targeted change in government spending