Optimal fiscal policy in times of uncertainty: a stochastic control approach

Abstract

This paper deals with the possibilities of designing optimal fiscal policy under uncertainty. First, different forms of uncertainty are discussed for economic policy analysis and design. For dynamic models under uncertainty, a stochastic optimum control framework is presented. Algorithms for nonlinear models are briefly reviewed: OPTCON1 for open-loop control, OPTCON2 for open-loop feedback (passive learning) control, and OPTCON3 for dual control with active learning. The OPTCON algorithms determine approximately optimal fiscal policies. The results from calculating these policies for a small macroeconometric model for Slovenia serve to illustrate the applicability of the OPTCON algorithms and compare their solutions. The results show that the most sophisticated and time intensive active-learning solution, which requires the use of an extremely small and simple model of the economy, is not necessarily superior to the simpler solutions. For actual policy design problems and policy advice, it will often be better to neglect the stochastic uncertainty and use deterministic optimization instead, especially since in practice, the most important forms of uncertainty are not stochastic but relate to the model specification, the behaviour of other policy makers or other agents, or fundamental uncertainty that cannot be dealt with at all.

1 Introduction

Over the last 15 years or so, European economies have been confronted with a series of unexpected crises: the Great Recession, the financial and economic crisis of 2007–2010; the euro crisis, the banking, economic, and sovereign debt crisis of 2009–2013; the COVID-19 pandemic crisis 2020–2023; and the crisis due to the Russian invasion of Ukraine in 2022 (actually since 2014) followed by Hamas terrorist attack and the subsequent war between Hamas and Israel since October 2023. All of these events have had an impact on key macroeconomic variables in most European countries, causing severe challenges for policy makers in the European Union as well as for national governments and their policies. While the European Central Bank designed its monetary policy in relation to pan-EU problems, national fiscal policy makers had to deal with difficult trade-offs in their own countries. This was aggravated by different, more local shocks. Slovenia, for instance, underwent a domestic crisis due to problems in its own banking sector from 2013 to 2017, with potential repercussions for other Central and Eastern European countries. The common feature of all of these crises was their unpredictability. In the Great Moderation of the 1990s, some economists even thought that most macroeconomic problems had been solved and no severe recession could happen again, e.g., Lucas (2003). The shaking of such beliefs also contributed to a more sceptical public attitude towards economists and mainstream economic theories.

In this paper, we investigate how optimal fiscal policy can deal with some forms of uncertainty. We consider the example of Slovenia, which became a member of the Eurozone in 2007 and, hence, has no monetary policy of its own; fiscal policy remains the primary tool with which to react to macroeconomic disturbances. Actually, Slovenia was the first country among those from former communist ones to join the Eurozone after a relatively short period of having its own currency, the Slovenian tolar. Moreover, in a series of research projects, partly with colleagues from Ljubljana, we acquired a deeper knowledge of the economic problems of this country, and contributed to analysing them by building several versions of macroeconomic medium-sized econometric models and using them for economic policy problems and for the design of optimal fiscal policies. As these models were used for deterministic optimizations, we want to know how one could introduce uncertainty with which fiscal policy making is inevitably confronted.

The structure of the paper is as follows: In the next section, we provide a classification of uncertainties a country may have to deal with when designing its fiscal policy in the best way possible. We point out that the theory and practice of economic policy, especially quantitative economic policy, can, at best, cope with stochastic disturbances, that is with disturbances whose probability distribution is (at least: assumed to be) known ahead of the event. Even this case cannot be said to be solved exactly for an optimal design of (in our case: fiscal) policies. We then concentrate on this stochastic uncertainty and present the results for a very simple model of the Slovenian economy using the OPTCON algorithms for optimal stochastic control of econometric models which we developed. The model is one of the well-known Phillips curve relation between inflation and unemployment (or the output gap).

Due to computational restrictions, our model is not in a position to give a comprehensive picture of the Slovenian economy; for a more realistic model, see, for instance, Weyerstrass et al. (2023) with results for the recent COVID-19 pandemic. We show that our results for the small model are relatively close to those obtained with a deterministic version of the same model. Finally, the relative advantages and disadvantages of the three versions of the OPTCON algorithm used are discussed and some conclusions drawn for fiscal policy design and for further research. We stress that the aim of this paper is not to derive results to be implemented by actual Slovenian fiscal policy makers. Instead, we explore whether the additional effort required to analyse stochastic uncertainty in the determination of an optimal fiscal policy is worthwhile given the restrictive assumptions it requires, especially about the model to be used. The answer is largely negative.

2 How to deal with different types of uncertainty

Ever since Brainard’s (1967) seminal paper, it has been well known that results derived from deterministic models of the theory of economic policy may have to be fundamentally modified when risk and uncertainty are taken into account. Therefore, the question arises as to which consequences different forms of uncertainty have on the decisions of policy makers. In particular, we ask whether endeavours to determine (in some sense) “optimal” conceptions of macroeconomic policy may be doomed to failure in the presence of uncertainty, as some economists from the Monetarist and the New Classical schools have claimed, e.g., Friedman (1948), Sargent and Wallace (1976). In particular, these authors assert that attempts at discretionary stabilization policy actions using optimizing procedures in the tradition of the theory of quantitative economic policy should be discarded when considerable uncertainty is present in the economy. Instead, they plead for fixed rules for economic policy instruments such as Friedman’s constant money stock rule for monetary policy or the rule of a permanently balanced budget for fiscal policy.

Several authors have argued against the prescription of fixed rules for policy making. For more arguments on this topic, see e.g. Neck (1986). It should be stressed that the question under consideration does not mean that policy makers really follow optimal stabilization policies but it is rather concerned with the possibility in principle that they can do so. For actual policy making, its explanation and evaluation, a positive theory of government behaviour is required, for instance a political economy or public choice approach. In this paper, we ask whether economic policy makers who aim at reaching certain objectives can and should do so in an “optimal” way even in the presence of uncertainty.

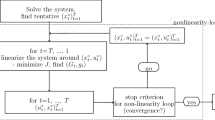
This question can be examined within a decision-theoretic approach to the theory of economic policy. This theory of quantitative economic policy originates from Jan Tinbergen (1952, 1967) and was extended to the dynamic case by using optimal control theory by Chow (1975, 1981) and Kendrick (1981), among others. Here policy makers have some instrument variables at their disposal whose values they can determine (within some limits). For fiscal policy, examples would include various categories of government expenditures and revenues or variables determining these components of the government budget. It is assumed that decisions about the values of these instrument variables have some effect on the policy makers’ objectives, such as low unemployment, low inflation, high output growth, sustainable public finance and balance of payments, environmental goals, etc. There some uncertainty at least regarding variables not under the control of a (national) policy maker, such as global developments or other unpredictable events, is present. Moreover, it is assumed that the policy makers have (more or less) well defined preferences about the values of the objective variables. In optimization approaches (Tinbergen’s so-called flexible-targets policy approach), it is assumed that the preferences of the policy makers can be summarized by an objective function to be maximized (or minimized) under the constraints of a model showing the relations between the instrument and the objective variables under alternative assumptions about the non-controlled exogenous variables. This can be represented schematically as shown in Fig. 1.

Fig. 1

Schematic representation of the approach of the theory of quantitative economic policy

It must be admitted that the assumption of an unambiguous and internally consistent objective function of one (or even the aggregate of all) of the policy makers may require unrealistic postulates about their rationality and knowledge. Such an objective function should therefore be interpreted not as a social welfare function in the sense of welfare economics, for which problems of social choice invariably arise, but as an expression of the values of certain policy makers or some consensus among them as to what to aim at. For such a restricted problem, the theory of economic policy and its decision-theoretic approach provide an adequate framework.

We may distinguish between three types of uncertainty in such a framework:

• 1. Stochastic uncertainty: Here probability distributions for the consequences of economic policy actions are known. These can either be objective ones, based on statistical frequencies, or subjective ones relating to the policy makers. An optimal policy is such that it maximize the expected utility of the results (in the dynamic case, the expected present value of the utility and costs of a time series of results).

• 2. Strategic uncertainty: This occurs when the results of economic policy actions are also determined by the actions of other decision makers and the interactions between them, where the other decision makers also follow (fully or boundedly) rational principles. The most interesting point here is the case of policy makers with different priorities in their objective functions. These fall under the subject of the theory of games (including dynamic games); they are not covered in this paper.

• 3. Fundamental uncertainty (nowadays often called “Black Swans”): In such situations, the policy makers know nothing about the probabilities of such events and do not have an idea how the event could come about, or even about the nature and the possibility of such an event. Such events can only be studied after they have occurred, although it may be possible to learn something about them as they evolve. The COVID-19 pandemic is an example of this type of uncertainty (although some scientists pointed out historical examples of similar pandemics ahead of the last one).

3 Approximate solutions to dynamic stochastic policy problems

Here we concentrate on the case of stochastic uncertainty. The framework is one of optimizing an intertemporal objective function with politically relevant variables (the rate of unemployment and the rate of inflation in our case) subject to constraints given by an estimated or calibrated dynamic econometric model. Such problems are the subject of stochastic control theory. The main source of uncertainty refers to the relations between different variables which are reflected in the probability distributions of the parameters of the econometric model of the economy. Unfortunately, stochastic optimal control theory has not been successful in deriving exact solutions for even very simple analytical problems of this kind and even less so for complex problems involving large models characterized by nonlinearities and a variety of sources of uncertainty. A famous example is Witsenhausen’s (1968) result that in a seemingly simple problem of (decentralized) control of a linear system with normally distributed error terms under a quadratic objective function, nonlinear solutions can be found that are superior to the optimal linear ones. This shows the impossibility of generalizing certainty equivalence (separation theorem) results for more complicated stochastic systems. A general solution for Witsenhausen’s counterexample is still unknown (Ho 2008), although for some variations of the counterexample a solution is known (Basar 2008); cf. also Yüksel and Basar (2024).

One reason why it is difficult to obtain analytic results from stochastic control problems is the so-called dual effect of controls in a stochastic dynamic system: Controls do not only serve to optimize the instantaneous objective in each period but can also be used to learn about the reactions of the system to policy measures, which in turn can contribute to improved policies in later periods. The fact that this interdependence between considerations of direct optimization and experimentation for learning about policy effects makes the stochastic optimal control problem intractable has been recognized by several authors in the past (Feldbaum 1965; Aoki 1989). Such problems can, therefore, only be studied numerically and only approximations to the unobtainable truly optimal policies can be obtained.

Such an approach was pursued by Kendrick (1981), who developed several algorithms, including one for active learning based on Bar-Shalom and Tse (1976), in which the dual effect of controls is explicitly taken into consideration. Extensions and applications of this algorithm are due to Amman and Kendrick (1995), Tucci (1998), and Amman et al. (2018), among others. These algorithms only applied to linear dynamic models, which is a severe restriction as even the simplest econometric models contain some nonlinearities. In a previous paper, we extended the Kendrick algorithm with active learning to a class of nonlinear models that can be approximated by time-varying linear models, called OPTCON3 (Blueschke-Nikolaeva et al. 2020). This is an extension of our earlier algorithms OPTCON1 and OPTCON2, which assume more special information patterns.

The OPTCON algorithms calculate approximate solutions to optimal control problems with a quadratic objective function (a loss function to be minimized) and a nonlinear multivariate discrete-time dynamic system under additive and parameter uncertainties. The intertemporal objective function is formulated in quadratic tracking form, which is quite often used in applications of optimal control theory to econometric models. This is then applied to the (approximately) optimal fiscal policy under uncertainty for a country, in our case Slovenia.

Formally, the optimal stochastic control or intertemporal optimization problem consists in finding values for the control variables (u_t) and the corresponding state variables (x_t) in each period t which minimize the objective function (in the case of a cost function and maximize it for a utility function):

$$\text{min}\,{\text{J}}=E\left[\sum_{t=1}^{T}{L}_{t}\left({{{x}}}_{{{t}}}, {{{u}}}_{{{t}}}\right)\right]$$

(1)

with

$$L_{t} \left( {x_{t} , u_{t} } \right) = \frac{1}{2}\left( {\begin{array}{*{20}c} {x_{t} - \tilde{x}_{t} } \\ {u_{t} - \tilde{u}_{t} } \\ \end{array} } \right)^{\prime } W_{t} \left( {\begin{array}{*{20}c} {x_{t} - \tilde{x}_{t} } \\ {u_{t} - \tilde{u}_{t} } \\ \end{array} } \right)$$

(2)

subject to constrains given by a dynamic system of nonlinear difference equations modelling the economy under consideration:

$${\varvec{x}}_{{\varvec{t}}} = f\left( {{\varvec{x}}_{{{\varvec{t}} - 1}} ,{ }{\varvec{x}}_{{\varvec{t}}} ,{ }{\varvec{u}}_{{\varvec{t}}} ,{ }{\varvec{\theta}},{ }{\varvec{z}}_{{\varvec{t}}} { }} \right) + {\varvec{\varepsilon}}_{{\varvec{t}}} ,t = 1, \, \ldots , \, T,$$

(3)

where ${{\varvec{x}}}_{{\varvec{t}}}$ is an n-dimensional vector of state variables that describes the state of the economic system at any point in time t. ${{\varvec{u}}}_{{\varvec{t}}}$ is an m-dimensional vector of control variables, ${\widetilde{{\varvec{x}}}}_{{\varvec{t}}}{\in R}^{n}$ and ${\widetilde{{\varvec{u}}}}_{{\varvec{t}}}{\in R}^{m}$ are given “ideal” (desired, target) levels of the state and control variables respectively. T denotes the terminal time period of the finite planning horizon. ${W}_{t}$ is an ((n + m) × (n + m)) matrix, specifying the relative weights of the state and control variables in the objective function. In a frequent special case, ${W}_{t}$ is a matrix including a discount factor $\alpha$ with ${W}_{t}=$ ${\alpha }_{t-1}W$. ${W}_{t}$(or W) is symmetric. ${\varvec{\theta}}$ is a p-dimensional vector of parameters whose values are assumed to be constant but unknown to the decision maker (parameter uncertainty), ${{\varvec{z}}}_{{\varvec{t}}}$ denotes an l-dimensional vector of non-controlled exogenous variables and ${{\varvec{\varepsilon}}}_{{\varvec{t}}}$ is an n-dimensional vector of additive disturbances (system error). ${\varvec{\theta}}$ and ${{\varvec{\varepsilon}}}_{{\varvec{t}}}$ are assumed to be independent random vectors with expectations $\widehat{{\varvec{\theta}}\boldsymbol{ }}$ and ${{\varvec{O}}}_{n }$ respectively and covariance matrices ${\boldsymbol{\Sigma }}^{{\varvec{\theta}}{\varvec{\theta}}}$ and ${\boldsymbol{\Sigma }}^{{\varvec{\varepsilon}}{\varvec{\varepsilon}}}$ respectively. f is a vector-valued function, ${f}_{i}$(…..) is the i-th component of f (…..), i = 1, …, n.

Next, we give a brief description of the three versions of the OPTCON algorithm with an open-loop, passive-learning, and active-learning strategy respectively. The first version of OPTCON, OPTCON1, delivers an open-loop (OL) solution and is described in detail in Matulka and Neck (1992). The open-loop strategy either ignores the stochastics of the system altogether or assumes the stochastics (expectation and covariance matrices of additive and multiplicative disturbances) to be given for all time periods at the beginning of the planning horizon. Following Chow (1975, 1981), the problem with the nonlinear system is tackled iteratively, starting with a tentative path of the control and state variables. The tentative path of the control variables is given for the first iteration. In order to find the corresponding tentative path for the state variables, the nonlinear system is solved numerically using the Levenberg–Marquardt method or trust region methods. Next, the iterative approximation of the optimal solution starts. The solution is iterated from one time path to the next until the algorithm converges or the maximum number of iterations is reached. During the optimization process, the system is linearized around the previous iteration’s result as a tentative path and the problem is solved for the resulting time-varying linearized system. The optimal solution of the problem for the linearized system is found under the above-mentioned simplifying assumptions about the information pattern; this solution is then used as the tentative path for the next iteration, starting off the procedure all over again. In every iteration, i.e., for every solution of the problem for the linearized system, the objective function is minimized using the dynamic programming principle of optimality to obtain the parameters of the feedback control rule. Finally, the value of the objective function is calculated for the obtained solution.

The second version of the algorithm, called OPTCON2 and described in Blueschke-Nikolaeva et al. (2012), includes the passive-learning or open-loop feedback (OLF) strategy, which uses the idea of re-estimating the model at the end of each time period. For this re-estimation, the model builder and, hence, the policy makers observe what has happened and use the current values of the state variables, that is, the new information, to improve their knowledge of the system. The stochastics in the problem is again represented by two kinds of errors, namely additive (random system errors ${{\varvec{\varepsilon}}}_{{\varvec{t}}}$) and multiplicative (“structural” errors, errors in the parameters ${\varvec{\theta}}$). It is assumed that “true” parameters $\widehat{{\varvec{\theta}}}$ generate the model. However, the policy maker does not know these true parameters and works with the “wrong” parameters resulting from the estimates using the realization of a random variable, which is the sum of $\widehat{{\varvec{\theta}}}$ and a purely random disturbance.

To determine the passive-learning strategy, first a forward loop is started from time 1 to T. In each time period S, an (approximately) optimal open-loop solution for the subproblem is determined, the problem for the time periods from S to T. Then the predicted x^∗ and u^∗ are fixed for the time period S. At the end of each time period, the policy maker observes the realized values of the state variables x^S, which are, however, disturbed by the additive errors. The difference between consecutive estimates of the state vector comes from the realization of the random numbers. Next, the new information is used by the policy maker to update and adjust the parameter estimate. After that, the same procedure is applied to the remaining subproblems from S + 1 to T, and so on. The update of the parameter estimates is conducted via the Kalman Filter.

The same update procedure is used in the third version of the OPTCON algorithm, called OPTCON3. This version of the OPTCON algorithm includes an active-learning strategy (also called closed-loop, adaptive-dual, or dual control). The active-learning strategy means the policy maker faces the dual problem of choosing the best strategy and simultaneously reducing the uncertainty about the system. The active-learning method differs from the passive-learning method in the OPTCON2 algorithm in the following way: When using the passive-learning method, new observations are obtained each period and are used to update the parameter estimates; however, no effort is made to choose control variables with the aim of improving the learning process about the dynamic system to be controlled. In contrast, in the active-learning methods, control variables are chosen with the dual purpose of moving the system in the desired direction and perturbing the system to improve the parameter estimates. Thus, the active-learning strategy delivers an optimal solution where the control is chosen with a view to reaching the desired states in the present and reducing uncertainty through learning, permitting an easier attainment of desired states in the future. This lets the policy maker deal with the dual problem of simultaneously choosing the best strategy and reducing the uncertainty about the system. The key idea is to make some use of information about future observations as well.

The procedure of finding the closed-loop solution in this paper corresponds to Kendrick (1981). The approximate cost-to-go is broken down into three terms: J_d = J_D + J_C + J_P, where J_d is the total cost-to-go (sum of the expected remaining costs) with T periods remaining; the deterministic component J_D includes only non-stochastic terms; the cautionary component J_C includes the stochastic component of the system known in the current period; and the probing term J_P contains the effect of dual learning on the future time periods. Each of these components faces special difficulties in computing due to the nonlinearity of the system. Especially the probing term includes the motivation to perturb the controls in the present time period in order to reduce future uncertainty about the parameter values and can therefore be considered the most challenging task. Thus, the terms J_C and J_P constitute a separate optimization problem with a quadratic criterion which is maximized subject to the nonlinear system. The system equations are derived from the expansion of the original system and can be calculated by rewriting the Taylor expansion of the nonlinear system in the perturbation form. Instead of the system (3), the objective function in perturbation form has to be minimized.

The structure of the OPTCON3 algorithm goes in line with the calculation of the open-loop strategy in OPTCON2. The optimization is carried out in a forward loop from 1 to T. In each time period S (S = 1,…,T), the following search procedure is conducted: The subproblem from S to T is solved via the open-loop (OL) strategy, and the OL solution of (x^∗, u^∗) for the time period S is fixed. After that, the core part of the dual control starts. The idea is to actively search for some solution paths which best deal with the dual problem of minimizing the current objective function and the future uncertainty in the model. In OPTCON3, a grid search method is used. The evaluation is repeated until the approximately optimal control is found. For details, see Blueschke-Nikolaeva et al. (2020).

The OPTCON3 algorithm essentially uses the approach introduced by Bar-Shalom and Tse (1976) and Kendrick (1981) but augments it by approximating, in each step, the nonlinear system by a series of linear systems (replacing the nonlinear autonomous system by a linear time-varying one). In the optimization process, the current state of the system has to be observed, which is crucial for the learning procedure. Because it is not possible to observe current and true values for a performance test, Monte-Carlo simulations have to be used. In this way, some “quasi-real” values can be created and used to compare the performance of an optimization without learning (both open-loop (OL) and certainty equivalence (CE) alternatives) as well as with passive learning (OLF) and active learning (AL). Thus, a large number (usually between 100 and 1000) of realizations of random noises is generated. It is assumed that there is an unknown “real” model with the “true” constant parameter vector but the policy maker does not know these “true” parameters and works with the “wrong” parameters resulting from the estimates using the realization of the random variables.

4 The macroeconometric model

We consider the following small macroeconomic model of an (expectations-augmented) Phillips curve relation with fiscal policy for the Slovenian economy, to be called SLOPOLMIN:

$$PI_{t\,} = C_{1} + C_{2} PI_{t - 1} + C_{3} GAP_{t - 1} + C_{4} GROIL$$

(4)

$$GAP_{t} = C_{5} SY_{t} + C_{6} SY_{t - 1} + C_{7} GEX_{t} + C_{8} GAP_{t - 4}$$

(5)

$$SY_{t} = S_{t} /YN_{t} *100$$

(6)

$$DT_{t} = DT_{t - 1} \left( {1 + ID_{t - 1} /100} \right) - S_{t} + EXDT_{t}$$

(7)

$$P_{t} = P_{t - 4} \left( {1 + PI_{t} /100} \right)$$

(8)

$$YN_{t} = YPOT_{t} \left( {1 + GAP_{t} /100} \right)P_{t} /100$$

(9)

The model consists of two behavioural equations: (4, 5), and 4 identities: (6–9). t is the time index. The 6 endogenous variables are: PI_t = rate of inflation, P_t = general price level (measured by the GDP deflator), GAP_t = output (Okun) gap (measured by real GDP), YN_t = nominal GDP, S_t = nominal government primary budget surplus, SY_t is the ratio of S_t to nominal GDP, DT_t = public debt (nominal). S_t is the control variable (fiscal policy instrument) for the optimization problem. There are 5 exogenous non-controlled variables: GROIL_t = rate of change of the oil price in euro, GEX_t = quarter-to-quarter rate of change of real exports, ID_t = interest on debt (measured as the ratio of interest payments on public debt to the value of public debt), EXDT_t = exogenous component of public debt (residual to fulfil identity (7); it includes revaluations of debt and some discretionary changes, among others), YPOT_t = potential real GDP (calculated from a production function). C_i (i = 1,…,8) are the parameters of the model which are uncertain and have to be estimated.

Equation (4) is an expectations-augmented Phillips curve and can be seen as analogous to the New Keynesian Phillips curve for the case of static expectations. (5) is a reduced-form equation explaining the output gap by a domestic fiscal policy variable and a proxy for global effects on the Slovenian economy. It corresponds to the aggregate demand function of conventional macroeconomic models. (6) defines the primary budget surplus-GDP ratio and links the fiscal instrument variable to nominal aggregate demand. (7) is the government budget constraint, and (8) and (9) define the left-hand side variable by the inverted definition of the inflation rate and the potential output respectively. Interest rates are exogenous, assumed to depend on monetary policies and international financial markets. The specification of the model and the lag structures were chosen in an extensive search for high significance of the parameter, with an attempt to keep the model as small as possible in order to make it usable for applying the rather complex optimal control algorithms.

For the estimation of the parameters, we used first OLS and then FIML (full information maximum likelihood), the latter method also delivering an estimate of the covariance matrix of the parameters. The sample was 1996Q2 until 2019Q4. The data come from the database of Weyerstrass et al. (2023), where more details are available. The results are shown in Table 1.

Table 1 Model SLOPOLMIN

The estimates of the parameters and the significance results are very close under the two estimation methods. Note that the coefficients of Eq. (2) imply a non-Keynesian effect of fiscal policy: Increasing the primary budget balance increases output and, hence, according to Eq. (1), also inflation. Thus, there is a trade-off between fighting unemployment (negative output gaps) and high rates of inflation, but the design of fiscal policy has to be non-Keynesian and there is no trade-off between output/employment and low budget deficits. This has to be borne in mind for the design of optimal fiscal policy and when interpreting the optimization results, although not necessarily the impact of uncertainty on them. It must be admitted that this result is unexpected as we estimated larger and more elaborate Keynesian macroeconometric models (e.g., in Weyerstrass et al. 2023) which fitted quite well for the same data. A source of uncertainty, which may be called model uncertainty, may, hence, be added to the ones discussed in the second section, which could also include uncertainty about the policy maker’s preferences (the objective function).

5 Optimal fiscal policies

To calculate the (approximately) optimal fiscal policy, we assume that the primary government budget balance is under the control of the policy maker, i.e., that it is the policy instrument. The objective variables are the rates of inflation, the output gap, and the control variable, which has to be given a weight in the objective function in order to make the control problem well defined. We assume that the “ideal” path for the policy maker is to hold the inflation rate constant at 2% and the output gap and primary balance at zero. Starting in the last quarter of 2007 (before the Great Recession), we take the time horizon of the optimization to be 28 periods: from 2008Q1 to 2019Q4 (before the pandemic crisis, which is considered to be the “Black Swan”). Using the model estimated over the entire time horizon to calculate policies over part of this time horizon as well may imply knowledge even a well-informed policy maker could not have when deciding on policy design. Rolling time horizons for the optimization can be a remedy when using such models for actual policy design; in our case, this would have complicated the task considerably, given our limited resources and the relatively short time span of the data available for Slovenia, which did not exist as an independent country before 1992.

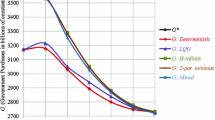
Figures 2, 3, 4 show the results of the optimal control calculations under deterministic and open-loop stochastic control, together with the simulation of the model using actual values of the control variable. The (approximately) optimal time paths of the control variable and the target variables under deterministic and open-loop stochastic control are nearly identical but very different from the simulated ones. The latter result is partly due to the non-Keynesian character of the model viz-à-viz the Keynesian practice of Slovenian (and other) policy makers. On the other hand, a general feature, which is also present in optimization analyses with larger and more elaborate models, is the smoother path of the variables of the model. Hence, at least the task of stabilizing an economy in terms of macroeconomic variables by reducing their volatility can be achieved by an optimization approach. The non-Keynesian character of the model implies a pro-cyclical design of the policy instrument, which in this case is stabilizing. Under this model, the optimal use of the fiscal policy instrument is less active than actual fiscal policy, with better results for the target variables. As noted above, in view of the more Keynesian policy recommendations from our larger previous models, this detail of the optimal policy in this small SLOPOLMIN model should be interpreted with great care.

Fig. 2

Time path of control variable S_t under simulation with historical values and with deterministic and open-loop stochastic optimization. The path denoted by “target” refers to the “ideal” values

Fig. 3

Time path of target variable inflation rate (PI_t) under simulation with historical values of the control variable and with deterministic and open-loop stochastic optimization. The path denoted by “target” refers to the “ideal” values

Fig. 4

Time path of target variable output gap (GAP_t) under simulation with historical values of the control variable and with deterministic and open-loop stochastic optimization. The path denoted by “target” refers to the “ideal” values”

The nearly identical time paths of the deterministic and open-loop stochastic policies are due to the near linearity of the model and, hence, the certainty equivalence of the optimization problem. The only nonlinearity in the model occurs in the debt Eq. (7), which exerts no feedback on the estimated equations and their endogenous variables. The situation might be different if we included government debt in the objective function or in an equation of the model with direct effects of public debt on the objective variables. However, the result above about the close similarity of deterministic and open-loop stochastic policies may also be interpreted to mean that open-loop stochastic control deals with uncertainty only in a superficial way, essentially neglecting the uncertainty in the parameters of the model.

For the open-loop feedback and the active-learning stochastic control solutions, we need information about some alternative realizations of the stochastic distribution. Stochastic simulations are the method to obtain this information. Of course, this does not correspond to actual realizations under alternative scenarios as these are non-existent. Instead, we assume that the estimated covariance matrix in the FIML estimation corresponds to the actual one in the unknown distribution of the parameters (how “God plays”, to paraphrase Albert Einstein). In this study, we conducted stochastic simulations with 100 draws of stochastic parameter combinations for the certainty equivalence (CE), the open-loop feedback (OLF), and the active-learning (AL) solutions using OPTCONi, i = 1,2,3 respectively to compare the influence of the stochastics under the three solution methods, all of which are approximations, but with AL using the most elaborated information about the stochastics. The good news was that the algorithms always converged. The bad news was that the running time on an Intel(R) Core(TM) i7-10,700 CPU @ 2.90GHz Windows PC was 181,643 s, which is approximately 50 h. This precludes similar exercises with a larger model or with a distinctly larger number of draws unless one has a supercomputer at one’s disposal.

The results can best be summarized in boxplots for each variable and each point of time, showing measures of tendency and variation and the outliers. Figures 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 (in the Appendix) give examples of such boxplots for some control and target variables and the value of the objective function as a measure of disutility or cost of the simulation run concerned. We chose some cases which can reveal preliminary results about the effect of the three algorithms. In the boxplots for each variable, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles of the variable over all 100 runs for the active-learning (AL), the passive-learning (OLF), and the certainty equivalence (CE) strategies. The whiskers extend to the most extreme data points within the interquartile range; the outliers are plotted individually using the “ + ” symbol.

At first glance, one result is the similarity, among the three strategies, of the values of the objective function despite some variation in the control and target variables. In the two first time periods, the active-learning strategy “probes” a little by a relatively low budget surplus to check the effects of a more active (less expansionary) fiscal policy. Soon it learns that this does not have a recognizable effect on its objective function, which, hence, remains closer to the median position. The larger variation in the values of the objective function with more outliers (cases with higher values of the objective function) in the last period is due to the well-known effect of a policy neglecting future developments in the last period of an optimization with finite time horizon and no terminal or scrap value; this is common to the three strategies under consideration. What is unexpected is the result that the most ambitious AL strategy, which looks explicitly at the dual effect of the controls, is not unambiguously the best one and may be dominated by the OLF strategy. As there is not much to learn about the effects of fiscal policy on the objective function, probing does not seem to be worthwhile in this experiment, and passive learning may be sufficient for an acceptable outcome of fiscal policy, at least in the model under consideration.

Figure 5 shows the values of the three components of the objective function, deterministic (J_D), cautionary (J_C), and probing terms (J_P), and the total objective function (J_d). The deterministic component comes from the deviations of the optimal time paths from their target values in the underlying deterministic optimization part, the cautionary component comes from the attempt to use the instrument in a tentative way to balance the costs of the controls with the costs of the target variables, and the probing component comes from the attempt to learn, during the earlier periods of time, about the model and its uncertainties to improve the performance in later periods.

Fig. 5

Objective function values; J_D – Deterministic term, J_C – Cautionary term, J_P – Probing terms, J_d – Total objective function, u_t=1 – Control variable

The cautionary component contributes most to the values of the total objective function J_d. The contribution of the deterministic component is much smaller but still substantial. In contrast, the probing component is responsible for by far the smallest part of the total cost. Thus, there is not much effort to be invested in the probing activity; in other words, the dual effect is nearly non-existent. A similar (but weaker) outcome than this was obtained by Blueschke-Nikolaeva et al. (2012) for a different model with an equally long time horizon. Interestingly, the values of all components and, hence the total value of the objective function as well do not depend on the values of the control variable. Both of these results can be interpreted to mean that there is not much influence of the instruments on the outcome of the economy. The reason for this is the feature of our model where there is a trade-off between the equally weighted target variables inflation rate and output gap and their rate of substitution is close to 1. Different actions increase the attainment of one goal at the expense of the other. The cost of the control action prevents the attainment of one goal only instead of a balanced mix of both. Thus, we have a kind of policy indifference, similar to the policy ineffectiveness in Monetarist and New Classical models but for reasons that differ.

6 Concluding remarks

In this paper, we discussed different forms of uncertainty for economic policy analysis and design and briefly reviewed the algorithms OPTCON1 for open-loop, OPTCON2 for open-loop feedback (passive learning), and OPTCON3 for dual control with active learning. We used our computer programs to implement approximately optimal policies according to the three OPTCON algorithms. The results from calculating these policies for a simple macroeconometric model for Slovenia served to test the OPTCON algorithms and compare the solutions of the stochastic optimal control problems. We found that the open-loop optimal solution is nearly identical to the deterministic one, at least in a model that does not contain too many nonlinearities. Another result points towards a trade-off between using the most sophisticated AL solution and the other variants: The AL solution is not necessarily (as we had expected) superior to the simpler solutions but uses vastly more input and time to calculate. Therefore, one should, depending on the properties of the model used, carefully deliberate whether the additional effort required for AL is worthwhile in a particular case. Open-loop feedback, open-loop, or even deterministic optimization may be recommendable, as the latter can be relatively easily applied to larger and better models in contrast to the extremely small model we had to use here.

We pointed out some weaknesses in our analysis and, hence, problems for further research. These include the question of model uncertainty, which can be dealt with in sensitivity analyses with respect to entire models and experimenting with different objective functions. Optimizations with rolling re-specification of the model, as is common practice when forecasts are made with econometric models, are a possibility, but this would require a larger economic research institute to do this and is much more expensive. These institutes usually build much more elaborate economic models than presented here, raising the question of a trade-off between costly modelling and high working, computing, and reaction time on the one hand and usually urgent demands for results and solutions for pressing problems by politicians and the public on the other, especially for active-learning control calculations. One question is whether an analysis like the one presented here should be done for a more elaborate model. To assess the influence of uncertainty, this might be a task for further research as the small differences between the policy designs presented here might just be due to the simplicity of the model used. However, unless significantly more research infrastructure is available, it would be unrealistic to do this on a regular basis for actual policy design.

At this point in time, it seems very questionable whether the additional effort to be invested in the optimization procedures taking account of stochastic uncertainty justifies the restriction to a very small model whose specification is necessarily problematic. The really big challenges in practical policy making do not originate from stochastic uncertainty but from uncertainty about the model to be used and from exogenous shocks whose probability distributions are not known or may even be non-existent. Especially the laborious implementation of the AL algorithm, which turned out to deliver worse results than the more straightforward open-loop or even deterministic algorithms, does not recommend itself for use in actual policy advice.

Appendix

See Figures 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

Fig. 6

Boxplot for the control variable in t = 1 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 7

Boxplot for the objective value J in t = 1 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 8

Boxplot for the control variable in t = 2 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 9

Boxplot for the target variable PI_t in t = 2 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 10

Boxplot for the state variable GAP_t in t = 2 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 11

Boxplot for the objective value J in t = 2 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 12

Boxplot for the control variable in t = 48 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 13

Boxplot for the target variable PI_t in t = 48 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 14

Boxplot for the target variable GAP_t in t = 48 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence

Fig. 15

Boxplot for the objective value J in t = 48 based on a Monte Carlo experiment with 100 draws. Solution strategies: AL – Active learning, OLF – Open-loop feedback (Passive Learning), CE – Certainty equivalence