On initial point selection of the steepest descent algorithm for general quadratic functions

Abstract

We prove some new results about the asymptotic behavior of the steepest descent algorithm for general quadratic functions. Some well-known results of this theory are developed and extended to non-convex functions. We propose an efficient strategy for choosing initial points in the algorithm and show that this strategy can dramatically enhance the performance of the method. Furthermore, a modified version of the steepest descent algorithm equipped with a pre-initialization step is introduced. We show that an initial guess near the optimal solution does not necessarily imply fast convergence. We also propose a new approach to investigate the behavior of the method for non-convex quadratic functions. Moreover, some interesting results about the role of initial points in convergence to saddle points are presented. Finally, we investigate the probability of divergence for uniform random initial points.

1 Introduction

Gradient descent method is indeed one of the simple algorithms for solving unconstrained optimization problems. It is the underlying idea in most of machine and deep learning algorithms, and some of its variants like stochastic and mini-batch gradient method constitute the main part of training algorithms which are popular in deep learning area; see [4, 20, 25].

By exploiting gradient information of the objective function, each step of this method provides an estimation of the minimizer by moving along the steepest descent direction. This method was originally proposed by Cauchy in 1847 and then investigated in detail by many researchers. Akaike [1] was the first author to prove theoretical properties of this method applied to strongly convex quadratic functions. He showed that gradient descent method with exact line search (Cauchy steps) takes small nearly orthogonal steps. This phenomenon, which is called zigzagging, also pointed out by Forsythe [12]. Gradient descent method usually behaves quite well in early iterations of the algorithm depending on the initialization point, but it works poorly near a stationary point. Akaike explained this phenomenon by showing that the search space becomes smaller, asymptotically, and finally falls into a two-dimensional space generated by the eigenvectors associated with two extreme eigenvalues.

Gradient descent is basically a first-order method which means that it builds on the first-order derivatives of the objective function and so its performance depends highly on the problem scaling and conditioning. It is in contrast to second-order methods that are faster and less sensitive to scaling and conditioning. We refer interested readers to Akaike [1], Forsythe [12], Nocedal et al. [21], Gonzaga and Schneider [14] and Gonzaga [13] for a clear explanation of the method.

Sum of all these problems and drawbacks made this method less popular for decades in comparison to second-order methods. By expansion of online business over last years, marketers became interested in analyzing and classification of consumer’s data. Everything was fine until that the data growth speed exceeded the ability of hardware to store them. At this time, first-order methods like gradient based algorithms and their variants returned to the scene owing to their abilities to solve large optimization problems with minimal memory requirements. Nowadays, the subject of large-scale optimization is an active field of research.

In an attempt to improve the method, some authors tried to make little changes in the current framework of the method to break its zigzagging pattern. Barzilai and Borwein [2] proposed a new step length with surprisingly good properties. Dai and Liao [8] showed R-linear convergence of it for convex quadratics. This method was extended to general problems by Raydan [23], and investigated by Dai [6], Raydan and Svaiter [24] and Birgin et al. [3]. Many authors also tried to hybridize gradient descent method by some variants of Barzilai and Borwein method; for example, see Asmundis et al. [9, 10], Sun et al. [26], Dai et al. [7], and Huang et al. [16, 17].

A major challenge in non-convex optimization is to design new algorithms with the ability of staying away from saddle points. It is well-known that a careless initialization of gradient descent method provably converges to saddle points [19]. There are some nice results about the behavior of the method in the vicinity of saddle points. Lee et al. [18] showed that gradient descent with constant short step-sizes stays away from strict saddle points almost surely with random initialization. Panageas et al. [22] extended this result to non-isolated critical points. Interested readers can also see [11, 27]. All attempts in this context are concerning to gradient descent method with constant step-size; we do not find anything about other step-size rules.

As we mentioned earlier, gradient descent method is a first-order method and its performance strongly depends on initialization. In this article, we are going to reveal some secrets behind the method, and more importantly, a good strategy of choosing initial points. The results presented in this article, to the best of our knowledge, are completely new.

Here, we investigate gradient descent algorithm with Cauchy step-size—steepest descent method—for solving quadratic problems. This article is presented in two parts with the following innovations.

In the first part, convex quadratic problems are investigated. We present the following results.

• 1. We improve some well-known results of this theory, and also develop them to non-convex quadratics.

• 2. A practical method for choosing a good initial point is proposed. We analyze it theoretically and demonstrate its efficiency by providing some examples.

• 3. A modified version of the steepest descent algorithm equipped with a pre-initial step is proposed.

In the second part, non-convex quadratic problems are investigated. We present the following results.

• 1. We determine a subset of quadratic problems for which independent of the choice of initial point, the steepest descent algorithm always diverges.

• 2. We provide some nice results about the probability of escaping from saddle points for a uniform random initialization.

• 3. We show for what choices of initial points the divergence of the algorithm can be guaranteed.

The rest of the paper is organized as follows.

We recall some well-known results about the theory of the steepest descent method in Sect. 2. The asymptotic behavior of the method for general quadratic functions are investigated in Sect. 3. In Sect. 4, we propose the idea of choosing suitable initial points and analyze it both theoretically and numerically. In Sect. 5, we present some numerical experiments. Finally, conclusions and discussions are given in Sect. 6.

2 A brief review

Gradient descent algorithm is an iterative routine originally designed by Cauchy for solving unconstrained optimization problems. Considering the problem

$$\begin{aligned} \min _{x\in \mathbb {R}^n} f(x), \end{aligned}$$

it generates a sequence of iterations starting from an initial point $x_0\in \mathbb {R}^n$ by

$$\begin{aligned} x_{k+1}=x_k-\alpha _k\nabla f(x_k), \end{aligned}$$

(1)

where $\nabla f(x_k)$ is the gradient of the objective function in $x_k$. The step-size $\alpha _k$ is an important term in this equation and determines the type of the method. Gradient descent algorithm with constant step-size ($\alpha _k$ is fixed during the iterations) is the main part of most algorithms in non-smooth and convex optimization [5, 19]. There is another well-known version of this algorithm, called steepest descent method, working with Cauchy step-size as follow

$$\begin{aligned} \alpha _k = \arg \min _{\alpha } f(x_k-\alpha \nabla f(x_k)). \end{aligned}$$

(2)

Here, we pay attention to quadratic objective functions. Considering

$$\begin{aligned} f(x)=\frac{1}{2}x^tAx-b^tx+c, \end{aligned}$$

(3)

where A is a symmetric matrix, and c and b are arbitrary vectors in $\mathbb {R}^n$, the general framework (1) takes the values $g_k:=\nabla f(x_k)=Ax_k-b$, and the Cauchy step-size (2) as

$$\begin{aligned} \alpha _k = \frac{g_k^tg_k}{g_k^tAg_k}. \end{aligned}$$

(4)

First-order necessary conditions imply that $x^*$ is a stationary point of (3) if it solves the system of linear equation $Ax^*=b$. Furthermore, it is a unique optimal point of (3) if A is positive definite.

Here, we assume that (3) has a stationary point $x^*$, so we can easily rewrite it as

$$\begin{aligned} f(x)= \frac{1}{2}(x-x^*)^tA(x-x^*)+f(x^*), \end{aligned}$$

which is a convenient form for the purpose of analysis. By a simple change of variable ($z=x-x^*$) and a constant elimination, we reach the function

$$\begin{aligned} {\bar{f}}(z)=\frac{1}{2}z^tAz \end{aligned}$$

(5)

with $z^*=0$ as its stationary point.

We further diagonalize A by setting $z=Mx$ where M has orthonormal eigenvectors of A as its columns. The new problem is related to the old one by

$$\begin{aligned} f(x)={\bar{f}}(Mx)=\frac{1}{2}x^t\varLambda x, \end{aligned}$$

(6)

where $\varLambda$ is a diagonal matrix whose elements are eigenvalues of A. It is easy to see that steepest descent iterations for minimizing ${\bar{f}}(z)$ from the initial point $z_0=Mx_0$ and f(x) from the initial point $x_0$ are related to each other by $z_k=Mx_k$.

We throughout this paper concentrate on minimizing (6) instead of (3). The following information are at hand at kth iteration of the steepest descent algorithm.

$$\begin{aligned} \nonumber x_{k+1}&= x_k-\alpha _k\varLambda x_k=(I-\alpha _k\varLambda )x_k, \\ g_{k+1}&=\varLambda x_{k+1}=(I-\alpha _k\varLambda )g_k\;\text {and} \\ \nonumber \mu _k&:=\frac{1}{\alpha _k}=\frac{g_k^t\varLambda g_k}{g_k^tg_k}, \end{aligned}$$

(7)

where I is the identity matrix. Furthermore,

$$\begin{aligned} {\bar{g}}_k=Mg_k,\;\; {\bar{g}}_k^t{\bar{g}}_k=g_k^tg_k,\;\; {\bar{g}}_k^tA^i{\bar{g}}_k=g_k^t\varLambda ^i g_k,\;\; and \; {\bar{\alpha }}_k=\alpha _k, \end{aligned}$$

(8)

where ${\bar{g}}_k:=\nabla {\bar{f}}(z_k)$, and i is an arbitrary positive integer.

We highlight the following remark about (5) and (6).

Remark 1

Assume that

$$\begin{aligned} {\bar{g}}_k=\sum _{i=1}^{n}\eta _k^iv_i \end{aligned}$$

is the eigenvector representation of ${\bar{g}}_k$, where $v_i$ ($i=1,\dots ,n$) are normalized eigenvectors of A, we have

$$\begin{aligned} g_k= M^t{\bar{g}}_k=\sum _{i=1}^{n}\eta _k^ie_i, \end{aligned}$$

where $e_i$ is the ith row of the identity matrix. Briefly speaking, ith component of $g_k$ is exactly $\eta _k^i$.

Throughout this paper, we consider the following assumptions regarding (6). They can be extended to original problem (5) by using (8) and Remark 1.

• 1. All components of the initial gradient vector are non-zero; namely,

  $$\begin{aligned} g_0^i:=g_i(x_0)\ne 0, \end{aligned}$$

  for $i=1,\ldots ,n$.

  It is clear from (7) that a zero component remains zero at all iterations. This assumption, in view of Remark 1, means that $\eta _0^i\ne 0$, for $i=1,\ldots ,n$.

• 2. $\varLambda$ has distinct non-zero eigenvalues arranged by

  $$\begin{aligned} \lambda _1< \lambda _2<\ldots <\lambda _n. \end{aligned}$$

  Equality (7) indicates that gradient vector components corresponding to two identical eigenvalues have the same rate of variations during the iterations. Furthermore, a zero eigenvalue can be removed because the steepest descent algorithm is blind in the sense that gradient vector components corresponding to zero eigenvalues do not change in the course of iterations. Therefore, we can remove multiple and zero eigenvalues for the purpose of analysis without losing of generality. We also assume that $|\lambda _1|\le \lambda _n$.

• 3. $\mu _k$ is non-zero at all iterations.

  If $\mu _k=0$, then (2) indicates that a best value for $\alpha _k$ is infinity which means that the problem is unbounded from below. The steepest descent algorithm is terminated here. The algorithm can start again with a different initial point hoping to find a local minima—this assumption is always satisfied for convex quadratics since $\lambda _1\le \mu _k\le \lambda _n$. In fact, $\mu _k$ is non-zero almost surely for a random initialization. Assuming that $\mu _{k}=0$, some tedious manipulation yields that the solution set of this equation is the level set of a polynomial function of $g_0$ with the degree $2(2^{k+1}-1)$, and clearly with a zero probability a random point lies in this set.

Remark 2

Assumptions 2 and 3 imply that both $g_k^1$ and $g_k^n$ are non-zero for all k. We prove it by induction.

It is clearly established for $k=0$. Assuming it holds for an arbitrary k; we will prove it for $k + 1$. First, we claim that

$$\begin{aligned} \mu _k= \frac{\sum _{i=1}^{n}\lambda _i(g_k^i)^2}{\sum _{i=1}^{n}(g_k^i)^2}\ne \lambda _1\;and\;\lambda _n. \end{aligned}$$

Because, an equality implies

$$\begin{aligned} \sum _{i=1}^{n}(\lambda _i-\lambda _1)(g_k^i)^2=0,\;or\;\sum _{i=1}^{n}(\lambda _i-\lambda _n)(g_k^i)^2=0, \end{aligned}$$

which means $g_k^n=0$ or $g_k^1=0$; a contradiction with the induction hypothesis. As a consequence, $g_{k+1}^1$ and $g_{k+1}^n$ are both non-zero in view of (7), the induction hypothesis and the fact that $\mu _k\ne \lambda _1\;and\;\lambda _n$.

We now intend to review some important results about the behavior of the steepest descent algorithm for quadratic functions. These results were first observed and established by Akaike [1] and then further investigated by Forsythe [12]. A simplified version of them can be found in Gonzaga and Schneider [14], and Nocedal et al. [21].

The following sequence plays an important role in this theory:

$$\begin{aligned} w_{k+1}=(\mu _k I-\varLambda )w_k,\;\;and \;w_0:=g_0. \end{aligned}$$

(9)

It is easy to see using (7) that $w_{k+1}=g_{k+1}\prod _{i=0}^{k}\mu _i$.

In the following lemma, we recall an important result of the theory and sketch the proof to emphasize on its validity for general quadratics.

Lemma 1

For the sequence $w_k$ generated by steepest descent iterations, we have

$$\begin{aligned} w_{k+2}^tw_k=||w_{k+2}||||w_k||\cos \psi _k=||w_{k+1}||^2, \end{aligned}$$

(10)

where $||\cdot ||$ is the Euclidean norm, and $\psi _k$ is the angle between $w_{k+2}$ and $w_k$.

Proof

We start by the definition of $w_k$ and have

$$\begin{aligned} w_{k+2}^tw_k-||w_{k+1}||^2&= w_k^t(\mu _{k+1}I-\varLambda )(\mu _kI-\varLambda )w_k-w_k^t(\mu _kI-\varLambda )^2w_k, \\&= w_k^t(\mu _kI-\varLambda )(\mu _{k+1}I-\mu _kI)w_k , \\&= (\mu _{k+1}-\mu _k)w_k^t(\mu _kI-\varLambda )w_k,\\&=(\mu _{k+1}I-\mu _kI)w_{k+1}^tw_k,\\&=0. \end{aligned}$$

The last equality is a straightforward result of (2). $\square$

We note that Lemma 1 is valid for non-convex quadratics. Moreover, (10) implies that $\cos \psi _k$ is always positive.

Many interesting results about the behavior of the steepest descent algorithm are derived from Lemma 1.

Theorem 1

Suppose that assumptions 1–3 hold and that the sequence $x_k$ is generated by applying steepest descent algorithm to (6). Then, there exists a real non-zero constant c such that

• i. $\lim _{k\rightarrow \infty }\psi _k = 0$; Consequently, $\lim _{k\rightarrow \infty }\cos \psi _k =1.$

• ii.
  $$\begin{aligned} \lim _{k\rightarrow \infty }\frac{(g_{2k}^i)^2}{||g_{2k}||^2}= \left\{ \begin{array}{ll} \frac{1}{1+c^2},\quad i=1; \\ 0, \quad i=2,\ldots ,n-1; \\ \frac{c^2}{1+c^2},\quad i=n. \end{array} \right. \end{aligned}$$
• iii.
  $$\begin{aligned} \lim _{k\rightarrow \infty }\frac{(g_{2k+1}^i)^2}{||g_{2k+1}||^2}= \left\{ \begin{array}{ll} \frac{c^2}{1+c^2},\quad i=1; \\ 0, \quad i=2,\ldots ,n-1; \\ \frac{1}{1+c^2},\quad i=n. \end{array} \right. \end{aligned}$$

• iv. $\lim _{k\rightarrow \infty }\mu _{2k} ={\hat{\mu }}$, $\lim _{k\rightarrow \infty }\mu _{2k+1} = {\check{\mu }}$, and ${\hat{\mu }}+{\check{\mu }}=\lambda _1+\lambda _n$.

• v.
  $$\begin{aligned} \lim _{k\rightarrow \infty }\frac{g_{k}^j}{g_k^i}=0,\;\text {for}\;j=2,\ldots ,n-1\;\text {,and}\;i=1\;\text {and}\;n. \end{aligned}$$

Proof

i. Lemma 1 indicates that the sequence $||w_{k+1}||/||w_k||$ is nondecreasing; Moreover, it is bounded from above because

$$\begin{aligned} ||w_{k+1}||\le ||\mu _kI-\varLambda ||w_k||\le (\lambda _n-\lambda _1)||w_k||. \end{aligned}$$

The rest of the proof is similar to part (ii) of Theorem 3 in [14].

ii-iii. The proof of these items for a convex quadratic function can be found in Akaike [1], Forsythe [12], Gonzaga and Schneider [14] (Theorems 3 and 4), and Nocedal et al. [21].

Now, assume that A has at least a negative and a positive eigenvalue. The new matrix ${\bar{A}}=A+mI_{n\times n}$ with $m>-\lambda _1$ is a positive definite matrix. Consider steepest descent iterations for problems

$$\begin{aligned} \min \frac{1}{2} x^tAx,\;\;\text {with a given initial point}\; x_0, \end{aligned}$$

and

$$\begin{aligned} \min \frac{1}{2} {\bar{x}}^t{\bar{A}}{\bar{x}},\;\;\text {with}\;{\bar{x}}_0\;\text {as the solution of}\;{\bar{A}}{\bar{x}}_0=Ax_0. \end{aligned}$$

(11)

We proceed by induction on k to prove ${\bar{\mu }}_k=\mu _k+m$ and ${\bar{w}}_k=w_k$.

It is easy to see using (11) that ${\bar{w}}_0={\bar{g}}_0=g_0=w_0$. Assuming ${\bar{w}}_k=w_k$, we have

$$\begin{aligned} {\bar{\mu }}_{k}=\frac{{\bar{w}}_k^t{\bar{A}}{\bar{w}}_k}{{\bar{w}}_k^t{\bar{w}}_k}=\frac{{\bar{w}}_k^t(A+mI){\bar{w}}_k}{{\bar{w}}_k^t{\bar{w}}_k}=\frac{w_k^tAw_k}{w_k^tw_k}+m=\mu _k +m, \end{aligned}$$

and consequently

$$\begin{aligned} {\bar{w}}_{k+1}=({\bar{\mu }}_kI-{\bar{A}}){\bar{w}}_k=(\mu _kI+mI-A-mI)w_k=w_{k+1}. \end{aligned}$$

We now apply this argument again with ${\bar{w}}_k$ and $w_k$ replaced by ${\bar{w}}_{k+1}$ and $w_{k+1}$ to obtain ${\bar{\mu }}_{k+1}=\mu _{k+1}+m$. Hence, the proof of the induction step is completed.

As a result, we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{(g_{k}^i)^2}{||g_{k}||^2}=\lim _{k\rightarrow \infty }\frac{(w_{k}^i)^2}{||w_{k}||^2}=\lim _{k\rightarrow \infty }\frac{({\bar{w}}_{k}^i)^2}{||{\bar{w}}_{k}||^2}=\lim _{k\rightarrow \infty }\frac{({\bar{g}}_{k}^i)^2}{||{\bar{g}}_{k}||^2}. \end{aligned}$$

Now, the proof of items ii. and iii. for non-convex quadratic functions is completed by using the above equality and the fact that these items are valid for convex quadratics.

iv. It is a direct consequence of items ii. and iii.; see [21].

v. It is easy to see that

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{g_{k}^j}{g_k^i}=\lim _{k\rightarrow \infty }\frac{g_{k}^j}{||g_{k}||}\frac{||g_{k}||}{g_k^i}; \end{aligned}$$

thus, the proof is completed by using ii. and iii.. $\square$

Although it is also possible to prove ii. and iii. for general quadratics by following their proof for convex quadratics, our approach in the proof of Theorem 1 provides a method to investigate the behavior of the steepest descent method for non-convex quadratics using the existing results for convex quadratics.

3 The asymptotic analysis

The asymptotic behaviour of the steepest descent algorithm is highly dependent on the final value of $\mu _k\mu _{k+1}$. In the following lemma, we provide a new bound for this value. It is a better bound than the one proposed by Gonzaga and Schneider (Theorem 1 in [14]), and more importantly, is valid for general quadratics.

Lemma 2

Assume that assumptions 1–3 hold. Then, we have

$$\begin{aligned} \frac{\lambda _1\lambda _n + (\lambda _1+\lambda _n)\lambda _i-\lambda _i^2}{2}\le {\check{\mu }}{\hat{\mu }}\le \frac{(\lambda _1+\lambda _n)^2}{4}, \end{aligned}$$

(12)

for $i=1,\ldots ,n$.

Proof

It is easy to see by part iv. of Theorem 1 that ${\hat{\mu }}$ and ${\check{\mu }}$ are feasible solutions of the optimization problem

$$\begin{aligned} \min (\max )\;\; xy\quad \text {subject to}\quad x+y=\lambda _1+\lambda _n,\;\lambda _1\le x,y\le \lambda _n. \end{aligned}$$

This problem has a maximum point in $x=y=(\lambda _1+\lambda _n)/2$ and two minimum points in $x=\lambda _1$ and $y=\lambda _n$, and $x=\lambda _n$ and $y=\lambda _1$. In other words,

$$\begin{aligned} \lambda _1\lambda _n\le {\check{\mu }}{\hat{\mu }}\le \frac{(\lambda _1+\lambda _n)^2}{4}, \end{aligned}$$

(13)

so the proof of the right-hand side of (12) is completed.

Furthermore, the lower bound in (13) and item iv. of Theorem 1 imply that

$$\begin{aligned} R:=\lim _{k\rightarrow \infty }\bigg |\frac{g_k^jg_{k+2}^i}{g_{k+2}^jg_k^i}\bigg |=\lim _{k\rightarrow \infty }\frac{\big |(\mu _{k+1}-\lambda _i)(\mu _k-\lambda _i)\big |}{\big |(\mu _{k+1}-\lambda _j)(\mu _k-\lambda _j)\big |}=\frac{\big |({\hat{\mu }}-\lambda _i)({\check{\mu }}-\lambda _i)\big |}{{\hat{\mu }}{\check{\mu }}-\lambda _1\lambda _n}, \end{aligned}$$

where $i=2,\ldots ,n-1$ and $j=1$ or $n(n>2)$. The denominator of the last equality is a result of

$$\begin{aligned} \lim _{k\rightarrow \infty }|(\mu _{k+1}-\lambda _j)(\mu _k-\lambda _j)|&=|{\hat{\mu }}-\lambda _j)({\check{\mu }}-\lambda _j)| \\ {\mathop {\Longrightarrow }\limits ^{\text {{(item iv.)}}}}&=|{\check{\mu }}{\hat{\mu }}-(\lambda _1+\lambda _n)\lambda _j+\lambda _j^2|\\ {\mathop {\Longrightarrow }\limits ^{\text {{ (j=1,n)}}}}&={\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n. \end{aligned}$$

Assuming $R>1$, there exist an integer $k_0$ and a small value $\epsilon _0>0$ such that

$$\begin{aligned} 1<R-\epsilon _0\le \bigg |\frac{g_k^jg_{k+2}^i}{g_{k+2}^jg_k^i}\bigg |\Longrightarrow (R-\epsilon _0)\bigg |\frac{g_k^i}{g_k^j}\bigg |\le \bigg |\frac{g_{k+2}^i}{g_{k+2}^j}\bigg |, \end{aligned}$$

for all $k\ge k_0$; this implies

$$\begin{aligned} \bigg |\frac{g_{k}^i}{g_{k}^j}\bigg |\longrightarrow \infty , \end{aligned}$$

which is a contradiction in view of part v. of Theorem 1. Therefore, $R\le 1$ and consequently

$$\begin{aligned} \big |{\hat{\mu }}{\check{\mu }}-(\lambda _1+\lambda _n)\lambda _i+\lambda _i^2\big |\le {\hat{\mu }}{\check{\mu }}-\lambda _1\lambda _n. \end{aligned}$$

The left-hand side of (12) is a direct consequence of the above inequality. Finally, we note that if $n=2$, the inequality (12) converts to (13), and thus, the proof is completed. $\square$

Gradient vector components change during the steepest descent iterations according to the equality (7). To investigate the asymptotic behavior of the gradient vector, let us assume for a moment that ${\check{\mu }}{\hat{\mu }}\ne 0$ and define

$$\begin{aligned} Z(\theta ) := \bigg |(1-\frac{1}{{\hat{\mu }}}\theta )(1-\frac{1}{{\check{\mu }}}\theta )\bigg |, \end{aligned}$$

where $\theta \in [\lambda _1,\lambda _n]$. An easy computation shows that for $i=1,\ldots ,n$,

$$\begin{aligned}&Z_i:=Z(\lambda _i)=\bigg |(1-\frac{1}{{\hat{\mu }}}\lambda _i)(1-\frac{1}{{\check{\mu }}}\lambda _i)\bigg |=\lim _{k\rightarrow \infty }\big |(1-\alpha _{k+1}\lambda _i)(1-\alpha _k\lambda _i)\big |\nonumber \\&\quad =\lim _{k\rightarrow \infty }\bigg |\frac{g_{k+2}^i}{g_k^i}\bigg |. \end{aligned}$$

(14)

Furthermore,

$$\begin{aligned} Z_1=Z_n= \big |1-\frac{\lambda _1\lambda _n}{{\hat{\mu }}{\check{\mu }}}\big |,\;\;Z({\hat{\mu }})=Z({\check{\mu }})=0,\;\;\text {and}\;Z(0)=Z(\lambda _1+\lambda _n)=1. \end{aligned}$$

(15)

It is obvious that $Z_i$ determines the asymptotic rate of change in gradient vector components for two subsequent even or odd iterations. An argument similar to the one used in the last part of the proof of Lemma 2 (nothing that $R=Z_i/Z_j$) indicates $Z_i\le Z_j$, for $i=2,\ldots ,n-1$ and $j=1,n$. It means that the asymptotic rate of change in $g_k^1$(or $g_k^n$) always dominates the one in $g_k^i$.

In the rest of this section, we intend to investigate (14) for two cases of convex and non-convex quadratics.

3.1 Convex quadratic functions

It is easy to see that ${\check{\mu }}{\hat{\mu }}$ is always non-zero for a convex quadratic function and so (14) is well-defined. We have depicted $Z(\theta )$ for a convex quadratic function in Fig. 1. This function has obviously a local maximum in

$$\begin{aligned} \theta _{max}:=\frac{{\check{\mu }}+{\hat{\mu }}}{2}=\frac{\lambda _1+\lambda _n}{2}. \end{aligned}$$

Fig. 1

$Z(\theta )$ for a convex quadratic function

From this figure and our discussion after the proof of Lemma 2, we find that the smaller is the value of $Z(\lambda _1)=Z(\lambda _n)=Z_1$, the better is the asymptotic rate of convergence.

Let us assume for a moment that ${\hat{\mu }}$ and ${\check{\mu }}$ are near $\lambda _1$ and $\lambda _n$, respectively. It is equivalent in view of part iv. of Theorem 1 to say that ${\hat{\mu }}{\check{\mu }}$ is near $\lambda _1\lambda _n$. As a consequence, $Z_1$ approaches zero accelerating the asymptotic rate of convergence. In other words, a desirable value for ${\hat{\mu }}{\check{\mu }}$ is $\lambda _1\lambda _n$.

Unfortunately, ${\hat{\mu }}{\check{\mu }}$ is bounded away from $\lambda _1\lambda _n$ in view of (12). In other words, if A is an ill-condition matrix with some eigenvalues near $\theta _{max}$, the left-hand side of (12) approaches its maximum value, and ${\hat{\mu }}{\check{\mu }}$ stays more away from its ideal value independent of the choice of initial point. The performance of the method is disappointing for such problems.

3.2 Non-convex quadratic functions

We now suppose that A has at least a negative and a positive eigenvalue. As a consequence, using assumptions 1–3, the objective function (3) has a unique stationary point which is clearly a saddle point.

Figure 2 shows the graph of $Z(\theta )$ for a non-convex quadratic function—we here consider that ${\hat{\mu }}{\check{\mu }}<0$ to show all the possible scenarios that can happen for a non-convex function. We have the following observations:

Fig. 2

$Z(\theta )$ for a non-convex quadratic function

• 1. The steepest descent algorithm converges if $Z_n(=Z_1)<1$. In view of Fig. 2, it means that either

  $$\begin{aligned} \lambda _1 \in (\theta _3,0)\;\;\text {or}\;\;\lambda _n\in (\lambda _1+\lambda _n,\theta _4), \end{aligned}$$

  where $\theta _3$ and $\theta _4$ are the roots of

  $$\begin{aligned} \theta ^2-(\lambda _1+\lambda _n)\theta +2{\hat{\mu }}{\check{\mu }}=0 \end{aligned}$$

  satisfying $Z(\theta _3)=Z(\theta _4)=1$; we have marked these intervals by (C). The following lemma provides a practical criterion.

Lemma 3

Assume that assumptions 1–3 hold. The steepest descent algorithm converges to a saddle point if

$$\begin{aligned} {\check{\mu }}{\hat{\mu }}<\frac{\lambda _1\lambda _n}{2}. \end{aligned}$$

(16)

Proof

Assuming (16) holds, we have ${\check{\mu }}{\hat{\mu }}<0$ and therefore

$$\begin{aligned} Z_n=Z_1=\frac{{\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n}{-{\check{\mu }}{\hat{\mu }}}< 1. \end{aligned}$$

Consequently, the definition of $Z_i$ in (14) implies that both $g_k^1$ and $g_k^n$ converge to zero. The proof is completed using the fact that $Z_i\le Z_1$, for $i=1,\ldots ,n$. $\square$

• 2. The steepest descent algorithm diverges to infinity if $Z_i>1$, for some $i=1,\ldots ,n$. In view of Fig. 2, it means that $\lambda _i$ belongs to some intervals marked by (D). The following lemma provides a practical criterion.

Lemma 4

Assume that assumptions 1–3 hold. The steepest descent algorithm diverges to infinity if

$$\begin{aligned} {\check{\mu }}{\hat{\mu }}>\frac{\lambda _1\lambda _n}{2}. \end{aligned}$$

(17)

Proof

If ${\check{\mu }}{\hat{\mu }}<0$, we have by using (17) that

$$\begin{aligned} Z_n=Z_1=\frac{{\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n}{-{\check{\mu }}{\hat{\mu }}}> 1. \end{aligned}$$

Thus, the definition of $Z_i$ in (14) implies that both $g_k^1$ and $g_k^n$ diverges to infinity. If ${\check{\mu }}{\hat{\mu }}>0$, we have obviously

$$\begin{aligned} Z_1=Z_n= 1-\frac{\lambda _1\lambda _n}{{\hat{\mu }}{\check{\mu }}}>1; \end{aligned}$$

the rest of the proof runs as before. If ${\check{\mu }}{\hat{\mu }}=0$, one of the step-lengths $\alpha _k$ or $\alpha _{k+1}$ should inevitably approach infinity. As a consequence, Remark 2 and equality (7) imply that the method diverges to infinity. Hence, the proof is completed. $\square$

We have the following observations in view of Remark 2:

• If there exist some $\lambda _i\in (0,\lambda _1+\lambda _n)$, then the method diverges to infinity independent of the choice of the initial point; in fact, it is easy to see by investigating the graph of $Z(\theta )$ that $Z(\lambda _1)=Z(\lambda _n)>1$ whenever there are some $\lambda _i\in (0,\lambda _1+\lambda _n)$ and therefore (17) is always held. Here, we have implicity assumed that $g_k^i\ne 0$, for all k—a similar argument as the one used after the Assumption 3 implies that $g_k^i\ne 0$ almost surely with a random initialization ($g_k^i=0$ if and only if $\mu _{k-1}=\lambda _i$).

Example 1

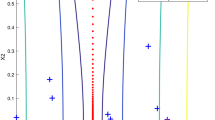
Consider the problem (3) with A a diagonal matrix with elements $(a_{11},a_{22},a_{33})=(-0.5 , \lambda _2 , 3)$ and $b=c=0$. We run the steepest descent algorithm starting from $x_0=10^{-6}(0.1606,0.0954,0.0897)$; it is so close to the stationary point. In Fig. 3, we have depicted the graph of $Z(\theta )$, in the logarithmic scale, as a function of $\theta =\lambda _2$. This figure indicates that for $\lambda _2\in (0,\lambda _1+\lambda _3)=(0,2.5)$, $Z(\lambda _2)$ is greater than one and, as a result of our analysis, the method diverges; see Fig. 4. Furthermore, Fig. 3 shows that $Z_2$ is always dominated by $Z_1$ and its variation does not follow any specific rule. These figures also show that the algorithm converges for $\lambda _2\in (2.78,3)$.

• The behavior of the steepest descent algorithm in the case of ${\check{\mu }}{\hat{\mu }}=\lambda _1\lambda _n/2$ needs careful investigation—it is the case only happen for non-convex quadratics. We show in follow that the method diverges if $n=2$.

  For two dimensional problems, there always exists a constant c such that $g_{k+2} = cg_k$. In other words, it is clear from (2) that both $g_k$ and $g_{k+2}$ are orthogonal to $g_{k+1}$ and therefore they should be inevitably parallel (since $n=2$). As a consequence,

  $$\begin{aligned} \mu _{k+2}=\frac{g_{k+2}^t\varLambda g_{k+2}}{g_{k+2}^tg_{k+2}}=\frac{g_{k}^t\varLambda g_{k}}{g_{k}^tg_{k}} =\mu _k \end{aligned}$$

  (18)

  and

  $$\begin{aligned} \mu _{k+2}\mu _{k+1}= \mu _{k+1}\mu _{k}=\ldots =\mu _0\mu _1, \end{aligned}$$

  for all k. Taking limit implies ${\check{\mu }}{\hat{\mu }}=\mu _k\mu _{k+1}=\mu _0\mu _{1}$. Again, we have by using (18) that

  $$\begin{aligned} \mu _{k+2}+\mu _{k+1}=\mu _{k+1}+\mu _{k}=\ldots =\mu _{0}+\mu _{1}, \end{aligned}$$

  which implies

  $$\begin{aligned} \mu _k+\mu _{k+1}=\mu _{0}+\mu _{1}={\check{\mu }}+{\hat{\mu }}=\lambda _1+\lambda _n. \end{aligned}$$

  Therefore, by the part iv. of Theorem 1,

  $$\begin{aligned} g_{k+2}=(1 - \frac{1}{\mu _{k+1}}\varLambda )(1 - \frac{1}{\mu _{k}}\varLambda )g_k=-I_{2\times 2}g_k=-g_k, \end{aligned}$$

  where the last equality is a result of the assumption ${\check{\mu }}{\hat{\mu }}=\lambda _1\lambda _n/2$. In other words, the gradient vector alternates between $\pm g_0$ and $\pm g_1$ without convergence. As a consequence, if assumptions 1–3 hold, then ${\check{\mu }}{\hat{\mu }}\ge \lambda _1\lambda _n/2$ is a sufficient and necessary condition for divergence when $n = 2$.

Fig. 3

The graph of $Z(\theta )$ for $\theta =\lambda _2$

Fig. 4

The graph of ||g|| as a function of $\lambda _2$

4 Initial point selection strategy

The choice of initial point is an important practical issue with a significant effect on the performance of the steepest descent algorithm. Our analysis of the previous section shows that

• steepest descent algorithm has generally a linear rate of convergence for a convex quadratic function. Its asymptotic rate of convergence is $Z_1$ according to (14), and a value of ${\check{\mu }}{\hat{\mu }}$ as close as possible to $\lambda _1\lambda _n$ increases the speed of convergence. The bound in (12) also indicates that a better rate of convergence is generally impossible for this algorithm;

• the behavior of the method for a non-convex quadratic function strongly depends on the value of ${\check{\mu }}{\hat{\mu }}$, and the distribution of eigenvalues between $\lambda _1$ and $\lambda _n$.

We here intend to introduce a new bound for ${\check{\mu }}{\hat{\mu }}$ which is valid for both convex and non-convex quadratic functions. This bound, in contrast to the one proposed in Lemma 2, shows the effect of the initial point on the final value of this parameter.

Theorem 2

Suppose that assumptions 1–3 hold. Then, for an arbitrary integer i,

$$\begin{aligned} {\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n= \frac{||w_{i+1}||^2}{L_i||w_i||^2}, \end{aligned}$$

(19)

where

$$\begin{aligned} L_i:=\lim _{k\rightarrow \infty }\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}, \end{aligned}$$

(20)

Proof

By Lemma 1 and the definition of $w_k$ in (9), we have

$$\begin{aligned} \frac{||w_{k+1}||}{||w_k||}=\cos \psi _k\frac{||w_{k+2}||}{||w_{k+1}||}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{||g_{k+1}|||\prod _{i=0}^{k}\mu _i|}{||g_k|||\prod _{i=0}^{k-1}\mu _i|}=\cos \psi _k\frac{||g_{k+2}|||\prod _{i=0}^{k+1}\mu _i|}{||g_{k+1}|||\prod _{i=0}^{k}\mu _i|}. \end{aligned}$$

Consequently,

$$\begin{aligned} \frac{||g_{k+1}|||\mu _k|}{||g_k||}=\cos \psi _k\frac{||g_{k+2}|||\mu _{k+1}|}{||g_{k+1}||} \end{aligned}$$

(21)

and, by replacing k by $k-1$,

$$\begin{aligned} \frac{||g_{k}|||\mu _{k-1}|}{||g_{k-1}||}=\cos \psi _{k-1}\frac{||g_{k+1}|||\mu _{k}|}{||g_k||}. \end{aligned}$$

(22)

We have by multiplying (21) and (22) by sides that

$$\begin{aligned} \frac{||g_{k+1}|||\mu _{k-1}\mu _k|}{||g_{k-1}||}=\cos \psi _{k-1}\cos \psi _k\frac{||g_{k+2}|||\mu _{k}\mu _{k+1}|}{||g_k||}, \end{aligned}$$

and equivalently

$$\begin{aligned} |\mu _{k}\mu _{k+1}|= \frac{||g_k||||g_{k+1}||}{||g_{k+2}||||g_{k-1}||\cos \psi _{k-1}\cos \psi _k}|\mu _{k-1}\mu _k|. \end{aligned}$$

(23)

Now, a repeated using (23) implies

$$\begin{aligned} |\mu _{k}\mu _{k+1}|= \frac{||g_{k}||||g_{i+1}||}{||g_{k+2}||||g_{i-1}||\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}\cos \psi _{i-1}}|\mu _{i}\mu _{i-1}|, \end{aligned}$$

which is equivalent, using (9) and Lemma 1, to

$$\begin{aligned} |\mu _{k}\mu _{k+1}|&= \frac{||g_{k}||||g_{i+1}||^2(\mu _{i}\mu _{i-1})^2(\prod _{j=0}^{i-2}\mu _j^2)}{||g_{k+2}||||g_{i-1}||||g_{i+1}|||\mu _{i}\mu _{i-1}|(\prod _{j=0}^{i-2}\mu _j^2)M_i}\\&= \frac{||g_{k}||||w_{i+1}||^2}{||g_{k+2}||w_{i+1}^tw_{i-1}\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}}\\&= \frac{||g_{k}||||w_{i+1}||^2}{||g_{k+2}||||w_i||^2\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}}, \end{aligned}$$

where $M_i=\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}\cos \psi _{i-1}$. As a consequence,

$$\begin{aligned} |\mu _{k}\mu _{k+1}|\frac{||g_{k+2}||}{||g_{k}||}=\frac{||w_{i+1}||^2}{||w_i||^2\cos \psi _k\cos ^2\psi _{k-1}\cos ^2\psi _{k-2}\ldots \cos ^2\psi _{i}}. \end{aligned}$$

(24)

On the other hand, (7) and items ii.-iii. of Theorem 1 imply

$$\begin{aligned} \nonumber \lim _{k\rightarrow \infty }(\mu _{k}\mu _{k+1})^2\frac{||g_{k+2}||^2}{||g_{k}||^2}&=\lim _{k\rightarrow \infty }\sum _{i=1}^n(\mu _{k+1}-\lambda _i)^2(\mu _{k}-\lambda _i)^2\frac{(g_k^i)^2}{||g_k||^2}\\ \nonumber&=\lim _{k\rightarrow \infty }\sum _{i=1,n}(\mu _{k+1}-\lambda _i)^2(\mu _{k}-\lambda _i)^2\frac{(g_k^i)^2}{||g_k||^2} \\ \nonumber&=({\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n)^2\lim _{k\rightarrow \infty }\bigg (\frac{(g_k^1)^2}{||g_k||^2}+\frac{(g_k^n)^2}{||g_k||^2}\bigg ) \\&=({\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n)^2. \end{aligned}$$

(25)

The proof is completed by taking limit from both sides of (24), and using (20) and (25). $\square$

We have the following remark about Theorem 2.

Remark 3

Unfortunately, the exact value of $L_i$ is unknown and depends on the problem structure. The only thing that we know is that $\cos \psi _k$ converges to 1 according to part i. of Theorem 1. Therefore, from a practical point of view, it is better to reduce the effect of the first cosine terms in $L_i$ by considering a large value of i. in (19).

We note that $L_i$ is neither zero, for a finite i, nor converging to zero. Assume for a moment that $\cos \psi _j=0$, for some j; then, Lemma 1 implies that $||w_{j+1}||=0$. This deduces using assumption 3 that $g_{j+1}=0$ and so the algorithm terminates. Moreover, if $L_i$ converges to zero, the left-side of (19) goes to infinity—$||w_{k+1}||/||w_k||$ is monotone increasing and upper bounded—it is a contradiction using Lemma 2.

The following lemma indicates that our proposed bound is exact for two dimensional problems.

Lemma 5

Suppose that assumptions 1–3 hold. If $n=2$,

$$\begin{aligned} {\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n= \frac{||w_{i+1}||^2}{||w_i||^2}=\frac{||w_{1}||^2}{||w_0||^2}, \end{aligned}$$

for all i.

Proof

Both $w_i$ and $w_{i+2}$ are orthogonal to $w_{i+1}$ by the definition of $\alpha _k$ in (2). Since $n=2$, they should be inevitably parallel. Therefore, $\cos \psi _i=1$, for all i, and the proof is completed by using (19). $\square$

4.1 Initial point and convex quadratic functions

Here, we use Remark 3 to find a good initial point according to our statements at the beginning of Sect. 4.

We conclude from (19) and the definition of $L_i$ that

$$\begin{aligned} {\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n= \frac{||w_{i+1}||^2}{L_i||w_i||^2}\ge \frac{||w_{i+1}||^2}{||w_i||^2}, \end{aligned}$$

(26)

for a fixed value of i. Now, it is easy to see that the bigger is the value of the right-hand side of (26), the bigger is the value of ${\check{\mu }}{\hat{\mu }}-\lambda _1\lambda _n$. As a consequence, ${\check{\mu }}{\hat{\mu }}$ stays more away from its ideal value destroying the speed of convergence. The following result is the main consequence of our analysis.

Remark 4

A good initial point for minimizing the convex quadratic function (3) by using steepest descent algorithm is the solution of the problem

$$\begin{aligned} \min _{x_0} \phi _i:= \frac{||w_{i+1}||^2}{||w_i||^2}, \end{aligned}$$

(27)

where $i\ge 1$ is a fixed constant. The bigger is the value of i, the tighter is the bound in (26) because $\phi _i$ is an increasing sequence. As a consequence, a good initial point is obtained by solving (27) for a large i.

We now provide some examples with regard to Remark 4. In the following example, we show that choosing an initial point near the optimal solution does not always imply a fast convergence.

Example 2

Consider problem (3) with $b=c=0$, and a diagonal matrix A with elements $(a_{11},a_{22})=(0.0157 , 4)$. The solution of this problem is clearly the zero vector. We run the algorithm two times using initial points $x_0^1=(0.01,0.01)$ and $x_0^2=(0.01,5)$—the algorithm terminates if $||g_k||\le 10^{-20}$. It is clear that $x_0^1$ is closer to optimal point than $x_0^2$. As Table 1 indicates, the value of $\phi _1$ is smaller for $x_0^2$ than $x_0^1$, and so the algorithm is terminated by fewer iterations. Figure 5 shows the detail of iterations.

We now investigate the effect of i and show that it is an important quantity in determining an ideal initial point.

Table 1 Steepest descent’s output for Example 2

Fig. 5

Steepest descent iterations for Example 2

Example 3

Consider problem (3) with $b=c=0$, and

$$\begin{aligned} A=\left( \begin{array}{cccc} 1.81 &{} 2 &{} 3 &{} 4 \\ 2 &{} 5.81 &{} 6 &{} 7 \\ 3 &{} 6 &{} 8.81 &{} 9 \\ 4 &{} 7 &{} 9 &{} 10.81 \\ \end{array} \right) . \end{aligned}$$

The spectrum and the condition number of A are (0.0045, 0.9949, 1.3680, 24.8725) and 5.5088e+03, respectively. We run the algorithm several times using initial points

$$\begin{aligned} x_0^1&= [0.1,0,0.25,5],\;\; x_0^2 = [1,0,0.25,5],\;\;x_0^3 = [1,0,2,5],\\ \;\; x_0^4&= [1,0.5,0,0.1],\;\;x_0^5 = [1,0,0.25,1],\;\text {and}\;\; x_0^6 = [1,0,0.25,0.25]. \end{aligned}$$

Table 2 illustrates the algorithms’ output—the algorithm terminates if $||g_k||\le 10^{-6}$. We denote by Iter the total number of iterations, $Iter_{inf}$ the last iteration number for which $| (\phi _{k}-\phi _{k-1})/\phi _{k-1}|> 10^{-6}$, and $\phi _{inf}$ the value of $\phi _k$ with $k=Iter_{inf}$. We have the following observations using Remark 4.

Table 2 Steepest descents’ output for Example 3

• Columns Iter and $Iter_{inf}$: The number of iterations in column $Iter_{inf}$ is extremely fewer than the one in column Iter.

  It can be seen from part v. of Theorem 1 that $g_k^i$, with i between 2 and $n-1$, converges faster than $g_k^1$ and $g_k^n$ to zero. As a consequence, the gradient vector lies asymptotically in a two-dimensional space generated by eigenvectors associated with two extreme eigenvalues. At this time, the steepest descent method acts similar to what we observed for two-dimensional problems. More precisely, the sequence $\phi _k$ converges and remains fixed at the rest of the iterations, and the algorithm takes so many iterations to decrease $g_k^1$ and $g_k^n$. Nocedal et al. [21] have also reported this situation in the study of the path followed by the iterates. It is the reason of why steepest descent algorithm is so slow.

  We note that unlike the gradient vector which converges if all its components converge to zero, the sequence $\phi _k$ converges only if $g_k$ falls and remains in a two-dimensional subspace of ${\mathbb {R}}^n$.

  Checking column Iter also shows that the optimal strategy for choosing initial points is

  $$\begin{aligned} x_0^5>x_0^6>x_0^3>x_0^4>x_0^2>x_0^1, \end{aligned}$$

  where $a>b$ means that a is preferred to b.

• Column $\phi _1$: The best strategy for choosing initial points by using this column is

  $$\begin{aligned} x_0^3>x_0^1>x_0^2>x_0^4>x_0^5>x_0^6. \end{aligned}$$

  Although it is clearly far from the optimal strategy, the column recommends choosing $x_0^3$ which is much better than $x^1_0$ and $x^2_0$.

• Columns $\phi _2,\ldots ,\phi _5$: The best strategy for choosing initial points by using these columns is

  $$\begin{aligned} x_0^6>x_0^5>x_0^3>x_0^4>x_0^2>x_0^1, \end{aligned}$$

  which is near the optimal strategy.

• Column $\phi _6$: The best strategy for choosing initial points by using this column is

  $$\begin{aligned} x_0^5>x_0^6>x_0^3>x_0^4>x_0^2>x_0^1, \end{aligned}$$

  which is exactly the optimal strategy.

Table 2 shows that we need only 36 iterations (6 iterations for all 6 initial points) to find a good initial point. We can also see that the sum of all iterations in column $Iter_{inf}$ is 128 which is much fewer than the minimum value in column iter. As we explained earlier, it is the case for most problems due to the steepest descent theory. It suggests us to design algorithms based on examining the value of $\phi _k$ for a set of random initial points. We follow this idea in the next section.

4.2 Steepest descent with a pre-initialization step

In view of Remark 4 and Example 3, we are able now to design a version of steepest descent algorithm suitable for large-scale ill-condition problems. The algorithm starts by generating a set of random initial points and then a suitable point is determined among them using a pre-initialization step. Finally, the steepest descent algorithm is run by using this point.

Algorithm 1

Steepest descent with a pre-initialization step Main body

• Step1.   Choose two integers $\xi$ and $\rho$, and small positive constants $\epsilon$ and $\eta$ with $\eta <\epsilon$.

• Step2.   Call Pre-Initial ($\xi$ , $\rho$ , $\eta$)

• Step3.   Set:

  • Condition: $||g_k||\le \epsilon$.

  • Output: The final solution $x_k$.

  • $x_0$ as the output of the function Pre-Initial in Step2.

• Step4.   Call SD ($x_0$ , Condition , Output).

Pre-Initial ($\xi$ , $\rho$ , $\eta$)

• Step1.   Generate a set $\mathbb {I}$ of random points in ${\mathbb {R}}^n$ with $|\mathbb {I}|=\xi$.

• Step2.   Set:

  • Condition: $\frac{\phi _k-\phi _{k-1}}{\phi _{k-1}}\le \eta$ or $k>\rho$.

  • Output: The final value of $\phi _k$.

• Step3.   For each $x_0\in \mathbb {I}$ do

  • Call SD ($x_0$ , Condition , Output).

• Step4.   Set $x_0$ to be a point in $\mathbb {I}$ with the corresponding minimal Output value.

• Step5.   Return $x_0$ and stop.

SD ($x_0$ , Condition , Output)

• Step1.   Set $k=0$.

• Step2.   Compute $g_k=Ax_0-b$, $\alpha _k=\frac{g_k^tg_k}{g_k^tAg_k}$, and $x_{k+1}=x_k-\alpha _k g_k$.

• Step3.   If Condition is satisfied, return Output and stop; else set $k=k+1$ and go to the Step2.

In Algorithm 1, the ordinary steepest descent algorithm (Function SD) is run two times with different stopping conditions. In the function Pre-Initial, we run it to find a suitable initial point by checking the value of $\phi _k$ for a subset of random initial points; we have also the condition $k>\rho$ to control the number of iterations in this function. In the Main body, the ordinary steepest descent algorithm is run with the output of the function Pre-Initial.

4.3 Initial point and non-convex quadratic functions

Remark 3 also helps us to say something about the choice of initial points for non-convex functions. Our first result shows that the steepest descent algorithm can converge to a saddle point with a non-zero probability.

Lemma 6

Suppose that assumptions 1 and 3 hold, $n=2$, and the initial point $x_0$ is chosen randomly from the uniform distribution. The steepest descent algorithm escapes from saddle points with the probability

$$\begin{aligned} P(\text {divergence})=\frac{2}{\pi }\big (\arctan (\frac{\lambda _1}{\lambda _2}\tan (\varpi ))-\arctan (\frac{\lambda _1}{\lambda _2}\tan (\frac{\pi }{2}-\varpi )) \big ), \end{aligned}$$

(28)

where

$$\begin{aligned} \varpi :=\frac{1}{2}\arcsin \frac{\sqrt{-2\lambda _1\lambda _2}}{\lambda _2-\lambda _1}. \end{aligned}$$

Proof

Assumptions 1 and 3 are established almost surely with random initialization. We can see by Lemma 5, (17) and the discussion after Lemma 4 that the steepest descent algorithm escapes from saddle points if and only if

$$\begin{aligned} \nonumber \frac{-\lambda _1\lambda _2}{2}\le \frac{||w_{1}||^2}{||w_0||^2}&=\frac{g_0^t(\mu _0I-\varLambda )^2g_0}{g_0^tg_0}\\&=\frac{g_0^t\varLambda ^2g_0}{g_0^tg_0}-\bigg (\frac{g_0^t\varLambda g_0}{g_0^tg_0}\bigg )^2. \end{aligned}$$

(29)

Let us define

$$\begin{aligned} x:=\frac{g_0^1}{||g_0||},\;\text {and}\;y:=\frac{g_0^2}{||g_0||}. \end{aligned}$$

Then, (29) is equivalent to

$$\begin{aligned} (\lambda _1^2x^2+\lambda _2^2y^2)-(\lambda _1x^2+\lambda _2y^2)^2\ge \frac{-\lambda _1\lambda _2}{2}, \end{aligned}$$

(30)

where $x^2+y^2=1$. Using polar coordinate, and by substituting $x=\cos \theta$ and $y=\sin \theta$ in (30), we find that

$$\begin{aligned} \sin ^2(2\theta )\ge \frac{-2\lambda _1\lambda _2}{(\lambda _1-\lambda _2)^2}. \end{aligned}$$

(31)

By solving (31) with respect to $\theta$, we have

$$\begin{aligned} \frac{k\pi }{2}+\varpi \le \theta \le \frac{k\pi }{2}+ \big (\frac{\pi }{2}-\varpi \big ), \end{aligned}$$

(32)

for $k=0,\ldots ,3$. In fact, the method diverges if $g_0$ belongs to the union of the regions marked by (D) in Fig. 6.

Assuming $x_0=(x_0^1,x_0^2)$ is chosen randomly, $g_0=(\lambda _1x_0^1,\lambda _2x_0^2)$ and the method diverges if (32) is established for $\theta =\arctan \big (\frac{\lambda _2x_0^2}{\lambda _1x_0^1}\big )$. Namely, if

$$\begin{aligned} \frac{\lambda _1}{\lambda _2}\tan (\frac{\pi }{2}-\varpi ) \le \tan ({\bar{\theta }})\le \frac{\lambda _1}{\lambda _2}\tan (\varpi ), \end{aligned}$$

(33)

or

$$\begin{aligned} \frac{\lambda _1}{\lambda _2}\tan (\pi -\varpi ) \le \tan ({\bar{\theta }})\le \frac{\lambda _1}{\lambda _2}\tan (\frac{\pi }{2}+\varpi ), \end{aligned}$$

(34)

where $\tan ({\bar{\theta }})=x_0^2/x_0^1$.

Four regions with the same area like the ones in Fig. 6 are determined by solving these inequalities with respect to ${\bar{\theta }}$.

It is easy to see that the probability of escaping from saddle points is equal to the probability of choosing a point on a unit circle satisfying (33) or (34), which is

$$\begin{aligned} P(\text {divergence})=\frac{4}{2\pi }\big (\arctan (\frac{\lambda _1}{\lambda _2}\tan (\varpi ))-\arctan (\frac{\lambda _1}{\lambda _2}\tan (\frac{\pi }{2}-\varpi )) \big ). \end{aligned}$$

$\square$

Fig. 6

Regions obtained by solving (31)

Remark 5

In Fig. 7, we have depicted the function (28) with respect to the variable $-\lambda _1/\lambda _2$ (the inverse of the condition number). It is easy to see that the smaller is the condition number, the more is the chance of divergence. Furthermore, we can see that

$$\begin{aligned} P(\text {divergence})\le \frac{1}{2}. \end{aligned}$$

Fig. 7

The probability of divergence as a function of the inverse of the condition number

The behavior of the method for ($2<n$)-dimensional problems is so complicated, and strongly depends on both the choice of initial point and the distribution of eigenvalues between $\lambda _1$ and $\lambda _n$.

Lemma 7

Assume that (3) is a non-convex function, and assumptions 1 and 3 hold . The steepest descent algorithm

• (a) diverges if at some iterations $k\ge 0$,

  $$\begin{aligned} \frac{-\lambda _1\lambda _n}{2}<\frac{g_k^tA^2g_k}{g_k^tg_k}-\bigg (\frac{g_k^tA g_k}{g_k^tg_k}\bigg )^2. \end{aligned}$$

  (35)

• (b) diverges with the probability of one, if there exists at least one $\lambda _i\in (0,\lambda _1+\lambda _n)$.

Proof

(a) It is easy to see by (26) that if

$$\begin{aligned} \frac{||w_{k+1}||^2}{||w_k||^2}=\frac{g_k^tA^2g_k}{g_k^tg_k}-\bigg (\frac{g_k^tA g_k}{g_k^tg_k}\bigg )^2>\frac{-\lambda _1\lambda _n}{2}, \end{aligned}$$

(17) holds and so the proof is completed.

(b) It is a direct consequence of our statement after Lemma 4, and the fact that assumptions 1 and 3 hold almost surely with random initialization. $\square$

In practice, the left-hand side of (35) is unknown, so a choice of $x_0$ that maximizes the right-hand side of it increases the chance of divergence.

We note that there always exists some initial points $x_0$ such that the steepest descent method diverges. For example, $g_0=Ax_0$ always satisfies (35) if $(\eta _0^1)^2=(\eta _0^n)^2=0.5$ and $\eta _0^i=0$, for $i=2,\ldots ,n-1$, where $g_0=\sum \eta _0^iv_i$ is the eigenvector representation of the gradient vector. As a consequence, in view of assumptions 1–3, the probability of divergence is always non-zero due to the continuity of the right-hand side of (35).

Finally, we note that (35) is always established at some iterations if there exists at least one $\lambda _i\in (0,\lambda _1+\lambda _n)$.

5 Numerical experiments

We now consider the numerical behaviour of Algorithm 1 as a tool for detecting good initial points. We first investigate the performance of the algorithm for finite values of $\rho$ and $\eta$. In this way, we considered 254 test problems including: 1. A subset of 240 randomly generated matrices (using Matlab randn function) with different dimensions, from 5 to 5000 (due to the device memory limit)), and condition numbers, from 9 to 8.18E+16. 2. A subset of 14 matrices with special structure borrowed from the test matrix toolbox for Matlab [15]; Table 3 shows the name, dimension (considered in experiments) and the condition number of these matrices. We tried to choose matrices with large condition number—about 80 percent of test problems have a condition number greater than 500—because the effect of an initial point on the speed of the algorithm is more noticeable for such problems. All runs were performed in Matlab 2015 on a 2.4 Intel Corei7 processor computer with 8GB of RAM.

Table 3 A subset of positive definite matrices from [15]

We used the approach explained in Example 3 to investigate the performance of the algorithm; namely, by checking the ability of the algorithm for detecting good initial points. In this manner, a set of $\xi =5$ random initial points were generated by Matlab rand, randn and randi functions for each problem. It is recommended to choose initial points from different distributions with different mean and standard deviation. Our strategy is

• $x_1 = rand(n,1)+5\times randn(n,1);$

• $x_2 = 10 \times randn(n,1)+ rand(1,1);$

• $x_3 = randi([-5,5],n,1)+rand(n,1);$

• $x_4 = randi([-10,10],n,1)+randn(n,1);$

• $x_5 = randi([-50,50],n,1),$

where n is the problem dimension. Table 4 shows the performance of Algorithm 1 for different values of $\rho$ and $\eta$. In this table, we have classified initial points into five sets from the best (most desirable), $x_0^1$, to the worst (undesirable), $x_0^5$, according to the number of iterations required for termination ($\epsilon =$10E−12). For example, $(\rho ,\eta ,x_0^1)=(1,0.1,60)$ means that the algorithm selects the most preferred initial point (among five) in 60 problems—it is 48 for the worst initial point by looking at $(\rho ,\eta ,x_0^5)$. We denote by SR the Success Ratio of the algorithm; it is defined by the percentage of problems for which the algorithm selects one of the two most preferred initial points; namely, $SR=100\;(|x_0^1|+|x_0^2|)/T$ where T is the total number of test problems. By checking the values of SR in Table 4, we find that

• the bigger is the value of $\rho$, the better is the success ratio—it shows the better performance of the algorithm for big values of $\rho$;

• the success ratio is almost constant for different values of $\eta$ and a fixed value of $\rho$—the role of $\eta$ is more prominent for big values of $\rho$ (see the rest of section);

• a best choice of $(\rho ,\eta )$ is (10, 0.1) or (20, 0.1); see the bold values.

Table 4 The performance of Algorithm 1 for finite values of $\eta$ and $\rho$

We now examine the performance of the algorithm for an infinite value of $\rho$ and different choices of $\eta$. For this purpose, we generated a new set of 328 random matrices having different dimensions and condition numbers greater than 500. Tables 5, 6, 7 show the performance of the algorithm when $\xi =5$. We denote by PR the Performance Ratio of the algorithm; it is defined as the worst-case ratio of the number of iterations required to stop inner iterations to the number of iterations required to stop outer iterations; more exactly,

$$\begin{aligned}&PR=100\;\max _{i\in {\mathbb {I}}}\max _{x_j\in {\mathbb {S}}_i}\\&\quad \frac{\text { Starting from }x_j\text {, the number of iterations for which}\;{\scriptstyle (\phi _k-\phi _{k-1})/\phi _{k-1}<\eta }}{\text { Starting from }x_j\text {, the number of iterations for which}\;{\scriptstyle ||g_k||<\epsilon }}, \end{aligned}$$

where ${\mathbb {S}}_i$ is the set of random initial points for the ith problem, and ${\mathbb {I}}$ is the set of all test problems. For a given value of $\eta$, it is reasonable to say the algorithm cost-effective if $(|\xi |\times PR)<20\%$ because the inner loop is repeated $|\xi |$ times—it is 5 in our experiments. As the column PR, bold values, shows, a good value of $\eta$ depends on the matrix condition number.

To sum all up, we do not recommend the second scenario (infinite value of $\rho$) because it is possible that the algorithm selects a point $x_0$ in the Step4 of the function Pre-Initial for which the value of $\phi _k$ is minimal, but k is large; while there exist some random initial points for which the value of $\phi _k$ is slightly bigger than the minimal, but k is very small. In other words, the final value of k at the termination point of the inner loop can significantly affect the performance of the algorithm. Therefore, it is better to limit the number of iterations in the inner loop by choosing a finite value of $\rho$.

Tables 8, 9, 10 show the numerical behaviour of Algorithm 1 for non-convex problems. We generated a set of 800 non-convex test problems with different dimensions ($n=5,10,15$ and 20) and condition numbers using Matlab randn function with zero mean and standard deviation of 50. All test problems have the common property that they don’t have any eigenvalues in $(0,\lambda _1+\lambda _n)$, because by part (b) of Lemma 7, the algorithm diverges. The performance of the algorithm for different values of $\rho =5$ and 10 (20 and 40 just for $n=20$), and a fixed value of $\xi =5$ were investigated. We use the notation in (27) and define

$$\begin{aligned} \phi \rho \max (\min ):=\max _{\mathbb {J}_i}(\min )\phi _\rho +\frac{\lambda _1\lambda _n}{2}, \end{aligned}$$

where $\mathbb {J}_i$ is the set of random initial points considered for problem i. Moreover, $|\mathbb {I}|$ denotes the total number of test problems, and $\kappa$ stands for the condition number of matrix A in (3).

We evaluate (35) by checking the sign of $\phi \rho \max (\min )$; for example, the bold value in Table 8 indicates that when $\phi \rho \max (\min )$ is negative, the algorithm converges for 39 problems (out of 100) whenever the random initial point with minimal value of $\phi _5$ is selected as the starting point—it diverges for 12 problems. By checking the column $\phi \rho \max (\min )>0$, we see that the algorithm always diverges. In fact, a positive value of $\phi \rho \max (\min )$ means that (35) holds and so divergence is a direct result of part (a) of Lemma 7.

When $\phi \rho \max (\min )$ is negative, we need to investigate the method more carefully because (35) is only a sufficient condition. We have the following observations by checking the corresponding column in all tables.

• Rows $\phi 5\max$ and $\phi 10\max$: Almost all values in these rows are zero. This indicates that the proposed strategy of choosing an initial point with a big value of $\phi _\rho$ can successfully result in divergence and escaping from saddle points even for small problems.

• Rows $\phi 5\min$ and $\phi 10\min$: The probability of convergence reduces by growing n. Moreover, $\phi 10\min$ can detect convergence better than $\phi 5\min$; it recommends choosing a big value of $\rho$ specially for large and ill-condition problems.

• Rows $\phi 20\min (\max )$ and $\phi 40\min (\max )$: The probability of divergence increases for large n independent of the choice of initial points.

Table 5 The performance of Algorithm 1 for an infinite value of $\rho$—328 problems with condition number greater than 500

Table 6 The performance of Algorithm 1 for an infinite value of $\rho$—272 problems with condition number greater than 1000

Table 7 The performance of Algorithm 1 for an infinite value of $\rho$—186 problems with condition number greater than 2000

Table 8 The performance of Algorithm 1 for non-convex problems with a condition number smaller than $10^3$

Table 9 The performance of Algorithm 1 for non-convex problems with a condition number between $10^3$ and $10^4$

Table 10 The performance of Algorithm 1 for non-convex problems with a condition number greater than $10^4$

6 Conclusions

In this paper, we paid attention to quadratic functions and investigated the effect of initial points on the behavior of the steepest descent algorithm. We extended and developed some well-known results of this theory to non-convex quadratics. A practical method for choosing initial points in the steepest descent algorithm was proposed. We proved theoretically and showed numerically that the method can accelerate the speed of convergence. We provided two examples and showed some good features of the proposed initial point selection strategy. Finally, non-convex quadratic functions were investigated. We showed how an initial point should be selected to guarantee divergence. The probability of divergence was also investigated for a class of problems. The following challenges lie ahead:

• Inequality (35) can be used to find a lower bound for the probability of divergence. We tried to compute it for $n=3$ using spherical coordinate, but we faced with a so complicated and hard to solve equation.

• The behaviour of the method is unknown for $(2<n)$-dimensional problems when ${\check{\mu }}{\hat{\mu }}=\lambda _1\lambda _n/2$. It seems the method diverges in this case, but we couldn’t find any proof.

The chance of convergence increases for non-convex ill-condition problems for which all eigenvalues of the Hessian are distributed around minimal and maximal ones.