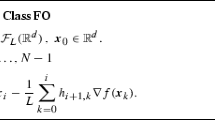On the worst case performance of the steepest descent algorithm for quadratic functions

Abstract

The existing choices for the step lengths used by the classical steepest descent algorithm for minimizing a convex quadratic function require in the worst case $\mathcal{{O}}(C\log (1/\varepsilon ))$ iterations to achieve a precision $\varepsilon$, where C is the Hessian condition number. We show how to construct a sequence of step lengths with which the algorithm stops in $\mathcal{{O}}(\sqrt{C}\log (1/\varepsilon ))$ iterations, with a bound almost exactly equal to that of the Conjugate Gradient method.

1 Introduction

We study the quadratic minimization problem

$$\begin{aligned} (P_z)\quad \mathop {\mathrm{minimize }}_{z\in {{\mathbb {R}}}^n}\bar{f}(z)=c^Tz+\dfrac{1}{2} z^THz, \end{aligned}$$

where $c\in {{\mathbb {R}}}^n$ and $H\in {{\mathbb {R}}}^{n\times n}$ is symmetric with eigenvalues

$$\begin{aligned} 0<\mu _1\le \mu _2\le \cdots \le \mu _n, \end{aligned}$$

and condition number $C=\mu _n/\mu _1$. The problem has a unique solution $z^*\in {{\mathbb {R}}}^n$.

The steepest descent algorithm, also called gradient method, is a memoryless method defined by

$$\begin{aligned} z^0\in {{\mathbb {R}}}^n\hbox { given, } z^{k+1}=z^k-\lambda _k\nabla f(z^k). \end{aligned}$$

(1)

The only distinction among different steepest descent algorithms is in the choice of the step lengths $\lambda _k$. The worst-case performance of a scheme is based on a stopping rule, which depends on a precision $\varepsilon >0$.

Assume that an initial point $z^0\in {{\mathbb {R}}}^n$ is given. Let $\varepsilon >0$ be a given precision. Let M be a matrix whose columns $M_i$, $i=1,\ldots ,m$, are orthonormal eigenvectors of H . We define four different stopping rules referred as $\tau _\varepsilon$, which will be used by algorithms:

• i. $\bar{f}(z)-\bar{f}(z^*)\le \varepsilon ^2(\bar{f}(z^0)-\bar{f}(z^*))$.

• ii. $\Vert z-z^* \Vert \le \varepsilon \Vert z^0-z^* \Vert$.

• iii. $\Vert \nabla \bar{f}(z) \Vert \le \varepsilon \Vert \nabla \bar{f}(z^0) \Vert$.

• iv. $|M_i^T(z-z^*)|\le \varepsilon |M_i^T(z^0-z^*)|$, i=1,...,n.

The first and second stopping rules are useful for characterizing the performance bounds for the algorithms, but they are usually not implementable. The third rule is practical. The fourth rule will be discussed in Sect. 3 and will be used in this paper. It means that all components of $z-z^*$ in the basis defined the columns of M are reduced by a factor of $\epsilon$ in absolute values. It implies all the others.

The steepest descent problem The problem to be solved in this paper is: given $\epsilon >0$ and $x^0\in {{\mathbb {R}}}^n$, find an integer $k>0$ and a set $\left\{ \lambda _0,\lambda _1,\ldots ,\lambda _{k-1} \right\}$ of positive numbers such that the point $z^k$ produced by the algorithm (1) satisfies the stopping rule (iv).

The steepest descent method, also called gradient method, was devised by Augustine Cauchy [3]. He studied a minimization problem and described a steepest descent step with exact line search, which we shall call “Cauchy step”. For (P$_z$), the Cauchy step is

$$\begin{aligned} \lambda _k=\mathop {\mathrm{argmin }}_{\lambda \ge 0} \bar{f}({x}^k-\lambda \nabla \bar{f}({x}^k)). \end{aligned}$$

(2)

The steepest descent method with Cauchy steps will be called Cauchy algorithm.

Steepest descent is the most basic algorithm for the unconstrained minimization of continuously differentiable functions, with step lengths computed by a multitude of line search schemes.

The quadratic problem is the simplest non-trivial non-linear programming problem. Being able to solve it is a pre-requisite for any method for more general problems, and this is the first reason for the great effort dedicated to its solution. A second reason is that the optimal solution of (P$_z$) is the solution of the linear system $Hz=-c$.

It was soon noticed that the Cauchy algorithm generates inefficient zig-zagging sequences. This phenomenon was established by Akaike [1], and further developed by Forsythe [7]. A clear explanation is found in Nocedal, Sartenaer and Zhu [13]. For some time the steepest descent method was displaced by methods using second order information.

In the last years gradient methods returned to the scene due to the need to tackle large scale problems, with millions of variables, and due to novel methods for computing the step lengths. Barzilai and Borwein [2] proposed a new step length computation with surprisingly good properties, which was further extended to non-quadratic problems by Raydan [15], and studied by Dai [4], Raydan and Svaiter [16] among others. In another line of research, several methods were developed to enhance the Cauchy algorithm by breaking its zig-zagging pattern. These methods, which will not be studied in this paper, are explained in De Asmundis et al. [5, 6] and in our paper [10].

None of these papers studies the worst-case performance of the algorithm applied to quadratic problems. This will be our task.

1.1 Complexity results

We are studying performance bounds for first-order methods – methods that use only function and derivative values. The best such method for the quadratic problem is the Conjugate Gradient method (and equivalent Krylov space methods): it is known that no first order method can be faster than it, and its performance bound (which then is the complexity of the problem with first order oracle) is given by

$$\begin{aligned} k \le \left\lceil \dfrac{\sqrt{\mathcal{{C}}}}{2} \log \left( \dfrac{2}{\varepsilon }\right) \right\rceil \end{aligned}$$

(3)

iterations to achieve the stopping rule (i), where $\lceil a\rceil$ denotes the smallest integer $\bar{a}$ such that $\bar{a}\ge a$.

This complexity study is found in Nemirovsky and Yudin [12], in Polyak [14], and a detailed proof of (3) is in Shewchuk [17]. See [9] for a tutorial on basic complexity results.

The two most widely known choices of step lengths for which there are complexity studies are:

• The Cauchy step, or exact step (2), the unique minimizer of f along the direction $-g$ with $g=\nabla f({x}^k)$, given by

  $$\begin{aligned} \lambda _k = \dfrac{g^T g}{g^T H g}. \end{aligned}$$

  (4)

• The short step: $\lambda _k = 1/{\mu _n}$, a fixed step length.

The complexity results for these methods are: the first stopping rule is achieved in

$$\begin{aligned} k \le \left\lceil \dfrac{\mathcal{{C}}}{4} \log \left( \dfrac{1}{\varepsilon }\right) \right\rceil ,\qquad k \le \left\lceil \dfrac{\mathcal{{C}}}{2} \log \left( \dfrac{1}{\varepsilon }\right) \right\rceil , \end{aligned}$$

respectively for the Cauchy and short step lengths. These bounds are tight, and we are unaware of any steepest descent algorithm with a better worst case performance.

In this paper we show that given $\mu _1$, $\mu _n$ and $\varepsilon$, there exist $k\in {\mathbb {N}}$ and a set $\left\{ \lambda _j\,|\,j=1\ldots k \right\}$ such that the steepest descent method applied from any initial point with the step lengths $\lambda _j$ in any order produces a point that satisfies all four stopping rules. The bound to be found in this paper is

$$\begin{aligned} k=\left\lceil \dfrac{\mathrm{cosh}^{-1} \left( \dfrac{2}{\varepsilon } \right) }{\mathrm{cosh}^{-1} \left( 1+\dfrac{2}{C-1} \right) } \right\rceil \approx \left\lceil \dfrac{\sqrt{\mathcal{{C}}}}{2} \log \left( \dfrac{2}{\varepsilon }\right) \right\rceil \end{aligned}$$

These two values differ by less than 1 for $\varepsilon <0.1$ and $C>2$, as can be seen by plotting both functions. A weaker relationship between both bounds will also be derived in Sect. 3.

The values $\lambda _j$ will be the inverses of the roots of a Chebyshev polynomial to be constructed in Sect. 3. In Sect. 2 we list some properties of Chebyshev polynomials and hyperbolic functions, which will be used in Sect. 4 to prove the performance bound.

The association of Chebyshev polynomials to steepest descent has been used by numerical analysts, but we are unaware of any complexity studies along this line. See Frank [8].

2 Tools

Let us list some well-known facts on Chebyshev polynomials¹ (see for instance [11]) and a technical result on hyperbolic functions.

Chebyshev polynomials. The Chebyshev polynomial of first kind $T_k(\cdot )$ satisfies:

• For $x\in [-1,1]$, $T_k(x)=\cos (k\, \mathrm{cos}^{-1} (x))\in [-1,1]$, with $T_k(1)=1$.

• For $x> 1$, $T_k(x)=\cosh (k\, \mathrm{cosh}^{-1} (x))>1$

• The roots of $T_k$ are

  $$\begin{aligned} x_j=\cos \left( \dfrac{1+2j}{2k}\pi \right) , j=0,1,\ldots ,k-1. \end{aligned}$$

• The maximizers of $|T_k(x)|$ in $[-1,1]$ are $\bar{x}_j=\cos (j\pi /k), j=0,1,\ldots ,k.$

Hyperbolic functions. The hyperbolic cosine satisfies

$$\begin{aligned} \cosh (x)=\dfrac{e^x+e^{-x}}{2}\ge \dfrac{e^x}{2},\, \cosh '(x)=\sinh (x),\, \cosh ''(x)=\cosh (x). \end{aligned}$$

Its Taylor approximation at 0 gives for $x\ge 0$

$$\begin{aligned} \cosh (x)=1+\dfrac{x^2}{2}+\dfrac{\cosh (\delta )x^4}{4!}\ge 1+\dfrac{x^2}{2}, \end{aligned}$$

where $\delta \in [0,x]$. It follows that $\cosh (x)-1$ is well approximated by $x^2/2$ for small values of $x\ge 0$. Setting $y=x^2/2$ and taking the inverse function, it follows that for small values of $y>0$,

$$\begin{aligned} \sqrt{2y}\ge \mathrm{cosh}^{-1} (1+y)\approx \sqrt{2y} . \end{aligned}$$

This fact will be useful, and so we give a formal proof here, whose only purpose is to quantify the ‘$\approx$’ above.

Lemma 1

Let $\bar{x}>0$ be a given real number. Then for any $x\in [0,\bar{x}]$,

$$\begin{aligned} \sqrt{2x}\ge \mathrm{cosh}^{-1} (1+x)\ge \gamma ({\bar{x}})\sqrt{2x}, \end{aligned}$$

where $\gamma (0)=1$ and for $y>0$, $\gamma (y)=\dfrac{\mathrm{cosh}^{-1} (1+y)}{\sqrt{2y}}<1.$

Proof

Note that for $x>0$, $\mathrm{cosh}^{-1} (1+x)=\gamma (x)\sqrt{2x}$. All we need is to prove that $x\in {\mathbb {R}}_+\mapsto \gamma (x)$ is continuous and decreases for $x>0$ (and then $\gamma (x)\ge \gamma (\bar{x})$ for $x\in [0,\bar{x}]$).

Continuity: using l’Hôspital’s rule,

$$\begin{aligned} \lim _{x\rightarrow 0+}\gamma (x)= \lim _{x\rightarrow 0+}\dfrac{\sqrt{2}}{\sqrt{x+2}}=1. \end{aligned}$$

Computing the derivative for $x>0$,

$$\begin{aligned} \dfrac{d}{dx}\gamma (x)=\dfrac{2\sqrt{\frac{x}{x+2}}-\mathrm{cosh}^{-1} (1+x)}{2x\sqrt{2x}}. \end{aligned}$$

The denominator is positive. So we must prove that the numerator

$$\begin{aligned} N(x)= 2\sqrt{\dfrac{x}{x+2}}-\mathrm{cosh}^{-1} (1+x) \end{aligned}$$

is negative for $x>0$.

Since $N(0)=0$, N(x) will be negative for $x>0$ if $N'(x)<0$. Computing this derivative, for $x>0$,

$$\begin{aligned} N'(x)=-\dfrac{\sqrt{x}}{(x+2)^{3/2}}<0, \end{aligned}$$

completing the proof.$\square$

3 An infinite dimensional problem

Problem (P$_z$) has a unique solution $z^*$. For the analysis, the problem may be simplified by assuming that $z^*=0$, and so $\bar{f}(z)= z^T Hz/2$. The matrix H may be diagonalized by setting $z=My$, where M has orthonormal eigenvectors of H as columns. Then the function becomes

$$\begin{aligned} f(y)=\dfrac{1}{2} y^TDy, \qquad D=\mathrm{diag}(\mu _1, \mu _2,\ldots ,\mu _n). \end{aligned}$$

(5)

M defines a similarity transformation, and hence for $z=My$,

$$\begin{aligned} \Vert z \Vert =\Vert y \Vert ,\,\Vert \nabla \bar{f}(z) \Vert = \Vert \nabla f(y) \Vert ,\,\nabla \bar{f}(z)=M\nabla f(y). \end{aligned}$$

We define the diagonalized problem

$$\begin{aligned} (P_y)\quad \mathop {\mathrm{minimize }}_{y\in {{\mathbb {R}}}^n} f(y)=\dfrac{1}{2} y^TDy. \end{aligned}$$

The steepest descent iterations with step lengths $\lambda _j$ for minimizing respectively $f(\cdot )$ from the initial point $y^0=M^Tz^0$, and $\bar{f}(\cdot )$ from the initial point $z^0$, are related by $z^k=My^k$. The stopping rule (iv) for the diagonalized problem becomes $|y_i|\le \epsilon |y_i^0|$, $i=1,\ldots ,n$, and clearly implies all the others. For instance, if rule (iv) holds at y ,

$$\begin{aligned} f(y)= \dfrac{1}{2} \sum _{i=1}^n \mu _i y_i^2 \le \dfrac{\epsilon ^2}{2} \sum _{i=1}^n \mu _i (y_i^0)^2 = \epsilon ^2 f(y^0), \end{aligned}$$

and rule (i) holds.

The stopping rules are equivalent for these two sequences. Thus, we may restrict our study to the diagonalized problem.

Given $y^0\in {{\mathbb {R}}}^n$, consider the sequence generated by the steepest descent algorithm defined by

$$\begin{aligned} {y}^{j+1}={y}^{j}-\lambda _j\nabla f({y}^{j}), \end{aligned}$$

(6)

where $\lambda _j$ is the step length at the j-iteration. As $\nabla f({y}^{j})=D{y}^{j}$ and D is diagonal, we have, for all $i=1,\ldots ,n$,

$$\begin{aligned} {y}^{j+1}_i=(1-\lambda _j\mu _i){y}^{j}_i. \end{aligned}$$

Using this recursively, we obtain

$$\begin{aligned} {y}^k_i=\prod _{j=0}^{k-1}(1-\lambda _j\mu _i)y^0_i. \end{aligned}$$

(7)

So, each variable may be seen independently, and the order of the step lengths $\left\{ \lambda _0,\ldots ,\lambda _{k-1} \right\}$ is irrelevant with respect to satisfying the stopping criterion. The stopping rule (iv), $|y_i^k|\le \varepsilon |y_i^0|$ for $i=1,\ldots ,n$, will be satisfied if

$$\begin{aligned} \left| \prod _{j=0}^{k-1}(1-\lambda _j\mu _i)\right| \le \varepsilon ,\quad i=1,\ldots ,n, \end{aligned}$$

which in its turn is implied by

$$\begin{aligned} \left| \prod _{j=0}^{k-1}(1-\lambda _jw)\right| \le \varepsilon ,\quad w\in [\mu _1,\mu _n]. \end{aligned}$$

The left hand side defines a polynomial $p(\cdot )$ such that $|p(w)|\le \epsilon$ for $w\in [\mu _1,\mu _n]$ and $p(0)=1$, with roots $1/\lambda _j$, $j=1,\ldots ,k$. Dividing this inequality by $\epsilon$, it can be satisfied by solving the following infinite dimensional problem:

Find a polynomial $p_k(\cdot )$ of degree $k\in {\mathbb {N}}$ such that $|p_k(w)|\le 1$ for $w\in [\mu _1,\mu _n]$ and $p(0)=1/\epsilon$, with roots $1/\lambda _j>0$, $j=1,\ldots ,k$.

This may be finally be formulated as

(P$_w$) Given $0<\mu _1<\mu _n$, find a polynomial $p_k(\cdot )$ of degree $k\in {\mathbb {N}}$ such that

$$\begin{aligned} \max _{w\in [\mu _1,\mu _n]}|p_k(w)|\le 1,\quad p(0)\ge 1/\epsilon , \end{aligned}$$

with roots $1/\lambda _j>0$, $j=1,\ldots ,k$.

The following fact summarizes our development up to now:

Let $p_k$ be a solution of (P$_w$). Then the steepest descent algorithm with step lengths $\left\{ \lambda _j,\, j=0,\ldots ,k-1 \right\}$ (in any order) applied to (P$_z$) from any initial point $z^0\in {\mathbb {R}}^n$ produces a point $z^k$ that satisfies all four stopping rules.

Solution of ($\mathbf{P} _w$). Our task is to find a polynomial with degree as low as we can which solves the problem. We do it by constructing a Chebyshev polynomial. First, we change variables so that the set $[\mu _1,\mu _n]$ is mapped onto $[-1,1]$. Set

$$\begin{aligned} w=\dfrac{\mu _n-\mu _1}{2} x +\dfrac{\mu _n+\mu _1}{2},\quad \hbox { or }\quad x=\dfrac{2w}{\mu _n-\mu _1}-\dfrac{\mu _n+\mu _1}{\mu _n-\mu _1}. \end{aligned}$$

Then $x=0$ for $w=(\mu _1+\mu _n)/2$, $x=-1$ for $w=\mu _1$ and $x=1$ for $w=\mu _n$.

For $w=0$, $x=-\dfrac{\mu _n+\mu _1}{\mu _n-\mu _1}= -\dfrac{C+1}{C-1}$.

Fig. 1

Chebyshev polynomial

With this change of variables, the problem is solved by a Chebyshev polynomial $T_k$ (see Fig. 1). We must satisfy the conditions $| T_k(x)|\le 1$ for $x\in [-1,1]$, which is trivial, and $|T_k(-(C+1)/(C-1))|\ge 1/\varepsilon$. Due to the symmetry of $|T_k|$ and to the fact that $T_k(x)>1$ for $x>1$, this condition is equivalent to

$$\begin{aligned} \left| T_k\left( \dfrac{C+1}{C-1}\right) \right| =T_k\left( 1+\dfrac{2}{C-1}\right) \ge \dfrac{1}{\varepsilon }. \end{aligned}$$

Thus, using the properties of Chebyshev polynomials, we must satisfy

$$\begin{aligned} \cosh \left( k\, \mathrm{cosh}^{-1} \left( 1+\dfrac{2}{C-1} \right) \right) \ge \dfrac{1}{\varepsilon }. \end{aligned}$$

The smallest integer that satisfies this is

$$\begin{aligned} k(C,\epsilon )= \left\lceil \dfrac{\mathrm{cosh}^{-1} \left( \dfrac{1}{\varepsilon } \right) }{\mathrm{cosh}^{-1} \left( 1+\dfrac{2}{C-1} \right) } \right\rceil . \end{aligned}$$

(8)

We have proved our main result, expressed in the next theorem.

Theorem 1

Consider the problem (P$_z$), assume that the eigenvalues of H belong to the interval $[\mu ^-,\mu ^+]$, $\mu ^->0$ and set $C= \mu ^+/\mu ^-$. Then the steepest descent algorithm with step lengths $\left\{ \lambda _j=1/w_j, j=0,1, \ldots ,k-1 \right\}$, where

$$\begin{aligned} w_j=\dfrac{\mu ^+-\mu ^-}{2} \cos \left( \dfrac{1+2j}{2k}\pi \right) + \dfrac{\mu ^++\mu ^-}{2} \end{aligned}$$

and $k=k(C,\epsilon )$ defined in (8), satisfies the stopping rule in k steps, for any initial point $z^0$. The step lengths $\lambda _j$ can be applied in any order.

Proof

The result follows directly by a change of variables and the reasoning above.$\square$

A simpler bound. Let us express the bound (8) in the shape $\mathcal{{O}}(\sqrt{C} \log (1/\varepsilon ))$. Numerical values for the parameter appearing in the corollary below will follow its proof.

Corollary 1

In the conditions of Theorem 1, for $C\ge \bar{C} >1$,

$$\begin{aligned} k \le \left\lceil \beta (\bar{C}) \dfrac{\sqrt{\mathcal{{C}}}}{2} \log \left( \dfrac{2}{\varepsilon }\right) \right\rceil , \end{aligned}$$

where

$$\begin{aligned} \beta (\bar{C})=\dfrac{2}{\mathrm{cosh}^{-1} (1+2/(\bar{C}-1))\sqrt{\bar{C} -1}} \end{aligned}$$

Proof

Let us examine numerator and denominator of (8).

Numerator: since $\cosh (x)> e^x/2$ for $x\in {\mathbb {R}}$, $\cosh (\log (2/\varepsilon ))> 1/\varepsilon$ for $\varepsilon <1$, and then $\mathrm{cosh}^{-1} (1/\varepsilon )<\log (2/\varepsilon )$.

Denominator: By Lemma 1, given $\bar{C}>1$ and $C\ge \bar{C}$ (and hence $2/(C-1)\le 2/(\bar{C}-1)$),

$$\begin{aligned} \mathrm{cosh}^{-1} \left( 1+\dfrac{2}{C-1}\right) \ge \gamma \left( \dfrac{2}{\bar{C}-1}\right) \sqrt{\dfrac{4}{C-1}}, \end{aligned}$$

(9)

with

$$\begin{aligned} \gamma \left( \dfrac{2}{\bar{C}-1}\right) =\dfrac{\mathrm{cosh}^{-1} \left( 1+\dfrac{2}{\bar{C}-1}\right) }{\sqrt{\dfrac{4}{\bar{C}-1}}} \end{aligned}$$

This value is near 1, as we see by calculating some values. Let us denote

$$\begin{aligned} \beta (\bar{C})=\dfrac{1}{\gamma (2/(\bar{C}-1))}=\dfrac{2}{\mathrm{cosh}^{-1} (1+2/(\bar{C}-1))\sqrt{\bar{C} -1}}, \end{aligned}$$

and obtain from (9):

$$\begin{aligned} \dfrac{1}{\mathrm{cosh}^{-1} (1+2/(C-1))}\le \beta (\bar{C})\dfrac{\sqrt{C-1} }{2}. \end{aligned}$$

Finally, putting together the results for numerator and denominator, (8) is satisfied by

$$\begin{aligned} k=\left\lceil \beta (\bar{C})\dfrac{\sqrt{C-1}}{2} \log (2/\varepsilon )\right\rceil \le \left\lceil \beta (\bar{C})\dfrac{\sqrt{C}}{2} \log (2/\varepsilon )\right\rceil , \end{aligned}$$

for any $C\ge \bar{C}$.$\square$

Numerical values: for $\bar{C}=2,4,10,100$, the values of $\beta$ are respectively 1.14, 1.06, 1.02, 1.002 . The corresponding values of $\gamma$ (which appears in the proof) are 0.88, 0.95, 0.98, 0.998.

4 Complexity for unknown eigenvalue bounds

In this section we study the diagonalized problem. All complexity results will also be valid for the original problem.

Let us study the problem (P$_y$) with no information on the eigenvalues. It is well-known (see for instance [1]) that the Cauchy step $\lambda _C(y)$ from a point $y\in {{\mathbb {R}}}^n$ with $g=\nabla f(y)$ satisfies

$$\begin{aligned} \lambda _C(y)=\dfrac{g^Tg}{g^TDg},\quad \dfrac{1}{\lambda _C}\in [\mu _1,\mu _n]. \end{aligned}$$

So, we may assume that a number $\mu \in [\mu _1,\mu _n]$ is known.

The Cheby algorithm. Consider the problem (P$_y$) and values $l<u$, not necessarily bounds for the eigenvalues. We shall call ‘Cheby’ algorithm the steepest descent with steps $\lambda _i$ given by Theorem 1 with $\mu ^-=l$ and $\mu ^+=u$. After its application from the initial point $y^0$, $g^0=\nabla f(y^0)$, we obtain a point $y=Cheby(y^0,l,u,\epsilon )$ such that

$$\begin{aligned} |y_j|\le \epsilon |y_j^0|,\quad |g_j|\le \epsilon |g_j^0| \end{aligned}$$

for $j\in \left\{ 1,\ldots ,n \right\}$ such that $l\le \mu _j\le u$.

The stopping rule. Let us use the stopping rule (iii), $\Vert \nabla f(y) \Vert \le \Vert \nabla f(y^0) \Vert$, because the other rules are not implementable. The following scheme expands an interval $[l_i,u_i]$ and applies the Cheby algorithm, until the stopping rule is satisfied. Note that we do not propose this as a practical method: our intent is to show a complexity bound.

Lemma 2

At an iteration i of the algorithm:

• (i) If $u_i\ge 2\mu _n$ then $\bar{u}=u_i$ ($u_i$ stops increasing).

• (ii) If $l_i\le \mu _1$ then $\bar{l}=l_i$ ($l_i$ stops decreasing).

• (iii) When the algorithm stops, $\bar{l}\ge \mu _1/4$, $\bar{u}\le 8\mu _n$ and $C_{\bar{i}}\le 32C$.

Proof

Assume without loss of generality that $\Vert g^0 \Vert =1$, and let us examine an iteration i (if $\Vert g^1 \Vert \le \epsilon$, the result is trivial).

• (i) Assume that $u_i\ge 2\mu _n$. We know that $\mu _C\in [\mu _1,\mu _n]$, and then $\mu _C\le \mu _n\le u_i/2$. By construction, $u_{i+1}=u_i$ ($u_i$ stops increasing).

• (ii) Assume that $l_i\le \mu _1$. We must prove that $\mu _C>u_i/2$.

Let $\bar{j}=\max \left\{ j\in \left\{ 1,\ldots ,n \right\} \,|\,\mu _j\le u_i \right\}$. By Theorem 1, after the application of the Cheby algorithm with precision $\epsilon /2$,

$$\begin{aligned} |g_j|\le \dfrac{\epsilon }{2} |g_j^0|,\quad \hbox { for } j=1,2,\ldots ,\bar{j}. \end{aligned}$$

Hence

$$\begin{aligned} \sum _{j\le \bar{j}}g_j^2\le \frac{\epsilon ^2}{4} \sum _{j\le \bar{j}}(g_j^0)^2 \le \frac{\epsilon ^2}{4}<\frac{\Vert g \Vert ^2}{4}, \end{aligned}$$

and consequently

$$\begin{aligned} \sum _{j>\bar{j}}g_j^2> \frac{3}{4} \Vert g \Vert ^2>\frac{3}{4} \epsilon ^2>\frac{1}{2} \epsilon ^2. \end{aligned}$$

It follows that

$$\begin{aligned} \sum _{j=1}^n \mu _jg_j^2\ge u_i \sum _{j>\bar{j}}g_j^2 >\frac{u_i}{2} \Vert g \Vert ^2. \end{aligned}$$

Dividing both sides by $\Vert g \Vert ^2$,

$$\begin{aligned} \mu _C=\frac{\sum _{j=1}^n \mu _jg_j^2}{\Vert g \Vert ^2} >\frac{u_i}{2}, \end{aligned}$$

proving (ii).

• (iii) Lower bound: if $\bar{l}=l_1$, the result is true because $l_1=\mu /2\ge \mu _1/2$. Otherwise, $\bar{l}=l_i/4$ for some i with $l_i>\mu _1$, and hence $\bar{l}>\mu _1/4$. Upper bound: if $\bar{u}=u_1$, $\bar{u}=2\mu \le 2\mu _n$. Otherwise, $\bar{u}=4 u_i$ for some i such that $u_i<2\mu _C\le 2\mu _n$, because $\mu _C\in [\mu _1,\mu _n]$. Hence $\bar{u}\le 8\mu _n$, completing the proof. $\square$

Lemma 3

Let p be the smallest integer such that $32 C\le 4^p$. The algorithm will stop with ${\bar{i}}\le p$, with a total number of steepest descent steps satisfying

$$\begin{aligned} K=\sum _{i=1}^p k_i\le 12\sqrt{C}\log (4/\epsilon ). \end{aligned}$$

Proof

The number of steps at each iteration with $C\ge 4$ and precision $\epsilon /2$ is given by Corollary 1: as $\lceil a\rceil \le a+1$ for $a\in {\mathbb {R}}$,

$$\begin{aligned} k_i\le 1.06\frac{\sqrt{C_i}}{2} \log (4/\epsilon )+1\le \sqrt{C_i}\log (4/\epsilon ). \end{aligned}$$

The last inequality is easily checked for $C_i\ge 4$ and $\epsilon <1$, because $1.06\log (4)+1<2\log (4)$.

The number of iterations satisfies ${\bar{i}}\le p$, because $4^{\bar{i}}=C_{\bar{i}}\le 32C$. Then $C\ge 4^{{\bar{i}}-2}/2$,

$$\begin{aligned} \sqrt{C} \ge 2^{{\bar{i}}-2}/\sqrt{2} . \end{aligned}$$

(10)

In ${\bar{i}}$ iterations, the total number of steepest descent steps is

$$\begin{aligned} K=\sum _{i=1}^{\bar{i}}k_i\le \sum _{i=1}^{\bar{i}}\sqrt{C_i}\log (4/\epsilon )=\log (4/\epsilon )\sum _{i=1}^{\bar{i}}2^i< \log (4/\epsilon )2^{{\bar{i}}+1}. \end{aligned}$$

Finally, using (10), $2^{{\bar{i}}+1}\le 8\sqrt{2}\sqrt{C}\le 12\sqrt{C}$, completing the proof.$\square$

Remark

If either a good lower bound or upper bound for the eigenvalues is known, the scheme becomes much easier, just update the unknown bound by multiplying or dividing it by 4 in each iteration. The bound on K will have a lower constant:

$$\begin{aligned} K\le 3\sqrt{C}\log (2/\epsilon ). \end{aligned}$$

Doing this simultaneously for both bounds would increase the complexity: the “difficult” thing was to decide which bound to change at each iteration, and it was done with the help of the inverse Cauchy step. If a scheme like this is to be used in practice, note that there must be more efficient ways of updating the upper bound (see for instance [5] for methods for estimating short steps). Estimating the smallest eigenvalue is more difficult. We assumed that all iterations start at the same initial point, which does not seem reasonable in practice: one should start each iteration i of the scheme from $y^i$.

5 Toward possible applications

The purpose of this paper is the establishment of a theoretical optimal performance bound. Nevertheless, some practical hints can be suggested from these results. These hints, together with efficient versions of steepest descent and practical methods for estimating the bounds $\bar{l}$ and $\bar{u}$, are explored in reference [10].

The Cauchy algorithm tends to generate steps that cycle around two limit points. Our results say that the steps should be spaced according to the Chebyshev roots: repeating step lengths is not as efficient as keeping them apart. They also suggest that the step lengths should have a sinusoidal distribution, with a higher density of step lengths near the extremities of the interval $[1/\mu _n,1/\mu _1]$.

This is illustrated by the following strategy: assuming that $\mu _1$, $\mu _n$ and $\epsilon$ are known, generate a list $L={l_1,l_2,\ldots ,l_k}$ of Chebyshev steps as in Theorem 1. Choose any steepest descent algorithm (Cauchy, short steps, Barzilai-Borwein,...) and do the following:

At iteration k , compute $\lambda _k$ by the algorithm.

Find the item $\bar{i}$ in L that minimizes $|\lambda _k-l_i|$.

Set $\lambda _k=l_{\bar{i}}$ and remove the item $l_{\bar{i}}$ from L .

The algorithm will necessarily stop for $k\le k(\mu _n/\mu _1,\epsilon )$. This procedure will hopefully enhance any steepest descent method, by forcing it to use Chebyshev steps. In Fig. 2 we show the effect of this enhancement on a run of the Cauchy and Barzilai-Borwein algorithms applied to a problem with logarithmically distributed eigenvalues, $C=10^6$, $n=10^4$, $\epsilon =10^{-5}$. The plots show the evolution of function values for the algorithm with ordered Chebyshev roots, modified Cauchy (original Cauchy is too slow, not shown), original Barzilai-Borwein and enhanced Barzilai-Borwein. We see that the enhancement really did improve the convergence in this example.

At left, the figure shows function values; at right, $\min \left\{ \Vert x^j \Vert _\infty \,|\,j\le k \right\}$.

Fig. 2

Algorithms using Chebyshev roots