1 Introduction

The development of semi-analytical orbital models dates back to the work of Brouwer (1959), who separated the influence of the \(J_2\) perturbation into short-period, long-period and secular variations. This perturbation is dominant in low orbits. For higher orbits, third-body perturbations must be taken into account. For example, in the high Earth orbit region, the lunisolar attraction becomes a dominant perturbation. One of the first models of third-body perturbations was developed by Kozai (1966), who published a comprehensive special report, which introduced the short-period solutions for the orbital elements. Kozai (1966) showed that in order to compute the position of a satellite with seven significant digits, even if the mean motion is as large as ten revolutions per day, lunisolar short-period perturbations should be taken into account.

Later Kozai (1973) used the ecliptic reference system for the Moon and the equatorial system for the satellite and introduced a new method for the evaluation of lunisolar perturbations, wherein it was proposed to compute secular and long-period perturbations by numerical integration and short-period perturbations by analytical formulae.

A simplified approximate model was introduced by Broucke (2003), who described the effect of the third-body perturbation on a satellite using double averaging over the mean anomaly of the satellite, as well as the mean anomaly of a distant third body. This yielded an analytic model for the evolution of the mean orbital elements during a long time period.

Solórzano and Prado (2007a, (2007b) studied the motion of a satellite using a singly averaged model. The disturbing function was expanded into Legendre polynomials up to fourth order. The single average was taken over the mean motion of the satellite to eliminate short-period perturbations.

Domingos et al. (2008) examined the third-body perturbations in the case of elliptic orbits with the disturbing function expanded into Legendre polynomials up to second order. The mentioned work was extended by Xiaodong et al. (2012), presenting the long-term perturbations due to a third body in an elliptic inclined orbit.

Nie et al. (2019) presented a semi-analytical model for third-body perturbations including the inclination and eccentricity of the third body and provided an analytical transformation between osculating and mean elements, in addition to developing the long-term dynamical equations.

The works discussed thus far assumed that the third-body perturbation is caused by a third body that orbits the primary in a radius larger than the semimajor axis of the perturbed object, e.g., a satellite. This assumption is justified as long as the primary does not have a third body in close orbit.

For example, consider Mars and its moons, Phobos and Deimos. Both are in relatively close orbit around Mars. The orbit of Phobos is especially close to Mars, and its semimajor axis is smaller than the areostationary radius. A third body that orbits a primary in a radius smaller than the semimajor axis of a satellite is called an inner third body.

A discussion of inner third-body dynamics was provided by Romero et al. (2015), in the context of station-keeping maneuvers required to control the inclination evolution of areostationary satellites. Such dynamics are different from the classical outer third-body case. In order to accurately predict the long-term motion of a satellite orbiting an inner third-body system, an appropriate model of the long-term effects caused by the inner third body is needed.

In this work, we develop a model for the long-term evolution of the orbital elements due to the inner third-body perturbation, while considering Legendre polynomials up to second order. We show that the resulting orbital element rates of the inner third-body problem are different from the classical problem. Whereas in the work of Romero et al. (2015), the non-averaged perturbing potential of an inner third body was used in order to examine its effects on the required station-keeping maneuvers, in this work, we study the long-term effects of the doubly averaged inner third-body perturbing potential on the orbital element evolution. We show that for near-circular orbits, the \(J_2\) problem and the inner third-body problem are equivalent and provide simulations to validate the model.

2 The perturbing potential

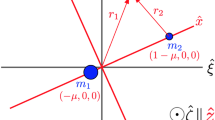
When the primary is located at the center of the reference system, the perturbing potential of an inner third body can be written as (Romero et al. 2015)

$$\begin{aligned} R=\frac{\mu _3}{r}\left[ 1+\left( \frac{d}{r}-\frac{r^2}{d^2}\right) \cos {S}+\sum \limits _{l=2}^\infty {{{\left( {\frac{d}{{{r}}}}\right) }^l}}{P_l}\left( {\cos {S}}\right) \right] , \end{aligned}$$
(1)

where \(\mu _3\) is the gravitational parameter of the third body, d is the distance between the primary and the third body, r is the distance between the primary and the satellite, S is the central elongation between the satellite and the third body, as shown in Fig. 1, and \(P_l\) are the Legendre polynomials of degree l.

Fig. 1
figure 1

An inner third-body configuration. The primary is located at the center of the reference system, and the orbit of the inner third body is in the XY plane

Full size image

Figure 2 depicts a comparison of the perturbing potential of an inner third body for different values of the maximum value of l. The examined satellite is a variant of Mars Odyssey, having the following orbital elements:

$$\begin{aligned}&a = 17000\text { km}, \quad e = 0.0091, \quad i = 92.977^{\circ } \nonumber \\&\Omega = 91.051^{\circ }, \quad \omega = 270.385^{\circ }, \quad f = 76.912^{\circ }. \end{aligned}$$
(2)

Except for the semimajor axis, these are the actual orbital elements of Mars Odyssey as of January 1, 2009, provided by NASA’s HORIZONS databaseFootnote 1. In such an orbit, Phobos induces an inner third-body perturbation upon the satellite.

Fig. 2
figure 2

The perturbing potential of Phobos on a Mars Odyssey orbiter variant

Full size image

As shown in Fig. 2, taking the first Legendre polynomial, \(l=2\), gives a reasonable approximation of the perturbing potential. We will refer to the region in which the model of the inner third body is valid as the inner third-body region. For a more accurate calculation of the total perturbing potential, the perturbation of Deimos should be taken into account. However, we will still use the Mars–Phobos system as a practical means to test the results of the model, by comparing it with the results of GMAT (NASA’s General Mission Analysis Tool) when Phobos is the only perturbation source. In what follows, we focus on modeling the dynamics given a single inner third body.

We start by approximating the perturbing potential while taking only \(P_2\). According to spherical trigonometry, the cosine of the central elongation is given by (Nie and Gurfil 2018)

$$\begin{aligned} \cos (S) = \sin {\left( M_{3} - \Omega \right) } \sin {\left( \omega + f \right) } \cos {\left( i \right) } + \cos {\left( M_{3} - \Omega \right) } \cos {\left( \omega + f \right) }, \end{aligned}$$
(3)

where \(M_3\) is the mean anomaly of the third body, \(\Omega \) is the satellite’s right ascension of ascending node (RAAN), \(\omega \) is its argument of periapsis, f is the true anomaly of the satellite, and i is the satellite’s inclination.

Substituting Eq. (3) into Eq. (1) yields the perturbing potential of an inner third body in terms of the orbital elements:

$$\begin{aligned} R= & {} \frac{\mu _{3}}{2 d^{2} r^{3}} \left[ d^{4} (3 (\sin {(M_{3} - \Omega )} \sin {(\omega + \theta )} \cos {(i )} + \cos {(M_{3} - \Omega )} \cos {(\omega + \theta )})^{2} - 1) \right. \nonumber \\&\left. +\, 2 d^{2} r^{2} + 2 r (d^{3} - r^{3}) (\sin {(M_{3} - \Omega )} \sin {(\omega + \theta )} \cos {(i )} \right. \nonumber \\&\left. +\, \cos {(M_{3} - \Omega )} \cos {(\omega + \theta )})\right] . \end{aligned}$$
(4)

In order to eliminate the short-period variations, the disturbing function is averaged with respect to the mean anomaly of the third body:

$$\begin{aligned} \begin{aligned} R_\mathrm{a}&= \frac{1}{{2\pi }}\int \limits _0^{2\pi }{R \mathrm{d}M_3} \\&= \frac{\mu _{3}}{4 r^{3}} \left[ 3 d^{2} \sin ^{2}{(\Omega )} \sin ^{2}{(\omega + f )} \cos ^{2}{(i )} + 3 d^{2} \sin ^{2}{(\Omega )} \cos ^{2}{(\omega + f )} + 4 r^{2} \right. \\&\left. \quad +\, 3 d^{2} \sin ^{2}{(\omega + f )} \cos ^{2}{(\Omega )} \cos ^{2}{(i )} + 3 d^{2} \cos ^{2}{(\Omega )} \cos ^{2}{(\omega + f )} - 2 d^{2}\right. ]. \end{aligned} \end{aligned}$$
(5)

The elimination of the medium-period variations is performed by integrating \(R_\mathrm{a}\) with respect to the mean anomaly of the satellite. This integration is somewhat more complicated, due to the dependency of r on f,

$$\begin{aligned} r=\frac{a\left( 1-e^2\right) }{1+e\cos (f)}. \end{aligned}$$
(6)

The doubly averaged perturbing potential is

$$\begin{aligned} R_\mathrm{da}=\dfrac{1}{{2\pi }}\int \limits _0^{2\pi }{R_\mathrm{a} \mathrm{d}M}=\dfrac{1}{{2\pi }}\int \limits _0^{2\pi }{I \mathrm{d}f}, \quad I=\dfrac{r^2}{a^2\sqrt{1-e^2}}R_\mathrm{a}, \end{aligned}$$
(7)

according to the relation \(\frac{\mathrm{d}f}{\mathrm{d}M}=\frac{a^2}{r^2}\sqrt{1-e^2}\).

Substituting Eqs. (5) and (6) into I, we get after some manipulations

$$\begin{aligned} \begin{aligned} I&= \frac{\mu _{3} g(e, f)}{8 \pi a^{3} (1 - e^{2})^{1.5}} \left[ 8 \pi a^{2} (1 - e^{2})^{2} + 3 d^{2} (e \cos {f } + 1)^{2} (\sin {\Omega } \cos ^{2}{(\omega + f )} \right. \\&\quad \left. -\, \sin {\Omega } \sin ^{2}{(\omega + f )} \cos ^{2}{i } + 2 \sin {(\omega + f )} \cos {\Omega } \cos {i } \cos {(\omega + f )}) \cos {\Omega } \right. \\&\quad \left. -\, \frac{d^{2}}{32} (e \cos {f } + 1)^{2} (12 \sin {(2 \Omega )} - 6 \sin {(2 \Omega - 2 i )} + 24 \pi \cos {(2 i + 2 \omega + 2 f )} \right. \\&\quad \left. -\, 18 \sin {(- 2 \Omega + 2 \omega + 2 f )} + 18 \sin {(2 \Omega + 2 \omega + 2 f )} + 24 \sin {(- i + 2 \omega + 2 f )} \right. \\&\quad \left. +\, 24 \sin {(i + 2 \omega + 2 f )} + 12 \sin {(- 2 \Omega + i + 2 \omega + 2 f )} - 48 \pi \cos {(2 \omega + 2 f )} \right. \\&\quad \left. + \,3 \sin {(2 \Omega - 2 i + 2 \omega + 2 f )} + 12 \sin {(2 \Omega - i + 2 \omega + 2 f )} - 48 \pi \cos {(2 i )} \right. \\&\quad \left. +\, 12 \sin {(2 \Omega + i + 2 \omega + 2 f )} + 3 \sin {(2 \Omega + 2 i - 2 \omega - 2 f )} - 6 \sin {(2 \Omega + 2 i )} \right. \\&\quad \left. +\, 3 \sin {(2 \Omega + 2 i + 2 \omega + 2 f )} - 3 \sin {(- 2 \Omega + 2 i + 2 \omega + 2 f )} - 16 \pi \right. \\&\quad \left. +\, 24 \pi \cos {(- 2 i + 2 \omega + 2 f )} - 12 \sin {(2 \Omega + i - 2 \omega - 2 f )})\right] , \end{aligned} \end{aligned}$$
(8)

where \(g(e, f)=\frac{1}{e \cos {(f )} + 1}\).

In order to facilitate the analysis, we will assume a small eccentricity for the satellite. In this case, we can approximate g(e, f) using its Taylor expansion up to the second order in e, i.e.,

$$\begin{aligned} g(e, f) \approx 1 - e \cos {\left( f \right) } + e^{2} \cos ^{2}{\left( f \right) }. \end{aligned}$$
(9)

Having simplified g(e, f), we can integrate I to get the doubly averaged perturbing potential of an inner third body:

$$\begin{aligned} \begin{aligned} R_\mathrm{da} = \frac{1}{{2\pi }}\int \limits _0^{2\pi }{I \mathrm{d}f} = \frac{\mu _{3}}{48 a^{3}} \left( 48 a^{2} - 27 d^{2} e^{2} \sin ^{2}{i} + 18 d^{2} e^{2} - 18 d^{2} \sin ^{2}{i} + 12 d^{2}\right) . \end{aligned}\nonumber \\ \end{aligned}$$
(10)

3 Orbital element evolution

In this section, we derive the rates of the orbital elements and present the equivalence to the \(J_2\) problem for near-circular orbits of the satellite.

3.1 Derivation of the orbital element rates

Having found \(R_\mathrm{da}\), its partial derivatives are given by

$$\begin{aligned} \frac{{\partial R_\mathrm{da}}}{{\partial a}}= & {} \frac{\mu _{3}}{a^{4}} \left( \frac{27}{16} d^{2} e^{2} \sin ^{2}{(i )} - a^{2} - \frac{9}{8} d^{2} e^{2} + \frac{9}{8} d^{2} \sin ^{2}{(i )} - \frac{3}{4} d^{2}\right) , \quad \frac{{\partial R_\mathrm{da}}}{{\partial \omega }} = 0 \nonumber \\ \frac{{\partial R_\mathrm{da}}}{{\partial e}}= & {} \frac{d^{2} e \mu _{3}}{24 a^{3}} (18 - 27 \sin ^{2}{(i )}), \quad \quad \frac{{\partial R_\mathrm{da}}}{{\partial i}} = - \frac{d^{2} \mu _{3}}{48 a^{3}} (18 + 27 e^{2}) \sin {(2 i )}. \end{aligned}$$
(11)

The partial derivatives \(\frac{{\partial R_\mathrm{da}}}{{\partial M}}\) and \(\frac{{\partial R_\mathrm{da}}}{{\partial \Omega }}\) are equal to zero due to the averaging of the perturbing potential over the anomalies of the satellite and the third body.

In order to find the doubly averaged rates of the orbital elements, the partial derivatives of the perturbing potential are substituted into the Lagrange planetary equations (Alfriend et al. 2010):

$$\begin{aligned} {\dot{a}}= & {} \frac{2}{na}\frac{{\partial R_\mathrm{da}}}{{\partial M}} \nonumber \\ {\dot{e}}= & {} -\frac{\sqrt{1-e^2}}{na^2e}\frac{{\partial R_\mathrm{da}}}{{\partial \omega }}+\frac{1-e^2}{na^2e}\frac{{\partial R_\mathrm{da}}}{{\partial M}} \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} -\frac{1}{na^2\sqrt{1-e^2}\sin (i)}\frac{{\partial R_\mathrm{da}}}{{\partial \Omega }}+\frac{\cot (i)}{na^2\sqrt{1-e^2}}\frac{{\partial R_\mathrm{da}}}{{\partial \omega }} \nonumber \\ {\dot{\Omega }}= & {} \frac{1}{na^2\sqrt{1-e^2}\sin (i)}\frac{{\partial R_\mathrm{da}}}{{\partial i}} \nonumber \\ {\dot{\omega }}= & {} \frac{\sqrt{1-e^2}}{na^2e}\frac{{\partial R_\mathrm{da}}}{{\partial e}}-\frac{\cot (i)}{na^2\sqrt{1-e^2}}\frac{{\partial R_\mathrm{da}}}{{\partial i}} \nonumber \\ {\dot{M}}= & {} n-\frac{2}{na}\frac{{\partial R_\mathrm{da}}}{{\partial a}}-\frac{1-e^2}{na^2e}\frac{{\partial R_\mathrm{da}}}{{\partial e}}, \end{aligned}$$
(12)

where \(n=\sqrt{\frac{\mu }{a^3}} = \sqrt{\frac{\mu _3}{Ka^3}}\), \(d=\root 3 \of {\frac{\mu }{n_m^2}}=\root 3 \of {\frac{\mu _3}{Kn_m^2}}\) with \(n_m\) being the mean motion of the third body, and \(K=\frac{\mu _3}{\mu }\). The resulting rates of the orbital elements due to the gravitational perturbation induced by an inner third body are, therefore,

$$\begin{aligned} {\dot{a}}= & {} {\dot{e}} = \frac{\mathrm{d}i}{\mathrm{d}t} = 0 \nonumber \\ {\dot{\Omega }}= & {} -C_1 \frac{3e^2 + 2}{\sqrt{\left( 1-e^2\right) a^7}}\cos (i) \nonumber \\ {\dot{\omega }}= & {} C_1 \frac{2e^2 + 5\cos (2i) + 3}{2\sqrt{\left( 1-e^2\right) a^7}} \nonumber \\ {\dot{M}}= & {} \frac{C_1}{2 \sqrt{a^{7}}} \left( 16e^2 - 24e^2 \sin ^2(i) + 3\cos (2i) + 1 \right) + \frac{C_2}{\sqrt{a^3}}, \end{aligned}$$
(13)

where \(C_1\) and \(C_2\) are given by

$$\begin{aligned} C_1=\frac{3}{8} \root 6 \of {\frac{\mu _3^7}{K n_m^8}}, \quad C_2 = \left( 2\sqrt{K}+\frac{1}{\sqrt{K}}\right) \sqrt{\mu _3}. \end{aligned}$$
(14)

There are several insights gained. First, the doubly averaged semimajor axis, eccentricity and inclination remain constant. Because the three mean momenta elements remain constant, the mean rates of change of \(\Omega \) and \(\omega \) are constant as well.

The analysis presented thus far could have been conducted while taking into consideration an additional Legendre polynomial. Doing so would have given a more accurate approximation of the perturbing potential,

$$\begin{aligned} \begin{aligned} R&= \frac{\mu _{3}}{2 d^{2} r^{4}} \left[ \cos (S) d^{5} (5 \cos ^{2}(S) - 3) + 2 \cos (S) r^{2} (d^{3} - r^{3}) + 2 d^{2} r^{3} \right. \\&\quad \left. +\, d^{4} r (3 \cos ^{2}(S) - 1)\right] , \end{aligned} \end{aligned}$$
(15)

which takes into account \(P_3\). However, using Eq. (15) leads to the same rates of the doubly averaged orbital elements presented in Eq. (13).

3.2 Model applicability limits

The model applicability limits can be developed as a function of the ratio between the semimajor axes of the perturbed and the perturbing bodies, denoted by Q. We can evaluate the errors introduced by neglecting the fourth Legendre polynomial, which provides a good estimate of the errors of the model in Eq. (13).

The orbital rates can be calculated while taking into account all Legendre polynomials up to the fourth degree in Eq. (1). Based on that calculation, and defining \(Q = {a}/{d}\),  \(d=\root 3 \of {\frac{\mu _3}{Kn_m^2}}\), the corresponding error of each orbital element is obtained as a function of Q:

$$\begin{aligned} {\dot{a}}_\mathrm{err}= & {} 0 \nonumber \\ {\dot{e}}_\mathrm{err}= & {} \frac{45 K n_{m}}{256 Q^{5.5}} e \sqrt{1 - e^{2}} \left( 6 - 7 \sin ^{2}{\left( i \right) }\right) \sin ^{2}{\left( i \right) } \sin {\left( 2 \omega \right) }\nonumber \\ \left( \frac{\mathrm{d}i}{\mathrm{d}t}\right) _\mathrm{err}= & {} \frac{45 K n_{m} e^{2}}{4096 Q^{5.5} \sqrt{1 - e^{2}}} (7 \left( \cos {\left( 4 i + 2 \omega \right) } - \cos {\left( 4 i - 2 \omega \right) }\right) \nonumber \\&\,+ 10 \left( \cos {\left( 2 i + 2 \omega \right) } - \cos {\left( 2 i - 2 \omega \right) }\right) )\nonumber \\ {\dot{\Omega }}_\mathrm{err}= & {} \frac{45 K n_{m}}{128 Q^{5.5} \sqrt{1 - e^{2}}} (14 e^{2} \sin ^{2}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 28 e^{2} \sin ^{2}{\left( i \right) } - 6 e^{2} \sin ^{2}{\left( \omega \right) } \nonumber \\&-\, 17 e^{2} + 7 \sin ^{2}{\left( i \right) } - 4) \cos {\left( i \right) }\nonumber \\ {\dot{\omega }}_\mathrm{err}= & {} \frac{45 K n_{m}}{128 Q^{5.5} \sqrt{1 - e^{2}}} (7 e^{2} \sin ^{4}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 14 e^{2} \sin ^{4}{\left( i \right) } - 28 e^{2} \sin ^{2}{\left( i \right) } + 13 e^{2} \nonumber \\&-\, 14 e^{2} \sin ^{2}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 6 e^{2} \sin ^{2}{\left( \omega \right) } - 28 \sin ^{2}{\left( i \right) } + 8\nonumber \\&+\, 7 \sin ^{4}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 21 \sin ^{4}{\left( i \right) } - 6 \sin ^{2}{\left( i \right) } \sin ^{2}{\left( \omega \right) })\nonumber \\ {\dot{M}}_\mathrm{err}= & {} \frac{45 K n_{m}}{256 Q^{5.5}} (84 e^{2} \sin ^{4}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 168 e^{2} \sin ^{4}{\left( i \right) } - 72 e^{2} \sin ^{2}{\left( i \right) } \sin ^{2}{\left( \omega \right) } \nonumber \\&-\, 204 e^{2} \sin ^{2}{\left( i \right) } + 48 e^{2} - 14 \sin ^{4}{\left( i \right) } \sin ^{2}{\left( \omega \right) } + 7 \sin ^{4}{\left( i \right) } \nonumber \\&+\, 12 \sin ^{2}{\left( i \right) } \sin ^{2}{\left( \omega \right) } - 6 \sin ^{2}{\left( i \right) }). \end{aligned}$$
(16)

As seen in Eq. (16), the resulting errors in the orbital element rates (except for the semimajor axis) are proportional to \(Q^{-5.5}\), which indicates that the error drops quickly as the ratio between the semimajor axes of the perturbed and perturbing bodies grows. Also, no error has been introduced in the rate of change of the semimajor axis by omitting the fourth Legendre polynomial.

3.3 Comparison to an external third-body perturbation model

Recall the known doubly averaged orbital rates of the classical external third-body perturbation (Nie et al. 2019):

$$\begin{aligned} {\dot{a}}= & {} 0 \nonumber \\ {\dot{e}}= & {} \frac{15 K n_m^2 a^{\frac{3}{2}}}{8 \sqrt{\mu }} e \sqrt{1 - e^2} \sin ^2(i) \sin (2 \omega ) \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} -\frac{15 K n_m^2 a^{\frac{3}{2}}}{16 \sqrt{\mu }} \frac{e^2}{\sqrt{1 - e^2}} \sin (2i) \sin (2 \omega ) \nonumber \\ {\dot{\Omega }}= & {} \frac{3K n_m^2 a^{\frac{3}{2}}}{8 \sqrt{(1 - e^2)\mu }} \left[ 5e^2 \cos (2 \omega ) - 3e^2 - 2\right] \cos (i) \nonumber \\ {\dot{\omega }}= & {} \frac{3K n_m^2 a^{\frac{3}{2}}}{8 \sqrt{(1 - e^2)\mu }} \left[ 5(\sin ^2(i) - e^2)\cos (2 \omega ) + 5 \cos ^2(i) + e^2 - 1\right] \nonumber \\ {\dot{M}}= & {} \frac{\sqrt{\mu }}{a^{\frac{3}{2}}} - \frac{K n_m^2 a^{\frac{3}{2}}}{8 \sqrt{\mu }}\left[ 15(e^2 + 1)\sin ^2(i)\cos (2 \omega ) + (3e^2 + 7)(3\cos ^2(i) - 1)\right] . \end{aligned}$$
(17)

Unlike Eq. (17), the resulting rates of the inner third-body problem, Eq. (13), do not depend on the argument of perigee. Furthermore, in the classical case of a third-body perturbation both the mean eccentricity and the mean inclination change over time. In the case of an inner third body, however, both the mean eccentricity and the mean inclination are constant. These changes compared to the classical model result from the fact that \(r>d\).

3.4 \(J_2\) analogy

We now consider the \(J_2\) problem and its similarities to the inner third-body problem. Both problems can be modeled by a rotating dipole of masses which generate a gravitational field. The concept of modeling the zonal harmonics as a mass dipole was first published by Aksenov et al. (1962) and is called two fixed centers (TFC).

We show here that for near-circular orbits, the \(J_2\) problem and the inner third-body problem are equivalent and share a general, unified solution. Recall the secular orbital element evolution of the \(J_2\) problem:

$$\begin{aligned} {\dot{a}}_{J2}= & {} {\dot{e}}_{J2} = \frac{\mathrm{d}i_{J2}}{\mathrm{d}t} = 0 \nonumber \\ {\dot{\Omega }}_{J2}= & {} -\frac{3 J_2 R_\mathrm{eq}^2 \sqrt{\mu }}{2 a^{\frac{7}{2}} (1-e^2)^2}\cos (i) \nonumber \\ {\dot{\omega }}_{J2}= & {} \frac{3 J_2 R_\mathrm{eq}^2 \sqrt{\mu }}{8 a^{\frac{7}{2}} (1-e^2)^2}(5\cos (2i)+3) \nonumber \\ {\dot{M}}_{J2}= & {} \frac{3 J_2 R_\mathrm{eq}^2 \sqrt{\mu }}{8 a^{\frac{7}{2}} (1-e^2)^{\frac{3}{2}}}(3\cos (2i)+1) + \sqrt{\frac{\mu }{a^3}}. \end{aligned}$$
(18)

For near-circular orbits, the rates of the inner third-body case can be approximated by the following form:

$$\begin{aligned} {\dot{a}}_{I3}= & {} {\dot{e}}_{I3} = \frac{\mathrm{d}i_{I3}}{\mathrm{d}t} = 0 \nonumber \\ {\dot{\Omega }}_{I3}= & {} -\frac{2C_1}{\sqrt{a^7}}\cos (i) \nonumber \\ {\dot{\omega }}_{I3}= & {} \frac{C_1}{2\sqrt{a^7}}\left[ 5\cos (2i) + 3\right] \nonumber \\ {\dot{M}}_{I3}= & {} \frac{C_1}{2 \sqrt{a^{7}}} \left[ 3\cos (2i) + 1 \right] + \frac{C_2}{\sqrt{a^3}}. \end{aligned}$$
(19)

Thus, in the near-circular approximation, both the \(J_2\) problem and the inner third-body problem yield orbital element rates of the form:

$$\begin{aligned} {\dot{a}}= & {} {\dot{e}} = \frac{\mathrm{d}i}{\mathrm{d}t} = 0 \nonumber \\ {\dot{\Omega }}= & {} \alpha a^{-3.5} \cos (i) \nonumber \\ {\dot{\omega }}= & {} \beta a^{-3.5} \left[ 5\cos (2i) + 3\right] \nonumber \\ {\dot{M}}= & {} \gamma a^{-3.5} \left[ 3\cos (2i) + 1 \right] + \delta , \end{aligned}$$
(20)

where \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \) are constants whose values are determined by the configuration of the system (whether it describes the gravitational field of an oblate planet or a planet with its moon). The values of \(\alpha , \beta , \gamma , \delta \) for the inner third-body configuration (I3) and the oblate planet configuration (J2) are:

$$\begin{aligned} \alpha _{I3}= & {} -2C_1, \beta _{I3} = \frac{C_1}{2}, \gamma _{I3} = \frac{C_1}{2}, \delta _{I3} = \frac{C_2}{\sqrt{a^3}} \nonumber \\ \alpha _{J2}= & {} -\frac{3}{2} J_2 R_\mathrm{eq}^2 \sqrt{\mu }, \beta _{J2} = \frac{3}{8} J_2 R_\mathrm{eq}^2 \sqrt{\mu }, \gamma _{J2} = \frac{3}{8} J_2 R_\mathrm{eq}^2 \sqrt{\mu }, \delta _{J2} = \sqrt{\frac{\mu }{a^3}}. \end{aligned}$$
(21)

Without assuming a near-circular orbit, the rate of change of the argument of perigee in Eq. (13) would have maintained its additional component of the order of \(e^2\), which does not exist in the rate of change of the argument of perigee in Eq. (18).

In order to describe the dynamics of a satellite in a near-circular orbit, Eq. (21) implies that a problem of an inner third body with \(\mu _3\), \(n_m\) and K can be replaced with a problem of an oblate planet with an effective standard gravitational parameter of \(\mu _\mathrm{eff} = C_2\) and effective zonal coefficient and equatorial radius that satisfy the relation

$$\begin{aligned} J_\mathrm{2,eff} R_\mathrm{eq,eff}^2 = \frac{4C_1}{3\sqrt{C_2}} = \frac{\mu _3^{\frac{11}{12}}}{2 n_m^{\frac{4}{3}} \sqrt{2K^{\frac{5}{6}} + K^{-\frac{1}{6}}}}. \end{aligned}$$
(22)

4 Applications

Here, we use the derived orbital element rates in order to calculate the long-term evolution of the orbital elements of a satellite in an inner third-body region of the Martian system, under the gravitational perturbation of Phobos.

To test the model, we used GMAT to simulate the orbit propagation of a satellite in the inner third-body region around Mars. The force model included the inner third-body perturbation of Phobos, taken as a point mass. Gravitational harmonics were disabled in order to exclusively examine the effects of the inner third body. The ephemeris source was mar085.bsp, an SPK SPICE kernel provided by the JPL database. Simulation results were calculated using the default GMAT integrator with respect to an inertial frame, with Mars at the origin.

We considered two satellites. The first satellite has a variant orbit of the orbiter MAVEN, with the following initial orbital elements:

$$\begin{aligned} a= & {} 28131\text { km}, \quad e = 0.1, \quad i = 160^{\circ } \nonumber \\ \Omega= & {} 29.16^{\circ }, \quad \omega = 29.075^{\circ }, \quad f = 114.256^{\circ }. \end{aligned}$$
(23)

\(\Omega \), \(\omega \) and f are the orbital elements of MAVEN as of January \(1^{\text {st}}\) 2019, provided by NASA’s HORIZONS database. \(e=0.1\) is small enough to justify the use of the model  (13), and \(a=28131\) km places the satellite in the inner third-body region.

The second satellite has the same initial orbital elements as in Eq. (23) except for the initial inclination, i.e.,

$$\begin{aligned} a= & {} 28131\text { km}, \quad e = 0.1, \quad i = 74.92^{\circ } \nonumber \\ \Omega= & {} 29.16^{\circ }, \quad \omega = 29.075^{\circ }, \quad f = 114.256^{\circ }. \end{aligned}$$
(24)

The inclination of the second satellite is the actual inclination of MAVEN at the said time.

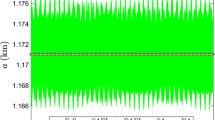
Figure 3 shows simulation results corresponding to the first satellite. Simulation time was 3 years. The results include the long-term change predicted by the model (13) and the osculating elements that were simulated using GMAT. As seen, there is a good correlation between the derived averaged model and the GMAT simulated non-averaged results.

Fig. 3
figure 3

The propagation of eccentricity, inclination, right ascension of ascending node and argument of perigee of a variant orbit of the orbiter MAVEN. Initial inclination is \(160^{\circ }\)

Full size image
Fig. 4
figure 4

The evolution of the orbital elements when propagating the inner third-body orbital element rates and the classical third-body orbital element rates in an inner third-body system

Full size image

Figure 4 shows the simulation results corresponding to the second satellite. Simulation time was 100 days. The results include the evolution of the orbital elements when propagating the inner third-body rates, Eq. (13), and the classical third-body rates, Eq. (17), in an inner third-body system. As expected, naïve integration of the classical third-body perturbation model cannot be used in an inner third-body system, as the evaluated averaged elements diverge away from their osculating counterparts.

It can be seen that the predicted rate of change in the right ascension of the ascending node is slightly different from the one simulated by GMAT. This difference is the result of assuming that the satellite is sufficiently farther from Mars compared with the orbital radius of the inner third body. When increasing the semimajor axis of the satellite, the predicted right ascension of the ascending node converges to the simulated results of GMAT.

The aforementioned simulations correspond to \(Q = 3\), which provides good accuracy. Because the errors in the orbital rates are proportional to \(Q^{-5.5}\), increasing the semimajor axis of the satellite by a factor of two will reduce the error by a factor of about 45.

As mentioned earlier, the simulations do not include the gravity model of Mars (except for the Keplerian term), in order to exclusively examine the effects of the inner third body. Although the gravity field of Mars is the dominant perturbation source, we disabled it without exploring the error introduced, as the focus herein is on modeling the inner third-body dynamics. A future work will focus on the possible applications of the model and the errors introduced when neglecting or approximating the gravity field.

5 Accommodating the third-body eccentricity

Here, we generalize the analytic model to consider a nonzero eccentricity for the orbit of the third body. In the case of a third body with an elliptical orbit, the cosine of the central elongation is given by

$$\begin{aligned} \cos (S) = \sin {\left( f_{3} + \omega _{3} - \Omega \right) } \sin {\left( \omega + f \right) } \cos {\left( i \right) } + \cos {\left( f_{3} + \omega _{3} - \Omega \right) } \cos {\left( \omega + f \right) }.\nonumber \\ \end{aligned}$$
(25)

Substituting Eq. (25) into Eq. (1), we get

$$\begin{aligned} R= & {} \frac{\mu _{3}}{2 d^{2} r^{3}} [d^{4} (3 (\sin {(\omega + f )} \sin {(- \Omega + \omega _{3} + f_{3} )} \cos {(i )} \nonumber \\&+\, \cos {(\omega + f )} \cos {(- \Omega + \omega _{3} + f_{3} )})^{2} - 1) \nonumber \\&+\, 2 d^{2} r^{2} + \cos {(\omega + f )} \cos {(- \Omega + \omega _{3} + f_{3} )} \nonumber \\&+\, 2 r (d^{3} - r^{3}) (\sin {(\omega + f )} \sin {(- \Omega + \omega _{3} + f_{3} )} \cos {(i )})]. \end{aligned}$$
(26)

Given R in terms of the orbital elements, we can integrate the potential with respect to the anomalies of the third body and the satellite. The doubly averaged perturbing potential is thus obtained by

$$\begin{aligned} R_\mathrm{da}=\frac{1}{{4\pi ^2}}\int \limits _0^{2\pi }{\int \limits _0^{2\pi }{R \mathrm{d}M_3} \mathrm{d}M} = \frac{1}{{4\pi ^2}}\int \limits _0^{2\pi }{\int \limits _0^{2\pi }{\tilde{I} \mathrm{d}f_3} \mathrm{d}f}, \end{aligned}$$
(27)

where

$$\begin{aligned} \tilde{I}=\left( \dfrac{r r_3}{a a_3}\right) ^2\dfrac{R}{\sqrt{\left( 1-e^2\right) \left( 1-e_3^2\right) }}. \end{aligned}$$
(28)

Substituting Eqs. (6), (26), and the relation \(r_3=\frac{a_3\left( 1-e_3^2\right) }{1+e_3\cos (f_3)}\) into Eq. (28), and assuming a near-circular orbit both for the satellite and for the third body, we can approximate \(\tilde{I}\) using a Taylor expansion up to the second order in \(e_3\) and then in e. The resulting doubly averaged perturbing potential is

$$\begin{aligned} R_\mathrm{da}= & {} \frac{\mu _{3}}{4a^{3}} \left[ \frac{45}{2} a_{3}^{2} e^{2} e_{3}^{2} \sin {(\Omega )} \sin ^{2}{(i )} \sin {(\omega _{3} )} \cos {(\Omega - \omega _{3} )} - \frac{9}{4} a_{3}^{2} e^{2} \sin ^{2}{(i )}\right. \nonumber \\&-\, \frac{45}{4} a_{3}^{2} e^{2} e_{3}^{2} \sin ^{2}{(i )} \sin ^{2}{(\omega _{3} )} + \frac{9}{4} a_{3}^{2} e^{2} e_{3}^{2} \sin ^{2}{(i )} - \frac{3}{2} a_{3}^{2} \sin ^{2}{(i )} \nonumber \\&-\, \frac{45}{4} a_{3}^{2} e^{2} e_{3}^{2} \sin ^{2}{(\Omega )} \sin ^{2}{(i )} + \frac{3}{2} a_{3}^{2} e^{2} - \frac{15}{2} a_{3}^{2} e_{3}^{2} \sin ^{2}{(\Omega )} \sin ^{2}{(i )} \nonumber \\&-\, \frac{15}{2} a_{3}^{2} e_{3}^{2} \sin ^{2}{(i )} \sin ^{2}{(\omega _{3} )} + \frac{3}{2} a_{3}^{2} e_{3}^{2} \sin ^{2}{(i )} + \frac{3}{2} a_{3}^{2} e_{3}^{2} + 4 a^{2} + a_{3}^{2} \nonumber \\&\left. +\, 15 a_{3}^{2} e_{3}^{2} \sin {(\Omega )} \sin ^{2}{(i )} \sin {(\omega _{3} )} \cos {(\Omega - \omega _{3} )} + \frac{9}{4} a_{3}^{2} e^{2} e_{3}^{2}\right] , \end{aligned}$$
(29)

where \(a_3=\root 3 \of {\frac{\mu _3}{Kn_m^2}}\). The corresponding rates of the doubly averaged orbital elements are obtained as previously using the Lagrange planetary equations:

$$\begin{aligned} {\dot{a}}= & {} {\dot{e}} = 0 \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} \frac{e_3^2 C_1}{2\sqrt{\left( 1 - e^2\right) a^7}} (15 e^{2} + 10) \sin {(i )} \sin {(2 \Omega - 2 \omega _{3} )} \nonumber \\ {\dot{\Omega }}= & {} -C_1\frac{3 e^{2} + 2 + e_3^2 h_1\left( e,\omega _{3},\Omega \right) }{\sqrt{\left( 1 - e^2\right) a^7}} \cos {(i )} \nonumber \\ {\dot{\omega }}= & {} C_1 \frac{2e^2 + 5\cos (2i) + 3 + e_3^2h_2\left( e,i,\omega _{3},\Omega \right) }{2\sqrt{\left( 1 - e^2\right) a^7}} \nonumber \\ {\dot{M}}= & {} \frac{C_1}{2\sqrt{a^7}} (16 e^{2} - 24 e^{2} \sin ^{2}{(i )} + 3 \cos (2i) + 1 +e_3^2h_3\left( e,i,\omega _{3},\Omega \right) ) + \frac{C_2}{\sqrt{a^3}},\nonumber \\ \end{aligned}$$
(30)

where \(C_1\) and \(C_2\) are given in Eq. (14) and

$$\begin{aligned} h_1\left( e,\omega _{3},\Omega \right)= & {} 15 e^{2} \sin ^{2}{\Omega } - 30 e^{2} \sin {\Omega } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} + 15 e^{2} \sin ^{2}{\omega _{3} } - 2 \nonumber \\&+\, 10 \sin ^{2}{\Omega } - 20 \sin {\Omega } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} + 10 \sin ^{2}{\omega _{3} } - 3 e^{2} \nonumber \\ h_2\left( e,i,\omega _{3},\Omega \right)= & {} 30 e^{2} \sin ^{2}{\Omega } - 60 e^{2} \sin {\Omega } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} + 30 e^{2} \sin ^{2}{\omega _{3} } \nonumber \\&-\, 50 \sin ^{2}{i } \sin ^{2}{\omega _{3} } - 12 e^{2} - 50 \sin ^{2}{\Omega } \sin ^{2}{i } + 20 \sin ^{2}{\Omega } + 2 \nonumber \\&+\, 100 \sin {\Omega } \sin ^{2}{i } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} + 20 \sin ^{2}{\omega _{3} } + 10 \sin ^{2}{i } \nonumber \\&-\, 40 \sin {\Omega } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} \nonumber \\ h_3\left( e,i,\omega _{3},\Omega \right)= & {} 240 e^{2} \sin {\Omega } \sin ^{2}{i } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} - 120 e^{2} \sin ^{2}{\Omega } \sin ^{2}{i } \nonumber \\&-\, 30 \sin ^{2}{\Omega } \sin ^{2}{i } - 120 e^{2} \sin ^{2}{i } \sin ^{2}{\omega _{3} } + 24 e^{2} \sin ^{2}{i } + 24 e^{2} \nonumber \\&+\, 6 + 60 \sin {\Omega } \sin ^{2}{i } \sin {\omega _{3} } \cos {(\Omega - \omega _{3} )} - 30 \sin ^{2}{i } \sin ^{2}{\omega _{3} } \nonumber \\&+\, 6 \sin ^{2}{i }. \end{aligned}$$
(31)

In contrast to the case of a third body in a circular orbit, here we see a long-periodic change in the inclination. Another insight is that the effects of the third body’s eccentricity are proportional to the second order of \(e_3\), which renders its influence rather small. In order to illustrate how small the influence is, we consider a hypothetical case wherein Phobos has an eccentricity of 0.15.

Fig. 5
figure 5

The rates of the doubly averaged eccentricity, right ascension of the ascending node, argument of perigee and inclination, in cases of zero and nonzero third-body eccentricities in the case of Mars—when Phobos has a hypothetical eccentricity of 0.15

Full size image

Figure 5 shows a comparison between the rates of the doubly averaged eccentricity, inclination, right ascension of the ascending node and argument of perigee, in the cases of zero and nonzero third-body eccentricities. The setup is the same as presented earlier, with the satellite having the initial orbital elements as in Eq. (24). It can be seen that the differences between the two cases are indeed small, even when the eccentricity of the third body’s orbit was taken to be 0.15. The simulation was set to start in January 1, 2019, lasting about one Earth month during which Phobos’ mean argument of perigee was around \(145^{\circ }\).

6 Conclusions

An expansion of the perturbing potential of an inner third body in terms of Legendre polynomials was examined, and an analysis of the corresponding long-term rates of the orbital elements was introduced. It was shown that for small eccentricity orbits of the satellite, the inner third-body problem is equivalent to the \(J_2\) problem.

We used only the first nonzero Legendre polynomial (\(P_2\)) for the analysis and showed that adding \(P_3\) results in the same rates for a third body in a circular orbit. We applied the inner third-body model on the Mars–Phobos system. The results were compared with a GMAT simulation, demonstrating the validity of the model.

We analyzed the errors introduced by truncating the series of Legendre polynomials at \(P_4\) and gave error estimates for each orbital element rate. The proposed method provides accurate long-term rates if the ratio between the semimajor axes of the perturbed and the perturbing bodies is at least 3.

The presented model was generalized to account for a nonzero eccentricity of the orbit of the third body, and a resulting change in inclination of the satellite has been detected. We showed that the effect of the third body’s eccentricity, \(e_3\), was proportional to \({\left( e_3\right) }^2\), which renders its influence rather small even for eccentricities around \(e_3 = 0.1\).