1 Introduction

Air-quality standards for acute health responses are usually prescribed in terms of concentration means over 1-h, 8-h or 24-h periods, while annual means are more appropriate for long-term effects. Such averaging periods pose no problem for assessing the impact of continuous or instantaneous sources using common dispersion models, as these are normally able to estimate at least 1-h mean concentrations (using ensemble-averaged computational models). However, for the impact assessment of odorant sources, flammable gases and the accidental or intentional release of toxic gases, the estimation of short-term-averaged maximum concentration is often required. For instance, for odour assessment, while a single breath is enough to perceive an odorant gas, regulation from different countries may use rather longer averaging times to identify a nuisance based on the fact that the nuisance arises after a certain number of odour occurrences, and also on odour recognition (which generally occurs at a higher concentration than that for odour perception). For flammable gases, one single occurrence of exceedance of the flash point may be sufficient to ignite a flame, which has to be accounted for in risk assessment. For toxic gases emitted from accidental or intentional releases, although one single breath could be enough to cause acute health impacts, the interest lies in predicting events that occur over a period in which an action can be performed to evacuate the area, i.e. at least minutes after the event has occurred. Therefore, estimating the maximum mean concentration value (peak) in a short time interval as a function of the duration of that interval is of foremost importance, but the averaging time \( \left( {\Delta \tau } \right) \) used for the impact assessment is very dependent on the actual application.

Different techniques have been employed to estimate the maximum mean concentration value for a short time interval, including the maximum instantaneous concentration, i.e., the concentration averaged over the sampling time or the measurement resolution Δt. A technique commonly employed to obtain the maximum instantaneous concentration is to use the concentration cumulative distribution function (CDF), which, according to Bartzis et al. (2008), can be applied for the time-averaged concentration \( \bar{C}\left( {\Delta T} \right) \) provided that the time interval \( \Delta T \) falls well within the inertial range of concentration spectra. The time series of instantaneous concentration can be obtained by high-frequency experimental measurements or numerical simulations using either direct numerical simulation or large-eddy simulation (LES) techniques. For instance, Xie et al. (2004, 2007) obtained a time series of instantaneous concentration using the LES technique to simulate the dispersion of pollutants emitted from ground-level and elevated sources in open terrain under neutral stability conditions, and proposed the use of extreme value theory to post-process LES data for the estimation of the maximum instantaneous concentration. Extreme value theory predicts the extreme concentration by first assuming that the upper tail of the CDF of the concentration time series follows the generalized Pareto distribution. In Xie et al. (2004, 2007), the measured or computed CDF was fitted to that distribution, yielding the necessary parameters, and so enabling the maximum instantaneous (normalized) concentration α to be deduced from

$$ \alpha \equiv \frac{{\bar{C}\left( {\Delta t} \right)_{max} }}{{\bar{C}\left( {\Delta T} \right)}}. $$
(1)

Here, \( \Delta T \) is the long-time averaging period of sufficient length to ensure that the mean concentration \( \bar{C}\left( {\Delta T} \right) \) does not change with further increases in \( \Delta T \), and \( \bar{C}\left( {\Delta t} \right)_{max} \) is the maximum instantaneous concentration, which represents the mean concentration averaged over the sampling time or the measurement resolution Δt.

Xie et al. (2007) found for the highest maximum-relative instantaneous concentration α = 60 at a location nearly three dimensionless distances from an elevated source within a turbulent boundary layer, and about α = 10 at a dimensionless distance around 0.5 from a ground-level source. Other authors have also attempted to estimate maximum instantaneous concentration values by using extreme value theory (Mole et al. 1995; Munro et al. 2001; Bartzis et al. 2015). However, the main criticism of the extreme-value-theory approach is the assumption that the data are independent and identically distributed, which is not in general true for data from turbulent flows. A ‘declustering’ process is, therefore, usually applied to the data before fitting the CDF tail to the Pareto distribution (see, e.g., Xie et al. 2007).

Although it is important to estimate the maximum possible instantaneous concentration, it is also necessary to estimate the maximum mean concentration value over a short time interval \( \Delta \tau \), i.e., for a time interval short enough to identify peak concentrations that may be a nuisance (or dangerous) because of, for example, odours, health responses, and flammability. The value of \( \Delta \tau \) can be larger or even much larger than the sampling rate \( \Delta t \) depending on the desired application. A widely-used technique to estimate the maximum mean concentration as a function of averaging time based on the mean concentration, averaged over a time interval ΔT large enough to stabilize the mean value in real situations (e.g. in the atmosphere), is to assume the validity of the model

$$ \frac{{\bar{C}\left( {\Delta \tau } \right)_{max} }}{{\bar{C}\left( {\Delta T} \right)}} = \left( {\frac{\Delta \tau }{\Delta T}} \right)^{ - p} , $$
(2)

where the exponent p is a real number between zero and one. Example studies are presented by Gifford (1960), Singer (1961), Singer et al. (1963), Hinds (1969), Ramsdell and Hinds (1971), Barry (1971) and Smith (1973). Equation 2, which has no obvious theoretical basis, has also been applied by Mavroidis (2009), Schauberger et al. (2012) and Piringer et al. (2014) and, with some insightful modifications (adjustment to the power-law formulation to include the integral time scale and concentration fluctuation intensity), by Bartzis et al. (2008, 2015).

The ratio of the peak (instantaneous or averaged over a short time interval) to the mean concentration depends on the dispersion processes in the flow, which are predominantly influenced by the degree of turbulent mixing. Therefore, as described by Schauberger et al. (2012) in the context of the atmosphere, the turbulence depends on the atmospheric stability, intermittency, travel time or distance from the source, emission height and source configuration, as well as on the presence of buildings. While the neutrally-stable homogeneous boundary-layer flow containing a single ground-level or elevated source studied by Xie et al. (2004, 2007) is relatively straightforward, several studies have also been made to investigated the influence of a single building, an array of buildings and/or atmospheric stability conditions on the peak-to-mean concentration ratio. Santos et al. (2009) and Liu et al. (2011) investigated the influence of a complex-shaped building on concentration peak values focusing on building orientation and atmospheric stability using, respectively, field and wind-tunnel experiments. De Melo et al. (2012) used well-known Gaussian dispersion models, including the California Puff Model (CALPUFF, Scire et al. 2000) and the American Meteorological Society and U.S. Environmental Protection Agency Regulatory Model (AERMOD, Cimorelli et al. 2005) coupled with the Plume Rise Model Enhancements (PRIME) algorithm to include the effects of a complex-shaped building to estimate the hourly mean concentration, and used Eq. 2 to determine the maximum mean concentrations for shorter averaging times. Dourado et al. (2014) used a fluctuating plume model, also coupled with the PRIME algorithm, to include the effects of a cubic and a complex-shaped building, applied Eq. 2 to calculate the peak-to-mean ratio, and compared the results with field and wind-tunnel data, respectively. According to the authors, the advantage of a fluctuating plume model in relation to analytical models such as AERMOD and CALPUFF is the possibility of estimating the intermittency and other fluctuation statistics, which are additional parameters useful in assessing the impact of short-term concentrations.

Efthimiou and Bartzis (2011) used numerical simulations of the Reynolds-averaged Navier–Stokes equations (RANS) including the concentration fluctuation equation, from which they derived the concentration fluctuation intensity \( C_{rms} /\bar{C}\left( {\Delta T} \right) \) and integral time scale of concentration to calculate the maximum dosage during a time interval \( \Delta \tau \) based on the formulation previously proposed by Bartzis et al. (2008). However, wall-mounted obstacles were treated implicitly using a rough-wall formulation for the surface conditions, rather than explicitly as individual obstacles. Bartzis et al. (2008) compared the modelled peak dosages for a time interval \( \Delta \tau = 0.02\,{\text{s}} \) against field experimental data. The errors found (typically a factor of five) were explained by the poor prediction of the values of \( \bar{C}\left( {\Delta T} \right) \) and \( C_{rms} \) by the particular RANS model they employed. Again, Efthimiou et al. (2017) used a RANS model to predict dosage-base parameters, including the peak concentration due to a puff release in an urban environment, and stated that the peak concentrations were the most challenging parameter to estimate, being systematically underpredicted by the numerical simulations compared with wind-tunnel data. Dourado et al. (2012) used the AERMOD and CALPUFF models together with the power-law function (Eq. 2) and LES models (using two subgrid-scale models: the dynamic Smagorinsky model of Germano et al. 1991, and the wall-adapting local eddy-viscosity model of Nicoud and Ducros 1999) to assess the peak-to-mean concentration ratio around a single cubic building, and compared the results with wind-tunnel data. Perhaps not surprisingly, the peak-to-mean concentration ratio estimated by the Gaussian models through the use of Eq. 2 was underestimated when compared with LES results and wind-tunnel data.

Despite these earlier efforts, there is a general lack of literature addressing the estimation of peak concentrations from sources within an array of obstacles simulating an urban environment and, in particular, evaluating the use of the LES approach to predict such peak concentrations. Our objective is, therefore, to examine the maximum mean concentration values obtained using different averaging times and using wind-tunnel datasets collected over long periods at locations downwind of sources within an urban array, and then to investigate the adequacy of the LES approach for estimating such peak concentrations.

2 Methodology

Wind-tunnel data and results from a LES model are used to investigate the peak-to-mean concentration ratio as a function of the averaging time. It is important to note here that both techniques produce a representation of the full-scale boundary layer. In the full-scale urban boundary layer, mesoscale unsteadiness plays a role in the near-source dispersion (Xie 2011), because the wind direction can usually change significantly, even within a 15-min interval. A conventional wind tunnel cannot simulate large-scale unsteadiness, whereas the LES approach can (again see Xie 2011), making it a worthwhile tool for the investigation of the effects of averaging time on the mean concentrations.

Table 1 presents the characteristic parameters used to represent the domain and fluid flow in both techniques, and also the characteristic parameters representing full scale based on a representative building height of 20 m in a low-density residential area and a central business district in Europe, and assuming that the duration of the wind-tunnel experiments matches 1 h at full scale, which is considered sufficient to integrate all turbulence scales within the planetary boundary layer (micrometeorological effects). Then, the non-dimensional time ΔT should be identical in the wind tunnel and full scale, so that the velocity at full scale may be calculated. Liu et al. (2011) stated that a dimensionless averaging time \( \Delta T^{*} = \Delta T/\left( {L_{ref} /U_{ref} } \right) \) between 200 and 400 yields an acceptable experimental error in the results compared with fully-converged statistical results for \( \Delta T^{*} = 3.6 \times 10^{4} \). However, they also found that the minimum averaging time to reach a sufficiently-converged standard deviation is about \( \Delta T^{*} = 195 \). The ΔT* value (2100, see Table 1) used herein is well in excess of this minimal requirement.

Table 1 Characteristic parameters
Full size table

2.1 Wind-Tunnel Details

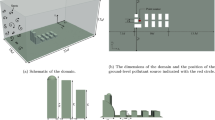
The experimental methodology has been described in Fuka et al. (2017) and Castro et al. (2017) and is only summarized here. All the experiments were conducted in the EnFlo environmental wind tunnel at the University of Surrey, UK, which has a working section of 3.5 m (width) × 20 m (length) × 1.5 m (height). The data analyzed are from an experimental campaign for a uniform array of buildings mounted in a thick, simulated, neutrally-stable atmospheric boundary layer. A flow direction of 0° (i.e. perpendicular to the larger faces of the buildings) was used for all data included herein. Source S1 is identified as in Fuka et al. (2017) and positioned in a long street in the middle of two buildings on the floor, with building dimensions of 2H (width) × H (length) × H (height). The array consists of 14 blocks in the flow direction by 21 blocks in the crosswind direction, and is shown in Fig. 1.

Fig. 1
figure 1

Schematic configuration of a uniform building array and computational and experimental domains. a Three-dimensional schematic domain; b lateral view of sensors 1; c top view of the wind-tunnel domain including the sensor positions and the limits of the LES domain. The letters in the sensor numbers indicate either different vertical positions or different experimental runs

Full size image

The freestream velocity U∞ = 2 m s−1, which gives a Reynolds number \( Re_{\infty } \) ≡ U∞H/ν =7400 or Reτ ≡ uτH/ν = 830 based on the wall friction velocity, where uτ is the friction velocity and ν is the kinematic viscosity, ensures that the 1-m-deep boundary layer is well into the fully-rough regime (Castro et al. 2017). Velocity and turbulence measurements were made using a two-component Dantec laser Doppler anemometer system with a FibreFlow probe of outside diameter 27 mm and focal length 160 mm (150 Hz). Tracer-concentration measurements were performed using a Cambustion fast flame ionization detector sampling at 200 Hz, and the source was a neutrally-buoyant propane/air mixture released from a round tube with a 20-mm internal diameter. The sampling rates are included in Table 1.

2.2 Large-Eddy-Simulation Details

The numerical results used here have been obtained and reported by Castro et al. (2017), whose computations were undertaken using the widely-used OpenFOAM code run on the University of Southampton’s Iridis4 high-performance computing system with typically 256 processor cores. A second-order differencing scheme for the convective and diffusive terms was used, and the time integration employed a second-order backward-differencing scheme. The computational domain size was 12H × 12H × 12H with an array of 24 obstacles (H = 1 m), as shown in Fig. 1. No-slip conditions were imposed on all surfaces (smooth), except at the top of the domain where a stress-free boundary condition was set, with periodicity enforced in the other two directions. The flow was maintained by enforcing a fixed-axial mass flux set to yield a Reynolds number (Reτ ≡ uτH/ν) of approximately 1000. A uniform mesh was used with a grid size equal to H/16. The mixed-time-scale subgrid model proposed by Inagaki et al. (2005) was used, with statistics obtained by averaging over at least \( \Delta T_{\tau }^{*} \)= 710 after an initial development period of at least \( \Delta T_{\tau }^{*} \)= 420. The timestep and scaling parameters are included in Table 1.

2.3 Peak-to-Mean Concentration Ratio

The range of locations used for sampling concentrations is shown in Fig. 1. The peak-to-mean concentration ratio \( \alpha \) (see Eq. 1) is calculated using the whole wind-tunnel and LES datasets (Table 1) for each sensor location. A running average was performed for 22 different averaging times \( \Delta \tau \), and in each case (for each \( \Delta \tau \)) a maximum mean concentration peak \( \bar{C}\left( {\Delta \tau } \right)_{max} \) is found. The value of \( \bar{C}\left( {\Delta T} \right) \) is calculated as the mean concentration over the entire dataset and, thus, for each dataset, the value of α is determined as a function of the averaging time \( \Delta \tau \) to investigate the behaviour in different regions of the array. The three specific (geometric) regions are named as ‘long street’ (e.g. locations 1, 2, 3..), ‘short street’ (e.g. locations 9a, 11a… and 9b, 11b…) and ‘street intersection’ (i.e. locations 8a, 10a… and 8b, 10b…), as shown in Fig. 1.

It is important to note in Fig. 1 that, for the sensors located in the short streets and street intersections, the subscripts ‘a’ and ‘b’ refer to symmetric positions in the array and, therefore, ideally, data from those locations are expected to be very similar. For the sensors located in the central position (long streets), the subscripts ‘a’ and ‘b’ refer to data obtained at identical locations, but from two different experimental runs under the same conditions.

We also note the physical inconsistencies in the peak/mean ratio expressed by Eq. 2: as \( \Delta \tau \to 0 \), \( \bar{C}\left( {\Delta \tau } \right)_{max} \to \infty \) and as \( \Delta \tau \to \infty \), \( \bar{C}\left( {\Delta \tau } \right)_{max} \to 0 \). However, neither can be true in practice since we expect that, as \( \Delta \tau \to \Delta T \), \( \bar{C}\left( {\Delta \tau } \right)_{max} \to \bar{C}\left( {\Delta T} \right) \) and, as the value of \( \Delta \tau \) decreases without reaching zero, the value of \( \bar{C}\left( {\Delta \tau } \right)_{max} \) increases. Therefore, Eq. 2 should be used for \( \Delta t < \Delta \tau < \Delta T \) only. We emphasize that Eq. 2 is simply a reasonably well-attested model, and is not a theoretical result in any sense.

3 Results and Discussion

3.1 Analysis of the Instantaneous Maximum Concentration Data

Figure 2a, b shows the relative maximum instantaneous concentration α measured in the wind tunnel and calculated using the LES model for different monitoring locations. Note that the value of \( \bar{C}\left( {\Delta t} \right)_{max} \) represents the instantaneous concentration measured in the wind-tunnel experiments and estimated from the LES results using a different resolution (sampling rate, as shown in Table 1). Therefore, the value of \( \bar{C}\left( {\Delta t} \right)_{max} \) represents the largest peak concentration (instantaneous maximum concentration) that can be provided by each technique (modelling and experimental).

Fig. 2
figure 2

Longitudinal profile at half the building height of relative concentration fluctuations, the intermittency and the 99th percentile normalized by the mean value measured in the wind tunnel (W) and calculated using the LES model for all monitoring positions. Sensors located in short streets/intersections and in the long street (central position behind the buildings) are shown on the left- and right-hand side, respectively, and X/H indicates the non-dimensional sensor distance from the source. The sensor numbers are as those indicated in Fig. 1

Full size image

In general, it can be seen that the LES results predict smaller peaks than those measured in the wind tunnel, and this difference slightly decreases as the sensor distance from the source increases. As a matter of fact, the wind-tunnel data show a more significant decrease of the peak values with distance from the source than the LES data. The measured wind-tunnel peak values for the sensors located behind the buildings (e.g. location 1, Fig. 2b) are up to six times smaller than for those sensors located in the short streets and intersections (e.g. location 8, Fig. 2a). Recall that sensors 8a and 8b are located at symmetrically-opposite positions and represent different experimental runs under the same conditions. In contrast, the calculated LES peak values for the sensors located behind the buildings are less than about one half of those values obtained at sensors located in the short streets and street intersections. These behaviours are further discussed in Sect. 3.2.

However, it can be seen that, although the data are indeed similar, the sensors at the ‘a’ locations always yield higher relative maximum instantaneous concentrations, especially for the sensors located in the short streets and intersections (Fig. 2a), which can be explained either by a naturally (dynamically) stable but slightly-asymmetric mean flow, despite the nominally-symmetric set-up, and/or by the existence of small asymmetries in the set-up—this whole issue is discussed by Fuka et al. (2017). The asymmetry in the source release in the wind tunnel may have shifted the plume centreline towards the ‘b’ sensors, leaving the ‘a’ sensors to be more affected by eddies in the plume borderline. In contrast, sensors located in the central position are not so much affected by the source-release asymmetry, as expected.

As noted earlier, Xie et al. (2007) used the generalized Pareto distribution to post-process the probability distributions obtained from LES data to predict extreme concentrations in open terrain, finding that the maximum concentration normalized by the local maximum mean concentration (the value of α deduced from the Pareto distribution fitted to the CDF tail) is about 60 at nearly three dimensionless distances from the source for the elevated source, and about 10 at nearly 0.5 dimensionless distances from the ground-level source. These values are similar to the LES results obtained here at the short streets and intersections, but note that we have made no attempt to deduce the maximum possible value of α with our values of α based on the Δt values fixed by the sampling resolution.

The wind-tunnel data show that the relative maximum instantaneous concentration in all regions (intersections, short streets, and central positions) decreases rapidly up to 8H downstream of the source, and then starts to decrease very smoothly, apparently towards a constant. Some discrepancies between the wind-tunnel data and LES results are found closer to the source where the influence of high-frequency eddies on the peak values is stronger.

Figure 2c, d shows that the relative concentration fluctuation (defined as the variance divided by the mean) calculated using the LES results agrees quite well with the wind-tunnel data, which show that the relative concentration fluctuation decreases with distance from the source very rapidly up to 10H, and then continues to decrease slowly. The relative concentration fluctuation is about twice as high for the sensors located in the short streets and intersections than in the central position (behind the buildings), which may be explained by the fact that the source is located in the middle of a long street (central position at half the building height) and, therefore, short street and intersection data are more susceptible to plume meander and any small asymmetrical effects of the wind-tunnel set-up. In contrast, in the central position behind the buildings, the plume is trapped between the buildings and is relatively well mixed.

Xie et al. (2004, 2007) studied the relative concentration fluctuations in plumes over open terrain from passive elevated and ground sources using LES results and wind-tunnel experimental data, finding that the relative concentration fluctuation for a ground source increases significantly with distance from the source up to a distance of 0.25D, where D is the boundary-layer depth, before decreasing to a nearly constant value. In contrast, for an elevated source, the relative concentration fluctuation increases significantly up to a distance of D, and then decreases significantly. Comparing the results obtained here for an urban region with the results obtained by Xie et al. (2004, 2007), the wind-tunnel results yield relative concentration fluctuations of the same order of magnitude. Our results also indicate that the relative concentration fluctuation remains constant far downstream, which is consistent with Xie et al. (2004, 2007), who explained this phenomenon using dimensional analysis, and proved that, for a given constant height (in which case the velocity variance and turbulent Schmidt number are constant), the derivative of turbulence intensity tends to zero as the distance from the source increases.

Intermittency is defined here as the proportion of the concentration time series for which the concentration is at or below a threshold value, which is set here as a nominal zero concentration (Santos et al. 2009). We also calculate the intermittency based on a threshold value defined as the standard error (as proposed for the original wind-tunnel data made available by Fuka et al. 2017), and both sets of results are presented in Fig. 2e, f. In general, the LES results show an intermittency near zero, whilst the wind-tunnel data show higher intermittency in the short streets and intersections, and much lower intermittency in the long streets. It is also clear that intermittency decreases with source distance, with the intermittency almost vanishing from about 12H from the source. Intermittencies in the long streets are an order of magnitude smaller than that in the short streets and intersections. As in open terrain close to the source, the larger eddies are expected to play an important role in moving the (at that stage thin) plume into and away from the sensor location. However, in the immediate building wakes, smaller eddies cause the concentration to be uniformly spread. Note that the intermittencies are much higher if the threshold is defined as the standard error, which is not surprising. The differences between the intermittency calculated by the LES model and that indicated by the wind-tunnel data may explain the results presented in Fig. 2a, b. This is because the value of \( \bar{C}\left( {\Delta T} \right) \) is calculated as a complete mean (i.e. including the nominal zero concentration), implying that the wind-tunnel data produce a lower value of \( \bar{C}\left( {\Delta T} \right) \) and, therefore, a larger relative maximum instantaneous concentration and relative concentration fluctuation, especially closer to the source.

The 99th percentiles, defined as the instantaneous concentration value exceeding 1% of the time, are presented in non-dimensional form in Fig. 2g, h, and calculated based on the instantaneous measurements taken from the complete datasets. The results obtained from the LES results and wind-tunnel data agree well for the sensor locations in the central positions, while the sensors located in the short streets and intersections show the same trend, and agree within a factor of about 1.5. Wind-tunnel data from the short streets and intersections show that the ratio between the 99th percentile and the mean is as high as 14 at 2H downstream from the source, and decreases to four at 11H downstream. The sensors located at the central position show 99th percentiles some two to three times higher than the mean value, depending on the distance from the source. All the above factors would be reduced if lower value percentiles (e.g. 90th rather than 99th) were used. Liu et al. (2011), for example, suggested the use of 90th percentile values calculated using 2-s averaged data for odour assessment, and found that the ratio between the 90th percentile and the mean values ranges from two to five.

3.2 Non-dimensional Concentration Fluctuation Spectra

Figure 3 shows the non-dimensional concentration fluctuation spectra measured in the wind tunnel and calculated using the LES results for a non-dimensional resolution frequency of 5.24 (150 Hz) and 25.9 (100 Hz), respectively. The aliasing frequency, which is half of the resolution frequency above which spectral values mean little, is represented by the dotted line in Fig. 3b for the wind-tunnel data, whereas the non-dimensional aliasing frequency for the LES results is outside the plotting region.

Fig. 3
figure 3

Spectra of non-dimensional concentration fluctuations at half the building height measured in the wind tunnel (W) and calculated using the LES model. Here S is the spectral density. The dotted line in b represents the non-dimensional aliasing frequency (f*H/U∞) for the wind tunnel. Sensors located at the central position are shown on the right-hand side, and sensors located in the intersections and short streets are presented on the left-hand side. Note that locations 6, 7, 19 and 20, g and h, are outside the LES computational domain

Full size image

For all monitoring points, it can be seen that, over a non-dimensional frequency range of two to three decades, the LES and wind-tunnel data essentially collapse. For higher frequencies, however, the LES data decrease unphysically, as also shown by Xie et al. (2007), which indicates that our LES results are not capable of predicting the largest concentration peaks observed in the wind-tunnel data over the shortest time scales. The LES model underpredicts the concentration fluctuation intensities governed by the smaller eddy motions, and we conclude that the particular choice of subgrid-scale model, as well as the grid size, are important in describing the smallest wavelength concentration motions, which is not surprising. In typical LES results, a significant part of the dissipation arises via the subgrid-scale model (Dairay et al. 2017), which certainly has more impact on the simulation of the high-frequency motions, and subsequently the peak concentrations. Another important feature is related to the fact that the LES model underpredicts slightly more for the monitoring points located in the central position (or in the long street, behind the building, see Fig. 3b, d, f, h), since on the short streets and intersections, the advective flows (which are the lowest-frequency motions) are relatively more important for mass transport. It can also be noted in Fig. 3 that, as the source distance increases, the differences between the wind-tunnel data and LES results slightly decrease, as further from the source the pollutants are expected to be better mixed with a low influence of high-frequency eddies on the peak values.

Note that, although the measurement frequency for the wind-tunnel experiments is slightly higher than the frequency implied by the LES timestep (Table 1), the LES spectra show data over a larger non-dimensional frequency range than that for the wind-tunnel spectra, which is simply because the dimensionless LES timestep is much smaller (Table 1). The non-dimensional sampling rate for the wind-tunnel data is thus smaller than the corresponding LES value. It is interesting to note that, despite the fact that the LES spectra display energy at higher frequencies, the amount of energy is almost entirely negligible.

Slopes of − 5/3 and − 1 are shown in Fig. 3, with the former slope indicating the inertial subrange in the velocity spectra. For the wind-tunnel data, for all sensors, the data is better fitted to the − 5/3 slope for non-dimensional frequencies larger than about 0.2, and to − 1 for lower frequencies. In contrast, the LES results fit the − 5/3 slope reasonably from 0.2 to 0.5, and fit a − 1 slope for low frequencies, but spectral values drop drastically for higher frequencies. This behaviour is consistent with that in Xie et al. (2004, 2007), and it is certainly caused by the limited spatial resolution of the LES model.

As discussed by Xie et al. (2007) for dispersion from a point source over open terrain, the characteristics of the concentration-fluctuation spectrum depend on the distance from the source. Close to the source, the turbulence characteristic length scale is large compared with the plume width and, therefore, the turbulence generates significant plume meandering with respect to the source location. As the plume travels, its width becomes much larger than any individual turbulent eddy, turbulence mixing becomes dominant within the plume, and the concentration variance is effectively transferred from low to high frequencies, developing an inertial subrange in the scalar spectrum. For the case in which the source is immersed in an array of buildings, the building dimension becomes a reference length scale. Within the uniform array in which the larger building walls are oriented at 90° to the wind direction, the plume is affected by the flow characteristics in the building wake (behind the obstacle, long street), and in the short streets and intersections where turbulent transport plays an important role. Nonetheless, the spectra do not change significantly downstream beyond about 5 or 6H from the source location for all sensor locations.

3.3 Peak-to-Mean Concentration Ratio

Figure 4 shows the variation of the peak-to-mean ratio with dimensionless averaging time Δτ* for different sensor locations and distances from the source. For all regions (long street, short street and intersections) inside the array of buildings, as the distance from the source increases (as shown, for instance, in Fig. 4j, sensors 13, 15, 17 and 21 located at the intersections) the peak-to-mean concentration ratio decreases more slowly with averaging time, i.e. the slope of the curve is lower for the sensors farther from the source. While these results agree with the experiments carried out by Mavroidis (2009), this author found that the absolute p values in the near-wake region for an isolated cubical building and staggered-array configurations are slightly lower than those in open terrain, and also lower than those found in the present work, which can be explained by the larger source distance from the building (2H) in the experimental configuration of Mavroidis (2009). Santos et al. (2009) also found lower p values near the windward and leeward walls of an isolated complex-shaped building than those reported for open fields. In this case, the source distance from the complex-shaped building was 3.5H, which implies that the building arrangement (separation distance and relative position) and source location influence the p values in Eq. 2.

Fig. 4
figure 4

Peak-to-mean concentration ratio as a function of averaging time measured in the wind tunnel (W) and calculated using the LES model at half the building height (left). The same data along with the corresponding linear fits (using logarithmic scales, log10) to determine the p values (Eq. 2) are shown in the right column

Full size image

Closer to the source, the larger eddies affect the plume intermittently, while farther away, the smaller eddies influence more strongly the peak-to-mean ratio in the same way as in an open terrain. However, due to the presence of buildings, which leads to higher turbulence shear stresses in comparison with open terrain and turbulent eddies of a scale similar to the building size, the decrease in the peak-to-mean ratio with averaging time as the sensors move farther away from the source is less pronounced than that expected for the open terrain. Piringer et al. (2014) evaluated the variation of peak-to-mean concentration ratio with distance from the source for open terrain, indicating that the peak-to-mean ratio (α, for a fixed value of Δτ) in the plume centreline is larger close to the source, and decreases with distance due to turbulence mixing. They find the value of α varies with the distance from the source, and is described by an exponential attenuation, approaching the value of \( \alpha \approx 1 \) within a few hundred metres or less, which means that, for this location, the peak concentration no longer varies with averaging time.

The LES results and wind-tunnel data agree very well for the larger averaging times down to a value of Δτ* between 1 and 10 depending on the sensor location (Fig. 4a, c, e, g, i). For a value of Δτ* smaller than that, for all sensor locations, the LES results give a value of α tending towards a constant independent of the dimensionless averaging time Δτ*, while the wind-tunnel measurements continue to indicate an increase. This behaviour again suggests that unphysical LES filtering of small scales does not allow for the prediction of concentration peaks for very short averaging times as the fluctuations are modelled at the subgrid scale (in this case, with the mixed-time-scale subgrid model proposed by Inagaki et al. (2005), which is a dynamic Smagorinsky model). Therefore, as discussed before, the choice of the filter size and subgrid model directly influences these results.

However, by analyzing the fits in Fig. 4b, d, f, h, j, one can observe that linear fitting (using logarithmic scales) works quite well for the LES results, provided the LES data for averaging times Δτ* below the value for which the peak-to-mean ratio remains constant are excluded. Therefore, even though the LES results are not able to predict the peak-to-mean values for very short averaging times, the resulting p values can be used to extrapolate for shorter averaging times.

It can be noted that the discrepancies between the two different wind-tunnel measurements for the same or symmetrically-opposed positions are very small for some sensor locations (sensors 1 and 2, Fig. 4a, c) but rather larger for others (sensors 9 and 12, Fig. 4e, g), which may be due to inaccuracies in the repositioning of the wind-tunnel sensors during the preparation for the experiments; they were sometimes displaced by up to 5 mm (in the vertical, lateral or windward direction). Also, the sensors labelled ‘a’ and ‘b’, as previously discussed, are located on the left and right side of the building facing the source, and there are small asymmetries in the flow. Comparing the LES results and wind-tunnel data, the LES results are always within the range of the two different wind-tunnel measurements.

The influence of the sensor height on the peak-to-mean ratio as a function of the averaging time was also investigated. Figure 5a, c shows that, for these monitoring positions, there was no substantial difference in data from sensors located at 0.5H and H, i.e., within the canopy. In contrast, there is a significant difference for sensors located above the building height (at 1.5H), with linear fits (Fig. 5b, d) showing that the p values are 1.5–2 times higher above the canopy since the source is embedded within the building array and, therefore, the sensors located above the canopy may be at the plume’s border, especially for sensors close to the source. Another interesting feature is that p values decrease more rapidly with distance from the source as the sensor height increases. Note that the p values are shown in Figs. 4 and 5 as the angular coefficient of the fitted lines in the log–log graphs based on Eq. 2.

Fig. 5
figure 5

Peak-to-mean concentration ratio as a function of averaging time measured in the wind tunnel (W) at different heights (on the left-hand side) and the corresponding linear fits (using logarithmic scales) to determine the p value as in Eq. 2 (on the right-hand side)

Full size image

Finally, Fig. 6 indicates that p values are smaller for the sensor in the central position (about half of the value) than for those located in short streets or at intersections, and it also decreases more slowly with distance from the source. Figure 6c shows that the p value at the same height decreases as the distance to the source increases. At the same distance to the source, the p value increases as the height increases, and increases more rapidly for the sampling station closer to the source. In general, the p values calculated using the LES results differ from those estimated using wind-tunnel data by less than 25%.

Fig. 6
figure 6

Variation of the p value with distance from the source for sensors located at a intersections and short street and b central positions. c The p value variation with height for sensors located at the central position at different source distances. The parameters X/H and Y/H indicate the non-dimensional sensor distance from the source and the sensor height, respectively

Full size image

4 Conclusions

As the LES model underpredicts the concentration fluctuation intensities governed by the smaller eddy motions, we conclude, not surprisingly, that the particular choice of subgrid-scale model and grid size is important in describing the smallest wavelength concentration motions. Linear fits of the data to Eq. 2 (using logarithmic scales) worked quite well for the LES results, provided the LES data for Δτ* values below the value for which the peak-to-mean ratio remains constant are excluded. Therefore, even though the LES results are not able to predict peak-to-mean values for very short averaging times, the fit can be extrapolated to produce a valid relation for shorter averaging times, implying that the LES technique can be used to assess the p value in the commonly-used power-law function.

Although the main aim of this work is to assess the performance of the LES approach in producing information to aid the use of Eq. 2 in urban areas, from the wind-tunnel data alone, some useful conclusions may be drawn for researchers working in a similar area. The instantaneous peak values for the sensors located behind the buildings are up to six times smaller than for those sensors located in the short streets and intersections. The relative concentration fluctuation is about twice as high for the sensors located in the short streets and intersections than behind the buildings since the source is also located behind the building on the floor and, therefore, the short streets and intersections are more susceptible to plume meander and asymmetrical effects of the wind-tunnel set-up. In contrast, in the central position behind the buildings, the plume is relatively well-mixed. The relative concentration fluctuations decrease with distance from the source very rapidly up to 10H, and then continue to decrease slowly. For all regions inside the array of buildings, for sensors further from the source, the peak-to-mean concentration ratio decreases more slowly with decreasing averaging time. The p values in the power-law function are smaller for the sensors in the central position (about half of the value) than for those located in short streets or at intersections, and also decrease more slowly with distance from the source. The influence of the sensor height on the peak-to-mean ratio as a function of the averaging time was also investigated. No substantial difference was found between sensors located at 0.5H and H, i.e., within the canopy, whilst in contrast, there was a significant difference for sensors located above the building height (at 1.5H).