Measurements and Computations of Flow in an Urban Street System

Abstract

We present results from laboratory and computational experiments on the turbulent flow over an array of rectangular blocks modelling a typical, asymmetric urban canopy at various orientations to the approach flow. The work forms part of a larger study on dispersion within such arrays (project DIPLOS) and concentrates on the nature of the mean flow and turbulence fields within the canopy region, recognising that unless the flow field is adequately represented in computational models there is no reason to expect realistic simulations of the nature of the dispersion of pollutants emitted within the canopy. Comparisons between the experimental data and those obtained from both large-eddy simulation (LES) and direct numerical simulation (DNS) are shown and it is concluded that careful use of LES can produce generally excellent agreement with laboratory and DNS results, lending further confidence in the use of LES for such situations. Various crucial issues are discussed and advice offered to both experimentalists and those seeking to compute canopy flows with turbulence resolving models.

1 Introduction

The use of large-eddy simulation (LES) to compute flow, turbulence and dispersion processes within urban environments is becoming ever more prevalent. This is partly because of continuously increasing computer power available to industry as well as in the academic environment, but also because of the recognition that lower order approaches such as Reynolds-averaged Navier–Stokes (RANS) do not adequately capture some of the important physics. Whilst LES has been common at larger scales since Deardorff (1970) and, indeed, forms the basis of most large-scale numerical weather forecasting models (in that processes on scales smaller than the grid are parametrized), it has only within the last fifteen years or so been applied to the range of much smaller scales and arguably greater complexities inherent in flow within urban canopies. In such work, the urban canopy has normally been resolved (to varying degrees of adequacy), rather than modelled in some way as is common in larger-scale (mesoscale) computations. Initially, work concentrated on the flow field itself and was generally aimed at computing cases that had been studied in the laboratory (e.g. Hanna et al. 2002; Kanda et al. 2004; Xie and Castro 2006; Smolarkiewicz et al. 2007). More recently studies have included the assessment of scalar dispersion and have also addressed specific field situations (e.g. Xie and Castro 2009; Moonen et al. 2013). A useful recent review of the use of computational fluid dynamics for dispersion in the urban environment has been provided by Tominaga and Stathopoulos (2013), but the field continues to expand rapidly. (See also the review of Belcher et al. 2013). It is clear that model evaluation is important and this was addressed comprehensively in the European COST action 732 programme (e.g. Schatzmann and Leitl 2011). However, it is noteworthy that many such attempts (apart from COST732) have concentrated largely on the adequacy of pollutant concentration results and not on the underlying flow field. It is a truism to state that there is little reason to expect dispersion characteristics to be accurate if the underlying turbulent flow field is inadequately predicted, unless there are counterbalancing errors of some kind.

In this paper attention is concentrated on (mostly) the canopy flow field for a neutrally stratified boundary layer developing over an array of rectangular obstacles. Experiments in a large wind tunnel, in which the array is placed within a thick, simulated atmospheric boundary layer (ABL), are reported and compared with corresponding LES data and also with fully resolved direct numerical simulations. The work forms the first stage of a major project, DIPLOS (DIsPersion of LOcalised releases in Street networks, www.diplos.org) whose objectives include generating greater understanding of canopy flows so that rapid response modelling approaches based on improved parametrizations can be developed for assessing the transport of potentially hazardous releases in the urban environment. Reporting of the associated concentration fields along with discussion of the extent to which current street-network models adequately predict them will follow in a subsequent paper. Here we address both the nature of the canopy flows for different wind directions and the extent to which LES captures both the mean and the fluctuating flow, using comparisons between the LES data and both laboratory and DNS data. The experimental and numerical approaches are described in Sect. 2. This is followed in Sect. 3 by a discussion of the upstream and above-canopy flows and then, in Sects. 4 and 5, by consideration of the within-canopy flow. Conclusions are summarized in Sect. 6.

2 Methodologies

It has been traditional to use arrays of cubes (height h) in work of this kind because this provides a geometry that leads to efficient DNS and LES computations (in terms of the resources required). The typical case studied has a cube-to-cube spacing equal to the cube size, which results in a rather open array compared with conditions in many city centres. The ‘streets’ between the intersections in such arrays are only h in extent and this is inadequate for the establishment of the developed street-canyon flows that form the basis of street-network dispersion models (e.g. Soulhac et al. 2011; Belcher et al. 2015) that are a focus of the current research. Ideally, the street canyons should be long compared to h and of 1:1 or smaller aspect ratio (width:height). A compromise solution of $h\times 2h\times h$ blocks with h spacing was adopted, acknowledging both these arguments and the implications in terms of computing resource. The latter consideration is all the more significant because an array of at least 18 blocks was needed in the computations to attain results that were essentially independent of domain size. Note also that, despite its simplicity, the array is a significant departure from the classical cube array in that it introduces geometrical asymmetry and is thus more typical of real urban areas.

Nonetheless, there are many features of real urban areas that are not captured, e.g. sloped roofs of different pitches on different buildings and non-parallel street configurations. Although complex areas containing such features are occasionally modelled in the laboratory and numerically (e.g. Yassin et al. 2005; Klein and Young 2011, as examples of specific city areas) and it is known that, for example, roof effects can play an important role in dispersion, our eventual objective is to assess the adequacy of street-network dispersion models and these are not yet available for more complex situations. We can view the array used herein as a stepping stone between classical cube arrays and the more complex situations, but specifically chosen to allow eventual comparisons of dispersion behaviour with that predicted by existing network models.

2.1 Laboratory Experiments

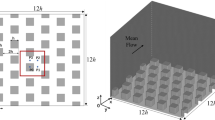
All experiments were conducted in the environmental wind tunnel in the EnFlo laboratory at the University of Surrey. This is an open-circuit tunnel with a working section that is 20 m long and $3.5\times 1.5$ m in cross-section. The model canopy comprised a square array of 294 ($14\times 21$) $h\times 2h\times h$ rectangular blocks with height $h=70$ mm, mounted on a turntable whose axis of rotation was some 14 m downstream of the test-section entrance. The origin of the rectangular coordinate system was set at the turntable (and model) centre, with x in the streamwise direction and z upwards. Figure 1 shows the arrangement for the orientation defined as $\theta =0^{\text {o}}$—i.e. with the oncoming flow perpendicular to the longer sides of the array obstacles. The array was curtailed at its corners in order to fit the turntable (Fig.1b) and thus allow ease of rotation to any desired angle. Note that the boundary layer upstream of the array was initiated by a set of five Irwin spires, 1.26 m in height, and developed over surface roughness comprising a staggered array of relatively sparsely distributed thin plates 80 $\hbox {mm}\times 20$ mm (width and height, respectively), with spacing 240 mm in both x and y. The boundary layer at the start of the urban array ($x=-2$ m) was thus about 14h in depth and was found to be reasonably homogeneous across the span with no systematic spanwise variations. Measured velocities were within $\pm 5\,\%$ of the spanwise mean. An internal boundary layer grew from the leading edge of the array, but conditions within the canopy, assessed for example by measurements along a spanwise street for the $\theta =0^{\text {o}}$ orientation, were essentially independent (i.e. within the experimental uncertainty) of the particular street downwind of the fifth street from the start of the array. Two reference ultrasonic anemometers mounted downstream of the array in the tunnel exit ducts were used to ensure that all the experiments were undertaken at the same freestream velocity in the approach flow (2 m s$^{-1}$). The Reynolds number based on obstacle height and the velocity at that height in the upstream boundary layer was about 7400, or about 830 when based on the friction velocity $u_\tau$ (i.e. $Re_\tau =hu_\tau /\nu$, where $\nu$ is the kinematic viscosity). The boundary layer was thus well within the fully-rough-wall regime.

Fig. 1

a Plan view of the full array, showing coordinate notation and the domain size used for most of the LES and DNS (outlined in red). b Looking upstream in the wind tunnel. The array is in the $\theta =0^{\text {o}}$ orientation with an laser Doppler anemometer probe body visible above the array and the upstream spires that help to set the oncoming boundary layer just discernible in the distance

Velocity and turbulence measurements were made using a two-component Dantec laser Doppler anemometer (LDA) system with a FibreFlow probe of outside diameter 27 mm and focal length 160 mm. This provided a measuring volume with a diameter of 0.074 mm and a length of 1.57 mm. Measurements in the local $U-W$ plane within the street network (i.e. in planes aligned with the streets) were obtained by use of a small mirror set at $45^{\text {o}}$ beneath a downward pointing probe. The flow was seeded with micron sized sugar particles at a sufficient level to attain data rates around 150 Hz. In general, data collection times were 2.5 min, selected to control the standard error in the results. This led to a typical standard error in U of 2 %, in $\overline{u^2}$ of 10 % and in $\overline{w^2}$ of 5 %, and corresponds to an averaging time of about 200T, where T is defined as an eddy turnover time, $T=h/u_\tau$. Our confidence is based on use of this LDA system over a long period of time, with a range or orientations and geometries (with or without the mirror system). There were many instances of the same variables being measured in different ways, without (for example) probe blockage problems becoming apparent. However, a potential source of significant error in the measurements was due to positioning uncertainty relative to the local buildings and tunnel co-ordinates. For example, an orientation error of $0.1^{\text {o}}$ in the array alignment to the wind-tunnel axis would result in a positioning error of about 2.5 mm relative to the buildings over a 1.5-m lateral traverse (i.e. in the y-direction), assuming the traverse itself to be perfectly aligned with the tunnel co-ordinates. There are inevitable imperfections in any wind tunnel and traverse installation and these had particular significance in this case because of the large volume over which results were required. In broad terms, the positional error in any horizontal plane was typically 2 mm. The implications obviously depend on the gradients of flow properties at any given location and resulting uncertainties were greatest in the thin shear layers downstream of the block surfaces (i.e. the side-walls and roof). The consequence of small errors in height relative to the local building roof level were obvious in initial experiments. This particular issue was resolved by use of a small ultrasonic height gauge attached to the traversing arm—in this way local height uncertainties (i.e. relative to the adjacent block) were reduced to about $\pm 0.5$ mm. The results presented here were obtained with this device in use (but see Sect. 4; Fig. 11).

Further practical issues directly affecting the flow were the accuracy of rotation of the array and its alignment relative to the approach flow. The $0^\mathrm{o}$ orientation proved by far the most demanding in these respects as any, albeit small, departure from the ideal set-up generated a small cross-flow in the street network (see Sect. 4). Dispersion measurements would then show a plume axis that drifted to one side, as indeed was observed in preliminary experiments that became the motivation for technique and hardware improvements. Ultimately, these resulted in plume-axis drift that was less than $1^{\text {o}}$; it is hard to see that anything substantially better can be achieved. Finally, it is worth noting that the $45^{\text {o}}$ array orientation case was far less sensitive to these matters, or rather that any consequent effects were far less obvious.

2.2 Salient LES Details

The computations for array orientations of $\theta =0^{\text {o}}$, $45^{\text {o}}$ and $90^{\text {o}}$ were undertaken using the well-known OpenFOAM code, run on the University of Southampton’s Iridis4 high performance computing system using typically 768 processor cores. Second-order differencing for the convective and diffusive terms was used everywhere and time-stepping employed a second-order backward differencing scheme. Flow in a planar channel whose domain size was $12h\times 12h\times 12h$ was simulated, although some comparative cases were computed with smaller domain sizes (see Sect. 4, where it is shown that arrays much smaller were insufficient). The array of (smooth-walled) obstacles was on the bottom (smooth) wall and comprised 24 obstacles—as shown in Fig. 1a—with no-slip conditions imposed on all surfaces, whereas at the top of the domain stress-free boundary conditions were imposed. Periodicity was enforced in the other two directions. All the statistics were obtained by averaging over at least $\varDelta T=710T$, after an initial development period of at least $\varDelta T=420T$. Comments about flow convergence will be made in due course. Whilst this approach to computing rough-wall flows is common, we emphasise that the flow system is fundamentally different to that in the wind tunnel where, as mentioned above, an internal boundary layer develops over the array. However, the emphasis in this project is on the nature of the flow and dispersion within the canopy rather than well above it. One of the interesting questions we address in Sect. 3 is the extent to which this canopy region (below, say, $z/h=1.2$) depends on the precise details of the outer boundary layer (or channel) flow, at least for the range of outer flow conditions modelled in the laboratory and by the numerics. It was anticipated that the dependence would not be very significant and, indeed, this turned out to be the case.

A uniform mesh was used (providing formally better numerical accuracy than more common expanding meshes) with a grid size of $\varDelta =h/16$. Because the Reynolds number was not very high ($Re_{\tau }\equiv u_{\tau }h/\nu \approx 1000$) this was chosen to be near (but above) the lower end of the range recommended by Xie and Castro (2006) for adequate simulation of urban areas and was a compromise driven by computer time limitations. The mixed time scale subgrid model proposed by Inagaki et al. (2005) was used; this circumvents either the (generally rather unsatisfactory) van Driest damping function near the walls or the difficulties in removing the numerical instabilities that can arise near the walls if, to avoid using damping models, a dynamic Smagorinsky model is implemented instead. These two difficulties can be particularly severe for cases (like the present) of multi-faceted wall geometry. However, computations were also performed using the standard Smagorinsky model and only small differences were observed in the spatially averaged mean velocities and turbulence stresses (less than 2 % in mean velocities). Computations using smaller domain heights ($H=6h$, 8h or 10h) were also undertaken; some representative results are shown in Sect. 4, confirming the weak effects of the outer flow on canopy-flow statistics. The flow was maintained by enforcing a fixed axial mass flux.

2.3 Salient DNS Details

Direct numerical simulations were carried out for the same building geometry at orientations of $0^{\circ }$ and $45^{\circ }$, with simulations performed on the UK national supercomputer, ARCHER, using typically 240 cores. For detailed descriptions of the development of the DNS code and the numerical techniques within it, see Yao et al. (2001), and for examples of its use for urban boundary-layer flows, see Coceal et al. (2006, (2007).

For the $0^{\circ }$ case, the DNS was conducted in a somewhat smaller domain of size $12h \times 9h \times 8h$, whereas the simulation of the $45^{\circ }$ case was carried out in a domain of size $12h \times 12h \times 12h$ (as used for the LES). In both cases, a uniform grid resolution of $\varDelta = h/32$ was used and the roughness Reynolds number achieved was $Re_{\tau } = 500$. This combination of mesh spacing and roughness Reynolds number was previously verified in similar studies to be adequate for a genuinely resolved DNS (e,g Coceal et al. 2006, 2007).

Periodic boundary conditions in horizontal directions were imposed. No-slip and impermeability conditions were prescribed at the bottom of the domain and on all solid surfaces, whereas free-slip boundary conditions were imposed at the domain’s upper boundary. For both orientations, the flow was driven by a constant body force. The flow Reynolds numbers based on the velocity at the top of the domain, $U_e$, and the cube height, h, were typically about $Re_{0} = 6600$ and $Re_{45} = 7500$ for the $0^{\circ }$ and $45^{\circ }$ directions, respectively. By way of comparison, the corresponding Reynolds numbers in the LES computations were in the range 14,500–16,000 and, in the wind-tunnel experiments, about 9300.

Both simulations were initially spun up until the turbulent flow was fully developed, which was monitored by the convergence of statistical turbulence measures. The timestep for the simulations was set to $\varDelta t = 0.00025T$ in both cases. Statistics were obtained from the converged simulations after a spin-up time of approximately 210T ($0^{\circ }$) and 380T ($45^{\circ }$), over averaging periods of $\varDelta T_{0} \approx 650T$ and $\varDelta T_{45} \approx 320T$.

3 Results and Initial Discussion

3.1 The Upstream Boundary Layer and its Influence Downstream

Fig. 2

a Mean velocity profiles measured upstream of and over the array and; b the corresponding shear-stress profiles. Note that red symbols refer to the upstream boundary layer, blue symbols are profiles taken above the urban array. The vertical dashed lines in (b) indicate the estimated value of $u_\tau ^2/U_e^2$ in the two cases

For reference purposes the major characteristics of the developed wind-tunnel boundary layer just upstream of the urban array are presented first. Figure 2a shows profiles of axial mean velocity obtained just upstream of the array and also close to its centre and within three streets of its downwind edge ($x=-2000$, $-70$ and 1190 mm, respectively). Data have been spanwise averaged at each height, using the values from various profiles taken at different spanwise locations; U is normalized by the freestream velocity at each location. It is clear that there is very little boundary-layer growth over that fetch (although it is perhaps just noticeable by close inspection of locations where $U/U_e=0.95$, say). There is nonetheless a small increase in $U_e$ with fetch; normalizing by the tunnel reference velocity yields values of 1.013, 1.028 and 1.043 for the three locations. These changes imply a freestream acceleration parameter defined by $(\nu /U_e^2)(dP/dx)$ of below $10^{-6}$, normally considered to have a negligible effect on a regular turbulent boundary layer. The changes in $U_e$ largely reflect the additional mass-flux reduction in the inner part of the boundary layer over the array, evident in Fig. 2a. The corresponding shear-stress profiles are shown in Fig. 2b, similarly normalized.

Note first that above a height of about 3h both the mean velocity and the shear-stress profiles at the downstream end of the array are very close to those upstream. This suggests that the inner boundary layer growing as a result of the change of surface condition does not reach beyond about $z=3h$. Above that height, the flow characteristics are essentially those of the upstream boundary layer. The immediate implication is that the channel-flow LES and DNS data might not be expected to collapse onto the laboratory data above $z\approx 3h$. We return to this point in due course.

Fig. 3

Wind-tunnel profiles in the upstream boundary layer (near the front edge of the urban array). a Reynolds stresses normalized by $u_\tau ^2$; $\bigcirc$, $\overline{u'^2}^+$; $\triangle$, $\overline{v'^2}^+$; $\square$, $\overline{w'^2}^+$ $\times$, $\overline{u'w'}^+$. Note that h here remains the urban-array height, whereas the height of the upstream roughness elements is $h_u=0.29h$. b Mean velocity data in logarithmic law form. The dashed line is the logarithmic law with $d=0$, $z_o=1.8$ mm ($z_o/h_u=0.09$) and $\kappa =0.41$

Spanwise-averaged centreline values of all the (non-zero) Reynolds stresses at $x=-2000$ mm are plotted in Fig. 3a, all normalized by $u_\tau ^2$. The friction velocity, $u_\tau$, was estimated by assuming that the measured (spanwise-averaged) value of $-\overline{u'w'}$ in the region just above the roughness is lower than $u_\tau ^2$ by a factor of 1.3, in accordance with Cheng and Castro (2002) for a similar (but not identical) canopy morphology. They showed that for arrays like these, this gave both a better match to the measured form drag on the elements and a more satisfactory fit of the mean velocity data to the logarithmic velocity law. In the near-wall region at least, the stresses are all typical for a naturally grown boundary layer and, overall, they are similar to typical wind-tunnel simulations of a neutrally stable atmospheric boundary layer. (Close inspection of the outer region shows differences from a naturally grown layer, but these are immaterial for the present purposes). A measure of the adequacy of the estimated friction velocity ($u_\tau /U_e=0.067$) is provided by Fig. 3b, which shows the mean velocity plotted in the usual logarithmic law form, $U^+={\kappa }^{-1}\ln [(z-d)/z_{o}]$, and compared with the standard logarithmic law assuming $\kappa =0.41$. For the quite sparse roughness of this upstream boundary layer, $d=0$ provides a satisfactory fit even beyond what would normally be expected as the logarithmic law range. This is an indication of the non-natural nature of the outer flow. Note that the top of the roughness is at $z/z_o\approx 11$; depending on the precise location of the measurement point in the $x-y$ plane one would not necessarily expect the logarithmic law to be followed much below $z/h_u=2$ ($z/z_o=22$), where $h_u$ is the height of the roughness (20 mm), since such heights would be in the roughness sublayer region where the flow must be inhomogeneous in both x and y.

As noted earlier, over the urban canopy an inner boundary layer grows and we expect significant changes in the friction velocity and the two logarithmic law parameters d and $z_o$ after the upstream edge of the array. This is explored in the following section, where comparisons with the LES and DNS data are included.

Fig. 4

Mean velocity profiles (a) and shear-stress profiles (b) for the three urban array orientations. Note the location of the top of the canopy, shown as a dashed line at $z/h=1$ in (b)

3.2 Flow Above the Urban Array

The major focus within the DIPLOS project is the canopy region itself (i.e. flow, turbulence and dispersion in and just above the $z\le h$ region) but it is of interest first to consider the flows above the canopy and for various wind directions. Figure 4 presents mean velocity and shear stress profiles for array orientations of $\theta =0^{\text {o}}$, $45^{\text {o}}$ and $90^{\text {o}}$, comparing laboratory, LES and DNS data. The computed profiles have been obtained by averaging not only in time but also over the entire computational domain. They are therefore not expected necessarily to agree with the laboratory data in the roughness sublayer region (were the flow is homogeneous in neither x nor y), since the latter data were obtained at specific x, y locations. Although the plan area density is $\lambda _p=\frac{1}{3}$ independent of wind direction (with $\lambda _p$ defined in the usual way by the ratio of the plan area of the elements to the total plan area), intuitively one would expect the surface drag for the zero degree case to be higher than for the $90^{\text {o}}$ case. The frontal area density ($\lambda _f$, the ratio of the element frontal area ‘seen’ by the oncoming flow to the total plan area for a repeating unit) is $\frac{1}{3}$ for $\theta =0^{\text {o}}$, i.e. twice that for $\theta =90^{\text {o}}$, so the former orientation provides a greater flow ‘blockage’. This larger drag for $\theta =0^{\text {o}}$ is immediately evident: just above the canopy both the measured and the computed shear stress for $\theta =90^{\text {o}}$ are significantly higher and the computed mean velocity profile shows a greater velocity deficit. The largest drag, however, occurs in the $\theta =45^{\text {o}}$ case, for which the near-wall shear stress reaches values some 13 % higher than the $0^{\text {o}}$ values. This is consistent with a slightly higher value of $\lambda _f$ (0.35, cf. 0.33 for $0^{\text {o}}$) but perhaps more importantly with the fact that there are no continuous streets in the prevailing wind direction for this particular orientation of the array.

Fig. 5

Data of Fig. 4 normalized using wall units. In (b), the dashed straight line joins the points (12,0) and (1,0)

The flow parameters are normalized using the freestream velocity (or the velocity at the top of the domain in the LES and DNS cases), so do not collapse across the three orientations. Normalizing using the appropriate friction velocity leads to the corresponding profiles in Fig. 5, from which it is evident that computational data in the inner region are in as good agreement with experiment as can be expected, especially given the uncertainty in establishing the friction velocity for the laboratory profiles (discussed above).

Note, first, that above the canopy neither the LES nor the DNS stress profiles (Fig. 5b) collapse exactly onto the expected straight line between (0, 12) and (1, 0). ($12h=840$ mm, the domain height). However, they do collapse when the dispersive shear stresses are added in (not shown) and it was the slope of these total stress lines in un-normalized form that provided the LES wall-stress values. (In these computations the OpenFoam code was set to maintain a constant mass flux at each timestep so, without time-averaging the computed pressure difference across the two ends of the channel, this was the most straightforward way to deduce the effectively imposed but initially unknown wall stress. In the DNS, the known $u_\tau$ was forced by the applied, constant pressure gradient.) The fact that the dispersive stresses (particularly in the $0^{\text {o}}$ and $90^{\text {o}}$ cases) were not exactly zero above, say, $z/h=2$ could be a result either of insufficient time averaging or, more likely, the presence of axial rollers in the outer flow which, as a result of the rather small span, could not move around much in the spanwise direction. It is interesting, however, that in the $45^{\text {o}}$ case the dispersive stresses above the canopy were closely zero. The effective span of the domain actually varies with x in this case and it may be that this (and the effectively variable domain length across the span) prevents altogether the appearance of essentially fixed outer layer axial structures. Incidentally, it is worth emphasising that the issue of domain width for channel-flow computations and whether or not it is sufficient to allow the possible presence of axial rollers in the outer flow is also important for smooth-wall flows (Fishpool et al. 2009).

Secondly, note that the only DNS data obtained with the $H=12h$ domain height were for the $\theta =45^{\text {o}}$ case and these data suggest a somewhat lower surface drag, yielding a higher value of $U_e/u_\tau$, most evident in Fig. 5a. The LES and DNS profiles in Fig. 4a collapse quite well, but the corresponding collapse seen in Fig. 4b required the 6 % higher value of $U_e/u_\tau$ (implied by Fig. 5a) for the DNS case. This could be a result of slight inadequacies in the subgrid model used in the LES but it could also be partly explained by the difference in $Re_\tau$, with the DNS value of 500 being about one half that used for the LES. The issue is not important for the present purposes, given our focus on flow variables (normalized by $u_\tau$) in the canopy region, but it will be fully explored in a subsequent paper in which results from computations using various subgrid models and Reynolds numbers will be compared with the fully resolved DNS data.

Thirdly, it is seen that for the $90^{\text {o}}$ case the LES and laboratory mean velocity and shear-stress profiles agree quite well over much of the domain. In this case the obstacle array in the wind tunnel provides the least perturbation to the upstream boundary layer. There is a much more significant perturbation in the other two cases, so the wind-tunnel profiles over the centre of the array consist more obviously of an inner region in equilibrium with the new surface and whose depth grows with fetch over the array, and an outer region that reflects the characteristics of the upstream surface. The friction velocity consistent with the inner region (increasingly large in the sequence $90^{\text {o}}$, $0^{\text {o}}$, $45^{\text {o}}$ for a fixed $U_e$) is thus appropriate for collapsing the LES and laboratory data only in this inner region, consistent with the behaviour shown in the figure.

Table 1 Parameter values deduced from laboratory, LES and DNS data

Fourthly, as explained in Sect. 3.1, the laboratory friction velocities were estimated by increasing the shear stresses obtained just above the canopy by the factor 1.3, in accordance with the findings of Cheng and Castro (2002). Table 1 lists the wall stresses for all three orientations, along with corresponding best-fit logarithmic law parameters, which are discussed next. For the fits, the zero-plane displacement height, d was assumed to be the height at which the surface drag appears to act (Jackson 1981) and was calculated from the LES and DNS data using the computed pressure field on the elements and the frictional forces on the surfaces. This leaves only $\kappa$ and $z_o$, the roughness height, as free parameters. The former was chosen to ensure a good match for the slope in the U versus $(u_{*}/\kappa )\ln [(z-d)/z_o]$ plot and the latter was chosen to ensure the correct amplitude. For the experimental data, a similar value of d was used but slightly different values of $z_o$ emerged (compared with those deduced from the LES data).

It is worth noting here that the values of $\kappa$ in Table 1 are often quite different to the more classical value of 0.41, which was adequate for fitting the wind-tunnel’s upstream boundary-layer data. The Kármán measure defined by $z^{+} dU^+/{dz^+}$ (where $z^+=zu_\tau /\nu$) was not always very closely constant over a reasonable range of z in the computations; one expects a constant value of $1/\kappa$ for a significant logarithmic law region. There is therefore some uncertainty in the estimate of $z_o$ and, of course, different values of $\kappa$ make a direct link between the value of $z_o/h$ and surface drag for different cases problematic. A change in $\kappa$ from 0.33 to 0.4, for example, typically leads to about a factor of two change in $z_o$. Note too that there is no reason to expect the ‘universal’ value of $\kappa$ to emerge—0.39 is a recent suggestion for this by Marusic et al. (2013)—because the ratio $\delta /h$ is not really large enough to imply adequate scale separation between inner and outer layers. An example of the changes that occur if $\kappa$ is fixed and d is allowed to vary is included in (the fourth line of) Table 1 for the $\theta =90^{\text {o}}$ case. Using the method described above this has the lowest $\kappa$ (0.265). However, fixing $\kappa$ at 0.39 (for example) and adjusting d to give the best fit to the experimental data requires a rather higher d / h and a very much smaller $z_o/h$. This latter value is unrealistically small, but fixing d / h as the ‘Jackson value’ yielded quite a poor fit and no region of constant Kármán measure (indeed, values were quite far from the expected 1/0.39). We believe our method, given a known $u_\tau$ and known d and adjusting $\kappa$ to yield the correct logarithmic law slope, is the most self-consistent.

Fig. 6

Mean velocity profiles in logarithmic law form. The logarithmic law parameters (d / h, $z_o/h$ and $\kappa$) are given in Table 1. In b ‘Upper set’ data refer to those from a probe traverse largely above the canopy height, whereas ‘Lower set’ data are from a separate traverse concentrating on the canopy region only

Despite these inevitable uncertainties, there is reasonable agreement between the laboratory and LES and DNS data and the resulting logarithmic law profiles for each wind direction are shown in Fig. 6. For consistency with the LES, the DNS logarithmic law parameters used in Fig. 6b were those used for the corresponding LES case. They differ slightly from the values (shown in Table 1) that produced the best fit to the Kármán measure.

Fig. 7

Normalized stress profiles for $\theta =0^{\text {o}}$. a axial; b spanwise; c vertical stresses. d Comparison of the LES axial stress for the three wind directions

As a final illustration of the boundary-layer flow above the canopy, Figs. 7a–c shows the turbulence normal stress profiles for the $\theta =0^{\text {o}}$ case. Comparisons for the LES axial stress for different wind directions are shown in Fig. 7d. Note first that the experimental profiles of both axial and vertical stresses ($\overline{u'^2}^+$ and $\overline{w'^2}^+$), approximately collapse at different x locations, because they reflect the characteristics of the upstream boundary layer. Only in the inner region would one expect significant differences at different axial locations. Nonetheless, these is a hint that data values in the region $1\le z/h\le 4$ at the downstream end of the array ($x=1190$ mm) are a little higher than further upstream. This is consistent with that downstream part of the flow being more closely in equilibrium with the rougher surface, although it should be borne in mind that stress profiles normalized by the friction velocity are very similar in smooth-wall and rough-wall channels (Leonardi and Castro 2010). It is notable that the LES axial stress in the outer region (Fig. 7a) is significantly larger than the experimental data whilst the differences in the other two components are smaller. This is almost certainly because of the presence of a significantly non-zero dispersive axial stress (not shown), suggesting either that the computation had not yet converged (in time), or perhaps that there are residual large-scale motions in the outer flow, probably as a result of the finite domain span, although if the latter were true one might expect non-zero dispersive stresses in the other two stress components (and there were none). Figure 7d shows that there seems to be a significant dependence on wind direction in the axial stresses in the outer flow. The axial stress is noticeably lower for the $45^{\text {o}}$ wind direction; this is the case that has no residual dispersive stress in the outer region. What is more significant is that the stresses within the canopy ($z/h\le 1$) are very strongly dependent on wind direction, as expected. It is to this canopy region that we now turn.

Fig. 8

Ensemble-averaged mean velocity profiles at the long-street centreline for $\theta =0^{\text {o}}$; a $U_s^+$, b $V_s^+$

4 Flow Within the Canopy Region

Consideration of the flow field within the near-wall region begins by presenting, as examples, the axial and vertical mean velocity ensemble-averaged profiles (for the $\theta =0^{\text {o}}$ case) for a location at the centre of the long street, defined as the street parallel to the longer sides of the array obstacles. In this section velocities oriented in the street directions are used, so $U_s$, $V_s$ are velocities normal and parallel, respectively, to the long side of the obstacles. Only for $\theta =0^{\text {o}}$ does $U_s=U$, $V_s=V$. There is very good collapse between laboratory, LES and DNS profiles of $U_s^+$ obtained using the 12h domain length (Fig. 8a), despite the different domain heights and widths used; the agreement continues all the way to $z=6h$ and 8h (not shown). However, a profile given by an LES run using a domain size significantly smaller in plan ($6h\times 6h$) differs from the others once $z/h>1$. This must be a result of the narrower (and perhaps also the shorter) domain used and the effect is further illustrated by the $V_s^+$ profiles seen in Fig. 8b. For this array orientation ($0^{\text {o}}$) and symmetrical location of the profiles with respect to the array blocks, one would anticipate a zero spanwise velocity at all heights. However, this is not found in either the experiments or the numerical computations and is indicative of a small, but definitely non-zero difference between the canopy and the domain-top mean velocity orientations. Note that the fact that the V profiles within the canopy in Fig. 8b are all the same sign is in one sense a coincidence (whether the y-coordinate is at $+90^{\text {o}}$ or $-90^{\text {o}}$ to the x-direction in either the laboratory or the numerical domain is completely arbitrary).

Some limited tests in the laboratory showed that the unexpected non-zero V could be removed by an appropriate rotation of the array (by only a degree or two). In the numerical computations, the periodic conditions imposed at the spanwise extents of the domain allow non-zero V and it appears that too small a domain width can promote a spanwise flow through the entire domain height, leading to an effective (and small) ‘freestream’ flow angle at the domain top. By far the largest flow angle at the top (about $1.3^{\text {o}}$) is given by the LES on the $6h\times 6h\times 6h$ domain and it appears that this is sufficient to trigger much larger flow angles within the canopy, not dissimilar, in fact, to the laboratory values (see Fig. 8b). At $z/h=0.5$, for example, this smaller domain LES run yields a flow angle in excess of $45^{\text {o}}$ relative to the sides of the obstacles (rather than the expected value of zero, but note that at that height the axial velocity is very small). This whole issue emphasises the care that is required in undertaking either laboratory or numerical experiments for these types of canopies. The reason for the non-zero spanwise flow at all heights in the computations is unclear; it may be that the total drag (and thus energy expended) is lowest for a small non-zero flow angle and the computation naturally picks out this lowest-energy flow. Further work is needed before a definitive answer could be identified. It is possible that the zero-degree case is somewhat pathological, as it is presumably relatively easy for the flow to ‘switch’ intermittently to conditions either side of a strictly symmetric state. Imposing a small non-zero wind angle could thus arguably provide a more satisfactory case for comparing wind-tunnel data and numerical simulations.

Fig. 9

Ensemble-averaged mean velocity profiles in street coordinates at the centre of the street intersection for $\theta =45^{\text {o}}$; a $U_s^+$, b $V_s^+$

Similar examples of velocity profiles are shown in Fig. 9 for $\theta =45^{\text {o}}$. Again, these are ensemble averaged across all corresponding street locations in the whole domain. In this case, the LES and DNS results for $U_s$ diverge for $z/h>1$, consistent with the plan-averaged profiles shown in Fig. 6b and with a small difference in the computed flow angles at the top of the domain (not shown). It is not clear why this difference occurs. Because of the array asymmetry with respect to the flow at $\theta =45^{\text {o}}$ this topology is expected to yield a non-zero lateral force in a numerical channel-flow computation (i.e. a force at $90^{\text {o}}$ to the drag force, defining the latter as the array force in line with the flow direction at the top of the domain). As Claus et al. (2012) discuss, such a non-zero force implies that the mean flow angle at the top of the domain must be slightly inclined to the forcing direction. Our results are qualitatively consistent with the earlier Claus et al. (2012) findings in that a non-zero angle shift occurs up to some height above the array, although the deviation appears more pronounced in the case of the LES (extending all the way to the top of the domain).

Fig. 10

Normalized velocity and stress profiles at $z/h=0.53$ along streets for $\theta =0^{\text {o}}$ (a, c, e) and $\theta =45^{\text {o}}$ (b, d, f). Street coordinates are used throughout and the location of the array blocks is indicated at the bottom of each figure. In a, c, e the laboratory y locations have, for convenience in comparison, been shifted by 9h and in all plots the origin of coordinates in the numerical data files has been shifted to cover the laboratory range conveniently. Symbols refer to laboratory data. Filled black triangles (in b, d, f) are from more closely resolved traverses. The legend for c, e is that for a and the legend for f is that for b

We turn now to profiles along the streets (rather than vertically through them), focussing first on street centrelines near $z/h=0.5$. Figure 10 shows examples of these and includes mean velocity ($U_s$) and the two major shear stresses along the y street for the $\theta =0^{\text {o}}$ array orientation (Fig. 10a,c,e) and both mean velocities and $\overline{u'_sv'_s}\,^+$ for the $\theta =45^{\text {o}}$ orientation. As before, the computed data are ensemble averaged across all available parallel streets in the domain. Consider first the $\theta =0^{\text {o}}$ case (the left hand column of Fig. 10). Note that the mean velocity shown ($U^+$, Fig. 10a) is the velocity across the street, i.e. in the freestream flow direction. So behind the blocks the velocity is negative and relatively small, whereas between them it is positive and much larger as the flow tends to sweep down the x streets in the main flow direction. There is good agreement between the laboratory and computational data, not just for this mean velocity (Fig. 10a) but also for the Reynolds shear stresses (Fig. 10c,e). The fact that the local magnitudes of the $\overline{u'v'}^+$ stress (Fig. 10e), which on average across the span must be zero by symmetry, is about the same as those of the other dominant stress (Fig. 10c) is a clear indication of the very three-dimensional and anisotropic nature of the turbulence field within the canopy. It is significant that the domain height, which is different for all three computation profiles, again has no significant effect on the canopy flow.

The level of agreement for the $\theta =45^{\text {o}}$ case is not quite so good, although it is interesting that the shear stress data shown in Fig. 10f all collapse reasonably well. On the other hand, whilst the computed LES and DNS mean velocities are satisfyingly close (Fig. 10b,d, and all obtained with a 12h domain height), there is a rather larger level of disagreement between them and the laboratory data. However, the latter are quite scattered and clearly vary significantly depending which axial (x) location was chosen for the traverse. For this array orientation the experiments to obtain data within the canopy were particularly tricky, but special care was taken over the final traverses at $x/h=1$ ($x=70$ mm), with data taken at much closer intervals in an attempt to identify the various peaks and troughs. These data are satisfyingly close to the computed profiles.

Fig. 11

Lateral $U^+$ profiles at $\theta =0^{\text {o}}$ along the y streets, near $z/h=1$. Block locations are indicated at the bottom of the figure

Very accurate vertical positioning of the LDA probe is not crucial at $z/h=0.5$, where the slopes in vertical profiles of the flow variables are not large. At $z/h=1$, however, slopes are large (see Fig. 8a for example) so that lateral profiles taken near this ‘roof-top’ position are subject to rather more uncertainty when compared with computed profiles. This is illustrated in Fig. 11, which shows DNS lateral profiles of $U^+$ along the y streets at three mesh node points nearest $z/h=1$, compared with laboratory data taken nominally at $z/h=1$. It is clear that except near the peaks, most of the laboratory data points lie between the lateral DNS profiles at $z/h=0.984$ and 1.016, as expected. Although the mesh was coarser, LES results (not shown) are quite similar. It is worth noting that the DNS profiles show small differences in successive sections of the array—for the $z/h=1.047$ profile, for example, the peak $U^+$ around $y/h=9$ is larger than at the equivalent locations around $y/h=6$ and 3. This may suggest either incomplete statistical convergence or, more likely, it is the effect of essentially stationary longitudinal rollers above the array indicated by the non-zero dispersive stresses there, discussed in Sect. 3.2.

Fig. 12

Mean vertical velocity along the long (y) street centreline at $z/h=1.03$ for the $\theta =0^{\text {o}}$ case. The left-hand axes refer to both $W^+$ and $W/U_{vec}$ whereas the right-hand axes refer to the flow angle, $\alpha$, in the vertical plane. Block locations are shown at the bottom of the figures. a LES; b DNS

5 Further Results and Discussion

Dispersion of pollutants within the canopy region depends partly on the extent to which the flow can transport material into or out of the canopy. Despite the important influences of turbulence, this will clearly depend somewhat on the nature of the mean vertical flow at the canopy top. Figure 12 shows the variation of mean vertical normalized velocity ($W^+$) along the centreline of the y-streets (i.e. parallel to the long faces of the obstacles) for the $\theta =0^{\text {o}}$ case. Data were ensamble averaged across all available street centrelines in the domain and for the LES (Fig. 12a) are at the first mesh point height above $z/h=1$ ($z/h=1.03$) whereas, for the DNS (Fig. 12b), they are interpolated to the same height (from the data corresponding to the $U^+$ data shown in Fig. 11). Data at the lower LES mesh point ($z/h=0.97$) are similar to those shown in Fig. 12a. The figure includes variations of the ratio $W/U_{vec}$, where $U_{vec}$ is the magnitude of the velocity in the horizontal plane, and the angle to the horizontal of the total mean flow vector. It is evident that there are regions of both inflow and outflow—i.e. negative and positive W (as there must be when spatially averaged, but not necessarily in individual profiles such as those at a specific x) . The strength of the mean flow is not particularly large, as seen by the variations of the flow angle (in the vertical plane), which do not exceed about $5^{\text {o}}$ at most. Similarly, although the DNS $W^+$ values differ noticeably from the LES (cf. Fig. 12a, b), they are small compared with the horizontal component—the $W/U_{vec}$ ratio is below 0.1 everywhere.

Perhaps the most interesting feature of Fig. 12 is that over each repeating unit (e.g. from $y/h=3$ to $y/h=6$) there is significant asymmetry in $W^+$ about the centre ($y/h=4.5$), independent of whether LES or DNS results are considered. This is also evident in Fig. 11. If the approach flow were at $90^{\text {o}}$ to the block face and the lateral side force on the canopy were zero, W should be symmetric about that point. One must conclude that one or both of those requirements are not precisely satisfied or, alternatively, that small numerical inaccuracies are sufficient to produce this asymmetry. Unexpected asymmetry evidenced by non-zero lateral (V) velocities was discussed in Sect. 4 (in relation to Fig. 8b) and it is perhaps not surprising that this small asymmetry is most clearly seen within the separated shear layer around $z/h=1$ in quantities that have large gradients there and are anyway very small. The computed flow angle at the top of the domain was only about $0.1^{\text {o}}$ for this case and the lateral array force (normal to the flow direction at the top of the domain and the sum of pressure and viscous contributions) was also practically zero, as expected. Note that the lateral force normal to the forcing direction must inevitably be zero in a numerical computation, as explained by Claus et al. (2012). We therefore conclude that small numerical inaccuracies are sufficient to produce the asymmetry in W and, indeed, yield noticeable differences between the LES and DNS data in Fig. 12 (there were, likewise, differences between DNS and LES in the unexpected non-zero V values within the canopy, Fig. 8b). These differences might also be a result of small differences in dispersive stresses just above the canopy. This all emphasises the point that numerical computations of these kinds of flow are not as straightforward as one might at first imagine—a salutary warning to computationalists!

Fig. 13

a Contour plots of the normalized mean vertical velocity, $W^+$, at $z/h=1$, from the LES data at all three array orientations. b For $\theta =45^{\text {o}}$ and $z/h=0.5$, contour plots of $W^+$ (left) and flow vectors (right) in the horizontal plane

Contour plots of $W^+$ at $z/h=1.0$ are shown in Fig. 13a for all array orientations. In every case, there are significant areas of outflow, as must inevitably be the case since the spatially-averaged mean value must be zero (at all heights, in fact, by mass continuity). The regions of outflow, however, are different: for $\theta =0^{\text {o}}$ they are concentrated at the trailing edge of the obstacle roofs and downstream of the side edges whereas, for $\theta =90^{\text {o}}$, they lie along the side edges and front face. Since one might intuitively have expected the obstacles to generate delta-wing type vortex motions in the $\theta =45^{\text {o}}$ case, it is interesting that there is, nonetheless, a region of outflow downstream of the rearmost corner. If the influence of turbulent fluxes at $z/h=1$ was negligible, these plots would indicate the regions where any pollutants emitted within the canopy would be expected to be transported out to the boundary layer above. Likewise, some would be transported back into the canopy from aloft in the regions of negative $W^+$. However, it is likely that the effects of turbulent transport are equally if not more important; the issue will be explored in the subsequent dispersion paper, but it is worth noting here that Belcher et al. (2015) (for an array of cubical obstacles) suggest that, indeed, turbulent transport is dominant compared to advection with mean W, but this is probably not true near the upwind edge of the array or if the obstacle height varies significantly.

A similar contour plot is shown in Fig. 13b for $\theta =45^{\text {o}}$, but at the canopy half-height, $z/h=0.5$. It is evident (see the left-hand plot) that the upward flows (positive $W^+$) are considerably stronger and more extensive than those at the top of the canopy, seen in Fig. 13a (centre plot). To compensate, the downward flows, although restricted to thinner regions near the edges of the blocks, have significantly greater magnitude. The horizontal component of the total mean flow is shown in the vector plot (at the right-hand side of Fig. 13b). The recirculating region behind the rearward short faces of the blocks can be seen, but the dominant feature is that the flow in the long streets (parallel to the longer side faces) is predominantly in the along-street ($y_s$) direction, despite the $45^{\text {o}}$ wind direction aloft. This feature of canopy flows for wind directions not normal to obstacle faces was discussed by Claus et al. (2012) and is likely to remain a strong feature of urban canopies independently of the precise array geometries, unless the obstacle sizes and orientations are different from one another so the array does not embody any long continuous streets. A similar ‘street steering’ effect has also been observed in the field (e.g. Balogun et al. 2010; Carpentieri and Robins 2010). Figure 13b suggests that the 2h streets of the present array are just long enough to be representative for the street network modelling approach.

Fig. 14

a Tracers following the mean flow (i.e. mean flow pathlines) for the $\theta =45^{\text {o}}$ case. The arrow shows the wind direction aloft. The right-hand sketch shows the origins of the nine coloured traces—equi-spaced in the street cross-section. The LES data were used. b Snapshot from video taken for $\theta =45^{\text {o}}$. The ground-based square smoke source ($70\times 70$ mm ), outlined by the white square, is located at the centre of a long street and the (green) laser sheet showing the smoke is coincident with the horizontal plane at $z/h=0.64$ and is viewed from above

As an example of possible pollutant pathways in the absence of any turbulence effects Fig. 14a shows (from LES data) mean flow pathlines originating from a grid of nine points in the vertical plane at the centre of the long ($y_s$) street and equally spaced between themselves and the obstacle side walls. There is a helical flow within the street but from some points the ‘tracers’ can escape above the canopy (via the positive vertical mean flow regions discussed above) and then they rapidly align with the mean flow aloft. Side views of the same results show that in no case do the tracers reach heights above $z/h\approx 1.1$.

Fig. 15

Vertical profiles of dispersive stresses within the canopy from the LES for $\theta =0^{\text {o}}$ (a) and $\theta =45^{\text {o}}$ (b). Each dispersive stress, at each height, is normalized by the corresponding (time- and domain-averaged) Reynolds stress at that height

It is worth noting that data like those presented in Figs. 13 and 14a would be almost impossible to obtain from laboratory or field experiments. (An indication of what can be achieved, however, is seen in Carpentieri et al. 2009). The figures are therefore examples of the added value provided by numerical computations and are clearly helpful in providing further understanding of the canopy flows. They should be interpreted with care, however. As indicated earlier, the presence of large-amplitude turbulent motions will ensure that tracers would not actually follow the mean flow particle paths shown in Fig. 14a. We illustrate this by showing in Fig. 14b, for comparison with Fig. 14a, a corresponding but instantaneous snapshot of the smoke pattern arising in a laboratory experiment on a plane not far from the mid-height of the canopy. The source of smoke laden air was an area of size $h\times h$ at $z=0$ and located at the centre of a long ($y_s$-direction) street. It is clear that, (i) some smoke can move ‘upstream’ of the source location, and (ii) some can arrive at considerable distances laterally within the canopy, much further than would be suggested by the selected mean flow tracers of Fig. 14a. The consequences of this rapid lateral spread are sometimes seen in dispersion measurements in the field, for example, the measurements in central London described by Wood et al. (2009). Views of a horizontal plane at $z/h=2$ (not shown) indicate (iii) that the smoke can reach heights well in excess of the $z/h=1.1$ suggested by mean flow tracers and certainly above $z/h=2$. These three facts alone are sufficient to demonstrate that the turbulence fluxes are very significant, so that mean flow tracers like those shown in Fig. 14a should indeed be interpreted with caution. It is crucial to study these fluxes in detail and this will be a topic for the subsequent dispersion paper describing the concentration fields within and above the canopy.

Not only are the turbulent fluxes important but it should be noted that, within the canopy, dispersive fluxes, arising from the spatial variability of the local time-mean velocities in horizontal planes, are also large. This is illustrated in Fig. 15, using the LES data. The data have been normalized in each case by the corresponding Reynolds stress at the appropriate height and it is clear that they can be of the same order as the latter over large parts of the canopy height, as found in previous studies (e.g. Coceal et al. 2006). This emphasises the high degree of spatial variability of flow properties within the canopy. Although in some circumstances pollutants may be well mixed (so that concentrations are not too non-uniform) this does not imply uniformity in the flow variables. Since the flows are strongly three-dimensional and inhomogeneous within the canopy, the usual decomposition of stresses in coordinates aligned with (e.g.) the forcing direction is perhaps not particularly useful; one could argue that principle stress coordinates should be used. However, this seems an unnecessary complication in the present context and would not add very much to physical understanding.

6 Final Discussion and Conclusions

We remark first on conclusions arising from the wind-tunnel experiments. Measurements in an extensive array of this kind are particularly challenging, not least because of the need to maintain positional accuracy relative to the array blocks whilst moving across several modules. The consequences are most obvious when traversing across the shear layers in the flow separating from the building block roof and walls, as is made very clear from inspection of the DNS results in Fig. 11. Related issues arise from the sensitivity of the flow to slight errors in alignment in the $0^{\text {o}}$ and $90^{\text {o}}$ cases. Although considerable efforts were made to improve experimental techniques, these matters remained the main cause of uncertainty in the data. The weak mean cross-flow seen in the computations for the $0^{\text {o}}$ case implies a consistent, though weak drift in the centreline of a plume dispersing through the array. Drift of this nature is likely to be of greater magnitude in the wind-tunnel work, due to overall alignment error, though variable to some degree, reflecting local errors in block alignment. These matters will be returned to in comparing measured and predicted dispersion in the subsequent paper.

Next, conclusions arising from the numerical computations are given. Firstly, it has been shown that the computed flows within the present urban-type canopy are not very sensitive to the domain height. This is significant, as smaller domain heights make it computationally more efficient when modeling pollutant releases within the canopy. Nonetheless, we recommend a domain height of at least six canopy heights in order to capture the most important turbulence features just above the canopy, some of which are necessarily linked to the turbulent flow at greater heights.

In common with previous work, some of our results suggest the possible presence of longitudinal, slowly-evolving rolls above the canopy. These can be strongly attenuated, if not completely damped out, if the computational domain is too small. For the present canopy morphology, a domain plan area of $6h \times 6h$ seems too small (see Sect. 4), especially for flow directions normal to the obstacle faces; these directions are in one sense pathological and allow the computed flow to break symmetry and contain a mean spanwise flow that is increasingly enhanced as the domain size decreases. The presence of slowly-moving rolls aloft also has implications for modelling limited-duration pollutant releases, because downstream concentration patterns could depend somewhat on the location of the rolls (with respect to that of the source) over the particular release and dispersion times. At this stage it is not clear how sensitive this feature is to the specific array morphology, but it is certainly something that should be considered in designing numerical experiments on such flows.

Secondly, as noted above, the present results illustrate the difficulty in achieving perfect flow symmetry for cases where the geometry would lead one to expect it. This is true both for laboratory and numerical modelling. It may be a result of the specific canopy morphology having its lowest drag condition at some small angle to that for which symmetry is expected, but further work would be needed to confirm this and, if this is the cause, the behaviour would certainly vary with canopy morphology. Whatever the cause, this asymmetric feature is a further indication of the care needed in designing and executing such experiments. In nearly all the extant literature, insufficient data are shown to give confidence that such a spanwise (symmetry-breaking) flow is not present, so the present results provide a further cautionary lesson.

Fig. 16

Mid-height ($z/h=0.5$) flow vectors for $\theta =45^{\text {o}}$. a Square cube array—from Claus et al. (2012). b the present array; note that only half of each $h\times 2h\times h$ obstacle is shown, so that only downwind half of the obstacles is shown at the top of the figure and the upstream half at the bottom

Thirdly, the present canopy has obstacles sufficiently long compared with their heights to yield extensive flow channelling along streets. This is most clearly illustrated by Fig. 16. The region in which the flow turns to become parallel to the long sides of the obstacles is no more than 1h in extent (in both $x_s$ and $y_s$ directions), a little smaller than that found in the more classical (square) cube array studies of Claus et al. (2012), shown on the left of the figure. Across the whole of the downwind half of the long street the flow for the present canopy is closely aligned with the obstacle faces, despite the $45^{\text {o}}$ flow orientation aloft. This supports the suggestion made in Sect. 5 that the streets are long enough to be representative for street-network modelling approaches; shorter streets would probably not be sufficient and it will be interesting to see how well network models can predict concentrations in the present canopy.

Finally, it is worth noting that the domain-averaged axial mean velocity profiles through the canopy cannot be sensibly fitted by an exponential profile, for any of the wind directions considered. MacDonald (2000) was perhaps the first to make the suggestion that profiles could be so fitted [although such profiles in vegetation canopies had long been proposed Cionco (1965)] and recently Yang et al. (2016) have suggested that good fits to exponentials can be obtained for a wide range of arrays comprising cubical obstacles. However, although they studied arrays of cubes with $\lambda _p=0.25$, identical to those studied by Coceal et al. (2006), Leonardi and Castro (2010) and Claus et al. (2012), the canopy velocity profiles they obtained differed significantly from those obtained by all these latter authors. It seems likely that their mesh was not fine enough (having only eight points across the height of the canopy) to resolve the thin shear layer at the canopy top. A 25 % area coverage is almost within the full ‘skimming’ regime (‘d-type’ roughness, in the classical roughness terminology) and it may well be that for much lower $\lambda _p$ typical of ‘k-type’ roughness when sheltering between obstacles is less prevalent, the velocity profiles can be reasonably modelled by exponentials. This remains an open question that will be considered in a further paper, but there is no doubt that the present computations can be used to show that assumptions typically made to derive an analytical (exponential) velocity profile model are generally far from valid in urban type canopies.

Despite the various uncertainties discussed in both the laboratory and the computational studies, an important general conclusion of the work is that the computations, whether by LES or DNS, satisfactorily capture the salient details of the complex, three-dimensional flow within the canopy, in that the results agree as well as can be expected with the wind-tunnel data. This is very encouraging, for it suggests that any subsequent differences found between computed and laboratory statistics of dispersion behaviour, for the same configurations and using the same methods, will not be a result of inadequate flow computations.