Assessing the Internal Variability of Large-Eddy Simulations for Microscale Pollutant Dispersion Prediction in an Idealized Urban Environment

Abstract

This study aims at estimating the inherent variability of microscale boundary-layer flows and its impact on air pollutant dispersion in urban environments. For this purpose, we present a methodology combining high-fidelity large-eddy simulation (LES) and a stationary bootstrap algorithm, to estimate the internal variability of time-averaged quantities over a given analysis period thanks to sub-average samples. A detailed validation of an LES microscale air pollutant dispersion model in the framework of the Mock Urban Setting Test (MUST) field-scale experiment is performed. We show that the LES results are in overall good agreement with the experimental measurements of wind velocity and tracer concentration, especially in terms of fluctuations and peaks of concentrations. We also show that both LES estimates and the MUST experimental measurements are subject to significant internal variability, which is therefore essential to take into account in the model validation. Moreover, we demonstrate that the LES model can accurately reproduce the observed internal variability.

1 Introduction

Air pollutants (trace gases and aerosols) released as a result of natural hazards (e.g. wildfires, Langmann et al. 2009), daily anthropogenic emissions (Crippa et al. 2016), or industrial plant accidents (Armand and Duchenne 2022; Dumont Le Brazidec et al. 2023) can degrade air quality and have significant short- and long-term health and environmental impacts (EEA 2020). They are dispersed over a wide range of lengths and time scales, making air quality prediction a multi-scale problem (Britter and Hanna 2003).

Simulating microscale dispersion is particularly challenging. Pollutant concentrations can locally vary by orders of magnitude in time and space due to the complex turbulent flow dynamics induced by interactions between atmospheric boundary-layer (ABL) processes and surface heterogeneity. This is particularly the case in urban areas where separation and recirculation zones are caused by the presence of buildings of varying heights and geometry (Fernando et al. 2001; Klein et al. 2007; Hertwig et al. 2019). Relevant insight into these processes has been obtained via microscale Computational Fluid Dynamics (CFD) (Baklanov 2000; Antonioni et al. 2012; Tominaga and Stathopoulos 2013; Hayati et al. 2017; Toparlar et al. 2017). This approach solves the Navier–Stokes equation for the velocity field and the pollutant concentration transport equation based on Reynolds-Averaged Navier–Stokes (RANS) formalism (Meroney et al. 1999; Milliez and Carissimo 2007; Koutsourakis et al. 2012) and Large-Eddy Simulation (LES) (Patnaik et al. 2007; Gousseau et al. 2011; Harms et al. 2011; Vervecken et al. 2015a; Merlier et al. 2018) approaches. In the RANS framework, all the scales of turbulence are modelled to predict ensemble-averaged flow and dispersion field, whereas in LES the turbulent scales above the filter scale are explicitly resolved. The advantage of the latter approach is twofold: (i) it reduces uncertainties related to turbulence modelling (García-Sanchez et al. 2018) at the expense of higher computational cost; (ii) since LES provides instantaneous realizations of the physical processes it can represent the effect of the inherent temporal variability of the ABL on pollutant dispersion. This important knowledge is not accessible with the averaged formalism of the RANS approach. LES is now used to evaluate operational air quality models (Hertwig et al. 2018; Grylls et al. 2019) and to parametrize urban canopy flows in mesoscale climate models (Nazarian et al. 2020; Nagel et al. 2023).

Experimental validation is required to assess the quality and fidelity of CFD approaches (Meyers et al. 2008; Schatzmann and Leitl 2011; Blocken and Gualtieri 2012). Among the limited number of full-scale experiments available, the MUST (Mock Urban Setting Test) field experiment (Yee and Biltoft 2004) is an attractive test case to assess LES reliability for microscale air pollution prediction because (i) it features an idealized urban canopy made up of a regular array of shipping containers, simplifying the model construction; (ii) the experimental test site is isolated which reduces uncertainties on the inflow wind; (iii) observations of wind, turbulence, and tracer concentration are available at different locations throughout the field; and (iv) several studies comparing CFD model predictions with experimental measurements using both RANS (Hanna et al. 2004; Milliez and Carissimo 2007; Donnelly et al. 2009; Kumar et al. 2015) and LES (Camelli et al. 2005; Dejoan et al. 2010; Santiago et al. 2010; König 2014; Nagel et al. 2022) approaches are already reported in the literature.

However, despite their high computational cost, CFD microscale atmospheric models may still lack accuracy because of the different uncertainties involved (Montazeri and Blocken 2013; Wise et al. 2018; García-Sanchez and Gorlé 2018). The uncertainties of an LES model can be grouped into three categories: (i) aleatory uncertainties, i.e. irreducible uncertainties inherent to the stochastic nature of the physical system under consideration; (ii) structural uncertainties, i.e. uncertainties due to the choice of the code and the underlying model assumptions such as turbulence modelling; and (iii) boundary conditions uncertainties, i.e. linked to meteorological forcing, representation of the urban geometry and characterization of the pollutant source. Aleatory uncertainties come from the ABL internal variability, due to its turbulent nature and changes in the meteorological conditions (García-Sanchez and Gorlé 2018). To reduce these uncertainties, it is necessary to acquire and simulate periods long enough to achieve statistical convergence of the flow and transport phenomena. This is possible in wind-tunnel experiments and numerical simulations, but not in experimental field-scale campaigns (Schatzmann and Leitl 2011). Longer acquisitions are indeed affected by transient phenomena such as large-scale fluctuations of the ABL or day-night cycle. In microscale studies, it is therefore common to select periods that minimize the influence of the large-scale fluctuations; for instance, 200-s quasi-stationary periods have been extracted from each 15-min trial of the MUST experiments (Yee and Biltoft 2004). However, temporal averages are then calculated over relatively short periods and are thus subject to sampling errors, which correspond to the microscale internal variability of the physical system. With LES models, time windows obtained by simulation are often limited by the computational cost, implying that the time-averaged LES estimates are also subject to microscale internal variability (Sood et al. 2022). Studies report internal variability as one of the reasons for the discrepancies between field-scale experiments and CFD simulations or wind-tunnel experiments and express the need to go beyond deterministic point-wise model/observations comparison (Schatzmann and Leitl 2011; Harms et al. 2011; Dauxois et al. 2021). Quantifying internal variability would therefore be a major methodological advance for robust atmospheric CFD model validation when data are acquired over limited periods, but also for model sensitivity analysis and multi-model comparisons.

The main contribution of this study is to provide a method for quantifying the internal variability of microscale boundary-layer flows and pollutant dispersion. The proposed approach relies on sub-averages resampling using the stationary bootstrap algorithm from Politis and Romano (1994) to take into account of temporal correlations in the data. It is a promising and efficient technique that does not require long acquisition and relies on minimal statistical assumptions. Since LES provides a temporal representation of the resolved wind fluctuations, this method can also be used to estimate the aleatory uncertainty of LES predictions in any kind of context. As an illustration, the internal variability is then estimated in a neutral case of the MUST field experiment to provide confidence intervals for both LES predictions and observations of wind velocity and pollutant concentration statistics. This enables robust validation of the model as it avoids misleading conclusions and makes it possible to dissociate errors due to model biases from those explained by internal variability alone. Finally, assessing this internal variability is useful to support future model development efforts and estimate which level of accuracy is achievable, in particular for designing reduction strategies to improve operational models (Vervecken et al. 2015b; Grylls et al. 2019; Dauxois et al. 2021).

The outline of this paper is as follows. The MUST trial is first presented in Sect. 2. The main features of the LES model are described in Sect. 3. The bootstrap procedure used to estimate internal variability is explained in Sect. 4. Results are finally presented and discussed in Sect. 5.

2 The Mock Urban Setting Test Experiment (MUST)

2.1 Experimental Site Description

MUST is a field-scale experiment performed in September 2001 at the US Army Dugway Proving Ground test site in the Utah desert (USA). Its objective was to provide extensive measurements in the short-to-medium range of a plume within an urban-like canopy in support of the development and validation of urban dispersion models (Biltoft 2001; Yee and Biltoft 2004).

The idealized urban canopy is mimicked by an array of $10\times 12$ regularly-spaced shipping containers covering an area of about $200\times 200\,\hbox {m}^2$ (Fig. 1). The array (in its x–y coordinate system) makes an angle of $30^{\circ }$ to the north. The containers are 12.2-m long, 2.42-m wide and 2.54-m high. The average distance between two containers is 12.9 m along the x-axis and 7.9 m along the y-axis. The terrain is flat and homogeneous with a mix of sparse greasewood and sagebrush ranging from 0.4 to 0.75 m high. It is worth mentioning that the geometry of the idealized canopy was slightly irregular, as the containers were not all perfectly aligned, and one container was replaced by a van (Biltoft 2001). Their impact on the flow field was studied in Santiago et al. (2010), but we consider in this study a regular case as in Milliez and Carissimo (2007) and Nagel et al. (2022).

Fig. 1

Schematic view of the MUST array configuration adapted from Kumar et al. (2015), the coordinate system used is the same as in Yee and Biltoft (2004) such that north corresponds to the angle of $-\,30^{\circ }$ in the x–y coordinate system. Black rectangles represent the shipping containers used to mimic the urban canopy. Triangles correspond to the anemometers mounted on towers S, T, and N. Yellow plus symbols correspond to the masts V equipped with WDTC anemometers, and the purple plus symbol to the ASU anemometer. Coloured circles correspond to the DPID concentration samplers (one colour for each line of sensors), and coloured squares correspond to the UVIC concentration samplers mounted on towers A, B, C, and D (note that there is a DPID sampler at the same location as tower D). The upstream mean wind direction (red arrow) and the propylene-source location (red star) of the trial 2681829 retained for the present study are also indicated

During the experiments of the MUST field campaign, a non-reactive gas (propylene) was released, passively, at different horizontal and vertical locations, and for different atmospheric conditions (in terms of wind direction, wind speed, and atmospheric stability condition). This gas can be considered a passive tracer.

2.2 Available Experimental Data

The MUST experimental dataset includes wind velocity and tracer concentration measurements within and outside the container array. This section summarizes the data of primary importance for the design and evaluation of our LES modelling approach. The reader should refer to Biltoft (2001) for full details of the instruments used during the MUST field campaign. For wind velocity measurements, two-dimensional and three-dimensional sonic anemometers were provided by the Dugway Proving Ground’s West Desert Test Center (WDTC) and deployed vertically on different masts (triangles in Fig. 1): four anemometers were mounted on the central tower T at $z = 4$, 8, 16 and 32 m; and three anemometers were mounted at $z = 4$, 8 and 16 m on each of the towers S and N (located 30 m upstream and downstream from the canopy, respectively). WDTC three-dimensional sonic anemometers were also positioned within the canopy at $z=1.15$ m on four tripods V (yellow plus-symbols in Fig. 1). An additional three-dimensional sonic anemometer, provided by the Arizona State University (ASU), measured wind velocity upstream of the containers, near tower S, at $z = 1.6$ m (purple plus-symbol in Fig. 1).

For tracer concentration measurements, 48 digi-photoionization detectors (DPIDs, coloured circles in Fig. 1) were used as well as 24 ultraviolet ion collectors (UVICs, coloured squares in Fig. 1). The DPIDs have a detection threshold of 0.04 ppm against 0.01 ppm for the UVICs. 40 DPIDs were placed within the canopy at $z = 1.6$ m, forming four sensor lines aligned with the y-axis (referred to as the DPIDs lines in Fig. 1); eight were placed on the central tower T at $z = 1$, 2, 4, 6, 8, 10, 12 and 16 m. Also, six UVICs were mounted within the canopy on each of the four 6-m towers A, B, C, and D at $z = 1$, 2, 3, 4, 5, 5.9 m to obtain vertical concentration profiles.

2.3 Selected Case

From all the available observations, 21 trials were chosen by Yee and Biltoft (2004) for their high quality (i.e. tracer detection on the tower T and for three of the four DPID lines). In addition, Yee and Biltoft (2004) extracted a 200-s quasi-stationary (in the statistical sense) period in each 15-min experiment that minimizes the effect of mesoscale meteorological fluctuations on the tracer concentration time series. This time window (referred to as the analysis period in the following) was chosen as the sequence with the smallest variation in mean wind speed and direction at the upstream tower S for each trial.

In this work, we simulate one of the 21 trials referred to as 2681829, which has been studied in the literature with LES (König 2014; Nagel et al. 2022) and in RANS mode as part of a set of MUST trials (Milliez and Carissimo 2007; Donnelly et al. 2009; Kumar et al. 2015). The trial main characteristics extracted from the data of Yee and Biltoft (2004) are summarized in Table 1. This case is a configuration with neutral atmospheric conditions (i.e. afternoon transition from unstable to stable conditions), characterized by a high value of the surface Obukhov length $L_\text {{o}}$ ($L_\text {{o}} \gg 2500$ m) estimated by Yee and Biltoft (2004), no latent and sensible heat fluxes, and a weak influence of buoyancy. The time-averaged wind speed $u_4$ and direction $\alpha _4$ at $z = 4$ m at the upstream tower S are respectively $7.93\,\textrm{m}\,\hbox {s}^{-1}$ and $-\,41^{\circ }$ (this angle is defined with respect to the x-axis of the container array indicated in Fig. 1, the north direction corresponding to an angle of $-\,30^{\circ }$). The gas was released, passively, at $z_s = 1.8\,$m near the inlet of the canopy (red star symbol in Fig. 1) with a constant flow rate $Q = 225\,$L$\,\hbox {min}^{-1}$.

For this selected trial, the analysis period is between 300 and 500 s after the start of the acquisition. The objective of this study is to estimate the internal variability associated with this limited acquisition time, and then to take it into account for the validation of the meteorological and tracer concentration statistics forecasts provided by our LES modelling approach.

Table 1 Main characteristics of the MUST trial 2681829 (Yee and Biltoft 2004): $\alpha _4$ and $u_4$ are respectively the time-averaged wind direction and wind speed at $z = 4$ m of the upstream tower S, $L_\text {{o}}$ is the surface Obukhov length estimated by Yee and Biltoft (2004) using the vertical fluxes of temperature and velocity measured at $z = 4$ m of the central tower T, Q is the constant tracer release rate at the source, and $z_s$ is the source height. The flow statistics are computed on the [300; 500 s] analysis period

3 Large-Eddy Simulation (LES) Model of the MUST Trial 2681829

In this section, the LES solver and numerical setup to model the microscale flow and plume dispersion within the canopy during the MUST trial 2681829 are described. The validation metrics in terms of flow and tracer concentrations for comparison with the experiments are also presented.

3.1 Numerical Large-Eddy Simulation (LES) Solver

The massively parallel LES code AVBP (Schönfeld and Rudgyard 1999; Gicquel et al. 2011)¹ developed by CERFACS is used to perform LES of the microscale flow and plume dispersion within the canopy during the MUST trial 2681829. It solves the LES-filtered compressible Navier–Stokes equations for flow dynamics and tracer advection–diffusion equation on unstructured grids. AVBP is widely used to resolve non-reactive or reactive unsteady flows in simple or complex geometry (Gicquel et al. 2011). It is also relevant to predict pollutant formation and atmospheric dispersion (Poubeau et al. 2016; Paoli et al. 2020).

In terms of numerical discretization, the second-order Lax-Wendroff (LW) finite-volume centered scheme (Schönfeld and Rudgyard 1999) is used in this study. Because of explicit time advancement and a fully compressible formulation, the LES timestep is subject to an acoustic CFL condition. In the context of very low Mach ABL flow, to increase the timestep and thereby save computational time, an artificial compressibility approach (pressure gradient scaling, Ramshaw et al. (1986)) is adopted.

In terms of subgrid-scale modelling, the Wall-Adaptative Local Eddy-Viscosity (WALE) model (Nicoud and Ducros 1999) accounts for the subgrid momentum transport. It represents the effect of unresolved small scales on the flow with a subgrid eddy-viscosity hypothesis, with a model form that is well adapted for shear-driven flows (Nicoud and Ducros 1999). The constant involved in the subgrid-scale turbulent viscosity estimation is set to $C_w = 0.5$ as recommended by Nicoud and Ducros (1999).

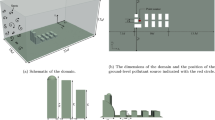
3.2 Computational Domain and Mesh

The computational domain in which the Navier–Stokes and the tracer transport equations are solved is a rectangular cuboid oriented so that the inlet boundary is normal to the mean upstream wind direction. In the x–y plane, the domain is a $420\times 420\,\hbox {m}^2$ square centred on the container array. Along the z-axis, the height of the domain is 50 m. To avoid lateral or vertical confinement effects, the distance between the lateral boundaries and the container array is at least 80 m (corresponding to $30\,H$, with $H = 2.54$ m the container height), and the distance between the top boundary and the top of the containers is 18 H. This geometry ensures compliance with the guidelines for CFD simulation of urban atmospheric flows (Tominaga et al. 2008; Franke et al. 2011). Consistently, Nagel et al. (2022) found that there was no significant influence of domain height on the microscale flow dynamics and plume dispersion predictions obtained using LES in a CFD-like configuration.

At the domain inlet, a turbulent inflow boundary condition is imposed to represent the upstream unsteady wind conditions that have an impact on the microscale flow dynamics and tracer dispersion (more details are given in Sect. 3.3). At the outlet and top boundaries, the static pressure is softly imposed to evacuate acoustic waves (Poinsot and Lele 1992). Symmetry boundary conditions are used for the lateral boundaries. The ground boundary is modelled as a rough surface with imposed shear stress evaluated using a law-of-the-wall based on the roughness length $z_0$. Similarly, for the container surfaces, the shear stress is imposed from the law-of-the-wall for a smooth surface based on a viscous length (Larsson et al. 2016).

An unstructured and boundary-fitted mesh of 91 million tetrahedra is used to discretize the computational domain. In the region of interest (in a box of $246\times 266\times 3.6\,\hbox {m}^3$ that contains the full container array), the mesh is uniform with a resolution equal to $\Delta x = \Delta y = \Delta z = 0.3$ m (this resolution corresponds to at least 8 cells over the height of the obstacle). In the rest of the domain, the mesh has a resolution of 0.3 m at the ground level except near the outlet and the lateral boundaries, where the resolution was coarsened to 2 m to reduce the number of cells. On the vertical, the mesh is gradually stretched to reach a 5-m resolution at the top boundary.

The mesh resolution used in this study is in line with the resolutions used in the literature, which typically range from 50 cm in König (2014) to 30 cm in Nagel et al. (2022). Such high-resolution LES is useful for examining the turbulent structures near the surface induced by the containers in the MUST experiments.

3.3 Inflow Boundary Condition Modelling

One challenge in LES of near-field pollutant dispersion relates to the modelling of inflow boundary conditions (Muñoz-Esparza et al. 2014; Dauxois et al. 2021). In field-scale applications, there is usually a limited amount of information available to represent the complexity of actual microscale inflow conditions that are influenced by the ABL variability. One way to represent the mesoscale/microscale interactions is to perform a dynamical downscaling of the atmospheric flow using a multi-scale meteorological model based on grid nesting (Wiersema et al. 2020; Nagel et al. 2022). This multi-scale approach resulted in significant improvement of the microscale flow velocity and tracer concentration predictions for the Oklahoma City Joint Urban 2003 experiment (Wiersema et al. 2020). However, this finding did not hold for the MUST idealized urban environment, where a standalone microscale LES configuration based on idealized inflow boundary conditions achieved the same level of accuracy as a multi-scale approach (Nagel et al. 2022). We therefore represent the turbulent inflow boundary condition using an idealized approach in this work.

3.3.1 Inlet Mean Wind Profile

The logarithmic wind profile from Richards and Hoxey (1993), representing a fully developed neutral atmospheric surface layer, is imposed at the inlet. This description is sufficient as (i) the selected trial corresponds to a neutral stratification condition; and (ii) we focus on the near-surface flow inside and just above the canopy. The mean horizontal wind velocity $\overline{u_{inlet}}$ at height z reads:

$$\begin{aligned} \overline{u_{inlet}}(z) = \frac{u_*}{\kappa } \ln \left( \frac{z + z_0}{z_0} \right) , \end{aligned}$$

(1)

where $z_0$ (m) is the aerodynamic roughness length equal to $0.045 \pm 0.005$ m according to observations (Yee and Biltoft 2004), $\kappa$ is the von Kármán constant equal to 0.4, and $u_*$ (m $\hbox {s}^{-1}$) is the friction velocity. The parameter $u_*$ is calibrated here by fitting the profile (Eq. 1) through a least-square regression on wind speed measurements available at the upstream tower S and for the ASU anemometer (these data are described in Sect. 2.2). This leads to $u_* = 0.73$ m $\hbox {s}^{-1}$, with an associated uncertainty of 0.12 m $\hbox {s}^{-1}$ estimated by uncertainty propagation. The corresponding vertical profile for the inlet mean wind is shown in Fig. 2a along with the measurements used for regression.

A constant wind direction $\overline{\alpha _{inlet}}$ is imposed on the vertical at the inlet so that the inlet wind vector reads $\overline{\textbf{u}} = \left( \overline{u_{inlet}} \,\cos (\overline{\alpha _{inlet}}),\ \overline{u_{inlet}} \,\sin (\overline{\alpha _{inlet}}),\ 0 \right) ^\textrm{T}$ in the MUST frame of reference (see Fig. 1). The constant wind direction is obtained by spatially averaging the four wind direction measurements available at tower S and for the ASU anemometer. This leads to $\overline{\alpha _{inlet}} = -40.95^{\circ }$, a value that remains very close to the observation at $z = 4$ m (see Table 1, page 7).

Fig. 2

Vertical profiles (solid lines) of the a inlet mean wind speed $\overline{u_{inlet}}(z)$, and the b inlet wind speed fluctuations $\overline{u_i'u_j'}(z)$ predicted by a precursor simulation and used to define the LES inflow boundary condition. Symbols correspond to experimental data

3.3.2 Inlet Wind Fluctuations

To provide an inflow boundary condition that is representative of boundary-layer turbulence, temporal wind fluctuations $\mathbf {u'}$ are added to the mean inlet wind profile (Eq. 1) according to Reynolds’ decomposition. The fluctuations are obtained from Fourier pseudo-random modes using the Kraichnan-Smirnov synthetic turbulence injection method (Kraichnan 1970; Smirnov et al. 2001) constructed so that they follow the Passot–Pouquet turbulence spectrum (Passot and Pouquet 1987). The fluctuations are defined based on the full turbulent Reynolds stress tensor since the Kraichnan method allows prescribing anisotropic and heterogeneous turbulence. It was verified that the distance between the inlet and the first obstacle, $d_{inlet} = 80$ m, is large enough to ensure the transition from the synthetic spectrum to a fully developed turbulence energy cascade. One drawback of the method is that the eddy length scale is limited by the inlet surface size (in this work, the maximum size of the eddies is equal to half the domain height, i.e. 25 m).

The components of the Reynolds stress tensor are estimated using a preliminary simulation with the same surface roughness but without obstacles, and with periodic boundary conditions at the inlet and outlet (Keating et al. 2004; Munters et al. 2016; Vasaturo et al. 2018). This periodic simulation is run at a 6.25-m resolution over a $400\times 400\times 250\,\hbox {m}^3$ computational domain and a 2-hour period to obtain converged velocity fluctuation statistics. The resulting mean velocity fluctuations are shown in Fig. 2b alongside fluctuation measurements. Even though experimental measurements of fluctuations were not used to calibrate the precursor simulation, it reproduces overall well the level of fluctuations measured at tower S upstream of the containers. The $\overline{u_x'^2}$ fluctuation profile is accurately predicted, however, the precursor tends to underestimate $\overline{u_y'^2}$ and overestimate $\left|\overline{u_x'u_y'}\right|$, especially below 5 m. These fluctuations statistics form the Reynolds stress tensor, which is imposed at the inlet of the microscale domain.

Fig. 3

Horizontal cuts at $z=1.6$ m of instantaneous a horizontal wind speed magnitude $u_h$ (m s^-1) and b propylene concentration c (ppm) at $t=60$ s. c Horizontal cut of the time-averaged concentration over the 200-s analysis period. White rectangles represent containers. The red star represents the tracer source, and the green line represents the mean wind direction imposed at the inlet. The plume centerline, identified by the positions of the mean concentration maximum on lines orthogonal to the incident wind angle, is represented as a red line (c)

3.4 Initial Condition and Simulation Spin-up

The LES simulation is initialized using a homogeneous flow field in the horizontal directions equal to the inlet mean field (Sect. 3.3.1). A spin-up time of 60 s, which corresponds to 1.5 times the convective time scale, is used so that first- and second-order statistics of the flow and the tracer reach a stationary state. A 200-s time window corresponding to the [300; 500 s] analysis period (Sect. 2.3) is then simulated, from which statistics of the flow and tracer concentration variables can be collected. At probe location, outputs are saved with a resolution of 0.05 s.

3.5 Tracer Modelling

Tracer dispersion is modelled by the LES-filtered advection–diffusion equation using an Eulerian approach. The effect of the subgrid scales on the tracer transport is modelled using a gradient-diffusion hypothesis with a turbulent Schmidt number $\textrm{S}_c^t$ set equal to 0.6. Sensitivity tests demonstrate that the choice of $\textrm{S}_c^t$ has a very limited impact on the model predictions (not shown here).

As in other simulations of the MUST experiment (Milliez and Carissimo 2007; Dejoan et al. 2010), the pollutant source is simulated by a local source term in the transport equation so the volumetric flow rate matches the experimental value Q defined in Table 1. A Gaussian-shaped volumetric source term is imposed with a half-width set to cover approximately 6 cells in each direction in order to avoid concentration discontinuities.

Illustrative examples of instantaneous flow and tracer concentration fields obtained by the LES model after the spin-up period are given in Fig. 3a, b. The transition from large-scale turbulence provided by the turbulent inlet forcing to small-scale turbulent structures induced by the containers is visible in Fig. 3a. The resulting instantaneous tracer concentration field is shown in Fig. 3b, highlighting the scale disparity of local tracer concentration values that can reach 10 ppm near the emission source. Figure 3c shows the time-averaged propylene concentration over the 200-s analysis period within the canopy. It highlights the deviation of the mean plume centerline from the incident mean wind direction because of the wind channeling effect induced by the obstacles.

In terms of computational cost, simulating a 260-s physical period (including the spin-up and the 200-s analysis period) for this MUST configuration costs 20,000 core hours, using 1344 CPU cores on the TGCC Irene SKL supercomputing facility (Intel Skylake architecture).

3.6 Model Validation Metrics

3.6.1 Wind Speed and Direction Metrics

To assess the model’s ability to quantitatively predict the flow field within and over the canopy, three metrics based on time-averaged quantities are used to quantify the difference between model predictions and flow measurements. The hit rate (q) and the mean absolute error (MAE) evaluate discrepancies for the horizontal flow velocity $u_h$ while the scaled averaged angle (SAA) quantifies the deviations for the horizontal direction of the flow $\overline{\alpha }$:

$$\begin{aligned}{} & {} q = \frac{1}{N_{obs}}\,\sum _{k=1}^{N_{obs}} \xi _k \text { with } \xi _k = {\left\{ \begin{array}{ll} 1 \text { if } \left|~\overline{{u_h}}_p^{(k)} - \overline{{u_h}}_o^{(k)}\right| \le AD \\ 1 \text { if } \frac{\left|~\overline{{u_h}}_p^{(k)} - \overline{{u_h}}_o^{(k)}\right|}{\left|~\overline{{u_h}}_o^{(k)}\right|} \le RD \\ 0 \text { else,} \end{array}\right. }, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} MAE = \langle ~\left|\overline{{u_h}}_p - \overline{{u_h}}_o\right|~\rangle , \end{aligned}$$

(3)

$$\begin{aligned}{} & {} SAA = \frac{\langle ~\overline{{u_h}}_p \left|\overline{\alpha }_p - \overline{\alpha }_o\right|~\rangle }{\langle ~\overline{{u_h}}_p~\rangle }, \end{aligned}$$

(4)

where ${\overline{u_h}}_o$ and $\overline{\alpha }_o$ are the observed time-averaged horizontal wind speed and direction, and ${\overline{u_h}}_p$ and $\overline{\alpha }_p$ are the model colocated predictions. Each element of the $N_{obs}$ dataset is indexed by the superscript (k) in Eq. 2, while the angle brackets $\langle \cdot \rangle$ indicate the average over the $N_{obs}$ elements in Eqs. 3–4. To compute the hit rate (Eq. 2), we use the same values of absolute deviation (AD) and relative deviation (RD) as Nagel et al. (2022), i.e. $AD = 1\,$m $\hbox {s}^{-1}$ and $RD = 0$.

The hit rate and SAA metrics have been used in other MUST modelling validation studies (Santiago et al. 2010; Nagel et al. 2022) and we use in addition the MAE following recommendations by Santiago et al. (2010). The perfect scores associated with these metrics are reported in Table 3. The metrics in Eqs. 2–4 are evaluated on the full set of WDTC sonic anemometer measurements, which are located on the towers S, T and N as well as on the four masts V (Sect. 2.2). Note that the first anemometer of the tower N downstream of the containers (located at $z = 4\,$m) was excluded because of its failure during the trial. The total number of measurements for LES model validation for flow prediction is, therefore, $N_{obs} = 13$. The accuracy of the wind flow estimates is only assessed for the horizontal velocity because most of the experimental measurements were provided by 2-D anemometers.

3.6.2 Tracer Concentration Metrics

LES model performance for tracer concentration prediction (in ppm) is evaluated using the standard statistical metrics for air quality model evaluation (Chang and Hanna 2004), which were also used in previous MUST studies with CFD modelling approaches (Milliez and Carissimo 2007; Antonioni et al. 2012; Nagel et al. 2022). These metrics compare the simulated and observed tracer concentrations in terms of fractional bias (FB), normalized mean square error (NMSE), fraction of predictions within a factor of two of observations (FAC2), geometric mean bias (MG), and geometric variance (VG):

$$\begin{aligned}{} & {} FB = \frac{\langle \overline{c}_{o}\rangle - \langle \overline{c}_{p}\rangle }{\frac{1}{2} \left( \,\langle \overline{c}_{o} \rangle + \langle \overline{c}_{p} \rangle \,\right) }, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} NMSE = \frac{\langle \,\left( \overline{c}_{o} - \overline{c}_{p}\right) ^2\,\rangle }{\langle \overline{c}_{o} \rangle \,\langle \overline{c}_{p} \rangle }, \end{aligned}$$

(6)

$$\begin{aligned}{} & {} FAC2 = \frac{1}{N_{obs}}\,\sum _{k=1}^{N_{obs}} \xi _k \text { with } \xi _k = {\left\{ \begin{array}{ll} 1 \text { if } 0.5 \le \overline{c}_p^{(k)}\,/~\overline{c}_o^{(k)} \le 2.0, \\ 0 \text { else,} \end{array}\right. } \end{aligned}$$

(7)

$$\begin{aligned}{} & {} MG = \exp \left( \,\langle \ln \widetilde{c}_{o} \rangle - \langle \ln \widetilde{c}_{p} \rangle \,\right) , \end{aligned}$$

(8)

$$\begin{aligned}{} & {} VG = \exp \left( \langle \,\left( \ln \widetilde{c}_{o} - \ln \widetilde{c}_{p} \right) ^2\,\rangle \right) , \end{aligned}$$

(9)

where $\overline{c}_o$ is the observed time-averaged concentration and $\overline{c}_p$ is the simulated counterpart. The tilde indicates that a threshold is applied to the concentration, i.e. $\widetilde{c} = \max (\overline{c},\,c_t)$, where $c_t$ is the concentration threshold, following recommendations from Chang and Hanna (2004) and Schatzmann et al. (2010).

For this analysis, the observation data are made of the tracer concentration measurements at the 40 DPID sensors located at $z =1.6$ m throughout the array of containers, at the 8 DPID sensors mounted on the tower T as well as at the 24 UVIC sensors mounted on the towers A, B, C, and D (Fig. 1). The threshold $c_t$ used to estimate the MG and VG metrics is taken as the instrument detection threshold (0.04 ppm for DPIDs and 0.01 ppm for UVICs as detailed in Sect. 2.2). The sensors that measure a time-averaged concentration below this threshold (over the [300; 500 s] analysis period) are excluded from the metrics estimations. This implies that only $N_{obs} = 47$ out of 72 concentration sensor measurements are used in the validation process in this study.

4 Internal Variability Estimation

4.1 Motivation

The internal variability associated with the atmospheric surface-layer processes induces an aleatory uncertainty in the observations and in the LES model predictions. As an illustration, Fig. 4a shows that the time-averaged concentration at a height of $z = 2$ m on tower B significantly changes between five LES estimates obtained over five consecutive 200-s time periods after the spin-up. This variability also extends to the whole vertical range of the plume, as illustrated by the vertical profile changes in Fig. 4b (see Sect. 5.2 for a more detailed analysis). Note that the five LES estimates are obtained for the exact same model configuration. This suggests that the aleatory uncertainty induced by the internal variability of the ABL is significant and should be accounted for, especially for model validation.

Fig. 4

Tracer concentration simulated using LES at tower B. a Time series at $z = 2$ m. b Time-averaged vertical profiles. Coloured lines correspond to three different realizations of the time-averaged concentration obtained with different 200-s averaging windows ([60; 260s] in orange, [260; 460s] in green, [460; 660s] in red, [660; 860s] in cyan and [260; 460s] in magenta)

In this section, we first formalize the effect of the ABL microscale internal variability on the quantities of interest (Sect. 4.2) and review existing methods to quantify it (Sect. 4.3). The method best suited to our context is then described in Sect. 4.4, with detailed information on how to choose its parameters and how to apply it to LES model predictions, experimental measurements and validation metrics.

4.2 Definition

Let $\overline{Y}$ be the 200-s time-averaged estimation of a given field Y, for example, the mean concentration field. It can be written as the mean of sub-samples averaged over shorter time windows :

(10)

where $\delta _t$ is a fraction of the total time-averaging window $T_{avg} = 200$ s such that $N_t = \lfloor T_{avg} / \delta _t \rfloor$ is the corresponding number of sub-samples. It is worth noting that extracting sub-samples over small averaging periods is feasible with an LES simulation, which provides instantaneous realizations of the turbulent phenomena, contrary to other dispersion modelling techniques such as RANS.

Written this way, the time-average $\overline{Y}$ can be seen as the sample estimator of the mean:

(11)

and internal variability corresponds to the variability of $\mu (\overline{Y})$ when the sample of sub-averages changes. In this sense, internal variability describes sampling noise error due to limited sample size $N_t$, i.e. limited acquisition time. The objective of this section is to estimate the variance of the sample mean estimator $\mathbb {V}(\mu )$.

4.3 Methods to Quantify Internal Variability

To quantify model internal variability, the most straightforward approach is to run several independent simulations and characterize the variance of the predictions (Costes et al. 2021). However, this is very computationally intensive (each LES estimation costs about 20,000 CPU hours), and unfeasible for observations because one cannot reproduce 200-s acquisitions with the same atmospheric conditions.

Another method is to apply the central limit theorem that provides a confidence interval for the sample mean estimator $\mu (\overline{Y})$ (Eq. 11). However, this interval is asymptotic and a large number of realizations of $\mu (\overline{Y})$ is needed for the sample mean to converge in law to a normal distribution, which is not feasible in our case because of the model computational cost.

Alternatively, one could model the statistical distribution of the sub-average samples to deduce, either analytically or through Monte Carlo estimation, the distribution of the sample mean $\mu (\overline{Y})$ and hence its variance. For example, the Gamma distribution is well suited for tracer concentration modelling (Cassiani et al. 2020; Orsi et al. 2021). However, this distribution assumption is not always appropriate. For example in our case, the Kolmogorov–Smirnov test (Massey 1951) shows that it is rejected for 4 probes out of 47. More importantly, when Y is a vector, it is difficult to find a statistical distribution that properly accounts for the correlation between its components. Yet, this is essential to propagate internal variability to validation metrics without error compensation (see Sect. 4.4.5).

To circumvent these issues, it is possible to rely on the empirical distribution of the available sub-average samples instead of assuming a priori their distribution. This is the fundamental principle of Jackknife resampling and bootstrap methods (Efron 1979), which are used in statistics for variance estimation and which are also widely used in climate science for model internal variability estimation (Huybers et al. 2014; Diffenbaugh et al. 2017; Risser et al. 2019; Chan et al. 2020). In our field of interest, Hanna (1989) used bootstrap to quantify confidence intervals for air quality model validation metrics; this is for instance implemented in the BOOT statistical model evaluation tool (Chang and Hanna 2005). More recently, Sood et al. (2022) used bootstrap to assess confidence intervals of ABL time-averaged estimates obtained with LES.

4.4 Application of a Bootstrap Method

4.4.1 On the Independance of the Samples

The standard bootstrap method relies on the assumption that the sub-average samples are independent and identically distributed (Efron 1979).

In the current study, the latter assumption is ensured for the LES model because it is stationary by construction: first, we use a spin-up period to remove the transient state; then, the inflow boundary conditions are stationary at the scale of the total averaging period of 200 s. However, observations from field campaigns are not necessarily stationary because of mesoscale fluctuations and daily variability in weather conditions. In this regard, the 200-s analysis period for the present case was chosen to minimize the large-scale variability (Yee and Biltoft 2004), and can thus be considered quasi-stationary.

To quantify the dependency between the sub-average samples , we use the correlation length $\lambda$, defined as the maximum inter-sample distance such that the auto-correlation function is larger than 20%. Figure 5a shows the auto-correlation of the sub-averages and the corresponding correlation length $\lambda$ for the concentration at 2-m high at tower D for both LES predictions and observations, using a sub-averaging period of $\delta _t = 10\,$s ($N_t = 20$). It shows that observed concentration sub-averages are not independent, with a correlation length of $\lambda _{obs} = 2$. Moreover, it appears to be the case for the majority of the probes over the detection threshold (Fig. 5b). Note that LES tends to underestimate the correlation of the concentration sub-averages compared to the measurements. This is because the size of the largest eddies in the LES setup is limited by the size of the computational domain, as explained in Sect. 3.3.2, thus limiting long-term correlations related to large-scale fluctuations. The fact that sample independence is not verified should not be overlooked, as it yields internal variability underestimation when using the standard bootstrap, as shown in Fig. 7.

Fig. 5

a Example of auto-correlation function versus discrete time-lag k of the concentration sub-averages over 10 s, for both measured and simulated concentration at tower D at $z=2\,$m. Vertical dashed lines correspond to the correlation length (in red for measurements and in blue for simulations). b, c Correlation lengths computed at every probe location for measurements (in red) and simulation sub-averages (in blue). Horizontal black dashed lines correspond to the averaged correlation length over all the probes

To deal with sample dependency, several methods for stationary weakly dependent samples are reported in the literature such as block bootstrap (Carlstein 1986), moving block bootstrap (Kunsch 1989) and stationary bootstrap (Politis and Romano 1994). In this study, we adopt the latter as (i) it allows for compromise in the choice of the block length as explained in Sect. 4.4.3, (ii) it does not undersample the first and last sub-samples, and (iii) it ensures that the bootstrap replicates remain stationary, unlike the other methods mentioned (Politis and Romano 1994). Note that the assumption of weak dependency is verified in the current study as the correlation between sub-average samples rapidly tends to zero for both simulation and observations (Fig. 5a). This is the case at every probe location since the estimated correlation lengths are always small compared to the number of sub-average samples $N_t$ (Fig. 5b, c).

4.4.2 Stationary Bootstrap Principle

The fundamental principle of bootstrap techniques is to resample with replacement the elements of the original sample (Fig. 6a) to generate B new samples called bootstrap replicates (Fig. 6b). In the stationary bootstrap method from Politis and Romano (1994), this is done by resampling blocks of consecutive elements instead of individual elements to account for the dependency between samples. The number of sub-averages in each block is randomly selected according to a geometrical law, implying that not all blocks are the same size, as illustrated in Fig. 6b.

Fig. 6

Stationary bootstrap algorithm applied to LES average concentration estimation at tower B ($z = 2$ m). a Sub-averages $\breve{c_k}$ over 10 s (coloured bars) are computed over the 200-s simulated time series (grey solid line). b Three examples of bootstrap replicates generated by resampling with repetition of blocks of the original 10-s sub-averages, their sample means $\lbrace \mu ^{(1)}, \mu ^{(2)}, \mu ^{(B)} \rbrace$ (Eq. 11) are shown as horizontal lines and illustrate the variability induced by the resampling. c The statistical distribution of the sample mean estimator $\mu$ is inferred from the B bootstrap replicates. The three examples of bootstrap realizations of time-averages of concentration over 200 s $\lbrace \mu ^{(1)}, \mu ^{(2)}, \mu ^{(B)} \rbrace$ are also represented as vertical dashed lines (c). In this example, the mean block length is $\ell = 2.5$

Because of the occurrence of repetitions in the resampling, the sample means of the bootstrap replicates $\left\{ \mu ^{(i)}(\overline{Y})\right\} _{i=1}^B$ always slightly differ, as shown by the horizontal dashed lines in Fig. 6b. This describes the variability of $\mu (\overline{Y})$ due to sampling error, which is precisely the internal variability of the 200-s average with the decomposition in sub-averages we propose in Eq. 10. Internal variability can thus be quantified in terms of variance as follows:

$$\begin{aligned} s^2\left( \,\mu (\overline{Y})\,\right) = \frac{1}{B-1}\,\displaystyle \sum _{i=1}^{B} \left( ~{\mu }^{(i)}(\overline{Y}) - \widehat{\mu (\overline{Y})}~\right) ^2, \end{aligned}$$

(12)

with $\widehat{\mu (\overline{Y})} = \frac{1}{B} \sum _{i=1}^B \mu ^{(i)}(\overline{Y})$. Bootstrap methods also estimate the complete distribution of the sample mean (shaded histogram in Fig. 6c). This allows providing confidence intervals for the original estimate $\mu (\overline{Y})$ based on the percentiles of the empirical bootstrap distribution.

4.4.3 Stationary Bootstrap Parameters

The stationary bootstrap strongly depends on three parameters: the number of bootstrap replicates B, the original sample size $N_t$, and the mean block length $\ell$.

It is important to use a large enough number of bootstrap replicates B to avoid sampling noise in the bootstrap estimates (Eq. 12). Note that the minimum number of required replicates depends on the target statistical moment from the estimator $\mu$. Here we are mainly interested in 95% confidence intervals, which require larger B than first-order moments (Davison and Hinkley (1997) suggested $B \ge 1000$). Results of the convergence tests performed for the current study case are presented in Appendix I.

On the other hand, the sample size $N_t$ depends on the physical context and also on the statistical moment of interest. In this study, our objective is to characterize the mean estimator (Eq. 11), which does not need as large $N_t$ as the variance estimator or the median estimator (Davison and Hinkley 1997). Still, a too small value for $N_t$ would result in too short confidence intervals (Davison and Hinkley 1997; Scheiner and Gurevitch 2001) and hence internal variability underestimation. Since the original samples are sub-averages (Eq. 10), one could simply reduce the averaging window $\delta _t$ to increase the number of sub-average samples $N_t$. However, it increases the dependency between samples which thus may not bring additional information on the underlying distribution. In this study, based on this compromise, we retain sub-averages computed over $\delta _t = 10\,$s, which yields $N_t = 20$ (see Appendix I for further details). Alternatively, it is possible to increase the number of sub-average samples by increasing the duration of the simulations. Comparison between bootstrap estimates over 200-s, 400-s and 600-s simulations is described in Appendix I. Results show that the acquisition of 200 s is enough to assess the variability of the time-averaged quantities over 200 s. It is therefore not necessary to run extended LES simulations to properly estimate microscale internal variability for the considered MUST trial.

Fig. 7

Relative standard deviations of the concentration mean over 200 s estimated with stationary bootstrap and averaged over every probe, for different mean block length $\ell$. Results for observations and simulations are indicated in cyan and magenta, respectively. The dashed line corresponds to the relative standard deviation estimated by the stationary bootstrap

Finally, the choice of the mean block length $\ell$ used in the stationary bootstrap is crucial as it has a strong influence on the final internal variability estimation as shown in Fig. 7. In practice, the choice of $\ell$ results from a careful trade-off as using larger blocks reduces the number of samples within each bootstrap replicate: too few samples often result in internal variability underestimation (Davison and Hinkley 1997; Scheiner and Gurevitch 2001), however, using shorter blocks may also lead to internal variability underestimation as it implies neglecting sample dependency (Fig. 7). In the limit case $\ell =1$, stationary bootstrap is equivalent to the standard bootstrap. In this study, we define the mean block length as the averaged value of the correlation length over all probe locations, i.e. $\ell = \langle \lambda \rangle + 1$, as done by Diffenbaugh et al. (2017). This approach leads to $\ell _{sim} = 1.17$ and $\ell _{obs} = 1.85$ for the mean concentration $\overline{c}$ (Table 2).

Note that a compromise is made since a single value of $\ell$ is used for the whole vector of concentration measurements (and its model counterpart), while the probes have different correlation lengths (Fig. 5b, c). Indeed, to propagate the internal variability to the validation scores (see Sect. 4.4.5), the same stationary bootstrap resampling must be used for every probe at once in order to preserve the spatial correlations between them. Otherwise, the variability of the validation metrics would be underestimated because of error compensation.

4.4.4 Application to Statistics of Interest

In this study, the stationary bootstrap method is used to assess the variability of the average concentration $\overline{c}$ but also of the average wind horizontal velocity (in terms of amplitude $\overline{u_h}$ and direction $\overline{\alpha }$). As the richer description of LES provides access to higher-order statistics beyond mean predictions, the stationary bootstrap method is also applied to assess the variability of concentration fluctuation $\overline{c'^2} = \overline{(c - \overline{c})^2}$ and flow turbulent kinetic energy $k = \frac{1}{2} (\overline{u_x'^2} + \overline{u_y'^2} + \overline{u_z'^2})$. However, the fluctuations of a quantity over a given averaging period are not equal to the average of its fluctuations over shorter periods. This implies that the decomposition in Eq. 10 does not hold for second-order statistics. To overcome this issue, one can use a bootstrap sample of both the quantity of interest and its squared value to draw the fluctuation bootstrap distribution:

$$\begin{aligned} \mu (\,\overline{c'^2}\,)^{(i)} = \mu (\,\overline{c^2}\,)^{(i)} - \left[ \mu (\,\overline{c}\,)^{(i)} \right] ^2, \ 1 \le i \le B, \end{aligned}$$

(13)

where $\mu (\overline{Y})^{(i)}$ is the ith bootstrap sample mean estimator of the quantity Y. Note that the sub-averages used to compute $\mu (\overline{c})^{(i)}$ and $\mu (\overline{c^2})^{(i)}$ must come from the same bootstrap resampling of the original sample. The bootstrap samples of the turbulent kinetic energy estimator are computed similarly. With these samples, the variability can be described by sample variance (Eq. 12) or percentile confidence intervals.

Table 2 summarizes the mean block length $\ell$ used in this work for all these quantities. Block lengths for observations are larger than for simulations because LES quantities are less temporally correlated (as shown in Fig. 5b, c). In addition, larger block lengths are obtained for flow-related variables than for concentration, because the wind measurement samples have relatively more data acquired at high altitudes, where temporal correlations are expected to be larger.

Table 2 Mean block lengths $\ell$ used for stationary bootstrap applied to the average concentration $\overline{c}$, mean squared concentration fluctuation $\overline{c'^2}$, amplitude $\overline{u_h}$ and direction $\overline{\alpha }$ of the mean horizontal wind vector and turbulent kinetic energy k. Values are determined for both simulated and observed data

4.4.5 Internal Variability Propagation to Validation Metrics

To take into account internal variability in the LES model validation, bootstrap distribution of the validation metrics (Sect. 3.6) can be obtained by propagating the internal variability of both LES and observations.

Let f be a metric quantifying how close two vectors are:

$$\begin{aligned} f :\ {}&\mathbb {R}^N \times \mathbb {R}^N \rightarrow \mathbb {R} \\&(\overline{Y}_{sim}, \overline{Y}_{obs}) \mapsto f(\overline{Y}_{sim}, \overline{Y}_{obs}), \end{aligned}$$

with $\overline{Y}_{sim}, \overline{Y}_{obs}$ typically the vectors of observations and model predictions at N different probe locations. The distribution of f is directly constructed by evaluating f for each pair of bootstrap replicates of the mean estimators of $\overline{Y}_{sim}$ and $\overline{Y}_{obs}$:

$$\begin{aligned} \mu (f)^{(i)} = f \left( \,\mu ( \overline{Y}_{sim})^{(i)}, \mu (\overline{Y}_{obs})^{(i)}\,\right) , \ 1 \le i \le B. \end{aligned}$$

(14)

Note that the bootstrap replicates $\left\{ \mu (\overline{Y}_{sim})^{(i)} \right\} _{i=1}^B$ and $\left\{ \mu (\overline{Y}_{obs})^{(i)} \right\} _{i=1}^B$ are obtained independently using stationary bootstrap with different block lengths (see Table 2). The metrics bootstrap replicates obtained from Eq. 14 can then be used to estimate the variance and confidence intervals of the validation scores, in the same way as in Sect. 4.4.2.

5 Results

In this section, the LES model presented in Sect. 3 is validated against MUST field trial 2681829 measurements for both microscale wind flow statistics (Sect. 5.1) and tracer plume-related quantities (Sect. 5.2). The impact of the internal variability of the ABL on these quantities is quantified using the bootstrap approach presented in Sect. 4. The same procedure is applied to both the experimental measurements and the LES field estimates, only the mean block length used in the stationary bootstrap differs (see Table 2). Then we demonstrate the impact of the estimated internal variability on the model validation.

The number of bootstrap replicates used is $B = 5000$; the samples are composed of $N_t=20$ sub-averages over 10 s. Convergence tests and validation of the bootstrap procedure are given in Appendix I. The stationary bootstrap algorithm used is from the Python module Recombinator.²

5.1 Validation of Microscale Meteorology Statistics

The accuracy of the LES model is assessed in terms of prediction of mean horizontal wind velocity $\overline{u_h}$, direction $\overline{\alpha }$, and wind turbulent kinetic energy k. These quantities are key features for the prediction of the plume dispersion within and above the container canopy, as they control the tracer advection by the mean flow and the turbulent dispersion process.

5.1.1 Wind Flow Vertical Profiles

Fig. 8

Vertical profiles of a mean horizontal wind velocity (m $\hbox {s}^{-1}$), b mean wind direction ($^{\circ }$), and c turbulent kinetic energy k ($\hbox {m}^2\,\hbox {s}^{-2}$) at the central tower T (Fig. 1). Available experimental data are represented by circles, black solid lines correspond to the LES time-averaged profiles (two additional realizations of LES estimations over 200 s are also represented as coloured dotted lines). Shaded grey areas correspond to the uncertainty induced by LES internal variability and are estimated by stationary bootstrap (the counterpart for the experimental data is indicated as error bars). The part of the domain affected by the top boundary condition according to Calaf et al. (2011) is indicated as a pink shaded area

Figure 8 shows the vertical profiles of $\overline{u_h}$, $\overline{\alpha }$ and k obtained with LES at tower T (this tower location is indicated in Fig. 1). On the one hand, results show very good agreement with the sonic anemometer measurements for the mean horizontal velocity and direction. The flow deceleration induced by the urban canopy compared to the inlet profile (Fig. 2) is well reproduced. However, the model slightly overestimates the channeling effect caused by the container array, as the flow deviation towards the negative angles is larger than the measured one, especially at $z=4\,$m and 8 m. On the other hand, the turbulent kinetic energy profile shows that the peak of fluctuations just above the containers is well estimated, whereas the model underestimates the turbulent kinetic energy as altitude increases. The reason for this discrepancy is twofold: (i) the synthetic turbulence injection cuts off turbulence length scales larger than the domain scale and (ii) the internal region of the boundary-layer flow is known to be unaffected by the finite vertical extent of the domain up to 0.2 time the height of the computational domain (Calaf et al. 2011). In this case, it corresponds to a height of 10 m; above this level, the vertical turbulent transport and other turbulent statistics start to be affected by the top boundary layer which imposes zero vertical turbulent transport.

Figure 8 also shows the 95% confidence intervals corresponding to the bootstrap estimations of the microscale internal variability as profile envelopes for the LES and as error bars for the observations. It is found that the variability is overall quite low for the mean horizontal wind velocity and direction. It is more important for the turbulent kinetic energy but not sufficient to explain the model bias at altitude. Moreover, the LES model tends to significantly underestimate the internal variability of $\overline{u_h}$ and k compared to that observed. This is attributed to the larger turbulent and mesoscale fluctuations which are not taken into account in the representation of the ABL by the LES model. This is consistent with the results from Nagel et al. (2022) showing that including the mesoscale processes improves the prediction of k at these locations.

Two additional LES estimations of time-averaged quantities over 200 s were obtained by extending the original simulation. The resulting vertical profiles are shown as coloured dotted lines in Fig. 8. The deviations from the baseline estimate (black solid line) illustrate the effect of internal variability on the time averages. Overall, the estimated envelopes cover well these independent realizations, which supports the plausibility of the stationary bootstrap estimates.

5.1.2 Quantification of Wind Flow Predictions Accuracy

In addition to the profiles at tower T (Fig. 8), we also compare LES predictions and observations using the wind flow metrics (Sect. 3.6.1). Table 3 presents the scores obtained over the obstacles (towers S, T and N), within the obstacles (masts V) and for all sensors at once. For every set, the hit rate is 100%, which means that the departure between LES estimates and measurements for the wind horizontal velocity is always less than the absolute deviation $AD=1$ m $\hbox {s}^{-1}$ used in Eq. 2 by Nagel et al. (2022). Indeed, the MAE metric shows the limited level of error for the wind velocity. However, the error is larger for sensors located within the container array, as shown by the higher MAE in this region, and this is even more pronounced for the SAA metric. This is due to the proximity of the masts V to the containers (Fig. 1), where there are strong wind direction gradients as explained by Nagel et al. (2022). Still, the overall accuracy of the LES flow estimations is satisfactory.

By computing two bootstrap samples of each measurement and colocated LES estimation, we can obtain an ensemble of metrics realizations as explained in Sect. 4.4.5, and then quantify how uncertain the model validation scores are, given the internal variability of the system. The resulting standard deviations of the flow validation metrics are given in Table 3. Results show that the internal variability has a limited effect on velocities, with a standard deviation of MAE of approximately 0.1 m $\hbox {s}^{-1}$. Note that this variability is however larger than the sonic anemometer accuracy (between 0.01 and 0.05 m $\hbox {s}^{-1}$). In contrast, the variability is less important for the wind direction. Moreover, the effect of variability is rather homogeneous over the different datasets, which is coherent with the vertical distribution of the internal variability envelopes at tower T (Fig. 8).

Table 3 Mean horizontal wind velocity and direction: comparison between the LES model and the experimental measurements at tower S, T and N, and the sensors at the container levels on the masts V (Fig. 1). The differences are assessed in terms of hit rate q, mean absolue error MAE, and scaled averaged angle SAA defined in Sect. 3.6.1. The stationary bootstrap method presented in Sect. 4.4 is used to estimate standard deviations of the scores

5.2 Validation of Tracer Dispersion Statistics

5.2.1 Mean Concentration Horizontal and Vertical Profiles

Model performance is first analyzed in terms of mean concentration horizontal profiles within the container array in Fig. 9a–d. At $z=1.6\,$m, the model underestimates tracer concentration along the four DPID sensor sampling lines, which could be due to a plume elevation overestimation, as discussed later. Still, the shape of the profiles is rather well reproduced by the model. The decrease in concentration is consistent with the observations, both in the flow direction (between each line) and in the transverse direction (on a given line). The plume deviation is also well predicted by the model as illustrated by the concentration maximum position.

Fig. 9

Horizontal profiles of average concentration $\overline{c}$ (ppm) (a–d) and concentration fluctuation intensity i (e–h) between the containers at $z=1.6$ m. The profiles are given for each line of DPID sensors represented with a distinct colour in Fig. 1. Circles correspond to measurements, black solid lines correspond to simulated time-averaged profiles (two additional realizations of LES estimations over 200 s are also represented as coloured dotted lines). Shaded grey areas correspond to the uncertainty induced by LES internal variability and are estimated by stationary bootstrap (the counterpart for the experimental data is indicated as error bars)

Model performance is then analyzed along the vertical (above the container array) by comparing the estimated mean concentration vertical profiles with measurements from towers B, T, C, and D (Fig. 10a–d). Overall, the LES predictions are in acceptable agreement with the observations. The model tends to overestimate the mean concentration at towers B and C. The same tendency was observed with other LES models by Camelli et al. (2005) and Nagel et al. (2022) for tower B. The model also underestimates the mean concentration at tower D due to a lack of lateral spread of the simulated plume (Fig. 9a), tower D being far from the plume centerline (Fig. 1). In addition, the predicted maximum concentration is located too high above the canopy, especially at tower B (if we disregard the highest sensor that is inconsistent with the others). For tower C, there are not enough sensors at high heights to conclude. This could mean that the predicted plume rises too much, which would explain the near-ground concentration underestimation (Fig. 9a–d).

Note that there seems to be an inconsistency between the UVIC measurements from tower C (Fig. 10c) and those from the fourth line of DPIDs (Fig. 9d), although they are arranged on the same transverse line. Indeed, the UVIC sensor at tower C at $z = 2$ m measures 0.21 ppm, while the two closest DPID sensors (10 m away) measure 0.54 ppm and 1.10 ppm. This may also concern other UVIC measurements, explaining why LES overestimates concentration at towers B and C.

5.2.2 Mean Concentration Internal Variability

The internal variability of the mean concentration is shown in Figs. 9 and 10 with the 95% confidence intervals estimated by stationary bootstrap. This internal variability increases with altitude (Fig. 10a–d), because, outside the canopy, the flow statistics are more sensitive to incoming fluctuations from the ABL. LES profile envelopes are generally consistent with the observed variability (Figs. 9, 10). Analysis of the relative internal variability aggregated over all sensors (Fig. 7, p. 20) confirms that the LES model can reproduce the observed internal variability overall, with a slight tendency to underestimate it as for instance at tower D (even if the relative variability $s(\overline{c})/\overline{c}$ is similar to that of the measurements).

Note that the stationary bootstrap estimations of the internal variability look plausible regarding the two independent LES realizations of 200-s averaged concentration. The bootstrap profile envelopes globally cover these realizations both inside and above the canopy (Figs. 9, 10). However, one or both realizations can be locally slightly outside the 95% confidence interval, for example at the concentration peak location (Fig. 9a) or at high altitude at tower T (Fig. 10b). This indicates that the internal variability is underestimated there, which is likely caused by an insufficient number of independent sub-average samples $N_t$, as stated by Davison and Hinkley (1997) and Scheiner and Gurevitch (2001).

Finally, although significant, the internal variability alone does not explain the mismatch between LES estimates and vertical tower measurements (Fig. 10a–d). The lack of accuracy comes rather from another source of uncertainty. For instance, Milliez and Carissimo (2007) explain that the vertical profiles are difficult to estimate accurately because of their important sensitivity to the wind direction. This sensitivity is exacerbated in our case at tower B and to a lesser extent at tower T, because both towers are located near the steepest edge of the plume where concentration gradients are very large (Fig. 9a–d). In these areas, plume position errors have a larger impact on model accuracy than microscale internal variability.

5.2.3 Concentration Fluctuation Intensity

In addition to time-averaged values, LES models provide an explicit temporal resolution of the flow. In this section, we propose to further validate the model by examining its ability to predict resolved concentration fluctuations, which are directly accessible from LES data. To characterize concentration fluctuations, we use the fluctuation intensity i as Yee and Biltoft (2004). It reads $i = \sqrt{\overline{c'^2}} / (\overline{c} + c_t)$, where $\overline{c'^2} = \overline{(c - \overline{c})^2}$ is the squared resolved fluctuation of the concentration. The concentration threshold $c_t$, equal to the detection threshold of the sensors, i.e. 0.01ppm for UVICs or 0.04ppm for DPIDs, is added to the normalization term to avoid ill-posed values for very small concentrations.

Fig. 10

Vertical profiles of average concentration $\overline{c}$ (ppm) (a–d) and concentration fluctuation intensity i (e–h) at towers B, T, C, and D, respectively (Fig. 1). Circles correspond to measurements, black solid lines correspond to simulated time-averaged profiles (two additional realizations of LES estimations over 200 s are also represented as coloured dotted lines). Shaded grey areas correspond to the uncertainty induced by LES internal variability and are estimated by stationary bootstrap (the counterpart for the experimental data is indicated as error bars)

Fig. 11

Scatter plots of simulated versus measured concentration statistics: a temporal mean, b fluctuation intensity, c normalized 95th percentile at each sensor over the detection threshold. Each type of sensor is represented with the same colour as in Fig. 1. The correlation coefficient R is indicated for each statistic. The error bars represent the 95% confidence intervals estimated through stationary bootstrap and account for the sampling error of both simulated and measured statistics (error bars are not given for the concentration maximum as the bootstrap procedure is not suitable for this statistic)

There is a very good agreement between LES estimations and observations of fluctuation intensity. Among the containers, the LES model finely reproduces the observed horizontal distributions (Fig. 9e–h), including their asymmetry. However, the fluctuation peak is slightly overestimated for the first line of sensors and lacks horizontal extent for lines #3 and #4. Moreover, the LES model also appears to be very accurate for the estimation of vertical fluctuation profiles (Fig. 10e–h), except for the T tower where the model overestimates them but still predicts a consistent profile. By normalizing the fluctuations, we show that, despite being biased for the mean concentration vertical profiles at towers B, C, and D, the LES model is still able to reproduce a physically-consistent estimation of the concentration second-order statistics.

The internal variability is also estimated for the concentration fluctuation intensity with the bootstrap samples from Eq. 13. Figures 9e–h show that internal variability is very large at the location of the peak fluctuation. Overall, the LES-predicted fluctuation envelopes are in good agreement with the observed variability and the two independent LES runs. Contrary to the average concentrations, and except for tower T, the differences between the model and the observations can be attributed to the internal variability, which is particularly visible for the tower D where the fluctuations are very important.

5.2.4 Quantification of Dispersion Predictions Accuracy

In the following, the accuracy of the LES model tracer transport is assessed from a more synthetic viewpoint. We also illustrate how the internal variability of the tracer concentration field should be taken into account in this model validation exercise.

Figure 11 shows the scatter plots of the simulated versus measured concentration main statistics. First, for the averaged concentration, the model estimates are overall consistent with the observations (Fig. 11a) with a correlation coefficient $R = 0.78$. Higher tracer concentration values (above 0.5–1 ppm) are well represented, but the LES model notably underestimates the lower concentration values. The same trend is found for the concentration fluctuations (not shown). The current model would therefore underestimate pollution exposure and dosage in this situation. However, if we remove the bias on the averages, the LES is able to accurately reproduce the fluctuations with a correlation coefficient $R = 0.91$ for the concentration fluctuation intensity (Fig. 11b), but with a tendency to overestimate.

In addition, the microscale internal variability is depicted in the scatter plots of the averaged concentration (Fig. 11a) and fluctuation intensity (Fig. 11b) with the 95% confidence intervals obtained with bootstrap and depicted as two error bars for each tracer concentration sensor measurement and colocated LES estimation. The internal variability is heterogeneous, with locations for which it is negligible and others for which it is very important. Note that, for most of the points the x-error and y-error bars have similar lengths, which shows that LES estimates well the variability of predicted quantities.

As suggested by Chang and Hanna (2005), we assess if the difference between simulated and observed values is significantly different from zero at the 95% confidence interval. This test is performed for each sensor, and we find that, given the internal variability, the LES model fits only 13% and 45% of the measurements, for the mean concentration and fluctuation intensity, respectively. Although internal variability is high in areas where the model lacks precision (i.e. for the low mean concentrations and high fluctuation intensities), it only explains a limited part of the misfit between simulation estimates and measurements. Therefore most of the model errors, especially for the mean concentration, must come from other sources.

Besides, Fig. 11c also shows a fine agreement for the 95th percentile of concentration time series over the 200-s analysis period. The LES model appears to well predict the peak concentrations with a correlation coefficient $R = 0.86$. This demonstrates that the LES model can represent all the complexity of the dispersion phenomenon and not only mean concentration levels. The effect of internal variability on the peak concentrations is not assessed, since it is not accessible with the bootstrap procedure described in Sect. 4.4. Nevertheless, the peak concentrations are expected to be subject to a strong variability, as they correspond to extreme events in the LES realizations of the tracer plume. Quantifying it would therefore be an interesting prospect.

Table 4 Comparison between the LES model mean concentration prediction and experimental measurements assessed in terms of fractional bias (FB), normalized mean square error (NMSE), fraction of predictions within a factor of two of observations (FAC2), geometric mean bias (MG), and geometric variance (VG). Definition of these metrics are given in Sect. 3.6.2. They are computed for the horizontal sensors (i.e. the DPID sensors located at $z=1.6\,$m), the vertical sensors (i.e. towers A, B, C, D and T), and all sensors. Sensors for which the experimental mean concentration is under the detection threshold are excluded. LES results for the same trial reported in the literature are given as an indicative basis

The accuracy of the LES mean concentration estimations is finally evaluated using the standard air quality metrics from Chang and Hanna (2004), following the methodology presented in Sect. 3.6. As in previous works (Milliez and Carissimo 2007; Kumar et al. 2015; Nagel et al. 2022), metrics are computed separately for the DPIDs sensors on the horizontal $z=1.6\,$m plane on the one hand, and for the vertical sensors on towers A, B, C, D and T on the other hand. Metrics are then evaluated for all sensors. Results gathered in Table 4 show an overall good agreement with observations, with only the geometric mean bias (MG) and variance (VG) out of the range of acceptable scores. This seems to indicate that LES models have some difficulty in capturing low tracer concentration values. Except for the MG, the scores obtained are in line with those obtained by Nagel et al. (2022) with another LES model and for the same trial. They are also comparable to the scores obtained with RANS models on a larger number of trials including the present trial 2681829 (Milliez and Carissimo 2007; Donnelly et al. 2009; Kumar et al. 2015).

The LES model appears to be less accurate on the horizontal plane within the canopy than above. In this region, the concentration is overall underestimated by the model ($FB>0$ and $MG>1$), which is seen in the horizontal profiles (Fig. 9a–d). Interestingly, the opposite behaviour, i.e. better performances on the horizontal than on the vertical, was observed by Nagel et al. (2022).

As explained in Sect. 4.4.5, the internal variability of the time-averaged concentrations is propagated to the air quality metrics to quantify their uncertainty. The resulting distributions for each metric are summarized with box-and-whisker plots of the bootstrap samples (Fig. 12). It demonstrates that the scores obtained in this model validation exercise are significantly uncertain. Moreover, it shows that the internal variability of the concentration affects each metric differently. Fractional and geometric mean biases (FB, MG) are less sensitive to internal variability because of error compensation, while wider spreads are found for the normalized mean square error (NMSE), and geometric variance (VG). This is because NMSE and VG are quadratic metrics and thus measure the dataset dispersion. The fraction of predictions within a factor of two of observations (FAC2) also shows an important variability as it is a discrete and non-linear metric computed over a small number of sensors. The effect of the internal variability is also higher on the vertical than on the horizontal, which is consistent with the observed envelopes in Figs. 9 and 10.

Figure 12 also shows the validation scores obtained for three independent LES predictions of time-averaged concentration over 200 s. Despite having identical model configurations, the discrepancies between each score are not negligible. The bootstrap estimation of the variability of the metrics, obtained using only the sub-averages of the first simulation ($[60,\ 260]\,$s), explains quite well this variability as only three outliers are found: one for the horizontal FB, one for the horizontal NMSE and one for the horizontal MG.

In summary, we show that, for microscale dispersion experiments with small acquisition times and/or limited analysis periods, validation scores feature a high range of variability. It is thus vital to take this variability into account in a model validation exercise, but also for sensitivity analysis or multi-model comparison, to avoid drawing insignificant conclusions about the trends in the metrics. The bootstrap procedure based on sub-average samples presented in this work appears to be well-suited to answer this need.

Fig. 12

Box plots of the air quality metrics distributions obtained by taking into account the internal variability of both simulated and observed data using stationary bootstrap. Point estimations corresponding to the reference and two independent realizations of 200 s simulation are shown as red squares, blue circles and green triangles. Results are given for a FB, b NMSE, c FAC2, d MG, and e VG metrics (Sect. 3.6). These metrics are computed for all tracer concentration sensors over the detection thresholds (blue box), but also for the subsets of the horizontal probes (i.e. the DPID sensors at $z=1.6\,$m) and vertical probes (i.e. towers A, B, C, D and T), respectively represented as green and pink boxes

6 Conclusions

This study aims at assessing the confidence one can have in the LES estimates of microscale meteorology and air pollutant dispersion, given the internal variability of microscale processes for a field-scale case. For this purpose, an LES model of the neutral MUST trial 2681829 was designed with significant grid resolution (at least 8 cells over the height of the obstacle) and with a synthetic turbulence injection approach to represent the ABL fluctuations smaller than the domain scale. A stationary bootstrap algorithm was implemented and applied to both experimental measurements and LES estimates, in order to estimate the internal variability of time-averaged quantities by resampling sub-averages over smaller periods. It is worth mentioning that this approach requires temporal realizations of the fields, and could not be applied with other dispersion models such as a RANS model, which predicts only ensemble-averaged quantities.

This study shows that the LES model is overall in acceptable agreement with the observations. The numerical prediction of the wind flow is very accurate, with a departure of turbulent kinetic energy above the canopy and a larger error in the wind direction for the sensors located very close to the obstacles. For the tracer mean concentration, the model is more accurate above the obstacles than between them. The LES underestimates the concentrations compared to the measurements of the DPID sensors (at $z=1.6\,$m and at tower T) and tends to overestimate them compared to the UVIC sensors (at towers B and C). Standard air quality metric scores are in line with previous RANS and LES studies reported in the literature. Finally, the LES model is very accurate at predicting relative fluctuations and concentration peaks.

This study also demonstrates that, in the context of the MUST field campaign, the time-averaged quantities characterizing wind flow and tracer dispersion for both LES estimates and experimental observations are subject to significant aleatory uncertainty due to the short analysis period typically used in the literature (200 s). This internal variability induces substantial uncertainty in the model evaluation scores. To avoid misleading results, we thus advise switching from point-wise validation to probabilistic validation to account for this internal variability. In our case, the LES model reproduces very well the observed variability, despite the simplistic representation of the ABL inflow (stationary flow with synthetic turbulence). Nevertheless, some of the discrepancies between observations and LES estimates cannot be explained by internal variability alone. This leads to the conclusion that there are either structural model errors and/or errors in the representation of the boundary conditions. In particular, CFD model predictions are known to be strongly affected by inflow uncertainties (García-Sánchez et al. 2014) and by the level of detail in the urban canopy geometry (Santiago et al. 2010).

This work was limited to the quantification of internal variability due to microscale processes and under quasi-stationary meteorological conditions. Indeed, the present LES model has stationary boundary conditions and limits the size for the largest eddies, it mainly reproduces the variability induced by the turbulence at the obstacle scale. Therefore, a rather direct and promising perspective would be to quantify the mesoscale variability, especially for longer analysis periods. For this purpose, a solution would be to use an LES model with inflow boundary conditions that are dynamically changing through a multi-scale meteorological model based on grid nesting (Wiersema et al. 2020; Nagel et al. 2022).

More generally, by addressing the aleatory uncertainties of the physical system, this work constitutes a first step towards a complete understanding of the total uncertainties in microscale LES. An exciting prospect would be to quantify other sources of uncertainties, i.e. uncertainties in the representation of the boundary conditions (Santiago et al. 2010; García-Sánchez et al. 2014) and structural model uncertainties. The latter could be estimated through sensitivity analysis and multi-model comparison. The methodology presented in this work would then allow assessing which of these uncertainties have a meaningful impact on the LES model predictions compared to internal variability. These diagnostics could support the construction and validation of operational dispersion models, including machine-learning-based reduced-order models (Nony et al. 2023). They are also very interesting for the construction of a data assimilation approach that is effective at correcting the largest sources of uncertainties in CFD predictions using in-situ measurements (Sousa and Gorlé 2019; Defforge et al. 2021).

Appendix I: Validation of the Stationary Bootstrap Approach

In this appendix, several convergence tests of the stationary bootstrap approach applied to the MUST trial are shown to verify the robustness and plausibility of the confidence intervals predicted by bootstrap as a complement to Sect. 4.

1.1 Convergence with the Number of Bootstrap Replicates

With bootstrap methods, such as the stationary bootstrap, bootstrap replicates of one original sample are used to compute Monte Carlo estimates of several statistics of the physical quantities of interest (time-averages or fluctuations), such as their variance (Eq. 12) or confidence intervals. The convergence of the estimator error is therefore in $\mathcal {O}(1/\sqrt{B})$ with B the number of bootstrap replicates.

Table 5 Values of 2.5th percentiles evaluated with stationary bootstrap for different numbers of replicates B. Estimations are given for one example of simulated and observed mean concentration (at tower B at $z=2\,$m), as well as for the air quality metrics (Sect. 3.6.2) and flow validation metrics (Sect. 3.6.1)

We assess the convergence for the 2.5th and 97.5th percentiles as it requires more bootstrap replicates than for bias or variance estimation (Davison and Hinkley 1997). Table 5 shows the evolution of the 2.5th percentile of the mean concentration at tower B at $z=2\,$m and of the model validation metrics evaluated according to the bootstrap procedure (Eq. 14) for different values of B. The bootstrap estimations of the 2.5th percentiles show some variability for very low numbers of bootstrap replicates (between 100 and 500), but then quickly converge for all the considered quantities. The same analysis was carried out for the 97.5th percentile and gave similar results. We conclude that B = 5000 bootstrap samples are more than sufficient to achieve convergence. This result is in line with the literature, which recommends between 1000 and 10,000 replicates (Davison and Hinkley 1997; Chang and Hanna 2005).

1.2 Effect of the Sub-Averaging Period

Since both simulated and measured time series are well sampled in time, it is possible to change the sub-averaging period $\delta _t$ to adjust the number of sub-average samples $N_t$ (Eq. 10). To assess the effect of the sub-averaging period on the internal variability estimation, the estimated percentiles obtained with a stationary bootstrap of sub-averages over $\delta _t =10\,\textrm{s}$ and $\delta _t =5\,\textrm{s}$ are compared. By reducing the sub-averaging period, the samples are getting more dependent. It is therefore mandatory to adapt the mean block length parameter $\ell$ of the stationary bootstrap method. For $\delta _t =5\,\textrm{s}$, it results to new values of $\ell _{sim}=1.38$ and $\ell _{obs}=2.62$ for the time-averaged concentrations. This is consistent since it means that, for more dependent data, the blocks should be larger than the ones used for $\delta _t =10\,\textrm{s}$ (Table 2, page 21). Table 6 shows the 2.5th percentile estimates for the main quantities of interest for the two different values of $\delta _t$. Results indicate that changing the sub-averaging period has a very limited impact on the stationary bootstrap estimations. This is because changing the sub-averaging period only changes the division of the original sample (Eq. 10) and so does not provide any additional information on the underlying distribution of the time-averaged quantities.

Table 6 Values of 2.5th percentiles evaluated with stationary bootstrap for different sub-averaging period $\delta _t$. Estimations are given for one example of simulated and observed mean concentration (at tower B at $z=2\,$m), as well as for the air quality metrics (Sect. 3.6.2)

1.3 Convergence with the Number of Sub-average Samples

As mentioned in Sect. 4.4.3, it is essential to have a sufficient number of sub-average samples $N_t$ in the original sample. In particular, too few samples may result in internal variability underestimation. To increase $N_t$, the LES simulation acquisition time is increased from 200 s to 400 s, and then 600 s (Fig. 4). With $\delta _t = 10$ s the resulting number of sub-averages is 40, and 60 respectively, against 20 for the reference sample. In any case, the bootstrap replicates are obtained by resampling only 20 sub-averages over the $N_t$ available, even if $N_t = 60$. Indeed, the objective is still to quantify the variability over the 200-s analysis period and not over 600 s. Two additional realizations of 200-s averages (in cyan and magenta in Fig. 4) are used for validation purposes.

Fig. 13

Box plots of the air quality metrics distributions obtained with stationary bootstrap with resampling of 20 sub-averages among 20, 40 and 60, in orange, green and red, respectively. Point estimations corresponding to the reference and two independent realizations of 200-s simulation are represented as orange squares, cyan circles and magenta triangles. Results are given for a FB, b NMSE, c FAC2, d MG, and e VG metrics (Sect. 3.6)

The distributions of the air quality metrics estimated by stationary bootstrap with resampling of 20 sub-averages among $Nt=20$, 40 and 60 are shown in Fig. 13. The bootstrap ensemble averages slightly change because the time-averaged quantities over 200, 400 and 600 s are different. Nevertheless, increasing the number of samples for stationary bootstrap gives similar estimations of the metrics dispersion. For FAC2, MG and VG metrics, which are nonlinear, the tails of the distributions seem more dependent on the number of samples. In all cases, the three bootstrap estimates cover the two independent realizations, once again supporting the validity of the stationary bootstrap.

As the orders of magnitude of the three estimates are overall consistent with each other, we conclude that $N_t = 20$ samples of sub-averages are sufficient for the stationary bootstrap method to converge. This implies that it is not required to run longer simulations to capture internal variability. The convergence with the number of samples is similarly verified for the envelopes of tracer concentration and wind velocity statistics presented in Sect. 4.