Abstract
We prove convergence of a finite difference scheme to the unique entropy solution of a general form of the Ostrovsky–Hunter equation on a bounded domain with non-homogeneous Dirichlet boundary conditions. Our scheme is an extension of monotone schemes for conservation laws to the equation at hand. The convergence result at the center of this article also proves existence of entropy solutions for the initial-boundary value problem for the general Ostrovsky–Hunter equation. Additionally, we show uniqueness using Kružkov’s doubling of variables technique. We also include numerical examples to confirm the convergence results and determine rates of convergence experimentally.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the initial-boundary value problem
with  and \(\gamma >0\). Equation (1a) is derived by integrating the nonlinear evolution equation
and \(\gamma >0\). Equation (1a) is derived by integrating the nonlinear evolution equation
in space. This equation was posed by Ostrovsky [27] and Hunter [18] with \(f(u)=\frac{1}{2}u^2\) as a model for small-amplitude long waves on a shallow rotating fluid and is referred to as the Ostrovsky–Hunter equation [3, 7, 23], short wave equation [18], Vakhnenko equation [25, 28, 34,35,36], Ostrovsky–Vakhnenko equation [4, 24] and reduced Ostrovsky equation [27, 29, 33]. If \(f(u)=-\frac{1}{6}u^3\), Eq. (2) is known as the short pulse equation, which was introduced by Schäfer and Wayne [32] as a model for the propagation of ultra-short light pulses in silica optical fibers (see also [1, 22]). In the present paper, however, we will consider an arbitrary flux  and will refer to Eq. (1a) with general f as Ostrovsky–Hunter equation.
and will refer to Eq. (1a) with general f as Ostrovsky–Hunter equation.
In order to derive Eq. (1a), we integrate Eq. (2) in space to get
The function P must then be further specified by an additional constraint, e.g. \(P(-\infty ,t)=0\) (which leads to \(P=\int _{-\infty }^x u \); see [8]) or \(\int P=0\) (implying \(P=\int _{-\infty }^x u - \int _{-\infty }^{\infty } u\) on the real line or \(P=\int _0^x u -\int _0^1 u\) in the unit interval; see [6, 18, 23, 33]). Here we will consider the unit interval and choose \(P(0,t)=0\), which gives
Concerning the initial and boundary data, we will assume

Coclite et al. developed a global well-posedness analysis utilizing the concept of entropy solutions defined in a distributional sense [see (6) in Definition 1 below] on the domains \(\mathbb {R}\times \mathbb {R}^+\) and \(\mathbb {R}^+\times \mathbb {R}^+\) in [7,8,9,10,11,12, 30] and on \([0,1]\times \mathbb {R}^+\) with non-homogeneous Dirichlet boundary conditions in [13]. Their proofs are based on a vanishing viscosity regularization and a compensated compactness argument.
In this paper, we aim to show existence of entropy solutions (as defined in Definition 1 below) to the initial-boundary value problem (1) by proving the convergence of a finite difference scheme. We will base our construction of the numerical scheme on the classical theory of monotone schemes for conservation laws and use central differences for the nonlocal source term. In order to get compactness of the scheme, we will employ Helly’s theorem together with appropriate a priori bounds of the piecewise constant interpolation. Then, we will show convergence towards the entropy solution using discrete versions of the entropy conditions in the interior of the domain and at the boundary. Furthermore, we prove uniqueness of entropy solutions by showing  stability using Kružkov’s ‘doubling of variables’ technique.
stability using Kružkov’s ‘doubling of variables’ technique.
Without convergence proof, numerical methods for Eq. (2) are used in [15, 18, 23], including Fourier pseudo-spectral methods and a finite difference scheme based on the Engquist–Osher scheme. So far the only rigorous numerical analysis of the Ostrovsky–Hunter equation is performed by Coclite et al. [6]. The authors, however, consider the case of periodic boundary conditions and initial data with zero mean. The present paper directly extends these results to the setting of non-periodic boundary conditions. Although we follow the general strategy of [6], the non-periodicity complicates matters throughout. In particular, we will present new versions of Harten’s lemma and Kružkov’s ‘doubling of variables’ technique that properly address the contributions of the boundary terms.
We will consider entropy solutions of (1) based on the following definition:
Definition 1
(Entropy solution) A function  is called an entropy solution of the Ostrovsky–Hunter equation (1) if for all entropy pairs \((\eta ,q)\), i.e. convex functions
is called an entropy solution of the Ostrovsky–Hunter equation (1) if for all entropy pairs \((\eta ,q)\), i.e. convex functions  , and q such that \(q'=\eta 'f'\),
, and q such that \(q'=\eta 'f'\),
for all nonnegative  , and
, and
holds for a. e. \(t\in (0,T)\). Here P[u] is as in (4) and \(u_0^{\tau }\) and \(u_1^{\tau }\) denote the strong traces of u at the boundary \(x=0\) respectively \(x=1\).
Remark 1
Note that by an approximation argument, cf. [17, pp. 57–58], a function  is an entropy solution if and only if inequalities (6) and (7) hold for all Kružkov entropy pairs,
is an entropy solution if and only if inequalities (6) and (7) hold for all Kružkov entropy pairs,
Remark 2
This is the usual definition of entropy solutions of Eq. (1). However, regarding the entropy boundary condition instead of working with the original condition due to Bardos et al. [2], we will use the entropy boundary condition (7) introduced by Dubois and LeFloch [14]. Due to the regularizing effect of the P Eq. (4) we have that  implies
implies  . Therefore, if
. Therefore, if  satisfies the entropy condition (6), then [5, Theorem 1.1] assures the existence of strong traces \(u^{\tau }_0, u^{\tau }_1\) and hence boundary entropy condition (7) is well-defined.
satisfies the entropy condition (6), then [5, Theorem 1.1] assures the existence of strong traces \(u^{\tau }_0, u^{\tau }_1\) and hence boundary entropy condition (7) is well-defined.
The paper is organized as follows. In Sect. 2 we specify the numerical scheme under consideration. Section 3 contains discrete a priori bounds which are used to show compactness of the scheme. In the next section we will develop discrete entropy inequalities both in the interior and at the boundary which will lead to our first main result, the convergence of the numerical solutions to an entropy solution, see Theorem 1 in Sect. 4. Our second main result, the  stability and thus uniqueness of entropy solutions, is shown in Sect. 5, Theorem 2, using Kružkovs ‘doubling of variables’ technique. Finally, the last section provides some numerical experiments.
stability and thus uniqueness of entropy solutions, is shown in Sect. 5, Theorem 2, using Kružkovs ‘doubling of variables’ technique. Finally, the last section provides some numerical experiments.
2 The numerical scheme
We discretize the domain \([0,1]\times [0,T]\) using \((N+1)\cdot (M+2)\) grid points with \(\Delta x = 1/N\) and \(\Delta t = \frac{T}{M+1}\), such that for \(j=0,\ldots ,N\) and \(n=0,\ldots ,M+1\),
As a shorthand notation for the sequence \((u_j^n)_{j=0}^N\) we will write \(u^n\). We will also frequently use the notation \(I_j=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}})\) for the interval in space, \(I^n=[t^n,t^{n+1})\) for the interval in time and \(I_j^n = I_j\times I^n\) for the rectangle in \([0,1]\times [0,T]\). Here, we fix the convention that \(x_{j+\frac{1}{2}}=(j+\frac{1}{2})\Delta x\), \(j=0,\ldots ,N-1\), as well as \(x_{-\frac{1}{2}} = x_0=0\) and \(x_{N+\frac{1}{2}}=x_N=1\). In order to get from the sequence \(u^n\) to a function on \([0,1]\times [0,T]\) we define the piecewise constant interpolation
The discrete initial datum \(u^0\) is constructed from  via
via
Then, the numerical scheme we want to employ reads as follows: For \(n\ge 0\) we set
where \(P_j^n\) is the following approximation to the integral of u,
and the flux at \((x_{j+\frac{1}{2}},t^n)\) is approximated by
where the discrete flux F is a Lipschitz continuous function in two variables. We will assume that F can be written in the form
where  , and that F is consistent with f and monotone in the sense that
, and that F is consistent with f and monotone in the sense that
Furthermore, we will assume
where \(\lambda = \frac{\Delta t}{\Delta x}\). Two examples for discrete flux functions with the assumed properties are the Lax–Friedrichs flux, i.e.
and the Engquist–Osher flux, i.e.
which satisfy (10) and (11) provided that the grid satisfies the CFL condition
Note that, using our scheme, we can recover a discrete version of (3), since
were we used the following difference operators:
3 Discrete a priori estimates
In this section we aim to prove compactness of the scheme using Helly’s theorem. This requires an  bound, a BV bound and a bound on the discrete time derivative of the numerical solution. These bounds are similar to the ones in [6], but the boundary conditions lead to additional terms.
bound, a BV bound and a bound on the discrete time derivative of the numerical solution. These bounds are similar to the ones in [6], but the boundary conditions lead to additional terms.
Lemma 1
( bound) For \(n\Delta t \le T\), the solution \(u^n\) of the numerical scheme (8) satisfies
bound) For \(n\Delta t \le T\), the solution \(u^n\) of the numerical scheme (8) satisfies

Proof
For \(j=1,\ldots ,N-1\) we define  . Then \(v_j^n\ge u_j^n\) for all \(j=1,\ldots ,N-1\) and thus, by monotonicity and consistency of the scheme (10)–(11),
. Then \(v_j^n\ge u_j^n\) for all \(j=1,\ldots ,N-1\) and thus, by monotonicity and consistency of the scheme (10)–(11),
Hence, we have

for \(j=1,2,\ldots ,N-1\). Because \(N\Delta x=1\), also \(P_j^n\) is bounded:

Regarding the boundary terms, clearly

Thus, we have

for \(n\Delta t\le T\).\(\square \)
The next lemma is a version of Harten’s lemma [16] on bounded domains that additionally uses the  bound from Lemma 1 to estimate the contribution of the source term to the total variation.
bound from Lemma 1 to estimate the contribution of the source term to the total variation.
Lemma 2
(B.V. bound) For \(n\Delta t\le T\), the solution \(u^n\) of the numerical scheme (8) satisfies

where \(C_T\) denotes a constant depending on \(\gamma \) and T.
Proof
For \(n=0,\ldots ,M\), we have

The scheme (8) can then be written in conservative form, i.e. for \(j=1,\ldots ,N-1\) we have
where
Using the consistency of the numerical flux and the mean value theorem, we get
and similarly
for all j in \(\{1,\ldots ,N-1\}\) and \(\{0,\ldots ,N-2\}\) respectively. Furthermore, using the mean value theorem on the difference \(F_1-F_2\) a similar calculation shows that the CFL condition (11) assures \(C_{j+\frac{1}{2}}^n+D_{j+\frac{1}{2}}^n \le 1\) for \(j=1,\ldots ,N-2\). Now, regarding the sum on the right hand side of (13), we can estimate
Regarding the first sum, we get
On the other hand, regarding the boundary terms in (13), since \(D_{\frac{1}{2}}^n\le 1\) and (12), we find

Moreover, we will estimate the P term with the help of Lemma (1) as follows

In summary we get

Furthermore, we note that

and similarly for the right boundary. Therefore we get

\(\square \)
Lastly, we have a bound on the discrete time derivative of \(u_{\Delta t}\).
Lemma 3
(Bound of the time derivative) For \(n\Delta t\le T\), the solution of the numerical scheme (8) satisfies

where \(C_{\lambda }\) depends on \(\gamma , T\), the Lipschitz constant of the discrete flux F and \(\lambda \).
Proof
Using the definition of the numerical scheme (8), the Lipschitz continuity of F, the  bound for P as seen in (12), and the BV and
bound for P as seen in (12), and the BV and  bounds of \(u^n\) from Lemma 2 and 1, we get
bounds of \(u^n\) from Lemma 2 and 1, we get

\(\square \)
With the help of these three bounds we finally can apply a version of Helly’s theorem to show compactness of the scheme.
Lemma 4
(Convergence) Let \(u_{\Delta t}\) be the family of solutions of the numerical scheme (8) defined by \(u_{\Delta t}(x,t)=u_j^n\) for \((x,t)\in [x_{j-\frac{1}{2}},x_{j+\frac{1}{2}})\times [t^n,t^{n+1})\). Further, let \(\lambda =\frac{\Delta t}{\Delta x}\) be fixed such that the discrete flux satisfies (10) and (11). Then there is a sequence \(\Delta t_k\) and a function  such that \(\Delta t_k\rightarrow 0\) and \(u_{\Delta t_k}\) converges to u in
such that \(\Delta t_k\rightarrow 0\) and \(u_{\Delta t_k}\) converges to u in  .
.
Proof
We want to apply Helly’s theorem [17, Theorem A.11]. This requires an  bound, a bound on the variation in space that is independent of \(\Delta t\), and
bound, a bound on the variation in space that is independent of \(\Delta t\), and  continuity in time as \(\Delta t\rightarrow 0\). An application of Lemma 1 gives
continuity in time as \(\Delta t\rightarrow 0\). An application of Lemma 1 gives

Furthermore, by using Lemma 2, we find

Finally, in order to show continuity in time, we employ Lemma 3. For \(t\in [t^n,t^{n+1})\) and \(s\in [t^{\overline{n}},t^{\overline{n}+1})\) with \(n>\overline{n}\) we find

An application of Helly’s theorem assures the existence of a sequence \(\Delta t_k\rightarrow 0\) and a function  such that such that \(u_{\Delta t_k}\) converges to u in the space
such that such that \(u_{\Delta t_k}\) converges to u in the space  as \(k\rightarrow \infty \).\(\square \)
as \(k\rightarrow \infty \).\(\square \)
4 Convergence towards the entropy solution
In this section we prove that the numerical scheme converges to an entropy solution of the Ostrovsky–Hunter equation. This fact hinges on discrete entropy inequalities for the interior of the domain and the boundary. These inequalities require a discrete version of the entropy flux that is consistent with the numerical flux function (9):
where
and \(c\in \mathbb {R}\) is an arbitrary constant. Note that since \(F_1\) and \(F_2\) are Lipschitz continuous, and if \(\eta '\) is bounded, also Q is Lipschitz continuous in both variables.
We will now derive discrete versions of the entropy conditions (6) and (7). The entropy condition in the interior of the domain has already been proven in [6].
Lemma 5
(Discrete entropy inequalities) For any convex entropy  with entropy flux q given by \(q'=\eta 'f'\), let \(Q_{j+\frac{1}{2}}^n\) and \(Q_{j-\frac{1}{2}}^n\) be defined by (14). Then the solutions of the scheme satisfies for each n
with entropy flux q given by \(q'=\eta 'f'\), let \(Q_{j+\frac{1}{2}}^n\) and \(Q_{j-\frac{1}{2}}^n\) be defined by (14). Then the solutions of the scheme satisfies for each n
for \(j=1,\ldots ,N-1\), as well as
and
Proof
The first inequality is derived in [6, Lemma 5] (see also [19, Lemma 6.1]). For the second inequality we use a Taylor approximation and the convexity of the flux
The proof of the third inequality can be done analogously.\(\square \)
Thus far, we only know that a sequence of solutions of the numerical scheme (8) converges to some  . By passing to the limit in the discrete entropy conditions of Lemma 5 we can now show that u is in fact an entropy solution. To accomplish that we will employ similar techniques as in [6] in regards to the entropy condition and as in [31] in regards to the entropy boundary condition. While the following theorem only provides the convergence of a subsequence of \(u_{\Delta t}\), the uniqueness result in Sect. 5 ensures that the whole sequence converges to the unique entropy solution.
. By passing to the limit in the discrete entropy conditions of Lemma 5 we can now show that u is in fact an entropy solution. To accomplish that we will employ similar techniques as in [6] in regards to the entropy condition and as in [31] in regards to the entropy boundary condition. While the following theorem only provides the convergence of a subsequence of \(u_{\Delta t}\), the uniqueness result in Sect. 5 ensures that the whole sequence converges to the unique entropy solution.
Theorem 1
(Convergence towards the entropy solution) Let  and
and  and fix \(\lambda =\frac{\Delta t}{\Delta x}\) such that the discrete flux in the scheme defined by (8) satisfies the (10) and (11). Then for any sequence \((\Delta t_n)_n\) such that \(\Delta t_n\rightarrow 0\), there is a subsequence \(\Delta t_{n_k}\) such that the piecewise constant interpolations \(u_{\Delta t_{n_k}}\) defined by the scheme (8) converge in
and fix \(\lambda =\frac{\Delta t}{\Delta x}\) such that the discrete flux in the scheme defined by (8) satisfies the (10) and (11). Then for any sequence \((\Delta t_n)_n\) such that \(\Delta t_n\rightarrow 0\), there is a subsequence \(\Delta t_{n_k}\) such that the piecewise constant interpolations \(u_{\Delta t_{n_k}}\) defined by the scheme (8) converge in  towards an entropy solution of the Ostrovsky–Hunter equation as \(k\rightarrow \infty \).
towards an entropy solution of the Ostrovsky–Hunter equation as \(k\rightarrow \infty \).
Proof
Let \((u_{\Delta t_{n_k}})\) be a sequence of approximate solutions that converges to u in the space  as \(\Delta t_{n_k}\rightarrow 0\) (cf. Lemma 4). For simplicity, we will omit any indices on \(\Delta t\). According to Lemma 5, the function \(u_{\Delta t}\) satisfies the discrete entropy and entropy boundary conditions.
as \(\Delta t_{n_k}\rightarrow 0\) (cf. Lemma 4). For simplicity, we will omit any indices on \(\Delta t\). According to Lemma 5, the function \(u_{\Delta t}\) satisfies the discrete entropy and entropy boundary conditions.
First, we show that u satisfies the entropy condition (6). Multiplying the discrete entropy condition (15) by \(\Delta t\Delta x \phi _j^n\), where \(\phi _j^n = \frac{1}{\Delta t\Delta x}\iint _{I_j^n}\phi (x,t){\text {dx}}{\text {dt}}\) for some nonnegative test function  , and taking the sum over \(n=0,\ldots ,M\) and \(j=1,\ldots ,N-1\) gives
, and taking the sum over \(n=0,\ldots ,M\) and \(j=1,\ldots ,N-1\) gives
where we have used that \(\phi _0^n=\phi _N^n=0\) for \(\Delta x\) small enough. As in [6] we can pass to the limit \(\Delta t\rightarrow 0\) in inequality (17).
More precisely, the continuity of \(\eta \) and the convergence of \(u_{\Delta t}\) imply that \(\eta (u_{\Delta t})\) converges to \(\eta (u)\) in  . On the other hand, since both the numerical and continuous entropy fluxes are Lipschitz continuous and \(u_{\Delta t}(\cdot ,t)\) has bounded variation for all \(t\in [0,T]\), we find
. On the other hand, since both the numerical and continuous entropy fluxes are Lipschitz continuous and \(u_{\Delta t}(\cdot ,t)\) has bounded variation for all \(t\in [0,T]\), we find
Finally, the  convergence of \(u_{\Delta t}\) implies
convergence of \(u_{\Delta t}\) implies  convergence of the P term, since for \(x\in I_j\) we have
convergence of the P term, since for \(x\in I_j\) we have

Thus we can pass to the limit \(\Delta t\rightarrow 0\) in (17) and get
and therefore u satisfies the entropy condition in the interior of the domain.
Regarding the entropy boundary condition (7), rearranging (15) yields
Multiplying by \(\Delta t \psi ^n\), where \(\psi ^n = \frac{1}{\Delta t}\int _{t^n}^{t^{n+1}}\psi (s){\text {ds}}\) for some nonnegative test function  , and summing over \(n=0,\ldots ,M\), we get
, and summing over \(n=0,\ldots ,M\), we get

Repeating this argument and using the discrete entropy boundary condition (16) yields
In order to recover the entropy boundary condition (7) we now pass to the limit \(\Delta t\rightarrow 0\) and then \(x\rightarrow 0\).
Firstly, since \(u_{\Delta t}\) converges to u in  and thus also in
and thus also in  , using the Lipschitz continuity of Q, we find
, using the Lipschitz continuity of Q, we find

Thus the left hand side of (18) converges to \(\int _0^T q(u(x,t))\psi (t){\text {dt}}\) for almost every \(x\in (0,1)\).
Because of the Lipschitz continuity of F and the  bound in Lemma 1, the piecewise constant interpolation in time of the values \(F_{\frac{1}{2}}^n\) is bounded in
bound in Lemma 1, the piecewise constant interpolation in time of the values \(F_{\frac{1}{2}}^n\) is bounded in  . Thus there exists a subsequence such that
. Thus there exists a subsequence such that  in
in  for some
for some  .
.
Since \(u_0^n = \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} \alpha (s){\text {ds}}\) converges to \(\alpha (t)\) for almost all \(t\in (0,T)\), the continuity of \(q,\eta '\) and f assures convergence of the remaining terms on the right hand side of (18).
Thus, by passing to the limit \(\Delta t\rightarrow 0\) in (18), we get
Because \(u(x,\cdot )\) is of bounded variation in time, we have strong convergence in  . The limit can only be the strong trace, i.e. \(u(x,\cdot )\rightarrow u_0^{\tau }\), as \(x\rightarrow 0\). Thus, by passing to the limit \(x\rightarrow 0\) in the foregoing inequality, we get
. The limit can only be the strong trace, i.e. \(u(x,\cdot )\rightarrow u_0^{\tau }\), as \(x\rightarrow 0\). Thus, by passing to the limit \(x\rightarrow 0\) in the foregoing inequality, we get
and since  is arbitrary
is arbitrary
for almost every \(t\in (0,T)\). It remains to show that \(\widetilde{f}_0(t) = f(u_0^{\tau }(t))\). By an approximation argument, (19) also holds true for Kružkov entropy pairs \(\eta (u)=|u-k|\), \(q(u)={\text {sign}}(u-k)(f(u)-f(k))\) with arbitrary \(k\in \mathbb {R}\). Choosing \(k>\max (u_0^{\tau }(t),\alpha (t))\) yields
and thus
On the other hand, choosing \(k<\min (u_0^{\tau }(t),\alpha (t))\) gives \(f(u_0^{\tau }(t)) \le \widetilde{f}_0(t)\), and therefore \(\widetilde{f}_0(t) = f(u_0^{\tau }(t))\). This proves the entropy boundary condition at \(x=0\). The boundary at \(x=1\) can be handled similarly.\(\square \)
5
 stability and uniqueness
stability and uniqueness
We now want to prove  stability of solutions following the ‘doubling of variables’ method introduced by Kružkov [20].
stability of solutions following the ‘doubling of variables’ method introduced by Kružkov [20].
Theorem 2
( stability) If u and v are entropy solutions of the Ostrovsky–Hunter equation with initial datum \(u_0\) and \(v_0\) respectively, then
stability) If u and v are entropy solutions of the Ostrovsky–Hunter equation with initial datum \(u_0\) and \(v_0\) respectively, then

In particular, this implies that entropy solutions to the initial-boundary value problem are unique.
Proof
Let u and v be entropy solutions with initial datum \(u_0\) and \(v_0\) respectively. We will now consider the entropy inequality (6) with Kružkov entropy pairs and a nonnegative test function \(\phi \) with support away from \(t=0\) and \(t=T\). By taking (6) for u in the variables (x, t) and for v in the variables (y, s) both with the test function \(\phi (x,t,y,s)\), integrating each with respect to the respective other two variables and adding them we get
Now, let \(\phi = \psi (\frac{x+y}{2},\frac{t+s}{2})\omega _{\varepsilon }(x-y)\omega _{\varepsilon _0}(t-s)\), where \(0\le \psi \le 1\) is a test function to be chosen later and \(\omega _{\varepsilon ,\varepsilon _0}\) are symmetric standard mollifiers. Then, using [17, Lemma 2.9], we find that the terms not involving P converge towards
as \(\varepsilon ,\varepsilon _0\rightarrow 0\). Regarding the remaining term, we use

Hence, using that weak solutions of bounded variation are Lipschitz continuous in time [17, Theorem 7.10], we find

as \(\varepsilon ,\varepsilon _0\rightarrow 0\). Consequently, u and v satisfy

Let now
which is a smooth approximation to \(\chi _{[0,a]}\). Then we define \(\psi (x,t) = \chi _{\delta ,1}(x)\chi _{\delta ,T}(t)\). Taking \(\delta \rightarrow 0\), we get

Note that by choosing
in the boundary entropy condition (7) we get
and similarly \(q(u^{\tau }_1(t),v^{\tau }_1(t)) \ge 0\) for a.e. t. Thus the right-hand side of (20) is nonnegative. An application of Gronwall’s lemma finishes the proof.\(\square \)
6 Numerical experiments
In this section we want to conduct two numerical experiments to illustrate our results. Here, we choose \(f(u)=u^2/2\) and \(\gamma =1\). Our first numerical experiment uses a well-studied travelling wave solution of the Ostrovsky–Hunter equation with initial datum given by the ‘corner wave’:
The ‘corner wave’ consists of two parabolas forming a sharp corner at \(x=\frac{1}{2}\) (cf. Fig. 1). The travelling wave solution is
which returns to its initial state after a period of \(T=36\). The ‘corner wave’ is the limit case of a family of smooth travelling wave solutions that has been investigated by several authors [3, 18, 27, 29, 33]. In this section we will not consider \(P(0)=0\), but \(\int _0^1 P =0\), which gives
This is motivated by the fact that the latter choice limits the growth of the  norm of the solution for our experiments. Figure 2 shows the exact entropy solution and a numerical solution both at \(T=36\). The numerical solution is calculated by the Lax–Friedrichs method with boundary conditions set as the explicit solution at \(x=0\) and \(x=1\) respectively and a grid discretization parameter of \(\Delta x=2^{-7}\).
norm of the solution for our experiments. Figure 2 shows the exact entropy solution and a numerical solution both at \(T=36\). The numerical solution is calculated by the Lax–Friedrichs method with boundary conditions set as the explicit solution at \(x=0\) and \(x=1\) respectively and a grid discretization parameter of \(\Delta x=2^{-7}\).
For this and all subsequent numerical experiments we useFootnote 1\(\Delta t/\Delta x=25\). Additionally, for the first experiment the known exact entropy solution is used to calculate the error:

Table 1 shows the  error between various numerical solutions and the exact solution, as well as the respective experimental convergence rates. Comparing these results to Table 1 in [6], we see that our numerical scheme is consistent with the periodic case.
error between various numerical solutions and the exact solution, as well as the respective experimental convergence rates. Comparing these results to Table 1 in [6], we see that our numerical scheme is consistent with the periodic case.
 errors and convergence rates for Experiment 1
errors and convergence rates for Experiment 1In our second experiment we use the same initial datum, but set the right boundary datum to zero. Figure 3 displays two numerical solutions, one on a moderate mesh (\(\Delta x =2^{-7}\)) calculated with the Lax–Friedrichs flux and one on a fine mesh (\(\Delta x^*=2^{-11}\)) calculated with the Engquist–Osher flux. With no explicit entropy solution at hand we consider a numerical solution on a fine grid (\(\Delta x^*=2^{-11}\)) in order to calculate the  errors in the second experiment, i.e.,
errors in the second experiment, i.e.,

Here, \(u_{\Delta t}\) and \(u_{\Delta t^*}\) are always calculated based on the same numerical method. Finally, in Table 2 we compare the  errors between various numerical solutions and provide the experimental convergence rates. One clearly sees that the Engquist–Osher flux leads to a better approximation in this experiment. This is due to the fact that the homogeneous boundary condition at \(x=1\) constitutes a shock that propagates into the domain and that shocks are resolved better with the Engquist–Osher flux.
errors between various numerical solutions and provide the experimental convergence rates. One clearly sees that the Engquist–Osher flux leads to a better approximation in this experiment. This is due to the fact that the homogeneous boundary condition at \(x=1\) constitutes a shock that propagates into the domain and that shocks are resolved better with the Engquist–Osher flux.
 errors and convergence rates for Experiment 2
errors and convergence rates for Experiment 2For conservation laws in \(\mathbb {R}\) without source term the classical result concerning convergence rates in  , due to Kuznetsov [21], gives a convergence rate of \(O(\Delta x^{1/2})\). The same convergence rate was shown in [6] for the Ostrovsky–Hunter equation with periodic boundary conditions. Although theoretical results estimating the convergence rate in the case of Dirichlet boundary conditions are highly desirable, such results are currently not at hand. However, in the absence of source terms Ohlberger and Vovelle [26] proof a rate of \(O(\Delta x^{1/6})\) in a very general setting.
, due to Kuznetsov [21], gives a convergence rate of \(O(\Delta x^{1/2})\). The same convergence rate was shown in [6] for the Ostrovsky–Hunter equation with periodic boundary conditions. Although theoretical results estimating the convergence rate in the case of Dirichlet boundary conditions are highly desirable, such results are currently not at hand. However, in the absence of source terms Ohlberger and Vovelle [26] proof a rate of \(O(\Delta x^{1/6})\) in a very general setting.
Notes
Here, we have
 and therefore \(\lambda =\Delta t/\Delta x\) should satisfy \(\lambda \le 36\). However, since the
and therefore \(\lambda =\Delta t/\Delta x\) should satisfy \(\lambda \le 36\). However, since the 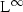 bound from Lemma 1 allows for some growth of
bound from Lemma 1 allows for some growth of 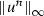 choosing a smaller \(\lambda \) can be neccessary.
choosing a smaller \(\lambda \) can be neccessary.
References
Amiranashvili, S., Vladimirov, A.G., Bandelow, U.: A model equation for ultrashort optical pulses around the zero dispersion frequency. Eur. Phys. J. D 58(2), 219–226 (2010)
Bardos, C., Leroux, A.Y., Nedelec, J.C.: First order quasilinear equations with boundary conditions. Commun. Partial Differ. Equ. 4(9), 1017–1034 (1979)
Boyd, J.P.: Ostrovsky and Hunter’s generic wave equation for weakly dispersive waves: matched asymptotic and pseudospectral study of the paraboloidal travelling waves (corner and near-corner waves). Eur. J. Appl. Math. 16(1), 65–81 (2005)
Brunelli, J.C., Sakovich, S.: Hamiltonian structures for the Ostrovsky–Vakhnenko equation. Commun. Nonlinear Sci. Numer. Simul. 18(1), 56–62 (2013)
Coclite, G., Karlsen, K., Kwon, Y.S.: Initial-boundary value problems for conservation laws with source terms and the Degasperis–Procesi equation. J. Funct. Anal. 257(12), 3823–3857 (2009)
Coclite, G., Ridder, J., Risebro, N.: A convergent finite difference scheme for the Ostrovsky–Hunter equation on a bounded domain. BIT Numer. Math. 57(1), 93–122 (2017)
Coclite, G., di Ruvo, L., Karlsen, K.: Some wellposedness results for the Ostrovsky–Hunter equation. In: Hyperbolic Conservation Laws and Related Analysis with Applications, pp. 143–159. Springer (2014)
Coclite, G.M., di Ruvo, L.: Oleinik type estimates for the Ostrovsky–Hunter equation. J. Math. Anal. Appl. 423(1), 162–190 (2015)
Coclite, G.M., di Ruvo, L.: Well-posedness of bounded solutions of the non-homogeneous initial-boundary value problem for the Ostrovsky–Hunter equation. J. Hyperbolic Differ. Equ. 12(02), 221–248 (2015)
Coclite, G.M., di Ruvo, L.: Well-posedness results for the short pulse equation. Z. Angew. Math. Phys. 66(4), 1529–1557 (2015)
Coclite, G.M., di Ruvo, L.: Wellposedness of bounded solutions of the non-homogeneous initial boundary for the short pulse equation. Boll. Unione Mat. Italiana 8(1), 31–44 (2015)
Coclite, G.M., di Ruvo, L.: Well-posedness of the Ostrovsky–Hunter equation under the combined effects of dissipation and short-wave dispersion. J. Evol. Equ. 16(2), 365–389 (2016)
Coclite, G.M., di Ruvo, L., Karlsen, K.H.: The initial-boundary-value problem for an Ostrovsky–Hunter type equation. In: Non-Linear Partial Differential Equations, Mathematical Physics, and Stochastic Analysis pp. 97–109 (2018)
Dubois, F., Le Floch, P.: Boundary Conditions for Nonlinear Hyperbolic Systems of Conservation Laws, pp. 96–104. Vieweg+Teubner Verlag, Wiesbaden (1989)
Grimshaw, R.H., Helfrich, K., Johnson, E.R.: The reduced Ostrovsky equation: integrability and breaking. Stud. Appl. Math. 129(4), 414–436 (2012)
Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49(3), 357–393 (1983)
Holden, H., Risebro, N.H.: Front Tracking for Hyperbolic Conservation Laws, vol. 152. Springer, New York (2015)
Hunter, J.K.: Numerical solutions of some nonlinear dispersive wave equations. Lect. Appl. Math. 26, 301–316 (1990)
Karlsen, K., Risebro, N., Storrøsten, E.: \(L^1\) error estimates for difference approximations of degenerate convection–diffusion equations. Math. Comput. 83(290), 2717–2762 (2014)
Kružkov, S.N.: First order quasilinear equations in several independent variables. Math. USSR Sb. 10(2), 217 (1970)
Kuznetsov, N.: Accuracy of some approximate methods for computing the weak solutions of a first-order quasi-linear equation. USSR Comput. Math. Math. Phys. 16(6), 105–119 (1976)
Liu, Y., Pelinovsky, D., Sakovich, A.: Wave breaking in the short-pulse equation. Dyn. PDE 6(4), 291–310 (2009)
Liu, Y., Pelinovsky, D., Sakovich, A.: Wave breaking in the Ostrovsky–Hunter equation. SIAM J. Math. Anal. 42(5), 1967–1985 (2010)
de Monvel, A.B., Shepelsky, D.: The Ostrovsky–Vakhnenko equation: a Riemann–Hilbert approach. C. R. Math. 352(3), 189–195 (2014)
Morrison, A., Parkes, E., Vakhnenko, V.: The N loop soliton solution of the Vakhnenko equation. Nonlinearity 12(5), 1427 (1999)
Ohlberger, M., Vovelle, J.: Error estimate for the approximation of nonlinear conservation laws on bounded domains by the finite volume method. Math. Comput. 75(253), 113–150 (2006)
Ostrovsky, L.: Nonlinear internal waves in a rotating ocean. Oceanology 18(2), 119–125 (1978)
Parkes, E.: The stability of solutions of Vakhnenko’s equation. J. Phys. A Math. Gen. 26(22), 6469 (1993)
Parkes, E.: Explicit solutions of the reduced Ostrovsky equation. Chaos Solitons Fractals 31(3), 602–610 (2007)
di Ruvo, L.: Discontinuous solutions for the Ostrovsky–Hunter equation and two-phase flows. Ph.D. thesis, University of Bari (2013)
Strub, S.I., Bayen, M.A.: Weak formulation of boundary conditions for scalar conservation laws: an application to highway traffic modelling. Int. J. Robust Nonlinear Control 16(16), 733–748 (2006)
Schäfer, T., Wayne, C.: Propagation of ultra-short optical pulses in cubic nonlinear media. Physica D Nonlinear Phenom. 196(1), 90–105 (2004)
Stepanyants, Y.A.: On stationary solutions of the reduced Ostrovsky equation: periodic waves, compactons and compound solitons. Chaos Solitons Fractals 28(1), 193–204 (2006)
Vakhnenko, V.: Solitons in a nonlinear model medium. J. Phys. A Math. Gen. 25(15), 4181 (1992)
Vakhnenko, V., Parkes, E.: The two loop soliton solution of the Vakhnenko equation. Nonlinearity 11(6), 1457 (1998)
Vakhnenko, V., Parkes, E.: The calculation of multi-soliton solutions of the Vakhnenko equation by the inverse scattering method. Chaos Solitons Fractals 13(9), 1819–1826 (2002)
Acknowledgements
The authors want to thank Nils Henrik Risebro from the University of Oslo for many insightful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jan Nordström.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The second author has received funding from the European Union’s Framework Programme for Research and Innovation Horizon 2020 (2014-2020) under the Marie Skłodowska-Curie Grant Agreement No. 642768.
Rights and permissions
About this article
Cite this article
Ridder, J., Ruf, A.M. A convergent finite difference scheme for the Ostrovsky–Hunter equation with Dirichlet boundary conditions. Bit Numer Math 59, 775–796 (2019). https://doi.org/10.1007/s10543-019-00746-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-019-00746-7
Keywords
- Ostrovsky–Hunter equation
- Short-pulse equation
- Vakhnenko equation
- Finite difference methods
- Monotone scheme
- Existence
- Uniqueness
- Stability
- Convergence
- Entropy solution
- Dirichlet boundary conditions




 stability and uniqueness
stability and uniqueness


 and therefore
and therefore 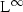 bound from Lemma
bound from Lemma 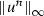 choosing a smaller
choosing a smaller