Model errors caused by rigid-foundation assumption in soil-structure interaction: a comparison of responses of a soil-structure-flexible foundation system and a rigid foundation system

Abstract

This study investigates model errors caused by the rigid-foundation assumption in dynamic Soil-Structure Interaction (SSI), which has been widely accepted in the past decades to reduce computational effort. A linear two-dimensional model is used for a qualitative analysis that compares the dynamic responses of a rigid system, comprising a rigid foundation embedded in a layered half-space with a superstructure mounted on top, and a corresponding flexible system with the same parameters but a flexible foundation with a variable stiffness. The Indirect Boundary Element Method combined with non-singular Green’s functions of distributed line loads is employed to calculate the system responses accurately. Transfer functions computed for a range of parameters show that the rigid-foundation assumption leads to overestimating the system natural frequency and changes the peak deformations to a different extent. It is also shown through a case study of 42 earthquakes that the rigid-foundation assumption may either overestimate or underestimate the system responses by up to approximately 50%, and in some cases even by approximately 100%, depending on the frequency content of excitation and SSI dynamic characteristics.

1 Introduction

The two or three-dimensional rigid-foundation model with the foundation on the surface of, or embedded in, a half-space representing the soil, with or without a superstructure on top, has commonly been assumed in studies of Soil–Structure Interaction (SSI) in the past decades. This assumption, by reducing the number of degrees of freedoms, facilitates computationally efficient analyses, while still providing relatively accurate results. However, it leads to overestimating wave scattering by the foundation and the overall flexibility of an SSI system, especially for short wavelengths (Trifunac et al. 1999). This paper addresses these issues by formulating a flexible-system model, which considers a foundation with variable stiffnesses, to investigate the errors produced by the rigid-foundation assumption in SSI problems. A specific focus of this study is on the effects of foundation flexibility on the system responses and its dynamic characteristics.

The rigid foundation model for SSI studies was established around 1970 and has widely been used since then. This was acceptable several decades ago when computer abilities were limited. For the model, the structures and the half-space are usually treated as two independent substructures at first, and system responses are then obtained by interfacing the two parts together via dynamic equilibrium of the rigid foundation. For this process, foundation impedance functions play an important role in describing both the stiffness and damping characteristics of underlying soil, as well as relating superstructure to the underlying soil. In the past few decades, many researches were dedicated on calculation of impedance functions through various methods, most of which are numerical ones. (Luco and Wong 1987; Gucunski 1993; Zhao et al. 2018; Fu et al. 2017, 2019). The substructure method is used in this paper to provide a benchmark to verify the results.

For the SSI model with a foundation of limited flexibility, it is challenging to separate each constituent part of the substructure model and use impedance functions in modelling and calculations, it is, therefore, less common to involve foundation flexibility in SSI-related studies (Spyrakos and Beskos 1986; Jeremić et al. 2009; Anastasopoulos and Kontoroupi 2014; Romero 2013; Pitilakis and Karatzetzou 2015). On the other hand, a foundation may behave rigidly when its stiffness is large enough (Liou and Huang 1994; Chen and Hou 2009; Gaitanaros and Karabalis 1988), however, many building foundations encountered in engineering practice do not have a large enough stiffness for this assumption to be justified. Nevertheless, the validity of rigid foundation assumption in SSI is seldomly verified and the role of foundation flexibility is rarely studied. From the limited existing studies, it can be concluded that foundation flexibility is important for assessing the dynamic behaviours of embedded foundations by a hybrid boundary element method—finite element method (BEM–FEM) approach (Iguchi and Luco 1981). It is also shown that the radiation damping for flexible foundations is significantly lower than that for rigid foundations in the same soil, that motions of the foundation are highly dependent on its flexibility (Todorovska et al. 2001a), and that both the vertical and horizontal motions are significantly influenced by the relative stiffness ratio of the foundation and the soil medium (Chen and Hou 2015). A clear reduction of the system frequency has been reported for a single-degree-of-freedom oscillator model on a semi-circular foundation to incident harmonic waves, because a non-rigid foundation adds extra flexibility to the system (Liang et al. 2016; Jin and Liang 2018). Also, a flexible foundation allows intermediate and short waves to enter the foundation-building interface, which makes building responses spatially complex (Gičev et al. 2015, 2016; Wolf 1985).

While many of the above-mentioned investigations concentrated only on the foundation responses without superstructure taken into account (Liou and Huang 1994; Chen and Hou 2009, 2015; Gaitanaros and Karabalis 1988; Iguchi and Luco 1981), this paper presents an SSI model consisting of a flexible embedded foundation with a superstructure on top of it for calculation of system responses. The half-space is simplified to a multi-layered site to consider the site dynamic characteristics in the model. Note that the terms flexible foundation or rigid foundation used in the paper refer specifically to the foundation itself, whereas these terms in some other studies correspond to the SSI system and fixed-base structure, respectively. The objectives of the paper are to: (1) propose an Indirect Boundary Element Method (IBEM) approach to obtain results of high accuracy, (2) propose a method to represent transfer functions of a flexible system whose motions are strongly spatially varied, (3) investigate the effects of foundation flexibility on the system responses and characteristics, (4) evaluate errors of the rigid foundation assumption in SSI problems for a qualitatively to guide future related studies, and (5) perform a series of case study analyses, for which the building and site data are available to provide reference values for engineering practice.

2 Methodology

2.1 Modelling of flexible foundation

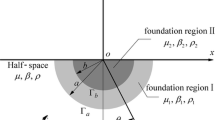
A two-dimensional SSI model, shown in Fig. 1, consists of a structure supported by a foundation embedded in a layered half-space. Both the structure and the foundation are reduced to a rectangular body, while, together with the half-space, they are assumed to be linear-elastic, viscously-damped and homogeneous. Although during strong earthquake events, both the soil and the structure are likely to experience some degree of non-linearity, evaluation of rigid foundation models under such conditions is out of the scope of this paper. The structure has a height of H, is characterized by shear-wave velocity β_b, Poisson’s ratio ν_b, mass density ρ_b per unit length in the y-direction and damping ratio ξ_b, whereas the foundation has dimensions 2a × c in the x- and z-directions, respectively, and is characterized by shear-wave velocity β_f, Poisson’s ratio ν_f, mass density ρ_f per unit length in the y-direction, and damping ratio ξ_f, respectively. No relative displacements are permitted at the structure-foundation interface. The entire soil layer has a thickness D, and the material properties of jth sub-layer are shear-wave velocity β_j, Poisson’s ratio ν_j, mass density ρ_j per unit length in the y-direction and damping ratio ξ_j, respectively, whereas the bedrock is characterized by shear-wave velocity β_R, Poisson’s ratio ν_R, mass density ρ_R per unit length in the y-direction and damping ratio ξ_R, respectively. The system is excited by a harmonic incident wave propagating from the bedrock, with particle motions in XOZ-plane, circular frequency ω, and incident angle θ with respect to the horizontal direction.

Fig. 1

SSI model consisting of an elastic foundation and superstructure embedded in a layered half-space and subjected to incident harmonic waves from the bedrock

For convenience of the following calculations, symbol Γ₁ represents the foundation-soil interface, and perfect bond is assumed along Γ₁ with no separation or uplift, while Γ₂ represents the two vertical outlines of the superstructure. Domain Ω₁ is the half-space except the foundation, and Ω₂ is the superstructure with the foundation, respectively.

2.2 IBEM approach

Two scattering fields within domains Ω₁ and Ω₂, respectively, are produced by incident harmonic waves, and an IBEM approach is used to calculate the scattering fields. To that end, the domains are divided into horizontal sub-layers, and, accordingly, it is assumed that N₁ elements are used along boundary Γ₁ (including the foundation bottom), and N₂ elements are used along boundary Γ₂, respectively. Then a set of fictitious horizontal harmonic loads, $p_{j} e^{{{\text{i}}\omega t}}$, and fictitious vertical harmonic loads, $r_{j} e^{{{\text{i}}\omega t}}$, whose amplitudes are unknown, are imposed onto each element of two domains, as shown in Fig. 1. The loads acting on the elements of Γ₁ of domain Ω₁ comprise fictitious-load vector ${\textbf{P}}_{{\textbf {1}}}$:

$${\textbf{P}_{\textbf {1}}} = \{ p_{1}^{1} , \, p_{1}^{2} , \, ... \, p_{1}^{j} , \, ... \, , \, p_{1}^{{N_{1} }} , \, r_{1}^{1} , \, r_{1}^{2} , \, ... \, , \, r_{1}^{j} , \, ... \, , \, r_{1}^{{N_{1} }} \}^{{\text{T}}}$$

(1)

and those acting on the elements of both Γ₁ and Γ₂, of domain Ω₂ comprise vector P₂:

$${\textbf{P}_{\textbf {2}}} = \{ p_{2}^{1} , \, p_{2}^{2} , \, ... \, p_{2}^{j} , \, ... \, , \, p_{2}^{{N_{1} + N_{2} }} , \, r_{2}^{1} , \, r_{2}^{2} , \, ... \, , \, r_{2}^{j} , \, ... \, , \, r_{2}^{{N_{1} + N_{2} }} \}^{{\text{T}}}$$

(2)

where superscript T denotes vector transpose. The time factor, $e^{{{\text{i}}\omega t}}$, in which, ${\text{i}} = \sqrt { - 1}$ is the imaginary unit, is omitted hereafter for convenience.

The displacements and tractions of a point x in domain Ω₁ are

$${\textbf{U}}_{{{\textbf{S1}}}} \left( {\textbf{x}} \right) = {\textbf{G}}_{{{\textbf{u1}}}} \left( {\textbf{x}} \right){\textbf{P}_{\textbf 1}} \quad {\textbf{ x}} \in \Omega_{1}$$

(3a)

$${\textbf{T}}_{{{\textbf{S1}}}} \left( {\textbf{x}} \right) = {\textbf{G}}_{{{\mathbf{\sigma} 1}}} \left( {\textbf{x}} \right){\textbf{P}_{\textbf {1}}} \quad {\textbf{ x}} \in \Omega_{{{\textbf{1}}}}$$

(3b)

where ${\textbf{G}}_{{{\textbf{u1}}}} ({\textbf{x}})$ and ${\textbf{G}}_{{\mathbf{ \sigma {1}}}} ({\textbf{x}})$ are the matrices of displacement Green’s functions and traction Green’s functions, respectively (Wolf 1985; Liang et al. 2013a, b):

$${\textbf{G}}_{{{\textbf {{u1}}}}} ({\textbf{x}}) = \left\{ \begin{gathered} G_{u1} ({\textbf{x}},p_{1}^{1} ), \, G_{u1} ({\textbf{x}},p_{1}^{2} ), \, ... \, G_{u1} ({\textbf{x}},p_{1}^{j} ), \, ... \, , \, G_{u1} ({\textbf{x}},p_{1}^{{N_{1} }} ), \, G_{u1} ({\textbf{x}},r_{1}^{1} ), \, G_{u1} ({\textbf{x}},r_{1}^{2} ), \, ... \, G_{u1} ({\textbf{x}},r_{1}^{j} ), \, ... \, , \, G_{u1} ({\textbf{x}},r_{1}^{{N_{1} }} ) \hfill \\ G_{w1} ({\textbf{x}},p_{1}^{1} ), \, G_{w1} ({\textbf{x}},p_{1}^{2} ), \, ... \, G_{w1} ({\textbf{x}},p_{1}^{j} ), \, ... \, , \, G_{w1} ({\textbf{x}},p_{1}^{{N_{1} }} ), \, G_{w1} ({\textbf{x}},r_{1}^{1} ), \, G_{w1} ({\textbf{x}},r_{1}^{2} ), \, ... \, G_{w1} ({\textbf{x}},r_{1}^{j} ), \, ... \, , \, G_{w1} ({\textbf{x}},r_{1}^{{N_{1} }} ) \hfill \\ \end{gathered} \right\}$$

(4a)

$${\textbf{G}}_{{\mathbf{\sigma 1}}} ({\textbf{x}}) = \left\{ \begin{gathered} G_{x1} ({\textbf{x}},p_{1}^{1} ), \, G_{x1} ({\textbf{x}},p_{1}^{2} ), \, ... \, G_{x1} ({\textbf{x}},p_{1}^{j} ), \, ... \, , \, G_{x1} ({\textbf{x}},p_{1}^{{N_{1} }} ), \, G_{x1} ({\textbf{x}},r_{1}^{1} ), \, G_{x1} ({\textbf{x}},r_{1}^{2} ), \, ... \, G_{x1} ({\textbf{x}},r_{1}^{j} ), \, ... \, , \, G_{x1} ({\textbf{x}},r_{1}^{{N_{1} }} ) \hfill \\ G_{z1} ({\textbf{x}},p_{1}^{1} ), \, G_{z1} ({\textbf{x}},p_{1}^{2} ), \, ... \, G_{z1} ({\textbf{x}},p_{1}^{j} ), \, ... \, , \, G_{z1} ({\textbf{x}},p_{1}^{{N_{1} }} ), \, G_{z1} ({\textbf{x}},r_{1}^{1} ), \, G_{z1} ({\textbf{x}},r_{1}^{2} ), \, ... \, G_{z1} ({\textbf{x}},r_{1}^{j} ), \, ... \, , \, G_{z1} ({\textbf{x}},r_{1}^{{N_{1} }} ) \hfill \\ \end{gathered} \right\}$$

(4b)

The components of the matrices in Eq. (4) are the Green’s functions of distributed loads acting along straight lines; for example, symbol $G_{u1} ({\mathbf{x}},p_{1}^{j} {)}$ corresponds to the horizonal displacement response of point x to the excitation from the distributed line load acting in the horizontal direction on the jth element. By using this type of Green’s functions, no singularity is anticipated in the IBEM model, which results in good accuracy and efficiency of numerical calculations. Also, this type of Green’s functions satisfies automatically the traction-free conditions on the top horizontal surface of the domain, thus, no meshing is needed on the ground surface and structure top. Similarly, the displacements and tractions of a point in domain Ω₂ are as follows:

$${\textbf{U}}_{{{\textbf{S2}}}} \left( {\textbf{x}} \right) = {\textbf{G}}_{{{\textbf{u2}}}} \left( {\textbf{x}} \right){\textbf{P}}_{\textbf {2}} \quad {\textbf{ x}}\in \Omega_{2}$$

(5a)

$${\textbf{T}}_{{{\textbf{S2}}}} \left( {\textbf{x}} \right) = {\textbf{G}}_{{\mathbf{\sigma 2}}} \left( {\textbf{x}} \right){\textbf{P}}_{\textbf {2}} \quad {\textbf{ x}} \in \Omega_{2}$$

(5b)

The boundary conditions of the model are, first, the continuity of displacements and tractions along boundary Γ₁:

$${\textbf{U}}_{{{\textbf{S1}}}} \left( {\textbf{x}} \right) + {\textbf{U}}_{{\textbf{f}}} \left( {\textbf{x}} \right) = {\textbf{U}}_{{{\textbf{S2}}}} \left( {\textbf{x}} \right)\,{\textbf{ x}} \in \Gamma_{1}$$

(6a)

$${\textbf{T}}_{{{\textbf{S1}}}} \left( {\textbf{x}} \right) + {\textbf{T}}_{{\textbf{f}}} \left( {\textbf{x}} \right) = {\textbf{T}}_{{{\textbf{S2}}}} \left( {\textbf{x}} \right)\,{\textbf{ x}} \in \Gamma_{1}$$

(6b)

where ${\textbf {U}}_{{\mathbf {\text{f}}}} ({\textbf {{x}}})$ and ${\mathbf {\text{T}}}_{{\mathbf {\text{f}}}} ({\textbf {{x}}})$ are the displacements and tractions of the free-field ground motion for incident harmonic waves. Second, the boundary Γ₂ must be traction-free:

$${\textbf{T}}_{{{\textbf {{S2}}}}} ({\textbf{x}}) = 0 \quad {\textbf{ x}} \in \Gamma_{2}$$

(7)

If N₁ target points are chosen from boundary Γ₁ (${\textbf{x}} = {\textbf{x}}_{1} ,{\textbf{x}}_{2} , \, ... \, ,{\textbf{ x}}_{{N_{1} }}$) and N₂ target points are chosen from boundary Γ₂ (${\textbf{x}} = {\textbf{x}}_{1} ,{\textbf{x}}_{2} , \, ... \, ,{\textbf{ x}}_{{N_{2} }}$) (usually one target point from one element for IBEM perform optimally), a set of linear equations of order N₁ + N₂ can be written as follows:

$$ \left[ {\begin{array}{*{20}c} {{\textbf{G}}_{{{\textbf{u1}}}} } & { - {\textbf{G}}_{{{\textbf{u2}}}}^{{\Gamma_{1} }} } \\ {{\textbf{G}}_{{\upsigma 1}} } & { - {\textbf{G}}_{{\upsigma 2}}^{{\Gamma_{1} }} } \\ 0 & {{\textbf{G}}_{{\upsigma 2}}^{{\Gamma_{2} }} } \\ \end{array} } \right]\left\{ \begin{gathered} {\textbf{P}}_{\textbf {1}} \hfill \\ {\textbf{P}}_{\textbf {2}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {\textbf{U}}_{{\textbf{f}}} \hfill \\ {\textbf{T}}_{{\textbf{f}}} \hfill \\ 0 \hfill \\ \end{gathered} \right\} $$

(8)

in which

$${\textbf{G}}_{{{\textbf{u1}}}} = \{ {\textbf{G}}_{{{\textbf{u1}}}} ({\textbf{x}}_{1} ),{\textbf{ G}}_{{{\textbf{u1}}}} ({\textbf{x}}_{2} ), \, ... \, ,{\textbf{ G}}_{{{\textbf{u1}}}} ({\textbf{x}}_{j} ), \, ... \, ,{\textbf{ G}}_{{{\textbf{u1}}}} ({\textbf{x}}_{{N_{1} }} )\}^{{\text{T}}} \quad {\textbf{ x}}_{j} \in \Gamma_{1}$$

(9a)

$${\textbf{G}}_{{\mathbf{\sigma} 1}} = \{ {\textbf{G}}_{{\mathbf{\sigma} 1}} ({\textbf{x}}_{1} ),{\textbf{ G}}_{{\mathbf{\sigma} 1}} ({\textbf{x}}_{2} ), \, ... \, ,{\textbf{ G}}_{{\mathbf{\sigma} 1}} ({\textbf{x}}_{j} ), \, ... \, ,{\textbf{ G}}_{{\mathbf{\sigma} 1}} ({\textbf{x}}_{{N_{1} }} )\}^{{\text{T}}} \quad {\textbf{ x}}_{j} \in \Gamma_{1}$$

(9b)

$${\textbf{G}}_{{{\textbf{u2}}}}^{{\Gamma_{1} }} = \{ {\textbf{G}}_{{{\textbf{u2}}}} ({\textbf{x}}_{1} ),{\textbf{ G}}_{{{\textbf{u2}}}} ({\textbf{x}}_{2} ), \, ... \, ,{\textbf{ G}}_{{{\textbf{u2}}}} ({\textbf{x}}_{j} ), \, ... \, ,{\textbf{ G}}_{{{\textbf{u2}}}} ({\textbf{x}}_{{N_{1} }} )\}^{{\text{T}}} \quad {\textbf{ x}}_{j} \in \Gamma_{1}$$

(9c)

$${\textbf{G}}_{{{\varvec \upsigma 2}}}^{{\Gamma_{1} }} = \{ {\textbf{G}}_{{\varvec {\upsigma} {\mathbf{2}}}} ({\textbf{x}}_{1} ),{\textbf{ G}}_{{\varvec {\upsigma} {\mathbf{2}}}} ({\textbf{x}}_{2} ), \, ... \, ,{\textbf{ G}}_{{\varvec{\upsigma} {\mathbf{2}}}} ({\textbf{x}}_{j} ), \, ... \, ,{\textbf{ G}}_{{\varvec{\upsigma} {\mathbf{2}}}} ({\textbf{x}}_{{N_{1} }} )\}^{{\text{T}}} \quad {\textbf{ x}}_{j} \in \Gamma_{1}$$

(9d)

$${\textbf{G}}_{{\boldsymbol{\upsigma} 2}}^{{\Gamma_{2} }} = \{ {\textbf{G}}_{{\boldsymbol{\upsigma} 2}} ({\textbf{x}}_{{N_{1} + 1}} ),{\textbf{ G}}_{{\boldsymbol{\upsigma} 2}} ({\textbf{x}}_{{N_{1} + 2}} ), \, \ldots \, ,{\textbf{ G}}_{{\boldsymbol{\upsigma} 2}} ({\textbf{x}}_{{N_{1} + j}} ), \, \ldots \, ,{\textbf{ G}}_{{\boldsymbol{\upsigma} 2}} ({\textbf{x}}_{{N_{1} + N_{2} }} )\}^{{\text{T}}} \quad {\textbf{ x}}_{{N_{1} + j}} \in \Gamma_{2}$$

(9e)

Then unknown vectors ${\textbf{P}}_{\bf 1}$ and ${\textbf{P}}_{\bf 2}$ are solved from Eq. (8). The responses at the structure top, ${\textbf{U}}_{{{\textbf{S2}}}} ({\textbf{x}})_{(\left| x \right| \le a, \, z = - H)} = \{ u_{s2\_x} ({\textbf{x}}), \, u_{s2\_z} ({\textbf{x}})\}$, are calculated by substituting locations ${\textbf{x}} = \left. {\mathop {(x,z)}\limits_{{}}^{{}} } \right|\left| x \right| \le a, \, z = - H$ into Eq. (5a).

The horizontal, vertical and rotational components of displacements are coupled in a flexible system, which is described by the transfer functions of the system, but can be decoupled by the following operations:

$$u_{b} ({\textbf{x}}) = u_{s1\_x} ({\textbf{x}}) \quad {\textbf{x}} \in (\left| x \right| \le a, \, z = - H)$$

(10a)

$$w_{b} ({\textbf{x}}) = \frac{{u_{s1\_z} ({\textbf{x}}) + u_{s1\_z} ( - {\textbf{x}})}}{2} \quad {\textbf{x}} \in (\left| x \right| \le a, \, z = - H)$$

(10b)

$$\theta_{b} ({\textbf{x}}) = \frac{{u_{s1\_x} ({\textbf{x}}) - w_{b} ({\textbf{x}})}}{\left| x \right|} \quad {\textbf{x}} \in (\left| x \right| \le a, \, z = - H).$$

(10c)

2.3 Verification of accuracy

Figure 2 is a comparison of the spectral amplitudes of transfer functions, $\left| u_{{\text{b}}} ({\textbf{x}}) \right|$ and $\left| {w_{{\text{b}}} \left( {\textbf{x}} \right)} \right|$, of a rigid system (with a rigid foundation and a rigid structure) between the method presented in this paper and that of Liang et al. (2013b). The numerical parameters are assumed as follows: ρ_R/ρ_j/ρ_b/ρ₀ = 1, ν_R = ν_j=ν_b = ν₀ = 1/4, ξ_R = ξ_j=ξ_b = ξ₀ = 0, β_R/β_j = 2 (j = 1, 2, 3, …), b/a = 0.5, H/a = 0.5, and vertically incident P- or SV-waves are used as excitations. The dimensionless frequency is defined as $\eta = \lambda_{j} /2a = \omega a/\pi \beta_{j}$, where $\lambda_{j}$ is the shear wavelength in the soil layer.

Fig. 2

Comparison of transfer functions between the method proposed herein (circles) and that in Liang et al. (2013b) (solid line) for vertically incident waves: a SV-wave, and b P-wave

In Liang et al. (2013b), a model of a shear wall supported by a rigid foundation is used, and the system responses are calculated by a substructure method, for which no wave motions are assumed within the foundation. Furthermore, the structure (i.e. the shear wall) is also simplified as a rigid body for comparison. While for the method presented in this paper, the stiffness of foundation and structure is set to be 10 times that of the soil layer, i.e., β_f/β_j = 10 and β_b/β_j = 10, so that the foundation and the structure are essentially reduced to rigid bodies. However, it should be noted that their wavelength is only 1/10 of that in the soil layer, thus, their element meshing needs to be at least 10 times that of the soil layer to ensure accuracy. For the modelling purposes in this study, we use N₁ = 1800 (300 for each lateral side and 600 for half of the bottom) and N₂ = 600 (300 for each lateral side), which results in a computationally demanding task, while only 1/10 of elements are used in Liang et al. (2013b).

The transfer functions are independent of spatial location along x-axis for rigid structures. The two results agree well, validating the method proposed in this paper. A small discrepancy is, nevertheless, observed for $\eta \ge 0.4$, because even denser meshing than N₁ = 1800 and N₂ = 600 is necessary for high frequencies. However, since the results presented so far are acceptable, it was deemed that enough calculations have been carried out to verify the proposed approach.

3 Numerical results and analysis

3.1 Model parameters

The results discussed in this chapter are presented in terms of the following dimensionless parameters of the uniform half-space: ρ_R/ρ_j=1, ν_R = ν_j=1/4, ξ_R = ξ_j=0.02 and β_R/β_j = 1 (j = 1, 2, 3, …), respectively. The foundation embedment is b/a = 0.5, mass density ρ_f/ρ_j = 0.2 (which makes it generally correspond to a basement-type foundation), damping ratio ξ_f = 0.02 and Poisson’s ratio ν_f = 1/4. The structure mass density is also taken as ρ_b/ρ_j = 0.2, damping ratio as ξ_b = 0.02 and Poisson’s ratio as ν_b = 1/4. The foundation flexibility is represented by a dimensionless ratio of foundation-to-soil shear wave velocity, β_f/β_j, while the structure flexibility is represented by a similar ratio of structure-to-soil shear wave velocity, β_b/β_j, respectively. The two ratios are referred hereafter to as foundation stiffness and structure stiffness for short.

Complex-valued material parameters are obtained by the correspondence principle and denoted by an asterisk:

$$\beta^{*} \approx \beta (1 + {\text{i}}\xi )$$

(11)

As the values of β_f/β_j and β_b/β_j vary in the following analysis, we use the following approximations:

$$\beta_{j}^{*} \approx \beta_{j} + {\text{i}}\beta_{j} \xi_{j}$$

(12a)

$$\beta_{{\text{f}}}^{*} \approx \beta_{{\text{f}}} + {\text{i}}\beta_{j} \xi_{j}$$

(12b)

$$\beta_{{\text{b}}}^{*} \approx \beta_{{\text{b}}} + {\text{i}}\beta_{j} \xi_{j}$$

(12c)

to ensure a constant damping in the structure and foundation, i.e., the energy dissipation caused by material damping is linked to the shear wave velocity of the soil, instead of that of their own.

A measurement of equivalent shear-wave velocity of the structure β_b is not easy, so this value of the structure may be roughly evaluated from the following formula

$$\omega_{{\text{ b}}} = \frac{{\beta_{{\text{b}}} \pi }}{2H}$$

(13)

or from a recommended method for a framed structure (Todorovska etal 2001b). The equivalent shear-wave velocity β_f of a basement-type foundation may be taken approximately the same as that of the structure, while for a piled foundation, this value is roughly evaluated from the following formula

$$\beta_{{{\text{pile}}}} = \frac{{A_{{{\text{piles}}}} \times \beta_{{{\text{concrete}}}} + A_{{{\text{soil}}}} \times \beta_{j} }}{{A_{{{\text{base}}}} }}$$

(14)

in which, β_concrete and β₁ are shear-wave velocities of reinforced concrete, and A_piles and A_soil are the projection areas of piles on XOY-plane and of the soil on XOY-plane except the piles, respectively. For a nine-story reinforced concrete building in Pasadena, California (Millikan Library) whose shear wave velocity is roughly evaluated as β_b = 379.3 m/s by Eq. (13) in the NS direction, it gives β_b/β_f = 1 for the building with basement-type foundation, and it gives β_b/β_f = 1.44 for a hypothesis Millikan Library with piled foundation for an pile area A_piles = A_base/15 and a hypothesis shear-wave velocity of reinforced concrete piles β_concrete = 4000 m/s, while it gives β_b/β_f = 1.76 for A_piles = A_base/10 and β_concrete = 4000 m/s. The foundation stiffness β_f/β_j generally corresponds to a representation of foundation types. Although β_f < β_j is rare in engineering practice, β_f /β_j = 0.5 is considered in the following study, to give a group of values (β_j/β_f = 0.5, 1, 2 and ∞) to study the roles of foundation flexibility in soil-structure interaction.

The variation of values for ratio β_b/β_j corresponds to different site classifications from hard to soft soil. The site classification criterion according to a design code (ASCE/SEI 7–10; 2010) is listed in Table 1. For a nine-story reinforced concrete building in Pasadena, California (Millikan Library), whose shear wave velocity is roughly evaluated as β_b = 379.3 m/s by Eq. (13) in the NS direction, it gives β_b/β_j = 1.27 for its own site (β_j = 298.7 m/s, site class D), and β_b/β_j = 3.79 for a soft site in Mexico City (β_j = 100 m/s, site class E), while in our case β_b/β_j = 0.76 for a moderately hard site (β_j = 500 m/s, site class C), β_b/β_j = 0.47 for a hard site (β_j = 800 m/s, site class B), and β_b/β_j = 0.25 for a rock site (β_j = 1500 m/s, site class A), respectively.

Table 1 Site Classification in ASCE/SEI-10 (ASCE/SEI 7–10; 2010)

3.2 Analysis of structural responses

Figure 3 shows the spectral amplitude of the transfer functions, $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$, $\left| {w_{{\text{b}}} ({\textbf{x}})} \right|$ and $\left| {\theta_{{\text{b}}} ({\textbf{x}})} \right|$, at the structure top for parameters β_f/β_j = 0.5, β_b/β_j = 0.5 and H = 2. The dimensionless frequency varies as $0 < \eta < 0.8$, and four incident angles, $\theta = 5^{ \circ } , \, 30^{ \circ } , \, 60^{ \circ } , \, 90^{ \circ }$, are assumed for incident P- and SV-waves, i.e., eight wave passages in total are considered. It is observed that although the structure and its foundation are very flexible, with stiffnesses only half of the surrounding soil, the transfer functions are approximately independent of x-coordinate for up to the first 2 resonances ($\eta < 0.3$). For the rigid foundation assumption, the structural responses in two directions are uncoupled, i.e. $u_{{\text{b}}} ({\textbf{x}}) = 0$ for the vertically incident P- waves, and $w_{{\text{b}}} ({\textbf{x}}) = 0$ and $\theta_{{\text{b}}} ({\textbf{x}}) = 0$ for vertically incident SV-waves. For the flexible foundation assumption, the conclusion that motions are uncoupled in two directions at least until first two resonances.

Fig. 3

Spectral amplitude of transfer functions at the structure top for: a horizontal displacement b vertical displacement, and c rotational displacement. (a) $u_{{\text{b}}} ({\text{x}})$ (b) $w_{{\text{b}}} ({\text{x}})$ (c) $\theta_{{\text{b}}} ({\text{x}})$

For medium and high frequencies (higher than the first two resonances, $\eta > 0.3$), the 3 transfer functions $u_{{\text{b}}} ({\textbf{x}})$, $w_{{\text{b}}} ({\textbf{x}})$ and $\theta_{{\text{b}}} ({\textbf{x}})$ gradually begin to vary along x-axis, but their resonances are still recognizable in the frequency domain. It is noted that the structural rotation, $\left| {\theta_{{\text{b}}} ({\textbf{x}})} \right|$, tends to concentrate in the middle of the structure top, the horizontal translation, $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$, at the two edges, but the vertical translation, $\left| {w_{{\text{b}}} ({\textbf{x}})} \right|$, appears to be distributed arbitrarily.

Figure 4 shows the spectral amplitude, $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$ of the transfer function at the structure top for the vertically incident SV-wave and for structural stiffness β_b/β_j = 0.5. Four values of the foundation stiffness are considered, β_f/β_j = 0.5, 1, 2 and ∞ (from left to right), and three structure heights are as assumed, H = 1, 2 and 3 (from top to bottom). For the short structure (H = 1), even when foundations are very flexible (β_f/β_j=0.5 and 1), the transfer function is still nearly independent of the x-coordinate for frequencies $\eta < 0.4$. This upper limit of $\eta$ is higher than what is shown in Fig. 4 for stiffer structures (β_b/β_j = 1 and 2). For the medium-height and high structures (H = 2 and 3), the upper limit may reach up to $\eta = 0.3$. It is concluded that the transfer functions hardly depend on the x-coordinate at least up to the first resonance for all cases. It is also noted that the local crests and troughs of the spectrum retain a similar shape, when the foundation stiffness varies, despite being shifted in frequency. The rigidity of the SSI system depends evidently on the frequency such that a system may act rigidly at low frequencies but becomes flexible at high frequencies.

Fig. 4

Spectral amplitude of transfer function $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$ at the structure top for different structure heights and foundation stiffness values for vertically incident SV-waves (β_b/β_j = 0.5)

Further, since the spectral shapes in Fig. 3 are similar to one another in the resonant frequency range for different wave passage effects, the transfer functions are normalized as follows and shown in Fig. 5:

$$\left| {\overline{u}_{{\text{b}}} } \right| = \left| {u_{{\text{b}}} /u_{{\text{f}}} } \right|$$

(15a)

$$\left| {\overline{w}_{{\text{b}}} } \right| = \left| {w_{{\text{b}}} /w_{{\text{f}}} } \right|$$

(15b)

$$\left| {\overline{\theta }_{{\text{b}}} } \right| = \left| {\theta_{{\text{b}}} /u_{{\text{f}}} } \right|$$

(15c)

Fig. 5

Spectral amplitude of normalized transfer functions for different wave passage effects (β_f/β_j = 0.5, β_b/β_j = 0.5, H = 2)

where $u_{{\text{b}}}$, $w_{{\text{b}}}$ and $\theta_{{\text{b}}}$ are the mean values of transfer functions amplitudes $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$, $\left| {w_{{\text{b}}} ({\textbf{x}})} \right|$ and $\left| {\theta_{{\text{b}}} ({\textbf{x}})} \right|$ at the structure top, respectively, $u_{{\text{f}}}$ and $w_{{\text{f}}}$ are the free-field ground motion amplitudes in the two directions. Figure 5 is for the same parameters as Fig. 3, i.e. β_f/β_j = 0.5, β_b/β_j = 0.5 and H = 2. The critical angle for incident harmonic waves is known to be:

$$\theta_{{_{{{\text{critical}}}} }} = \tan^{ - 1} \sqrt {\frac{1}{1 - 2\nu }}$$

(16)

It is shown that the wave passage effects are generally absent in the normalized responses until the first resonance, except for incident SV-waves with $\theta < \theta_{{_{{{\text{critical}}}} }}$, because of wave type transformation. The absence of wave passage effects is helpful in the study of this paper, because the amplitudes of foundation input excitations are eliminated from system responses, and only the natural characteristics of system manifest themselves.

For frequencies above the first resonance, the wave passage effects have more variations along x-axis for rotation amplitude $\left| {\overline{\theta }_{{\text{b}}} } \right|$ than for translation amplitudes $\left| {\overline{u}_{{\text{b}}} } \right|$ and $\left| {\overline{w}_{{\text{b}}} } \right|$. It is difficult to remove wave passage effects at frequencies where transfer functions begin to depend on x-coordinate. As the following analysis mainly concentrates on the resonances in the horizontal direction corresponding to the first peak of $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$, the normalized amplitude $\left| {\overline{u}_{{\text{b}}} } \right|$ for vertically incident SV-waves is used to represent the system responses to study the errors caused by the rigid foundation assumption. The vertical displacement transfer function, $\left| {\overline{w}_{{\text{b}}} } \right|$, will be studied in future papers.

Both transfer functions $\left| {\overline{u}_{{\text{b}}} } \right|$ and $\left| {\overline{\theta }_{{\text{b}}} } \right|$ have the same resonant frequencies, but the second resonance of $\left| {\overline{\theta }_{{\text{b}}} } \right|$ is much more clear than that of $\left| {\overline{u}_{{\text{b}}} } \right|$. The resonant frequency of $\left| {\overline{w}_{{\text{b}}} } \right|$ is larger, because the wave propagation velocity in the vertical direction is mainly related to P-wave velocity in the structure.

3.3 Effects of foundation stiffness

Figure 6 shows the spectral amplitude of the normalized transfer function of $\left| {\overline{u}_{{\text{b}}} } \right|$ under the excitation of vertically incident SV-waves for a range of structural and foundation properties. In each plot, the different lines correspond to four values of foundation stiffness (β_f/β_j = 0.5, 1, 2 and ∞). The plots in the different columns show results for three cases of structure height (H = 1, 2 and 3), and the plots in the different rows correspond to three structural stiffness values (β_b/β_j = 0.5, 1 and 2), respectively. It is shown that as the foundation flexibility ratio β_f/β_j increases, the transfer function has a higher resonant frequency and a wider peak, approaching the case of the rigid foundation. The vertical transfer function $\left| {\overline{w}_{{\text{b}}} } \right|$ has similar properties. The flexibility of foundation is more influential for rigid structures (β_b/β_j = 0.5) than for flexible structures (β_b/β_j = 1, 2), i.e., the rigid foundation assumption introduces more errors for models with rigid structures.

Fig. 6

Spectral amplitude of normalized transfer function $\left| {\overline{u}_{{\text{b}}} } \right|$ for different foundation stiffness

Figure 7 shows the spectral amplitude of the normalized transfer function $\left| {u_{{\text{b}}} ({\textbf{x}})} \right|$ along structure height, i.e. for ${\textbf{x}} \in ( - H \le z \le b, \, x = \pm a)$, at resonant frequency for vertically incident SV-waves. It is known that compared with a fixed-base structure, flexible half-space in a soil-structure-rigid foundation system dampens down the amplitude of system responses and decreases the resonant frequency of the responses. While for a soil-structure-flexible foundation system, flexible foundation amplifies the amplitude of foundation displacement and structure displacement for most cases, whereas it still decreases the resonant frequency. However, it is also noticed in the figure that, for less cases of slender flexible structures (β_f/β_j = 0.5 and H/a = 3; β_f/β_j = 1 and H/a = 3), foundation flexibility yet dampens down the spectral amplitude slightly. For this case, structure displacement is characterized by an inflection point on structure height, above which, foundation flexibility begins to dampen down the amplitude of structure response.

Fig. 7

Spectral amplitude of normalized transfer function $\left| {\overline{u}_{{\text{b}}} ({\textbf{x}})} \right|$ along structure height, i.e. for ${\textbf{x}} \in ( - H \le z \le b, \, x = \pm a)$, at resonant frequency for vertically incident SV-waves

Foundation flexibility plays two roles in an SSI system in the way that, a flexible foundation may act as a weak local layer in the half-space and amplifies the responses, while on the other hand, it may also act as an additional damper in the half-space and dampens down the responses. The predominance of the two roles depends on particular parameters of an SSI system. As the rigid foundation assumption is widely used in SSI-related studies, the assumption may probably underestimate structure responses and leads to unconservative evaluation.

In order to describe the properties of the transfer functions, especially near the resonant frequency, three indicators are introduced, namely the system frequency, system damping and system peak amplitude. The system frequency, $\tilde{\omega }_{{\text{b}}}$, is defined as the peak frequency of the transfer functions. The system damping is measured from the transfer function by the half-power method:

$$\tilde{\xi }_{{\text{b}}} = \frac{{\omega_{2} - \omega_{1} }}{{\omega_{2} + \omega_{1} }}$$

(17)

where $\omega_{1}$ and $\omega_{2}$ are the frequencies to the left and right of the system frequency, respectively, at which the response drops to $1/\sqrt 2$ of its maximum value. The system damping is reflected in the general shape of the transfer function peak. It was considered that the half-power method was adequate for evaluating the system damping (Fu et al. 2018).

Figure 8 shows the 3 indices of transfer function $\left| {\overline{u}_{{\text{b}}} } \right|$ with respect to structural stiffness described by β_b/β_j, for a range of 0 < β_b/β_j<2 in this study. For very flexible structures with β_b/β_j < 0.5, it makes generally no differences whether the flexible foundation model or the rigid foundation model is assumed, because the large flexibility of the structure makes that of the foundation uninfluential. With structures becoming stiffer (β_b/β_j > 0.5), the system frequency (normalized as $\tilde{\eta }_{{\text{b}}} = \lambda_{j} /2a = \tilde{\omega }_{{\text{b}}} a/\pi \beta_{j}$ for convenience) of the flexible foundation model is evidently smaller than that of rigid foundation model, especially for short and light structures (H/a = 1, 2), because the structure itself is rigid. For the case of β_f/β_j = 0.5, the ratio $\tilde{\eta }_{{{\text{b}}({\text{flex}})}} /\tilde{\eta }_{{{\text{b}}({\text{rigid}})}}$ may fall as low as 50%, and for the case β_f/β_j = 1, the ratio may reach 70%, while for β_f/β_j = 0.5, the ratio is less than 90%.

Fig. 8

Parameters of transfer function $\left| {\overline{u}_{{\text{b}}} } \right|$ for different foundation stiffness

It is noticed that the system frequency for some short structures (H/a = 1) is as high as 0.6. For this case, the transfer function is still approximately independent from x-coordinate before the first resonance. For example, for structural parameters β_f/β_j = 2, β_b/β_j = 2 and H/a = 1, the transfer function is generally constant along x-axis up to $\eta = 0.8$.

The system damping of the flexible foundation model is smaller than that of the rigid foundation model, especially for short structures (H/a = 1, 2), and the flexible foundation models are characterized by a sharper peak of the transfer function. Correspondingly, the system peak amplitude of the former is larger than the latter, although an abnormality can be observed for β/β_j = 0.5 and H/a = 3. On the other hand, the system damping tends to be independent of the foundation stiffness for high structures (H/a = 3), whose transfer functions have also very sharp peaks.

4 Responses in time domain

Four instrumented buildings located in California are chosen to establish their SSI models to study the errors produced by the rigid foundation assumption in time domain for actual recorded earthquakes: the Hollywood Storage Building (CSMIP Station No. 24236, CSMIP stands for California Strong Motion Instrumentation Program) (Trifunac et al. 2001; Duke et al. 1970), the Millikan Library (NSMP No. 5407, NSMP stands for National Strong Motion Program) (Luco et al. 1986, 1987), a building in Sherman Oaks (CSMIP Station No. 24322) (NIST GCR 2012), and a building in Walnut Creek (CSMIP Station No. 58364) (NIST GCR 2012). Strong motion observation data collected on the buildings in several earthquake events, instead of arbitrary earthquake records, are used as input excitation to be in agreement with the site dynamic characteristics of the buildings. The 3D building structures were simplified to 2D models to obtain an estimation of the errors produced by the rigid foundation assumption.

The Hollywood Storage Building is supported by a reinforced concrete basement on Raymond concrete piles, whose penetration lengths are 3–9 m below the basement. No data on foundation mass was found, so the assumed values ρ_base = ρ_b and ρ_pile = ρ₁ are used in the model, where ρ_base and ρ_pile are the mass density of the basement of a depth of 2.74 m and of the piles of a penetration length of 6 m (an average penetration length of 6 m is used for convenience), respectively, and ρ₁ is the mass density of the first soil layer. From these assumptions, foundation mass M_f = 1.34 × 10⁷ kg is obtained for the model. No data on the shear-wave velocities were available either, thus, the shear-wave velocity of the structure and of the basement is approximately evaluated from Eqs. (13) and (14). Poisson’s ratio ν_b = 1/3 is used for the structure, and structural mass, M_b, is assumed as uniformly distributed along its height. For the SSI model with a rigid foundation, M_f = 1.34 × 10⁷ kg is assumed to be distributed uniformly within the foundation. The parameters of the Hollywood Storage Building are listed in Table 2, and the building site is simplified to a multi-layered half-space with parameters listed in Table 3.

Table 2 Buildings for case studies

Table 3 Site parameters for case studies

For the Sherman Oaks building, its foundation consists of a two-story basement, beams-on-grade and friction piles, and the assumed values ρ_base = ρ_b and ρ_pile = ρ₁ are also used for its model. According to NIST GCR (2012), the fixed-base periods in 2 directions were estimated from an FEM model to be 2.72 s and 2.67 s, however, it seems that such long periods are unreasonable for the building. We re-estimated the fixed-base periods to be 0.65 s and 0.59 s according to a Chinese design code (GB 50,009–2012).

The Millikan Library and the Walnut Creek building both have a basement-type foundation. No data on the mass of the Walnut Creek building was found, so a rational estimation of the mass of the Millikan Library was also used for the Walnut Creek building. The structural parameters of other three buildings, evaluated by a similar process as for the Hollywood Storage Building as well as site parameters are all listed in Tables 2 and 3, respectively.

Table 4 shows the ratios of system frequency, $\tilde{\eta }_{{\text{b}}}$, and peak amplitudes, $\left| {\overline{u}_{{\text{b}}}^{{\max}} } \right|$, for the flexible and rigid foundation models for the 4 buildings. The rigid foundation model introduces a 10% error in the system frequency, and about 10%–20% error in the peak amplitude. The errors in the system frequency indicate a shift of the whole spectrum along η-axis, which may result in significant errors in evaluating structural responses to seismic excitations in the time domain.

Table 4 Ratios of system frequency $\tilde{\eta }_{{\text{b}}}$ and peak amplitude $\left| {\overline{u}_{{\text{b}}}^{{\max}} } \right|$ between flexible and rigid foundation model

Figure 9 shows the dynamic responses on the structure top of the Hollywood Storage Building in the time domain in the NS direction. The excitation, as shown in Fig. 9a, is a normalized acceleration record with a peak value of 0.1 g obtained at the ground floor of the building in the NS direction during the San Fernando earthquake in 1971. It is assumed in the building model that the input excitation propagates from the bedrock. Figure 9b shows the responses of the flexible foundation model, presented as a time history, $\ddot{\overline{u}}_{{\text{b}}} (t)$, (left) and a response spectrum of that time history, $RS\;\left\{ {\ddot{\overline{u}}_{{\text{b}}} } \right\}$, (right). Finally, Fig. 9c shows the responses of the rigid foundation model. In the left-hand-side column, the value next to the asterisk is the maximum roof acceleration, while that in the bottom right-hand-side corner is the mean roof acceleration from the time window between 0 and 80 s. The calculation of responses in the time domain was conducted in three steps. First, the time history of acceleration records was mapped to the frequency domain by the Fourier transformation. Then structural responses, such as those shown in Fig. 6, were calculated at 2048 + 1 equally spaced frequency points from 0 to 25 Hz, and were multiplied by the acceleration records at the corresponding points to obtain the response in the frequency domain. Finally, the responses were mapped back into the time domain by the inverse Fourier transformation.

Fig. 9

Analysis of the Hollywood Storage Building model in the NS direction during the San Fernando earthquake: a acceleration data recorded at the ground floor, b roof response of flexible foundation model, and c roof response of rigid foundation model

It can be seen that the maximum response found in the time history of the rigid foundation model is 84.8% that of the flexible foundation model, while the mean responses found in the time history and the maximum value of response spectrum of the rigid foundation model are 110.3% and 83.7%, respectively, those of the flexible foundation model. The dynamic responses in the time domain for the four buildings in 42 earthquakes are summarized in Table 5 (for the building short direction) and Table 6 (for the building long direction), for which the excitations were the acceleration records obtained on the ground floor of each building in the respective direction (https://strongmotioncenter.org/).

Table 5 Dynamic responses in time domain of four buildings in short direction

Table 6 Dynamic responses in time domain of 4 buildings in long direction

Figure 10 shows the ratio of the 3 responses (the maximum response in the time history, mean response in time history, and maximum response spectrum) of the rigid foundation model to these of the flexible foundation model. The x-axis corresponds to each event in Tables 5 and 6, and y-axis is the percentage value. The responses of the rigid foundation model are about 50%–150% those of the flexible foundation model, i.e. the errors of the rigid foundation model are up to about 50% in evaluating the dynamic responses of the SSI problem, and sometimes may even reach 100%. As a flexible foundation itself adds extra flexibility to the system, it is sometimes assumed that a rigid foundation model is conservative for evaluating the system responses. But this is not always the case—a rigid foundation model may either overestimate or underestimate the system responses. Further, it is interesting to observe that both overestimation or underestimation may occur equally frequently, depending on the frequency content of seismic excitation. The Hollywood Storage Building and the Sherman Oaks building both have pile foundations, while the Millikan Library and the Walnut Creek Building have a basement-type foundation, and it is also noticed that the errors produced by the rigid foundation model appear similar for all four buildings, irrespective of their foundation type.

Fig. 10

Ratios between rigid foundation model and flexible foundation model for: a maximum response in time history, b mean response in time history, and c maximum value of response spectrum. (Red circle—Hollywood Storage Building, gray star—Sherman Oaks building; green rectangle—Millikan Library, blue triangle—Walnuts Creek building.)

For the Hollywood Storage Building analyzed in the NS direction, the shear-wave velocity of foundation is about twice that of the underlying soil (β_f/β₁≈2), and the errors produced by of the rigid foundation model are smaller than average. For the Sherman Oaks Building, which is similar, the model errors do not differ significantly from the average. It is, therefore, incorrect to use the rigid foundation model to evaluate structural responses in the time domain for β_f/β₁ = 2 at least.

5 Conclusions

The errors produced by the rigid foundation assumption in SSI problems are studied using linear-elastic two-dimensional models comprising a foundation with variable stiffness values, embedded in a layered half-space and with a superstructure on top of it. The accuracy of simulations is investigated by reducing the model to a rigid system, whose solutions were obtained previously by a substructure method. The results were presented for varying foundation-to-soil stiffness ratios and for different values of the structural stiffness and height, in both the frequency and the time domain. The main findings of the study are as follows:

• 1. Case studies are carried out on 4 buildings of a height between approximately 40–50 m. Two of them had pile foundations on a soft soil with the shear wave velocity less than 200 m/s (one building is of plan configuration 15 m × 66 m and of fixed-base frequency 0.83 Hz–2.0 Hz in 2 directions, respectively; another is of plan configuration 26 m × 58 m and of fixed-base frequency 1.54 Hz–1.69 Hz in 2 directions, respectively), and other 2 had basement-type foundations on a moderately stiff soil with the shear wave velocity of about 300 m/s (one building is of plane configuration 23 m × 25 m and of fixed-base frequency 2.16 Hz–1.26 Hz in 2 directions, respectively; another is of plan configuration 32 m × 45 m and of fixed-base frequency 1.52 Hz–2.1 Hz in 2 directions, respectively). It is shown that the errors produced by the rigid foundation assumption in SSI problems may be up to 50% in evaluating the dynamic responses, and sometimes may even reach 100%. A rigid foundation model may either overestimate or underestimate the dynamic responses, and the overestimation or underestimation was approximately equally probable in the 42 analyzed earthquake events. This conclusion applies to both the basement-type and the pile foundations.

• 2. There is a difference in the system frequency between the flexible foundation model and the rigid foundation model, and the rigid foundation model leads to larger discrepancies in the system frequency with increasing structural stiffness. The system damping of the flexible foundation model is usually lower than that of rigid foundation model.

• 3. For a linear-elastic SSI system with a flexible foundation, the transfer functions are nearly independent from spatial location up to the first resonance. Although the transfer functions begin to be spatially dependent with increasing frequency, higher-order resonances are still recognizable. Also, the horizontal and vertical motions are uncoupled for the systems with a flexible foundation up to the first resonance, while they begin to be slightly coupled in the higher frequency range.

• 4. For the shear-wave velocity ratio of foundation to underlying soil less than 2, it is incorrect to use the rigid foundation model assumption to evaluate the structural responses.

The conclusions in this paper were reached using 2D models with uniformly distributed mass and stiffness and give an initial estimation of the accuracy of the rigid foundation assumption in SSI problems. However, real buildings are 3D structures; moreover, the foundation exterior and interior walls may significantly influence the bending stiffness. A further research using full 3D models of realistic buildings is, therefore, planned in future.