1 Introduction

Dynamic soil–structure interaction (SSI) is one fundamental problem in the field of earthquake engineering. In actual SSI process, foundation flexibility (foundation deformation) is very significant, which has been proved by many tests and observation records (Wong et al. 1977; Hudson 1977; Trifunac et al. 1999). Some scholars made efforts on flexible foundation to try to make the theoretical models more suitable to the actual situation.

The earlier research works (Iguchi and Luco 1981; Rajapakse 1989; Wang et al. 1991; Gucunski and Peek 1993; Liou and Huang 1994) pointed out that foundation flexibility has strong effect on foundation impedance function and contact stresses distribution beneath the foundation. The theoretical models in these earlier research works are usually the circular-shaped surface plate ignoring the embedding effect, and these earlier research works did not investigate how foundation flexibility influence structural response. Hayir et al. (2001 and Todorovska et al. 2001) first noticed that and carried some research works. The results illustrated that the structure near the foundation has larger deformations when taking account of foundation flexibility into the analysis. Liang et al. (2016) presented an analytical solution of dynamic soil–structure interaction with a SDOF oscillator on a homogenous embedded semi-circular flexible foundation. The analysis showed that foundation flexibility has strong effect on system response and system frequency. Le et al. (2016) presented an analytical solution to the response of a shear wall standing on a rigid–flexible composite foundation. They compared the results with that of the shear wall with rigid foundation (Trifunac 1972), but they did not investigate the effect of foundation flexibility on system response and system frequency. Liang and Jin (2016) presented an analytical solution of dynamic soil–structure interaction with a SDOF oscillator on a rigid–flexible composite foundation, and studied how foundation flexibility influences system response and system frequency.

It is worth to note the forced vibration test of Millikan Library Building (Wong et al. 1977). The results showed that foundation has very significant deformation and the distribution of the contact stresses beneath the foundation focus on the stiffer elements of structure, which is different to that of rigid foundation. Take a foundation base plate surrounded by shear walls for example. When the stiffness of the shear walls is very large, the region that the plate connected with the shear walls will be very stiff. The stiff region brings flexibility variation in the plate, which makes the response of the plate is different to that of completely rigid plate assumption. Thus, in SSI analysis, it is of significance to consider the effect of the stiff region that foundation connected with structure on foundation response and structural response.

However, the models in the current researches on flexible foundation are either homogenous flexible foundation models or rigid–flexible composite foundation models. The homogenous flexible foundation models ignore the flexibility variation in foundation caused by superstructure, while the rigid–flexible composite foundation models treat the stiff region in foundation caused by superstructure completely rigid, which will exaggerate scattering of the waves and the effective input motion to the superstructure. Therefore, it is of significance to study the dynamic soil–structure interaction based on the completely flexible composite foundation model, in which, the stiff region is treated as a flexible region, rather than completely rigid region.

This paper presents a closed-form analytical solution of dynamic soil–structure interaction with a SDOF oscillator on semi-circular flexible composite foundation in elastic half-space for incident plane SH waves, and analyzes the effects of the foundation flexibility variation on the dynamic response of the foundation, the relative response of the SDOF oscillator and the system frequency.

2 Methodology

2.1 The model

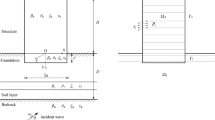
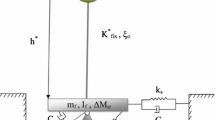
The two-dimensional (2D) model, shown in Fig. 1, consists of a SDOF oscillator, with only out-of-plane shear deformation, supported by a semi-circular flexible composite foundation embedded in the half-space, representing a structure and its foundation. Point o is the origin of the Cartesian x–y–z and cylindrical r–θ–y coordinate systems, and the flexible composite foundation is infinite long in y direction (axis y points to the reader). The flexible composite foundation has radius a, and its interior is composed of region I and region II. Region I is between the boundary Γ a and Γ b with smaller stiffness, and Region II has radius b with larger stiffness. The half-space has respectively shear modulus μ, shear-wave velocity β, and mass density ρ; the region I has respectively shear modulus μ 1, shear-wave velocity β 1, and mass density ρ 1; the region II has respectively shear modulus μ 2, shear-wave velocity β 2, and mass density ρ 2. Further, the foundation has total mass M 0 per unit length (in the y-direction), and the mass of the soil replaced by the flexible composite foundation is M S per unit length. The SDOF oscillator has mass M b per unit length, undamped circular frequency ω b, and is connected with the foundation through a finite width δ (δ ≪ a). The excitation is an incident plane SH wave with circular frequency ω, incidence angle γ (measured from the vertical z-axis) and unit amplitude.

Fig. 1
figure 1

The model of dynamic soil–structure interaction with flexible composite foundation

Full size image

The superstructure is simplified into a single-degree-of-freedom (SDOF) oscillator as a pole attached to the flexible foundation below at the center point. This approximation, which is simple, is a worthwhile attempt to study such SSI of flexible foundations. Indeed, this approximation was first used by Lee and Trifunac (1982) to investigate three-dimensional (3D) SSI problem for rigid hemispherical foundation.

The solution steps are as follows. In Sect. 2.1, the model is introduced, while, in Sect. 2.2, the excitation, the free-field motion and the wave functions are defined, and the solution is presented.

2.2 Governing equations and solution

The free-field motion caused by incident plane SH wave can be expressed as \(v_{{}}^{i + r}\) (Trifunac 1972)

$$\begin{aligned}{} v_{{}}^{i + r} & = 2J_{0} (kr) + 4\sum\limits_{n = 1}^{\infty } {( - 1)^{n} J_{2n} (kr) \cdot \cos (2n\gamma ) \cdot \cos (2n\theta )} \\& \quad - 4i\sum\limits_{n = 0}^{\infty } {( - 1)^{n} J_{2n + 1} (kr) \cdot \sin (2n + 1)\gamma \cdot \sin (2n + 1)\theta } \, \\ \end{aligned}$$
(1)

where \(k = \omega /\beta\), and J p (x) are the Bessel function of the first kind with argument x and order p.

In the half-space, the scattered wave v R outgoing from the foundation is represented as

$$v_{{}}^{R} = \sum\limits_{n = 0}^{\infty } {\left[ {a_{n} H_{2n}^{( 2)} (kr) \cdot \cos (2n\theta ) + b_{n} H_{2n + 1}^{( 2)} (kr) \cdot \sin (2n + 1)\theta } \right]}$$
(2)

The wave motion in region I of the flexible composite foundation can be written as

$$v_{ 1}^{S} = \,\sum\limits_{n = 0}^{\infty } {\left[ {c_{n} H_{2n}^{( 2)} (k_{ 1} r) + d_{n} J_{2n} (k_{ 1} r)} \right]} \cdot \cos (2n\theta ) + \sum\limits_{n = 0}^{\infty } {\left[ {e_{n} H_{2n + 1}^{( 2)} (k_{ 1} r) + f_{n} J_{2n + 1} (k_{ 1} r)} \right]} \cdot \sin (2n + 1)\theta \,$$
(3)

where \(k_{ 1} = {\omega \mathord{\left/ {\vphantom {\omega {\beta_{ 1} }}} \right. \kern-0pt} {\beta_{ 1} }}\), H (2) P (x) is the Hankel function of the second kind with argument x and order p.

The wave motion in region II of the flexible composite foundation can be written as

$$v_{ 2}^{S} = \,g_{0} J_{0} (k_{2} r) + \sum\limits_{n = 1}^{\infty } {g_{n} J_{2n} (k_{2} r)} \cdot \cos (2n\theta ) + \sum\limits_{n = 0}^{\infty } {h_{n} J_{2n + 1} (k_{2} r)} \cdot \sin (2n + 1)\theta \,$$
(4)

where \(k_{2} = {\omega \mathord{\left/ {\vphantom {\omega {\beta_{2} }}} \right. \kern-0pt} {\beta_{2} }}\).

Motion v F in foundation region II, due to the inertia load from the oscillator, F, acting on the point o is represented as (Liang et al. 2016)

$$v_{{}}^{F} = \, - \frac{F}{{2\mu_{2} }}\, \cdot i \cdot H_{0}^{(2)} (k_{2} r)$$
(5)

All the wave motions must satisfy the wave differential equation given by

$$\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }} = \frac{1}{{\beta^{2} }}\frac{{\partial^{2} v}}{{\partial t^{2} }}$$
(6)

where v stands for the motions \(v_{{}}^{i + r}\), \(v_{{}}^{R}\), \(v_{ 1}^{S}\), \(v_{2}^{S}\) and \(v_{{}}^{F}\) respectively, and β stands for β, β 1 and β 2 respectively.

All the wave motions must also satisfy the boundary conditions given by

$$\sigma_{\theta y} = \frac{\mu }{r}\frac{\partial v}{\partial \theta } = 0\quad at\quad \theta = \pm \frac{\pi }{2}$$
(7)
$$v_{{}}^{i + r} + v_{{}}^{R} = v_{1}^{S} \quad at\quad r = a$$
(8)
$$\mu \frac{{\partial (v_{{}}^{i + r} + v_{{}}^{R} )}}{\partial r} = \mu_{1} \frac{{\partial v_{1}^{S} }}{\partial r}\quad at\quad r = a$$
(9)
$$v_{1}^{S} = v_{2}^{S} + v_{{}}^{F} \quad at\quad r = b$$
(10)
$$\mu_{1} \frac{{\partial v_{1}^{S} }}{\partial r} = \mu_{2} \frac{{\partial (v_{2}^{S} + v_{{}}^{F} )}}{\partial r}\quad at\quad r = b$$
(11)
$$v_{{}}^{F} = \Delta \quad at\quad r = 0$$
(12)

In Eq. (5), v stands for the motions \(v_{{}}^{i + r}\), \(v_{{}}^{R}\), \(v_{ 1}^{S}\), \(v_{2}^{S}\) and \(v_{{}}^{F}\) respectively, and μ stands for μ, μ 1 and μ 2 respectively. In Eqs. (2), (3) and (4), the a n , b n , c n , d n , e n , f n , g n , and h n are the complex constants that can be determined by boundary conditions (8), (9), (10), (11) and (12). Δ is the effective input motion at point o to the SDOF oscillator.

The inertia load F that the SDOF oscillator acts at point o of the flexible foundation can be determined as follows. The system equilibrium equation of the undamped SDOF oscillator subjected to effective input motion Δ can be written as

$$(\ddot{\Delta }_{b} + \ddot{\Delta }) + \omega_{b}^{2} \Delta_{b} = 0$$
(13)

where, Δ b is the relative motion of the SDOF oscillator to point o, and

$$\Delta_{b} = \frac{{\omega_{{}}^{2} }}{{\omega_{b}^{2} - \omega_{{}}^{2} }}\Delta$$
(14)

So, the inertia load F is

$$F = \omega^{2} M_{b} (\Delta_{b} + \Delta ) = \omega^{2} M_{b} \frac{{\omega_{b}^{2} }}{{\omega_{b}^{2} - \omega^{2} }}\Delta$$
(15)

The complex expansion coefficients a n , c n , d n , and g n can be determined by substituting Eqs. (1) through (5) into boundary conditions (8), (9), (10), (11) and (12). This gives for n = 1, 2, 3 …

$$a_{n} \cdot H_{2n}^{(2)} (ka) - c_{n} \cdot H_{2n}^{(2)} (k_{1} a) - d_{n} \cdot J_{2n} (k_{1} a) = - 4 \times ( - 1)^{n} J_{2n} (ka) \cdot \cos (2n\gamma )$$
(16a)
$$a_{n} \cdot \mu W_{2,n} - c_{n} \cdot \mu_{1} W_{3,n} - d_{n} \cdot \mu_{1} W_{4,n} = - \mu W_{1,n}$$
(16b)
$$c_{n} \cdot H_{2n}^{(2)} (k_{1} b) + d_{n} \cdot J_{2n} (k_{1} b) - g_{n} \cdot J_{2n} (k_{2} b) = 0$$
(16c)
$$\begin{aligned} c_{n} \cdot \mu_{1} \left[ {\frac{2n}{b}H_{2n}^{(2)} (k_{1} b) - k_{1} H_{2n + 1}^{(2)} (k_{1} b)} \right] + d_{n} \cdot \mu_{1} \left[ {\frac{2n}{b}J_{2n} (k_{1} b) - k_{1} J_{2n + 1} (k_{1} b)} \right] \hfill \\ \quad \quad - g_{n} \cdot \mu_{2} \left[ {\frac{2n}{b}J_{2n} (k_{2} b) - k_{2} J_{2n + 1} (k_{2} b)} \right] = 0 \hfill \\ \end{aligned}$$
(16d)

where,

$$W_{1,n} = 4 \times ( - 1)^{n} \left[ {\frac{2n}{r}J_{2n} (kr) - kJ_{2n + 1} (kr)} \right]\cos (2n\gamma )$$
(17a)
$$W_{2,n} = \frac{2n}{r}H_{2n}^{(2)} (kr) - kH_{2n + 1}^{(2)} (kr)$$
(17b)
$$W_{3,n} = \frac{2n}{r}H_{2n}^{(2)} (k_{1} r) - k_{1} H_{2n + 1}^{(2)} (k_{1} r)$$
(17c)
$$W_{4,n} = \frac{2n}{r}J_{2n} (k_{1} r) - k_{1} J_{2n + 1} (k_{1} r)$$
(17d)

The complex expansion coefficients b n , e n , f n , and h n can be determined by solving Eqs. (18a) through (18d) together, and it gives for n = 0, 1, 2, 3 …

$$b_{n} \cdot H_{2n + 1}^{(2)} (ka) - e_{n} \cdot H_{2n + 1}^{(2)} (k_{1} a) - f_{n} \cdot J_{2n + 1} (k_{1} a) = 4i \times ( - 1)^{n} J_{2n + 1} (ka) \cdot \sin (2n + 1)\gamma$$
(18a)
$$b_{n} \cdot \mu P_{2,n} - e_{n} \cdot \mu_{1} P_{3,n} - f_{n} \cdot \mu_{1} P_{4,n} = - \mu P_{1,n}$$
(18b)
$$e_{n} \cdot H_{2n + 1}^{(2)} (k_{1} b) + f_{n} \cdot J_{2n + 1} (k_{1} b) - h_{n} \cdot J_{2n + 1} (k_{2} b) = 0$$
(18c)
$$\begin{aligned} e_{n} \cdot \mu_{1} \left[ {\frac{2n + 1}{b}H_{2n + 1}^{(2)} (k_{1} b) - k_{1} H_{2n + 2}^{(2)} (k_{1} b)} \right] + f_{n} \cdot \mu_{1} \left[ {\frac{2n + 1}{b}J_{2n + 1} (k_{1} b) - k_{1} J_{2n + 2} (k_{1} b)} \right] \hfill \\ \quad \quad - h_{n} \cdot \mu_{2} \left[ {\frac{2n + 1}{b}J_{2n + 1} (k_{2} b) - k_{2} J_{2n + 2} (k_{2} b)} \right] = 0 \hfill \\ \end{aligned}$$
(18d)

where,

$$P_{1,n} = - 4i \times ( - 1)^{n} \left[ {\frac{2n + 1}{r}J_{2n + 1} (kr) - kJ_{2n + 2} (kr)} \right]\sin (2n + 1)\gamma$$
(19a)
$$P_{2,n} = \frac{2n + 1}{r}H_{2n + 1}^{(2)} (kr) - kH_{2n + 2}^{(2)} (kr)$$
(19b)
$$P_{3,n} = \frac{2n + 1}{r}H_{2n + 1}^{(2)} (k_{1} r) - k_{1} H_{2n + 2}^{(2)} (k_{1} r)$$
(19c)
$$P_{4,n} = \frac{2n + 1}{r}J_{2n + 1} (k_{1} r) - k_{1} J_{2n + 2} (k_{1} r)$$
(19d)

Especially, for n = 0, the complex expansion coefficients a 0, c 0, d 0, g 0 and Δ can be determined by solving Eqs. (20a) through (20e) together, and it gives

$$a_{0} \cdot H_{0}^{(2)} (ka) - c_{0} \cdot H_{0}^{(2)} (k_{1} a) - d_{0} \cdot J_{0} (k_{1} a) = - 2J_{0} (ka)$$
(20a)
$$a_{0} \cdot \mu kH_{1}^{(2)} (ka) - c_{0} \cdot \mu_{1} k_{1} H_{1}^{(2)} (k_{1} a) - d_{0} \cdot \mu_{1} k_{1} J_{1} (k_{1} a) = - 2\mu kJ_{1} (ka)$$
(20b)
$$c_{0} \cdot H_{0}^{(2)} (k_{1} b) + d_{0} \cdot J_{0} (k_{1} b) - g_{0} \cdot J_{0} (k_{2} b) + \frac{i}{{2\mu_{2} }}\omega^{2} M_{b} T(\omega )H_{0}^{(2)} (k_{2} b) \cdot \Delta = 0$$
(20c)
$$c_{0} \cdot \mu_{1} k_{1} H_{1}^{(2)} (k_{1} b) + d_{0} \cdot \mu_{1} k_{1} J_{1} (k_{1} b) - g_{0} \cdot \mu_{2} k_{2} J_{1} (k_{2} b) + \frac{i}{2}k_{2} \cdot \omega^{2} M_{b} T(\omega )H_{1}^{(2)} (k_{2} b) \cdot \Delta = 0$$
(20d)
$$g_{0} \cdot J_{0} (k_{2} \delta ) - \left[ {\frac{i}{{2\mu_{2} }}\omega^{2} M_{b} T(\omega )H_{0}^{(2)} (k_{2} \delta ) + 1} \right] \cdot \Delta = - Sum\;\;\;(\delta \;is\;a\;small\;value)$$
(20e)

where,

$$T(\omega ) = \frac{{\omega_{b}^{2} }}{{\omega_{b}^{2} - \omega^{2} }}$$
(21a)
$$Sum = \sum\limits_{n = 1}^{\infty } {g_{n} J_{2n} (k_{2} \delta )} \cdot \cos (2n\theta ) + \sum\limits_{n = 0}^{\infty } {h_{n} J_{2n + 1} (k_{2} \delta )} \cdot \sin (2n + 1)\theta$$
(21b)

Because the inertia load F is applied at point o of the flexible composite foundation, the motion at point o cannot be calculated directly by letting r = 0 due to singularity. So, we let r = δ in Eq. (20e), where δ is a number that tends to zero, but not equal to zero. θ can be an arbitrary value due to δ tending to zero. Here, we let θ = 0, and so

$$Sum = \sum\limits_{n = 1}^{\infty } {g_{n} J_{2n} (k_{2} \delta )}$$
(22)

It should be noted that, a 0, c 0, d 0, g 0 and Δ are independent with the incident angle, which is due to that, except for the unknowns a 0, c 0, d 0, g 0 and Δ, all the other parameters are independent with the incident angle in Eqs. (20a) through (20e).

Both Δ and Δ b are normalized by surface displacement amplitude of the free-field motion v i+r

$$\bar{\Delta } = \Delta /\left| {v^{i + r} } \right|,\quad \bar{\Delta }_{b} = \Delta_{b} /\left| {v^{i + r} } \right|.$$
(23)

3 Verification by comparison with results for homogenous flexible foundation and rigid–flexible composite foundation

For the SDOF oscillator, the dimensionless parameter η is defined as (Todorovska and Trifunac 1992)

$$\eta = \frac{{\omega_{b} a}}{\pi \beta }$$
(24)

which depends on the relative stiffness of the SDOF oscillator to the half-space and the relative mass of the SDOF oscillator to the foundation mass. In this study we call it “structural stiffness” for short in the following. Small η means a flexible SDOF oscillator and/or stiff soil and large η means a stiff SDOF oscillator and/or very flexible soil. The limiting value η → ∞ corresponds to a rigid SDOF oscillator, and η → 0 corresponds to a flexible SDOF oscillator on a rigid half-space (Todorovska and Trifunac 1992). Figure 2 shows the results of this paper with that of the homogenous flexible foundation model (Liang et al. 2016), and Fig. 3 shows the results of this paper with that of the rigid–flexible composite foundation model (Liang and Jin 2016). It can be seen that our results agree very well with those of the two limiting cases.

Fig. 2
figure 2

Comparison with the results of homogenous flexible foundation with SDOF oscillator (Liang et al. 2016)

Full size image
Fig. 3
figure 3

Comparison with the results of rigid–flexible composite foundation with SDOF oscillator (Liang and Jin 2016)

Full size image

4 Numerical results and analysis

4.1 Calculation parameters

Figures 4, 5, 6, 7, 8 and 9 illustrate the effect of foundation flexibility variation on foundation dynamic response and structural relative response. To easily make comparison, the results of two limiting cases [homogenous flexible foundation (Liang et al. 2016) and rigid–flexible composite foundation (Liang and Jin 2016)] are also plotted in each sub-figure. The parameters are as follows. The shear-velocity contrast between the foundation region I and the half-space β 1/β = 2, and foundation flexibility variation β 2/β 1 = 2/2, 3/2, 5/2 and 100/2. Especially, for β 2/β 1 = 2/2, it means that the flexible composite foundation is homogeneous flexible foundation. The mass-density contrast between the foundation and the half-space ρ 1/ρ 2/ρ = 1/1/2, which is equivalent to M 0/M S  = 1/2. We call the parameter b/a as “foundation flexibility variation region” for short in the following, and b/a = 0.25, 0.50 and 0.75. The mass contrast between the SDOF oscillator and the foundation (we call it “structural mass” for short in the following) M b/M 0 = 1, 2 and 4. The structural stiffness η = 1/12, 1/6 and 1/3. The wave incident angle γ = 0°, 30°, 60° and 90°. δ/a = 0.05, which is a practical value for common structures (Liang et al. 2016).

Fig. 4
figure 4

Dynamic response of point o (structural stiffness η = 1/3)

Full size image
Fig. 5
figure 5

Dynamic response of point o (structural stiffness η = 1/6)

Full size image
Fig. 6
figure 6

Dynamic response of point o (structural stiffness η = 1/12)

Full size image
Fig. 7
figure 7

Relative response of the superstructure (structural stiffness η = 1/3)

Full size image
Fig. 8
figure 8

Relative response of the superstructure (structural stiffness η = 1/6)

Full size image
Fig. 9
figure 9

Relative response of the superstructure (structural stiffness η = 1/12)

Full size image

4.2 Foundation effective input motion

Figures 4, 5 and 6 show how foundation flexibility variation (β 2/β 1) influence the effective input motion that foundation to structure. It can be seen that when taking account of foundation flexibility variation (β 2/β 1) into the analysis, the input motion that foundation to structure is different to that of the homogenous flexible foundation model and that of the rigid–flexible composite foundation model. For η = 1/3, b/a = 0.25 and M b/M 0 = 4, when β 2/β 1 = 2/2, 3/2, 5/2 and 100/2, the peak responses of point o are 1.827, 1.548, 1.417 and 1.349, respectively, and the frequencies corresponding to the peaks are 0.497, 0.509, 0.509 and 0.504, respectively. While, the peak response of point o for homogenous flexible foundation model is 1.827 and its corresponding frequency is 0.497, and the peak response of point o for rigid–flexible composite foundation model is 1.349 and its corresponding frequency is 0.504. This shows that for β 2/β 1 = 100/2, the results of flexible composite foundation are very close to that of rigid–flexible composite foundation and the flexible composite foundation can be treated as rigid–flexible composite foundation approximately.

This also illustrates the effective input motion that foundation to structure is highly dependent on foundation flexibility variation. The larger the foundation flexibility variation (β 2/β 1) is, the result will more approach to the result of the rigid–flexible composite foundation model. The smaller the foundation flexibility variation (β 2/β 1) is, the result will more approach to that of the homogenous flexible foundation model. This means when foundation flexibility variation (β 2/β 1) increases, the peak of effective input motion will be smaller and the frequency corresponding to the peak will shift to higher frequency.

The reason why the effective input motion occurs the above phenomenon is that foundation flexibility variation highly influences foundation stiffness. Depending on the degree of foundation flexibility variation, flexible composite foundation is between rigid–flexible composite foundation and homogenous flexible foundation. It is necessary to consider foundation flexibility variation (β 2/β 1) in actual SSI analysis, because both the homogenous flexible foundation model and the rigid–flexible composite foundation model are limiting cases.

Foundation flexibility variation region (b/a), structural mass (M b/M 0) and structural stiffness (η) also influence the effective input motion.

For fixed η and M b/M 0, when b/a increase, the peak of point o will decrease. For η = 1/3, M b/M 0 = 4 and β 2/β 1 = 3/2, when b/a = 0.25, 0.50 and 0.75, the peak of point o are 1.548, 1.435 and 1.370, respectively.

For fixed η and β 2/β 1, when M b/M 0 increases, the frequency corresponding to the peak of point o will shift to lower frequency. For η = 1/3, b/a = 0.25 and β 2/β 1 = 3/2, when M b/M 0 = 1, 2 and 4, the frequencies corresponding to the peaks of point o are 0.801, 0.670 and 0.509.

For fixed b/a and M b/M 0, when η decreases, the peak of point o will increase and the frequency corresponding to the peak will shift to lower frequency. For b/a = 0.25, β 2/β 1 = 3 and M b/M 0 = 2, when η = 1/3, 1/6 and 1/12, the peaks of point o are 1.430, 1.621 and 1.917 respectively, and the frequencies corresponding to the peaks are 0.670, 0.442 and 0.248, respectively. While for b/a = 0.25, β 2/β 1 = 5 and M b/M 0 = 2, when η = 1/3, 1/6 and 1/12, the peaks of point o are 1.299, 1.492 and 1.787 respectively, and the frequencies corresponding to the peaks are 0.667, 0.444 and 0.248, respectively.

4.3 Structural relative response

Figures 7, 8 and 9 show how foundation flexibility variation (β 2/β 1) influences the structural relative response. It can be seen that the peak of structural relative response is close to that of the homogenous flexible foundation model and that of the rigid–flexible composite foundation model, but the frequency corresponding to the peak is significantly different. The frequency corresponding to the peak for flexible composite foundation model is strongly affected by foundation flexibility variation (β 2/β 1). For η = 1/3, b/a = 0.75 and M b/M 0 = 2, when β 2/β 1 = 2/2, 3/2, 5/2 and 100/2, the peaks of structural relative response are 1.351, 1.405, 1.446 and 1.477, respectively, and the frequencies corresponding to the peaks are 0.733, 0.841, 0.921 and 0.976, respectively. While, the peak of structural relative response for the homogenous flexible foundation is 1.351 and its corresponding frequency is 0.733, and the peak of structural relative response for the rigid–flexible composite foundation is 1.477 and its corresponding frequency is 0.976.

Foundation flexibility variation region (b/a) also influences the structural relative response. For η = 1/3, M b/M 0 = 2 and β 2/β 1 = 3/2, when b/a = 0.25, 0.50 and 0.75, the peaks of structural relative response are 1.371, 1.387 and 1.405, respectively, and the frequencies corresponding to the peaks of point o are 0.789, 0.820 and 0.841, respectively.

Structural stiffness (η) and structural mass (M b/M 0) also influence the structural relative response. When structural stiffness (η) is very small, the effect of foundation flexibility variation (β 2/β 1) on the structural relative response is very little. For η = 1/12, b/a = 0.25 and M b/M 0 = 1, when β 2/β 1 = 2/2, 3/2, 5/2 and 100/2, the peaks of structural relative response are 38.073, 38.187, 38.507 and 38.472, respectively, and the frequencies corresponding to the peaks are 0.255, 0.256, 0.257 and 0.257, respectively. For fixed η, when structural mass (M b/M 0) increases, the frequency corresponding to the peak of structural relative response will shift to lower frequency. For η = 1/13, b/a = 0.25 and β 2/β 1 = 3/2, when M b/M 0 = 1, 2 and 4, the frequencies corresponding to the peaks of structural relative response are 0.898, 0.789 and 0.638, respectively.

4.4 System frequency

Todorovska and Trifunac (1992) defined a system frequency for rigid foundation with a SDOF oscillator, by the frequency corresponding to the peak of the ratio of the structural relative response to the system input. This paper follows this definition, and the dimensionless system frequency can be expressed as

$$\eta^{sys} = {{\omega a} \mathord{\left/ {\vphantom {{\omega a} \beta }} \right. \kern-0pt} \beta }$$
(37)

Based on this definition, the effect of foundation flexibility variation on the system frequency can well be described by the shift of peak frequency in Figs. 7, 8 and 9.

Figures 7, 8 and 9 show that when considering foundation flexibility variation (β 2/β 1), system frequency of flexible composite foundation is highly dependent on foundation flexibility variation (β 2/β 1). With foundation flexibility variation (β 2/β 1) decreasing, system frequency of flexible composite foundation will shift to lower frequency, and the shift value (relative to the system frequency of rigid–flexible composite foundation) is dependent on foundation flexibility variation (β 2/β 1). For η = 1/3, b/a = 0.75 and M b/M 0 = 2, when β 2/β 1 = 2/2, 3/3, 5/2, 100/2, the system frequencies are 0.733, 0.841, 0.921 and 0.976, respectively, while that of the homogenous flexible foundation model is 0.733 and that of the rigid–flexible composite foundation model is 0.976, and the shift value (relative to the system frequency of rigid–flexible composite foundation) are 0.243, 0.135, 0.055 and 0.000.

Foundation flexibility variation region (b/a) and structural stiffness (η) also influence the system frequency. When b/a increases, the system frequency will shift to higher frequency. For η = 1/3, M b/M 0 = 2 and β 2/β 1 = 3/2, when b/a = 0.25, 0.50 and 0.75, the system frequencies of flexible composite foundation are 0.789, 0.820 and 0.841, respectively. When structural stiffness (η) is very small, the effect of foundation flexibility variation (β 2/β 1) on system frequency is very little. For η = 1/12, b/a = 0.25 and M b/M 0 = 1, when β 2/β 1 = 2/2, 3/2, 5/2 and 100/2, the system frequencies are 0.255, 0.256, 0.257 and 0.257, respectively. However, as the structural stiffness (η) increases, the effect of foundation flexibility variation (β 2/β 1) on system frequency becomes large. For η = 1/3, b/a = 0.25 and M b/M 0 = 1, when β 2/β 1 = 2/2, 3/2, 5/2 and 100/2, the system frequencies are 0.857, 0.898, 0.922 and 0.936, respectively. From the two examples, it can be seen that for larger structural stiffness (η), the effect of foundation flexibility variation on system frequency will become larger.

5 Conclusion

This paper derived an analytical solution of a SDOF oscillator on a semi-circular flexible composite foundation in half-space for incident plane SH waves, and studied the effects of foundation flexibility variation on system response and system frequency. Some conclusions are as follows.

  1. 1.

    Foundation flexibility variation has strong effect on the effective input motion of the foundation to the structure, but has small effect on the peak of structural relative response. The peak and the frequency corresponding to the peak of the effective input motion are highly dependent on foundation flexibility variation. When foundation flexibility variation become larger, the peak of input motion will be smaller and the peak frequency will shift to higher frequency. The peaks of structural relative response correspond to different foundation flexibility variation have little different.

  2. 2.

    Foundation flexibility variation also has strong effect on system frequency. When foundation flexibility variation decreases, system frequency will shift to lower frequency, and the shift value (relative to the system frequency of rigid–flexible composite foundation) is also highly dependent on foundation flexibility variation.

  3. 3.

    The influence of foundation flexibility variation on system response is also dependent on structure stiffness. For larger structural stiffness, the influence of foundation flexibility variation on system frequency becomes larger.