Distributed information-based guidance of multiple mobile sensors for urban target search

Abstract

We present a framework for distributed mobile sensor guidance to locate and track a target inside an urban environment. Our approach leverages the communications between robots when a link is available, but it also allows them to act independently. Each robot actively seeks the target using information maximization. The robots are assumed to be capable of communicating with their peers within some distance radius, and the sensor payload of each robot is a camera modeled to have target detection errors of types I and II. Our contributions include an optimal information fusion algorithm for discrete distributions which allows each agent to combine its local information with that of its neighbors, and a path planner that uses the fused estimate and a recent coverage result for information maximization to guide the agents. We include simulations and laboratory experiments involving multiple robots searching for a moving target within model cities of different sizes.

1 Introduction

Many applications require time-efficient location of a target, and these tasks are made more difficult in urban environments. For example, Urban Search and Rescue (USAR) may be time-critical after a natural disaster or an accident calls for the rapid location of survivors (Tomić et al. 2012; Liu and Nejat 2013, 2015). Surveillance tasks are also examples of a search and tracking problem (Pennisi et al. 2015). While a single, autonomous agent can successfully locate a target, it has been shown that increasing the number of agents that participate in a distributed search task is always beneficial (Chung and Burdick 2008). In this work, we are concerned with the problem of locating a moving target inside an urban environment, using multiple Unmanned Aerial Vehicles (UAVs) equipped with camera sensors. We study the efficient distribution of search effort among the UAV platforms, which must also be capable of operating autonomously.

One of the challenges for multiple agent searching is the need for communication and coordination among them. A centralized structure with sufficient computing power can plan optimal paths, even though the search problem is known to be NP-hard (Trummel and Weisinger 1986). For example, sensor guidance can be posed in a game-theoretical context as a cooperative strategy if the sensor motions and measurements have a central processor (Choi and Lee 2015). The work of Haugen and Imsland (2016) plans the motions of fixed-wing UAVs with sensor payloads by using dynamic optimization of convex programs. Multiple target detection and tracking with a central planner is demonstrated in Dames et al. (2015), with an application of the Probability Hypothesis Density filter. When the targets to localize are static, the application of information-theoretical tools in a centralized motion planner for multiple sensors results in substantial gains over exhaustive coverage strategies (Charrow et al. 2015b). As the authors show in Hausman et al. (2015), if the communication topology among sensors can be controlled, it can be optimized to enhance the estimation of the location of the sensors and a target.

Optimal path planning becomes intractable as the number of agents and the complexity of the map increase. Furthermore, a centralized controller requires a fully connected network. Line of sight communications are difficult in urban canyons, and many tasks cannot assume the presence of communication networks. Alternatively, the search can be performed in a distributed manner if each agent has access to the target location estimates of one or more of its peers. However, if the communication network of the agents is not fully connected, they will not have shared access to a target location estimate. In Pimenta et al. (2009), the authors propose a distributed control framework to track an intruder while keeping coverage of the search area. An example of distributed estimation in urban environments is Dames et al. (2016), where teams of UAVs equipped with magnetometers use information gradients to locate ground targets.

Different methods have been proposed to address the problem of distributed data fusion. The average consensus algorithm is one of the most widespread (Olfati-Saber and Murray 2003; Moreau 2005). The nodes share a belief with certain neighbors. As long as the graph is connected, all of the agents will reach consensus as the average of the estimates. In Scoy et al. (2015), the average consensus algorithm is extended with local nonlinear oscillators to ensure that the estimator is robust to the initial internal node states. The framework in Atanasov et al. (2015) includes average consensus for particle filter estimators, with a distributed sensor guidance algorithm that uses the gradient of mutual information to locate a signal source. Instead of using information-based approaches to position mobile sensors, Kantaros and Zavlanos (2016) focuses on maximizing a sensor coverage cost function while optimizing the communication topology, with both alternating optimizations being performed in a distributed manner. An alternative approach is the channel filter. In this case, the nodes fuse their local estimates with those of their neighbors, but they have to remove shared information before the fusion to avoid overemphasizing their agreement (Ong et al. 2008). This mode of operation allows for asynchronous communications.

We propose a framework to allow a team of multiple agents to locate a target within an urban environment that does not assume full connectedness of the communication graph. This paper presents two major contributions to solve the afforementioned challenges. First, we propose a solution to the optimal information fusion problem for the case of two, one-dimensional, discrete probability mass functions (pmfs). We derive a closed-form equation that, given two pmfs, finds a third one that simultaneously minimizes the measurement space distance to both. This result removes the need to compute the information shared by two agents and allows for a straightforward combination of their beliefs.

Our second contribution builds on the availability of a local map and a local target position estimator per each agent, and formulates an information-based path planner that guides the target search. The planner is based on a recent result linking mutual information maximization to sensor coverage, which is used as part of a cost function that also includes a collision avoidance term.

The UAVs can operate independently in case of no communication and share information when it is available. In the case of full or guaranteed intermittent connectivity, their target position estimates will converge. This is supported by Monte Carlo analysis using different sets of communication distances and path planning lengths. We also include laboratory experiments using UAVs searching for a ground robot while running our algorithms in real time.

The rest of this paper is organized as follows. Sect. 2 presents background material relative to our estimator and map model. The algorithm applied for distributed target location estimation is described in Sect. 3. We then explain our approach to path planning in Sect. 4, after which Sect. 5 presents simulation and experimental results. Our conclusions and remarks are in Sect. 6.

2 Preliminaries

2.1 Particle filter estimator

The particle filter is an estimator that can be used in the case of nonlinear system dynamics and non-Gaussian process and measurement noise (Arulampalam et al. 2002). Let $\mathbf {x}_k$ denote the target state at time k. An initial estimate of the target state probability distribution function (pdf), $p(\mathbf {x}_0)$ may be arbitrarily chosen and is described by the set of N particles $\mathcal {X}=\{\mathbf {x}_0^i: i=1,\ldots ,N\}$, with associated weights $w_0^i$ such that $\sum _{i=1}^N w_k^i = 1$ at any time k. The particle filter follows a prediction-correction pattern similar to other schemes such as the Kalman filter. The state pdf at time k is approximated by a sum of delta functions

$$\begin{aligned} p \left( \mathbf {x}_{k} \right) \approx \sum _{i=1}^{N} w_k^i \delta (\mathbf {x}_{k}- \mathbf {x}_{k}^i) . \end{aligned}$$

(1)

The prediction step consists of propagating the particles forward in time according to the dynamic model, $\mathbf {x}^i_k = f_{k-1}(\mathbf {x}^i_{k-1},\mathbf {u}_{k-1})$. This yields the predicted state pdf, $p \left( \mathbf {x}_{k} \mid \mathbf {z}_{k-1} \right)$. When a measurement $\mathbf {z}_k$ is received, the state pdf is updated in the correction step

$$\begin{aligned} p \left( \mathbf {x}_{k} \mid \mathbf {z}_{k}\right) = \frac{p \left( \mathbf {z}_{k} \mid \mathbf {x}_{k}\right) p \left( \mathbf {x}_{k} \mid \mathbf {z}_{k-1}\right) }{p \left( \mathbf {z}_{k} \mid \mathbf {z}_{k-1}\right) } . \end{aligned}$$

(2)

The measurement likelihood function, $p \left( \mathbf {z}_{k} \mid \mathbf {x}_{k} \right)$, is used to update the particle weights according to Bayes’ Rule

$$\begin{aligned} w_k^i = \frac{w_{k-1}^i p \left( \mathbf {z}_{k} \mid \mathbf {x}_{k}^i\right) }{\sum _{j=1}^N w_{k-1}^j p \left( \mathbf {z}_{k} \mid \mathbf {x}_{k}^j\right) } . \end{aligned}$$

(3)

Over time, as more information about the target is gathered, many of the particles may have their weights drop down to or near zero. This means that the effective number of particles decreases, leading to a degeneration of the particle set. To cope with this phenomenon, various resampling techniques have been devised (Li et al. 2015). The resampling may be performed when the number of effective particles drops below a threshold by using an approximate metric

$$\begin{aligned} N_{eff} = \frac{1}{\sum _{i=1}^N w_k^{(i)}} \end{aligned}$$

(4)

although it can also be performed at every time step in what is known as systematic resampling, whenever the computation constraints allow it.

2.2 Urban map model

The urban environment can be modeled as a graph $\mathcal {M}=(V,E)$, where the set of vertices $V=\{1,\ldots ,n\}$ represents either one end of a road segment or an intersection of multiple roads, and the set of edges $E \subseteq V \times V$ represents road segments. The use of a directed graph allows us to represent one or two-way roads (Ramirez-Paredes et al. 2015).

In this context, the location of a vehicle can be represented as tuple $\theta = \{ e, p, v \}$, where e is an identifier for the edge where the vehicle is located, $p \in [0, 1]$ is the position of the vehicle relative along the length of the road segment, and $v \in \mathbb {R}$ is the velocity of the vehicle. We can always define a mapping $R: E \times [0,1] \times \mathbb {R} \mapsto \mathbb {R}^2 \times [-\pi ,\pi ] \times \mathbb {R}$ to change to a representation consisting of a location in $\mathbb {R}^2$, an orientation and a linear velocity, i.e., the current pose and velocity in the world. The target vehicle is modeled as having first-order kinematics with velocity saturation, such that it may follow a sequence of map graph nodes as waypoints, accelerating and stopping in a manner that resembles a car in a city environment.

Two examples of graph-based descriptions of urban environments are shown in Fig. 1. The square grid is used later in this text as a test environment for laboratory experiments involving multiple robots. The bottom graph represents a portion of downtown Dallas, TX. In both cases, the directions of the roads E are represented as arrows joining intersections, which are the nodes V.

Fig. 1

Two graphs representing urban environments. Top: a $5\times 5$ grid. Botton: a model of downtown Dallas, TX

3 Distributed target search and tracking

3.1 System overview

The agents (e.g., one or more UAVs) perform distributed data fusion, and each agent runs a particle filter estimator for the target location. The kinematic model for each UAV is based on the common first-order approximation for quadrotor helicopters. Each agent plans its movements using mutual information maximization between its sensor and the distribution of target locations based on its local estimator, and is capable of individually pursuing its goal. The path generation is based on the result from Ramirez-Paredes et al. (2016) linking sensor coverage to mutual information. The sensors are assumed to be capable of detecting their peers if within some distance radius, and each sensor is allowed to have target detection errors of types I and II. Our approach leverages available communications between the mobile sensor and also allows them to act independently. The information exchange lets the agents agree on an improved estimate of the target location distribution and continue their individual search. The agents can locate the target without communicating, but they will perform a more efficient search if the communication links exist at least occasionally.

A diagram of the control components of a single agent is shown in Fig. 2. Each agent is equipped with a camera for target detection, and it is capable of self localizing in a global frame. This can be accomplished by using a Global Positioning System (GPS) receiver, for example. The radio link can be used to transmit and receive both the estimates of the target location and the location of the agent in the global frame to other agents within a radius. Also included in the diagram are a path planning and a trajectory controller modules. The trajectory control can be achieved by a combination of autopilot module and waypoint navigation, while the path planner is described later in this text.

Fig. 2

Inner components of a single agent

We begin by formally establishing the set of agents as $N_A > 1$ identical UAVs equipped with electro-optical sensors capable of detecting a designated target. Let each agent be identified by an integer $i \in \{1,\ldots ,N_A\}$. The agents are connected in a communication network, represented by a digraph $G_c = (V_c,E_c)$, with $N_A$ vertices, where $V_c = \{1, \ldots , N_A\}$.

An example of a network configuration is illustrated in Fig. 3. Each UAV is considered a single agent, and two radii are associated with it. The first, $r_d$, is a communication radius. This indicates that any other agent within $r_d$ units will be able to exchange positions and beliefs with the agent being analyzed. Similarly, $r_c$ is a collision radius. Whenever two agents are closer than $r_c$ units of each other, a collision is considered imminent and must be avoided. In Fig. 3, agent 1 is disconnected from the others and gets no information from their estimators.

Fig. 3

A team of four UAVs, showing the communication radius $r_c$ and the collision avoidance radius $r_c$ for each

Consider the scenario where each agent i has a local particle filter estimator of the target location. Hence each agent maintains its own particle set $\theta (i), w(i)$, as covered in Sect. 2.1. Each particle is $\theta \in E \times [0,1] \times \mathbb {R}$. At any time instant, a particle set can be transferred from agent i to agent j if $(i,j) \in E$. Whenever unambiguous, we will drop the time index of the particles and weights to simplify notation. We could design the system such that only measurements are shared by the agents, but by exchanging particle sets they implicitly transmit their measurement history. Assuming that agent i is then provided with a copy of the particle set $[\theta (j), w(j)]$, we need an approach to compute $p(\theta (i) | \theta (j))$. Ideally, under the assumption that the measurements from each agent are independent,

$$\begin{aligned} p(\theta (i) | z(i) \cup z(j)) = \eta \frac{\displaystyle p(\theta (i) | z(i)) p(\theta (i) | z(j)) }{\displaystyle p(\theta (i) | z(i) \cap z(j)) } \end{aligned}$$

(5)

where $\eta$ is a normalization constant. The denominator of this expression is computed using a channel filter, the purpose of which is to compensate for duplicated information shared by agents i and j. Our choice to use a channel filter approximation comes from the work of Makarenko and Durrant-Whyte (2006), where the distributed data fusion architecture assumes that each and every node is an information fusor.

Depending on the estimator used, it may not be possible to properly construct a channel filter, which can then be substituted by an approximation, such as the covariance intersect algorithm (Julier and Uhlmann 1997; Franken and Hupper 2005). This requires pdfs that can be completely described by covariance matrices, which is not the case for the urban search scenarios discussed in this work. In our case, the particle filter allows us to construct a representation of the target pdf.

3.2 Optimal information fusion

We present a reliable and simpler alternative to approximate a channel filter. Since the channel filter is used to remove the common information between two nodes, an effective approximation has to achieve the same effect. The target pdf can be represented with varying degrees of precision by dividing each road segment into a set of discrete sections and formulating a normalized histogram. Taking this to an extreme, each road portion or graph edge can be represented by a single histogram bin. Let us define a function to retrieve the edge on which a particle travels $E_s(i,k) = \{e : \theta ^k(i) \in e\}$, where the superscript denotes the k-th particle in the set maintained by agent i. We can then construct a representation for the probability mass of edge e, as perceived by agent i

$$\begin{aligned} E_w(i,e) = \sum _{\displaystyle k : \theta ^k(i) \in e} w^k(i) . \end{aligned}$$

(6)

Thus, $E_w(i,e)$ constitutes a bin in the normalized histogram or pmf for agent i over E. When combining the information from agents i and j, we seek for a fused estimate of the target pmf, $\mathcal {F}$, that minimizes some metric between $\mathcal {F}$ and both $E_w(i,e)$ and $E_w(j,e)$ over E.

When comparing pdfs (or pmfs) p and q, it is commonly accepted to use the Kullback-Lieber divergence (KLD), given by

$$\begin{aligned} D(p||q) = \int p(x) \log \frac{p(x)}{q(x)} dx . \end{aligned}$$

This quantity is, however, not symmetrical and hence not a metric. An alternative metric is the Hellinger distance (Fannes and Spincemaille 2003), which is symmetrical, and its square has the important property of being the lower bound of the KLD, so $H^2 (p,q) \le D(p||q)$. In the context of describing metrics between discrete distributions, we will temporarily use the symbols i and j to enumerate their elements. The Hellinger distance is defined as

$$\begin{aligned} H(p,q) = \frac{1}{\sqrt{2}} \left[ \int \left( \sqrt{p(x)} - \sqrt{q(x)} \right) ^2 dx \right] ^{1/2} \end{aligned}$$

(7)

and for the discrete case as

$$\begin{aligned} H(p,q) = \frac{1}{\sqrt{2}} \left[ \sum _i \left( \sqrt{p(i)} - \sqrt{q(i)} \right) ^2 \right] ^{1/2} \end{aligned}$$

(8)

where the factor of $1/\sqrt{2}$ is used to normalize the distance in the interval [0, 1]. Taking the squared Hellinger distance and expanding the binomial expression for each term of the sum, an alternative form is

$$\begin{aligned} H^2(p,q) = 1 - \sum _i \sqrt{p(i) q(i)} \end{aligned}$$

(9)

where the sum term is called the affinity between distributions.

Let us define a metric to minimize in order to find the pmf r that results from the optimal fusion of p and q. A sensible choice based on (8) is

$$\begin{aligned} g(p,q,r)= & {} H^2(p,r) + H^2(q,r) \end{aligned}$$

(10)

$$\begin{aligned} g(p,q,r)= & {} 2 - \sum _i \sqrt{p(i)r(i)} - \sum _i \sqrt{q(i) r(i)} \end{aligned}$$

(11)

$$\begin{aligned}= & {} 2 - \sum _i \sqrt{r(i)} \left[ \sqrt{p(i)} + \sqrt{q(i)} \right] \end{aligned}$$

(12)

which adds the distances of some pmf r to both p and q.

Proposition 1

The optimal choice of r, which minimizes the sum of the squared Hellinger distances (10), is given by the element-wise function of p and q

$$\begin{aligned} r^* (i) = \frac{(\sqrt{p(i)}+\sqrt{q(i)})^2}{2 + 2 \sum _j \sqrt{p(j) q(j)}} . \end{aligned}$$

(13)

Proof

Finding the r that minimizes g(p, q, r) can be stated as an optimization problem.

$$\begin{aligned} \begin{aligned}&\underset{\displaystyle r}{\text {maximize}}&f(r) = \sum _i \sqrt{r(i)} [ \sqrt{p(i)} + \sqrt{q(i)} ] \\&\text {subject to}&\sum _i r(i) = 1 \\&0 \le r_i \le 1, ~~i=1, \ldots , n \end{aligned} \end{aligned}$$

(14)

The objective function, which consists of a sum of square roots, has a minimum at $r = 0$. Taking the gradient with respect to r gives

$$\begin{aligned} \frac{\partial f}{\partial r(i)} = \frac{\sqrt{p(i)} + \sqrt{q(i)}}{2 \sqrt{r(i)}} \end{aligned}$$

which has no critical points within the feasible set. An inspection of the components of the Hessian shows that

$$\begin{aligned} \frac{\partial ^2 f}{\partial r(j) \partial r(i)} = {\left\{ \begin{array}{ll} -\frac{\sqrt{p(i)}+\sqrt{q(i)}}{4 \sqrt{r(i)^3}} &{} \text{ if }~i=j \\ 0 &{} \text{ if } ~i \ne j \end{array}\right. } \end{aligned}$$

(15)

which indicates that f(r) is concave in $\mathbb {R}^n_{+}$, the positive real n-vectors.

Given that the arguments are all real in [0, 1], the extremum of (14) can be found using Lagrange multipliers. We will consider p, q as constant in this derivation. The Lagrangian is

$$\begin{aligned} \Lambda (r,\lambda ) = \sum _i \sqrt{r(i)} [ \sqrt{p(i)} + \sqrt{q(i)} ] - \lambda \left( \sum _i r(i) - 1 \right) \nonumber \\ \end{aligned}$$

(16)

Let us compute the derivative of (16) with respect to each r(i), and also with respect to $\lambda$, and equate them to zero.

$$\begin{aligned} \frac{\partial \Lambda }{\partial r(i)}&= \frac{\sqrt{p(i)} + \sqrt{q(i)}}{2 \sqrt{r(i)}} - \lambda = 0 \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial \Lambda }{\partial \lambda }&= 1 - \sum _i r(i) = 0 \end{aligned}$$

(18)

Then we arrange all of the equations involving $\lambda$ as a series of equalities, and square them.

$$\begin{aligned} \frac{\sqrt{p(1)}+\sqrt{q(1)}}{2 \sqrt{r(1)}}&= \frac{\sqrt{p(2)}+\sqrt{q(2)}}{2 \sqrt{r(2)}}\nonumber \\&= \cdots = \frac{\sqrt{p(n)}+\sqrt{q(n)}}{2 \sqrt{r(n)}} \end{aligned}$$

(19)

$$\begin{aligned} \frac{(\sqrt{p(1)}+\sqrt{q(1)})^2}{4 r(1)}&= \frac{(\sqrt{p(2)}+\sqrt{q(2)})^2}{4 r(2)} \nonumber \\&= \cdots = \frac{(\sqrt{p(n)}+\sqrt{q(n)})^2}{4 r(n)} \end{aligned}$$

(20)

Here n is the total number of elements for each pmf. The common factor of 1 / 4 can be removed. At this point, it is convenient to define the shorthand $l_i = (\sqrt{p(i)}+\sqrt{q(i)})^2$. The quantity $l_i=0$ iff both $p(i)=q(i)=0$. From (10), it is clear that in this case any choice of r(i) results in zero contribution to the distance computation.

Taking pairs of equations from (20), we can use the following relationships to find the solution to the system formed by (17) and (18).

$$\begin{aligned} l_2 r(1)&= l_1 r(2) \nonumber \\ l_3 r(2)&= l_2 r(3) \nonumber \\&\vdots \nonumber \\ l_{n} r(n-1)&= l_{n-1} r(n) \end{aligned}$$

(21)

These can be condensed along with (18) in a single matrix equation.

$$\begin{aligned} \begin{bmatrix} l_2&\quad -l_1&\quad 0&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad l_3&\quad -l_2&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad 0&\quad l_4&\quad -l_3&\quad \cdots&\quad 0 \\&\quad&\quad \vdots&\quad&\quad \ddots&\quad \vdots \\ 0&\quad 0&\quad 0&\quad 0&\quad \cdots&\quad -l_{n-1} \\ 1&\quad 1&\quad 1&\quad 1&\quad \cdots&\quad 1 \end{bmatrix} r = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix} \end{aligned}$$

(22)

Assuming the left-hand $n \times n$ matrix is full rank, the solution can be found using Gaussian elimination as

$$\begin{aligned} r(i)&= \frac{l_i}{\sum _j l_j} = \frac{(\sqrt{p(i)}+\sqrt{q(i)})^2}{\sum _j (\sqrt{p(j)}+\sqrt{q(j)})^2} \nonumber \\&= \frac{(\sqrt{p(i)}+\sqrt{q(i)})^2}{\sum _j \left( p(j)+q(j)+2 \sqrt{p(j) q(j)} \right) } \end{aligned}$$

(23)

and we reach the stationary point of (16), $r^*$.

The special case of $l_i=0$ for some i can be handled by carefully selecting the pairs of equations from (21), i.e., taking care not to choose a pair $l_i r(j) = l_j r(i)$ where $l_i=l_j=0$, but either can be zero. That makes the matrix full rank since, with the exception of its last row, it is upper triangular with non-zero elements along the diagonal.

If $l_i=0 ~~ \forall ~~ i$, then $p=q=0$ and $r^*=0$ by definition. $\square$

Furthermore, we can get bounds on (10). First, by being the sum of two squared Hellinger distances, the absolute bounds on (10) for arbitrary r are

$$\begin{aligned} 0 \le g(p,q,r) \le 2 . \end{aligned}$$

(24)

Let us now state the bounds for using the optimal r.

Proposition 2

By computing the optimal distribution $r^*$ with (13), the sum of the squared Hellinger distances (10) is bounded by

$$\begin{aligned} 0 \le g(p,q,r^*) \le 2 - \sqrt{2}. \end{aligned}$$

(25)

Proof

We can get bounds for (10) for $r^*$ by first substituting (13) in (10)

$$\begin{aligned} g(p,q,r^*) = 2 - \frac{2 + 2 \sum _i \sqrt{p(i)q(i)}}{\sqrt{2+2\sum _j \sqrt{p(j)q(j)}}} \end{aligned}$$

(26)

and then considering the extrema of the affinity term for p and q, which are $\{0, 1\}$. $\square$

Using Proposition 1, we can compute the distribution that optimally fuses the information from two nodes. Let us call this optimal fusion $\mathcal {F}$, distributed over E. Then, for agents i and j, the fusion for edge e is given by

$$\begin{aligned} \mathcal {F}(i, j, e) = \frac{E_w(i,e) + E_w(j,e) + 2\sqrt{E_w(i,e) E_w(j,e)}}{2 + 2\sum _{e \in E} \sqrt{E_w(i,e) E_w(j,e)}}\nonumber \\ \end{aligned}$$

(27)

and the data fusion step for agent i incorporating the information from agent j is an update of the weight of the k-th particle

$$\begin{aligned} w^k(i)|\theta (j) \leftarrow w^k(i) \frac{\displaystyle \mathcal {F}(i, j, E_s(i,k))}{\displaystyle E_w(i, E_s(i,k))} . \end{aligned}$$

(28)

The denominator is the sum of the particle weights in the edge that contains particle $w^k(i)$. This division ensures that the weights of the particles on edge $E_s(i,k)$ add up to the new weight from the fusion step with agent j, $\mathcal {F}(i,j,E_s(i,k))$.

3.3 Distributed estimation convergence

A condition for distributed estimation is the existence of a connected communication network graph among the agents. Otherwise, there would be no information exchange among them. When the communication distance between agents is limited but they still are expected to periodically exchange information, we can refer to a result from the random networks and distributed data fusion literature in order to discuss connectivity. A random graph G has a set $V=\{1,\ldots ,n\}$ of vertices, and a probability p that determines the existence of edge (i, j), $i\ne j$. These parameters define the sample space of all random graphs, which is denoted by $\mathcal {G}(n,p)$. The union of two graphs that have the same vertex set V is the graph $G_1 \cup G_2 = (V, E_1 \cup E_2)$. The graphs G and $G_i$ are not to be confused with $\mathcal {M}$, which represents the urban map.

Let us first review a lemma from (Hatano and Mesbahi 2005).

Lemma 1

Consider the sequence of random graphs $G_k \in \mathcal {G}(n,p)$, with $k = \{1,2,\ldots \}$. Then, if $k \rightarrow \infty$, $\cup _k G_k$ is connected w.p.1.

The proof is brief and comes from noting that the probability of existence of edge (i, j) is p for any $G_k$, so the probability of two vertices not being connected in $\cup _k G_k$ is $\lim _{k\rightarrow \infty }(1-p)^k = 0$. In the case of multiple agents that have communication links as in our system, most of the time the network graph L is $K_n$, the complete graph on n vertices. There is a probability $1-p$ of having a broken link, but we may not have information to determine p. Lemma 1 helps us ensure that the information about the target will get disseminated among the agents w.p.1.

It is also useful to consider the communication topology as a random network because in real implementations it would be considerably difficult to guarantee a complete or even connected graph at a given time instant $t_f$. Consider agent i simultaneously receiving measurements from its m neighbors $d_1 \dots d_m$ at time $t_f$. These measurements will normally be processed asynchronously, resulting in a sequence of subgraphs of G given by $G_{t_f + \Delta t} = (V, (i,j))$, with $j \in d_1 \dots d_m$, and $\Delta t$ is some random delay will be introduced to the reception of each measurement. The asynchronous nature of the measurement processing makes it necessary for the nodes to perform a local filtering of the common information between their estimates and those from their neighbors.

We now present a proposition regarding the convergence of the distributed estimation approach from the previous section, under the assumption that the communication graph is connected.

Proposition 3

Consider an undirected communication network $G_c = (V_c, E_c)$ established among the agents, such that $|V_c|=N_A$. Assume that $G_c$ is connected. Define, per agent i, a local estimate of the probability weights assigned to each edge $e_1, e_2, \ldots , e_{|E|} \in E$ denoted as a vector

$$\begin{aligned} \mathcal {E}_i = [E_w(i,e_1) ~ E_w(i,e_2), ~\ldots , ~E_w(i, e_{|E|})]^T . \end{aligned}$$

Then define the fusion process as a per-element substitution operating on two agents that exchange estimates, so $E_w(i,e) \leftarrow F(i,j,e), E_w(j,e) \leftarrow F(i,j,e) ~ \forall ~e \in E$. Let us denote this process as $\mathcal {E}_i \rightleftarrows \mathcal {E}_j$. Consider a time index to indicate the local estimate of edge probabilities for agent i at time k, as in $\mathcal {E}_i(k)$. The total disagreement among all agents at time k can be expressed as

$$\begin{aligned} \Delta (k) = \sum _{i=1}^{N_A} \sum _{j=1}^{N_A} H^2 (\mathcal {E}_i(k), \mathcal {E}_j(k)) . \end{aligned}$$

Under the conditions above,

$$\begin{aligned} \mathcal {E}_i(k-1) \rightleftarrows \mathcal {E}_j(k-1)&\implies \mathcal {E}_i(k) \equiv \mathcal {E}_j(k) \\&\implies \Delta (k-1) > \Delta (k) \end{aligned}$$

such that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Delta (k) = 0 \end{aligned}$$

Proof

By definition, for two identical pmfs the value of (8) is zero. We have defined the fusion operation as a substitution of two fused pmfs with the best approximation to them both, using (13). For a connected graph, it follows by inspection that at least one term of the sum in $\Delta (k)$ will become zero after the fusion is applied at time $k-1$. The number of zero terms in $\Delta (k)$ can only increase as time progresses. The requirement that the graph is connected guarantees that all terms of $\Delta (k)$ eventually become zero. $\square$

If the communication network is strictly connected at all times, the number of iterations for convergence of this discrete-time data fusion is, in the worst case, equal to the number of edges in the connected graph $G_c$.

4 Information-based path planning

Using a graph as the road network representation enables the use of well-established graph search algorithms. One notable example is the shortest paths algorithm by Dijkstra (Dijkstra 1959). In graph theory, a path is an alternating sequence of vertices and edges in which (a) each edge is incident with the vertex that precedes it and the vertex that follows it, and (b) all edges and vertices are distinct, with the possible exception of the first and last ones. The particle weights can be used to compute an edge traversal cost to guide the UAVs in their search for the target over some path. The planning horizon can be specified according to the application.

The objective of our path planner is to guide the agents such that the mutual information between their sensors and the target pdf is maximized, while the search effort is efficiently distributed. One additional challenge that our work addresses is intermittent connectivity of the communication network $G_c$. We require the agents to be able to work in isolation if the connectivity of $G_c$ is compromised, and to be able to resume working as a team once $G_c$ becomes connected.

In order to achieve this distributed planning, each agent uses its own estimate of the target pdf $p(\theta )$, which may include information fused from other agents, and plans its own path. The local planner also needs the location of the other agents in order to trace a path that does not overlap with them. When the planner has no knowledge of the locations of other agents, collisions are avoided when they are within sensing range, defined by the collision radius. The emergent behavior of the system distributes the search effort if communications are available.

4.1 Mutual information maximization and sensor coverage

The objective of the path planning algorithm is to maximize the mutual information (MI) between the sensors and the target. The larger this quantity is, the more knowledge about the target location we can extract from the sensor data. The MI is commonly defined in terms of the information entropy. For a certain continuous random variable $\varTheta$ defined in a domain $\varOmega$, its differential entropy is given by

$$\begin{aligned} h(\varTheta ) = - \int _\varOmega p(\theta ) \ln p(\theta ) d\theta . \end{aligned}$$

Using this definition, we can introduce the MI in terms of the conditional distribution $p(\theta | Z)$ after a measurement Z is acquired.

$$\begin{aligned} I(\varTheta ;Z) = h(\varTheta ) - h(\varTheta |Z) . \end{aligned}$$

Computing $I(\varTheta ;Z)$ can be difficult, and many works in the literature resort to the information gradient instead, so under the common first-order dynamics assumption for a hypothetical mobile sensor the control law

$$\begin{aligned} \mathbf {u} = \zeta \frac{\partial I}{\partial \theta } \end{aligned}$$

(29)

with $\zeta > 0$ would guide the sensor in the most informative direction (Hoffmann and Tomlin 2010; Ryan and Hendrick 2010; Julian et al. 2012). This has also been referred to as myopic search given the very limited horizon employed (Charrow et al. 2015a).

A recent work by our group has found a simple solution to compute the points that maximize MI for a class of binary sensors, which can detect a target once it falls inside a region of coverage (Ramirez-Paredes et al. 2016). A notable example of this sensor class are surveillance cameras.

The sensors under consideration are modeled as capable of giving misreports, also known as Type I (false positive) and II (false negative) errors. A binary sensor covers a region S of the search domain $\varOmega$. Defining the probability of a Type I error as $\alpha$ and that of a Type II error as $\beta$, we have

$$\begin{aligned} p(z=1|\theta \notin S)&= \alpha \end{aligned}$$

(30)

$$\begin{aligned} p(z=0|\theta \in S)&= \beta \end{aligned}$$

(31)

$$\begin{aligned} p(z=0|\theta \notin S)&= 1- \alpha \end{aligned}$$

(32)

$$\begin{aligned} p(z=1|\theta \in S)&= 1 - \beta \end{aligned}$$

(33)

as the detection probabilities for a given target position $\theta$.

The connection between sensor coverage and MI maximization requires the definition of an auxiliary function, C(S).

$$\begin{aligned} C(S) = \int _S p(\theta ) d \theta \end{aligned}$$

(34)

The main result from Ramirez-Paredes et al. (2016) is the following proposition that links sensor coverage to MI maximization.

Proposition 4

(Ramirez-Paredes et al. (2016)) For a binary sensor satisfying (30) to (33), the value of C(S) that maximizes $I(\varTheta ; Z)$ is

$$\begin{aligned} C_{opt} = \frac{1-\alpha (\gamma +1)}{(1 -\alpha - \beta ) (\gamma + 1)} \end{aligned}$$

(35)

where the constant $\gamma$ is defined as

$$\begin{aligned} \gamma = \left[ \frac{\alpha ^\alpha (1-\alpha )^{(1-\alpha )}}{\beta ^\beta (1-\beta )^{(1-\beta )}} \right] ^{\frac{1}{1-\alpha -\beta }} . \end{aligned}$$

(36)

We apply this result to our path planner by making the sensor coverage of each UAV a part of its cost function. Since $C_{opt}$ is always known, we can define a per-edge information cost for the path planner.

$$\begin{aligned} \mathcal {I}_e = \left| \sum _{k: \theta ^k\in e} w^k - C_{opt} \right| \end{aligned}$$

(37)

4.2 Collision avoidance

To avoid inter-agent collisions, we propose a cost-based approach to bias the path planning stage. Assuming that each agent knows the positions of the others, the planner can assign a large cost to any graph edge that contains an agent, thus deviating the path from collisions.

For all agents flying at approximately the same altitude, we can simplify the collision avoidance by considering the configuration space as a subset of $\mathbb {R}^2$. We denote the position of agent i in the global frame as $\xi _i$. Then, for each agent i, a ball of collision $\mathcal {B}(\xi _i, r_c^i) \subset \mathbb {R}^2$ is an open set centered at the position of agent i.

With these definitions in place, we can proceed to present a cost function for each edge to be traversed by an agent.

$$\begin{aligned} \kappa _e = {\left\{ \begin{array}{ll} c &{} \bigcup _{i=1}^N \left[ e \cap \mathcal {B}(\xi _i, r_c^i) \right] \ne \emptyset \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(38)

The constant c can be arbitrarily large, but as a minimum $c > \mathcal {I}_e ~~ \forall ~ e$.

Even under this scheme, the lowest cost path for a given agent may guide it to collide in the presence of a large number of agents on the graph, depending on the scale of the road network. For those situations, and considering the extra degree of freedom that altitude provides, a natural approach is to vary the height at which each agent moves. The agents start climbing or descending to their designated collision-avoidance altitudes whenever another agent moves within a safety radius.

4.3 Unified path planning and collision avoidance

We can now combine the previous expressions for edge cost in a single procedure that simultaneously guides the agents to informative locations while avoiding collisions. This can be expressed as an optimization problem, where the objective is to find some set of map edges and vertices $\mathcal {P} \subset \mathcal {M}$, such that the edges of $\mathcal {P}$ minimize a joint information and collision cost

$$\begin{aligned} \begin{aligned}&\underset{\mathcal {P}}{\text {minimize}}&\sum _{e \in \mathcal {P}} \left( \kappa _e + \mathcal {I} _e \right) \\&\text {subject to}&\mathcal {P} ~~ \text {forms a path}. \\ \end{aligned} \end{aligned}$$

(39)

Under no communication, collisions are possible since $\kappa _e = 0 ~ \forall ~ e$. Hence we assume that an agent can detect others that are within its collision radius. Having all of the edge costs, Dijkstra’s algorithm is applied at each iteration to compute the path that solves (39). This choice of algorithm is driven by the availability of fast implementations.

5 Results

5.1 Simulations

Monte Carlo simulations were used to evaluate the performance of our approach. The simulator was developed using the Robot Operating System (ROS). To simulate changing communication network topologies due to the environment, we used different communication radii for the agents. We get the fully connected case by increasing the radius to be larger than the size of the map. We used a scaled-down map of downtown Dallas, Texas, USA for the evaluation, as in Fig. 1. The original size of the region is approximately $800\times 500$ m. The scale used was 1:20.

We modeled four quad-rotor helicopters carrying monocular cameras to search for a single moving target. Each camera had false positive and negative detection probabilities of $\alpha =0.01$ and $\beta =0.05$. The target is modeled by a differential drive robot that follows the directions of the roads and chooses a new road at random at each intersection, with uniform probability. The target is not allowed to return if it was traversing a one-way road. The starting location of the target was randomized at the beginning of each simulation, always within the urban map. The linear velocity of the target reached a maximum of 0.2 m/s.

The initial location of the agents for every simulation was fixed at opposite corners of the map. The maximum linear velocity of each agent was set at 0.5 m/s. All agents know the street map and their own location on the map. Each agent employs a local particle filter using 4000 particles. We had scenarios with 2, 4 and 6 agents searching for the target. The communication distances used in the simulations were 5, 20 and 100% of the map size, and the planning lengths were 1, 3 and 5 map edges ahead. Additionally, we present the results of a naive search, in which the agents choose the road sections to explore at random with equal probability, without making use of the target location estimation or exchanging any information other than for collision avoidance purposes. This random search can be used to illustrate the effect of simply adding more agents to the search, and provides a baseline for comparison. We ran 120 trials for each choice of number of agents, communication distance and path planning length, including the random searches, totaling 30 combinations.

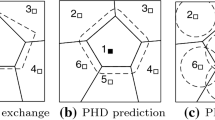
Figure 4 shows the simulation environment, as understood by Agent 1. In this example, the communication network is complete, and all of the agents are aware of the positions of other agents and exchange particle sets. Lines represent streets, and tall buildings are assumed to prevent the target or agent from moving off the streets. The red rectangle represents the ground region covered by the on-board camera. The red circles signal the collision prevention regions of the other agents, in case they come in close proximity. We used a 5 m radius. The green path indicates the roads which the planner has selected as the best route for Agent 1. The cyan dots represent particles with low weights, while the magenta dots are the particles with higher weights. Thus, the magenta regions have a higher probability of containing the target. A general view of the path planners and the estimators for the 4 agent case can be seen in Fig. 5. The four plots depict the same instant in time. A comparison of the particle sets of each estimator reveals that they have reached an approximate consensus. A perspective view of the simulation environment is shown in Fig. 6.

Fig. 4

Urban map overlaid with different markers, corresponding to several aspects of the internal target position estimator for Agent 1

Fig. 5

Visualization of the path planners and target location estimators for the four agents case in the search task

Fig. 6

Visualization of the simulation environment with four quadrotor helicopters present. The target is the red ground robot (Color figure online)

We present statistics for the target acquisition time corresponding to different parameter selection in Fig. 7. For each combination of communication distance and planning horizon, the 0.25, 0.5 and 0.75 quantiles are plotted in standard box format. The 0.5 quantile or median is shown as the horizontal line amidst the box for each configuration. The top and bottom of the boxes are the 0.25 and 0.75 quantiles. The whisker markers indicate the range of the measurements. The labels on the x axis indicate the planning horizon P, or the special case of a random search, denoted by the letter R.

The color of the boxes indicates the communication distance used, where blue is 5%, green is 50% and red is 100% of the map size. As the communication and planning distances increase, a general trend in acquisition time reduction can be noticed in the different boxes. Including a comparison of our scheme with the random searches is useful to discern between the time reduction due to the different communication distances and planning lengths, and the effect of simply adding more agents to the task. These comparisons further demonstrate the advantages of having agents that can plan and communicate their internal estimator states.

Fig. 7

Quantiles for the acquisition times of different communication distances and planning horizons for the agents. The box colors denote the communication distance between agents as a percentage of the map size. The horizontal axis labels denote the planning path length, as a number of map edges. The special cases of yellow boxes with the label ’R’ denote a random search, with no communication among robots. We present results for the 2, 4 and 6 agents cases (Color figure online)

5.2 Statistical analysis

Although the results presented so far are compelling, a rigorous analysis provides insight about the effect that each choice of parameters (communication distance, planning path length, the number of agents) has on the time to acquire the target. This can be achieved by the application of hypothesis testing. The results of such tests indicate which choices of simulation parameters are significantly better.

Our sets of simulations constitute samples from a random process, with unmodeled probability distributions. The Kolmogorov-Smirnov (KS) test can be used to determine the goodness of fit for a certain distribution with respect to a sample. We tried fitting our simulation data to exponential and geometric distribution models, under the reasoning that the time to capture a target can be thought of as a series of failing Bernoulli trials until a success occurs. The null hypothesis for the KS test is that the sample corresponds to the distribution with the specified parameters. However, this hypothesis was rejected for our data for both the exponential and geometric models at a 5% significance level.

When performing hypothesis testing, it is possible to choose either parametric or non-parametric tests depending on the underlying distribution of the data. Given that our data is not normally distributed, there is no strong indication that parametric tests will be inherently better. Under this reasoning, we will present the results from a non-parametric test.

The non-parametric test is the Wilcoxon rank sum test (Wilcoxon et al. 1970), which can determine whether two samples come from the same distribution. We would like to know if two sets of our simulations take a significantly different amount of time to capture the target. In particular, if a certain selection of communication radius and planning horizon is faster than another. This test uses the median of the data.

Fig. 8

Results for the statistical analysis of our simulations. The labels denote the number of agents used after the letter A, the communication radius as a percentage of the map size after the letter D, and the planning path length as map edges after the letter P. The $(\circ )$ symbol indicates that the null hypothesis is rejected at a 5% significance level, meaning that the parameters from a certain row cause the target acquisition to take significantly longer than the parameters from the corresponding column. On the other hand, the $(\cdot )$ symbol indicates that the null hypothesis cannot be rejected

The null hypothesis $H_0:t^i \le t^j$ refers to the situation in which sample i contains smaller or equal target acquisition times than sample j, in general. Note that this is a one-tailed test since our intention is to confirm if a given set of simulation parameters is strictly faster to acquire the target than another, hence the null hypothesis is not an equality condition. The alternative hypothesis $H_1:t^i > t^j$ is that sample j contains significantly shorter acquisition times than sample i.

We used a p-value of 0.05 for our hypothesis tests. Since we have 30 different sets of parameters to compare, resulting in $30^2$ tests, we do not present the results as a table. Instead, we show for which pairs of parameter sets the Wilcoxon rank sum test rejects the null hypothesis for the chosen p-value. The results are shown in Fig. 8. The rejection of the null hypothesis is denoted by a $(\circ )$ symbol, whereas a failure to reject $H_0$ is denoted by $(\cdot )$.

Fig. 9

Two miniature UAVs equipped with cameras search for a moving target, represented by a ground robot. The grid illustrates the city map used by the robots

Fig. 10

Two agents searching for a moving target inside a grid map, with a communication radius that exceeded the size of the map. The target acquisition times for these experiments were, from top to bottom: 28.19, 47.90 and 78.57 s

There are several text labels associated with the data. The letter A represents the number of agents used for those trials. The letter D is the percentage of the map size that corresponds to the communication range of the agents, and the letter P is the number of map edges used by each agent for planning its path. The random searches are denoted as A2Rand, A4Rand and A6Rand for the 2, 4 and 6 agent cases, respectively. Thus, for some row i and column j of Fig. 8, finding a $(\circ )$ symbol at their intersection means that $H_1:t^i > t^j$ is accepted and the parameter selection of column j is significanly faster than that of row i.

We can find an overall trend in Fig. 8 that signals faster target acquisition times as the communication distance, path planning horizon and number of agents increase. However, we cannot claim that these increases result in improvements for all cases. For example, the parameter selection A6D100P5 outperforms most other selections, but it is not significantly better than A6D20P1. It seems that as the number of agents is increased, the benefit from increasing communication distances becomes less important, which may come from the role that the map size plays in the target acquisition times.

Fig. 11

Experiments with the agents limited to communicate within a 1.5 m radius. Their capture times, from top to bottom: 21.50, 46.51 and 23.05 s

5.3 Laboratory experiments

Our distributed estimation algorithm was tested inside a laboratory environment, using two agents to search for a moving target. The scenario was a $5 \times 5$ grid, representing an urban environment. Each square was 0.75 m per side. The target was a Pioneer 3DX ground robot, traversing the simulated streets at a maximum linear velocity of 0.2 m/s. Each time the ground robot reached an intersection, it took one of the allowable road at random with uniform probability.

The agents were two AR Drone 2.0 UAVs, equipped with downward-facing cameras. The false positive and negative probabilities for the target detector were experimentally determined to be $\alpha =0.0247$ and $\beta =0.2304$, and the local estimators for each agent used 4000 particles. As in the simulations, the maximum linear velocity of the agents was limited to 0.5 m/s. The motion of all robots was recorded using a Vicon capture system. Although all of the guidance and control algorithms were being executed in the same computer, the path planners for the UAVs did not have access to the pose information for the ground robot. The target search was purely based on the camera feedback from the UAVs. Two instances of the path planner were running in parallel, connected to a single UAV each. These instances could communicate but did not have direct access to the target location estimate of the other. Each path planner transmitted its local particle set at 4 Hz. Figure 9 shows our UAVs pursuing a target inside the laboratory. The ground robot can be seen moving on top of the simulated roads, while the UAVs are executing the search task.

We present two sets of experiments. The first three, represented by Fig. 10, used a complete graph for communications. These trials took different acquisition times to locate the target, but they all end in capture. The path followed by the target is depicted in green. The position of the first agent over time is the bold red curve, while the blue curve corresponds to the motion of the second agent. In all cases, the starting position of a robot is marked by a ($\mathbf {\times }$) symbol, while the final position is indicated by ($\mathbf {\star }$).

The second set of experiments, illustrated in Fig. 11, were executed with the agents being restricted in their communication radii. They exchanged beliefs only when they became closer than 1.5 m (i.e., two edge lengths). The target was located even though the agents were mostly working independently.

In the laboratory environment we encountered results that were not as uniform as those in presented in the simulation section. An inspection of the target acquisition times from the experiments in Figs. 10, 11 does not show gains from increasing the communication radius. In all cases, the UAVs found the target, whether by communicating their particle sets or acting almost fully independently. This is indicative of the robustness of our approach to disruptions in the communication network of the agents.

6 Conclusions

The use of multiple agents to search for a target presents a series of challenges in order to coordinate them and to distribute the search effort efficiently. The approach presented in this work focuses on enabling each agent to search for the target in an individual manner, while also letting them leverage any information that the other agents may share with them. Since the map representation is a graph, with the edges corresponding to road segments, we propose to consider each edge as a bin in a histogram, and as such, construct an implementation of the channel filter well suited for a particle filter estimator. Of course, finer partitions of the edges would be possible, making it a design choice.

We present an algorithm that uses the entirety of each edge as a histogram bin, and which updates the weights of the local particles with the information shared by the other agents as their particle sets. The information-based path planner that each agent uses generates routes over the road network based on the local estimator, which may include information fused from other nodes or not. When said information from other agents is available, the planner will avoid repeated exploration of areas already covered since the probability mass contained in them is far from the optimum.

Simulations and experiments indicate the performance of this approach. The agents successfully completed their search tasks under different communication distance conditions, both in simulation and laboratory experiments. However, it is only with persistent communication that the agent behaviors indicate cooperation, since they avoid regions that others have explored and concentrate on more informative areas.