Abstract
Classifying objects in complex unknown environments is a challenging problem in robotics and is fundamental in many applications. Modern sensors and sophisticated perception algorithms extract rich 3D textured information, but are limited to the data that are collected from a given location or path. We are interested in closing the loop around perception and planning, in particular to plan paths for better perceptual data, and focus on the problem of planning scanning sequences to improve object classification from range data. We formulate a novel time-constrained active classification problem and propose solution algorithms that employ a variation of Monte Carlo tree search to plan non-myopically. Our algorithms use a particle filter combined with Gaussian process regression to estimate joint distributions of object class and pose. This estimator is used in planning to generate a probabilistic belief about the state of objects in a scene, and also to generate beliefs for predicted sensor observations from future viewpoints. These predictions consider occlusions arising from predicted object positions and shapes. We evaluate our algorithms in simulation, in comparison to passive and greedy strategies. We also describe similar experiments where the algorithms are implemented online, using a mobile ground robot in a farm environment. Results indicate that our non-myopic approach outperforms both passive and myopic strategies, and clearly show the benefit of active perception for outdoor object classification.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Information gathering is an important family of tasks for outdoor robots that is central to a wide variety of applications including agriculture, environmental monitoring, mining, defence, surveillance, and disaster management. Many information gathering tasks, such as searching (Gan et al. 2014), localising (Cliff et al. 2015), and tracking (Xu et al. 2013), naturally involve a planning component that seeks to choose future observation locations in order to maximise an information-theoretic objective. Object segmentation and classification, however, is traditionally cast as a passive perception problem where data are generated as part of a disconnected navigation process and fed into a perception processing pipeline. This paper advocates an active approach for outdoor object classification, and attempts to close the loop around planning and perception in this context.
Object recognition is fundamental to the general application of outdoor robots. Manipulation tasks require the robot to identify and localise objects of interest among many other objects present in the natural world. Non-manipulation tasks, such as semantic mapping, also require the robot to identify the class and pose of objects in order to perform useful work outdoors. A good example is agricultural robotics, where object recognition is applied in autonomous crop surveillance (Hung et al. 2013), weeding (Underwood et al. 2015), and harvesting (Bac et al. 2014).
Outdoor environments are challenging for robots because they comprise complex 3D geometry, usually with little high-level structure. Robots often rely on data from range sensors to perceive this complex geometry. The problem of how to collect range data from such sensors is vital to the accuracy and efficiency of identifying objects. In this situation, choosing the proper viewpoint of the robot is key to perception quality because data from these sensors is highly viewpoint dependent; variation in the position and orientation of the sensor relative to the environment can result in large changes in the distribution of 3D points in the scene. Achieving high-quality perception is therefore strongly coupled to planning robot motion, and there is exciting potential to dramatically improve the quality of outdoor object classification through an active perception approach.
In this paper, we focus on the problem of planning scanning sequences to improve estimates of object class labels from 3D laser scans. We are interested in unknown outdoor scenes which are cluttered and potentially large. One immediate challenge is how to quantify the benefit of any active approach to this problem, in comparison to passive perception, in a meaningful way. An active approach may perform better simply due to more available observations. Moreover, there is an inherent exploration/exploitation trade-off between covering a large area (exploration) and improving semantic understanding (exploitation).
Our idea is to both disentangle the exploration problem and to construct a fair comparison by proposing a problem formulation based on a resource-budgeted goal. We call this the time-constrained active object classification problem. The robot must navigate to a given location in its workspace in a specified time or distance while making high-value observations. This formulation is strongly motivated by many applications, such as agriculture, where a natural roadmap exists from which the robot may deviate in order to improve perception, and where resource constraints could necessitate refuelling at a known location. It is also then possible to compare to passive strategies given the same budget.
Solving this problem involves two main technical challenges. First, it is necessary to consider planning and perception algorithms in an integrated manner. In order for planning and perception to operate in a closed loop, planning algorithms must be efficient enough to operate online while considering many possible viewpoints with uncertain utility, in addition to traditional geometric path planning. Perception algorithms must provide a principled estimate of such utility, also online, while considering occlusions and possibly sparse training data. Second, evaluation necessarily involves online experiments with real robots. Simulation is limited in its ability to accurately model sensor noise and control uncertainty that affect the quality of data in real robot systems. Thus, algorithmic challenges are supplemented by systems challenges in performing experimental evaluation.
Our approach is to plan observation sequences using Monte Carlo methods coupled with a classifier based on non-parametric Bayesian regression. We assume a set of known objects and attempt to recognise them in an outdoor scene, while obeying the time/distance constraint. We present a novel planning algorithm, Monte Carlo active perception (MCAP), that chooses viewpoints by considering information gain, travel cost, time/distance budget, and goal location. MCAP is non-myopic in that it simulates full paths to the goal with Monte Carlo rollouts, and combines the information gained from these different paths. We treat the class and pose of objects as partially observable states, and maintain state estimates as joint probability distributions. The process of predicting future observations considers occlusions by generating simulated point clouds based on the current object beliefs. It makes no other assumptions about objects (e.g., touching or stacked), only that samples from their probability distributions can be obtained. MCAP is an any-time algorithm and will continue to operate until a given computation limit is exceeded. Although we present the algorithm in a replanning context, where a new plan is generated following each sensor observation, it can also be used to plan full sequences of observations if desired.
The information gain evaluation in MCAP is assumed to be provided by a separate algorithm. Here, we present a novel algorithm for jointly estimating object class and pose that learns global feature vectors using Gaussian process (GP) regression combined with a particle filter estimation framework. The particle filter maintains a joint distribution, represented as a collection of particles, for each observed point cloud segment. Mutual information is computed using the particle estimate based on expected observations.
We show that MCAP converges to the optimal value function in the limit, and then evaluate its performance both in simulation and using an outdoor mobile robot in a farm setting. Simulation experiments use synthetic data in manually constructed and randomly constructed scenarios. We compare MCAP with passive perception approximated by a random walk (Patten et al. 2016), and by a myopic (one-step greedy) strategy, for various time budgets. Algorithm performance is measured using the Brier score, a well-known measure of the quality of probabilistic estimates. Simulation results indicate that MCAP outperforms passive perception and the myopic strategy with increasing budget, which shows that MCAP uses available time more effectively to improve object classification.
Our experiments with a real robot demonstrate the behaviour of our algorithms online in real-world conditions. We report results from a total of 12 trials comprising passive perception, one-step greedy, and MCAP in two scenes. The scenes include five object classes typical of those found on a farm. The robot has a single, side-mounted 2D laser scanner oriented vertically, and thus the robot must build 3D point clouds from successive scans while the robot is in motion. This side-mounted configuration is motivated by applications in agriculture (Bargoti et al. 2015; Rosell and Sanz 2012) and is challenging because simple straight-line paths generate limited views of objects and are unlikely to lead to sufficient data for classification. Algorithm performance in these trials is similar to the simulation experiments.
This paper offers four main contributions. First, we introduce a novel non-myopic planning algorithm for active object classification. Second, we provide a supporting perception framework that estimates object class and pose distributions jointly in a principled manner. Third, we establish a problem formulation designed to directly compare passive and active perception. Finally, we report extensive experimental results to evaluate our methods. We believe that our real-robot experiments are the first demonstration of online active object classification from 3D range data in the outdoor setting.
The remainder of the paper is organised as follows. Section 2 discusses related work and Sect. 3 defines the time-constrained active object classification problem. Section 4 presents the MCAP algorithm. Section 5 describes the classification and estimation algorithms. Sections 6 and 7 report experimental results. The paper concludes and discusses future work in Sect. 8.
2 Related work
The problem of classifying 3D objects with range sensors is traditionally performed with a predetermined set of objects of interest, as we do here, but using data collected offline or from preselected locations (Douillard et al. 2014). Recent interest has focused on long-term and long-range operation (Collet et al. 2015). However, the passive perception approach means that these methods do not perform online decision making to improve data quality during execution.
The Monte Carlo planner we propose for online decision making is related to the large body of work in the area of Monte Carlo state estimation and planning. Sequential Monte Carlo (SMC) methods (e.g., particle filters) (Andrieu et al. 2010; Doucet et al. 2001) are commonly used for inference in state space models. SMC methods are well established in robotics and are now a topic of resurgent interest for various applications (Lindsten and Schön 2013).
One relatively recent application is planning in game AI, where determining the value/cost of a search node in a large search tree is treated as a state estimation problem and solved using SMC methods. Monte Carlo tree search (MCTS) (Browne et al. 2012) is an important example that very recently has achieved success in solving the notoriously difficult game of Go (Silver et al. 2016). Previously, we have applied MCTS to the robotics domain for information gathering with an aerial glider (Nguyen et al. 2016). MCTS has also been applied to object recognition where online planning minimises the costs of movement and incorrect decisions (Lauri et al. 2015).
We formulate a similar problem, but base our approach on the partially observable Monte Carlo Planning (POMCP) algorithm, proposed by Silver and Veness (2010), to explicitly consider the partially observable states of objects. Similar ideas have been used for general active sensing problems in combination with information maximisation (Lauri 2016; Lauri and Ritala 2014). Our MCAP algorithm extends POMCP to the specific problem of active object classification with state uncertainty, and similarly exploits sampling to compute an information-theoretic reward function. However, instead of using a black-box simulator to generate observations, we develop a sensor model to explicitly predict observations. The immediate rewards (information gained by taking an observation) are stored at each node in the search tree. Unlike POMCP, the rewards are used to evaluate mutual information for observation sequences, and we show that equivalent convergence properties are retained.
Outdoor active perception is typically studied in the context of information gathering by maximising the rate of information gain, which has been applied in areas such as exploration (Bourgault et al. 2002), search (Gan et al. 2014), tracking (Xu et al. 2013), search and rescue (Pineda et al. 2015), active localisation (Vander Hook et al. 2015), active underwater inspection (Hollinger et al. 2013), environmental monitoring (Binney et al. 2013), object detection (Vélez et al. 2012), and model construction (Blaer and Allen 2007; Fentanes et al. 2011). In these tasks, actions are chosen by predicting the information gain of observations, commonly measured by the resulting reduction in uncertainty (entropy) and quantified with mutual information.
Solutions to the related informative path planning problem (Guestrin et al. 2005; Krause et al. 2008) provide provable guarantees for information gain planning by leveraging the property of submodularity (Nemhauser et al. 1978). Although maximising mutual information is known to be a submodular objective function, our problem does not satisfy a number of other requirements, such as knowing all possible observation locations beforehand. This class of approaches is not applicable to our case.
Outdoor active object classification is related to work in passive perception that studies multiple object recognition from multiple views (Faulhammer et al. 2015; Tang et al. 2012; Xie et al. 2013) and shows that the availability of multiple views can improve recognition performance (Karasev et al. 2012). One of the challenges is how to associate the data acquired from different observations to the objects in the scene (Wong et al. 2015). An approach is to perform data association as a pre-processing step (Patten et al. 2015, 2016; Wu et al. 2015). Another challenge is that estimating the pose and class of objects from multiple observations involves estimating a state that is a mix of continuous and discrete variables. We approach this problem using a non-parametric Bayesian method combined with a particle filter.
Our development of a classifier based on GP regression is motivated by the need for robust performance in the case of limited training data. Supervised classifiers use training sets that typically are collected and labelled by hand, which is time-consuming in the field robotics context. Our method is inspired by the work of Huber et al. (2012) who learn object models with GP regression. Their method learns the likelihood of image features of predefined object models for camera parameters. We apply the approach to 3D data by learning global features of point clouds, generalise the task to object classification, and analyse the performance with dimensionality reduction.
Active perception has a long history in robotics, beginning with active vision (Bajcsy 1988; Aloimonos et al. 1988), which is still of considerable interest (Chen et al. 2011). Current research in this area has a strong focus on indoor applications and finding the next-best-view. Often, this is formulated as a state estimation problem (Denzler and Brown 2002; Huber et al. 2012; Meger et al. 2010). The choice of classifier, in addition to viewpoint, has also been explored (Potthast et al. 2015), as well as variants such as active object detection (Becerra et al. 2016). Work that is most similar to ours considers a long planning horizon and a time budget (Eidenberger and Scharinger 2010; Atanasov et al. 2014). Like ours, this work formulates the problem as a partially observable Markov decision process (POMDP). However, our approach exploits Monte Carlo methods to avoid full-width expansion in the search space.
A main challenge in active classification is to identify objects by selecting only a subset of possible views, and in the presence of occlusions (Wu et al. 2015; Patten et al. 2016). Many approaches are limited to observing a small number of objects (often household) with viewpoints constrained to an orbit around the scene (Huber et al. 2012; Denzler and Brown 2002; Eidenberger and Scharinger 2010). In contrast, we consider the problem of moving in a large outdoor environment with a potentially large number of objects. For this problem it is not meaningful to restrict the number of observations; rather, it is more intuitive to constrain the amount of available time for a robot to move in an environment while making observations. Therefore, we formulate a new problem that formalises this objective.
3 Problem formulation
In this section, we define the time-constrained active object classification problem. We introduce the problem in general form, and then model it as a partially-observable Markov decision process. The algorithms presented in subsequent sections provide a solution to this POMDP.
3.1 Time-constrained active object classification
The objective is for a mobile robot to actively classify unidentified objects in an unknown environment while arriving at a goal location within a strict time or distance budget. For this problem, the robot is equipped with a range sensor and it is deployed in an environment with an unknown number of static objects with unknown identities.
The environment is composed of a finite number of objects where each object is assumed to belong to one of a set of classes \(\ell \in \mathcal {L} = \{1,2,\ldots ,N_L\}\) of size \(N_L\). We assume a known set of object models \(\mathcal {M} = \{m_i\}_{i=1}^{N_M}\) of size \(N_M\) that are partitioned into independent subsets \(\mathcal {C}_{\ell } = \{m_i\}_{i=1}^{N_{\ell }} \subset \mathcal {M}\) to define each class \(\ell \). Each subset \(\mathcal {C}_{\ell } \subset \mathcal {M}\) is composed of \({N_{\ell }}\) models. The classes are independent subsets and each object model belongs to only one set. In each set, the number of models may not necessarily be the same.
Let t index time such that the total number of observed objects at time t is denoted by \(N^t\). The state of each observed object \(n \in \{1,\ldots ,N^t\}\) is maintained in a global belief \(\mathcal {B}^t = \{ b_n^t \}_{n=1}^{N^t}\). Each \(b_n^t = (\mathcal {N}({\varvec{\mu }}^t_n, {\varvec{\varSigma }}^t_n), {\varvec{p}}^t_n)\) is a probabilistic interpretation of an object. The x-y location and orientation of an object are assumed to be normally distributed with mean vector \({\varvec{\mu }}^t_n = [\mu ^t_{n,x}, \mu ^t_{n,y}, \mu ^t_{n,\theta }]\) and covariance matrix \({\varvec{\varSigma }}^t_n = \text {diag}(\sigma ^t_{n,x}, \sigma ^t_{n,y}, \sigma ^t_{n,\theta })\). The vector \({\varvec{p}}^t_n = [p^t_{n,\ell }]_{\ell =1}^{N_L}\) maintains the probability for each class, where
for the discrete random variable \(L_n\), and with \(\sum _{\ell =1}^{N_L} p^t_{n,\ell } = 1\) and \(p^t_{n,\ell } \ge 0\) \(\forall \) \(t,n,\ell \).
The pose of the robot at time t is given by \({\varvec{x}}^t = (x^t, y^t, \theta ^t)\) and represents the robot’s x-y location and orientation. The path travelled by the robot from its initial location \({\varvec{x}}^0\) and ending at the current location \({\varvec{x}}^t\) is denoted by the sequence \(X^{0:t} = [ {\varvec{x}}^i ]_{i=0}^{t}\). At each location, the robot makes a 3D point cloud observation \(\mathcal {Z}^t = \{ {\varvec{z}}^t_n\}_{n=1}^{N^t}\) that is partitioned into subsets (using 3D segmentation) such that each \({\varvec{z}}^t_n \in \mathcal {Z}^t\) corresponds to an object. Every observation updates the belief \(\mathcal {B}^t\) to a new belief \(\mathcal {B}^{t+1}\) by modifying each \(b_n^t\). Observations also update a global 3D occupancy grid \(\mathcal {G}^t\) composed of voxels that have a state of free, occupied, or unknown.
The robot is given a budget B, which is the maximum amount of time it can operate (or distance it can travel) before it needs to arrive at the goal \({\varvec{x}}_G\). The budget reduces according to a cost function \(C({\varvec{x}}^t, {\varvec{x}}^{t+1})\) that measures the time (or distance) to travel between two locations or \(C_P(X^{0:t}) = \sum _{i=0}^t C({\varvec{x}}^i, {\varvec{x}}^{i+1})\) that measures the time (or distance) to traverse a path. At each time, the remaining budget is given by \(B^t = B - C_P(X^{0:t})\). We define \(t = t_E\) for when the budget is exhausted, in other words \(B^{t_E} = 0\).
The set of robot locations over time forms a path and the aim is to select a path such that \({\varvec{x}}^{t_E} = {\varvec{x}}_G\) as well as maximising a measure of informativeness given by a utility function. The utility of observing object n from a candidate path \(X^{t:t_E} = [{\varvec{x}}^i]_{i=t}^{t_E}\) is denoted \(U_b(X^{t:t_E},b_n^t,\mathcal {G}^t,{\varvec{x}}_G, B^t)\). This is a function of the candidate path, the object’s state estimate, the occupancy grid, the goal, and the remaining budget. If the path cannot reach the goal within the remaining budget then it has utility 0. Objects are assumed independent; therefore, the total utility of observing all objects is
For online planning, the robot replans after each observation. Therefore, at each stage the robot moves to the first location on the path that yields the largest expected utility.
With the outline above, the problem is defined as follows. Given the current pose \({\varvec{x}}^t\), the current belief \(\mathcal {B}^t\), the occupancy grid \(\mathcal {G}^t\), the goal location \({\varvec{x}}_G\), and the remaining budget \(B^t\), plan a path to the goal such that \({\varvec{x}}^{t_E} = {\varvec{x}}_G\) by iteratively selecting the first location of the path that maximises the utility function
3.2 Sequential decision-making formulation
The underlying classification problem is considered to be a stochastic process that obeys the Markov property. Objects are observed, from which their class and pose are estimated. The true state of an object is only inferred from noisy observations, therefore we model the system as a POMDP. In our approach we assume the action-value function is known (or well approximated) and so we do not consider model uncertainty, for which reinforcement learning techniques would apply (Sutton and Barto 1998). Instead we focus on state uncertainty with a POMDP, defined as follows.
A set of unique states \(\mathcal {S}^t\) is defined at each time t. Each state \(s^t = ({\varvec{x}}^t, \tilde{\mathcal {B}}^t)\) \(\forall \) \(s^t\in \mathcal {S}^t\) comprises the robot’s pose and a set of object states \(\tilde{\mathcal {B}}^t = \{ \tilde{b}^t_n \}_{n=1}^{N^t}\). Each \(\tilde{b}^t_n = (\tilde{x}_n, \tilde{y}_n, \tilde{\theta }_n, \tilde{\ell }_n)\) is a single x location, y location, orientation, and class label that can be considered as a sample of the object belief \(b^t_n\); \(\tilde{\mathcal {B}}^t\) can be considered as a set of samples of \(\mathcal {B}^t\). The belief state characterises the probability distribution over the state space \(\mathcal {S}^t\). The probability assigned to a state \(s^t\) is denoted \(bel^t(s^t)\) where \(0 \le bel^t(s^t) \le 1\) and \(\sum _{s^t \in \mathcal {S}^t} bel^t(s^t) = 1\).
The robot is given a set of discrete actions \(\mathcal {A}\) where each action \(a \in \mathcal {A}\) stochastically affects the robot’s state. The next pose \({\varvec{x}}^{t+1} = A({\varvec{x}}^t, a^t)\) is determined by the action process A, characterised by the probability distribution \(p({\varvec{x}}^{t+1} | {\varvec{x}}^t, a^t)\).
With each action, the robot receives a single observation \(\mathcal {Z}^{t+1}\). In general, the observation is characterised by the path from \({\varvec{x}}^t\) to \({\varvec{x}}^{t+1}\), the object beliefs, and the action taken. The observation function \(O(s^t, a^t, \mathcal {Z}^{t+1}) = p(\mathcal {Z}^{t+1} | s^t, a^t)\) represents a probability distribution over possible observations, given action \(a^t\) was taken from state \(s^t\). When an observation is made, the belief state is updated \(bel^{t+1}(s^{t+1}) = E(bel^t(s^t), \mathcal {Z}^{t+1})\) through an estimation process E (defined later in Sect. 5). Together, the action process A and estimation process E represent a full update process of the state.
Illustration of the five main stages of the MCAP algorithm
The transition function T specifies the probability of transitioning to a new state. Given action \(a^t\) is taken in state \(s^t\), the transition function is defined as \(T(s^t, a^t, s^{t+1}) = p(s^{t+1} | s^t, a^t)\).
The reward function \(R(s^t,a^t)\) assigns a numerical value to quantify the utility of performing action \(a^t\) from state \(s^t\) (defined later in Sect. 4). For active object classification, this reward can only be determined by anticipating future observations for a given state, which we specify through a prediction function, \(\hat{\mathcal {Z}}^t = P(s^t,a^t)\).
The goal of the robot is to maximise the sum of rewards collected along a path from the current location to the goal by sequentially selecting actions. The robot should consider the value of actions while considering the uncertainty of the underlying belief state. Therefore, we define the reward for the belief state as \(R_{bel}(bel^t(s^t),a^t) = \mathbb {E} [R(s^t,a^t)] = \sum _{s^t \in \mathcal {S}^t} bel^t(s^t)R(s^t,a^t)\). In addition, the robot should consider a non-myopic approach by optimising the sum of future rewards along a path to the goal. As such, the utility function (2) can be defined as the sum of cumulative rewards
where each action \(a^t, \dots , a^{t_E}\) results in the updated belief with corresponding robot positions \({\varvec{x}}^{t+1}, \dots , {\varvec{x}}^{t_E}\) in \(X^{t:t_E}\), and \(0 < \eta \le 1\) is a discount factor that weights the importance of earlier actions over later actions.
Thus, substituting (4) into (3), the objective is as follows. Plan a path to the goal such that \({\varvec{x}}^{t_E} = {\varvec{x}}_G\) by iteratively selecting the first location (or corresponding action) on the path that maximises the total expected cumulative reward
4 Monte Carlo active perception
In this section we present the Monte Carlo active perception algorithm. MCAP plans observation actions non-myopically by building on ideas from Monte Carlo tree search (Browne et al. 2012), a method for stochastic planning that constructs a search tree using random samples in the decision space. MCTS approximates the true value of an action by simulating, or rolling out, a subsequent chain of actions according to a default policy, and then uses reward statistics to adjust the tree search policy. Many rollouts are performed, and thus the expected value of a tree node approaches its true value. Tree search uses best-first search, enabling computation time to be spent in the most promising areas of the search space.
The MCTS algorithm assumes that the environment is fully observable. However, in many problems, such as active perception, this is not the case. The work by Silver and Veness (2010) proposes the POMCP algorithm, which extends MCTS to partially observable environments. The key idea is to represent action and observation histories with the tree nodes, draw samples from the belief space, and then proceed with the standard MCTS algorithm.
MCAP is an extension of MCTS and POMCP for active perception, where the states of objects are partially observable. In contrast to POMCP, MCAP does not generate random observations with a black box simulator. Instead, it predicts maximum-likelihood observations given sampled states and sensor model. Our reward function uses mutual information (Sect. 4.2), which requires solving an intractable integral for conditional entropy. To deal with this problem, we exploit sampling to update the integral calculation with each iteration. Updating mutual information with each observation (due to the samples), allows the reward value to be collapsed into the action transition. Thus, the search tree branches only on actions, and not on observations. This generates a deep and focused tree that would otherwise be shallow due to the excessive branching factor at chance (observation) nodes.
Furthermore, predicted observations are computed differently during tree search and rollouts. Belief updates during tree search (from the root to a leaf node) use maximum-likelihood observations (Sect. 4.4). Rollouts from the leaf node update the belief using offline data, selected from simplified geometric occlusion reasoning (Sect. 4.5). These rewards are maintained separately by tree nodes, motivating further modification in reward computation.
We first give an overview of the MCAP algorithm. Then we define its reward function and show its convergence properties. We then present the viewpoint estimation methods used in our implementation.
4.1 Algorithm overview
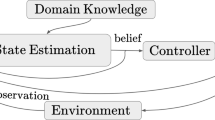
The main stages of MCAP are shown in Fig. 1. Intuitively, MCAP builds a tree where nodes represent viewpoints. First, a node is chosen for expansion in the select stage using a variant of best-first search as in MCTS. Then, a sample is drawn from the belief state. Using the sample, the belief and internal node rewards are updated for each observation along the path from the root to the chosen node. Next, the chosen node is expanded by adding a new child node to the tree following a random action. The simulate stage performs a rollout of random actions for the entire planning horizon (until the time budget is exceeded). The final reward resulting from the expansion is backed-up to update the expected future reward for each node along the path from the new child node to the root. This process is repeated until available computation time is exceeded. The algorithm finishes by returning the child of the root node (or corresponding edge action) with the highest expected reward.
MCAP is listed as pseudocode in Algorithm 1. The algorithm takes as input the current belief state, the occupancy grid, the goal location, the current travel-time budget remaining, and a user-defined computation time allowance. Each node in the search tree V, defined as \(v = \langle \mathcal {X}_v, W_v, R_v, r_v, \bar{Q}_v \rangle \), represents a history of actions. \(\mathcal {X}_v\) is the history of robot poses. \(W_v\) is the visit count. \(R_v\) is the immediate reward of the node representing the value of the action from the parent node. This value is modified with independent calculations each time the node is visited. \(r_v\) is the reward for a rollout from the initial simulation when the node was added. This accounts only for the accumulated reward between the leaf node and the terminal state. Finally, \(\bar{Q}_v\) is the weighted sum of the immediate reward and all child node rewards. Our representation differs from standard MCTS by the definition of incremental rewards between nodes. The reason is that it allows the mutual information reward for a node to be updated with each iteration, separately from other nodes. As a result, the average rewards \(\bar{Q}_v\) are defined differently, through recursion, in order to retrieve the equivalent average value.
The algorithm proceeds by initialising the search tree V with the root node \(v_0\) (line 2). The algorithm then iterates until the desired computation time (an input parameter) is exhausted (line 3). In the limit, the tree would grow to a maximum depth that depends on the budget, but in practice this may take a considerable amount of time. Active object classification benefits significantly from online replanning because real data improves the estimates, which in turn enables better paths to be planned. In our implementation we plan for a fixed number of iterations of 50, before taking an action and then replan while considering the new observation.
At each iteration of the algorithm, a node is chosen for expansion by the function \(\textsc {Select}\) and its path from the root is returned (line 4) according to the upper confidence bound (UCT) algorithm (Kocsis and Szepesvári 2006)
This sums an exploitation value (first term) for promising nodes with high value and an exploration value (second term) for nodes visited less frequently. The parameter \(c_{\text {uct}}\) balances exploration/exploitation and controls the trade-off between the solution quality and computational complexity.
In MCAP, the remaining budget from the chosen node to the terminal state is computed (line 5). With the updated budget, the node is expanded by a simulation in the function \(\textsc {SampleExpandSimulate}\) to compute an expected reward (line 6). First, a set of object states are sampled from the initial belief state (line 20). Then the nodes along the path from the root to the selected node are traversed, updating the belief with each transition, and updating immediate rewards \(R_v\) for the sampled state (line 27). Once the chosen node is reached, a Monte Carlo rollout is performed that selects actions randomly. Actions from \(\mathcal {A}\) are selected by the function \(\textsc {SelectAction}\) such that the subsequent path reaches the goal (without collisions in \(\mathcal {G}\)) within the remaining time budget (line 32). The first node from the first action is added to the tree V as a new child node of the expanded node (line 38). The remaining actions create a path to the goal, and a final reward is computed from the final state (line 40). The final reward is stored at the new node as \(r_v\) (line 44).
The simulated reward is then propagated from the expanded node to the root in the function \(\textsc {BackUp}\) (line 7). The cumulative reward of each node is updated so that it stores the average reward of all rollouts starting at the node. In MCAP, the rewards are defined incrementally and therefore they are computed recursively by summing the immediate reward of the node and the rewards of its child nodes (all sub-trees), and appropriately normalising (line 49). This is in contrast to standard MCTS, which averages the total reward of all rollout paths that include the node.
Lastly, the algorithm iterates by expanding a new node with a new set of object samples. The algorithm terminates when the allowed computation time is reached. When the algorithm finishes, or if it possibly terminated prematurely by a user, it returns the child node of the root node with highest expected reward (line 9).
4.2 Reward function
We define the reward function for active object classification as the combination of increase in mutual information and exploration of unknown space. This could be used for other tasks where mutual information is an appropriate measure.
4.2.1 Information reward
Let \(Z_n\) be a random variable to represent observations. Mutual information for a single object n is defined as
where \(H(b_n)\) is the entropy of an object belief, \(H(b_n|Z_n = \tilde{{\varvec{z}}}_n)\) is the entropy conditioned on the observation \(\tilde{{\varvec{z}}}_n\), and \(p(\tilde{{\varvec{z}}}_n)\) is the probability of the observation. Entropy computation for our belief definition is provided in “Appendix 1”.
Computing the conditional entropy requires summing over all possible observations, which is intractable. In MCAP, each iteration samples a new state s from the belief state and each sample can be used to generate a predicted point cloud from the prediction function \(\hat{\mathcal {Z}} = P(s,a)\) defined previously in Sect. 3.2. Thus, given many samples, the summation in (7) can be approximated.
Let \(b^{\tau }_n\) denote an object belief for node v at depth \(\tau \) given the sequence of observations from the root to v, generated according to the sample s. Then, with \(W_v\) iterations (number of samples), the accumulated reward can be computed as
This defines an incremental information reward at node v as the mutual information with respect to the belief of its parent node. The total mutual information in (7) is given by averaging over all samples, as is done in MCAP (line 27).
Objects are assumed independent; therefore the total information content for all objects at a node, with belief state \(b^{\tau }_n\), sample s, and action a, is given by
Dividing the entropy of the object belief by the entropy of the parent node \(b^0_n\) scales the total information content at any node in the tree to lie within the interval [0, 1].
4.2.2 Exploration reward
The onboard sensor is considered to have a limited range and field of view (FoV). This means the environment is never fully observed from a single observation. Consequently, objects will only ever be inspected if they have been detected. To guide the robot to actively seek new objects, we introduce the concept of exploration
The numerator \(\varDelta V_{\text {unknown}}\) measures the increase of observable volume of unknown space for an observation at a node with respect to the parent node in a similar way to (8). The denominator \(V_{\text {total}}\) measures the total volume of the work space. Dividing by \(V_{\text {total}}\) enforces exploration to be a value in the interval [0, 1] because it measures the proportion of unexplored space within the total workspace. Determining \(\varDelta V_{\text {unknown}}\) exploits the occupancy grid \(\mathcal {G}\) by counting the number of unknown cells that have a clear line-of-sight to the sensor. The total volume is simply given by the dimensions of the environment.
4.2.3 Combined reward function
The reward function is given by combining (9) and (10)
where \(\alpha \) is a tuning parameter that balances between exploration (\(\alpha = 0\)) and exploitation (\(\alpha = 1\)). Scaling the information content in (9) and exploration in (10) restricts the final reward to the domain [0, 1].
4.2.4 Recursive reward computation
The motivation for storing immediate rewards at each node is so that each iteration can separately update the conditional entropy term in (7). In general, MCTS does not store immediate rewards but instead stores the sum of rewards from all rollouts that pass through the node. The empirical average can be computed incrementally by
where \(q_i\) is the total cumulative reward of the simulation from the root to a terminal state.
For the case of incremental rewards between nodes, as in MCAP, we propose to compute the average rewards recursively according to
This differs from (12) in that rewards are defined by the subsequent action sequences from a node, instead of the full path from the root to a terminal state. That is, nodes comprise their immediate reward plus the average of all sub-tree rewards. Nodes do not consider the accumulated rewards for sequence of actions corresponding to the portion of the path higher in the tree. The discount factor \(\eta \) is applied at each depth \(\tau \). These are also applied to the incremental values accumulated for \(r_v\) in MCAP (line 40) to correctly weight the overall rollout value.
4.3 Analysis
In the original UCT algorithm, setting \(c_{\text {uct}} = 1/\sqrt{2}\) is known to satisfy Hoeffding’s inequality which admits the bound \(\mathcal {O}(\log (n)/n)\) on the rate of regret (Kocsis and Szepesvári 2006; Auer et al. 2002). This is derived under the assumption that the expected values of the averages converge for reward values in the interval [0, 1]. In MCAP, reward calculation is decomposed so that the conditional entropy term in (7) can be directly updated and this motivates the recursive formulation in (13). We show this formulation is equivalent to the empirical average and subsequently that MCAP maintains the same bound on the rate of regret as UCT.
Lemma 1
The average reward value
for node v at depth \(\tau \) in the search tree of MCAP is equivalent to the empirical average of all simulations starting from the node, \(\bar{Q}_v = \frac{1}{W_v} \sum _{i=1}^{W_v} R_v^i\). Here, \(W_v\) is the visit count of the node, which is equivalent to the number of simulations. \(R_v^i = \sum _{j=\tau }^{\tau _{\text {max}}} \eta ^i r^i_j\) is the cumulative reward of the \(i^{\text {th}}\) simulation from the node to a terminal state at depth \(\tau _{\text {max}}\). The cumulative reward is defined as the discounted sum of immediate rewards \(r^i_j = R(s,a)\).
The proof of this is given in “Appendix 2”. We now state our convergence theorem.
Theorem 1
For suitable choices of \(c_{\mathrm {uct}}\) and a sufficiently large number of samples n, the bias of the estimated expected reward \(\bar{Q}_v\) is \(\mathcal {O}(\log (n)/n)\).
Proof
As the number of samples increases, the empirical averages of all immediate node rewards converge to the true mean value. By Lemma 1, the expected payoffs \(\bar{Q}_v\) are the expected averages of all simulations starting at a node. Therefore, the assumption in (Kocsis and Szepesvári 2006) that the expected values of all rollout returns converge is satisfied. The average reward values lie in the interval [0, 1] due to normalisation in (9) and (10) which implies that the tail conditions are satisfied with \(c_{\text {uct}} = 1/\sqrt{2}\) by Hoeffding’s inequality. The remainder of the proof follows from (Kocsis and Szepesvári 2006). \(\square \)
4.4 Predicting point clouds for viewpoint evaluation
The reward function assumes predicted point clouds from future viewpoints (as defined in Sect. 3). We define the prediction function P(s, a), listed in pseudocode as Algorithm 2, that takes as input a set of object states and outputs an expected point cloud observation \(\hat{\mathcal {Z}}\). This method uses ray tracing that is similar to our previous work (Patten et al. 2016).
4.4.1 Predicting occupied space
The first step to predict visible point clouds is to determine which cells in the occupancy grid belong to which object. Each object is associated a set of occupied cells denoted by \(\tilde{\mathcal {G}}_n \subset \mathcal {G}\) (line 4). Cells can only belong to one object, which implies that the sets are mutually exclusive. Assigning a cell \({\varvec{g}}_i = [g_{i,x}, g_{i,y}, g_{i,z}]\) to an object is done by computing a scalar weight value according to
The weights are proportional to the distance between the centre of the grid cell and the centres of the objects; larger for objects that are nearer and smaller for objects that are further. The weights are normalised by dividing by the sum of the weights so that they can be interpreted as a probability. Cell ownership is performed by sampling an object index from the cumulative probability distribution.
A small probability is introduced to allow association of cells to no observed object. This is useful in situations involving real sensors where sensor noise may temporarily generate artificial returns. The probability of assigning a cell to no object is controlled by the parameter \(\epsilon _{\text {non}}\).
4.4.2 Predicting point clouds
Once cells are assigned to objects, the algorithm then determines the expected point cloud observation for each object independently. For object n, surface points are determined by casting rays from the sensor location to an occupancy grid representation of the object. For clarity, let the future location of the robot, as determined by the input action a, be denoted \({\varvec{x}}_{\text {new}} = A({\varvec{x}},a)\) and let \({\varvec{x}}_{\text {rel}}\) denote the relative location between \({\varvec{x}}_{\text {new}}\) and the object. In an offline phase, a 3D occupancy grid \(\gamma _{m_i} \in \varGamma \) is created for each object model \(m_i \in \mathcal {M}\). Online, the model that matches the object belief of the sampled state, denoted by \(\gamma _{n,m_i}\), is selected and rays are cast from \({\varvec{x}}_{\text {rel}}\) in the \(\textsc {CastForward}\) function (line 7). In this function, rays are cast according to the characteristics of the sensor. Any ray that intersects with an occupied cell in \(\gamma _{n,m_i}\) is maintained in the set of points \({\varvec{z}}_{\text {forw}}\) at the corresponding intersection point with the cell. This set of points represents the observable points on the surface of the object.
The points in \({\varvec{z}}_{\text {forw}}\) are processed individually to determine which points are visible with respect to the global occupancy grid \(\mathcal {G}\). The points are first transformed to the world coordinate frame and then rays are cast to the sensor location \({\varvec{x}}_{\text {rel}}\) in the function \(\textsc {CastBackward}\) (line 9). Any point that does not intersect with an occupied cell is stored in the set \({\varvec{z}}_{\text {back}}\). Careful consideration is taken not to exclude points that only intersect with the occupied space belonging to the object of interest. Thus, \({\varvec{z}}_{\text {back}}\) consists of points corresponding to the rays that have no intersection or only intersect with occupied cells associated to the object in \(\tilde{\mathcal {G}}_n\).
The procedure for predicting the visible points is performed for each observed object. The point clouds are combined together to form a complete observation \(\hat{\mathcal {Z}}\) (line 10) and this is returned by the prediction function (line 12).
4.5 Predicting point clouds for rollouts
The algorithm outline above computes precise point clouds and is used for computing future rewards. However, it can be time consuming, which is prohibitive when many rollout simulations need to be performed. For this reason, we present an alternative method for use with the rollouts.
The point cloud prediction procedure for rollouts is listed in Algorithm 3. First, occupied cells are assigned to each object, as in Algorthim 2. Then, the 3D convex hull is computed for each set of occupied cells using the centroids of the cells as points (line 5). These are then projected to a 2D plane (line 6).
Each object is then analysed sequentially. The function \(\textsc {Overlap}\) determines the occlusion level of an object by using the projected convex hulls (line 9). First, it determines which other objects can potentially occlude the object by computing the distance from the observation location \({\varvec{x}}_{\text {new}}\) to the centre of each convex hull. Any object that is nearer to \({\varvec{x}}_{\text {new}}\) than object n is an occluding object. Next, the area of overlap between the combined convex hulls of the occluding objects with the convex hull of object n is calculated. This calculation outputs a scaler value o, indicating the proportion of occlusion for the object.
The occlusion level o, along with the relative observation location \({\varvec{x}}_{\text {rel}}\), and the class of the object \(\tilde{\ell }_n\) (determined from \(\tilde{s}\)) are input to a lookup table (line 10). This returns a point cloud that is then combined with the point clouds of other objects (line 11). The combined point cloud is finally returned at the end of the algorithm (line 13).
The lookup table is constructed offline in a training phase. Object models are observed from random locations and the point clouds are stored with their relative observation location. To consider occlusion, the object models are also observed with random occlusions with specific size such that the observed point clouds represent an occluded point cloud with known occlusion level. Using the lookup table in Algorithm 3 simply requests a point cloud for a given class, observation location, and occlusion level. In our experiments, we discretise the occlusion to the levels \(\{0, 0.2, 0.4, 0.6, 0.8\}\).
5 Class and pose estimation
MCAP requires the availability of an application-specific algorithm to generate and update belief states. Here, we define an estimator that computes this belief state as a joint distribution of object class and pose. MCAP uses this estimator in two contexts: (1) when a real observation is taken by an onboard sensor, and (2) when a simulated observation is created using the point cloud predictor.
Our estimation algorithm consists of a particle filter combined with a classifier based on GP regression. An informal description of the estimation process is as follows. First, a point cloud is provided as input (real or simulated) and is segmented such that each segment corresponds to a single object. The choice of segmentation algorithm is not critical to the description of the estimator; in our implemented system we use a simple nearest-neighbour approach. Then, a set of particles is assigned to each point cloud segment. Each particle corresponds to a single class/pose hypothesis for its associated point cloud segment, and the set of particles represents a distribution over states. A weight is computed for each particle to represent the likelihood of the associated class/pose hypothesis. Using these weights, particles are resampled to generate a new set of particles, which is returned to MCAP as the belief state distribution. MCAP samples from this distribution by drawing a single particle from each object’s associated set of particles.
We begin this section by describing the GP method used to compute class/pose likelihoods. Then, we describe the particle filter estimator.
5.1 Gaussian process classifier
Here we describe our approach for computing object class and pose likelihoods given point cloud observations. We explain our method for learning global feature vectors of object models using GP regression, and how the likelihood values are determined for query data.
We first present a short description of Gaussian process regression for convenience. Although GPs can be used directly for classification (GP classification), e.g., (Paul et al. 2012), in this paper we use GP regression to learn a continuous function, which is then used as a classifier.
5.1.1 Background: Gaussian process regression
GPs are a non-parametric Bayesian technique for learning a latent function from noisy data (Rasmussen and Williams 2006). A GP defines a prior over functions, from which a posterior can be derived for new data. In other words, a GP provides a prediction of output values from input queries with an additional measure of prediction uncertainty that depends on the noise and variability of the data.
GP regression assumes a training set \(\mathcal {D} = \{ ({\varvec{\phi }}_i, f_i) \}_{i=1}^{N_D}\) with size \(N_D\) of inputs \({\varvec{\phi }}_i \in \varPhi \subseteq \mathbb {R}^d\), with dimension d, and outputs \(f_i \in {\varvec{\mathcal {F}}} \subseteq \mathbb {R}\). The aggregation of all \(N_D\) inputs form the design matrix \({\varvec{\varPhi }} \subseteq \mathbb {R}^{d \times N_D}\) and the aggregated output values form the column vector \({\varvec{f}}\). The outputs are assumed to be drawn from a noisy process
where \(F(\cdot )\) is the latent function that is to be determined from the training data and \(\epsilon \) is zero-mean Gaussian noise with variance \(\sigma _{\text {noise}}^2\).
A GP denoted by
is completely specified by its mean function \(\mu ({\varvec{\phi }})\) and covariance function \(\kappa ({\varvec{\phi }},{\varvec{\phi }}')\) which are defined as
for any two inputs \({\varvec{\phi }}\) and \({\varvec{\phi }}'\) and where \(\kappa (\cdot , \cdot )\) is a positive definite kernel. The most popular kernel is the squared exponential, given by
where \(\sigma _{\text {var}}^2\) is the signal variance and \({\varvec{M}}\) is a square matrix of size d characterised by the length scales in each dimension. If an isotropic matrix is used then only one length scale parameter \(\sigma _{\text {len}}\) is required resulting in \({\varvec{M}} = \sigma _{\text {len}}^{-2} {\varvec{I}}\), where \({\varvec{I}} \in \mathbb {R}^{d \times d}\) is the identity matrix.
Given the training set \(\mathcal {D}\), the predictive distribution for a test input \({\varvec{\phi }}_*\) is a Gaussian characterised by the mean \(\bar{f}_*\) and variance \(\sigma ^2_*\),
where the vector \({\varvec{\kappa }}_* = \kappa ({\varvec{\phi }}_*, {\varvec{\varPhi }}) = [ \kappa ({\varvec{\phi }}_*, {\varvec{\phi }}_i)]_{i=1}^{N_D}\), \({\varvec{\kappa }}_{**} = \kappa ({\varvec{\phi }}_*, {\varvec{\phi }}_*)\), \({\varvec{K}} \in \mathbb {R}^{N_D \times N_D}\) is the covariance matrix with elements defined by \({\varvec{K}}_{(i,i')} = \kappa ({\varvec{\phi }}_i, {\varvec{\phi }}_{i'})\), and \({\varvec{I}} \in \mathbb {R}^{N_D \times N_D}\) is the identity matrix. These expressions fully describe the predicted outputs of a GP for query inputs. They specify the expected mean of the output with a corresponding variance as a measure of the uncertainty about the prediction.
The hyper-parameters \(\sigma _{\text {noise}}\), \(\sigma _{\text {var}}\), and \(\sigma _{\text {len}}\) can be learned from the training data. The most common method is to maximise the log marginal likelihood using standard optimisation techniques (Rasmussen and Williams 2006).
5.1.2 Learning global features with Gaussian processes
The first step in our algorithm for computing object class and pose likelihoods is to learn global features from training data. The output of this process is a set of GPs, one for each feature element/object pair. Class and pose likelihoods are generated online from observed data with these GPs.
In a training phase, each model \(m_i \in \mathcal {M}\) is observed from a random set of locations \(\varPhi _i = \{\phi _{ih}\}_{h=1}^{N_D}\) and a point cloud is acquired from a sensor. Each point cloud is processed to compute a global feature vector \({\varvec{f}}_{ih} = [ f_{ihj}]_{j=1}^{N_F}\), where \(N_F\) is the number of elements in the vector. The set of locations \(\varPhi _i\) yields a set of training feature vectors \({\varvec{\mathcal {F}}}_i = \{{\varvec{f}}_{ih}\}_{h=1}^{N_D}\) for each training object. A separate GP, denoted by \(\mathcal {GP}_{ij}\), is learned for each training object i and each element j in the feature vectors from the set of inputs \(\varPhi _i\) and outputs \({\varvec{\mathcal {F}}}_i\). For \(N_M\) objects in the training set, a total of \(N_M \times N_F\) GPs are learned offline. The result is a set of GP models \(\mathcal {GP}_i = \{ \mathcal {GP}_{ij} \}_{j=1}^{N_F}\) for each training object, that return a mean \(\bar{f}_{*ij}\) and variance \(\sigma _{*ij}^2\) for any query input \(\phi _*\).
5.1.3 Observation likelihoods
We now describe how to compute the likelihood of an input point cloud given a class label and object pose. The likelihood of a test observation \({\varvec{f}}_o\) acquired from a location \({\varvec{\phi }}_o\) (relative to the observed object) is computed by matching the feature vector to the predicted features from the learned GPs. In the case of a single object model \(m_i\) and a single feature vector element j, the likelihood of the observed feature value given the model is
We model the feature vector components as independent, thus the likelihood of the observed feature vector is given by the product of the univariate normal distributions
5.1.4 Dimensionality reduction
Point cloud feature vectors are often very high dimensional, which means that many GPs need to be learned. Various dimensionality reduction methods can be applied to project the feature vectors onto a lower-dimensional space. Here, we use Principle Component Analysis (PCA) (Jolliffe 2002) to reduce the size of the feature vectors.
The training outputs \({\varvec{\mathcal {F}}}_i\) for training object i are combined into a matrix \({\varvec{F}}_i \in \mathbb {R}^{N_D \times N_F}\), where rows correspond to data inputs and columns correspond to feature components. The reduced feature vectors are derived from the original feature vectors by
where \({\varvec{W}}_i \subseteq \mathbb {R}^{N_F \times N_W}\) is a transformation matrix resulting from Singular Value Decomposition (SVD). The transformation maps each feature vector \({\varvec{f}}_{ih} \in {\varvec{\mathcal {F}}}_i\) from the original dimension of \(N_F\) to a lower dimension \(N_W\). The rows of \({\varvec{F}}^w_i\) are extracted to form a new training set \({\varvec{\mathcal {F}}}^w_i = \{ {\varvec{f}}^w_{ih} \}_{i=1}^{N_D}\).
Computing the likelihood of an observation \({\varvec{f}}_o\) for training object i requires the feature vector to be transformed into the lower-dimensional space. This is done by applying the transformation matrix \({\varvec{W}}_i\) that was determined for the models in training. The likelihood function (23) for the test observation \({\varvec{f}}_o\) becomes
where \(f^w_{oj}\) are the components of the transformed observed feature vector \({\varvec{f}}^w_{oi} = {\varvec{f}}_o {\varvec{W}}_i\), and \(\bar{f}^w_{oij}\) are the components of the transformed predicted feature vector from \(\mathcal {GP}_i\) with corresponding variances \((\sigma ^w_{oij})^2\).
Dimensionality reduction decreases the computation time for calculating observation likelihoods because fewer GPs need to be queried. It also has the benefit of inducing independence amongst the components, which justifies our approximation for computing the likelihood by a product of independent normal distributions.
5.2 Belief representation with a particle filter
The likelihood function described above requires a class label and pose estimate as input. Here, we describe a particle filter estimator that maintains a joint distribution over class and pose for each object. The method updates beliefs through recursive Bayesian estimation. This is beneficial for multi-view classification because it is robust to small amounts of noise (e.g., small localisation errors).
Each particle represents a single class and pose hypothesis for an object, where its weight (likelihood) is computed as above, and a collection of these particles represents a joint distribution. The full set of particles is partitioned into two subsets, one for particles associated to objects, and the other for particles that represent unknown areas of the workspace. Particles are reassociated and updated after each point cloud observation, then resampled according to their weights. This particle representation is very convenient for the MCAP algorithm because sampled states are retrieved simply by selecting a single particle from each object’s set of particles.
The set of particles \(\varPi \) consists of \(N_{\varPi }\) particles that represent a single state estimate of an object,
with x location \(\xi _{\upsilon }\), y location \(\eta _{\upsilon }\), orientation \(\psi _{\upsilon }\), and class label \(\lambda _{\upsilon }\). The set \(\varPi \) is divided into two unique sets: an unobserved set \(\varPi _U\) and an observed set \(\varPi _O\). The unobserved set consists of particles that are out of the sensor FoV or particles that are occluded behind occupied space, in other words in unknown space. The observed set consists of all other particles that may be in free or occupied space. Initially all particles belong to the unobserved set.
The observed particles estimate the states of all objects in the environment and the unobserved particles estimate the unknown space. Particles move from the unobserved set to the observed set if they become visible with a new observation. The visibility of a particle is determined by checking for line-of-sight through the global occupancy grid \(\mathcal {G}\). Any previous particles that were in the observed set remain in the observed set, and once a particle is in the observed set it cannot move to the unobserved set.
5.2.1 Probabilistic particle association
A single set of particles is used to estimate all the objects simultaneously, which means that particles must be associated to each object. Each observed particle that is in the observed set as well as within the sensor’s range and FoV is assigned to an observed object. The assignment of a particle to an object is determined probabilistically.
The location of an object is approximated by its mean, and the distance from the location of each particle to each object is used to compute a weight according to
The weights are normalised in order to interpret the associations as a probability. The cumulative probability distribution is constructed from the weights and an object index n is sampled for each particle to determine the final association.
Particles that are in the observed set but are not directly in the sensor’s FoV and range, or are occluded, remain associated to the same object they were associated to in the previous observation. This means that objects that have been observed in previous observations, but are unobserved in the current observation, still remain in the belief.
5.2.2 Particle resampling
New observations provide additional information about the observed objects. Accordingly, the state estimates must be updated. This is done by updating the set of particles that are associated to each object.
Following from the likelihood functions (23) or (25), a weight is computed for each particle according to
where \({\varvec{f}}_n\) is the feature vector extracted from the point cloud \({\varvec{z}}_n\) belonging to object n. The weights are normalised by dividing by the sum of the weights so that \(\sum _{\upsilon =1}^{N_{\varPi }} \omega _{\upsilon ,n} = 1\).
Given the weights, particles are resampled using Sequential Importance Resampling (SIR) (Doucet et al. 2001) to generate a new set of particles. New particles are drawn (with replacement) from the original set of particles in proportion to their weights until the new set of particles is the same size as the original set. Gaussian white noise is added to the \(\xi _{\upsilon }\), \(\eta _{\upsilon }\), and \(\psi _{\upsilon }\) components of each particle to introduce a small amount of diversity. Finally, once all particles have been drawn, the particle weights are reset to a uniform distribution. The set of particles will converge to a tighter estimate with more observations because particle hypotheses with stronger likelihoods are more likely to be resampled.
6 Experiments in simulation
This section presents results obtained in simulation. We first describe experiments that validate the performance of our estimation algorithm. Then, we give results for two specific simulation environments and results for a further 10 randomly generated environments. Lastly, we present results relating to the computation time of MCAP in comparison to a myopic planning strategy.
6.1 Experiment 1: classification performance
This section presents results that evaluate the estimator presented in Sect. 5. These experiments use simulated and real 3D LIDAR data.
6.1.1 Observation likelihoods for classification
For classification, the pose dependency can be removed by taking the expectation over observation locations
where \(\varPhi _o'\) is the set of observation locations relative to the object. This is approximated by locations on a circle with centre given by the centre of the observed point cloud and radius given by the distance to \({\varvec{\phi }}_o\). A discrete set of points are selected so that all query inputs have an even density of sampled locations. In our experiments, we select locations with a separation of \(0.2\hbox {m}\).
The observations from the sampled locations are considered equally likely. This means that \(p ({\varvec{\phi }}_o')\) is uniform for all \({\varvec{\phi }}_o'\), allowing the expression to be written as
where \(|\varPhi _o'|\) is the number of sampled locations.
Classifying an object means determining the probability of the object belonging to each class \(\ell \) given the observations, which is expressed as \(p(\ell | {\varvec{f}}_o)\). The partition of models into subsets \(\mathcal {C}_{\ell }\) means that the class probability can be computed from the average of the model probabilities
The term \(p (m_i | {\varvec{f}}_o)\) is calculated from the observation likelihoods in (29) by applying Bayes’ rule,
where we assume uniform priors on the object models.
Averaging the probabilities in (31) accounts for the variation of the number of models in each class and removes the bias of larger classes. The final probability for each class is determined by normalising the probability distribution.
6.1.2 Results with simulated data
Classification performance was evaluated with synthetic LIDAR (sparse 3D range) data from a Velodyne HDL-64E. The data was generated using the Blensor simulation toolbox (Gschwandtner et al. 2011) and used to train the classifier. The training set consisted of 11 CAD-like models, grouped into 5 classes (car, motorbike, person, sign, tree). Each object was viewed from 150 random locations between \(3-25\hbox {m}\) from the object centres. The same set of locations were used for each model. At each location, a point cloud observation was recorded and the viewpoint feature histogram (VFH) (Rusu et al. 2010) descriptor was computed using the Point cloud library (PCL) (Rusu and Cousins 2011). This feature descriptor has 308 elements, which was reduced to as few as 20 elements using PCA. GPs were trained with 2D data inputs (x and y locations of training locations) and function values given by the components of the reduced feature vectors. The squared exponential kernel function was used for the 2D inputs. Although VFH descriptors are scale invariant, we observed variations of the descriptors at different distances due to the sparsity and variable density of the data from the LIDAR scanner. For this reason, location distances were considered and descriptors were not assumed to be identical for the same viewing angle.
A separate test set was created by generating point clouds from a set of random locations for each object model. The total size of the test set was 926 point clouds. The VFH descriptor was computed for each test point cloud and the class estimate was computed using the trained classifier. For classification, the final decision was made by taking the class with the largest probability.
The confusion matrix in Table 1 summarises classification results for unoccluded single views (descriptors with 100 components). Most point cloud instances are classified correctly and the overall result achieves an F1 score of 0.84. All classes return high precision and recall except the tree class (precision\(\,=\,0.75\), recall\(\,=\,0.53\)). This is seen by the large number of false negatives with the person and sign classes, and the large number of false positives with the car class.
F1 scores for synthetic LIDAR data with varying size of feature vector and training set. k-NN clustering and spin image matching with full training set shown for comparison
For comparison, classification with VFH descriptors using k-NN clustering was performed. The full length VFH descriptors computed in training from all training point clouds were added to a k-d tree. Given a test feature vector as input, the number of nearest-neighbours in the k-d tree were tallied to determine the score for a class. The final classification result was selected as the class with the highest score. We found the best performance was with 25 nearest-neighbours.
We also compared with local feature matching by computing spin images (Johnson 1997) of point clouds at keypoints chosen by the Intrinsic Shape Signature (ISS) keypoint detector (Zhong 2009). Matching a test observation to a training example proceeded by determining keypoints and then finding, for each one, the most similar keypoint in the training point cloud. The most similar keypoint was determined by the nearest-neighbour in a k-d tree that contained the feature vectors of the training object’s keypoints. Overlapping matches (corresponding to the same keypoint in the training point cloud) were removed. The total matching score for a test observation was the sum of the distances in feature space of the matched keypoints. An extra penalty was added for any unmatched keypoint. The final class was selected as the class of the training example with the smallest total distance. In our experiments we used an image width of 8 bins, and a large search radius of \(0.5\,\hbox {m}\) for the support cylinder, which was necessary to capture enough points from the sparse data.
A comparison of our method with dimensionality reduction as well as with k-NN clustering and spin image matching is shown in Fig. 2. As expected, more reduction of the descriptors leads to worse classification performance. The F1 score reduces from 0.84 with 100 components to 0.70 with 20 components with 150 training instances. Compared to the other methods, however, our method still performs well. k-NN clustering achieves an F1 score of 0.78 and spin image matching achieves an F1 score of 0.58. The poor performance of spin image matching can be explained by the difficulty of computing keypoints and local features with sparse and variable density data. The best performance is our approach with 100 components in the feature descriptors, however, with fewer components k-NN performs best.
6.1.3 Results with limited training data
One motivation for this method is the difficulty of collecting large amounts of field data to train classifiers. For this reason, we compared the performance with a reduced training set. The same data from Sect. 6.1.2 was used but the training data was reduced from 1650 to 1100 by removing 50 examples randomly from the training sets of each instance model (a total of 550 examples all together). This is a reduction of \(30\%\), which is a significant amount of time that translates to many hours saved in the acquisition process.
We performed classification with the same test set as the previous experiment. The F1 score for varying size of the feature vectors is shown in Fig. 2 and a comparison of the size of the training set is summarised in Table 2. The table presents the F1 scores for each method and the reduction of the classification accuracy as a percentage when the training set is reduced. The table shows that using the GP classifier with feature vectors of more than 40 elements is much more robust than performing k-NN clustering or spin image matching. It degrades by as little as \(1.28\%\) when 80 feature elements are used, compared with \(6.41\%\) for k-NN clustering and \(10.34\%\) for spin image matching. With smaller feature vectors, however, the performance degradation of our approach is significantly worse, up to \(11.30\%\) with 20 components. This indicates that the compression is too large and the boundaries between the features are not strong enough to distinguish between the classes.
The reason for the robust performance of our approach with large feature vectors is that a GP interpolates between the elements in the training set. This behaviour offers predictions for queries that are not in the training set, which can capture good matches. The standard methods are restricted to only finding matches with examples in the training set. If the training set is sparse then there are many “blind spots” where queries have very few close neighbours. GPs, on the other hand, have infinite resolution to make queries and therefore perform better with limited training data.
6.1.4 Results with real data and occlusions
Classification performance was further evaluated with real LIDAR data (Velodyne HDL-64E), collected outdoors at the University of Sydney (Patten et al. 2015). The objects (barbecue, box, desk, motorbike, picnic table, tree, wheelie bin) were observed from locations on a circle with radius \(8{-}10\,\hbox {m}\). The training set size for each object was between 105 and 125 point clouds. VFH descriptors were computed for the point clouds and separate GPs were learned.
The training locations were constrained to a circle to ensure that the point clouds were not occluded. As such, we used the orientation of the viewpoint locations for the data inputs. Given the data was collected along a circle, the periodic exponential kernel function defined as
was used instead of the squared exponential kernel function. The data inputs are given by a single dimension, corresponding to the orientation of the viewpoint with respect to the ground truth object. The parameters \(\sigma _{\text {var}}\) and \(\sigma _{\text {len}}\) are defined (and learned) in a similar way to the squared exponential kernel function, and \(\rho \) is the period, which we set to \(2\pi \).
The test set was collected from a separate drive. Point clouds were segmented into the different objects and stored separately. Point clouds within a distance of \(6{-}12\,\hbox {m}\) were stored, in order to maintain a similar distance to the training viewpoints. In total, the test set comprised 241 point clouds. The pose was marginalised out by taking the expectation over orientations uniformly separated by \(15^{\circ }\).
The experiment with the real outdoor LIDAR data is more difficult than the synthetic data because of the occlusions in the test data. Overall, the classification is not as strong as with the synthetic data, as shown by the confusion matrix in Table 3 (feature vectors reduced to 80 components). The table shows that all objects are recognised but there is more confusion than with the synthetic data, indicated by the lower F1 score of 0.53. The table shows there is particular confusion of the picnic table with the desk, and confusion of the wheelie bin with the box. This is to be expected as these pairs of objects are visually similar.
Our method with varying dimensionality reduction is presented in Fig. 3. This reveals the same trend as the synthetic data: more dimensionality reduction leads to worse classification performance. With this dataset, the F1 score reduces from 0.53 with 80 components to 0.25 with 20 components. Also shown is the classification performance with k-NN clustering and spin image matching. In this case, spin image matching (F1 score of 0.49) outperforms k-NN clustering (F1 score of 0.3). This supports the known notion that classification with local features is more robust than global features when dealing with occlusions. Our method, however, still outperforms spin image matching with 80 components.
F1 scores for real LIDAR data with varying size of feature vector. k-NN clustering and spin image matching shown for comparison
6.2 Experiment 2: fork environment
6.2.1 Experiment set up
Planning simulations were performed with synthetic LIDAR data generated with Blensor, similar to Experiment 1. The data was restricted to a \(180^{\circ }\) FoV by only keeping points in the domain \([\theta -\pi /2, \theta +\pi /2]\), where \(\theta \) is the heading of the robot. The sensor range was also restricted to 20 m.
Observations were segmented to extract point cloud observations of each object. First, the ground was removed by detecting the dominant plane in the point cloud data using the RANSAC algorithm (Fischler and Bolles 1981) and then removing points belonging to the plane. The remaining points were partitioned by Euclidean clustering. Both procedures were implemented with PCL.
The classifier was trained using the data described in Sect. 6.1, which comprised 5 object classes. This experiment used the reduced training set of 100 training inputs for each object and a feature descriptor length of 80 elements. The reduced training dataset was used because it results in faster computation, but as seen in Fig. 2 and Table 2 this set of parameters still gives good classification accuracy, therefore we consider this a good balance between speed and performance.
The robot was required to navigate between observation locations and eventually to the goal. Locations were preselected from a uniform grid, with a separation of \(2\,\hbox {m}\), and from these locations a roadmap was generated. The robot could move in the environment with a step size of \(4\,\hbox {m}\) by using the underlying roadmap. Initially, the roadmap was known to the robot, however, obstacles were not known. Obstacles were added at each stage by projecting the 3D occupancy grid to the 2D ground plane, and adjusting edge weights between roadmap nodes accordingly. The robot was constrained to move on the 8-grid, excluding the backward motions, and always faced the direction of travel, as shown in Fig. 4.
Robot motions and sensor FoV for simulations
Simulations were performed with a number of variations of our approach. We compared with different settings of \(\alpha = \{0, 0.5, 1\}\) where \(\alpha = 0\) is pure exploration, \(\alpha = 1\) is pure exploitation, and \(\alpha = 0.5\) balances both. Our method was also applied without rollouts (MCAP w/o) such that only the tree search part of the algorithm was implemented. We compared with a greedy strategy that only considered the value of the first expansion of actions. This strategy randomly drew samples from the object beliefs to compute the information gain in (11). This strategy is comparable to MCAP that only expands the first set of actions and without rollouts. Unless stated otherwise, the MCAP algorithm and its variations were given 50 iterations and the greedy strategy was given 25 samples per available action. In many cases, the greedy strategy has an advantage because it can potentially plan up to 125 cycles. Finally, we compared with a passive strategy that randomly selected the next location.
Performance was evaluated with two different metrics. The first metric used was the total entropy of the observed objects, computed from the joint state of class and pose. This was determined by clustering the particles of the estimation to the ground truth object locations and summing the entropy of the particles of each cluster.
The second metric used was the Brier score (BS) (Brier 1950), which is a score function that measures the accuracy of probabilistic predictions. It is different to other measures, such as precision and recall, which measure classification correctness based on the class with the highest probability. BS accounts for the probabilities of each class hypothesis and is useful for evaluating probabilistic classifiers.
The original BS is in the range [0, 2]. We scaled the values to the range [0, 1] with the definition
for a cluster of particles. The class probability \(p_{\ell }\) was computed by tallying the number of particles with class label \(\ell \) and normalising over all classes. This score measures the squared error of the predicted probability of a class \(p_{\ell }\) with respect to the object’s ground truth probability \(p^{gt}_{\ell }\). Each object has a ground truth probability of 1 for the true class and 0 for every other class. If a prediction is perfectly correct, then \(\text {BS} = 0\), the best score possible. If a prediction is perfectly incorrect, that is a \(100\%\) probability of a false class, then \(\text {BS} = (1+1)/2 = 1\), the worst score possible. Any other distribution of the probabilities is in the range [0, 1].
Simulation environment 1 (fork) with 10 objects. Robot start location is near bottom-left corner and goal location is near top-right corner. Size is \(28\,\hbox {m}\times 28\,\hbox {m}\)
The first planning experiment was performed with the environment in Fig. 5. This set up consisted of 10 objects in a \(28\,\hbox {m}\times 28\,\hbox {m}\) square with minimum object separation of \(1\,\hbox {m}\). The robot began at coordinate \((-12, -12)\) (near the bottom-left corner) with orientation \(\pi /2\) and was given the goal location at coordinate (12, 12) (near the top-right corner). As can be seen in the figure, there is a large tree that blocks the straight line path between the start and goal. Due to the tree, the robot must quickly decide to take the left or the right path, which gives this environment the name fork. For this set up, the estimation used 4000 particles, initially randomly distributed within the bounds of the environment and with randomly selected class types.
Final total entropy and Brier score for experiments in simulation environment 1 for different planners and budgets
Example paths (red) of MCAP algorithm with illustration of observations (grey) for different budgets in simulation environment 1. Ground truth objects shown in black (Color figure online)
Each planning method was executed 10 times for 5 budgets of 40, 45, 50, 55, and \(60\,\hbox {m}\). The increment of \(5\,\hbox {m}\) is approximately one observation. At the end of each trial, the total entropy and BS were measured.
6.2.2 Discussion
The results from the 10 trials for each planning method are summarised in Fig. 6. The figure shows that balanced MCAP has the lowest entropy and BS (best classification) for most budgets. Exploitation is the second best performing method, especially for classification as it is only marginally worse than balanced MCAP in some cases, and marginally better in other cases. In terms of entropy, random is significantly worse (all p values \({<} 0.05\) Footnote 1), which advocates an active method. Similarly to balanced MCAP, the other strategies (MCAP w/o, exploit, and greedy) improve with larger budgets. For the largest budget, these methods have entropy values similar to balanced MCAP. The reason is that the number of observations allowed by the large budget is sufficient for most objects to be confidently classified. In terms of classification, balanced MCAP and exploitation perform best. The other strategies are worse, having similar scores to random.
Exploration is the worst performing active method. Even as the budget increases, the final entropy and BS do not improve. The reason is that the environment is sufficiently small to be fully explored with the allowed number of observations. Once fully explored, the strategy has no more to explore and the robot moves to the goal. The other strategies, that also maximise information content, often decide to improve object estimates before exploring new area. This results in the robot making more useful observations early on and overall within the allocated budget.
Example paths for the MCAP algorithm with different budgets are shown in Fig. 7. For the smallest budget, the robot travels to the right and then along the shortest path to the goal. As the budget increases, the robot still prefers to take the path to the right. However, the robot begins to detour from the shortest path and even performs loops to observe more of the environment (Fig. 7c, d). With the longest budget, the robot can explore all parts of the environment; it first detours to the right, and on the return path, it travels towards the top (Fig. 7e).
6.3 Experiment 3: corridor environment
6.3.1 Experiment set up
The second planning experiment was performed with the environment in Fig. 8. The simulations were similar to the first planning experiment, with the same sensor parameters, classifier, and robot motion. In this experiment the environment was larger, here a \(44\,\hbox {m}\times 44\,\hbox {m}\) square, and it consisted of 16 objects with minimum separation of \(2\hbox {m}\). The robot began at \((-20, -20)\) (near the bottom-left corner) with orientation \(\pi /2\) and goal location (20, 20) (near the top-right corner). Due to the size of the environment, 5000 particles were used for the estimation. In this environment, there is an unimpeded straight line path from the start to the goal. Along the path there are options to deviate left or right in order to investigate other regions. We call this environment a corridor because of the narrow passage connecting the start and goal.
Each planning method was performed 10 times. For this environment the experiments were performed for 5 budgets of 65, 75, 85, 95, and \(105\,\hbox {m}\).
Simulation environment 2 (corridor) with 16 objects. Robot start location is near bottom-left corner and goal location is near top-right corner. Size is \(44\,\hbox {m}\times 44\,\hbox {m}\)
6.3.2 Discussion
The results for entropy and BS from the 10 trials for each planning method are shown in Fig. 9. These show that balanced MCAP is the best performing strategy. For most budgets, balanced MCAP has the lowest entropy and BS. The entropy for the shortest budget is very similar for balanced MCAP, MCAP w/o, and exploration. However, as the budget increases, balanced MCAP and MCAP w/o begin to perform better than exploration. In terms of BS, balanced MCAP and MCAP w/o perform best. The trend here, however, is different to entropy in that balanced MCAP more significantly outperforms MCAP w/o with the two largest budgets. The results also show that random is the worst performing method. While the final entropy and BS reduce with larger budgets, it is significantly outperformed by the other methods (all p values \({<} 0.05\) for entropy and BS). The strength of non-myopic planning is more emphasised in this larger environment than the previous smaller environment. In terms of entropy, greedy is significantly outperformed (all p values \({<} 0.05\)). In terms of BS, greedy is most often the worst strategy (p values \({<} 0.05\) for budgets 65, 75, and \(95\,\hbox {m}\)).
In comparison to the fork environment, exploitation is now the worst performing active strategy and exploration is much more comparable to balanced MCAP. The reason for this is that the environment is larger, meaning that it cannot be completely explored with the limited number of observations. Exploitation is too focused on improving object estimates, as a result it does not have the foresight to detect more objects in unknown regions. Unobserved objects penalise entropy because particles are clustered to the ground truth object locations. In contrast, an exploration strategy observes more objects, so its final entropy and even its BS are better.
Final total entropy and Brier score for experiments in simulation environment 2 for different planners and budgets
Example paths (red) of MCAP algorithm with illustration of observations (grey) for different budgets in simulation environment 2. Ground truth objects shown in black (Color figure online)
Example paths for MCAP with different budgets are shown in Fig. 10. The paths show the same trend as the fork environment: the robot travels along the shortest path with the smallest budget and begins to deviate from this path with larger budgets. There are some cases, for all algorithms, when objects are missed, as illustrated in Fig. 10a. Additionally, in some trials, objects are only observed from a single viewpoint, particularly the small objects at the bottom-right of the environment (see Fig. 10a, b, c). This highlights the difficulty of planning with a small budget because the robot can only observe a subset of the objects. With longer budgets, the robot has time to observe the environment more completely and manages to view all objects with more than a single observation (Fig. 10d, e).
6.4 Experiment 4: random environments
6.4.1 Experiment set up
The third planning experiment was performed with multiple random environments. The previous experiments analysed the average performance of multiple trials of each planning method given the environment. In these random experiments, the average is taken over different environments.
A total of 10 environments were randomly generated, consisting of 10 objects (2 cars, 4 trees, 2 people, and 2 signs) in a \(32\hbox {m}\times 32\hbox {m}\) square. Each planner was run once in each environment with budgets 50 and \(100\hbox {m}\). Similar to previous experiments, we used the same sensor model, classifier, and motion model. The robot also began near the bottom-left corner and was given the goal location near the top-right corner. Differently, 4500 particles were used for estimation.
6.4.2 Discussion
The mean (and standard deviation) entropy and BS from the 10 trials for the different planning methods and budgets are given in Tables 4 and 5. They show that balanced MCAP has the lowest entropy and BS for both budgets. MCAP w/o is the second best performing method, except for the BS with a budget of \(50\,\hbox {m}\). Greedy is the worst active strategy and random is worst overall (both greedy and random have all p values \({<} 0.05\) for entropy and BS).
The experiment also emphasises the benefit of considering both exploration and exploitation when planning. In the previous experiments, exploitation performed relatively well in the smaller fork environment, but exploration performed relatively well in the larger corridor environment. The environments for the random experiments have a size in between that of the fork and corridor environments, and the results show that explore and exploit have very similar performance. In all cases, however, balanced MCAP and MCAP w/o are superior because they can benefit from both aspects.
The results indicate that there is a clear trade-off between exploration and exploitation that may depend on the given environment. It is an interesting area of research to better analyse this trade-off and it is left for future work.
6.5 Experiment 5: computation time
6.5.1 Experiment set up
The computation time of the proposed algorithms were analysed using the fork environment with the same start and goal configuration. For the analysis, we compared the planning time of MCAP, MCAP w/o, and greedy. Each planner was run 10 times with tree search iterations of 25, 50, 75, and 100. For the greedy algorithm, the number of iterations corresponded to the number of samples taken for each candidate observation location.
6.5.2 Discussion
The planning times for a budget of \(50\hbox {m}\) are presented in Table 6. The times reported in the table correspond to the average times for each planning cycle over the 10 trials. The point cloud prediction operation is the most computationally demanding component of the planning system. In particular, the ray-tracing operations take the most time because they involve checking the state of (possibly many) voxels.
The results show that more iterations increase the planning time for each strategy. Initially, with 25 iterations MCAP w/o has the smallest planning time, with greedy and MCAP having similar times. With more iterations, however, the planning time for MCAP increases more significantly than greedy. MCAP w/o also increases but the average planning time is always less than MCAP. So while the full MCAP strategy is superior in terms of object classification certainty and correctness, it comes at a cost of computation.
Planning time histograms. Columns (left to right) correspond to greedy, MCAP w/o, and MCAP. Rows (top to bottom) correspond to number of iterations 25, 50, 75, and 100. The x axes are measured in seconds (intervals of 25 seconds) and the y axes measure the frequency per bin
The histograms in Fig. 11 provide a more detailed description of the computation times to help illustrate why MCAP has longer planning times. The figure shows the distribution of planning times for different number of iterations used by the algorithms. An important observation is that both greedy and MCAP w/o have many cycles with 0s planning time. The reason is that the robot is often in situations with only one valid available action. This can be explained by two possible scenarios: (1) the robot is located near obstacles and all but one option is blocked, and (2) the remaining budget is very small and the robot only has the option to move towards the goal. These two scenarios occur less frequently with MCAP. This indicates that a longer planning horizon prevents the robot from moving into restrictive areas, where many obstacles may block future paths, or from exhausting its budget too quickly. Non-myopic planning enables the robot to have more options at every planning stage. So while the computation time is longer for MCAP, it is because it actually has the opportunity to plan more often.
The data reveals that greedy plans only \(36\%\) of the time, in contrast to MCAP w/o that plans \(76\%\) and MCAP that plans \(84\%\) of the time. In Table 6, MCAP plans \(3\times \) longer than greedy or \(1.5\times \) longer than MCAP w/o in the worst case with 100 iterations. However, when the 0s planning times are not included, MCAP plans on average 563 s, which is only \(1.5\times \) longer than greedy (386 s) and only \(1.2\times \) longer than MCAP w/o (451 s).
7 Experiments with an outdoor robot
In this section, we describe experiments with an outdoor ground robot with a vertically-mounted 2D laser. We implemented MCAP and two other algorithms (greedy and random) for comparison. We first describe the experimental set up, and then report results from two farm scenarios.
7.1 Experiment set up
7.1.1 Robot platform
Experiments were performed with the robot show in Fig. 12. The robot has “Load-Haul-Dump” (LHD) kinematics; a front and back chassis articulate around a single central joint. The maximum angle the articulation joint can move is 0.9 rad, corresponding to a minimum turning radius of \(2.85\,\hbox {m}\) given the \(1.38\,\hbox {m}\) distance from the joint to each chassis.
Robot platform and sensor used in outdoor hardware experiments
The robot was equipped with a vertical 2D SICK laser on the front left side as shown in Fig. 12b. The vertical mounting means that each scan returned points on a vertical semi-circle. Scans were continuously captured while the robot drove between locations and the scans were combined to form a 3D point cloud. The point clouds were restricted to \(20\,\hbox {m}\). Prior to the experiments, the sensor was calibrated using the method of Underwood et al. (2010).
The robot was given five motion primitives, illustrated in Fig. 13a, that provided the observations shown in Fig. 13b–e. The curved motion primitives were approximately \(5\,\hbox {m}\) and the forward action was approximately \(3\,\hbox {m}\). The primary use of the forward motion was to navigate. Due to the narrow FoV for the action, point cloud returns were ignored.
During the experiments, there was motion and localisation noise, and consequently observation noise. The noise was modelled in the predicted belief updates in the tree expansion of MCAP by adding noise to the next location in each node expansion. New nodes were expanded with the ideal arc length and turning angle for each primitive. Then a small amount of noise was added to the x and y locations, and to the final heading angle. The predicted observations were computed from the noisy locations.
During online execution, the robot location was updated by GPS (RTK), which provided good accuracy outdoors. The heading of the robot was updated using an onboard IMU. The robot was equipped with a Nuvo-3000 industrial PC; all code for planning and point cloud processing was written in C++ and ran on the robot using ROS (Quigley et al. 2009).
Motion primitives and sensor FoVs for hardware experiments with outdoor robot
7.1.2 Experimental details
The classifier was trained with pre-collected data. This was collected by manually driving the robot around training objects with motions similar to the right primitive. Data was collected from random locations from all angles around the objects at distances between 2 and \(20\,\hbox {m}\). The number of training observations for each object varied, between 50 and 80. The combined 3D point clouds were processed to remove the ground and background objects. From the remaining points, VFH descriptors were computed and used to train the GP classifier. The full descriptors of 308 elements were used in these experiments because of two reasons. First, the fewer training examples limited the compressibility of the vectors. Second, more severe performance reduction was observed with smaller descriptors due to the noise and unpredictability of the real data. In addition to training, the collected point clouds were also used to construct the model occupancy grids for the CastForward function (Algorithm 2).
The set of objects used in the experiment were a ute (pick-up truck), hatch-back car, drum, small utility vehicle, petrol tank on trailer, and a water tank on a trailer. The petrol tank on trailer and water tank on trailer were grouped into a single class due to their similar appearance and application.
Similar to the simulation experiments, the robot was given a start and goal location. For these experiments, the robot started at the bottom-left corner of the environment. The goal was selected as any location within \(5\,\hbox {m}\) of a chosen corner because of the difficulty to reach a precise location with the limited motions. Each experiment began with the right motion to capture an initial observation.
7.2 Experiment 1
Set up for hardware experiment 1 with 5 objects (ute, small utility vehicle, petrol tank on trailer, two drums). Robot start location is bottom-left corner and goal region is top-right corner. Size is \(24\,\hbox {m}\times 36\,\hbox {m}\)
The set up for the first hardware experiment is shown in Fig. 14, which consisted of 5 objects (ute, small utility vehicle, petrol tank on trailer, two drums) arranged in a \(24\,\hbox {m}\times 36\,\hbox {m}\) rectangle. For safety, navigation was only allowed if the robot had reasonable clearance from all objects on predicted trajectories. Due to this constraint, objects were separated by at least \(5\,\hbox {m}\) so that more complex paths could be considered.
Three trials were performed for MCAP, greedy, and random. The robot was allocated a distance budget of \(70\,\hbox {m}\) and the goal region was selected as the top-right corner. Each trial used 3000 particles for estimation.
The final entropy, BS, percentage volume of unknown space, and computation time are reported in Table 7. The mean values from the three trials are reported in the bottom row. The results show that our proposed method achieves the lowest mean entropy and BS. The values report that random is consistently worst, having the highest entropy and BS for every trial. For trial 2, greedy achieves a very low entropy but the values for the other trials are not as good. This demonstrates how greedy can sometimes perform well, but also it can perform arbitrarily poorly. Greedy is very sensitive to the initial conditions as well as to the action and observation noise, while MCAP is much more consistent.
In addition to entropy and classification performance, MCAP also explores the most area. The table reports the percentage volume of unknown space, which is lowest for MCAP. This is beneficial for active exploration in unknown environments, when the number of objects is unknown and the robot must explore the area in order to detect objects.
The table also reports the average planning times. As expected, MCAP has the longest planning time, spending on average 103s, while greedy spends on average 62s. Although MCAP must plan for longer, the result is better estimates about the objects in the environment.
The point clouds of the observed objects with their entropy and BS are shown in Fig. 15. In the figure, each point cloud observation is coloured differently. The point clouds show that MCAP has a stronger focus on the utility vehicle and the ute, which are observed three or more times. Greedy is similar, except for one trial that does not observe the ute at all. In comparison to random, more observations of these objects result in lower entropies and BSs. In particular, in trial 1 and 2, random only observes the utility vehicle once, resulting in a considerably larger entropy and BS.
Observed point clouds for all trials in hardware experiment 1. Each row shows final result of a single trial. Row labels indicate algorithm (\(\mathrm{R} = \mathrm{random}, \mathrm{G} = \mathrm{greedy}, \mathrm{M} = \mathrm{MCAP}\)) and trial number. BS is Brier score, E is entropy
Travelled paths (red) with illustration of observations (grey) for all trials in hardware experiment 1. Ground truth objects shown in black. (Trajectories as measured by the GPS unit mounted on the articulation joint. Apparent side-stepping is due to lateral movement of articulation joint between successive motions.) (Color figure online)
The random strategy has the most uniform point density across objects, indicating that it does not focus on the uncertain objects. Even though all objects are observed, the viewpoints are not necessarily profitable and in many cases the entropy and BS of objects are worse than MCAP or greedy. An example of this is the ute in trial 1 for random. The ute is observed four times, but due to its length many observations only have partial coverage. The partial observations make the ute more difficult to classify and they are the reason why it has high entropy and BS. MCAP and greedy also suffer this problem, but they still better classify the ute with the same (or fewer) number of observations.
The sub-optimality of the random strategy when given a budget is highlighted by the traversed paths in Fig. 16. In all random trials, the robot spends more time in the beginning travelling to the far right of the environment or performing a large loop. After this initial period, the remainder of the path is almost a straight line to the goal region. The outcome is that time is wasted in the beginning, resulting in poor classification of the objects further from the start.
The figure also highlights the benefit of non-myopic planning. Both MCAP and greedy generate more consistent paths than random but MCAP better utilises its observations given the budget. In all greedy trials, the robot moves to the top of the environment and with the unaccounted excess budget it backtracks. MCAP, on the other hand, plans a longer horizon, which allows the robot to be more flexible in the beginning and make useful observations. The behaviour results in a better balance between object certainty and object discovery.
7.3 Experiment 2
The set up for the second hardware experiment is shown in Fig. 17. It consisted of 4 objects (small utility vehicle, petrol tank on trailer, two drums) arranged in the same rectangle as the first hardware experiment with similar separation conditions. Similar to the first hardware experiment, 3000 particles were used for estimation.
The purpose of this experiment was to investigate the behaviour of the planning algorithms in a significantly difficult environment. To this end, a drum was intentionally placed in a highly occluded location at the top-right of the environment, the goal region was selected as the top-left corner, and a small budget of \(60\hbox {m}\) was allocated. This combination made observing the drum difficult and planning more imperative.
The results for one trial of MCAP, greedy, and random are presented in Table 8. MCAP has the lowest total entropy of all the methods. In terms of BS, however, random has a slightly smaller value than MCAP and greedy.
The point clouds of the observed objects are shown in Fig. 18 and the paths with the illustrated observations are shown in Fig. 19. These reveal that MCAP was the only strategy to detect the occluded drum. The path generated by MCAP takes the robot to the right of the environment, which enables the robot to observe the drum. Both greedy and random perform a circle near the start, after which the budget is nearly exhausted and the robot drives towards the goal region. Along the second half of their paths, they do not make many useful observations, in particular they do not observe the top-right corner of the environment. Althoughthe planning time for MCAP is significantly more than for greedy, it is because MCAP plans more often. Without the foresight, greedy exhausts its budget too quickly and has no opportunity in the later part of the mission to make decisions, except for the straight path to the goal. MCAP, on the other hand, positions the robot in a better region of the environment that enables the robot to make more observations of all objects and the free space. As seen in Table 8, MCAP completely explores the environment, while greedy (and random) have over \(20 \%\) of the environment unexplored.
Set up for hardware experiment 2 with 4 objects (small utility vehicle, petrol tank on trailer, two drums). Robot start location is bottom-left corner and goal region is top-left corner. Size is \(24\,\hbox {m}\times 36\,\hbox {m}\)
Observed point clouds for all trials in hardware experiment 2. Each row shows final result of a single trial. Row labels indicate algorithm (\(\mathrm{R} = \mathrm{random}, \mathrm{G} = \mathrm{greedy}, \mathrm{M} = \mathrm{MCAP}\)). BS is Brier score, E is entropy
Travelled paths (red) with illustration of observations (grey) for all trials in hardware experiment setup 2. Ground truth objects shown in black (Color figure online)
8 Discussion and future work
In this paper, we have presented a new approach for active object classification from 3D range data in outdoor environments. We proposed a new problem formulation, time-constrained active object classification, and presented an initial solution algorithm, MCAP, that retains the convergence properties of MCTS and POMCP. We also presented an estimation algorithm that uses a particle filter and Gaussian process regression to compute the joint likelihood of pose and class from point cloud observations.
We began by evaluating our algorithms in simulation in comparison with passive perception and a one-step greedy approach. Because the time-constrained active object classification problem takes a time/distance budget as a parameter, we evaluated these algorithms for a range of budget values. The results indicated that MCAP used the available budget more efficiently than the other algorithms and planned more informative views. This result supports our expectation that non-myopic planning is beneficial for this problem.
We also demonstrated MCAP using a real robot in an outdoor environment. This demonstration showed that it is feasible to implement our algorithms online, onboard a robot. We compared the performance of MCAP to passive perception and a greedy approach as in the simulation experiments. Here, the training data and sensor observations were subject to sensor noise. The pattern of behaviour observed in these experiments was similar to that in simulation.
Although we did not optimise our code, its performance was sufficient for our demonstrations. Planning time ranged from seconds to minutes per observation. However, optimising online execution time is an important area of future work. Certain aspects of our algorithms are parallelisable and can exploit the current trend towards increased availability of embedded multi-core computing. Combined with a tuned implementation, it is reasonable to expect that our algorithms are feasible for use in practical applications.
MCAP is presented as a general algorithm for active perception, not just for object classification. Another rich area of future work is to replace the estimation algorithm with estimators for other tasks, or with variants tuned for specific scenarios. MCAP could also benefit from application-specific rollout policies that exploit domain knowledge. This has been shown to improve the performance of similar algorithms in other contexts, and it would also apply here.
The main conclusion we draw from our work is that active perception is key to robust perception outdoors. Our experiments clearly show cases where traditional passive perception is severely limited in its ability to gather high-quality data efficiently. This efficiency is necessary to advance the practical application of outdoor robots, particularly in agriculture, where crop surveillance, autonomous weed management, and autonomous harvesting rely on robust perception of objects in the natural world.
Notes
t-Tests with respect to balanced MCAP.
References
Aloimonos, J., Weiss, I., & Bandopadhay, A. (1988). Active vision. International Journal of Computer Vision, 1(4), 333–356.
Andrieu, C., Doucet, A., & Holenstein, R. (2010). Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72(3), 269–342.
Atanasov, N., Sankaran, B., Le Ny, J., Pappas, G., & Daniilidis, K. (2014). Nonmyopic view planning for active object classification and pose estimation. IEEE Transactions on Robotics, 30(5), 1078–1090.
Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine Learning, 47(2–3), 235–256.
Bac, C. W., Henten, E. J., Hemming, J., & Edan, Y. (2014). Harvesting robots for high-value crops: State-of-the-art review and challenges ahead. Journal of Field Robotics, 31(6), 888–911.
Bajcsy, R. (1988). Active perception. Proceedings of the IEEE, 76(8), 966–1005.
Bargoti, S., Underwood, J. P., Nieto, J. I., & Sukkarieh, S. (2015). A pipeline for trunk detection in trellis structured apple orchards. Journal of Field Robotics, 32(8), 1075–1094.
Becerra, I., Valentín-Coronado, L. M., Murrieta-Cid, R., & Latombe, J. C. (2016). Reliable confirmation of an object identity by a mobile robot: a mixed appearance/localization-driven motion approach. International Journal of Robotics Research, 35(10), 1207–1233.
Binney, J., Krause, A., & Sukhatme, G. (2013). Optimizing waypoints for monitoring spatiotemporal phenomena. International Journal of Robotics Research, 32(8), 873–888.
Blaer, P. S., & Allen, P. K. (2007). Data acquisition and view planning for 3-D modeling tasks. In: Proceedings of IEEE/RSJ IROS (pp. 417–422)
Bourgault, F., Makarenko, A., Williams, S., Grocholsky, B., & Durrant-Whyte, H. (2002). Information based adaptive robotic exploration. In Proceedings of IEEE/RSJ IROS (pp. 540–545).
Brier, G. W. (1950). Verification of forecasts expressed in terms of probability. Monthly Weather Review, 78(1), 1–3.
Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M., Cowling, P. I., Rohlfshagen, P., et al. (2012). A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 4(1), 1–43.
Chen, S., Li, Y., & Kwok, N. (2011). Active vision in robotic systems: A survey of recent developments. International Journal of Robotics Research, 30(11), 1343–1377.
Cliff, O., Fitch, R., Sukkarieh, S., Saunders, D., & Heinsohn, R. (2015). Online localization of radio-tagged wildlife with an autonomous aerial robot system. In Proceedings of RSS.
Collet, A., Xiong, B., Gurau, C., Hebert, M., & Srinivasa, S. (2015). Herbdisc: Towards lifelong robotic object discovery. International Journal of Robotics Research, 34(1), 3–25.
Denzler, J., & Brown, C. (2002). Information theoretic sensor data selection for active object recognition and state estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(2), 145–157.
Doucet, A., Smith, A., de Freitas, N., & Gordon, N. (2001). Sequential Monte Carlo methods in practice. Information science and statistics. Berlin: Springer.
Douillard, B., Underwood, J., Vlaskine, V., Quadros, A., & Singh, S. (2014). A pipeline for the segmentation and classification of 3D point clouds. In Experimental robotics (Vol. 79, pp. 585–600). Springer, STAR.
Eidenberger, R., & Scharinger, J. (2010). Active perception and scene modeling by planning with probabilistic 6D object poses. In Proceedings of IEEE/RSJ IROS (pp. 1036–1043).
Faulhammer, T., Aldoma, A., Zillich, M., & Vincze, M. (2015). Temporal integration of feature correspondences for enhanced recognition in cluttered and dynamic environments. In Proceedings of IEEE ICRA (pp. 3003–3009).
Fentanes, J.P., Zalama, E., & Gómez-García-Bermejo, J. (2011). Algorithm for efficient 3D reconstruction of outdoor environments using mobile robots. In Proceedings of IEEE ICRA (pp. 3275–3280).
Fischler, M. A., & Bolles, R. C. (1981). Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6), 381–395.
Gan, S., Fitch, R., & Sukkarieh, S. (2014). Online decentralized information gathering with spatial-temporal constraints. Autonomous Robots, 37(1), 1–25.
Gschwandtner, M., Kwitt, R., Uhl, A., & Pree, W. (2011). BlenSor: Blender sensor simulation toolbox. In Advances in visual computing (Vol. 6939, pp. 199–208), . Springer.
Guestrin, C., Krause, A., & Singh, A. (2005). Near-optimal sensor placements in Gaussian processes. In Proceedings of ICML (pp. 265–272).
Hollinger, G., Englot, B., Hover, F., Mitra, U., & Sukhatme, G. (2013). Active planning for underwater inspection and the benefit of adaptivity. International Journal of Robotics Research, 32(1), 3–18.
Huber, M., Dencker, T., Roschani, M., & Beyerer, J. (2012). Bayesian active object recognition via Gaussian process regression. In Proceedings of fusion (pp. 1718–1725).
Hung, C. C., Nieto, J., Taylor, Z., Underwood, J., & Sukkarieh, S. (2013). Orchard fruit segmentation using multi-spectral feature learning. In Proceedings of IEEE/RSJ IROS (pp. 5314–5320).
Johnson, A. E. (1997). Spin-images: A representation for 3-D surface matching. Ph.D. thesis, Carnegie Mellon University.
Jolliffe, I. (2002). Principal component analysis. Wiley StatsRef: Statistics Reference Online.
Karasev, V., Chiuso, A., & Soatto, S. (2012). Controlled recognition bounds for visual learning and exploration. In Advances in neural information processing systems 25 (pp. 2915–2923). Curran Associates, Inc..
Kocsis, L., & Szepesvári, C. (2006). Bandit based Monte-Carlo planning. In Proceedings of ECML (pp. 282–293). Springer.
Krause, A., Singh, A., & Guestrin, C. (2008). Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies. Journal of Machine Learning Research, 9, 235–284.
Lauri, M. (2016). Sequential decision making under uncertainty for sensor management in mobile robotics. PhD thesis, Tampere University of Technology.
Lauri, M., & Ritala, R. (2014). Stochastic control for maximizing mutual information in active sensing. In Proceedings of IEEE ICRA, workshop on robots in homes and industry: Where to look first?
Lauri, M., Atanasov, N., Pappas, G. J., & Ritala, R. (2015). Active object recognition via Monte Carlo tree search. In Proceedings of IEEE ICRA, workshop on beyond geometric constraints.
Lindsten, F., & Schön, T. B. (2013). Backward simulation methods for Monte Carlo statistical inference. Foundations and Trends in Machine Learning, 6(1), 1–143.
Meger, D., Gupta, A., & Little, J. (2010). Viewpoint detection models for sequential embodied object category recognition. In Proceedings of IEEE ICRA (pp. 5055–5061).
Nemhauser, G., Wolsey, L., & Fisher, M. (1978). An analysis of approximations for maximizing submodular set functions—I. Mathematical Programming, 14(1), 265–294.
Nguyen, J. L., Lawrance, N. R. J., Fitch, R., & Sukkarieh, S. (2016). Real-time path planning for long-term information gathering with an aerial glider. Autonomous Robots, 40(6), 1017–1039.
Patten, T., Kassir, A., Martens, W., Douillard, B., Fitch, R., & Sukkarieh, S. (2015). A Bayesian approach for time-constrained 3D outdoor object recognition. In Proceedings of IEEE ICRA, workshop on scaling up active perception.
Patten, T., Zillich, M., Fitch, R., Vincze, M., & Sukkarieh, S. (2016). Viewpoint evaluation for online 3-D active object classification. IEEE Robotics and Automation Letters, 1(1), 73–81.
Paul, R., Triebel, R., Rus, D., & Newman, P. (2012). Semantic categorization of outdoor scenes with uncertainty estimates using multi-class Gaussian process classification. In Proceedings of IEEE/RSJ IROS (pp. 2404–2410).
Pineda, L., Takahashi, T., Jung, H. T., Zilberstein, S., & Grupen, R. (2015). Continual planning for search and rescue robots. In Proceedings of IEEE RAS humanoids (pp. 243–248).
Potthast, C., Breitenmosero, A., Sha, F., & Sukhatme, G. (2015). Active multi-view object recognition and online feature selection. In Proceedings of ISRR.
Quigley, M., Conley, K., Gerkey, B. P., Faust, J., Foote, T., Leibs, J., Wheeler, R., & Ng, A. Y. (2009). ROS: an open-source robot operating system. In Proceedings of IEEE ICRA, workshop on open source software.
Rasmussen, C. E., & Williams, C. K. I. (2006). Gaussian processes for machine learning. Cambridge, MA: MIT Press.
Rosell, J., & Sanz, R. (2012). A review of methods and applications of the geometric characterization of tree crops in agricultural activities. Computers and Electronics in Agriculture, 81, 124–141.
Rusu, R., & Cousins, S. (2011). 3D is here: Point Cloud Library (PCL). In Proceedings of IEEE ICRA (pp. 1–4).
Rusu, R. B., Bradski, G., Thibaux, R., Hsu, J. (2010). Fast 3D recognition and pose using the viewpoint feature histogram. In Proceedings of IEEE/RSJ IROS (pp. 2155–2162).
Silver, D., & Veness, J. (2010). Monte-Carlo planning in large POMDPs. In Advances in neural information processing systems 23 (pp. 2164–2172). Curran Associates, Inc.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., van den Driessche, G., et al. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489.
Sutton, R. S., & Barto, A. G. (1998). Introduction to reinforcement learning (1st ed.). Cambridge, MA: MIT Press.
Tang, J., Miller, S., Singh, A., & Abbeel, P. (2012). A textured object recognition pipeline for color and depth image data. In Proceedings of IEEE ICRA (pp. 3467–3474).
Underwood, J. P., Hill, A., Peynot, T., & Scheding, S. J. (2010). Error modeling and calibration of exteroceptive sensors for accurate mapping applications. Journal of Field Robotics, 27(1), 2–20.
Underwood, J. P., Calleija, M., Taylor, Z., Hung, C., Nieto, J., Fitch, R., & Sukkarieh, S. (2015). Real-time target detection and steerable spray for vegetable crops. In Proceedings of IEEE ICRA, workshop on robotics in agriculture.
Vander Hook, J., Tokekar, P., & Isler, V. (2015). Algorithms for cooperative active localization of static targets with mobile bearing sensors under communication constraints. IEEE Transactions on Robotics, 31(4), 864–876.
Vélez, J., Hemann, G., Huang, A. S., Posner, I., & Roy, N. (2012). Modelling observation correlations for active exploration and robust object detection. Journal of Artificial Intelligence Research, 44, 423–453.
Wong, L. L. S., Kaelbling, L. P., & Lozano-Prez, T. (2015). Data association for semantic world modeling from partial views. International Journal of Robotics Research, 34(7), 1064–1082.
Wu, K., Ranasinghe, R., & Dissanayake, G. (2015). Active recognition and pose estimation of household objects in clutter. In Proceedings of IEEE ICRA (pp. 4230–4237).
Xie, Z., Singh, A., Uang, J., Narayan, K. S., & Abbeel, P. (2013). Multimodal blending for high-accuracy instance recognition. In Proceedings of IEEE/RSJ IROS (pp. 2214–2221).
Xu, Z., Fitch, R., Underwood, J., & Sukkarieh, S. (2013). Decentralized coordinated tracking with mixed discrete-continuous decisions. Journal of Field Robotics, 30(5), 717–740.
Zhong, Y. (2009). Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of ICCV workshops (pp. 689–696).
Acknowledgements
This research is supported in part by the Australian Centre for Field Robotics, the New South Wales State Government, the Australian Research Council’s Discovery Projects funding scheme (Project Number DP140104203), and the Faculty of Engineering and Information Technologies at The University of Sydney under the Faculty Research Cluster Program. We thank Joel Veness, Oliver Cliff, and Graeme Best for helpful discussions. Thanks to Andrew Bate, Jocie Bate, Lasitha Piyathilaka, and Grant Louat at SwarmFarm Robotics for use of the robot and assistance with the hardware experiments. Thanks also to James Underwood and Alen Alempijevic for assistance with sensor calibration.
Author information
Authors and Affiliations
Corresponding author
Additional information
This is one of several papers published in Autonomous Robots comprising the Special Issue on Active Perception.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mpeg 55018 KB)
Appendix 1: Calculating entropy
Appendix 1: Calculating entropy
The state vector of an object is given by \(b = (\mathcal {N}({\varvec{\mu }}, \varSigma ), {\varvec{p}})\) where the components of the pose are assumed to be normally distributed with mean vector \({\varvec{\mu }} = [\mu _x, \mu _y, \mu _{\theta }]\) and covariance matrix \(\varSigma = \text {diag}(\sigma _x, \sigma _y, \sigma _{\theta })\) for the x location , y location, and orientation angle. The class of the object is represented by the probability vector \({\varvec{p}} = [p_{\ell }]_{\ell =1}^{N_L}\).
For the state vector of an object, the entropy of the joint state can be expressed as
which can be decomposed up into the continuous variable (pose) and the discrete class label to give
where \({\varvec{x}} = (x,y,\theta )\).
From the definition of conditional entropy
where \({\varvec{X}} = [X, Y, \varTheta ]\) is a continuous random vector for the pose components, and L is a discrete random variable for the class label. The first term is the probability over the classes which is simply given by
Expanding the second term yields
For the estimation method described in this paper, the conditional entropy \(H({\varvec{X}}|L = \ell )\) is computed from the particles with class label \(\ell \) and calculating the entropy of a multivariate Gaussian distribution
where \(|\cdot |\) is the determinant of the matrix, and the power 3 comes from the dimension of \({\varvec{x}}\). We simplify this expression and assume each dimension \((x,y,\theta )\) to be independent, therefore, \(|\varSigma | = \sigma _{x}^2 \sigma _{y}^2 \sigma _{\theta }^2\).
1.1 Appendix 2: Proof of Lemma 1
In this proof we show that the recursive reward value for a node is equivalent to the empirical average of all rollout reward values for all simulations beginning at the node.
Let \(T = \tau _{\text {max}}\) represent the maximum depth of the tree. For a leaf node, that has no children or rollout reward, the average reward is given by \(\bar{Q}_T = \eta ^T R_T = \eta ^T \frac{1}{W_T} \sum _{i=1}^{W_T} R^i_T\).
Now consider a node one level above the leaf nodes at depth \(T-1\). The immediate reward is the average of all sample rewards \(Q_{T-1} = \frac{1}{W_{T-1}} \sum _{i=1}^{W_{T-1}} r^i_{T-1}\). The rollout reward consists of one step such that \(r_{T-1} = \eta ^{T} r^r_T\). Expanding the recursive definition gives
where the cumulative reward \(R^i_{T-1} = \sum _{j=T-1}^{T} \eta ^j r^i_j = \eta ^{T-1} r^i_{T-1} + \eta ^T r^i_T\) is the sum of the immediate reward and the immediate reward of the leaf node. The third line is obtained by moving the rollout reward into the last summation and using the definition of MCTS that the visit count of a parent equals the sum of the visit counts of its children plus one for the rollout. In other words, \(W_{T-1} = 1 + \sum \limits _{{{v_c \in \textsc {Children}(v)}}} W_{v_c}\). By induction, the result holds for all higher-level nodes. \(\square \)
Rights and permissions
About this article
Cite this article
Patten, T., Martens, W. & Fitch, R. Monte Carlo planning for active object classification. Auton Robot 42, 391–421 (2018). https://doi.org/10.1007/s10514-017-9626-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-017-9626-0