Spin-orbit coupling dynamics in a planar synchronous binary asteroid

Abstract

Purpose: The 1:1 spin-orbit resonance phenomenon is widely observed in binary asteroid systems. We aim to investigate the intrinsic dynamic mechanism behind the phenomenon under the coupled influence of the secondary’s rotation and orbital motion. Methods: The planar sphere–ellipsoid model is used to approximate the synchronous binary asteroid. The Lindstedt–Poincaré method is applied on the spin-orbit problem to find its explicit quasi-periodic solution. Results: Numerical simulations demonstrate that analytical solutions truncated at high orders are accurate enough to describe the orbital and rotational motions of the synchronous binary asteroid. With the help of the solution, we are able to identify in a more accurate way the stable region for the synchronous state by using the Lyapunov characteristic exponent. Moreover, the resonances that determine the boundary of the stability region are identified. Conclusion: The stable synchronous state requires a small eccentricity $e$ of the mutual orbit but permits a large libration angle $\theta$ of the secondary. The anti-correlation of $\theta$ and $e$ is confirmed. The stable region for a very elongated secondary is small, which helps explain the lack of such secondaries in observations (see Table 1 in Pravec et al. in Icarus 267:267–295, 2016). Findings of this study provide insights into the inherent dynamics that determine the rotational states of a synchronous binary asteroid.

1 Introduction

Many moons in the solar system have been confirmed to be trapped in the 1:1 spin-orbit resonance, where moon’s rotational period approximately synchronizes with its orbital period (Antognini et al. 2014). The synchronization makes one side of the moon always point toward the center body. The 1:1 spin-orbit resonance is also called the synchronous state. The fascinating phenomenon also present for binary asteroid systems through radar and photometric observations (Ostro et al. 2006; Pravec et al. 2006, 2016). With an increasing interest in asteroid explorations (Daly et al. 2023; Li et al. 2023; Chen 2023), studying the intrinsic dynamics of spin-orbit resonances is important because it helps us better constrain properties of the asteroids with limited observations (Wang and Hou 2020).

Studies till now have found some important dynamic mechanisms that shape the evolution history of binary asteroids. For example, the binary Yarkovsky–O’Keefe–Radzievskii–Paddack (BYORP) effect of a synchronous or doubly-synchronous binary asteroid system can constantly modify the mutual orbit (Ćuk and Burns 2005). A satellite orbit drift, presumably caused by the BYORP effect, has been already observed in two binary near-Earth asteroids (Scheirich et al. 2021). Jacobson et al. (2014) propose the hypothesis that additional energy from the BYORP effect can cause the loss of synchronicity in binary asteroids. Another typical mechanism is the tide which produces a torque that transfers the angular momentum between the rotation and the revolution. The tidal torque may drive the satellite’s rotation toward the synchronous state even if its magnitude is smaller than the radiative torque (Goldreich and Sari 2009). Evidence suggests that the spin-orbit dynamics, together with other mechanisms plays an important role in the evolution processes of binary asteroids (Jacobson and Scheeres 2011a). In the current study, we focus only on the spin-orbit dynamics, more specifically, the 1:1 spin-orbit resonance in a synchronous binary asteroid system.

Due to the strong spin-orbit coupling (Compère and Lemaître 2014; Hou et al. 2017), assuming the mutual orbit as an invariant ellipse (see examples in Goldreich and Peale (1966), Murray and Dermott (2000)) is not suitable for a binary asteroid with a large secondary and a very close mutual orbit distance. Such a state, i.e., a non-negligible secondary, irregular shapes of the two asteroids, and a close mutual distance, is widespread in the population of observed binary asteroids (Margot et al. 2015). The full two-body problem (F2BP) is often used to describe the spin-orbit coupling in binary asteroid systems (Scheeres 2002, 2009; Chappaz and Howell 2015; Wang and Hou 2021). Considering the importance of the strong coupling between the secondary’s rotation and the mutual orbit, the F2BP is reduced to a two-degree-of-freedom system, namely planar sphere–ellipsoid model (Scheeres 2009; McMahon and Scheeres 2013), under the following assumptions: (1) The primary body $P$ is regarded as a rigid sphere with a radius $r_{\mathrm{{P}}}$, which is equivalent to the mass point $m_{\mathrm{{P}}}$. That is to say, the primary’s spin is ignored. (2) The secondary $S$ with mass $m_{\mathrm{{S}}}$ is regarded as a triaxial rigid ellipsoid with three semi-major axes $a_{\mathrm{{S}}} \ge b_{\mathrm{{S}}} \ge c_{\mathrm{{S}}}$. The main non-spherical gravity, $J_{2}$ and $J_{22}$ terms are considered. (3) The secondary spins along its shortest axis with its equator coinciding with the orbital plane. Note that the mutual motion no longer moves on a given Keplerian orbit but interacts with the secondary’s rotation.

Equations of motion (EOM) of the planar sphere–ellipsoid model in secondary’s body-fixed frame admit that the strict 1:1 spin-orbit resonance is the equilibrium point (EP) and periodic orbits exist in the vicinity of the EP. To study the stability of librational motion around the EP, McMahon and Scheeres (2013) utilize energy to determine a sufficiency condition of the stability bound by zero-velocity curves (ZVCs). They find bounded periodic orbits with open ZVCs and study sufficient conditions for unbounded motion. Wang and Hou (2020) compute two families of periodic orbits for a synchronous secondary by the predict–correct algorithm and use the two families to study the stability of the 1:1 spin-orbit resonance. The limitation of their study is that the analytical solution is truncated at the lowest order, making them improper for large values of orbit eccentricity or libration amplitude. On the other hand, analytical expressions of invariant tori, i.e., periodic and quasi-periodic motions, in the spin-orbit problem are already investigated by Celletti (1994), Celletti and Chierchia (2008), Calleja et al. (2022), but their model assumes an invariant mutual orbit which may be invalid for a binary asteroid.

Inspired by these studies, we construct analytical solutions to high orders in the planar sphere–ellipsoid model. The method used is the well-known Lindstedt–Poincaré (LP) method (Jorba and Masdemont 1999; Li and Hou 2023), which is seldom applied to the study of the sphere–ellipsoid model. In contrast to the numerical approach (Zhang et al. 2023), or the approach of normalizing the Hamiltonian (Gkolias et al. 2016), the LP method directly obtains explicit high-order analytic solutions. The high-order solution allows us to describe the motion of the synchronous binary asteroid in a more accurate way. Based on the solution, the contour map of Lyapunov characteristic exponent (LCE) on the ‘momentum’ plane is generated. Specific structures appear at the boundary of the stability region in the contour maps, and these structures are found to be related with resonances. By this way, we are able to identify the major resonances that determine the stability boundary of a secondary’s rotational motion in a synchronous binary asteroid. By changing values of the mass ratio, the mutual orbit distance, the orbital eccentricity, and the secondary’s elongation, we are able to describe these parameters’ influence on the stability of the 1:1 spin-orbit resonance.

The remaining of the paper is as follows: Sect. 2 introduces the planar sphere–ellipsoid model, including the EOM in the secondary’s body-fixed frame, the EP which corresponds to the exact synchronous state, and the expansion of the EOM around the EP. Then, an algorithm based on the LP method is proposed to construct high order analytical solutions in Sect. 3. Section 4 checks the accuracy of the analytical solution by comparing it with numerical integration. Based on the analytical solution, Sect. 5 generates contour maps of the LCEs on the ‘momentum’ plane and identifies the resonances that determine the boundary of the stability region for the secondary’s rotational motion in the synchronous binary asteroid. By changing values of the parameters such as the mass ratio and the mutual orbit distance, we are able to describe their influence on the stability region. Section 6 concludes the study.

2 Model description

2.1 Planar sphere–ellipsoid model

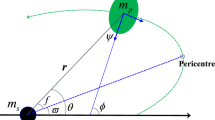
Our model focuses on the planar motion of a synchronous secondary. It is convenient to describe the rotation of the secondary by taking its centroid as the origin of the coordinate system. As shown in Fig. 1, the $X$-axis is fixed on the secondary’s longest equatorial axis, and the $x$-axis points to the inertial direction. The angle between the two axes, $\theta _{\mathrm{{S}}}$ represents the secondary’s rotation. $\boldsymbol{r}$ is the position vector and $\theta$ is the primary’s revolution angle (so-called the secondary’s libration angle with respect to $\boldsymbol{r}$ in many papers) in the body-fixed frame. The dashed line indicates that we approximate the real binary asteroid as a sphere and an ellipsoid. In this study, we derive the system’s EOM from its Hamiltonian. The potential function $V$ and kinetic energy $T$ of the system are

$$ \begin{aligned} V & = G{m_{\mathrm{{P}}}}{m_{\mathrm{{S}}}}\left [ {\frac{1}{r} + \frac{1}{{2{r^{3}}}}\left ( {{A_{1}} + {A_{2}}\cos 2\theta } \right )} \right ], \\ T & = 0.5\mu \left [ {{{\dot{r}}^{2}} + {r^{2}}{{\left ( {\dot{\theta}+ {{\dot{\theta}}_{\mathrm{{S}}}}} \right )}^{2}}} \right ] + 0.5I_{\mathrm{{S}}} \dot{\theta}_{\mathrm{{S}}}^{2}, \end{aligned} $$

(1)

where $m_{\mathrm{{P}}}$ and $m_{\mathrm{{S}}}$ are the masses of the primary and the secondary, respectively; $G$ is the gravitational constant; $A_{1}$ and $A_{2}$ are coefficients related to the $J_{2}$, $J_{22}$ terms; $\mu$ is the system’s reduced mass; $I_{\mathrm{{S}}}$ is the secondary’s moment of inertia; and their expressions are

$$ \begin{aligned} & {A_{1}} = 0.1\left ( {a_{\mathrm{{S}}}^{2} + b_{\mathrm{{S}}}^{2} - 2c_{\mathrm{{S}}}^{2}} \right ), \quad A_{2} = 0.3\left ( {a_{\mathrm{{S}}}^{2} - b_{ \mathrm{{S}}}^{2}} \right ), \\ & \mu = {m_{\mathrm{{P}}}}{m_{\mathrm{{S}}}}/\left ( {{m_{\mathrm{{P}}}} + {m_{\mathrm{{S}}}}} \right ), \quad I_{\mathrm{{S}}} = 0.2{m_{\mathrm{{S}}}}\left ( {a_{\mathrm{{S}}}^{2} + b_{ \mathrm{{S}}}^{2}} \right ), \end{aligned} $$

(2)

Where $a_{\normalfont{\mathrm{{S}}}}$, $b_{\normalfont{\mathrm{{S}}}}$ and $c_{\normalfont{\mathrm{{S}}}}$ are the secondary’s three semi-major axes. Immediately we obtain the conservative system’s Lagrangian function,

$$ \begin{aligned} \mathscr{L} = T + V. \end{aligned} $$

(3)

Define $r$, $\theta$, $\theta _{\mathrm{{S}}}$ as the generalized coordinates, corresponding conjugated variables are

$$ \begin{aligned} {p_{1}} &= \mu \dot{r}, \quad {p_{2}} = \mu {r^{2}}\left ( { \dot{\theta}+ {{\dot{\theta}}_{\mathrm{{S}}}}} \right ), \\ {p_{3}} &= \mu {r^{2}}\left ( {\dot{\theta}+ {{\dot{\theta}}_{\mathrm{{S}}}}} \right ) + I_{\mathrm{{S}}}{\dot{\theta}_{\mathrm{{S}}}}. \end{aligned} $$

(4)

Substituting Equation (4) into Equation (1), we obtain the Hamiltonian,

$$\begin{aligned} \begin{aligned} H & = T - V\\ & = \frac{1}{{2\mu }}\left ( {p_{1}^{2} + \frac{{p_{2}^{2}}}{{{r^{2}}}}} \right ) + \frac{{{{\left ( {{p_{3}} - {p_{2}}} \right )}^{2}}}}{{2{I_{\mathrm{{S}}}}}} \\ &\quad {}- G{m_{\mathrm{{P}}}}{m_{\mathrm{{S}}}}\left [ {\frac{1}{r} + \frac{1}{{2{r^{3}}}}\left ( {{A_{1}} + {A_{2}}\cos 2\theta } \right )} \right ]. \end{aligned} \end{aligned}$$

(5)

Furthermore, the EOM in the canonical form is

$$ \left \{ \begin{aligned} & \dot{r} = \partial H/\partial {p_{1}} = {p_{1}}/\mu \\ & \dot{\theta}= \partial H/\partial {p_{2}} = {p_{2}}/\left ( {\mu {r^{2}}} \right ) - \left ( {{p_{3}} - {p_{2}}} \right )/{I_{\mathrm{{S}}}} \\ & {{\dot{\theta}}_{\mathrm{{S}}}} = \partial H/\partial {p_{3}} = \left ( {{p_{3}} - {p_{2}}} \right )/{I_{\mathrm{{S}}}} \\ & {{\dot{p}}_{1}} = - \partial H/\partial r \\ &\hphantom{{{\dot{p}}_{1}}}{}= p_{2}^{2}/\left ( {\mu {r^{3}}} \right ) \\ &\hphantom{{{\dot{p}}_{1}}}\quad {}- G{m_{\mathrm{{P}}}}{m_{\mathrm{{S}}}}\left [ {1/{r^{2}} + 1.5\left ( {{A_{1}} + {A_{2}}\cos 2\theta } \right )/{r^{4}}} \right ] \\ & {{\dot{p}}_{2}} = - \partial H/\partial \theta = - G{m_{\mathrm{{P}}}}{m_{ \mathrm{{S}}}}{A_{2}}\sin 2\theta /{r^{3}} \\ & {{\dot{p}}_{3}} = - \partial H/\partial {\theta _{\mathrm{{S}}}} = 0 \end{aligned} \right .. $$

(6)

The system seems to have three degrees of freedom. Since $\theta _{\mathrm{{S}}}$ called the cyclic coordinate does not appear in the Hamiltonian, $p_{3}$ is an integral of motion. Obviously, $p_{3}$ is the system’s total angular momentum and it is conserved, i.e. $p_{3} \equiv K$. We use the integral of motion to reduce one degree of freedom, and obtain the EOM in the form of second-order ordinary differential equations,

$$ \left \{ \begin{aligned} & \ddot{r} = r{\left ( { \frac{{{I_{\mathrm{{S}}}}\dot{\theta}+ K}}{{\mu {r^{2}} + {I_{\mathrm{{S}}}}}}} \right )^{2}} \\ &\hphantom{\ddot{r} =} {}- G\left ( {{m_{\mathrm{{P}}}} + {m_{\mathrm{{S}}}}} \right )\left [ {\frac{1}{{{r^{2}}}} + \frac{3}{{2{r^{4}}}}\left ( {{A_{1}} + {A_{2}} \cos 2\theta } \right )} \right ] \\ & \ddot{\theta}= - 2 \frac{{\dot{r}\left ( {{I_{\mathrm{{S}}}}\dot{\theta}+ K} \right )}}{{r\left ( {\mu {r^{2}} + {I_{\mathrm{{S}}}}} \right )}} \\ &\hphantom{\ddot{\theta}=}{}- \frac{{G\left ( {{m_{\mathrm{{P}}}} + {m_{\mathrm{{S}}}}} \right ){A_{2}}\sin 2\theta }}{{{r^{5}}}} - \frac{{G{m_{\mathrm{{P}}}}{m_{\mathrm{{S}}}}{A_{2}}\sin 2\theta }}{{{I_{\mathrm{{S}}}}{r^{3}}}} \end{aligned} \right .. $$

(7)

We have to remark that conservation of the angular momentum has already been used by many previous studies (Scheeres 2009; McMahon and Scheeres 2013; Wang and Hou 2020).

Fig. 1

A perpendicular view of the relative geometry of the sphere–ellipsoid model. The primary body moves around the secondary. $O-XY$ is the body-fixed frame of the secondary

2.2 Expansion of the EOM

If the binary asteroid is trapped in the strict synchronous state, the primary’s orbital period is equal to the secondary’s rotation period. As a result, $P$ appears stationary in the body-fixed frame. That is to say, the strict 1:1 spin-orbit resonance is equivalent to an EP of Equation (7). For the planar sphere–ellipsoid model, there are two types of EPs. One type of EP is at the $X$-axis of the secondary’s body-fixed frame ($\theta = 0$), i.e., the secondary always has its longest axis pointing towards the primary. The other type of EP is at the $Y$-axis ($\theta = \pi /2$), i.e., the secondary always has its short axis pointing towards the primary. The EP’s Lyapunov stability is discussed in Scheeres (2004), Bellerose and Scheeres (2008), based on the planar sphere-ellipsoid model. Depending on the mass ratio, the secondary’s elongation, and the mutual orbit distance, the stability of the two types of EP may be different. For example, the EP on the $X$-axis is assumed to be stable in our work, but it is not always the case. It can be unstable when the secondary is too elongated or is too close to the primary, or its mass ratio with respect to the primary is too large (Scheeres 2009). Even though, most of the time, the EP on the $X$-axis is stable, such as the example binary asteroid systems used in this study. In the following study, we will focus on this type of EP. In a real synchronous binary asteroid, the secondary is usually not in an exact resonance state. This means the primary $P$ oscillates around the EP in the secondary’s body-fixed frame. We study the synchronous state, i.e., the 1:1 spin-orbit resonance by expanding the EOM around the stable EP. To simplify the following derivation, and make the calculation at a reasonable scale, hereafter we adopt the following dimensionless units of mass, length, and time:

$$ \begin{aligned} \left [M\right ]=m_{\mathrm{{P}}} + m_{\mathrm{{S}}}, \quad \left [L\right ]=r_{0}, \quad \left [T\right ]=\sqrt{\left [L\right ]^{3}/G\left [M\right ]}, \end{aligned} $$

(8)

where $r_{0}$ is the distance from the origin to the stable EP. Substituting the above dimensionless units and $r=r_{0}+\rho$ into Equation (7), we obtain

$$ \left \{ \begin{aligned} & \ddot{\rho}= \frac{{\left ( {{r_{0}} + \rho } \right ){{\left ( {{I_{\mathrm{{S}}}}\dot{\theta}+ K} \right )}^{2}}}}{{{{\left [ {\mu {{\left ( {{r_{0}} + \rho } \right )}^{2}} + {I_{\mathrm{{S}}}}} \right ]}^{2}}}} - \frac{1}{{{{\left ( {{r_{0}} + \rho } \right )}^{2}}}} \\ &\hphantom{\ddot{\rho}=}{}- \frac{3}{{2{{\left ( {{r_{0}} + \rho } \right )}^{4}}}}\left ( {{A_{1}} + {A_{2}}\cos 2\theta } \right ) \\ & \ddot{\theta}= - 2 \frac{{\dot{\rho}\left ( {{I_{\mathrm{{S}}}}\dot{\theta}+ K} \right )}}{{\left ( {{r_{0}} + \rho } \right )\left [ {\mu {{\left ( {{r_{0}} + \rho } \right )}^{2}} + {I_{\mathrm{{S}}}}} \right ]}} \\ &\hphantom{\ddot{\theta}=}{}- {A_{2}}\sin 2\theta \left [ { \frac{1}{{{{\left ( {{r_{0}} + \rho } \right )}^{5}}}} - \frac{\mu }{{{I_{\mathrm{{S}}}}{{\left ( {{r_{0}} + \rho } \right )}^{3}}}}} \right ] \end{aligned} \right .. $$

(9)

For the purpose of using the Lindstedt–Poincaré method (see Sect. 3) to construct the high-order analytical solution of Equation (9), we further expand its right function into the power series of $\rho$ and $\theta$. Neglecting the tedious (but not difficult) process of Taylor expansion, the final expressions of EOM are

$$ \left \{ \begin{aligned} & \ddot{\rho}= {c_{1}} + {c_{2}}\rho + {c_{3}}\dot{\theta}+ {c_{4}}{{ \dot{\theta}}^{2}} + \mathop {\sum }\limits _{i = 1}^{\infty }{c_{5}}{ \rho ^{i}}\dot{\theta}\\ &\hphantom{\ddot{\rho}=}{}+ \mathop {\sum }\limits _{i = 1}^{\infty }{c_{6}}{ \rho ^{i}}{{\dot{\theta}}^{2}} + \sum \limits _{i = 2}^{\infty }{ \sum \limits _{j = 0}^{\lfloor i/2 \rfloor} {{\varphi _{ij}}{\rho ^{i - 2j}}{\theta ^{2j}}} } \\ & \ddot{\theta}= {c_{7}}\theta + {c_{8}}\dot{\rho}+ {c_{9}}\dot{\rho}\dot{\theta}+ \sum \limits _{i = 1}^{\infty }{{c_{10}} {\rho ^{i}} \dot{\rho}}+ \sum \limits _{i = 1}^{\infty }{{c_{11}} {\rho ^{i}} \dot{\rho}\dot{\theta}}\\ &\hphantom{\ddot{\theta}=} {} + \sum \limits _{i = 2}^{\infty }{\sum \limits _{j = 1}^{\lfloor {\left ( {i + 1} \right )/2} \rfloor} {{ \psi _{ij}}{\rho ^{i - 2j + 1}}{\theta ^{2j - 1}}} } \end{aligned} \right ., $$

(10)

where $c_{n}$, $n=1,2,\ldots,11$, ${{\varphi _{ij}}}$, ${{\psi _{ij}}}$ are coefficients and their detailed expressions are given in the Appendix.

3 Quasi-periodic solution

In this section, an algorithm based on the LP method is proposed to solve Equation (10). Generally speaking, the LP method divides the nonlinear EOM into many linear systems of equations with orders (to be defined later) from zero to infinity, and the higher-order equations are obtained by substituting the low-order solutions into the EOM. As a starting point, the 1st order solution is easily found. Though the general solution of a complex nonlinear system is unavailable, its quasi-periodic solution can be asymptotically approached. The major benefit of this approach is that the explicit analytical solution can be computed to very high orders on the computer.

3.1 0th and 1th order equations

Collecting all the constant terms in Equation (10), we have its 0th order part,

$$ \begin{aligned} c_{1} = - 1.5\left ( {{A_{1}} + {A_{2}}} \right )r_{0}^{ - 4} - r_{0}^{ - 2} + {K^{2}}{r_{0}}{\left ( {{I_{\mathrm{{S}}}} + \mu r_{0}^{2}} \right )^{ - 2}}=0. \end{aligned} $$

(11)

The above equation indicates that the EP’s position is determined by the total angular momentum for a system of defined shape and mass. We remark that there are usually two solutions satisfying Eq. (11) for a fixed value of $K$. One is stable and further away from the secondary, and the other is usually unstable and closer to the secondary (Scheeres 2009). Our study focuses on the outer stable equilibrium point. The 1st order part, namely the linear part of the EOM is

$$ \left \{ \begin{aligned} \ddot{\rho}= {c_{2}}\rho + {c_{3}}\dot{\theta}\\ \ddot{\theta}= {c_{7}}\theta + {c_{8}}\dot{\rho}\end{aligned} \right . , $$

(12)

and its characteristic equation is

$$ \begin{aligned} {\lambda ^{4}} - \left ( {{c_{2}} + {c_{7}} + {c_{3}}{c_{8}}} \right ){ \lambda ^{2}} + {c_{2}}{c_{7}} = 0. \end{aligned} $$

(13)

For motion around the stable EP, there are two pairs of imaginary roots of Equation (13), i.e. $\lambda = \pm i {\omega _{0}}$, $\pm i {\nu _{0}} \; \left ( {{ \omega _{0}} < {\nu _{0}}} \right )$. Lyapunov’s center theorem tells us that two families of periodic orbits emanate from the stable EP if $\omega _{0}$ and $\nu _{0}$ are incommensurable. Since the two basic frequencies both exist, we aim to find the quasi-periodic solution of Equation (10). The free solution of Equation (12) can be written as

$$ \left \{ \begin{aligned} & \rho = \alpha \cos {\theta _{1}} + \beta \cos {\theta _{2}} \\ & \theta = - \left ( {{\omega _{0}}^{2} + {c_{2}}} \right ){\left ( {{ \omega _{0}}{c_{3}}} \right )^{ - 1}}\alpha \sin {\theta _{1}}\\ & \hphantom{\theta =}{}- \left ( {{\nu _{0}}^{2} + {c_{2}}} \right ){\left ( {{\nu _{0}}{c_{3}}} \right )^{ - 1}}\beta \sin {\theta _{2}} \end{aligned} \right ., $$

(14)

where ${\theta _{1}} = {\omega _{0}}t + {\theta _{1\mathrm{{i}}}}$, ${\theta _{2}} = {\nu _{0}}t + {\theta _{2\mathrm{{i}}}}$. ${\theta _{1\mathrm{{i}}}}$ and ${\theta _{2\mathrm{{i}}}}$ are initial phase angles. $\alpha$ and $\beta$ are the amplitude parameters of the long and the short period component, respectively. Wang and Hou (2020) gave the physical interpretation of the two components. If we approximatively treat the libration around the EP as a pendulum motion, the long-period frequency $\dot{\theta}_{1}$ is the free libration frequency, and the short-period frequency $\dot{\theta}_{2}$ is the forced libration frequency. Moreover, the long-period amplitude $\alpha$ and the short-period amplitude $\beta$ are indicators of the maximal libration angle $\theta _{\max }$ and the mutual orbit eccentricity $e$, respectively. There exists approximate relations that $\left ( {{\omega _{0}}^{2} + {c_{2}}} \right ){\left ( {{\omega _{0}}{c_{3}}} \right )^{ - 1}}\alpha \sim {\theta _{\max }}$ and $\beta r_{0}^{ - 1} \sim e$. A particular quasi-periodic orbit is defined by given values of the four integral constants, $\alpha$, $\beta$, ${\theta _{1\mathrm{{i}}}}$, ${\theta _{2\mathrm{{i}}}}$.

3.2 High-order analytical solution

The part of Equation (10) beyond order 2 is

$$ \left \{ \begin{aligned} & \ddot{\rho}= {c_{4}}{{\dot{\theta}}^{2}} + \sum \limits _{i = 1}^{ \infty }{{c_{5}}} {\rho ^{i}}\dot{\theta}+ \sum \limits _{i = 1}^{ \infty }{{c_{6}}} {\rho ^{i}}{{\dot{\theta}}^{2}} \\ &\hphantom{\ddot{\rho}=}{}+ \sum \limits _{i = 2}^{\infty }{\sum \limits _{j = 0}^{ \lfloor i/2 \rfloor } {{\varphi _{ij}}{ \rho ^{i - 2j}}{\theta ^{2j}}} } \\ & \ddot{\theta}= {c_{9}}\dot{\rho}\dot{\theta}+ \sum \limits _{i = 1}^{ \infty }{{c_{10}}{\rho ^{i}}\dot{\rho}} + \sum \limits _{i = 1}^{ \infty }{{c_{11}}{\rho ^{i}}\dot{\rho}\dot{\theta}} \\ &\hphantom{\ddot{\theta}=}{}+ \sum \limits _{i = 2}^{\infty }{\sum \limits _{j = 1}^{ \lfloor \left ( {i + 1} \right )/2 \rfloor } {{\psi _{ij}}{\rho ^{i - 2j + 1}}{\theta ^{2j - 1}}} } \end{aligned} \right .. $$

(15)

Substituting Equation (14) into Equation (15), we can obtain the 2nd order equations, from which the solution of order 2 is solved. Substituting the solutions of order 1 and order 2 into Equation (15), we can obtain the 3rd-order equations. The process is repeated to obtain higher-order solutions. The quasi-periodic solution of arbitrary order can be written in the general form,

$$ \left \{ \begin{aligned} & \rho = \sum \limits _{i,j,p,q} {{\rho _{ijpq}}{\alpha ^{i}}{\beta ^{j}} \cos \left ( {p{\theta _{1}} + q{\theta _{2}}} \right )} \\ & \theta = \sum \limits _{i,j,p,q} {{\theta _{ijpq}}{\alpha ^{i}}{ \beta ^{j}}\sin \left ( {p{\theta _{1}} + q{\theta _{2}}} \right )} \end{aligned} \right ., $$

(16)

where $i$, $j$, $p$, $q$ are integers. $i$ and $j$ are the exponents of the small parameters $\alpha$ and $\beta$, and they define the order $n$ ($n=i+j$). $p$ and $q$ are the linear coefficients of $\theta _{1}$ and $\theta _{2}$. Taking the nonlinear effect into account, the LP method expands the two basic frequencies as the power series of $\alpha$, $\beta$, in the form of

$$ \left \{ \begin{aligned} & {{\dot{\theta}}_{1}} = \sum \limits _{i,j} {{\omega _{ij}}{\alpha ^{i}}{ \beta ^{j}}} \\ & {{\dot{\theta}}_{2}} = \sum \limits _{i,j} {{\nu _{ij}}{\alpha ^{i}}{ \beta ^{j}}} \end{aligned} \right .. $$

(17)

We have obtained the lowest-order solution in Sect. 3.1:

$$ \begin{aligned} {\rho _{1010}} &= 1,{\rho _{0101}} = 1,\\ {\theta _{1010}} &= - \frac{{\omega _{0}^{2} + {c_{2}}}}{{{\omega _{0}}{c_{3}}}},{\theta _{0101}} = - \frac{{\nu _{0}^{2} + {c_{2}}}}{{{\nu _{0}}{c_{3}}}},\\ {\omega _{00}} &= {\omega _{0}},{\nu _{00}} = {\nu _{0}}. \end{aligned} $$

The lowest-order solution contains only cosine terms or sine terms in $\rho$ or $\theta$, respectively. Suppose that there are only cosine terms in $\rho$ and only sine terms in $\theta$ for the solution of order $n-1$ ($n > 1$). Substituting the previous solutions into Equation (15), its right functions only produce cosine terms in $\rho$ and only sine terms in $\theta$. As a result, the solution of order $n$ also satisfies the rule. In a word, the quasi-periodic solution of arbitrary order satisfying Equation (16) is proved by Mathematical Induction.

The above recursive process can be carried out to high orders with the aid of a computer. For symbolic computations on computers, actually the coefficients in Eq. (16) are treated. When solving the $n$-th order solution, extracting all terms of order $n$, one can obtain linear equations of the unknown and the known in the general form that

$$ \left \{ \begin{aligned} & \left [ { - {{\left ( {{\omega _{0}}p + {\nu _{0}}q} \right )}^{2}} - {c_{2}}} \right ]{\rho _{ijpq}} - {c_{3}}\left ( {{\omega _{0}}p + { \nu _{0}}q} \right ){\theta _{ijpq}} \\ &\quad = {\Phi _{ijpq}} + {\delta _{p1}}{\delta _{q0}}\left ( {2{\omega _{0}} + {c_{3}}{\theta _{1010}}} \right ){\omega _{i - 1,j}} \\ &\qquad {}+ {\delta _{p0}}{ \delta _{q1}}\left ( {2{\nu _{0}} + {c_{3}}{\theta _{0101}}} \right ){ \nu _{i,j - 1}} \\ & \left [ { - {{\left ( {{\omega _{0}}p + {\nu _{0}}q} \right )}^{2}} - {c_{7}}} \right ]{\theta _{ijpq}} + {c_{8}}\left ( {{\omega _{0}}p + { \nu _{0}}q} \right ){\rho _{ijpq}} \\ &\quad = {\phi _{ijpq}} + {\delta _{p1}}{\delta _{q0}}\left ( {2{\omega _{0}}{ \theta _{1010}} - {c_{8}}} \right ){\omega _{i - 1,j}} \\ &\qquad {}+ {\delta _{p0}}{ \delta _{q1}}\left ( {2{\nu _{0}}{\theta _{0101}} - {c_{8}}} \right ){ \nu _{i,j - 1}} \end{aligned} \right ., $$

(18)

where ${\Phi _{ijpq}}$ and ${\phi _{ijpq}}$ are the coefficients of the known terms produced by the right functions of Equation (15). The unknown $\rho _{ijpq}$, $\theta _{ijpq}$, $\omega _{i,j - 1}$, $\nu _{i,j - 1}$ are obtained from Equation (18) in the following three cases:

(1) If $p=1$ and $q=0$, Equation (18) can be reduced to

$$ \left \{ \begin{aligned} & \left ( { - {\omega _{0}}^{2} - {c_{2}}} \right ){\rho _{ijpq}} - {c_{3}}{ \omega _{0}}{\theta _{ijpq}} \\ &\quad = {\Phi _{ijpq}} + \left ( {2{\omega _{0}} + {c_{3}}{\theta _{1010}}} \right ){\omega _{i - 1,j}} \\ & {c_{8}}{\omega _{0}}{\rho _{ijpq}} + \left ( { - {\omega _{0}}^{2} - {c_{7}}} \right ){\theta _{ijpq}} \\ &\quad = {\phi _{ijpq}} + \left ( {2{ \omega _{0}}{\theta _{1010}} - {c_{8}}} \right ){\omega _{i - 1,j}} \end{aligned} \right .. $$

(19)

Since $\left ( { - {\omega _{0}}^{2} - {c_{2}}} \right )\left ( { - { \omega _{0}}^{2} - {c_{7}}} \right ) + {c_{3}}{c_{8}}\omega _{0}^{2} = 0$, for the above equation to have a solution, one requires that

$$ \begin{aligned} \frac{{ - \omega _{0}^{2} - {c_{2}}}}{{{c_{8}}{\omega _{0}}}} = \frac{{{\Phi _{ijpq}} + \left ( {2{\omega _{0}} + {c_{3}}{\theta _{1010}}} \right ){\omega _{i - 1,j}}}}{{{\phi _{ijpq}} + \left ( {2{\omega _{0}}{\theta _{1010}} - {c_{8}}} \right ){\omega _{i - 1,j}}}}. \end{aligned} $$

(20)

$\omega _{i - 1,j}$ is obtained from the above equation, in the form of

$$ \begin{aligned} &{\omega _{i - 1,j}} \\ & = - \frac{{\left ( {\omega _{0}^{2} + {c_{2}}} \right ){\phi _{ijpq}} + {c_{8}}{\omega _{0}}{\Phi _{ijpq}}}}{{\left [ {{\omega _{0}}\left ( {2{\omega _{0}} - 1} \right ) - {c_{2}}} \right ]{c_{8}} + \left [ {2\left ( {{\omega _{0}} + {c_{2}}} \right ) + {c_{3}}{c_{8}}} \right ]{\omega _{0}}{\theta _{1010}}}}. \end{aligned} $$

(21)

We set ${\theta _{ijpq}} = 0$, then

$$ {\rho _{ijpq}} = \left [ {{\Phi _{ijpq}} + \left ( {2{\omega _{0}} + {c_{3}}{ \theta _{1010}}} \right ){\omega _{i - 1,j}}} \right ]{\left ( { - { \omega _{0}}^{2} - {c_{2}}} \right )^{ - 1}}. $$

(2) If $p=0$ and $q=1$, Equation (18) can be reduced to

$$ \left \{ \begin{aligned} & \left ( { - {\nu _{0}}^{2} - {c_{2}}} \right ){\rho _{ijpq}} - {c_{3}}{ \nu _{0}}{\theta _{ijpq}} \\ &\quad = {\Phi _{ijpq}} + \left ( {2{\nu _{0}} + {c_{3}}{ \theta _{0101}}} \right ){\nu _{i,j - 1}} \\ & {c_{8}}{\nu _{0}}{\rho _{ijpq}} + \left ( { - {\nu _{0}}^{2} - {c_{7}}} \right ){\theta _{ijpq}} \\ &\quad = {\phi _{ijpq}} + \left ( {2{\nu _{0}}{ \theta _{0101}} - {c_{8}}} \right ){\nu _{i,j - 1}} \end{aligned} \right .. $$

(22)

Since $\left ( { - {\nu _{0}}^{2} - {c_{2}}} \right )\left ( { - {\nu _{0}}^{2} - {c_{7}}} \right ) + {c_{3}}{c_{8}}\nu _{0}^{2} = 0$, for the above equation to have a solution, one requires that

$$ \begin{aligned} \frac{{ - \nu _{0}^{2} - {c_{2}}}}{{{c_{8}}{\nu _{0}}}} = \frac{{{\Phi _{ijpq}} + \left ( {2{\nu _{0}} + {c_{3}}{\theta _{0101}}} \right ){\nu _{i,j - 1}}}}{{{\phi _{ijpq}} + \left ( {2{\nu _{0}}{\theta _{0101}} - {c_{8}}} \right ){\nu _{i,j - 1}}}}. \end{aligned} $$

(23)

$\nu _{i ,j-1}$ is obtained from the above equation, in the form of

$$ \begin{aligned} &{\nu _{i,j - 1}} \\ &= - \frac{{\left ( {\nu _{0}^{2} + {c_{2}}} \right ){\phi _{ijpq}} + {c_{8}}{\nu _{0}}{\Phi _{ijpq}}}}{{\left [ {{\nu _{0}}\left ( {2{\nu _{0}} - 1} \right ) - {c_{2}}} \right ]{c_{8}} + \left [ {2\left ( {{\nu _{0}} + {c_{2}}} \right ) + {c_{3}}{c_{8}}} \right ]{\nu _{0}}{\theta _{0101}}}}. \end{aligned} $$

(24)

We set ${\theta _{ijpq}} = 0$, then

$$ {\rho _{ijpq}} = \left [ {{\varphi _{ijpq}} + \left ( {2{\nu _{0}} + {c_{3}}{ \theta _{0101}}} \right ){\nu _{i,j - 1}}} \right ]{\left ( { - {\nu _{0}}^{2} - {c_{2}}} \right )^{ - 1}}. $$

(3) $\rho _{ijpq}$ and $\theta _{ijpq}$ can be directly solved from Equation (18) except the above two cases. There are no corrections to the basic frequencies in these general cases.

The indexes $i$, $j$, $p$, $q$ are loop variables in the LP algorithm. $\lvert p \rvert \le i$, $\lvert q \rvert \le j$, $p \ge 0$, and $p$, $q$ have the same parity as $i$, $j$, respectively. This is similar to the example in Jorba and Masdemont (1999). These properties of the loop variables ensure that all of the coordinates’ coefficients of order $n$ and the basic frequencies’ coefficients of order $n-1$ are computed from the equations of order $n$. The solution computed by the algorithm has to be truncated at finite orders in practice. Nevertheless, our quasi-periodic solution truncated at a high order provides a good approximation of the original system, and we will show that in the next section.

4 Numerical simulations

4.1 An example based on DPM

On one hand, we construct the high-order analytical solution based on the dynamical and physical properties of Didymos’s predicted model (DPM) in Michel et al. (2016). These properties are ${a_{\mathrm{{S}}}} = 103{\mathrm{{~m}}}$, ${b_{\mathrm{{S}}}} = 79{\mathrm{{~m}}}$, ${c_{\mathrm{{S}}}} = 66{\mathrm{{~m}}}$, $[L] = 1180~m$, $[M] = 5.3 \times {10^{11}}{\mathrm{{~kg}}}$, ${m_{\mathrm{{S}}}}/[M] = 0.0092$. We note that these values are different from the recent results obtained by Daly et al. (2023). The predicted model’s secondary is more elongated. Nevertheless, we still use the predicted model in accordance with the previous work by Wang and Hou (2020). Influence of the secondary’s shape on the stability will be discussed later. Table 1 lists coefficients of the analytical solution. We set $\alpha = 0.0003$, $\beta = 0.02$, ${\theta _{1\mathrm{{i}}}} = {\theta _{2\mathrm{{i}}}} = 45 ^{\circ}$ as an example, whose maximal libration angle is about $2^{\circ}$. Then the analytical orbit $\left ( {{\rho _{A}},{\theta _{A}}} \right )$ is obtained by Equation (16). On the other hand, we compute the numerical orbit $\left ( {{\rho _{N}},{\theta _{N}}} \right )$ by integrating the original EOM (see Equation (9)) with the initial values given by the analytical solution. To check the accuracy of the analytical solution, we compare it with the numerical results. Obviously, $\rho _{A} = \rho _{N}$, $\theta _{A} = \theta _{N}$ at the initial moment. The difference between $\left ( {{\rho _{A}},{\theta _{A}}} \right )$ and $\left ( {{\rho _{N}},{\theta _{N}}} \right )$ increases along with the time. The norm of the deviation $D\left ( t \right )$ in the phase space is used as an indicator of measuring the accuracy,

$$ \begin{aligned} D\left ( t \right ) &= \bigl({{\left ( {{\rho _{A}} - {\rho _{N}}} \right )}^{2}} + {{\left ( {{\theta _{A}} - {\theta _{N}}} \right )}^{2}} \\ &\quad {}+ {{\left ( {{p_{1A}} - {p_{1N}}} \right )}^{2}} + {{\left ( {{p_{2A}} - {p_{2N}}} \right )}^{2}}\bigr)^{1/2}, \end{aligned} $$

(25)

where $p_{1}$ and $p_{2}$ are the conjugated variables defined in Equation (4). In addition, it is convenient to define ${D_{\max }}\left ( t \right ) = \max \left ( {D(t)} \right )$, $t \in \left [ {{t_{0}},t} \right ]$ to eliminate the effect of periodic terms.

Table 1 Coefficients of the analytical solution

Figure 2 shows the accuracy of the analytical solution in the time interval $0 \le t \le {10^{3}}$. An obvious phenomenon in the figure is that the accuracy increases with an increase in the order of the analytical solution, which verifies the accuracy of the expansion (see Equation (10)) and the LP algorithm (see Sect. 3.2). However, the computational accuracy prevents the increase of the analytical solution’s accuracy when it is constructed to a high order. Currently, the double-precision floating point is used to compute the analytical solution in our FORTRAN program. Under the example parameters, the analytical solution of order 11 has the best performance, so the red line in the figure nearly coincides with the gold one. In our work, the analytical solution is always constructed to reach the best-performance order. The analytical solution’s accuracy can be further improved by using floating point with more bytes, but it is accurate enough to do further study. As shown in the left panel of Fig. 2, these lines rapidly oscillate in the short run due to the effect of periodic terms. Besides, there is a continual growth of the deviation in long-term evolution due to the truncation in the analytical frequencies.

Fig. 2

Time history of $D\left ( t \right )$ and ${D_{\max }}\left ( t \right )$. Dimensionless units are used in the coordinate axes. The deviations between the numerical solution and the analytical one of orders 5, 8, 11, and 12, are plotted in different colors

4.2 Valid domain in $\alpha -\beta$ plane

Since the discrepancy in the frequencies dominates the long-term accuracy of the analytical orbit, we introduce another accuracy criteria,

$$ \begin{aligned} {\Delta _{i}} = \lg \left ( {\lvert {{{{\dot{\theta}}_{i}}} - {f_{i}}} \rvert /{{{\dot{\theta}}_{i}}} } \right ), \quad i=1 \; or \; 2, \end{aligned} $$

(26)

which indicates the relative error between the basic frequency obtained from Equation (17) and its true value $f_{i}$. The accuracy criteria of the analytical solution of order 11 in $\alpha - \beta$ plane are calculated by the following four steps: (1) We fix the two initial phase angles, ${\theta _{1\mathrm{{i}}}} = {\theta _{2\mathrm{{i}}}} = 45 ^{\circ}$, and change the values of $\alpha$ and $\beta$. The $\alpha - \beta$ plane is divided into a $50\times 50$ grid, and every node indicates a particular orbit. (2) As for a specific node, the analytical solution of order 11 gives the positions and velocities at time $t = 0$. The discrete trajectory is computed by numerically integrating Equation (9). (3) $f_{1}$ and $f_{2}$ are then obtained by using the NAFF_UV code to analyze the two basic frequencies of the discrete trajectory (Skoufaris 2021; Laskar 1990; Laskar et al. 1992; Papaphilippou 2014). In a trajectory, we sample a value of $\theta$ every time step $\pi /2$, and a total of $2^{10}$ data are input into the NAFF_UV code for frequency analysis. (4) Substituting $f_{i}$ and the analytical ${{{\dot{\theta}}_{i}}}$ into Equation (26), $\Delta _{i}$ are immediately obtained.

Figure 3 can be used to estimate the valid domain of the analytical solution (truncated at order 11) for DPM in the $\alpha -\beta$ plane. What can be clearly seen in this figure is that the analytical solution’s accuracy decreases with an increase in the amplitude parameters $\alpha$ and $\beta$. The deeper the red, the larger the discrepancy in the frequencies. We believe that the analytical solution is not valid for those regions with very dark red color. In addition, some special structures remind us of the existence of resonance, and we will discuss this interesting dynamical mechanism in Sect. 5.

Fig. 3

Contour maps of $\Delta _{1}$ (left panel) and $\Delta _{2}$ (right panel) in the $\alpha -\beta$ plane. The bar is colored according to the values of $\Delta _{i}$

4.3 Quasi-periodic orbits

Once the initial conditions are given, the orbit is uniquely determined by Equation (9). We use the analytical solution to provide the initial conditions and transform the integrating results from the polar coordinates $\left ( {r,\theta } \right )$ to the Cartesian coordinates $\left ( {X, Y} \right )$ by $X = \left ( {{r_{0}} + \rho } \right ){\mathrm{{cos}}}\theta$ and $Y = \left ( {{r_{0}} + \rho } \right )\sin \theta$. Some example orbits are illustrated in Fig. 4. The blue orbit ($\alpha =0.005$) is far more elongated than the red orbit ($\beta =0.005$), which indicates that $\alpha$ has a main influence on the orbital amplitude if the two amplitude parameters are equal. When both of the long and the short period components exit, the quasi-periodic orbits never come back to previous positions in a ‘period’ due to the incommensurability of the two basic frequencies but move within limits for a long time.

Fig. 4

Some example orbits with different amplitude parameters. We set the maximal integration time $t_{\max}=10^{3}$, and ${\theta _{1\mathrm{{i}}}} = {\theta _{2\mathrm{{i}}}} = 45 ^{\circ}$ in the computation of these orbits

5 Stability, chaos and resonance

The numerical simulation reveals that the analytical solution is a good approximation of the quasi-periodic motion in the planar synchronous binary asteroid. In this section, we investigate the dynamics of the synchronous state with the help of the high-order solution. DPM is taken as an example to show the results.

5.1 Stable region for the synchronous state

When the 1:1 spin-orbit resonance occurs, the resonance angle $\theta$ librates within $\left ( {0^{\circ},360^{\circ}} \right )$. If $\theta > 90^{\circ}$, the angle would circulate because of the rotational symmetry in the planar sphere–ellipsoid model. Thus, the libration threshold is set at $90^{\circ}$ to judge whether the synchronous state is broken. As mentioned above, a combination of $\alpha$ and $\beta$ represents a particular orbit after fixing the two initial phases. We still set the maximal integration time $t_{\max}=10^{3}$, and ${\theta _{1\mathrm{{i}}}} = {\theta _{2\mathrm{{i}}}} = 45 ^{\circ}$. If $\theta _{N}$ is within the libration threshold of $90^{\circ}$ for a specific combination of $\alpha$ and $\beta$, it means that the corresponding synchronous state is stable, at least within the integration time.

As shown in Figs. 5(a) and 5(b), the synchronous state is preserved at the blue points, while it is broken at the red points within the integration time. The abscissa and the ordinate are the indicators of $\theta _{\max}$ and $e$, respectively. By using the linear solution to provide the initial conditions, Wang and Hou (2020) draw the stable region within a short integration time, and find the anti-correlation of $\theta$ and $e$. That is to say, for a synchronous binary asteroid, the larger its orbit eccentricity, the smaller the secondary’s libration amplitude. However, the stability contour map based on the linear solution and a short time integration (150 dimensionless time in Wang and Hou (2020) approximates to 38 dimensionless time in this paper) is unreliable, due to the accuracy limit of the solution and the inability for the short time integration to separate the stable orbits from the unstable ones. For example, extending the integration time from 38 to $10^{3}$ and still use the linear solution, the stability contour map is shown in Fig. 5(a). It seems that there is no longer an obvious anti-correlation in Fig. 5(a). However, the anti-correlation is further confirmed on a longer timescale by using the high-accuracy solution (truncated at order 11) to provide the initial conditions in Fig. 5(b). The figure also shows that the stable synchronous state of the system requires a small orbit eccentricity. Moreover, some special structures appear. For example, the red unstable ‘island’ encircled by the blue stable ‘water’ below the pentagram is related to the resonance of $\omega$ and $\nu$. We compute the discrete trajectory at the pentagram where $\alpha =0.0076$, $\beta =0.048$ as an example. The trajectory is shown in Fig. 5(c). Interestingly, the difference between the ratio of its two basic frequencies and 0.75 is less than $10^{-5}$, which confirms that the basic frequencies are trapped in 3:4 resonance. One should notice that the LP method is actually not feasible to construct the analytical solution of a resonance orbit due to the well-known small divisor problem, and the resonance orbit in Fig. 5(c) is computed by numerical integration.

Fig. 5

Stable region for the synchronous state and an example of the resonance orbit. Blue represents stable synchronous state while red represents broken synchronous state within $10^{3}$ dimensionless time in the stability contour maps (left and middle frames). The contour maps are firstly drawn on the $\alpha - \beta$ plane. Then we approximately transform the $\alpha - \beta$ plane into the $\theta _{\max} - e$ plane by the relationships shown in the abscissa and the ordinate. There are many 3:4 resonance orbits with different amplitudes around the pentagram, but they have similar shape shown in the right frame

5.2 Chaos in the 1-mLCE maps

The one-dimensional maximal Lyapunov characteristic exponent (1-mLCE) $\chi _{1}$ is widely used as a criterion to measure the chaoticity of an orbit (Tan et al. 2022; Dermott et al. 2021; Suková and Semerák 2013; Breiter et al. 2005). A very tiny disturbation on a chaotic orbit would cause rapid divergence. Denote the deviation between the original orbit and the disturbed one as $\boldsymbol{w}\left ( t \right )$. The 1-mLCE is defined as $\chi _{1}=\mathop {\lim }\limits _{t \to \infty } {t^{ - 1}}\ln \left ( {\left \| {\boldsymbol{w}\left ( t \right )} \right \|/\left \| { \boldsymbol{w}\left ( 0 \right )} \right \|} \right )$, and $\chi _{1}=0$ for a regular orbit (Skokos 2010). To compute the 1-mLCEs of the orbits in our model, we need the Hamilton equations (6) and the variational equations,

$$ \left \{ \begin{aligned} & {{\dot{w}}_{1}} = \frac{{{w_{3}}}}{\mu } \\ & {{\dot{w}}_{2}} = - \frac{{2{p_{2}}}}{{\mu {r^{3}}}}{w_{1}} + \left ( {\frac{1}{{\mu {r^{2}}}} + \frac{1}{{I_{\mathrm{{S}}}}}} \right ){w_{4}} \\ & {{\dot{w}}_{3}} = \left [ {\frac{{2\mu }}{{{r^{3}}}} + \frac{{6\mu \left ( {{A_{1}} + {A_{2}}\cos 2\theta } \right )}}{{{r^{5}}}} - \frac{{3p_{2}^{2}}}{{\mu {r^{4}}}}} \right ]{w_{1}}\\ &\hphantom{{{\dot{w}}_{3}} =}{} + \frac{{3\mu {A_{2}}\sin 2\theta }}{{{r^{4}}}}{w_{2}} + \frac{{2{p_{2}}}}{{\mu {r^{3}}}}{w_{4}} \\ & {{\dot{w}}_{4}} = \frac{{3\mu {A_{2}}\sin 2\theta }}{{{r^{4}}}}{w_{1}} - \frac{{2\mu {A_{2}}\cos 2\theta }}{{{r^{3}}}}{w_{2}} \end{aligned} \right .. $$

(27)

In practice, we cannot integrate the equations to infinity but compute the finite time 1-mLCE,

$$ \chi _{1}(t) = {t^{ - 1}}\ln \left ( {\left \| {\boldsymbol{w}\left ( t \right )} \right \|/\left \| {\boldsymbol{w}\left ( 0 \right )} \right \|} \right ), $$

through the numerical algorithm in Skokos (2010). The Lyapunov time, $t_{L}=1/\chi _{1}(t)$, is a conventional timescale for an orbit to become chaotic. Using the LP solution of order 11 (see Table 1) to provide initial orbital conditions, we compute the 1-mLCE maps for the dynamical system described in Sect. 4.1. The 1-mLCE map in our paper refers to the contour map of $\lg \chi _{1}(t)$ in the $\alpha -\beta$ plane with a fixed integration time $t_{\max}$ and fixed initial phase angles $\theta _{1 \mathrm{{i}}}$, $\theta _{2 \mathrm{{i}}}$. A total of forty-eight 1-mLCE maps in different combinations of ($t_{\max}$, $\theta _{1 \mathrm{{i}}}$, $\theta _{2 \mathrm{{i}}}$) are investigated in our study, and that is

$$ \begin{aligned} \left ( {{t_{\max }},{\theta _{1\mathrm{{i}}}},{\theta _{2\mathrm{{i}}}}} \right ) &\in \left \{ {{{10}^{3}},{{10}^{4}},{{10}^{5}}} \right \} \times \left \{ {\frac{\pi }{4},\frac{{3\pi }}{4},\frac{{5\pi }}{4}, \frac{{7\pi }}{4}} \right \} \\ &\quad {}\times \left \{ {\frac{\pi }{4}, \frac{{3\pi }}{4},\frac{{5\pi }}{4},\frac{{7\pi }}{4}} \right \}. \end{aligned} $$

(28)

For simplicity, some of the maps are presented in Fig. 6. After analyzing all of the maps, three plain facts are obtained: (1) The orbits in deep-red regions encircled by black lines are chaotic in the sense that $t_{L} \le t_{\max}$. The chaoticity increases with an increase in $\alpha$ and $\beta$. As mentioned above, if $r_{0}$ is taken as the dimensionless unit of length, $\beta$ is an indicator of the orbit eccentricity. The chaoticity of large eccentricity orbits forbid the stable synchronous state. (2) From the vertical view of Fig. 6, the finite time 1-mLCEs of regular orbit decrease with an increase in the integration time. (3) From the horizontal view of Fig. 6, different structures appear with different values of $\theta _{1 \mathrm{{i}}}$ and $\theta _{2 \mathrm{{i}}}$. These different structures are produced by periodic terms in the LP solution. Interestingly, some special structures do not change with different combinations of ($t_{\max}$, $\theta _{1 \mathrm{{i}}}$, $\theta _{2 \mathrm{{i}}}$) and appear in all of the maps. We believe that the unchangeable structures are related with the resonance of the basic frequencies.

Fig. 6

The 1-mLCE maps for the planar sphere–ellipsoid model of the DPM. In every panel, the corresponding fixed values of ($t_{\max}$, $\theta _{1 \mathrm{{i}}}$, $\theta _{2 \mathrm{{i}}}$) are given in the title and the black line where $t_{L}= t_{\max}$ is regarded as the boundary of chaotic and regular orbits. The bar is colored according to the values of $\lg \chi _{1}(t)$

5.3 Resonance of the basic frequencies

The resonance of the basic frequencies means $\dot{\theta}_{1}:\dot{\theta}_{2} = q:p$ where $p$ and $q$ are integers. We locate the resonances in the $\alpha -\beta$ plane in two ways. The first way is to substitute Equation (17) (truncated at order 10) into $p \dot{\theta}_{1} - q \dot{\theta}_{2}=0$, and then all of its feasible roots $(\alpha ,\beta )$ form the so-called resonance curve. Note that the resonance curve is computed with the help of the truncated analytical frequencies, so it gives the approximate locations of the $q:p$ resonance center. The second way is to utilize the NAFF_UV code to numerically analyze the frequencies of the orbits around the resonance curves. As shown in Fig. 7(b), there are only two main frequency peaks $f_{1}$ and $f_{2}$ for the regular orbit, but many haphazard peaks appear for the chaotic orbit. Thus, the analytical solution for the quasi-periodic motion is invalid at the chaotic region, even though $\alpha$ and $\beta$ are not large. Here we identify an orbit trapped into the $q:p$ resonance if the difference between $f_{1}: f_{2}$ and $q:p$ is less than 0.005. Figure 7(a) shows only the part of the 1-mLCE map where special structures appear. As can be seen from the figure, the numerical results of frequency analysis are in good agreement with the resonance curves. Some special structures of the map appear in the resonance regions, which indicates that the resonance is the mechanism to determine the stability boundary of the synchronous state.

Fig. 7

Left panel: resonance in the zoom-in 1-mLCE map. The solid lines of different colors indicate different types of resonances. Numerical frequency analysis verifies that these orbits in the marked points around the curves are trapped into corresponding $q:p$ resonance. Right panel: example amplitude–frequency chart of the regular orbit and the chaotic one

6 Conclusion and discussion

The main goal of the current study was to investigate the resonances that determine the stability boundary of the 1:1 spin-orbit resonance in a synchronous binary asteroid. The difference between our study and previous ones is twofold. First, the explicit high-order analytical solution is constructed and the complete spin-orbit coupling model is considered. We use the two-degree-of-freedom model consisting of a sphere and an ellipsoid to approximate the binary asteroid. The high-order analytical solution is constructed by the LP algorithm to describe the quasi-periodic motion around the EP where the strict 1:1 spin-orbit resonance locates. Second, stability, chaos, and resonance are studied. Specific resonances that determine the boundary of the stability region are identified with the help of the explicit solution. Findings of this study suggest that secondary resonances of basic frequencies play an important role in the evolution of a binary asteroid. During the evolution of binary asteroids, the mutual orbit may gradually migrate due to the tide and the BYORP effect (Jacobson and Scheeres 2011b). During this process, the secondary, being initially trapped in a synchronous state, may change its synchronous state during the migration when it crosses the boundary of the stability region (Jacobson et al. 2014).

Moreover, influence on the stability region from the mass parameter $m_{\mathrm{{S}}}$, the angular momentum parameter $r_{0}$ of the system, and the secondary’s shape parameters are investigated. Figure 8 presents contour maps for these general cases. The secondary’s mass and the mutual distance have little influence on the stable region, while the secondary’s elongation contributes more obviously to the instability. The upper limit of the libration angle reported in Fig. 8 puts a theoretical upper boundary on the secondary’s libration amplitude beyond which the synchronous state can no longer hold. The synchronous state can permit a large libration angle of the secondary. However, in the real world, due to its close distance from the primary, the secondary’s libration amplitude gradually damps to zero by the tidal dissipation, even if it is already tidally locked (Murray and Dermott 2000). The time scale of tidal dissipation is much shorter than the average lifetime of binary asteroids (Goldreich and Sari 2009; Jacobson and Scheeres 2011a), which means that the secondaries have enough time to damp its libration amplitude during its lifetime. As a result, most of the synchronous secondaries have small libration amplitudes (Pravec et al. 2016). We believe synchronous binaries with a secondary in libration with an large amplitude exist because theoretical simulations allow the binaries to do so (see Sect. 5.3 in Pravec et al. (2016)), and some physical processes such as the not-very-close planetary flyby can provide such a mechanism to excite the libration amplitude of the synchronous secondary (Meyer and Scheeres 2021). According to Pravec et al. (2016), the 3-$\sigma$ upper limit on the eccentricity of synchronous binaries can reach 0.20, which agrees with the result in Fig. 8. We agree that the reported orbit eccentricities of synchronous binaries are generally small. This phenomenon again can be explained by the tidal dissipation. The tide can continue to damp the orbit eccentricity even when the secondary is tidally locked. So synchronous binaries tend to have an orbit eccentricity smaller than the upper limit. Results in the current study put an upper limit on the orbit eccentricity once the mass ratio and distance w.r.t. the primary, and the elongation of the secondary are available. The general conclusion is that the maximum eccentricity is smaller when the secondary is more elongated. As a result, the general small orbit eccentricity may also be related to the generally large elongations of the secondary.

Fig. 8

Stable regions for the synchronous state and resonance curves in the test systems. To compute these figures, we set $t_{\max}=10^{3}$, ${\theta _{1\mathrm{{i}}}} = {\theta _{2\mathrm{{i}}}} = 45 ^{\circ}$. In the figures per column, we change a parameter among $r_{0}$, $m_{\mathrm{{S}}}/[M]$, and $a_{\mathrm{{S}}}/b_{\mathrm{{S}}}$, and fix other parameters described in Sect. 4.1

The current study focuses on the planar configuration, with the purpose of finding the planar secondary resonances that limit the free libration amplitude and the mutual orbit eccentricity of synchronous binary asteroids. One possible extension is to construct non-planar analytical solutions around the exact synchronous state. In such a case, even using the constraint from the conservation of total angular momentum, the reduced dynamical system is much more complicated (Tan et al. 2023), but the construction of an analytical solution to high order is possible. By investigating the relationship between the fundamental frequencies and the out-of-plane amplitude, we are able to find the secondary resonances influencing the secondary’s obliquity.

Appendix:  The coefficients in Equation (10)

$$\begin{aligned} & {c_{1}} = - \frac{{3\left ( {{A_{1}} + {A_{2}}} \right )}}{{2r_{0}^{4}}} - \frac{1}{{r_{0}^{2}}} + \frac{{{K^{2}}{r_{0}}}}{{{\Upsilon ^{2}}}}, \\ &{c_{2}} = \frac{{6\left ( {{A_{1}} + {A_{2}}} \right )}}{{r_{0}^{5}}} + \frac{2}{{r_{0}^{3}}} + \frac{{{K^{2}}\left ( {{I_{\mathrm{{S}}}} - 3\mu r_{0}^{2}} \right )}}{{{\Upsilon ^{3}}}}, \\ & {c_{3}} = \frac{{2{r_{0}}{I_{\mathrm{{S}}}}K}}{{{\Upsilon ^{2}}}},\quad {c_{4}} = \frac{{{r_{0}}I_{\mathrm{{S}}}^{2}}}{{{\Upsilon ^{2}}}},\quad {c_{7}} = - \frac{{2{A_{2}}\Upsilon }}{{{I_{\mathrm{{S}}}}r_{0}^{5}}}, \\ &{c_{8}} = - \frac{{2K}}{{{r_{0}}\Upsilon }},\quad {c_{9}} = - \frac{{2{I_{\mathrm{{S}}}}}}{{{r_{0}}\Upsilon }}, \\ & {c_{5}} = 2\frac{{{I_{\mathrm{{S}}}}K}}{{{\mu ^{2}}}}\left [ {{r_{0}}F \left ( i \right ) + F\left ( {i - 1} \right )} \right ], \\ & {c_{10}} = \frac{{2K}}{{{I_{\mathrm{{S}}}}}}\left [ {{{\left ( { - {r_{0}}} \right )}^{ - i - 1}} + {r_{0}}f\left ( i \right ) + f\left ( {i - 1} \right )} \right ], \\ & {c_{6}} = \frac{{I_{\mathrm{{S}}}^{2}}}{{{\mu ^{2}}}}\left [ {{r_{0}}F \left ( i \right ) + F\left ( {i - 1} \right )} \right ], \\ & {c_{11}} = 2\left [ {{{\left ( { - {r_{0}}} \right )}^{ - i - 1}} + {r_{0}}f \left ( i \right ) + f\left ( {i - 1} \right )} \right ] \end{aligned}$$

(A.1)

$$ \begin{aligned} {\varphi _{ij}} & = {\delta _{j,0}} \left\{ \frac{{{K^{2}}}}{{{\mu ^{2}}}}\left [ {{r_{0}}F\left ( i \right ) + F \left ( {i - 1} \right )} \right ] \right.\\ &\left.\quad {}+ {{\left ( { - 1} \right )}^{i + 1}} \frac{{\left ( {i + 1} \right )}}{{r_{0}^{i + 2}}}\left [ {1 + \frac{{\left ( {i + 2} \right )\left ( {i + 3} \right )\left ( {{A_{1}} + {A_{2}}} \right )}}{{4r_{0}^{2}}}} \right ] \right\} \\ &\quad {} + {\Delta _{i,1}}{\Delta _{i,2}}{\Delta _{j,0}}{\Delta _{j,\lfloor \left ( {i + 1} \right )/2 \rfloor}}{\left ( { - 1} \right )^{i - j + 1}} \\ &\quad {}\times\frac{{{2^{2j - 2}}\left ( {i - 2j + 1} \right )\left ( {i - 2j + 2} \right )\left ( {i - 2j + 3} \right ){A_{2}}}}{{\left ( {2j} \right )!r_{0}^{i - 2j + 4}}} \\ &\quad {} + {\delta _{i \bmod 2,0}}{\delta _{j,\lfloor \left ( {i + 1} \right )/2 \rfloor}}{\left ( { - 1} \right )^{j + 1}} \frac{{3{A_{2}}}}{{2r_{0}^{4}}} \frac{{{2^{2j}}}}{{\left ( {2j} \right )!}} \end{aligned} $$

(A.2)

$$ \begin{aligned} {\psi _{ij}} &= {\left ( { - 1} \right )^{i - j + 1}} \frac{{{2^{2j - 2}}\left ( {i - 2j + 2} \right )\left ( {i - 2j + 3} \right )}}{{\left ( {2j - 1} \right )!r_{0}^{i - 2j + 4}}} \\ &\quad {}\times\left [ { \frac{{\left ( {i - 2j + 4} \right )\left ( {i - 2j + 5} \right )}}{{12r_{0}^{2}}} + \frac{\mu }{{{I_{\mathrm{{S}}}}}}} \right ]{A_{2}} \end{aligned} $$

(A.3)

Note that we introduce the following functions in the above expressions,

$$ \begin{aligned} f\left ( i \right ) &= \frac{1}{{2\sqrt { - {I_{\mathrm{{S}}}}/\mu } }} \left [ {{\left ( { \frac{{\sqrt { - {I_{\mathrm{{S}}}}/\mu } - {r_{0}}}}{{{I_{\mathrm{{S}}}}/\mu + r_{0}^{2}}}} \right )}^{i + 1}}\right.\\ &\quad {}\left. + {{\left ( { - 1} \right )}^{i}}{{\left ( { \frac{{\sqrt { - {I_{\mathrm{{S}}}}/\mu } + {r_{0}}}}{{{I_{\mathrm{{S}}}}/\mu + r_{0}^{2}}}} \right )}^{i + 1}} \right ], \\ F\left ( i \right ) &=\! \left \{ \textstyle\begin{array}{l} \left [ {{r_{0}}\sqrt { - {I_{\mathrm{{S}}}}/\mu } - {I_{\mathrm{{S}}}}/\mu \left ( {2 + i} \right )} \right ]{\left ( {\sqrt { - {I_{\mathrm{{S}}}}/ \mu } - {r_{0}}} \right )^{i + 2}} \\ - {\left ( { - 1} \right )^{i}}\left [ {r{{\sqrt { - {I_{\mathrm{{S}}}}/ \mu } }_{0}} + {I_{\mathrm{{S}}}}/\mu \left ( {2 + i} \right )} \right ] \\\quad {}\times{\left ( {\sqrt { - {I_{\mathrm{{S}}}}/\mu } + {r_{0}}} \right )^{i + 2}} \end{array}\displaystyle \hspace{-3pt} \right \} \\ &\quad {\left [ {4{{\left ( {{I_{\mathrm{{S}}}}/\mu } \right )}^{2}}{{\left ( {{I_{ \mathrm{{S}}}}/\mu + r_{0}^{2}} \right )}^{i + 2}}} \right ]^{ - 1}}, \\ {\delta _{i,j}}& = \left \{ \textstyle\begin{array}{cc} {1,} & {i = j} \\ {0,} & {i \ne j} \end{array}\displaystyle \right ., \quad {\Delta _{i,j}} = \left \{ \textstyle\begin{array}{cc} {0,} & {i = j} \\ {1,} & {i \ne j} \end{array}\displaystyle \right ., \quad \Upsilon = \mu r_{0}^{2} + {I_{\mathrm{{S}}}}. \end{aligned} $$

(A.4)