The Spin–Orbit Resonances of the Solar System: A Mathematical Treatment Matching Physical Data

Abstract

In the mathematical framework of a restricted, slightly dissipative spin–orbit model, we prove the existence of periodic orbits for astronomical parameter values corresponding to all satellites of the Solar System observed in exact spin–orbit resonance.

1 Introduction and Results

1.1 Satellites in Spin–Orbit Resonance

One of the many fascinating features of the Solar System is the presence of moons moving in a “synchronous” way around their planet, as experienced, for example, by earthlings looking always on the same, familiar face of their satellite. Indeed, 18 moons of our Solar System move in so-called 1:1 spin–orbit resonance: while performing a complete revolution on an (approximately) Keplerian ellipse around their principal body, they also complete a rotation around their spin axis (which is—again, approximately—perpendicular to the revolution plane); in this way, these moons always show the same side to their host planet.

The list of these 18 moons is as follows: Moon (Earth); Io, Europa, Ganymede, Callisto (Jupiter); Mimas, Enceladus, Tethys, Dione, Rhea, Titan, Iapetus (Saturn); Ariel, Umbriel, Titania, Oberon, Miranda (Uranus); Charon (Pluto); minor bodies with mean radius smaller than 100 km are not considered (see, however, Appendix 3).

There is only one more occurrence of spin–orbit resonance in the Solar System: the strange case of the 3:2 resonance of Mercury around the Sun (i.e., Mercury rotates three times on its spin axis, while making two orbital revolutions around the Sun).

In this paper we discuss a mathematical theory which is consistent with the existence of all spin–orbit resonances of the Solar System; in other words, we prove a theorem, in a framework of a well-known simple “restricted spin–orbit model,” establishing the existence of periodic orbits for parameter values corresponding to all the satellites (or Mercury) in our Solar System observed in spin–orbit resonance.

We remark that, in dealing with mathematical models trying to describe physical phenomena, one may be able to rigorously prove theorems only for parameter values, typically, somewhat smaller than the physical ones; on the other hand, for the true physical values, typically, one only obtains numerical evidence. In the present case, thanks to sharp estimates, we are able to fill such a gap and prove rigorous results for the real parameter values. Moreover, such results might also be an indication that the mathematical model adopted is quite effective in describing the physics.

1.2 The Mathematical Model

We consider a simple—albeit nontrivial—model in which the center of mass of the satellite moves on a given two-body Keplerian orbit focused on a massive point (primary body) exerting gravitational attraction on the body of the satellite modeled by a triaxial ellipsoid with equatorial axes $a\ge b>0$ and polar axis $c$; the spin polar axis is assumed to be perpendicular to the Keplerian orbit plane;¹ finally, we include also small dissipative effects (due to the possible internal nonrigid structure of the satellite), according to the “viscous-tidal model, with a linear dependence on the tidal frequency” (Correia and Laskar 2004): essentially, the dissipative term is given by the average over one revolution period of the so-called MacDonald’s torque (MacDonald 1964); compare (Peale 2005).

For a discussion of this model, see (Celletti 1990); for further references, see (Danby 1962; Goldreich and Peale 1967; Wisdom 1987; Celletti 2010); for a different [partial differential equation (PDE)] model, see (Bambusi and Haus 2012).

The differential equation governing the motion of the satellite is then given by

$$\begin{aligned} \ddot{x} + {\eta } (\dot{x} - {\nu })+{\varepsilon }f_x(x,t)=0, \end{aligned}$$

(1)

where:

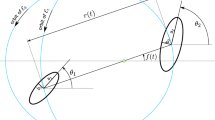
• (a) $x$ is the angle (mod $2{\pi }$) formed by the direction of (say) the major equatorial axis of the satellite with the direction of the semi-major axis of the Keplerian ellipse plane; “dot” represents derivative with respect to $t$, where $t$ (also defined mod $2{\pi }$) is the mean anomaly (i.e., the ellipse area between the semi-major axis and the orbital radius $\rho _{\mathbf{e}}$ divided by the total area times $2{\pi }$) and $\mathbf{e}$ is the eccentricity of the ellipse;

• (b) The dissipation parameters ${\eta } = K \Omega _\mathbf{e}$ and ${\nu }=\nu _\mathbf{e}$ are real-analytic functions of the eccentricity $\mathbf{e}$: $K \ge 0$ is a physical constant depending on the internal (nonrigid) structure of the satellite, and²

  $$\begin{aligned} \Omega _\mathbf{e}&:= \left( 1 + 3\mathbf{e}^2 + \frac{3}{8}\mathbf{e}^4 \right) \frac{1}{\left( 1-\mathbf{e}^2\right) ^{9/2} },\nonumber \\ N_\mathbf{e}&:= \left( 1 + \frac{15}{2}\mathbf{e}^2 + \frac{45}{8}\mathbf{e}^4 + \frac{5}{16}\mathbf{e}^6 \right) \frac{1}{\left( 1-\mathbf{e}^2\right) ^{6} },\nonumber \\ \nu _\mathbf{e}&:= \frac{N_\mathbf{e}}{\Omega _\mathbf{e}}\ . \end{aligned}$$

  (2)

• (c) The constant ${\varepsilon }$ measures the oblateness (or “equatorial ellipticity”) of the satellite and is defined as $\varepsilon =\frac{3}{2}\, \frac{B-A}{C}$, where $A\le B$ and $C$ are the principal moments of inertia of the satellite ($C$ being referred to the polar axis);

• (d) The function $f$ is the (“dimensionless”) Newtonian potential given by

  $$\begin{aligned} f(x,t):=-\frac{1}{2 \rho _\mathbf{e}(t)^3} \cos (2x-2\mathrm{f}_\mathbf{e}(t)), \end{aligned}$$

  (3)

  where $\rho _\mathbf{e}(t)$ and $\mathrm{f}_\mathbf{e}(t)$ are, respectively, the (normalized) orbital radius

  $$\begin{aligned} \rho _\mathbf{e}(t):=1-\mathbf{e}\cos (u_\mathbf{e}(t)) \end{aligned}$$

  (4)

  and the polar angle (see³ Fig. 1); the eccentric anomaly $u=u_\mathbf{e}(t)$ is defined implicitly by the Kepler equation⁴

  $$\begin{aligned} t=u-\mathbf{e}\sin (u). \end{aligned}$$

  (5)

  Notice that the Newtonian potential $f(x,t)$ is a doubly periodic function of $x$ and $t$, with periods $2{\pi }$.

Fig. 1

Triaxial satellite revolving on a rescaled Keplerian ellipse (equatorial section)

Remarks

• (i) The principal moments of an ellipsoid of mass $m$ and with axes $a$, $b$, and $c$ are given by

  $$\begin{aligned} A = \frac{1}{5} m \left( b^2 + c^2\right) ,\quad B = \frac{1}{5} m \left( a^2 + c^2\right) , \quad C = \frac{1}{5} m \left( a^2 + b^2\right) . \end{aligned}$$

  The oblateness $\varepsilon$ is then given by

  $$\begin{aligned} \varepsilon = \frac{3}{2} \frac{B-A}{C} = \frac{3}{2} \frac{a^2 - b^2}{a^2 + b^2} . \end{aligned}$$

  (6)

• (ii) There is no universally accepted determination of the internal rigidity constant $K$ for most satellites of the Solar System.⁵ For the Moon and Mercury an accepted value is ${\sim }10^{-8}$; see, e.g., (Celletti 1990). However, for our analysis to hold it will be enough that $\eta \le 0.008$ for the moons and $\eta \le 0.001$ for Mercury.

The known physical parameter values of the 18 moons of the Solar System needed for our analysis are reported in Table 1.⁶

Table 1 Physical data of the moons in 1:1 spin–orbit resonance (http://ssd.jpl.nasa.gov/?sat_phys_par and http://ssd.jpl.nasa.gov/?sat_elem)

The corresponding data for Mercury are presented in Table 2.

Table 2 Physical data for Mercury in 3:2 spin–orbit resonance (http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html and http://solarsystem.nasa.gov/planets/charchart.cfm)

1.3 Existence Theorem for Solar System Spin–Orbit Resonances

In this framework, a $p$:$q$ spin–orbit resonance (with $p$ and $q$ co-prime nonvanishing integers) is, by definition, a solution $t\in {\mathbb {R}}\rightarrow x(t)\in {\mathbb {R}}$ of (1) such that

$$\begin{aligned} x(t+ 2 \pi q) = x(t) + 2 \pi p; \end{aligned}$$

(7)

indeed, for such orbits, after $q$ revolutions of the orbital radius, $x$ has made $p$ complete rotations.⁷

Our main result can, now, be stated as follows:

Theorem

(Moons) The differential equation (1) (a)$\div$(d) admits spin–orbit resonances (7) with $p=q=1$ provided e, $\nu$, and $\varepsilon$ are as in Table 1 and $0 \le \eta \le 0.008$.

(Mercury) The differential equation (1) (a)$\div$(d) admits spin–orbit resonances (7) with $p=3$ and $q=2$ provided e, $\nu$, and $\varepsilon$ are as in Table 2 and $0 \le \eta \le 0.001$.

In Biasco and Chierchia (2009) (compare Theorem 1.2), existence of spin–orbit resonances with $q=1,2,4$ and any $p$ (co-prime with $q$) is proved,⁸ while in Celletti and Chierchia (2009), quasi-periodic solutions corresponding to $p/q$ irrational are studied in the same model. In Biasco and Chierchia (2009), no explicit computations of constants (size of admissible $\varepsilon$, size of admissible $\eta$, etc.) were carried out.

The main point of this paper is to compute all constants explicitly in order to get nearly optimal estimates and include all cases of physical interest.

2 Proof of the Theorem

2.1 Step 1: Reformulation of the Problem of Finding Spin–Orbit Resonances

Let $x(t)$ be a $p$:$q$ spin–orbit resonance and let $u(t):= x(qt)-pt-\xi$. Then, by (7) and choosing $\xi$ suitably, one sees immediately that $u$ is $2{\pi }$-periodic and satisfies the differential equation

$$\begin{aligned} u''(t)+{\hat{\eta }}\,\left( u'(t)-{\hat{\nu }}\,\right) +{\hat{\varepsilon }}\,f_x\left( \xi + pt +u(t), qt\right) =0\ ,\quad \langle u\rangle = 0, \end{aligned}$$

(8)

where $\langle \cdot \rangle$ denotes the average over the period⁹ and

$$\begin{aligned} {\hat{\eta }}\,:= q \eta ,\quad {\hat{\nu }}\,:= q \nu -p,\quad {\hat{\varepsilon }}\,:= q^2 \varepsilon . \end{aligned}$$

(9)

Separating the linear part from the nonlinear one, we can rewrite (8) as follows: let

$$\begin{aligned} \left\{ \begin{array}{l} Lu:=u''+{\hat{\eta }}\,u'\\ \left[ \Phi _\xi (u)\right] (t) := {\hat{\eta }}\,{\hat{\nu }}\,-{\hat{\varepsilon }}\,f_x\left( \xi + pt +u(t),qt\right) \end{array}\right. \end{aligned}$$

(10)

then, the differential equation in (8) is equivalent to

$$\begin{aligned} Lu=\Phi _\xi (u). \end{aligned}$$

(11)

2.2 Step 2: The Green Operator ${\mathcal G}=L^{-1}$

Let $C^k_\mathrm{per}$ be the Banach space of $2\pi$-periodic $C^k({\mathbb {R}})$ functions endowed with the $C^k$-norm;¹⁰ let ${C^{k}_\mathrm{per,0}}$ be the closed subspace of $C^k_\mathrm{per}$ formed by functions with vanishing average over $[0,2\pi ]$; finally, denote by ${\mathbb {B}}:={C^{0}_\mathrm{per,0}}$ the Banach space of $2{\pi }$-periodic continuous functions with zero average (endowed with the sup-norm).

The linear operator $L$ defined in (10) maps injectively $C^2_\mathrm{per, 0}$ onto ${\mathbb {B}}$; the inverse operator (the “Green operator”) ${\mathcal G}=L^{-1}$ is a bounded linear isomorphism. Indeed, the following elementary lemma holds:

Lemma 2.1

Let ${\hat{\eta }}\,<2/\pi$. Then¹¹

$$\begin{aligned} \Vert {\mathcal G}\Vert _{L({\mathbb {B}},{\mathbb {B}})} \le \left( 1+{\hat{\eta }}\,\frac{\pi }{2}\left( 1-{\hat{\eta }}\,\frac{\pi }{2}\right) ^{-1}\right) \frac{\pi ^2}{8}. \end{aligned}$$

In particular, assuming

$$\begin{aligned} {\hat{\eta }}\,\le \frac{\pi }{5}\left( \frac{10}{\pi ^2}-1 \right) ,\;\mathrm{i.e.},\;\eta \le \left\{ \begin{array}{ll} \frac{\pi }{5}\left( \frac{10}{\pi ^2}-1 \right) =0.0083\ldots ,\quad &{} \mathrm{if}\ (p,q)=(1,1) \\ \frac{\pi }{10}\left( \frac{10}{\pi ^2}-1 \right) =0.0041\ldots ,\quad &{} \mathrm{if}\ (p,q)=(3,2) \end{array}\right. \nonumber \\ \end{aligned}$$

(12)

one gets

$$\begin{aligned} \Vert {\mathcal G}\Vert _{L({\mathbb {B}},{\mathbb {B}})} \le \frac{5}{4}. \end{aligned}$$

(13)

The proof of the above lemma is based on the following elementary result, whose proof is given in¹² Appendix 1:

Lemma 2.2

$$\begin{aligned}&\qquad \qquad v\in {C^{1}_\mathrm{per,0}} \qquad \Longrightarrow \qquad \Vert v\Vert _{C^0}\le \frac{\pi }{2}\Vert v'\Vert _{C^0}\end{aligned}$$

(14)

$$\begin{aligned}&\qquad \qquad v\in {C^{2}_\mathrm{per,0}} \qquad \Longrightarrow \qquad \Vert v\Vert _{C^0}\le \frac{\pi ^2}{8}\Vert v''\Vert _{C^0} \end{aligned}$$

(15)

Proof of Lemma 2.1

Given $g\in {\mathbb {B}}$ with $\Vert g\Vert _{C^0}=1$ we have to prove that, if $u\in {C^{2}_\mathrm{per,0}}$ is the unique solution of $u''+{\hat{\eta }}\,u'=g$ with $\langle u\rangle =0$, then

$$\begin{aligned} \Vert u\Vert _{C^0} \le \left( 1+{\hat{\eta }}\,\frac{\pi }{2}\left( 1-{\hat{\eta }}\,\frac{\pi }{2}\right) ^{-1}\right) \frac{\pi ^2}{8}. \end{aligned}$$

(16)

We note that, setting $v:=u'$, we have that $v\in {\mathbb {B}}$ and $v'=-{\hat{\eta }}\,v+g$. Then, we get

$$\begin{aligned} \Vert v\Vert _{C^0} \mathop {\le }\limits ^{(14)}\frac{\pi }{2}\Vert -{\hat{\eta }}\,v+g\Vert _{C^0} \le \frac{\pi }{2} \left( {\hat{\eta }}\,\Vert v\Vert _{C^0}+1\right) , \end{aligned}$$

which implies

$$\begin{aligned} \Vert u'\Vert _{C^0}=\Vert v\Vert _{C^0} \le \left( 1-\frac{\pi }{2}{\hat{\eta }}\,\right) ^{-1} \frac{\pi }{2}. \end{aligned}$$

(17)

Since $u''=-{\hat{\eta }}\,u' +g$, we have

$$\begin{aligned} \Vert u\Vert _{C^0} \mathop {\le }\limits ^{(15)}\frac{\pi ^2}{8}\Vert -{\hat{\eta }}\,u'+g\Vert _{C^0} \le \frac{\pi ^2}{8} \left( 1+{\hat{\eta }}\,\Vert u'\Vert _{C^0}\right) , \end{aligned}$$

and (16) follows by (17). $\square$

2.3 Step 3: Lyapunov–Schmidt Decomposition

Solutions of (11) are recognized as fixed points of the operator ${\mathcal G}\circ \Phi _\xi$:

$$\begin{aligned} u={\mathcal G}\circ \Phi _\xi (u)\ , \end{aligned}$$

(18)

where $\xi$ appears as a parameter.

To solve Eq. (18), we shall perform a Lyapunov–Schmidt decomposition. Let us denote by $\hat{\Phi }_\xi : C^0_\mathrm{per}\rightarrow {\mathbb {B}}={C^{0}_\mathrm{per,0}}$ the operator

$$\begin{aligned} {\hat{\Phi }}_\xi (u)&:= \frac{1}{{\hat{\varepsilon }}\,}\, \left[ \Phi _\xi (u) -\langle \Phi _\xi (u) \rangle \right] \\&:= - f_x\left( \xi + pt +u(t), qt\right) + \phi _u(\xi ) , \nonumber \end{aligned}$$

(19)

where

$$\begin{aligned} \phi _u(\xi ) :=\frac{1}{2\pi }\int \limits _0^{2\pi } f_x\left( \xi + pt +u(t;\xi ), qt \right) \mathrm{d}t\ . \end{aligned}$$

(20)

Then, Eq. (18) can be split into a “range equation”

$$\begin{aligned} u ={\hat{\varepsilon }}\,{\mathcal G} \circ {\hat{\Phi }}_\xi (u) \end{aligned}$$

(21)

[where $u=u(\cdot ;\xi )$] and a “bifurcation (or kernel) equation”

$$\begin{aligned} \phi _u(\xi )=\frac{{\hat{\eta }}\,{\hat{\nu }}\,}{{\hat{\varepsilon }}\,}\quad \Longleftrightarrow \quad \left\langle \Phi _\xi \left( u(\cdot ;\xi \right) \right\rangle =0 . \end{aligned}$$

(22)

Remark 2.3

• (i) If $(u,\xi )\in {\mathbb {B}}\times [0,2\pi ]$ solves (21) and (22), then $x (t)$ solves (1).

• (ii) $\forall \xi \in [0,2\pi ]$, ${\hat{\Phi }}_\xi \in {C}^1({\mathbb {B}},{\mathbb {B}})$; indeed, $\forall (u,\xi )\in {\mathbb {B}}\times [0,2\pi ]$,

  $$\begin{aligned} \Vert {\hat{\Phi }}_\xi (u)\Vert _{{C}^0}\le 2\sup _{\mathbb {T}^2}|f_x|,\quad \Vert D_u{\hat{\Phi }}_\xi \Vert _{\mathcal {L}({\mathbb {B}},{\mathbb {B}})}\le 2\sup _{\mathbb {T}^2}|f_{xx}|. \end{aligned}$$

  (23)

The usual way to proceed to solve (21) and (22) is the following:

• 1. For any $\xi \in [0,2\pi ]$, find $u=u(\cdot ;{\xi })$ solving (21);

• 2. Insert $u=u(\cdot ,\xi )$ into the kernel equation (22) and determine $\xi \in [0,2\pi ]$ so that (22) holds.

2.4 Step 4: Solving the Range Equation (Contracting Map Method)

For ${\hat{\varepsilon }}\,$ small the range equation is easily solved by standard contraction arguments.

Let $R:=\frac{5}{2}{\hat{\varepsilon }}\,\sup _{\mathbb {T}^2}|f_x|$ and let

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbb {B}}_{R}:=\left\{ v\in {\mathbb {B}}:\ \Vert v\Vert _{C^0}\le R\right\} \\ \varphi :\ v\in {\mathbb {B}}_{R}\rightarrow \varphi (v):={\hat{\varepsilon }}\,{\mathcal G} \circ \hat{\Phi }_\xi (v). \end{array}\right. \end{aligned}$$

(24)

Proposition 2.4

Assume that ${\hat{\eta }}\,$ satisfies (12) and that

$$\begin{aligned} \frac{5}{2}{\hat{\varepsilon }}\,\sup _{\mathbb {T}^2}|f_{xx}|<1. \end{aligned}$$

(25)

Then, for every ${\xi }\in [0,2{\pi }]$, there exists a unique $u:=u(\cdot ;{\xi })\in {\mathbb {B}}_{R}$ such that ${\varphi }(u)=u$.

Proof

By (12) and (23) the map ${\varphi }$ in (24) maps ${\mathbb {B}}_{R}$ into itself and is a contraction with Lipschitz constant smaller than 1 by (25). The proof follows by the standard fixed point theorem. $\square$

Recalling (3), (4), and (9), the “range condition” (25) writes

$$\begin{aligned} \varepsilon <\left\{ \begin{array}{ll} \frac{(1-\mathbf{e})^3}{5},\quad &{} \mathrm{if}\ (p,q)=(1,1), \\ \ \\ \frac{(1-\mathbf{e})^3}{20},\quad &{} \mathrm{if}\ (p,q)=(3,2). \end{array}\right. \end{aligned}$$

(26)

2.5 Step 5: Solving the Bifurcation Eq. (22)

The function $\phi _u(\xi )$ in (20) can be written as

$$\begin{aligned} \phi (\xi )&= \phi ^{(0)}(\xi )+{\hat{\varepsilon }}\,\tilde{\phi }^{(1)}_u(\xi ;{\hat{\varepsilon }}\,) \end{aligned}$$

(27)

with

$$\begin{aligned} \phi ^{(0)}(\xi ) := \frac{1}{2\pi }\int \limits _0^{2\pi }f_x (\xi +pt,qt)\mathrm{d}t. \end{aligned}$$

(28)

By (24), for $\varepsilon$ satisfying (26),

$$\begin{aligned} \sup _{ \xi \in [0,2\pi ] } |\tilde{\phi }^{(1)}_u| \le \sup _{\mathbb {T}^2}|f_{xx}| \frac{R}{{\hat{\varepsilon }}\,}\le \frac{5}{2} \left( \sup _{\mathbb {T}^2}|f_{x}|\right) \left( \sup _{\mathbb {T}^2}|f_{xx}|\right) . \end{aligned}$$

(29)

By (3), (4), for $\varepsilon$ satisfying (26), one finds immediately that

$$\begin{aligned} \sup _{ \xi \in [0,2\pi ] } |\tilde{\phi }^{(1)}_u|\le M_1:=\frac{5}{(1-\mathbf{e})^6}. \end{aligned}$$

(30)

Let us, now, have a closer look at the zero-order part $\phi ^{(0)}$. The Newtonian potential $f$ has the Fourier expansion

$$\begin{aligned} f(x,t) = \sum _{j \in \mathbb Z, j \ne 0} \alpha _j \cos (2x - jt), \end{aligned}$$

(31)

where the Fourier coefficients $\alpha _j=\alpha _j(\mathbf{e})$ coincide with the Fourier coefficients of

$$\begin{aligned} G_\mathbf{e}(t):= -\frac{e^{2i \mathrm{f}_\mathbf{e}(t)}}{2\rho _e(t)^3}= \sum _{j\in {\mathbb {Z}},j\ne 0} \alpha _j \exp (ijt) \end{aligned}$$

(32)

(see Appendix 2). Thus,

$$\begin{aligned} f_x (\xi +pt,qt)=-2 \sum _{j\in {\mathbb Z},\ j\ne 0}\alpha _j \sin (2\xi +(2p-jq)t), \end{aligned}$$

and one finds

$$\begin{aligned} \phi ^{(0)}(\xi ) =\left\{ \begin{aligned} -2\alpha _{2}\sin (2\xi ),&\quad \mathrm{if}\ (p,q)=(1, 1), \\ -2\alpha _{3}\sin (2\xi ),&\quad \mathrm{if}\ (p,q)=(3,2).\end{aligned}\right. \end{aligned}$$

(33)

Define

$$\begin{aligned} a_{pq}:= \left\{ \begin{aligned} 2|\alpha _{2}|- \hat{\varepsilon }M_1,&\quad \mathrm{if}\ (p,q)=(1,1), \\ 2|\alpha _{3}|- \hat{\varepsilon }M_1,&\quad \mathrm{if}\ (p,q)=(3,2).\end{aligned}\right. \end{aligned}$$

(34)

Then, from (27), (30), (33), and (34), it follows that $\phi ([0,2{\pi }])$ contains the interval $[-a_{pq},a_{pq}]$, which is not empty provided [recall (9) and (30)]

$$\begin{aligned} \varepsilon <\left\{ \begin{aligned} \frac{2(1-\mathbf{e})^6}{5}|\alpha _2(\mathbf{e})|,&\quad \mathrm{if}\ (p,q)=(1,1), \\ \frac{(1-\mathbf{e})^6}{10}|\alpha _3(\mathbf{e})|,&\quad \mathrm{if}\ (p,q)=(3,2). \end{aligned}\right. \end{aligned}$$

(35)

Therefore, we can conclude that the bifurcation equation (22) is solved if one assumes that $|\frac{{\hat{\eta }}\,{\hat{\nu }}\,}{{\hat{\varepsilon }}\,}|\le a_{pq}$, i.e. (recall again (9), (30), and (34)), if

$$\begin{aligned} \eta <\left\{ \begin{aligned} \frac{\varepsilon }{| \nu -1|} \left( 2|\alpha _2(\mathbf{e})|-\frac{5 \varepsilon }{(1-\mathbf{e})^6} \right) ,\quad&\mathrm{if}\ (p,q)=(1,1), \\ \frac{2\varepsilon }{|2 \nu -3|} \left( 2|\alpha _3(\mathbf{e})|-\frac{20 \varepsilon }{(1-\mathbf{e})^6} \right) ,\quad&\mathrm{if}\ (p,q)=(3,2).\ \end{aligned}\right. \end{aligned}$$

(36)

We have proven the following:

Proposition 1

Let $(p,q)=(1,1)$ or $(p,q)=(3,2)$ and assume (12), (26), (35), and (36). Then, (1) admits $p$:$q$ spin–orbit resonances $x(t)$ as in (7).

2.6 Step 6: Lower Bounds on $|\alpha _2(\mathbf{e})|$ and $|\alpha _3(\mathbf{e})|$

In order to complete the proof of the theorem, by checking the conditions of Proposition 1 for the resonant satellites of the Solar System, we need to give lower bounds on the absolute values of the Fourier coefficients $\alpha _2(\mathbf{e})$ and $\alpha _3(\mathbf{e})$. To do this we will simply use a Taylor formula to develop $\alpha _j(\mathbf{e})$ in powers of $\mathbf{e}$ up to suitably large order¹³

$$\begin{aligned} \alpha _j(\mathbf{e})= \sum _{k=0}^h \alpha _j^{(k)} \mathbf{e}^k +R_j^{(h)}(\mathbf{e}) \end{aligned}$$

(37)

and use the analyticity property of $G_\mathbf{e}$ to get an upper bound on $R_j^{(h)}$ by means of standard Cauchy estimates for holomorphic functions. To use Cauchy estimates, we need an upper bound of $G_\mathbf{e}$ in a complex eccentricity region. The following simple result will be enough:

Lemma 2

Fix $0<b<1$. The solution $u_\mathbf{e}(t)$ of the Kepler equation (5) is, for every $t\in {\mathbb {R}}$, holomorphic with respect to $\mathbf{e}$ in the complex disk

$$\begin{aligned} |\mathbf{e}|< e_*:= \frac{b}{\cosh b} \end{aligned}$$

(38)

and satisfies

$$\begin{aligned} \sup _{t\in {\mathbb {R}}} |u_{\mathbf{e}}(t)-t| \le b. \end{aligned}$$

(39)

Moreover, $\rho _\mathbf{e}(t)=1-\mathbf{e}\cos (u_\mathbf{e}(t))$ satisfies

$$\begin{aligned} |\rho _\mathbf{e}(t)|\ge 1-b,\quad \forall \, t\in \mathbb R,\quad |\mathbf{e}|<e_* \end{aligned}$$

(40)

and $G_\mathbf{e}(t)$ (defined in (32)) satisfies

$$\begin{aligned} |G_\mathbf{e}(t)| \le \frac{2}{(1-b)^5}\left( |1-\mathbf{e}| (1+\cosh b) +1-b \right) ^2, \quad \forall \, t\in \mathbb R,\quad |\mathbf{e}|<e_*. \end{aligned}$$

(41)

Proof

Using that

$$\begin{aligned} \sup _{|{\, \mathrm{Im} \,}z|<b} |\sin z|=\sup _{|{\, \mathrm{Im} \,}z|<b} |\cos z|= \cosh b, \end{aligned}$$

(42)

one sees that for $|\mathbf{e}|< e_*$ the map $v \mapsto \chi _\mathbf{e}(v)$ with $\left[ \chi _\mathbf{e}(v) \right] (t):=\mathbf{e}\sin \left( v(t)+t\right)$ is a contraction in the closed ball of radius $b$ in the space of continuous functions endowed with the $\sup$-norm. Moreover, since $\chi _\mathbf{e}(v)$ is holomorphic in $\mathbf{e}$, the same holds for the fixed point $v_{\mathbf{e}}(t)$ of $\chi _\mathbf{e}$. The estimate in (39) follows by observing that $u_{\mathbf{e}}(t)=v_{\mathbf{e}}(t)+t$. Since by (39) we get

$$\begin{aligned} \left| {\, \mathrm{Im} \,}\left( u_{\mathbf{e}}(t)\right) \right| \le b ,\quad \forall \, t\in \mathbb R,\quad |\mathbf{e}|<e_*, \end{aligned}$$

(43)

estimate (40) follows by

$$\begin{aligned} |\rho _\mathbf{e}(t)|\ge 1- |\mathbf{e}| |\cos (u_\mathbf{e}(t))| \mathop {\ge }\limits ^{(42)}1-e_* \cosh b=1-b. \end{aligned}$$

Next, let $w_\mathbf{e}(t):=\sqrt{\frac{1+\mathbf{e}}{1-\mathbf{e}}} \tan \left( \frac{u_\mathbf{e}(t)}{2} \right)$ so that $\mathrm{f}_\mathbf{e}= 2 \arctan w_\mathbf{e}$. Then,¹⁴

$$\begin{aligned} |e^{2i \mathrm{f}_\mathbf{e}(t)}| = \frac{|w-i|^4 }{|w^2+1|^2} \le \left( \frac{4}{|w^2+1|}+2 \right) ^2 =4\left( \frac{|1-\mathbf{e}||1+\cos u_\mathbf{e}|}{|1-\mathbf{e}\cos u_\mathbf{e}|}+1 \right) ^2\!\!\!. \end{aligned}$$

Then, (41) follows by (40), (42), and (43).

Lemma 3

Let $R^{(h)}_j(\mathbf{e})$ be as in (37), $0<b<1$, and $0<\mathbf{e}<b/\cosh b$. Then,

$$\begin{aligned} |R_j^{(h)}(\mathbf{e})| \le R^{(h)}(\mathbf{e};b) \end{aligned}$$

with

$$\begin{aligned} R^{(h)}(\mathbf{e};b)&:= \frac{2}{(1-b)^5}\\&\times \left( \left( 1+\frac{b}{\cosh b}-\mathbf{e}\right) (1+\cosh b) +1-b \right) ^2 \frac{\mathbf{e}^{h+1}}{\left( \frac{b}{\cosh b}-\mathbf{e}\right) ^{h+1}}\ . \end{aligned}$$

Proof

For $\mathbf{e},\rho >0$ we set

$$\begin{aligned}{}[0,\mathbf{e}]_{\rho }:=\{\ z\in \mathbb C,\ \ \mathrm{s.t.}\ \ z=z_1+z_2,\ \ z_1\in [0,\mathbf{e}],\ \ |z_2|<\rho \ \}. \end{aligned}$$

Lemma 2 and standard (complex) Cauchy estimates imply, for $0\le s\le 1$,

$$\begin{aligned} |{D^{h+1}}\alpha _j(s\mathbf{e})| \le \frac{(h+1)!}{(e_*-\mathbf{e})^{h+1}} \sup _{[0,\mathbf{e}]_{e_*-\mathbf{e}}}|\alpha _j| \end{aligned}$$

and, therefore,

$$\begin{aligned} |R_j^{(h)}(\mathbf{e})| \le \frac{\mathbf{e}^{h+1}}{(e_*-\mathbf{e})^{h+1}} \sup _{[0,\mathbf{e}]_{e_*-\mathbf{e}}}|\alpha _j|\ . \end{aligned}$$

By (41) we obtain

$$\begin{aligned} \sup _{[0,\mathbf{e}]_{e_*-\mathbf{e}}}|\alpha _j| \le \frac{2}{(1-b)^5}\left( (1+e_*-\mathbf{e}) (1+\cosh b) +1-b \right) ^2 \end{aligned}$$

from which, recalling (38), the lemma follows.

Now, in order to check the conditions of Proposition 1, we will expand $\alpha _2$ in powers of $\mathbf{e}$ up to order $h=4$ and $\alpha _3$ up to order $h=21$. Using the representation formula (53) for the $\alpha _j$ given in Appendix 2, we find

$$\begin{aligned} \alpha _2(\mathbf{e})&= - \frac{1}{2} + \frac{5}{4} \mathbf{e}^2 - \frac{13}{32} \mathbf{e}^4 + R^{(4)}_2(\mathbf{e})\ ,\\ \alpha _3(\mathbf{e})&= -\frac{7}{4} \mathbf{e}+ \frac{123}{32} \mathbf{e}^3 - \frac{489}{256} \mathbf{e}^5 + \frac{1763}{4096} \mathbf{e}^7 - \frac{13527}{327680} \mathbf{e}^9+ \frac{180369}{13107200} \mathbf{e}^{11} \\&+ \frac{5986093}{734003200} \mathbf{e}^{13} + \frac{24606987}{3355443200} \mathbf{e}^{15} + \frac{33790034193}{5261334937600} \mathbf{e}^{17} \\&+\frac{1193558821627}{210453397504000} \mathbf{e}^{19} + \frac{467145991400853}{92599494901760000}\mathbf{e}^{21} + R^{(21)}_3(\mathbf{e}). \end{aligned}$$

In view of Lemma 3, we choose, respectively, $b=0.462678$ and¹⁵ $b=0.768368$ to get lower bounds:

$$\begin{aligned} |\alpha _2(\mathbf{e})|&\ge \left| \frac{1}{2} - \frac{5}{4} \mathbf{e}^2 + \frac{13}{32} \mathbf{e}^4\right| - |R^{(4)}(\mathbf{e};0.462678)|\end{aligned}$$

(44)

$$\begin{aligned} |\alpha _3(\mathbf{e})|&\ge \left| \sum _{k=1}^{21} \alpha _3^{(k)} \mathbf{e}^k\right| - | R^{(21)}(\mathbf{e};0.768368)|. \end{aligned}$$

(45)

2.7 Step 7: Check of the Conditions and Conclusion of the Proof

We are now ready to check all conditions of Proposition 1 with the parameters of the satellites in spin–orbit resonance given in Tables 1 and 2.

In Table 3 we report:

• In column 2: the lower bounds on $|\alpha _q(\mathbf{e})|$ as obtained in step 6 using (44) and (45) (with the eccentricities listed in Tables 1 and 2)

• In column 3: the difference between the right-hand side and the left-hand side of the inequality¹⁶ (26)

• In column 4: the difference between the right-hand side and the left-hand side of the inequality (35)

• In column 5: the right-hand side of the inequality (36), which is an upper bound for the admissible values of the dissipative parameter $\eta$

Table 3 Check of the hypotheses of Proposition 1 for the satellites in spin–orbit resonance

The positive values reported in the third and fourth column mean that the range condition (26) and the topological condition (35) are satisfied for all the moons in 1:1 resonance and for Mercury; the bifurcation condition (36) yields an upper bound on the admissible value for ${\eta }$ (fifth column). Thus, ${\eta }$ has to be smaller than the minimum between the value in the fifth column of Table 3 and the value in the right-hand side of Eq. (12) (needed to give a bound on the Green operator): this minimum value is $0.008$ for the moons in 1:1 resonance and $0.001$ for Mercury.

The proof of the theorem is complete.

Appendices

Appendix 1: Proof of Lemma 2.2

Proof

We first prove (14). Up to a rescaling we can prove (14) assuming $\Vert v'\Vert _{C^0}=1$. Assume by contradiction that

$$\begin{aligned} \Vert v\Vert _{C^0}=:c>\pi /2. \end{aligned}$$

Note that it is obvious that $c\le \pi$, since v has zero average and, therefore, must vanish at some point. Since |v| is a continuous periodic function it attains a maximum at some point; up to a translation we can assume that |v| attains its maximum in $-c$. In that case, multiplying by $-1$, we can also assume that $-c$ is a minimum, namely

$$\begin{aligned} \Vert v\Vert _{C^0}=c=-v(-c). \end{aligned}$$

Since $\Vert v'\Vert _{C^0}=1$, we get

$$\begin{aligned} v(t)\le -c +|t+c|, \quad \forall t\in [-2c,0] \end{aligned}$$

and, therefore,

$$\begin{aligned} v(0)\le 0,\ \ v(-2c)\le 0,\quad \int \limits _{-2c}^0 v\le -c^2. \end{aligned}$$

(46)

Since $\Vert v'\Vert _{C^0}=1$, we also get

$$\begin{aligned} v(t)\le \pi -c -|t-\pi +c|,\quad \forall \, t\in [0,2\pi -2c]. \end{aligned}$$

Then,

$$\begin{aligned} \int \limits _0^{2\pi -2c}v\le (\pi -c)^2. \end{aligned}$$

Combining with the last inequality in (46), we get

$$\begin{aligned} \int \limits _{-2c}^{2\pi -2c}v\le (\pi -c)^2-c^2=\pi (\pi -2c)<0, \end{aligned}$$

which contradicts the fact that $v$ has zero average, proving (14).

We now prove (15). Up to a rescaling we can prove (15) assuming $\Vert v''\Vert _{C^0}=1$. Assume by contradiction that

$$\begin{aligned} \Vert v\Vert _{C^0}=:c>\pi ^2/8. \end{aligned}$$

(47)

Up to a translation we can assume that $|v|$ attains maximum at $0$. In that case, multiplying by $-1$, we can also assume that $-c$ is a minimum, namely

$$\begin{aligned} \Vert v\Vert _{C^0}=c=-v(0). \end{aligned}$$

Since $\Vert v''\Vert _{C^0}=1$, we get

$$\begin{aligned} v(t)\le -c +t^2/2, \quad \forall t\in \mathbb R. \end{aligned}$$

Since v has zero average must exist $t_1 < 0 < t_2$

$$\begin{aligned} s.t. v(t_1) = v(t_2) = 0, v(t) < 0 \ \forall \ t \in (t_1, t_2), \end{aligned}$$

(48)

Moreover,

$$\begin{aligned} \hbox {and} \ \ t_1 \le - \sqrt{2 c}, t_2 \ge \sqrt{2 c}, t_2 - t_1 < 2 \pi . \end{aligned}$$

Since $v$ has zero average and is $2\pi$-periodic,

$$\begin{aligned} \int \limits _{t_2}^{2\pi +t_1} v= -\int \limits _{t_1}^{t_2}v \ge \frac{2}{3} (2c)^{3/2}. \end{aligned}$$

(49)

Set

$$\begin{aligned} a:=\pi + (t_1-t_2)/2 \end{aligned}$$

and note that

$$\begin{aligned} 0<a\le \pi -\sqrt{2c}<\pi /2, \quad a^2<2c \end{aligned}$$

(50)

by (48) and (47). Set

$$\begin{aligned} u(t):=v\left( t+\pi +(t_1+t_2)/2\right) . \end{aligned}$$

Note that $u\in \mathbb B\cap C^2$ and, by (48),

$$\begin{aligned} \Vert u\Vert _{C^0}=c,\quad \Vert u''\Vert _{C^0}=1,\quad \ u(-a)=u(a)=0,\quad \int \limits _{-a}^a u = \int \limits _{t_2}^{2\pi +t_1} v \mathop {\ge }\limits ^{(49)}\frac{2}{3} (2c)^{3/2}. \end{aligned}$$

Consider now the even function

$$\begin{aligned} w(t):=\frac{1}{2}(u(t)+u(-t)). \end{aligned}$$

Note that $w\in \mathbb B\cap C^2$ and

$$\begin{aligned} \Vert w\Vert _{C^0}\le c,\ \ \Vert w''\Vert _{C^0}\le 1,\ \ w(-a)=0,\ \ \int \limits _{-a}^0 w =\frac{1}{2} \int \limits _{-a}^{a} u \ge \frac{1}{3} (2c)^{3/2}. \end{aligned}$$

(51)

Set

$$\begin{aligned} z(t):=c-\frac{c}{a^2}t^2. \end{aligned}$$

We claim that

$$\begin{aligned} z(t)\ge w(t),\quad \forall \, -a\le t\le 0. \end{aligned}$$

(52)

Then,

$$\begin{aligned} \int \limits _{-a}^0 w\le \int \limits _{-a}^0 z= \frac{2}{3} ca \mathop {<}\limits ^{(50)} \frac{1}{3} (2c)^{3/2} \mathop {\le }\limits ^{(51)}\int \limits _{-a}^0 w, \end{aligned}$$

which is a contradiction.

Let us prove the claim in (52). Note that $z(-a)=w(-a)=0$. Assume by contradiction that there exists $\bar{t}\in [-a,0)$ such that

$$\begin{aligned} z(\bar{t})=w(\bar{t}),\quad z(t)\ge w(t),\quad \forall \, t\in [-a,\bar{t}],\quad z'(\bar{t})\le w'(\bar{t}). \end{aligned}$$

Then, since $\Vert w''\Vert _{C^0}\le 1$,

$$\begin{aligned} w(t)&\ge w(\bar{t}) +w'(\bar{t})(t-\bar{t}) -\frac{1}{2} (t-\bar{t})^2\\&\mathop {>}\limits ^{(50)} z(\bar{t}) +z'(\bar{t})(t-\bar{t}) -\frac{c}{a^2} (t-\bar{t})^2 =z(t) ,\quad \forall \, t\in (\bar{t},0]. \end{aligned}$$

Then,

$$\begin{aligned} w(0)>z(0)=c, \end{aligned}$$

which contradicts the first inequality in (51). This completes the proof of (15). $\square$

Appendix 2: Fourier Coefficients of the Newtonian Potential

Properties of the Fourier coefficients $\alpha _j$ of the Newtonian potential $f$, including Eq. (32), have been discussed, e.g., in Appendix 1 of¹⁷ Biasco and Chierchia (2009).

Here we provide a simple formula for the Fourier coefficients $\alpha _j$ of the Newtonian potential $f$ in (3) [compare (d) of §1, and (31)–(32)]; namely we prove that

$$\begin{aligned} \alpha _j= -\frac{1}{4 \pi } \int \limits _0^{2 \pi } \frac{1}{\rho ^2(w^2+1)^2} \left[ (w^4-6w^2+1) c_j (u) -4w(w^2-1)s_j (u) \right] \mathrm{d}u,\quad \end{aligned}$$

(53)

where $w=w(u;\mathbf{e}) :=\sqrt{\frac{1+\mathbf{e}}{1-\mathbf{e}}} \tan \frac{u}{2}$, $\rho =1-\mathbf{e}\cos u$, and

$$\begin{aligned} c_j(u):=\cos (ju-j\mathbf{e}\sin u),\quad s_j(u):=\sin (ju-j\mathbf{e}\sin u). \end{aligned}$$

Proof

If $z=\arctan w$, then

$$\begin{aligned} e^{2iz}=\frac{i- w }{w+i}=-\frac{(w-i)^2}{w^2+1}, \end{aligned}$$

(54)

so that if $w_\mathbf{e}(t):=w(u_{\mathbf{e}}(t),\mathbf{e})$ one has $f_\mathbf{e}= 2 \arctan w_\mathbf{e}$ and

$$\begin{aligned} G_\mathbf{e}&= -\frac{1}{2\rho _\mathbf{e}^3} \frac{(w_\mathbf{e}-i)^2}{(w_\mathbf{e}+i)^2} = -\frac{1}{2\rho _\mathbf{e}^3} \frac{(w_\mathbf{e}-i)^4}{(w_\mathbf{e}^2+1)^2}\\&= -\frac{1}{2\rho _\mathbf{e}^3} \frac{1}{(w_\mathbf{e}^2+1)^2} \left( w_\mathbf{e}^4-6w_\mathbf{e}^2+1 -4iw_\mathbf{e}(w_\mathbf{e}^2-1) \right) . \nonumber \end{aligned}$$

(55)

By parity properties, it is easy to see that the $G_j$’s are real, namely $G_j=\bar{G}_j$, so that

$$\begin{aligned} \alpha _j&= G_j = \frac{1}{2 \pi } \int \limits _0^{2 \pi } G(t) e^{-ijt} \, \mathrm{d}t = -\frac{1}{4 \pi } \int \limits _0^{2 \pi } \frac{e^{i2f_\mathbf{e}(t) - ijt}}{\rho _\mathbf{e}(t)^3} \, \mathrm{d}t \\&= -\frac{1}{4 \pi } \int \limits _0^{2 \pi } \frac{1}{\rho _\mathbf{e}^3(w_\mathbf{e}^2+1)^2} \left[ (w_\mathbf{e}^4-6w_\mathbf{e}^2+1)\cos (jt) -4w_\mathbf{e}(w_\mathbf{e}^2-1)\sin (jt) \right] \mathrm{d}t. \end{aligned}$$

Making the change of variable given by the Kepler equation (5), i.e., integrating from $t$ to $u=u_\mathbf{e}$ and setting $u_\mathbf{e}(t)' = \frac{1}{\rho _\mathbf{e}(t)}$, one gets (53). $\square$

Appendix 3: Small Bodies

In the Solar System, besides the 18 moons listed in Table 1 and Mercury, there are five other minor bodies with mean radius smaller than 100 km observed in 1:1 spin–orbit resonance around their planet: Phobos and Deimos (Mars), Amalthea (Jupiter), and Janus and Epimetheus (Saturn), as listed in Table 4.

Table 4 Physical data of minor bodies in 1:1 spin–orbit resonance

Besides being small, such bodies have also a quite irregular shape and only Janus and Epimetheus have good equatorial symmetry.¹⁸ Indeed, for these two small moons (and only for them among the minor bodies), our theorem holds as shown by the data reported in Table 5.¹⁹

Table 5 Check of the hypotheses of Proposition 1 for the small satellites in spin–orbit resonance