1 Introduction

Regarding the general relativity of the geometric interpretation of gravity, it is no longer a force, but rather a representation of the non-Euclidean geometry of host space-time. The theory was based on the Riemannian assumption geometry, according to which the deviations are from Euclidean flatness described by the symmetric Levi-Civita connection, that is, with Christoffel symbols. Affine connection presents space-time twisting; therefore a new degree of geometric freedom appears in the system because there is an independent torsion field in addition to the scale. The literature abounds with a number of suggestions for experimenting with theories of gravity with nonzero torsions (Hammond 2002; Mao et al. 2007; Wanas 2007; Kostelecký et al. 2008; March et al. 2011; Hehl et al. 2013; Puetzfeld and Obukhov 2014; Lin et al. 2017; Dimitrios et al. 2019; Capozziello et al. 2017; Vignolo and Fabbri 2012). However, so far, there has been no demonstration to support the existence of time and space. The twist begins to become tangible with very high energy densities. These densities can only be achieved at depth within compact objects, such as neutron stars and black holes, or during the early stages of the expansion of the universe. Such environments are still beyond our experimental capabilities. Just like the Friedman–Robertson–Walker (\(\mathit{FRW}\)) model of standard cosmology, warping is not naturally suitable for very symmetrical gaskets. Given the spatial homogeneity and isotropic universe of the latter, it must meet the permissible torsional field. In practical terms, space-time torsion and associated complete rotation are determined by a numerical function that only depends on time. These are options that allow us to build and study torsional analogs from the classic Friedman universes. In these options, it turns out that despite the torsion, the opposite Einstein’s tensors and energy-momentum tensors are symmetric as well. Researchers have been trying to offer a better understanding of general relativity in the presence of matter to be obtained, given that the intrinsic angular momentum of fermion particles (spin) improves the bending effects of space-time. This can be attained by having an asymmetric affine connection in the manifold construction, which causes space-time to twist, and thus allows new geometric degrees of freedom to appear in the system. It thus becomes the source of convolution with more general prescriptions. One example is based on well-established studies of gravity, Einstein—Cartan–Keppel–Siyama (ECKS) theory (Lu and Chee 2016; Pereira et al. 2019; Cruz et al. 2020). In the past few years the recently revised far-parallel gravity theory has become an area of intensive research. Based on the Einstein idea to use torsion instead of curvature to describe the deviation of the metric from the Minkowski one (Einstein 1930), this theory gives rise to a set of possible modifications of \(\mathit{GR}\), which cannot be constructed within the classical curvature formalism. If the torsion scalar is inserted in the action of the theory in the same way as the curvature scalar \(R\) enters in the Hilbert action, then the theory appears to be equivalent to \(\mathit{GR}\) and thus is usually called Teleparallel Equivalent of General Relativity (\(\mathit{TEGR}\)) (Aldrovandi and Pereira 2012). \(\mathit{TEGR}\) is constructed in the context of absolute parallelism (AP) geometry. The Lagrangian function used to derive the field equations of this theory is a torsion scalar \(T_{s}\). Torsion of the \(\mathit{AP}\)-geometry is the skew-symmetric part of the Weitzenböck linear connection. The curvature of this connection vanishes identically. So, in the context of \(\mathit{TEGR}\), gravity is attributed to torsion, not to curvature. This represents one of the differences between \(\mathit{GR}\) and \(\mathit{TEGR}\). As it is well known, the geometric structure used to construct \(\mathit{GR}\) has a nonvanishing curvature and a vanishing torsion. On the other hand, \(\mathit{TEGR}\) is constructed in the \(\mathit{AP}\)-geometry having a vanishing curvature and a nonvanishing torsion. However, a version of the \(\mathit{AP}\)-geometry, known in the literature as the parameterized absolute parallelism (\(\mathit{PAP}\)) geometry, has simultaneously a nonvanishing curvature and torsion. This motivates us to explore the consequence of writing a gravity theory using the curvature of the parameterized Weitzenböck linear connection. This may help us in reattributing gravity to the curvature of a linear connection, preserving Einstein’s principal ideas. In general, the resulting theory is not a metric but a teleparallel theory. In other words, the gravitational potential is defined in terms of the building blocks (\(\mathit{BB}\)) of the \(\mathit{PAP}\)-geometry, the teleparallel vector fields. It can be reduced to \(\mathit{GR}\) under certain conditions (Wanas et al. 2018a).

In this paper, we use \(\mathit{PAP}\). It offers numerous possibilities for describing curvature and torsion in such a way as to explain the role each of them plays in the development of the universe in its early and advanced stages. Therefore the aim of this paper is to examine the effect of the torsion and shear terms on Universe evolution behavior. The study is especially concerned with those effects caused by torsion on the geometric of space-time, in their different stages, from the beginning of the universe to the Big Rip state. On the other hand, the latest observations and predictions that our universe is undergoing an accelerated expansion stage (Riess et al. 1998; Perlmutter et al. 1999; de Bernardis et al. 2000; Perlmutter and Brian 2003) provide a new approach for modern cosmology. A cosmology class of researchers is making attempts to accommodate this observational fact by choosing some exotic matter \(\mathbf{s}\) (known as dark energy) in the framework of general relativity. There are several choices for this exotic matter, namely, the quintessence scalar fields models (Ratra and Philip 1988), the phantom field (Nojiri and Sergei 2003), K-essence (Mukhanov and Steinhardt 2001), the dark energy models, including Chaplygin gas (Bento et al. 2002), and so on. In this paper, we take another approach to explain expansion depending on the effect of the geometric torsion instead of the concept of dark energy. In the following section, we explain the geometry used in this paper and define torsion and its relationship to the expansion of the universe.

2 A review of the AP-geometry

In what follows, we provide a review of the \(\mathit{AP}\)-geometry. The building of the conventional absolute parallelism geometry \(\mathit{AP}\) is defined completely in four dimensions by a tattered vector \(\lambda _{i}^{ \gamma } \) (\(i = 1, 2, 3, 4\)) to indicate the vector number. Furthermore, \(\gamma = 1, 2, 3, 4\) indicate the coordinate components. The covariant vector of \(\lambda _{i}^{ \gamma } \) yields (Mikhail and Wanas 1977)

$$ \lambda _{i}^{ \gamma } \lambda _{i \alpha } = \delta _{\alpha }^{ \gamma }\quad \text{and}\quad \lambda _{i}^{ \alpha } \lambda _{j \alpha } = \delta _{i j}. $$
(1)

Consider the following symmetric tensors:

$$ g_{\alpha \beta } = \lambda _{i\alpha } \lambda _{i\beta },\qquad g^{\alpha \beta } = \lambda _{i}^{ \alpha } \lambda _{i}^{ \beta },\quad \text{and}\quad g_{\beta \gamma } g^{\alpha \beta } = \delta _{\gamma }^{ \alpha }. $$
(2)

At any point in the \(\mathit{AP}\) geometry, we can define the Riemannian space at which the symmetric tensor (2) gives the following metric tensor:

$$ ds^{2} = g_{\alpha \beta } dx^{\alpha } dx^{\beta }. $$
(3)

The generalization of the partial differentiation in the Riemannian space is defined in the covariant vectors as follows:

$$ A_{\beta ;\gamma } = A_{\beta ,\gamma } - \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} A_{\alpha }, $$
(4)

where

$$ \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} = g^{\gamma \varepsilon } (g_{\alpha \varepsilon ,\beta } + g_{\beta \varepsilon ,\alpha } - g_{\alpha \beta ,\varepsilon } )/2. $$
(5)

We can define a nonsymmetric connection (affine connection) \(\Gamma _{ \alpha \beta }^{\gamma } \) as follows (Mikhail 1962):

$$ \Gamma _{ \alpha \beta }^{\gamma } = \lambda _{i}^{ \gamma } \lambda _{i \alpha ,\beta } = - \lambda _{i \alpha } \lambda _{i, \beta }^{ \gamma }. $$
(6)

This nonsymmetric connection is a consequence of the following absolute parallelism condition:

$$ \lambda _{i \alpha | \beta } = \lambda _{i \alpha , \beta } - \Gamma _{ \alpha \beta }^{\gamma } \lambda _{i \gamma }. $$
(7)

The torsion tensor \(\Lambda _{ \alpha \beta }^{\gamma } \) of a general space-time coincides with the antisymmetric component of the affine connection, that is,

$$ \Lambda _{ \alpha \beta }^{\gamma } = \left ( \Gamma _{ \alpha \beta }^{\gamma } - \Gamma _{ \beta \alpha }^{\gamma } \right ) = 2 \Gamma _{ [\alpha \beta ]}^{\gamma } = - \Lambda _{ \beta \alpha }^{\gamma }. $$
(8)

According to the metricity condition (\(g_{ \alpha \beta ; \gamma } = 0\)), the generalized (asymmetric) connection is given by

$$ \Gamma _{ \alpha \beta }^{\gamma } = \Psi _{ \alpha \beta }^{\gamma } + \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} $$
(9)

and

$$ \psi _{ \alpha \beta }^{\gamma } = \Gamma _{ \alpha \beta }^{\gamma } - \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} = \lambda _{i}^{ \gamma } \lambda _{i \alpha ; \beta } = - \lambda _{i \alpha } \lambda _{i; \beta }^{ \gamma } , $$
(10)

where \(\left \{ \begin{array}{c} \gamma \\ \alpha \beta \end{array} \right \}\) defines Christoffel symbols, and \(\Psi _{ \alpha \beta }^{\gamma } \) is the contortion tensor given by (Hammond 2002; Wanas 2008)

$$ \psi ^{\alpha }_{\beta \gamma } = \frac{1}{2}\left ( \Lambda ^{\alpha }_{\beta \gamma } - \Lambda _{\beta . \gamma }^{ \alpha } + \Lambda _{\gamma . \beta }^{ \alpha } \right ). $$
(11)

From the geometrical point of view, torsion prevents infinitesimal parallelograms from closing (Hehl et al. 1976; Hehl and Obukhov 2007). Physically, torsion provides a link between the intrinsic angular momentum (i.e., the spin) of the matter and the geometry of the host space-time. The antisymmetry of \(\Lambda _{ \alpha \beta }^{\gamma } \) guarantees that it has only one nontrivial contraction, leading to the torsion vector

$$ C_{\alpha } = \Lambda _{ \alpha \beta }^{\beta } = - \Lambda _{ \beta \alpha }^{\beta }. $$
(12)

As we will see later, the torsion vector becomes the sole carrier of the torsion effects in spatially homogeneous and isotropic space-times. Following (11), there is only one independent contraction of the contortion tensor as well. In particular, we have

$$ \Psi _{ \alpha \beta }^{\beta } = C_{\alpha } = - \Psi _{ \beta \alpha }^{ \beta }\quad \text{with}\ \Psi _{ \beta \alpha }^{\alpha } = 0. $$
(13)

The general absolute derivative has been earlier defined by (Wanas 2000)

$$ A_{ \alpha || \beta } = A_{\alpha , \beta } - \nabla _{ \alpha \beta }^{\gamma } A_{\gamma } $$
(14)

and

$$ A^{\alpha }_{ || \beta } = A^{\alpha , \beta } + \nabla _{ \gamma \beta }^{\alpha } A^{\gamma } . $$
(15)

In addition, the connection \(\nabla _{ \alpha \beta }^{\gamma }\) is given by (Wanas 2000),

$$ \nabla _{ \alpha \beta }^{\gamma } = \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} + b \psi _{ \alpha \beta }^{\gamma }, $$
(16)

where \(b\) is a dimensionless parameter. It can be easily shown that object (16) is a linear connection having the following properties:

  1. (i)

    It is nonsymmetric, that is, it has a nonvanishing torsion.

  2. (ii)

    It covers the domain of Riemannian geometry for \(b = 0\).

  3. (iii)

    It reduces to the conventional \(\mathit{AP}\)-geometry for \(b = 1\).

  4. (iv)

    It has simultaneously nonvanishing torsion and curvature.

  5. (v)

    This connection will be called parameterized canonical connection or parameterized Weitzenböck connection (Wanas et al. 2018a). It is clearly nonsymmetric, so its symmetric part is \(\nabla _{ (\alpha \beta )}^{\gamma } = \frac{1}{2}(\nabla _{ \alpha \beta }^{\gamma } + \nabla _{ \beta \alpha }^{\gamma } )\).

  6. (vi)

    For the entire values of \(b\), all possible values of the parameter \(b\) are called the \(\mathit{PAP}\)-geometry.

  7. (vii)

    The \(\mathit{PAP}\)-geometry has the same \(\mathit{BB}\) as the \(\mathit{AP}\)-geometry.

It is easy to show that the object given by (16) is a metric linear connection, that is,

$$ g_{ \alpha \beta || \gamma } = 0. $$
(17)

3 The field equations with torsion

Earlier in the last century, the relationship between spin and torsion was studied by numerous researchers, who showed that the torsion may be attributed to rotation (spin). Einstein–Cartan–Sciama–Kibble theory (Cartan 1923; Sciama 1962; Kibble 1961; Trautman 1972) is one of the outcomes of these studies, which is simplified to the standard of the GR field equation when the spin is finished. As is well known, the geometry used to create the GR has a nonvanishing curvature and a vanishing torsion. On the other hand, the teleparallel equivalent of general relativity (\(\mathit{TFGR}\)) is built in AP-geometry with vanishing curvature and non-vanishing torsion. However, a version of AP-geometry, known in the literature as \(\mathit{PAP}\)-geometry, has curvature and nonvanishing curvature at the same time. This motivates us to explore the result of writing the theory of gravity using curvature Weitzenböck linear connection parameters. This may help redistribute gravity on the curvature of the linear contact, preserving Einstein’s main ideas. In general, the resulting theory is not a metric but rather a parallel theory. In other words, the gravitational potential is defined in terms of the basic building blocks of \(\mathit{PAP}\) architecture and teleparallel vector fields. It can be reduced to GR under certain conditions. To investigate the effect of torsion on the Big Rip models, the field equations that describe this situation will be inferred, and then the field equations that describe the cosmological models will be solved. Connection (16) gives rise to the following simultaneous nonvanishing torsion and curvature tensor (Wanas 2000):

$$\begin{aligned} B_{ \mu \nu \sigma }^{ \varepsilon } &= \nabla _{ \mu \sigma ,\nu }^{ \varepsilon } - \nabla _{ \mu \nu , \sigma }^{ \varepsilon } + \nabla _{ \mu \sigma }^{ \alpha } \nabla _{ \alpha \nu }^{ \varepsilon } - \nabla _{ \mu \nu }^{ \alpha } \nabla _{ \alpha \sigma }^{ \varepsilon } \\ &= R_{ \mu \nu \sigma }^{ \varepsilon } + b L_{ \mu \nu \sigma }^{ \varepsilon }, \end{aligned}$$
(18)

where the Riemann–Christoffel curvature tensor is

$$\begin{aligned} R_{ \mu \nu \sigma }^{ \varepsilon } &= \left \{ \textstyle\begin{array}{c} \varepsilon \\ \mu \sigma \end{array}\displaystyle \right \} _{, \nu } \_\left \{ \textstyle\begin{array}{c} \varepsilon \\ \mu \nu \end{array}\displaystyle \right \} _{, \sigma } + \left \{ \textstyle\begin{array}{c} \alpha \\ \mu \sigma \end{array}\displaystyle \right \} \left \{ \textstyle\begin{array}{c} \varepsilon \\ \alpha \nu \end{array}\displaystyle \right \} \\ &\quad {}- \left \{ \textstyle\begin{array}{c} \alpha \\ \mu \nu \end{array}\displaystyle \right \} \left \{ \textstyle\begin{array}{c} \varepsilon \\ \alpha \sigma \end{array}\displaystyle \right \} , \end{aligned}$$
(19)

and the torsion tensor is

$$\begin{aligned} L^{\varepsilon }_{\mu \nu \sigma } &= \Psi _{ \mu \sigma , \nu }^{\varepsilon } - \Psi ^{\varepsilon }_{\mu \nu ,\sigma } - \Psi _{ \mu \sigma }^{\alpha } \Psi _{ \alpha \nu }^{\varepsilon } + \Psi _{ \mu \nu }^{\alpha } \Psi _{ \alpha \sigma }^{\varepsilon } \\ &\quad {}+ \left \{ \textstyle\begin{array}{c} \alpha \\ \mu \sigma \end{array}\displaystyle \right \} \Psi _{ \alpha \nu }^{\varepsilon } + \left \{ \textstyle\begin{array}{c} \varepsilon \\ \alpha \nu \end{array}\displaystyle \right \} \Psi _{ \mu \sigma }^{\alpha } \\ &\quad {}- \left \{ \textstyle\begin{array}{c} \alpha \\ \mu \nu \end{array}\displaystyle \right \} \Psi _{ \alpha \sigma }^{\varepsilon } - \left \{ \textstyle\begin{array}{c} \varepsilon \\ \alpha \sigma \end{array}\displaystyle \right \} \Psi _{ \mu \nu }^{\alpha }. \end{aligned}$$
(20)

The parameterized linear connection (16) has some properties. Taking \(b = 0\), it covers the domain of Riemannian geometry with its Levi-Civita linear connection. Also, if we take \(b = 1\), then it will reduce to Weitzenböck linear connection for the case of \(\mathit{AP}\)-geometry. As stated above, Weitzenböck connection has a vanishing curvature, but its parameterized linear connection has a simultaneously nonvanishing curvature and torsion. Due to the importance of curvature in describing gravity, it would be of interest to explore the consequences of constructing a \(\mathit{GFT}\) depending on the curvature of (16). Also, it is worth mentioning that the tensor given by (18) is in general nonsymmetric and is completely formed from the \(\mathit{BB}\) of the \(\mathit{PAP}\)-geometry. So the field equations of the theory (18) satisfy the general covariance principle and unification principle (Wanas et al. 2018a). In a modern approach, which is called covariant formulation of teleparallel gravity, instead of the definition of Weitzenböck connection (8), a more general expression is used,

$$ \Gamma _{ \alpha \beta }^{\gamma } = \lambda _{i}^{ \gamma } \left ( \lambda _{i \alpha ,\beta } + \lambda _{j \beta } \omega _{ \alpha }^{i j} \right ), $$
(21)

where \(\omega _{ \alpha }^{i j} = - \omega _{ \alpha }^{j i}\) is the so-called spin connection.

Equation (21) is used to study the spin connection to ensure the covariance of any theory; see (Toporensky and Tretyakov 2020; Cahill 2020). We hope to work on this topic in the future.

The formulation of the gravitational field with torsion equations (\(\mathit{GFT}\)) is given in the following form (Bakry and Shafeek 2021):

$$ B_{\mu \nu } = R_{\mu \nu } - L_{\mu \nu } = 8\pi (T_{\mu \nu } - \frac{1}{2}g_{\mu \nu } T). $$
(22)

This equation represents the special case from the gravitational field with torsion (18) when \(b = - 1\). The value \(b = - 1\) was chosen to show the effect of the torsion force on the field. In this case, Eq. (16) takes the form

$$ \nabla _{ \alpha \beta }^{\gamma } = 2 \left \{ \textstyle\begin{array}{c} \gamma \\ \alpha \beta \end{array}\displaystyle \right \} - \Gamma _{ \alpha \beta }^{\gamma }. $$
(23)

The energy-momentum tensor concerned with perfect fluid is given by (Brans and Robert 1961)

$$ T_{\alpha \beta } = - (P + \rho )U_{ \alpha } U_{ \beta } + Pg_{\alpha \beta }, $$
(24)

which gives rise to

$$ T = - \rho + 3P, $$
(25)

where \(\rho \) is the energy density of the matter in comoving coordinates, and \(P\) is the pressure in the fluid.

To use the field Eq. (22) to study the emergence of the universe in homogeneous and isotropic world models, Robertson (1932) gives the basic components of the cosmological model:

$$ \lambda _{0}^{ \mu } = \left \{ 1, 0, 0, 0 \right \} , $$
$$\begin{aligned} \lambda _{1}^{ \mu } = &\left \{ 0,\frac{W^{ +} \sin \theta \cos \varphi }{4S},\frac{W^{ -} \cos \theta \cos \varphi - 4\sqrt{K} r \sin \varphi }{4r S},\right. \\ &\quad \left.\frac{ - (W^{ -} \sin \varphi + 4\sqrt{K} r\cos \theta \cos \varphi )}{4rS \sin \theta } \right \} , \end{aligned}$$
$$\begin{aligned} \lambda _{2}^{ \mu } = &\left \{ 0,\frac{W^{ +} \sin \theta \sin \varphi }{4S},\frac{W^{ -} \cos \theta \sin \varphi + 4\sqrt{K} r \cos \varphi }{4r S},\right. \\ &\quad \left.\frac{W^{ -} \cos \varphi - 4\sqrt{K} r\cos \theta \sin \varphi }{4rS \sin \theta } \right \} , \end{aligned}$$
$$ \lambda _{3}^{ \mu } = \left \{ 0,\frac{W^{ +} \cos \theta }{4S},\frac{ - W^{ -} \sin \theta }{4r S},\frac{\sqrt{K}}{S} \right \} , $$
(26)

where \(\mu = 0,1,2,3\) represent the coordinate components, \(W^{ \pm } = 4 \pm Kr^{2}\), \(K = - 1, 1, 0\) is the curvature parameter, and \(S(t)\) is the scale factor. The coordinates \(r\), \(\theta \), and \(\varphi \) in tetrad vectors (24) are comoving coordinates.

For comparison with the results of orthodox \(\mathit{GR}\), we may replace definition (2) by

$$ g_{\alpha \beta } = \eta _{ij}\lambda _{i \alpha } \lambda _{j \beta }, $$
(27)

where \(\eta _{ij} = \operatorname{diag}(1, - 1, - 1, - 1)\).

Equation (25) defines a pseudo-Riemannian structure associated with the \(\mathit{AP}\) structure. The metric tensor corresponding to the tetrad (26) and (27) is given by

$$ \begin{aligned}[b] &g_{00} = 1,\quad g_{11} = - (4S/W^{ +} )^{2},\quad g_{22} = g_{11} r^{2}, \\ &\quad \text{and}\ g_{33} = g_{11} r^{2}\sin ^{2}\theta , \end{aligned} $$
(28)
$$ \begin{aligned}[b] &g^{00} = 1,\qquad g^{11} = - (W^{ +} /4S)^{2},\qquad g^{22} = 1/g_{11} r^{2}, \\ &\quad \text{and}\ g^{33} = 1/g_{11} r^{2}\sin ^{2}\theta . \end{aligned} $$
(29)

The Riemannian space associated with \(\mathit{AP}\) space (3) and (28) is the space having the well-known \(\mathit{FRW}\) metric given by

$$ d\tau ^{2} = dt^{2} - \frac{16S^{2}(t)}{W^{ + 2}}\left [ dr^{2} + r^{2}(d\theta ^{2} + \sin ^{2}\theta d\varphi ^{2}) \right ]. $$
(30)

This metric is written explicitly in comoving coordinates attached to the point of expanding space. The comoving coordinate system is characterized by

$$ U^{1} = U^{2} = U^{3} = 0,\quad \text{and} U^{0} = 1, $$
(31)

where \(U^{\alpha } \) is the velocity vector in the comoving coordinate system satisfying the condition \(U_{\alpha } U^{\beta } = 1\).

The nonvanishing Christoffel symbols of the second kind for the metric (28) are given by

$$\begin{aligned} &\left \{ \textstyle\begin{array}{c} 0 \\ 1 1 \end{array}\displaystyle \right \} = 16S\dot{S} / W^{ + 2},\qquad \left \{ \textstyle\begin{array}{c} 0 \\ 2 2 \end{array}\displaystyle \right \} = 16 r^{2}S\dot{S} / W^{ + 2},\qquad \\ &\left \{\textstyle\begin{array}{c} 0 \\ 3 3 \end{array}\displaystyle \right \} = 16 r^{2} \sin ^{2}\theta S\dot{S} / W^{ + 2}, \end{aligned}$$
$$\begin{aligned} &\left \{ \textstyle\begin{array}{c} 1 \\ 1 1 \end{array}\displaystyle \right \} = - 2K r / W^{ +},\qquad \left \{ \textstyle\begin{array}{c} 1 \\ 0 1 \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} 2 \\ 0 2 \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} 3 \\ 0 3 \end{array}\displaystyle \right \} = \frac{\dot{S}}{S}, \end{aligned}$$
(32)
$$\begin{aligned} \left \{ \textstyle\begin{array}{c} 1 \\ 2 2 \end{array}\displaystyle \right \} = \frac{K^{2}r^{5} - 16 r}{W^{ + 2}},\qquad \left \{ \textstyle\begin{array}{c} 1 \\ 3 3 \end{array}\displaystyle \right \} = \frac{(K^{2}r^{4} - 16) r \sin ^{2}\theta }{W^{ + 2}}, \end{aligned}$$
$$ \begin{aligned} &\left \{ \textstyle\begin{array}{c} 2 \\ 1 2 \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} 3 \\ 1 3 \end{array}\displaystyle \right \} = W^{ -} /r W^{ +}, \\ &\left \{ \textstyle\begin{array}{c} 2 \\ 3 3 \end{array}\displaystyle \right \} = - \sin \theta \cos \theta ,\qquad \left \{ \textstyle\begin{array}{c} 3 \\ 2 3 \end{array}\displaystyle \right \} = \cot \theta , \end{aligned} $$

where \(\dot{S} = dS/dt\).

The geometric objects necessary to solve the field equations (22) have the following nonvanishing components of the torsion tensor:

$$ \Lambda _{ 01}^{1} = \Lambda _{ 02}^{2} = \Lambda _{ 03}^{3} = - \dot{S}/S, $$
$$ \Lambda _{ 32}^{1} = - \Lambda _{ 23}^{1} = 8\sqrt{K} r^{2}\sin \theta /W^{ +}, $$
$$ \Lambda _{ 13}^{2} = - \Lambda _{ 31}^{2} = 8\sqrt{K} \sin \theta /W^{ +}, $$
$$ \Lambda _{ 21}^{3} = - \Lambda _{ 12}^{3} = 8\sqrt{K} /W^{ +} \sin \theta . $$
(33)

Using (6), (10), and (32), the nonvanishing contortion components and the torsion vector are given by

$$ \Psi _{ 01}^{1} = \Psi _{ 02}^{2} = \Psi _{ 03}^{3} = - \dot{S}/S,\qquad \Psi _{ 11}^{0} = - 16S\dot{S}/W^{ + 2}, $$
$$ \Psi _{ 22}^{0} = \Psi _{ 11}^{0} r^{2},\qquad \Psi _{ 33}^{0} = \Psi _{ 11}^{0} r^{2}\sin ^{2}\theta , $$
$$ \Psi _{ 13}^{2} = - \Psi _{ 31}^{2} = 4\sqrt{K} \sin \theta /W^{ +}, $$
$$ \Psi _{ 21}^{3} = - \Psi _{ 12}^{3} = 4\sqrt{K} /W^{ +} \sin \theta , $$
(34)

and the nonvanishing torsion vector \(C_{\alpha } \) of the \(\mathit{PAP}\)-space can be written as

$$ C_{0} = - 3 \dot{S}/S. $$

Substituting from (23), (24), (32), and (34) into the field Eqs. (22), we get

$$ 3 \ddot{S} = - 2 \pi (\rho + 3P)S, $$
(35)
$$ 3 \dot{S}^{2} = 2 \pi \rho S^{2}. $$
(36)

We can observe that the field Eqs. (35) and (36) are the same as in (Bakry and Shafeek 2021) when \(b = - 1\). It is clear that these equations do not depend on the curvature constant.

From Eq. (36) we get

$$ \rho = 3 \dot{S}^{2}/ 2\pi S^{2}. $$
(37)

Substituting (37) into Eq. (35), we obtain

$$ P = - \left ( \frac{ \dot{S}^{2} + S \ddot{S}}{2 \pi S^{2}} \right ). $$
(38)

The differential Eqs. (37) and (38) are in three unknowns: the scale factor \(S(t)\), the density \(\rho (t)\), and the pressure \(P(t)\). To get exact solutions for these equations, we must use an equation of state, as in an extra solution, which gives \(P = \omega \rho \) in the following form:

$$ \omega = - \left ( \frac{\dot{S}^{2} + S \ddot{S}}{3 \dot{S}^{2}} \right ). $$
(39)

From Eqs. (37) and (38) we can note that the field equations do not depend on the curvature parameter \(K\).

4 Kinematics of Big Rip model in \(\mathit{GFT}\)

In fact, a critical analysis of the solution systems of Einstein field equations in general relativity theory or in modified theories has two sides. The first side incorporates the parameterization of geometrical parameters, the scale factor \(S(t)\), the Hubble parameter \(H\), the deceleration parameter \(\mathit{DP}\), and the cosmic jerk parameter, giving the time-dependent function of all the cosmological parameters. The second side covers the parameterization of the physical parameters, the energy density of the matter \(\rho \), the pressure in the fluid \(P\), and the equation of state, giving the scale factor dependence or redshift dependence of all the cosmological parameters. The \(\mathit{DP}\) is one of the geometrical parameters through which the dynamics of the universe can be counted. Many parameterized forms of \(\mathit{DP}\) such as constant \(\mathit{DP}\) (Berman 1983; Berman and de Mello Gomide 1988), linearly varying \(\mathit{DP}\) (Akarsu and Tekin 2012), quadratic varying \(\mathit{DP}\) (Bakry and Shafeek 2019), and periodic varying \(\mathit{DP}\) (Sahoo et al. 2018) are used to find new cosmological models. Linear parameterization of the \(\mathit{DP}\) shows quite natural phenomena toward the future evolution of the universe; it either expands forever or ends up with the Big Rip in future. Such a parameterization has been frequently used in the following works: (Caldwell and Kamionkowski 2003; Akarsu and Tekin 2012; Bakry and Shafeek 2019; Sahoo and Sivakumar 2015; Sahoo et al. 2018; Mishra et al. 2012, 2013a, 2013b; Wanas and Hassan 2014). Also, many researchers have studied cosmological models in the gravitational theory; for example, see Refs (Pawar and Solanke 2014; Dagwal and Pawar 2018; Xiao and Wang 2020; Pawar et al. 2021). By using the linearly varying deceleration parameter (\(\mathit{LVDP}\)) law we can generalize the cosmological solutions. As is known, the universe would exhibit expansion phases such as expansion with constant rate for \(q = 0\), exponential expansion phase for \(- 1 \le q < 0\), superexponential expansion for \(q < - 1\), and de Sitter expansion for \(q = - 1\). Note that the superexponential expansion is a rapid rate of expansion if \(q < -1\) under \(\mathit{LVDP}\). The linearly varying deceleration parameter is given by (Akarsu and Tekin 2012)

$$ q = m - 1 - at, $$
(40)

where \(m\) (is in dimensionless) and \(a\) (is in units of sec−1) are constants greater than zero.

From Eq. (40) we can observe that the universe starts with a Big Bang at \(t_{bb} = 0\) with \(q_{bb} = m - 1\). Then it enters the accelerating stage at \(t_{a} = (m - 1)/a\) with \(q_{a} \le 0\). Next, it enters the superexponential expansion phase at \(t_{se} = m/a\) with \(q_{se} \le - 1\), and the universe finally ends at \(t_{br} = 2m/a\) with \(q_{br} = - (m + 1)\).

The \(\mathit{DP}\) is defined as follows:

$$ q + 1 = \frac{dH^{ - 1}}{dt}, $$
(41)

where \(H\) is the Hubble parameter defined through \(H = \dot{S}/S\).

Integration of Eq. (41) yields

$$ H = \frac{2}{t (2m - at)} = \frac{\dot{S}}{S}. $$
(42)

Equation (42) leads to

$$ \dot{S} = \frac{2 S}{t (2m - at)} $$
(43)

and

$$ \ddot{S} = \frac{4S (1 - m + a t)}{t^{2} (2m - at)^{2}}. $$
(44)

The scale factor \(S(t)\) is obtained by integrating the Hubble parameter in Eq. (42) as (Bakry et al. 2021)

$$ S = S_{0}\left ( \frac{t}{2m - at} \right )^{1 / m}, $$
(45)

where \(S_{0}\) is a constant of integration.

The scale factor (45) differs from the result obtained by Akarsu and Tekin (2012).

Substituting Eqs. (43)–(45) into (37)–(39), we get

$$ \rho = \frac{6}{ \pi t^{2} (2m - at)^{2}}, $$
(46)
$$ P = - \left ( \frac{2 (2 - m + at)}{ \pi t^{2} (2m - at)^{2}} \right ), $$
(47)
$$ \omega = - \frac{1}{3} \left ( 2 - m + at \right ) = - \frac{1}{3}(1 - q). $$
(48)

The relationship between the scale factor and the redshift \(z\) is given by the expression (Akarsu and Tekin 2012)

$$ 1 + z = \frac{S_{z = 0}}{S(t)}, $$
(49)

where \(S_{z = 0}\) is the present value of the scale factor.

We can also solve the deceleration parameter \(q\) as a function of the redshift. Using Eqs. (41), (45), and (49), we obtain

$$ q(z) = m - 1 - \frac{2ma S^{m}_{z = 0}}{(1 + z)^{m} + a S^{m}_{z = 0}}, $$
(50)

where \(S_{z = 0} = 2.46\); see Table 1.

Table 1 The limits of the torsion, shear, and expansion effects on the evolution of the universe
Full size table

The Jerk parameter \(j(t)\) is defined as follows (Visser 2004):

$$ j(t) = \frac{1}{\mathit{SH}^{3}}\frac{d{}^{3}S}{dt^{3}} = q(t) + 2q^{2}(t) - \frac{1}{H(t)}\frac{dq(t)}{dt}. $$
(51)

This is used to discuss the models close to \(\Lambda\mathit{CDM}\). The complete sets of \(\Lambda\mathit{CDM}\) models characterized by \(j (t) = 1\) (constant) are provided by David et al. (2007). It is said that the universe undergoes a smooth transition from deceleration to acceleration for models with negative values of deceleration parameter or with positive value of jerk parameter. Substituting Eqs. (39) and (42) into (48), the cosmic jerk parameter is as follows:

$$ j(t) = (2m - 1) (m - 1) + 3 a t (1 - m) + \frac{3 a^{2}t^{2}}{2}. $$
(52)

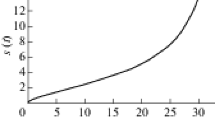
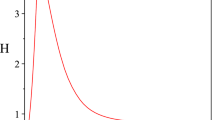
To compare the findings of the current study with the observed cosmological kinematics and to provide further predictions, the cosmological parameters are plotted by selecting \(m = 2\) and \(a = 0.126\). In Fig. 1, the scale factor is plotted versus the cosmic time \(t\). The universe starts with the Big Bang at \(t_{bb} = 0\) and ends at \(t_{br} = 30.75~\text{Gyr}\). In Fig. 2 the deceleration parameter \(q(t)\) is plotted against the cosmic time \(t\). The deceleration parameter is initially \(q_{bb} = 1\) and then reaches \(q_{br} = - 3\) at the end of the universe. The universe enters into the hastening development stage at \(t_{a} = 7.937~\text{Gyr}\), and then it reaches \(q_{\mathit{day}} = - 0.73\) at \(t_{\mathit{day}} = 13.7~\text{Gyr}\). Next, it enters the superexponential expansion stage at \(t_{se} = 15.873~\text{Gyr}\). In Fig. 3 the Hubble parameter \(H\) is plotted versus the cosmic time \(t\). This parameter diverges at the beginning and the end of the universe. The deceleration parameter \(q(z)\) is also graphed versus redshift \(z\) in Fig. 4. Note that the rapid development begins at \(z_{t} = 0.51\), which is consistent with the observational data, where the cosmological observations for the transition redshift of the hurrying expansion are given by \(0.3 < z_{t} < 0.8\) (Riess et al. 2007; Cunha and Lima 2008; Frieman et al. 2008; Ishida et al. 2008; Cunha 2009; Pandolfi 2009; Lima et al. 2010; Li et al. 2011). In Fig. 5 the energy density \(\rho (t)\) of the fluid is plotted versus the cosmic time \(t\). Note in the current model that the positivity of the energy density is satisfied. The energy density of the fluid deviates at the beginning and the end of the universe. In Fig. 6 the pressure of the fluid \(P\) is plotted versus the cosmic time \(t\). The pressure also deviates at the beginning and the end of the universe. In Fig. 7 the state parameter of the fluid \(\omega \) is plotted versus the cosmic time \(t\). Observe that the value of \(\omega = 0\) at \(q_{bb} = 1\) and \(t_{bb} = 0\) enters to \(\omega = - 1 / 3\) at \(q_{a} = 0\) and \(t_{a} = 7.937~\text{Gyr}\), and reaches \(\omega = - 4 / 3\) at the end of the universe. The plot between the jerk and cosmic time in Fig. 8 reveals that the cosmic jerk parameter is positive throughout the whole circle of the universe and tends to be 15 at late times. The jerk curve changes at \(q_{a} = 0\) and \(t_{a} = 7.937~\text{Gyr}\). The value of the jerk is consistent with observational value \(j = 2.4\) for \(t = 1.5~\text{Gyr}\) (Riess et al. 2004; Astier et al. 2006; Capozziello et al. 2007). In Fig. 9 the Hubble parameter \(H\) is plotted versus redshift \(z\). It is clear that acceleration occurs when \(z = 0.5\) and that there is a strong acceleration when \(z = - 0.5\). The value of the redshift decreases with the increase of time until it reaches its lowest value at the Big Rip, as shown in the Fig. 10.

Fig. 1
figure 1

Scale factor vs. cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 2
figure 2

Deceleration parameter vs. cosmic time \(t: 0 \to 31.75\)

Full size image
Fig. 3
figure 3

Hubble parameter vs. cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 4
figure 4

Deceleration parameter \(q(z)\) vs. redshift \(z: - 1 \to 2\)

Full size image
Fig. 5
figure 5

Energy density of the fluid \(\rho \) vs. cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 6
figure 6

Pressure \(P(t)\) vs. cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 7
figure 7

Equation of state parameter \(\omega \) vs. the cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 8
figure 8

Displays the evolution of the jerk parameter vs. cosmic time \(t:0 \to 31.75\)

Full size image
Fig. 9
figure 9

Hubble parameter \(H(z)\) vs. redshift \(z: - 1 \to 2\)

Full size image
Fig. 10
figure 10

Cosmic time vs. redshift \(z: - 1 \to 2\)

Full size image

5 The limits of the torsion effect on the universe in \(\mathit{GFT}\)

In this section, we discuss the effect of torsion on the cosmological parameters and on the evolution of the universe. The scalar torsion \(\mathrm{T}_{s}\) is defined by (Wanas and Hassan 2014)

$$ \mathrm{T}_{s} = \sqrt{g^{\alpha \beta } C_{\alpha } C_{\beta }} = 3\dot{S}/S = 3H. $$
(53)

This equation implies that the physical behavior of both the Hubble parameter and the scalar torsion are similar.

Comparing Eqs. (42), and (53), we obtain

$$ \mathrm{T}_{s} = \frac{6}{t (2m - at)}, $$
(54)

where \(\mathrm{T}_{s}\) is in units of sec−1.

Using Eqs. (41) and (46), we obtain

$$ q (\mathrm{T}_{s}) = - \left ( 1 + \frac{3\dot{\mathrm{T}}_{s}}{\mathrm{T}_{s}^{2}} \right ). $$
(55)

Also, substituting (47) and (48) into (37–39), we get

$$ \rho _{\mathrm{T}_{s}} = \frac{\mathrm{T}_{s}^{2}}{6 \pi }. $$
(56)

This equation implies that the positivity of the energy density \(\rho \ge 0\) is satisfied, and it does not depend on the curvature constant. Also, this means that the density of matter is the source of torsion:

$$ P_{\mathrm{T}_{s}} = - \frac{1}{6 \pi } \left ( \frac{d\mathrm{T}_{s}}{dt} + \frac{2}{3}\mathrm{T}_{ s}^{2} \right ), $$
(57)

which shows that pressures can act as a source of torsion.

Equations (56) and (57) show that the energy density and pressure contain torsion contributions (Capozziello et al. 2017)

$$ \omega (\mathrm{T}_{s}) = - \left ( \frac{2}{3} + \frac{ \dot{\mathrm{T}}_{s}}{\mathrm{T}_{s}^{2}} \right ) = - \frac{1}{3}\left ( 1 - q \right ). $$
(58)

Equations (56)–(58) are the dynamical equations of \(\mathit{FRW}\) standard cosmology, written in the context of

\(\mathit{PAP}\)-geometry (a geometry with nonvanishing torsion).

On the other hand, substituting (46) and (48) into (51), we get

$$ j(\mathrm{T}_{s}) = \left ( 1 + \frac{3\dot{\mathrm{T}}_{s}}{\mathrm{T}_{s}^{2}} \right ) \left ( 1 + \frac{6\dot{\mathrm{T}}_{s}}{\mathrm{T}_{s}^{2}} \right ) + \frac{9}{\mathrm{T}_{s}^{3}}\left ( \ddot{\mathrm{T}}_{s} - \frac{2\dot{\mathrm{T}}_{s}^{2}}{\mathrm{T}_{s}} \right ). $$
(59)

To find the relationship between the torsion scalar and the redshift \(z\), we use Eqs. (49) and (54) to get the expression

$$ \mathrm{T}_{s}(z) = \frac{3 \left ( (1 + z)^{m} + a S_{ z = 0}^{m} \right )^{2}}{2 m^{2} S_{ z = 0}^{m}(1 + z)^{m}}, $$
(60)

where \(S_{z = 0} = 2.46\); see Table 1.

From Eq. (55) we can observe that the universe starts with a Big Bang at \(t_{bb} = 0\) with \(\mathrm{T}_{s} = \infty \), and then it enters the accelerating stage at \(t_{a} = (m - 1)/a\) with \(\mathrm{T}_{s} = \frac{6a}{m^{2} - 1}\). Next, it enters the superexponential expansion phase at \(t_{se} = m/a\) with \(\mathrm{T}_{s} = \frac{6 a}{m^{2}}\), and finally ends at \(t_{br} = 2m/a\) with \(\mathrm{T}_{s} = \infty \). The scalar torsion \(\mathrm{T}_{s}\) diverges at the Big Bang and the Big Rip. Also, from Eqs. (45), (49) and (54), the scale factor, the energy density of the fluid, and the scalar torsion diverge at \(t \to t_{\mathit{end}}\). This is the Big Rip behavior first suggested by Caldwell et al. (2003).

In Fig. 11, we plot the scalar torsion \(\mathrm{T}_{s}\) versus the cosmic time \(t\). This parameter diverges at the beginning and the end of the universe. The model accelerates at (\(t_{a} = 7.937~\text{Gyr}\) and \(\mathrm{T}_{s} = 0.252\)) and enters into the superexponential expansion phase at (\(t_{se} = 15.873 \mathit{Gyr}\) and \(\mathrm{T}_{s} = 0.189\)). As a result, the universe ends at (\(t_{br} = 31.75~\text{Gyr}\) and \(\mathrm{T}_{s} = \infty \)). We can say that the torsion of the geometric origin is introduced in GR and can lead to an accelerated behavior of the universe due to a repulsive nonlinear interaction of the (baryon) matter with itself. A discussion of this opinion is given in (Capozziello et al. 2007). In Fig. 12, we plot the torsion scalar versus redshift \(z\). We can observe that the present value of the torsion scalar is \(\mathrm{T}_{s z = 0} = 0.19\).

Fig. 11
figure 11

Torsion scalar \(\mathrm{T}_{s}\) vs. cosmic time \(t:0 \to 30.15\)

Full size image
Fig. 12
figure 12

Torsion scalar \(\mathrm{T}_{s}\) vs. redshift \(z: - 1 \to 2\)

Full size image

Using Eqs. (37) and (38) with \(P = \omega \rho \), the continuity equation reads

$$ \frac{\dot{\rho }}{\rho } = - 3\frac{\dot{S}}{S} \left ( \frac{4}{3} + 2 \omega \right ). $$
(61)

Equation (61) gives

$$ \rho = \rho _{0}\left ( \frac{S}{S_{0}} \right )^{ - (4 + 6 \omega )} $$
(62)

with \(\rho _{0} = \rho (t = t_{0})\) and \(S_{0} = S(t = t_{0})\).

Using Eqs. (45), (54), and (62), we get

$$ \rho _{\mathrm{T}_{s}} = 0.41\rho _{0} \mathrm{T}_{s}^{ - (2 + 3 \omega )} t^{ - 2 (2 + 3 \omega )}. $$
(63)

Accordingly, the torsion effect on the energy-density evolution carried by the term on the right-hand side of Eq. (60) also depends on the matter equation of state \(\omega \). The torsion contribution vanishes in media with zero effective gravitational mass/energy (i.e., when \(\omega = - 2/3\)). On the other hand, the energy-density evolution becomes essentially torsion dominated in the case of a vacuum stage when \(\omega = - 1\) and

$$ (\rho _{\mathrm{T}_{s}})_{\omega = - 1} = 0.41 \rho _{0} (\mathrm{T}_{s})_{\omega = - 1} (t^{2})_{\omega = - 1}. $$
(64)

Therefore \(\rho = \rho (t)\) due to the presence of only torsion and time. Thus torsion cosmology is a competitive model to explain the cosmic acceleration, which does not need to introduce some exotic matter composition.

6 Big Rip model with shear

To better understand the accelerated expansion of the universe, many researchers depend on the type Ia supernova (SNe Ia) (Riess et al. 2004). What happened in the Big Bang and its relationship to the expansion of the universe, shear, and dark energy is still a debatable issue (Wolfgang and Niemeyer 2000). Therefore, in this section, we review the relationship between shear and torsion and its role in the evolution of the universe.

Now the rate of convergence/divergence of world-line congruence is governed by the modified Raychaudhuri equation in \(\mathit{AP}\)-geometry. In the presence of torsion, the latter reads as (Wanas and Bakry 2009)

$$\begin{aligned} &\frac{d\Theta }{d\tau } - 2 (\Omega ^{2} - \Sigma ^{2}) + \frac{\Theta {}^{2}}{3} + U^{\alpha } U^{\beta } (R_{\alpha \beta } - L_{\alpha \beta } ) \\ &\quad {}+ U^{\alpha } (\Omega _{\sigma }^{ \beta } + \Sigma _{\sigma }^{ \beta } ) \Lambda _{ \alpha \beta }^{\sigma } + \frac{1}{3}\Theta U^{\alpha } C_{\alpha } = 0, \end{aligned}$$
(65)

where \(U^{\alpha } \) is the unit tangent along the geodesic, \(\Theta \) is the expansion scalar, \(\Omega \) is the rotation scalar, and \(\Sigma \) is the shear scalar defined by

$$ \Theta = U^{\alpha }_{| | \alpha },\qquad \Omega _{\alpha \beta } = U_{[\alpha || \beta ]},\qquad \Omega ^{2} = \frac{1}{2}\Omega ^{\alpha \beta } \Omega _{\alpha \beta }, $$
$$ \Sigma _{\alpha \beta } = U_{(\alpha || \beta )} - \frac{\Theta }{3}P_{\alpha \beta },\qquad \Sigma ^{2} = \frac{1}{2}\Sigma ^{\alpha \beta } \Sigma _{\alpha \beta }, $$
$$ P_{\alpha \beta } = g_{\alpha \beta } - U_{\alpha } U_{\beta }, $$

and

$$ U^{\alpha } U_{\alpha } = 1,\qquad U_{\sigma } U^{\alpha } U^{\beta } \Lambda _{ \alpha \beta }^{\sigma } = 0, $$
(66)

where \(\Sigma _{\alpha \beta } \) is a shearing tensor, and \(\Omega _{\alpha \beta } \) is a rotation tensor.

Substituting the values given by (33) and (34) into the modified Raychaudhuri Eq. (65), after some calculations, we get

$$ \frac{d\Theta }{d\tau } = 6 \left ( \frac{\ddot{S}}{S} - \frac{\dot{S}^{2}}{S^{2}} \right ). $$
(67)

This equation is the same as that obtained by Wanas et al. (2018b) when \(b = - 1\).

Substitution from (53) into (67), one obtains

$$ \frac{d\Theta }{d\tau } = \left ( \frac{6 \ddot{S}}{S} - \frac{2 \mathrm{T}_{s}^{2}}{3} \right ). $$
(68)

Note that the last term on the right-hand side of Eq. (18), which implies that torsion assists or inhibits the expansion/contraction of the time-like congruence tangent to the \(U_{\alpha } \)-field, depends on the value of \(\mathrm{T}_{s}\). The model is considered superexpansion when \(d\Theta /dt > 0\), that is,

$$ \frac{ \ddot{S}}{S} > \frac{1}{9}\mathrm{T}_{s}^{2}. $$
(69)

This condition is met in our model when \(t_{se} = m/a\).

On the other hand, by using Eqs. (32)–(34), (43), and (66), we get

$$ \Theta = \frac{6\dot{S}}{S} = \frac{12}{t (2m - at)}. $$
(70)

Observe that the expansion scalar is infinite at \(t = 0\) and \(t = 2m/a\). As \(t \to m/a\), we obtain

\(\Theta \to 12a/m^{2}\), \(q = - 1\), \(dH/dt = 0\), which implies the smallest value of Hubble’s parameter:

$$ \Omega = 0, $$
(71)
$$ \Sigma _{11} = - \frac{16S \dot{S}}{W^{ + 2}},\qquad \Sigma _{22} = \Sigma _{33} = r^{2}\Sigma _{11}. $$
(72)

Thus the shear scalar can be obtained from Eqs. (36), (66), and (72) as follows:

$$ \Sigma ^{2} = \frac{1}{6}\left ( \frac{3 \dot{S}}{S} \right )^{2} = \pi \rho , $$
(73)

where \(\Sigma \) is in units of sec−1, and

$$ \rho _{\Sigma } = \frac{\Sigma ^{2}}{\pi }. $$

This equation means that the density of matter is the source of shear.

Using Eq. (73), we can rewrite Eq. (57) as follows:

$$ P_{\Sigma } = - \frac{2.5}{6 \pi } \left ( \frac{d \Sigma }{dt} + \frac{5}{3}\Sigma ^{2} \right ). $$
(74)

Also, Eq. (74) shows that pressures can act as a source of the shear.

Substituting from (53) and (54) into (73), we obtain

$$ \Sigma = 0.4 \mathrm{T}_{s} = \left ( \frac{2.5}{t (2m - at)} \right ). $$
(75)

Substituting (53) into (70), we obtain

$$ \Theta = 2 \mathrm{T}_{s}. $$
(76)

From Eqs. (73) and (75) we get

$$ \mathrm{T}_{s} = 2.5 \Sigma = 0.5 \Theta . $$
(77)

Equation (77) represents the relationship between the torsion scalar, the shear scalar, and the expansion scalar. Since \(\Sigma ^{2}/\Theta ^{2} = 0.04 \ne 0\), our model is anisotropic.

Using Eqs. (38) and (43), we obtain

$$ q (\Sigma ) = - \left ( 1 + \frac{1.2}{\Sigma ^{2}}\frac{d \Sigma }{dt} \right ). $$
(78)

From Eq. (35) we can read off the condition for the expansion of the universe to be accelerating:

$$ P < - \frac{1}{3}\rho . $$
(79)

Substituting (56) and (77) into (79), we get

$$ P < - 0.02 \mathrm{T}_{ s}^{2} = - 0.1 \Sigma ^{2}. $$
(80)

Also, the relationship between the shear scalar and the redshift \(z\) can be obtained as follows:

$$ \Sigma _{z} = \frac{0.6 \left ( (1 + z)^{m} + a S_{ z = 0}^{m} \right )^{2}}{ m^{2} S_{ z = 0}^{m}(1 + z)^{m}}, $$
(81)

where \(S_{z = 0} = 2.46\); see Table 1.

Now, to demonstrate how \(\mathit{GR}\) with shear matches the observed kinematics of the universe and makes additional predictions, we plot the shear scalar by choosing \(m = 2\) and \(a = 0.126\). We also plot the scalar shear versus redshift \(z\) in Fig. 13; one can observe that the present value of the shear scalar is \(\Sigma _{z = 0} = 0.08\), which is the expected \(1\sigma \) constrain for an Euclid-like experiment (Heavens et al. 2006; Taylor et al. 2018). The shear scalar diverges at an initial epoch as depicted in Fig. 14 and also diverges at the Big Rip.

Fig. 13
figure 13

Shear scalar \(\Sigma \) vs. redshift \(z: - 1 \to 2\)

Full size image
Fig. 14
figure 14

Shear scalar \(\Sigma \) vs. cosmic time \(t:0 \to 30.15\)

Full size image

On the other hand, it is well known that the modified Raychaudhuri equation (65) plays an important role in studying space-time singularities (Wanas et al. 2018b). The meaning of singularity in physics, in general, is connected to a point where space-time curvature becomes infinite or divergent. However, Geroch (1967, 1968a, 1968b) has pointed out that a more precise meaning of singularity would require the idea of geodesic incompleteness. Established singularity theorems using the Raychaudhuri equation show that the existence of singularity in the solution of GR field equations is inevitable (Narlikar 1979).

It is widely accepted that the universe in its early stages was very hot. Consequently, matter was degenerated into its elementary constituents. These constituents are spinning elementary particles with different spins. So, if there is an interaction between the gravitational field and the spin of the particle, as suggested by (Wanas 1996), then it will be interesting to explore the effect of this interaction on the initial singularity of the universe. Now, we are going to use the modified Raychaudhuri equation (65) to study the singularity problem in our model. The existence of initial singularity depends mainly on the solution of Eq. (65). In particular, it depends on the resulting sign of the left-hand side term \(d\Theta /dt\). This can be studied using the standard conventions of the singularity theorems of GR, that is, singular models are characterized by \(d\Theta /dt < 0\). The initial singularity exists when

$$ T_{s}^{2} > \frac{9 \ddot{S}}{S}. $$
(82)

Substituting (44) and (54) into (82), we get the existence of the initial singularity at

$$ \tau < \frac{ m}{a}, $$
(83)

that is, inequality (79) implies that the initial singularity is realized within a proper time given by inequality (70).

Also, substituting (20), (66), (71), and (72) into the modified Raychaudhuri equation (65), after some calculations, we get

$$ \frac{1}{2}\frac{d\Theta }{d\tau } = - \frac{1}{12}\Theta ^{2} - U^{\alpha } U^{\beta } R_{\alpha \beta }. $$
(84)

If the strong energy condition holds, that is, \(U^{\alpha } U^{\beta } R_{\alpha \beta } \ge 0\), then Eq. (74) takes the form

$$ \frac{d\Theta }{d\tau } \le - \frac{1}{6}\Theta ^{2}. $$
(85)

Equation (75) can be rewritten as follows:

$$ \frac{d\Theta ^{ - 1}}{d\tau } \ge \frac{1}{6}. $$
(86)

Integrating this inequality, we get

$$ \Theta ^{ - 1} \ge \frac{\tau }{6} + \Theta _{0}^{ - 1}, $$
(87)

where \(\Theta _{0}\) is the initial value of \(\Theta \).

Let \(\Theta _{0} < o\), that is, the congruence is initially converging at a point on a path in the congruence. Then inequality (78) takes the form

$$ \Theta ^{ - 1} \ge \frac{\tau }{6} - | \Theta _{0}^{ - 1}|. $$
(88)

This inequality implies that the expansion \(\Theta \to - \infty \) along the path within a proper time is given by

$$ \tau \le \frac{6}{|\Theta _{0}|}. $$
(89)

Comparing Eqs. (73) and (79), the initial value of \(\Theta \) is given by

$$ |\Theta _{0}| = \frac{6 a}{m} = 0.378. $$
(90)

This value corresponds to Table 1, where the acceleration starts at that value.

7 Results and discussion

Torsion can force the worlds of Milne and Einstein–de Sitter to a stage of exponential expansion similar to that of its de Sitter counterpart (Bakry and Shafeek 2021). These examples indicate that a torsion-dominated early universe, or a late, dust-dominated universe with torsion, could go through a phase of accelerated expansion without the need for a cosmological constant, enlargement field, or dark energy. Similar effects are stated in (Siamak et al. 2017; Rabin et al. 2018; Kranas et al. 2019), suggesting that torsional cosmology may merit further scrutiny. For this reason, we use AP-geometry by incorporating the effects of space-time torsion into the theory; asymmetric affine connections are allowed to provide the simplest classical extension of general relativity by joining the effects of space-time torsion into the theory. In this paper, we adopt a specific profile for the torsion tensor that belongs to the class of the vectorial torsion fields, and it is monitored by a single scalar function of time. Through the study, we found that the field equation does not depend on the curvature constant because the curvature constant disappears automatically. Therefore the energy density of the matter, the pressure in the fluid, and our Big Rip model do not depend on this constant. In the present paper, we introduce the evolution of a universe that does not exhibit a cosmological constant such as Poincaré’s gauge theory of gravity (\(\mathit{PGT}\)). Given the homogeneity and isotropy of the universe, the temporal component of the torsion \(\mathrm{T}_{s}\) is only what survives and has bearing on the emergence of the universe in advanced and late times (Yo and Nester 1999; Chui and Ni 1993; Ni 1996). From Eqs. (53)–(59) and (74)–(76) we can discuss the limits of the torsion, shear, and expansion effects on the evolution of the universe in Table 1.

8 Conclusions

From Table 1 we can conclude that the torsion and shear have a major role at the beginning of the universe at the Big Bang. Then its effect diminishes until it reaches its lowest value in the middle of the universe’s age, then increases again, and reaches its first value at the Big Rip (because in the Big Bang and Big Rip stages the matter of the universe is spinning elementary particles). Torsion’s effect on the evolution of the universe is greater than the effect of shearing. The torsion of time and space produced a gravitational repulsion in the early universe full of quarks and leptons, thereby preventing the singularity of the universe. This idea suggests that our universe shrinks by a minimum radius before rebounding, which may explain the origin of the Big Bang. The torsion energy can solve the problem of \(\mathit{SN}\)-type observations since it gives rise to a repulsive force. We can substitute the exotic term dark energy with the term torsion energy; the latter has a pure geometric origin; for more detail, see (Wanas 2007, 2008, 2010). The value of the torsion density parameter is \(\Omega _{\mathrm{T}_{s}} = 2 \pi \rho _{\mathrm{T}_{s}}/3 H^{2} \approx 1\) at \(t \in \mathopen{]} 0, 31.75 \mathclose{[}\). Also, the value of the shear density parameter is \(\Omega _{\Sigma } = 2 \pi \rho _{\Sigma } /3 H^{2} \approx 1\) at \(t \in \mathopen{]}0, 31.75 \mathclose{[}\). The overall density parameter is \(\Omega = \Omega _{\mathrm{T}_{s}} \approx 1\) or \(\Omega = \Omega _{\Sigma } \approx 1\). Therefore the model can predict the flat universe at \(t \in \mathopen{]} 0, 31.75 \mathclose{[}\). Hence the derived model is compatible with the observational results (Spergel et al. 2003, 2007). When assuming the flat \(\mathit{FRW}\) cosmology, we can find that the limitation of the torsion scalar is \(\mathrm{T}_{s} = 0.22 \pm 0.03\) at \(t \in \mathopen{]} 0, 31.75 \mathclose{[}\). The field Eq. (35)–(36) does not depend on the curvature constant, and thus the curvature density parameter \(\Omega _{K} = 0\). Consequently, our model assumes that the space is flat, which is consistent with the expansion prediction of the disappearance of the curvature density parameter [69], and the results obtained by the \(\mathit{CMB}\) experiment (Spergel et al. 2003, 2007). From Eq. (74) and Table 1 we can observe the condition of negative pressure at \(\Sigma > 3/5 t_{\Sigma } \). The pressure has negative values although this could be physically considered unreasonable. However, due to the shear force, the energy conditions are always satisfied. The pressure at the beginning of the universe is isotropic, but due to the presence of the shear, the pressure becomes more and more anisotropic. From Eq. (64) and Table 1 we can obtain the value of the initial energy density as \(\rho _{0} = 5.6\times 10^{ - 5}\) sec−1. Table 1 shows that the dynamic scalar torsion model can display features similar to those of the currently observed accelerating universe. The energy density, torsion, shear, and expansion diverge at the beginning and end of the universe, as shown in Table 1 and Figs. (5) and (11). Fluids with \(\omega < - 0.33\) are usually considered in the context of dark energy because they cause accelerated expansion. The terms dark energy and the cosmological constant are foreign terms. They have neither a geometric origin nor a clearly defined physical origin (Wanas 2010). On this basis, we can explain the expansion of the universe due to the influence of torsion and shear forces, thus getting rid of the concept of dark energy. From the field equations we can see that the effect of the “dark energy” mainly comes from the nonlinearity of the field equation driven by the dynamic scalar torsion. It is shown in Table 1 that \(\omega \) emerges within a range about \(- 1.7 \le \omega \le 0\), which is compatible with the \(\mathit{SNe} Ia\) observations (Knop et al. 2003; Spergel et al. 2007). The parameter \(\mathit{EoS}\) displays the same singularity represented by the Hubble parameter, that is, at the initial phase and at the Big Rip, which conforms to the investigations of Sahoo and Sivakumar (2015). Bearing in mind homogeneous and isotropic cosmological models, the terms produced by torsion and shear give rise to accelerated expansion. This means that acceleration can be a geometric source in GR cosmology with torsion and shear forces. There is general agreement that the universe has reached a state of accelerating expansion at redshift \(z_{t} = 0.5\) (Cunha and Lima 2008; Cunha 2009). We can observe that the accelerating expansion in our model begins at \(q = 0\), \(z_{t} = 0.51\), \(\mathrm{T}_{s} = 0.25\), and \(\Sigma = 0.10\). The model also enters the accelerating expansion stage at \(t_{z = 0} = 13.7~\text{Gyr}\), and the present value of the deceleration parameter is \(q_{z = 0} = - 0.73\), \(\mathrm{T}_{s} = 0.19\), and \(\Sigma = 0.08\). Some of these values are consistent with the observational results (Heavens et al. 2006; Cunha and Lima 2008; Taylor et al. 2018). Finally, Figs. (3), (5), (11), and (14) reveal that the Hubble parameter, the energy density, the torsion scalar, and the shear scalar have similar behavior and exhibit opposite behavior of the pressure in the fluid.