Big Rip and Big Crunch Cosmological Models in a Gravitational Field with Torsion

Abstract

The gravitational field with torsion is being constructed by using the parametrized absolute parallelism geometry. A generalized law of variation of Hubble’s parameter in evolutionary cosmological models is used. The cosmological models under the influence of the gravitational field with torsion are obtained and discussed. A new model of the Universe is presented using a special class of Riemann–Cartan geometry. This model is oscillating with expansion and contraction at different stages. It behaves normally as the conventional Big Bang model in the first half-age until it reaches the moment of a Big Rip, then reverses its behavior as a result of a changes in the pressure and torsion until it reaches a Big Crunch at the end of the second half-age. We suppose that the Big Rip singularity is replaced by a regular maximum of the scale factor at the Big Rip due to a possible physical mechanism of quantum nature. The positivity condition for the energy density of matter leads to exclusion of open and closed universes.

1 INTRODUCTION

Lately, there has been some renewed interest in torsion looking into the Einstein–Cartan construction of General Relativity (GR) [1–5] and into the physical effects it may imply [6–9]. The standard $\Lambda$CDM cosmological model is the simplest and arguably the one that most effectively designates the evolution of the observed universe [10].

Although being the best fit to a wide range of data, it suffers from several theoretical shortcomings [11], so it fails in tracking cosmic dynamics at every redshift and fails in according observational cosmology to some fundamental theory of physical interactions. Among the flaws of this model, there is the lack of final probes, at a fundamental level, for dark energy and dark matter candidates which frustrates the possibility to reduce $\Lambda$CDM to some self-consistent scheme, despite the fact that it is a fair “snapshot” of the present status of the universe.

These facts motivate the search for other models, among which alternative theories of gravity that should reproduce the successes of $\Lambda$CDM but should be more appropriate in describing the cosmological dynamics [12].

Specifically, the large amount of dark energy models depend on the implied assumption that Einstein’s GR is the correct theory of gravity indeed. Yet, its cogency on cosmological scales and large astrophysical scales has never been tested but only expected [13], and it is therefore imaginable that both cosmic speed-up and missing matter, respectively, dark energy and dark matter, are nothing else but signals of a breakdown of GR at large scales.

In other arguments, GR could fail in giving self-consistent pictures both at ultraviolet scales (early universe) and at infrared scales (late universe), also it is fairly working at the Solar System scales and in the weak field. For these reasons, the “full” geometric sector of GR has to be investigated considering also the role of torsion. Such an “ingredient” has been firstly considered by Cartan and then by Sciama and Kibble in order to deal with spin in GR (see [14] for a review).

Being spin as fundamental as the mass of the particles, torsion was introduced in order to complete the scheme that mass (energy) is the source of curvature and spin is the source of torsion. Unfortunately, torsion in the context of GR seems not to produce models with observable effects since the gravitational coupling is extremely weak in all torsion phenomena, and only in the very early universe its effect could have been significant.

However, it has been proven that spin is not the only source for torsion. As a matter of fact, torsion can be decomposed in three irreducible tensors, with different properties. In [15], a systematic classification of these different types of torsion and their possible sources was discussed.

In this article, we discuss the cosmological applications of the gravitational field with torsion, considering the possibility that the Big Rip, Big Crunch and the singularity problem could be geometrically interpreted by curvature and torsion. Examples in which repulsive gravity and clustered structures could be implemented considering torsion are present in the literature [14, 16], and [17] but, in that case, GR has been adopted, and the whole dark sector has not been addressed.

When the parameterized absolute parallelism (PAP) geometry is considered, the terms originated by torsion can lead to an accelerated expansion. This means that in the gravitational field with torsion (GFT), torsion can be a geometric source for acceleration and solve the initial singularity problem.

The aim of the present article is to study the effect of torsion on the dynamics of the Friedmann–Robertson–Walker (FRW) Cosmology.

To clarify the organization of the current manuscript, the rest of the paper is developed as follows: Section 2 is devoted to investigating the torsion tensor and the equations of GFT. The period of the revolution of a satellite in an equatorial orbit with zero inclination is illustrated in Section 3. Section 4 is devoted to introducing the stability condition of a satellite with zero inclination.

The motion of a satellite with a variable inclination from the equatorial plane is discussed in Section 5. In Section 6, the observational bounds on cosmic torsion are discussed. Finally, concluding remarks based on the main findings are outlined in Section 7.

2 THE TORSION TENSOR AND GFT EQUATIONS

It is well known that the spin can be one of the sources of torsion. In 1923, Cartan showed that the intrinsic angular momentum (spin) could have an important role in a geometric theory of space-time like GR [18]. He showed that spin could create torsion. This idea was considered also by Sciama [19] and Kibble [20] and, more recently, by Hehl et al. [14] and Trautmann et al. [21]. The path followed in this stream of research was to extend GR to a theory (the Einstein–Cartan–Sciama–Kibble, ECSK, theory) in which spin is the source of torsion. In the limit of zero spin distribution, the theory reduces to standard GR.

The PAP is more comprehensive than the absolute parallelism (AP) geometry and the Riemannian geometry, in the sense that it contains these geometries. So, we used this generalized PP geometry to study the evolution of the universe. The PAP geometry is a generalized parallelism to include the contortion effect in addition to the Christoffel symbol in Riemannian geometry with a parameter ($b$). This geometry gives a clearer explanation of the future of the universe. In this article, we are studying the effect of the contortion term on the evolution of the universe. In 2000, Wanas created the PAP geometry; this geometry describes gravity and torsion in specified quantities. The PAP geometry contains the parameter $b$, from which the effect of both gravity and torsion can be determined on cosmological models. The structure of the conventional AP geometry is defined in 4-dimensions by a tetrad vector $\lambda_{i}^{\gamma}$ ($i=1,2,3,4$ indicates the vector number, and $\gamma=1,2,3,4$ indicates the coordinate component). The covariant vector of ${\lambda}^{\gamma}_{i}$ is defined as [22]

$$\lambda_{i}^{\,\,\gamma}\lambda_{i\,\alpha}=\delta_{\alpha}^{\,\,\gamma}\quad\text{and}\quad\lambda_{i}^{\,\,\alpha}\lambda_{j\,\alpha}=\delta_{i\,j}.$$

(1)

One can define the following symmetric tensors:

$$g_{\alpha\beta}=\lambda_{i\alpha}\lambda_{i\beta},\quad g^{\alpha\beta}=\lambda_{i}^{\,\,\alpha}\lambda_{i}^{\,\,\beta},\quad\text{and}$$

$$g_{\beta\gamma}g^{\alpha\beta}=\delta_{\gamma}^{\,\,\alpha}.$$

(2)

At any point of the AP space, we can define a Riemannian space, in which the symmetric tensor (2) plays the role of the metric tensor,

$$ds^{2}=g_{\alpha\beta}dx^{\alpha}dx^{\beta}.$$

(3)

The generalization of partial differentiation in Riemannian space is given by a semi-colon as defined for contravariant and covariant vectors are follows:

$$A^{\beta}{}_{;\gamma}=A^{\beta}{}_{,\gamma}+\left\{{\beta}\atop{\alpha\gamma}\right\}A^{\alpha},$$

(4)

$$A_{\beta;\gamma}=A_{\beta,\gamma}-\left\{{\alpha}\atop{\beta\gamma}\right\}A_{\alpha},$$

(5)

where

$$\left\{{\gamma}\atop{\alpha\beta}\right\}=\frac{1}{2}g^{\gamma\varepsilon}(g_{\alpha\varepsilon\,,\beta}+g_{\beta\varepsilon\,,\alpha}-g_{\alpha\beta\,,\varepsilon}).$$

(6)

In addition to the symmetric affine connection (6), one can define a nonsymmetric connection $\Gamma_{\alpha\beta}^{\gamma}$ as follows:

$$\Gamma_{\alpha\beta}^{\gamma}=\lambda_{i}^{\gamma}\lambda_{i\alpha,\beta}=-\lambda_{i\alpha}\lambda_{i\beta}^{\gamma}.$$

(7)

It is a consequence of the absolute parallelism condition

$$\lambda_{i\alpha|\beta}=\lambda_{i\alpha,\beta}-\Gamma_{\alpha\beta}^{\gamma}\lambda_{i\gamma}.$$

(8)

Consequently, we have two different types of absolute derivatives,

$$A_{|\beta}^{{}_{+}^{\alpha}}=A_{,\beta}^{\alpha}+\Gamma_{\gamma\,\beta}^{\,\alpha}A^{\gamma},\quad\mbox{and}$$

(9)

$$A_{|\beta}^{{}_{-}^{\alpha}}=A_{,\beta}^{\alpha}+\Gamma_{\beta\gamma}^{\alpha}A^{\gamma}.$$

(10)

Using the affine connection (7), the torsion tensor is defined as the antisymmetric part of the connection in a coordinate basis as follows:

$$\Lambda_{\alpha\beta}^{\gamma}=\Gamma_{\alpha\beta}^{\gamma}-\Gamma_{\beta\alpha}^{\gamma}=-\Lambda_{\beta\alpha}^{\gamma}.$$

(11)

A connection with torsion has the form

$$\Psi_{\,\,\,\,\,\alpha\beta}^{\gamma}=\Gamma_{\,\,\,\,\alpha\beta}^{\gamma}-\left\{{\gamma}\atop{\alpha\beta}\right\}=\lambda_{i}^{\,\,\gamma}\lambda_{i\,\alpha\,;\,\beta}$$

$${}=-\lambda_{i\,\alpha}\lambda_{i\,;\,\beta}^{\,\gamma},$$

(12)

where

$$K_{\alpha\beta}^{\gamma}=\Gamma_{\alpha\beta}^{\gamma}+\left\{{\gamma}\atop{\alpha\beta}\right\},$$

(13)

$$\Psi_{[\alpha\beta]}^{\gamma}=\frac{1}{2}(\Gamma_{\alpha\beta}^{\gamma}-\Gamma_{\beta\alpha}^{\gamma})=\frac{1}{2}\Lambda_{\beta\alpha}^{\gamma}.$$

(14)

It is clear that the skew part of the connection ${\mathrm{\Gamma}}^{\gamma}_{\alpha\beta}$ and the symmetric part of the tensor ${\mathrm{\Psi}}^{\gamma}_{\alpha\beta}$ are

$$\Gamma_{[\alpha\beta]}^{\gamma}=\frac{1}{2}\Lambda_{\alpha\beta}^{\gamma},$$

(15)

$$\Psi_{(\alpha\beta)}^{\gamma}=\Gamma_{[\alpha\beta]}^{\gamma}-K_{\beta\alpha}^{\gamma}.$$

(16)

From these third-order tensors, one can define the basic vector as follows:

$$C_{\alpha}=\Psi_{\alpha\beta}^{\beta}.$$

(17)

Certain considerations lead to the following general linear connection [23]:

$$\nabla_{\alpha\beta}^{\gamma}=\left\{{\gamma}\atop{\alpha\beta}\right\}+b\Psi_{\alpha\beta}^{\gamma},$$

(18)

where $b$ is a dimensionless parameter.

It is clear from this equation that we have parametrized the contortion (or equivalently the torsion) term in a general connection of the AP geometry. The parametrized connection represents simultaneously a nonvanishing curvature and a nonvanishing torsion. This result is contrary to what is obtained by some authors [24]. For the entire values of ($b$), all its possible values lead to what is called the PAP geometry.

The general absolute derivative using the connection (18) is defined as [20]

$$A_{\alpha||\beta}=A_{\alpha,\beta}-\nabla_{\alpha\beta}^{\gamma}A_{\gamma},$$

(19)

$$A^{\alpha}{}_{||\beta}=A^{\alpha}{}_{,\beta}-\nabla_{\gamma\beta}^{\alpha}A^{\gamma}.$$

(20)

Note that the double stroke (||) is reduced to a single stroke (|) for the AP geometry and to a semicolon (;) for Riemannian geometry, on taking $b=1$ and $b=0$, respectively.

From equations (12), (18) and (19), one can prove that

$$g_{\alpha\beta}{}_{||\gamma}=0.$$

(21)

In this section, we are going to study the consequences of the modified torsion gravitational effects on the cosmological models, especially those caused by torsion, the geometric effect of torsion in space-time (analogously to mass causing the space-time curvature). We will begin to deduce the field equations that describe this situation, we solve the field equations that describe the cosmological models, and then study the effect of torsion on them. The noncommutation of covariant differentiation using the parametrized connection (18) gives rise to the following simultaneous nonvanishing parametrized torsion and curvature tensor [23]:

$$B_{\,\,\,\mu\nu\sigma}^{\,\varepsilon}=\nabla_{\mu\,\sigma\,,\nu}^{\,\varepsilon}-\nabla_{\mu\,\nu\,,\,\sigma}^{\,\varepsilon}+\nabla_{\mu\,\sigma}^{\,\alpha}\nabla_{\alpha\,\nu}^{\,\varepsilon}-\nabla_{\mu\,\nu}^{\,\alpha}\nabla_{\alpha\,\sigma}^{\,\varepsilon}$$

$${}=R_{\,\,\,\mu\,\nu\,\sigma}^{\,\varepsilon}+b\,L_{\,\,\mu\,\nu\,\sigma}^{\,\varepsilon},$$

(22)

where the Riemann–Christoffel curvature tensor is

$$R_{\,\,\,\,\mu\,\nu\,\sigma}^{\,\varepsilon}=\left\{{\varepsilon}\atop{\mu\sigma}\right\}_{,\,\nu}-\left\{{\varepsilon}\atop{\mu\nu}\right\}_{,\,\sigma}$$

$${}+\left\{{\alpha}\atop{\mu\sigma}\right\}\left\{{\varepsilon}\atop{\alpha\nu}\right\}-\left\{{\alpha}\atop{\mu\nu}\right\}\left\{{\varepsilon}\atop{\alpha\sigma}\right\},$$

(23)

and the parameterized anti-curvature tensor is [21]

$$L_{\mu\sigma}=(\Psi_{\,\,\,\,\mu\sigma\,,\,\,\alpha}^{\alpha}-\Psi_{\,\,\,\mu\alpha\,,\,\sigma}^{\alpha})$$

$${}+b\,(\Psi_{\,\,\,\,\varepsilon\,\alpha}^{\alpha}\Psi_{\,\,\,\,\mu\,\sigma}^{\varepsilon}-\Psi_{\,\,\,\,\,\varepsilon\,\sigma}^{\alpha}\Psi_{\,\,\,\,\mu\,\alpha}^{\varepsilon})$$

$${}+\left\{{\varepsilon}\atop{\mu\sigma}\right\}\Psi_{\,\,\,\,\varepsilon\,\alpha}^{\alpha}-\left\{{\varepsilon}\atop{\alpha\mu}\right\}\Psi_{\,\,\,\,\,\varepsilon\,\sigma}^{\alpha}$$

$${}+\left\{{\alpha}\atop{\alpha\varepsilon}\right\}\Psi_{\,\,\,\,\,\mu\,\sigma}^{\varepsilon}-\left\{{\alpha}\atop{\varepsilon\sigma}\right\}\Psi_{\,\,\,\,\mu\,\alpha}^{\varepsilon}.$$

(24)

The tensor (24) is called the parametrized anti-curvature tensor [25] for the following reasons:

(i) When $b=0$, Eq. (22) turns into $B_{\mu\,\nu\,\sigma}^{\,\varepsilon}=R_{\,\,\,\mu\,\nu\,\sigma}^{\,\varepsilon}$ as in GR.

(ii) When $b=1$, Eq. (22) turns into $B_{\mu\,\nu\,\sigma}^{\,\varepsilon}=0$, as in AP geometry.

(iii) When $b=2$, the curvature tensor (22) is transformed to the inverse of the curvature tensor in GR.

(iv) When $b=n\geq 2$, Eq. (18) gives

$$\nabla_{\alpha\beta}^{\gamma}=n\,\Gamma_{\alpha\,\beta}^{\,\alpha}-(n-1)\left\{{\gamma}\atop{\alpha\beta}\right\}.$$

(25)

(v) The parameter $b$ is defined as $b=[(d/2)MF]$, where $d$ is a number taking the values $0,1,2,\ldots$. for particles with quantum spin $0,1/2,1,\ldots$, respectively; $M$ is the fine structure constant (1/137), and $F$ is a dimensionless parameter depending on the size of the system under consideration. The vanishing of $b$ switches off the antigravity in any system and reduces any suggested theory, constructed in the PAP geometry, to the conventional gravity theory (e.g., the orthodox GR) [25].

Based on this, due to Eq. (25), we find that the effect of torsion is more influential than attraction.

The tensor $B_{\mu\nu}$ is the only tensor to be obtained from (22) by contraction, which is defined as

$$B_{\,\mu\,\nu}=B_{\mu\,\nu\,\varepsilon}^{\,\varepsilon},$$

(26)

and the corresponding scalar is given by

$$B=g^{\mu\,\nu}B_{\,\mu\,\nu}.$$

(27)

We chose the tensor ($B_{\,\mu\,\nu}-\frac{1}{2}g_{\mu\,\nu}B$) to represent the gravitational field with torsion, depending on the property that its covariant divergence (||) vanishes identically (as a result of the Bianchi identity)

$$B_{\,\lambda\,\mu\,\nu\,\alpha\,||\eta}+B_{\,\lambda\,\mu\,\eta\,\nu\,||\alpha}+B_{\,\lambda\,\mu\,\alpha\,\eta\,||\nu}=0,$$

(28)

which can be written concisely as follows:

$$B_{\sigma[\lambda\,\mu\,||\,\nu]}^{\,\varepsilon}=0,$$

(29)

where $A_{[\alpha,\beta,\gamma...]}$ denotes antisymmetry.

One may interpret this geometrical property physically as the conservation of matter and energy; we can use the Bianchi identity (28) to formulate the torsion gravitational field GFT, in the following form:

$$B_{\mu\,\nu}-\frac{1}{2}g_{\mu\,\nu}B=8\pi T_{\mu\,\nu}.$$

(30)

The field equations (30) can be written in the alternative form

$$B_{\mu\,\nu}=8\pi\Big{(}T_{\mu\,\nu}-\frac{1}{2}g_{\mu\,\nu}T\Big{)}.$$

(31)

The energy-momentum tensor of a perfect fluid [26] is given by

$$T_{\alpha\,\beta}=-(P+\rho)U_{\,\alpha}U_{\,\beta}+Pg_{\alpha\,\beta},$$

(32)

so that

$$T=-\rho+3P,$$

(33)

where $\rho$ is the energy density of matter in comoving coordinates, and $p$ is the fluid pressure.

One may note that if $b=0$, the field equation (31) can be reduced to Einstein’s famous field equations [27]. Now, we are going to apply GFT to the structure of the AP geometry having homogeneity and isotropy. Many researchers have used the general tetrad giving the structure of the AP geometry having homogeneity and isotropy, which is given by Robertson (1932) in spherical polar coordinates $(t,r,\theta,\phi)$ [28] as

$$\lambda_{0}^{\,\mu}=\left\{\,1,\,0,\,0,\,0\,\right\},$$

$$\lambda_{1}^{\,\mu}=\Bigg{\{}0,\ \frac{L^{+}\sin\theta\cos\phi}{4S},$$

$$\frac{L^{-}\cos\theta\cos\phi-4\sqrt{K}r\,\sin\phi}{4r\,S},$$

$$\frac{-\,(L^{-}\sin\phi+4\sqrt{K}\,r\cos\theta\cos\phi)}{4rS\,\sin\theta}\Bigg{\}},$$

$$\lambda_{2}^{\,\mu}=\Bigg{\{}0,\ \frac{L^{+}\sin\theta\sin\phi}{4S},$$

$$\frac{L^{-}\cos\theta\sin\phi+4\sqrt{K}r\,\cos\phi}{4r\,S},$$

$$\frac{L^{-}\cos\phi-4\sqrt{K}\,r\cos\theta\sin\phi}{4rS\,\sin\theta}\Bigg{\}},$$

$$\lambda_{3}^{\,\mu}=\left\{0,\frac{L^{+}\cos\theta}{4S},\frac{-L^{-}\sin\theta}{4r\,S},\frac{\sqrt{K}\,}{S\,}\right\},$$

(34)

where $\mu=0,1,2,3$ represents the coordinate components, $L^{\pm}=4\pm Kr^{2}$, $K$ is the curvature constant $=(-1,0,1)$, and $S(t)$ is the scale factor.

The tensors (2) have the same properties of the metric tensor as in Riemannian geometry. Consequently, they can be used to define a Riemannian structure associated with the AP structure. For comparison with the results of the orthodox GR, we replace the definition (2) with

$$g_{\alpha\beta}=\eta_{ij}\lambda_{i\,\alpha}\lambda_{i\,\beta},$$

(35)

where $\eta_{ij}=\text{diag}\,(1,-1,-1,-1)$.

There, (35) defines a pseudo-Riemannian structure associated with the AP structure. The metric tensor corresponding to the tetrad (34) and (35) is given by

$$g_{00}=1,\quad g_{11}={-}(4S/L^{+})^{2},$$

$$g_{22}=g_{11}\,r^{2},\quad\text{and}\quad g_{33}=g_{11}\,r^{2}\sin^{2}\theta,$$

(36)

$$g^{00}=1,\quad g^{11}={-}(L^{+}/4S)^{2},$$

$$g^{22}=\frac{1}{g_{11}r^{2}},\quad\text{and}\ \ g^{33}=\frac{1}{g_{11}r^{2}\sin^{2}\theta}.$$

(37)

The Riemannian space associated with the AP space (34), (35) and (36), is the space having the well-known FRW metric

$$ds^{2}=dt^{2}$$

$${}-\frac{16S^{2}(t)}{L^{+\,2}}\left[dr^{2}+r^{2}(d\theta^{2}+\sin^{2}\theta\,d\phi^{2})\right].$$

(38)

The nonvanishing Christoffel symbols of the second kind for the metric (38) are given by

$$\left\{0\atop 11\right\}=\dfrac{16S\dot{S}}{L^{+\,2}},\quad\left\{0\atop 22\right\}=\dfrac{16\,r^{2}S\dot{S}}{L^{+\,2}},$$

$$\left\{0\atop 33\right\}=\dfrac{16\,r^{2}\sin^{2}\theta\,S\dot{S}}{L^{+\,2}},\quad\left\{1\atop 11\right\}=-\dfrac{2K\,r}{L^{+}},$$

$$\left\{0\atop 01\right\}=\left\{2\atop 02\right\}=\left\{3\atop 03\right\}=\dfrac{\dot{S}}{S},$$

$$\left\{1\atop 22\right\}=\dfrac{K^{2}r^{5}-16r}{L^{+2}},\quad\left\{1\atop 33\right\}=\dfrac{L^{-}r\sin^{2}\theta}{L^{+2}},$$

$$\left\{2\atop 12\right\}=\left\{3\atop 13\right\}=\dfrac{L^{-}}{rL^{+}},$$

$$\left\{2\atop 33\right\}=-\sin\theta\cos\theta,\quad\left\{3\atop 23\right\}=\cot\theta,$$

(39)

where $\dot{S}=dS/dt$.

The nonvanishing contortion components are given by

$$\Psi_{01}^{1}=\Psi_{\,02}^{2}=\Psi_{03}^{3}=-\dot{S}/S,$$

$$\Psi_{11}^{0}=-16S\dot{S}/L^{+2},$$

$$\Psi_{22}^{2}=\Psi_{11}^{0}\,r^{2},\quad\Psi_{33}^{0}=\Psi_{11}^{0}\,r^{2}\sin^{2}\theta,$$

$$\Psi_{13}^{2}={-}\Psi_{\,\,\,\,31}^{2}=4\sqrt{K}\,\sin\theta/L^{+},$$

$$\Psi_{\,\,\,\,\,21}^{3}={-}\Psi_{\,\,\,\,12}^{3}=\,4\sqrt{K}\,/(L^{+}\sin\theta).$$

(40)

The nonvanishing symmetric torsion components are

$$\Lambda_{(11)}^{0}=16S\dot{S}/L^{+2},$$

$$\Lambda_{(22)}^{0}=16\,r^{2}S\,\dot{S}/L^{+2},$$

$$\Lambda_{(3\,3)}^{0}=16r^{2}\,\sin^{2}\theta S,\dot{S}/L^{+2},$$

$$\Lambda_{(10)}^{1}=\Lambda_{\left(2\,0\right)}^{2}=\Lambda_{\left(3\,0\right)}^{3}=-\dot{S}/(2S).$$

(41)

Substituting (39) and (40) into (26), we get after some calculations

$$B_{00}=3(b-1)\ddot{S}/S,$$

(42)

$$B_{11}=\frac{-16(b-1)\left(2(1-b)\dot{S}^{2}+2K(1+b)S\,\ddot{S}\right)}{L^{+2}},$$

(43)

$$B_{22}=r^{2}B_{11}\quad B_{33}=r^{2}\sin^{2}\theta\,B_{11}.$$

(44)

Now, since the geometric structure used for this study satisfies the cosmological principle (homogeneity and isotropy), we can use the comoving coordinate system characterized by

$$U^{1}=U^{2}=U^{3}=0,\quad\text{and}\quad U^{0}=1.$$

(45)

Substituting these values into (38), one gets

$$T_{\,0\,0}=\rho,\quad T_{\,1\,1}=g_{1\,1}P,$$

$$T_{\,2\,2}=g_{2\,2}P,\quad T_{\,3\,3}=g_{3\,3}P.$$

(46)

Now, the field equations (31) are solved using (32), (33), (41)–(45), and (46), and the resulting differential equations are

$$6(b-1)\ddot{S}=8\pi(\rho+3P)S,$$

(47)

$$(b-1)\left(3(1-b)\dot{S}^{2}+3K(1+b)\right)$$

$${}=-8\pi\rho S^{2}.$$

(48)

For differential equations (47) and (48) the following remarks are clear:

• 1. If $b=0$, the equations are reduced to the Einstein field equations in Riemannian geometry.

• 2. Equations (47) and (48) are in three unknowns: the scale factor $S(t)$, the density $\rho(t)$, and the pressure $P(t)$. To get exact solutions for these equations, we must use an equation of state, for example, $P=\omega\,\rho$.

From Eq. (48) one gets

$$\rho=\left(3(1-b)^{2}\dot{S}^{2}+3K(1-b^{2})\right)/(8\pi\,S^{2}).$$

(49)

Substituting from Eq. (49) into (47), one obtains

$$P=-\frac{(1-b)^{2}\dot{S}^{2}+2(1-b)S\ddot{S}+K(1-b^{2})}{8\,\pi\,S^{2}}.$$

(50)

In the following sections, we will use the previous equations to study the physical development of the universe. We start with a constant deceleration parameter as follows.

3 INFLATIONARY COSMOLOGICAL MODEL WITH A CONSTANT DECELERATION PARAMETER

In this section, we solve the differential equations of GFT using the generalized variation law for Hubble’s parameter to find the deceleration parameter $q$ and the scale factor $S(t)$.

The special variation law for Hubble’s parameter is given by [29, 30]

$$H=\frac{\dot{S}}{S}=D\,S^{\,-m},$$

(51)

where $m$ and $D$ are positive constants. From Eq. (51) we get:

$$\dot{S}=D\,S^{\,1-m},$$

(52)

$$\ddot{S}=D^{2}\,(1-m)\,S^{\,1-2m}.$$

(53)

Integrating Eq. (52), one gets

$$S(t)=(Dt)^{1/m}.$$

(54)

The deceleration parameter $q$ is defined as

$$q=\frac{dH^{-\,1}}{dt}-1.$$

(55)

Substituting from (52) and (53) into (49) and (50), one finds

$$\rho=\frac{3(1-b)^{2}\,D^{2}S^{\,2(1-m)}+3K(1-b^{2})}{8\pi\,S^{\,2}},$$

(56)

$$P=-\frac{1}{8\pi\,S^{2}}\big{[}K(1-b^{2})$$

$${}+(1-b)(3-b-2m)\,D^{2}S^{2(1-m)}\big{]}.$$

(57)

In this part, we shall deal only with the energy-momentum tensors for dust and perfect fluids.

In the case of dust, the equation of state is $P=0$, and one studies three cases.

In the first case, where $P=0$ and $K=0$, Eq. (57) can be written in the form

$$m=(3-b)/2.$$

(58)

Substituting from (52) and (53) into (55), one gets

$$q=m-1=(1-b)/2.$$

(59)

Also, using (59) and (54), one obtains

$$S(t)=(Dt)^{2/(3-b)}.$$

(60)

In the second case, where $P=0$ and $K=-1$, Eqs. (57) and (59) give

$$m<(3-b)/2,\quad q<(1-b)/2.$$

(61)

In the third case, where $P=0$ and $K=1$, Eqs. (57) and (59) lead to

$$m>(3-b)/2,\quad q>(1-b)/2.$$

(62)

In the case of radiation, the equation of state is $P=\rho/3$, and from Eqs. (56) and (57) one gets

$$(m-2+b)D^{\,2}S^{\,2-2m}=K(1+b).$$

(63)

From this equation, one can study three cases.

In the first case, $K=0$, Eq. (63) gives

$$m=2-b,\quad q=1-b.$$

(64)

Substituting from (64) into (54), one can obtain

$$S(t)=(Dt)^{1/(2-b)}.$$

(65)

In the second case, $K=-1$, Eq. (63) gives

$$m<2-b,\quad q<1-b.$$

(66)

In the third case, $K=1$, Eq. (63) leads to

$$m>2-b,\quad q>1-b.$$

(67)

It is worth mentioning that for $b=0$, the cosmological models reduces to the ordinary models of GR.

From Eq. (56), we see that the condition of positive energy density depends on the value of $b$ and $K$; for ($b=0$), closed and flat cosmological model possible because they achieve this condition, while an open cosmological model is impossible; this result was reached by Bremen [29].

In the cases of ($b=2,\,3,\,4,\,\cdots)$, the effect of torsion is greater than the effect of gravity.

Accordingly, the most accepted cosmological model is the flat model because it is the only one that achieves a positive energy density, that is why we exclude the open and closed cosmological model. The deceleration parameter is $q=-1/2,\,-1,\,-3/2,\,\cdots$ (in dust flat models), and $q=-1,\,-2,\,-3,\,\cdots.$ (in radiation flat models).

Consequently, the GFT gives inflationary cosmological models with a constant deceleration parameter.

These results are clear indications that the geometric torsion can be an effective source for inflation. But these kinds of models are not consistent with cosmological observations.

This is why we use a variable deceleration parameter in the following sections (4 and 5).

In GR, the de Sitter model represents inflation with a constant deceleration parameter.

4 THE BIG RIP MODEL

In this section, we suggest that the Hubble parameter of the universe is given by

$$H=\frac{\dot{S}}{S}=\frac{2}{t\,(2m-at)}.$$

(68)

Integrating (68), one obtains

$$S=S_{0}\left(\frac{t}{2m-at}\right)^{1/m},$$

(69)

where $S_{0}$ is an integration constant.

From Eq. (69) one obtains

$$\dot{S}=\frac{2\,S\,}{t\,(2m-at)},$$

(70)

$$\ddot{S}=\frac{4S\,(1-m\,+a\,t)}{t^{2}\,(2m-at)^{2}}.$$

(71)

Substituting from (68) into (55), one obtains:

$$q=m-1-at.$$

(72)

The scale factor a related to the redshift $z$ by the expression [31]

$$1+z=\frac{S_{z=0}}{S(t)},$$

(73)

where $S_{z=0}$ is the present value of the scale factor.

One can also solve for the deceleration parameter $q$ as a function of the redshift. Using Eqs. (69) and (73), one obtains,

$$q(z)=m-1-\frac{2ma\,S^{m}{}_{z=0}}{(1+z)^{m}+a\,S^{m}{}_{z=0}}.$$

(74)

Substituting (69), (70), and (71) into (49) and (50), one gets for the density and pressure:

$$\rho=\Big{[}3K(1-b^{2})(2m-at)^{2+2/m}t^{2}$$

$${}+12(1-b)^{2}\,t^{2/m}\Big{]}\Big{[}8\pi(2m-at)^{2}t^{2+2/m}\Big{]}^{-1},$$

(75)

$$P=-\Big{[}4(1-b)(3-b-2m+2at)t^{2/m}$$

$${}+K(1-b^{2})(2m-at)^{2+2/m}t^{2}\Big{]}$$

$${}\times\Big{[}8\pi(2m-at)^{2}t^{2+2/m}\Big{]}^{-1}.$$

(76)

From (75) and (76) we obtain the equation-of-state parameter $\omega=P/\rho$ as

$$\omega=-\Big{[}4(1-b)(3-b-2m+2at)t^{2/m}$$

$${}+K(1-b^{2})(2m-at)^{2+2/m}t^{2}\Big{]}$$

$${}\times\Big{[}3K(1-b^{2})(2m-at)^{2+2/m}t^{2}$$

$${}+12(1-b)^{2}\,t^{2/m}\Big{]}^{-1}.$$

(77)

According to Eq. (72), the universe passes through the following stages:

• (i) The universe arises with ($q=(m-1)$ at $t_{bb}=0$),

• (ii) The accelerating stage ($q\leq 0$ at $t_{a}\geq(m-1)/a$),

• (iii) The strong exponential expansion stage ($q\leq-1$ at $t_{se}\geq m/a$ ),

• (iv) The universe ends with ($q={-}(m+1)$ at $t_{\textrm{end}}=2m/a$).

This event is a Big Rip behavior.

Now, one can discuss the physical behavior of the Big Rip model and its observational validation. To clarify how the linear disparity deceleration parameter corresponds to the observable universe dynamics and expects additional predictions of methods of variety, let us choose $m=1.65$, and $a=0.097$ (compared with Özgür Akarsu and Tekin Dereli [31]).

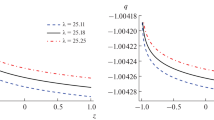
In Fig. 1 we plot the scale factor versus cosmic time $t$. The universe starts with a Big Bang at $t_{\textrm{bb}}=0$, $S=0$, and ends at $t_{\textrm{br}}=34.0$, $S=\infty$. In Fig. 2 we plot the Hubble parameter $H$ versus cosmic time $t$, it diverges at the beginning and at end of the universe. In Fig. 3 we plot the deceleration parameter $q$ versus cosmic time $t$. The deceleration parameter is initially $q_{\textrm{bb}}=0.56$ and reaches $q_{\textrm{br}}={-}2.5$ at the end of the universe.

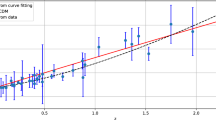
The universe enters into the accelerated expansion phase at$t_{\textrm{ae}}=6.7$. These values are consistent with the observational results. We also plot the deceleration parameter $q$ versus redshift $z$ in Fig. 4, where one may observe that the accelerated expansion begins at $z\approx 0.6$, consistent with the observational data.

In Figs. 5–7 we plot the energy density of the fluid $\rho$ versus cosmic time $t$. In the case $b=0$, one can observe that the condition ($\rho\geq 0$) holds for the closed and flat cosmological models but is violated for the open cosmological models.

Fig. 1

The scale factor versus cosmic time $t:\ 0\to 33$.

Fig. 2

The Hubble parameter versus cosmic time $t:\ 0\to 33$.

Fig. 3

The deceleration parameter versus cosmic time $t:\ 0\to 33$.

Fig. 4

The deceleration parameter $q$ versus redshift, $z:0\to 2$.

Fig. 5

The energy density of the fluid $\rho$ versus cosmic time $t:\ 0\to 33.$ ($K=1$).

Fig. 6

The energy density of the fluid $\rho$ versus cosmic time $t:\ 0\to 33.$ ($K=0$).

Fig. 7

The energy density of the fluid $\rho$ versus cosmic time $t:\ 0\to 33.$ ($K=1$).

Fig. 8

The pressure $P$ versus cosmic time $t:\ 0\to 33$.

Fig. 9

The pressure $P(t)$ versus cosmic time $t:0\to 33$.

Fig. 10

The pressure $P(t)$ versus cosmic time $t:0\to 33$.

Hence, under the energy positivity condition, the closed and flat cosmological models are possible, while open ones are excluded.

In that case, Berman also reached the same conclusion in GR [29]. In the case $b=2$, in GFT one can observe that the condition ($\rho\geq 0$) is adequate for open and flat cosmological models, but a closed one is impossible.

The energy density of the fluid diverges at the end, which mean that the universe ends with a Big Rip.

According to these results, we can only accept the flat model. This outcome is consistent with the fact that the universe must be flat [32, 33]. In Figs. 8–10 we plot the pressure of the fluid $P$ versus cosmic time $t$. The pressure also diverges at the beginning and the end of the evolution but exhibits different behaviors for the closed, flat and open universes.

In Figs. 11–13 we plot the equation of state parameter $\omega$ versus cosmic time $t$. It shows different behaviors for the closed, flat and open universes, but converges to the same value $\omega={-}1/3$ at the very late times of the universe.

Fig. 11

The equation of state parameter $\omega$ versus cosmic time $t:0\to 33$.

Fig. 12

The equation of state parameter $\omega$ versus cosmic time $t:0\to 33$.

Fig. 13

The equation of state parameter $\omega$ versus cosmic time $t:0\to 33$.

In the next section, we will study the Hubble variation law which contains three parameters.

5 THE BIG CRUNCH MODEL

In the present section, we suggest the Hubble variation law, such that,

$$H=\frac{2(1-\eta)}{(2m-at)(t-\frac{2m\eta}{a})},\quad H=\frac{\dot{S}}{S},$$

(78)

where $m$ and $\eta$ are positive quantities.

From Eqs. (78) and (55), one gets a linearly varying deceleration parameter which contains the parameter ($\eta$) as

$$q=\frac{m(1+\eta)-at}{1-\eta}-1.$$

(79)

where $\eta\neq 1$. Equation (78) gives

$$\dot{S}=\frac{2\,S(1-\eta)\,}{(2m-at)(t-\frac{2m\eta}{a})},$$

(80)

$$\ddot{S}=\frac{4S\,((1-\eta)^{2}-2m\,(1-\eta^{2})+2a\,t)}{(2m-at)^{2}(t-\frac{2m\eta}{a}){}^{2}}.$$

(81)

Accordingly, integrating Eq. (80), one finds

$$S=S_{0}\left(\frac{t-2m\eta/a}{2m-at}\right)^{1/m},$$

(82)

where $S_{0}$ is an integration constant.

Using Eqs. (73), (79) and (82), one gets

$$q(z)=\frac{m(1+\eta)}{1-\eta}-1$$

$${}-\frac{2ma\,S^{m}{}_{z=0}+2m\eta(1+z)^{m}}{(1-\eta)\,((1+z)^{m}+a\,S^{m}{}_{z=0})}$$

(83)

From this equation, one can obtain for $\eta=0$

$$q(z)=m-1-\frac{2ma\,S^{m}{}_{z=0}}{\,((1+z)^{m}+a\,S^{m}{}_{z=0})},$$

(84)

and for $\eta=2$,

$$q(z)=-3m-1$$

$${}+\frac{2ma\,S^{m}{}_{z=0}+4m(1+z)^{m}}{\,((1+z)^{m}+a\,S^{m}{}_{z=0})}.$$

(85)

Table 1 The deceleration parameter, the scale factor and the expansion scalar

Table 2 The singularity conditions in the Big Crunch model of the Universe

Substituting from (80), (81), and (82) into (49), (50), we get, respectively,

$$\rho=\Big{[}12(1-b)^{2}(1-\eta)^{2}(t-2m\eta/a)^{2/m}$$

$${}+3K(1-b^{2})(2m-at)^{2+2/m}(t-2m\eta/a)^{2}\Big{]}$$

$${}\times\Big{[}8\pi(2m-at)^{2}(t-2m\eta/a)^{2+2/m}\Big{]}^{-1},$$

(86)

$$P=-\frac{A}{B},$$

(87)

where

$$A=4(1-b)(t-2m\eta/a)^{2/m}\Big{[}(1-b)(1-\eta)^{2}$$

$${}+4at+2(1-\eta)^{2}-4m(1-\eta^{2})\Big{]}$$

$${}+K(1-b^{2})(2m-at)^{2+2/m}(t-2m\eta/a)^{2},$$

and

$$B=8\pi(2m-at)^{2}(t-2m\eta/a)^{2+2/m}.$$

The equation-of-state parameter is given by

$$\omega=-\frac{A}{C}$$

(88)

where

$$C=12(1-b)^{2}(1-\eta)^{2}(t-2m\eta/a)^{2/m}$$

$${}+3K(1-b^{2})(2m-at)^{2+2/m}(t-2m\eta/a)^{2}.$$

The generalization of the expansion scalar $\Theta$ of the universe in PAP is given by [34]

$$\Theta=U_{\,\,\,\,||\,\,\alpha}^{\,\alpha}.$$

(89)

Equation (89) gives [34],

$$\Theta=\frac{3(1-b)\dot{S}}{S}=3(1-b)H.$$

(90)

Substituting from (78) into (90), one obtains

$$\Theta=\frac{6\,(1-b)\,(1-\eta)}{(2m-at)(t-\frac{2m\eta}{a})}.$$

(91)

By differentiation of Eq. (91) with respect to cosmic time, one obtains

$$\frac{d\Theta}{dt}=\frac{12\,(b-1)\,\left(m(1-\eta^{2})-(1-\eta)at\right)}{(2m-at)^{2}(t-\frac{2m\eta}{a})^{2}}.$$

(92)

We use Eq. (90) to study the singularity of the universe. The Big Crunch model passes through three stages, as explained below:

• (i) The first half-age of the chronological age of the universe ($\eta=0$ and $b=0$). The universe starts with a Big Bang at $t_{\textrm{bb}}=0$, with $q_{\textrm{bb}}=m-1$, enters into the acceleration stage $q\leq 0$ at $t_{a\,1}\geq(m-1)/a$, enters into a strong expansion stage $q\leq-1$ at $t_{\textrm{se}1}\geq m/a$, enters into the half-age stage at $t_{\textrm{ha}}=2m/a$, with $q_{\textrm{ha}}={-}(1+m)$.

• (ii) The Big Rip stage ($\eta=0$ or $\eta=2$, $q={-}(m+1)$ and $S(t)=\infty$ $,$ at $t_{br}=2m/a$. For the universe to move from the first stage to the second one through the Big Rip, we assume that there is a physical mechanism of probably quantum nature that replaces the singularity with a regular maximum of the scale factor $S(t)$. The evolution of the universe is affected by this physical mechanism at the second stage, as we will explain in the following part of this article.

• (iii) The second half-age of the chronological age of the universe ($\eta=2$). The behavior of this stage is reverse to the first stage (contraction instead of expansion), the universe starts this stage with $t_{\textrm{hf}}=2m/a$, $q_{\textrm{ha}}={-}(1+m)$. A reversal is mainly caused by the changes in pressure and torsion after a Big Rip, and the particles with spin $1/2,1,\ldots$ correspond to $F=548,274,\ldots$, respectively. The universe enters into a strong contraction stage ($q\leq 0$) at $t_{a\,2}\leq(1+3m)/a$ and ends at $t_{\textrm{end}}=4m/a$ with $q_{\textrm{end}}=m-1$ such as the beginning.

The scale factor $S(t)$ starts with a Big Bang at $\eta=0$, $t_{\textrm{bb}}=0$ and $S(t)=0$, enters into a divergent case at $t_{\textrm{br}}=2m/a$. It represents the Big Rip moment and ends at $\eta=2$, $t_{\textrm{end}}=4m/a$ and $S(t)=0$. One sees that the deceleration parameter $q$ and the scale factor $S(t)$ start and end with the same values.

To study the singularity of the universe for our Big Crunch model, the actuality of the first singularity mainly depends on the solution of Eq. (92). Specifically, it depends on the resulting sign of the left-hand side term. This issue can be studied using the normal agreements of the singularity theorems of GR, i.e., the initial singularity is considered by the condition ${d\mathrm{\Theta}}/{dt}<0$ [35].

Accordingly, we have three cases presented in Table 2.

From Table 2, one may see that the first half-age of the universe is beginning with an initial singularity, when $b=0$ as in GR. In GFT ($b=2$), the second half-age of the universe is not free from an initial singularity.

Now, by choosing $m=1.65$ and $a=0.097$ (compared to Özgür Akarsu and Tekin Dereli [31]) to show how the linearly changing deceleration parameter can compete with the observed cosmic kinematics and make other predictions.

Fig. 14

The deceleration parameter $q$ against cosmic time $t:0\to 33$ at $\eta=0$, and $t:\ 33\to 66$ at $\eta=2$.

Fig. 15

The scale factor $S(t)$ against cosmic time $t:\ 0\to 33$ at $\eta=0$, and $t:\ 33\to 66$ at $\eta=2$.

Fig. 16

The deceleration parameter $q$ versus redshift $z:\ 0\to 2$.

Fig. 17

The energy density of the fluid $\rho$ versus cosmic time. The curve is plotted by choosing $(b=0$, $\eta=0)$ at $t:\ 0\to 33$, and ($b=2$, $\eta=2$) at $t:\ 33\to 66$.

Fig. 18

The energy density of the fluid $\rho$ versus cosmic time. The curve is plotted by choosing ($b=0$, $\eta=0$) at $t:\ 0\to 33$, and ($b=2$, $\eta=2$) at $t:\ 33\to 66$.

Fig. 19

The energy density of the fluid $\rho$ versus cosmic time. The curve is plotted by choosing $(b=0$, $\eta=0)$ at $t:\ 0\to 33$, and ($b=2$, $\eta=2$) at $t:\ 33\to 66$.

In what follows, the kinematic analysis will be displayed throughout Figs. 14–19.

In Fig. 14 the deceleration parameter $q$ is depicted versus cosmic time $t$. It is observed that the behavior of $q(t)$ in the second half-age is inverse to its behavior in the first half of it. Moreover, the deceleration parameter starts with $q_{\textrm{bb}}=0.6$ and ends at a Big Rip with $q_{\textrm{br}}=-2.5$. In Fig. 15, the scale factor $S$ is plotted versus cosmic time $t$ . As can be seen, the universe in the first half-age starts with a Big Bang at $t_{\textrm{bb}}=0$ and ends with a Big Rip at $t_{\textrm{br}}=34$, entering the initial state at the end of the second half-age.

In Fig. 16 one may note that in the first half-age of the universe, the dynamic transition from deceleration to acceleration happens at $z=0.8$. This stage agrees with the (LVDP) model [31]. In Figs. 17, 18, 19, the energy density of the fluid $\rho$ versus cosmic time $t$ is plotted. It is observed that, in our proposed model, the flat model is physically accepted. This is happening due to the positivity of the energy density of the matter. Meanwhile, the closed and open models do not achieve this characteristic.

6 OBSERVATIONAL BOUNDS ON COSMIC TORSION

The literature contains a number of proposals for observational tests of torsion, the majority of which work within our Solar system [36–42]. Here, we will try to put cosmological bounds on the torsion field by exploiting the fact that it “gravitates” and therefore modifies the expansion dynamics of the host universe. In the present section, we investigate the effect of torsion on the cosmological solutions of the GFT equations (47), (48). To facilitate comparison with standard cosmology, we take $K=0$. For this case (47) and (48) reduce to

$$\ddot{S}/S=4\pi(\rho_{0}+3P_{0})/[3(b-1)],$$

(93)

$$(\dot{S}/S)^{2}=8\pi\,\rho_{0}/[3(1-b)^{2}],$$

(94)

which are the dynamic equations of FRW standard cosmology, written in the context of the PAP geometry.

Now, using the contortion components (40) and the basic vector (17), the only non-vanishing components of the basic vector is

$$C_{0}=3\dot{S}/S,$$

(95)

and from Eq. (95) one can get the scalar torsion $\kappa$ defined by [43],

$$\kappa=\sqrt{g^{\alpha\beta}C_{\alpha}C_{\beta}}=3\dot{S}/S=3H,$$

(96)

From this equation, one obtains

$$\dot{\kappa}=3\bigg{(}\frac{\ddot{S}}{S}-\frac{\dot{S}{}^{2}}{S^{2}}\bigg{)},$$

(97)

and hence,

$$\frac{\ddot{S}}{S}=\frac{\dot{\kappa}}{3}+\frac{\kappa^{2}}{9}.$$

(98)

Let us assume that the dominant energetic content of the universe, after a Big Rip, is purely induced by the torsion field $\kappa$, then the dynamic equations (93) and (94) may be written in the form

$$\ddot{S}/S=4\pi(\rho_{\kappa}+3P_{\kappa})/[3(b-1)],$$

(99)

$$(\dot{S}/S)^{2}=8\pi\,\rho_{\kappa}/[3(1-b)^{2}],$$

(100)

where $\rho_{\kappa}$ annd $P_{\kappa}$ are the energy density and pressure induced by the torsion field $\kappa$, respectively.

Substituting (96) and (98) into (99) and (100), one gets

$$\rho_{\kappa}=\frac{\kappa^{2}}{24\pi},\quad P_{\kappa}=\frac{1}{12\pi}\bigg{(}\dot{\kappa}+\frac{\kappa^{2}}{6}\bigg{)}.$$

(101)

From Eq. (101), the equation of state for a perfect fluid induced by the torsion field $\kappa$ is

$$P_{\kappa}=-(\varepsilon-1/3)\,\rho_{\kappa},$$

(102)

where

$$\varepsilon=\frac{6\,\dot{\kappa}+2\,\kappa^{2}}{3\,\kappa^{2}(1-b)}.$$

(103)

Comparing the equation (102) with the equation of state $P_{\kappa}=\omega\rho_{\kappa}$, one obtains

$$\omega=1/3-\varepsilon.$$

(104)

The three most common examples of cosmological fluids with this $\varepsilon$ are radiation ($\varepsilon=0$), dust ($\varepsilon=1/3$) and the vacuum energy ($\varepsilon=4/3$), which is mathematically equivalent to a cosmological constant $\Lambda$. It is well recognized that fluids with $\varepsilon>4/3$ are usually considered in the background of dark energy (DE), since they give rise to accelerated expansion. Besides the fluids with $\varepsilon>2/3$, there have been proposed in this article various scalar field models that can be described by a time-dependent $\varepsilon$ that can evolve below $2/3$, that is, quintessence $-2/3\leq\varepsilon\leq 4/3$, phantom $\varepsilon\leq 4/3$, quintom that can evolve across the cosmological constant boundary $\varepsilon=4/3$.

Employing Eqs. (70) and (96), the value of the scalar torsion $\kappa$ is given by

$$\kappa=\frac{6\,}{t\,\left(2\,m-a\,t\right)\,}.$$

(105)

From Eqs. (105) and (102), the expressions for the energy density and pressure read

$$\rho_{\kappa}=\frac{3\,}{2\,\pi\,t^{2}\left(2\,m-a\,t\right)^{2}\,},$$

(106)

$$P_{\kappa}=-\rho_{\kappa}.$$

(107)

By Eqs. (105)–(107), the Big Rip happens at $t_{\textrm{br}}=2m/a$. In this case,

$$\kappa\to\infty,\quad\ \rho_{\kappa}(t)\to\infty,\quad\ P_{\kappa}(t)\to-\,\infty,$$

(108)

where $b=0$, and $\varepsilon=4/3$.

From the above discussion, the Universe inevitable evolves to a Big Rip phase, which is one of the possible fates of the Universe according to the cosmological observations [44, 45]. Torsion plays an important role in the evolution of the universe. In the Big Rip model, the Universe has a finite lifetime. It starts with a Big Bang at $t_{\textrm{bb}}=0$ with $\kappa\to\infty$ and ends at $t_{\textrm{br}}=2m/a$ with $\kappa\to\infty$. The scalar torsion reaches its minimum value at $t=m/a$. Finally, we hope to extend on this topic in detail in our future work.

7 DISCUSSION AND CONCLUSION

Table 3 Evolution of the deceleration parameter and the scale factor with cosmic time for the Big Crunch model

In Section 1, we presented a summary of the PAP geometry, which is most suitable for physical applications, especially for constructing theories that require both torsion and curvature to describe different interactions. For example, attempts to geometrize strings [46], theories accounting for Dirac fields [47] and theories gauging gravity [48], are among this class of theories. In Section 2, the field equations in GR are generalized in the PAP geometry. This version of absolute parallelism is more general than the conventional AP geometry. The generalization regards the effect of torsion of the background gravitational field, the GFT obtained contains some extra terms, depending on space-time torsion that would have some effects on the cosmological models. Under a certain condition, these models could be reduced to the original models of GR without any need for a vanishing torsion. However, we would like to point out that the interaction of matter with space- time curvature gives rise to an attractive force, while its interaction with space-time torsion gives rise to a repulsive one (anti-gravity) [25]. In Section 3, the effect of torsion leads to inflationary cosmological models with a constant deceleration parameter. In Section 4, we suggested a special law for the deceleration parameter to study a Big Rip model. The model has a different behavior, we note that the three models with $\omega=-1/3$ at $t=m-1$ show that there is presently an inflationary universe. We see that the closed and open model are impossible since the condition of the energy density ($\rho=0)$ is unreliable, but the flat case is possible since the condition ($\rho=0)$ is satisfied in this model, this result differs from GR. In Section 5, we suggest here a Big Crunch model; the temporal age of the universe can be divided into three stages:

$\bullet$ The first half-age of the Universe ($b=0$, $\eta=0$, $t:\ 0\to 34$).

$\bullet$ The Big Rip stage at $t=34$.

$\bullet$ The second half-age of the Universe ($b=2$, $\eta=2$, $t:\ 34\to 68$), the behavior at this stage is reverse to the first stage.

Finally, in brief the results of the Big Crunch model are displayed in Table 3.

From Table 3, the second half-age of the Universe has an inverse physical behavior to the first half-age. In our cosmological model, the first half-age begins with a singular stage and ends with a nonsingular stage. The second half-age of the universe is free from an initial singularity.

In the early universe, torsion could play a relevant role but then quickly disappears, as shown in GR, when $b=0$. As agreed in GFT when $b=2$, the torsion plays a relevant role in the second half-age of the Universe. At that stage, the torsion causes the Universe to restructure to the past. The torsion effect on the energy density evolution, see Eq. (49), carried by the parameter $b$, also depends on the matter equation of state. Astronomical observations expect a Big Rip to happen at late time [49–61]. Section 6 discusses the observational bounds on the presence of torsion in the late Universe. But so far, no actual observation can be found to make sure that the results are correct, excluding the data from SNIa, BAO and CMB about the redshift. In our Big Rip and Big Crunch models, we discussed the redshift, see Eqs. (74), (84), (85), and Figs. 4 and 16. So far, our results are consistent with astronomical observations [48–53].

Our model can be considered as a generalization of the special law of variation of the Hubble parameter, which was used by many authors from the beginning [29, 62, 63], Berman et al. [30], Özgür and Tekin [31], Maharaj and Naidoo [64]. The model of a Big Crunch that was suggested in this article closely corresponds to the Periodic Universe with varying deceleration parameter of the second degree [65]. Finally, after the Big Rip, quantitative mechanisms that depend on the parameter $b$ can be used to study the evolution of the universe. This parameter represents the spin value, as shown in Section 5, for more details see [22, 23, 25]. In this article, we were trying to combine quantum cosmology with well-known particle physics or basic theories. We hope that another work in this field can be extended.