Existence and stability of equilibrium points in the photogravitational restricted four-body problem with Stokes drag effect

Abstract

The restricted four-body problem consists of an infinitesimal particle which is moving under the Newtonian gravitational attraction of three finite bodies, $m_{1}$, $m_{2}$ and $m_{3}$. The three bodies (called primaries) are moving in circular orbits around their common centre of mass fixed at the origin of the coordinate system. Moreover, according to the solution of Lagrange, these primaries are fixed at the vertices of an equilateral triangle. The fourth body does not affect the motion of the three bodies. In this paper, we deal with the photogravitational version of the problem with Stokes drag acting as a dissipative force. We consider the case where all the primaries are sources of radiation and that two of the bodies, $m_{2}$ and $m_{3}$, have equal masses ($m _{2} = m_{3} = \mu$) and equal radiation factors ($q_{2} = q_{3} = q$) while the dominant primary body $m_{1}$ is of mass $1 - 2\mu$. We investigate the dynamical behaviour of an infinitesimal mass in the gravitational field of radiating primaries coupled with the Stokes drag effect. It is found that under constant dissipative force, collinear equilibrium points do not exist (numerically and of course analytically) whereas the existence and positions of the non-collinear equilibrium points depend on the parameters values. The linear stability of the non-collinear equilibrium points ($L_{i},i = 1,2, \ldots ,8$) is also studied and it is found that they are all unstable except $L_{1}$, $L _{7}$ and $L_{8}$ which may be stable for a range of values of $\mu$ and various values of radiation factors. Finally, we justify the relevance of the model in astronomy by applying it to a stellar system (Ross 104-Ross775a-Ross775b), for which all the equilibrium points have been seen to be unstable.

1 Introduction

The equilibrium solution of $n$-body celestial systems and related equilibrium points analysis have always been an attractive and important field of research, especially these days due to the detection of more than 2500 extra-solar planetary systems (see, e.g., Murray and Dermott 1999; Marchand et al. 2007 for the list of references and for some interesting historical notes). Among extra-solar systems we can find some of them with only one star and several planets, others with several stars and none or several planets. Among the possible scenarios of extra-solar planets, those involving multiple star systems are perhaps the most interesting in terms of dynamics (Campo and Docobo 2014). Since there is no general analytical solution to the $n$-body problem for $n\ge 3$, several simplifications have been introduced with the most prominent being the restricted three and four-body problems (Meyer et al. 2008). The restricted three-body problem (R3BP) describes the motion of an infinitesimal mass moving under the gravitational effects of two finite bodies, called primaries, which move in circular or elliptical orbits around their center of mass on account of their mutual attraction and the infinitesimal mass is not influencing the motion of the primaries. It is well-known that, in the rotating frame this problem possesses five equilibrium points three of which lie on the line connecting the primaries are called collinear points while the other two form in the plane of motion equilateral configuration with the primaries and are called triangular points. The restricted four-body problem (R4BP) is perhaps the simplest model after the R3BP and a natural generalization of it. It describes the motion of a body of infinitesimal mass under the Newtonian gravitational attraction of three much bigger bodies (called the primaries) moving in circular or elliptic orbits around their centre of mass fixed at the origin of the coordinate system. The fourth body does not affect the motion of the three primaries. Two different configurations of the three bodies have been considered in this case: collinear configuration of the primaries (see, e.g., Kalvouridis et al. 2006, 2007; Arribas et al. 2016a, 2016b; Barrabés et al. 2017) and equilateral triangle for the three main bodies (see, e.g., Baltagiannis and Papadakis 2011; Papadouris and Papadakis 2013; Singh and Vincent 2015; Singh and Omale 2019).

In this paper, we deal with the latter case since, from a natural point of view there are astronomical bodies that exhibit a triangular configuration when considered geometrically. For instance, the Trojan asteroids of Jupiter and the four Martian asteroids. For details on the examples of such configuration we refer to Alvarez-Ramirez and Barrabes (2015), Zotos (2016) and references therein. This problem has been used by many scientists for practical applications such as, among others, Robutel and Gabern (2006, Sun, Jupiter and Saturn system), Schwarz et al. (2009a, star, two massive planets and a massless Trojan), Schwarz et al. (2009b, star, brown dwarf, gas giant and a massless Trojan), Ceccaroni and Biggs (2012, Sun, Jupiter, Trojan Asteroid, Spacecraft), Baltagiannis and Papadakis (2013, Sun, Jupiter, Trojan Asteroid, Spacecraft), and references therein.

The case of R3BP where one or both primaries are sources of radiation is a long-standing, well-known problem usually referred to as “the photogravitational problem of three bodies”; this case was initially studied by Radzievskii (1950, 1953). Since then, a number of publications have been reported on this topic (see, Burns et al. 1979; Schuerman 1980; Bhatnagar and Chawla 1979; Simmons et al. 1985; Manju and Choudhry 1985; Luk’yanov 1987, 1988; Ragos and Zagouras 1988; Papadakis 1996; Ishwar and Elipe 2001, and references therein). However, dissipative effects play a key role in Solar system dynamics. One of the most important mechanism of dissipation is the Poynting-Robertson (P-R) drag, which models the Solar radiation effect on dust grains. The restricted three-body problem with P-R drag force has been studied by many scientists in recent times. Some of them are Murray (1994), Ishwar and Kushvah (2006), Ragos and Zafiropoulos (1995), Celletti et al. (2011). Another important kind of non gravitational effect is the so-called Stokes drag; this effect is due to the collisions of particles with the molecules of the gas nebula being present during the formation of a planetary system (Beaugé and Ferraz-Mello 1993; Celletti et al. 2011). In this context, Jain and Aggarwal (2015a) have studied the R3BP with Stokes drag effect considering the primaries as point mass. Also, Jain and Aggarwal (2015b) discussed the same problem under Stokes drag effect when the smaller primary is an oblate body. In both papers, they have shown that there exist two non-collinear libration points which are linearly unstable and collinear libration points do not exist.

On the other hand, the generalization of the R4BP can include the consideration of various types of effects such as Coriolis and centrifugal forces, variation of masses, oblateness of bodies, P-R drag, radiation pressure force, Stokes drag, triaxiality, etc.

The study of radiation and its effects on the dynamics of small bodies has attracted much attention in recent years. This interest is absolutely justified, since a great number of strong radiation sources exist in the Universe (see Baguhl et al. 1995; Jackson 2001 for details). For example, Kalvouridis et al. (2006) discussed the effect of radiation force due to primaries in the R4BP using Radzievskii’s model and noticed that there are some variations in the result which are unstable for all values of the assumed parameters and later studied the parametric evolution of periodic orbits of the problem (Kalvouridis et al. 2007). The photogravitational case, but of the Lagrangian R4BP, was introduced by Papadouris and Papadakis (2013) where they studied the equilibrium points of the problem for the case of two equal masses. Also, the linear stability of each equilibrium point was examined. Further, the periodic solutions in the photogravitational case of this problem were studied by Papadouris and Papadakis (2014). Several authors, among others, Suraj and Hassan (2014), Singh and Vincent (2015, 2016) and references therein, studied the effects of radiation pressure on the equilibrium points of the problem (Lagrange configuration). Similarly, the R4BP with effects of drag has received attention with respect to real systems in Celestial Mechanics. Recently, Kumari and Kushvah (2013) examined equilibrium points and regions of motion in the restricted four-body problem with solar wind drag effect. Singh and Omale (2019) studied the combined effect of Stokes drag, oblateness and radiation pressure on the existence and stability of equilibrium points in the restricted four-body problem.

In this paper, we intend to study the motion of an infinitesimal body in the R4BP in which the dissipative force (Stokes drag) is considered in the case where the three primary bodies are sources of radiation. Our goal is to investigate numerically the combined effect of radiation factors and Stokes drag on the motion of a small particle in the force field of three bodies much bigger than the particle, which are always in Lagrangian configuration. Our target is not to provide a systematic search of their location and existence but to detect them for several combinations of the parameters of the problem. To do so, we firstly choose such $q_{i}$, $m_{i}$ and constant dissipative force ($k$) in order that the Lagrangian configuration is stable, finally, then we compute numerically the number and positions of the equilibrium points and then their stability. We find that, in contrast to the photogravitational one, the current problem does not admit collinear equilibrium points which would have increased the dynamical richness of the problem.

It is also interesting to observe that there are natural bodies that are equal in mass and whose orbits are nearly circular. For two stars of equal masses it is expected that, in general, they should be of the same age and composition and, consequently, they should exert radiation of the same order. This means that the choice of $q_{2} = q_{3} = q$ would be physically compatible.

The paper proceeds as follows: In Sect. 2, we present the equations of motion of the considered dynamical system. In Sect. 3, we determine the equilibrium points of the problem. Specifically, we study the existence and location of the equilibrium points under the influence of the system parameters. Section 4 investigates the linear stability of the equilibrium points; Sect. 5 is the validation of the model by its application to a stellar system, while Sect. 6 discusses the obtained results and conclusions of the paper.

2 Equations of motion

We consider three bodies of masses $m_{1}$, $m_{2}$ and $m_{3}$ ($m_{1} \gg m_{2} = m_{3}$) always lying at the vertices of an equilateral triangle and one of them, say $m_{1}$, is on the positive $x$-axis at the origin of time. The motion of the system is referred to axes rotating with uniform angular velocity. The three bodies move in the same plane and their mutual distances remain unchanged with respect to time (see e.g., Papadouris and Papadakis 2013). We suppose that the origin is taken as the center of gravity of the system and that the motion of the infinitesimal mass $m$ is governed by the gravitational force of the primaries. We adopt the sum of the masses of the primaries and the distance between them as the units of mass and length. We choose the unit of time such as to make the gravitation constant equal to unity. Let the coordinates of the infinitesimal mass be ($x$, $y$) and those of masses $m_{1}$, $m_{2}$ and $m_{3}$ are:

$$\begin{aligned} &{ (x_{1},y_{1}) = (\sqrt{3} \mu ,0),\qquad (x_{2},y_{2}) = \biggl( - \frac{ \sqrt{3}}{2}(1 - 2\mu ),\frac{1}{2}\biggr),}\\ &{ (x_{3},y_{3}) = (x_{2}, - y _{2}),} \end{aligned}$$

respectively, relative to a rotating frame of reference $\mathit{Oxyz}$, where $O$ is the origin, $\mu = \frac{m_{2}}{m_{1} + m_{2} + m_{3}} = \frac{m_{3}}{m_{1} + m_{2} + m_{3}}$ is the mass parameter, where $\mu \in (0,1/3)$.

The equations of motion of the infinitesimal mass $m$ in the photogravitational restricted four-body problem with the origin resting at the centre of mass, in a rotating system of coordinates can be described in the dimensionless variables as (see Papadouris and Papadakis 2013 and Singh and Omale 2019):

$$\begin{aligned} &{ \ddot{x} - 2\dot{y} = \varOmega _{x} - S_{x},} \end{aligned}$$

(1)

$$\begin{aligned} &{ \ddot{y} + 2\dot{x} = \varOmega _{y} - S_{y},} \end{aligned}$$

(2)

where,

$$ \varOmega = \frac{(x^{2} + \mathrm{y}^{2})}{2} + \frac{(1 - 2\mu )q_{1}}{r _{1}} + \frac{\mu q_{2}}{r_{2}} + \frac{\mu q_{3}}{r_{3}}, $$

(3)

with

$$ \begin{aligned} S_{x} &= k\bigl(\dot{x} - y + \alpha S'y\bigr) = k \biggl(\dot{x} - y - \frac{3\alpha y}{2r ^{\frac{7}{2}}}\biggr), \\ S_{y} &= k \bigl(x + \dot{y} - \alpha S'x\bigr) = k\biggl(x + \dot{y} + \frac{3\alpha x}{2r^{\frac{7}{2}}}\biggr), \\ S' &= S'(r) = r ^{ - \frac{3}{2}}, \end{aligned} $$

(4)

while

$$ \begin{aligned} r_{1} &= \sqrt{(x - \sqrt{3} \mu )^{2} + \mathrm{y}^{2}},\\ r _{2} &= \sqrt{\biggl(x + \frac{\sqrt{3}}{2}(1 - 2\mu )\biggr)^{2} + \biggl( \mathrm{y} - \frac{1}{2}\biggr)^{2}}, \\ r_{3} &= \sqrt{\biggl(x + \frac{\sqrt{3}}{2}(1 - 2\mu ) \biggr)^{2} + \biggl(y + \frac{1}{2}\biggr)^{2}}, \\ r &= \sqrt{x^{2} + y^{2}}. \end{aligned} $$

(5)

Here $r_{1}$, $r_{2}$ and $r_{3}$ are the distances of the infinitesimal body from the primaries, $\varOmega$ is the gravitational potential, dots denote time derivatives, the suffixes $x$ and $y$ indicate the partial derivatives of $\varOmega$ with respect to $x$ and $y$, respectively. $k \in [0, 1)$ is the dissipative constant, depending on several physical parameters (Beaugé and Ferraz-Mello 1993) like the viscosity of the gas, the radius and the mass of the particle and $\alpha \in [0, 1)$ is the ratio of the gas and keplerian velocities (Murray 1994). The Stokes drag effect is of order of $k = 10^{ - 5}$, $\alpha = 0.05$ (Jain and Aggarwal 2015a, 2015b; Celletti et al. 2011) for all numerical results. The radiation pressure parameters of the primaries are expressed by means of the relations $0 < q_{i} = (1 - b _{i}) \le 1$, $i = 1, 2, 3$, where $b_{1}$, $b_{2}$ and $b_{3}$ are the ratios of the force $F_{r}$ which is caused by radiation to the force $F_{g}$ which results from gravitation due to the three primary bodies $m_{1}$, $m_{2}$ and $m_{3}$, respectively. It is interesting to note that an increase in the radiation pressure implies a decrease in the mass reduction factor at constant gravitational force.

2.1 Linear stability of the Lagrange configuration in the gravitational case

In Newtonian gravity, Gascheau (1843) proved that Lagrange’s equilateral triangular configuration for circular motion is stable, if:

$$ \frac{m_{1}m_{2} + m_{2}m_{3} + m_{1}m_{3}}{(m_{1} + m_{2} + m_{3})^{2}} < \frac{1}{27}, $$

(6)

where $m_{1}$, $m_{2}$ and $m_{3}$ are the three primary bodies. The gravitational interaction is usually considered to be the Newtonian one in most of the studies concerning the Trojans. However, if one wants to consider the problem in the framework of General Relativity, we may refer here the article by Yamada and Tsuchiya (2017).

2.2 Linear stability of the Lagrange configuration in the photogravitational case

In the photogravitational case, the necessary condition for the stability of the configuration is the inequality (see Papadouris and Papadakis 2013):

$$ \frac{q_{1}m_{1}q_{2}m_{2} + q_{2}m_{2}q_{3}m_{3} + q_{1}m_{1}q_{3}m _{3}}{ ( q_{1}m_{1} + q_{2}m_{2} + q_{3}m_{3} )^{2}} < \frac{1}{27}, $$

(7)

where $q_{1}$, $q_{2}$ and $q_{3}$ are the corresponding radiation pressure forces of the primaries.

In the gravitational case (see Baltagiannis and Papadakis 2011) where the two small primary bodies have the same mass, we know that only for a large value of $m_{1}$ and small masses $m_{2}$ and $m_{3}$, the Routh’s inequality is fulfilled. In the case where the dominant primary body $m_{1}$ is a radiation source ($q_{1} \ne 1$, $q_{2} = q_{3} = 1$) while the other two small primaries have equal masses ($m_{2} = m_{3}$), then a detailed study of the equilibrium points of the problem has been done by Papadouris and Papadakis (2013).

Next, we shall discuss the positions of the equilibrium points of the test body under the above condition (7). As we have already mentioned, our target is not to provide a systematic search of their existence and location but to gain more insight about their dynamics.

3 Existence and locations of equilibrium points

The equilibrium points are those points at which the velocity and acceleration of the fourth body are zero. Therefore, the locations of these points are given by the solutions of the equations:

$$\frac{\partial \varOmega }{\partial x} = \frac{\partial \varOmega }{\partial y} = 0,\quad \mbox{i.e.}, $$

$$\begin{aligned} &{ x - \frac{(1 - 2\mu )(x - \sqrt{3} \mu )q_{1}}{r_{1}^{3}}- \frac{q _{2}(x + \frac{\sqrt{3}}{2}(1 - 2\mu ))\mu }{r_{2}^{3}}} \\ &{ \quad {}- \frac{q _{3}(x + \frac{\sqrt{3}}{2}(1 - 2\mu ))\mu }{r_{3}^{3}} + k \biggl(y + \frac{3y \alpha }{2r^{\frac{7}{2}}}\biggr)= 0,} \end{aligned}$$

(8)

$$\begin{aligned} &{ y - \frac{(1 - 2\mu )yq_{1}}{r_{1}^{3}} - \frac{q_{2}(y - \frac{1}{2})\mu }{r_{2}^{3}}- \frac{q_{3}(y + \frac{1}{2})\mu }{r_{3}^{3}}} \\ &{ \quad {}- k\biggl(x + \frac{3\alpha x}{2r^{ \frac{7}{2}}}\biggr)= 0.} \end{aligned}$$

(9)

Their positions are hard to be obtained with analytical expressions; however, they can be approximated by using any numerical method for solving non-linear algebraic systems. For the numerical computation of the number and the position of these equilibria, we shall do a graphical study of the two curves. Using the Newton-Raphson (N-R) method of solution, our experimental results on a wide range of parameter values show that the system admits only eight equilibria in the ($x$, $y$) plane. The aforementioned method has been successfully applied by Baltagiannis and Papadakis (2011), Papadouris and Papadakis (2013) and references therein for the determination of equilibrium points in a different model-problem of Celestial Mechanics.

It is interesting to note that for $k = 0$, $q_{1} = q_{2} = q_{3} = 1$, we obtain the classical case of the restricted four-body problem and the solutions are reported in Baltagiannis and Papadakis (2011); while for $k = 0$, $q_{1} < 1$, $q_{2} = q_{3} = 1$, we have a photogravitational case and some of the results can be found in Papadouris and Papadakis (2013). In the absence of dissipative force ($k = 0$) and $q_{1} < 1$, $q_{2} = q _{3} < 1$, the photogravitational case of Singh and Vincent (2016) is verified. Also, the restricted three body problem with Stokes drag effect of Jain and Aggarwal (2015a, 2015b) is recovered for $k \ne 0$, $m_{3} = 0$, and $q_{1} = q_{2} = q_{3} = 1$.

3.1 Collinear equilibrium points

The positions of the collinear equilibrium points are given by solving (8) and (9) for $y = 0$. If, $y = 0$, equation (9) is not fulfilled since it gives $\frac{q_{2}\mu }{2r_{2}^{3}} - \frac{q_{3} \mu }{2r_{3}^{3}} - k(x + \frac{3\alpha x}{2r^{\frac{7}{2}}}) = 0$ which is satisfied for $q_{2} = q_{3} = k = 0$. Thus, the solutions of (8) will not correspond to equilibrium points (i.e. they are not solution of the initial system: $\{\varOmega _{x} = 0,\ \varOmega _{y} = 0\}$, or in other words, do not lie exactly on the $x$-axis), called collinear equilibrium points. Hence, collinear equilibrium points do not exist (numerically and of course neither analytically) in the present problem. This result agrees with Baltagiannis and Papadakis (2011), who determined the positions and stability of equilibrium points in the equilateral triangle configuration of the four-body problem when $m_{1} \ne m_{2} \ne m_{3}$, Singh and Vincent (2017), when $m_{1} m_{2} = m_{3}$, and the studies carried out by Jain and Aggarwal (2015b). So, in this problem there are cases where collinear equilibria do not exist.

3.2 Non-collinear equilibrium points

The positions of the non-collinear equilibrium points are given by solving (8) and (9) for $y \neq 0$, that can be written as:

$$\begin{aligned} &{ x - \frac{(1 - 2\mu )(x - \sqrt{3} \mu )q_{1}}{r_{1}^{3}}- \frac{q _{2}(x + \frac{\sqrt{3}}{2}(1 - 2\mu ))\mu }{r_{2}^{3}}} \\ &{ \quad - \frac{q _{3}(x + \frac{\sqrt{3}}{2}(1 - 2\mu ))\mu }{r_{3}^{3}}+k \biggl(y + \frac{3y \alpha }{2r^{\frac{7}{2}}}\biggr)= 0,} \end{aligned}$$

(10)

$$\begin{aligned} &{ y - \frac{(1 - 2\mu )yq_{1}}{r_{1}^{3}} - \frac{q_{2}(y - \frac{1}{2})\mu }{r_{2}^{3}} - \frac{q_{3}(y + \frac{1}{2})\mu }{r_{3}^{3}}} \\ &{ \quad {} - k\biggl(x + \frac{3\alpha x}{2r^{ \frac{7}{2}}}\biggr)= 0,} \end{aligned}$$

(11)

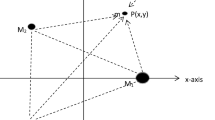
and the problem, for $\mu = 0.01$, $q_{1} = 0.99$, $q = q_{2} = q_{3} = 0.85$, $k = 10^{ - 5}$, and $\alpha = 0.05$ admits eight non-collinear equilibrium points, $L _{i}$, $i =1, 2, \ldots ,8$ (Fig. 1). One can easily see eight points of intersection of the curves $\varOmega _{x} = 0$ (light blue line in the figure) and $\varOmega _{y} = 0$ (orange line in the figure), which correspond to eight equilibrium positions of the infinitesimal body $m$. The three blue points are the positions of the primary bodies and the red dots are the positions of the eight non-collinear equilibrium points of the problem. In the figure, points $L_{1}$ and $L_{2}$ seem to correspond to collinear equilibrium points as solution of (10) and (11) [arising from (8) and (9)] when $y = 0$. However, this solution does not verify (11), hence $L_{1}$ and $L_{2}$ do not constitute collinear points (i.e. do not lie exactly on the $x$-axis).

Fig. 1

The eight non-collinear equilibrium points and the positions of the primary bodies for $\mu = 0.01$, $q_{1} = 0.99$, $q = q_{2} = q_{3} = 0.85$, $k = 10^{ - 5}$, and $\alpha = 0.05$. Blue dots indicate the coordinates of the primaries ($m_{i}$), while red dots ($L_{i}$) represent the positions of the equilibrium points

We note that the existence, number and location of these equilibrium points depend on the system parameters (mass parameter $\mu$, dissipative constant $k$ and the radiation factors $q_{i},i = 1,2,3$) of the problem. For example, the problem admits seven non-collinear equilibrium points for constant values of $\mu = 0.01$, $q_{1} = 0.5$, $q = q_{2} = q_{3} = 0.7$, $k = 10^{ - 5}$, and $\alpha = 0.05$ (Fig. 2 panel (a)) because $L_{5}$ in Fig. 1 does not exist, while for constant values of $\mu = 0.005$, $q_{1} = 0.6$, $q = q_{2} = q_{3} = 0.3$, the problem has one less (six) equilibrium points (Fig. 2 panel (b)) since $L_{5}$ and $L_{6}$ in Fig. 1 do not exist. Further, we observe that when radiation factors are relatively weak, all the equilibrium points existing in the gravitational case appear; however, when the coefficients are strong, only some points are likely to appear.

Fig. 2

(a) Positions of the seven equilibrium points for $\mu = 0.01$, $q_{1} = 0.5$, $q = q_{2} = q_{3} = 0.7$, $k = 10^{ - 5}$, and $\alpha = 0.05$, (b) the six equilibrium points for $\mu = 0.005$, $q_{1} = 0.6$, $q = q_{2} = q_{3} = 0.3$, $k = 10^{ - 5}$, and $\alpha = 0.05$. Blue dots indicate the coordinates of the primaries ($m_{i}$), while red dots ($L_{i}$) represent the positions of the equilibrium points

Next, we shall discuss the positions of the non-collinear equilibrium points of the infinitesimal body for $\mu = 0.01$, $k = 10^{ - 5}$ and $\alpha = 0.05$ whereas the radiation factors $q_{1}$ and $q_{2,3}$ vary in the interval $q_{i} \in [1, 0)$; $i = 1,2,3$, while they always satisfy the above condition (7).

To investigate the influence of the radiation factors on the positions of the equilibria under consideration, the radiation factor of the two equal primaries ($q_{2} = q_{3}$) is arbitrary set to be $q = 0.9985$ while that of the dominant primary $q_{1}$ ($0 < q_{1} \le 1$) varies. The coordinates of the numerically determined non-collinear equilibrium points are shown in Table 1 for various values of the radiation factor $q _{1}$. We observe that with the increase of values of the radiation factor $q_{1}$, the coordinates of the equilibria $L_{5}$ and $L_{6}$ tend to the primaries $m_{3}$ and $m_{2}$, correspondingly while all the equilibrium points of the problem approach the dominant primary $m_{1}$. The aforementioned discussion are presented in Fig. 3 where we have shown the positions of the equilibrium points for a fixed value of $q = 0.9985$ and for three different values of $q_{1} = 1$, $q_{1} = 0.75$ and $q_{1} = 0.516$. In the figure, we have plotted using the following color code: panel (a) $q_{1} = 1$ (green, gray), panel (b) $q_{1} = 0.75$ (black, gray), and panel (c) $q_{1} = 0.516$ (magenta, gray). From Fig. 3, we observe that the variational trend of the equilibria is similar to the scenario presented in Table 1, that is, equilibria $L_{5}$ and $L_{6}$ tend to the primaries $m_{3}$ and $m_{2}$, correspondingly while all the equilibrium points of the problem approach the dominant primary $m_{1}$ as the radiation pressure $q_{1}$ increases (i.e. $q_{1}$ decreases) for a fixed value of $q=0.9985$.

Fig. 3

The positions of the eight non-collinear equilibrium points for $\mu = 0.01$, $k = 10^{ - 5}$, $\alpha = 0.05$, and $q= 0.9985$ as $q_{1}$ radiates, i.e. panels: (a) $q_{1} = 1$ (green, gray), (b) $q_{1} = 0.75$ (black, gray), and (c) $q_{1} = 0.516$ (magenta, gray). Blue dots ($m_{i}$) correspond to the coordinates of the primaries, while red dots ($L_{i}$) show the positions of the equilibrium points

Table 1 The positions of the eight non-collinear equilibrium points as a function of $q_{1}$ for $\mu = 0.01$, $k = 10^{ - 5}$ and $\alpha = 0.05$

Similarly, for the investigation of the influence of the radiation factor of the two equal primaries ($q_{2} = q_{3}$) on the positions of the non-collinear equilibrium points, we set $q_{1} = 0.9985$ as $q$ varies for the same fixed values of $\mu = 0.01$, $k = 10^{ - 5}$, $\alpha = 0.05$. The coordinates of the numerically determined non-collinear equilibrium points are shown in Table 2 for various values of the radiation factor $q$. We observe that with the increase of the radiation pressure parameter $q$, the equilibria $L_{1}$ and $L_{2}$ approach the primary body $m_{1}$, the equilibria $L_{4}$ and $L_{8}$ increase towards $m_{2}$, $L_{3}$ and $L_{7}$ increase towards $m_{3}$ whereas $L_{5}$ and $L_{6}$ decrease towards the primaries $m_{3}$ and $m_{2}$ correspondingly. In Fig. 4, we have shown the positions of the non-collinear equilibrium points for a fixed value of $q_{1} = 0.9985$ and for three different values of $q = 1$, $q =$0.75 and $q =$ 0.516 while the remaining parameters are $\mu = 0.01$, $k = 10^{ - 5}$ and $\alpha = 0.05$. In the figure, we have plotted using the following color code: panel (a) $q = 1$ (green, gray), panel (b) $q = 0.75$ (black, gray), and panel (c) $q = 0.516$ (magenta, gray). Panel (d) shows the combined plots of panels ((a)–(c)) with arrows signifying the directions of the equilibrium points. The points of intersections: (red), (yellow) and (black) are when $q=1$, $q=0.75$ and $q=0.516$, correspondingly, for a fixed value of $q_{1}=0.9985$. From Fig. 4, we observe that the variational trend of the equilibria is similar to the scenario presented in Table 2, that is, for fixed a value of $q_{1}=0.9985$ and for increasing $q$, the equilibria $L_{1}$ and $L_{2}$ approach the primary body $m_{1}$, the equilibria $L_{4}$ and $L_{8}$ increase towards $m_{2}$, $L_{3}$ and $L_{7}$ increase towards $m_{3}$ whereas $L_{5}$ and $L_{6}$ decrease towards the primaries $m_{3}$ and $m_{2}$, correspondingly. Also, we see that $L_{1}$ and $L_{2}$ have very less dependence on the parameters as there is almost no change in the positions of the equilibria.

Fig. 4

The positions of the eight non-collinear equilibrium points for $\mu = 0.01$, $k = 10^{ - 5}$, $\alpha = 0.05$, and $q_{1}= 0.9985$ as $q$ radiates, i.e. panels: (a) $q = 1$ (green, gray), (b) $q = 0.75$ (black, gray), and (c) $q = 0.516$ (magenta, gray), (d) shows the combined plots of panels ((a)–(c)) with arrows showing the directions of the equilibrium points. Blue dots ($m_{i}$) correspond to the coordinates of the primaries, while red dots ($L_{i}$) show the positions of the equilibrium point

Table 2 The positions of the eight non-collinear equilibrium points as a function of $q$ for $\mu = 0.01$, $k = 10^{ - 5}$ and $\alpha = 0.05$

4 Linear stability of the non-collinear equilibrium points

In this section, we attempt to examine the linear stability of an equilibrium configuration, that is, its ability to restrain the body motion in its vicinity. To do so, we displace the infinitesimal body a little from an equilibrium point with a small velocity. Let the position of an equilibrium point be denoted by ($x_{0}$, $y_{0}$), and consider a small displacement ($\xi$, $\eta$) from the point such that $x = x_{0} + \xi$ and $y = y_{0} + \eta$. Substituting these values into (1) and (2), we obtain the variational equations:

$$\begin{aligned} &{ \ddot{\xi } - 2\dot{\eta } = \xi (\varOmega _{xx}^{0} - S_{xx}^{0}) + \eta (\varOmega _{xy}^{0} - S_{xy}^{0}) - S_{\dot{x}x}^{0}\dot{\xi },} \end{aligned}$$

(12)

$$\begin{aligned} &{ \ddot{\eta } + 2\dot{\xi } = \xi \bigl(\varOmega _{yx}^{0} - S_{yx}^{0}\bigr) + \eta \bigl(\varOmega _{yy}^{0} - S_{yy}^{0}\bigr) - S_{y\dot{y}}^{0}\dot{\eta }.} \end{aligned}$$

(13)

Here, only linear terms in $\xi$ and $\eta$ have been taken. The second partial derivatives are denoted by subscripts $x$ and $y$ while the dots represent the derivatives w.r.t the actual time $t$. The superscript ‘0’ indicates that the partial derivatives have been evaluated at the equilibrium point with $S_{x\dot{x}}^{0}=k =\ S_{y\dot{y}}^{0}$.

The characteristic equation corresponding to (12) and (13) is given by:

$$ \lambda ^{4} + a\lambda ^{3} + b\lambda^{2} + c\lambda + d = 0, $$

(14)

where

$$ \begin{aligned} a &= S_{x\dot{x}}^{0} + S_{y\dot{y}}^{0}, \qquad b = 4 + S_{x\dot{x}}^{0}S_{y\dot{y}}^{0} - J_{xx}^{0} - K_{yy}^{0}, \\ c &= 2J_{xy}^{0} - 2K_{yx}^{0} - S_{x\dot{x}}^{0}K_{yy}^{0} - S_{y \dot{y}}^{0}J_{xx}^{0},\\ d &= J_{xx}^{0}K_{yy}^{0} - J_{xy}^{0}K _{yx}^{0} \end{aligned} $$

(15)

with

$$ \begin{aligned} J_{xx}^{0} &= \bigl(\varOmega _{xx}^{0} - S_{xx}^{0}\bigr), \qquad J_{xy}^{0} = \bigl(\varOmega _{xy}^{0} - S_{xy}^{0} \bigr), \\ K_{yx}^{0} &= \bigl(\varOmega _{yx}^{0} - S_{yx}^{0}\bigr), \qquad K_{yy}^{0} = \bigl(\varOmega _{yy}^{0} - S_{yy}^{0}\bigr). \end{aligned} $$

(16)

Evaluating the partial derivatives at the equilibrium points, we obtain:

$$\begin{aligned} J_{xx}^{0} =& 1 - \frac{(1 - 2\mu )q_{1}}{r_{10}^{3}} + \frac{3q_{1}(1 - 2\mu )(x_{0} - \sqrt{3} \mu )^{2}}{r_{10}^{5}} \\ &{}- \frac{\mu q_{2}}{r _{20}^{3}} +\frac{3\mu q_{2}(x_{0} + \frac{\sqrt{3}}{2}(1 - 2 \mu ))^{2}}{r_{20}^{5}} - \frac{\mu q_{3}}{r_{30}^{3}} \\ &{}+ \frac{3\mu q_{3}(x_{0} + \frac{\sqrt{3}}{2}(1 - 2\mu ))^{2}}{r _{30}^{5}} - \frac{21kx_{0}y_{0}\alpha }{4r_{0}^{\frac{11}{2}}}, \end{aligned}$$

(17)

$$\begin{aligned} J_{xy}^{0} =& \frac{3y_{0}q_{1}(1 - 2\mu )(x_{0} - \sqrt{3} \mu )}{r _{10}^{5}} \\ &{}+ \frac{3\mu q_{2}(y_{0} - \frac{1}{2})(x_{0} + \frac{ \sqrt{3}}{2}(1 - 2\mu ))}{r_{20}^{5}} \\ &{} + \frac{3\mu q_{3}(y_{0} + \frac{1}{2})(x_{0} + \frac{\sqrt{3}}{2}(1 - 2\mu ))}{r_{30}^{5}} \\ &{}- k\biggl( - 1 - \frac{3\alpha }{2r_{0}^{\frac{7}{2}}} + \frac{21\alpha y _{0}^{2}}{4r_{0}^{\frac{11}{2}}}\biggr), \end{aligned}$$

(18)

$$\begin{aligned} K_{yx}^{0} =& \frac{3y_{0}q_{1}(1 - 2\mu )(x_{0} - \sqrt{3} \mu )}{r _{10}^{5}} \\ &{} + \frac{3\mu q_{2}(y_{0} - \frac{1}{2})(x_{0} + \frac{ \sqrt{3}}{2}(1 - 2\mu ))}{r_{20}^{5}} \\ &{}+ \frac{3\mu q_{3}(y_{0} + \frac{1}{2})(x_{0} + \frac{\sqrt{3}}{2}(1 - 2\mu ))}{r_{30}^{5}} \\ &{} - k\biggl(1 + \frac{3\alpha }{2r_{0}^{\frac{7}{2}}} - \frac{21\alpha x_{0} ^{2}}{4r_{0}^{\frac{11}{2}}}\biggr), \end{aligned}$$

(19)

$$\begin{aligned} K_{yy}^{0} =& 1 - \frac{(1 - 2\mu )q_{1}}{r_{10}^{3}} + \frac{3q_{1}y _{0}^{2}(1 - 2\mu )}{r_{10}^{5}} - \frac{\mu q_{2}}{r_{20}^{3}} \\ &{}+ \frac{3 \mu q_{2}(y_{0} - \frac{1}{2})^{2}}{r_{20}^{5}} - \frac{\mu q_{3}}{r _{30}^{3}} + \frac{3\mu q_{3}(y_{0} + \frac{1}{2})^{2}}{r_{30}^{5}} \\ &{}+ \frac{21k\alpha x_{0}y_{0}}{4r_{0}^{\frac{11}{2}}} \end{aligned}$$

(20)

with

$$\begin{aligned} r_{10} &= \sqrt{(x_{0} - \sqrt{3} \mu )^{2} + \mathrm{y}_{0}^{2}}, \\ r_{20} &= \sqrt{ \biggl(x_{0} + \frac{\sqrt{3}}{2}(1 - 2\mu )\biggr)^{2} + \biggl( \mathrm{y}_{0} - \frac{1}{2}\biggr)^{2}}, \\ r_{30} &= \sqrt{\biggl(x_{0} + \frac{\sqrt{3}}{2}(1 - 2\mu )\biggr)^{2} + \biggl(y _{0} + \frac{1}{2} \biggr)^{2}}, \\ r_{0} &= \sqrt{x_{0}^{2} + y_{0}^{2}}. \end{aligned}$$

(21)

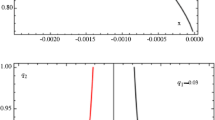
The equilibrium points are stable if all the roots of (14) evaluated at the equilibrium points are purely imaginary roots or complex roots with negative real parts; otherwise, they are unstable. It is known (Papadouris and Papadakis 2013) that the condition of stability of triangular configuration in linear approximation is given by (7). It is expedient to make stability analysis of the obtained equilibrium solutions in the domain restricted by (7). A numerical check of the stability analysis for the equilibrium points $L_{2}, \ldots, L_{6}$ showed that under any values of the parameters, satisfying thus the requested equation (7) when exist, the eigenvalues are of the form $\lambda _{1,2} = \pm a$, $\lambda _{3,4} = - a \pm ib$ where $a$ and $b$ are real numbers. Consequently, they are unstable. On the contrary, there are values of $\mu$ and radiation factors where the equilibrium points $L_{1}$, $L_{7}$ and $L_{8}$ may be stable. In Fig. 5, we have plotted the stability regions of the non-collinear equilibrium points. We observed that when we increase the radiation factors along with the increase of the mass ratio, the stability interval of $L_{1}$ increases. For the specific three pairs of values of $q_{1}$ and $q$; $(1, 1)$, $(0.995, 0.99)$ and $(0.8, 0.7)$, the equilibrium point $L_{1}$ is stable for $\mu \in (0,0.00256]$, $\mu \in (0,0.00257]$ and $\mu \in (0,0.0030]$ correspondingly. Now, we have found the stability regions on the $(\lambda , \mu )$-plane as shown in Fig. 5, panel (a). The figures are obtained for different values of $\mu$ which can be as representative for other cases. It can be seen from the figure that for $\mu = 0.00256$, $q_{1}=1$ and $q=1$ (green line), the trajectory rotates around the position of $L_{1}$ and does not leave it essentially. For $\mu = 0.00257$, $q_{1}= 0.995$ and $q= 0.99$ (red line) and $\mu = 0.0030$, $q_{1}= 0.8$ and $q= 0.7$ (black line), the trajectory rotates around $L_{1}$ as well, but together with the growth of $\mu$ and radiation factors begins more and more to move away from it. Hence, we conclude that the regions of stability increase with the increase of the radiation factors and mass ratio. On the other hand, for the same three pairs of values of $q_{1}$ and $q$; $(1, 1)$, $(0.995, 0.99)$ and $(0.8, 0.7)$, the equilibrium points $L_{7,8}$ are stable for $\mu \in (0,0.018]$, $\mu \in (0,0.0175]$ and $\mu \in (0,0.0132]$ correspondingly. In Fig. 5 panel (b) we have drawn the stability regions on the $(\lambda , \mu )$-plane of the equilibrium points $L_{7,8}$. We observed that for $\mu = 0.018$, $q_{1}=1$ and $q=1$ (green line), the trajectory rotates around the positions of $L_{7,8}$ and does not leave it essentially. For $\mu = 0.0175$, $q_{1}= 0.995$ and $q= 0.99$ (red line) and $\mu = 0.0132$, $q_{1}= 0.8$ and $q= 0.7$ (black line), the trajectory rotates around $L_{7,8}$ as well, but together with the increase of radiation factors along with the decrease of mass ratio begins more and more to come close to the equilibrium points. We also conclude that the regions of stability decrease with the increase of the radiation factors.

Fig. 5

(a) Stability region of $L_{1}$ for $\mu = 0.00256$, $q_{1} = 1$, $q = 1$ (green line); $\mu = 0.00257$, $q_{1} = 0.995$, $q = 0.99$ (red line) and $\mu = 0.0030$, $q_{1} = 0.8$, $q = 0.7$ (black line). (b) Stability region of $L_{7,8}$ for $\mu = 0.018$, $q_{1} = 1$, $q = 1$ (green line); $\mu = 0.0175$, $q_{1} = 0.995$, $q = 0.99$ (red line) and $\mu = 0.0132$, $q_{1} = 0.8$, $q = 0.7$ (black line). We have fixed the values of $k = 10^{ -5}$ and $\alpha = 0.05$ in all cases. For complex eigenvalues ${\pm} a \pm ib$, both the positives real and imaginary parts are plotted

From the results we can conclude that radiation factors have strong effect on the stability regions for large deviations of it values from the gravitational case. In the same conclusion we have reached, for the mass parameter $\mu$, comparing each frame of the figures.

5 Model applications to (Ross 104-Ross775a-Ross775b) stellar system

In this section, we apply the model to study the motion of a test particle in the vicinity of a star, Ross 104 whose mass is 0.42 $M_{ \mathit{Sun}}$ and bolometric luminosity of 0.020 along with its binary star, Ross 775a and Ross 775b each having equal mass 0.23 $M_{\mathit{Sun}}$ and bolometric luminosity of 0.20, respectively. According to Xuetang and Lizhong (1993), the mass reduction factors are expressed by means of the relations $q_{i} = 1 - \frac{A\kappa L}{ \alpha \rho M}$, $i = 1,2,3$, where $M$ and $L$ are the mass and the luminosity of a star respectively, $\alpha$ and $\rho$ are the radius and density of the test particle, $A = 2.9838 \times 10^{ - 5}$ in the C.G.S system, and $\kappa$ is the radiation pressure efficiency factor of a star, and it is considered as a unity following Stefan-Boltzmsnn’s law. Now given a test particle with radius $\alpha = 2 \times 10^{ - 3} \mbox{ cm}$ and density $\rho = 1.4~\mbox{g}\,\mbox{cm}^{-3}$, then $q_{\mathrm{ROSS}~104}=q_{1} = 0.9995264$, and $q_{\mathrm{ROSS}~775A}=q_{2} = q_{3} = 0.9913514$ and the mass parameter $\mu$ of the system is 0.261363636. Using these data, we have computed the positions of the non-collinear equilibrium points as shown in Fig. 6. It can be seen that there exist eight non-collinear equilibrium points of the problem. In addition, with the help of the software package Mathematica, we obtain the roots of the characteristic equation (14) as given in Table 3 for the stellar system (Ross 104-Ross775a-Ross775b), for the assumed values of $k = 10^{ - 5}$ and $\alpha = 0.05$. An analysis of the numerical results shows the non existence of pure imaginary roots. Hence, the non-collinear equilibrium points are unstable.

Fig. 6

Equilibrium points for the (Ross 104-Ross775a-Ross775b) stellar system

Table 3 Existence and stability of equilibrium points in the stellar system: Ross 104-Ross775a-Ross775b under the combined effect of radiation pressure and Stokes drag

6 Discussion and conclusion

We have studied the photogravitational restricted four-body problem with Stokes drag when the primary bodies $m_{1}$, $m_{2}$ and $m_{3}$ are always at the vertices of an equilateral triangle (Lagrangian configuration). The fourth particle in this system has negligible mass $m$ with respect to the primaries, and its motion is perturbed by radiation factors and Stokes drag from the primaries. We studied the existence, location and stability of the equilibrium points as the parameters vary. It was found that in the presence of Stokes drag, collinear equilibrium points do not exist, both analytically and numerically. The eight non-collinear equilibrium points were seen to be affected by the radiation factors for fixed values of mass parameter and Stokes drag. It was also found that the number of the equilibrium points depends on the values of system parameters (Figs. 1 and 2). The effects of the involved parameters on the positions of the equilibrium points are given in Tables 1 and 2. These are shown graphically in Figs. 3 and 4. Finally, the stability investigation has been achieved by determining the roots of the characteristic equation. The numerical investigations of these roots revealed that all the equilibrium points are unstable except $L_{1}$, $L _{7}$ and $L_{8}$ which may be stable for a range of values of $\mu$ provided that the remaining parameters are fixed. Also, the stability regions of these equilibria are plotted in Fig. 5 and we observed that the regions of $L_{1}$ increased with the increase of the radiation factors and mass ratio whereas, the stability regions of $L_{7,8}$ decreased with the increase of the radiation factors. The model has been applied to a stellar system: Ross 104-Ross775a-Ross775b as seen in Fig. 6 and Table 3. It was found that the stellar system under consideration has no roots which are purely imaginary or complex roots with negative real parts; consequently, the equilibrium points are all linearly unstable.