Out-of-plane equilibrium points in the photogravitational restricted four-body problem

Abstract

The photogravitational restricted four-body problem is employed to describe the motion of an infinitesimal particle in the vicinity of three finite radiating bodies. The fourth body $P_{4}$ of infinitesimal mass does not affect the motion of the three bodies ($P_{1}, P_{2}, P_{3}$) that are always at the vertices of an equilateral triangle. We consider that two of the bodies ($P_{2}$ and $P_{3}$) have the same radiation and mass value $\mu$ while the dominant primary body $P_{1}$ is of mass $1 - 2\mu$. The equilibrium points ($L_{1}^{z},L_{2}^{z}$) lying out of the orbital plane of the primaries as well as the allowed regions of motion as determined by the zero velocity curves are studied numerically. Finally the stability of these points is studied and they are found to be unstable.

1 Introduction

To study the motion of celestial bodies, restricted four-body problem (RFBP, for short) is one of the important problem in the dynamical system. The restricted four body has many possible uses in the dynamical system for example, the fourth body is very useful for saving fuel and time in the trajectory transfers in the restricted four-body problem (Machuy et al. 2007). The restricted four-body problem describes the motion of negligible mass under the Newtonian gravitational attraction of three much bigger bodies (called the primaries) moving in circular orbits around their center of mass fixed at the origin of the coordinate system. Few bodies problems have been studied for long time in celestial mechanics, either as simplified models of more complex planetary systems or as benchmark models where new mathematical theories can be tested. Today the few-body problem is recognized as a standard tool in astronomy and astrophysics, from solar system dynamics to galactic dynamics (Murray and Dermott 1999). It is known that in the planar problem of three bodies attracting each other according to Newtonian gravitational law, there exist only two permanent central configurations, namely, the collinear (Eulerian) and the triangular (Lagrangian). In the first case, the primaries of the problem lie on a single straight line while in the second one, the primary bodies lie at the vertices of an equilateral triangle. We will consider the latter case which are solutions of the central configuration equations for which the three bodies with nonzero mass are at the vertices of an equilateral triangle. The model was used, among others, by Pedersen (1944, 1952), Simo (1978), Alvarez-Ramirez and Vidal (2009), Baltagiannis and Papadakis (2011), Papadouris and Papadakis (2013), Reena and Badam (2014), etc. A different version of the problem arises when some or all the primaries are sources of radiation. The existence of strong radiation sources in the universe has repeatedly been confirmed from a very early period. In 1891, the Russian physicist Labedev experimentally demonstrated the minute pressure exerted by light on bodies and stated a law carrying his name, according to which, this pressure is inversely proportional to the square of the distance between the light source and the illuminated body (Labedev 1891). The existence of the out of the orbital plane equilibrium points, in the photogravitational restricted three-body problem, was first pointed out by Radzievskii (1950) studying the case Sun-Planet-particle and Galaxy Kernel-Sun-particle. He found two equilibrium points on the $(x,z)$ plane in symmetrical positions with respect to the $(x,y)$ plane. The stability of these points was first studied in the solar problem by Perezhogin (1976) and by the same author (1982) in the whole range of existence when the smaller body is considered non-luminous.

Later Simmons et al. (1985) proved the existence of two more out of plane equilibrium points both on the $(x,z)$ plane, when both primary bodies are radiation sources and certain relations between the mass and the radiation pressure parameters hold.

As we have already mentioned, several authors based their works on Radzievskii’s model (Chernikov, 1970; Perezhogin, 1976; Schuerman, 1980; Simmons et al., 1985; Kunitsyn and Polyakhova, 1995; Ragos and Zagouras, 1988a, 1988b; Douskos and Markellos, 2006; Shankaran et al., 2011; Das et al., 2009; Singh, 2012, etc.) to understand various issues related to the dynamics of a particle around radiating primaries. This model has interesting applications for artificial satellites, future space colonizations or even for ‘sailing’ vehicles and spacecraft ‘parking’ (Friedman 1976).

The classical restricted four-body problem may be generalized to include different types of effects such as radiation pressure force, Poynting-Robertson drag, oblateness coefficient, Coriolis and centrifugal force, variation of the masses of the primaries, etc. So, using the equations of the three-dimensional problem given in the literature we wish to study the existence and stability of “out-of- plane” equilibrium points.

Here, we consider the three primary bodies $P_{1}$, $P_{2}$, $P_{3}$ of masses $m_{1}$, $m_{2}$, $m_{3}$ as radiation sources while two of the bodies ($P_{2}$ and $P_{3}$) have the same radiation and mass value. Also, the infinitesimal body is assumed to have no influence on the motion of the primaries. The model may be applied to examine the dynamic behavior of small objects such as cosmic dust, grains, etc.

Our goal in this paper is to study the effects of radiation pressure on the motion of a small particle in the force field of three radiating bodies much bigger than the particle, which are always in Lagrangian configuration. More precisely, we study the equilibrium points, the zero velocity curves and the linear stability of the problem under the effects of radiation pressure from the primaries.

This work may be applicable to the study of a test particle in the Sun-Jupiter-Trojan-spacecraft system and the results obtained in this study will have thus practical application in astrophysics.

The paper is organized in six sections. Section 2 provides the equations of motion for the system under investigation. Section 3 locates the positions of the out of plane points. Section 4 is devoted to the surfaces and curves of zero velocity. The regions of allowed motion as determined by the zero velocity curves as well as the positions of out of plane points are given. Section 5 established their stability; while Sect. 6 discusses the obtained results and conclusion of the paper.

2 Equations of motion

The system we consider is the motion of an infinitesimal object, e.g. a spacecraft, in the presence of three finite celestial objects ($P_{1},P_{2},P_{3}$) with masses $m_{1}$, $m_{2}$ and $m_{3}$, which we treat as point mass. We suppose that $P_{1},P_{2},P_{3}(m_{1} \gg m_{2} =m_{3})$ always lie at the vertices of an equilateral triangle and one of them, $P_{1}$ (say), is on the negative $x$-axis at the origin of time. This configuration is well known to be stable if the masses satisfy the condition of Gascheau’s inequality (see for details Gascheau, 1843 and Baltagiannis and Papadakis, 2011). This system is also dimensionless, i.e., we normalize the units with the supposition such that the sum of the masses, the separation between the primaries, the Gaussian constant and unit of time are equal to unity. The equilateral configuration is possible for all distributions of the masses, whilst the fourth body of negligible mass moves in the same plane. The factors characterizing the radiation effects of the primaries are also taken into account. These are related to the notation of Schuerman (1980) given by the relation $q_{i} = 1 -\beta_{i}$, $i= 1, 2, 3$ where $q_{1},q_{2} = q_{3}$ stand for the mass reduction factors, $\beta_{1},\beta_{2}$ and $\beta_{3}$ are the ratios of the magnitude of radiation ($F_{r}$) to gravitational ($F_{g}$) forces, from the respective primaries. For $i = 1,2,3$, it is clear that: If $q_{i}=1$, the radiation pressure has no effect. If $0< q_{i}<1$, the gravitational force is greater than the radiational one. If $q_{i}=0$, the radiation force balances the gravitational one. If $q_{i}<0$, the radiation pressure overrides the gravitational attraction. Let the coordinates of the infinitesimal mass be $(x,y)$ and masses $m_{1}$, $m_{2}$, and $m_{3}$ are

$$\begin{aligned} &{(- \sqrt{3} \mu,0),} \\ &{\biggl(\frac{\sqrt{3}}{2}(1 - 2\mu), - \frac{1}{2} \biggr) \quad \mbox{and}\quad \biggl(\frac{\sqrt{3}}{2}(1 - 2\mu), \frac{1}{2}\biggr)} \end{aligned}$$

respectively, relative to the rotating frame of reference Oxyz, where

$$\begin{aligned} \mu= \frac{m_{2}}{m_{1} + m_{2} + m_{3}}= \frac{m_{3}}{m_{1} + m_{2} + m_{3}}< \frac{1}{2} \end{aligned}$$

is the mass parameter.

The differential equations of motion in three dimensions in the dimensionless variables and the barycentric – synodic coordinate system are written as (Papadouris and Papadakis (2013)):

$$\begin{aligned} &{\ddot{x} - 2\dot{y}= \varOmega_{x} } \\ &{\ddot{y} + 2\dot{x}= \varOmega_{y} } \\ &{\ddot{z} = \varOmega_{z} } \end{aligned}$$

(1)

where

$$\begin{aligned} \varOmega=\frac{1}{2}\bigl( x^{2} + y^{2} \bigr)+\frac{q_{1}(1 - 2\mu)}{r_{1}} + \frac{q_{2}\mu}{r_{2}} + \frac{q_{3}\mu}{r_{3}} \end{aligned}$$

(2)

and

$$\begin{aligned} &{r_{1}^{2}= (x + \sqrt{3} \mu)^{2} + y^{2} + z^{2}} \\ &{r_{2}^{2} = \biggl(x - \frac{\sqrt{3}}{2}(1 - 2\mu) \biggr)^{2} + \biggl(y + \frac{1}{2}\biggr)^{2} + z^{2}} \\ &{r_{3}^{2} = \biggl(x - \frac{\sqrt{3}}{2}(1 - 2\mu) \biggr)^{2} + \biggl(y - \frac{1}{2}\biggr)^{2} + z^{2}} \end{aligned}$$

where $r_{1}$, $r_{2}$ and $r_{3}$ are the distances of the infinitesimal body from the primaries, $\varOmega$ is the photogravitational potential, dots denote time derivatives, the suffixes $x$ and $y$ indicate the partial derivatives of $\varOmega$ with respect to $x$ and $y$ respectively.

System (1) admits the Jacobian integral

$$ \dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} = 2 \varOmega- C $$

(3)

where $C$ is the Jacobi Integral Constant.

3 Positions of out-of-plane equilibrium points

The locations of the out-of-plane equilibrium points can be found from the equations of motion by setting all velocity and acceleration components equal to zero and solving the resulting system

$$ \varOmega_{x} = \varOmega_{y} = \varOmega_{z} =0, $$

(4)

numerically for $x, y, z$.

Considering $z\neq0$ we thus obtain that

$$\begin{aligned} &{\begin{aligned}[b] &x - \frac{(1 - 2\mu)(x + \sqrt{3} \mu)q_{1}}{r{}_{1}^{3}} - \frac{q_{2}(x - \frac{\sqrt{3}}{2}(1 - 2\mu))\mu}{r{}_{2}^{3}} \\ &\quad {} - \frac{q_{3}(x - \frac{\sqrt{3}}{2}(1 - 2\mu))\mu}{r{}_{3}^{3}}= 0\end{aligned} } \end{aligned}$$

(5)

$$\begin{aligned} &{y - \frac{(1 - 2\mu)yq_{1}}{r{}_{1}^{3}} - \frac{(y + \frac{1}{2})\mu q_{2}}{r{}_{2}^{3}} - \frac{q_{3}(y - \frac{1}{2})\mu}{r{}_{3}^{3}}= 0 } \end{aligned}$$

(6)

$$\begin{aligned} &{\biggl(\frac{(1 - 2\mu)q_{1}}{r{}_{1}^{3}} + \frac{\mu q_{2}}{r{}_{2}^{3}} + \frac{\mu q_{3}}{r{}_{3}^{3}} \biggr)z = 0 } \end{aligned}$$

(7)

with

$$\begin{aligned} &{r_{1}^{2}= (x + \sqrt{3} \mu)^{2} + y^{2} + z^{2}} \\ &{r_{2}^{2} = \biggl(x - \frac{\sqrt{3}}{2}(1 - 2\mu) \biggr)^{2} + \biggl(y + \frac{1}{2}\biggr)^{2} + z^{2}} \\ \ &{r_{3}^{2} = \biggl(x - \frac{\sqrt{3}}{2}(1 - 2\mu) \biggr)^{2} + \biggl(y - \frac{1}{2}\biggr)^{2} + z^{2}} \end{aligned}$$

If $y = 0$, Eq. (6) is fulfilled (since $q_{2} = q_{3}$) and we solve Eqs. (5) and (7) for $y = 0$ and $z\neq0$. This results in the following equations

$$\begin{aligned} &{\begin{aligned}[b] &x_{0} - \frac{(1 - 2\mu)(x_{0} + \sqrt{3} \mu)q_{1}}{r_{10}^{3}} \\ &\quad{} - \frac{2q_{2}(x_{0} - \frac{\sqrt{3}}{2}(1 - 2\mu))\mu}{r_{20}^{3}} = 0\end{aligned} } \end{aligned}$$

(8)

$$\begin{aligned} &{\frac{(1 - 2\mu)q_{1}}{r{}_{10}^{3}} + \frac{2q_{2}\mu}{r{}_{20}^{3}} = 0 } \end{aligned}$$

(9)

where

$$\begin{aligned} &{r_{10}^{2} = (x_{0} + \sqrt{3} \mu)^{2} + z{}_{0}^{2}} \\ &{r_{20}^{2} = r_{30}^{2} = \biggl(x_{0} - \frac{\sqrt{3}}{2}(1 - 2\mu)\biggr)^{2} + \frac{1}{4} + z{}_{0}^{2},\qquad q_{2} = q_{3}} \end{aligned}$$

and the subscript ‘0’ is used to denote the equilibrium values.

From Eq. (9) we have that

$$ \frac{r_{20}}{r_{10}} = \biggl[ \biggl( \frac{ - q_{2}}{q_{1}} \biggr) \frac{2\mu}{1 - 2\mu} \biggr]^{\frac{1}{3}} \equiv k $$

(10)

which means that if $k=\mathrm{constant}$ the locus of these points is an Apollonius circle (http://en.wikipedia.org/wiki/CirclesofApollonius).

From Eq. (10) it can be seen that, for the existence of any real solution, one of the following conditions is necessary to hold:

$$ q_{1}q_{2} < 0\quad\mbox{or}\quad q_{1} = q_{2} = 0 $$

(11)

The second conditions means that the gravitational attractions balance the corresponding radiation pressure forces. This case will not be considered here.

The first condition means that the radiation pressure force of just one of the primaries exceeds its gravitational attraction.

The existence of these points is of particular astronomical interest in connection with planetary system formation, satellite motion, etc. These points are found to be located in the $(x,z)$ plane in symmetrical positions with respect to the $(x,y)$ plane. They are dynamically equivalent, which means that are characterized by the same Jacobian constant $C$ and by the same state of stability. For any given $\mu$, the existence, position and stability of these points depend on $q_{1}$ and $q_{2}$. So, the value of radiation factors could be taken in $0 < q_{2} \le1$, $- 1 \le q_{1} \le0$.

Now, for $\mu= 0.019$ and $0 < q_{2} \le1$ there are intervals of $q_{1}$ of the form $- 1 \le q_{1} \le0$ for which there exist out of the plane equilibrium points, which we call here $L_{1}^{z}$ and $L_{2}^{z}$. In Figs. 1, 2 and 3 we show graphically their positions in $(x, q_{2})$ and $(z, q_{2})$, as $q_{2}$ varies, for fixed values of $q_{1}$. Figures 1, 2 and 3 show the effects of radiation parameters i.e. $q_{1} = - 0.03$, $q_{2}$ in the interval $[1, 0.77]$, $q_{1} = -0.01$, $q_{2}$ in the interval $[1, 0.26]$ and $q_{1} = - 0.001$, $q_{2}$ in the interval $[1, 0.03]$, correspondingly on the positions of our out of plane points $L_{1}^{z}$ and $L_{2}^{z}$. From the results in Figs. 1, 2 and 3 it is obvious that as the radiation parameters increases the positions of out of plane equilibrium points are significantly affected.

Fig. 1

Position of $L_{1}^{z}$ and $L_{2}^{z}$ in the $(x\mbox{--}z)$ plane as a function of $q_{2}$ in the interval $[1, 0.77]$, for $q_{1} = - 0.03$, $\mu= 0.019$

Fig. 2

Position of $L_{1}^{z}$ and $L_{2}^{z}$ in the $(x\mbox{--}z)$ plane as a function of $q_{2}$ in the interval $[1, 0.26]$, for $q_{1} = -0.01$, $\mu= 0.019$

Fig. 3

Position of $L_{1}^{z}$ and $L_{2}^{z}$ in the $(x\mbox{--}z)$ plane as a function of $q_{2}$ in the interval $[1, 0.03]$, for $q_{1} = -0.001$, $\mu= 0.019$

4 Zero-velocity curves in the $(x, z)$ plane

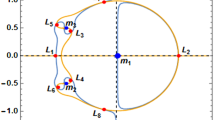
The usefulness of the Jacobi constant integral in clarifying certain general properties of the relative motion of a small body by the construction and investigation of zero velocity curves in every problem of celestial dynamics was pointed out by many investigators in the past. In this section we present the contours of the surface (3) on the $(x,z)$ plane, for zero velocity, which provide the zero velocity curves. In Fig. 4 we plot these zero velocity curves for $\mu= 0.019$, $q_{1} = - 0.01$ and for various values of the Jacobi constant $C$. The green curves corresponds to the Jacobi constant value $C$ of the out of plane equilibrium point $L_{1}^{z}$ and $L_{2}^{z}$. Large (black) dots indicate the primary bodies, while the small ones are the out of plane equilibrium points of the problem. We note here that between center of the dominant primary $P_{1}$ and its companion out of plane equilibrium points, the zero velocity curves form small rhombus of regions not allowed to motion.

Fig. 4

Zero velocity curves in the $(x,z)$ plane for $\mu= 0.019$, $q_{1} = - 0.01$ and for various values of the Jacobi constant $C$

5 Linear stability of out-of-plane equilibrium points

In order to study the linear stability of the out of plane equilibrium point $(x_{0}, 0, z_{0})$ we displace the infinitesimal body to the point ($x_{0}+\xi,\eta,z_{0} + \zeta$) where $\xi \eta,\zeta$, are the corresponding perturbations along the axes $Ox$, $Oy$ and $Oz$. So we linearize the system (1) to obtain the variational equations of motion as

$$\begin{aligned} &{\ddot{\xi} - 2\dot{\eta} = \xi\bigl(\varOmega^{\mathrm{o}}_{xx} \bigr) +\eta\bigl(\varOmega^{\mathrm{o}}_{xy}\bigr) +\zeta\bigl( \varOmega^{\mathrm{o}}_{xz}\bigr) } \\ &{\ddot{\eta} + 2\dot{\xi} = \xi\bigl(\varOmega^{\mathrm{o}}_{yx} \bigr) +\eta \bigl(\varOmega^{\mathrm{o}}_{yy}\bigr) +\zeta\bigl( \varOmega^{\mathrm{o}}_{yz}\bigr) } \\ &{\ddot{\zeta} = \xi\bigl(\varOmega^{\mathrm{o}}_{zx}\bigr) + \eta\bigl(\varOmega^{\mathrm{o}}_{zy}\bigr) +\zeta\bigl( \varOmega^{\mathrm{o}}_{zz}\bigr) } \end{aligned}$$

(12)

where the superscript ‘o’ indicates that the partial derivatives are to be evaluated at out of plane points $(x_{0},0,z_{0})$

Explicitly, the partial derivatives of system (12) are

$$\begin{aligned} &{\varOmega^{\mathrm{o}}_{xy} = \varOmega^{\mathrm{o}}_{yx} = \varOmega^{\mathrm{o}}_{yz} = \varOmega^{\mathrm{o}}_{zy} =0,} \\ &{\begin{aligned}[b] \varOmega^{\mathrm{o}}_{xx}&=1- \frac{q_{1}(1 - 2\mu)}{r{}_{10}^{3}}\biggl[1 - \frac{3(x_{0} + \sqrt{3} \mu)^{2}}{r{}_{10}^{2}}\biggr] \\ &\quad {} - \frac{2q_{2}\mu}{ r{}_{20}^{3}}\biggl[1 - \frac{3(x_{0} - \frac{\sqrt{3}}{2}(1 - 2\mu ))^{2}}{r{}_{20}^{2}}\biggr]\end{aligned}} \\ &{\begin{aligned}[b] \varOmega^{\mathrm{o}}zx &= \varOmega^{\mathrm{o}}xz = 3z_{0}\biggl[\frac {q_{1}(1 - 2\mu)(x_{0} + \sqrt{3} \mu)}{r{}_{10}^{5}} \\ &\quad{} + \frac{2q_{2}\mu(x_{0} - \frac{\sqrt{3}}{2}(1 - 2\mu))}{r{}_{20}^{5}}\biggr]\end{aligned}} \\ &{\varOmega^{\mathrm{o}}yy = 1 - \frac{q_{1}(1 - 2\mu)}{r{}_{10}^{3}} + \frac{2\mu q_{2}}{r_{20}^{5}} \biggl[\frac{3}{4} - r_{20}^{2}\biggr]} \\ &{\varOmega^{\mathrm{o}}zz = \frac{(1 - 2\mu )q_{1}}{r_{10}^{3}}\biggl[\frac{3z{}_{0}^{2}}{r{}_{10}^{2}} - 1\biggr] + \frac{2\mu q_{2}}{r{}_{20}^{3}}\biggl[\frac{3z{}_{0}^{2}}{r{}_{20}^{2}} - 1\biggr]} \end{aligned}$$

with

$$\begin{aligned} &{r{}_{10}^{2} = (x_{0} + \sqrt{3} \mu)^{2} + z{}_{0}^{2}} \\ &{r{}_{20}^{2} = r_{30}^{2} = \biggl(x_{0} - \frac{\sqrt{3}}{2}(1 - 2\mu )\biggr)^{2} + \frac{1}{4} + z{}_{0}^{2},\qquad q_{2} = q_{3}} \end{aligned}$$

The characteristic equation corresponding to system (12) is

$$ \lambda^{6} + a\lambda^{4} + b \lambda^{2} + c = 0 $$

(13)

with

$$\begin{aligned} &{a = 4 - \varOmega^{\mathrm{o}}xx - \varOmega^{\mathrm{o}}yy - \varOmega^{\mathrm{o}}zz} \\ &{\begin{aligned}[b]b &= \varOmega^{\mathrm{o}}xx\varOmega^{\mathrm{o}}yy + \varOmega^{\mathrm{o}}yy\varOmega^{\mathrm{o}}zz + \varOmega^{\mathrm{o}}zz \varOmega^{0}xx \\ &\quad{} - 4\varOmega^{\mathrm{o}}zz - \bigl(\varOmega^{\mathrm{o}}xz \bigr)^{2}\end{aligned}} \\ &{c = \bigl(\varOmega^{\mathrm{o}}xz\bigr)^{2} \varOmega^{\mathrm{o}}yy - \varOmega^{\mathrm{o}}xx\varOmega^{\mathrm{o}}yy \varOmega^{\mathrm{o}}zz} \end{aligned}$$

which is a polynomial of sixth degree in $\lambda$.

The eigenvalues of the characteristic Eq. (13) determine the stability or instability of the respective equilibrium points. An equilibrium point will be stable if the characteristic equation has six imaginary roots or complex roots with non-positive real parts.

We have computed the characteristic roots $\lambda_{i}$, $i = 1,2,\ldots,6$ as the radiation parameters varies in the interval $0 < q_{2} \le1$, $- 1 \le q_{1} \le0$ with an arbitrary small step and found no case in which all the roots are all imaginary. This lead to the instability of the out of plane points.

6 Discussion and conclusion

In this paper we study the location and the stability of the out of plane equilibrium points for particles moving in the vicinity of three massive bodies which emit light radiation formulated on the basis of Lagrangian configuration. As it is known, such points do not appear if only the gravitational forces are considered. There are two out of plane equilibrium points that lie in the $(x,z)$ plane in symmetrical positions with respect to the $(x,y)$ plane. We found that as the radiation parameters increases, the positions of out of plane equilibrium points are significantly affected. The effects of the parameters involved on the positions of the out of plane points are shown graphically (Figs. 1, 2 and 3). The existence of these points is of particular astronomical interest in connection with planetary system formation, satellite motion, etc. Radiation parameters is also seen to have significant effects on the topology of the zero velocity curves in the $(x,z)$ plane (Fig. 4). In particular, between the center of the dominant primary body and its companion out of plane equilibrium points, the zero velocity curves form small rhombus of regions not allowed to motion. Finally, the stability of these points has been achieved numerically by determining the roots of the characteristic equation. The numerical investigation of these roots shows no case in which the roots are all imaginary. Consequently, the motion is unbounded, and thus unstable, which agree with Papadouris and Papadakis (2013) when only the dominant primary body is a radiation source.