1 Introduction

Over the years, it is under the discussion that universe is facing an accelerated cosmic expansion. According to most of the observations, it is due to the exotic energy component, known as dark energy (DE) (Perlmutter et al. 1997, 1998, 1999), but the nature and behavior of DE is anonymous. Currently, there are two main ways for the discussion of this accelerated expansion. One way is to introduced scalar fields models in Einstein gravity like phantom (Caldwell 2002; Nojiri and Odintsov 2003), quintessence (Sahni and Starobinsky 2000; Sahni 2004; Padmanabhan 2008) and anisotropic fluids (Akarsu and Kilinc 2010; Sharif and Zubair 2010), etc. An alternative way is modifications of Einstein Hilbert action to obtain alternate theories of gravity like \(f(R)\) gravity (Starobinsky 1980), \(f(\tau)\) (where \(\tau\) being the torsion scalar) gravity (Ferraro and Fiorini 2007; Bengochea and Ferraro 2009; Zubair 2015, 2016) and Gauss-Bonnet gravity (Carroll et al. 2005; Cognola 2006), etc. DE is linked with the modification of Einstein gravity in such a way that it would give an alternative way to describe its nature.

Recently, Harko et al. (2011) introduced \(f(R,T)\) gravity by defining a function of \(R\) and \(T\) in Einstein Lagrangian. The action for this theory is described by

$$ \mathcal{I}=\frac{1}{2\kappa^{2}} \int{f(R,T)\sqrt{-g}dx^{4}}+ \int\mathcal{L}_{m} \sqrt{-g}dx^{4}, $$
(1)

in above equation, \(\mathcal{L}_{m}\) is matter lagrangian and \(\kappa^{2}=8\pi G\). The matter energy momentum tensor can be stated as (Land and Lifshitz 2002)

$$ T_{\alpha\beta}=-\frac{2}{\sqrt{-g}}\frac{\delta(\sqrt{-g} {\mathcal{\mathcal{L}}_{m}})}{\delta{g^{\alpha\beta}}}. $$
(2)

Harko et al. (2011) formulated the modified dynamical equations in metric formalism for different choices of the Lagrangian. The motion of massive test particles is found to be non-geodesic leading to the presence of extra force. This version of modified theories has gained significant importance and various issues have been presented in literature (Houndjo et al. 2012; Jamil et al. 2012; Alvarenga et al. 2013; Chakraborty 2013; Zubair and Noureen 2015; Noureen et al. 2015). Houndjo and Piattella (2012) considered \(f(R,T)\) theories of gravity and numerically reconstructed the \(f(R,T)\) function which can reproduce the standard transition era from matter dominated phase to the acceleration phase. In Houndjo and Piattella (2012) presented the cosmic evolution in the presence of dark matter and holographic DE. The chaplygin gas \(f(R,T)\) models are also explored in Houndjo et al. (2012) and Jamil et al. (2012) and it is shown that dust fluid can reproduce \(\varLambda\)CDM, Einstein static cosmos and phantom cosmology. Alvarenga et al. (2013) studied the scalar cosmological perturbations in the metric formalism in the context of \(f(R,T)\) gravity and set an explicit model in these theories to guarantee the standard continuity equation.

Chakraborty (2013) obtained particular \(f(R,T)\) functions by taking the conservation of stress-energy tensor for homogeneous and isotropic cosmic model. Reddy et al. (2012) used \(f(R,T)=R+2f(T)\) model in the presence of perfect fluid to develop a viable cosmological model and studied some physical features for Bianchi III model. Ahmad and Pradhan (2014) used the similar model for perfect fluid and found cosmological solutions for Bianchi type \(V\) spacetime. Shamir et al. (2015) found exact solutions of LRS Bianchi type \(I\) in the context of \(f(R,T)\) gravity using the proportionality relation between expansion and shear scalars. Sharif and Zubair (2013, 2012, 2014) discussed cosmic evolution of LRS Bianchi I model in the background of \(f(R,T)=f(R)+\lambda T\), by exploring the null energy condition (NEC) and \(\omega_{DE}\). The exact solution were obtained in two different scenarios; employing the anisotropic feature of model and assuming a particular from of function \(f(R)\). Moreover, the behavior of dynamical parameters was also presented for exponential and power law expansion cases. The objective of this paper is to find more consistent \(f(R,T)\) model which counts the current cosmic era. We will solve modified field equations with the help of anisotropic nature of spacetime and discuss some dynamical features for generic model which represents the Bianchi type I, III and Kantowski-Sachs space-times. This paper has following sequence. In Sect. 2, we develop the field equations and find their solutions as well as some physical parameters. Section 3 relates to the discussion of some important cases. Finally, Sect. 4, comprises of concluding remarks.

2 \(f(R,T)\) gravity

The field equations corresponding to action (1) are

$$\begin{aligned} &\kappa^{2}T_{\alpha\beta}-f_{T}(R,T)T_{\alpha\beta}-f_{T}(R,T) \varTheta_{\alpha\beta} \\ &\quad{}-R_{\alpha\beta}f_{R}(R,T)+ \frac{1}{2}g_{\alpha\beta}f(R,T) \\ &\quad{}+({\nabla}_{\alpha}{\nabla}_{\beta}-g_{\alpha\beta}{ \Box})f_{R} (R,T)=0, \end{aligned}$$
(3)

where \(f_{R}=\frac{df}{dR}\), \(f_{T}=\frac{df}{dT}\) and \({\Box}=\nabla_{\alpha}\nabla^{\alpha}\), \(\nabla_{\alpha}\) represents the covariant derivative and \(\varTheta_{\mu\nu}\) is represented by

$$\begin{aligned} \varTheta_{{\mu}{\nu}} =&\frac{g^{\alpha{\beta}}{\delta}T_{{\alpha}{\beta}}}{ {\delta}g^{\mu{\nu}}} \\ =&-2T_{{\mu}{\nu}}+g_{\mu\nu} \mathcal{L}_{m} -2g^{\alpha\beta}\frac{\partial^{2}\mathcal{L}_{m}}{{\partial} g^{\mu\nu}{\partial}g^{\alpha\beta}}. \end{aligned}$$
(4)

We can represent trace of Eq. (3) as

$$\begin{aligned} \kappa^{2}T-f_{T}(R,T)T-f_{T}(R,T) \varTheta-Rf_{R}(R,T) \\ \quad{}-2f(R,T) + 3{\Box}f_{R}(R,T)=0, \end{aligned}$$
(5)

where \(\varTheta=\varTheta_{\alpha}^{\alpha}\). From Eqs. (3) and (5), we get

$$\begin{aligned} &\kappa^{2}\biggl(T_{\alpha\beta}-\frac{1}{4}Tg_{\alpha\beta} \biggr)-f_{T}(R,T) \biggl(T_{\alpha\beta}-\frac{1}{4}Tg_{\alpha\beta} \biggr) \\ &\quad{}-f_{T}(R,T) \biggl(\varTheta_{\alpha\beta}- \frac{1}{4}{ \varTheta}g_{\alpha\beta}\biggr) \\ &\quad{}-\biggl(R_{\alpha\beta}-\frac{1}{4}Rg_{\alpha\beta} \biggr)f_{R}(R,T) \\ &\quad{}-\biggl(\frac{1}{4}g_{\alpha\beta}{\Box}-{ \nabla}_{\alpha}{\nabla}_{\beta}\biggr)f_{R}(R,T)=0. \end{aligned}$$
(6)

The energy momentum tensor for perfect fluid is defined as

$$T_{\alpha\beta}=({\rho}+p)u_{\alpha}u_{\beta}-pg_{\alpha\beta}, $$

where \(p\) and \(\rho\) indicate the pressure and energy density respectively. For matter configuration equation of state (EoS) is defined as \(\omega=p/\rho\) which determines different eras depending on its values. \(\omega=-1\) denotes the \(\varLambda\)CDM model, \(\omega>-1\) represents quintessence phase and phantom phase is represented by \(\omega<-1\). We have two alternatives for \(L_{m}\) to be selected for perfect fluid either \(L_{m}=-p\) or \(L_{m}=\rho\) which have been studied in the literature (Sotiriou and Faraoni 2008; Bertolami et al. 2007; Bisabr 2013). In our case, we choose \(L_{m}=-p\) which helps to find \(\varTheta_{\alpha\beta}\) of the form

$$ \varTheta_{\alpha\beta}=-2T_{\alpha\beta}-pg_{\alpha\beta}. $$
(7)

So, the field equations become

$$\begin{aligned} &\kappa^{2}\biggl(T_{\alpha\beta}-\frac{1}{4}Tg_{\alpha\beta} \biggr)+f_{T}(R,T) (T_{\alpha\beta}+pg_{\alpha\beta}) \\ &\quad{}-\frac{1}{4}f_{T}(R,T) (\rho+p)g_{\alpha\beta} -\biggl(R_{\alpha\beta}-\frac{1}{4}Rg_{\alpha\beta} \biggr)f_{R}(R,T) \\ &\quad{}- \biggl(\frac{1}{4}g_{\alpha\beta}{\Box}-{ \nabla}_{\alpha}{\nabla}_{\beta}\biggr) f_{R}(R,T)=0. \end{aligned}$$
(8)

If one takes \(f_{T}=0\), in above equation, then field equations convert to that in \(f(R)\) gravity. In this work, we choose the following \(f(R,T)\) model (Harko et al. 2011)

$$ f(R,T)=f(R)+\lambda{T}, $$
(9)

where \(\lambda\) being the coupling parameter. The general model representing Bianchi type I, III and Kantowski-Sachs spacetimes can be defined as

$$\begin{aligned} ds^{2} =&dt^{2}-A^{2}(t)dr^{2}-B^{2}(t)d \theta^{2} \\ &{}-B^{2}(t)K^{2}(\theta)d\phi^{2}, \end{aligned}$$
(10)

where \(k(\theta)\) is the function of \(\theta\), \(A(t)\) and \(B(t)\) represent the scale factors dependent on cosmic time. For metric (10), we get the field equations as follows

$$\begin{aligned} & \biggl(\frac{\ddot{A}}{A}+2\frac{\ddot{B}}{B}- \frac{\dot{A}\dot{B}}{AB} -\frac{\dot{B}^{2}}{B^{2}}+\frac{K''(\theta)}{{B^{2}K(\theta)}} \biggr)F \\ &\qquad{}-\frac{1}{2} \biggl(\frac{\dot{A}}{A} +2\frac{\dot{B}}{B} \biggr) \frac{d}{dt}F+\frac{3}{2}\frac{d^{2}}{dt^{2}}{F} \\ &\quad{}=-\frac{3}{2}\bigl(\kappa^{2}+\lambda\bigr) (\rho+p), \end{aligned}$$
(11)
$$\begin{aligned} & \biggl(\frac{\ddot{A}}{A}-2\frac{\ddot{B}}{B}+2 \frac{\dot{A}\dot{B}}{AB} -\frac{\dot{B}^{2}}{B^{2}}+\frac{K''(\theta)}{{B^{2}K(\theta)}} \biggr)F \\ &\qquad{}- \biggl( \frac{\dot{B}}{B} \biggr)\frac{d}{dt}F-\frac{1}{2}\frac{d^{2}}{dt^{2}}F \\ &\quad{}=\frac{1}{2}\bigl(\kappa^{2}+\lambda\bigr) (\rho+p), \end{aligned}$$
(12)
$$\begin{aligned} & \biggl(\frac{\dot{B}^{2}}{B^{2}}-\frac{\ddot{A}}{A}-\frac{K''(\theta)}{ {B^{2}K(\theta)}} \biggr)F-\frac{1}{2} \biggl(\frac{\dot{A}}{A}+ \frac{\dot{B}}{B} \biggr) \frac{d}{dt}F -\frac{1}{2}\frac{d^{2}}{dt^{2}}F \\ &\qquad{}=\frac{1}{2} \bigl(\kappa^{2}+\lambda\bigr) (\rho+p), \end{aligned}$$
(13)

where \(F(R)=f_{R}(R)\), \(R=-2 (\frac{\ddot{A}}{A}+2\frac{\ddot{B}}{B}+2\frac{\dot{A}\dot{B}}{AB} +\frac{\dot{B}^{2}}{B^{2}}-\frac{K''(\theta)}{{B^{2}K(\theta)}} )\) and dot is the time derivative.

Now we identify some quantities including volume \(V\), expansion scalar \(\varTheta\) and shear scalar \(\sigma\)

$$\begin{aligned} &V=a^{3}=AB^{2}, \qquad \theta=u_{;a}^{a}=\frac{\dot{A}}{A}+2\frac{\dot{B}}{B}, \\ &\sigma^{2}=\frac{1}{2}\sigma_{ab}\sigma^{ab}=\frac{1}{3} \biggl(\frac{\dot{A}}{A}- \frac{\dot{B}}{B} \biggr)^{2}. \end{aligned}$$

The anisotropy parameter of expansion, mean Hubble parameters and deceleration parameter q are given by

$$ \begin{aligned} &\Delta=\frac{2}{9} \biggl(\frac{H_{x}-H_{y}}{H} \biggr)^{2},\\ &H=(\ln \dot{a})=\frac{1}{3} \biggl( \frac{\dot{A}}{A}+2\frac{\dot{B}}{B} \biggr),\\ &q=\frac{d}{dt} \biggl(\frac{1}{H} \biggr)-1, \end{aligned} $$
(14)

where \(H_{x}=\frac{\dot{A}}{A}\) and \(H_{y}=\frac{\dot{B}}{B}\).

Now subtracting Eqs. (12) and (13), we find

$$\begin{aligned} &\biggl(\frac{\ddot{A}}{A}+\frac{\dot{A}\dot{B}}{AB}-\frac{\ddot{B}}{B}- \frac{\dot{B^{2}}}{B^{2}} +\frac{K''(\theta)}{B^{2}K(\theta)} \biggr)F \\ &\quad{}+ \biggl(\frac{\dot{A}}{A} - \frac{\dot{B}}{B} \biggr)\frac{d}{dt}F=0. \end{aligned}$$
(15)

For the solution of above equation, we utilize a physical form that expansion scalar is proportional to shear scalar (Sharif and Zubair 2012, 2014; Roy et al. 1985; Adhav et al. 2007; Reddy and Kumar 2013). Thorne (1967) found that the velocity redshift relation for extragalactic sources imply the isotropic nature of cosmos within the 30 % range approximately i.e., \(\frac{\sigma}{H}\leq 0.30\) (Kantowski and Sachs 1966). Collins (1977) studied physical importance of this form for perfect fluid and barotropic EoS in a more general case. This condition results in following relation

$$ A=B^{\alpha}, \quad \alpha\neq1, \ \alpha>0. $$
(16)

By using the above condition and simplifying, we find

$$ \frac{\ddot{B}}{B}+\frac{\dot{B}\dot{F}}{BF}+(\alpha+1) \frac{\dot{B}^{2}}{B^{2}}- (\alpha-1)\frac{K''(\theta)}{B^{2}K(\theta)}=0. $$
(17)

To solve the above equation, we assume a relation between \(F\) and \(a\) as the \(F\varpropto a^{\beta}\) (Sharif and Shamir 2009, 2010; Sharif and Zubair 2013, 2014),

$$ F=la^{\beta}, $$
(18)

where \(\beta\) can be any scalar and \(l\) determines the proportionality sign.

$$ {\ddot{B}}+\bigl(1+\alpha+\beta(\alpha+2)\bigr)\frac{\dot{B}^{2}}{B}- \frac{(\alpha-1)K''(\theta)}{ BK(\theta)}=0. $$
(19)

Substituting \(\dot{B}=f(B)\), it becomes

$$ \frac{df^{2}}{dB}+\bigl(1+\alpha+\beta(\alpha+2)\bigr) \frac{f^{2}}{B}=\frac{(\alpha-1)K''(\theta)}{Bk(\theta)}, $$
(20)

whose solution is

$$\begin{aligned} f^{2} = \biggl(\frac{dB}{dt} \biggr)^{2} =& \frac{(\alpha-1)k''(\theta)}{(1+\alpha+\beta(\alpha+2))K(\theta)} \\ &{}+ \frac{C}{B^{(1+\alpha+\beta(\alpha+2))}}, \end{aligned}$$
(21)

where \(c\) represents constant of integration. So the space time Eq. (10) goes to be

$$\begin{aligned} ds^{2} =& \biggl(\frac{dt}{dB} \biggr)^{2}~dB^{2}-B^{2\alpha}(t)dr^{2}-B^{2}(t)d \theta^{2} \\ &{}- B^{2}(t)K^{2}(\theta)d\phi^{2} \\ =&\frac{dT^{2}}{\frac{(\alpha-1) k''(\theta)}{(1+\alpha+\beta(\alpha+2))k(\theta)} +\frac{C}{T^{(1+\alpha+\beta(\alpha+2))}}} \\ &{}-T^{2\alpha}dr^{2}-T^{2}d \theta^{2} -T^{2}k^{2}(\theta)d\phi^{2}, \end{aligned}$$
(22)

where \(B=T\). We describe physical features of model (22). The directional Hubble parameter and mean Hubble parameter takes the form

$$\begin{aligned} \begin{aligned} &H_{x}=\alpha H{y}=\alpha \biggl[\frac{(\alpha-1)k''(\theta)}{T^{2}(1+\alpha+\beta(\alpha+2))k(\theta)}\\ &\phantom{H_{x}=\alpha H{y}=}+ \frac{c}{T^{3+\alpha+\beta(\alpha+2)}} \biggr]^{\frac{1}{2}}, \\ &H=\frac{\alpha+2}{3} \biggl[\frac{(\alpha-1)k''(\theta)}{T^{2}(1+\alpha+\beta(\alpha+2))k(\theta)}\\ &\phantom{H=}+\frac{c}{T^{3+\alpha+\beta(\alpha+2)}} \biggr]^{\frac{1}{2}}. \end{aligned} \end{aligned}$$
(23)

It can be seen that these quantities appear to be dynamical and approach to zero as \(T\rightarrow\infty\) subject to the condition that \(3+\alpha+\beta(\alpha+2)>0\), which can satisfied only if \(\beta\geq-1\) with \(\alpha>1\). Moreover, for earlier times these parameters take infinitely large values for \(3+\alpha+\beta(\alpha+2)>0\). In present discussion we find similar results for volume and anisotropy parameter as shown in Sharif and Zubair (2012, 2014).

The deceleration parameter, shear scalar and expansion scalar are set to be

$$\begin{aligned} &q=\partial_{t} \biggl(\frac{1}{\frac{\alpha+2}{3}[{\frac{(\alpha-1)k''(\theta)}{T^{2}(1+\alpha+\beta(\alpha+2))k(\theta)} +\frac{c}{T^{3+\alpha+\beta(\alpha+2)}}}]^{\frac{1}{2}}} \biggr)-1, \end{aligned}$$
(24)
$$\begin{aligned} &\theta=3H=(\alpha+2) \biggl[\frac{(\alpha-1)k''(\theta)}{T^{2}(1+\alpha+\beta(\alpha+2))k(\theta)} \\ &\phantom{\theta=3H=}+ \frac{c}{T^{3+\alpha+\beta(\alpha+2)}}\biggr]^{\frac{1}{2}}, \end{aligned}$$
(25)
$$\begin{aligned} &\sigma=\frac{(\alpha-1)^{2}}{3} \biggl[\frac{(\alpha-1)k''(\theta)}{T^{2}(1+\alpha+\beta(\alpha+2))k(\theta)} \\ &\phantom{\sigma=}+ \frac{c}{T^{3+\alpha+\beta(\alpha+2)}} \biggr]. \end{aligned}$$
(26)

We present the evolution of \(q\) for subcases in next section and evolution of \(\theta\) and \(\sigma\) is very similar to that for the Hubble parameter \(H\). Using Eq. (21) in field equations (11)–(13), we find the following relations for null energy condition (NEC) and energy density \(\rho\)

$$\begin{aligned} &\rho+p= \bigl[T^{-3-\alpha}lk(\theta) \bigl(1+ \alpha+k(\theta)\beta(2+\alpha)\bigr) \\ &\phantom{\rho+p=}\times \bigl(2T^{1+\alpha+\beta(2+\alpha)}\bigl(2\beta+ (2+\beta)\alpha\bigr) \\ &\phantom{\rho+p=}+c\bigl(2+\alpha\bigl(2-2\alpha+\beta(2+\alpha) \bigr)\bigr) \bigr)+ T^{1+\alpha+\beta(2+\alpha)} \\ &\phantom{\rho+p=}\times \bigl(-2(1+\alpha)+k(\theta) \bigl(-2+(-2+\alpha) \\ &\phantom{\rho+p=}\times \bigl(-2 \alpha^{2}+\beta(1+\alpha) (2+\alpha) \bigr) \bigr)\bigr) k''(\theta) \bigr] \\ &\phantom{\rho+p=}\times \bigl[k(\theta) \bigl(1+ \alpha+k(\theta)\beta(2+\alpha)\bigr) \bigl(\kappa^{2}+\lambda\bigr) \bigr]^{-1}, \end{aligned}$$
(27)
$$\begin{aligned} &\rho = \bigl[T^{-3-\alpha} l \bigl[k(\theta) \bigl(1+\alpha+k(\theta)\beta (2+\alpha) \bigr) \\ &\phantom{\rho =}\times\bigl[2 T^{1+\alpha+\beta (2+\alpha)}\bigl(2 \beta +(2+\beta) \alpha\bigr) \\ &\phantom{\rho =}+c \bigl(2+\alpha \bigl(2-2 \alpha+\beta (2+ \alpha)\bigr)\bigr) \bigr]+T^{1+\alpha+\beta (2+\alpha)} \\ &\phantom{\rho =} \times \bigl[k(\theta) \bigl[-2+(-2+\alpha) \bigl[\beta (1+\alpha) (2+ \alpha)-2 \alpha^{2} \bigr] \bigr] \\ &\phantom{\rho =}-2 (1+\alpha) \bigr] k''(\theta) \bigr] \bigr] \bigl[k(\theta) \bigl(1+ \alpha+k(\theta)\beta(2+\alpha)\bigr) \\ &\phantom{\rho =}\times\bigl(\kappa ^{2}+\lambda\bigr) (1+\omega ) \bigr]^{-1}. \end{aligned}$$
(28)

Putting the Eqs. (21) and (27) in Eq. (5) results in following function of \(f(R,T)\)

$$\begin{aligned} f(R,T) =&\frac{T^{(2+\alpha)\beta}l}{2} \biggl[R+\frac{1}{T^{3}} \biggl[3 \beta (2+\alpha) \\ &{}\times\biggl(-2 T+T^{-\alpha-\beta (2+\alpha)}c(1+\alpha) \\ &{}+ \frac{T (-1+\alpha^{2} ) k''(\theta)}{1+\alpha+k(\theta)\beta (2+\alpha)} \biggr) \biggr] \\ &{}- \bigl[ \bigl(T^{-3-\alpha-\beta (2+\alpha)}(1-3 \omega) \\ &{}\times \bigl(k(\theta) \bigl(1+\alpha +k(\theta)\beta(2+\alpha)\bigr) \\ &{}\times\bigl(2T^{1+\alpha+\beta(2+\alpha)} \bigl(2 \beta+(2+\beta)\alpha\bigr) \\ &{}+c\bigl(2+\alpha\bigl(2-2\alpha+\beta(2 +\alpha)\bigr)\bigr) \bigr) \\ &{}+T^{1+\alpha+ \beta(2+\alpha)} \bigl(-2(1+\alpha) \\ &{}+k(\theta) \bigl(-2+(-2+\alpha) \\ &{}\times \bigl(-2\alpha^{2} + \beta(1+\alpha) (2+\alpha) \bigr) \bigr) \bigr)k''( \theta) \bigr) \bigr) \\ &{}/\bigl(k(\theta) \bigl(1+\alpha+k(\theta)\beta(2+\alpha)\bigr) (1+\omega)\bigr) \bigr] \\ &+ \bigl[ \bigl(2T^{-3-\alpha-\beta(2+\alpha)}\lambda(-1+\omega) \\ &{}\times\bigl(k(\theta) \bigl(1+\alpha+k(\theta)\beta(2+\alpha)\bigr) \\ &{}\times \bigl(2T^{1+\alpha +\beta(2+\alpha)} \bigl(2\beta(2+\beta)\alpha\bigr) \\ &{}+c\bigl(2+\alpha\bigl(2-2\alpha+ \beta(2+\alpha)\bigr)\bigr) \bigr) \\ &{}+T^{1+\alpha+\beta(2+\alpha)} \bigl(-2(1+\alpha) +k(\theta) \\ &{}\times \bigl(-2+(-2+\alpha) \bigl(-2\alpha^{2}+\beta(1+ \alpha) \\ &{}\times(2+\alpha) \bigr) \bigr) \bigr)k''(\theta) \bigr) \bigr) \\ &{}/ \bigl(k(\theta) \bigl(1+\alpha +k(\theta)\beta(2+\alpha)\bigr) \\ &{}\times\bigl(\kappa^{2}+ \lambda \bigr) (1+\omega ) \bigr) \bigr] \biggr]. \end{aligned}$$
(29)

3 Some important cases

Now we discuss some particular cases depending on \(k(\theta)\).

  • LRS Bianchi type-I Model

For \(k(\theta)=\theta\), we get LRS Bianchi type-I model, which reduces to flat FRW spacetime if \(A(t)=B(t)=a(t)\). This spacetime has one transverse direction \(x\) and two equivalent longitudinal directions \(y\) and \(z\).

We can define the relations of NEC and \(\rho\) for this model as

$$\begin{aligned} &\rho+p= \bigl[T^{-3-\alpha}l \bigl[ \bigl(T^{1+\alpha+\beta (2+\alpha)}(1+\alpha) \bigl(2\alpha+\beta(2+\alpha)\bigr) \\ &\phantom{\rho+p=}+c\bigl(2+ \alpha\bigl(2 -2\alpha+\beta(2+\alpha)\bigr)\bigr) \bigr) \bigr] \bigr] \\ &\phantom{\rho+p=}\times \bigl[ \kappa^{2}+\lambda \bigr]^{-1}, \end{aligned}$$
(30)
$$\begin{aligned} &\rho= \bigl[T^{-3-\alpha} l \bigl(T^{1+\alpha+\beta (2+\alpha)}(1+ \alpha) \bigl(2 \alpha+\beta (2+\alpha)\bigr) \\ &\phantom{\rho=}+c \bigl(2+\alpha \bigl(2-2 \alpha+\beta (2+\alpha)\bigr)\bigr) \bigr) \bigr] \\ &\phantom{\rho=}\times\bigl[ \bigl(\kappa ^{2}+\lambda \bigr) (1+\omega ) \bigr]^{-1}. \end{aligned}$$
(31)

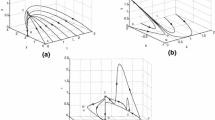
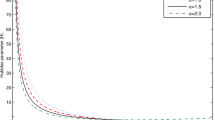
In Figs. 1 and 2, we present the evolution of NEC and \(\rho\) for LRS Bianchi I model. In our studies we focus on both positive and negative values of the coupling parameter \(\lambda\). One can see that NEC is satisfied so that is the energy density for the choice of parameters \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\) as shown in Fig. 1. The validity of NEC implies that EoS parameter \(\omega>-1\) (the quintessence model). If \(c>0\), then \(\rho+p<0\) so that NEC is violated, \(\omega<-1\) representing phantom era of DE as shown in Fig. 2. Hence the evolution of cosmological parameters is consistent with the current observational data (Perlmutter et al. 1999; Ade et al. 2013).

Fig. 1
figure 1

Behavior of NEC (left plot) and \(\rho\) (right plot) for LRS Bianchi I model versus \(T\) and \(\lambda\). Herein, we set \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\)

Full size image
Fig. 2
figure 2

Behavior of NEC (left plot) and \(\rho\) (right plot) for LRS Bianchi I model versus \(T\) and \(\lambda\). We set \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\)

Full size image

The deceleration parameter for LRS Bianchi I model is given as

$$ q=\frac{5+6\beta+\alpha+3\beta\alpha}{4+2\alpha}. $$
(32)

Here, the value of \(q\) is independent of the choice of \(\alpha\) if \(\beta=-2\) and \(q<-1\) for this choice of parameters. \(q<-1\), is consistent with the above shown evolution of \(\rho+p\). It is a cumbersome task to find the explicit form of the function \(f(R,T)\), we present the plot of \(f(R,T)\) versus \(\lambda\) and \(T\) as shown in Fig. 3.

  • Bianchi type-III Model

When \(k(\theta)=\sin\theta\) then we get the Bianchi III model. This model also describes the homogeneous and anisotropic behavior of the universe. In literature (Shamir et al. 2015; Kiran and Reddy 2013; Chandel and Ram 2013), people have discussed the Bianchi type III in the background of \(f(R,T)\) gravity. Kiran and Reddy (2013) found that the bulk viscous string Bianchi type III model does not exist in \(f(R,T)\) gravity for the choice of \(f(R,T)=R+2f(T)\).

Fig. 3
figure 3

Plot of \(f(R,T)\) versus \(\lambda\) and \(T\)

Full size image

The expression of the NEC, energy density and deceleration parameter for Bianchi type III model can be expressed as

$$\begin{aligned} &\rho+p= \bigl[\bigl(1+\alpha+\beta(2+\alpha)\bigr) \bigl(\kappa^{2}+\lambda \bigr) \bigr]^{-1} \\ &\phantom{\rho+p=}\times \bigl[T^{-3-\alpha}lc\bigl(1+\alpha+\beta(2+\alpha)\bigr) \\ &\phantom{\rho+p=}\times\bigl(2+\alpha\bigl(2-2\alpha+\beta (2+\alpha)\bigr) \bigr) \\ &\phantom{\rho+p=}+T^{1+\alpha+\beta(2+\alpha)}(2\beta^{2}\alpha(2+\alpha)^{2} \\ &\phantom{\rho+p=}+2\bigl(2+\alpha+3\alpha^{3}\bigr) \\ &\phantom{\rho+p=}+\beta(2+\alpha) \bigl(2+\alpha(3+5\alpha) \bigr) \bigr], \end{aligned}$$
(33)
$$\begin{aligned} &\rho= \bigl[T^{-3-\alpha}l \bigl[c \bigl(1+\alpha+\beta (2+\alpha)\bigr) \\ &\phantom{\rho=}\times\bigl(2+\alpha\bigl(2-2\alpha+\beta(2+\alpha)\bigr)\bigr) \\ &\phantom{\rho=}+T^{1+\alpha+\beta (2+\alpha)} \bigl[2 \beta^{2} \alpha (2+ \alpha)^{2}+2 \bigl(2+\alpha+3 \alpha^{3} \bigr) \\ &\phantom{\rho=} +\beta (2+\alpha) \bigl(2+\alpha(3+5\alpha)\bigr) \bigr] \bigr] \bigr] \\ &\phantom{\rho=}\times\bigl[\bigl(1+\alpha+ \beta(2+\alpha)\bigr) \bigl(\kappa^{2}+\lambda \bigr) (1+\omega) \bigr]^{-1}, \end{aligned}$$
(34)
$$\begin{aligned} &q=-1-\frac{3}{2 T^{4} (2+\alpha)} \\ &\phantom{q=}\times\sqrt{T^{-1-\alpha-\beta (2+\alpha)} c+ \frac{1-\alpha}{1+\alpha+\beta (2+\alpha)}} \\ &\phantom{q=}\times \biggl(\frac{2 T (-1+\alpha)}{1+\alpha+\beta (2+\alpha)} \\ &\phantom{q=}-T^{-\alpha-\beta (2+\alpha)} c \bigl(3+\alpha+\beta (2+ \alpha)\bigr) \biggr) \\ &\phantom{q=}\times \biggl(T^{-3-\alpha-\beta (2+\alpha)} c \\ &\phantom{q=}+\frac{1-\alpha}{T^{2} (1+\alpha+\beta (2+\alpha))} \biggr)^{-3/2}. \end{aligned}$$
(35)

To explore the dynamics of Bianchi type III model, we first see the evolution of \(q\) which helps to constrain the parameters including \(\beta\) and \(c\). \(q\) is found to be imaginary if we set \(\beta<0\) and \(c<0\) with \(\alpha\gtrsim1\). Now \(-1< q<0\) if \(-0.7\leqslant \beta \leqslant-1.3\) and \(q<-1\) if \(\beta\geqslant -1.4\), later case appears to be more viable favoring the phantom model, we present its evolution in Fig. 4.

Fig. 4
figure 4

Plot of deceleration parameter for Bianchi type III model with \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\)

Full size image

Now we will see the behavior of the energy density and NEC for Bianchi III model. Here, we set \(c=2\) and \(\beta=-2\) according to the evolution of \(q\). Figure 5 shows the evolution of \(\rho\) and \(\rho+p\) versus \(\lambda\) and \(T\). Left plot shows that NEC is violated which implies the EoS parameter as \(\omega<-1\), also it depicts the picture of \(q\) in more convincingly way. Moreover, in this era of DE, we have \(\rho>0\) as shown in right plot of the Fig. 5. The plot of the function \(f(R,T)\) for this model is shown in Fig. 6.

  • Kantowski-Sachs Model

When \(k(\theta)=\sinh\theta\), we get Kantowski-Sachs model. Authors have explored the solutions of modified dynamical equation for this model in \(f(R,T)\) gravity (Samanta 2013; Reddy et al. 2014). Samanta (2013) discussed the \(H(z)\), luminosity distance and distance modulus \(\mu(z)\) for Kantowski-Sachs model in the background of particular function \(f(R,T)=R+\lambda T\). Using the similar \(f(R,T)\) function, Reddy et al. (2014) presented the dynamics of bulk viscous fluid and discussed some physical properties for Kantowski-Sachs model. Here, in our case \(\rho\) and \(\rho+p\) takes the following form.

$$\begin{aligned} &\rho+p= \bigl[T^{-3-\alpha}l\bigl(T^{1+\alpha+\beta(2+\alpha)} \bigl(-4+2\beta^{2}(2+\alpha)^{2} \\ &\phantom{\rho+p=}+\beta \alpha(2+\alpha) (5+ \alpha) \\ &\phantom{\rho+p=} -2\alpha\bigl(-1+(-4+\alpha)\alpha\bigr)\bigr)+c\bigl(1+\alpha+ \beta(2+\alpha)\bigr) \\ &\phantom{\rho+p=}\times \bigl(2+\alpha \bigl(2-2\alpha+\beta(2+\alpha)\bigr)\bigr) \bigr) \bigr] \\ &\phantom{\rho+p=}\times \bigl[1+\alpha+\beta(2+\alpha) \bigl(\kappa^{2}+\lambda\bigr) \bigr]^{-1}, \end{aligned}$$
(36)
$$\begin{aligned} & \rho= \bigl[T^{-3-\alpha}l \bigl[T^{1+\alpha+\beta (2+\alpha)} \bigl[-4+2 \beta^{2}(2+\alpha)^{2} \\ &\phantom{\rho=}+ \beta \alpha (2+\alpha) (5+\alpha) -2\alpha\bigl(-1+(-4+\alpha) \alpha\bigr) \bigr] \\ &\phantom{\rho=}+c\bigl(1+\alpha+\beta (2+\alpha)\bigr) \bigl(2+\alpha \bigl(2-2\alpha +\beta (2+\alpha)\bigr)\bigr) \bigr] \bigr] \\ &\phantom{\rho=}\times \bigl[\bigl(1+\alpha+\beta (2+ \alpha)\bigr) \bigl(\kappa ^{2}+\lambda \bigr) (1+\omega ) \bigr]^{-1} \end{aligned}$$
(37)

The relation of \(q\) for the above model is obtained of the form

$$\begin{aligned} q =&-1+\frac{3}{2 T^{4}(2+\alpha)} \\ &{}\times\sqrt{T^{-1-\alpha-\beta (2+\alpha)} c+ \frac{-1+\alpha}{ 1+\alpha+\beta (2+\alpha)}} \\ &{}\times \biggl(\frac{2 T (-1+\alpha)}{1+\alpha+\beta (2+\alpha)} \\ &{} +T^{-\alpha-\beta (2+\alpha)} c \bigl(3+\alpha+\beta (2+ \alpha)\bigr) \biggr) \\ &{}\times \biggl(T^{-3-\alpha-\beta (2+\alpha)} c \\ &{}+\frac{-1+\alpha}{T^{2} (1+\alpha+\beta (2+\alpha))} \biggr)^{-3/2} \end{aligned}$$
(38)
Fig. 5
figure 5

Behavior of NEC (left plot) and \(\rho\) (right plot) for Bianchi III model versus \(T\) and \(\lambda\). We set \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\)

Full size image
Fig. 6
figure 6

Evolution of \(f(R,T)\) for Bianchi III model

Full size image

Figure 7 shows the evolution of deceleration parameter versus \(\lambda\) and \(T\). In this case we find that for positive \(\beta\), \(q>0\) at earlier times. Here, we set \(T\geq1.1\), if \(\beta\geq54\), it results in \(-1< q<0\), however for phantom cosmic era, we need to set \(\beta\leq-1.4\). As in previous case, we are interested to discuss the phantom era in accordance with recent observations (Ade et al. 2013). For the evolution of NEC we set \(\beta=-2\), it found that NEC is violated which favors the evolution of \(q\) as shown in left plot of Fig. 8. Moreover, \(\rho>0\) for thick choice of parameters.

Fig. 7
figure 7

Plot of deceleration parameter for Kantowski-Sachs model with \(\alpha=1.1\), \(\beta=-2\) and \(c=2\)

Full size image
Fig. 8
figure 8

Behavior of NEC (left plot) and \(\rho\) (right plot) for Kantowski-Sachs model versus \(T\) and \(\lambda\). We set \(\alpha=1.1\), \(\beta=-2\), \(l=1\), \(c=2\) and \(\kappa=8\pi\)

Full size image

Figure 9, shows the evolution of \(f(R,T)\) for Kantowski-Sachs model.

Fig. 9
figure 9

Evolution of \(f(R,T)\) for Kantowski-Sachs model with \(\alpha=1.1\), \(\beta=-2\), \(l=1\) and \(c=2\)

Full size image

4 Conclusion

The \(f(R,T)\) theory can be regarded as a potential candidate in explaining the role of DE to accelerate the cosmic expansion. In such theory, cosmic acceleration may appear as an outcome of unified contribution from geometrical and matter components. A suitable form of Lagrangian which can explain the cosmic evolution in a definite way is still under consideration. People have studied various issues in \(f(R,T)\) gravity including the evolution of cosmic parameters for anisotropic cosmic models (Houndjo et al. 2012; Chakraborty 2013; Reddy et al. 2012; Ahmad and Pradhan 2014; Shamir et al. 2015; Sharif and Zubair 2012, 2013, 2014). In this study we have obtained the exact solutions of the modified field equations for the general model representing Bianchi type I, III and Kantowski-Sachs spacetimes. In literature people have discussed these anisotropic models for more specific case \(R+\lambda T\) (Kiran and Reddy 2013; Samanta 2013; Reddy et al. 2014). However, we have employed more general function \(f(R)+\lambda T\), which has already been discussed in Sharif and Shamir (2009, 2010), Sharif and Zubair (2013, 2014) for LRS Bianchi type \(I\) model.

In finding the solution we restrict the anisotropic nature of universe using the condition that expansion scalar is proportional to shear scalar, which results in power law relation between scale factors as \(A=B^{\alpha}\). Moreover, following Sharif and Shamir (2009, 2010), Sharif and Zubair (2013, 2014), we assume the relation between \(F\) and \(a\). We explain the evolutionary paradigm of Hubble parameters, expansion and shear scalars. The dynamical quantities of the model are explored in three different cases namely, Bianchi type I, Bianchi type III and Kantowski Sachs models. In this discussion we set the parameters as \(\alpha=1.1\), \(\beta=-2\), \(l=1\) and \(c=2\). For this choice we find that \(q<-1\), \(\rho+p<0\) with \(\rho>0\) in all the three cases, which indicates the phantom evolution of the universe in accordance with the recent observations (Perlmutter et al. 1999; Ade et al. 2013).