Global gravito-electrostatic fluctuations in self-gravitating spherical non-uniform charged dust clouds

Abstract

We formulate exact non-local linear analysis for identification and characterization of the global collective gravito-electrostatic eigenmodes, discrete oscillations and associated instabilities in interstellar charged dust molecular cloud (DMC) sphere with mass-radius above the stability critical values on the astrophysical fluid scales of space and time. The realistic relevant zeroth-order effects, hitherto remaining unaccounted for, are concurrently included. It avoids using any kind of the Jeansian swindles against usual viewpoint. Armed with the modified Fourier plane-wave method, the dispersion relations (eigenvalues) and amplitude-variations (eigenfunctions) of the relevant perturbations about the inhomogenous equilibrium are procedurally derived and analyzed together with numerical illustrations. It is seen that the entire cloud supports spectrally heterogeneous mixture of the Jeans (gravitational) and electrostatic (acoustic) modes, coupled via quasi-linear discrete oscillations of mixed pattern. The lowest-order non-rigid diffused cloud surface boundary (CSB), sourced by active gravito-electrostatic interplay, is the most unstable interfacial plasma layer. Three distinct and spatio-spectrally isolated classes of global eigenmodes—dispersive, non-dispersive and hybrid types—are keyed together with idiosyncratic prolific features. Dispersive features are prominent in the ultra-high $k$-regime (acoustic) with modified form due to self-gravitational condensation of the Jeans modes; whereas, non-dispersive characteristics in the ultra-low $k$-regime (gravitational) dominated by the Jeans waves; where, $k = 2\pi/ \lambda$ is the angular wave number of the fluctuations on the Jeans scale. We further demonstrate that the grain-charge (grain-mass) plays destabilizing (stabilizing) influential role for the electrostatic fluctuations, but stabilizing (destabilizing) role for the self-gravitational counterparts. The results can be useful to realize diverse complex global astrophysical matter stabilities, instability-caused energy-cascading processes and self-gravitational cloud collapse dynamics leading to star clusters and galactic associations.

1 Introduction

Application of conventional local stability theory in self-gravitating astrophysical plasmas is indeed inadequate and incorrect due to their non-uniform nature ensuing from the differential scale-heights of the gravitationally stratified constituent species in establishing gravito-thermal equilibrium. The existence of gravity-induced ambipolar electrostatic space-charge polarization effects in the plasmas with large-scale non-zero equilibrium electric field, in fact, needs inclusive attention (Bally and Harrison 1978; Vranjes and Tanaka 2005). An isolated isothermal gravitating dusty plasma gas or dust molecular cloud (DMC) in gravito-thermal equilibrium organizes itself in such a fashion that the heavier constituents (grains) preponderantly fill lower layers toward the central region, leaving the lighter species (electrons and ions) re-distributed in upper layers relative to the center. In the usual DMC conditions (Vranjes and Tanaka 2005) at plasma temperature $T~\mbox{eV}$, the grain-to-electron and grain-to-ion scale heights ($H_{s}$) may, with all the usual notations, be respectively compared as, $H_{d} / H_{e}\sim ( m_{d} / m_{i} ) ( T / T_{d} )\sim 10^{13} \gg 1$ and $H_{d} / H_{i}\sim ( m_{d} / m_{i} ) ( T / T_{d} )\sim10^{9} \gg 1$. For a few km of scale-heights of the electrons and ions, the dust density scale-height may go a few parsecs. It clearly indicates that a large-scale non-zero electrostatic potential is evolved in association with the gravity-induced stratification effects. As a consequence, astrophysical plasmas are indeed inhomogeneous and non-uniform in nature containing free energy sources stored in their equilibrium inhomogeneities themselves. The free energies naturally tend to relax into lower energy states via instabilities or diffusive fluctuations. This implies that gravity-induced ambipolar electrostatic space-charge polarization effects in the plasmas with large-scale non-zero equilibrium electric field giving large-scale plasma flow dynamics on the zeroth-order must be considered in their instability analyses. This entails, at least in principle, that the existence of the gravity-induced non-zero zeroth-order electric field acting as an active source for the inhomogeneities requires non-local analyses in astrophysical environments. It may be noted that the global (non-local) collective plasma wave fluctuations in the complex astrophysical grainy cloud environments with the unipolar gravitationally-induced bipolar electrostatic polarization effects needed for maintaining the cloud equilibria taken into account has hitherto not been realized completely amid the non-uniform equilibrium.

It may furthermore be pertinent to mention that contemplates of collective waves, oscillations and associated instabilities in ionized self-gravitating dusty plasmas (viz. DMCs, protostellar disks, interstellar and circumstellar clouds, cores, and so on) are very essential due to their important role in the formation process of stars, planets and other galactic elements (Verheest 1996, 2000; Shukla and Mamun 2000; Mamun and Shukla 2001; Spitzer 2004). The presence of inertially massive and electrically charged dust particulates makes it more interesting to empathize the nascence mechanism of bounded astrophysical objects.

The interstellar dust mostly consists of Silicates $((\mathrm{SiO}_{4})^{4-})$, Graphite (C), Amorphous Carbon (aC), Polycyclic Aromatic Hydrocarbon (PAH) molecules, Silicon Carbide (SiC), Magnesium Sulfide (MgS), Icy grain mantles composed of simple molecules (e.g., $\mathrm{H}_{2}\mathrm{O}$, NH₃, CH₃OH and CO), and organic refractory grain mantles rich in carbon and oxygen (Tielens and Allamandola 1987; Hoyle and Wickramasinghe 1991; Spitzer 2004). The grain morphologies are usually non-uniform in composition (Tielens and Allamandola 1987; Hoyle and Wickramasinghe 1991; Spitzer 2004). These are composed of heterogeneous multilayers of different constituents starting from the grain core to outer surface. The core is made up of silicates and carbon. The inner surface, just adjacent to the core, is formed with water and ammonia at normal temperature (far below the plasma temperature); and the outer surface with oxygen, carbon monoxide and nitrogen (Tielens and Allamandola 1987; Hoyle and Wickramasinghe 1991; Spitzer 2004). The grain mass is $\sim10^{ - 9}\mbox{--}10^{ - 21}~\mbox{kg}$, with the volume density of mass, $\rho_{d} = m_{d}n_{d}\sim3 \times10^{ - 21}~\mbox{kg}\,\mbox{m}^{-3}$ in interstellar media (Vaisberg et al. 1987; Hoyle and Wickramasinghe 1991; Verheest 2000; Spitzer 2004). There are different DMC classes depending on their physical properties (Friberg and Hajalmarson 1990; Kutner 2003; Stahler and Palla 2004). For example, these are Globular Clouds (GCs) ($n_{\mathrm{GC}}\sim10^{9}\mbox{--}10^{10}~\mbox{m}^{-3}$, $T_{\mathrm{GC}}\sim10^{ - 3}~\mbox{eV}$), Dark Clouds (DCs) ($n_{\mathrm{DC}}\sim10^{9}~\mbox{m}^{-3}$, $T_{\mathrm{DC}}\sim 10^{-3}~\mbox{eV}$); Giant Molecular Clouds (GMCs) ($n_{\mathrm{GMC}} > 3 \times10^{8}~\mbox{m}^{-3}$, $T_{\mathrm{GMC}}\sim1.4 \times10^{ - 3}\mbox{--}5.0 \times10^{ - 3}~\mbox{eV}$); Dense Dust Clouds (DDCs) ($n_{\mathrm{DDC}}\sim10^{11}\mbox{--}10^{12}~\mbox{m}^{-3}$, $T_{\mathrm{DDC}}\sim3.0 \times10^{ - 3}\mbox{--}1.0 \times10^{ - 2}~\mbox{eV}$); Diffuse Dust Molecular Clouds (DDMCs) ($n_{\mathrm{DDMC}} > 10^{7}~\mbox{m}^{-3}$, $T_{\mathrm{DDMC}}\sim5.0 \times10^{ - 3}\mbox{--}1.0 \times10^{ - 2}~\mbox{eV}$); Cirrus Clouds (CCs) ($n_{\mathrm{CC}}\sim10^{7}\mbox{--}10^{9}~\mbox{m}^{-3}$, $T_{\mathrm{CC}}\sim10^{-3}\mbox{--}10^{-2}~\mbox{eV}$); Supernova Remnant Clouds (SRCs) ($n_{\mathrm{SRC}}\sim10^{6}~\mbox{m}^{-3}$, $T_{\mathrm{SRC}}\sim1\mbox{--}10^{3}~\mbox{eV}$); etc.

As is well-known, the star-formation processes are governed by complex interplay between the gravitational attraction due to the massive grains; and agents such as, instability in the atmosphere, magnetic field, radiation and thermal pressure that resist free-fall compression. The supersonic turbulence and thermal instability lead to transient, dense clumpy structures. Some of the clumps begin to collapse under the condition that the gravitational force pulling inward exceeds the gas pressure pushing them outward. Once the collapse starts, the process feeds on itself and makes it denser, and so on. Thus, the clumps fragment into many pieces. Fragmented pieces again continue to collapse on its own self-gravity until the gas temperature raises enough to balance gravitational effects. A consequence of the gravito-thermal balancing results in bounded structures in the form of protostars or pre-stellar cores (Peratt 2015). The presence of flow and inhomogeneity is an integral part here. For example, interplay between self-gravity and flow can destabilize the dusty fluid; where, both the electrostatic and Jeans instabilities may operate simultaneously. Jeans has predicted the instabilities of self-gravitating large gas clouds in the last century (Jeans 1902). Later, Chandrasekhar has worked on comparative investigation of the Jeans instability in self-gravitating fluids and plasmas; and has found that the hydrostatic gas pressure gradient and the Lorentz force stabilize the Jeans instability (Chandrasekhar 1957). In this direction, Pudritz has performed a local linear instability analysis of self-gravitating partially ionized magnetoplasma (Pudritz 1990). His main interesting result is that the fluctuation growth rate reduces to that of the Jeans instability for the large-wavelength limit with frictional modulation in the short-wavelength regime only. Recently, other authors have also studied local stabilities to explore the magnetic Jeans and tearing instabilities for understanding the involved fragmentation processes (Mamun et al. 1999; Mamun and Shukla 2000, 2001; Shukla and Mamun 2000). It can thus be seen that, there might have been many other earlier linear (Pudritz 1990; Avinash and Shukla 1994; Pandey et al. 1994; Shukla and Mamun 2000; Verheest et al. 2003) and nonlinear (Rao et al. 1990; Pandey et al. 1994) stability analyses in the direction. Recently, Mamun and Schlickeiser have reported an interesting result on nonlinear fluctuations in self-gravitating dusty plasma (Mamun and Schlickeiser 2015). They have investigated the existence of different solitary gravito-electrostatic potential structures in an inertial bi-dust-fluidic plasma system with bi-polar charges evolving on the dust-acoustic scales of space and time. They have applied local nonlinear perturbation theory, with presumptively homogeneous equilibrium; but on the ground that their perturbation wavelength is much shorter in comparison with the inhomogeneity scale-length. Based on the existing reports, it can be noted that the realistic DMC dynamics is indeed very complex to formulate. Equilibrium inhomogeneities and non-uniformities further add to the factors complicating it. So, to the best of our knowledge, none has heretofore studied the non-local linear fluctuations in such a convoluted cloudy configuration. In this paper, we, therefore, construct a theoretical methodological model for the same.

In astrophysical berths, the grain dynamics is mainly controlled by gravitation; while, those of the electrons and ions are influenced overwhelmingly by electromagnetic counterparts. The two forces operate on two widely distinct scales. For micron and sub-micron sized grains, these forces become comparable, at least in principle, within an order of magnitude (Avinash and Shukla 1994). Our model is specially focused on the particular class of the DMCs, where the dust self-gravity is balanced by the force arising from shielded electric field on the charged dust (Avinash and Shukla 2006). The principal goal is centered on the choice that the mass- and scale-size of the cloud are greater than the Avinash-Shukla critical mass limit ($M_{D} > M_{\mathrm{AS}}\sim10^{18}~\mbox{kg}$, but $\sim10^{21}~\mbox{kg}$, in our case) and critical scale length ($R_{D} > L_{\mathrm{AS}}\sim10^{9}~\mbox{m}$) for the maximum cloud mass, respectively. We develop standard eigenvalue formalism around the inhomogeneous and non-uniform equilibrium. It uses the inhomogeneous plane wave analysis (Ostashev and Wilson 2016). The derived eigenvalue and eigenfunction equations are numerically illustrated and analyzed. The unique characteristics found here are the co-excitation and co-evolution of new instability and interplaying spectral fluctuations sourced by the gravito-electrostatics.

Apart from the “introduction” described in Sect. 1 above, this paper is structurally organized in a standard format as follows. Section 2 contains physical model and necessary basic governing structure equations. Section 3 presents analytical derivations of the DMC stability threshold values of the mass and size. Section 4 contains the non-local fluctuation analysis, subdivided into Sects. 4.1 and 4.2, showing the electrostatic Poisson and self-gravitational Poisson formalisms, respectively. Results and discussions are summarized in Sect. 5. Lastly, Sect. 6 depicts the main conclusions and astrophysical applicability in futuristic directions.

2 Physical model and basic governing equations

A spherical self-gravitating charged DMC in astrophysical environment is considered in quasi-neutral hydrodynamic inhomogeneous equilibrium configuration on the astrophysical scales of space and time. The plasma constituents are the thermal electrons, singly ionized positive ions and inertial spherical micron-sized dust grains of identical nature. The solid matter of the massive dust grains is embedded in the gaseous phase of the plasma enclosed in a giant spherically symmetric chamber. A bulk uniform (divergence-free) flow is presumed to exist globally amid quasi-neutrality. On the Jeans scales of space and time, we neglect the inertia of the electrons and ions, treated as the Boltzmannian species. The dust kinetic pressure, which is appropriate for the cloud much larger than the plasma Debye radius, is ignored. Moreover, the dust charge is not constant, but taken as function of dust population density. It decreases with increase in the dust concentration, and vice versa. The equilibrium (zeroth-order) electric field is finite non-zero arising due to gravity-induced electrostatic polarization effects of the plasma (Bally and Harrison 1978; Pandey et al. 2002; Vranjes and Tanaka 2005). The electrostatic fragmentation of the like charged grains due to the Coulombic repulsive fields (Bliokh et al. 1995) is ignored. The origin of such polarization lies in the mass-dependent gravitational stratification of the plasma constituents to establish reorganized gravito-thermal equilibrium. Besides, all the realistic zeroth-order effects hitherto remaining unaccounted for—like equilibrium inhomogeneities, diverse gradient forces, dust flow-convection dynamics, and so forth—are all concurrently included. Thus, it avoids using any kind of the Jeansian swindles to handle the inhomogeneities against the traditional viewpoint of assuming the equilibrium initially as “homogeneous” one. Furthermore, influences by external cosmic agencies, such as dark matter or stars, are neglected. All other equilibrium characteristic features, as described by Avinash and Shukla, are retained without any loss of generality (Avinash and Shukla 2006). We consider that the total cloud mass contributed collectively by the heavier grains is greater than the Avinash–Shukla critical mass-size limiting values. The velocity convection dynamics in the dust fluid is afresh included. For realizing the macroscopic state of such clouds, the electrons and ions with all usual notations are respectively drew as

$$\begin{aligned} &qn_{e}\vec{\nabla} \varphi- \vec{\nabla} p_{e} = 0,\quad \mbox{and} \end{aligned}$$

(1)

$$\begin{aligned} &- qn_{i}\vec{\nabla} \varphi- \vec{\nabla} p_{i} = 0. \end{aligned}$$

(2)

We apply the hydrodynamic model approximation (low-frequency), which enables us to assume the phase velocity $v_{p} = \omega/ k$ of the fluctuations in the range $v_{te}, v_{ti} \gg v_{p} \gg v_{td}$; where $v_{te}$, $v_{ti}$, and $v_{td}$ are thermal velocities of the electrons, ions and the charged grains, respectively. So, the electrons and ions are justifiably treated as the Boltzmannian particles (derivable from Eqs. (1)–(2)). The dynamics of the dust fluid with all conventional notations is collectively governed by

$$\begin{aligned} &\frac{\partial n_{d}}{\partial t} + \vec{\nabla}. ( n_{d}\vec{v}_{d} ) = 0,\quad\mbox{and} \end{aligned}$$

(3)

$$\begin{aligned} &\rho_{d} \biggl[ \frac{\partial\vec{v}_{d}}{\partial t} + ( \vec{v}_{d}.\vec{ \nabla} )\vec{v}_{d} \biggr] = - q_{d}n_{d}\vec{ \nabla} \varphi- \rho_{d}\vec{\nabla} \psi. \end{aligned}$$

(4)

The system is finally closed by the coupling Poisson equations of the electrostatic and self-gravitational potential distributions, given respectively in closed form, as follows,

$$\begin{aligned} &\nabla^{2}\varphi= - 4\pi \bigl[ e ( n_{i} - n_{e} ) + q_{d}n_{d} \bigr],\quad\mbox{and} \end{aligned}$$

(5)

$$\begin{aligned} &\nabla^{2}\psi= 4\pi G\rho_{d}. \end{aligned}$$

(6)

Here, $n_{e}$, $n_{i}$, and $n_{d}$ are the unnormalized electron (with charge “$-q$”, temperature “$T_{e}$”, and mass “$m_{e}$”), ion (with charge “$+q$”, temperature “$T_{e}$”, and mass “$m_{i}$”), and dust (with charge “$q_{d} = - Z_{d}q$”, temperature “$T_{d}$”, and mass “$m_{d}$”) number densities, respectively. The notations $\varphi$ and $\psi$ stand for the unnormalized electrostatic and self-gravitational potentials, respectively. The dust flow velocity is designated by $v_{d}$. The electronic and ionic thermal pressures are dictated by their respective isothermal equations of state, $p_{e} = n_{e}T_{e}$ and $p_{i} = n_{i}T_{i}$, with temperature-scaling $T_{d} \ll T_{e} \approx T_{i} = T$ (in eV) due to the differential mass-scaling $m_{d} \gg m_{i} > m_{e}$, respectively. Lastly, $G = 6.67 \times10^{-11}~\mbox{N}\,\mbox{m}^{2}\,\mbox{kg}^{-2}$ is the universal gravitational constant via which the gravitating dusty gaseous matter interacts.

3 Derivation of the stability mass limit

Avinash and Shukla have shown an upper limit of the total mass and spatial extension of astrophysical dusty clouds for stable configuration (Avinash and Shukla 2006), as originally understood in case of the Chandrasekhar mass limit for compact astrophysical objects (Chandrasekhar 1957). For the present DMC, we first derive its mass- and size-limits, in the light of our formalism. This implies that, if the mass and size are less than the Avinash-Shukla critical values, then the cloud is stable; otherwise, the cloud becomes unstable and undergoes collapse self-gravitationally. The equation of force balance for the charged dust fluid can be written as,

$$ \vec{\nabla} p_{e} = - \rho_{d}\vec{\nabla} \psi, $$

(7)

where, $p_{e}$ is the electrostatic pressure (superscript ‘$e$’ for ‘electrostatic’). Now, spatially differentiating Eq. (7) and using Eq. (6), we derive the Lane-Emden equation (LEE) on the self-gravitational pressure with spherical symmetry in the normalized form as follows,

$$ \biggl( \frac{R_{D}}{\lambda_{J}} \biggr)^{2} \biggl\{ \frac{1}{\xi^{2}} \frac{\partial}{\partial\xi} \biggl( \frac{\xi^{2}}{\rho_{D}}\frac{\partial P_{E}}{\partial\xi} \biggr) \biggr\} = - \rho_{D}, $$

(8)

where, $R_{D} = ( n_{o}T / 4\pi G m_{d}^{2} n_{do}^{2} )^{1 / 2}$ is the DMC scale-size and $\lambda_{J}$ is the critical Jeans length. Further, $\xi$ is the radial distance normalized by $\lambda_{J}$, $P_{E}$ is the electric pressure normalized by the plasma thermal pressure $P_{Eo} = n_{o}T$, and $\rho_{D} = m_{d}n_{d}$ is the cloud mass density normalized by equilibrium cloud mass density, $\rho_{Do} = m_{d}n_{do}$.

It is seen that $R_{D} = 100\lambda_{J}~\mbox{m}$ in the proposed model for $\lambda_{J}\sim4.21 \times10^{9}~\mbox{m}$, $m_{d}\sim10^{ - 14}~\mbox{kg}$, $n_{o} / n_{do}\sim10^{4}$, and $T\sim1~\mbox{eV}$ (Vaisberg et al. 1987; Hoyle and Wickramasinghe 1991; Verheest 2000; Spitzer 2004). To derive the critical mass limit, the total mass (Chandrasekhar 1957; Avinash and Shukla 2006) of the DMC can analytically be calculated as,

$$ M_{D} = \frac{TR_{D}^{2}}{Gm_{d}\lambda_{J}^{2}}I, $$

(9)

where, the integral $I = \int_{0}^{\xi} \rho_{D}r^{2}dr \sim1$, is a dimensionless number (Avinash and Shukla 2006).

Now, from Eq. (9), we find that $M_{D}\sim10^{21}~\mbox{kg}$. Avinash and Shukla have given the critical DMC mass limit as $M_{\mathrm{AS}}\sim10^{18}~\mbox{kg}$ and critical length as $L_{\mathrm{AS}}\sim10^{9}~\mbox{m}$ for equilibrium (stable) state (Avinash and Shukla 2006). In our model, the DMC mass ($M_{D} \gg M_{\mathrm{AS}}$) and scale-size ($R_{D} \gg L_{\mathrm{AS}}$) exceed the Avinash-Shukla critical values. Thus, by critical value estimation, the cloud model here is unstable and hence, an interesting site for global fluctuation analysis.

A schematic diagram of the considered dust cloud model is portrayed in Fig. 1. The fluctuating non-rigid surface is well-known to be located at $\xi= 3.5\lambda_{J}$ (Dwivedi et al. 2007; Karmakar 2012; Borah and Karmakar 2015), which is the lowest-order cloud surface boundary (CSB). The terminology “lowest-order CSB”, means the nearest concentric spherical electric potential surface boundary (formed by gravito-electrostatic force balancing) relative to the center of entire cloud mass distribution. The CSB acts as an interfacial surface, coupling the cloud interior plasma (CIP) and cloud exterior plasma, as clearly shown in Fig. 1. Thus, it is seen that the concentric cloud surface located at $\xi= 6\lambda_{J}$ is the physical extension boundary for our stability study, which corresponds to the unstable cloud size, $R_{D} = 100\lambda_{J}$. For clarity, we re-state that $L_{\mathrm{AS}}\sim 10^{9} \approx2.37 \times10^{ - 1}\lambda_{J}$, which indicates $\xi= 6\lambda_{J} \approx25L_{\mathrm{AS}}$. This justifies that the spherical cloud extension $\xi= 0-6\lambda_{J} ( > L_{\mathrm{AS}} )$, containing net mass $M_{D} \approx25M_{\mathrm{AS}} ( > M_{\mathrm{AS}} )$, is sensibly a good choice in physical parameter window for instability investigation in the considered cloud.

Fig. 1

Schematic diagram of the spherical DMC considered in the analysis. Various concentric spherical layers are described in the text

4 Non-local fluctuation analysis

The normalized (by standard astrophysical parameters) form of Eqs. (1)–(2), describing the electron-ion dynamics in spherically symmetric geometry, is respectively given as follows,

$$\begin{aligned} &N_{e}\frac{\partial\theta}{\partial\xi} - \frac{\partial N_{e}}{\partial \xi} = 0,\quad\mbox{and} \end{aligned}$$

(10)

$$\begin{aligned} &N_{i}\frac{\partial\theta}{\partial\xi} + \frac{\partial N_{i}}{\partial \xi} = 0. \end{aligned}$$

(11)

Integrating Eqs. (10)–(11) spatially, we obtain the normalized Boltzmann population distribution for the electrons and ions, respectively, as written below,

$$\begin{aligned} &N_{e} = N_{eo}\exp ( \theta ),\quad\mbox{and} \end{aligned}$$

(12)

$$\begin{aligned} &N_{i} = N_{io}\exp ( - \theta ). \end{aligned}$$

(13)

Similarly, the normalized form of Eqs. (3)–(4) for the dust is obtained as below

$$\begin{aligned} &\frac{1}{M_{d}}\frac{\partial N_{d}}{\partial\tau} + N_{d}\frac{2}{\xi} + \frac{N_{d}}{M_{d}}\frac{\partial M_{d}}{\partial\xi} + \frac{\partial N_{d}}{\partial\xi} = 0,\quad\mbox{and} \end{aligned}$$

(14)

$$\begin{aligned} &\frac{\partial M_{d}}{\partial\tau} + M_{d}\frac{\partial M_{d}}{\partial \xi} = - \frac{q_{d}}{q} \frac{\partial\theta}{\partial\xi} - \frac{m_{d}}{q}\frac{\partial\eta}{\partial\xi}. \end{aligned}$$

(15)

Lastly, the normalized form of the coupling Poisson equations, Eqs. (5)–(6), under spherical symmetry is respectively transformed as

$$\begin{aligned} &\frac{\partial^{2}\theta}{\partial\xi^{2}} + \frac{2}{\xi} \frac {\partial \theta}{\partial\xi} = \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} [ N_{e} - N_{i} + Z_{d}N_{d} ],\quad\mbox{and} \end{aligned}$$

(16)

$$\begin{aligned} &\frac{\partial^{2}\eta}{\partial\xi^{2}} + \frac{2}{\xi} \frac {\partial \eta}{\partial\xi} = \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{Gm_{d}N_{d}}{q}. \end{aligned}$$

(17)

The time, $\tau$, is here normalized by the Jeans time $\omega_{J}^{ - 1}$ scale. The electrostatic potential $\theta$ and self-gravitational potential $\eta$ are normalized by the plasma thermal potential $T / q$, so as to compare the fluctuation levels on a common base. Next, $N_{e}$, $N_{i}$, and $N_{d}$ are the concentrations of the electrons, ions, and grains, normalized by the equilibrium plasma density $n_{o}$ each. Moreover, $M_{d}$ is the dust flow velocity normalized by the dust sound phase speed $C_{ss} = ( T / m_{d} )^{1 / 2}$.

4.1 Electrostatic fluctuations

We apply non-local linear perturbation on the relevant physical parameters around the inhomogeneous equilibrium point as shown below,

$$ F ( \xi,\tau ) = F_{o} ( \xi ) + F_{1} ( \xi ,\tau ), $$

(18)

where, $F = N_{e}, N_{i}, N_{d}, M_{d}, \theta \mbox{ and } \eta$; with $F_{o}$ as the corresponding spatially inhomogeneous equilibrium counterparts. Here, we consider inhomogeneous equilibrium mainly due to gravity-induced plasma polarization effects (Bally and Harrison 1978; Vranjes and Tanaka 2005). Using Eq. (18) in Eqs. (12)–(17), the corresponding linearized set of equations is as follows,

$$\begin{aligned} &N_{e1} ( \xi,\tau ) = N_{eo} ( \xi )\exp \bigl\{ \theta_{o} ( \xi ) \bigr\} \theta_{1} ( \xi,\tau ), \end{aligned}$$

(19)

$$\begin{aligned} &N_{i1} ( \xi,\tau ) = - N_{io} ( \xi )\exp \bigl\{ - \theta_{o} ( \xi ) \bigr\} \theta_{1} ( \xi,\tau ), \end{aligned}$$

(20)

$$\begin{aligned} &\frac{\partial N_{d1} ( \xi,\tau )}{\partial\tau} + N_{d1} ( \xi,\tau )\frac{\partial M_{do} ( \xi )}{\partial\xi} + N_{do} ( \xi )\frac{\partial M_{d1} ( \xi,\tau )}{\partial\xi} \\ &\quad {}+ M_{d1} ( \xi,\tau )\frac{\partial N_{do} ( \xi )}{\partial\xi} + M_{do} ( \xi )\frac{\partial N_{d1} ( \xi,\tau )}{\partial\xi} \\ &\quad {} + \bigl\{ M_{do} ( \xi )N_{d1} ( \xi,\tau ) + N_{do} ( \xi )M_{d1} ( \xi,\tau ) \bigr\} \frac{2}{\xi} = 0, \end{aligned}$$

(21)

$$\begin{aligned} &\frac{\partial M_{d1} ( \xi,\tau )}{\partial\tau} + M_{d1} ( \xi,\tau )\frac{\partial M_{do} ( \xi )}{\partial\xi} + M_{do} ( \xi )\frac{\partial M_{d1} ( \xi,\tau )}{\partial\xi} \\ &\quad {} + \frac{q_{d}}{q}\frac{\partial\theta_{1} ( \xi,\tau )}{\partial\xi} + \frac{m_{d}}{q} \frac{\partial \eta_{1} ( \xi,\tau )}{\partial\xi} = 0, \end{aligned}$$

(22)

$$\begin{aligned} &\frac{\partial^{2}\theta_{1} ( \xi,\tau )}{\partial\xi^{2}} + \frac{2}{\xi} \frac{\partial\theta_{1} ( \xi,\tau )}{\partial\xi} \\ &\quad = \biggl(\frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl[ N_{e1} ( \xi,\tau ) - N_{i1} ( \xi,\tau ) + Z_{d}N_{d1} ( \xi,\tau ) \bigr], \end{aligned}$$

(23)

$$\begin{aligned} &\mbox{and} \\ &\frac{\partial^{2}\eta_{1} ( \xi,\tau )}{\partial\xi^{2}} + \frac{2}{\xi} \frac{\partial\eta_{1} ( \xi,\tau )}{\partial\xi} = \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{Gm_{d}}{q}N_{d1} ( \xi, \tau ). \end{aligned}$$

(24)

Now, we apply the Fourier technique for a first-order inhomogeneous plane wave analysis over Eqs. (19)–(24) as inhomogeneous planar (radial) fluctuations (Melrose 1986)—a natural justified choice to describe the fields in non-uniform complex media in inhomogeneous equilibrium.

The following key points on the plane wave analysis, both as a methodical theory and as a strategic tool, may be worth mentioning. A plane harmonic wave may be assumed as a limiting special structure of a spherical wave from a considerably distant source (idealistically, induced point-source, in pure electromagnetic sense); where, the spherical wave front becomes almost planar. Although, realistic astrophysical clouds are known to have finite extension, the assumption of perturbations propagating as plane wave is valid under the condition that the dust cloud is unbounded, expanded infinitely and boundary effects are not directly of any great immensity for the phenomena happening in the bulk plasma system (Carbonell et al. 2004; Cattaert and Verheest 2005). The plane wave approximation under spherically symmetric geometry is a simpler way (than other existing analytical methods and strategies) of concentrating on only one dimension (radial), thereby enabling us for the structure solutions in which the other two dimensions (azimuthal and co-latitudinal) do not enter at all. Another advantage in the analysis of translationally invariant systems derives from the fact that the natural representation of the system physical variables is in terms of plane waves with canonically minimum reduced degrees of freedom (only $\xi$, in the present case). This simplicity translates into faster computer run times with less memory requirements for exact analysis. The name “plane wave” is appropriate because the field vectors in the wave have the same value everywhere on each plane of constant $\xi$, for any fixed time $\tau$, such that $\xi$ is typically greater than the size of wave-scale length. In a broader and stricter sense, its phase is the same over a plane normal to the direction of wave propagation, even if the strength of the wave varies within that plane; but, function of $\xi$ only. These planes propagate in the radial direction at constant phase velocity of the considered fluctuations. Even for non-homogeneous, but isotropic and slowly-varying plasma medium with trifling viscosity, such approximations indeed represent a good starting point to the actual solutions. We adopt the short-wavelength approximation in the form of the Fourier plane waves, validated by $k \xi\gg 1$, which in principle, implicates the wavelength $\lambda\ll \xi$ (Ostashev and Wilson 2016). Armed with this technique, with $\xi\sim\lambda_{J}$ as inhomogeneity scale length, the relevant sinusoidal fluctuations can be written as follows,

$$ F_{1} ( \xi,\tau ) = \widetilde{F}_{1} ( \xi ) e^{ - i\omega\tau+ ik\xi}. $$

(25)

Here, $\omega$ is the fluctuation frequency normalized to the Jeans frequency $\omega_{J} ( = \sqrt{4\pi Gm_{d}n_{do}} )$ and $k$ is the wave vector (angular wave number) normalized to the critical Jeans wave vector $k_{J} ( = 2\pi/ \lambda_{J} )$. Now, applying Eq. (25) in Eqs. (19)–(24), we get

$$\begin{aligned} &\widetilde{N}_{e1}( \xi ) = N_{eo} ( \xi )\exp \bigl\{ \theta_{o} ( \xi ) \bigr\} \widetilde{\theta}_{1} ( \xi ), \end{aligned}$$

(26)

$$\begin{aligned} &\widetilde{N}_{i1} ( \xi ) = - N_{io} ( \xi )\exp \bigl\{ - \theta_{o} ( \xi ) \bigr\} \widetilde{\theta}_{1} ( \xi ), \end{aligned}$$

(27)

$$\begin{aligned} & \biggl\{ - i\varOmega+ \frac{\partial M_{do} ( \xi )}{\partial \xi} + M_{do} ( \xi ) \biggl( \frac{\partial}{\partial\xi} + \frac{2}{\xi} \biggr) \biggr\} \widetilde{N}_{d1} ( \xi ) \\ &\quad {} + \biggl\{ N_{do} ( \xi ) \biggl( \frac{\partial}{ \partial \xi} + \frac{2}{\xi} + ik \biggr) + \frac{\partial N_{do} ( \xi )}{\partial\xi} \biggr\} \widetilde{M}_{d1}( \xi ) = 0, \end{aligned}$$

(28)

where, $\varOmega= \{ \omega- kM_{do} ( \xi ) \}$ is the Doppler-shifted frequency of the fluctuations.

$$\begin{aligned} & \biggl\{ - i\varOmega+ \frac{\partial M_{do} ( \xi )}{\partial \xi} + M_{do} ( \xi ) \frac{\partial}{\partial\xi} \biggr\} \widetilde{M}_{d1} ( \xi ) \\ &\quad = - \frac{q_{d}}{q} \biggl( \frac{\partial}{\partial\xi} + ik \biggr) \widetilde{\theta}_{1} ( \xi ) - \frac{m_{d}}{q} \biggl( \frac{\partial}{\partial\xi} + ik \biggr) \widetilde{\eta}_{1} ( \xi ), \end{aligned}$$

(29)

$$\begin{aligned} &\frac{\partial^{2}\widetilde{\theta}_{1} ( \xi )}{\partial\xi^{2}} + \biggl( \frac{2}{\xi} + 2ik \biggr) \frac{\partial\widetilde{\theta}_{1} ( \xi )}{\partial\xi } + \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \widetilde{\theta}_{1} ( \xi ) \\ &\quad = \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \Bigl[ \widetilde{N}_{e1}( \xi ) - \widetilde{N}_{i1}(\xi ) + Z_{d}\widetilde{N}_{d1}( \xi ) \Bigr] , \quad \mbox{and} \end{aligned}$$

(30)

$$\begin{aligned} &\frac{\partial^{2}\widetilde{\eta}_{1} ( \xi )}{\partial\xi^{2}} + \biggl( \frac{2}{\xi} + 2ik \biggr)\frac{\partial\widetilde{\eta}_{1} ( \xi )}{\partial\xi} + \biggl( \frac{2ik}{\xi} - k^{2} \biggr)\widetilde{\eta}_{1} ( \xi ) \\ &\quad = \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{Gm_{d}}{q} \widetilde{N}_{d1} ( \xi ). \end{aligned}$$

(31)

We solve Eq. (30) for $\widetilde{N}_{d1} ( \xi )$, $\partial/\partial\xi \{ \widetilde{N}_{d1} ( \xi ) \}$, $\partial^{2} / \partial \xi^{2} \{ \widetilde{N}_{d1} ( \xi ) \}$; Eq. (31) for $\widetilde{\eta}_{1} ( \xi )$; and use them in Eqs. (28)–(29). After rigorous calculation and simplification with the assumption that $\{-i\varOmega+ \partial M_{do} ( \xi ) / \partial\xi+ M_{do} ( \xi )\partial/ \partial\xi \}\times\widetilde{M}_{d1}( \xi )\sim0$ (for fairly massive quasi-stationary grains in cold-dust approximation), we get the non-local electrostatic eigenfunction equation as,

$$\begin{aligned} &\frac{\partial^{4}\widetilde{\theta}_{1} ( \xi )}{\partial\xi ^{4}} + \biggl( \frac{\alpha_{2}}{\alpha_{1}} \biggr)\frac{\partial^{3}\widetilde{\theta}_{1} ( \xi )}{\partial \xi^{3}} + \biggl( \frac{\alpha_{3}}{\alpha_{1}} \biggr)\frac{\partial^{2}\widetilde{\theta}_{1} ( \xi )}{\partial \xi^{2}} \\ &\quad {}+ \biggl( \frac{\alpha_{4}}{\alpha_{1}} \biggr)\frac{\partial \widetilde{\theta}_{1} ( \xi )}{\partial\xi} + \biggl( \frac{\alpha_{5}}{\alpha_{1}} \biggr) \widetilde{\theta}_{1} ( \xi ) = 0. \end{aligned}$$

(32)

The various coefficients, involved in Eq. (32), are expressed as,

$$\begin{aligned} &\alpha_{1} = \frac{M_{do}^{2} ( \xi )}{Z_{d}} \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2}, \end{aligned}$$

(33)

$$\begin{aligned} &\alpha_{2} = \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2} \frac{1}{Z_{d}} \biggl\{ M_{do}^{2} ( \xi ) \biggl( \frac{2}{\xi} + ik \biggr) + A_{2} \biggr\} , \end{aligned}$$

(34)

$$\begin{aligned} &\alpha_{3} = \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2} \frac{1}{Z_{d}} \biggl[ A_{1} + A_{2} \biggl( \frac{2}{\xi} + ik \biggr) \\ &\phantom{\alpha_{3} =}+ M_{do}^{2} ( \xi ) \biggl\{ \frac{2ik}{\xi} - k^{2} - \frac{4}{\xi^{2}} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl( N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &\phantom{\alpha_{3} =} + N_{io} ( \xi )e^{ - \theta_{o} ( \xi )} \bigr) \biggr\} \biggr] - \biggl( 1 + \frac{Gm_{d}^{2}}{Z_{d}q^{2}} \biggr) \biggl( \frac{2ik}{\xi} - k^{2} \biggr)^{ - 1} \\ &\phantom{\alpha_{3} =}\times \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} , \end{aligned}$$

(35)

$$\begin{aligned} &\alpha_{4} = \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2} \frac{1}{Z_{d}} \biggl\{ A_{1} \biggl( \frac{2}{\xi} + 2ik \biggr) \\ &\phantom{\alpha_{4} =} + A_{2} \biggl( \frac{2ik}{\xi} - k^{2} - \frac{2}{\xi^{2}} \biggr) + \frac{4M_{do}^{2} ( \xi )}{\xi^{3}} \biggr\} \\ &\phantom{\alpha_{4} =} - \frac{A_{2}}{Z_{d}}\left \{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \right \} \\ &\phantom{\alpha_{4} =} - \biggl( 1 + \frac{Gm_{d}^{2}}{Z_{d}q^{2}} \biggr) \biggl\{ ik \frac {\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} , \end{aligned}$$

(36)

$$\begin{aligned} &\alpha_{5} = \frac{A_{2}}{Z_{d}}\frac{\partial}{\partial\xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi )e^{ - \theta_{o} ( \xi )} \bigr\} \\ &\phantom{\alpha_{4} =} - \frac{A_{1}}{Z_{d}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} (\xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \\ &\phantom{\alpha_{4} =} + \frac{M_{do}^{2} ( \xi )}{Z_{d}}\frac{\partial^{2}}{\partial \xi^{2}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \\ &\phantom{\alpha_{4} =} + \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2} \frac{1}{Z_{d}} \biggl\{ A_{1} \biggl( \frac{2ik}{\xi} - k^{2} \biggr) + \frac{2ikA_{2}}{\xi^{2}} \\ &\phantom{\alpha_{4} =}- M_{do}^{2} ( \xi ) \frac{4ik}{\xi^{3}} \biggl( 1 + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{Z_{d}^{2}N_{do}\xi^{2}}{2M_{do}^{2} ( \xi )} \biggr) \biggr\} \\ &\phantom{\alpha_{4} =} - \frac{q_{d}}{q} \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} \\ &\phantom{\alpha_{4} =} \times \biggl[ 1 + \frac{m_{d}}{q} \biggl( \frac{2ik}{\xi} - k^{2} \biggr)^{ - 1} \biggl\{ \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \\ &\phantom{\alpha_{4} =} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr\} \biggr], \end{aligned}$$

(37)

$$\begin{aligned} &A_{1} = - \varOmega^{2} - 2i\varOmega\frac{\partial M_{do} ( \xi )}{\partial\xi} + \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} ^{2} \\ &\phantom{A_{1} =} + M_{do} ( \xi ) \frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}} + \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} - i\varOmega- \frac{M_{do} ( \xi )}{\xi} \biggr\} \\ &\phantom{A_{1} =}\times M_{do} ( \xi )\frac{2}{\xi},\quad \mbox{and} \end{aligned}$$

(38)

$$\begin{aligned} &A_{2} = - 2i\varOmega M_{do} ( \xi ) \biggl( 1 - M_{do} ( \xi )\frac{2}{\xi} \biggr) + 3M_{do} ( \xi ) \frac{\partial M_{do} ( \xi )}{\partial\xi}. \end{aligned}$$

(39)

In Eq. (32), the term involving the lowest-order non-locality, ($\partial^{0} / \partial\xi^{0}$), is the last term, where all other higher-order non-local terms would be absent in case of homogeneous equilibrium (local stability analysis). In all other remaining terms, different orders of non-locality appear in the form of different-order $\partial/ \partial\xi$-operations. We equate the coefficient of the last term to derive the non-local dispersion relation of the considered fluctuations as,

$$\begin{aligned} \alpha_{5} =& \frac{A_{2}}{Z_{d}}\frac{\partial}{ \partial \xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \\ &{} - \frac{A_{1}}{Z_{d}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} (\xi)} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \\ &{} + \frac{M_{do}^{2} ( \xi )}{Z_{d}}\frac{\partial^{2}}{\partial \xi^{2}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \\ &{}+ \biggl( \frac{\lambda_{De}}{\lambda_{J}} \biggr)^{2}\frac{1}{Z_{d}} \biggl\{ A_{1} \biggl( \frac{2ik}{\xi} - k^{2} \biggr) + \frac{2ikA_{2}}{\xi^{2}} \\ &{}- M_{do}^{2} ( \xi ) \frac{4ik}{\xi^{3}} \biggl( 1 + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{Z_{d}^{2}N_{do}\xi^{2}}{2M_{do}^{2} ( \xi )} \biggr) \biggr\} \\ &{}- \frac{q_{d}}{q} \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} \\ &{}\times \biggl[ 1 + \frac{m_{d}}{q} \biggl( \frac{2ik}{\xi} - k^{2} \biggr)^{ - 1} \biggl\{ \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \\ &{}- \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr\} \biggr] \\ =&0. \end{aligned}$$

(40)

The presence of equilibrium gradients in Eq. (40) reflects conversely that astrophysical plasma equilibria are indeed inhomogeneous and non-uniform in nature. It gives the eigenvalue equation describing the non-local electrostatic fluctuations in simplified form as,

$$ D_{E} ( \omega,k ) \equiv\omega^{2} + E_{1} \omega+ E_{o} = 0, $$

(41)

where,

$$\begin{aligned} E_{o} =& kM_{do} ( \xi ) \biggl\{ kM_{do} ( \xi ) - 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} - \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} ^{2} \\ &{}- M_{do} ( \xi )\frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}} + M_{do}^{2} ( \xi )\frac{2}{\xi} \biggl( \frac{1}{\xi} - ik \biggr) \\ &{}- \frac{2}{\xi} M_{do} ( \xi ) \frac{\partial M_{do} ( \xi )}{\partial\xi} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \frac{q_{d}Z_{d}}{q} \\ &{}\times \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} \\ &{}\times \biggl\{ 1 + \frac{m_{d}}{q} \biggl( \frac{2ik}{\xi} - k^{2} \biggr)^{ - 1} \biggr\} \\ &{}+ \biggl[ \frac{2ik}{\xi} - k^{2} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]^{ - 1} \biggl[ \biggl\{ - 3\frac{\partial M_{do} ( \xi )}{\partial\xi} - 2ikM_{do} ( \xi ) \\ &{}- M_{do}^{2}(\xi)\frac{2}{\xi} \biggr\} M_{do} ( \xi ) \biggl\{ \frac{2ik}{\xi^{2}} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \\ &{}\times\frac{\partial}{\partial\xi} \left \{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \right \} \biggr\} \\ &{}+ M_{do}^{2} ( \xi ) \biggl\{ \frac{4ik}{\xi^{3}} \biggl( 1 + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \frac{Z_{d}^{2}N_{do}\xi^{2}}{2M_{do}^{2} ( \xi )} \biggr) \\ &{}- \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \frac{\partial^{2}}{\partial\xi^{2}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{-\theta_{o} ( \xi )} \bigr\} \biggr\} \biggr], \end{aligned}$$

(42)

and

$$\begin{aligned} E_{1} =& 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} - 2M_{do} ( \xi ) \biggl( k - \frac {i}{\xi} \biggr) \\ &{}+ \biggl[ \frac{2ik}{\xi} - k^{2} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]^{ - 1} 2iM_{do} ( \xi ) \biggl[ \frac{2ik}{\xi} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \\ &{}\times\frac{\partial}{\partial\xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} +N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]. \end{aligned}$$

(43)

In case of infinite degree of spherical curvature $( \xi\to0 )$, Eqs. (42)–(43) get respectively modified to the following,

$$ \textstyle\begin{cases} E_{o} \approx\infty, \quad \mbox{and} \\ E_{1} \approx\infty. \end{cases} $$

(44)

Again, for the zeroth-degree of spherical curvature $(\xi\to \infty)$, Eqs. (42)–(43) get reduced, respectively, to

$$\begin{aligned} E_{o} \approx& \biggl[ kM_{do} ( \xi ) \biggl\{ kM_{do} ( \xi ) - 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} - \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} ^{2} \\ &{}- M_{do} ( \xi ) \frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}} \biggr]_{\xi= \infty} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \frac{q_{d}Z_{d}}{q} \\ &{}\times \biggl[ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr]_{\xi= \infty} \biggl( 1 + \frac{m_{d}}{qk^{2}} \biggr) \\ &{}- \biggl[ k^{2} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} _{\xi= \infty} \biggr]^{ - 1} \\ &{}\times \biggl[ \biggl\{ - 3M_{do} ( \xi ) \frac{\partial M_{do} ( \xi )}{\partial\xi} - 2ikM_{do}^{2} ( \xi ) \biggr\} \\ &{}\times \left \{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \frac{\partial}{\partial\xi} \left \{N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )}\right \} \right \} \\ &{} -M_{do}^{2} ( \xi ) \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{\partial^{2}}{\partial\xi^{2}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi)} \\ &{} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr\} \biggr]_{\xi= \infty}, \quad\mbox{and} \end{aligned}$$

(45)

$$\begin{aligned} E_{1} \approx& \biggl[ 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} - 2kM_{do} ( \xi ) \biggr]_{\xi= \infty} \\ &{} -2i \bigl[ M_{do} ( \xi ) \bigr]_{\xi= \infty} \biggl[ k^{2} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} _{\xi= \infty} \biggr]^{ - 1} \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \\ &{}\times \biggl[ \frac{\partial}{\partial\xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )}+ N_{io} ( \xi )e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]_{\xi= \infty}. \end{aligned}$$

(46)

Now, the following special cases may be worth mentioning and explaining. In the Jeans limit $( k \to0 )$, the coefficients of Eq. (41) get modified to the following respective forms,

$$\begin{aligned} E_{o} \approx& - \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} ^{2} \\ &{}+ M_{do}^{2} ( \xi )\frac{2}{\xi^{2}} \biggl( 1 - \frac{\xi}{M_{do} ( \xi )}\frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr) \\ &{}+ \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} ^{ - 1} \\ &{}\times \biggl[ \biggl\{ 3M_{do} ( \xi ) \frac{\partial M_{do} ( \xi )}{\partial\xi} + M_{do}^{2} ( \xi )\frac{2}{\xi} \biggr\} \\ &{}\times \biggl\{ \frac{\partial}{\partial\xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr\} \\ &{}+ M_{do}^{2} ( \xi ) \biggl\{ \frac{\partial^{2}}{\partial \xi^{2}} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr\} \biggr] \\ &{}- M_{do} ( \xi ) \frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}},\quad\mbox{and} \end{aligned}$$

(47)

$$\begin{aligned} E_{1} \approx& 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} + i\frac{2}{\xi} M_{do} ( \xi ) - 2iM_{do} ( \xi ) \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} ^{ - 1} \frac{\partial}{\partial\xi} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} . \end{aligned}$$

(48)

Again, in the electrostatic limit of the fluctuations $(k \to \infty )$, Eqs. (42)–(43) get reduced to the following respective forms,

$$ \textstyle\begin{cases} E_{o} \approx\infty, \quad \mbox{and} \\ E_{1} \approx\infty. \end{cases} $$

(49)

In case of homogeneous equilibrium configuration; for which $M_{do}$, $\theta_{o} = 0$, $N_{eo}$, $N_{io}$, $N_{do} = 1$, and $\partial/ \partial\xi ( N_{eo},N_{io}, N_{do},M_{do},\theta_{o} ) = 0$; Eq. (41) becomes,

$$\begin{aligned} \omega =& \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} k \biggl\{ 1 - \frac{1}{k^{2}} \biggl( \frac{m_{d}}{q_{d}} \biggr) \\ &{}\times \biggl( 1 - \frac {2i}{k\xi} \biggr)^{ - 1} \biggr\} ^{1 / 2}. \end{aligned}$$

(50)

Now, for investigating the stability behavior, we use $\omega= \omega_{r} + i\omega_{i}$ in Eq. (50), which on simplification results in

$$\begin{aligned} &\omega_{r} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} k \biggl\{ 1 - \biggl( \frac{m_{d}}{2q_{d}} \biggr)\frac{1}{k^{2}} \biggr\} ,\quad\mbox{and} \end{aligned}$$

(51)

$$\begin{aligned} &\omega_{i} = - \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2}\frac{m_{d}}{q_{d}} \biggr\} \frac{1}{k^{2}\xi}. \end{aligned}$$

(52)

Here, it is observed from Eq. (51) that, the real part of frequency depends on the ratio of the Jeans-to-Debye lengths, wave vector, charge and mass of the grains. Likewise, it is seen from Eq. (52) that, the imaginary part of frequency depends on ratio of the Jeans-to-Debye lengths, charge and mass of the grains, wave vector and in addition, on the geometrical configuration as well. We can see that $\omega_{i}<0$, so the fluctuations should show damping behaviors. For infinite degree of curvature $( \xi \to0 )$, for a given $k$, one finds, $\omega_{r} = \omega_{r}$, and $\omega_{i} \to0$. So, it is clear that, the damping or growth of the fluctuations depend on the cloud geometry. Again, for the zero-degree of curvature $( \xi\to\infty )$, $\omega_{r} = \omega_{r}$, and $\vert \omega_{i} \vert \to\infty$. Under such geometrical configurations, the fluctuations show infinite damping nature. In the Jeans limit $( k \to0 )$, one gets $\omega_{r} \to0$, and $\vert \omega_{i} \vert \to\infty$. On the other hand, in the electrostatic limit $( k \to\infty )$, one finds $\omega_{r} \to\infty$, and $\omega_{i} \to0$. In this limit, one can further see that $\omega_{r} \propto k$, which reveals purely acoustic behavior of the fluctuations. Now, the ratio between imaginary-to-real frequencies ($D_{P_{E}} = \omega_{i} / \omega_{r}$, or $G_{P_{E}} = \omega_{i} / \omega_{r}$), which is defined as damping (or, growth) rate per period (Carbonell et al. 2004) depending on the nature of the mode evolution, reads as,

$$ D_{P_{E}} = \frac{2}{k\xi} \biggl\{ 1 + \biggl( \frac{2q_{d}}{m_{d}} \biggr) k^{2} \biggr\} . $$

(53)

For a given $k$, Eq. (53) further reduces to

$$ D_{P_{E}} = \frac{\omega_{i}}{\omega_{r}} \propto\frac{1}{\xi}. $$

(54)

So, at $\xi, k \to0$, one finds $D_{P_{E}} \to\infty$; and at $\xi, k \to \infty$, one sees $D_{P_{E}} \to0$. So, in case of homogeneous equilibrium, it is observed that the damping rate per period is infinitely large at the center, in the Jeans limit. The damping rate per period is zero for infinite distance, which corresponds to the electrostatic limit. The phase velocity and group velocity of the fluctuations in homogeneous equilibrium configuration are respectively given by,

$$\begin{aligned} &V_{p_{E}} = \frac{\omega}{k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} \biggl\{ 1 - \biggl( \frac{m_{d}}{2q_{d}} \biggr)\frac{1}{k^{2}} \biggr\} ,\ \ \mbox{and} \end{aligned}$$

(55)

$$\begin{aligned} &V_{g_{E}} = \frac{\partial\omega}{\partial k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} \biggl\{ 1 + \biggl( \frac{m_{d}}{2q_{d}} \biggr)\frac{1}{k^{2}} \biggr\} . \end{aligned}$$

(56)

Equations (55) and (56) reveal that the phase velocity and group velocity are inversely proportional to the wave vector. For a given $k$, $V_{p_{E}} \propto ( - V_{g_{E}} )$, which shows that $V_{p_{E}}$ and $V_{g_{E}}$ are of opposite evolutionary phase. At $\xi\to0, \infty$, we see that $V_{p_{E}}$ and $V_{g_{E}}$ remain unchanged. Again, at $k \to0$, it is found that $\vert V_{p_{E}} \vert$, $V_{g_{E}} \to\infty$. As $k \to\infty$, we find that $V_{p_{E}}$, $V_{g_{E}} \to ( \lambda _{J} / \lambda_{De} ) ( Z_{d}q_{d} / q )^{1 / 2}$. Thus, in the Jeans limit, $V_{p_{E}}$ and $V_{g_{E}}$ are of infinite strength. In contrast, in the electrostatic limit, both are constant thereby revealing the acoustic-nature of the fluctuations. The phase dispersion and group dispersion (Nishikawa and Wakatani 1990; Chen 2007) are derived respectively as,

$$\begin{aligned} &\Delta_{p_{E}} = \frac{\partial V_{p_{E}}}{\partial k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{m_{d}}{q_{d}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} \frac {1}{k^{3}},\quad \mbox{and} \end{aligned}$$

(57)

$$\begin{aligned} &\Delta_{g_{E}} = \frac{\partial V_{g_{E}}}{\partial k} = - \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr) \biggl( \frac{m_{d}}{q_{d}} \biggr) \biggl( \frac{Z_{d}q_{d}}{q} \biggr)^{1 / 2} \biggr\} \frac{1}{k^{3}}. \end{aligned}$$

(58)

Equations (57)–(58) show that $\Delta_{p_{E}} \propto ( - \Delta_{g_{E}} ) \propto k^{-3}$. Thus, the phase and group dispersions are of opposite evolutionary phase, each depending inversely upon the wave vector cubed. At, $\xi\to0, \infty$; we see that $\Delta_{p_{E}}$, $\Delta_{g_{E}}$ remain unchanged as $V_{p_{E}}$ and $V_{g_{E}}$. Similarly, $\Delta_{p_{E}}$, $\vert \Delta_{g_{E}} \vert \to\infty$, at $k \to0$, and $\Delta_{p_{E}}$, $\Delta_{g_{E}} \to0$, at $k \to \infty$. It provides an analytic scheme to see the dispersion properties of the electrostatic fluctuations in the limiting case of pure homogeneity.

4.2 Self-gravitational fluctuations

To study the self-gravitational potential fluctuations, we deduce self-gravitational eigenfunction equation by using Eqs. (26)–(31). In the derivation, we solve Eq. (31) for $\widetilde{N}_{d1} ( \xi )$, $\partial/ \partial\xi \{ \widetilde{N}_{d1} ( \xi ) \}$, $\partial^{2} / \partial\xi^{2} \{ \widetilde{N}_{d1} ( \xi ) \}$, Eq. (30) for $\widetilde{\theta}_{1} ( \xi )$ and use them in Eqs. (28)–(29). After rigorous calculation with the assumption of $\{ - i\varOmega+ \partial M_{do} ( \xi ) / \partial\xi+ M_{do} ( \xi )\partial / \partial\xi \}\widetilde{M}_{d1} ( \xi )\sim 0$ (for relatively massive quasi-stationary cold dust grains), we obtain

$$\begin{aligned} &\frac{\partial^{4}\widetilde{\eta}_{1} ( \xi )}{\partial\xi^{4}} + \biggl( \frac{\beta_{2}}{\beta_{1}} \biggr)\frac{\partial^{3}\widetilde{\eta}_{1} ( \xi )}{\partial\xi^{3}} + \biggl( \frac{\beta_{3}}{\beta_{1}} \biggr)\frac{\partial^{2}\widetilde{\eta}_{1} ( \xi )}{\partial \xi^{2}} \\ &\quad {}+ \biggl( \frac{\beta_{4}}{\beta_{1}} \biggr)\frac{\partial \widetilde{\eta}_{1} ( \xi )}{\partial\xi} + \biggl( \frac{\beta_{5}}{\beta_{1}} \biggr) \widetilde{\eta}_{1} ( \xi ) = 0, \end{aligned}$$

(59)

where, the various coefficients involved in Eq. (59) are,

$$\begin{aligned} \beta_{1} =& M_{do}^{2} ( \xi ), \end{aligned}$$

(60)

$$\begin{aligned} \beta_{2} =& M_{do}^{2} ( \xi ) \biggl( \frac{2}{\xi} + 2ik \biggr) + A_{2}, \end{aligned}$$

(61)

$$\begin{aligned} \beta_{3} =& A_{1} + \biggl( \frac{2}{\xi} + 2ik \biggr)A_{2} + \frac{2M_{do}^{2} ( \xi )k}{\xi} \biggl( i - \frac{2i}{\xi} - \frac{2}{\xi^{2}k} \biggr) \\ &{} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \biggl\{ ik \frac{\partial N_{do} ( \xi )}{\partial\xi} - k^{2}N_{do} ( \xi ) \biggr\} \frac{Gm_{d}^{2}q_{d}}{q^{2}} \\ &{}\times \biggl[ \biggl( \frac{2ik}{\xi} - k^{2} \biggr) - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]^{ - 1} \biggl( \frac{Z_{d}q}{Gm_{d}} + \frac{m_{d}}{q} \biggr) , \end{aligned}$$

(62)

$$\begin{aligned} \beta_{4} =& A_{1} \biggl( \frac{2}{\xi} + 2ik \biggr) + \biggl( \frac{2ik}{\xi} - \frac{2}{\xi^{2}} - k^{2} \biggr)A_{2} \\ &{}+ M_{do}^{2} \biggl( \frac{4}{\xi^{3}} - \frac{4ik}{\xi^{2}} \biggr) - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} \\ &{}- k^{2}N_{do} ( \xi ) \biggr\} \frac{Gm_{d}^{2}q_{d}}{q^{2}} \biggl( \frac{2}{\xi} + 2ik \biggr) \biggl[ \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \\ &{}- \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} + N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \bigr\} \biggr]^{-1} \\ &{}\times \biggl( \frac{Z_{d}q}{Gm_{d}} + \frac{m_{d}}{q} \biggr) , \quad \mbox{and} \end{aligned}$$

(63)

$$\begin{aligned} \beta_{5} =& A_{1} \biggl( \frac{2ik}{\xi} - k^{2} \biggr) - \frac{2ik}{\xi^{2}}A_{2} + M^{2}_{do}\frac{4ik}{\xi^{3}}- \biggl(\frac{\lambda_{J}}{\lambda _{De}} \biggr)^{2} \\ &{}\times \biggl\{ ik\frac{\partial N_{do}(\xi)}{\partial\xi} - k^{2}N_{do}( \xi ) \biggr\} \frac{Gm^{2}_{d}}{q^{2}} \biggl(\frac{2}{\xi}+2ik \biggr) \\ &{}\times \biggl[1 + \frac{Z_{d}q_{d}q}{Gm_{d}} \biggl(\frac{2ik}{\xi}-k^{2} \biggr) \biggl[ \biggl(\frac {2ik}{\xi}-k^{2} \biggr) \\ &{}- \biggl(\frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo}( \xi)e^{\theta_{o}(\xi)} + N_{io}(\xi)e^{-\theta_{o}(\xi)} \bigr\} \biggr]^{-1} \biggr]. \end{aligned}$$

(64)

Similar to the electrostatic counterpart, we equate the coefficient of the lowest-order non-locality term in Eq. (59) to zero and get the eigenvalue equation as follows,

$$ D_{S} ( \omega,k ) \equiv\omega^{2} + S_{1} \omega+ S_{o} = 0, $$

(65)

where,

$$\begin{aligned} S_{o} =& M_{do} ( \xi ) \biggl\{ k^{2}M_{do} ( \xi ) - \frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}} - \frac{2}{\xi} \biggl( \frac{\partial M_{do} ( \xi )}{\partial \xi} \\ &{}+ \biggl( ik - \frac{1}{\xi} \biggr)M_{do} ( \xi ) \biggr) \biggr\} - \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggl\{ 2ikM_{do} ( \xi ) \\ &{}+ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} - \biggl( k^{2} - \frac{2ik}{\xi} \biggr)^{ - 1} \biggl[ \frac{2ik}{\xi^{2}} \biggl\{ 2ikM_{do}^{2} ( \xi ) \\ &{}+ 3M_{do} ( \xi )\frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \biggl\{ ik\frac{\partial N_{do} ( \xi )}{\partial\xi} \\ &{}- k^{2}N_{do} ( \xi ) + ikN_{do} ( \xi ) \frac{2}{\xi} \biggr\} \frac{Gm_{d}^{2}}{q^{2}} \\ &{}\times \biggl[ 1 + \frac{Z_{d} q_{d} q}{Gm_{d}} \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \biggl[ \biggl( \frac{2ik}{\xi} - k^{2} \biggr) \\ &{} - \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \bigl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ -\theta_{o} ( \xi )} \bigr\} \biggr]^{ - 1} \biggr] \biggr] , \end{aligned}$$

(66)

and

$$\begin{aligned} S_{1} =& 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} - 2kM_{do} ( \xi ) + \frac{2}{\xi} iM_{do} ( \xi ) \\ &{}- \biggl( k^{2} - \frac{2ik}{\xi} \biggr)^{ - 1} \frac{4M_{do} ( \xi ) k}{\xi^{2}}. \end{aligned}$$

(67)

It is seen that the coefficients of the non-local fluctuations, given by Eqs. (66)–(67), get modified in case of infinite degree of geometrical curvature $( \xi\to0 )$, as shown below,

$$ \textstyle\begin{cases} S_{o} \approx\infty, \quad \mbox{and} \\ S_{1} \approx\infty. \end{cases} $$

(68)

Again, for the zeroth-degree of curvature $( \xi\to\infty )$, Eqs. (66)–(67) become,

$$\begin{aligned} S_{o} \approx& \biggl[ M_{do} ( \xi ) \biggl\{ k^{2}M_{do} ( \xi ) - \frac{\partial^{2}M_{do} (\xi)}{\partial\xi^{2}} \biggr\} \\ &{}- \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggl\{ 2ikM_{do} ( \xi ) + \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} \biggr]_{\xi= \infty} \\ &{}- \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2} \biggl\{ \frac{i}{k}\frac{\partial N_{do} ( \xi )}{\partial\xi} - N_{do} ( \xi )\biggr\} _{\xi= \infty} \frac{Gm_{d}^{2}}{q^{2}} \\ &{}\times\Biggl[ 1 + \frac{Z_{d} q_{d} q}{Gm_{d}}\Biggl[ 1 + \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}\frac{1}{k^{2}} \biggl\{ N_{eo} ( \xi ) e^{\theta_{o} ( \xi )} \\ &{}+ N_{io} ( \xi ) e^{ - \theta_{o} ( \xi )} \biggr\} _{\xi= \infty} \Biggr]^{ - 1} \Biggr],\quad\mbox{and} \end{aligned}$$

(69)

$$\begin{aligned} S_{1} \approx& 2i \biggl[ \frac{\partial M_{do} ( \xi )}{\partial \xi} \biggr]_{\xi= \infty} - 2k \bigl[ M_{do} ( \xi ) \bigr]_{\xi= \infty}. \end{aligned}$$

(70)

In the Jeans limit $( k \to0 )$, Eqs. (66)–(67) get reduced to the following forms,

$$\begin{aligned} S_{o} \approx& -M_{do} ( \xi ) \biggl( \frac{\partial^{2}M_{do} ( \xi )}{\partial\xi^{2}} - \frac{2}{\xi} \frac{\partial M_{do} ( \xi )}{\partial\xi} + M_{do} ( \xi ) \frac{2}{\xi^{2}} \biggr) \\ &{}- \biggl\{ \frac{\partial M_{do} ( \xi )}{\partial\xi} \biggr\} ^{2}, \quad\mbox{and} \end{aligned}$$

(71)

$$\begin{aligned} S_{1} \approx& 2i\frac{\partial M_{do} ( \xi )}{\partial\xi} + \frac{2}{\xi} iM_{do} ( \xi ). \end{aligned}$$

(72)

Similarly, in the electrostatic limit $( k \to\infty )$, Eqs. (66)–(67) get altered to the following respective forms,

$$ \textstyle\begin{cases} S_{o} \approx\infty, \quad \mbox{and} \\ S_{1} \approx\infty. \end{cases} $$

(73)

For homogeneous equilibrium with $M_{do}$, $\theta_{o} = 0$; $N_{eo}$, $N_{io}$, $N_{do} = 1$, and $\partial/\partial\xi (N_{eo},N_{io},N_{do},M_{do},\theta_{o} = 0)$, Eq. (65) becomes,

$$ \omega= \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}2m_{d}^{1 / 2}Z_{d} \biggl( \frac{1}{k} \biggr) \biggl( 1 + \frac{2i}{k\xi} \biggr)^{1 / 2}. $$

(74)

Now, again using $\omega= \omega_{r} + i\omega_{i}$ in Eq. (74) and after simplification, we get

$$\begin{aligned} &\omega_{r} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}2Z_{d} m_{d}^{1 / 2} \biggr\} \frac{1}{k},\quad\mbox{and} \end{aligned}$$

(75)

$$\begin{aligned} &\omega_{i} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}2Z_{d} m_{d}^{1 / 2} \biggr\} \frac{1}{k^{2}\xi}. \end{aligned}$$

(76)

Thus, the real and imaginary parts of frequency depend on the ratio of the Jeans-to-Debye lengths, charge and mass of the grains, wave vector and geometrical configuration. For a given $k$, at $\xi\to0$; one has $\omega_{r} = \omega_{r}$, $\omega_{i} \to\infty$. Again, at $\xi\to \infty$; we see that $\omega_{r} = \omega_{r}$, $\omega_{i} \to0$. This reveals that near the center of the cloud, self-gravitational fluctuations have infinite growing character. Similar to the electrostatic analysis, at $k \to0$; one gets $\omega_{r}, \omega_{i} \to\infty$. Also, at $k \to \infty$; one derives $\omega_{r}, \omega_{i} \to0$. Now, damping (or, growth) rate per period (Carbonell et al. 2004) depending on the nature of the mode-evolution comes out as,

$$ D_{P_{G}} = \frac{1}{k\xi}. $$

(77)

For a given $k$, the damping rate per period given by Eq. (77) becomes

$$ D_{P_{G}} = \frac{\omega_{i}}{\omega_{r}} \propto \biggl( \frac{1}{\xi} \biggr). $$

(78)

So, when $\xi, k \to0$, $D_{P_{G}} \to\infty$; and $\xi, k \to\infty$, $D_{P_{G}} \to 0$. Thus, in case of homogeneous equilibrium, it is observed that, both at the center and in the large-wavelength regime, the damping rate per period is infinitely large. At infinite distance and in the small-wavelength regime, the damping rate per period is zero. The phase velocity and group velocity of the fluctuations under homogeneous equilibrium configuration are deduced as,

$$\begin{aligned} &V_{p_{G}} = \frac{\omega}{k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}2Z_{d} m_{d}^{1 / 2} \biggr\} \frac{1}{k^{2}},\quad\mbox{and} \end{aligned}$$

(79)

$$\begin{aligned} &V_{g_{G}} = \frac{\partial\omega}{\partial k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}2Z_{d} m_{d}^{1 / 2} \biggr\} \biggl( - \frac{1}{k^{2}} \biggr). \end{aligned}$$

(80)

Thus, it is seen that $V_{p_{G}} = - V_{g_{G}}$. This indicates that, for homogeneous equilibrium without any Jeans swindle, $V_{p_{G}} \propto ( - V_{g_{G}} )$, which in turn reveals that $V_{p_{G}}$ and $V_{g_{G}}$ propagate with opposite phase. Further, we see that, at $k \to 0$, both $V_{p_{G}}$, $V_{g_{G}} \to\infty$; and at $k \to\infty$, both $V_{p_{G}}$, $V_{g_{G}} \to 0$. This implies that, in the small-wavelength regime, no self-gravitational fluctuations propagate. The corresponding phase dispersion and group dispersion (Nishikawa and Wakatani 1990; Chen 2007) are now obtained and given by

$$\begin{aligned} &\Delta_{p_{G}} = \frac{\partial V_{p_{G}}}{\partial k} = - \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}4Z_{d} m_{d}^{1 / 2} \biggr\} \biggl( \frac{1}{k^{3}} \biggr),\quad\mbox{and} \end{aligned}$$

(81)

$$\begin{aligned} &\Delta_{g_{G}} = \frac{\partial V_{g_{G}}}{\partial k} = \biggl\{ \biggl( \frac{\lambda_{J}}{\lambda_{De}} \biggr)^{2}4Z_{d} m_{d}^{1 / 2} \biggr\} \biggl( \frac{1}{k^{3}} \biggr). \end{aligned}$$

(82)

From Eqs. (81)–(82), we see that $\Delta_{p_{G}} = ( - \Delta_{g_{G}} )\alpha ( k^{ - 3} )$. Thus, $\Delta_{p_{G}}$ and $\Delta_{g_{G}}$ are of opposite evolutionary phase and depend on $k$. If $k \to0$, we see that $\Delta_{p_{G}}$, $\Delta_{g_{G}} \to\infty$; and at $k \to\infty$, one finds that $\Delta_{p_{G}}$, $\Delta_{g_{G}} \to0$, like $V_{p_{G}}$ and $V_{g_{G}}$. It is noted that $\Delta_{p_{G}}$ and $\Delta_{g_{G}}$ are independent of any kind of geometrical curvature influences in correlation with the electrostatic counterparts.

5 Results and discussions

An evolutionary model to study the properties of global electro-gravitational modes in self-gravitating inhomogeneous interstellar DMC with all the characterizing equilibrium parameters varying radially is constructed under spherical symmetry. To study excitation and evolution of the fluctuations globally, we numerically integrate the electrostatic eigenfunction equation [Eq. (32)] with suitable initial input values by the fourth-order Runge–Kutta method (Otto and Denier 2005). Before the numerical illustrations, different normalization constants are estimated methodologically from the judicious inputs available in the literature (Vaisberg et al. 1987; Hoyle and Wickramasinghe 1991; Verheest 2000; Spitzer 2004) as shown in Table 1.

Table 1 Normalization constants with estimated typical values

Figure 2 shows the profile of the normalized electrostatic potential fluctuations $( \tilde{\theta}_{1} ( \xi ) )$ with variation in normalized distance $( \xi )$ and in normalized wave vector $( k )$ of the fluctuations. Different initial values used are $( \theta )_{i} = - 1.00 \times10^{ - 2}$, $( \theta_{\xi} )_{i} = - 1.00 \times10^{ - 3}$, $( N_{e} )_{i} = 9.50 \times10^{ - 1}$, $( N_{i} )_{i} = 9.00 \times10^{ - 1}$, $( N_{d} )_{i} = 1.00 \times10^{ - 3}$, $( M_{d} )_{i} = 1.01 \times10^{ - 3}$, $( \eta )_{i} = - 1.00 \times10^{ - 5}$, $( \eta )_{i} = - 1.00 \times10^{ - 5}$, $( \theta_{\xi} )_{i} = - 1.00 \times 10^{ - 3}$, $( \theta_{1\xi} )_{i} = 1.00 \times10^{ - 4}$, $( \theta_{1\xi\xi} )_{i} = - 1.00 \times10^{ - 7}$, and $( \theta_{1\xi\xi\xi} )_{i} = - 1.00 \times10^{ - 9}$. The other input parameters kept constant are $m_{d} = 2.50 \times10^{ - 14}~\mbox{kg}$ and $Z_{d} = 1.00 \times10^{2}$ (Vaisberg et al. 1987; Hoyle and Wickramasinghe 1991; Verheest 2000; Spitzer 2004). The level of fluctuations is found maximum at 3.5 (on the Jeans scale), which is the lowest-order cloud surface boundary (CSB) (Karmakar 2012; Borah and Karmakar 2015). On the exterior, the fluctuations show a damped periodic oscillatory behavior. The oscillatory behavior indicates that the electro-gravitational interaction is not static, but dynamic in a periodic fashion via gravito-electrostatic coupling interplay. The periodic oscillations are due to the compression of one species and rarefaction of the other, and vice versa. The damping nature in the Cloud Exterior Plasma (CEP) is attributable to the decrease in the dynamic coupling strength. In the $k$-space, no fluctuation propagates up to $k = 1$ (which corresponds to $\lambda= 6.28 \lambda_{J}$). This large-wavelength region is dominated by the self-gravitational fluctuations, which are due to the inertial dust grains, concentrated near the center. So, $k = 1$ is a critical point for propagation of the eigenfluctuations undergoing quasi-linear transformation into pure gravitational form via self-gravity. As $k$ increases, the fluctuations grow linearly with a super-growth at $k = 3.5\ (\lambda= 1.79\lambda_{J})$. The growth occurs in the Cloud Interior Plasma (CIP) due to the combined effect of the self-gravity, equilibrium inhomogeneities and gravity-induced plasma polarization. For $k > 3.5$, the instability decays due to the gradually decreasing charge density in the CEP outward.

Fig. 2

Profile of the normalized electrostatic potential fluctuations $( \tilde{\theta}_{1} ( \xi ) )$ with variation in normalized distance $( \xi )$ and in normalized wave vector $( k )$ of the fluctuations. Different initial values used here are $( \theta )_{i} = - 1.00 \times10^{ - 2}$, $( \theta_{\xi} )_{i} = - 1.00 \times10^{ - 3}$, $( N_{e} )_{i} = 9.50 \times10^{ - 1}$, $( N_{i} )_{i} = 9.00 \times10^{ - 1}$, $( N_{d} )_{i} = 1.00 \times10^{ - 3}$, $( M_{d} )_{i} = 1.01 \times10^{ - 3}$, $( \eta )_{i} = - 1.00 \times10^{ - 5}$, $( \eta )_{i} = - 1.00 \times10^{ - 5}$, $( \theta_{\xi} )_{i} = - 1.00 \times 10^{ - 3}$, $( \theta_{1\xi} )_{i} = 1.00 \times10^{ - 4}$, $( \theta_{1\xi\xi} )_{i} = - 1.00 \times10^{ - 7}$ and $( \theta_{1\xi\xi\xi} )_{i} = - 1.00 \times10^{ - 9}$. The other input parameter values kept constant are $m_{d} = 2.50 \times10^{ - 14}~\mbox{kg}$ and $Z_{d} = 1.00 \times10^{2}$

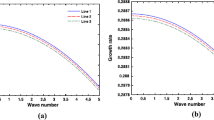
Figure 3 consecrates the profile of the normalized (a) real part of frequency, (b) imaginary part of frequency and (c) imaginary-to-real frequency ratio of the fluctuations with variation in normalized distance $( \xi )$ and normalized wave vector $( k )$. The different input initial values used are the same as Fig. 2. The real part (Fig. 3(a)) is maximum at $\xi= 3.5$. This reveals that the CSB is the most unstable interfacial zone (as seen before in Fig. 2, too). It decreases from the center to $\xi= 1.5$ outward. This is due to the fact that the global mode-spectrum is dominated by the Jeans modes near the center. In the CEP, the real part of frequency gets attenuated due to the dispersive nature of the medium. The instability decays from the center with a super-decay at $k = 3$ ($\lambda= 2.09\lambda_{J}$), which coincides with the Jeans mode. In this local neighborhood, discrete oscillations are found to exist as mode-mode coupler. After $k = 3$, the instability grows linearly with wave vector, which is the electrostatic acoustic mode-behavior. This linear growth of the global instability is due to the density inhomogeneity and gravity-induced polarization effects (Bally and Harrison 1978; Vranjes and Tanaka 2005). In the long-wavelength region, the global instability behaves as the usual Jeans mode; and in the short-wavelength region, the Jeans mode is quasi-linearly converted into acoustic mode via gravitational condensation of large-wavelength waves. So, the instability evolves as a hybrid structure due to mode-mode coupling of electro-gravitational fluctuations. Moreover, we see a three-scale behavior in the $\xi$-space (Fig. 3(b)). The imaginary frequency decreases from the center to $\xi= 1.5$, and then, it increases linearly with a maximum and saturated value at $\xi= 4$ outward. The instability is damped in the long-wavelength region with a super-decay at $k = 4$ ($\lambda= 1.57\lambda_{J}$) and grows linearly in the short-wavelength region. Figure 3(c) shows the ratio of imaginary-to-real frequency. In the $\xi$-space, the ratio again shows three-scale behavior with a transition from slight damping to growth rate per period. The growth rate per period is 1 at $\xi = 3.5$. So, the linear theory is applicable for the CIP, and beyond the CSB, the nonlinear theory has to be applied for the CEP. In the $k$-space, the frequency ratio grows with a super-growth at $k = 3$ ($\lambda= 2.09\lambda_{J}$). Hereafter, there is a sharp damping with a super-decay at $k = 4$ ($\lambda= 1.57\lambda_{J}$) and then, it shows a linear growing behavior.

Fig. 3

Profile of the normalized (a) real part of frequency, (b) imaginary part of frequency and (c) imaginary-to-real frequency ratio of the fluctuations with variation in normalized distance $(\xi)$ and in normalized wave vector $(k)$. Different input initial values used are the same as Fig. 2

Figure 4 shows the same as Fig. 3, but in the large-wavelength regime ($k \to 0$). It is seen that, in the ultra-low $k$ limit, non-dispersive nature of the fluctuations prevails due to the Jeans instability, with domination in the large-wavelength regime, together with all other properties re-organized accordingly.

Fig. 4

Same as Fig. 3, but in the large-wavelength regime ($k \to0$)

Similarly, Fig. 5 indicates the same as Fig. 3, but in the highlighted small-wavelength regime ($k \to\infty$). In this ultra-high $k$ limit, the dispersive characteristics of the fluctuations are prevalent. The real part of frequency (Fig. 5(a)) grows quasi-linearly with some background discrete oscillations, which depicts the acoustic behavior, which corresponds to small wavelength. The imaginary part displays damping oscillatory behavior in the small-wavelength regime (Fig. 5(b)). The ratio of imaginary-to-real frequency, likewise, signifies the damping nature of the instability in the ultra-high $k$ limit (Fig. 5(c)).

Fig. 5

Same as Fig. 3, but in the small-wavelength regime ($k \to\infty$)

Figure 6 displays the profile constructs of the normalized (a) phase velocity and (b) group velocity of the fluctuations with variation in normalized distance $( \xi )$ and in normalized wave vector $( k )$. The different input initial values used are the same as Fig. 2. We see that the phase velocity decreases from the center to $\xi= 1.5$ due to the strong self-gravitational attractive force sourced by the massive grains. In the $\xi$-region, spanned with $1.5 < \xi< 3.5$, the phase velocity increases linearly with the maximum value at $\xi= 3.5$, thereby showing the most unstable nature of the CSB. In the CEP, the phase velocity decreases due to the small drifting of charged species from the CIP to CEP due relatively high self-gravity. In the $k$-space, the phase velocity decays sharply from $k = 0$ to $k = 1.5$. For $k > 1$, it decays with very small gradient. Thus, the fluctuations are dispersive in nature with maximum dispersive behavior in the large-wavelength region ($k = 1$) due to strong self-gravitational effects. The velocity of the wave envelope is found to be maximum at $\xi= 3.5$ due to the most unstable nature of the CSB. The group velocity shows nonlinear behavior in the CEP, as the growth rate per period exceeds unity beyond the CSB. It is seen that the group velocity shows almost constant, but with slight damping nature, in the long-wavelength region. In $2.1 < k \le4.5$, the group velocity increases linearly with the maximum value at $k = 4.5$ ($\lambda= 1.39\lambda_{J}$). The velocity of the imbalance is damped out in the very short-wavelength regime ($k > 4.5$) due to very small drifting of the charged species in the CEP.

Fig. 6

Profile of the normalized (a) phase velocity and (b) group velocity of the fluctuations with variation in normalized distance $(\xi)$ and in normalized wave vector $( k )$. The different input initial values used are the same as Fig. 2

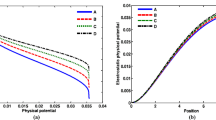
Figure 7 graphically displays the spatial profiles of the real part (A, B, C, D) and imaginary part (a, b, c, d) (rescaled by dividing with 1.28) of the $\theta ( \xi )$-fluctuation frequency with variation in (a) $Z_{d}$ and (b) $m_{d}$, correspondingly, under the same condition as Fig. 2. Different lines in (a) correspond to $Z_{d} = 100$ (blue), 102 (red), 104 (green), and 106 (black), respectively. Again, different lines in (b) link to $m_{d} = 2.49 \times10^{ - 14}~\mbox{kg}$ (blue), $2.50 \times10^{ - 14}~\mbox{kg}$ (red), $2.51 \times10^{ - 14}~\mbox{kg}$ (green), and $2.52 \times 10^{ - 14}~\mbox{kg}$ (black), respectively. The real and imaginary parts of fluctuation frequency (Fig. 7(a)) increase with increase in $Z_{d}$, and decrease (Fig. 7(b)) with increase in $m_{d}$. It may be noted that, as $Z_{d}$ increases, the electrostatic repulsive force increases. Hence, the growth rate increases. As $m_{d}$ increases, the self-gravitational attractive force increases. This dominates the fluctuation growth rate. As a result, the growth rate decreases. Thus, grain charge ($Z_{d}$) behaves as destabilizing source and grain mass ($m_{d}$) acts as a stabilizing source of the fluctuations. The observed features are quite in good agreement with those obtained by others in the past (Shadmehri and Dib 2009). From Fig. 7(a), the values of real and imaginary parts at the CSB are $( \omega_{r} )_{E}$, $( \omega_{i} )_{E}\sim2.25$ each. Similarly, from Fig. 7(b), we see $( \omega_{r} )_{E}$, $( \omega_{i} )_{E}\sim2.2$ each at the CSB. It is found that, for both the cases (Figs. 7(a)–7(b)), the real part shows constant value for $0 \le \xi\le0.5\lambda_{J}$ and variation increases as frequency evolves away from the region $\xi= 0.5\lambda_{J}$.

Fig. 7

Spatial profile of the real part (A, B, C, D) and imaginary part (a, b, c, d) of the $\theta ( \xi )$-fluctuation frequency with variation in (a) $Z_{d}$ and (b) $m_{d}$, correspondingly, under the same condition as Fig. 2. Different lines in (a) correspond to $Z_{d} = 100$ (blue), 102 (red), 104 (green), and 106 (black), respectively. Again, different lines in (b) link to $m_{d} = 2.49 \times10^{ - 14}$ (blue), $2.50 \times10^{ - 14}$ (red), $2.51 \times10^{ - 14}$ (green), and $2.52 \times10^{ - 14}~\mbox{kg}$ (black), respectively

Figure 8 gives the profiles of the normalized self-gravitational potential fluctuations $( \tilde{\eta}_{1} ( \xi ) )$ with normalized distance $( \xi )$ and normalized wave vector $( k )$. Different initial values used here are $( \theta )_{i} = - 1.00 \times10^{ - 3}$, $( \theta_{\xi} )_{i} = - 1.00 \times10^{ - 4}$, $( N_{e} )_{i} = 8.10 \times10^{ - 1}$, $( N_{i} )_{i} = 8.00 \times10^{ - 1}$, $( N_{d} )_{i} = 1.00 \times10^{ - 2}$, $( M_{d} )_{i} = 5.00 \times10^{ - 3}$, $( \eta )_{i} = - 1.00 \times10^{ - 4}$, $( \eta_{\xi} )_{i} = - 9.00 \times10^{ - 2}$, $( \eta_{1} )_{i} = 1.00 \times10^{ - 2}$, $( \eta_{1\xi} )_{i} = - 1.00 \times10^{ - 5}$, $( \eta_{1\xi\xi} )_{i} = - 1.00 \times 10^{ - 9}$, and $( \eta_{1\xi\xi\xi} )_{i} = - 1.00 \times 10^{ - 10}$. The other input parameters kept constant are the same as in Fig. 2. It is interesting to see that the CSB is the most unstable interfacial zone, as the self-gravitational fluctuation is again maximum at $\xi= 3.5$, like in the electrostatic counterparts, presented before. It is clear that the electrostatic (Fig. 2) and self-gravitational (Fig. 8) fluctuations evolve with opposite polarities on strength due to the electro-gravitational coupling of the electrostatic repulsive and self-gravitational attractive effects. In the CEP, the self-gravitational fluctuations decrease due to decrease in dust density distribution as well as the coupling between the two counteracting forces. The self-gravitational fluctuations show a unique characteristic feature of almost zero-value from the center up to $\xi= 0.5$ and $k = 0.5$ in the CIP. The fluctuation grows linearly in the large-wavelength region ($0.5 < k \le2$) with a super-growth at $k = 2$ ($\lambda= 3.14\lambda_{J}$). For $k > 2$, the self-gravitational instability decays gradually due to low-concentration of the massive grains in the CEP.

Fig. 8

Profile of the normalized self-gravitational potential fluctuations $( \tilde{\eta}_{1} ( \xi ) )$ with normalized distance $( \xi )$ and in normalized wave vector $( k )$ of the fluctuations. Different initial values used here are $( \theta )_{i} = - 1.00 \times10^{ - 3}$, $( \theta_{\xi} )_{i} = - 1.00 \times10^{ - 4}$, $( N_{e} )_{i} = 8.10 \times10^{ - 1}$, $( N_{i} )_{i} = 8.00 \times10^{ - 1}$, $( N_{d} )_{i} = 1.00 \times10^{ - 2}$, $( M_{d} )_{i} = 5.00 \times10^{ - 3}$, $( \eta )_{i} = - 1.00 \times10^{ - 4}$, $( \eta_{\xi} )_{i} = - 9.00 \times10^{ - 2}$, $( \eta_{1} )_{i} = 1.00 \times10^{ - 2}$, $( \eta_{1\xi} )_{i} = - 1.00 \times10^{ - 5}$, $( \eta_{1\xi\xi} )_{i} = - 1.00 \times10^{ - 9}$ and $( \eta_{1\xi\xi\xi} )_{i} = - 1.00 \times10^{ - 10}$. The other input parameter values kept constant are the same as Fig. 2

Figure 9 exhibits profiles of the normalized (a) real part of frequency, (b) imaginary part of frequency, (c) imaginary part of frequency with different view-orientation and (d) imaginary-to-real frequency ratio of the fluctuations with normalized distance $( \xi )$ and normalized wave vector $( k )$. The different input initial values used are the same as in Fig. 8. The real part shows the maximum value at the center, and it decreases linearly with distance (Fig. 9(a)). So, it is clear that near the center, the Jeans mode plays the dominating role due to the large-accumulation of the massive grains. In the $k$-space, the real frequency part shows a linearly damping characteristic feature from the center with a super-decay at $k = 2.5$ ($\lambda= 2.51\lambda_{J}$). Then, the real part increases linearly with wave vector. The long-wavelength region, in which damping behavior is prominent, is the Jeans mode-dominated region. Furthermore, the short-wavelength region, in which instability grows linearly, is the electrostatic mode-dominated region. Thus, a unique transition from the Jeans mode to electrostatic mode via quasi-linear coupling is found to survive in the DMC (Fig. 9(a)). So, the instability evolves as a hybrid structure due to intrinsic mode-mode coupling of electro-gravitational nature. The imaginary part shows the maximum value at $\xi= 3.5$, which re-confirms the most unstable nature of the CSB (Fig. 9(b)). In the $k$-space, the imaginary part gradually grows with a super-growth value at $k = 3.7$ ($\lambda= 1.69\lambda_{J}$). Beyond it, the instability damps out. Figure 9(c) shows the imaginary frequency in a different orientation to observe the evolution pattern more clearly. Figure 9(d) shows the profile of imaginary-to-real frequency ratio with variation in $\xi$ and $k$. In the $\xi$-space, it again shows a transition from growth-to-damping rate per period. The growth rate per period is 1 at $\xi = 1.5$. So, the linear theory is widely applicable for $\xi\le1.5$. The growth rate is maximum at $\xi= 3.5$, which again reveals the unstable CSB. Beyond the CSB, the growth turns into damping. In the $k$-space, the imaginary-to-real frequency ratio grows linearly from the center and shows a super-growth at $k = 3.4$ ($\lambda= 1.84\lambda_{J}$). So, in the long-wavelength region, the Jeans mode plays the dominating role. Beyond the super-growth point, there is a sharp damping with super-decay at $k = 6$ ($\lambda= 1.04 \lambda_{J}$).

Fig. 9

Profile of the normalized (a) real part of frequency, (b) imaginary part of frequency, (c) imaginary part of frequency with different orientation and (d) imaginary-to-real frequency ratio of the fluctuations with normalized distance $( \xi )$ and in normalized wave vector $( k )$. The different input initial values used are the same as Fig. 8

Figure 10 shows the same as Fig. 9, but in the large-wavelength regime ($k \to0$). All the profiles in the ultra-low $k$ limit show dispersive nature. The imaginary part shows the growing nature of the instability in the large-wavelength regime (Fig. 10(b)). This observation reveals that, the self-gravitational fluctuation instability, i.e., the Jeans instability grows only in the large-wavelength regime.

Fig. 10

Same as Fig. 9, but in the large-wavelength regime ($k \to0$)

Figure 11 shows the profile in the small-wavelength regime ($k \to\infty$) under the same condition as Fig. 9. In the ultra-high $k$ limit, the real part shows hybrid characteristics of the instabilities with rhythmic transitions from the Jeans to electrostatic modes (Fig. 11(a)). In the extremely high-$k$ limit, the instability behaves as purely acoustic mode like the electrostatic counterpart. The imaginary part (Fig. 11(b)) and imaginary-to-real frequency ratio (Fig. 11(c)) in the ultra-high $k$ limit show similar behaviors as the electrostatic ones.

Fig. 11

Same as Fig. 9, but in the small-wavelength regime ($k \to\infty$)

Figure 12 graphically presents the profile of normalized (a) phase velocity and (b) group velocity of the fluctuations with normalized distance $( \xi )$ and normalized wave vector $(k)$. The different input initial values used are the same as Fig. 8. In the $\xi$-space, the phase velocity (Fig. 12(a)) shows a linearly damping behavior from the center outwards due to decrease in the dust concentration. In the $k$-space, the phase velocity shows resonantly sharp decay from the center with a super-decay at $k = 1.5$ ($\lambda= 4.18\lambda_{J}$). After that, it shows slow variation. This shows that the Jeans mode dominates in the long-wavelength region and it is highly dispersive for the regime, $k \le 1.5$. Also, the velocity of the Jeans mode amplitude is maximum at the center and it linearly decreases outwards (Fig. 12(b)). This again signifies that the Jeans mode dominates in the CIP with the maximum value at the center. In the $k$-space, the group velocity shows a sharp damping from the center with a super-decay at $k = 1.5$ ($\lambda= 4.18\lambda_{J}$). Again, after that, it grows linearly. Therefore, the group velocity shows dispersive nature of the fluctuations with mode-mode coupling characteristics of the wave-amplitude toward shorter-wavelengths via self-gravitational condensation of larger wavelength perturbations.

Fig. 12

Profile of the normalized (a) phase velocity and (b) group velocity of the fluctuations with normalized distance $( \xi )$ and in normalized wave vector $( k )$. The different input initial values used are the same as Fig. 8

Figure 13 shows the same as Fig. 7, but for the $\eta ( \xi )$-fluctuations. It is seen that the real and imaginary parts of the fluctuation frequency decrease with increase in $Z_{d}$ (Fig. 13(a)), and increase with increase in $m_{d}$ (Fig. 13(b)). For both the cases (Figs. 13(a)–13(b)), the real part shows no rational variation in the regime $0 \le\xi\le0.5\lambda_{J}$. The variation increases as the frequency shifts away from $\xi= 0.5\lambda_{J}$. The imaginary part reveals that, with increase in $Z_{d}$ (Fig. 13(a)), the growth rate remains the same in the CIP ($0 \le\xi\le3.5\lambda_{J}$); but after CSB, it decreases with increase in $Z_{d}$. It is observed that, the growth rate increases from the center outward with increase in $m_{d}$ (Fig. 13(b)). The electrostatic repulsive force in the cloud increases with increase in $Z_{d}$, which dominates over the self-gravitational counterparts. Thus, the growth rate decreases with increase in $Z_{d}$ in the CEP. Again, when $m_{d}$ increases, the self-gravitational attractive force increases; which in turn, increases the growth rate. From Fig. 13(a), the real and imaginary parts at the CSB are $( \omega_{r} )_{G} \sim1.7$, and $( \omega_{i} )_{G}\sim2.0$, respectively. Similarly, from Fig. 13(b), one gets $( \omega_{r} )_{G}\sim1.75$, and $(\omega_{i})_{G}\sim2.0$ at the CSB.

Fig. 13

Same as Fig. 7, but now for the $\eta(\xi)$-fluctuations. The different input initial values used are the same as Fig. 8

Thus, it is confirmed by all the techniques, that the CSB is most unstable electrostatic potential boundary, which is non-rigid in nature. It is also observed that the ratio of imaginary-to-real frequency at the CSB for the electrostatic case (Fig. 3(c)) is $( \omega_{i} / \omega_{r} )_{E}\sim1$. The same for the self-gravitational counterpart (Fig. 9(d)) is $( \omega_{i} / \omega_{r} )_{G}\sim 1.12$. The ratio of both the values is $R = ( \omega_{i} / \omega_{r} )_{E} / ( \omega_{i} / \omega_{r} )_{G}\sim0.89$. At the CSB, we get the real frequency ratio of the two classes of fluctuations as, $( f_{Z_{d}} )_{r} = ( \omega_{r} )_{E} / ( \omega_{r} )_{G} = 2.25 / 1.7\sim1.32$ (from Figs. 7(a), 13(a)), and $( f_{Z_{d}} )_{i} = ( \omega_{i} )_{E} / ( \omega_{i} )_{G} = 2.25 / 2\sim1.12$ (from Figs. 7(a), 13(a)). Thus, at the CSB, the electrostatic instabilities are more dominant than the corresponding self-gravitational ones with increasing $Z_{d}$-value. Similarly, at the CSB, we obtain $( f_{m_{d}} )_{r} = ( \omega_{r} )_{E} / ( \omega_{r} )_{G} = 2.2 / 1.75\sim1.25$ (from Figs. 7(b), 13(b)), and $( f_{m_{d}} )_{i} = ( \omega_{r} )_{E} / ( \omega_{r} )_{G} = 2.2 / 2\sim1.1$ (from Figs. 7(b), 13(b)). It implies that, at the CSB, the electrostatic instabilities dominate over the self-gravitational counterparts, although elsewhere, the net fluctuations can evolve in a dissimilar intermixed pattern.

6 Conclusions and remarks

We present a self-consistent evolutionary description of the non-local electro-gravitational instabilities supported in an inhomogeneous, non-uniform, self-gravitating charged DMC. We carry out a non-local linear normal mode analysis to study their excitation and evolution mode characteristics globally with hydrodynamic viewpoint. Then, we derive eigenvalue and eigenfunction equations for both the distinct classes of electrostatic and self-gravitational fluctuations. A numerical scheme for illustrations is constructed with suitable and judicious initial input values. It identifies three distinct categories of non-local eigenfluctuations. Here, it is admitted that the role of neutral dynamics in the intrinsic process of quasi-linear mode-modification is ignored. Besides, details of positively charged species surrounded by the density of electrons needed to make the plasma roughly neutral are dropped for simplification. Despite the facts and faults, the following concluding remarks may summarily be worth mentioning.

• 1. An analytic non-local linear model to investigate the discrete behavior of the collective dynamics of global gravito-electrostatic fluctuations in spherical charged dust cloud is developed on the astrophysical fluid scales of space and time.

• 2. Eigenvalue and eigenfunction equations are methodologically derived by applying the standard inhomogeneous (modified) Fourier technique exactly.

• 3. The considered DMC macroscopically is shown to be in unstable state, as the calculated mass ($M_{D}\sim10^{21}~\mbox{kg}$) and scale length ($R_{D}\sim 10^{11}~\mbox{m}$) are found greater than that of the Avinash-Shukla critical values for astrophysical objects to be in stable equilibrium state.

• 4. Both electrostatic and self-gravitational potential fluctuations are found to be maximum at the CSB, existing at radial coordinate $\xi= 3.5\lambda_{J}\sim1.47 \times10^{10}~\mbox{m}$, but with opposite polarities in strength. This implies that the CSB is the most unstable interfacial zone (coupling the CIP and CEP) due to the strong coupling of the self-gravitational attractive and electrostatic repulsive effects contributed by the collective charged grainy plasma species.

• 5. Three distinct and spatio-spectrally isolated classes of non-local eigenmodes—dispersive, non-dispersive and hybrid types—are identified and characterized with illustrations.

• 6. Dispersive features are prominent in the ultra-high $k$-regime, and non-dispersive characteristics dominate in the ultra-low $k$-regime.

• 7. The ratio of global electrostatic-to-self-gravitational potential fluctuations comes out as, $\tilde{\theta}_{1} / \tilde{\eta}_{1}\sim7 \times10^{1}$. This shows that the strength of self-gravitational potential fluctuations is much smaller than that of the electrostatic counterpart. This, in turn, implicates that the existence of considerably massive dust grains is needed for bounded structures to form.

• 8. The density and electro-gravitational coupling play the stabilizing role.

• 9. The density inhomogeneity, self-gravity and non-local wave characterization indicate a unique type of hybrid instability due to mode-mode coupling via quasi-linear processes. This type of instabilities leads to the mechanisms responsible for the formation of bounded structures like star clusters and other galactic associations via gravito-electrostatic polarization.

• 10. The entire DMC is a mixture of both the Jeans and electrostatic modes, coupled via discrete oscillatory features, but of intermixed pattern. Near the center, the Jeans mode plays the dominating role, and the electrostatic mode prevails outward.

• 11. The Jeans mode is more unstable in the long-wavelength region; whereas, the electrostatic mode is more unstable in the short-wavelength region.

• 12. In the Jeans limit and electrostatic limit for the special case of homogeneous equilibrium, the fluctuations exhibit extreme behaviors immaterial of the geometrical curvature considered.

• 13. The growth rate of the electrostatic fluctuations increases and that of the gravitational fluctuations decreases with the increase in electrical charge of the massive dust grains. However, it shows reverse characteristics with the increase in mass of the massive dust grains.

• 14. The grain-charge has destabilizing influential role for the electrostatic fluctuations; but stabilizing role for the self-gravitational ones. In contrast, the grain-mass plays stabilizing influential role for the former; but, destabilizing protagonist for the latter.

• 15. Lastly, we believe that our results can provide extensive inputs for exploration of self-gravitational cloud collapse dynamics (via fragmentation and filamentation processes) leading to the formation mechanism of diverse galactic eigenunits and eigenstructures. It can further find application to see instability-triggered energy cascading processes in thermal regions of diverse astrophysical objects and their circumvented atmospheres. It is moreover empathized that further refinements with inclusion of neutral particle dynamics, bi-polar grain charge fluctuations, kinematic viscosity and non-static cloud rotational behavior in the framework of multi-fluid approach using the WKB method are necessary. These are in progress for more accurate outcomes yet to be reported elsewhere.