1 Introduction

The dusty plasma is the fascinating research area as the dust is omnipresent in astrophysical situations (Shukla and Mamun 2002) for example in protostellar disks, interstellar and circumstellar clouds, molecular clouds, planetary atmospheres, cometary tails, asteroid zones, interstellar media, nebula and earth’s surroundings. The presence of dust adds new changes in the phenomenon of “gravitational collapsing” and requires revision of the study of gravitational effects in the astrophysical objects. In cosmic circumstances, self-gravitation of the medium is important in understanding the formation of dust clouds and equilibrium structures, as well as for the study of collective processes. The propagation of waves and related instabilities corresponding to dusty plasma has been studied widely in dusty plasma. Pandey et al. (1994) have investigated the linear and nonlinear Jeans instability of dusty plasma. The Jeans instability in collisional dusty plasma has been investigated by Shukla and Verheest (1999). The Jeans instability in partially ionized self-gravitating plasma is observed to study the fragmentation of molecular dusty clouds by Verheest et al. (2003). The effect of non-thermal ion distributions on the Jeans instability in dusty plasmas has been observed by Pillay and Verheest (2005). Tsintsadze et al. (2008) have studied the importance of thermal radiation on the Jeans instability for magnetized dusty plasma with gravitational effects. Mamun et al. (2010) have studied the effects of dust temperature and fast ions on gravitational instability in self-gravitating magnetized dusty plasma.

In addition, magnetohydrodynamics (MHD) is the most useful fluid model for determining the macroscopic equilibrium and stability properties of plasma. Kossacki (1961) has studied the magneto gravitational instability considering the electrical conductivity of viscous rotating plasma using MHD theory. In this direction, for ultra-cold dense quantum plasma, Haas (2005) presented a modified quantum magnetohydrodynamic model to produce a quantum counterpart of magnetohydrodynamics. Similarly, it is of much interest to discuss MHD model for dusty plasma. Shukla and Rahman (1996) presented magnetohydrodynamics of dusty plasma. In this work, a set of magnetohydrodynamic equations for multi-component dusty plasma has been derived. The effective one-fluid model for dusty plasma has been used by many researchers to study waves and instabilities. The modulational instability with dust Alfvén ordinary and cusp solitons in self-gravitating magneto-radiative plasma have been studied by Masood et al. (2010). The study of shear flow instabilities in magnetized partially ionized dense dusty plasmas is done by Birk and Wiechen (2002) using dust MHD model. Linear and nonlinear properties of an obliquely propagating dust magnetosonic wave are discussed by Masood et al. (2009) using dust MHD model. Zamanian et al. (2009) used a Hall-MHD type of model to derive general dispersion relation describing the fast and slow dust-magnetosonic modes and the shear dust-Alfvén waves including magnetization of the system. In their studies they assumed that the dust particles have a magnetic dipole moment. Radiation (thermal) instability in weakly ionized plasma with continuous ionization and recombination is studied by Baruah et al. (2010). Jamil et al. (2012) have studied the shear Alfvén waves in quantum dusty magneto plasmas using quantum magnetohydrodynamic model.

In recent years, the importance of viscosity and resistive parameters have been shown in many astrophysical dusty objects (Fortov et al. 2012; Prasad and Rama 1997; Zaburdaev 2001; Knobloch and Julien 2005) and laboratory dusty plasma (Ji et al. 2001; Mikhailovskii et al. 2008). Magnetorotational instability in dissipative dusty plasmas has been studied by Ren et al. (2009a). With this background and considerations, the present study is motivated by the Tsintsadze et al. (2008) and Masood et al. (2010). Thus, considering the significance of present problem in the collapse process of dense astrophysical dusty plasma, we have studied the self-gravitational instability of dusty magneto plasma using magnetohydrodynamic model for dust incorporating the dissipation effects due to viscosity and electrical resistivity.

The paper is organized as follows: Sect. 2 presents concise summary of basic equations with magnetohydrodynamic model for dusty system. The derivation of general dispersion relation from linearized perturbation equations is given in Sect. 3. Section 4 presents analytical and numerical discussion of modified dispersion relation considering different propagation directions (with respect to magnetic field). The interpretation of the graphs plotted using actual and normalized parameters of considered astrophysical situation are also given in the same section. Conclusion of the work is presented in the last section.

2 The model

Let us consider a three component magnetized dusty plasma having electrons, ions and dust grains. The governing equations used are the effective one-fluid MHD equations for dusty plasma. Based on the condition of quasi neutrality and the fact that the temperature of the dust grains is normally less than the temperature of the electrons and ions, it is possible to neglect the gas dynamics. The electron and ion inertia is ignored as we are interested in very low frequency regime. We also ignore the displacement current term in Ampere’s law owing to the same reason. The system is considered in the presence of an external one dimensional magnetic field \(\boldsymbol{B} = \boldsymbol{B}_{0}\hat{z}\), where \(\hat{z}\) is unit vector along z direction. In general, the dust grains have distributions in mass, size and charge. However, for simplicity, we have assumed that all the dust grains are of the same size, same mass \(m_{d}\), and equal charge \(q_{d}e\) and are mobile with respect to the rest species. The quasi neutrality condition is \(n_{i} = n_{e} + q_{d}n_{d}\). Here, \(n_{j}\) is the number density of species \(j\) (\(j=i, e, \mbox{ and } d\) represent ions, electrons and dusty grains, respectively) and \(q_{d}\) is the charge on dust grains. The basic set of MHD equations for dusty plasma with these assumptions reads as follows.

The equation of motion for magnetized dusty fluid is (Tsintsadze et al. 2008; Shukla and Rahman 1996)

$$ \begin{aligned}[b] & \rho_{d} \biggl( \frac{\partial}{\partial t} + \boldsymbol{v}_{d}. \nabla \biggr)\boldsymbol{v}_{d} \\ &\quad = \rho_{d}\nabla \psi - \nabla P + \frac{1}{4\pi} ( \nabla \times \boldsymbol{B} ) \times \boldsymbol{B} + \mu \rho_{d}\nabla^{2}\boldsymbol{v}_{d}, \end{aligned} $$
(1)

The equation of continuity is given by

$$ \frac{\partial}{\partial t}\rho_{d} + \nabla. ( \rho_{d} \boldsymbol{v}_{d} ) = 0, $$
(2)

The equation for magnetic force is written as

$$ \frac{\partial \boldsymbol{B}}{\partial t} = \nabla \times ( \boldsymbol{v}_{d} \times \boldsymbol{B} ) + \eta \nabla^{2}\boldsymbol{B} $$
(3)

The Poisson’s equation for self-gravitational potential is

$$ \nabla^{2}\psi = - 4\pi G\rho_{d} $$
(4)

where pressure \(P = \sum_{s} p_{s} = n_{d}k_{B} ( T_{d} + q_{d}T_{i} ) + n_{e}k_{B} ( T_{e} + T_{i} )\) (Shukla and Rahman 1996) and \(p_{s}\) (\(= n_{s}k_{B}T_{s}\)) and \(T_{s}\) are the pressure and temperature of s species (\(s = i, e, d\)), respectively. The electrical resistivity of the conducting fluid is expressed as \(\eta = c^{2} / 4\pi \zeta\) where \(\zeta\) is the electrical conductivity, \(\mu\) the fluid viscosity, \(v_{d}\), \(\rho_{d}\), \(G\), \(P\) and \(\psi\) represent the equilibrium dust fluid velocity, dust fluid density, gravitational constant, fluid pressure and gravitational potential respectively.

3 Linearized perturbation equations and dispersion relation

For the process of linearization, all space and time dependent variables are considered as made of two parts viz. equilibrium and perturbed parts. The terms followed by ‘\(\delta\)’ show the perturbed part and the terms with subscript ‘0’ represent the equilibrium one.

$$ \begin{aligned} & \psi = \psi_{0} + \delta \psi,\qquad \boldsymbol{B} = \boldsymbol{B}_{0} + \delta \boldsymbol{B}, \qquad \boldsymbol{v}_{d} = \boldsymbol{v}_{d0} + \delta \boldsymbol{v}_{d}, \\ & P = P_{0} + \delta P,\qquad \rho_{d} = \rho_{d0} + \delta \rho_{d} \end{aligned} $$
(5)

The terms \(\delta \boldsymbol{B}\) symbolize the perturbations in magnetic field, \(\delta \rho_{d}\) signifies the perturbations in fluid density, \(\delta P\) shows perturbations in fluid pressure, \(\delta \boldsymbol{v}_{d}\) gives perturbations in fluid velocity, \(\delta \psi\) is perturbations in gravitational potential. The viscous magnetized plasma is considered with \(\boldsymbol{v}_{d0} = 0\). Further, we do not use ‘0’ in the equilibrium quantities. Using (1)–(5), we write the linearized perturbation equations of finitely conducting, viscous dusty plasma as

$$ \begin{aligned}[b] \rho_{d}\frac{\partial \delta \boldsymbol{v}_{d}}{\partial t} &= \rho_{d}\nabla \delta \psi - \nabla \delta P + \frac{1}{4\pi} ( \nabla \times \delta \boldsymbol{B} ) \times \boldsymbol{B} \\ &\quad {} + \mu \rho_{d}\nabla^{2}\delta \boldsymbol{v}_{d}, \end{aligned} $$
(6)
$$ \frac{\partial}{\partial t}\delta \rho_{d} + \rho_{d}\nabla. \delta \boldsymbol{v}_{d} = 0, $$
(7)
$$ \nabla^{2}\delta \psi = - 4\pi G\delta \rho_{d} $$
(8)
$$ \frac{\partial \delta \boldsymbol{B}}{\partial t} = \nabla \times ( \delta \boldsymbol{v}_{d} \times \boldsymbol{B} ) + \eta \nabla^{2}\delta \boldsymbol{B} $$
(9)

However, we assume the variation of perturbation as \(\exp (i\boldsymbol{k}.\boldsymbol{r} + i\omega t)\), (where \(\omega\) is the frequency of disturbance and \(k = k_{x}\hat{x} + k_{z}\hat{z}\) denotes wave number) and using this type of perturbation (6)–(9) can be written as

$$ \begin{aligned}[b] \rho_{d}i\omega \delta \boldsymbol{v}_{d} &= - i \boldsymbol{k}\delta P + \frac{1}{4\pi} ( i\boldsymbol{k} \times \delta \boldsymbol{B}) \times \boldsymbol{B} \\ &\quad {} - \mu \rho_{d}k^{2} \delta \boldsymbol{v}_{d} + \rho_{d} i\boldsymbol{k}\delta \psi \end{aligned} $$
(10)
$$ i\omega \delta \rho_{d} = - \rho_{d} i\boldsymbol{k}. \delta \boldsymbol{v}_{d}, $$
(11)
$$ i\omega \delta \boldsymbol{B} = i\boldsymbol{k} \times (\delta \boldsymbol{v}_{d} \times \boldsymbol{B}) - \eta k^{2}\delta \boldsymbol{B} $$
(12)

and

$$ - k^{2}\delta \psi = - 4\pi G\delta \rho_{d}, $$
(13)

Using the linearized set of equations and assuming \(n_{d}k_{B} ( T_{d} + q_{d}T_{i} ) \gg n_{e}k_{B} ( T_{e} + T_{i} )\), we obtain the following expressions for the three components of \(\delta \boldsymbol{v}_{d}\) (\(v_{dx}\) \(v_{dy}\) and \(v_{dz}\)) and can be written in the matrix form as follows

$$ {}[X_{m n}] [Y_{n}] = 0\quad m,n = 1, 2, 3, $$
(14)

where \([X_{m,n}]\) is \(3 \times 3\) and \([Y_{n}]\) is \(3 \times 1\) matrix, having elements as

$$ \begin{aligned} &X_{11} = - \omega^{2} + k_{x}^{2}T^{2} + i\omega \mu k^{2}+ \frac{i\omega k^{2}V_{dA}^{2}}{ ( i\omega + \eta k^{2} )},\qquad X_{12} = 0, \\ &X_{13} = k_{x}k_{z}T^{2} \\ &X_{21} = 0, \qquad X_{22} = i\omega + \mu k^{2} + \frac{k_{z}^{2}V_{dA}^{2}}{ ( i\omega + \eta k^{2} )}, \\ & X_{23} =0, \\ &X_{31} = k_{x}k_{z}T^{2}, \qquad X_{32} = 0, \\ & X_{33} = - \omega^{2} + k_{z}^{2}T^{2} + i\omega \mu k^{2} \\ &Y_{1} = v_{d x},\qquad Y_{2} = v_{d y},\qquad Y_{3} = v_{d z}, \end{aligned} $$
(15)

where \(\varOmega_{Jd} = ( 4\pi G\rho_{d} )^{1 / 2}\) is the plasma dust Jeans frequency, \(V_{dS} = [ ( q_{d}k_{B}T_{i} + k_{B}T_{d} ) / m_{d} ]^{1 / 2}\) is the modified dust acoustic speed and \(T^{2} = V_{dS}^{2} - \varOmega_{Jd}^{2} / k^{2}\). Moreover, using \(i\omega = \sigma\) in the determinant of matrix (15) offers the general dispersion relation as

$$ \begin{aligned}[b] &\biggl[ \sigma^{4} + \sigma^{3}k^{2} \biggl( 2\mu + \frac{V_{dA}^{2}}{ ( \sigma + \eta k^{2} )} \biggr) \\ &\quad {}+\sigma^{2}k^{2} \biggl( T^{2} + \mu^{2}k^{2} + \frac{\mu k^{2}V_{dA}^{2}}{ ( \sigma + \eta k^{2} )} \biggr) \\ &\quad {}+ \sigma k^{2}T^{2} \biggl( \mu k^{2} + \frac{ ( k. V_{dA} )^{2}}{ ( \sigma + \eta k^{2} )} \biggr) \biggr] \\ &\quad {}\times \biggl( \sigma + \mu k^{2} + \frac{ ( k. V_{dA} )^{2}}{ ( \sigma + \eta k^{2} )} \biggr) = 0 \end{aligned} $$
(16)

and \(V_{dA} = \sqrt{B / 4 \pi \rho_{d}}\) is the dust Alfvén velocity. The general dispersion relation of Jeans instability of dusty plasma considering dissipation due to the resistive and viscous effects is represented by (16). If we consider the situations where the value of viscosity is ignorable (\(\mu = 0\)), the gravitational mode of (16) can be written as

$$ \begin{aligned}[b] & \sigma^{4} + \sigma^{2} \biggl\{ \frac{V_{dA}^{2}\sigma}{ ( \sigma + \eta k^{2} )} + T^{2} \biggr\} k^{2} + \frac{\sigma}{ ( \sigma + \eta k^{2} )}k^{2}T^{2} ( k. V_{dA} )^{2} \\ &\quad = 0 \end{aligned} $$
(17)

Equation (17) shows fast and the slow dust magnetosonic waves modified by gravitational potential and resistive effects. In absence of gravitational and resistive effects the above Eq. (17) takes the shape as \(\sigma^{4} + \sigma^{2}k^{2} \{ V_{dA}^{2} + V_{dS}^{2} \} + k^{2}V_{dS}^{2} ( k. V_{dA} )^{2} = 0\) that represents typical dust magnetohydrodynamic wave. Equation (17) resembles the result given by Ren et al. (2009b) for electron ion plasma excluding quantum effect of electrons in that case. If we consider the ignorable values of both resistivity and viscosity i.e. \(\eta = 0\), \(\mu = 0\) in that case (16) describes Jeans instability in dusty plasma which is studied by Tsintsadze et al. (2008) excluding radiative effects in that case, and also recovers the result given for electron ion plasma by Lundin et al. (2008) excluding effect of magnetization due to the spin and quantum effects of electrons in that case. The analysis of (16) gives the solutions, for non-viscous, infinitely conducting (\(\eta = 0\), \(\mu = 0\)) case as

$$ \begin{aligned}[b] \sigma_{F,S}^{2} &= \frac{1}{2} \bigl[ - k^{2} \bigl( T^{2} + V_{dA}^{2} \bigr) \\ &\quad {}\pm \bigl\{ k^{4} \bigl( T^{2} + V_{dA}^{2} \bigr)^{2} - 4k^{2}T^{2} ( k. V_{dA} )^{2} \bigr\} ^{1 / 2} \bigr] \end{aligned} $$
(18)

and the subscripts \(F\) and \(S\) stand for ‘fast’ and ‘slow’ respectively. If we consider the situation where the propagation of perturbation is along the magnetic field, there will be two independent propagating waves represented as \(\sigma_{\parallel F}^{2} = - k^{2}V_{dA}^{2}\) and \(\sigma_{\parallel S}^{2} = - k^{2}T^{2}\) respectively. If we observe these two waves, it is obvious that one is non-gravitating (Alfvén) mode and other is gravitating mode.

Moreover, in the presence of resistivity and viscosity the gravitational mode gets separated from Alfvén mode for general propagation and can be written as

$$\begin{aligned} &{\sigma^{4} + \sigma^{3} ( 2\mu + \eta )k^{2} } \\ &{\quad {} + \sigma^{2} \biggl\{ 2\mu \eta k^{4} + ( k. V_{dA} )^{2} + k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) + \mu^{2}k^{4} \biggr\} } \\ &{\quad {}+ \sigma k^{2} \biggl\{ \mu^{2}\eta k^{4} + \eta k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) + \mu ( k. V_{dA} )^{2} } \\ &{\quad {} + \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr)\mu k^{2} \biggr\} } \\ &{\quad {} + k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) \bigl\{ \mu \eta k^{4} + ( k. V_{dA} )^{2} \bigr\} = 0 } \end{aligned}$$
(19)

Since parameter \(\mu\), \(\eta\), \(V_{dA}\) are always positive, and, if value of \(T^{2}\) is positive, all coefficients of (19) are positive. Further, it is well known that an equation with all positive real coefficients, (19) can have no positive real roots. Therefore, in the case of \(T^{2} > 0\) the solutions of (19) describes the stable state of the medium. Since (19) is quartic equation in \(\sigma\), it follows that there are in general four modes in which a wave can be propagated in the medium; and if \(\sigma_{1}\), \(\sigma_{2}\), \(\sigma_{3}\) and \(\sigma_{4}\) denote the frequencies of these four modes, in all cases the following dependence must be satisfied by the roots of (19)

$$ \sigma_{1} \sigma_{2} \sigma_{3} \sigma_{4} = k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) \bigl( \mu \eta k^{4} + k^{2}V_{dA}^{2} \bigr) $$
(20)

Therefore, we can say if \(( V_{dS}^{2} - \varOmega_{Jd}^{2} / k^{2} ) < 0\), at least one of the real roots must be positive and the considered system is unstable. If (19) has complex roots, we can obtain an equation that must be satisfied by real parts of the roots. In the case of \(( V_{dS}^{2} - \varOmega_{Jd}^{2} / k^{2} ) > 0\), all coefficients of this equation are positive, and thus complex roots with positive real parts cannot exist. Hence, the medium must be stable. Thus, it is proved that the medium is stable in respect to small perturbations, if \(( V_{dS}^{2} - \varOmega_{Jd}^{2} / k^{2} )\) is positive, and unstable, if \(( V_{dS}^{2} - \varOmega_{Jd}^{2} / k^{2} )\) is negative.

To investigate the instability of the system the general dispersion relation can be discussed in following ways: when the perturbation propagates perpendicular and along the direction of magnetic field and when the perturbation propagates to the oblique direction of the magnetic field.

4 Discussions

4.1 Propagation transverse to the magnetic field

First, we consider the situation where the perturbations are propagating transverse to the direction of magnetic field, in that case, we place \(k_{x} = k\), \(k_{z} = 0\) in (16) and we acquire

$$ \begin{aligned}[b] & \bigl\{ \sigma + \mu k^{2} \bigr\} ^{2} \biggl\{ \sigma^{2} + k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) + \sigma \mu k^{2} \\ &\quad {}+ \frac{\sigma k^{2}V_{dA}^{2}}{ ( \sigma + \eta k^{2} )} \biggr\} = 0 \end{aligned} $$
(21)

It is clear from the above dispersion relation that it separates the wave propagation into two different modes for transverse propagation. The first mode is viscous mode given as

$$ \sigma + \mu k^{2} = 0 $$
(22)

Equation (22) evidently shows the mode is due to viscosity of the medium only. The second gravitating mode can be written as

$$ \begin{aligned}[b] & \sigma^{3} + \sigma^{2} \{ \eta + \mu \}k^{2} \\ &\quad {}+ \sigma \biggl\{ k^{2} \biggl\{ V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr\} + k^{2}V_{dA}^{2} + \mu \eta k^{4} \biggr\} \\ &\quad {}+ \eta \biggl\{ V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr\} k^{4} = 0 \end{aligned} $$
(23)

It is clear that the gravitating mode is modified due to the presence of magnetic field (dust Alfvén velocity), viscosity and resistivity effects. In absence of resistivity and viscosity the dispersion relation reduces to

$$ \sigma^{2} + k^{2} \biggl( V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr) + k^{2}V_{dA}^{2} = 0 $$
(24)

In absence of gravitational effect above dispersion relation matches with (19) obtained by Zamanian et al. (2009) excluding intrinsic magnetization in that case. They studied the dust dynamics using Hall MHD type model incorporating the magnetic moment of dust. The above dispersion relation is identical to (28) obtained by Tsintsadze et al. (2008). It is clearly visible form (24) that the solution of the equation has the following form:

$$ \sigma = \pm ik \biggl\{ V_{dS}^{2} + V_{dA}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr\} $$
(25)

This shows that in absence of gravitational effects there will be two waves propagating in the opposite directions which will be the combination of Alfvén and dust acoustic modes. However, (23) is cubic equation and if the constant term of (23) is less than zero, the condition of instability can be written as

$$ \bigl[ ( q_{d}k_{B}T_{i} + k_{B}T_{d} ) / m_{d} \bigr] < \varOmega_{Jd}^{2} / k^{2} $$
(26)

The above equation represents the condition of instability and it is clear that the condition is not affected by viscosity and resistivity parameter but from (23) it is clear that the growth rate of instability will be modified by viscosity and resistivity parameter of the system.

If one observes the gravitating mode given by (23), it is clearly visible that the growth rate of instability is depending upon resistivity and viscosity. For our numerical analysis of (23), we have chosen the plasma parameters that are typical for a number of space and astrophysical plasma systems, particularly for molecular clouds, protostellar disks, interstellar and circumstellar clouds, the ionosphere of the Earth, etc. (Evans 1994; Verheest and Cadez 2002; Whittet 1992). The dust number density has been assumed as \(n_{d0} = 10^{ - 1}\mbox{ m}^{ - 3}\), \(m_{d} = 4 \times 10^{ - 15}\mbox{ kg}\), \(G = 6.67 \times 10^{ - 11}\mbox{ m}^{3}\,\mbox{kg}^{ - 1}\,\mbox{s}^{ - 2}\), the magnetic field is of the order of \(B = 3 \times 10^{ - 10}\mbox{ T}\), dust Alfvén velocity \(V_{dA} = 13.4\mbox{ m/s}\), and dust temperature is \(T_{d} = 30\mbox{ K}\), dust acoustic speed is \(V_{ds} \simeq 2.8\mbox{ m/s}\). Thus, the Jeans dust frequency is calculated considering the above parameters, which is found to be \(\varOmega_{Jd} = 10^{ - 13}\mbox{ s}^{ - 1}\).

The above mentioned astrophysical situations are rich in dust and the magnetic field induced current in the magneto dust fluid modifies the dynamics of the fluid. The viscous and resistive processes are of much importance in the dynamics of these astrophysical medium as the energy is dissipated via. viscous and resistive processes. The distribution of dust particles in the interstellar, protostellar, circumstellar and molecular local sheet of cloud (with the size and charge distribution of dust) is connected with the overall energy dissipation properties and leads to wide range of viscosity and conductivity. This can be achieved using a number of ex situ and in situ technique. The observed wide range of parameters suggests the local sheet to sheet variation of specific dusty cloud characteristics. Reviewing the literature for the interstellar dusty, molecular dusty and protostellar disks and circumstellar clouds, (Verheest and Cadez 2002; Mamun and Shukla 2000; Zhukhovitskii et al. 2015; Mamun and Shukla 2001; Goerz 1989; Spitzer 1941; Angelis 1992) it is clear that the value of viscosity and resistivity covers extensive range depending upon the density, temperature and magnetic field of the region. Therefore the range of viscosity and resistivity parameters for the specific local sheet of cloud of astrophysical situation chosen as \(\mu = 10^{10\text{--}16}\mbox{ m}^{ - 2} \,\mbox{s}^{ - 1}\), \(\eta = 10^{ 8\text{--}15}\mbox{ m}^{2}\,\mbox{s}^{ - 1}\) (Evans 1994; Whittet 1992; Shukla 2002; Krugel 2002; Verheest 2012; Crutcher 1998; Lizano and Galli 2014). Here, we restrict ourselves to the case in which viscosity and resistivity are almost of the same order. The numerical analysis of these environments is performed using both the dimensionless and real (actual) parameters of the astrophysical situation. However, the predictions of the analytical results are well described and verified by the numerical results.

In particular, the relevance of the resistive and viscous effects to the dusty interstellar, protostellar and circumstellar clouds is discussed using the real parameters. The results clearly show that for the above mentioned dusty situations the gravitational instability is affected directly with the dissipative effects. The parameters mentioned above are used for the numerical calculation. The effect of viscous parameter on the growth rate of self-gravitational instability (when the perturbation propagates in the transverse propagation) has been described in the form of Fig. 1 using (23). Equation (23) is cubic equation and the positive roots of (23) are picked up to observe the growth rate of instability. Figure 1 clearly shows that the threshold of instability is independent from the viscosity parameter. It is also verified from condition (26). It is clear from the figure that as the value of viscosity parameter increases the growth rate of instability decreases and hence it shows stabilization effect on the growth rate of gravitational instability. Similarly, Fig. 2 shows the effect of resistivity parameter on the growth rate of gravitational instability in the transverse direction of propagation. The analysis of the figure displays that as the value resistivity increases the growth rate of instability also increases. It is also obvious from the figure that the threshold of instability is independent from the resistive parameter. Figure 3 shows the effect of magnetic field strength on growth rate and clearly shows the stabilizing effect on the instability. It is also clear from Fig. 3 that the critical wave number is independent from the magnetic field. It is important to note that the value of threshold for Jeans instability is estimated as 35.714286.

Fig. 1
figure 1

Growth rate of Jeans instability with wave number for various values of viscosity parameter for transverse propagation. The parameters used are \(V_{dA} = 13.4\), \(V_{dS} = 2.8\), \(\eta = 10^{15}\), \(\varOmega_{Jd} = 10^{ - 13}\)

Full size image
Fig. 2
figure 2

Growth rate of Jeans instability with wave number for various values of resistivity parameter for transverse propagation. The parameters used are \(V_{dA} = 13.4\), \(V_{dS} = 2.8\), \(\mu = 10^{13}\), \(\varOmega_{Jd} = 10^{ - 13}\)

Full size image
Fig. 3
figure 3

Growth rate of Jeans instability with wave number for various values of magnetic field parameter for transverse propagation. The parameters used are \(V_{dA} = 13.4\), \(V_{dS} = 2.8\), \(\eta = 10^{15}\), \(\mu = 10^{13}\), \(\varOmega_{Jd} = 10^{ - 13}\)

Full size image

Further, the normalization is performed with the help of Jeans dust frequency and dust acoustic speed and can be applied to the different ranges of plasma parameters. Hence, the corresponding parameters, which stand for our numerical analysis, are \(V_{dA} / V_{ds} = 4.78\mbox{--}5.5\), \(\mu^{*}= 0.1\mbox{--}0.3\), \(\eta^{*} = 0.1\mbox{--}0.3\). These parameters have been constantly used by various researchers to study effect of viscosity and resistivity on waves and instabilities. Thus, the results of the present investigation should help us to explain the basic features of the dynamics of various parts of protostellar disks, interstellar, circumstellar and molecular clouds.

The effects of electrical resistivity and viscosity corrections on the growth rate of Jeans instability in dusty plasma can be readily analyzed numerically using normalized parameters. The following dimensionless parameters are used

$$ \begin{aligned} & \sigma^{*} = \frac{\sigma}{\varOmega_{Jd}}, \qquad k^{*} = \frac{kV_{ds}}{\varOmega_{Jd}},\qquad \eta^{*} = \frac{\eta \varOmega_{Jd}}{V_{ds}^{2}}, \\ & V_{dA}^{*} = \frac{V_{dA}}{V_{ds}}, \qquad \mu^{*} = \frac{\mu \varOmega_{Jd}}{V_{ds}^{2}} \end{aligned} $$
(27)

First, we write Eq. (23) in dimensionless form, using Eq. (27). The normalized form of Eq. (23) can be written as

$$ \begin{aligned}[b] & \sigma^{*3} + \sigma^{*2} \bigl( \eta^{*} + \mu^{*} \bigr)k^{*2} \\ &\quad {}+ \sigma^{*} \bigl( k^{*2} - 1 + k^{*2}V_{dA}^{*2} + \mu^{*}\eta^{*}k^{*4} \bigr) \\ &\quad {}+\eta^{*}k^{*2} \bigl( k^{*2} - 1 \bigr) = 0 \end{aligned} $$
(28)

For the purpose of study the influence of resistivity and viscosity corrections in the transverse direction of propagation on the growth rate of Jeans instability, we solve (28) numerically. The solution of normalized dispersion relation (28) relates to the frequency \(\sigma\) and wave vector k and thereby determines the normal modes of plasma. The dispersion relation can be solved with the initial value problem in which k is given real and wave frequency \(\omega\) can be written as \(\omega = \omega_{r} + i\gamma\), where \(\gamma\) is the growth rate or damping rate. Now, if we take real positive value of \(\sigma\) it will determine growth rate, if we take real negative value of \(\sigma\) it determines damping rate and taking the imaginary value (either positive or negative) it shows oscillations. So in the present case to observe instability real positive roots are chosen that will give growth rate of instability. Moreover, using (28) the growth rate of Jeans instability has been examined in Figs. 4, 5, and 6 for different values of dimensionless viscosity, resistivity and magnetic field strength. In Fig. 4, we have plotted the growth rate of instability against the normalized wave number (\(k^{*}\)) for various values of dimensionless viscosity parameter \(\mu^{*}\) keeping the fix value of dimensionless resistivity \(\eta^{*}\) and dimensionless dust Alfvén speed \(V_{dA}^{*}\). Figure 4 clearly displays the influence of viscosity parameter \(\mu^{*}\) on the growth rate of Jeans instability. If we analyze this figure with three curves for different viscosity values, we can see that at \(k=0\) all curves show that the growth rate is unity, which can also be verified analytically from the dispersion relation. However, as the wave number advances the curve proceeds picking up different values of growth rate for different values of viscosity and hence each curve moves in a different way. The figure shows that for initial wave numbers the peak value of the perturbation growth rate is constant for all the values of viscosity parameter, but further, (with the increase of wave number) the growth rate of instability decreases with increase in the parameter \(\mu^{*}\). So, one can conclude the influence of viscosity parameter is found as stabilizing on the growth rate of Jeans instability of dusty plasma. The unstable region is found to be decreased with growing value of \(\mu^{*}\). However, it is to be noted that the threshold remains the same for different values of viscosity, this is also in agreement with the threshold condition given by (26). In the same manner further, Fig. 5 represents the growth rate of instability \(\sigma^{*}\) with the normalized wave number \(k^{*}\) for several values of resistivity parameter \(\eta^{*}\). Figure shows that with the increasing value of resistivity, growth rate increases and hence electrical resistivity has destabilizing effect on the Jeans instability. It is again clearly seen from the figure that threshold of instability remains the same for all values of resistivity, since the instability condition is independent from the resistivity parameter. Further, the evaluation of these two figures tells us that on similar background condition the effect of viscosity parameter is more dominating in comparison to the resistivity parameter. It is to be mentioned here that viscosity appears in the momentum equation, and the resistivity comes in the induction equation. In the momentum equation the viscous stresses due to viscous forces tending to resist the relative movement of adjacent layers of the fluid, and lead to stabilizing effect. While, the finite resistivity allows plasma to slip up across the field lines, and thus the restrictive effect of the field in infinite conductivity disappears, and finite resistivity shows a destabilizing influence. Moreover, Fig. 6 describes the effect of magnetic field on growth rate of instability. An increase in the value of magnetic field tends to decrease the instability growth rate. It describes that the magnetic field has stabilizing effect on growth rate of Jeans instability. The growth rate decreases fast with rise in the magnetic field. Actually, higher value of magnetic field led to higher cyclotron frequency and thus a lesser amount of energy is shared to the low frequency mode. However, it is clearly seen from the figure as the magnetic field is increased, the threshold value of wave vector remains constant it can be verified by the threshold condition also that the Jeans condition of instability does not depend upon the magnetic field.

Fig. 4
figure 4

The normalized growth rate of Jeans instability versus normalized wavenumber in transverse propagation for various values of the viscosity parameter (\(\mu^{*}\)) for dusty fluid. The values of constant parameters are taken to be \(V_{dA}^{*} = 4.78\), \(\eta^{*} = 0.3\)

Full size image
Fig. 5
figure 5

The normalized growth rate of Jeans instability versus normalized wavenumber in transverse propagation for various values of the viscosity parameter (\(\eta^{*}\)) for dusty fluid. The values of constant parameters are taken to be \(V_{dA}^{*} = 4.78\), \(\mu^{*} = 0.3\)

Full size image
Fig. 6
figure 6

The normalized growth rate of Jeans instability versus normalized wavenumber in transverse direction for various values of the magnetic field parameter (\(V_{dA}^{*}\)) for dusty fluid. The values of constant parameters are taken to be \(\mu^{*} = 0.1\), \(\eta^{*} = 0.1\)

Full size image

4.2 Propagation along the magnetic field

We consider only the wave mode which propagates along the direction of the magnetic field. We put \(k_{x} = 0\), \(k_{z} = k\) in (16). The dispersion relation obtained in the longitudinal propagation case can be written as

$$ \bigl\{ \sigma^{2} + \sigma \mu k^{2} + k^{2}T^{2} \bigr\} \biggl\{ \sigma + \mu k^{2} + \frac{k^{2}V_{dA}^{2}}{ ( \sigma + \eta k^{2} )} \biggr\} ^{2} = 0 $$
(29)

The first factor of the (29) gives gravitational mode as

$$ \sigma^{2} + \sigma \mu k^{2} + k^{2} \biggl\{ V_{dS}^{2} - \frac{\varOmega_{Jd}^{2}}{k^{2}} \biggr\} = 0 $$
(30)

It is clear from above equation that the resistivity parameter does not influence the Jeans instability of magneto dusty plasma. Equation (30) is quadratic equation in \(\sigma\) with constant term. When constant term of (30) is less than zero this allows at least one positive real root which corresponds to the instability of the system. Thus, when perturbation propagates along the direction of magnetic field, the general condition of instability is obtained from constant term of (30) is given as

$$ k^{2}V_{dS}^{2} < 4\pi G\rho_{d} $$
(31)

It is clear from the above equation that the Jeans criterion for the gravitational instability of a medium is unaffected even if viscosity and resistivity effects are included. The Jeans condition resembles the condition of instability obtained by Zamanian et al. (2009) and Tsintsadze et al. (2008) The condition also matches with the one obtained by Ren et al. (2009a) as well as Lundin et al. (2008) for the electron ion case excluding quantum effects in that case.

However, from (29) the Alfvén mode is given as

$$ \sigma^{2} + \sigma ( \mu + \eta )k^{2} + \mu \eta k^{4} + k^{2}V_{dA}^{2} = 0 $$
(32)

The solutions of Eq. (32) have the following form

$$ \sigma_{1,2} = - \frac{1}{2} ( \mu + \eta )k^{2} \pm \frac{1}{2} \bigl[ ( \mu - \eta )^{2}k^{4} - 4k^{2}V_{dA}^{2} \bigr]^{1/2} $$
(33)

It is important to mention that in presence of viscosity and resistivity the propagation of Alfven waves does not get affected due to gravitational potential in the general propagation. If we put \(\eta = 0\), \(\mu = 0\) we have two Alfvén waves along the z axis in opposite directions. The presence of terms \(\mu\) and \(\eta\) in (32) describes damping due to viscosity and electrical resistance. Since the solution of (33) will always be an imaginary number. Hence, the Alfvén waves cannot cause instability in the considered system.

Further, in the longitudinal direction of propagation growth rate of Jeans instability is observed using real (actual) parameters from (30). Figure 7 shows the effect of viscous parameter on the growth rate of gravitational instability and the growth rate decreases with the increase of viscosity parameter and hence the viscosity shows stabilizing effect. Figure 8 is plotted for the various real (actual) values of dust acoustic speed and it shows that since the threshold of instability depends on the value of \(V_{d s}\), figure shows different threshold values for different value of \(V_{d s}\). These values are estimated as 55.555556, 35.714286 and 26.31579. It is clearly observed from figure that as the value of \(V_{d s}\) increases the growth rate of Jeans instability decreases. Thus, \(V_{d s}\) describes stabilization effect and verifies the condition (31) for gravitational instability.

Fig. 7
figure 7

Growth rate of Jeans instability with wave number for various values of viscosity parameter for longitudinal propagation. The parameters used are \(V_{dS} = 2.8\), \(\varOmega_{Jd} = 10^{ - 13}\)

Full size image
Fig. 8
figure 8

Growth rate of Jeans instability with wave number for various values of dust acoustic speed for longitudinal propagation. The parameters used are \(\mu = 10^{13}\), \(\varOmega_{Jd} = 10^{ - 13}\)

Full size image

For the purpose to observe the effects of viscosity corrections (using the normalized parameters) on the growth rate of Jeans instability of dusty plasma along the direction of magnetic field, we discuss the dispersion relation indicated by (30) numerically. Equation (30) is normalized using Eq. (27) as

$$ \sigma^{*2} + \sigma^{*}\mu^{*}k^{*2} + k^{*2} - 1 = 0 $$
(34)

The growth rate of instability is to be studied for longitudinal propagation using (34). Numerical analysis of (34) is displayed in the form of Fig. 9. Figure 9 displays the growth rate of instability with the normalized wave number (\(k^{*}\)) for different values of dimensionless viscosity in longitudinal direction. Figure 9 clearly shows the growth rate decreases with increasing the value of viscosity. So, the influence of viscosity on the growth rate of instability is stabilizing. Figure 9 displays that initially the highest value of the growth rate and the threshold of instability remains the same for all values of viscosities which are in agreement with the analytical results. The comparison of Fig. 7 obtained using real (actual) parameters, and Fig. 9 obtained using normalized parameters shows that both figures exhibit same conclusions for the growth rate of Jeans instability.

Fig. 9
figure 9

The normalized growth rate of Jeans instability versus normalized wavenumber for various values of viscosity parameter (\(\mu^{*}\)) in longitudinal direction

Full size image

However, for the longitudinal and transverse propagation, we have presented graphs using both real (actual) data and the normalized data. It is important to mention that the graph plotted with the actual values can be used to study the dynamics of specific situation and specify how effective a particular physical effect would be for that system. On the other hand the graphs plotted using normalized data can be applied to study various situations in the astrophysical region using appropriate data from that region.

4.3 Propagation at an angle \(\theta\) to the magnetic field:

We study the case when perturbation propagates in an arbitrary direction with respect to the magnetic field \(\boldsymbol{B}\). The coordinates are considered such that y axis is perpendicular to the plane of propagation \(\boldsymbol{k}\) and the magnetic field \(\boldsymbol{B}\). The magnetic field \(\boldsymbol{B}\) is considered along z axis and the angle between \(\boldsymbol{k}\) and \(\boldsymbol{B}\) is \(\theta\) as \(\boldsymbol{k} = k\) (\(\sin\theta \hat{x} + \cos\theta \hat{z}\)), therefore (15) takes the shape as

$$ \begin{aligned} & X_{11} = - \omega^{2} + k^{2} \sin^{2}\theta T^{2} + i\omega \mu k^{2} + \frac{i\omega k^{2}V_{dA}^{2}\cos^{2}\theta}{ ( i\omega + \eta k^{2} )}, \\ & X_{12} = 0, \qquad X_{13} = k^{2}\sin \theta \cos \theta T^{2} \\ & X_{21} = 0, \qquad X_{22} = i\omega + \mu k^{2} + \frac{k^{2}\cos^{2}\theta V_{dA}^{2}}{ ( i\omega + \eta k^{2} )}, \\ & X_{23} = 0, \\ & X_{31} = k^{2}\sin \theta \cos \theta T^{2},\qquad X_{ 3 2} = 0, \\ & X_{33} = - \omega^{2} + k^{2} \cos^{2}\theta T^{2} + i\omega \mu k^{2} \end{aligned} $$
(35)

after solving this matrix (using \(\sigma = i\omega\)) we get the following dispersion relation as

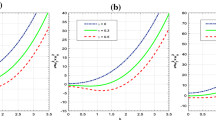
$$ \begin{aligned}[b] & \sigma^{4} + \sigma^{3} ( 2\mu + \eta )k^{2} + \sigma^{2} \bigl( 2\mu \eta k^{4} + V_{dA}^{2}k^{2}\cos^{2} \theta + k^{2}V_{dS}^{2} \\ &\quad {}- \varOmega_{Jd}^{2} + \mu^{2}k^{4} \bigr) + \sigma k^{2} \bigl\{ \mu^{2}\eta k^{4} + \eta \bigl( k^{2}V_{dS}^{2} - \varOmega_{Jd}^{2} \bigr) \\ &\quad {} + \mu k^{2}V_{dA}^{2}\cos^{2}\theta + \mu \bigl( k^{2}V_{dS}^{2} - \varOmega_{Jd}^{2} \bigr) \bigr\} \\ &\quad {}+ \bigl( k^{2}V_{dS}^{2} - \varOmega_{Jd}^{2} \bigr) \bigl( \mu \eta k^{4} + k^{2}V_{dA}^{2}\cos^{2}\theta \bigr) = 0 \end{aligned} $$
(36)

Further, we will discuss the dispersion relation (36) numerically at \(\theta = \pi / 4\) and at \(\theta = \pi / 6\) by normalizing it using (27). The results are shown in the form of Figs. 10 and 11 which discusses the effect of viscosity and resistivity respectively. Figure 10a shows the effect of viscosity parameter when the angle between the magnetic field and propagation direction is \(\theta = 30^{\circ}\) and Fig. 10b describes the same for \(\theta = 45^{\circ}\). Both the figures show stabilizing effect of viscosity parameter on growth rate of Jeans instability. Since the condition of instability does not depends upon angle \(\theta\) so the threshold will also stay the same for both the angles. Similarly, Fig. 11a displays the effect of resistivity parameter when direction of propagation is at an angle \(30^{\circ}\) to the magnetic field and Fig. 11b shows the same for \(\theta = 45^{\circ}\). It is clear that resistivity parameter shows destabilizing effect for both the angles \(30^{\circ}\) and \(45^{\circ}\). Thus, we can conclude that viscosity has stabilizing effect and resistivity has destabilizing effect on the growth rate of gravitational instability for both \(\theta = 30^{\circ}\) and \(\theta = 45^{\circ}\).

Fig. 10
figure 10

The normalized growth rate of Jeans instability versus normalized wavenumber for various values of viscosity parameter (\(\mu^{*}\)) (a) at \(\theta = \pi / 6\), (b) at \(\theta = \pi / 4\). The values of constant parameters are taken to be \(V_{dA}^{*} = 4.78\), \(\eta^{*} = 0.1\)

Full size image
Fig. 11
figure 11

The normalized growth rate of Jeans instability versus normalized wavenumber for various values of resistivity parameter (\(\eta^{*}\)) (a) at \(\theta = \pi / 6\), (b) at \(\theta = \pi / 4\). The values of constant parameters are taken to be \(V_{dA}^{*} = 4.78\), \(\mu^{*} = 0.1\)

Full size image

5 Conclusions

In the present work, self-gravitational instability of a magnetized dusty plasma is examined. The general dispersion relation is derived using the linearized perturbation method and discussed to get condition of instability and it is found that the Jeans criterion is unaffected with the resistivity and viscosity parameters. Further, the general dispersion relation is analyzed in different direction of propagation with respect to magnetic field. When perturbation is considered to be propagated in the transverse direction it splits into two modes one is stable viscous and other is gravitating mode coupled with Alfvén mode. In longitudinal direction of propagation resistivity separates the Alfvén mode from gravitational mode. In oblique direction of propagation the gravitating mode is modified by resistivity, viscosity and magnetic field parameter. The numerical results show destabilizing influence of resistivity parameter in the transverse, longitudinal and oblique direction of propagation, while viscosity parameter stabilizes the growth rate of Jeans gravitational instability in transverse, longitudinal and oblique directions of propagation. The results are obtained from both the real parameters of astrophysical plasma as well as the normalized dimensionless data.