Radiative and Gravitational Modes and Instabilities in an Inhomogeneous Magneto Dusty Plasma with Charge Variation

Abstract

The Jeans instability of collisional magnetized dusty plasmas is examined incorporating polarization force, charge variation of dust grains, and radiative cooling of ion and electron species. The collisional effects of dust grains with neutrals are considered with sufficient background of neutral particles. A general dispersion relation is obtained using normal mode analysis technique which is found to be modified due to polarization force, dust charge fluctuation, and radiative effects of electrons and ions. The analytical discussion of general dispersion relation is presented in parallel and perpendicular mode of propagation. The Routh Hurwitz criterion is applied to analyze the stability of the considered system. We report the existence of a modified cyclotron mode in parallel propagation and a purely collisional mode in perpendicular propagation along with the gravitational mode. These modes are discussed analytically, as well as numerically, to show the importance of different parameters considering different situations. The implications of the result have been discussed for the molecular clouds.

1 INTRODUCTION

The wide range of applications of dusty plasma in space and astrophysical situations (such as planetary nebulae, cometary tails, interstellar molecular clouds, and stellar atmospheres) make it an interesting area of research [1–4]. A lot of research has widely been done in the dusty plasma [5–8]. The presence of massive dust and neutrals in a cloud significantly alters the cloud mass such that it exceeds the Jeans mass of the cloud and leads to the collapse. The mechanism involved in cloud collapse is attributable to the self-gravitational instability, which results in further fragmentation of the cloud. In various astrophysical phenomena, for example, star formation and planet formation, the self-gravitational instability plays a central role. Ali and Shukla [9] explored the self-gravitational instability in collisional dusty plasma. Self-gravitational instability in dusty plasma considering degenerate and nondegenerate cases has been studied by Jain and Sharma [10]. Sharma [11] has observed the self-gravitational instability in dissipative dusty plasma. The Jeans instability in magnetized dusty plasma considering the effect of thermal radiations has been studied by Tsintsadze et al. [12]. The effect of Boltzmann distributed negative ions on self-gravitational instability has been observed by Roy and Mukherjee [13]. Along with this, the charging of dust grains via plasma current flowing on dust grains, field emission, photoelectric effect, etc. [14], also modifies the characteristics of dusty plasma. The charge on the dust does not remain constant, and, therefore, the effect of dust charge fluctuation is important to consider [15]. Tsytovich et al. [16] have investigated the dust charging in dusty plasma. Popel et al. [17] have studied the shock structures incorporating the dust charge fluctuation in complex plasma. The effect of dust charge variation on self-gravitational instability in radiative dusty plasma has been discussed by Prajapati and Bhakta [18]. Tsytovich and de Angelis [19] observed the effect of dust charge variation in dusty plasma. Morfill et al. [20] have described the elementary processes considering the dust charge fluctuation in dusty plasma.

In the present work, one of the important effect of dusty plasma, i.e., polarization force, is also important to study as we have considered the massive and highly charged dust grains. The presence of large number of ion number density on negatively charged dust grains deforms the Debye sheath, due to which an electrostatic force experienced by dust particles which polarized the dust. As a result, new force generates in the dusty plasma system which modifies the features of dusty plasma. Khrapak et al. [21] have investigated the dust acoustic wave propagation in dusty plasma with the presence of polarization force. Sharma [22] has studied the effect of polarization force on the Jeans instability in magnetized strongly coupled dusty plasma. Pervin et al. [23] have considered the effect of fast electrons and dust polarization force in strongly coupled dusty plasma to study the dust acoustic shock waves. Influence of polarization force on electrostatic dust acoustic modes in quantum plasma has been discussed by Sharma and Jain [24]. Dutta et al. [25] have explored the effects of polarization force gravito-electromagnetic stability with dust charge variation in nonthermal dusty plasma. The effect of polarization force on dust charge variation in dusty plasma is examined by Shahmansoori and Mamun [26]. They have also studied the influence of generalized polarization force on the propagation of dust acoustic waves. Recently, Abbasi and Vaziri [27] have observed the effect of polarization force on self-gravitational instability in partially ionized dusty plasma considering dust–neutral and ion–neutral drags.

The structure formation of many astrophysical bodies and their existence is believed due to self-gravitation. However, the existence in some small regions, e.g., planetary nebulae, a solar prominence, etc., is due to some kind of radiative condensation process. Moreover, Gammie [28] observed that the self-gravitational collapse of disk can not proceed until its cooling is not enough. So, this notion that there is an interplay between self-gravitational collapse and cooling of plasma species. In this direction, the radiative condensation has been studied in several research works. The role of thermal instability in molecular cloud has been discussed by Gilden [29]. The effect of radiative cooling on self-gravitational instability in partially ionized dusty plasma including the dust charge fluctuation has been examined by Pandey and Krishan [30]. Sharma and Jain [31] have investigated the radiative condensation instability in self-gravitating partially ionized magneto dusty plasma including polarization force. Pandey et al. [32] have investigated the self-gravitational instability in dusty plasma with radiative effect and dust charge fluctuation. Bora [33] has studied thermal instability in dusty plasma including radiative effects of electron, as well as of ions. The role of radiative condensations on Jeans instability in collisional dusty plasma considering dust charge fluctuation has been studied by Sharma and Patidar [34].

In the previous investigations, the influence of radiative condensation of electron and ion on self-gravitational instability in dusty plasma has been studied, but nobody have studied the effect of magnetic field along with the self-gravitation, polarization force, and radiative cooling of ion in partially ionized dusty plasma. Shukla and Sandberg [35] have observed the radiative condensation instability due to electron species in either magnetized or unmagnetized dusty plasma including self-gravitation. They have excluded the effects of radiative cooling of ions, dust charge fluctuation, and polarization force. Pandey and Krishan [30] considered the unmagnetized partially ionized dusty plasma to study the dust charge fluctuation and electron’s radiative effects on self-gravitational instability. However, the external magnetic field greatly modifies the dynamics of dust particles and affects the instability of the system. Therefore, looking toward the importance of the presence of magnetic field, we have incorporated its effect to study the self-gravitational instability in collisional dusty plasma with radiative condensation of ions and electrons, and charge variation and polarization force of dust grains. The present work is performed in the region near by the newly born stars of dark molecular cloud [36, 37].

The manuscript is arranged in the following manner. In Section 2, we have presented the formulation of the considered dusty plasma system, which consists basic and linearized sets of equations, and derivation of general dispersion relation. Section 3 is devoted to the analytical discussion of the general dispersion relation. The graphical discussion is explored in Section 4. The last section considers the conclusion and applications of the presented work.

2 FORMULATION

Let us consider partially ionized self-gravitating dusty plasma with the influence of external magnetic field ${\mathbf{H}} (0,0,H)$. The plasma system is treated as a mixture of four components. The dust particles introduce the collective effects in the system, which modifies the characteristics of the plasma. It has been suggested that the consideration of interaction of plasma species with dust grains is a good approximation [38].

The collisional cross section of plasma particles with dust grains in the study of dusty plasma is ${{\sigma }_{s}} = \pi r_{d}^{2}\left( {1 - 2{{e}_{s}}{{q}_{d}}{\text{/}}{{r}_{d}}{{m}_{d}}\left| {v_{d}^{2}} \right|} \right)$, where $s = e,i$; ${{r}_{d}}$ is the dust grain radius; ${{m}_{d}}$ is the mass of dust particle; and ${{e}_{s}}$ is the electric charge of the sth species.

For the interaction of ion with the dust, the rate of absorption on dust surface (${{\nu }_{{{\text{ch}}}}}$), can be expressed as

$${{\nu }_{{{\text{ch}}}}} = {{\nu }_{q}}\left( {\frac{{{{Z}_{{d0}}}d}}{{1 + {{Z}_{{d0}}}d}}} \right)\frac{{\tau + {{z}_{0}}}}{{1 + \tau + {{z}_{0}}}}$$

and the rate of loss of momentum by ions due to C-oulomb collisions and its absorption on the grain surface is

$$\bar {\nu } = {{\nu }_{q}}\left( {\frac{{{{Z}_{{d0}}}d}}{{1 + {{Z}_{{d0}}}d}}} \right)\frac{{{{z}_{0}} + \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right)\tau + \left( {{{2z_{0}^{2}} \mathord{\left/ {\vphantom {{2z_{0}^{2}} {3\tau }}} \right. \kern-0em} {3\tau }}} \right)\Lambda '}}{{{{z}_{0}}\left( {1 + \tau + {{z}_{0}}} \right)}},$$

where ${{Z}_{{d0}}}$ is number of charges on dust grains in equilibrium, ${{\nu }_{q}}$ is equilibrium charging rate of dust, $\Lambda '$ is the Coulomb logarithm, $d = \left( {{{{{n}_{{d0}}}} \mathord{\left/ {\vphantom {{{{n}_{{d0}}}} {{{n}_{{e0}}}}}} \right. \kern-0em} {{{n}_{{e0}}}}}} \right)\,$, $\tau = {{{{T}_{{i0}}}} \mathord{\left/ {\vphantom {{{{T}_{{i0}}}} {{{T}_{{e0}}}}}} \right. \kern-0em} {{{T}_{{e0}}}}}$, and ${{z}_{0}} = {{{{Z}_{d}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{Z}_{d}}{{e}^{2}}} {{{r}_{d}}{{T}_{{e0}}}}}} \right. \kern-0em} {{{r}_{d}}{{T}_{{e0}}}}}$.

Thus, considering the above effects in the continuity and momentum equations of plasma particles, the modified ionization source model was developed [39, 40]. But in the present work, we have ignored the collisions of electrons with dust particles as electrons are considered to be inertialess and it is assumed that the size of ion in the present system is much smaller in comparison to the dust radius, due to which the cross section of interaction of ion with dust can be ignored. Therefore, the trapped plasma particles on the dust surface have insignificant role. In addition to this, the charging of dust particles is considered only due to the plasma current flowing over the surface of dust grains and we have not incorporated the other mechanisms like secondary emission, photoelectric effect, Coulomb collisional charging, etc., in the present model. The contribution of interaction of plasma particles on the dust surface yields more interesting results that would be examined in future work.

2.1 Basic Equations

The self-gravitating, magnetized, collisional, inhomogeneous dusty plasma we are studying is made of four components, i.e., electrons, ions, neutrals, and massive negatively charged dust grains. We have chosen a set of hydrodynamic equations showing the dynamics of each species in the plasma system. The system is enclosed by Poisson’s equation [41] as follows:

$${{\nabla }^{2}}{{\phi }_{E}} = 4\pi \left( {{{n}_{e}}e - {{n}_{i}}e + {{n}_{d}}{{Z}_{d}}e} \right),$$

((1))

where ${{n}_{e}}$ is electron number density, ${{n}_{i}}$ is ion number density, ${{n}_{d}}$ is dust number density, and ${{\phi }_{E}}$ is the electrostatic potential.

2.1.1. Dynamics of dust grains. We consider that the dust particulates are of uniform radius ${{r}_{d}}$ and same mass ${{m}_{d}}$ and having the charge ${{q}_{d}} = - {{Z}_{d}}e$. The polarization force of dust grains is considered as the Debye sheath of the highly negatively charged dust grains contains high number of ion species, due to which the Debye cloud of dust deforms and dust becomes elongated. As a result, the electric field sets up between the dust grains and ions, which polarized the dust grains in the plasma system. Here, we have ignored the inhomogeneous dust density as the inhomogeneity scale length for density of dust particles must be comparable to the considered Jeans instability scale length.

A single-fluid model (comprises continuity equation and momentum equation) which describes the dynamics of dust grains is given by

$$\frac{{\partial {{n}_{d}}}}{{\partial t}} + \boldsymbol{\nabla} \cdot ({{n}_{d}}{{{\mathbf{v}}}_{d}}) = 0,$$

((2))

$$\begin{gathered} {{m}_{d}}{{n}_{d}}\left( {\frac{{\partial {{{\mathbf{v}}}_{d}}}}{{\partial t}} + \left( {{{{\mathbf{v}}}_{d}} \cdot \boldsymbol{\nabla} } \right){{{\mathbf{v}}}_{d}}} \right) \\ = - {{q}_{d}}{{n}_{d}}(1 - \Gamma )\nabla {{\phi }_{E}} - {{m}_{d}}v_{{td}}^{2}\nabla {{n}_{d}} - {{m}_{d}}{{n}_{d}}\nabla {{\phi }_{g}} \\ - \;\frac{{{{q}_{d}}{{n}_{d}}}}{c}\left( {{{{\mathbf{v}}}_{d}} \times {\mathbf{H}}} \right) - \beta {{m}_{d}}{{n}_{d}}{{\nu }_{d}}({{{\mathbf{v}}}_{d}} - {{{\mathbf{v}}}_{n}}). \\ \end{gathered} $$

((3))

Here, ${{{\mathbf{v}}}_{d}}$,${{{\mathbf{v}}}_{n}}$, ${{v}_{{td}}}$, and ${{T}_{d}}$ stand for the velocity of dust grains, velocity of neutrals, dust thermal velocity, and dust temperature, respectively. The symbol Γ = $\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right)\left( {{{\left| {{{q}_{d}}} \right|e} \mathord{\left/ {\vphantom {{\left| {{{q}_{d}}} \right|e} {{{\lambda }_{D}}{{T}_{i}}}}} \right. \kern-0em} {{{\lambda }_{D}}{{T}_{i}}}}} \right)\left( {1 - {{{{T}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{i}}} {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}} \right)$ represents the dust polarization interaction parameter, and β = ${{m}_{n}}{{n}_{n}}{\text{/}}{{m}_{d}}{{n}_{d}}$ represents the ratio of densities of neutral particles and dust grains, where ${{n}_{n}}$ and ${{m}_{n}}$ are the number and mass density of neutrals. Considering the physical parameters ${{m}_{d}} = {{10}^{{ - 12}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 7}}}$ g, ${{r}_{d}} = {{10}^{{ - 6}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 4}}}$ cm, ${{n}_{i}} = {{10}^{{ - 3}}}$ cm⁻³, ${{n}_{d}} = {{10}^{{ - 3}}}$ cm⁻³, ${{n}_{n}} = {{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{9}}$ cm⁻³, $H = 10$ μG, Z_d = $2 \times {{10}^{3}}$, ${{T}_{e}} = 30$ K, and ${{T}_{i}} = 10$ K in the region of dense molecular cloud [8, 21, 35, 42], it is found that collisions of dust with neutrals ${{\nu }_{d}}$ is of the order of the dust Jeans frequency ${{\Omega }_{{Jd}}}$ ($\approx {\kern 1pt} {{10}^{{ - 9}}}$ s⁻¹). Thus, the collisional frequency between dust and neutrals is considered in both the dust and neutral dynamics.

Poisson’s equation for self-gravitational potential ${{\phi }_{g}}$ is

$${{\nabla }^{2}}{{\phi }_{g}} = 4\pi G{{m}_{d}}{{n}_{d}}.$$

((4))

The charge dynamics of dust grains are given by current balance equation as

$$\begin{gathered} \frac{{\partial {{Z}_{d}}}}{{\partial t}} = \pi r_{d}^{2}\left[ {{{n}_{e}}\sqrt {8{{T}_{e}}{\text{/}}\pi {{m}_{e}}} \exp \left( {e\left( {{{\phi }_{f}} - V} \right){\text{/}}{{T}_{e}}} \right)} \right. \\ \left. { - \;{{n}_{i}}\sqrt {8{{T}_{i}}{\text{/}}\pi {{m}_{i}}} \left( {1 - e\left( {{{\phi }_{f}} - V} \right){\text{/}}{{T}_{i}}} \right)} \right], \\ \end{gathered} $$

((5))

where ${{\phi }_{f}} = {{{{q}_{d}}} \mathord{\left/ {\vphantom {{{{q}_{d}}} C}} \right. \kern-0em} C}$ and V show the dust floating and bulk plasma potential, respectively, with capacitance C and the symbols ${{T}_{{e,i}}}$ and ${{m}_{{e,i}}}$ are for the temperature and mass of electrons and ions, respectively.

2.1.2. Dynamics of neutral particles. In the dynamics of neutrals, the collisional effect of neutrals and dust is considered. The continuity and force balance equations are given as

$$\frac{{\partial {{n}_{n}}}}{{\partial t}} + \boldsymbol{\nabla} \cdot ({{n}_{n}}{{{\mathbf{v}}}_{n}}) = 0,$$

((6))

$${{m}_{n}}{{n}_{n}}\left( {\frac{{\partial {{{\mathbf{v}}}_{n}}}}{{\partial t}} + \left( {{{{\mathbf{v}}}_{n}} \cdot \nabla } \right){{{\mathbf{v}}}_{n}}} \right) = - {{m}_{n}}{{n}_{n}}{{\nu }_{d}}({{{\mathbf{v}}}_{n}} - {{{\mathbf{v}}}_{d}}).$$

((7))

2.1.3. Dynamics of radiative electron and ion species. In the molecular cloud, the plasma species show radiative effects. The heating and cooling effect of both species are important as it drives the collapse in the system. Therefore, we have considered the radiative effects of both species [33, 35] in the dynamics of electrons and ions,

$$\frac{{\partial {{n}_{e}}}}{{\partial t}} + \nabla \cdot \left( {{{n}_{e}}{{{\mathbf{v}}}_{e}}} \right) = 0,$$

((8))

$$\frac{3}{2}{{n}_{e}}\frac{{\partial {{T}_{e}}}}{{\partial t}} + {{P}_{e}}\nabla \cdot {{{\mathbf{v}}}_{e}} = {{\chi }_{e}}{{\nabla }^{2}}{{T}_{e}} - L\left( {{{n}_{e}},{{T}_{e}}} \right),$$

((9))

$$0 = e{{n}_{e}}\nabla {{\phi }_{E}} - \nabla \left( {{{n}_{e}}{{T}_{e}}} \right).$$

((10))

Similarly, for ion species, we have

$$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \nabla \cdot \left( {{{n}_{i}}{{{\mathbf{v}}}_{i}}} \right) = 0,$$

((11))

$$\frac{3}{2}{{n}_{i}}\frac{{\partial {{T}_{i}}}}{{\partial t}} + {{P}_{i}}\nabla \cdot {{{\mathbf{v}}}_{i}} = {{\chi }_{i}}{{\nabla }^{2}}{{T}_{i}} - L\left( {{{n}_{i}},{{T}_{i}}} \right),$$

((12))

$${{m}_{i}}{{n}_{i}}\frac{{\partial {{{\mathbf{v}}}_{i}}}}{{\partial t}} + \left( {{{{\mathbf{v}}}_{i}} \cdot \nabla } \right){{{\mathbf{v}}}_{i}} = - e{{n}_{i}}\nabla {{\phi }_{E}} - \nabla \left( {{{n}_{i}}{{T}_{i}}} \right).$$

((13))

In Eqs. (8)−(13), ${{{\mathbf{v}}}_{e}}$, ${{\chi }_{e}}$, and $L\left( {{{n}_{e}},{{T}_{e}}} \right)$ are for the velocity, thermal conductivity, and heat loss function of electrons, respectively, while ${{{\mathbf{v}}}_{i}}$, ${{\chi }_{i}}$, and $L\left( {{{n}_{i}},{{T}_{i}}} \right)$ are for the velocity, thermal conductivity, and heat loss function of ions, respectively.

2.2 Linearized Equations

Now, to derive the dispersion relation for collisional plasma with self-gravitation, we first linearize the basic set of equations by putting the combination of equilibrium state and a perturbation in each physical variable. For the linearization process the physical quantities are written as ${{T}_{{e,i}}} = {{T}_{{e,i0}}} + \delta {{T}_{{e,i}}}$, ${{\phi }_{E}} =$${{\phi }_{{E0}}}\, + \,\delta {{\phi }_{E}}$, ${{Z}_{d}}\, = \,{{Z}_{{d0}}}\, + \,\delta {{Z}_{d}}$, ${{\phi }_{g}}\, = \,{{\phi }_{{g0}}}\, + \,\delta {{\phi }_{g}}$, ${{n}_{j}}\, = \,{{n}_{{j0}}}\, + \,\delta {{n}_{j}}$, and ${{{\mathbf{v}}}_{j}} = {{{\mathbf{v}}}_{{j0}}} + \delta {{{\mathbf{v}}}_{j}}$, where j stands for ion (i), electron (e), dust (d), and neutral (n) species.

As a consequence of linearization, the basic sets of equations can be represented as

$${{\nabla }^{2}}\delta {{\phi }_{E}} = 4\pi \left( {\delta {{n}_{e}}e - \delta {{n}_{i}}e + {{n}_{{d0}}}e\delta {{Z}_{d}} + \delta {{n}_{d}}e{{Z}_{{d0}}}} \right).$$

((14))

Linearized equations for dust and neutral particles are

$$\frac{{\partial \delta {{n}_{d}}}}{{\partial t}} + {{n}_{{d0}}}\nabla \cdot \delta {{{\mathbf{v}}}_{d}} = 0,$$

((15))

$$\begin{gathered} \frac{{\partial \delta {{{\mathbf{v}}}_{d}}}}{{\partial t}} + \frac{{v_{{td}}^{2}}}{{{{n}_{{d0}}}}}\nabla \delta {{n}_{d}} - \frac{{e{{Z}_{{d0}}}}}{{{{m}_{d}}}}(1 - \Gamma )\nabla \delta {{\phi }_{E}} + \nabla \delta {{\phi }_{g}} \\ - \;\frac{{e{{Z}_{{d0}}}}}{{{{m}_{d}}}}\left( {\delta {{{\mathbf{v}}}_{d}} \times {\mathbf{H}}} \right) + \beta {{\nu }_{d}}(\delta {{{\mathbf{v}}}_{d}} - \delta {{{\mathbf{v}}}_{n}}) = 0, \\ \end{gathered} $$

((16))

$$\frac{{\partial \delta {{Z}_{d}}}}{{\partial t}} = \frac{{{{I}_{{e0}}}}}{e}\left( {\frac{{\delta {{n}_{e}}}}{{{{n}_{{e0}}}}} + \frac{{e\delta {{\phi }_{f}}}}{{{{T}_{{e0}}}}}} \right) + \frac{{{{I}_{{i0}}}}}{e}\left( {\frac{{\delta {{n}_{i}}}}{{{{n}_{{i0}}}}} + \frac{{e\delta {{\phi }_{f}}}}{{{{T}_{{i0}}} - e{{\phi }_{{f0}}}}}} \right),$$

((17))

$${{\nabla }^{2}}\delta {{\phi }_{g}} = 4\pi G\left( {{{m}_{d}}\delta {{n}_{d}}} \right),$$

((18))

$$\frac{{\partial \delta {{n}_{n}}}}{{\partial t}} + {{n}_{{n0}}}\nabla \cdot \delta {{{\mathbf{v}}}_{n}} = 0,$$

((19))

$$\frac{{\partial \delta {{{\mathbf{v}}}_{n}}}}{{\partial t}} + {{\nu }_{d}}(\delta {{{\mathbf{v}}}_{n}} - \delta {{{\mathbf{v}}}_{d}}) = 0.$$

((20))

The dynamics of the electron species can be given in the linearized form as

$$\begin{gathered} \frac{{\partial \delta {{n}_{e}}}}{{\partial t}} + {{n}_{{e0}}}\nabla \cdot \delta {{{\mathbf{v}}}_{e}} = 0, \\ \frac{{\partial \delta {{{\mathbf{v}}}_{e}}}}{{\partial t}} = \frac{e}{{{{m}_{e}}}}\nabla \delta {{\phi }_{E}} - \frac{{{{n}_{{e0}}}\nabla \delta {{T}_{e}} + {{T}_{{e0}}}\nabla \delta {{n}_{e}}}}{{{{m}_{e}}{{n}_{{e0}}}}}, \\ \end{gathered} $$

((21))

$$\begin{gathered} \frac{{3{{n}_{{e0}}}}}{2}\frac{{\partial \delta {{T}_{e}}}}{{\partial t}} + {{n}_{{e0}}}{{T}_{{e0}}}\nabla \cdot {{{\mathbf{v}}}_{{e1}}} \\ = {{\chi }_{e}}{{\nabla }^{2}}\delta {{T}_{e}} - {{\left( {\frac{{\partial L}}{{\partial {{T}_{e}}}}} \right)}_{{{{T}_{{e0}}}}}}\delta {{T}_{e}} - {{\left( {\frac{{\partial L}}{{\partial {{n}_{e}}}}} \right)}_{{{{n}_{{e0}}}}}}\delta {{n}_{e}}, \\ \end{gathered} $$

((22))

where ${{L}_{{Te}}} = \left( {{1 \mathord{\left/ {\vphantom {1 {{{n}_{{e0}}}}}} \right. \kern-0em} {{{n}_{{e0}}}}}} \right){{\left( {{{\partial L} \mathord{\left/ {\vphantom {{\partial L} {\partial \delta {{T}_{e}}}}} \right. \kern-0em} {\partial \delta {{T}_{e}}}}} \right)}_{{{{T}_{{e0}}}}}}$ and ${{L}_{{ne}}} =$$\left( {{1 \mathord{\left/ {\vphantom {1 {{{T}_{{e0}}}}}} \right. \kern-0em} {{{T}_{{e0}}}}}} \right){{\left( {{{\partial L} \mathord{\left/ {\vphantom {{\partial L} {\partial \delta {{n}_{e}}}}} \right. \kern-0em} {\partial \delta {{n}_{e}}}}} \right)}_{{{{n}_{{e0}}}}}}$ are temperature and density dependent heat loss functions for the electron species, respectively. For the ion species, we have

$$\begin{gathered} \frac{{\partial \delta {{n}_{i}}}}{{\partial t}} + {{n}_{{i0}}}\nabla \cdot \delta {{{\mathbf{v}}}_{i}} = 0, \\ \frac{{\partial \delta {{{\mathbf{v}}}_{i}}}}{{\partial t}} = - \frac{e}{{{{m}_{i}}}}\nabla \delta {{\phi }_{E}} - \frac{{{{n}_{{i0}}}\nabla \delta {{T}_{i}} + {{T}_{{i0}}}\nabla \delta {{n}_{i}}}}{{{{m}_{i}}{{n}_{{i0}}}}}, \\ \end{gathered} $$

((23))

$$\begin{gathered} \frac{{3{{n}_{{i0}}}}}{2}\frac{{\partial \delta {{T}_{i}}}}{{\partial t}} + {{n}_{{i0}}}{{T}_{{i0}}}\nabla \cdot {\mathbf{v}_{{i1}}} \\ = {{\chi }_{i}}{{\nabla }^{2}}\delta {{T}_{i}} - {{\left( {\frac{{\partial L}}{{\partial {{T}_{i}}}}} \right)}_{{{{T}_{{i0}}}}}}\delta {{T}_{i}} - {{\left( {\frac{{\partial L}}{{\partial {{n}_{i}}}}} \right)}_{{{{n}_{{i0}}}}}}\delta {{n}_{i}}, \\ \end{gathered} $$

((24))

where ${{L}_{{Ti}}} = \left( {{1 \mathord{\left/ {\vphantom {1 {{{n}_{{i0}}}}}} \right. \kern-0em} {{{n}_{{i0}}}}}} \right){{\left( {{{\partial L} \mathord{\left/ {\vphantom {{\partial L} {\partial \delta {{T}_{i}}}}} \right. \kern-0em} {\partial \delta {{T}_{i}}}}} \right)}_{{{{T}_{{i0}}}}}}$ and ${{L}_{{ni}}} =$$\left( {{1 \mathord{\left/ {\vphantom {1 {{{T}_{{i0}}}}}} \right. \kern-0em} {{{T}_{{i0}}}}}} \right){{\left( {{{\partial L} \mathord{\left/ {\vphantom {{\partial L} {\partial \delta {{n}_{i}}}}} \right. \kern-0em} {\partial \delta {{n}_{i}}}}} \right)}_{{{{n}_{{i0}}}}}}$ are temperature and density dependent heat loss functions for the ion species, respectively.

Furthermore using the wave perturbation  $\varphi (\mathbf{r},t) =$$\hat {\varphi }(r){{e}^{{(i\mathbf{k} \cdot \mathbf{r} - i\sigma \,t)}}}$ in the above linearized set of equations, the perturbed dust number density, perturbed dust charge density, perturbed electron number density, and perturbed ion number density are estimated. The amplitude of oscillating variable is given by $\hat {\varphi }(r)$, the symbol σ stands for harmonic perturbation frequency and k is the wave vector in the x and z directions. Now, the obtained value of perturbed dust density $\delta {{n}_{d}}$ and perturbed dust charge $\delta {{Z}_{d}}$ are

$$\begin{gathered} \frac{{\delta {{n}_{d}}}}{{{{n}_{{d0}}}}} = \frac{{ - e{{Z}_{{d0}}}\delta {{\phi }_{E}}\left( {1 - \Gamma } \right)}}{{{{m}_{d}}}}\left[ {k_{ \bot }^{2}\frac{{\left( {i{{\sigma }^{2}} - \left( {1 + \beta } \right)\sigma {{\nu }_{d}}} \right)}}{{\sigma + i{{\nu }_{d}}}}} \right. \\ + \;\left. {k_{{||}}^{2}\left\{ {i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}} + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\}} \right] \\ \end{gathered} $$

$$ \times \;\left[ {\left\{ {i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}}} \right.} \right.\left. { + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\}$$

((25))

$$\begin{gathered} \times \;\left( { - i{{\sigma }^{3}} - \frac{{i\beta {{\nu }_{d}}{{\sigma }^{3}}}}{{ - i\sigma + {{\nu }_{d}}}} + i\sigma v_{{td}}^{2}k_{{||}}^{2} - \frac{{i\sigma \Omega _{{Jd}}^{2}k_{{||}}^{2}}}{{{{k}^{2}}}}} \right) \\ + \;{{\left. {\left( {v_{{td}}^{2}k_{ \bot }^{2} - \frac{{\Omega _{{Jd}}^{2}k_{ \bot }^{2}}}{{{{k}^{2}}}}} \right)\frac{{\left( {i{{\sigma }^{2}} - \left( {1 + \beta } \right)\sigma {{\nu }_{d}}} \right)}}{{\left( {\sigma + i{{\nu }_{d}}} \right)}}} \right]}^{{ - 1}}}, \\ \end{gathered} $$

$$\delta {{Z}_{d}} = \frac{{i\left| {{{I}_{{e0}}}} \right|}}{{\sigma + i\Lambda }}\left( {\frac{{\delta {{n}_{e}}}}{{e{{n}_{{e0}}}}} - \frac{{\delta {{n}_{i}}}}{{e{{n}_{{i0}}}}}} \right).$$

((26))

In calculating perturbed dust density, we have neglected the terms appearing in multiplication of ${{k}_{ \bot }}{{k}_{{||}}}$. The symbol ${{\Omega }_{{cd}}} = {{q}_{d}}H{\text{/}}{{m}_{d}}c$ represents the dust cyclotron frequency, and $\Omega _{{Jd}}^{2} = 4\pi G{{m}_{d}}{{n}_{{d0}}}$ is the dust Jeans frequency.

Similarly the perturbed electron number density $\delta {{n}_{e}}$ and ion number density $\delta {{n}_{i}}$ are given in the form of following equations:

$$\frac{{\delta {{n}_{e}}}}{{{{n}_{{e0}}}}} = \frac{e}{{{{T}_{{e0}}}}}{{\left( {1 - \frac{{\left( {i\sigma + {{L}_{{ne}}}} \right)}}{{{{R}_{{ce}}}}}} \right)}^{{ - 1}}}\delta {{\phi }_{E}},$$

((27))

$$\frac{{\delta {{n}_{i}}}}{{{{n}_{{i0}}}}} = \frac{e}{{{{T}_{{i0}}}}}{{\left( {\frac{{{{\sigma }^{2}}}}{{v_{{ti}}^{2}{{k}^{2}}}} - \frac{{\left( {{{R}_{{ci}}} - (i\sigma + {{L}_{{ni}}})} \right)}}{{{{R}_{{ci}}}}}} \right)}^{{ - 1}}}\delta {{\phi }_{E}},$$

((28))

where $v_{{ti}}^{2} = {{T}_{{i0}}}{\text{/}}{{m}_{i}}$, ${{R}_{{ce}}} = ( - 3{\text{/}}2)i\sigma + ({{\chi }_{e}}{{k}^{2}}{\text{/}}({{n}_{{e0}}}) + {{L}_{{Te}}})$, and ${{R}_{{ci}}} = ( - 3{\text{/}}2)i\sigma + ({{\chi }_{i}}{{k}^{2}}{\text{/}}({{n}_{{i0}}}) + {{L}_{{Ti}}}).$

The substitution of the values of $\delta {{n}_{d}}$, $\delta {{n}_{e}}$, $\delta {{n}_{i}}$, and $\delta {{Z}_{d}}$ in Poisson’s equation yields general dispersion relation as

$$\begin{gathered} \left[ {\left\{ {i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}} + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\}} \right. \\ \times \;\left( { - {{\sigma }^{2}} - \frac{{\beta {{\nu }_{d}}{{\sigma }^{2}}}}{{ - i\sigma + {{\nu }_{d}}}} + v_{{td}}^{2}k_{{||}}^{2} - \frac{{\Omega _{{Jd}}^{2}k_{{||}}^{2}}}{{{{k}^{2}}}}} \right) \\ \end{gathered} $$

$$\begin{gathered} + \;\left( {v_{{td}}^{2}k_{ \bot }^{2} - \frac{{\Omega _{{Jd}}^{2}k_{ \bot }^{2}}}{{{{k}^{2}}}}} \right)\left. {\frac{{\sigma \left( {i\sigma - \left( {1 + \beta } \right){{\nu }_{d}}} \right)}}{{\left( {\sigma + i{{\nu }_{d}}} \right)}}} \right] \\ \times \;\left[ {1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)} \right.\left( {\frac{{{{R}_{{ce}}}}}{{{{R}_{{ce}}} - (i\sigma + {{L}_{{ne}}})}}} \right) \\ - \;\left( {\frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right) \\ \times \;\left. {\frac{{v_{{ti}}^{2}{{k}^{2}}}}{{{{\sigma }^{2}} - v_{{ti}}^{2}{{k}^{2}}\left( {1 - (i\sigma + {{L}_{{ni}}})/{{R}_{{ci}}}} \right)}}} \right] + \frac{{\Omega _{{pd}}^{2}(1 - \Gamma )k_{{||}}^{2}}}{{{{k}^{2}}}} \\ \end{gathered} $$

((29))

$$\begin{gathered} \times \;\left\{ {i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}} + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\} \\ + \;\frac{{\Omega _{{pd}}^{2}(1 - \Gamma )k_{ \bot }^{2}}}{{\left( {\sigma + i{{\nu }_{d}}} \right){{k}^{2}}}}\left( {i{{\sigma }^{2}} - \left( {1 + \beta } \right)\sigma {{\nu }_{d}}} \right) = 0. \\ \end{gathered} $$

Here, $\Im = {{\left| {{{I}_{{e0}}}} \right|\omega _{{pd}}^{2}} \mathord{\left/ {\vphantom {{\left| {{{I}_{{e0}}}} \right|\omega _{{pd}}^{2}} {{{q}_{{d0}}}c_{d}^{2}}}} \right. \kern-0em} {{{q}_{{d0}}}c_{d}^{2}}}$, where $c_{d}^{2} = {{Z_{{d0}}^{{}}{{T}_{{e0}}}} \mathord{\left/ {\vphantom {{Z_{{d0}}^{{}}{{T}_{{e0}}}} {{{m}_{d}}}}} \right. \kern-0em} {{{m}_{d}}}}$ and $\Omega _{{pd}}^{2} = {{4\pi {{n}_{{d0}}}Z_{{d0}}^{2}{{e}^{2}}} \mathord{\left/ {\vphantom {{4\pi {{n}_{{d0}}}Z_{{d0}}^{2}{{e}^{2}}} {{{m}_{d}}}}} \right. \kern-0em} {{{m}_{d}}}}$. The expression for the Debye lengths of electron and ion species is $\lambda _{{De,i}}^{2} =$${{{{T}_{{e,i0}}}} \mathord{\left/ {\vphantom {{{{T}_{{e,i0}}}} {4\pi {{n}_{{e,i0}}}{{e}^{2}}}}} \right. \kern-0em} {4\pi {{n}_{{e,i0}}}{{e}^{2}}}}$.

Equation (29) describes the linear general dispersion relation of self-gravitating dusty plasma where the effects of dust neutral collision frequency, polarization force, cyclotron frequency, variation of dust charge, and radiative cooling of electrons and ions are taken into consideration. If we ignore the effects of polarization force, magnetic field, dust charge fluctuation, and radiative cooling from general dispersion relation (29), the reduced result recovers the result obtained by Verheest et al. [43] under some limitations. Further, in the case of nonradiative Maxwellian ions and for unmagnetized fully ionized dusty plasma, general dispersion relation (29) is similar to the result given by Prajapati and Bhakta [18] for self-gravitating dusty plasma. Under the assumption of constant dust charge and inertialess Maxwellian ion in unmagnetized collisionless dusty plasma, Eq. (29) exactly takes the form of result (25) given by Prajapati et al. [44], excluding strong coupling terms in that work. Therefore, the present work is the improvement of the previous work done by Prajapati et al. [44] due to the combined study of the magnetic field, polarization force, dust charge variation, and radiative effect of ions.

3 DISCUSSION OF DISPERSION RELATION

The propagations of the system are in two different directions; therefore, for the sake of simplicity, general dispersion relation (29) is discussed in parallel and perpendicular directions separately.

3.1 Mode of Propagation Parallel to the Magnetic Field

In parallel propagation, we consider the case when perturbations of the system and magnetic field both are in the same direction for collisional radiative dusty plasma in the presence of dust charge variation and polarization force. Therefore, we assume that the perturbations of the system are parallel to the direction of magnetic field and put ${{k}_{ \bot }} = 0$ and ${{k}_{{||}}} = k$ in dispersion relation (29). In this case, Eq. (29) reduces to

$$\begin{gathered} \left\{ {i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}} + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\} \\ \times \;\left[ {1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)\left( {\frac{{{{R}_{{ce}}}}}{{{{R}_{{ce}}} - (i\sigma + {{L}_{{ne}}})}}} \right)} \right. \\ \end{gathered} $$

$$ - \;\left( {\frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}} - } \right.\left. {\frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)$$

((30))

$$\begin{gathered} \times \;\frac{{v_{{ti}}^{2}{{k}^{2}}}}{{{{\sigma }^{2}} - v_{{ti}}^{2}{{k}^{2}}\left( {1 - (i\sigma + {{L}_{{ni}}}){\text{/}}{{R}_{{ci}}}} \right)}} + \Omega _{{pd}}^{2}(1 - \Gamma ) \\ \times \;\left. {{{{\left( { - {{\sigma }^{2}} - \frac{{\beta {{\nu }_{d}}{{\sigma }^{2}}}}{{ - i\sigma + {{\nu }_{d}}}} + v_{{td}}^{2}k_{{||}}^{2} - \Omega _{{Jd}}^{2}} \right)}}^{{ - 1}}}} \right] = 0. \\ \end{gathered} $$

It is clear from Eq. (30) that the magnetic field term gets separated from the radiative terms in the parallel mode of propagation. Dispersion relation (30) has two factors out of which the first factor gives modified cyclotron mode, whereas the other factor shows the gravitational mode. It is obvious from dispersion relation (30) that the dust neutral collision frequency shows its effect on both the cyclotron mode, as well as gravitational mode. In the absence of ion thermal velocity, collision frequency, magnetic field, and ion radiative cooling, dispersion relation (30) becomes similar to Eq. (31) of Prajapati et al. [44] for weakly coupled dusty plasma. The first factor of dispersion relation (30) contributes

$$i\sigma - \frac{{\sigma \beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}} + \frac{{\Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}} - {{\sigma }^{2}}\beta {{\nu }_{d}}} \right)}} = 0.$$

((31))

This equation shows the cyclotron mode modified by dust neutral collision frequency. We can find an interesting consequence from Eq. (31) that, in the absence of neutrals, Eq. (31) gives a pure cyclotron mode for fully ionized plasma, i.e., $\sigma = \pm \Omega _{{cd}}^{{}}$, whereas in the absence of magnetic field, it gives pure collisional mode $i\sigma - {{\nu }_{d}}\left( {1 + \beta } \right) = 0$ for partially ionized dusty plasma.

Using the limit $\sigma \ll {{L}_{{ne,i}}}$, ${{L}_{{Te,i}}}$, ${{{{\chi }_{{e,i}}}{{k}^{2}}} \mathord{\left/ {\vphantom {{{{\chi }_{{e,i}}}{{k}^{2}}} {{{n}_{{e,i0}}}}}} \right. \kern-0em} {{{n}_{{e,i0}}}}}$ and substituting $- i\sigma = \omega$ in the second factor of Eq. (30), we get the polynomial form of gravitational mode as follows:

$$\begin{gathered} {{\omega }^{5}} + {{\omega }^{4}}\left( {1 + \beta } \right){{\nu }_{d}} + {{\omega }^{3}}\left\{ {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right. \\ + \;v_{{ti}}^{2}{{k}^{2}}(1 - {{L}_{{ni}}}R_{{ci}}^{{'0}})\left. { + \;\xi _{{De}}^{0}\left( {{{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}} + \Omega _{{pd}}^{2}(1 - \Gamma )} \right)} \right\} \\ + \;{{\omega }^{2}}\left\{ {\left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right)} \right.{{\nu }_{d}} + \left( {1 + \beta } \right){{\nu }_{d}}{{k}^{2}}v_{{ti}}^{2} \\ \end{gathered} $$

$$\begin{gathered} \times \;\left. {\left( {(1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}) + {{\alpha }_{D}}\xi _{{De}}^{0}} \right) + \Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}} \right\} \\ + \;\omega \left\{ {{{k}^{2}}v_{{ti}}^{2}(1 - {{L}_{{ni}}}R_{{ci}}^{{'0}})\left( {\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0} + {{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right)} \right. \\ \end{gathered} $$

((32))

$$\begin{gathered} \left. { + \;{{\alpha }_{D}}\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right)} \right\} \\ + \;\left\{ {\Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}(1 - {{L}_{{ni}}}R_{{ci}}^{{'0}})} \right. \\ + \;\left. {\left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right){{\nu }_{d}}{{k}^{2}}v_{{ti}}^{2}(1 - {{L}_{{ni}}}R_{{ci}}^{{'0}} + {{\alpha }_{D}}\xi _{{De}}^{0})} \right\} = 0, \\ \end{gathered} $$

where ${{\alpha }_{D}}\, = \,1{\text{/}}\lambda _{{Di}}^{2}{{k}^{2}}\, - \,\Im {\text{/}}\Lambda {{k}^{2}}$, $R_{{ci}}^{{'0}}\, = \,{{\{ {{\chi }_{i}}{{k}^{2}}{\text{/}}({{n}_{{i0}}})\, + \,{{L}_{{Ti}}}\} }^{{ - 1}}}$, and $\xi _{{De}}^{0} = {{\{ 1 + (1{\text{/}}\lambda _{{De}}^{2}{{k}^{2}} - \Im {\text{/}}\Lambda {{k}^{2}})R_{{ce}}^{'}{\text{/(}}R_{{ce}}^{'} - {{L}_{{ne}}}{\text{)\} }}}^{{ - 1}}}$ with $R_{{ce}}^{'} = {{\chi }_{e}}{{{{k}^{2}}} \mathord{\left/ {\vphantom {{{{k}^{2}}} {({{n}_{{e0}}}}}} \right. \kern-0em} {({{n}_{{e0}}}}}) + {{L}_{{Te}}}$.

Equation (32) shows the self-gravitational instability of inhomogeneous radiative dusty plasma. This equation describes the combined effects of dust thermal velocity, ion thermal velocity, dust charge fluctuation, dust neutral collision frequency, radiative effects of electrons and ions, and polarization force on the growth rate of instability. If we ignore the effects of dust neutral collisional frequency, polarization force, self-gravitation, and dust dynamics from dispersion relation (32), the obtained result is similar to Eq. (14) of Pandey et al. [32]. Further, if we neglect the radiative effects of ions, polarization force, magnetic field, and ion thermal velocity from Eq. (32), then the reduced dispersion relation matches to the result obtained by Shukla and Sandberg [35] under some limitations. Therefore, we can say that the result obtained in this section is an important finding in the regions of molecular clouds, where polarization force and radiative effects of electron and ion species along with dust−neutral collision frequency take part in the gravitational collapse.

Moreover, the condition of the Jeans instability can be obtained from the constant term of Eq. (32). If this term is less than zero, then it will give necessarily one real positive root, which makes the system unstable. Hence, the modified gravitational instability condition from Eq. (32) can be written as

$${{k}^{2}}v_{{td}}^{2} + \frac{{\Omega _{{pd}}^{2}(1 - \Gamma )\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)\xi _{{De}}^{0}}}{{\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) + {{\alpha }_{D}}\xi _{{De}}^{0}}} < \Omega _{{Jd}}^{2}.$$

((33))

The above expression displays the condition of the Jeans instability for collisional dusty plasma with radiative effects. This condition is influenced by radiative effects of electrons and ions, dust thermal velocity, and polarization force, whereas completely unaffected by dust neutral collision frequency. We can say from Eq. (33) that the dust thermal velocity tries to stabilize the system as it is against the dust Jeans frequency, whereas polarization force and radiative cooling of ions and electrons move the system toward destabilization. If we ignore the dust charge fluctuation and radiative effects of electrons and ions from condition (33), the obtained condition of Jeans instability is in good agreement with condition (26) of Prajapati and Bhakta [18].

To determine the stability of the present collisional dusty plasma system including radiative effects, we apply the Routh Hurwitz criterion on expression (32). It is clear that all the coefficients of Eq. (32) are positive; thus, the necessary condition of stability is satisfied. Further, for the fulfillment of sufficient condition of the Routh Hurwitz matrix, we rewrite dispersion relation (32) as

$${{c}_{0}}{{\omega }^{5}} + {{c}_{1}}{{\omega }^{4}} + {{c}_{2}}{{\omega }^{3}} + {{c}_{3}}{{\omega }^{2}} + {{c}_{4}}\omega + {{c}_{5}} = 0,$$

where

$$\begin{gathered} {{c}_{0}} = 1, \\ {{c}_{1}} = \left( {1 + \beta } \right){{\nu }_{d}}, \\ \end{gathered} $$

$$\begin{gathered} {{c}_{2}} = {{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2} + v_{{ti}}^{2}{{k}^{2}}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) \\ + \;\xi _{{De}}^{0}\left( {{{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}} + \Omega _{{pd}}^{2}(1 - \Gamma )} \right), \\ \end{gathered} $$

$$\begin{gathered} {{c}_{3}} = \left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right){{\nu }_{d}} + \left( {1 + \beta } \right){{\nu }_{d}}{{k}^{2}}v_{{ti}}^{2} \\ \times \;\left( {\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) + {{\alpha }_{D}}\xi _{{De}}^{0}} \right) + \Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}, \\ \end{gathered} $$

$$\begin{gathered} {{c}_{4}} = {{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)\left( {\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0} + {{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right) \\ + \;{{\alpha }_{D}}\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{c}_{5}} = \Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) \\ + \;\left( {{{k}^{2}}v_{{td}}^{2} - \Omega _{{Jd}}^{2}} \right){{\nu }_{d}}{{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}} + {{\alpha }_{D}}\xi _{{De}}^{0}} \right). \\ \end{gathered} $$

The principle minors of Eq. (32) are

$$\begin{gathered} {{\Delta }_{1}} = {{c}_{1}} > 0, \\ {{\Delta }_{2}} = {{c}_{1}}{{c}_{2}} - {{c}_{0}}{{c}_{3}} > 0, \\ \end{gathered} $$

$${{\Delta }_{3}} = {{c}_{3}}{{\Delta }_{2}} - {{c}_{1}}\left( {{{c}_{1}}{{c}_{4}} - {{c}_{0}}{{c}_{5}}} \right) > 0,$$

((34))

$$\begin{gathered} {{\Delta }_{4}} = {{c}_{2}}{{c}_{3}}{{c}_{4}}{{c}_{5}} - {{c}_{0}}{{c}_{2}}c_{3}^{2} \\ - \;c_{2}^{2}c_{5}^{2} - c_{5}^{2}({{c}_{1}}{{c}_{4}} - {{c}_{0}}{{c}_{5}}) > 0, \\ \end{gathered} $$

which are all positive. Therefore, if condition of Routh Hurwitz matrix (34) is satisfied, the considered system given by Eq. (32) will be stable.

Further, for negligible self-gravitation, Eq. (32) provides the dispersion relation for radiative condensation mode as

$$\begin{gathered} {{\omega }^{5}} + {{\omega }^{4}}\left( {1 + \beta } \right){{\nu }_{d}} + {{\omega }^{3}}\left\{ {{{k}^{2}}v_{{td}}^{2} + {{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)} \right. \\ + \;\left. {\xi _{{De}}^{0}\left( {{{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}} + \Omega _{{pd}}^{2}(1 - \Gamma )} \right)} \right\} \\ \end{gathered} $$

$$\begin{gathered} + \;{{\omega }^{2}}\left\{ {\left\{ {{{k}^{2}}v_{{td}}^{2}{{\nu }_{d}} + \left( {1 + \beta } \right)} \right.{{\nu }_{d}}{{k}^{2}}v_{{ti}}^{2}} \right. \\ \times \;\left. {\left( {\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) + {{\alpha }_{D}}\xi _{{De}}^{0}} \right) + \Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}} \right\} \\ + \;\omega \left\{ {\left\{ {{{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)\left( {\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0} + {{k}^{2}}v_{{td}}^{2}} \right)} \right.} \right. \\ \end{gathered} $$

((35))

$$\begin{gathered} + \;\left. {{{\alpha }_{D}}\xi _{{De}}^{0}v_{{ti}}^{2}{{k}^{4}}v_{{td}}^{2}} \right\} + \left\{ {\Omega _{{pd}}^{2}(1 - \Gamma ){{\nu }_{d}}\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)} \right. \\ + \;{{k}^{2}}v_{{td}}^{2}{{\nu }_{d}}\left. {\left( {{{k}^{2}}v_{{ti}}^{2}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) + {{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}}\xi _{{De}}^{0}} \right)} \right\} = 0. \\ \end{gathered} $$

The dispersion relation of this mode is modified due to the dust thermal velocity, collision frequency, polarization force, and radiative effects of electrons and ions. It can be understood from the constant term of Eq. (35) that the ion thermal velocity has no effect on the instability criterion. The condition of radiative condensation instability can be obtained from Eq. (35) as

$$\begin{gathered} \Omega _{{pd}}^{2}\left( {1 - \Gamma } \right)\left( {1 - \frac{{{{L}_{{ni}}}}}{{R_{{ci}}^{'}}}} \right) + {{k}^{2}}v_{{td}}^{2} \\ \times \;\frac{{\left\{ {1 - \frac{{{{L}_{{ni}}}}}{{R_{{ci}}^{'}}} + \frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}}\left( {\left( {1 + \frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{\Im }{{\Lambda {{k}^{2}}}}} \right)\frac{{R_{{ce}}^{'}}}{{R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right)} \right\}}}{{\left\{ {1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{\Im }{{\Lambda {{k}^{2}}}}} \right)\left( {\frac{{R_{{ce}}^{'}}}{{R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right)} \right\}}} < 0. \\ \end{gathered} $$

((36))

This is modified due to polarization force, dust thermal velocity, and radiative effects of electrons and ions. In the absence of dust thermal velocity, polarization force, and radiative cooling of ions, it gives the usual isobaric condition of radiative condensation instability for electrons, i.e., ${{\chi }_{e}}{{k}^{2}}{\text{/}}{{n}_{{e0}}} + {{L}_{{Te}}} < {{L}_{{ne}}}$, whereas if we neglect the effects of dust thermal velocity, polarization force, and radiative cooling of electrons, it takes the shape of radiative condensation criterion of ions, i.e., ${{\chi }_{i}}{{k}^{2}}{\text{/}}{{n}_{{i0}}} + {{L}_{{Ti}}} < {{L}_{{ni}}}$.

3.2 Mode of Propagation Perpendicular to the Magnetic Field

To analyze the effect of magnetic field on instability of radiative self-gravitating dusty plasma in this mode of propagation, we have considered the wave vector in the direction perpendicular to the magnetic field and ignored all other directions of the wave vector. Therefore, we kept ${{k}_{ \bot }} = k$ and ${{k}_{{||}}} = 0$ in general dispersion relation (29) of partially ionized radiative self-gravitating dusty plasma.

Thus, the obtained form is

$$\begin{gathered} \left[ {\frac{{i{{\sigma }^{2}} - \left( {1 + \beta } \right)\sigma {{\nu }_{d}}}}{{\left( {\sigma + i{{\nu }_{d}}} \right)}}} \right] \\ \times \;\left[ {\left\{ {1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)} \right.\left( {\frac{{{{R}_{{ce}}}}}{{{{R}_{{ce}}} - (i\sigma + {{L}_{{ne}}})}}} \right)} \right. \\ - \;\frac{{v_{{ti}}^{2}{{k}^{2}}}}{{{{\sigma }^{2}} - v_{{ti}}^{2}{{k}^{2}}\left( {1 - (i\sigma + {{L}_{{ni}}}){\text{/}}{{R}_{{ci}}}} \right)}} \\ \times \;\left. {\left( {\frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)} \right\} + \Omega _{{pd}}^{2}(1 - \Gamma ) \\ \times \;\left\{ { - {{\sigma }^{2}} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}} - \frac{{i{{\sigma }^{2}}\beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}}} \right. \\ \left. {{{{\left. { + \;\frac{{i\sigma \Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\}}}^{{ - 1}}}} \right] = 0, \\ \end{gathered} $$

((37))

which gives two factors.

The first factor represents pure collisional mode ($\sigma = - i\left( {1 + \beta } \right){{\nu }_{d}}$), which has damping behavior in the magnetized dusty plasma with self-gravitating. The effect of magnetic field, dust charge fluctuation, and radiative condensation can be analyzed from the second factor

$$\begin{gathered} \left[ {\left\{ {1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)} \right.} \right.\left( {\frac{{{{R}_{{ce}}}}}{{{{R}_{{ce}}} - (i\sigma + {{L}_{{ne}}})}}} \right) \\ - \;\frac{{v_{{ti}}^{2}{{k}^{2}}}}{{{{\sigma }^{2}} - v_{{ti}}^{2}{{k}^{2}}\left( {1 - (i\sigma + {{L}_{{ni}}}){\text{/}}{{R}_{{ci}}}} \right)}} \\ \times \;\left( {\frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}} - } \right.\left. {\left. {\frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)} \right\} \\ + \;\Omega _{{pd}}^{2}(1 - \Gamma )\left\{ { - {{\sigma }^{2}} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}} - \frac{{i{{\sigma }^{2}}\beta {{\nu }_{d}}}}{{\sigma + i{{\nu }_{d}}}}} \right. \\ \left. {{{{\left. { + \;\frac{{i\sigma \Omega _{{cd}}^{2}\left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right)}}{{i\sigma \left( {{{\sigma }^{2}} + i\sigma {{\nu }_{d}}} \right) - {{\sigma }^{2}}\beta {{\nu }_{d}}}}} \right\}}}^{{ - 1}}}} \right] = 0, \\ \end{gathered} $$

((38))

which is written in the algebraic polynomial form as follows:

$$\begin{gathered} {{\omega }^{6}} + {{\omega }^{5}}2{{\nu }_{d}}\left( {1 + \beta } \right) + {{\omega }^{4}}\left\{ { - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}} + \nu _{d}^{2}{{{\left( {1 + \beta } \right)}}^{2}}} \right. \\ + \,\Omega _{{cd}}^{2}\, + \,v_{{ti}}^{2}{{k}^{2}}\left( {1\, - \,{{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)\, + \left. {\xi _{{De}}^{0}\left( {{{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}}\, + \Omega _{{pd}}^{2}(1 - \Gamma )} \right)} \right\} \\ + \;{{\omega }^{3}}\left\{ {\left( {v_{{td}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2}} \right)\left( {2 + \beta } \right){{\nu }_{d}} + 2\Omega _{{cd}}^{2}{{\nu }_{d}}} \right. \\ \end{gathered} $$

$$\begin{gathered} + \;2\left( {1 + \beta } \right){{\nu }_{d}}v_{{ti}}^{2}{{k}^{2}}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) \\ \left. { + \;2\left( {1 + \beta } \right){{\nu }_{d}}\xi _{{De}}^{0}\left( {{{k}^{2}}v_{{ti}}^{2}{{\alpha }_{D}} + \Omega _{{pd}}^{2}(1 - \Gamma )} \right)} \right\} \\ + \;{{\omega }^{2}}\left\{ {\left( {v_{{td}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2}} \right)\left( {1 + \beta } \right)\nu _{d}^{2} + } \right.\Omega _{{cd}}^{2}\nu _{d}^{2} \\ \end{gathered} $$

$$\begin{gathered} + \;\left( {\nu _{d}^{2}{{{\left( {1 + \beta } \right)}}^{2}} + v_{{td}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2} + \Omega _{{cd}}^{2}} \right) \\ \times \;v_{{ti}}^{2}{{k}^{2}}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right) + \xi _{{De}}^{0}{{\alpha }_{D}}{{k}^{2}}v_{{ti}}^{2} \\ \times \;\left( {\nu _{d}^{2}{{{\left( {1 + \beta } \right)}}^{2}} + v_{{td}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2} + \Omega _{{cd}}^{2}} \right) \\ \end{gathered} $$

((39))

$$\begin{gathered} + \;\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0}\left. {\left( {\nu _{d}^{2}\left( {1 + \beta } \right) + v_{{ti}}^{2}{{k}^{2}}\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)} \right)} \right\} \\ + \;\omega \left\{ {{{k}^{2}}v_{{ti}}^{2}\left( {\xi _{{De}}^{0}{{\alpha }_{D}} + \left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)} \right)} \right. \\ \times \;\left( {\left( {v_{{td}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2}} \right)\left( {2 + \beta } \right){{\nu }_{d}} + 2{{\nu }_{d}}\Omega _{{cd}}^{2}} \right) \\ \end{gathered} $$

$$\begin{gathered} + \;\left. {\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {2 + \beta } \right)\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right){{\nu }_{d}}} \right\} + \left\{ {v_{{ti}}^{2}{{k}^{2}}} \right. \\ \times \;\left( {\xi _{{De}}^{0}{{\alpha }_{D}} + \left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)} \right)\left( { - \Omega _{{Jd}}^{2}\nu _{d}^{2}\left( {1 + \beta } \right) + \Omega _{{cd}}^{2}\nu _{d}^{2}} \right) \\ + \;\left. {\Omega _{{pd}}^{2}(1 - \Gamma )\xi _{{De}}^{0}{{k}^{2}}v_{{ti}}^{2}\left( {2 + \beta } \right)\left( {1 - {{L}_{{ni}}}R_{{ci}}^{{'0}}} \right)\nu _{d}^{2}} \right\} = 0. \\ \end{gathered} $$

Expression (39) is a sixth-order polynomial equation, which shows the combined effect of polarization force, radiative condensation of electrons and ions, self-gravitation, magnetic field, dust charge fluctuation, and collision frequency. Dispersion relation (39) recovers the result of Shukla and Sandberg [35] in the absence of radiative condensation of ion, magnetic field, dust charge fluctuation, and polarization force. In order to analyze the effect of considered parameter on self-gravitation instability in convenient form, we apply some limits in dispersion relation (39). If we consider the collisionless self-gravitating plasma in which the electron and ion species follow a Maxwell−Boltzmann distribution and the charge on the dust grains is constant, then the dispersion relation yields as

$$\begin{gathered} {{\omega }^{4}} + \left\{ {\left( {1 + {{\lambda _{{De}}^{2}} \mathord{\left/ {\vphantom {{\lambda _{{De}}^{2}} {\lambda _{{Di}}^{2}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}}}} \right)v_{{ti}}^{2}{{k}^{2}} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}}} \right. \\ \left. { + \;\Omega _{{cd}}^{2} + \Omega _{{pd}}^{2}\lambda _{{De}}^{2}{{k}^{2}}(1 - \Gamma )} \right\}{{\omega }^{2}} \\ + \;v_{{ti}}^{2}{{k}^{2}}\left\{ {\left( {1 + {{\lambda _{{De}}^{2}} \mathord{\left/ {\vphantom {{\lambda _{{De}}^{2}} {\lambda _{{Di}}^{2}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}}}} \right)\left( {\Omega _{{cd}}^{2} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}}} \right)} \right. \\ \left. { + \;\Omega _{{pd}}^{2}\lambda _{{De}}^{2}{{k}^{2}}(1 - \Gamma )} \right\} = 0. \\ \end{gathered} $$

((40))

Equation (40) is a quadratic in the power of ${{\omega }^{2}}$ and the sum and product of the roots of Eq. (40) can be given as $\omega _{1}^{2} + \omega _{2}^{2}$ = $\left\{ { - \left( {1 + {{\lambda _{{De}}^{2}} \mathord{\left/ {\vphantom {{\lambda _{{De}}^{2}} {\lambda _{{Di}}^{2}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}}}} \right)v_{{ti}}^{2}{{k}^{2}}} \right.$ + $\Omega _{{Jd}}^{2}$ – $\Omega _{{cd}}^{2}$ – $v_{{td}}^{2}{{k}^{2}}$ – $\left. {\Omega _{{pd}}^{2}\lambda _{{De}}^{2}{{k}^{2}}(1\, - \,\Gamma )} \right\}$ and $\omega _{1}^{2}\omega _{2}^{2}$ = $\left\{ {\Omega _{{pd}}^{2}\lambda _{{De}}^{2}{{k}^{2}}(1\, - \,\Gamma )} \right.$ + $\left. {\left( {1 + {{\lambda _{{De}}^{2}} \mathord{\left/ {\vphantom {{\lambda _{{De}}^{2}} {\lambda _{{Di}}^{2}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}}}} \right)\left( {\Omega _{{cd}}^{2} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}}} \right)} \right\}v_{{ti}}^{2}{{k}^{2}}$, respectively. From the product of the roots, one can notice that $\Omega _{{cd}}^{2} + v_{{td}}^{2}{{k}^{2}}$ + $\Omega _{{pd}}^{2}\lambda _{{De}}^{2}{{k}^{2}}(1 - \Gamma ){{\left( {1 + {{\lambda _{{De}}^{2}} \mathord{\left/ {\vphantom {{\lambda _{{De}}^{2}} {\lambda _{{Di}}^{2}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}}}} \right)}^{{ - 1}}} < \Omega _{{Jd}}^{2}$; then, Eq. (40) satisfied by at least one real positive root which gives the instability in the self-gravitating dusty plasma. The inequality reveals that thermal velocity of ion has no connection with self-gravitational instability criterion. The increasing value of cyclotron frequency suppresses the effect of the gravitational wave frequency, while the dust polarization force increases the effect of gravitational free energy.

Furthermore, if we ignore the thermal velocity of ions and dust charge fluctuation in collisionless self-gravitating plasma and consider the radiative condensations of electrons and ions, then Eq. (39) reduces as

$${{\omega }^{2}} - \Omega _{{Jd}}^{2} + v_{{td}}^{2}{{k}^{2}} + \Omega _{{cd}}^{2} + \frac{{\Omega _{{pd}}^{2}(1 - \Gamma )}}{{\left\{ {1 + \left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{De}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{De}}^{2}{{k}^{2}}}}} \right)\left( {{{R_{{ce}}^{'}} \mathord{\left/ {\vphantom {{R_{{ce}}^{'}} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right. \kern-0em} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right)} \right. + \left. {\left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right)\left( {{{R_{{ci}}^{'}} \mathord{\left/ {\vphantom {{R_{{ci}}^{'}} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right. \kern-0em} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right)} \right\}}} = 0.$$

((41))

Equation (41) shows the effect of radiative condensation of electrons and ions, magnetic field, and polarization force in a dusty plasma including self-gravitation. In the absence of magnetic field and polarization force, the obtained result becomes identical with Eq. (32) of Sharma and Patidar [34], excluding the neutrals in that case. Equation (41) recovers the result of Shukla and Sandberg [35] in the absence of polarization force, ion radiative cooling, and magnetic field. The obtained condition of self-gravitational instability from Eq. (41) is

$$v_{{td}}^{2}{{k}^{2}} + \Omega _{{cd}}^{2} + \frac{{\Omega _{{pd}}^{2}(1 - \Gamma )}}{{\left\{ {1 + \left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{De}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{De}}^{2}{{k}^{2}}}}} \right)\left( {{{R_{{ce}}^{'}} \mathord{\left/ {\vphantom {{R_{{ce}}^{'}} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right. \kern-0em} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right)} \right. + \left. {\left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right)\left( {{{R_{{ci}}^{'}} \mathord{\left/ {\vphantom {{R_{{ci}}^{'}} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right. \kern-0em} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right)} \right\}}} < \Omega _{{Jd}}^{2}.$$

((42))

Equation (42) indicates that the combined influence of radiative condensation and polarization force reduce the damping effect of dust plasma frequency over the Jeans frequency. Inequality (42) becomes similar to Eq. (34) of Sharma and Patidar [34] in the absence of magnetic field and polarization force. Thus, the combined effect of polarization force and ion radiative cooling on Jeans instability in the presence of magnetic field is our new result of the present work which has been not reported yet.

Further, if we consider the effect of variable dust charge and polarization force and exclude the effect of collisions and ion and dust thermal velocities in radiative self-gravitating dusty plasma, then dispersion relation (37) yields

$$\begin{gathered} 1 + \left( {\frac{1}{{\lambda _{{De}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)\left( {\frac{{{{R}_{{ce}}}}}{{{{R}_{{ce}}} - (i\sigma + {{L}_{{ne}}})}}} \right) \\ - \;\left( {\frac{1}{{\lambda _{{Di}}^{2}{{k}^{2}}}} - \frac{{i\Im }}{{(\sigma + i\Lambda ){{k}^{2}}}}} \right)\left( {\frac{{{{R}_{{ci}}}}}{{{{R}_{{ci}}} - (i\sigma + {{L}_{{ni}}})}}} \right) \\ - \;\frac{{\Omega _{{pd}}^{2}(1 - \Gamma )}}{{{{\sigma }^{2}} + \Omega _{{Jd}}^{2} - \Omega _{{cd}}^{2}}} = 0, \\ \end{gathered} $$

((43))

which gives the condition of gravitational instability

$$\Omega _{{cd}}^{2} + \Omega _{{pd}}^{2}(1 - \Gamma ){{\left[ \begin{gathered} 1 + \left\{ {\left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{De}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{De}}^{2}{{k}^{2}}}}} \right) - \left( {{\Im \mathord{\left/ {\vphantom {\Im {\Lambda {{k}^{2}}}}} \right. \kern-0em} {\Lambda {{k}^{2}}}}} \right)} \right\}\left( {{{R_{{ce}}^{'}} \mathord{\left/ {\vphantom {{R_{{ce}}^{'}} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right. \kern-0em} {R_{{ce}}^{'} - {{L}_{{ne}}}}}} \right) \hfill \\ + \;\left\{ {\left( {{1 \mathord{\left/ {\vphantom {1 {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right. \kern-0em} {\lambda _{{Di}}^{2}{{k}^{2}}}}} \right) - \left( {{\Im \mathord{\left/ {\vphantom {\Im {\Lambda {{k}^{2}}}}} \right. \kern-0em} {\Lambda {{k}^{2}}}}} \right)} \right\}\left( {{{R_{{ci}}^{'}} \mathord{\left/ {\vphantom {{R_{{ci}}^{'}} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right. \kern-0em} {R_{{ci}}^{'} - {{L}_{{ni}}}}}} \right) \hfill \\ \end{gathered} \right]}^{{ - 1}}} < \Omega _{{Jd}}^{2}.$$

The obtained criterion indicates that the fluctuation in dust charge supports the gravitational free energy to grow.

In the magnetized dusty plasma, if the influence of self-gravitation is very small and the plasma species follow the Maxwell−Boltzmann distribution, dispersion relation (38) yields the modified cyclotron mode in terms of dust charge fluctuation, collision frequency, and polarization force as follows:

$$\begin{gathered} {{\omega }^{6}} + {{\omega }^{5}}2{{\nu }_{d}}\left( {1 + \beta } \right) + {{\omega }^{4}}\left\{ {\nu _{d}^{2}{{{\left( {1 + \beta } \right)}}^{2}}} \right. + v_{{td}}^{2}{{k}^{2}} + \Omega _{{cd}}^{2} \\ + \;v_{{ti}}^{2}{{k}^{2}} + \left. {v_{{ti}}^{2}{{k}^{2}}{{{{\alpha }_{D}}} \mathord{\left/ {\vphantom {{{{\alpha }_{D}}} {\left( {1 + {{B}_{e}}} \right) + {{\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right)} \mathord{\left/ {\vphantom {{\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right)} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right) + {{\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right)} \mathord{\left/ {\vphantom {{\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right)} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}}}} \right\} \\ + \;{{\omega }^{3}}\left\{ {v_{{td}}^{2}{{k}^{2}}\left( {2 + \beta } \right){{\nu }_{d}} + } \right.2\Omega _{{cd}}^{2}{{\nu }_{d}} + 2\left( {1 + \beta } \right){{\nu }_{d}}v_{{ti}}^{2}{{k}^{2}} \\ \end{gathered} $$

$$\begin{gathered} + \;2\left( {1 + \beta } \right){{\nu }_{d}}v_{{ti}}^{2}{{k}^{2}}{{{{\alpha }_{D}}} \mathord{\left/ {\vphantom {{{{\alpha }_{D}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}} + \Omega _{{pd}}^{2}{{\nu }_{d}}\left( {1 - \Gamma } \right) \\ \left. {{{ \times \;\left( {2 + \beta } \right)} \mathord{\left/ {\vphantom {{ \times \;\left( {2 + \beta } \right)} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right\} + {{\omega }^{2}}\left\{ {v_{{td}}^{2}{{k}^{2}}\nu _{d}^{2}\left( {1 + \beta } \right) + \Omega _{{cd}}^{2}\nu _{d}^{2}} \right. \\ \end{gathered} $$

$$\begin{gathered} + \;v_{{ti}}^{2}{{k}^{2}}{\kern 1pt} \left( {1 + {{{{\alpha }_{D}}} \mathord{\left/ {\vphantom {{{{\alpha }_{D}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right)\left( {{{{\left( {1 + \beta } \right)}}^{2}}\nu _{d}^{2} + v_{{td}}^{2}{{k}^{2}} + \Omega _{{cd}}^{2}} \right) \\ + \;\Omega _{{pd}}^{2}\nu _{d}^{2}\left( {1 - \Gamma } \right){{\left( {1 + \beta } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \beta } \right)} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}} \\ \end{gathered} $$

((44))

$$\begin{gathered} \times \;\left. {\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right){{v_{{ti}}^{2}{{k}^{2}}} \mathord{\left/ {\vphantom {{v_{{ti}}^{2}{{k}^{2}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right\} + \omega \left\{ {{{k}^{2}}v_{{ti}}^{2}} \right. \\ \times \;\left( {1 + {{{{\alpha }_{D}}} \mathord{\left/ {\vphantom {{{{\alpha }_{D}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right)\left( {v_{{td}}^{2}{{k}^{2}}\left( {2 + \beta } \right){{\nu }_{d}} + 2{{\nu }_{d}}\Omega _{{cd}}^{2}} \right) \\ \end{gathered} $$

$$\begin{gathered} + \left. {\;\Omega _{{pd}}^{2}(1 - \Gamma ){{k}^{2}}v_{{ti}}^{2}{{\left( {2 + \beta } \right){{\nu }_{d}}} \mathord{\left/ {\vphantom {{\left( {2 + \beta } \right){{\nu }_{d}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right\} \\ + \;\left\{ {{{k}^{2}}v_{{ti}}^{2}\left( {1 + {{{{\alpha }_{D}}} \mathord{\left/ {\vphantom {{{{\alpha }_{D}}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right)} \right.\left( {v_{{td}}^{2}{{k}^{2}}\left( {1 + \beta } \right) + \Omega _{{cd}}^{2}} \right)\nu _{d}^{2} \\ + \;\left. {\Omega _{{pd}}^{2}(1 - \Gamma ){{k}^{2}}v_{{ti}}^{2}{{\left( {1 + \beta } \right)\nu _{d}^{2}} \mathord{\left/ {\vphantom {{\left( {1 + \beta } \right)\nu _{d}^{2}} {\left( {1 + {{B}_{e}}} \right)}}} \right. \kern-0em} {\left( {1 + {{B}_{e}}} \right)}}} \right\} = 0, \\ \end{gathered} $$

where ${{B}_{e}} = {1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}\lambda _{{De}}^{2}}}} \right. \kern-0em} {{{k}^{2}}\lambda _{{De}}^{2}}} - {\Im \mathord{\left/ {\vphantom {\Im {\Lambda {{k}^{2}}}}} \right. \kern-0em} {\Lambda {{k}^{2}}}}$.

Equation (44) describes the effect of dust neutral collisions, dust charge fluctuation, and polarization force on the propagation of dust cyclotron mode. If we consider the dust charge variation and ignore the self-gravitational and radiative effects in Eq. (41), the obtained mode takes the shape as $\left( {\omega = - i\sigma } \right)$

$$\begin{gathered} {{\sigma }^{2}} - \Omega _{{cd}}^{2} - v_{{td}}^{2}{{k}^{2}} \\ - \;\Omega _{{pd}}^{2}\left( {1 - \Gamma } \right){{\left( {{1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}\lambda _{{De}}^{2}}}} \right. \kern-0em} {{{k}^{2}}\lambda _{{De}}^{2}}} - {\Im \mathord{\left/ {\vphantom {\Im {\Lambda {{k}^{2}}}}} \right. \kern-0em} {\Lambda {{k}^{2}}}}} \right)}^{{ - 1}}} = 0. \\ \end{gathered} $$

((45))

Quadratic equation (45) satisfied by the two roots: ${{\sigma }_{1}}$ and ${{\sigma }_{2}}$, whose value can be written as

$$\begin{gathered} {{\sigma }_{{1,2}}} \\ = \pm \sqrt {\Omega _{{cd}}^{2} + v_{{td}}^{2}{{k}^{2}} + \Omega _{{pd}}^{2}\left( {1 - \Gamma } \right){{{\left( {{1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}\lambda _{{De}}^{2}}}} \right. \kern-0em} {{{k}^{2}}\lambda _{{De}}^{2}}} - {\Im \mathord{\left/ {\vphantom {\Im {\Lambda {{k}^{2}}}}} \right. \kern-0em} {\Lambda {{k}^{2}}}}} \right)}}^{{ - 1}}}} , \\ \end{gathered} $$

((46))

which gives two oscillating cyclotron mode modified by thermal velocity, polarization force and charge fluctuation of dust.

4 NUMERICAL DISCUSSION

In the previous section, the analytical discussion of the properties of general dispersion relation has been performed, but in order to know the influence of specific considered parameter on the growth rate of gravitational instability, we perform the numerical estimation of general dispersion relation in both parallel and perpendicular mode of propagation. Now, to analyze the effect of collisions, magnetic field, dust charge fluctuation, and polarization force on the growth rate of Jeans instability in the presence of radiative condensation of electrons and ions, we rewrite the dispersion relation of parallel (32) and perpendicular (39) mode of propagation in normalized form as

$$\begin{gathered} {{\omega }^{{*5}}} + {{\omega }^{{*4}}}\left( {1 + \beta } \right)\nu _{d}^{*} + {{\omega }^{{*3}}}\left\{ {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1 + {{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right. \\ \left. { + \;\xi _{{De}}^{*}\left( {\alpha _{D}^{*}{{k}^{{*2}}} + \Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)} \right)} \right\} + {{\omega }^{{*2}}}\left\{ {\nu _{d}^{*}\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)} \right. \\ + \;\left( {1 + \beta } \right)\nu _{d}^{*}{{k}^{{*2}}}\left. {\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right) + \Omega _{{pd}}^{{*2}}\nu _{d}^{*}\xi _{{De}}^{*}\left( {1 - \Gamma } \right)} \right\} \\ \end{gathered} $$

$$ + \;\omega {\text{*}}\left\{ {{{k}^{{*2}}}} \right.\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right)$$

((47))

$$\begin{gathered} \left. { + \;\Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\xi _{{De}}^{*}\left( {{{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right)} \right\} \\ + \;\left\{ {\nu _{d}^{*}{{k}^{{*2}}}\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)} \right.\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right) \\ \left. {\; + \Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\nu _{d}^{*}{{k}^{{*2}}}\xi _{{De}}^{*}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right\} = 0, \\ \end{gathered} $$

and

$$\begin{gathered} {{\omega }^{{*6}}} + {{\omega }^{{*5}}}2\nu _{d}^{*}\left( {1 + \beta } \right) + {{\omega }^{{*4}}}\left\{ {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1 + \nu _{d}^{{*2}}{{{\left( {1 + \beta } \right)}}^{2}}} \right. \\ + \;\left. {\Omega _{{cd}}^{{*2}} + {{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right) + \xi _{{De}}^{*}\left( {\alpha _{D}^{*}{{k}^{{*2}}} + \Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)} \right)} \right\} \\ + \;{{\omega }^{{*3}}}\left\{ {\left( {2 + \beta } \right)\nu _{d}^{*}\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)} \right. + 2\nu _{d}^{*}\Omega _{{cd}}^{{*2}} \\ \end{gathered} $$

$$\begin{gathered} + \;2{{k}^{{*2}}}\nu _{d}^{*}\left( {1 + \beta } \right)\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right) \\ \left. { + \;\Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\xi _{{De}}^{*}\nu _{d}^{*}\left( {2 + \beta } \right)} \right\} + {{\omega }^{{*2}}}\left\{ {\nu _{d}^{{*2}}\left( {1 + \beta } \right)} \right. \\ \times \;\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right) + \Omega _{{cd}}^{{*2}}\nu _{d}^{{*2}} + {{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right) \\ \end{gathered} $$

$$ \times \;\left\{ {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1 + \nu _{d}^{{*2}}{{{\left( {1 + \beta } \right)}}^{2}} + \Omega _{{cd}}^{{*2}}} \right\}$$

((48))

$$\begin{gathered} + \;\Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\xi _{{De}}^{*}\left( {{{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right.\left. {\left. { + \nu _{d}^{{*2}}(1 + \beta )} \right)} \right\} \\ + \;\omega {\text{*}}\left\{ {{{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right)} \right. \\ \times \;\left\{ {\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)(2 + \beta ) + \left. {2\Omega _{{cd}}^{{*2}}} \right\}\nu _{d}^{*}} \right. \\ \end{gathered} $$

$$\begin{gathered} + \;\Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\xi _{{De}}^{*}\nu _{d}^{*}{{k}^{{*2}}}\left( {2 + \beta } \right)\left. {\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right\} \\ + \;{{k}^{{*2}}}\left( {1 - L_{{ni}}^{*}\xi _{i}^{*} + \alpha _{D}^{*}\xi _{{De}}^{*}} \right)\nu _{d}^{{*2}}\left\{ {\left( {{{k}^{{*2}}}v_{{td}}^{{*2}} - 1} \right)(1 + \beta )} \right. \\ \left. { + \;\Omega _{{cd}}^{{*2}}} \right\} + \Omega _{{pd}}^{{*2}}\left( {1 - \Gamma } \right)\xi _{{De}}^{*}\nu _{d}^{{*2}}{{k}^{*}}^{2}\left( {1 + \beta } \right)\left. {\left( {1 - L_{{ni}}^{*}\xi _{i}^{*}} \right)} \right\} = 0, \\ \end{gathered} $$

where

$$\begin{gathered} \omega \text{*} = \frac{\omega }{{{{\Omega }_{{Jd}}}}},\quad k{\text{*}} = \frac{{k{{v}_{{ti}}}}}{{{{\Omega }_{{Jd}}}}},\quad \chi _{e}^{*} = \frac{{{{{{\chi }_{e}}{{\Omega }_{{Jd}}}} \mathord{\left/ {\vphantom {{{{\chi }_{e}}{{\Omega }_{{Jd}}}} {{{n}_{{e0}}}}}} \right. \kern-0em} {{{n}_{{e0}}}}}}}{{v_{{ti}}^{2}}}, \\ L_{{ne}}^{*} = \frac{{{{L}_{{ne}}}}}{{{{\Omega }_{{Jd}}}}},\quad L_{{Te}}^{*} = \frac{{{{L}_{{Te}}}}}{{{{\Omega }_{{Jd}}}}},\quad \nu _{d}^{*} = \frac{{{{\nu }_{d}}}}{{{{\Omega }_{{Jd}}}}}, \\ \chi _{i}^{*} = \frac{{{{{{\chi }_{i}}{{\Omega }_{{Jd}}}} \mathord{\left/ {\vphantom {{{{\chi }_{i}}{{\Omega }_{{Jd}}}} {{{n}_{{i0}}}}}} \right. \kern-0em} {{{n}_{{i0}}}}}}}{{v_{{ti}}^{2}}},\quad L_{{ni}}^{*} = \frac{{{{L}_{{ni}}}}}{{{{\Omega }_{{Jd}}}}},\quad L_{{Ti}}^{*} = \frac{{{{L}_{{Ti}}}}}{{{{\Omega }_{{Jd}}}}}, \\ \end{gathered} $$

$$\begin{gathered} \lambda _{{Di}}^{*} = \frac{{{{\lambda }_{{Di}}}{{\Omega }_{{Jd}}}}}{{{{v}_{{ti}}}}},\quad \lambda _{{De}}^{*} = \frac{{{{\lambda }_{{De}}}{{\Omega }_{{Jd}}}}}{{{{v}_{{ti}}}}},\quad \Im \text{*} = \frac{{\Im v_{{ti}}^{2}}}{{\Lambda \Omega _{{Jd}}^{2}}}, \\ v_{{td}}^{*} = \frac{{{{v}_{{td}}}}}{{{{v}_{{ti}}}}},\quad \Omega _{{cd}}^{*} = \frac{{{{\Omega }_{{cd}}}}}{{{{\Omega }_{{Jd}}}}},\quad \Omega _{{pd}}^{*} = \frac{{{{\Omega }_{{pd}}}}}{{{{\Omega }_{{Jd}}}}}, \\ \end{gathered} $$

((49))

$$\begin{gathered} \xi _{i}^{*} = {{\left( {\chi _{i}^{*}{{k}^{{*2}}} + L_{{Ti}}^{*}} \right)}^{{ - 1}}}, \\ \xi _{{De}}^{*} = 1 + \left( {\frac{1}{{{{k}^{{*2}}}\lambda _{{De}}^{{*2}}}} + \frac{{\Im {\text{*}}}}{{{{k}^{{*2}}}}}} \right)\left( {\frac{{\chi _{e}^{*}{{k}^{{*2}}} + L_{{Te}}^{*} - L_{{ne}}^{*}}}{{\chi _{e}^{*}{{k}^{{*2}}} + L_{{Te}}^{*}}}} \right), \\ \alpha _{D}^{*} = \left( {\frac{1}{{{{k}^{{*2}}}\lambda _{{Di}}^{{*2}}}} + \frac{{\Im {\text{*}}}}{{{{k}^{{*2}}}}}} \right). \\ \end{gathered} $$

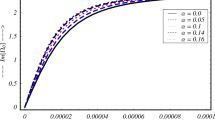
The influence of polarization force on growth rate of instability with wavenumber in parallel mode of propagation has been displayed in Fig. 1. The four curves stand for different value of polarization force $\Gamma = 0.0$, 0.1, 0.3, and 0.5. The value of other parameters are taken as $\beta = 0.8$, $\nu _{d}^{*} = 2.5$, $\Omega _{{pd}}^{*} = 0.5$, $L_{{Te}}^{*} = 0.1$, $L_{{Ti}}^{*} = 0.1$, $\lambda _{{De}}^{*} = \lambda _{{Di}}^{*} = 0.01$, $\chi _{i}^{*} = 0.1$, $L_{{ne}}^{*} = 0.1$, $\chi _{e}^{*} = 0.1$, and $L_{{ni}}^{*} = 0.1$.

Fig. 1.

Growth rate of gravitational instability is plotted against wavenumber in parallel mode of propagation for different values of polarization force Γ.

The nature of curves reveals that, as the effect of polarization force increases in the system, the growth rate of self-gravitational instability becomes stronger. Thus, one can say that the polarization force has destabilizing effect on the growth rate of self-gravitational instability of collisional magnetized radiative dusty plasma.

In Fig. 2 the dimensionless growth rate of the Jeans instability is displayed with the dimensionless wavenumber for different values of collision frequency in parallel mode of propagation. The fixed values of plasma parameters are taken as $\beta = 0.8$, $L_{{Te}}^{*} = 0.1$, $L_{{Ti}}^{*} = 0.1$, $\lambda _{{De}}^{*} = 0.01$, $\Omega _{{pd}}^{*} = 0.1$, $\lambda _{{Di}}^{*} = 0.01$, $\Omega _{{cd}}^{*} =$ 0.1, $L_{{ne}}^{*} = 0.1$, $L_{{ni}}^{*} = 0.1$, $\chi _{e}^{*} = 0.0$, $\chi _{i}^{*} = 0.0$, $\Gamma = 0.2$, and $\Im \text{*} = 0.05$. Figure 2 contains three curves for different values of dust neutral collision frequency. It can be seen from curves that the growth rate of instability is higher for lowest value of dust neutral collision frequency. Further, for the positive increasing of collision frequency, the growth rate of instability decreases.

Fig. 2.

Growth rate of Jeans instability versus wavenumber in parallel mode of propagation is plotted for different values of dust−neutral collision frequency $\nu _{d}^{*}$.

In Fig. 3, the normalized growth rate is plotted against the normalized wavenumber in the parallel mode of propagation for various values of dust charge fluctuation ($\Im \text{*} = 0.0$, 3.0, and 6.0) by taking the fixed values of remaining parameters as $\chi _{e}^{*} = 0.1$, $\chi _{i}^{*} = 0.1$, $\nu _{d}^{*} = 0.0$, $v_{{td}}^{*} = 0.2$, $L_{{Te}}^{*} = 0.1$, $L_{{Ti}}^{*} = 0.1$, $\lambda _{{De}}^{*} = 0.1$, $\Omega _{{pd}}^{*} = 0.1$, $\lambda _{{Di}}^{*} = 0.1$, $L_{{ne}}^{*} = 0.1$, and $L_{{ni}}^{*} = 0.1$. It is clear from the figure that the growth rate of instability increases with increase in dust charge fluctuation.

Fig. 3.

Growth rate against wavenumber in parallel mode of propagation is plotted for different values of dust charge fluctuation $\Im {\text{*}}$.

Figure 4 shows the influence of cyclotron frequency on the growth rate of Jeans instability in the perpendicular mode of propagation. In the figure, the solid curve is for $\Omega _{{cd}}^{*} = 0.1$, while dashed and dotted curves are for $\Omega _{{cd}}^{*} = 0.3$ and $\Omega _{{cd}}^{*} = 0.5$, respectively.

Fig. 4.

Growth rate of Jeans instability versus wavenumber in perpendicular mode of propagation is plotted for different values of dust cyclotron frequency $\Omega _{{cd}}^{*}$.

The values of other normalized parameters are selected as $\beta =$ 0.2, $v_{{td}}^{*} = 0.2$, $\Im \text{*} = 0.2$, $L_{{Te}}^{*} = 0.5$, $L_{{Ti}}^{*} =$ 0.1, $\lambda _{{De}}^{*} = 0.01$, $\Omega _{{pd}}^{*} = 0.1$, $\lambda _{{Di}}^{*} = 0.01$, $\chi _{e}^{*} = 0.5$, $L_{{ne}}^{*} = 0.5$, $L_{{ni}}^{*} = 0.1$, $\chi _{i}^{*} = 0.1$, $\Gamma = 0.4$, and $\nu _{d}^{*} = 0.2$. The figure shows that the growth rate of instability decreases on increasing the value of the magnetic field; therefore, increase in the magnetic field moves the system toward stabilization.

To observe the effect of dust neutral collisions ($\nu _{d}^{*}$) on the growth rate of the Jeans instability against wavenumber in perpendicular mode of propagation, Fig. 5 has been plotted. The right panel is for $\nu _{d}^{*} = 0.0$, and the left panel is plotted for $\nu _{d}^{*} = 0.1$, 0.2, and 0.3. It can be seen that the increasing value of dust neutral collision frequency decreases the growth rate of instability. The dissipative effect of the dust neutral collision frequency reduces the effect of free energy available to increase the growth rate of self-gravitational instability. Thus, the dust neutral collision frequency has stabilizing behavior on the growth rate of Jeans instability in perpendicular mode of propagation of magnetized radiative dusty plasma with polarization force.

Fig. 5.

Growth rate of Jeans instability against wavenumber in perpendicular propagation is plotted for different values of dust−neutral collision frequency $\nu _{d}^{*}$.

The positive roots of normalized growth rate in perpendicular propagation are plotted against the normalized wavenumber in Fig. 6 for four different values of polarization force (Γ = 0.0, 0.3, 0.6, and 0.9). The figure shows four curves (Γ = 0.0 in the right panel and Γ = 0.3, 0.6, and 0.9 in the left panel). It is observed from the figure that the growth rate of the Jeans instability increases with increasing the values of polarization force. The system tends to move toward destabilization; thus, the polarization force shows the destabilizing effect on the collisional radiative self-gravitating dusty plasma. Hence, the existence of the polarization forces has a vital role in the instability of the system.

Fig. 6.

Growth rate of Jeans instability against wavenumber in perpendicular mode of propagation is plotted for different values of polarization force.

Now, we have plotted Eq. (45) in Figs. 7 and 8 in order to study the influence of dust thermal velocity and polarization force on the dust cyclotron mode in perpendicular mode of propagation.

Fig. 7.

Dispersion frequency against wave number in perpendicular of propagation is plotted for presence and absence of dust thermal velocity $v_{{td}}^{*}$.

Fig. 8.

Dispersion frequency against wavenumber in perpendicular mode of propagation is plotted for different values of dust polarization force Γ.

The dispersion frequency versus wavenumber is plotted in Fig. 7 for the absence and presence of dust thermal velocity. We have kept the dust plasma frequency ${{\Omega }_{{pd}}} = 5.37 \times {{10}^{{ - 2}}}$, dust cyclotron frequency ${{\Omega }_{{cd}}} = 1.6 \times {{10}^{{ - 3}}}$, and polarization force $\Gamma = 0.3$. The solid curve shows the absence and dotted curve shows the presence of dust thermal velocity. Figure 7 illustrates that the dispersion frequency is greater in the presence of dust thermal velocity and the dispersion frequency increases with increasing the wavenumber in the plasma system.

Figure 8 demonstrates the variation of dispersion frequency of dust cyclotron mode with the wavenumber for three different value of dust polarization force. The solid curve is for the value of polarization force $\Gamma = 0.0$, dashed curve represents $\Gamma = 0.5$, and dotted curve represents $\Gamma = 0.9$, while the value of other fixed parameters are chosen as ${{\Omega }_{{pd}}} = 5.37 \times {{10}^{{ - 2}}}$, ${{\Omega }_{{cd}}} = 1.6 \times {{10}^{{ - 3}}}$, and ${{v}_{{td}}} = 8.4 \times {{10}^{{ - 2}}}$. The behavior of curves describes that the growing value of polarization force reduces the dispersion frequency of dust cyclotron mode.

Furthermore, the dispersion frequency of pure dust cyclotron in parallel mode of propagation and modified dust cyclotron mode in perpendicular mode of propagation is plotted in Fig. 9. The variation of dispersion frequency of dust cyclotron mode against the dust cyclotron frequency is shown in Fig. 9. The cyclotron mode (in perpendicular propagation) modified in terms of dust thermal velocity, polarization force, and dust charge fluctuation is represented by solid curve, while the pure cyclotron mode (in parallel propagation) is signified by dotted curve. Figure 9 indicates that the dispersion frequency increases with increasing value of dust cyclotron frequency. It can also be seen that the cyclotron mode in perpendicular mode of propagation has higher value of dispersion frequency in comparison to the pure cyclotron mode.

Fig. 9.

Dispersion frequency against dust cyclotron frequency in parallel and perpendicular modes of propagation is plotted.

5 CONCLUSIONS

The influences of polarization force, magnetic field, and dust−neutral collision frequency on the self-gravitational instability of partially ionized radiative dusty plasma are studied in the present work. The discussion of general dispersion relation is done in both the parallel and perpendicular modes of propagations. We get cyclotron and radiative gravitating mode in parallel mode of propagation, while the collisional and radiative gravitating mode modified by magnetic field is observed in perpendicular mode of propagation. In parallel mode of propagation, the dust−neutral collision frequency and the ratio of densities of neutrals and dust particles modify the cyclotron mode, while the mode remains unaffected from the dust self-gravity. The radiative condensation instability condition is affected by the presence of dust charge variation, dust thermal velocity, and polarization force. The condition and growth rate of gravitational instability of dust grains is affected by the magnetic field in perpendicular mode only. The numerical results show that the dust−neutral collision frequency and magnetic field have a stabilizing effect on growth rate of the Jeans instability of dust, whereas dust charge fluctuation and radiative cooling of electrons and ions have the destabilizing effect on growth rate of the Jeans instability. Furthermore, the influence of dust polarization force enhances in the system and increases the growth rate of self-gravitational instability. The polarization force and thermal velocity of dust has significant influence the dust cyclotron mode. The obtained results are important for the study of molecular clouds.

ADDITIONAL INFORMATION

The article is published in the original.