On the photogravitational R4BP when the third primary is an oblate/prolate spheroid

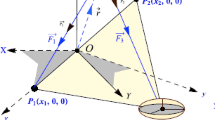
Abstract

The present paper deals with the photogravitational restricted four-body problem, when the third primary placed at the triangular libration point of the restricted three-body problem is an oblate/prolate body. The third primary $m_{3}$ is not influencing the motion of the dominating primaries $m_{1}$ and $m_{2}$. We have studied the motion of $m_{4}$, moving under the influence of the three primaries $m_{i}, i=1,2,3$, but the motion of the primaries is not being influenced by infinitesimal mass $m_{4}$. The aim of this study is to find the locations of the libration points and their stability. We obtain three collinear and five non-collinear libration points when the third body is an oblate spheroid and source of radiation. The collinear libration points are unstable for all the mass parameter. The non-collinear libration points are stable for different mass parameters and oblateness factors. Further there exist 12 libration points, depending on the mass ratio of dominating primaries, the prolateness, and the radiation pressure of the third primary. We have drawn the zero velocity surface to determine the possible allowed boundary region. We observed that for increasing values of the oblateness coefficient $A$, the corresponding possible boundary region increases where the particle can freely move from one side to another side. Further, for different values of the Jacobi constant $C$, we can find the boundary region where the particle can move in the possible allowed partitions. The stability region of the libration points expanded due to the presence of the oblateness coefficient and various values of $C$. We further apply these findings to the Sun–Jupiter–asteroid–spacecraft system.

1 Introduction

In celestial mechanics, the restricted three-body problem with different perturbations as oblateness, prolateness, and radiation of the primaries has been studied by many scientists. The R3BP has been the beginning of inspiration and field of study since Newton and Euler. In our solar system the Sun–Jupiter–asteroid system represents a good model of the restricted four-body problem. We have considered the generalization of the three-body problem to the restricted four-body problem by taking three bodies as the governing primaries and the fourth body as an infinitesimal mass. In analogy with the R3BP, we have also taken the different perturbations as the oblateness and the radiating force in R4BP consisting of three primaries moving in circular orbits keeping an equilateral-triangle configuration in which the third body is fixed at the libration point of R3BP and the fourth particle is moving under the gravitational attraction of the three primaries.

There exist strong radiation sources in the universe. Thus, we have investigated the photogravitational restricted four-body problem (PRFBP). For this investigation, we shall acquire the basic idea of Radzievskii’s (1950, 1951) theory for the photogravitational R4BP. In this study, we have shown the effect of radiation pressure and the result on the non-collinear libration points $L_{i},i=4,5,6,7$. The radiation due to the third primary influences the motion of the infinitesimal mass but does not affect the motion of the other dominating primaries. The impact due to radiating primaries has been studied by many scientists (Simmons et al. 1985; Ragos et al. 1995; Bhatnagar and Chawla 1979). Moulton (1900) discussed a class of particular solutions of the problem of four bodies. Recently, the four-body problem has been studied by many scientists; Baltagiannis and Papadakis (2011), Ceccaroni and Biggs (2010), Ceccaroni and Biggs (2012), and Croustalloudi and Kalvouridis (2013). Suraj and Hassan (2014) studied the photogravitational four-body problem in the sense of Sitnikov by taking all the three primaries as a source of radiation. Suraj et al. (2014) studied the photogravitational R3BP when the primaries are heterogeneous spheroids with three layers. Papadouris and Papadakis (2014) studied the libration points in the photogravitational restricted four-body problem and observed that the existence and the number of collinear and non-collinear libration points of the problem depends on the mass parameters of the primaries and the radiation factor. Alvarez-Ramírez and Barrabés (2015) studied the transport orbits in an equilateral restricted four-body problem. One studied homoclinic and heteroclinic connections, as well as transit orbits traveling from and to different regions in dependence on the existence of families of unstable periodic orbits, with invariant stable and unstable manifolds.

Chand et al. (2015) has studied the R4BP when the third primary is an oblate body. In the present paper we have taken the radiation pressure due to the third primary into account. Also, we have discussed the problem by taking the third primary as a prolate body and a source of radiation as well.

The present paper is organized as follows: In Sect. 2 we derive the equations of motion of the infinitesimal mass with the oblateness and the radiation due to the third primary. Section 3 deals with the existence of coplanar libration points, Sect. 3.1 shows the existence of the libration points when the third primary is an oblate body and Sect. 3.2 shows the existence of the libration points when the third primary is a prolate body and a source of radiation as well. In Sect. 4 we discuss the ZVC. Further, Sect. 5 deals with the stability of the obtained libration points. In Sect. 6, we apply our technique to find the libration points and to discuss their stability in Sun–Jupiter–asteroid–spacecraft system. Finally, in Sect. 7 we analyze and discuss the obtained results.

2 Equations of motion

In this photogravitational version of restricted four-body problem we adopt the notation and formulation used in Chand et al. (2015). The scaled equations of motion of the infinitesimal mass of the four-body problem when the third primary is an oblate (prolate) spheroid and a source of radiation in the usual dimensionless rectangular rotating coordinate system are

$$ \begin{aligned}[c] &\ddot{x}-2n\dot{y}=\varOmega_{x},\\ &\ddot{y}+2n\dot{x}=\varOmega_{y},\\ &\ddot{z}=\varOmega_{z}, \end{aligned} $$

(1)

where

$$\begin{aligned} &{\varOmega=\frac{1}{2}\bigl(x^{2}+y^{2}\bigr)+ \frac{1-\mu}{r_{1}}+\frac{\mu}{r_{2}}+\frac{\varepsilon q}{r_{3}} \biggl(1+\frac{A}{2r_{3}^{2}}- \frac{3Az^{2}}{2r_{3}^{4}} \biggr),} \\ &{r_{1}=\sqrt{(x+\mu)^{2}+y^{2}+z^{2}},} \\ &{r_{2}=\sqrt{(x-1+\mu)^{2}+y^{2}+z^{2}},} \\ &{r_{3}=\sqrt{ \biggl(x-\frac{1}{2}+\mu \biggr)^{2}+ \biggl(y-\frac{\sqrt{3}}{2} \biggr)^{2}+z^{2}},} \\ &{p=\frac{\mbox{Radiation pressure due to primary}\quad m_{3}}{ \mbox{Gravitational force due to primary}\quad m_{3}},} \\ &{q=1-p,} \\ &{A=\frac{a^{2}-c^{2}}{5R^{2}},} \\ &{n=1,} \\ &{R=\mbox{Dimensional distance between the main primaries}.} \end{aligned}$$

Chand et al. (2015) has discussed the case $A>0$, which represents the oblateness of the third primary. Here, in addition we have also taken the radiation due to the third primary into the consideration. Further, we have discussed the case $A<0$ (Douskos et al. 2012), corresponding to a prolate primary. The radiation pressure parameter of the primary $m_{3}$ is used in the same notation as in the classical three-body problem (Schuerman 1980). In the PRFBP (Photogravitational Restricted Four-Body Problem), we have adopted the basic idea discussed by Radzievskii (1950, 1951). Equation (1) possesses the well-known Jacobi integral,

$$ J(x,y,z,\dot{x},\dot{y},\dot{z})=2\varOmega(x,y,z)-(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})=C, $$

(2)

where $\dot{x},\dot{y}$, and $\dot{z}$ are the velocities and $C$ is the Jacobi constant.

3 Locations of coplanar libration points

The coordinates $(x_{0},y_{0})$ of the coplanar non-collinear libration points are the solutions of the first two equations of motion, i.e. Eq. (1), after setting the velocities $\dot{x},\dot{y},\dot{z}$ and the accelerations $\ddot{x},\ddot{y},\ddot{z}$ equal to zero. Thus we get

$$ \begin{aligned}[c] &\frac{\partial{\varOmega}}{\partial{x}}=x_{0}- \frac{(1-\mu)(x_{0}+\mu)}{r_{01}^{3}}-\frac{\mu(x_{0}-1+\mu)}{r_{02}^{3}} \\ &\phantom{\frac{\partial{\varOmega}}{\partial{x}}=}{}-q\varepsilon\frac{(x_{0}-\frac{1}{2}+\mu)}{r_{03}^{3}} \biggl\{ 1+\frac{3A}{2r_{03}^{2}} \biggr\} =0, \\ &\frac{\partial{\varOmega}}{\partial{y}}=y_{0} \biggl\{ 1-\frac{1-\mu}{r_{01}^{3}}-\frac{\mu}{r_{02}^{3}} \biggr\} -\frac{q\varepsilon(y_{0}-\frac{\sqrt{3}}{2})}{r_{03}^{3}} \\ &\phantom{\frac{\partial{\varOmega}}{\partial{y}}=}{}\times \biggl\{ 1+\frac{3A}{2r_{03}^{2}} \biggr\} =0, \end{aligned} $$

(3)

where $r_{01}, r_{02}$, and $r_{03}$ are the distances of $m_{4}$ from each of the primaries $m_{1}, m_{2}$, and $m_{3}$, respectively, at the libration points.

3.1 Case I: The primary $m_{3}$ as an oblate body

In this subsection we wish to observe the effect of the oblateness and the radiation pressure due to the third body on the location of the non-collinear libration points. In the photogravitational case, when the third primary is an oblate spheroid and radiates as well, the considered problem admits three collinear libration points $L_{i}, i=1,2,3$, but these collinear libration points are not being affected by the oblateness and radiation pressure of the third primary. The non-collinear points are solutions of Eq. (3). We observed that our problem admits five non-collinear libration points $L_{i},i=4,5,6,7,8$. These libration points are plotted in Fig. 1(a) for $A=1$ and in Fig. 1(b) for $A=0.35$. The four non-collinear libration points $L_{i},i=4,5,6,7$ exist near the third primary and are being affected by the oblateness and the radiation pressure of the third primary, but the change in the non-collinear libration point $L_{8}$ is negligible. We observed that as the oblateness increases the non-collinear libration points $L_{4,5, 6,7}$ move away from the third primary. In Table 1, we have evaluated the non-collinear libration points for $\mu=0.3$, $\varepsilon=0.02$ and for different values of the oblateness ($A$) and the radiation pressure parameter ($q$). Here $1-\mu$, $\mu$, and $\varepsilon$ are the scaled masses of the primaries $m_{1},m_{2}$ ($m_{1}\geq m_{2}$), and $m_{3}$ ($m_{3}\ll m_{1}, m_{2}$), respectively (Chand et al. 2015).

Fig. 1

(a, b) Location of eight equilibrium points for $\mu=0.3$, $\epsilon=0.03$ and $A=1$ (frame-1) $A=0.35$ (frame-2). The red-blue, green-orange, magenta-cyan and purple-yellow line shows contour for $q=0.1$, $q=0.25$, $q=0.35$ and $q=0.45$, respectively

Table 1 Non-collinear libration points

3.2 Case II: The primary $m_{3}$ as a prolate body

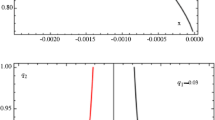
In this subsection we discuss the effect on the non-collinear libration points due to the prolateness and the photogravitational effect of the primary $m_{3}$. When the third primary is a prolate spheroid and radiates as well, the problem admits three collinear libration points $L_{i}$, $i=1,2,3$ which are not being affected by the prolateness and the radiation pressure of the third primary. The non-collinear libration points are solutions of Eq. (3). We observed that our problem admits nine non-collinear libration points $L_{i}$, $i=4,5,\ldots,12$. These libration points are plotted in Fig. 2(a, b) for $\mu =0.3$, $\epsilon =0.02$, $A=-0.0005$ to −0.001, and $q=0.1$. The eight non-collinear libration points $L_{i},i=4,5,\ldots,11$ (Table 2) exist near the third primary and are being affected due to the prolateness and the radiation of the third primary, but the change in the non-collinear libration point $L_{12}$ (Figs. 2(a, b)) is negligible. We also observed that for the prolateness $A=-0.01$ and $q=0.65$, there exist five non-collinear libration points and for the prolateness $A=-0.1$ and $q=0.65$, there is only one non-collinear libration point $L_{8}$. There does not exist any non-collinear libration point near the third primary.

Fig. 2

(a, b) Locations of 12 equilibrium points for prolate primary and zoomed part near third primary. Here $A=-0.0005$ and $q=0.1$

Table 2 Coordinates of collinear and non-collinear libration points for ($q= 0.1$ and $A=-0.0005$) radiating and prolate primary

4 Zero velocity curves

The contours of the surface (2), gives the zero velocity curves of the R4BP when the third primary is an oblate spheroid and a source of radiation. In Figs. 3(a, b, c, d) we obtained these zero velocity curves for the fixed value of the oblateness parameter $A=0.25$ and radiation parameter $q=0.1, 0.25, 0.50, 0.75$ with $\mu =0.3$ and $\varepsilon=0.02$. In the frames (a, b, c, d) of Fig. 3 we have plotted the zero velocity curves for $C=C_{L_{i}}=C_{i}$, $i=1,2,3,4$, evaluated at $L_{i}, i=4,5,6,7$, respectively. The infinitesimal mass is free to move only in the regions outside the bounded curves. We observe that as the radiation parameter increases the value of the Jacobian constant increases and the bounded region where the motion is not possible also increases. From frames (a, c, d) (Fig. 3), we observe that the infinitesimal mass can move from one primary to other. But in frame (b) (Fig. 3), the infinitesimal mass can move only around the third primary or from one dominating primary to another one, but it cannot move from the third primary to any dominating primaries.

Fig. 3

(a, b, c, d) ZVC for different value of $C$ evaluated at $L_{4}, L_{5}, L_{6}$ and $L_{8}$. Here black dots represents the eight equilibrium points and the blue dots are the primary bodies

5 Stability of the non-collinear libration points

In this section we wish to study the stability of the non-collinear libration points of the problem, as it indeed is very important for any dynamical system. Thus, we investigated the stability of the non-collinear libration points of the problem when the third primary $m_{3}$ is an oblate spheroid and a source of radiation.

The equations of motion of the infinitesimal body $m_{4}$ are

$$ \begin{aligned}[c] &\ddot{x}-2\dot{y}=\varOmega_{x},\\ &\ddot{y}+2\dot{x}=\varOmega_{y}. \end{aligned} $$

(4)

Now we wish to study the possible motion of the infinitesimal mass around the non-collinear libration points. Let the coordinates of these non-collinear libration points be $(x_{0}, y_{0})$. Now we apply a small displacement $(\alpha_{1},\alpha_{2})$ to $(x_{0}, y_{0})$. Thus, the variations ($\alpha_{1}$ and $\alpha_{2}$) can be written $\alpha_{1} = x-x_{0}$ and $\alpha_{2} = y-y_{0}$, and the variational equations of the motion become

$$ \begin{aligned}[c] &\ddot{\alpha_{1}}-2\dot{\alpha_{2}}=\varOmega_{x}(x_{0}+\alpha_{1},y_{0}+\alpha_{2})\\ &\phantom{\ddot{\alpha_{1}}-2\dot{\alpha_{2}}}{}=\alpha_{1}\overset{*}{\varOmega}_{xx}+\alpha_{2}\overset{*}{\varOmega}_{xy},\\ &\ddot{\alpha_{2}}+2\dot{\alpha_{1}}=\varOmega_{y}(x_{0}+\alpha_{1},y_{0}+\alpha_{2})\\ &\phantom{\ddot{\alpha_{2}}+2\dot{\alpha_{1}}}{}=\alpha_{1}\overset{*}{\varOmega}_{yx}+\alpha_{2}\overset{*}{\varOmega}_{yy}, \end{aligned} $$

(5)

where ‘*’ indicates that the partial derivatives are to be calculated at the respective libration points.

Since the solutions of the variational equations are of the form $\xi=A_{1}e^{\lambda t}$, $\eta=A_{2}e^{\lambda t}$, substituting these values in Eq. (5) and simplifying, we obtain

$$ \begin{aligned}[c] &\bigl(\lambda^{2}-\overset{*}{ \varOmega}_{xx}\bigr)A_{1}+(-2\lambda-\overset{*}{ \varOmega}_{xy})A_{2}=0, \\ &(2\lambda-\overset{*}{\varOmega}_{yx})A_{1}+\bigl( \lambda^{2}-\overset{*}{\varOmega}_{yy}\bigr)A_{2}=0. \end{aligned} $$

(6)

Now, for the nontrivial solution the determinant of the coefficients matrix of the above system must be zero i.e.

$$\begin{aligned} \left| \textstyle\begin{array}{c@{\quad}c} \lambda^{2}-\overset{*}{\varOmega}_{xx} & -2\lambda-\overset{*}{\varOmega}_{xy} \\ 2\lambda-\overset{*}{\varOmega}_{yx} & \lambda^{2}-\overset{*}{\varOmega}_{yy} \\ \end{array}\displaystyle \right|=0. \end{aligned}$$

(7)

Therefore, the characteristic equation of Eqs. (4) is

$$\begin{aligned} \lambda^{4}-(4-\overset{*}{\varOmega}_{xx}- \overset{*}{\varOmega}_{yy})\lambda^{2}+\overset{*}{ \varOmega}_{xx}\overset{*}{\varOmega}_{yy}-\overset{*}{ \varOmega}_{xy}^{2}=0, \end{aligned}$$

(8)

which is a fourth degree equation in $\lambda$. The libration point $(x_{0}, y_{0})$ is said to be stable if all the four roots of Eq. (8) are either negative real numbers or pure imaginary.

Here $\overset{*}{\varOmega}_{xx}$, $\overset{*}{\varOmega}_{yy}$, and $\overset{*}{\varOmega}_{xy}$ are as follows:

$$\begin{aligned} &{\overset{*}{\varOmega}_{xx}=1+ \frac{(1-\mu)[2(x_{0}+\mu)^{2}-y_{0}^{2}]}{\sqrt{(x_{0}+\mu)^{2}+y_{0}^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{xx}=}{} +\frac{\mu[2(x_{0}+\mu-1)^{2}-y_{0}^{2}]}{\sqrt{(x_{0}+\mu-1)^{2}+y_{0}^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{xx}=}{}+\frac{q\varepsilon[2(x_{0}+\mu-\frac{1}{2})^{2}-\frac{1}{4}(\sqrt{3}-2y_{0})^{2}]}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{xx}=}{} +\frac{3qA\varepsilon[4(x_{0}+\mu-\frac{1}{2})^{2}-\frac{1}{4}(\sqrt{3}-2y_{0})^{2}]}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{7}},}\\ &{\overset{*}{\varOmega}_{yy}=1+\frac{\mu[2y_{0}^{2}-(x_{0}+\mu-1)^{2}]}{\sqrt{(x_{0}+\mu-1)^{2}+y_{0}^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{yy}=}{} -\frac{(1-\mu)[(x_{0}+\mu)^{2}-2y_{0}^{2}]}{\sqrt{(x_{0}+\mu)^{2}+y_{0}^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{yy}=}{} +\frac{q\varepsilon[\frac{1}{2}(\sqrt{3}-2y_{0})^{2}-(x_{0}+\mu-\frac{1}{2})^{2}]}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{yy}=}{} +\frac{3qA\varepsilon[(\sqrt{3}-2y_{0})^{2}-(x_{0}+\mu-\frac{1}{2})^{2}]}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{7}},} \\ &{\overset{*}{\varOmega}_{xy}=3 \biggl[\frac{y_{0}\mu(x_{0}+\mu-1)}{\sqrt{(x_{0}+\mu-1)^{2}+y_{0}^{2}}^{5}}- \frac{y_{0}(1-\mu)(x_{0}+\mu)}{\sqrt{(x_{0}+\mu)^{2}+y_{0}^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{xy}=}{} +\frac{q\varepsilon(y_{0}-\frac{\sqrt{3}}{2})(x_{0}+\mu-\frac{1}{2})}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{5}}} \\ &{\phantom{\overset{*}{\varOmega}_{xy}=}{} +\frac{5qA\varepsilon(y_{0}-\frac{\sqrt{3}}{2})(x_{0}+\mu-\frac{1}{2})}{\sqrt{(y_{0}-\frac{\sqrt{3}}{2})^{2}+(x_{0}+\mu-\frac{1}{2})^{2}}^{7}} \biggr].} \end{aligned}$$

(9)

6 Application

Let us apply the methodology and technique developed in this paper to the Sun–Jupiter–asteroid–spacecraft system by taking the shape of the asteroid as an oblate or prolate body and a source of radiation as well. Also we take the bigger primary $m_{1}$ as the Sun. The astrophysical data are as follows:

$\mbox{mass of Sun}=1.98892\times10^{30}~\mbox{kg}$,

$\mbox{mass of Jupiter}=1.8986\times10^{27}~\mbox{kg}$,

$\mbox{mass of asteroid}=1.4\times10^{19}~\mbox{kg}$,

$\mbox{mass of spacecraft}=1000~\mbox{kg}$, $G=6.67\times10^{11}~\frac{\mathrm{Nm}^{2}}{\mathrm{kg}^{2}}$,

$\mbox{distance between Sun and Jupiter}=778\,547\,200~\mbox{km}$.

We have considered as $m_{\mathrm{asteroid}}$ the mass of an actual asteroid of the Trojan group, 624 Hektor, a major one of the group. Thus in dimensionless units, $m_{1}=m_{\mathrm{Sun}}/(m_{\mathrm{Sun}}+m_{\mathrm{Jupiter}})=0.999045619393$, $m_{2}=m_{\mathrm{Jupiter}}/ (m_{\mathrm{Sun}}+m_{\mathrm{Jupiter}})=0.000953677379$ and $m_{3}= \frac{m_{\mathrm{asteroid}}}{m_{\mathrm{Sun}}+m_{\mathrm{Jupiter}}}=0.703227815673\times 10^{-11}$ with $1m= 1.28444\times 10^{-12}$. Solving Eq. (3), there exist five non-collinear libration points given in Table 3 for different values of the oblateness $A>0$ and $q$ for the Sun–Jupiter–asteroid system. The collinear libration points for $A=0.25$ are $L_{1}=-1.0003971309$, $L_{2}=0.9323702081$, and $L_{3}=1.0688257109$. In Figs. 4(a, b), we have plotted the eight libration points in the Sun–Jupiter–asteroid system for different values of the oblateness parameter $A$ and the radiation parameter $q$. We observed that as the radiation parameter increases the non-collinear libration points $L_{4,5,6,7}$ move away from the third primary and all the remaining libration points remain unchanged. The stability of the non-collinear libration points for the Sun–Jupiter–asteroid system obtained in Table 3 are studied and presented in Tables 5, 6, 7, and 8. In the Sun–Jupiter–asteroid system for the prolateness $A=-0.1$, we have obtained three non-collinear libration points, in which two exist near the third primary (Fig. 5(a, b), Table 4).

Fig. 4

(a, b) The five non-collinear equilibrium points in the Sun–Jupiter asteroid system and zoomed part (for oblate primary). Here $A=0.25$ and the red-blue, green-orange, magenta-cyan and purple-yellow line shows contour for $q=0.1$, $q=0.25$, $q=0.50$ and $q=0.75$, respectively

Fig. 5

(a, b) The three non-collinear equilibrium points in the Sun–Jupiter asteroid system and zoomed part (for prolate primary). Here $A=-0.1$ and the red–blue, green–orange, magenta–cyan and purple–yellow line shows contour for $q=0.1$, $q=0.25$, $q=0.50$ and $q=0.75$, respectively

Table 3 Non-collinear libration points in Sun–Jupiter–asteroid system for different values of $q$

Table 4 Non-collinear libration points and their stability in the Sun–Jupiter–asteroid system for a prolate body and different values of $q$

7 Discussion and conclusions

In the present paper, we have studied the autonomous circular restricted four-body problem (CRFBP) introducing the third primary as an oblate/prolate spheroid and a source of radiation as well. Further, all the three primaries are set in the Lagrangian equilateral-triangle configuration.

We have derived the equations of motion in the mentioned mathematical setup. In the next section we found the existence of the libration points by taking the third body as: (a) an oblate spheroid; (b) a prolate spheroid, and a source of radiation. We have found that for the oblate primary, there exist three collinear libration points and five non-collinear libration points for different values of $A$ and $q$. The first collinear libration point lies to the left of $m_{1}$, the second collinear point exists between $m_{1}$ and $m_{2}$ and the last one lies to the right of $m_{2}$. Further, four non-collinear libration points exist near the third primary and one non-collinear libration point lies opposite and away from the third primary. Also we have observed that as the oblateness and radiation of the third primary increases the four non-collinear libration points near the third primary moves away from the third primary and the fifth non-collinear libration point is unaffected by these perturbations. But for a prolate primary the number of libration points varies according to the prolateness coefficient $A$. We have observed that there exist a maximum of 12 libration points (Table 2), eight non-collinear libration points lie near the third primary and one non-collinear libration point lies away and opposite to the third primary. Further we have applied these methods in the Sun–Jupiter–asteroid–spacecraft system. We found that for this configuration there exist three collinear and five non-collinear libration points (presented in Table 3, when the third primary is an oblate spheroid. Also for a prolate primary, in this system there exist three collinear and two non-collinear libration points (presented in Table 4). Further, we have discussed the stability of the Sun–Jupiter–asteroid–spacecraft system and presented the results in Tables 5, 6, 7, and 8. We observed for an oblate primary $m_{3}$ that the libration points $L_{6}$ and $L_{7}$ are stable for $A=0.25, 0.35, 0.45$ and $q=0.1,0.25,0.50,0.75$, respectively. Also $L_{6}$ and $L_{7}$ are stable for $A=1$ and $q=0.1,0.25,0.50$. But $L_{6}$ and $L_{7}$ are unstable for $A=1$ and $q=0.75$. Further, we observed that $L_{4}$ and $L_{5}$ are always unstable for all values of $A$ and $q$. In the Sun–Jupiter–asteroid–spacecraft system the non-collinear libration points $L_{4}$ and $L_{5}$, presented in Table 4, are always stable for all values of $q=0.1,0.25,0.50,0.75$ and $A=-0.01$. In Figs. 6(a, b, c, d), we have plotted the ZVC in the Sun–Jupiter–asteroid system when the asteroid is supposed to be an oblate spheroid and a source of radiation. We observed that as $C$ increases, the forbidden region shown in gray color becomes bigger and the fourth body cannot move from the dominating primaries to the other primaries and vice versa.

Fig. 6

(a, b, c, d) ZVC in the Sun–Jupiter asteroid system when Asteroid is supposed to be an oblate spheroid and source of radiation. The white domains correspond to the Hill’s region, gray shaded domains indicate the forbidden regions, while the thick black lines depict the Zero Velocity Curves (ZVCs). The red dots shows the position of the Lagrangian points, while the blue dots indicate the positions of three primaries

Table 5 Stability of non-collinear libration points in the Sun–Jupiter–asteroid system for $A=1$ and different values of $q$

Table 6 Stability of non-collinear libration points in the Sun–Jupiter–asteroid system for $A=0.25$ and different values of $q$

Table 7 Stability of non-collinear libration points in the Sun–Jupiter–asteroid system for $A=0.35$ and different values of $q$

Table 8 Stability of non-collinear libration points in the Sun–Jupiter–asteroid system for $A=0.45$ and different values of $q$