1 Introduction

The spherically symmetric static exterior and interior Schwarzschild solutions of the Einstein field equations are well-known staples in the elementary courses of General Relativity (GR). On the other hand cylindrically symmetric static solutions (combining the translation along the axis and rotation around the axis) are less familiar among the general relativists. The static spherically vacuum solutions were found in early 20th century by Weyl (1917) and Levi-Civita (1919). They were interested in the more general problem of static geometries that are axially symmetric. In this paper, we construct and study cylindrically symmetric solutions of the anisotropic strange stars that the best candidates of X-rays bluster. For this purpose, we established the nonlinear differential equations for cylindrically anisotropic source in the presence of varying cosmological constant and find some analytic solutions which have been applied to a class of strange stars.

Recent observational data and theoretical results in modern cosmology revealed the facts that dark energy might be described in a scientific way by the cosmological constant. The measurements obtained by the Wilkinson Microwave Anisotropic Probe (WMAP) imply that three–fourth of total mass-energy in our universe is dark energy (DE) (Perlmutter et al. 1997, 1998, 1999 and Riess et al. 1998). The well-known leading theory of DE is mainly based on the cosmological constant. characterized by the repulsive pressure as defined by Einstein in 1917 for the formulation of static universe model. Later on, Zeldovich (1967) interpreted cosmological constant as a vacuum energy of quantum fluctuation which has a size of order of ∼3×10−56 cm−2 (Peebles and Ratra 2003). Recent astronomical observations like the study of type Ia supernova show that the expansion of the universe is accelerating and it is believed that this may be due to a non-vanishing positive cosmological constant. These observations have attracted attention to the study of astrophysical objects with cosmological constant.

In order to model the mass and radius of the Neutron star, Egeland (2007) predicted that the existence of cosmological constant depends upon the density of the vacuum. For this purpose Egeland used the Fermi equation of state with the relativistic equation of hydrostatic equilibrium. Motivated by this fact, we introduced the cosmological constant in a small scale to study the structure of strange stars and concluded that cosmological constant can describes the class of some strange stars for example X-ray bluster 4U1820-30 X-ray pulsar Her X-1, Millisecond pulsar SAX J 1808-3658 etc., in very good manners. Dey et al. (1998), Usov (2004), Ruderman (1972), Mak and Harko (2002, 2003) and many others have studied the structure of strange stars by using different approaches.

Mak and Harko (2004) presented a class of exact solutions of the field equation by using spherical symmetry. They also found that energy density as well as tangential and radial pressure are finite and positive inside the anisotropic star. Chaisi and Maharaj (2005) established an algorithm with an anisotropic matter distribution. By using Chaplygin gas equation of state (EoS), Rahaman et al. (2012) extended the Krori and Barua (1975) analysis of the charge anisotropic static spherically symmetric spacetime. Lobo (2006) generated the anisotropic exact models with a barotropic EOS for compact objects. He also generalized the Mazur–Mottola gravastar models by considering a matching of an interior solution governed by the dark energy EOS \(\omega=\frac{p}{\rho}<\frac{-1}{3}\) to an exterior Schwarzschild vacuum solution at a junction interface. In this paper, we have formulated the cylindrically symmetric models of strange stars which have been proposed earlier by Alcock et al. (1986) and Haensel et al. (1986). Herrera and his collaborators (Herrera 1992, Herrera et al. 2008a, 2008b, 2011) have discussed the stability and gravitational collapse of anisotropic stars. The related work in modified theory of gravity has also been done by Sharif and Abbas (2013a, 2013b, 2013c). Hossein et al. (2012) have studied the properties of the anisotropic compact stars in the presence of cosmological constant.

The cylindrically symmetric models proposed here are associated with cosmological constant and we have studied the stability of the model by calculating the speed of sound using the anisotropic property of the model. Finally, the surface red shift has been calculated using the observational data of a class of anisotropic stars. The plan of the paper is following. In the next section, we present the anisotropic source and Einstein field equations. Section 3 deals with the physical analysis of the proposed model. In the last section, the results of the paper are concluded.

2 Interior matter distribution and field equations

For solving Einstein equations with a cylindrically symmetric spacetime, firstly, we must assume the line element with which we would like to work. Let t denote a time coordinate, for a fixed time t, a cylindrically symmetric spacetime can be described as follows. There is a central axis of symmetry, with z denoting the coordinate along the static solutions of Einsteins equations. The general static cylindrically symmetric spacetime (Brito et al. 2012) is given by

$$ ds^2=-e^{\nu(r)}dt^2+e^{\mu(r)}dr^2+e^{\alpha(r)}dz^2+e^{\beta(r)}d{ \theta^2}, $$
(1)

where ν, μ, α and β are unknown functions. In analogy to standard spherically symmetric spacetime, we define coordinate r in such a way that co-efficient of dθ2 is equal to r2. This transformation is called tangential gauge, thus by setting eβ(r)=r2, metric (1) can be written as

$$ ds^2=-e^{\nu(r)}dt^2+e^{\mu(r)}dr^2+e^{\alpha(r)}dz^2+r^2d{ \theta^2}. $$
(2)

Since co-efficient of dr2 and dz2 have same dimensions, thus it is convenient to take eμ(r)=eα(r). Hence metric (2) reduces to

$$ ds^2=-e^{\nu(r)}dt^2+e^{\mu(r)} \bigl(dr^2+dz^2\bigr)+r^2d{ \theta^2}. $$
(3)

In this equation μ(r)=Ar2 and ν(r)=Br2+C (Krori and Barua 1975) where A, B and C are arbitrary constants to be determined by using some boundary conditions. The interior of compact object may be defined in terms of anisotropic fluid which has following form

$$ T_{\alpha\beta}=(\rho+P_t) U_{\alpha} U_{\beta}+P_{t} g_{\alpha\beta}+(P_r-P_t) \psi_{\alpha}\psi_{\beta}, $$
(4)

where \(U_{\alpha}=e^{\frac{\nu}{2}} \delta_{\alpha}^{0}\), \(\psi_{\alpha}=e^{\frac{\mu}{2}} \delta_{\alpha}^{1}\), ρ, P t and P r correspond to the energy density, transverse and radial pressures, respectively. In this case cosmological constant has radial dependence such that Λ=Λ(r)=Λ r . Therefore, the Einstein field equations

$$ G_{\alpha \beta}= R_{\alpha\beta}-\frac{1}{2}g_{\alpha\beta}R + g_{\alpha\beta}\varLambda \equiv \frac{{8\pi G}}{c^4}T_{\alpha\beta}, $$
(5)

for the metric in Eq. (3) (in the relativistic units G=c=1) are obtained as follows:

$$\begin{aligned} &8\pi\rho+{\varLambda}_r=\frac{1}{2} \biggl( \frac{\mu''}{e^{\mu(r)}} \biggr), \end{aligned}$$
(6)
$$\begin{aligned} &8\pi P_r-{\varLambda}_r= \frac{1}{4e^{\mu}} \biggl(\frac{\nu'^2(r)r+2r\nu''(r)+4\nu'(r)}{r} \biggr), \end{aligned}$$
(7)
$$\begin{aligned} &8\pi P_t-{\varLambda}_r= \frac{1}{4} \biggl[\frac{\nu'^2(r)+2\mu''(r)+2\nu''(r)}{e^{\mu(r)}} \biggr]. \end{aligned}$$
(8)

We assume that radial pressure of the compact star is proportional to the matter density, so

$$ P_r=m\rho,\quad m>0, $$
(9)

where m is the equation of state parameter. Now, from the metric (3) and Eqs. (6)–(8), we get the energy density ρ, tangential pressure P t , radial pressure P r and cosmological parameter Λ r . These quantities are

$$\begin{aligned} &\rho=\frac{(12B-A+4B^2r^2)e^{-Ar^2}}{8\pi(m+1)}, \end{aligned}$$
(10)
$$\begin{aligned} &P_r=\frac{e^{-Ar^2}[(m-7)(4B^2r^3+12Br)-8Arm]}{64\pi r (m+1)}, \end{aligned}$$
(11)
$$\begin{aligned} &P_t=\frac{e^{-Ar^2}[B^2r^2(m-3)+B(m-11)+A]}{8\pi(m+1)}, \end{aligned}$$
(12)
$$\begin{aligned} &{\varLambda}_r=\frac{e^{-Ar^2}}{m+1}\bigl[Am-4B \bigl(Br^2+3\bigr)\bigr]. \end{aligned}$$
(13)

The equation of state (EoS) parameters corresponding to normal and transverse directions can be written as,

$$P_r=\omega_r\rho, $$

then from Eqs. (9), we get

$$ \omega_r(r)=m. $$
(14)

Also, when

$$P_t=\omega_t\rho, $$

then from Eqs. (10) and (12), we get

$$ \omega_t(r)=\frac{B^2r^2(m-3)+B(m-11)+A}{12B-A+4B^2r^2}. $$
(15)

3 Physical analysis

In this section, we shall discuss following features of our model:

3.1 Anisotropic behavior

Taking derivative of Eqs. (10) and (11), we get

$$\begin{aligned} &\frac{d\rho}{dr}=- \biggl[\frac{(24BAr-2A^2r+8AB^2r^3)e^{-Ar^2}}{8\pi(m+1)} \\ &\phantom{\frac{d\rho}{dr}=\,}- \frac{8B^2re^{-Ar^2}}{8\pi(m+1)} \biggr]<0, \end{aligned}$$
(16)
$$\begin{aligned} &\frac{dP_r}{dr}=- \biggl[\frac{(24BAr-B^2r(1+Ar^2))e^{-Ar^2}}{8\pi(m+1)} \\ &\phantom{\frac{dP_r}{dr}=\,}- \frac{A^2mre^{-Ar^2}}{4\pi(m+1)} \biggr]<0. \end{aligned}$$
(17)

At center r=0, our model provides that

$$\begin{aligned} &\frac{d\rho}{dr}=0,\qquad \frac{dP_r}{dr}=0 \end{aligned}$$
(18)
$$\begin{aligned} &\frac{d^2\rho}{dr^2}<0,\qquad \frac{d^2P_r}{dr^2}<0 \end{aligned}$$
(19)

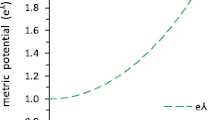
which indicate maximality of radial pressure and density. This implies the fact that ρ and P r are decreasing function of r as shown in Figs. 1–6 for a class of strange star. Similar behavior of P t and Λ r is shown in Figs. 7, 8, 9 and 10, 11, 12. The measure of anisotropy is

$$\Delta=\frac{2}{r}(P_t-Pr), $$

which takes the form

$$ \Delta=\frac{1}{16\pi r } \bigl[e^{-Ar^2} \bigl(B \bigl(Br^2+1\bigr)+2A \bigr) \bigr]. $$
(20)

The anisotropy will be directed outward when P t >P r this implies that Δ>0 and directed inward when P t <P r implying Δ>0. In this case Δ>0, for larger value of r for a class of strange stars as shown in Figs. 13–15. This implies that anisotropic force allows the construction of more massive star while near the center there is attractive force as Δ<0 in Figs. 14, 15. Note that the bound on the EoS parameter 0<ω t (r)<1 is shown in Fig. 16. This shows that star consists of ordinary matter and effect of cosmological constant Λ.

Fig. 1
figure 1

Density variation of Strange star candidate 4U 1820-30

Full size image
Fig. 2
figure 2

Density variation of Strange star candidate Her X-1

Full size image
Fig. 3
figure 3

Density variation of Strange star candidate SAX J 1808.4-3658(SS1)

Full size image
Fig. 4
figure 4

Radial pressure variation of Strange star candidate 4U 1820-30

Full size image
Fig. 5
figure 5

Radial pressure variation of strange star candidate Her X-1

Full size image
Fig. 6
figure 6

Radial pressure variation of strange star candidate SAX J 1808.4-3658(SS1)

Full size image
Fig. 7
figure 7

Tangential pressure variation of Strange star candidate 4U 1820-30

Full size image
Fig. 8
figure 8

Tangential pressure variation of strange star candidate Her X-1

Full size image
Fig. 9
figure 9

Tangential pressure variation of strange star candidate SAX J 1808.4-3658(SS1)

Full size image
Fig. 10
figure 10

Behavior of cosmological constant for strange star candidate 4U 1820-30

Full size image
Fig. 11
figure 11

Behavior of cosmological constant for strange star candidate Her X-1

Full size image
Fig. 12
figure 12

Behavior of cosmological constant for strange star candidate SAX J 1808.4-3658(SS1)

Full size image

3.2 Matching conditions

Here, we match the interior metric (3) to the vacuum exterior cylindrically symmetric metric (Lemos and Zanchin 1996) given by

$$\begin{aligned} ds^2 =&- \biggl({\varLambda r^2}- \frac{4M}{r} \biggr)dt^2+ \biggl({{\varLambda} r^2}- \frac{4M}{r} \biggr)^{-1}dr^2 \\ &{}+{\varLambda}r^2dz^2+r^2d\theta ^2, \end{aligned}$$
(21)

where Λ<0 is cosmological constant. At the boundary r=R continuity of the metric functions g tt , g rr and \(\frac{\partial g_{tt}}{\partial r}\) at the boundary surface yield,

$$\begin{aligned} g_{tt}^-=g_{tt}^+,\qquad g_{rr}^-=g_{rr}^+, \qquad \frac{\partial g_{tt}^-}{\partial r}=\frac{\partial g_{tt}^+}{\partial r}, \end{aligned}$$
(22)

where − and +, correspond to interior and exterior solutions. From the interior and exterior matrices, we get

$$\begin{aligned} A =&\frac{1}{R^2}ln \biggl(\frac{4M}{R}+\sqrt{ \frac{16M^2}{R^2}+4} \biggr), \end{aligned}$$
(23)
$$\begin{aligned} B =&\frac{1}{R^2} \biggl[\frac{\varLambda R^3+2M}{\varLambda R^3-4M} \biggr]. \end{aligned}$$
(24)

For the given values of M and R for given star, the constants A and B are given in Table 1.

Table 1 Values of constant for given Masses and Radii of stars
Full size table

3.3 Stability

We define sound speed as,

$$\begin{aligned} &\upsilon^2_{SR}=\frac{dP_r}{d \rho}= \biggl[\frac{4BAr-B^2r(1+Ar^2)-2A^2mr}{24BAr-2A^2r+8AB^2r^3-8B^2r} \biggr] \end{aligned}$$
(25)
$$\begin{aligned} &\upsilon ^2_{ST}=\frac{dP_t}{d \rho} \\ &\phantom{\upsilon ^2_{ST}}= \bigl[\bigl\{ 2B^2r(m-3)-2Ar\bigl(B^2r^2(m-3) \\ &\phantom{\upsilon ^2_{ST}=\,}+B(m-11)+A\bigr)\bigr\} \\ &\phantom{\upsilon ^2_{ST}=\,}\times\bigl\{ 24BAr-2A^2r+8AB^2r^3-8B^2r\bigr\} ^{-1} \bigr]. \end{aligned}$$
(26)

These quantities are shown in Fig. 17, in this figure I=R,S. From the above equations, we get

$$\begin{aligned} &\upsilon^2_{ST}-\upsilon^2_{SR} \\ &\quad{}=\bigl\{ 2B^2rm-5B^2r-2B^2Ar^3m+5B^2Ar^3 \\ &\qquad{}+18ABr-2ABrm-2A^2r+2A^2rm\bigr\} \\ &\qquad{}\times\bigl\{ 24BAr-2A^2r+8AB^2r^3-8B^2r\bigr\} ^{-1}, \end{aligned}$$
(27)

which can be simplified to the following form

$$\begin{aligned} &\upsilon^2_{ST}-\upsilon^2_{SR} \\ &\quad{}= \bigl\{ B^2\bigl(2rm-5r-2Ar^3m+5Ar^3\bigr) \\ &\qquad{}+2B(9Ar-2Arm)-2A^2r(1-m)\bigr\} \\ &\qquad{}\times\bigl\{ 24BAr-2A^2r+8AB^2r^3-8B^2r\bigr\} ^{-1}. \end{aligned}$$
(28)

From Fig. 17, we can see that \(|\upsilon^{2}_{st}-\upsilon^{2}_{sr}|\leq1\). This is used to check whether local anisotropic matter distribution is stable or not. For this, we use the cracking concept (Herrera and Santos 1997) which explain that potentially stable region is that region where radial speed of sound is greater than the transverse speed of sound. Hence, our proposed compact star model is stable.

3.4 Surface redshift

The compactness of the star is given by

$$\begin{aligned} u =&\frac{M}{b}=\frac{1}{2(m+1)} \biggl[\frac{2B^2e^{-Ar^2}}{A^2} \\ &{}- \frac{\sqrt{\pi}Erf[\sqrt{A}b](2B^2-A(A-12B))}{2bA^{\frac{5}{2}}} \biggr], \end{aligned}$$
(29)

where b=r. The surface redshift (Z s ) corresponding to the above compactness (u) is obtained

$$\begin{aligned} &1+{Z_s} \\ &\quad{}=[1-2u]^{-\frac{1}{2}}= \biggl[1-\frac{1}{(m+1)} \biggl( \frac{2B^2e^{-Ar^2}}{A^2} \\ &\qquad{}-\frac{\sqrt{\pi}Erf[\sqrt{A}b](2B^2-A(A-12B))}{2bA^{\frac{5}{2}}} \biggr) \biggr]^{\frac{1}{2}}. \end{aligned}$$
(30)

The maximum surface redshift for the compact objects is given by Fig. 18.

4 Conclusion

In GR cylindrically symmetric solution turns out to be analogous to spherically symmetric solutions in many ways but also remain quite different in many aspects. The first well-known static spherically symmetric vacuum solution of Einstein Field equation is Schwarzschild exterior solution characterized by mass, but there are some static vacuum cylindrically symmetric solutions other than cone or cosmic string solutions characterized by the defect angle. A cone solution is Lorentz-invariant along the cylinder axis and hence cannot arise from a matter source unless the matter source satisfies the physical equation of state.

In this paper, we have constructed analytical solutions for the compact stars with more general interior source and exterior geometry. The analysis has been done by considering that stars are anisotropic in their internal configuration. The present day acceleration of the Universe in the form of DE allows us to consider the cosmological constant as a variable in its character. The interior configuration of the cylindrical star has been treated by metric assumption. By the physical interpretation of the results, we conclude that bound on effective EoS parameter is given by 0<ω i <1 which is in agreement with normal matter distribution. The density and pressure attain the maximum value at the center. It has been found that the anisotropy will be directed outward when P t >P r this implies that Δ>0 and directed inward when P t <P r implying Δ>0. In this case Δ>0, for larger value of r for a class of strange stars as shown in Figs. 13–15. This implies that anisotropic force allows the construction of more massive star while near the center of the interior configuration there is attractive force as Δ<0 in Figs. 14, 15. The range of Z s for the compacts objects in this case lies in the range 0<Z s ≤0.003. In case of isotropic interior configuration without cosmological constant this range turnout to be Z s ≤2. Hence in present configuration redshift has been decreased to a certain range. According to Böhmer and Harko anisotropic stars in the presence of cosmological constant has the redshift value in the range Z s ≤5, which is consistent with the Ivanov (2002) bound Z s ≤5.211. On the basis of the cracking concept, we have discussed the stability of the proposed model and found that present model is stable.

Fig. 13
figure 13

Anisotropic behavior of strange star candidate 4U 1820-30

Full size image
Fig. 14
figure 14

Anisotropic behavior of strange star candidate Her X-1

Full size image
Fig. 15
figure 15

Anisotropic behavior of strange star candidate SAX J 1808.4-3658(SS1)

Full size image
Fig. 16
figure 16

Behavior of EoS parameter for 4U1820-30, Her X-1 and SAX J 1808.4-3658(SS1)

Full size image
Fig. 17
figure 17

Variation of v2 ST −v2 SR of Strange star candidate 4U1820-30, Her X-1 and SAX J 1808.4-3658(SS1)

Full size image
Fig. 18
figure 18

Behavior of redshift of Strange star candidate 4U1820-30, Her X-1 and SAX J 1808.4-3658(SS1)

Full size image