1 Introduction

Since the striking idea of white dwarf by Chandrasekhar (1931) the study of general relativistic compact objects received a tremendous thrust to carry out research in the field of ultra-dense objects. White dwarfs are composed of one of the densest forms of matter known, surpassed only by other compact stars such as neutron stars, quark stars/strange stars, boson stars, gravastars etc.

In the compact stars the matter is found to be in the stable ground state where the quarks are confined inside the hadrons. If it is composed of the de-confined quarks then also a stable ground state of matter, known as ‘strange matter’, is achievable which provides a ‘strange star’ (Witten 1984; Glendenning 1997; Xu 2003; De Paolis et al. 2007). The main theoretical motivation for postulating the existence of strange stars was to explain the exotic phenomena of gamma ray bursts and soft gamma ray repeaters (Cheng and Dai 1996, 1998). On the observational side, the Rossi X-ray Timing Explorer has now confirmed that SAX J1808.4-3658 is one of the candidates for a strange star (Li et al. 1999).

As a start of the astrophysical objects of compact nature of the above kind the theoretical investigation has been done by several researchers by using both analytical and numerical methods. Local isotropy, as it has been shown in recent years, is a too stringent condition, which may excessively constrain modeling of self-gravitating objects. Therefore it is always interesting to explore the consequences produced by departures from local isotropy under a variety of circumstances. As such the density distribution inside the compact stars need not be isotropic and homogeneous as proposed in the TOV model. In the early seventies Ruderman (1972) has investigated the stellar models and argued that the nuclear matter may have anisotropic features at least in certain very high density ranges (\({>} 10^{15}~\mbox{gm}/\mbox{c.c.}\)), where the nuclear interaction must be treated relativistically. Later on Bowers and Liang (1917) gave emphasis on the importance of locally anisotropic equations of state for relativistic fluid spheres. They showed that anisotropy might have non-negligible effects on such parameters like maximum equilibrium mass and surface redshift.

Therefore anisotropic matter distribution have been considered recently by several investigators as key feature in the configuration of compact stars (with or without cosmological constant) to model the objects physically more realistic (Mak and Harko 2002, 2003; Usov 2004; Varela et al. 2010; Rahaman et al. 2010a, 2012a,b; Kalam et al. 2012). However, to make well documented and well explained the case for the anisotropic pressure, the following reference list may be more relevant. An exhaustive review on the subject of anisotropic fluids presented by Herrera and Santos (1997), which provides almost all references until 1997, as well as a detailed discussion on some of the issues analyzed in this manuscript. More recently a comprehensive work on the influence of local anisotropy on the structure and evolution of compact objects has been published by Herrera et al. (2004). These references, we think, would provide the reader with an excellent source of information.

As one of the physical characteristics Mak and Harko (2000) have calculated the mass-radius ratio or compactness factor for compact relativistic star however in the presence of cosmological constant. To study mass and radii of neutron star Egeland (2007) incorporated the existence of cosmological constant of proportionality depending on the density of vacuum. Kalam et al. (2012) by using their model calculated mass-radius ratio for Strange Star Her X-1 of their model and found it out as \({M_{\mathrm{eff}}/R}_{\max} = 0.336\) which satisfies Buchdahl’s limit and corresponds to the same mass-radius ratio for the observed Strange Star Her X-1. This physical aspect is very important because of the fact that it helps to determine nature of the compact stars, its size, shape, matter contain and several other features.

Now to get more information, several studies have been done on charged or neutral fluid spheres with a spacetime geometry that admits a conformal symmetry, in the static as well as generalized non-static cases. In this line of conformal symmetry we note that there are lots of works available in the literature (Dev and Gleiser 2004; Yavuz et al. 2005; Pradhan et al. 2007; Sharma and Maharaj 2007; Rahaman et al. 2010b). However, we investigate in the present work a new anisotropic star admitting non-static conformal symmetry (mathematical formalism is provided in detail in Sect. 2).

Under this background and motivation we conduct an investigation in the present paper for a model of the relativistic compact star with anisotropy and find out exact spherically symmetric solutions which describe the interior of the dense star admitting non-static conformal symmetry. The scheme of this study is as follows: We provide mathematical formalism for non-static conformal motion in Sect. 2 whereas the Einstein field equations for anisotropic stellar source are given in Sect. 3. The solutions and general features of the field equations under the Dev-Gleiser energy density profile have been found out in Sect. 4 along with a special discussion on two prescriptions, in Sect. 5, viz. (Sect. 5.1) the Misner-Zapolsky prescription, and (Sect. 5.2) the Dev-Gleiser prescription are done to show that mass to size ratio clearly indicates that the model represents a strange compact star. In Sect. 6 we have made some concluding remarks.

2 Non-static conformal symmetry

Now, we consider the interior of a star under conformal motion through non-static Conformal Killing Vector as (Maartens and Maharaj 1990; Coley and Tupper 1994; Harko and Mak 2005; Böhmer et al. 2007; Rahaman et al. 2010b; Radinschi et al. 2010)

$$ L_{\xi }g_{ij}=g_{ij;k}\xi^{k}+g_{kj} \xi_{;i}^{k}+g_{ik}\xi_{;j}^{k}= \psi g_{ij}, $$
(1)

where \(L\) represents the Lie derivative operator, \(\xi \) is the four vector along which the derivative is taken, \(\psi \) is the conformal factor and \(g_{ij}\) are the metric potentials. It is to be noted that for \(\psi =0\), the equation above yields the Killing vector, whereas for \(\psi =\mathit{const.}\) corresponds to the homothetic vector. So, in general for \(\psi =\psi (x,t)\) we obtain conformal vectors. In this manner, one can perform a more general study of the spacetime geometry by using Conformal Killing Vector. It is therefore argued that in the case of fluid, spacetime admitting one-parameter group of conformal motions represents generalization (to general relativity) of the well-known self-similar solutions (Cahill and Taub 1971). However, for more physical justifications in favor of the conformal symmetry as adopted in our methodology interested readers can take a look on the following references (and references therein) (Herrera et al. 1990; Di Prisco et al. 1991).

The static spherically symmetric spacetime is given by the line element (Ray et al. 2008; Usmani et al. 2011)

$$ ds^{2}=-e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin ^{2}\theta d\phi^{2}\bigr), $$
(2)

where \(\nu (r)\) and \(\lambda (r)\) are the metric potentials and functions of radial coordinate \(r\) only. Here we have considered \(G=1=c\) in geometrized units.

The proposed charged fluid spacetime is mapped conformally onto itself along the direction \(\xi \). Here following Herrera et al. (1984) and Herrera and Ponce de Leon (1985) we assume \(\xi \) as non-static but \(\psi \) to be static as follows:

$$\begin{aligned}& \xi =\alpha (t,r)\partial_{t}+\beta (t,r)\partial_{r}, \end{aligned}$$
(3)
$$\begin{aligned}& \psi =\psi (r). \end{aligned}$$
(4)

The above set of Eqs. (1)–(4) give the following expressions (Maartens and Maharaj 1990; Coley and Tupper 1994; Harko and Mak 2005; Böhmer et al. 2007; Rahaman et al. 2010a; Radinschi et al. 2010) for \(\alpha \), \(\beta \), \(\psi \) and \(\nu\):

$$\begin{aligned}& \alpha =A+\frac{1}{2}kt, \end{aligned}$$
(5)
$$\begin{aligned}& \beta =\frac{1}{2}Bre^{-\frac{\lambda }{2}}, \end{aligned}$$
(6)
$$\begin{aligned}& \psi =Be^{-\frac{\lambda }{2}}, \end{aligned}$$
(7)
$$\begin{aligned}& e^{\nu }=C^{2}r^{2}\exp \biggl[ -2kB^{-1} \int \frac{e^{\frac{\lambda }{2}}}{r}dr \biggr] , \end{aligned}$$
(8)

where \(k\), \(A\), \(B\) and \(C\) are arbitrary constants. According to Maartens and Maharaj (1990) one can set \(A=0\) and \(B=1\) so that by rescaling we can get

$$\begin{aligned}& \alpha =\frac{1}{2}kt, \end{aligned}$$
(9)
$$\begin{aligned}& \beta =\frac{1}{2}re^{-\frac{\lambda }{2}}, \end{aligned}$$
(10)
$$\begin{aligned}& \psi =e^{-\frac{\lambda }{2}}, \end{aligned}$$
(11)
$$\begin{aligned}& e^{\nu }=C^{2}r^{2}\exp \biggl[ -2k \int \frac{e^{\frac{\lambda }{2}}}{r}dr \biggr] . \end{aligned}$$
(12)

However, one can note that the above considerations, i.e. \(A=0\) and \(B=1\), do not loss any generality. This is because the rescaling \(\xi \) and \(\psi \) in the following manner, \(\xi \rightarrow B^{-1} \xi \) and \(\psi \rightarrow B^{-1}\psi \), leaves Eq. (1) invariant.

3 The field equations for anisotropic stellar source

In the present investigation we consider the most general energy-momentum tensor compatible with spherically symmetry in the following form:

$$ T_{\nu }^{\mu }=(\rho +p_{r})u^{\mu }u_{\nu }+p_{r}g_{\nu }^{\mu }+(p _{t}-p_{r})\eta^{\mu }\eta_{\nu }, $$
(13)

with \(u^{\mu }u_{\mu }=-\eta^{\mu }\eta_{\mu }=1\), where \(\rho \) is the matter density, \(p_{r}\) and \(p_{t}\) are the radial and the transverse pressures of the anisotropic fluid respectively. In fact, the notion of the anisotropic fluid allows the pressures to differ among spatial directions. In particular, in the case of spherical symmetry the spatial directions split into the radial pressure \(p_{r}\) and the transverse pressure \(p_{t}\) which may have relation as \(\Delta = p_{r} - p_{t}\), known as the anisotropy of the spherical system (Lake 2009; Horvat et al. 2011; Bhar et al. 2015).

For the metric given in Eq. (2), the Einstein field equations are (Rahaman et al. 2010c)

$$\begin{aligned}& e^{-\lambda } \biggl[ \frac{\lambda^{\prime }}{r}-\frac{1}{r^{2}} \biggr] + \frac{1}{r ^{2}}=8\pi \rho , \end{aligned}$$
(14)
$$\begin{aligned}& e^{-\lambda } \biggl[ \frac{\nu^{\prime }}{r} + \frac{1}{r^{2}} \biggr] - \frac{1}{r ^{2}}=8\pi p_{r}, \end{aligned}$$
(15)
$$\begin{aligned}& \frac{1}{2}e^{-\lambda } \biggl[ \frac{1}{2}\bigl( \nu^{\prime }\bigr)^{2}+ \nu^{\prime \prime }-\frac{1}{2} \lambda^{\prime }\nu^{\prime }+ \frac{1}{r}\bigl( \nu^{\prime }-\lambda^{\prime }\bigr) \biggr] =8\pi p_{t}. \end{aligned}$$
(16)

Imposing the conformal motion, one can write the stress-energy components in terms of the conformal function as follows:

$$\begin{aligned}& 8\pi \rho =\frac{1}{r^{2}}\bigl(1-\psi^{2}-2r\psi { \psi^{\prime }}\bigr), \end{aligned}$$
(17)
$$\begin{aligned}& 8\pi p_{r}=\frac{1}{r^{2}}\bigl(3\psi^{2}-2k\psi -1 \bigr), \end{aligned}$$
(18)
$$\begin{aligned}& 8\pi p_{t}= \frac{1}{r^{2}} \bigl[ (\psi - k)^{2} +2r\psi {\psi^{\prime }} \bigr] . \end{aligned}$$
(19)

4 The solutions and features of the field equations for Dev-Gleiser energy density profile

Now our task is to find out solutions for the above set of the modified Einstein equations in terms of the conformal motion. However, to do so we would like to study the following case for specific energy density as proposed by Dev and Gleiser (2004) for stars with the energy density in the form

$$ \rho = \biggl( \frac{a}{r^{2}}+3b \biggr) /8\pi , $$
(20)

where \(a\) and \(b\) are constants, the dimension of \(a\) being equivalent to the radial distance \(r\) (i.e. here in km) whereas \(b\) is a dimensionless parameter. It is to be noted that the choice of the values for \(a\) and \(b\) is dictated by the physical configuration under consideration, e.g. \(a = 3/7\) and \(b = 0\), corresponds to a relativistic Fermi gas for ultradense cores of neutron stars (Misner and Zapolsky 1964) whereas the values \(a = 3/7\) and \(b \neq 0\) represent a relativistic Fermi gas with core immersed in a constant density background (Dev and Gleiser 2004). It can easily be observed from Eq. (21) that for large \(r\) the constant density term dominates (\(r^{2}_{c} \gg a/3b\)) so that the corresponding star can be modeled with shell-type feature surrounding the core.

Due to use of the above energy density, Eq. (17) will take the following form:

$$ \biggl( \frac{a}{r^{2}}+3b \biggr) = \frac{1}{r^{2}} \bigl( 1- \psi^{2}-2r \psi {\psi {\prime }} \bigr) , $$
(21)

Solving this Eq. (21), we get

$$ \psi^{2}=1-a-b{r^{2}}+\frac{d}{r}= g(r)~(\mbox{say}), $$
(22)

where \(d\) is an integration constant.

Substituting the value of \(\psi \) in Eqs. (18) and (19), expressions for radial and tangential pressures can be obtained as

$$\begin{aligned}& p_{r}= \frac{1}{8\pi {r^{2}}} \biggl[ 2-3a-3br^{2}+ \frac{3d}{r} -2k \sqrt{g(r)} \biggr] , \end{aligned}$$
(23)
$$\begin{aligned}& p_{t}= \frac{1}{8\pi {r^{2}}} \bigl[ 1-a-3br^{2}+k^{2}- 2k\sqrt{g(r)} \bigr] . \end{aligned}$$
(24)

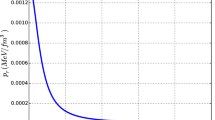
In Figs. 2–3 we have shown the behavior of the radial and tangential pressures whereas Fig. 1 represents the 3-dimensional presentation indicating the variation of radial pressure with respect to the parameters \(a,b\) for a fixed radius. All the curves are in accordance to the physical feasibility within the acceptable range.

Fig. 1
figure 1

Variation of radial pressure, \(p_{r}\), with respect to the parameters \(a\) and \(b\) for a fixed radial distance \(r=0.4\mbox{ km}\)

Full size image
Fig. 2
figure 2

Variation of radial pressure with respect to radial distance

Full size image
Fig. 3
figure 3

Variation of transverse pressure with respect to radial distance

Full size image

Let us now consider a simplest form of barotropic equation of state (EOS) as \(p_{i} = \omega_{i} \rho \), where \(\omega_{i}\) are the EOS parameters along the radial and transverse directions. In general, this EOS is used for a spatially homogeneous cosmic fluid, however, it can be extended to inhomogeneous spherically symmetric spacetime, by assuming that the radial pressure follows the above EOS (Rahaman et al. 2015). Here at present as such we are not considering different forms of \(\omega \) with it’s possible space and time dependence as are available in the literature (Chervon and Zhuravlev 2000; Zhuravlev 2001; Peebles and Ratra 2003; Usmani et al. 2008). Thus, the EOS parameters \(\omega \) can straightly be written in the following forms:

$$\begin{aligned}& \omega_{r} = \frac{p_{r}}{\rho }= \frac{1}{(a+3br^{2})} \biggl[ 2-3a-3br ^{2}+ \frac{3d}{r} -2k \sqrt{g(r)} \biggr] , \end{aligned}$$
(25)
$$\begin{aligned}& \omega_{t}= \frac{p_{t}}{\rho }= \frac{1}{(a+3br^{2})} \bigl[ 1-a-3br ^{2}+ k^{2} - 2k \sqrt{g(r)} \bigr] . \end{aligned}$$
(26)

In Figs. 4 and 5 we plot variations of the radial and transverse EOS parameter with respect to the radial distance, in which radial EOS represents expected nature with a decreasing pattern. However, the transverse EOS parameter indicates that it lies between \((- \frac{1}{3}, 0)\). It is negative like exotic matter in nature, however, later on we shall see that all energy conditions are satisfied for real matter situation.

Fig. 4
figure 4

Variation of radial EOS parameter with respect to radial distance

Full size image
Fig. 5
figure 5

Variation of transverse EOS parameter with respect to radial distance

Full size image

4.1 Anisotropic behavior

For the model under consideration the measure of anisotropy in pressures can be obtained, from Eqs. (23) and (24), as follows:

$$ \Delta \equiv (p_{t}-p_{r})= \frac{1}{8\pi r^{2}} \biggl[ k^{2}+2a- \frac{3d}{r}-1 \biggr] . $$
(27)

It can be seen that the ‘anisotropy’ will be directed outward when \(p_{t} > p_{r}\) i.e. \(\Delta > 0 \), and inward when \(p_{t} < p_{r}\) i.e. \(\Delta < 0\). This feature is obvious from Fig. 6 of our model that a repulsive ‘anisotropic’ force (\(\Delta < 0\)) allows the construction of a more massive stellar distribution (Hossein et al. 2012).

Fig. 6
figure 6

Anisotropic behavior at the stellar interior with respect to radial distance

Full size image

4.2 Energy conditions

In general relativity the distribution of the mass, momentum, and stress due to matter and to any non-gravitational fields is described by the energy-momentum tensor \(T^{ij}\). However, the Einstein field equation is not very conservative about what kinds of states of matter or non-gravitational fields are admissible in a spacetime model. The energy conditions represent such criteria and describe properties common to all states of matter and all non-gravitational fields which are well-established in physics, while being sufficiently strong to rule out many unphysical “solutions” of the Einstein field equation. In this line of thinking, the following rules are adopted in general relativity which are as follows: Null Energy Condition (NEC), Weak Energy Condition (WEC), Strong Energy Condition (SEC) and Dominant Energy Condition (DEC). However, it is to note that there are many matter configurations which violate the strong energy condition, at least from a mathematical perspective, e.g. for a scalar field with a positive potential can violate this condition and in any cosmological inflationary process (Hawking and Ellis 1973). It is argued that such a violation would violate the classical regime of general relativity, and one would be required to use an alternative theory of gravity (Poisson 2004).

We now put and verify the above mentioned different energy conditions of the stellar configuration as follows:

$$\begin{aligned}& \rho \geq 0, \quad \rho +p_{r} \geq 0, \quad \rho +p_{t} \geq 0,\quad \rho +p _{r}+2p_{t} \geq 0,\\& \rho > |p_{r}|\quad \mbox{and} \quad \rho > |p_{t}|. \end{aligned}$$

It is seen that NEC, WEC, SEC and DEC i.e. all the energy conditions for our particular choices of the values of mass and radius are satisfied which can also be observed from Fig. 7.

Fig. 7
figure 7

Energy conditions as a function of \(r\) are plotted for the specified range

Full size image

4.3 TOV equation

To search equilibrium situation of this anisotropic star under different forces, we write the generalized Tolman-Oppenheimer-Volkoff (TOV) equation as (Varela et al. 2010)

$$ -\frac{M_{G}(\rho +p_{r})}{r^{2}}e^{\frac{\lambda -\nu }{2}}-\frac{dp _{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0, $$
(28)

where \(M_{G}=M_{G}(r)\) is the effective gravitational mass inside a sphere of radius \(r\) which can be derived from the Tolman-Whittaker formula as

$$ M_{G}(r)=\frac{1}{2}r^{2}e^{\frac{\nu -\lambda }{2}}\nu '. $$
(29)

The above equation explains the equilibrium conditions of the fluid sphere due to the following hydrostatic, anisotropic and gravitational forces:

$$\begin{aligned} F_{h} =&-\frac{dp_{r}}{dr} \\ =&\frac{1}{8\pi } \biggl[ \frac{4}{r^{3}}-\frac{6a}{r^{3}} + \frac{9d}{r ^{4}}-\frac{4k\sqrt{g(r)}}{r^{3}} \\ &{}-\frac{k(2br^{2}+\frac{d}{r})}{r ^{3}\sqrt{g(r)}} \biggr] , \end{aligned}$$
(30)
$$\begin{aligned} F_{a} =&\frac{2}{r}(p_{t}-p_{r})= \frac{1}{8\pi } \biggl[ -\frac{2}{r^{3}}+\frac{4a}{r ^{3}}+ \frac{2k^{2}}{r^{3}} -\frac{6d}{r^{4}} \biggr] , \end{aligned}$$
(31)
$$\begin{aligned} F_{g} =&-\frac{\nu '}{2}(\rho +p_{r}) \\ =&-\frac{1}{8\pi } \biggl[ \frac{2}{g(r)r} \biggl\{ -\frac{12a}{r^{2}}+ \frac{2}{r ^{2}}+\frac{15d}{r^{3}} - \frac{10k\sqrt{g(r)}}{r^{2}} \\ &{}+\frac{10ak\sqrt{g(r)}}{r ^{2}}+\frac{18d^{2}}{r^{4}} + \frac{6a^{2}}{r^{2}} - \frac{15ad}{r^{3}}+6ab-6b \\ &{}-\frac{9bd}{r}+6bk\sqrt{g(r)} - \frac{12dk\sqrt{g(r)}}{r^{3}}+\frac{4k^{2} g(r)}{r^{2}}\biggr\} \\ &{}+ \frac{a}{r^{3}} -\frac{1}{r^{3}}-\frac{3d}{2r^{4}}+ \frac{k \sqrt{g(r)}}{r^{3}} \biggr] . \end{aligned}$$
(32)

Equation (28) can be rewritten in the form

$$ F_{g}+F_{h}+F_{a}=0. $$
(33)

The profiles of different forces \(F_{g}\), \(F_{h}\), \(F_{a}\) are shown in Fig. 8. The figure exposes that our model of anisotropic star is in static equilibrium under the gravitational \((F_{g})\), hydrostatics \((F_{h})\) and anisotropic \((F_{a})\) forces.

Fig. 8
figure 8

The anisotropic star is in static equilibrium under gravitational \((F_{g})\), hydrostatics \((F_{h})\) and anisotropy \((F_{a})\) forces

Full size image

4.4 Stability issue

The velocity of sound should follow the condition \(v_{s}^{2} = dp/d \rho < 1\) for a physically realistic model (Herrera et al. 1979; Herrera 1992; Chan et al. 1993; Abreu et al. 2007). We therefore calculate the radial and transverse sound speed for our anisotropic model as follows (Rahaman et al. 2012b):

$$\begin{aligned} v_{rs}^{2} =&\frac{dp_{r}}{d\rho } \\ =&\frac{1}{2a} \biggl[ 4-6a+\frac{9d}{r} -4k\sqrt{g(r)}- \frac{k(2br^{2}+ \frac{d}{r})}{\sqrt{g(r)}} \biggr] , \end{aligned}$$
(34)
$$\begin{aligned} v_{ts}^{2} =&\frac{dp_{t}}{d\rho } \\ =&\frac{1}{2a} \biggl[ 2-2a+2k^{2} -4k \sqrt{g(r)}- \frac{k(2br^{2}+ \frac{d}{r})}{\sqrt{g(r)}} \biggr] . \end{aligned}$$
(35)

Let us check whether the sound speeds lie between 0 and 1. For this requirement we plot the sound speeds in Figs. 9 and 10. It is observed that numerical values of these parameters satisfy the inequalities \(0 \leq v_{rs}^{2}\), \(|v_{ts}^{2}| \leq 1\) everywhere within the stellar object. However, for the radial sound velocity there is a prominent change over after attaining certain higher value which gradually goes down. Since the transverse sound velocity is negative (due to negative transverse pressure), we use numerical value. As sound speeds lie between 0 and 1, we should have \(|v_{ts}^{2}| - v_{rs}^{2} \leq 1\) as evident from Fig. 11.

Fig. 9
figure 9

Variation of radial sound velocity with respect to radial distance

Full size image
Fig. 10
figure 10

Variation of transverse sound velocity with respect to radial distance

Full size image
Fig. 11
figure 11

Variation of \(|v_{ts}^{2}| - v_{rs}^{2} \) with respect to radial distance

Full size image

Now, one can go through a technique for stability check of local anisotropic matter distribution as available in the literature (Herrera 1992). This technique is known as the cracking concept of Herrera and states that the region for which radial speed of sound is greater than the transverse speed is a potentially stable region. Figure 11 indicates that there is a change of sign for the term \(|v_{ts}^{2}| - v_{rs}^{2}\) within the specific configuration and thus confirming that the model has a transition from unstable to stable configuration. The present stellar model gradually gets stability with the increase of the radius.

4.5 Surface redshift

In terms of the maximum allowable compactness (mass-radius ratio) for a fluid sphere as given by Buchdahl (1959), the stability issue may be discussed now. Buchdahl has proposed an absolute constraint of the maximally allowable mass-to-radius ratio for isotropic fluid spheres in the form \(2M/R \leq 8/9\). One can now calculate the effective gravitational mass in terms of the energy density \(\rho \) as

$$ M_{\mathrm{eff}}=4\pi \int_{0}^{R}\rho r^{2} dr= \frac{1}{2}R \bigl[ a+bR^{2} \bigr] . $$
(36)

Therefore, the compactness of the star is given by

$$ u= \frac{M_{\mathrm{eff}}}{R}= \frac{1}{2} \bigl[ a+bR^{2} \bigr] . $$
(37)

The nature of variation of the above expression for compactness of the star can be seen in Fig. 12 which is gradually increasing. We now define the surface redshift corresponding to the above compactness as

$$ 1+z_{s}= [1-2u]^{-1/2}= \bigl[ 1 - \bigl( a+bR^{2} \bigr) \bigr] ^{-1/2}, $$
(38)

so that the surface redshift can be expressed as follows:

$$ z_{s}= \bigl[ 1-\bigl(a+bR^{2}\bigr) \bigr] ^{-\frac{1}{2}} - 1. $$
(39)
Fig. 12
figure 12

Mass vs radius relation is shown in the plot for the specified range

Full size image

We plot surface redshift in Fig. 13. Likewise compactness factor \(u\) this has also a behavior of gradual increase. This feature is also observed from the Table 1. The maximum surface redshift for the present stellar configuration of radius \(0.62\mbox{ km}\) turns out to be \(z_{s} = 0.35280\) (see Table 1) which seems well within the limit \(z_{s} < 2\) (Straumann 1984; Böhmer and Harko 2006).

Fig. 13
figure 13

Variation of redshift \(z_{s}\) with radial coordinate \(r\)

Full size image
Table 1 Calculation of masses and hence compactness factors for different values of constant \(b\) with \(a = 3/7\) and \(R=0.62\mbox{ km}\) (with the conversion \(1~\mbox{km} = 1.475~M_{\odot }\))
Full size table

5 Special physical analysis of the model based on the matter contained

If we look at Eq. (36) as well as Eq. (37) then it will at once reveal that there are lots of information inherently hidden inside these two equations. Let us therefore examine the present model for the specified values of \(a\) and \(b\), appearing in Eqs. (36) and (37), as follows:

5.1 The Misner-Zapolsky prescription

For the prescription of Misner and Zapolsky (1964) i.e. \(a = 3/7\) and \(b = 0\), we get the effective gravitational mass as \(M_{\mathrm{eff}}=(3/14)R\) which numerically comes out to be \(0.195~M_{\odot }\) so that the compactness factor becomes \(u=M_{\mathrm{eff}}/R =0.21428\) as can be seen from Table 1. Here to estimate mass we have taken radius of the star \(R=0.62\mbox{ km}\) by solving \(p_{r}=0\) at \(r=R\) graphically from Fig. 14. This therefore represents a relativistic Fermi gas for ultradense cores of the neutron stars as noticed in Misner and Zapolsky (1964).

Fig. 14
figure 14

Radius of the star where \(p_{r}=0\) increases with the increase of the parameter \(d\)

Full size image

5.2 The Dev-Gleiser prescription

In this prescription (Dev and Gleiser 2004), by substituting the values \(a = 3/7\) and \(b \neq 0\) one can get the expression for the effective gravitational mass as \(M_{\mathrm{eff}}= (1/2)R [ (3/7)+bR^{2} ] \). For this case we provide here a data sheet by choosing different values for \(b\) (for Case A, \(b=0\) whereas for Case B, \(b \geq 0\)) in Table 1. This corresponds to a relativistic Fermi gas with core immersed in a constant density background (Dev and Gleiser 2004).

6 Conclusion

The purpose of this paper consists in presenting a model of a static, spherical, fluid configuration, which is locally anisotropic, and which could serve, eventually, as a model for a compact star. The solution is obtained by assuming that the metric admits a one parameter group of conformal motions, with the conformal factor being a function, not only of the radial coordinate, but also of time. In this sense this solution generalizes the models presented in Herrera et al. (1984) and Herrera and Ponce de Leon (1985). The physical behavior of the presented model is reasonable, and therefore it might serve for modeling of ultracompact objects.

In the present investigations we have observed some interesting features which are as follows:

(1) Note that though the transverse pressure is negative, however, all energy conditions are satisfied. This indicates that the matter distribution of the star is real i.e. the star is composed of the normal matter.

(2) It is observed that the transverse sound velocity is negative (due to negative transverse pressure) so that we use numerical value. As the sound speeds lie between 0 and 1, we should have \(|v_{ts}^{2}| - v_{rs}^{2} \leq 1\) (Fig. 11).

(3) In connection to the isotropic case and in the absence of the cosmological constant it has been shown for the surface redshift analysis that \(z_{s} \leq 2\) (Buchdahl 1959; Straumann 1984; Böhmer and Harko 2006). On the other hand, Böhmer and Harko (2006) argued that for an anisotropic star in the presence of a cosmological constant the surface redshift must obey the general restriction \(z_{s} \leq 5\), which is consistent with the bound \(z_{s} \leq 5.211\) as obtained by Ivanov (2002). Therefore, for an anisotropic star without cosmological constant the above value \(z_{s} = 0.3\) seems to be within an acceptable range (Fig. 13).

(4) The radius of the star depends on the parameter \(d\), as appears in Eq. (23), with an increasing mode (Fig. 14).

(5) It is well known that the anisotropic factor \(\Delta =p_{t} - p _{r}\) should vanish at the origin. However, in the present model the energy density under consideration has an infinite central density. According to Misner and Zapolsky (1964) one may use it as an asymptotic solution with a cut-off density below which Eq. (27) will not valid.

(6) In the present model, the stability of the matter distribution comprised of the anisotropic star has been attained. We can conclude this by analyzing the TOV equation which describes the equilibrium condition for matter distribution subject to the gravitational force (\(F _{g}\)), hydrostatic force (\(F_{h}\)) and another force (\(F_{a}\)) due to anisotropic pressure (Fig. 8).

(7) For an overall view of the present study and also to have a physically viable model we put here the data which are available on some compact stars, e.g. Her X-1, SAX J 1808.4-3658 and Strange Star-4U 1820-30 (see Table 1 of Kalam et al. 2012). The compactness factor \(u\) for these stars are 0.168, 0.299 and 0.332 respectively. In comparison to these data we can conclude that our model represents a star with moderate compactness and also indicates that the star might be a compact star of Strange quark type rather than Neutron star. This is because, in general, superdense stars with mass-size ratio exceeding 0.3 are expected to be composed of strange matter (Tikekar and Jotania 2007).

Now according to Buchdahl (1959), the maximum allowable compactness for a fluid sphere is given by \(\frac{2M}{R} <\frac{8}{9}\). Our compactness values for the chosen model (see Table 1) fall within this acceptable range and hence provides a stable stellar configuration.

(8) Finally, it is noted that all static anisotropic solutions to Einstein equations (in the spherically symmetric case) can be obtained by a general method introduced by Herrera and co-workers (Herrera et al. 2008). As shown in this reference, all such solutions are produced by two generating functions. Accordingly, the solution presented by us is a particular case of the general solution described in the reference above. This particular aspect of identifying the two generators corresponding to our solution may be considered elsewhere.