Relative equilibria of full dynamics of a rigid body with gravitational orbit-attitude coupling in a uniformly rotating second degree and order gravity field

Abstract

The motion of a rigid body in a uniformly rotating second degree and order gravity field is a good model for the gravitationally coupled orbit-attitude motion of a spacecraft in the close proximity of an asteroid. The relative equilibria of this full dynamics model are investigated using geometric mechanics from a global point of view. Two types of relative equilibria are found based on the equilibrium conditions: one is the Lagrangian relative equilibria, at which the circular orbit of the rigid body is in the equatorial plane of the central body; the other is the non-Lagrangian relative equilibria, at which the circular orbit is parallel to but not in the equatorial plane of central body. The existences of the Lagrangian and non-Lagrangian relative equilibria are discussed numerically with respect to the parameters of the gravity field and the rigid body. The effect of the gravitational orbit-attitude coupling is especially assessed. The existence region of the Lagrangian relative equilibria is given on the plane of the system parameters. Numerical results suggest that the negative C₂₀ with a small absolute value and a negative C₂₂ with a large absolute value favor the existence of the non-Lagrangian relative equilibria. The effect of the gravitational orbit-attitude coupling of the rigid body on the existence of the non-Lagrangian relative equilibria can be positive or negative, which depends on the harmonics C₂₀ and C₂₂, and the angular velocity of the rotation of the gravity field.

1 Introduction

Space missions to the asteroids have long been of great interest to the space community, since the knowledge of these primitive bodies can provide answers to the fundamental questions concerning the solar system origin and early evolution, possibly including the development of life on Earth (Barucci et al. 2011). Several missions have been developed with big successes, such as NASA’s NEAR and Dawn, and JAXA’s Hayabusa. Moreover, near-Earth objects (NEOs) pose potential impact risk to our fragile ecosystem, which has made the space community turn its attention to NEO issue. All the major space agencies are involved on missions to asteroids for scientific exploration or NEO hazard mitigation.

The close-proximity operations are generally necessary during the asteroid scientific exploration mission and the asteroid deflection mission. The dynamical behavior of the spacecraft near asteroids is the basis of the design and implementation of the guidance and control during the close-proximity operations. Since an asteroid is always much smaller than the planets, the orbital radius will be very small for a spacecraft in the close proximity of a small asteroid. Therefore, the gravitational coupling between the orbital and attitude motions of the spacecraft can be significant due to the large ratio of its dimension to the orbit radius, as shown by Koon et al. (2004), Scheeres (2006b), Wang and Xu (2014a). The magnitude of the gravitational orbit-attitude coupling can be described by the parameter ε=ρ/r₀, where ρ is the characteristic dimension of the spacecraft and r₀ is the orbital radius. Due to the large dimension of Earth, the parameter ε is order of 10⁻⁶ for a spacecraft (ρ∼10 m) around Earth. However, the parameter ε can be order of 10⁻² for a spacecraft on a 1 km orbit around a small asteroid.

In the traditional spacecraft dynamics around Earth and in general deep space missions, the spacecraft is treated as a point mass in the orbital dynamics and the attitude motion, treated separately, is studied on a predetermined orbit (Maciejewski 1997). The traditional spacecraft dynamics is precise enough for these missions, because the spacecraft dimension is very small in comparison with the orbital radius and the gravitational orbit-attitude coupling is insignificant. However, it will no longer have a high precision in the close proximity of small asteroids due to the significant orbit-attitude coupling.

To take into account the gravitational orbit-attitude coupling, the spacecraft in the proximity of an asteroid can be modeled as a rigid body instead of a point mass. This full dynamics model with gravitational orbit-attitude coupling will be more precise than the previous orbital dynamics around asteroids with the point mass model. The full spacecraft dynamics will be also more faithful to the real motion than the attitude dynamics of spacecraft near an asteroid, such as Riverin and Misra (2002), Misra and Panchenko (2006), Kumar (2008), Wang and Xu (2013a, 2013b, 2013c, 2013d, 2014c). The studies on the full dynamics are very useful for the future asteroid mission design.

This full dynamics model in a non-central gravity field can be considered as a restricted model of the Full Two Body Problem (F2BP), i.e., the dynamics of two rigid bodies orbiting each other interacting through the mutual gravitational potential. That is to say, in our problem we only study the motion of the spacecraft, and assume that the motion of the central body is not affected by the spacecraft. The sphere-restricted model of F2BP, in which one body is assumed to be a homogeneous sphere, has been studied broadly, such as Kinoshita (1970, 1972a, 1972b), Aboelnaga and Barkin (1979), Barkin (1979, 1980, 1985), Koon et al. (2004), Scheeres (2004, 2006a), Breiter et al. (2005), Bellerose and Scheeres (2008a, 2008b), Balsas et al. (2008, 2009) and Vereshchagin et al. (2010). There are also several works on more general models of F2BP, in which both bodies are non-spherical, such as Maciejewski (1995), Mondéjar and Vigueras (1999), Scheeres (2002, 2009), Koon et al. (2004), Boué and Laskar (2009), McMahon and Scheeres (2013), and Woo et al. (2013).

The full dynamics of a rigid body with gravitational orbit-attitude coupling in a central gravity field has been investigated in several works (Wang et al. 1991, 1992; Teixidó Román 2010). The relative equilibria and their stability of the full dynamics of a rigid body with gravitational orbit-attitude coupling in a J₂ gravity field have been studied in Wang and Xu (2013e, 2013f) and Wang et al. (2014a). However, these results are only applicable to a spherical or spheroid central body, but not applicable to an irregular-shaped asteroid, the oblateness and ellipticity of which are both significant. Also notice that most of the asteroids are nearly in a uniform rotation about their maximum-moment principal axis. Therefore, studies of the full dynamics of a rigid body with gravitational orbit-attitude coupling in a uniformly rotating second degree and order-gravity field with harmonics C₂₀ and C₂₂ are necessary.

The relative equilibria act as “organizing centers” of the dynamics of the system. It is helpful to understand dynamical properties of the system by studying the existence of relative equilibria. Moreover, the relative equilibria provide some natural hovering positions for the spacecraft in the close-proximity operations, at which the hovering can be achieved at the cost of a low control effort.

In the present paper, the relative equilibria of the rigid body, especially their types and existence, are investigated using geometric mechanics from a global point of view. To our best knowledge, this problem has not been studied before either in the dynamics near asteroids or in F2BP. In our study, the effect of the gravitational orbit-attitude coupling will be especially assessed.

2 Statement of the problem

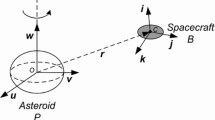
As described by Fig. 1, we consider a rigid body B moving around a uniformly rotating celestial body P, the gravity field of which is approximated by a second degree and order-gravity field with harmonics C₂₀ and C₂₂. The body-fixed reference frames of the central body and the rigid body are given by S _P ={u,v,w} and S _B ={i,j,k} with O and C as their origins respectively. The origins of the frame S _P and S _B are fixed at the mass centers of the bodies, and the coordinate axes are chosen to be aligned along the principal moments of inertia. The principal moments of inertia of the central body are assumed to satisfy

$$ I_{P,ww} > I_{P,vv},\qquad I_{P,ww} > I_{P,uu}. $$

(1)

The mass center of the central body is assumed to be stationary in the inertial space, and the central body is rotating uniformly around its maximum-moment principal axis, i.e., the w-axis.

Fig. 1

The rigid body moving in a uniformly rotating second degree and order-gravity field

The harmonic coefficients C₂₀ and C₂₂ of the 2nd degree and order-gravity field of the central body can be defined by

$$ \begin{aligned}[c] &C_{20} = - \frac{1}{2Ma_{e}^{2}} ( 2I_{P,ww} - I_{P,uu} - I_{P,vv} ) < 0,\\ &C_{22} = \frac{1}{4Ma_{e}^{2}} ( I_{P,vv} - I_{P,uu} ), \end{aligned} $$

(2)

where M and a _e are the mass and the mean equatorial radius of the central body respectively.

3 Equilibrium conditions

The relative equilibria of the rigid body are the stationary solutions of the equations of motion. Equilibrium conditions determining the relative equilibria can be obtained by setting the time change rates of the phase space variables all equal to zero. Equations of motion can be derived with the method of the geometric mechanics. Here we only give the equations of motion briefly, see Wang and Xu (2012, 2014b) and Wang et al. (2014b) for the details of the non-canonical Hamiltonian structure and the derivation of the equations of motion.

The attitude of the rigid body is described with respect to the body-fixed frame of the central body S _P by the attitude matrix A,

$$ \boldsymbol{A} = [\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} ]^{T} \in \mathit{SO}(3), $$

(3)

where α, β and γ are coordinates of the unit vectors u, v and w expressed in the body-fixed frame of the rigid body S _B respectively; SO(3) is the 3-dimensional special orthogonal group. The position vector of mass center C of the rigid body with respect to the mass center O of the central body expressed in the body-fixed frame S _P is denoted by r.

Therefore the configuration space of the problem is the Lie group

$$ Q = \mathit{SE}(3), $$

(4)

known as the special Euclidean group of three space with elements (A,r), which is the semidirect product of SO(3) and $\mathbb{R}^{3}$. We can choose the body-fixed coordinates for the phase space, i.e., the cotangent bundle T^∗ Q, as follows (Wang and Xu 2012, 2014b; Wang et al. 2014b):

$$ \boldsymbol{z} = \bigl[ \boldsymbol{\varPi}^{T},\boldsymbol{ \alpha}^{T}, \boldsymbol{\beta}^{T},\boldsymbol{ \gamma}^{T}, \boldsymbol{R}^{T},\boldsymbol{P}^{T} \bigr]^{T} \in \mathbb{R}^{18}, $$

(5)

where Π, R=A^T r and P are the angular momentum, position vector and linear momentum of the rigid body respectively expressed in the body-fixed frame S _B . The body-fixed coordinates z provide a global point of view to determine the relative equilibria.

This system has a non-canonical Hamiltonian structure with the Poisson bracket $\{ \cdot, \cdot \}_{\mathbb{R}^{18}}(\boldsymbol{z})$, which can be written in terms of the Poisson tensor as follows:

$$ \{ f, g\}_{\mathbb{R}^{18}}(\boldsymbol{z}) = ( \nabla_{\boldsymbol{z}}f )^{T}\boldsymbol{B}(\boldsymbol{z}) ( \nabla_{\boldsymbol{z}}g ). $$

(6)

The Poisson tensor B(z) is given by (Wang and Xu 2012):

$$ \boldsymbol{B}(\boldsymbol{z}) = \left[\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \hat{\boldsymbol{\varPi}} & \hat{\boldsymbol{\alpha}} & \hat{\boldsymbol{\beta}} & \hat{\boldsymbol{\gamma}} & \hat{\boldsymbol{R}} & \hat{\boldsymbol{P}} \\ \hat{\boldsymbol{\alpha}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \hat{\boldsymbol{\beta}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \hat{\boldsymbol{\gamma}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \hat{\boldsymbol{R}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} \\ \hat{\boldsymbol{P}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & - \mathbf{I}_{3 \times 3} & \mathbf{0} \end{array} \right], $$

(7)

where I_3×3 is the 3×3 identity matrix, and the hat map $\hat{\phantom{\cdot}}\hspace{-3pt}:\mathbb{R}^{3} \to \mathit{so}(3)$ is the usual Lie algebra isomorphism. For a vector w=[w^x,w^y,w^z], we have

$$ \hat{\boldsymbol{w}} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & - w^{z} & w^{y} \\ w^{z} & 0 & - w^{x} \\ - w^{y} & w^{x} & 0 \end{array} \right]. $$

(8)

The Hamiltonian of the system is given by (Wang et al. 2014b; Wang and Xu 2014b):

$$\begin{aligned} H ( \boldsymbol{z} ) =& \frac{1}{2}\boldsymbol{\varPi}^{T} \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} + \frac{\vert \boldsymbol{P} \vert ^{2}}{2m} - \omega_{T}\boldsymbol{\varPi}^{T}\boldsymbol{\gamma} \\ &{} - \omega_{T}\boldsymbol{P}^{T} ( \hat{\boldsymbol{\gamma}} \boldsymbol{R} ) + V ( \boldsymbol{z} ), \end{aligned}$$

(9)

where the diagonal matrix $\boldsymbol{I} = \operatorname{diag}\{ I_{xx}, I_{yy}, I_{zz} \}$ and m are the inertia tensor and mass of the rigid body respectively, ω _T is the angular velocity of the uniform rotation of the gravity field, and V(z) is the gravitational potential.

The second-order gravitational potential V(z) is given by:

$$\begin{aligned} &{V ( \boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )} \\ &{\quad{}=- \frac{\mu m}{R} - \frac{\mu}{2R^{3}} \bigl[ \operatorname{tr} ( \boldsymbol{I} ) - 3\bar{\boldsymbol{R}}^{T}\boldsymbol{I} \bar{ \boldsymbol{R}} - m\tau_{0} + 3m\tau_{0} ( \boldsymbol{\gamma} \cdot \bar{\boldsymbol{R}} )^{2}} \\ &{\qquad{}+ 6m\tau_{2} \bigl( ( \boldsymbol{\alpha} \cdot \bar{ \boldsymbol{R}} )^{2} - ( \boldsymbol{\beta} \cdot \bar{ \boldsymbol{R}} )^{2} \bigr) \bigr],} \end{aligned}$$

(10)

where μ=GM, G is the Gravitational Constant, $\tau_{0} = a_{e}^{2}C_{20}$, $\tau_{2} = a_{e}^{2}C_{22}$ and $\bar{\boldsymbol{R}}$ is the unit vector along the vector R (Wang and Xu 2013a).

The equations of motion can be written in the Hamiltonian form

$$ \dot{\boldsymbol{z}} = \boldsymbol{B}(\boldsymbol{z})\nabla_{\boldsymbol{z}}H(\boldsymbol{z}). $$

(11)

The explicit equations of motion can be obtained from Eqs. (9) and (11) as follows:

$$\begin{aligned} \left[ \begin{array}{@{}c@{}} \dot{\boldsymbol{\varPi}} \\ \dot{\boldsymbol{\alpha}} \\ \dot{\boldsymbol{\beta}} \\ \dot{\boldsymbol{\gamma}} \\ \dot{\boldsymbol{R}} \\ \dot{\boldsymbol{P}} \end{array} \right] =& \boldsymbol{B}(\boldsymbol{z}) \left[ \begin{array}{@{}c@{}} \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} - \omega_{T}\boldsymbol{\gamma} \\ \partial V / \partial \boldsymbol{\alpha} \\ \partial V / \partial \boldsymbol{\beta} \\ - \omega_{T}\boldsymbol{\varPi} - \omega_{T}\hat{\boldsymbol{R}}\boldsymbol{P} + \partial V / \partial \boldsymbol{\gamma}\\ - \omega_{T}\hat{\boldsymbol{P}}\boldsymbol{\gamma} + \partial V / \partial \boldsymbol{R}\\ - \omega_{T}\hat{\boldsymbol{\gamma}} \boldsymbol{R} + \boldsymbol{P} / m \end{array} \right] \\ =& \left[\begin{array}{@{}c@{}} \hat{\boldsymbol{ \varPi}} \boldsymbol{I}^{- 1}\boldsymbol{\varPi} + \sum _{\boldsymbol{b} = \boldsymbol{\alpha},\boldsymbol{\beta},\boldsymbol{\gamma},\boldsymbol{R}} \hat{\boldsymbol{b}} ( \partial V / \partial \boldsymbol{b} )\\ \hat{\boldsymbol{\alpha}} ( \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} - \omega_{T}\boldsymbol{\gamma} ) \\ \hat{\boldsymbol{\beta}}( \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} - \omega_{T}\boldsymbol{\gamma} ) \\ \hat{\boldsymbol{\gamma}} ( \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} ) \\ \hat{\boldsymbol{R}} ( \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} ) + \boldsymbol{P} / m \\ \hat{\boldsymbol{P}} ( \boldsymbol{I}^{ - 1}\boldsymbol{\varPi} ) - \partial V / \partial \boldsymbol{R} \end{array} \right]. \end{aligned}$$

(12)

Then equilibrium conditions that determine the relative equilibria are given by

$$\begin{aligned} &{\boldsymbol{I}\boldsymbol{\varOmega}_{e} \times \boldsymbol{ \varOmega}_{e} + \boldsymbol{R}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{R}} \bigg|_{e}} \\ &{\quad{} + \boldsymbol{\alpha}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\alpha}} \bigg|_{e}+\boldsymbol{\beta}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\beta}} \bigg|_{e}} \\ &{\quad{} + \boldsymbol{\gamma}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\gamma}} \bigg|_{e} = \mathbf{0},} \end{aligned}$$

(13)

$$\begin{aligned} &{\boldsymbol{\alpha}_{e} \times ( \boldsymbol{ \varOmega}_{e} - \omega_{T}\boldsymbol{\gamma}_{e} ) = \mathbf{0},} \end{aligned}$$

(14)

$$\begin{aligned} &{\boldsymbol{\beta}_{e} \times ( \boldsymbol{ \varOmega}_{e} - \omega_{T}\boldsymbol{\gamma}_{e} ) = \mathbf{0},} \end{aligned}$$

(15)

$$\begin{aligned} &{\boldsymbol{\gamma}_{e} \times \boldsymbol{ \varOmega}_{e} = \mathbf{0},} \end{aligned}$$

(16)

$$\begin{aligned} &{\boldsymbol{R}_{e} \times \boldsymbol{\varOmega}_{e} + \frac{\boldsymbol{P}_{e}}{m} = \mathbf{0},} \end{aligned}$$

(17)

$$\begin{aligned} &{\boldsymbol{P}_{e} \times \boldsymbol{\varOmega}_{e} - \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{R}}\bigg|_{e} = \mathbf{0},} \end{aligned}$$

(18)

where the subscript e is used to denote the value at the equilibrium. Here the angular momentum Π and the angular velocity I⁻¹ Π in Eq. (12) are denoted by IΩ and Ω respectively. Actually, Eqs. (13) and (18) are the torque and force balance equations respectively. Using the formulation of the second-order potential equation (10), we can write the torque and force balance equations (13) and (18) as follows

$$\begin{aligned} &{\boldsymbol{I}\boldsymbol{\varOmega}_e\times\boldsymbol{\varOmega}_e+\boldsymbol{T}_e=\mathbf{0},} \end{aligned}$$

(19)

$$\begin{aligned} &{\boldsymbol{P}_e\times\boldsymbol{\varOmega}_e+\boldsymbol{F}_e=\mathbf{0},} \end{aligned}$$

(20)

where T _e and F _e are the gravity gradient torque and gravitational force expressed in the body-fixed frame S _B respectively.

$$\begin{aligned} &{\boldsymbol{T}_{e} = \boldsymbol{R}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{R}}\bigg|_{e} + \boldsymbol{\alpha}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\alpha}} \bigg|_{e}} \\ &{\phantom{\boldsymbol{T}_{e} =}{}+ \boldsymbol{\beta}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\beta}} \bigg|_{e} + \boldsymbol{\gamma}_{e} \times \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{\gamma}} \bigg|_{e}} \\ &{\phantom{\boldsymbol{T}_{e}}{} = \frac{3\mu}{R_{e}^{5}}\boldsymbol{R}_{e} \times \boldsymbol{I}\boldsymbol{R}_{e},} \end{aligned}$$

(21)

$$\begin{aligned} &{\boldsymbol{F}_{e} = - \frac{\partial V(\boldsymbol{R}, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} )}{\partial \boldsymbol{R}} \bigg|_{e}} \\ &{\phantom{\boldsymbol{F}_{e}}{}=- \frac{\mu m}{R_{e}^{2}}\bar{\boldsymbol{R}}_{e}} \\ &{\phantom{\boldsymbol{F}_{e}=}{}+\frac{3\mu}{2R_{e}^{4}} \bigl\{ \bigl[ 5\bar{ \boldsymbol{R}}_{e}^{T}\boldsymbol{I}\bar{ \boldsymbol{R}}_{e} - \operatorname{tr} ( \boldsymbol{I} ) + \tau_{0}m \bigl( 1 - 5 ( \boldsymbol{\gamma}_{e} \cdot \bar{\boldsymbol{R}}_{e} )^{2} \bigr)} \\ &{\phantom{\boldsymbol{F}_{e}=}{} -10\tau_{2}m \bigl( ( \boldsymbol{ \alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )^{2} - ( \boldsymbol{\beta}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )^{2} \bigr) \bigr] \bar{ \boldsymbol{R}}_{e}} \\ &{\phantom{\boldsymbol{F}_{e}=}{}- 2\boldsymbol{I}\bar{\boldsymbol{R}}_{e} + 2\tau_{0}m ( \boldsymbol{\gamma}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )\boldsymbol{\gamma}_{e} + 4 \tau_{2}m \bigl( ( \boldsymbol{\alpha}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e}} \\ &{\phantom{\boldsymbol{F}_{e}=}{} - ( \boldsymbol{ \beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{ \beta}_{e} \bigr) \bigr\} .} \end{aligned}$$

(22)

It is worth our attention that the attitude parameters of the rigid body α, β and γ are included in Eq. (22) due to the gravitational orbit-attitude coupling.

Equations (14)–(17) describe the basic geometrical properties of the configuration of the relative equilibria. According to Eqs. (14)–(16), we can conclude that

$$ \boldsymbol{\varOmega}_{e} = \omega_{T}\boldsymbol{\gamma}_{e}. $$

(23)

That is to say, the rigid body has the same angular velocity as the central body and then the relative attitude is kept to be stationary.

From Eq. (17), we can know that

$$ \boldsymbol{P}_{e} = m\omega_{T}\boldsymbol{\gamma}_{e} \times \boldsymbol{R}_{e}. $$

(24)

The mass center of the rigid body is on a stationary orbit, moving synchronously with the rotation of the central body. The position vector r _e (t) of the mass center C of the rigid body will generate a cone in the inertial space with the unit vector w as its axis. When R _e is perpendicular to γ _e , this cone will degenerate into a plane. Therefore, the orbit of the mass center of the rigid body is a circle that is the base of the cone, and the angular velocity of the orbit is ω _T , same as the angular velocity of the rotation of the central body and the rigid body. Notice that there is no priori reason that the center of the circular orbit coincides with the origin O. The orbital plane is perpendicular to w, i.e., parallel to the equatorial plane of the central body P.

Insertion of Eq. (21) into the torque balance equation (19) yields:

$$ \omega_{T}^{2}\boldsymbol{I}\boldsymbol{\gamma}_{e} \times \boldsymbol{\gamma}_{e} = \frac{3\mu}{R_{e}^{5}}\boldsymbol{I}\boldsymbol{R}_{e} \times \boldsymbol{R}_{e}. $$

(25)

By taking the inner product of both sides of Eq. (25) with γ _e , we have

$$ ( \boldsymbol{I}\boldsymbol{R}_{e} \times \boldsymbol{R}_{e} ) \cdot \boldsymbol{\gamma}_{e} = \boldsymbol{I}\boldsymbol{R}_{e} \cdot ( \boldsymbol{R}_{e} \times \boldsymbol{\gamma}_{e} ) = 0. $$

(26)

Therefore, IR _e lies in the plane spanned by R _e and γ _e . In the same way we get

$$ ( \boldsymbol{I\gamma}_{e} \times \boldsymbol{\gamma}_{e} ) \cdot \boldsymbol{R}_{e} = \boldsymbol{I\gamma}_{e} \cdot ( \boldsymbol{\gamma}_{e} \times \boldsymbol{R}_{e} ) = 0. $$

(27)

Iγ _e also lies in the plane spanned by R _e and γ _e . Then the plane spanned by R _e and γ _e is parallel to a principal plane of the tensor of inertia I. According to Eq. (24), the linear momentum P _e is parallel to the principal axis, which is perpendicular to the principal plane spanned by R _e and γ _e .

According to Eqs. (22)–(24), the force balance equation (20) can be written as:

$$\begin{aligned} &{m\omega_{T}^{2} ( \boldsymbol{\gamma}_{e} \times \boldsymbol{R}_{e} ) \times \boldsymbol{\gamma}_{e}} \\ &{\quad{} = \frac{\mu m}{R_{e}^{2}}\bar{\boldsymbol{R}}_{e}} \\ &{\qquad{}- \frac{3\mu}{2R_{e}^{4}} \bigl\{ \bigl[ 5 \bar{\boldsymbol{R}}_{e}^{T}\boldsymbol{I}\bar{\boldsymbol{R}}_{e} - \operatorname{tr} ( \boldsymbol{I} ) + \tau_{0}m \bigl( 1 - 5 ( \boldsymbol{ \gamma}_{e} \cdot \bar{\boldsymbol{R}}_{e} )^{2} \bigr)} \\ &{\qquad{} - 10\tau_{2}m \bigl( ( \boldsymbol{ \alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )^{2} - ( \boldsymbol{\beta}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )^{2} \bigr) \bigr]\bar{ \boldsymbol{R}}_{e}} \\ &{\qquad{} - 2\boldsymbol{I}\bar{\boldsymbol{R}}_{e} + 2\tau_{0}m ( \boldsymbol{\gamma}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\gamma}_{e}} \\ &{\qquad{} + 4\tau_{2}m \bigl( ( \boldsymbol{ \alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{ \alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e} \bigr) \bigr\} .} \end{aligned}$$

(28)

4 Lagrangian relative equilibria

First we consider a particular case when R _e is parallel to a principal axis of the tensor of inertia I. From Eq. (25), we can know that

$$ \omega_{T}^{2}\boldsymbol{I\gamma}_{e} \times \boldsymbol{\gamma}_{e} = \mathbf{0}, $$

(29)

which means that γ _e is also parallel to a principal axis of the tensor of inertia I. For a general rigid body B without symmetry, this can mean either R _e ⋅γ _e =0 or R _e ×γ _e =0. From the physical intuition, the case of R _e ×γ _e =0 means that the mass center of the rigid body is always located above the pole of the central body P, which is impossible in the real situation of an asteroid orbiter. Therefore we have R _e ⋅γ _e =0. Thus, the orbit plane of the mass center of the rigid body is in the equatorial plane of body P, and the center of the circular orbit coincides with origin O. From the fact that R _e and γ _e are parallel to two different principal axes of the tensor of inertia I and Eq. (24), we can conclude that P _e is parallel to the third principal axis of the tensor of inertia.

Since the circular orbit of the mass center of the rigid body is within the equatorial plane of the central body P, and R _e , Ω _e and P _e are parallel to the three principal axis of the tensor of inertia I, this type of the relative equilibria is called the classical relative equilibria, or Lagrangian relative equilibria.

Without loss of generality, we assign R _e =[R _e 0 0]^T, γ _e =[0 0 1]^T, Ω _e =[0 0 ω _T ]^T and P _e =m[0 R _e ω _T 0]^T. Then the force balance equation (28) can be written as follows:

$$\begin{aligned} m\omega_{T}^{2}R_{e}\bar{ \boldsymbol{R}}_{e} =& \frac{\mu m}{R_{e}^{2}}\bar{\boldsymbol{R}}_{e} - \frac{3\mu}{2R_{e}^{4}} \bigl\{ \bigl[ 5\bar{\boldsymbol{R}}_{e}^{T} \boldsymbol{I}\bar{\boldsymbol{R}}_{e} - \operatorname{tr} ( \boldsymbol{I} ) + \tau_{0}m \\ &{} - 10\tau_{2}m \bigl( ( \boldsymbol{ \alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )^{2} - ( \boldsymbol{\beta}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )^{2} \bigr) \bigr]\bar{ \boldsymbol{R}}_{e} \\ &{}- 2I_{xx}\bar{\boldsymbol{R}}_{e} + 4 \tau_{2}m \bigl( ( \boldsymbol{\alpha}_{e} \cdot \bar{ \boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} \\ &{}- ( \boldsymbol{ \beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{ \beta}_{e} \bigr) \bigr\} . \end{aligned}$$

(30)

By checking the left and right sides of Eq. (30), it is easy to find that Eq. (30) requires the vector $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ on the right side to be parallel to the unit vector $\bar{\boldsymbol{R}}_{e}$. Notice that $\bar{\boldsymbol{R}}_{e}$, which is perpendicular to γ _e , is within the plane spanned by α _e and β _e . Then, the vector $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ is actually the reflection of the unit vector $\bar{\boldsymbol{R}}_{e}$ with respect to the vector α _e .

According to the fact that $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ is parallel to the unit vector $\bar{\boldsymbol{R}}_{e}$, we can conclude that $\bar{\boldsymbol{R}}_{e}$ is parallel or perpendicular to the vector α _e . That is to say,

$$ \boldsymbol{\alpha}_{e} = \left[ \begin{array}{@{}c@{}} 1 \\ 0 \\ 0 \end{array} \right],\ \left[ \begin{array}{@{}c@{}} 0 \\ 1 \\ 0 \end{array} \right],\ \left[ \begin{array}{@{}c@{}} - 1 \\ 0 \\ 0 \end{array} \right]\ \mbox{or}\ \left[ \begin{array}{@{}c@{}} 0 \\ - 1 \\ 0 \end{array} \right]. $$

(31)

Accordingly,

$$ \boldsymbol{\beta}_{e} = \left[ \begin{array}{@{}c@{}} 0 \\ 1 \\ 0 \end{array} \right],\ \left[ \begin{array}{@{}c@{}} - 1 \\ 0 \\ 0 \end{array} \right],\ \left[ \begin{array}{@{}c@{}} 0 \\ - 1 \\ 0 \end{array} \right]\ \mbox{or}\ \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right]. $$

(32)

Therefore, at the Lagrangian relative equilibria, the mass center of the rigid body is located at the principal axes of the asteroid in the equatorial plane, i.e., u and v, and the axes of the body-fixed frame of the rigid body S _B are parallel to those of the body-fixed frame S _P . The Lagrangian relative equilibria given here are the same with those in Wang and Xu (2014b) and Wang et al. (2014b) obtained by using the symmetry of the gravity field and the inertia tensor of the rigid body.

Without loss of generality, we assign and α _e =[1 0 0]^T β _e =[0 1 0]^T, as shown by Fig. 2. At this relative equilibrium, the mass center of the rigid body is located on the positive side of the principal axis u. Other Lagrangian relative equilibria can be converted into this equilibrium by changing the arrangement of the axes of the body-fixed reference frames S _B and S _P .

Fig. 2

A Lagrangian relative equilibrium of the rigid body

Then the force balance equation (30) can be written as

$$\begin{aligned} &{m\omega_{T}^{2}R_{e}\bar{ \boldsymbol{R}}_{e}} \\ &{\quad{}= \frac{\mu m}{R_{e}^{2}}\bar{\boldsymbol{R}}_{e} - \frac{3\mu}{2R_{e}^{4}} \bigl\{ \bigl[ 5I_{xx} - \operatorname{tr} ( \boldsymbol{I} ) + \tau_{0}m - 10\tau_{2}m \bigr]\bar{ \boldsymbol{R}}_{e}} \\ &{\qquad{}- 2I_{xx}\bar{\boldsymbol{R}}_{e} + 4 \tau_{2}m\bar{\boldsymbol{R}}_{e} \bigr\} ,} \end{aligned}$$

(33)

which can be rearranged further as

$$ \omega_{T}^{2} = \frac{\mu}{R_{e}^{3}} - \frac{3\mu}{2R_{e}^{5}} \biggl\{ 2\frac{I_{xx}}{m} - \frac{I_{yy}}{m} - \frac{I_{zz}}{m} + \tau_{0} - 6\tau_{2} \biggr\} . $$

(34)

Here we have solved out the Lagrangian relative equilibria based on the equilibrium conditions. The existence of the Lagrangian relative equilibria can be investigated based on Eq. (34).

To make studies in general cases instead of in specific cases, we first nondimensionalize the system by the characteristic time $\sqrt{a_{e}^{3} / \mu}$ and the characteristic length a _e . After nondimensionalization, the equatorial radius a _e and the gravitational constant μ of the central body are both equal to 1, and the unit of the angular velocity is $\sqrt{\mu/a^{3}_{e}}$. Then Eq. (34) can be written as:

$$\begin{aligned} \omega_{T}^{2} =& \frac{1}{R_{e}^{3}} - \frac{3}{2R_{e}^{5}} \biggl( 2\frac{I_{xx}}{m} - \frac{I_{yy}}{m} - \frac{I_{zz}}{m} + C_{20} - 6C_{22} \biggr) \\ =& \frac{1}{R_{e}^{3}} \biggl[ 1 + \frac{3}{2R_{e}^{2}} \biggl( - 2\frac{I_{xx}}{m} + \frac{I_{yy}}{m} + \frac{I_{zz}}{m} - C_{20} + 6C_{22} \biggr) \biggr] \\ =& \frac{1}{R_{e}^{3}} \biggl[ 1 + \frac{3}{2R_{e}^{2}} ( \Delta I - C_{20} + 6C_{22} ) \biggr], \end{aligned}$$

(35)

where ΔI=−2I _xx /m+I _yy /m+I _zz /m. The parameter ΔI is a comprehensive scale of the effect of the orbit-attitude coupling of the rigid body, since it describes both the non-spherical mass distribution and the characteristic dimension of the rigid body, which are two basic elements of the gravitational orbit-attitude coupling (Wang et al. 2014a). The effect of ΔI can be considered equivalently as a change of the oblateness and ellipticity of the central body in the sense of the point mass model.

As in Wang et al. (2014a), the characteristic dimension of the rigid body d _C can be defined by the following equation:

$$ I_{xx} = \frac{1}{2}md_{C}^{2},\quad\mbox{or}\quad\frac{1}{2}d_{C}^{2} = \frac{I_{xx}}{m}. $$

(36)

Notice that the characteristic dimension d _C is only an estimation of the dimension of the rigid body, but not the real dimension of the rigid body. Since the characteristic dimension d _C has a very simple relation with I _xx /m, we will also refer I _xx /m as the characteristic dimension in the following.

The mass distribution parameters of the rigid body can be defined as follows:

$$ \sigma_{x} = \biggl( \frac{I_{zz} - I_{yy}}{I_{xx}} \biggr),\qquad \sigma_{y} = \biggl( \frac{I_{zz} - I_{xx}}{I_{yy}} \biggr). $$

(37)

The parameters σ _y and σ _x have the following range:

$$ - 1 \le \sigma_{y} \le 1,\qquad - 1 \le \sigma_{x} \le 1. $$

(38)

As shown above, the ratio I _xx /m describes the characteristic dimension of the rigid body; the ratios σ _x and σ _y describe the shape of the rigid body. The parameter ΔI can be written in terms of the three ratios I _xx /m, σ _x , and σ _y as follows (Wang et al. 2014a):

$$ \Delta I = \frac{I_{xx}}{m} \biggl( - 2 + \frac{I_{yy}}{I_{xx}} + \frac{I_{zz}}{I_{xx}} \biggr) = \frac{I_{xx}}{m}f_{\sigma}, $$

(39)

where f _σ is defined as:

$$ f_{\sigma} = \frac{2\sigma_{y} - \sigma_{x} - \sigma_{x}\sigma_{y}}{1 - \sigma_{y}}. $$

(40)

We can estimate the range of the parameter ΔI through the upper limit of I _xx /m and the calculation of f _σ on the σ _y –σ _x plane. We assume that the upper limit of I _xx /m is equal to 0.5, which means that the characteristic dimension of the rigid body d _C is a _e , which is the upper limit in our study.

According to Wang et al. (2014a), the lower limit of f _σ is −1, which can be reached in the case of σ _y =−1. Theoretically, the upper limit of f _σ is the positive infinity, which can be reached when σ _y approaches 1 and it means that the mass distribution of the rigid body is a rod along the i-axis. In our study we will not consider this extreme case that would not exist in the real physical system. We choose the upper limit of f _σ as 16 as in Wang et al. (2014a).

Noticing that the upper limit of I _xx /m is equal to 0.5, we can obtain the range of the parameter ΔI as follows:

$$ - 0.5 < \Delta I < 8. $$

(41)

The practical range of the harmonic coefficients C₂₀ and C₂₂ of the 2nd degree and order-gravity field in our study are chosen as follows:

$$ \left\{ \begin{array}{@{}l} - 0.5 < C_{20} < 0, \\ - 0.25 < C_{22} < 0.25, \end{array} \right. $$

(42)

which should cover most asteroids in our solar system. Therefore, the range of ΔI−C₂₀+6C₂₂ is given by:

$$ - 2 < \Delta I - C_{20} + 6C_{22} < 10. $$

(43)

According to the results by Howard (1990) and Elipe and López-Moratalla (2006), through some calculation it is found that Eq. (35) has one positive root for R _e under the following condition:

$$ \Delta I-C_{20}+6C_{22}>0, $$

(44)

and the positive root R _e satisfies

$$ R_{e} \ge \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{1 / 3}. $$

(45)

Equation (35) has two positive roots for R _e under the following condition:

$$ 0 > \Delta I - C_{20} + 6C_{22} > - \frac{2}{5} \biggl( \frac{2}{5} \biggr)^{2 / 3} \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{2 / 3}, $$

(46)

and the two positive roots R_e1 and R_e2 satisfy

$$ 0 < R_{e2} \le \biggl( \frac{2}{5} \biggr)^{1 / 3} \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{1 / 3} \le R_{e1} < \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{1 / 3}. $$

(47)

In the case of

$$ \Delta I - C_{20} + 6C_{22} < - \frac{2}{5} \biggl( \frac{2}{5} \biggr)^{2 / 3} \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{2 / 3}, $$

(48)

Equation (35) has no positive root for R _e .

Since the unit of the angular velocity is $\sqrt{\mu / a_{e}^{3}}$, ω _T =1 means that the gravity of the particle on the surface of the asteroid is balanced by the centrifugal force. Therefore, it is reasonable to assume that ω _T <1. The existence of the Lagrangian relative equilibria can be investigated in the (ΔI−C₂₀+6C₂₂)–ω _T plane according to the value of the root R _e of Eq. (35). For simplification, if Eq. (35) has no positive root or its positive root R _e <1, which means that the mass center of the rigid body moves under the surface of the central body P, the Lagrangian relative equilibria will be regarded not to exist.

According to Eq. (45) and the range ω _T <1, Eq. (35) always has a positive root R _e >1 in the case of ΔI−C₂₀+6C₂₂>0, therefore the Lagrangian relative equilibria can always exist in the range 0<ΔI−C₂₀+6C₂₂<10.

According to Eqs. (46) and (48), the remaining part of the (ΔI−C₂₀+6C₂₂)–ω₇ plane can be divided into two regions by

$$ \Delta I - C_{20} + 6C_{22} = - \frac{2}{5} \biggl( \frac{2}{5} \biggr)^{2 / 3} \biggl( \frac{1}{\omega_{T}^{2}} \biggr)^{2 / 3}. $$

(49)

As shown by Fig. 3, the (ΔI−C₂₀+6C₂₂)–ω _T plane is divided into the region 1 and the region 2 by the blue curve, which is given by Eq. (49).

Fig. 3

The (ΔI−C₂₀+6C₂₂)–ω _T plane divided according to the root R _e

In the region 1, Eq. (48) is satisfied, therefore Eq. (35) has no positive root and then the Lagrangian relative equilibria cannot exist. Whereas the region 2, in which Eq. (46) is satisfied, can be divided into three subregions 2a, 2b and 2c corresponding to the three cases R_e1<1, R_e1>1>R_e2 and R_e2>1 respectively, as shown by Fig. 3.

In the subregion 2a, the two positive roots are both smaller than 1, therefore the Lagrangian relative equilibria cannot exist in this subregion. In the subregion 2b, only one of the two positive roots is larger than 1, therefore only one Lagrangian relative equilibrium can exist for each point of this subregion. In the subregion 2c, both the two positive roots are larger than 1, therefore two Lagrangian relative equilibria can exist for each point of this subregion.

To investigate the existence of the Lagrangian relative equilibria from another point of view, the curves of the orbital radius R _e versus the angular velocity ω _T in the cases of different values of ΔI−C₂₀+6C₂₂ are given in Fig. 4. The nine curves, from up to bottom, are corresponding to nine values of ΔI−C₂₀+6C₂₂: 10, 8, 6, 4, 2, 0, −0.5, −1, −2 respectively.

Fig. 4

The curves of the orbital radius R _e versus the angular velocity ω _T

According to Fig. 4, we can see that the upper six curves, which are corresponding to the six nonnegative values of ΔI−C₂₀+6C₂₂: 10, 8, 6, 4, 2, 0 respectively, are always above the critical strange line R _e =1. This means that the Lagrangian relative equilibria can always exist in the range ω _T <1 that is consistent with the conclusion obtained above. The lower three curves, which are corresponding to the three negative values of ΔI−C₂₀+6C₂₂: −0.5, −1, −2 respectively, are more complex. As the angular velocity ω _T decreases from 1 to 0, there exists a bifurcation, before which Eq. (35) has no positive root and after which two positive roots of Eq. (35) appear.

In the cases of ΔI−C₂₀+6C₂₂=−1,−2, both the curves of the two positive roots of Eq. (35) are above the critical strange line R _e =1. That is to say, after the bifurcation two Lagrangian relative equilibria can always exist. However, in the case of ΔI−C₂₀+6C₂₂=−0.5, after the bifurcation, as the angular velocity ω _T decreases to 0, the smaller positive root will decrease below the critical line R _e =1. Therefore, as the angular velocity ω _T decreases to 0 after the bifurcation, the number of the Lagrangian relative equilibria that can exist will decrease from two to one. These conclusions are consistent with the results in Fig. 3.

5 Non-Lagrangian relative equilibria

5.1 Existence condition of non-Lagrangian relative equilibria

Here we consider a general case when R _e is not parallel to any principal axis of the tensor of inertia I. Notice that the plane spanned by R _e and γ _e is parallel to a principal plane of the tensor of inertia I. Without loss of generality, we assume that the principal plane spanned by R _e and γ _e is the i–k plane, and P _e is parallel to the principal axis j. Then, we can have

$$\begin{aligned} &{\begin{array}{@{}l} \boldsymbol{R}_{e} = \bigl[R_{e}^{x}\quad 0\quad R_{e}^{z}\bigr]^{T},\qquad \boldsymbol{\gamma}_{e} = \bigl[\gamma_{e}^{x}\quad 0\quad \gamma_{e}^{z}\bigr]^{T},\\ \boldsymbol{\varOmega}_{e} = \omega_{T}\bigl[ \gamma_{e}^{x}\quad 0 \quad \gamma_{e}^{z}\bigr]^{T}, \end{array}} \end{aligned}$$

(50)

$$\begin{aligned} &{\boldsymbol{P}_{e} = m\omega_{T}\bigl[0\quad R_{e}^{x}\gamma_{e}^{z} - R_{e}^{z}\gamma_{e}^{x}\quad 0\bigr]^{T}.} \end{aligned}$$

(51)

Then Eq. (25) can be written as follows

$$ \omega_{T}^{2}\gamma_{e}^{x} \gamma_{e}^{z} ( I_{zz} - I_{xx} ) = \frac{3\mu}{R_{e}^{5}}R_{e}^{x}R_{e}^{z} ( I_{zz} - I_{xx} ). $$

(52)

Here a general rigid body with (I _zz −I _xx )≠0 is considered, therefore we have

$$ \omega_{T}^{2}\gamma_{e}^{x}\gamma_{e}^{z} = \frac{3\mu}{R_{e}^{5}}R_{e}^{x}R_{e}^{z}. $$

(53)

Since R _e is not parallel to any principal axis of the rigid body, we have $R_{e}^{x}R_{e}^{z} \ne 0$. From Eq. (53) and $R_{e}^{x}R_{e}^{z} \ne 0$, we know that γ _e is not parallel to any principal axis either, and

$$ \boldsymbol{R}_{e} \cdot \boldsymbol{\gamma}_{e} = \gamma_{e}^{x}R_{e}^{x} + \gamma_{e}^{z}R_{e}^{z} = \gamma_{e}^{x}R_{e}^{x} + \frac{3\mu}{ R_{e}^{5}\omega_{T}^{2}\gamma_{e}^{x}}R_{e}^{x} \bigl( R_{e}^{z} \bigr)^{2} \ne 0. $$

(54)

Therefore, the orbit of the mass center of the rigid body is a circle with its center located on w but not coinciding with origin O. The orbital plane is displaced, that is to say, parallel to but not in the equatorial plane of the central body P. Since the circular orbit of the mass center of the rigid body is not within the equatorial plane of the central body P, and neither of R _e and γ _e is parallel to the principal axis of the tensor of inertia I, this type of relative equilibria is called the non-classical relative equilibria, or non-Lagrangian relative equilibria.

Then the left side of the force balance equation (28) can be written as follows:

$$\begin{aligned} &{m\omega_{T}^{2}\left[ \begin{array}{c} 0 \\ R_{e}^{x}\gamma_{e}^{z} - R_{e}^{z}\gamma_{e}^{x} \\ 0 \end{array} \right] \times \left[ \begin{array}{c} \gamma_{e}^{x} \\ 0 \\ \gamma_{e}^{z} \end{array} \right]} \\ &{\quad{} = m\omega_{T}^{2}\left[ \begin{array}{c} R_{e}^{x}( \gamma_{e}^{z} )^{2} - R_{e}^{z}\gamma_{e}^{x}\gamma_{e}^{z} \\ 0 \\ R_{e}^{z}( \gamma_{e}^{x} )^{2} - R_{e}^{x}\gamma_{e}^{x}\gamma_{e}^{z} \end{array} \right],} \end{aligned}$$

(55)

which is within the plane spanned by R _e and γ _e , i.e., i–k plane. Therefore, the right side of Eq. (28) is required also to be within the plane spanned by R _e and γ _e , which means that the vector $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ is within the plane spanned by R _e and γ _e , since the remaining terms on the right side are within the plane naturally.

Notice that $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e})\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ is the reflection of the component of the unit vector $\bar{\boldsymbol{R}}_{e}$ in the α _e –β _e plane with respect to the vector α _e . According to the fact that $( \boldsymbol{\alpha}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\alpha}_{e} - ( \boldsymbol{\beta}_{e} \cdot \bar{\boldsymbol{R}}_{e} )\boldsymbol{\beta}_{e}$ is within the plane spanned by R _e and γ _e , we can conclude that α _e is within or perpendicular to the plane spanned by R _e and γ. That means that the mass center of the rigid body is located within the principal plane of the central body P. Without loss of generality, we assume that α _e is within the plane spanned by R _e and γ _e , and

$$ \boldsymbol{\alpha}_e=\bigl[\gamma^z_e\quad 0\quad -\gamma^x_e\bigr],\qquad \boldsymbol{\beta}_{e}= \bigl[ 0 \quad 1\quad 0\bigr]^{T}. $$

(56)

Figure 5 illustrates the geometry of this non-Lagrangian relative equilibrium. In Fig. 5, $\gamma_{e}^{z}$ and $\gamma_{e}^{x}$ are coordinates of the vector w (or γ _e ) on the axes k and i respectively; $R_{e}^{z}$ and $R_{e}^{x}$ are coordinates of the position vector r on the axes k and i respectively. θ is the angle between R _e and the equatorial plane of the central body P, θ₁ is the angle between R _e and i, and θ₂ is the angle between w (or γ _e ) and k. The angles θ, θ₁ and θ₂ are given by:

$$ \tan \theta_{1} = \frac{R_{e}^{z}}{R_{e}^{x}},\quad \tan \theta_{2} = \frac{\gamma_{e}^{x}}{\gamma_{e}^{z}},\quad \theta = \theta_{1} + \theta_{2}. $$

(57)

Fig. 5

The geometry of the non-Lagrangian relative equilibrium

According to Fig. 5, we can find that the principal plane of the rigid body i–k plane coincides with the principal plane of the central body u–w plane at the non-Lagrangian relative equilibria. Through the comparison between Figs. 2 and 5, it is easy to find that the locations of the Lagrangian and non-Lagrangian relative equilibria are close. That is to say, for a Lagrangian relative equilibrium, if we rotate the rigid body around its negative j axis for θ₂, and then lift up the orbit of the mass center of the rigid body to an equilibrium position, we can reach a non-Lagrangian relative equilibrium if it can exist.

After the nondimensionalization, the force balance equation (28) can be written as follows:

$$\begin{aligned} &{\omega_{T}^{2}\left[ \begin{array}{@{}c@{}} R_{e}^{x} ( \gamma_{e}^{z})^{2} - R_{e}^{z}\gamma_{e}^{x} \gamma_{e}^{z} \\ 0 \\ R_{e}^{z} ( \gamma_{e}^{x})^{2} - R_{e}^{x}\gamma_{e}^{x} \gamma_{e}^{z} \end{array} \right]} \\ &{\quad{} = \frac{1}{R_{e}^{3}}\left[ \begin{array}{@{}c@{}} R_{e}^{x} \\ 0 \\ R_{e}^{z} \end{array} \right] + \frac{3}{R_{e}^{5}} \left[ \begin{array}{@{}c@{}} R_{e}^{x} \frac{I_{xx}}{m} \\ 0 \\ R_{e}^{z}\frac{I_{zz}}{m} \end{array} \right]} \\ &{\qquad{}- \frac{3}{2R_{e}^{7}} \biggl\{ \bigl( 5\bigl(R_{e}^{x} \bigr)^{2} - R_{e}^{2} \bigr)\frac{I_{xx}}{m} - R_{e}^{2}\frac{I_{yy}}{m}} \\ &{\qquad{} + \bigl( 5\bigl(R_{e}^{z} \bigr)^{2} - R_{e}^{2} \bigr)\frac{I_{zz}}{m} + C_{20} \bigl( R_{e}^{2} - 5 \bigl( \gamma_{e}^{x}R_{e}^{x} + \gamma_{e}^{z}R_{e}^{z} \bigr)^{2} \bigr)} \\ &{\qquad{} - 10C_{22} \bigl( \gamma_{e}^{z}R_{e}^{x} - \gamma_{e}^{x}R_{e}^{z} \bigr)^{2} \biggr\} \left[ \begin{array}{@{}c@{}} R_{e}^{x} \\ 0 \\ R_{e}^{z} \end{array} \right]} \\ &{\qquad{}- \frac{3}{R_{e}^{5}}C_{20} \bigl( \gamma_{e}^{x}R_{e}^{x} + \gamma_{e}^{z}R_{e}^{z} \bigr)\left[\begin{array}{@{}c@{}} \gamma_{e}^{x} \\ 0 \\ \gamma_{e}^{z} \end{array} \right]} \\ &{\qquad{} - \frac{6}{R_{e}^{5}}C_{22} \bigl( \gamma_{e}^{z}R_{e}^{x} - \gamma_{e}^{x}R_{e}^{z} \bigr)\left[ \begin{array}{@{}c@{}} \gamma_{e}^{z} \\ 0 \\ - \gamma_{e}^{x} \end{array} \right].} \end{aligned}$$

(58)

According to $( \gamma_{e}^{x} )^{2} + ( \gamma_{e}^{z} )^{2} = 1$ and Eq. (53), $\gamma_{e}^{x}$ and $\gamma_{e}^{z}$ can be solved out as:

$$ \begin{aligned}[c] &\gamma_{e}^{x} = \biggl( \frac{1}{2} \mp \sqrt {\frac{1}{4} - \biggl( \frac{3}{\omega_{T}^{2}R_{e}^{5}}R_{e}^{x}R_{e}^{z} \biggr)^{2}} \biggr)^{\frac{1}{2}},\\ &\gamma_{e}^{z} = \biggl( \frac{1}{2} \pm \sqrt{\frac{1}{4} - \biggl( \frac{3}{\omega_{T}^{2}R_{e}^{5}}R_{e}^{x}R_{e}^{z} \biggr)^{2}} \biggr)^{\frac{1}{2}}. \end{aligned} $$

(59)

Equation (59) contains two cases

$$ \gamma_{e}^{z} > \gamma_{e}^{x}\quad \mbox{and}\quad \gamma_{e}^{x} > \gamma_{e}^{z}. $$

(60)

The non-Lagrangian relative equilibrium, i.e., $R_{e}^{x}$, $R_{e}^{z}$, $\gamma_{e}^{x}$ and $\gamma_{e}^{z}$, can be solved out by Eqs. (58) and (59). The existence condition of the non-Lagrangian relative equilibria is equivalent to the solvable condition of the algebraic equations (58) and (59).

5.2 Existence regions of non-Lagrangian relative equilibria

However, it is difficult to analyze the existence of the non-Lagrangian relative equilibria through theoretical studies of nonlinear algebraic equations (58) and (59). Therefore, we will try to solve Eqs. (58) and (59) using numerical method with different values of the parameters of the system.

Notice that all the six parameters of the system, i.e., C₂₀, C₂₂, ω _T , I _xx /m, σ _x and σ _y , need to be discussed. To investigate the existence of the non-Lagrangian relative equilibria and the effects of the system parameters on the existence, we only need to carry out the numerical studies for some chosen values of the system parameters. We will choose some different values for the harmonic coefficients C₂₀ and C₂₂, the angular velocity of the gravity field ω _T , and the characteristic dimension of the rigid body I _xx /m. Then for each combination of the values of C₂₀, C₂₂, ω _T and I _xx /m, we try to solve the algebraic equations (58) and (59) for a grid of points on the σ _y –σ _x plane with a certain step size. If the point (σ _y ,σ _x ) can guarantee the solvable condition of Eqs. (58) and (59), that is to say, guarantee the existence of the non-Lagrangian relative equilibria, we plot the point (σ _y ,σ _x ) on the σ _y –σ _x plane.

With this method, we can obtain the existence regions of the non-Lagrangian relative equilibria on the σ _y –σ _x plane with different values of the harmonic coefficients C₂₀ and C₂₂, the angular velocity ω _T , and the characteristic dimension I _xx /m. Through comparisons between existence regions with different values of C₂₀, C₂₂, ω _T and I _xx /m, we can find out the individual effect of the system parameters on the existence of the non-Lagrangian relative equilibria.

We choose three different values for the coefficient C₂₀ and five different values for the coefficient C₂₂ as follows:

$$ \begin{aligned}[c] &C_{20} = - 0.5, -0.3, 0.1,\\ &C_{22} = - 0.25, - 0.15, 0, 0.15, 0.25. \end{aligned} $$

(61)

That is to say, there are fifteen different cases for the pair (C₂₀,C₂₂). The upper limits of I _xx /m and ω _T are chosen the same as in the studies of the Lagrangian relative equilibria. Then, the different values of I _xx /m and ω _T for each case of (C₂₀,C₂₂) in the numerical studies are chosen as follows:

$$\begin{aligned} &{\frac{I_{xx}}{m} = 0.5, 0.5\mathrm{e} - 2, 0.5\mathrm{e} - 6;} \end{aligned}$$

(62)

$$\begin{aligned} &{\omega_{T} = 1, 0.5, 0.2.} \end{aligned}$$

(63)

Through the numerical studies, we find that only in the cases of three pairs of (C₂₀,C₂₂), including (−0.3,−0.25), (−0.1,−0.25) and (−0.1,−0.15), the non-Lagrangian relative equilibria can exist. The fifteen pairs of (C₂₀,C₂₂) are plotted on the C₂₀–C₂₂ plane in Fig. 6.

Fig. 6

The pairs of (C₂₀,C₂₂) on the C₂₀–C₂₂ plane

The three pairs of (C₂₀,C₂₂), in the cases of which the non-Lagrangian relative equilibria can exist, are given by pentagrams in Fig. 6, and the remaining twelve pairs are given by dots. The existence regions of the non-Lagrangian relative equilibria on the σ _y –σ _x plane with the three pairs of (C₂₀,C₂₂), including (−0.3,−0.25), (−0.1,−0.25) and (−0.1,−0.15), are given in Tables 1, 2 and 3 respectively. In these figures, the interval −0.02<σ _y <0.02 is not considered, since σ _y =0 is equivalent to I _zz =I _xx that is the singular point of the existence condition of the non-Lagrangian relative equilibria, as shown by Eqs. (52) and (53).

Table 1 The existence regions of the non-Lagrangian relative equilibria with C₂₀=−0.3 and C₂₂=−0.25

Table 2 The existence regions of the non-Lagrangian relative equilibria with C₂₀=−0.1 and C₂₂=−0.25

Table 3 The existence regions of the non-Lagrangian relative equilibria with C₂₀=−0.1 and C₂₂=−0.15

5.3 Effects of the system parameters

Through comparisons between existence regions on the σ _y –σ _x plane in Tables 1, 2 and 3 with different pairs of (C₂₀,C₂₂) and different values of I _xx /m and ω _T , we can assess the effects of the system parameters on the existence of the non-Lagrangian relative equilibria. Several conclusions can be reached as follows:

• (a) The effect of the harmonic C ₂₀ and C ₂₂

According to Fig. 6, the numerical results suggest that a C₂₀ with a small absolute value and a negative C₂₂ with a large absolute value favor the existence of the non-Lagrangian relative equilibria. This conclusion can be also verified through the comparisons between existence regions on the σ _y –σ _x plane with different values of C₂₀ and C₂₂ in Tables 1, 2 and 3. That is to say, with a smaller absolute value of the negative C₂₀, the existence region of the non-Lagrangian relative equilibria is larger, as shown by Tables 1 and 2. Generally, with a larger absolute value of the negative C₂₂, the existence region is larger, as shown by Tables 2 and 3.

• (b) The effect of the angular velocity of the gravity field ω _T

In Tables 1, 2 and 3, if we change the value of the angular velocity of the gravity field ω _T with other system parameters fixed, we can find that the effect of the angular velocity ω _T is not monotone. Generally, among the three values of ω _T in Eq. (63) the existence region is the largest in the case of ω _T =0.5.

• (c) The effect of the gravitational orbit-attitude coupling of the rigid body

Notice that the gravitational orbit-attitude coupling is more significant when the ratio of the characteristic dimension of the rigid body to the orbit radius is larger. The effect of the gravitational orbit-attitude coupling of the rigid body can be discussed through comparisons between existence regions with different values of I _xx /m.

As shown by Tables 1, 2 and 3, the effect of the orbit-attitude coupling of the rigid body on the existence of the non-Lagrangian relative equilibria is complex, since the effect can be positive or negative, depending on the values of C₂₀, C₂₂ and ω _T .

In the cases of

$$\begin{aligned} &{C_{20} = - 0.1,\qquad C_{22} = - 0.25,\qquad \omega_{T} = 0.5,} \end{aligned}$$

(64)

$$\begin{aligned} &{C_{20} = - 0.1,\qquad C_{22} = - 0.15,\qquad \omega_{T} = 0.5,} \end{aligned}$$

(65)

as the characteristic dimension of the rigid body I _xx /m decreases, the existence region of the non- Lagrangian relative equilibria is getting larger and larger, and is equal to the whole σ _y –σ _x plane eventually. That is to say, the gravitational orbit-attitude coupling of the rigid body B has a negative effect on the existence of the non-Lagrangian relative equilibria.

However, in some other cases, including

$$\begin{aligned} &{C_{20} = - 0.3,\qquad C_{22} = - 0.25,\qquad \omega_{T} = 1,} \end{aligned}$$

(66)

$$\begin{aligned} &{C_{20} = - 0.3,\qquad C_{22} = - 0.25,\qquad \omega_{T} = 0.5,} \end{aligned}$$

(67)

$$\begin{aligned} &{C_{20} = - 0.1,\qquad C_{22} = - 0.25,\qquad \omega_{T} = 1,} \end{aligned}$$

(68)

$$\begin{aligned} &{C_{20} = - 0.1,\qquad C_{22} = - 0.25,\qquad \omega_{T} = 0.2,} \end{aligned}$$

(69)

$$\begin{aligned} &{C_{20} = - 0.1,\qquad C_{22} = - 0.15,\qquad \omega_{T} = 1,} \end{aligned}$$

(70)

as the characteristic dimension of the rigid body I _xx /m decreases, the existence region of the non-Lagrangian relative equilibria is getting smaller and disappears eventually. That is to say, the gravitational orbit-attitude coupling of the rigid body B has a positive effect on the existence of the non-Lagrangian relative equilibria in these five cases.

When the characteristic dimension of the rigid body I _xx /m is very small, such as I _xx /m=0.5e−6, the effect of the gravitational orbit-attitude coupling is very weak and the mass distribution parameters σ _x and σ _y have no influence on the existence of the non-Lagrangian relative equilibria. The existence will be determined by the values of C₂₀, C₂₂ and ω _T . The non-Lagrangian relative equilibria can exist on the whole σ _y –σ _x plane when the values of C₂₀, C₂₂ and ω _T favor their existence, which are given by Eqs. (64) and (65); whereas the non-Lagrangian relative equilibria cannot exist on the whole σ _y –σ _x plane when the values of C₂₀, C₂₂ and ω _T do not favor their existence, which are given by Eqs. (66)–(70).

When the characteristic dimension of the rigid body is large, such as I _xx /m=0.5, the effect of the gravitational orbit-attitude coupling is dominant. Compared with the case of a smaller characteristic dimension, the orbit-attitude coupling can destroy the existence of non-Lagrangian relative equilibria in some regions on the σ _y –σ _x plane in the cases of Eqs. (64) and (65); whereas the orbit-attitude coupling can lead to the existence of non-Lagrangian relative equilibria in some regions on the σ _y –σ _x plane in the cases of Eqs. (66)–(70).

When the characteristic dimension of the rigid body is very small, the gravitational orbit-attitude coupling is insignificant and the rigid body can be considered as a point mass. According to our conclusions stated above, the displaced stationary orbit above the equatorial plane of the central body can exist even for a point mass in the cases of Eqs. (64) and (65). This is consistent with the results in Howard (1990).

6 Conclusions

Relative equilibria of the full dynamics of a rigid body with gravitational orbit-attitude coupling in a uniformly rotating second degree and order gravity field, especially their types and existences, have been investigated from a global point of view. Equilibrium conditions of the relative equilibria have been obtained based on the equation of motion of the system. It has been found that at the relative equilibria the attitude and position of the rigid body are both kept to be stationary with respect to the central body. The orbit of the mass center of the rigid body is a circle parallel to the equatorial plane of the central body, and the center of the orbit is located on the rotational axis of the central body.

Through the equilibrium conditions, we have found two types of relative equilibria: one is the Lagrangian relative equilibria, in which the circular orbit of the rigid body is in the equatorial plane of the central body; the other is the non-Lagrangian relative equilibria, in which the circular orbit is parallel to but not in the equatorial plane of central body. The geometrical properties of both the Lagrangian and non-Lagrangian relative equilibria have been given in details.

The existences of both the Lagrangian and non-Lagrangian relative equilibria have been discussed numerically with respect to the parameters of the gravity field and the rigid body. The effect of the gravitational orbit-attitude coupling has been especially assessed. The existence region of the Lagrangian relative equilibria has been given on the plane of the system parameters.

As for the non-Lagrangian relative equilibria, our numerical results suggested that a C₂₀ with a small absolute value and a negative C₂₂ with a large absolute value favor their existence. The effect of the gravitational orbit-attitude coupling of the rigid body on their existence could be positive or negative, depending on the values of the harmonics C₂₀ and C₂₂, and the angular velocity of the rotation of the gravity field. Our numerical results also suggested that the displaced stationary orbit above the equatorial plane of the central body could exist even for a point mass in a second degree and order-gravity field.