On the nonlinear stability of relative equilibria of the full spacecraft dynamics around an asteroid

Abstract

The full dynamics of a spacecraft around an asteroid, in which the gravitational orbit–attitude coupling is considered, has been shown to be of great value and interest. Nonlinear stability of the relative equilibria of the full dynamics of a rigid spacecraft around a uniformly rotating asteroid is studied with the method of geometric mechanics. The non-canonical Hamiltonian structure of the problem, i.e., Poisson tensor, Casimir functions and equations of motion, are given in the differential geometric method. A classical kind of relative equilibria of the spacecraft is determined from a global point of view, at which the mass center of the spacecraft is on a stationary orbit, and the attitude is constant with respect to the asteroid. The conditions of nonlinear stability of the relative equilibria are obtained with the energy-Casimir method through the semi-positive definiteness of the projected Hessian matrix of the variational Lagrangian. Finally, example asteroids with a wide range of parameters are considered, and the nonlinear stability criterion is calculated. However, it is found that the nonlinear stability condition cannot be satisfied by spacecraft with any mass distribution parameters. The nonlinear stability condition by us is only the sufficient condition, but not the necessary condition, for the nonlinear stability. It means that the energy-Casimir method cannot provide any information about nonlinear stability of the relative equilibria, and more powerful tools, which are the analogues of the Arnold’s theorem in the canonical Hamiltonian system with two degrees of freedom, are needed for a further investigation.

1 Introduction

Space missions to asteroids have been one of the most exciting space activities of the human beings in the recent two decades. Asteroid missions have triggered a major progress in our whole understanding of small bodies in our solar system, and several missions have been developed with big successes, such as NASA’s Near Earth Asteroid Rendezvous (NEAR) to the asteroid Eros and JAXA’s mission Hayabusa to the asteroid Itokawa. The impact risk near-Earth objects (NEOs) pose to our fragile ecosystem has made the space community turn its attention to NEO hazard mitigation. On average, every 26–30 million years a 10-km-sized asteroid strikes Earth, and every several hundred years there is a Tunguska-class (100-m diameter) asteroid impact [44]. Asteroid missions for NEO hazard mitigation may be necessary in the near future.

The investigation on the dynamical behavior of the spacecraft near asteroids is very important for the mission design and the navigation and control of the spacecraft. As shown in our paper [58], in comparison with the traditional spacecraft dynamics around Earth, the spacecraft dynamics near asteroids has a remarkable characteristic: the gravitational coupling between the orbital and rotational motions can be severe due to the large ratio of the dimension of spacecraft to the orbit radius.

The traditional spacecraft dynamics, in which the spacecraft is treated as a point mass in the orbital motion and the attitude motion is treated as a restricted problem on a predetermined orbit, is precise enough for the case around Earth, since the gravitational orbit–attitude coupling is negligible on an Earth orbit. However, it no longer has a high precision in the case around small asteroids, where the orbit–attitude coupling can be significant. The significant effects of the gravitational orbit–attitude coupling in the dynamics of the spacecraft near asteroids have also been pointed out and discussed by Koon et al. [24], Scheeres [37], Wang and Xu [47–51], and Wang et al. [57].

In the full dynamics of spacecraft around asteroids, the gravitationally coupled orbital and rotational motions of the spacecraft are modeled within a unified approach, as shown by Wang et al. [58]. The full dynamics should be more precise than the previous orbital dynamics around asteroids with the point mass model, such as the works by Hirabayashi et al. [18], Hu [19], Hu and Scheeres [20], San-Juan et al. [32], Scheeres [33, 39], Scheeres and Hu [40], Scheeres et al. [41–43]. The full spacecraft dynamics will be also more faithful to the real motion than the attitude dynamics of the spacecraft near an asteroid, such as Riverin and Misra [31], Misra and Panchenko [30], Kumar [25], Wang and Xu [46, 52–55].

Through studies on the full dynamics, more detailed properties of the dynamical behavior of spacecraft near asteroids can be uncovered. These results will be very useful for the design of future higher-precision technologies for the navigation and control of spacecraft around asteroids, which should be more precise than the current technologies developed based on the traditional spacecraft dynamics.

The full spacecraft dynamics around an asteroid can be considered as a restricted model of the Full Two Body Problem (F2BP), i.e., two rigid bodies orbiting each other interacting through mutual gravitational potential. That is to say, in our problem we only study the motion of the spacecraft, and assume that the motion of the asteroid is not affected by the spacecraft. The sphere-restricted model of F2BP, in which one body is assumed to be a homogeneous sphere, has been studied broadly. The gravity field of the non-spherical body is truncated on the second-order terms [2–4, 21–23], or the non-spherical body is assumed to be a general rigid body [1, 5, 6, 8, 24, 36], an ellipsoid [9, 10, 35], a symmetrical body [45] and a dumb-bell [16]. There are also several works on the more general models of the F2BP, in which both bodies are non-spherical, such as Maciejewski [26], Scheeres [34, 38], Koon et al. [24], Boué and Laskar [11], McMahon and Scheeres [29] and Woo et al. [59].

Notice that the relative equilibria are an important qualitative property and act as the “organizing centers” of the dynamics of the system. It is helpful to understand the dynamical properties of the system near the relative equilibria by studying the properties at the relative equilibria. Therefore, we choose relative equilibria as the starting point of the study of the full dynamics near asteroids. In our papers [51] and [58], the relative equilibria and their linear stability of the full dynamics of a rigid spacecraft around a uniformly rotating asteroid have been studied with the method of geometric mechanics. We found that the full spacecraft dynamics is intrinsically different from the traditional dynamics, and the unstable traditional stationary orbit can be stabilized through the gravitational orbit–attitude coupling, however, at the cost of the reduction of the traditional linear attitude stability region.

In our papers [51] and [58], non-canonical Hamiltonian structure of the problem, i.e., Poisson tensor, Casimir functions and equations of motion, which govern the phase flow and phase space structures of the system, have been derived in the differential geometric method. In those papers, a classical kind of relative equilibria of the problem has also been determined from a global point of view by using the planar symmetries of the gravity field and the inertia tensor of the spacecraft.

In this paper, we will further investigate the nonlinear stability of the relative equilibria obtained in [51] and [58] using the energy-Casimir method provided by the geometric mechanics.

2 Statement of the problem

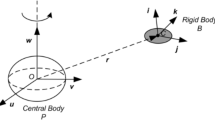
The problem we studied here is the same as that in Wang et al. [58]. As described by Fig. 1, a rigid spacecraft $B$ is moving around an asteroid $P$. The body-fixed reference frames of the asteroid and the spacecraft are given by $S_{P}$={${\varvec{u}}$, ${\varvec{v}}$, ${\varvec{w}}$ }and $S_{B}$={${\varvec{i}}$, ${\varvec{j}}$, ${\varvec{k}}$} with $O$ and $C$ as their origins, respectively. The origin of the frame $S_{P}$ is fixed at the mass center of the asteroid, and the coordinate axes are chosen to be aligned along the principal moments of inertia. The principal moments of inertia of the asteroid are assumed to satisfy the following inequations

$$\begin{aligned} I_{P,zz} >I_{P,yy} ,\;I_{P,zz} >I_{P,xx}. \end{aligned}$$

(1)

Fig. 1

The spacecraft moving around a uniformly rotating asteroid

Then the second degree and order-gravity field of the asteroid can be represented by the harmonic coefficients $C_{20}$ and $C_{22}$ with other harmonic coefficients vanished [19]. The harmonic coefficients $C_{20}$ and $C_{22}$ are defined by

$$\begin{aligned} \begin{aligned}&C_{20} =-\frac{1}{2Ma_e^2 }\left( {2I_{P,zz} -I_{P,xx} -I_{P,yy} }\right) <0,\\&\quad C_{22} =\frac{1}{4Ma_e^2 }\left( {I_{P,yy} -I_{P,xx} }\right) , \end{aligned} \end{aligned}$$

(2)

where $M$ and $a_{e}$ are the mass and the mean equatorial radius of the asteroid, respectively. The frame $S_{B}$ is attached to the mass center of the spacecraft and coincides with the principal axes reference frame. The mass center of the asteroid is assumed to be stationary in the inertial space, and the asteroid is in a uniform rotation around its maximum-moment principal axis, i.e., the ${\varvec{w}}$ axis.

3 Non-canonical Hamiltonian structure and relative equilibria

The non-canonical Hamiltonian structure of the problem, i.e., Poisson tensor, Casimir functions and equations of motion, and a classical kind of relative equilibria of the problem have already been obtained in the papers [51] and [58]. Here we only list the main results obtained there, see those papers for the details.

The attitude of the spacecraft is described with respect to the body-fixed frame of the asteroid $S_{P}$ by ${\varvec{A}}$,

$$\begin{aligned} \varvec{A}=[\varvec{i,\,j,\,k}]=[\varvec{\alpha } ,\,\varvec{\beta } ,\,\varvec{\gamma } ]^T\,\in \,SO(3), \end{aligned}$$

(3)

where the vectors ${\varvec{i}}$, ${\varvec{j}}$, and ${\varvec{k}}$ are components of the unit axial vectors of the body-fixed frame $S_{B}$ in the body-fixed frame $S_{P}$, respectively, $\varvec{\alpha }$, $\varvec{\beta }$, and $\varvec{\gamma }$ are coordinates of the unit vectors ${\varvec{u}}$, ${\varvec{v}}$, and ${\varvec{w}}$ in the body-fixed frame $S_{B}$, respectively, and SO(3) is the three-dimensional special orthogonal group. The matrix ${\varvec{A}}$ is also the coordinate transformation matrix from the body-fixed frame $S_{B}$ to the body-fixed frame $S_{P}$.

The position vector of the mass center of the spacecraft $C$ with respect to the mass center of the asteroid $O$ expressed in the body-fixed frame $S_{P}$ is given by the vector ${\varvec{r}}$. The configuration space of the problem is the Lie group

$$\begin{aligned} Q=SE(3), \end{aligned}$$

(4)

known as the special Euclidean group of three space with elements $(A,\,r)$, which is the semidirect product of SO (3) and ${\mathbb {R}}^3$.

The phase space of the system is the cotangent bundle $T^{*}Q$, the coordinates of which are chosen as the body-fixed coordinates given by

$$\begin{aligned} \varvec{z} = \left[ {\varvec{\Pi }^{T},\varvec{\alpha }^{T} \varvec{,}\,\varvec{\beta }^{T} \varvec{,}\,\varvec{\gamma }^{T} \varvec{,}\,\varvec{R}^{T} \varvec{,}\,\varvec{P}^{T} } \right] ^{T} \in \,\mathbb {R}^{{18}}, \end{aligned}$$

(5)

where $\varvec{\Pi }$ is the angular momentum of the spacecraft with respect to the inertial space, $\varvec{R}=\varvec{A}^{T}\varvec{r}$ is the position vector of the spacecraft, and $\varvec{P}$ is the linear momentum of the spacecraft with respect to the inertial space. $\varvec{\Pi }$, $\varvec{R}$, and $\varvec{P}$ are all expressed in the body-fixed frame $S_{B}$.

The Poisson bracket $\{\cdot ,\,\cdot \}_{{\mathbb {R}}^{18}} (z)$ of the non-canonical Hamiltonian system of the problem in the coordinates $z$ is given in terms of the Poisson tensor as follows:

$$\begin{aligned} \{ f,\,g\} _{{\mathbb {R}^{{18}} }} (\varvec{z}) = \left( {\nabla _{\varvec{z}} f} \right) ^{T} \varvec{B}(\varvec{z})\left( {\nabla _{\varvec{z}} g} \right) \end{aligned}$$

(6)

for any $f,\,g\in \,C^\infty ({\mathbb {R}}^{18})$. The Poisson tensor $\varvec{B}(\varvec{z})$, which has been derived in the differential geometric method by Wang and Xu [47], is given by

$$\begin{aligned} \varvec{B}(\varvec{z}) = \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \varvec{\hat{\Pi }} &{}{\varvec{\hat{\alpha }}} &{} {\varvec{\hat{\beta }}}&{} {\varvec{\hat{\gamma }}} &{} {\varvec{\hat{R}}} &{} {\varvec{\hat{P}}}\\ {\varvec{\hat{\alpha }}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\varvec{\hat{\beta }}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\varvec{\hat{\gamma }}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\varvec{\hat{R}}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {{\mathbf {I}}_{{3 \times 3}} }\\ {\varvec{\hat{P}}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {- {\mathbf {I}}_{{3 \times 3}} } &{} {\mathbf {0}} \\ \end{array} \right] , \end{aligned}$$

(7)

where ${\mathbf {I}}_{3\times 3}$ is the 3$\times$3 identity matrix. The hat map $\wedge :{\mathbb {R}}^3\rightarrow SO(3)$ is the usual Lie algebra isomorphism, and for a vector $\varvec{a}=\left[ {a^1,\,a^2,a^3} \right] ^T\in {\mathbb {R}}^3$,

$$\begin{aligned} \varvec{\hat{a}}=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} {-a^3} &{} {a^2}\\ {a^3} &{} 0 &{} {-a^1}\\ {-a^2} &{} {a^1} &{} 0\\ \end{array} }} \right] . \end{aligned}$$

(8)

The $18\times 18$ antisymmetric and degenerated Poisson tensor $\varvec{B}(\varvec{z})$ has six geometric integrals as independent Casimir functions

$$\begin{aligned}&C_{1} (\varvec{z}) = \frac{1}{2}\varvec{\alpha }^{T} \varvec{\alpha } \equiv \frac{1}{2},\,C_{2} (\varvec{z}) = \frac{1}{2}\varvec{\beta }^{T} \varvec{\beta } \equiv \frac{1}{2},\\&\quad C_{3} (\varvec{z}) = \frac{1}{2}\varvec{\gamma }^{T} \varvec{\gamma } \equiv \frac{1}{2},\\&C_{4} (\varvec{z}) = \varvec{\alpha }^{T} \varvec{\beta } \equiv 0,\,C_{5} (\varvec{z}) = \varvec{\alpha }^{T} \varvec{\gamma } \equiv 0,\,\\&\quad C_{6} (\varvec{z}) = \varvec{\beta }^{T} \varvec{\gamma } \equiv 0. \end{aligned}$$

The twelve-dimensional invariant manifold or symplectic leaf of the system can be defined in ${\mathbb {R}}^{18}$ by Casimir functions as follows:

$$\begin{aligned} \begin{array}{l} \displaystyle \Sigma = \left\{ \begin{array}{l} \left[ {\varvec{\Pi }^{T} ,\varvec{ \alpha }^{T} ,\,\varvec{\beta }^{T} ,\,\varvec{\gamma }^{T} ,\,\varvec{R}^{T} ,\,\varvec{P}^{T} } \right] ^{T} \in \mathbb {R}^{{18}} \, \end{array}\right. \\ \displaystyle |\,C_{1}(\varvec{z}) = C_{2} (\varvec{z}) = C_{3} (\varvec{z}) = \frac{1}{2},\\ \quad \displaystyle \left. {C_{4} (\varvec{z}) = C_{5} (\varvec{z}) = C_{6} (\varvec{z}) = 0} \right\} .\\ \end{array} \end{aligned}$$

(9)

The symplectic structure on this symplectic leaf is defined by restriction of the Poisson bracket $\{ \cdot ,\, \cdot \} _{{\mathbb {R}^{{18}} }} (\varvec{z})$ to $\Sigma$.

The six-dimensional nullspace of $\varvec{B}(\varvec{z})$ can be obtained from Casimir functions as follows:

$$\begin{aligned} {\text {N}}\left[ {\varvec{B}(\varvec{z})} \right]&= span\left\{ \left( {\begin{array}{l} {\mathbf {0}} \\ \varvec{\alpha } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} } \right) ,\,\left( {\begin{array}{l} {\mathbf {0}} \\ {\mathbf {0}} \\ \varvec{\beta } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} } \right) ,\,\left( {\begin{array}{l} {\mathbf {0}} \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \varvec{\gamma } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} } \right) ,\,\left( {\begin{array}{l} {\mathbf {0}} \\ \varvec{\beta } \\ \varvec{\alpha } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} } \right) ,\right. \nonumber \\&\left. \times \left( {\begin{array}{l} {\mathbf {0}} \\ \varvec{\gamma } \\ {\mathbf {0}} \\ \varvec{\alpha } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} } \right) ,\,\left( {\begin{array}{l} {\mathbf {0}} \\ {\mathbf {0}} \\ \varvec{\gamma } \\ {\beta } \\ {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array}} \right) \right\} . \end{aligned}$$

(10)

The Hamiltonian of the system in coordinates $\varvec{z}$ can be written as follows:

$$\begin{aligned} H( z)&= \frac{1}{2}\varvec{\Pi }^{T} \varvec{I}^{-1} \varvec{\Pi } +\frac{\left| \varvec{P} \right| ^2}{2m}-\omega _T \varvec{\Pi } ^T \varvec{\gamma }\nonumber \\&-\,\omega _T \varvec{P}^T(\varvec{\hat{\gamma }}\varvec{R})+V(\varvec{z}), \end{aligned}$$

(11)

where $m$ is the mass of the spacecraft, and the inertia tensor ${\varvec{I}}$ is given by

$$\begin{aligned} \varvec{I}={\hbox {diag}}\left\{ {I_{xx} ,\,I_{yy} ,\,I_{zz} } \right\} , \end{aligned}$$

(12)

with the principal moments of inertia of the spacecraft $I_{xx}$, $I_{yy}$, and $I_{zz}$. $\omega _{T}$ is the angular velocity of the uniform rotation of the asteroid. Based on the results by Wang and Xu [52], through some rearrangements, the explicit formulation of the second-order approximation of the gravitational potential $V(\varvec{z})$ in Eq. (11) can be written as follows:

$$\begin{aligned}&V\left( {\varvec{R},\,\varvec{\alpha },\,\varvec{\beta },\,\varvec{\gamma }} \right) =- \frac{{\mu m}}{R} \nonumber \\&\quad - \frac{\mu }{{2R^{3} }}\left[ {tr\left( \varvec{I} \right) - 3\varvec{\bar{R}}^{T} \varvec{I\bar{R}} - m\tau _{0} + 3m\tau _{0} \left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) ^{2} } \right. \nonumber \\&\quad \left. +\,{ 6m\tau _{2} \left( {\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) ^{2} - \left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) ^{2} } \right) } \right] \!, \end{aligned}$$

(13)

where $\mu \,=\, GM,\, G$ is the gravitational constant, $\tau _{0}$ = $a_{e}^{2}C_{20},\,\tau _{2} =a_{e}^{2}C_{22}$, $R=\left| \varvec{R} \right|$, and $\varvec{\bar{R}}=\varvec{R}/R$ is the unit vector along the vector $\varvec{R}$.

The equations of motion can be written in the Hamiltonian form as follows:

$$\begin{aligned} \varvec{\dot{z}}=\varvec{B}(\varvec{z})\nabla _z H(\varvec{z}). \end{aligned}$$

(14)

The explicit equations of motion can be obtained from Eqs. (11) and (14):

$$\begin{aligned} \left[ \begin{array}{l} {\varvec{\dot{\Pi }}} \\ {\varvec{\dot{\alpha }}}\\ {\varvec{\dot{\beta }}} \\ {\varvec{\dot{\gamma }}}\\ {\varvec{\dot{R}}} \\ {\varvec{\dot{P}}} \\ \end{array} \right]&= \varvec{B}(\varvec{z})\left[ \begin{array}{l} {\varvec{I}^{{ - 1}} \varvec{\Pi } - \omega _{T} \varvec{\gamma }}\\ {\partial V/\partial \varvec{\alpha }} \\ {\partial V/\partial \varvec{\beta }} \\ { - \omega _{T} \varvec{\Pi } -\omega _{T} \varvec{\hat{R}}\varvec{P} + \partial V/\partial \varvec{\gamma }} \\ { - \omega _{T}\varvec{\hat{P}}\varvec{\gamma } + \partial V/\partial \varvec{R}}\\ { - \omega _{T} \varvec{\hat{\gamma }}\varvec{R} + \varvec{P/}m}\\ \end{array}\right] \nonumber \\ \!&= \! \left[ \begin{array}{l} {\varvec{\hat{\Pi }}\,\varvec{I}^{{ - 1}} \varvec{\Pi } + \sum \limits _{{\varvec{b} = \varvec{\alpha },\varvec{\beta ,\gamma },\varvec{R}}} {\varvec{\hat{b}}\left( {\partial V/\partial \varvec{b}} \right) } }\\ {\varvec{\hat{\alpha }}\left( {\varvec{I}^{{ - 1}} \varvec{\Pi } - \omega _{T} \varvec{\gamma }} \right) } \\ {\varvec{\hat{\beta }}\left( {\varvec{I}^{{ - 1}} \varvec{\Pi } -\omega _{T} \varvec{\gamma }} \right) } \\ {\varvec{\hat{\gamma }}\left( {\varvec{I}^{{ - 1}} \varvec{\Pi }} \right) } \\ {\varvec{\hat{R}}\left( {\varvec{I}^{{ - 1}} \varvec{\Pi }} \right) + \varvec{P}/m}\\ {\varvec{\hat{P}}\left( {\varvec{I}^{{ - 1}} \varvec{\Pi }} \right) - \partial V/\partial \varvec{R}} \\ \end{array} \right] . \end{aligned}$$

(15)

According to Beck and Hall [7], and Hall [17], the relative equilibria of the system correspond to the stationary points of the Hamiltonian constrained by the Casimir functions. The stationary points can be determined by the first variation condition of the variational Lagrangian $\nabla F({\varvec{z}_e})={\mathbf {0}}$, where subscript $e$ is used to denote the value at relative equilibria. The variational Lagrangian $F(\varvec{z})$ is given by

$$\begin{aligned} F(\varvec{z})=H(\varvec{z})-\sum \limits _{i=1}^6 {\mu _i C_i (\varvec{z})}. \end{aligned}$$

(16)

By using the formulations of the Hamiltonian Eq. (11) and the Casimir functions, the equilibrium conditions are obtained as follows:

$$\begin{aligned}&\varvec{I}^{{ - 1}} \varvec{\Pi }_{e} - \omega _{T} \varvec{\gamma }_{e} = {\mathbf {0}},\end{aligned}$$

(17a)

$$\begin{aligned}&-\,\frac{\mu }{{2R_{e}^{3} }}\left[ {12m\,\tau _{2} \left( {\varvec{\alpha }_{e} \cdot \varvec{\bar{R}}_{e} } \right) \varvec{\bar{R}}_{e} } \right] - \mu _{1} \varvec{\alpha }_{e} \nonumber \\&\quad -\, \mu _{4} \varvec{\beta }_{e} - \mu _{5} \varvec{\gamma }_{e} = {\mathbf {0}},\end{aligned}$$

(17b)

$$\begin{aligned}&\frac{\mu }{{2R_{e}^{3} }}\left[ {12m\,\tau _{2} \left( {\varvec{\beta }_{e} \cdot \varvec{\bar{R}}_{e} } \right) \varvec{\bar{R}}_{e} } \right] - \mu _{2} \varvec{\beta }_{e} - \mu _{4} \varvec{\alpha }_{e} \nonumber \\&\quad -\, \mu _{6} \varvec{\gamma }_{e} = {\mathbf {0}},\end{aligned}$$

(17c)

$$\begin{aligned}&-\, \omega _{T} \varvec{\Pi }_{e} - \omega _{T} \varvec{\hat{R}}_{e} \varvec{P}_{e} - \frac{\mu }{{2R_{e}^{3}}}\left[ {6m\tau _{0} \left( {\varvec{\gamma }_{e} \cdot \varvec{\bar{R}}_{e} } \right) \varvec{\bar{R}}_{e} } \right] \nonumber \\&\quad -\, \mu _{3} \varvec{\gamma }_{e} - \mu _{5} \varvec{\alpha }_{e} - \mu _{6} \varvec{\beta }_{e} = {\mathbf {0}},\end{aligned}$$

(17d)

$$\begin{aligned}&-\, \omega _{T} \varvec{\hat{P}}_{e} \varvec{\gamma }_{e} + \left. {\frac{{\partial V}}{{\partial \varvec{R}}}} \right| _{e} = {\mathbf {0}},\end{aligned}$$

(17e)

$$\begin{aligned}&-\, \omega _{T} \varvec{\hat{\gamma }}_{e} \varvec{R}_{e} + \frac{{\varvec{P}_{e} }}{m} = {\mathbf {0}}, \end{aligned}$$

(17f)

where the partial derivate of the gravitational potential in Eq. (17e) is obtained as

$$\begin{aligned} &\frac{{\partial V}}{{\partial \varvec{R}}} = \frac{{\mu m}}{{R^{2} }}\varvec{\bar{R}} - \frac{{3\mu }}{{2R^{4} }}\nonumber \\ &\quad \times \left\{ \begin{array}{l} \left\{ \begin{array}{l} 5\varvec{\bar{R}}^{T} \varvec{I\bar{R}} - tr\left( \varvec{I} \right) + \tau _{0} m\left( {1 - 5\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) ^{2} } \right) \\ - 10\tau _{2} m\left( {\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) ^{2} - \left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) ^{2} } \right) \\ \end{array} \right\} \varvec{\bar{R}}\\ - 2\varvec{I\bar{R}} \!+\! 2\tau _{0} m\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) \varvec{\gamma } \!+\! 4\tau _{2} m\left( {\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) \varvec{\alpha } \!-\! \left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) \varvec{\beta }} \right) \\ \end{array} \!\right\} \!,\nonumber \\ \end{aligned}$$

(18)

which is actually the gravitational force of the spacecraft in the body-fixed frame $S_{B}$.

Equation (17a) implies that

$$\begin{aligned} \varvec{\Pi }_e =\omega _T \varvec{I}\varvec{\gamma }_e, \end{aligned}$$

(19)

i.e., the spacecraft has the same angular velocity as the asteroid and the attitude of the spacecraft is stationary with respect to the asteroid.

Equation (17f) implies that

$$\begin{aligned} \varvec{P}_e =m\omega _T \varvec{\hat{\gamma }}_e \varvec{R}_e, \end{aligned}$$

(20)

i.e., the mass center of the spacecraft is moving synchronously with the rotation of the asteroid. That is to say, at the relative equilibria the mass center of the spacecraft is on a stationary orbit. Insertion of Eq. (20) into Eq. (17e) yields the balance equation of the gravitational force

$$\begin{aligned} m\omega _T^2 \left[ {\varvec{R}_e -( {\varvec{R}_e \cdot \varvec{\gamma }_e })\varvec{\gamma }_e} \right] =\left. {\frac{\partial V}{\partial \varvec{R}}} \right| _e. \end{aligned}$$

(21)

The information of the attitude of the spacecraft $\varvec{\alpha }$, $\varvec{\beta }$, and $\varvec{\gamma }$ are included in Eq. (21) due to the orbit–attitude coupling, then the stationary orbit is the generalization of the traditional stationary orbit with the point mass model.

We can obtain several geometrical properties of the relative equilibria based on the equilibrium conditions Eq. (17). Taking the dot product of $\varvec{\beta }_e$ with Eq. (17b) yields $\mu _4 =-( {6m\tau _2 \mu /R_e^3 })( { \varvec{\alpha }_e \cdot \varvec{\bar{R}}_e })( { \varvec{\beta }_e \cdot \varvec{\bar{R}}_e })$, while the dot product of $\varvec{\alpha }_e$ with Eq. (17c) yields $\mu _4 =({6m\tau _2 \mu /R_e^3 })( { \varvec{\alpha }_e \cdot \varvec{\bar{R}}_e })( { \varvec{\beta }_e \cdot \varvec{\bar{R}}_e })$. Then we will have $\mu _{4}$ =0 and $({ \varvec{\alpha }_e \cdot \varvec{\bar{R}}_e })( { \varvec{\beta }_e \cdot \varvec{\bar{R}}_e })=0$, which means the mass center of the spacecraft is located within the principal plane of asteroid $\varvec{\alpha } _e - \varvec{\gamma }_e$ or $\varvec{\beta }_e - \varvec{\gamma }_e$. According to Eq. (21), we see that at the relative equilibria the gravitational force is within the same principal plane $\varvec{\alpha }_e - \varvec{\gamma }_e$ or $\varvec{\beta }_e - \varvec{\gamma }_e$, and is perpendicular to the rotational axis of the asteroid $\varvec{\gamma }_e$. That is to say, the gravitational force balances the centrifugal force of the orbital motion.

Different types of relative equilibria can exist in the equilibrium conditions Eq. (17). We have determined a kind of relative equilibria using the planar symmetries of the gravity field and the inertia tensor in Wang et al. [58].

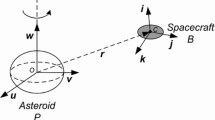
At this classical kind of relative equilibria, the mass center of the spacecraft is located at the principal axes of the asteroid, and $\varvec{\alpha }_e$, $\varvec{\beta }_e$ and $\varvec{\gamma }_e$ are principal axes of the inertia tensor of the spacecraft. As shown by Fig. 2, we assume that the mass center of the spacecraft is located on the principal axis ${\varvec{u}}$

$$\begin{aligned}&\varvec{\bar{R}}_e =\varvec{\alpha }_e =\left[ {1,\,0,\,0} \right] ^T,\,\varvec{\beta }_e =\left[ {0,\,1,\,0} \right] ^T,\nonumber \\&\quad \varvec{\gamma }_e =\left[ {0,\,0,\,1} \right] ^T. \end{aligned}$$

(22)

According to Eqs. (19) and (20), at this relative equilibrium we have

$$\begin{aligned} \varvec{\Pi }_e&= \left[ {0,\,0,\,\omega _T I_{zz} } \right] ^T,\end{aligned}$$

(23)

$$\begin{aligned} \varvec{P}_e&= \left[ {0,\,m\omega _T R_e ,\,0} \right] ^T. \end{aligned}$$

(24)

Fig. 2

A classical relative equilibrium of the spacecraft

The balance equation of the gravitational force Eq. (21) can be satisfied, with the radius of the orbit $R_{e}$ determined by

$$\begin{aligned} \omega _T^2 R_e \!=\!\frac{\mu }{R_e^2 }\!-\!\frac{3\mu }{2R_e^4 }\left\{ {2\frac{I_{xx} }{m}\!-\!\frac{I_{yy} }{m}\!-\!\frac{I_{zz} }{m}+\tau _0 -6\tau _2 } \!\right\} \!,\nonumber \\ \end{aligned}$$

(25)

which can be obtained through Eqs. (18) and (21). According to Eq. (25), the orbital motion of the spacecraft is affected by its moments of inertia. This effect can be considered equivalently as a change of the oblateness and ellipticity of the asteroid from the viewpoint of the point mass orbital model. This is the consequence of the mutual coupling between the orbital and rotational motions. Notice that in the case of $I_{xx}$ = $I_{yy}$ = $I_{zz}$, i.e., the mass distribution of the spacecraft is a homogeneous sphere under the second-order approximation, the effects of the moments of inertia in the orbital motion are vanished. This is consistent with the physical origin of the gravitational orbit–attitude coupling. If the gravitational orbit–attitude coupling is ignored, Eq. (25) is reduced to the classical result by Hu [19] on the stationary orbit of a point mass in a second-degree and order gravity field.

The Eqs. (17b–17d) can also been satisfied by

$$\begin{aligned}&\mu _1 =-\frac{6\mu m\tau _2 }{R_e^3 },\,\mu _2 =0,\,\mu _3 =-\omega _T^2 I_{zz} -m\omega _T^2 R_e^2 ,\nonumber \\&\quad \mu _4 =\mu _5 =\mu _6 =0. \end{aligned}$$

(26)

Then, the classical kind of relative equilibria are described by Eqs. (22–26).

4 Nonlinear stability of the relative equilibria

In this section, we will investigate the nonlinear stability of the relative equilibria obtained above using the modified energy-Casimir method provided by the geometric mechanics adopted by Beck and Hall [7] and Hall [17].

4.1 Nonlinear stability

The energy-Casimir method, which is the generalization of the Lagrange–Dirichlet criterion in the canonical Hamiltonian system, is a powerful tool provided by the geometric mechanics for determining the nonlinear stability of the relative equilibria in a non-canonical Hamiltonian system [28]. It is worth mentioning that a modified energy-Casimir method was adopted by Beck and Hall [7], and Hall [17] in the studies of the attitude stability of a rigid spacecraft on a circular orbit in a central gravitational field. This method was also discussed in the Appendix C of Wang et al. [56], where it was called Lagrange multiplier approach. This modified method, in which the stability problem is considered as a constrained variational problem, is more convenient for practical applications than the original energy-Casimir method, since there is no requirement to choose a particular Casimir function [56].

According to the Lagrange–Dirichlet criterion in the canonical Hamiltonian system, the nonlinear stability of the equilibrium point is determined by the distributions of the eigenvalues of the Hessian matrix of the Hamiltonian [28]. If all the eigenvalues of the Hessian matrix of the Hamiltonian are positive or negative, that is the Hessian matrix of the Hamiltonian is positive- or negative-definite, then the equilibrium point is nonlinear stable. This follows from the conservation of energy and the fact that the level sets of the Hamiltonian near the equilibrium point are approximately ellipsoids.

However, the Hamiltonian system we considered here is non-canonical, and the phase flow of the system is constrained on the twelve-dimensional invariant manifold or symplectic leaf $\Sigma$ by the Casimir functions. Therefore, rather than considering general perturbations in the whole phase space as in the Lagrange-Dirichlet criterion in the canonical Hamiltonian system, we need to restrict the consideration to perturbations on $\left. {T\Sigma } \right| _{\varvec{z}_e}$, the tangent space to the invariant manifold $\Sigma$ at the relative equilibria $\varvec{z}_e$, i.e., the range space the Poisson tensor $\varvec{B}(\varvec{z})$ at the relative equilibria $z_e$, denoted by $\text{ R }( {\varvec{B}(\varvec{z}_e)})$. This is the basic principle of the energy-Casimir method that the Hessian matrix needs to be considered restrictedly on the invariant manifold $\Sigma$ of the system. This restriction is constituted through the projected Hessian matrix of the variational Lagrangian $F(\varvec{z})$ in Beck and Hall [7], and Hall [17].

According to the modified energy-Casimir method adopted by Beck and Hall [7], and Hall [17], the conditions of nonlinear stability of the relative equilibria $\varvec{z}_e$ can be obtained through the distributions of the eigenvalues of the projected Hessian matrix of the variational Lagrangian $F(\varvec{z})$. The projected Hessian matrix of the variational Lagrangian $F(\varvec{z})$ has the same number of zero eigenvalues as the linearly independent Casimir functions of the system, which are associated with the nullspace $\text{ N }\left[ {\varvec{B}(\varvec{z}_e)} \right]$, i.e., the complement space of the tangent space to the invariant manifold at the relative equilibria $\varvec{z}_e$. The remaining eigenvalues of the projected Hessian matrix are associated with the tangent space to the invariant manifold $\left. {T\Sigma } \right| _{\varvec{z}_e }$, and if they are all positive, then the relative equilibria $\varvec{z}_e$ is a constrained minimum on the invariant manifold $\Sigma$ and therefore it is nonlinear stable.

According to Beck and Hall [7], the projected Hessian matrix is given by $\varvec{P}( {\varvec{z}_e })\nabla ^{2} F({\varvec{z}_e })\varvec{P}({\varvec{z}_e})$, where the projection operator is given by

$$\begin{aligned}&\varvec{P}\left( {\varvec{z}_{e} } \right) = {\mathbf {I}}_{{18 \times 18}} - \varvec{K}(\varvec{z}_{e} )\left( {\varvec{K}(\varvec{z}_{e} )^{T} \varvec{K}(\varvec{z}_{e} )} \right) ^{{ - 1}} \varvec{K}(\varvec{z}_{e} )^{T}\end{aligned}$$

(27)

$$\begin{aligned}&\varvec{K}(\varvec{z}_{e} ) \!=\! \left[ {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \left. {\nabla _{\varvec{z}} C_{1} \left( \varvec{z} \right) } \right| _{e} &{} \cdots &{} \left. {\nabla _{\varvec{z}} C_{i} \left( \varvec{z} \right) } \right| _{e} &{} \cdots &{} \left. {\nabla _{\varvec{z}} C_{6} \left( \varvec{z} \right) } \right| _{e}\\ \end{array} } \right] \nonumber \\&\quad =\left[ {\begin{array}{llllll} {\mathbf {0}} &{} {\mathbf {0}} &{}{\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\varvec{\alpha }_{e} } &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\varvec{\beta }_{e} } &{} {\varvec{\gamma }_{e} } &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\varvec{\beta }_{e} } &{} {\mathbf {0}} &{} {\varvec{\alpha }_{e} } &{} {\mathbf {0}} &{} {\varvec{\gamma }_{e} } \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\varvec{\gamma }_{e} } &{} {\mathbf {0}} &{} {\varvec{\alpha }_{e} } &{} {\varvec{\beta }_{e} } \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} \\ \end{array} } \right] \end{aligned}$$

(28)

By using the formulation of the second-order approximation of the gravitational potential Eq. (13), the Hessian of the variational Lagrangian $\nabla ^2F( z)$ is calculated as

$$\begin{aligned}&\nabla ^{2} F\left( \varvec{z} \right) \nonumber \\&\quad =\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\varvec{I}^{{ - 1}} } &{} {\mathbf {0}} &{} {\mathbf {0}} &{} { - \omega _{T} {\mathbf {I}}_{{3 \times 3}} } \\ {\mathbf {0}} &{} { - \frac{{6\mu m\tau _{2} }}{{R^{5}}}\varvec{RR}^{T} - \mu _{1} {\mathbf {I}}_{{3 \times 3}} } &{} { - \mu _{4} {\mathbf {I}}_{{3 \times 3}} } &{} { - \mu _{5} {\mathbf {I}}_{{3 \times 3}} } \\ {\mathbf {0}} &{} { - \mu _{4}{\mathbf {I}}_{{3 \times 3}} } &{} {\frac{{6\mu m\tau _{2} }}{{R^{5} }}\varvec{RR}^{T} - \mu _{2} {\mathbf {I}}_{{3 \times 3}} } &{} { - \mu _{6} {\mathbf {I}}_{{3 \times 3}} }\\ { - \omega _{T} {\mathbf {I}}_{{3 \times 3}} } &{} { - \mu _{5} {\mathbf {I}}_{{3 \times 3}} } &{} { - \mu _{6} {\mathbf {I}}_{{3 \times 3}} } &{} { - \frac{{3\mu m\tau _{0} }}{{R^{5}}}\varvec{RR}^{T} - \mu _{3} {\mathbf {I}}_{{3 \times 3}} } \\ {\mathbf {0}} &{} {\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}}} &{} {\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}}} &{} {\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}} - \omega _{T} \varvec{\hat{P}}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\omega _{T} \varvec{\hat{R}}} \\ \end{array} \right. \nonumber \\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \begin{array}{l@{\quad }l} {\mathbf {0}} &{} {\mathbf {0}} \\ {\left( {\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}}} \right) ^{T} } &{} {\mathbf {0}}\\ {\left( {\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}}} \right) ^{T} } &{} {\mathbf {0}} \\ {\left( {\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}}} \right) ^{T} + \omega _{T}\varvec{\hat{P}}} &{} { - \omega _{T} \varvec{\hat{R}}} \\ {\frac{{\partial ^{2} V}}{{\partial \varvec{R}^{2} }}} &{} {\omega _{T} \varvec{\hat{\gamma }}}\\ { - \omega _{T} \varvec{\hat{\gamma }}} &{}{\frac{1}{m}{\mathbf {I}}_{{3 \times 3}} } \\ \end{array} \right] \end{aligned}$$

(29)

The second-order partial derivates of the gravitational potential in Eq. (29) are obtained as follows:

$$\begin{aligned}&\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}} = \frac{\partial }{{\partial \varvec{\alpha }}}\left( {\frac{{\partial V}}{{\partial \varvec{R}}}} \right) =- \frac{{6\mu m\tau _{2} }}{{R^{4} }}\nonumber \\&\quad \times \left[ {\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) {\mathbf {I}}_{{3 \times 3}} + \varvec{\alpha \bar{R}}^{T} - 5\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) \varvec{\bar{R}\bar{R}}^{T} } \right] ,\end{aligned}$$

(30)

$$\begin{aligned}&\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}} = \frac{\partial }{{\partial \varvec{\beta }}}\left( {\frac{{\partial V}}{{\partial \varvec{R}}}} \right) =\frac{{6\mu m\tau _{2} }}{{R^{4} }}\nonumber \\&\quad \times \left[ {\left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) {\mathbf {I}}_{{3 \times 3}} + \varvec{\beta }\varvec{\bar{R}}^{T} - 5\left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) \varvec{\bar{R}\bar{R}}^{T} } \right] ,\end{aligned}$$

(31)

$$\begin{aligned}&\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}} = \frac{\partial }{{\partial \varvec{\gamma }}}\left( {\frac{{\partial V}}{{\partial \varvec{R}}}} \right) =- \frac{{3\mu m\tau _{0} }}{{R^{4} }} \nonumber \\&\quad \times \left[ {\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) {\mathbf {I}}_{{3 \times 3}} + \varvec{\gamma }\varvec{\bar{R}}^{T} - 5\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) \varvec{\bar{R}\bar{R}}^{T} } \right] ,\end{aligned}$$

(32)

$$\begin{aligned}&\frac{{\partial ^{2} V}}{{\partial \varvec{R}^{2} }} = \frac{{\mu m}}{{R^{3} }}\left( {{\mathbf {I}}_{{3 \times 3}} - 3\varvec{\bar{R}\bar{R}}^{T} } \right) \nonumber \\&\quad + \frac{{3\mu }}{{R^{5} }}\left\{ \begin{array}{l} \left[ {tr\left( \varvec{I} \right) - \tau _{0} m} \right] \varvec{\bar{R}\bar{R}}^{T}\\ \quad + \varvec{I} - \tau _{0} m\varvec{\gamma \gamma }^{T} - 2\tau _{2} m\left( {\varvec{\alpha \alpha }^{T} - \varvec{\beta \beta }^{T} } \right) \\ \end{array} \right\} \nonumber \\&\quad + \frac{{3\mu }}{{2R^{5} }}\left\{ \begin{array}{l} 5\varvec{\bar{R}}^{T} \varvec{I\bar{R}} - tr\left( \varvec{I} \right) + \tau _{0} m\left( {1 - 5\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) ^{2} } \right) \\ \quad - 10\tau _{2} m\left( {\left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) ^{2} - \left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) ^{2} } \right) \\ \end{array} \right\} \nonumber \\&\quad \times \left\{ {7\varvec{\bar{R}\bar{R}}^{T} - {\mathbf {I}}_{{3 \times 3}} } \right\} \nonumber \\&\quad + \frac{{15\mu }}{{R^{5} }}\left\{ \! \begin{array}{l} - \varvec{I\bar{R}\bar{R}}^{T} \!-\! \varvec{\bar{R}\bar{R}}^{T} \varvec{I} \!+\! \tau _{0} m\left( {\varvec{\gamma } \cdot \varvec{\bar{R}}} \right) \left( {\varvec{\gamma \bar{R}}^{T} \!+ \!\varvec{\bar{R}\gamma }^{T} } \right) \\ \quad + 2\tau _{2} m\left[ \begin{array}{l} \left( {\varvec{\alpha } \cdot \varvec{\bar{R}}} \right) \left( {\varvec{\alpha \bar{R}}^{T} + \varvec{\bar{R}\alpha }^{T} } \right) \\ - \left( {\varvec{\beta } \cdot \varvec{\bar{R}}} \right) \left( {\varvec{\beta \bar{R}}^{T} + \varvec{\bar{R}\beta }^{T} } \right) \\ \end{array} \right] \\ \end{array} \right\} .\nonumber \\ \end{aligned}$$

(33)

As described by Eqs. (22)-(26), at the relative equilibria $\varvec{z}_e$, we have $\varvec{\bar{R}}_{e} = \varvec{\alpha }_{e} = \left[ {1,\,0,\,0} \right] ^{T} ,\,\varvec{\beta }_{e} = \left[ {0,\,1,\,0} \right] ^{T} ,\,\varvec{\gamma }_{e} = \left[ {0,\,0,\,1} \right] ^{T} ,\,\varvec{\Pi }_{e} = \left[ {0,\,0,\,\omega _{T} I_{{zz}} } \right] ^{T} ,\varvec{P}_{e} = \left[ {0,\,m\omega _{T} R_{e} ,\,0} \right] ^{T} ,\,\omega _{T}^{2} R_{e} \!=\! \frac{\mu }{{R_{e}^{2} }} \!-\! \frac{{3\mu }}{{2R_{e}^{4} }}\left\{ 2\frac{{I_{{xx}} }}{m} \!-\! \frac{{I_{{yy}} }}{m}\right. \left. - \frac{{I_{{zz}} }}{m} + \tau _{0} - 6\tau _{2} \right\} ,\,\mu _{1} = - \frac{{6\mu m\tau _{2} }}{{R_{e}^{3} }}$, $\mu _{3} =-\omega _{T}^{2}I_{zz} -m\omega _{T}^{2}R_{e}^{2}$, and $\mu _{2}=\mu _{4}=\mu _{5}=\mu _{6}$ = 0. Then the Hessian $\nabla ^2F( {\varvec{z}_e })$ at the relative equilibria $z_e$ is:

$$\begin{aligned}&\nabla ^{2} F\left( {\varvec{z}_{e} } \right) \nonumber \\&\quad =\left[ {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\varvec{I}^{{ - 1}} } &{} {\mathbf {0}} &{} {\mathbf {0}} &{} { - \omega _{T} {\mathbf {I}}_{{3 \times 3}} } \\ {\mathbf {0}} &{} {\frac{{6\mu m\tau _{2} }}{{R_{e}^{3} }}\left( {{\mathbf {I}}_{{3 \times 3}} - \varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} } \right) } &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\frac{{6\mu m\tau _{2} }}{{R_{e}^{3} }}\varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} } &{} {\mathbf {0}} \\ { - \omega _{T} {\mathbf {I}}_{{3 \times 3}} } &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\omega _{T}^{2} \left( {I_{{zz}} + mR_{e}^{2} } \right) {\mathbf {I}}_{{3 \times 3}} - \frac{{3\mu m\tau _{0} }}{{R_{e}^{3} }}\varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} } \\ {\mathbf {0}} &{} {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}}} \right| _{e} } &{} {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}}} \right| _{e} } &{} {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}}} \right| _{e} - \omega _{T}^{2} mR_{e} \varvec{\hat{\beta }}_{e} } \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}} &{} {\omega _{T} R_{e} \varvec{\hat{\alpha }}_{e} } \\ \end{array}} \right. \nonumber \\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\begin{array}{l@{\quad }l} {\mathbf {0}} &{} {\mathbf {0}} \\ {\left( {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}}} \right| _{e} } \right) ^{T} } &{} {\mathbf {0}} \\ {\left( {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}}} \right| _{e} } \right) ^{T} } &{} {\mathbf {0}}\\ {\left( {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}}} \right| _{e} } \right) ^{T} + \omega _{T}^{2} mR_{e} \varvec{\hat{\beta }}_{e} } &{} { - \omega _{T} R_{e} \varvec{\hat{\alpha }}_{e} } \\ {\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{R}^{2} }}} \right| _{e} } &{} {\omega _{T} \varvec{\hat{\gamma }}_{e} } \\ { - \omega _{T} \varvec{\hat{\gamma }}_{e} } &{} {\frac{1}{m}{\mathbf {I}}_{{3 \times 3}} } \\ \end{array} } \right] \end{aligned}$$

(34)

The second-order partial derivates of the gravitational potential in Eq. (34) at the relative equilibria $\varvec{z}_e$ are obtained through Eqs. (30–33) as follows:

$$\begin{aligned}&\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\alpha }\partial \varvec{R}}}} \right| _{e} = - \frac{{6\mu m\tau _{2} }}{{R_{e}^{4} }}\left[ {{\mathbf {I}}_{{3 \times 3}} - 4\varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} } \right] ,\end{aligned}$$

(35)

$$\begin{aligned}&\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\beta }\partial \varvec{R}}}} \right| _{e} = \frac{{6\mu m\tau _{2} }}{{R_{e}^{4} }}\varvec{\beta }_{e} \varvec{\alpha }_{e}^{T},\end{aligned}$$

(36)

$$\begin{aligned}&\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{\gamma }\partial \varvec{R}}}} \right| _{e} = - \frac{{3\mu m\tau _{0} }}{{R_{e}^{4} }}\varvec{\gamma }_{e} \varvec{\alpha }_{e}^{T} ,\end{aligned}$$

(37)

$$\begin{aligned}&\left. {\frac{{\partial ^{2} V}}{{\partial \varvec{R}^{2} }}} \right| _{e} = \frac{{\mu m}}{{R_{e}^{3} }}\left( {{\mathbf {I}}_{{3 \times 3}} - 3\varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} } \right) \nonumber \\&+\frac{{3\mu }}{{2R_{e}^{5} }}\left\{ \! \begin{array}{l} \left[ {15I_{{xx}} - 5tr\left( \varvec{I} \right) \!+ \!5\tau _{0} m \!-\! 34\tau _{2} m} \right] \varvec{\alpha }_{e} \varvec{\alpha }_{e}^{T} \\ \quad + 4\tau _{2} m\varvec{\beta }_{e} \varvec{\beta }_{e}^{T}\\ - 2\tau _{0} m\varvec{\gamma }_{e} \varvec{\gamma }_{e}^{T} \!+\! 2\varvec{I} \!-\! \left[ 5I_{{xx}} \!-\! tr\left( \varvec{I} \right) \!+\! \tau _{0} m\right. \\ \quad -\left. 10\tau _{2} m \right] {\mathbf {I}}_{{3 \times 3}}\\ \end{array}\! \right\} \!.\nonumber \\ \end{aligned}$$

(38)

In Eqs. (34–38), we have

$$\begin{aligned} \varvec{\hat{\alpha }}_e&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {-1} \\ 0 &{} 1 &{} 0 \\ \end{array}}} \right] ,\,\varvec{\hat{\beta }}_e =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ {-1} &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\nonumber \\ \varvec{\hat{\gamma }}_e&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} {-1} &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\varvec{\alpha }_e \varvec{\alpha }_e^T =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\end{aligned}$$

(39)

$$\begin{aligned} \varvec{\beta }_e \varvec{\beta }_e^T&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\varvec{\gamma }_e \varvec{\gamma }_e^T =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} }} \right] ,\,\nonumber \\ \varvec{\beta }_e \varvec{\alpha }_e^T&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\varvec{\gamma }_e \varvec{\alpha }_e^T =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \\ \end{array} }} \right] . \end{aligned}$$

(40)

As stated above, the nonlinear stability of the relative equilibria $\varvec{z}_e$ depends on the eigenvalues of the projected Hessian matrix of the variational Lagrangian $F(\varvec{z})$. The characteristic polynomial of the projected Hessian matrix $\varvec{P}( {\varvec{z}_e })\nabla ^2 F( {\varvec{z}_e })\varvec{P}( {\varvec{z}_e })$ can be calculated by

$$\begin{aligned} P(s)=\det \left[ {s{\varvec{I}}_{18\times 18} -\varvec{P}( {\varvec{z}_e })\nabla ^2 F( {\varvec{z}_e })\varvec{P}( {\varvec{z}_e })} \right] . \end{aligned}$$

(41)

The eigenvalues of the projected Hessian matrix are roots of the characteristic equation, which is given by

$$\begin{aligned} \det \left[ {s\varvec{I}}_{18\times 18} -\varvec{P}( {\varvec{z}_e })\nabla ^2 F( {\varvec{z}_e })\varvec{P}( {\varvec{z}_e }) \right] =0.\nonumber \\ \end{aligned}$$

(42)

With the help of symbolic calculation in Matlab, the characteristic equation of Eq. (42) can be obtained with the following form:

$$\begin{aligned} \begin{aligned}&s^6(I_{zz} s-1)(mR_e^5 s^2+A_1 s+A_0 )\\&\quad (2mR_e^8 s^3+B_2 s^2+B_1 s+B_0 ) \\&(4I_{xx} R_e^8 s^3+C_2 s^2+C_1 s+C_0 )\\&\quad (2mI_{yy} s^3+D_2 s^2+D_1 s+D_0 )=0.\\ \end{aligned} \end{aligned}$$

(43)

The coefficients $A_{1}$, $A_{0}$, $B_{2}$, $B_{1}$, $B_{0}$, $C_{2}$, $C_{1}$, $C_{0}\,D_{2}$, $D_{1}$ and $D_{0}$ are functions of the parameters of the system: $\mu$, $R_{e}$, $\omega _{T}$, $\tau _{0}$, $\tau _{2}$, $m$, $I_{xx}$, $I_{yy}$ and $I_{zz}$. The explicit formulations of these coefficients are given in Appendix.

Notice that in our problem there are six linearly independent Casimir functions, then as shown by Eq. (43), the projected Hessian matrix have six zero eigenvalues associated with the six-dimensional complement space of the tangent space to the invariant manifold at the relative equilibria $\varvec{z}_e$. The remaining twelve eigenvalues are associated with the twelve-dimensional tangent space $\left. {T\Sigma } \right| _{\varvec{z}_e}$ to the invariant manifold, and if they are all positive, then the relative equilibria $\varvec{z}_e$ is a constrained minimum on the invariant manifold $\Sigma$, therefore it is nonlinear stable.

Since the projected Hessian matrix is symmetrical, the eigenvalues are guaranteed to be real by the coefficients of the polynomials in Eq. (43) intrinsically. Therefore, in the conditions of nonlinear stability of the relative equilibria, it is only needed to guarantee that the roots of the polynomial equations in Eq. (43) are positive.

According to the theory of the distribution of the roots of the polynomial equation, notice that $I_{zz}$ $>$ 0 is always satisfied, that the remaining twelve eigenvalues in Eq. (43) are positive is equivalent to

$$\begin{aligned} \begin{array}{c} A_1 <0,\,A_0 >0, \\ B_2 <0,\,B_1 >0,\,B_0 <0, \\ C_2 <0,\,C_1 >0,\,C_0 <0, \\ D_2 <0,\,D_1 >0,\,D_0 <0. \\ \end{array} \end{aligned}$$

(44)

We have given the conditions of the nonlinear stability of the relative equilibria in Eq. (44). Given the parameters of the system, we can determine whether the relative equilibria are nonlinear stable using the stable criterion in Eq. (44).

4.2 Case studies

However, the expressions of the coefficients $A_{1}$, $A_{0}$, $B_{2}$, $B_{1}$, $B_{0}$, $C_{2}$, $C_{1}$, $C_{0}\,D_{2}$, $D_{1}$ and $D_{0}$ in terms of the parameters of the system are tedious, because there are large amount of parameters in the system and the considered problem is a very high-dimensional system, the invariant manifold of which is twelve-dimensional. It is difficult to get general conditions of nonlinear stability through Eq. (44) in terms of the parameters of the system $\mu$, $R_{e}$, $\omega _{T}$, $\tau _{0}$, $\tau _{2}$, $m$, $I_{xx}$, $I_{yy}$ and $I_{zz}$.

Therefore, we will consider an example asteroid $P$, which has same mass, mean radius, and rotational velocity $\omega _{T}$ as the asteroid 4769 Castalia in Scheeres et al. [41], but has different parameters for the oblateness $\tau _{0}$ and ellipticity $\tau _{2}$. The parameters of the asteroid $P$ are as follows: $M=1.4091\times 10^{12}\,$kg, $\tau _{0}=-2.9485\times 10^{4}\,$ m$^{2}$, $\tau _{2}=-2.7954\times 10^{4}\,$ m$^{2}$ and $\omega _{T}=4.2883\times 10^{-4}\,$ s$^{-1}$ with the uniform rotational period equal to 4.07 h. Notice that the ellipticity $\tau _{2}$ is negative, and then the spacecraft is located on the intermediate-moment principal axis of the asteroid, i.e., the shorter-axis of the equatorial plane.

The nonlinear stability criterion in Eq. (44) can be determined by three mass distribution parameters of the spacecraft: $I_{xx}/m$, $I_{yy}/I_{xx}$, and $I_{zz}/I_{xx}$. The ratio $I_{xx}/m$ describes the characteristic dimension of the spacecraft; the ratios $I_{yy}/I_{xx}$ and $I_{zz}/I_{xx}$ describe the shape of the spacecraft to the second-order.

Next we will determine the nonlinear stability by Eq. (44) in a wide range of the three parameters of the spacecraft: $I_{xx}/m$, $I_{yy}/I_{xx}$, and $I_{zz}/I_{xx}$. Six different values of the parameter $I_{xx}/m$ are considered as follows:

$$\begin{aligned} \frac{I_{xx} }{m}=2,\,\,10,\,\,100,\,\,500,\,\,800,\,\,1250, \end{aligned}$$

(45)

which have covered spacecraft with the characteristic dimension order of 1–100 m.

In the case of each value of $I_{xx}/m$, the parameters $\sigma _{y}$ and $\sigma _{x}$ are considered in the following range

$$\begin{aligned} -1\le \sigma _y \le 1,\,-1\le \sigma _x \le 1, \end{aligned}$$

(46)

where $\sigma _{y}$ and $\sigma _{x}$ are defined as

$$\begin{aligned} \sigma _y =\left( {\frac{I_{zz} -I_{xx} }{I_{yy} }}\right) ,\,\sigma _x =\left( {\frac{I_{zz} -I_{yy} }{I_{xx} }}\right) . \end{aligned}$$

(47)

The range in Eq. (46) has covered all the possible mass distributions of the spacecraft to the second order.

For given mass distribution parameters of the spacecraft, the orbit radius $R_{e}$ at the relative equilibria can be calculated by Eq. (25). Then with all the parameters of the system known, i.e., $\mu$, $\omega _{T}$, $R_{e}$, $\tau _{0}$, $\tau _{2}$, $m$, $I_{xx}$, $I_{yy}$ and $I_{zz}$, the nonlinear stability criterion in Eq. (44) can be calculated.

We calculate the nonlinear stability criterion in Eq. (44) for spacecraft within the above range of the mass distribution parameters given by Eqs. (45) and (46). We try to plot the points, which correspond to the mass distribution parameters guaranteeing the nonlinear stability, on the $\sigma _{y}-\sigma _{x}$ plane in the six cases of different values of $I_{xx}/m$. Unfortunately, it is found that with any value of $I_{xx}/m$, no mass distribution parameters in Eq. (46) can guarantee that the nonlinear stability criterion in Eq. (44) is satisfied, i.e., that all the remaining twelve eigenvalues in Eq. (43) are positive.

Then, different example asteroids with a wide range of the parameters $\omega _{T}$, $\tau _{0}$, and $\tau _{2}$ are considered, and the nonlinear stability criterion in Eq. (44) is calculated. However, it is found that the criterion in Eq. (44) cannot be satisfied by the spacecraft with any mass distribution parameters in the case of any example asteroid.

4.3 Some discussions on the nonlinear stability condition

It is worth our special attention that the nonlinear stability condition that the relative equilibria $\varvec{z}_e$ is a constrained minimum on the invariant manifold $\Sigma$, i.e., all the remaining twelve eigenvalues in Eq. (43) are positive, is actually the definition of the formal stability of the relative equilibria. For a finite-dimensional system, the formal stability implies nonlinear stability, but the inverse is not true. That is to say, the nonlinear stability condition we obtained by the energy-Casimir method in this paper is only the sufficient condition, but not the necessary condition, for the nonlinear stability of the relative equilibria.

Therefore, the fact that the nonlinear stability criterion in Eq. (44) cannot be satisfied does not imply that the relative equilibria are always nonlinear unstable. Indeed, it means that the energy-Casimir method we adopted in this paper cannot provide any information about the nonlinear stability of the relative equilibria, and other more powerful tools are needed for a further investigation.

For a canonical Hamiltonian system, when the quadratic part of the Hamiltonian, i.e., the Hessian of the Hamiltonian, is not sign definite, the Lagrange–Dirichlet criterion is not applicable anymore. For the system with two degrees of freedom, the Arnold’s theorem can be used in the case of nonresonance, and in the case of the resonances other methods by Markeev [27], Cabral and Meyer [12] and Elipe et al. [13–15] should be adopted. However, in our problem, a non-canonical Hamiltonian system with six degrees of freedom is dealt with. These existing methods mentioned above are not applicable in our problem, and a new method needs to be adopted.

5 Conclusions

The nonlinear stability of the relative equilibria of the full dynamics of a rigid spacecraft around a uniformly rotating asteroid has been studied with the method of geometric mechanics. Unlike the traditional spacecraft dynamics, in the full dynamics the spacecraft is considered as a rigid body and the orbital and attitude motions of the spacecraft are modeled in a unified approach, i.e., the gravitational orbit–attitude coupling is taken into account.

Based on the non-canonical Hamiltonian structure and a classical kind of relative equilibria of the problem, we have investigated the nonlinear stability of the relative equilibria using the energy-Casimir method provided by geometric mechanics. The nonlinear stability criterion of the relative equilibria has been given through the semi-positive definiteness of the projected Hessian matrix of the variational Lagrangian.

Finally, example asteroids with a wide range of parameters were considered, and nonlinear stability criterion was calculated. However, it was found that the nonlinear stability condition cannot be satisfied by the spacecraft with any mass distribution parameters. Notice that the nonlinear stability condition that the relative equilibrium is a constrained minimum on the invariant manifold is actually the definition of the formal stability, and it is only the sufficient condition, but not the necessary condition, for the nonlinear stability of the relative equilibria. Therefore, the fact that the nonlinear stability condition cannot be satisfied does not imply that the relative equilibria are always nonlinear unstable. It means that the energy-Casimir method adopted by us in this paper cannot provide any information about the nonlinear stability of the relative equilibria, and more powerful tools, which are the analogues of the Arnold’s theorem in the canonical Hamiltonian system with two degrees of freedom, are needed for a further investigation.

Appendix: Formulations of coefficients in characteristic equation

The explicit formulations of the coefficients in Eq. (43) are given as follows:

$$\begin{aligned}&A_{1} = 36\,\tau _{2} \,m^{2} \mu - 6\,\tau _{0} \,m^{2} \mu + 2\,R_{e}^{2} m^{2} \mu \nonumber \\&\quad +\,6\,m\mu \,I_{{yy}} - 12\,I_{{xx}} \,m\mu + 6\,m\mu I_{{zz}} - R_{e}^{5}.\end{aligned}$$

(48)

$$\begin{aligned}&A_{0} = 6\,\mu \,m\tau _{0} - 2\,R_{e}^{2} m\mu - 36\,\mu \,m\tau _{2} - \omega _{T}^{2} R_{e}^{5} m \nonumber \\&\quad -\,6\,\mu \,I_{{yy}} + 12\,I_{{xx}} \,\mu - 6\,\mu \,I_{{zz}}.\end{aligned}$$

(49)

$$\begin{aligned}&B_{2} = - 9mR_{e}^{3} \mu \,I_{{yy}} + 3\,m^{2} R_{e}^{3} \mu \,\tau _{0} - 3\,mR_{e}^{3} \mu \,I_{{zz}} \nonumber \\&\quad -\, 42\,m^{2} R_{e}^{3} \mu \,\tau _{2} - 2\,m^{2} R_{e}^{5} \mu - 12\,m^{2} R_{e}^{5} \mu \,\tau _{2} \nonumber \\&\quad +\, 12\,mR_{e}^{3} I_{{xx}} \,\mu - 2\,R_{e} ^{8}. \end{aligned}$$

(50)

$$\begin{aligned}&B_{1} = - 72\,m^{2} \mu ^{2} \tau _{2} \,I_{{xx}} + 2\,\mu \,mR_{e}^{5} - 18\,m^{3} \mu ^{2} \tau _{2} \,\tau _{0}\nonumber \\&\quad -\, 3\,mR_{e}^{3} \mu \,\tau _{0} + 12\,\mu \,mR_{e}^{5} \tau _{2} + 12\,m^{3} \mu ^{2} \tau _{2} \,R_{e}^{2} \nonumber \\&\quad +\, 9\,R_{e}^{3} \mu \,I_{{yy}} + 54\,m^{2} \mu ^{2} \tau _{2} \,I_{{yy}} - 12\,R_{e}^{3} I_{{xx}} \,\mu \nonumber \\&\quad +\, 3\,R_{e}^{3} \mu \,I_{{zz}} + 18\,m^{2} \mu ^{2} \tau _{2} \,I_{{zz}} + 108\,m^{3} \mu ^{2} \tau _{2}^{2} \nonumber \\&\quad -\, 2\,m\omega _{T}^{2}R_{e}^{8} + 42\,mR_{e}^{3} \mu \,\tau _{2}. \end{aligned}$$

(51)

$$\begin{aligned}&B_{0} = - 18\,m\mu ^{2} \tau _{2} \,I_{{zz}} + 72\,mI_{{xx}} \,\mu ^{2} \tau _{2} - 12\,m^{2} R_{e}^{2} \mu ^{2} \tau _{2} \nonumber \\&\quad +\, 12\,m^{2} R_{e}^{5} \omega _{T}^{2} \tau _{2} \,\mu + 18\,m^{2} \mu ^{2} \tau _{2} \,\tau _{0} \nonumber \\&\quad -\, 108\,m^{2} \mu ^{2} \tau _{2}^{2} - 54\,m\mu ^{2} \tau _{2} \,I_{{yy}}. \end{aligned}$$

(52)

$$\begin{aligned}&C_2 =-2\,R_e^8 \omega _T^2 I_{xx} \,I_{zz} -4\,mR_e^5 I_{xx} \,\mu -4\,R_e^8\nonumber \\&\quad +\,24\,R_e^3 I_{xx}^2 \mu -6\,R_e^3 I_{xx} \,\mu \,I_{yy} -18\,R_e^3 I_{xx} \,\mu \,I_{zz} \nonumber \\&\quad -\,60\,mR_e^3 I_{xx} \,\mu \,\tau _2 -2\,m\omega _T^2 I_{xx} \,R_e^{10} +6\,mR_e^5 I_{xx} \,\mu \,\tau _0\nonumber \\&\quad -\,12\,mR_e^5 I_{xx} \,\mu \,\tau _2 +18\,mR_e^3 I_{xx} \,\mu \,\tau _0.\end{aligned}$$

(53)

$$\begin{aligned}&C_1 =-2\,R_e^8 \omega _T^2 I_{xx} +4\,\mu \,mR_e^5 +12\,\mu \,mR_e^5 \tau _2 -24\,R_e^3 I_{xx} \,\mu \nonumber \\&\quad +\,18\,R_e^3 \mu \,I_{zz} -9\,mR_e^3 I_{xx} \,\mu \,\omega _T^2 I_{zz} \,\tau _0 \nonumber \\&\quad -\,9\,mI_{xx} \,\mu ^2\tau _0 \,I_{yy} -72\,mI_{xx}^2 \mu ^2\tau _2 +11\,mR_e^5 I_{xx} \,\mu \,\omega _T^2 I_{zz} \nonumber \\&\quad +\,6\,m^2R_e^5 \omega _T^2 \tau _2 \,\mu \,I_{xx} +3\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{yy} \,I_{zz} \nonumber \\&\quad -\,6\,\mu \,mR_e^5 \tau _0 +3\,m^2R_e^5 \omega _T^2 \mu \,\tau _0 \,I_{xx} +2\,R_e^8 \omega _T^2 I_{zz} \nonumber \\&\quad +\,3\,mR_e^5 I_{xx} \,\mu \,\omega _T^2 I_{yy} +2\,m\omega _T^2 R_e^{10} +9\,R_e^3 I_{xx}\,\mu \,\omega _T^2 I_{zz}^2 \nonumber \\&\quad -\,2\,m^2\omega _T^4 I_{xx} \,R_e^{10} +2\,m^2I_{xx} \,\mu \,\omega _T^2 R_e^7 +18\,mI_{xx} \,\mu ^2\tau _2 \,I_{yy} \nonumber \\&\quad -\,72\,m^2\mu ^2\tau _2 \,\tau _0 \,I_{xx} -12\,R_e ^3I_{xx}^2 \mu \,\omega _T^2 I_{zz} \nonumber \\&\quad +\,108\,m^2I_{xx} \,\tau _2 ^2\mu ^2-6\,m^2R_e^2 I_{xx} \,\mu ^2\tau _0 +12\,m^2R_e^2 I_{xx}\,\mu ^2\tau _2 \nonumber \\&\quad -\,27\,mI_{xx} \,\mu ^2\tau _0 \,I_{zz} -12\,mR_e^5 I_{xx}^2 \mu \,\omega _T^2 \nonumber \\&\quad +\,9\,m^2\mu ^2\tau _0 ^2I_{xx} \!+\!54\,mI_{xx} \,\mu ^2\tau _2 \,I_{zz} \!+\!30\,mR_e^3 I_{xx} \,\mu \,\tau _2 \,\omega _T^2 I_{zz}\nonumber \\&\quad -\,18\,mR_e^3 \mu \,\tau _0 +36\,mI_{xx}^2 \mu ^2\tau _0 \nonumber \\&\quad +\,60\,mR_e^3 \mu \,\tau _2 +6\,R_e^3 \mu \,I_{yy}. \end{aligned}$$

(54)

$$\begin{aligned}&C_0 =-9\,m^2\mu ^2\tau _0^2 +2\,m^2\omega _T^4 R_e^{10} -11\,\mu \,mR_e^5 \omega _T^2 I_{zz} \nonumber \\&\quad -\,3\,\mu \,mR_e^5 \omega _T^2 I_{yy} +3\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{yy} +21\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{zz}\nonumber \\&\quad -\,3\,m^2R_e^5 \omega _T^2 \mu \,\tau _0 -3\,R_e^3 \mu \,\omega _T^2 I_{yy} \,I_{zz} +14\,\omega _T^2 R_e^5 mI_{xx} \,\mu \nonumber \\&\quad -\,6\,m^2R_e^5 \omega _T^2 \tau _2 \,\mu -9\,R_e^3 \mu \,\omega _T^2 I_{zz}^2\nonumber \\&\quad -\,18\,m\mu ^2\tau _2 \,I_{yy} +72\,mI_{xx} \,\tau _2 \,\mu ^2-36\,mI_{xx} \,\mu ^2\tau _0 \nonumber \\&\quad -\,54\,m\mu ^2\tau _2 \,I_{zz} +9\,m\mu ^2\tau _0 \,I_{yy} -108\,m^2\mu ^2\tau _2^2 \nonumber \\&\quad -\,2\,m^2\mu \,\omega _T^2 R_e^7 -12\,R_e ^3\omega _T^2 I_{xx}^2 \mu +72\,m^2\mu ^2\tau _2 \,\tau _0 \nonumber \\&\quad +\,6\,m^2R_e^2 \mu ^2\tau _0 -12\,m^2R_e^2 \mu ^2\tau _2 +27\,m\mu ^2\tau _0 \,I_{zz} \nonumber \\&\quad +\,9\,mR_e^3 \mu \,\omega _T^2 I_{zz} \,\tau _0 -9\,mR_e^3 \omega _T^2 I_{xx} \,\mu \,\tau _0 \nonumber \\&\quad -\,30\,mR_e^3 \mu \,\tau _2 \,\omega _T^2 I_{zz} +30\,mR_e^3 \omega _T^2 I_{xx} \,\tau _2 \,\mu . \end{aligned}$$

(55)

$$\begin{aligned}&D_2 =-2\,m-2\,I_{yy} -\omega _T^2 I_{yy} \,I_{zz} \,m-m^2\omega _T^2 I_{yy} \,R_e^2.\end{aligned}$$

(56)

$$\begin{aligned}&D_1 \!=\!2\!+\!\omega _T^2 I_{zz} \,m\!+\!m^2\omega _T^2 R_e^2 \!+\!\omega _T^2 I_{yy} \,I_{zz} \!-\!\omega _T^2 I_{yy} \,m.\end{aligned}$$

(57)

$$\begin{aligned}&D_0 =-\omega _T^2 I_{zz} +\omega _T^2 I_{yy}. \end{aligned}$$

(58)