1 Introduction

The possibility cannot be discarded that the collapse of spherical distribution of matter to a point singularity may be avoided if the matter acquires large amounts of electric charge during the gravitational collapse or during an accretion process onto a compact object. The gravitational attraction is then balanced by electrostatic repulsion due to the same charge and by the pressure gradient (Bekenstein 1971). Hence the study of the gravitational behavior of stellar charged object has been remaining as one of the main interests to the researchers (de Felice et al. 1995; Ghezzi 2005).

The analysis and the determination of maximum mass of very compact astrophysical objects has been a key issue in relativistic astrophysics for the last few decades. There are several astrophysical objects as well as cosmological phases where one needs to consider equation of state (EOS) of matter involving energy densities of the order of 1015 g cm−3 or higher, exceeding the normal nuclear matter density. Recent observations show that the estimated mass and radius of several compact objects associated with X-ray pulsar Her X-1, X-ray burster 4U 1820-30, millisecond pulsar SAX J 1808.4-3658, X-ray sources 4U 1728-34 are not compatible with the standard neutron star models (Dey et al. 1998; Li et al. 1999, for a recent review see Weber 2005).

The maximum mass of strange star is almost the same but the radius is less than as that of neutron stars, with higher compactness parameter (Weber et al. 2012). Compact objects like neutron stars or strange stars may be classified on the basis of mass–radius (M–R) relation. The approximate (M–R) relations of strange stars follow M∝R 3 are in surprising contrast to that of neutron stars (M∝R −3), and strange stars can have much small radii.

The EOS of compact objects such as neutron/strange stars are not well understood at least near the core region. Apart from the differences in the EOS, an important distinction between quark stars and conventional neutron stars is that the quark stars are self-bound by the strong interaction, whereas neutron stars are bound by gravity. This allows a quark star to rotate faster than would be possible for a neutron star.

There are also striking differences between the surfaces of bare strange stars and that of normal matter neutron stars. The very properties of the quark surface, e.g., strong bounding of particles, abrupt density change from 4×1014 g cm−3 to ∼0 in ∼1 fm. Another distinction between a strange star and a normal neutron star is by the surface electric fields associated with it. Strange stars, if bare, possess ultra-strong electric fields on their surfaces, which, for ordinary strange matter, is around 1018 V/cm (Alcock et al. 1986) and 1020 V/cm for color superconducting strange matter (Usov 2004; Usov et al. 2005; Negreiros et al. 2010). The influence of energy densities of ultra-high electric fields on the bulk properties of compact stars was explored by Ray et al. (2003), Malheiro et al. (2004). Weber et al. (2007, 2009, 2010), Negreiros et al. (2009) also have shown that electric fields of this magnitude, generated by charge distributions located near the surfaces of strange quark stars, increase the stellar mass by up to 30 % depending on the strength of the electric field. In contrast to the strange star the surface electric field in the case of neutron star is absent. These features may allow one to observationally distinguish quark stars from neutron stars.

Due to the absence of reliable information about equation of state of matter content in the interior of such compact stars, insight into the structure can be obtained by reference to applicable analytic solutions to the equation of relativistic stellar structure (Lattimer and Prakash 2001).

Two traditional approaches usually followed to obtain a realistic charged stellar model. One can start with an explicit EOS and suitable form of electric charge distribution and then integrating the equation of hydrostatic equilibrium, also known charged generalization of Oppenheimer-Volkoff equation (Oppenheimer and Volkoff 1939; Bekenstein 1971) which is obtained by requiring the conservation of mass-energy, as that determines the global structure of electrically charged stars. The integration starts at the center of the star with a prescribed central pressure. The integrations are iterated until the pressure decreases to zero, indicating the surface of the star has been reached (Some recent studies include de Felice et al. 1995; Anninos and Rothman 2001; Ray et al. 2003; Siffert et al. 2007; Negreiros and Malheiro 2007; Negreiros et al. 2009). Such input equations of state do not normally allow for closed-form solutions.

In the second approach one can have insight into such structures by solving the Einstein’s gravitational field equations. Einstein-Maxwell equations represent an under-determined system of nonlinear ordinary differential equations of the second order. For the special case of a static isotropic perfect fluid, the field equations of Einstein’s theory can be reduced to a set of four coupled ordinary differential equations in five unknowns and arrive to exact solutions by making an ad hoc assumption for one of the metric functions or for the energy density. The EOS can be computed from the resulting metric. The first exact solutions of Einstein’s equation in this approach known to have astrophysical significance may have been discovered by Tolman (1939). Out of the different types of exact solutions obtained by Tolman, model V and VI are not considered physically viable, as they correspond to singular solutions (infinite values of central density and pressure). Except these models, all other solutions are known as regular solutions (finite and positive pressure and density at the origin). Models IV and VII are found physically viable in the study of compact astrophysical stellar objects. Out of numerous works done following Tolman’s approach some include Nduka (1976, 1978), Mak and Fung (1995), Patel et al. (1997), Harko and Mak (2000), Sharma et al. (2001), Gupta and Kumar (2005a, 2005b, 2005c), Hansraj and Maharaj (2006), Maharaj and Komathiraj (2007), Komathiraj and Maharaj (2007), Thirukkanesh and Maharaj (2009), Bijalwan (2012), Takisa and Maharaj (2013). As might be expected with Tolman’s method, unphysical pressure-density configurations are found more frequently than physical ones (Delgaty and Lake 1998).

In recent years, however, several authors follow an alternative approach to present analytical stellar models of electrically neutral/charged compact strange stars within the framework of linear equation of state (EOS) based on MIT bag model together with a particular choice of metric potentials (Mak and Harko 2004; Hansraj and Maharaj 2006; Sharma and Maharaj 2007; Esculpi and Alomá 2010; Takisa and Maharaj 2012; Maharaj and Takisa 2012; Kalam et al. 2013; Rahaman et al. 2012).

Some works also studied the viability of nonlinear EOS based on suitable geometry for the description in the interior 3-spaces of such compact star (Vaidya and Tikekar 1982; Tikekar 1990). This approach leads to physically viable and easily tractable models of superdense stars in equilibrium. Tikekar and Jotania (2005) have shown that the ansatz suggested by Tikekar and Thomas (1998) has these features and the general three-parameter solution based on it also leads to physically plausible relativistic models of strange stars. Several aspects of physical relevance and the maximum mass of class of compact star models, based on Vaidya–Tikekar ansatz, have been investigated by Sharma et al. (2006) (also see Jotania and Tikekar 2006 for the relevant references). The charged analogues of Vaidya–Tikekar models have been derived by Patel and Koppar (1987), Koppar et al. (1991). Astrophysical consequences of the charged analogues of Vaidya–Tikekar solutions in modeling electrically charged compact star have been discussed by Patel and Pandya (1986), Gupta and Kumar (2011), Bijalwan and Gupta (2011), Chattopadhyay et al. (2012).

The known analytic solutions of Einstein’s gravitational field equations fall into two classes. The first class describes “normal” matter neutron stars for which density vanishes at the surface where the pressure vanishes. The Tolman VII solution with vanishing surface energy density falls into this class and hence is useful approximation to realistic neutron star models. And the class that describes stars for which density is finite, about 2–3 times the normal nuclear matter saturation density, at the surface where the pressure vanishes includes Tolman IV solution. This type of solutions is useful approximation to realistic models of “self-bound” strange quark star (Lattimer 2004).

In some recent studies (see Fatema and Murad 2013; Murad and Fatema 2013, hereafter paper I & II, for references) the ansatz for the metric function

$$ e^{\nu(r)} = B_{N}\bigl(1 + Cr^{2} \bigr)^{N} $$
(1.1)

where N is a positive integer and B N is a constant, known as Generalized Tolman IV solution, are found useful to construct stellar models of second class. The solutions corresponding to different values of N represent the charged analogues of Generalized Tolman IV model (for instance, see Table 1 of paper II for references).

The principal motivation of this work is to develop some new analytical relativistic stellar models by obtaining closed-form solutions of Einstein-Maxwell field equations with the help of Eq. (1.1) as a continuation of (paper I & II). The solutions obtained in this work are expected to provide simplified but easy to mathematically analyzed charged stellar models with nonzero high surface density which could reasonably model electrically charged strange quark stars, by satisfying applicable physical boundary conditions.

2 New interior solutions

2.1 Einstein–Maxwell field equations

As in paper I and II we consider a static, spherically symmetric stellar object whose interior metric is given in Schwarzschild coordinates x μ=(t,r,θ,ϕ)Footnote 1

$$ ds^{2} = e^{\nu(r)}dt^{2} - e^{\lambda(r)}dr^{2} - r^{2}\bigl(d\theta ^{2} + \sin^{2}\theta d\phi^{2}\bigr) $$
(2.1)

With the help of the following transformation x=Cr 2 and Eq. (1.1), the equation of “pressure isotropy” yields the following solution (paper I),

$$\begin{aligned} e^{ - \lambda}& = \frac{x}{ ( 1 + x )^{N - 2} [ 1 + (1 + N)x ]^{\frac{2}{1 + N}}} \\ &\quad \times \int\frac{ ( 1 + x )^{N - 1} [ 1 + (1 + N)x ]^{\frac{ ( 1 - N )}{ ( 1 + N )}}}{x^{2}} \\ &\quad \times \biggl( \frac{2Cq^{2}}{x} - 1 \biggr)dx \\ &\quad + A_{N}\frac{x}{ ( 1 + x )^{N - 2} [ 1 + (1 + N)x ]^{\frac{2}{1 + N}}} \end{aligned}$$
(2.2)

where A N is a constant of integration may be determined by imposing appropriate physical boundary conditions.

2.2 Model of electric charge distribution

To perform the integration in (2.2) a variety of choices has been made by various authors previously (for instance, see Table 1 of paper II). In this work we consider the following model of electric charge distribution:

$$ \frac{2Cq^{2}}{x^{2}} = Kx^{n + 1} ( 1 + x )^{l + 1 - N} \bigl[ 1 + ( 1 + N )x \bigr]^{m + \frac{N - 1}{N + 1}} $$
(2.3)

where l,m are nonnegative integers, n>0,K≥0

The assumption on the charge distribution function, 2Cq 2/x 2, for which the electric field intensity vanishes at the center and remains continuous and bounded in the interior of the star, is physically reasonable and useful in the study of the gravitational behavior of charged stellar objects (paper I, II).

3 Some new charged stellar models

As Lattimer and Prakash (2005) pointed out that the choice of metric potential (1.1) with N=2 yields the most relevant analytical EOS. Because the velocity of sound for this case was found \(v_{s} \approx 1/\sqrt{3}\) throughout most of the star, similar to the behavior of strange quark matter and hence the choice N=2 may be more relevant in modeling electrically charged strange stars than by other N. The complete closed-form solution of the Einstein–Maxwell system, for the electric charge distribution model (2.3) is then given by,

$$\begin{aligned} &e^{\nu} = B_{2} ( 1 + x )^{2} \end{aligned}$$
(3.1a)
$$\begin{aligned} & \begin{aligned}[b] e^{ - \lambda} &= K \sum_{i = 0}^{l} \sum _{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} \frac{x^{n + i + j + 2}}{ ( 1 + 3x )^{\frac{2}{3}}} \\ &\quad + 1 + A_{2}\frac{x}{ ( 1 + 3x )^{\frac{2}{3}}} \end{aligned} \end{aligned}$$
(3.1b)
$$\begin{aligned} & \frac{2Cq^{2}}{x^{2}} = Kx^{n + 1} ( 1 + x )^{l + 1 - N} \bigl[ 1 + ( 1 + N )x \bigr]^{m + \frac{N - 1}{N + 1}} \end{aligned}$$
(3.1c)
$$\begin{aligned} &\begin{aligned}[b] \frac{\kappa}{C}P &= K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j}\\ &\quad \times \frac{x^{n + i + j + 1} ( 1 + 5x )}{ ( 1 + 3x )^{\frac{2}{3}} ( 1 + x )}\\ &\quad + \frac{K}{2}x^{n + 1} ( 1 + x )^{l - 1} ( 1 + 3x )^{m + \frac{1}{3}}\\ &\quad + \frac{4}{ ( 1 + x )} + A_{2}\frac{ ( 1 + 5x )}{ ( 1 + 3x )^{\frac{2}{3}} ( 1 + x )} \end{aligned} \end{aligned}$$
(3.1d)
$$\begin{aligned} & \begin{aligned}[b] \frac{\kappa}{C}\rho&= - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} x^{n + i + j + 1}\\ &\quad \times \frac{ [ ( 2n + 2i + 2j + 5 ) + ( 6n + 6i + 6j + 11 )x ]}{ ( 1 + 3x )^{\frac{5}{3}}}\\ &\quad - \frac{K}{2}x^{n + 1} ( 1 + x )^{l - 1} ( 1 + 3x )^{m + \frac{1}{3}} \\ &\quad - A_{2}\frac{ ( 3 + 5x )}{ ( 1 + 3x )^{\frac{5}{3}}} \end{aligned} \end{aligned}$$
(3.1e)

Equations (3.1d)–(3.1e) constitute the analytical EOS in parametric form.

4 Elementary criteria for physical acceptability

To test the physical relevance of the obtained solutions and obtain physically meaningful distribution of charged matter some physical criteria have been adopted in this work [paper I],

4.1 Elementary conditions to construct regular and physically acceptable relativistic charged stellar models

  1. (i)

    The solution should be free from physical and geometric singularities i.e. e ν>0 and e λ>0 in the range 0≤r≤R

  2. (ii)

    The pressure and energy density are positive, P≥0 and ρ≥0 throughout the fluid sphere.

  3. (iii)

    Pressure P should be zero at boundary r=R i.e. P(r=R)=0. R is the radius of the fluid sphere.

  4. (iv)

    In order to have an equilibrium configuration the matter must be stable against the collapse of local regions. This requires, Le Chatelier’s principle also known as local or microscopic stability condition, that P must be a monotonically non-decreasing function of ρ,

    $$\frac{dP}{d\rho} \ge0$$
  5. (v)

    The causality condition \(\sqrt{dP/d\rho} \le1\) must be satisfied throughout the fluid sphere.

  6. (vi)

    ρ≥P. This is known as dominant energy condition.

  7. (vii)

    The trace of the energy momentum tensor must be nonnegative, i.e., ρ−3P≥0, 0≤r≤R.

  8. (viii)

    Pressure and energy density, should maximum at the centre and monotonically decreasing from the center to the pressure free interface (i.e. boundary of the fluid sphere). Mathematically,

    $$\begin{aligned}[t] &\biggl( \frac{dP}{dr} \biggr)_{r = 0}, \biggl( \frac{d\rho}{dr} \biggr)_{r = 0} = 0\quad\mbox{and}\\ & \biggl( \frac{d^{2}P}{dr^{2}} \biggr)_{r = 0}, \biggl( \frac{d^{2}\rho}{dr^{2}} \biggr)_{r = 0} < 0 \end{aligned} $$

    So that

    $$\frac{dP}{dr}, \frac{d\rho}{dr} < 0;\quad0 < r \le R $$
  9. (ix)

    The ratio of pressure to energy density P/ρ should be monotonically decreasing with increasing r i.e.

    $$\frac{d}{dr} \biggl( \frac{P}{\rho} \biggr)_{r = 0} = 0,\qquad \frac{d^{2}}{dr^{2}} \biggl( \frac{P}{\rho} \biggr)_{r = 0} < 0$$
  10. (x)

    In addition to (iv) and (v), the velocity of sound should be monotonically decreasing with increasing radius, i.e.

    $$\frac{d}{dr} \biggl( \frac{dP}{d\rho} \biggr) < 0,\quad0 < r \le R$$

    The condition will be satisfied if \(\frac{d}{dr} ( \frac{dP}{d\rho} )_{r = 0} < 0\) and (ix) are found satisfied.

  11. (xi)

    The interior solution should match continuously with an exterior Reissner–Nordström solution,

    $$\begin{aligned} ds^{2}& = \biggl( 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}} \biggr)dt^{2}\\ &\quad - \biggl( 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}} \biggr)^{ - 1}dr^{2}\\ &\quad - r^{2} \bigl( d\theta^{2} + \sin^{2}\theta d\phi^{2} \bigr) \end{aligned}$$

    This requires the continuity of the metric coefficients at the surface,

    $$e^{\nu(r)} = e^{ - \lambda(r)} = 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}};\quad r \ge R $$
  12. (xii)

    Electric field intensity E, such that E(0)=0, is taken to be monotonically increasing with increasing radius i.e.,

    $$\frac {dE}{dr} > 0;\quad0 < r \le R$$

4.2 Determination of the arbitrary constant A 2

To specify A 2 the boundary condition (iii) of previous subsection can be utilized,

$$\begin{aligned} A_{2} &= - K \sum_{i = 0}^{l} \sum _{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j}\\ &\quad \times X^{n + i + j + 1} - \frac{K}{2}\frac{X^{n + 1} ( 1 + X )^{l} ( 1 + 3X )^{m + 1}}{ ( 1 + 5X )} \\ &\quad - \frac{4 ( 1 + 3X )^{\frac {2}{3}}}{ ( 1 + 5X )} \end{aligned}$$

where X=CR 2.

4.3 Total charge to radius ratio Q/R

Using X=CR 2 in Eq. (2.3) we obtain the square of ratio Q/R,

$$ \frac{Q^{2}}{R^{2}} = \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} $$
(4.1)

4.4 Total mass to radius ratio M/R

By matching the metric coefficients obtained in (3.1a)–(3.1b) with the exterior Reissner–Nordström metric at the boundary and with reference to the Eq. (4.1) one can establish the equation of compactness,

$$\begin{aligned} \frac{2M}{R} &= - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} \\ &\quad\times \frac{X^{n + i + j + 2}}{ ( 1 + 3X )^{\frac{2}{3}}} + \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} \\ &\quad - A_{2}\frac{X}{ ( 1 + 3X )^{\frac{2}{3}}} \end{aligned}$$
(4.2)

4.5 Total charge to mass ratio Q/M

Dividing (4.1) by (4.2) we obtain the charge to mass ratio Q/M,

$$\begin{aligned} \frac{Q}{M}& = \frac{Q / R}{M / R} = \frac{2\sqrt{\frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}}}}{[ - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} \frac{X^{n + i + j + 2}}{ ( 1 + 3X )^{\frac{2}{3}}} + \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} - A_{2}\frac{X}{ ( 1 + 3X )^{\frac{2}{3}}} ]} \end{aligned}$$
(4.3)

4.6 Determination of the constant B 2

The constant B 2 can be specified by the boundary condition e ν(R)=e −λ(R), which gives,

$$\begin{aligned} B_{2} &= ( 1 + X )^{ - 2}\Biggl[ K \sum _{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j}\\ &\quad \times \frac{X^{n + i + j + 2}}{ ( 1 + 3X )^{\frac{2}{3}}} \\ &\quad + 1 + A_{2}\frac{X}{ ( 1 + 3X )^{\frac{2}{3}}} \Biggr] \end{aligned}$$

4.7 Central and surface redshifts

The central and surface redshift of the charged fluid sphere are given by

$$\begin{aligned} &z_{c} = \sqrt{e^{ - \nu(0)}} - 1 = \frac{1}{\sqrt{B_{N}}} - 1,\\ & z_{s} = \sqrt{e^{ - \nu(R)}} - 1 = \frac{ ( 1 + X )^{ - \frac{N}{2}}}{\sqrt{B_{N}}} - 1 \end{aligned}$$

5 Construction of physically realistic fluid spheres

5.1 Pressure and density gradients

Differentiating the pressure and density equations (3.1d) and (3.1e) respectively with respect to the auxiliary variable x one obtains the pressure and density gradients for the analytical EOS,

$$\begin{aligned} \frac{\kappa}{C}\frac{dP}{dx}& = K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j}\\ &\quad \times x^{n + i + j} \frac{P_{n,i}(x)}{ ( 1 + 3x )^{\frac{5}{3}} ( 1 + x )^{2}} \\ &\quad + \frac{K}{2}x^{n} ( 1 + x )^{l - 2} ( 1 + 3x )^{m - \frac{2}{3}}\\ &\quad \times \bigl[ (n + 1) + (4n + 3m + l + 4)x \\ &\quad \times+ (3n + 3m + 3l + 1)x^{2} \bigr] \\ &\quad - \frac{4}{ ( 1 + x )^{2}} + 2A_{2}\frac{ ( 1 - 5x^{2} )}{ ( 1 + 3x )^{\frac{5}{3}} ( 1 + x )^{2}}\\ \frac{\kappa}{C}\frac{d\rho}{dx}& = - K \sum_{l = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j}\\ &\quad \times x^{n + i + j} \frac{Q_{n,i}(x)}{ ( 1 + 3x )^{\frac{8}{3}}} \\ &\quad - \frac{K}{2}x^{n} ( 1 + x )^{l - 2} ( 1 + x )^{m - \frac{2}{3}}\bigl[ (n + 1) \\ &\quad + (4n + 3m + l + 4)x + (3n + 3m + 3l + 1)x^{2} \bigr] \\ &\quad + 10A_{2}\frac{ ( 1 + x )}{ ( 1 + 3x )^{\frac{8}{3}}} \end{aligned}$$

where,

$$\begin{aligned} P_{n,i} &= (n + i + j + 1) + (9n + 9i + 9j + 11)x \\ &\quad + 23(n + i + j + 1)x^{2} + 5(3n + 3i + 3j + 1)x^{3} \\ Q_{n,i}& = (n + i + j + 1)(2n + 2i + 2j + 5) + (12n^{2} + 24ni \\ &\quad + 24nj + 12i^{2} + 24ij + 12j^{2} + 34n + 34i \\ &\quad + 34j + 12)x + (3n + 3i + 3j + 1)(6n + 6i\\ &\quad + 6j + 11)x^{2} \end{aligned}$$

Once the ratios M/R and Q/R obtained then the total mass and total charge of the fluid sphere may be calculated by providing the values of one of the following physical quantities,

(i) For a given radius

  1. (a)

    Total Mass

    $$\begin{aligned} M &= \frac{R}{2}\Biggl[ - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} \\ &\quad \times \frac{X^{n + i + j + 2}}{ ( 1 + 3X )^{\frac{2}{3}}} + \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} \\ &\quad - A_{2}\frac{X}{ ( 1 + 3X )^{\frac{2}{3}}} \Biggr] \end{aligned}$$
    (5.1)

    where the mass M is in km.Footnote 2

  2. (b)

    Total Charge

    $$ Q = R\sqrt{\frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}}} $$
    (5.2)

    where the mass Q is in km.Footnote 3

  3. (c)

    Central density

    $$ \rho_{c} = - \frac{3XA_{2}}{\kappa R^{2}} $$
    (5.3)

    where the radius R is in unit of m and the central density in kg m−3.

  4. (d)

    Surface density

    $$\begin{aligned} \rho_{s}& = \frac{1}{R^{2}\kappa} \Biggl[ - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} \\ &\quad\times { l \choose i} { m \choose j} X^{n + i + j + 2} \\ &\quad\times\frac{ [ ( 2n + 2i + 2j + 5 ) + ( 6n + 6i + 6j + 11 )X ]}{ ( 1 + 3X )^{\frac{5}{3}}} \\ &\quad - \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} \\ &\quad\times- A_{2}X\frac{ ( 3 + 5X )}{ ( 1 + 3X )^{\frac{5}{3}}} \Biggr] \end{aligned}$$
    (5.4)

    where the radius R is in unit of m and the surface density in kg m−3.

(ii) For a given surface density

The radius of the charged fluid sphere can be calculated by the following eqn.

$$\begin{aligned} R^{2}& = \frac{1}{\rho_{s}\kappa} \Biggl[ - K \sum_{i = 0}^{l} \sum_{j = 0}^{m} \frac{3^{j}}{ ( n + i + j + 1 )} { l \choose i} { m \choose j} \\ &\quad \times X^{n + i + j + 2} \\ &\quad \times \frac{ [ ( 2n + 2i + 2j + 5 ) + ( 6n + 6i + 6j + 11 )X ]}{ ( 1 + 3X )^{\frac{5}{3}}} \\ &\quad - \frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}} \\ &\quad - A_{2}X\frac{ ( 3 + 5X )}{ ( 1 + 3X )^{\frac{5}{3}}} \Biggr] \end{aligned}$$
(5.5)

And the total mass, total charge, and the central density can be calculated by Eqs. (5.1)–(5.3).

(iii) For a given central density

Radius

$$ R = \sqrt{ - \frac{3XA_{2}}{\kappa\rho_{c}}} $$
(5.6)

where the central energy density ρ c is given in the unit kg m−3 and the radius in m.Footnote 4 The total mass, total charge, and the surface density then can be calculated by Eqs. (5.1), (5.2), and (5.4) respectively.

(iv) For a given central pressure

The radius can be calculated by the following equation

$$ R = \sqrt{\frac{ ( 4 + A_{2} )X}{\kappa P_{c}}} $$
(5.7)

where the central pressure P c is given in the unit N m−2.Footnote 5 The total mass, total charge, the central and surface densities then can be calculated by Eqs. (5.1)–(5.3), and (5.4) respectively.

(v) For a given electric charge

The radius can be calculated by the use of following equation

$$ R = Q / \sqrt{\frac{K}{2}X^{n + 2} ( 1 + X )^{l - 1} ( 1 + 3X )^{m + \frac{1}{3}}} $$
(5.8)

where the charge Q is given in the unit km. Then the total mass, total charge, the central and surface densities then can be calculated by Eqs. (5.1)–(5.3), and (5.4) respectively.

5.2 Physical analysis of the models

A fluid sphere satisfying the inequalities (i), (ii) and (viii)–(x) of Sect. 4.1 will be termed as well-behaved. For a particular set (l,m,n) the values of K, X have been put to the Eqs. (5.1)–(5.8) for which the fluid distribution satisfies the inequalities of Sect. 4.1 are reported in Table 1.

Table 1 Some values of parameters (l,m,n,K,X) for which well-behaved charge fluid sphere can be generated
Full size table

Case I: l=1, m=0, n=0.2

For this particular set (l,m,n) the range of values, K≥0.805,0≤X≤0.498 are obtained for which the fluid distribution are well-behaved. Numerical investigation shows that X decreases as K increases. And hence the maximum value of compactness parameter is obtained (2M/R)max=0.739068, using (4.1), at K min=0.805, X max=0.498. Corresponding to the values of K and X the total charge to radius ratio, and total charge to total mass ratio are found to be Q/R=0.34 and Q/M=0.93 using Eqs. (4.2) and (4.3) respectively. For a chosen stellar central density ρ c as parameter the radius, R, of the fluid sphere can be calculated by using Eq. (5.6). In particular we choose ρ c =3.4×1015 g cm−3 and we obtain R=7.91 km. Then the total mass and other physical quantities are calculated as M=1.96M ⊙, P c =318.6319 MeV fm−3, ρ s =8.26×1014 g cm−3, Q=3.15×1020 C. A lower choice of the stellar central density ρ c =1.65×1015 g cm−3 the total mass and other physical quantities are calculated as M=2.82M ⊙, R=11.36 km, P c =154.63 MeV fm−3, ρ s =4.009×1014 g cm−3, Q=4.52×1020 C.Footnote 6

Case II: l=0,m=1,n=0.2

Corresponding to the values K min=0.68,X max=0.408 the compactness parameter, total charge to radius ratio, and total charge to total mass ratio are found to be (2M/R)max=0.679556, Q/R=0.31, Q/M=0.92. Choosing stellar central density ρ c =3.4×1015 g cm−3 as parameter the mass and other physical values comes out to be M=1.66M ⊙, R=7.28 km, P c =287.86 MeV fm−3, ρ s =9.83×1014 g cm−3, Q=2.64×1020 C. Choosing stellar central density ρ c =1.39×1015 g cm−3as parameter the mass and other physical values comes out to be M=2.60M ⊙, R=11.39 km, P c =117.68 MeV fm−3, ρ s =4.02×1014 g cm−3, Q=4.13×1020 C.

Case III: l=1,m=1,n=0.2

$$\begin{aligned} &K_{\min} = 0.58,\quad X_{\max} = 0.368 \\ & 2M / R = 0.646764,\quad Q / R = 0.29,\quad Q / M = 0.91 \end{aligned}$$

Choosing stellar central density ρ c =3.4×1015 g cm−3 we obtain a charged fluid sphere with total mass, radius, central pressure, surface density and total charge M=1.51M ⊙, R=6.95 km, P c =277.60 MeV fm−3, ρ s =10.80×1014 g cm−3, Q=2.38×1020 C respectively. Choosing stellar central density ρ c =1.26×1015 g cm−3 we obtain a charged fluid sphere with total mass, radius, central pressure, surface density and total charge M=2.48M ⊙, R=11.43 km, P c =102.87 MeV fm−3, ρ s =4.002×1014 g cm−3, Q=3.9×1020 C respectively.

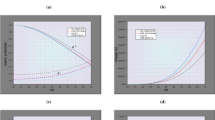
Though it is difficult to obtain an explicit analytical relation among n,K min,X max but for some particular choices of (l,m,n) the variations are plotted in Figs. 1–2a, 2b. The mass and other physical quantities of compact charged fluid spheres, can be obtained by specifying one of the following: (i) radius, (ii) central density, (iii) surface density, (iv) central pressure, (v) electric charge as parameter. We particularly choose central density (Table 2). Numerical investigations show that for each particular choice of l,m the maximum value of the compactness parameter, 2M/R, is obtained at n=0.2 (Fig. 3).

Fig. 1
figure 1

K–X relation for particular l, m, and n

Full size image
Fig. 2a
figure 2

K vs. X max(l=1,m=0) for 0<n<0.34. The maximum value X max=0.498, is obtained at K=0.805

Full size image
Fig. 2b
figure 3

n vs. X max(l=1,m=0) for 0.788<K<0.887. The maximum value X max=0.498, is obtained at n=0.2

Full size image
Fig. 3
figure 4

n vs. 2M/R(l=0,m=1) for 0<n<0.4. The maximum value of 2M/R is obtained at n=0.2

Full size image
Table 2 Maximum mass and the various physical variables of charged fluid spheres for given central density
Full size table

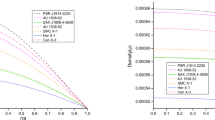
The behaviors of various physical variables in the interior of the star have been investigated and found regular and well behaved throughout the fluid sphere. To reduce the size of the paper the behaviors are not plotted in figures. From the Fig. 4 it can be observed that the speed of sound always remain less than the speed of light and the condition of causality is satisfied. Moreover, the speed of sound found \(v_{s} \approx 1/\sqrt{3}\) throughout most of the fluid sphere, similar to the behavior of strange quark matter. As in paper I and II the choice of electric charge distribution function (2.3) is physically reasonable in the study of gravitational behavior of electrically charged compact stellar objects as it is zero at the stellar center and monotonically increasing towards the pressure free interface (boundary). The analytical EOS obtained in Eqs. (3.1d) and (3.1e) is plotted for particular values of constant parameters in Fig. 5.

Fig. 4
figure 5

Behaviors of speed of sound \(\sqrt{dP/c^{2}d\rho}\) for the fluid spheres generated by the same input as in Fig. 1

Full size image
Fig. 5
figure 6

Pressure-density profile for a fluid sphere generated by the input (l, m, n, K, X)=(1, 0, 0.2, 0.805, 0.498) with given central density ρ c =3.4×1015 g cm−3

Full size image

The compactness parameter (mass to radius ratio) of charged fluid spheres are found to satisfy the lower limit of the allowable mass–to–radius ratio (M/R) for charged fluid sphere (Böhmer and Harko 2007)

$$\frac{3}{2}\frac{Q^{2}}{R^{2}}\frac{ ( 1 + \frac{Q^{2}}{18R^{2}} )}{ ( 1 + \frac{Q^{2}}{12R^{2}} )} \le\frac{2M}{R} $$

And the mass of the charged fluid sphere also satisfies the Andréasson inequality (Andréasson 2009),

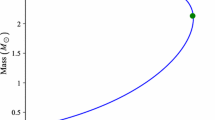
$$\sqrt{M} \le\frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9} + \frac{Q^{2}}{3R}} $$

The mass–radius relationship of electrically charged fluid spheres for the particular set of values (l,m,n,K)=(1,1,0.2,0.58) and a sequence of spheres described by 0≤X≤0.368 is plotted in Fig. 6. The behavior of Fig. 6 reproduces that of other quark star models (e.g., Negreiros et al. 2009).

Fig. 6
figure 7

Mass-radius relation for fluid spheres generated by the inputs (l, m, n, K)=(1, 1, 0.2, 0.58) and 0≤X≤0.368 with surface density ρ s =4.6×1014 g cm−3

Full size image

6 An application of the model for some strange star candidates

Based on the analytic model developed so far, to get an estimate of the range of various physical parameters, let us now consider some potential strange star candidates like Her X-1, SAX J 1808.4-3658, 4U 1820-30. Using the mass and radius reported in Gangopadhyay et al. (2013) for each of these pulsars we have calculated the values of the relevant physical quantities and the values are reported in Table 3.

Table 3 Physical values of energy density and pressure for different strange stars
Full size table

7 Concluding remarks

In this work we have studied a new family of analytical relativistic stellar models which may be considered as charged analogues of Generalized Tolman IV model. In contrast, so far the literature known to present authors, the charged analogues of Tolman V-VI models obtained by Pant and Sah (1979), Patiño and Rago (1989), Singh et al. (1995), Ray and Das (2002, 2004, 2007), Ray et al. (2007) are not physically viable in the description of compact astrophysical objects as the infinite values of central density and pressure. However, the charged analogues of Tolman IV and VII models obtained by Maurya and Gupta (2011), Kiess (2012), as the neutral ones, exhibit the physical features required for the construction of physically realizable relativistic compact stellar structure.

Numerical studies show that the solutions obtained in this work can generate charged fluid spheres with maximum mass 2.83M ⊙, radius 11.37 km, central and surface densities on the order 1.65×1015 g cm−3 and 4×1014 g cm−3 respectively, with electric charge on the order 1020 C. Moreover, the speed of sound is obtained \({\sim}1 / \sqrt{3}\) at the center and remains almost the same throughout most of the fluid sphere. An analytical stellar model with such physical features is most likely to present an approximated realistic model of strange quark star. And hence the analytical EOS given by our models could play a significant role, besides the usual linear EOS based on phenomenological MIT bag model, in the description of internal structure of electrically charged bare strange quark stars.