Abstract
A spatially homogeneous and anisotropic Bianchi type-VI0 space-time filled with perfect fluid in general relativity and also in the framework of f(R,T) gravity proposed by Harko et al. (in arXiv:1104.2669 [gr-qc], 2011) has been studied with an appropriate choice of the function f(R,T). The field equations have been solved by using the anisotropy feature of the universe in Bianchi type-VI0 space time. Some important features of the models, thus obtained, have been discussed. We noticed that the involvement of new function f(R,T) doesn’t affect the geometry of the space-time but slightly changes the matter distribution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, there has been a lot of interest in alternative theories of gravitation. In view of the late time acceleration of the universe and the existence of the dark matter and dark energy, very recently, modified theories of gravity have been developed. Noteworthy amongst them are f(R) theory of gravity formulated by Nojiri and Odintsov (2003a) and f(R,T) theory of gravity proposed by Harko et al. (2011). Carroll et al. (2004) explained the presence of a late time cosmic acceleration of the universe in f(R) gravity. Nojiri and Odintsov (2003b) demonstrated that phantom scalar in many respects looks like strange effective quantum field theory by introducing a non-minimal coupling of phantom field with gravity. Recently, Harko et al. (2011) developed f(R,T) modified theory of gravity, where the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and of the trace T of the stress-energy tensor. They have obtained the gravitational field equations in the metric formalism, as well as, the equations of motion for test particles, which follow from the covariant divergence of the stress-energy tensor. The f(R,T) gravity model depends on a source term, representing the variation of the matter stress energy tensor with respect to the metric. A general expression for this source term is obtained as a function of the matter Lagrangian L m so that each choice of L m would generate a specific set of field equations. Some particular models corresponding to specific choices of the function f(R,T) are also presented, they have also demonstrated the possibility of reconstruction of arbitrary FRW cosmologies by an appropriate choice of a function f(T). In the present model the covariant divergence of the stress energy tensor is nonzero. Hence the motion of test particles is non-geodesic and an extra acceleration due to the coupling between matter and geometry is always present.
In f(R,T) gravity, the field equations are obtained from the Hilbert-Einstein type variational principle.
The action principle for this modified theory of gravity is given by
where f(R,T) is an arbitrary function of the Ricci scalar R and of the trace T of the stress energy tensor of matter and L m is the matter Lagrangian.
The stress energy tensor of matter is
Using gravitational units (by taking G & c as unity) the corresponding field equations of f(R,T) gravity are obtained by varying the action principle (1.1) with respect to g ij as

where

Here ∇ i is the covariant derivative and T ij is usual matter energy-momentum tensor derived from the Lagrangian L m .
It can be observed that when f(R,T)=f(R), then (1.3) reduce to field equations of f(R) gravity.
It is mentioned here that these field equations depend on the physical nature of the matter field. Many theoretical models corresponding to different matter contributions for f(R,T) gravity are possible. However, Harko et al. gave three classes of these models
In this paper we are focused to the first class, i.e.
where f(T) is an arbitrary function of trace of the stress energy tensor of matter.
Then from (1.3) & (1.4), we get the gravitational field equations as

where the overhead prime indicates differentiation with respect to the argument.
Reddy et al. (2012a, 2012b) have obtained Kaluza-Klein cosmological model in the presence of perfect fluid source and Bianchi type-III cosmological model in f(R,T) gravity using the assumption of law of variation for the Hubble parameter proposed by Bermann (1983). Adhav (2012) has obtained LRS Bianchi type-I cosmological model in f(R,T) gravity using the same assumption of law of variation for the Hubble parameter proposed by Bermann (1983). Chaubey and Shukla (2013) have obtained a new class of Bianchi cosmological models in f(R,T) gravity. Reddy and Santi Kumar (2013) have presented some anisotropic cosmological models in this theory. Recently Rao and Neelima (2013) have discussed perfect fluid Einstein-Rosen universe in f(R,T) gravity.
Motivated by the above investigations, we study spatially homogeneous and anisotropic Bianchi type-VI0 cosmological models with perfect fluid matter source in f(R,T) gravity, where f(R,T)=R+2f(T). This model is very important in the discussion of large scale structure, to identify early stages and finally to study the evolution of the universe.
2 Metric and field equations
The Bianchi type-VI0 line element can be written in the form
where A,B&C are functions of time ‘t’ only.
The matter tensor for perfect fluid is
The field equations in f(R,T) theory of gravity for the function f(R,T)=R+2f(T) when the matter source is perfect fluid are given by

where the prime indicates the derivative with respect to the argument.
Now, choose the function f(T) as the trace of the stress energy tensor of the matter so that
where λ is a constant.
Using commoving coordinate system, the field equations for the metric (2.1) with the help of (2.2) to (2.4) can be written as





From (2.9), we get
Without loss of generality we can take α=1, so that we have
Using (2.10), the field equations (2.5) to (2.8) can reduce to



where the overhead dot(.) indicates the derivative with respect to ‘t’.
These are three linearly independent equations with four unknowns A,B,ρ and p. In order to solve the system completely, we assume that the expansion scalar is proportional to shear scalar. This condition leads to
From (2.11) and (2.12), we get
Using (2.14) in (2.15), we get


Then the metric (2.1) can now be written in the form

From (2.11) to (2.13), we obtain the pressure as

and the density

The metric (2.18) together with (2.19) and (2.20) represents an anisotropic Bianchi type-VI0 perfect fluid cosmological model in f(R,T) gravity.
3 Some important features of the model
The volume element of the model (2.18) is given by
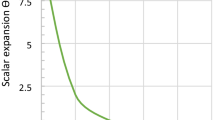
The scalar expansion θ, shear scalar σ are given by


The mean Hubble parameter (H) is given by
The deceleration parameter (q) is given by
The deceleration parameter q>0 for −∞<m<−2 and m>1 and q<0 for −2<m<1.
If q<0, the model accelerates and when q>0, the model decelerates in the standard way. Here the models sometimes decelerate in the standard way and later accelerate which is in accordance with the present day scenario. It may be noted that Bianchi models represent cosmos in its early stage of evolution. However, in spite of the fact that the universe, in this case, decelerates in the standard way it will accelerate in finite time due to cosmic re collapse where the universe in turns inflates “decelerates and then accelerates” (Nojiri and Odintsov 2003c).
The average anisotropy parameter A m is given by
The overall density parameter Ω is given by

5 Conclusions
In this paper, we have presented a spatially homogeneous and anisotropic Bianchi type-VI0 space-time filled with perfect fluid in the framework of f(R,T) gravity proposed by Harko et al. (2011) and in general relativity.
The following are the observations and conclusions.
-
(1)
The model (2.18) has no initial singularity for positive values of m.
-
(2)
The spatial volume increases with time.
At \(t = \frac{ - k_{2}}{k_{1}}\), the volume element of the model vanishes while all other parameters diverge.
-
(3)
Since the mean anisotropy parameter A m ≠0, the models do not approach isotropy for m≠1.
-
(4)
For m=1, from the field equations, we can easily see that we will get only isotropic Zeldovich universe.
-
(5)
The deceleration parameter q>0 for −∞<m<−2 and m>1 and q<0 for −2<m<1. If q<0, the model accelerates and when q>0, the model decelerates in the standard way. Here the models sometimes decelerate in the standard way and later accelerate which is in accordance with the present day scenario. It may be noted that Bianchi models represent cosmos in its early stage of evolution. However, in spite of the fact that the universe, in this case, decelerates in the standard way it will accelerate in finite time due to cosmic re collapse where the universe in turns inflates “decelerates and then accelerates” (Nojiri and Odintsov 2003c).
-
(6)
The involvement of new function f(R,T) doesn’t affect the geometry of the space-time but slightly changes the matter distribution.
References
Adhav, K.S.: Astrophys. Space Sci. 339, 365 (2012)
Bermann, M.S.: Nuovo Cimento B 74, 182 (1983)
Carroll, S.M., et al.: Phys. Rev. D, Part. Fields 70, 043528 (2004)
Chaubey, R., Shukla, A.K.: Astrophys. Space Sci. 343, 415 (2013)
Harko, T., Lobo, F.S.N., Nojiri, S., Odintsov, S.D.: (2011). arXiv:1104.2669 [gr-qc]
Nojiri, S., Odintsov, S.D.: arXiv:hep-th/0307288 (2003a)
Nojiri, S., Odintsov, S.D.: Phys. Lett. B 562, 147 (2003b)
Nojiri, S., Odintsov, S.D.: Phys. Rev. D 68, 123512 (2003c)
Rao, V.U.M., Neelima, D.: Eur. Phys. J. Plus. (2013) (accepted for publication)
Reddy, D.R.K., Santi Kumar, R.: Astrophys. Space Sci. 344, 253 (2013)
Reddy, D.R.K., Naidu, R.L., Satyanarayana, B.: Int. J. Theor. Phys. 51, 3222 (2012a)
Reddy, D.R.K., Santi Kumar, R., Naidu, R.L.: Astrophys. Space Sci. 342, 249 (2012b)
Acknowledgements
The second author (D. Neelima) is grateful to the Department of Science and Technology (DST), New Delhi, India for providing INSPIRE fellowship. The authors are thankful to the reviewer for constructive comments in improving this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rao, V.U.M., Neelima, D. Bianchi type-VI0 perfect fluid cosmological model in a modified theory of gravity. Astrophys Space Sci 345, 427–430 (2013). https://doi.org/10.1007/s10509-013-1406-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10509-013-1406-5