1 Introduction

“The universe is highly homogeneous and isotropic on large scales” has been indicated by the recent observations of large scale structure (LSS) (Tegmark et al. 2004) and cosmic microwave background radiation (CMBR) (Bennett et al., 2003; Spergel et al., 2003a, 2003b). In general, it has been observed that anisotropic models do not isotropize sufficiently as they evolve into future. This isotropy problem can be solved by inflation. Wald (1983) has proved that initially expanding Bianchi models with a cosmological constant approach asymptotically to spatially homogeneous & isotropic models like de Sitter model.

Ananda and Bruni (2005) studied the general relativistic dynamics of Robertson-Walker models with a non-linear equation of state. They have verified that the behavior of the anisotropy at the singularity found in the brane scenario can be recreated in the general relativistic context by considering a quadratic term in equation of state [EoS] given by

$$P = P_{0} + \alpha\rho+ \beta\rho^{2}, $$

where P 0, α and β are parameters.

This equation represents the first terms of the Taylor expansion of any equation of state of the form P=P(ρ) about ρ=0.

Ananda and Bruni (2006) used the simplified equation of state in the form

$$P = \alpha\rho+ \frac{\rho^{2}}{\rho_{c}} $$

to analyze the effects of quadratic equation of state in homogeneous & inhomogeneous anisotropic cosmological models in general relativity to isotropize the universe at early times when the initial singularity is approached.

Dark energy universe with different equations of state has been discussed by Nojiri and Odintsov (2005) with inhomogeneous Hubble parameter term. The observational constraints on dark energy with quadratic equation of state has been presented by Capozziello et al. (2006). According to Nojiri and Odintsov (2005), Capozziello et al. (2006) quadratic equation of state may describe dark energy or unified dark matter. Rahman et al. (2009) have modelled electron as a spherically symmetric charged perfect fluid distribution of matter characterized by quadratic equation of state in general relativity. Feroze and Siddiqui (2011) studied the charged anisotropic matter with quadratic equation of state and obtained new classes of static spherically symmetric models of relativistic stars. Maharaj and Takisa (2013) have obtained new exact solutions of the Einstein-Maxwell field equations with charged anisotropic matter distribution and a quadratic equation of state. Chavanis (2013a) studied a cosmological model based on a quadratic equation of state unifying vacuum energy, radiation and dark energy. Chavanis (2013b) has developed a cosmological model describing the early inflation, the intermediate decelerating expansion, and the late accelerating expansion by a quadratic equation of state. Sharma and Ratanpal (2013) have obtained a class of solutions describing the interior of a static spherically symmetric compact anisotropic star & shown that the model admits an equation of state which is quadratic in nature. Recently, Malaver (2014) studied the behavior of compact relativistic objects with anisotropic matter distribution considering quadratic equation of state and new solutions to the Einstein-Maxwell system of equations are found in terms of elementary functions.

In brane world models, inspired by string theory, the physical fields in our four dimensional universe are confined to three brane, while gravity can access the extra dimension. In brane world scenario, the gravity on brane can be described by the modified 4-dimensional Einstein’s equations which contain (i) Sμ which is quadratic in the stress energy tensor of matter confined on the brane and (ii) E which is trace less tensor originating from the 5D Weyl tensor. The quadratic term of energy density appears in the 4-dimensional effective energy momentum tensor in the Einstein’s equations and it plays a significant role of different characteristics of the cosmological brane models. Hence, motivation to consider a quadratic equation of state includes its importance in the brane world models and the study of dark energy and general relativistic dynamics for different models. So, it is not unnatural to choose quadratic form of equation of state to study anisotropy problems. Hence, the anisotropic Bianchi type-I homogeneous cosmological model containing a perfect fluid with quadratic equation of state has been studied.

2 Metric and field equations

We have considered the Bianchi type-I line element as

$$ ds^{2} = dt^{2} - A^{2}dx^{2} - B^{2}dy^{2} - C^{2}dz^{2}, $$
(2.1)

where A, B and C are scale factors and are functions of time t only.

The Einstein field equations, in natural limits (8πG=1 and c=1) are

$$ R_{ij} - \frac{1}{2}Rg_{ij} = - T_{ij}, $$
(2.2)

where R ij is the Ricci tensor; R is the Ricci scalar and T ij is the energy-momentum tensor.

The energy-momentum tensor T ij for the perfect fluid is given by

$$ T_{i j} = (\rho+ p) u_{i} u_{j} - p g_{i j}, $$
(2.3)

where ρ is the energy density, p is the pressure and u i is the four velocity vector satisfying g ij u i u j =1.

We have assumed an equation of state (EoS) in the general form p=p(ρ) for the matter distribution.

We consider it, in this case, in the quadratic form as

$$ p = \alpha\rho^{2} - \rho, $$
(2.4)

where α is constant and strictly α≠0.

This will not affect the quadratic nature of equation of state.

In co-moving coordinate system, the Einstein field equations (2.2) for the metric (2.1) with the help of Eqs. (2.3) reduce to following set of equations:

$$\begin{aligned} &{\frac{\dot{A}\dot{B}}{AB} + \frac{\dot{B}\dot{C}}{BC} + \frac{\dot{A}\dot{C}}{AC} = \rho, } \end{aligned}$$
(2.5)
$$\begin{aligned} &{\frac{\ddot{B}}{B} + \frac{\ddot{C}}{C} + \frac{\dot{B}\dot{C}}{BC} = - p, } \end{aligned}$$
(2.6)
$$\begin{aligned} &{\frac{\ddot{A}}{A} + \frac{\ddot{C}}{C} + \frac{\dot{A}\dot{C}}{AC} = - p, } \end{aligned}$$
(2.7)
$$\begin{aligned} &{\frac{\ddot{A}}{A} + \frac{\ddot{B}}{B} + \frac{\dot{A}\dot{B}}{AB} = - p, } \end{aligned}$$
(2.8)

where overhead dot (.) denote differentiation with respect to time t.

The energy conservation equation \(T_{; j}^{i j} = 0\) leads to the following simple expression

$$ \dot{\rho} + \biggl( \frac{\dot{A}}{A} + \frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) ( \rho+ p ) = 0. $$
(2.9)

We have defined the spatial volume V and average scale factor a for Bianchi type-I space-time as

$$ V = a^{3} = ABC. $$
(2.10)

The mean Hubble parameter H for Bianchi type-I universe is defined as

$$ H = \frac{\dot{a}}{a} = \frac{1}{3} ( H_{x} + H_{y} + H_{z} ), $$
(2.11)

where

$$H_{x} = \frac{\dot{A}}{A},\qquad H_{y} = \frac{\dot{B}}{B}, \qquad H_{z} = \frac{\dot{C}}{C} $$

are the directional Hubble parameters in the directions of x, y and z axes respectively.

3 Solutions of the field equations

Subtracting Eq. (2.6) from (2.7); Eq. (2.7) from (2.8) and Eq. (2.6) from (2.8) respectively, we get

$$\begin{aligned} &{\frac{\ddot{A}}{A} - \frac{\ddot{B}}{B} + \frac{\dot{C}}{C} \biggl( \frac{\dot{A}}{A} - \frac{\dot{B}}{B} \biggr) = 0, } \end{aligned}$$
(3.1)
$$\begin{aligned} &{\frac{\ddot{B}}{B} - \frac{\ddot{C}}{C} + \frac{\dot{A}}{A} \biggl( \frac{\dot{B}}{B} - \frac{\dot{C}}{C} \biggr) = 0, } \end{aligned}$$
(3.2)
$$\begin{aligned} &{\frac{\ddot{A}}{A} - \frac{\ddot{C}}{C} + \frac{\dot{B}}{B} \biggl( \frac{\dot{A}}{A} - \frac{\dot{C}}{C} \biggr) = 0. } \end{aligned}$$
(3.3)

After solving Eqs. (3.1) to (3.3) with some simplification, we get

$$\begin{aligned} &{\frac{A}{B} = d_{1}\exp \biggl( x_{1}\int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.4)
$$\begin{aligned} &{\frac{B}{C} = d_{2}\exp \biggl( x_{2}\int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.5)
$$\begin{aligned} &{\frac{A}{C} = d_{3}\exp \biggl( x_{3}\int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.6)

where x 1, x 2, x 3 and d 1, d 2, d 3 are constants of integration.

Using above Eqs. (3.4), (3.5) and (3.6), we can write the metric functions A, B and C explicitly as

$$\begin{aligned} &{A(t) = D_{1} V^{\frac{1}{3}}\exp \biggl( X_{1} \int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.7)
$$\begin{aligned} &{B(t) = D_{2} V^{\frac{1}{3}}\exp \biggl( X_{2}\int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.8)
$$\begin{aligned} &{C(t) = D_{3} V^{\frac{1}{3}}\exp \biggl( X_{3}\int \frac{dt}{V} \biggr), } \end{aligned}$$
(3.9)

where D 1, D 2, D 3 and X 1, X 2, X 3 are the constants of integration which satisfy the relations D 1 D 2 D 3=1 and X 1+X 2+X 3=0.

It should be noted that the isotropic subcase, A=B=C, is not possible here because X 1+X 2+X 3≠0 from Eq. (3.7) to Eq. (3.9).

Now, using Eq. (2.10) in Eq. (2.9), we get

$$ \dot{\rho} + \frac{\ddot{V}}{V} ( \rho+ p ) = 0. $$
(3.10)

Using equations from (2.5) to (2.8), we obtain

$$ \frac{\ddot{V}}{V} = \frac{3}{2}(\rho- p). $$
(3.11)

After solving Eq. (3.11) and integrating, we obtain

$$ \dot{V} = \sqrt{3 \rho V^{2} + c_{1}}, $$
(3.12)

where c 1 is an integration constant.

Again integrating above Eq. (3.12), we get

$$ \int\frac{dV}{\sqrt{3\rho V^{2} + c_{1}}} = t + t_{0}, $$
(3.13)

where the integration constant t 0 can be taken to be zero, since it gives a shift in time.

Now choosing β=−1 and γ=0 in Eq. (2.4) and using Eq. (3.10), we obtain energy density in terms of volume as,

$$ \rho= (\alpha\log V)^{ - 1}. $$
(3.14)

It can be observed that the energy density is a positive quantity.

Using Eqs. (3.14) in Eq. (3.13) and choosing c 1=t 0=0, we get

$$ \int\frac{dV}{\sqrt{3(\alpha\log V)^{ - 1} V^{2}}} = t. $$
(3.15)

Integrating above Eq. (3.15), we obtain

$$ V = e^{3 ( \frac{t^{2}}{4\alpha} )^{1/3}}. $$
(3.16)

Using Eq. (3.16) in Eqs. (3.7), (3.8) and (3.9), we obtain the scale factors A, B and C as

$$\begin{aligned} &{A(t) = D_{1} e^{ ( \frac{t^{2}}{4\alpha} )^{1/3}}\exp \bigl[X_{1}F(t) \bigr], } \end{aligned}$$
(3.17)
$$\begin{aligned} &{B(t) = D_{2} e^{ ( \frac{t^{2}}{4\alpha} )^{1/3}}\exp \bigl[X_{2}F(t) \bigr], } \end{aligned}$$
(3.18)
$$\begin{aligned} &{C(t) = D_{3} e^{ ( \frac{t^{2}}{4\alpha} )^{1/3}}\exp \bigl[X_{3}F(t) \bigr], } \end{aligned}$$
(3.19)

where

$$\begin{aligned} F(t) =& \frac{\alpha^{1/3}}{6} \bigl\{ \sqrt{3\alpha} \alpha^{1/3} \mathrm{erf} \bigl[ \sqrt{3/\alpha} ( t/2\alpha )^{1/3} \bigr] \\ &{} - 3 (4t)^{1/3} e^{ - 3 ( \frac{t^{2}}{4\alpha} )^{1/3}} \bigr\} \end{aligned}$$

and erf is the “error function”.

Using Eq. (3.16) in Eq. (3.14), we obtain energy density as

$$ \rho= \frac{1}{3} \biggl( \frac{2}{\alpha t} \biggr)^{2/3}. $$
(3.20)

From Eqs. (2.4) and (3.20), we obtain pressure as

$$ p = \frac{\alpha}{9} \biggl( \frac{2}{\alpha t} \biggr)^{4/3} - \frac {1}{ 3} \biggl( \frac{2}{\alpha t} \biggr)^{2/3}. $$
(3.21)

Now the physical quantities in cosmology, the mean Hubble parameter H, the expansion scalar θ, the mean anisotropy parameter Δ, the shear scalar σ 2 and deceleration parameter q are defined and found to be

$$\begin{aligned} &{H = \frac{1}{3} \biggl( \frac{\dot{A}}{A} + \frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) = \frac{2 t^{ - 1/3}}{3 (4\alpha )^{1/3}}, } \end{aligned}$$
(3.22)
$$\begin{aligned} &{\theta= 3H = \frac{2 t^{ - 1/3}}{(4\alpha)^{1/3}}, } \end{aligned}$$
(3.23)
$$\begin{aligned} &{\Delta= \frac{1}{3}\sum_{i = 1}^{3} \biggl( \frac{\Delta H_{i}}{H} \biggr)^{2} = \frac{3X}{4}t^{2/3} e^{ - 6 ( \frac{t^{2}}{4\alpha} )^{1/3}}, } \end{aligned}$$
(3.24)
$$\begin{aligned} &{\sigma^{2} = \frac{3}{2}\Delta H^{2} = \frac{X}{2 (4\alpha)^{2/3}}e^{ - 6 ( \frac{t^{2}}{4\alpha} )^{1/3}}, } \end{aligned}$$
(3.25)
$$\begin{aligned} &{q = \frac{d}{dt} \biggl( \frac{1}{H} \biggr) - 1 = \frac{(4\alpha)^{1/3}}{2 t^{2/3}} - 1, } \end{aligned}$$
(3.26)

where \(X = X_{1}^{2} + X_{2}^{2} + X_{3}^{2}\).

4 Discussion

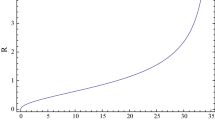
The spatial volume V is finite at t=0. It expands exponentially as time t increase and becomes infinitely large as t→∞ as shown in Fig. 1.

Fig. 1
figure 1

The variation of V vs. t for α=0.5

Full size image

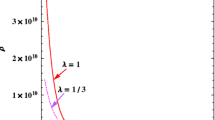
The evolution of expansion scalar θ for α=0.5 is as shown in Fig. 2, it is observed that the expansion scalar θ start with infinite value at t=0 but as cosmic time t increases it decreases and becomes constant after some finite time.

Fig. 2
figure 2

Expansion scalar θ vs. t for α=0.5

Full size image

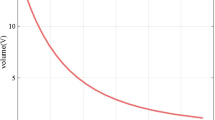
From Fig. 3, it is observed that the evolution of the energy density ρ is infinite at t=0 and as cosmic time t increases it decreases and becomes constant after some finite time for α=0.5.

Fig. 3
figure 3

Evolution of energy density ρ vs. t for α=0.5

Full size image

The deceleration parameter q is decelerating at t=0 and if time t increases then it decreases and becomes negative after some finite time for α=0.5 as shown in Fig. 4.

Fig. 4
figure 4

Deceleration parameter q vs. t for α=0.5

Full size image

It shows that the universe accelerates after an epoch of deceleration. The deceleration parameter q is in the range −1≤q≤0 (shaded region) which matches with the observations made by Riess et al. (1998) and Perlmutter et al. (1999).

5 Conclusion

A Bianchi type-I cosmological model has been investigated with a quadratic equation of state (EoS) parameter. The physical and kinematical parameters which are very important in the discussion of cosmological models have been obtained and a graphical representation of each of them is presented and studied. It is observed that the spatial volume of the model expands exponentially with time and the energy density decreases with time and becomes constant after a finite time. Observation of deceleration parameter shows early inflation and late time acceleration of the obtained universe which is in accordance with the present day scenario of accelerated expansion of our universe as per Riess et al. (1998) and Perlmutter et al. (1999).