1 Introduction

The subject of nonlinear waves in plasma have received considerable interest in plasma physics because of their importance in the environment of space and in laboratory. Among the nonlinear wave structures, solitons are of particular interest for researchers as the solitons offer a rich physical insight underlying the nonlinear phenomena. During the last several decades, the propagation of ion acoustic solitary waves (IASWs) in plasma has been extensively studied theoretically and also in laboratory (Ikeji et al. 1970; Cairns et al. 1996; Yoshimura and Watanabe 1991; Konotop 1996; Hashimoto and Ono 1972; Duan et al. 1997; Mahmood and Saleem 2002). Solitary wave propagation in unmagnetized plasmas without the dissipation can be described by the Korteweg-de Vries (KdV) equation or Kadomtsev-Petviashvili (KP) equation. In recent years quantum plasmas have received a great attention in investigating various aspects of plasma like quantum plasma echo (Manfredi and Feix 1996), dense plasma particularly in astrophysical and cosmological studies (Kremp et al. 1999; Opher et al. 2001; Jung 2001; Chabrier et al. 2002), quantum plasma instabilities in Fermi gases (Manfredi and Hass 2001), quantum landau damping (Suh et al. 1991). Among the prevalent models to study quantum effects in plasma, quantum hydrodynamic (QHD) (Acona and Iafrate 1989; Gardner 1994; Gasser and Markowich 1997; Gardner and Ringhofer 2000; Gasser et al. 2000) model has become popular because it extends the usual fluid model to one incorporating the quantum effect. The QHD model is closed to the classical fluid model as it is comprised of a set of equations describing transportation of charge momentum and energy. The derivation from the classical model occurs mainly due to the presence of a term which is called Bohm potential (Gardner 1994). This term contains the Planck’s constant ħ indicating the quantum effect. In ultra-small electronic devices, the QHD model describes negative differential resistance in resonant tunneling diodes and ultra-small high electron mobility transistors (Zhou and Ferry 1993; Chen et al. 1995). Another significant quantum plasma theory which must be mentioned here is the Wigner Poisson system (Gardner et al. 1989; Markowich et al. 1990; Gardner 1991) which involves the integro differential system. Haas et al. (2003) used the QHD model to study quantum ion acoustic waves in the weakly nonlinearized theory and obtained a deformed Korteweg-de Vries (dKdV) equation which involves the parameter H, proportional to the Planck’s constant ħ. They observed several characteristic features of pure quantum origin for the linear, weakly nonlinear and fully nonlinear waves. Malik et al. (1994) have derived modified KP equation to study two dimensional soliton propagation in an inhomogeneous plasma with finite temperature drifting ions. El-Shewy et al. (2011) have studied solitary solution and energy for the KP equation in two temperatures charged dusty grains. Lin and Duan (2005) have investigated the solitary waves in a two temperature dusty plasma by deriving KP equation. Gill et al. (2006) have derived KP equation for dusty plasma with variable dust charge and two temperature ions. Pakzad (2009, 2010) have studied solitary waves of the KP equation in warm dusty plasma with variable dust charge, two temperature ion and nonthermal electron. In the present paper, we studied the propagation of IASWs in an unmagnetized quantum plasma. By using the reductive perturbation method (RPM) on two dimensional unmagnetized case of this system, one can obtain the KP equation. Balancing between nonlinear and dispersion effects can result in the formation of symmetrically solitary waves. The organization of the paper is as follows. In Sect. 2 the basic set of equations are given and KP equation has been derived. In Sect. 3 results and discussions are given, while Sect. 4 is kept for conclusion.

2 Basic equations and derivation of the KP equation

We consider an unmagnetized quantum plasma system comprising electrons and ions and investigated the nonlinear propagation IASWs. The following set of normalized two-dimensional equations of continuity, motion and Poisson describe the nonlinear dynamics of IAWs in quantum plasma:

$$ \frac{\partial n_e}{\partial t}+\frac{\partial }{\partial x}(n_e u_e)+\frac{\partial }{\partial y}(n_e v_e)=0 $$
(1)
$$ \frac{\partial n_i}{\partial t}+\frac{\partial }{\partial x}(n_i u_i)+\frac{\partial }{\partial y}(n_i v_i)=0 $$
(2)
(3)
(4)
(5)
(6)
$$ \frac{\partial ^2 \phi}{ \partial x^2}+\frac{\partial ^2 \phi}{ \partial y^2} =n_e-n_i $$
(7)

where \(\nabla=(\frac{\partial }{\partial x},\frac{\partial }{\partial y} )\) and n e , u e , v e , m e , (n i , u i , v i , m i ) are the electron (ion) number density, velocity field in the x direction, y direction and mass respectively and \(H=\frac{\hbar \omega_{pe}}{2k_{B}T_{Fe}}\) is the nondimensional quantum parameter, ħ is the Planck constant divided by 2π, k B is the Boltzmann’s constant, T Fe is the Fermi temperature and \(\omega_{Pe}=(4 \pi n_{0} e^{2}/m_{e})^{\frac{1}{2}}\). ϕ is the electrostatic wave potential. n e and n i are normalized to unperturbed plasma density n 0, u e , v e (u i ,v i ) is the electron (ion) fluid speed normalized to the ion acoustic velocity \(C_{s}=(2 k_{B}T_{Fe}/m_{i})^{\frac{1}{2}}\), and ϕ is normalized to 2k B T Fe /e. The time and space variables are in units of the ion plasma period \({\omega_{Pi}}^{-1}=(m_{i}/4 \pi n_{0} e^{2})^{\frac{1}{2}}\) and the Debye radius \(\lambda_{D}=(2 k_{B}T_{Fe}/4 \pi n_{0} e^{2})^{\frac{1}{2}}\), respectively.

We assume that the electrons obey the equation of state in two-dimension (Manfredi and Hass 2001)

$$ p_e=\frac{m_e v_{Fe}^2}{4n_{0}}n_e^2 $$
(8)

where the electron Fermi velocity v Fe connected to the Fermi temperature T Fe by \(m_{e} v_{Fe}^{2}/2= k_{B}T_{Fe}\).

To derive the KP equations we use the stretched coordinates

$$ \xi={\varepsilon }(x-v_0 t),\quad\eta={\varepsilon }^{2}y \quad \mbox{and}\quad\tau={\varepsilon }^{3}t $$
(9)

The dependent variables are expanded as follows:

$$ n_e=1+\varepsilon ^2 {n}^{(1)}_e+{\varepsilon }^{4} {n}^{(2)}_e+ \cdots $$
(10)
$$ n_i=1+\varepsilon ^2 {n}^{(1)}_i+{\varepsilon }^{4} {n}^{(2)}_i+ \cdots $$
(11)
$$ u_e=\varepsilon ^2 {u}^{(1)}_e+{\varepsilon }^{4} {u}^{(2)}_e+ \cdots $$
(12)
$$ u_i=\varepsilon ^2 {u}^{(1)}_i+{\varepsilon }^{4} {u}^{(2)}_i+ \cdots $$
(13)
$$ v_e={\varepsilon }^{3} {v}^{(1)}_e+{\varepsilon }^{5} {v}^{(2)}_e+ \cdots $$
(14)
$$ v_i={\varepsilon }^{3} {v}^{(1)}_i+{\varepsilon }^{5} {v}^{(2)}_i+ \cdots $$
(15)
$$ \phi=\varepsilon ^2 {\phi}^{(1)}+{\varepsilon }^{4} {\phi}^{(2)}+ \cdots $$
(16)

Substituting (10)–(16) into (1)–(7), we obtain from the lowest order in ε,

where \(m=\frac{m_{i}}{m_{e}}\) and

$$ v_0=\sqrt{\frac{4 m}{m+1}} $$
(17)

And for the higher orders of ε, we obtain the following set of equations,

$$ -v_0 \frac{\partial v^{(1)}_e}{\partial \xi}=m\frac{\partial \phi^{(1)}}{\partial \eta}-2m\frac{\partial n^{(1)}_e}{\partial \eta} $$
(18)
$$ -v_0 \frac{\partial v^{(1)}_i}{\partial \xi}=-\frac{\partial \phi^{(1)}}{\partial \eta}-2\frac{\partial n^{(1)}_i}{\partial \eta} $$
(19)
$$ \frac{\partial ^2 \phi^{(1)}}{\partial \xi^2}=n^{(2)}_e-n^{(2)}_i $$
(20)
(21)
(22)
(23)
(24)
(25)
(26)

Combining above equations, we get the KP-equation as

$$ \frac{\partial }{\partial \xi} \biggl[\frac{\partial \phi^{(1)}}{\partial \tau} +A\phi^{(1)} \frac{\partial \phi^{(1)}}{\partial \xi} +B\frac{\partial ^3 \phi^{(1)}}{\partial \xi^3} \biggr]+C\frac{\partial ^2 \phi^{(1)}}{\partial \eta^2}=0 $$
(27)

where

$$ A=-\frac{3 v_0\{m(2-v_0^2)^2+(2m-v_0^2)^2\}}{2(m-1)(2m-v_0^2)(2-v_0^2)}, $$
(28)
$$ B=\frac{H^2\{v_0^2(1-m)-4(2m-v_0^2)^2(2-v_0^2)\}}{16mv_0(m-1)}, $$
(29)

and

$$ C=\frac{v_0}{2} $$
(30)

3 Solitonic solution and discussion

Introducing a new variable ζ=ξ+η−Uτ, where U is a constant velocity, the soliton solution of (27) can be written in the following form

$$ \phi^{(1)}(\zeta)=\phi_0 \mathit{Sech}^2(\zeta/W) $$
(31)

where the soliton amplitude ϕ 0 and the soliton width W are

(32)
(33)

The study of the amplitude and width of solitons is a common way to recognize waves in plasmas. The other way is the study of the soliton’s energy. The soliton solution (31) can give the soliton energy

$$ E=\int_{-\infty}^{\infty} {\phi^{(1)}}^2(\zeta) d\zeta $$
(34)

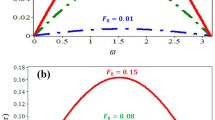
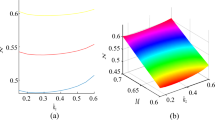
From Eq. (32) and (33) it is seen that the soliton width is significantly affected by the quantum diffraction parameter H, but the quantum correction does not affect the soliton amplitude. Also, from Eq. (34) it is found that the soliton energy is modified by the quantum parameter. The two fluid quantum magnetohydrodynamic model is used which includes the quantum diffraction effects which are proportional to ħ 2 and due to the density fluctuations. The quantum parameter H is a measure of quantum diffraction effects and only modifies the dispersive coefficient. Quantum effects are very important in astrophysical objects like white dwarfs, neutron stars where densities are enormous. In Fig. 1 we plot the solution (31) for different values of H. It is evident from the figure that the amplitude of the nonlinear potential structures remain constant with the increase in the quantum diffraction parameter H associated with the quantum Bohm potential. However, only the width of the solitary structure is broadened with the increase in the value of H. The quantum mechanical effects due to quantum correlation of electron number density fluctuation on the energy of soliton is shown in Fig. 2. This indicates that the energy of soliton increases by increasing the quantum Bohm potential. The quantum statistic effect enhances the energy of soliton.

Fig. 1
figure 1

Plot of ϕ (1) against ζ for different values of H=2.2 (solid line), H=1.8 (dotted line), H=1.5 (dashed line), for the solution (31), where U=1.2 and m=1836

Full size image
Fig. 2
figure 2

Plot of soliton energy (34) against H, where the other parameters are same as given in Fig. 1

Full size image

4 Conclusion

In the present study we have investigated the nature of nonlinear propagation of IASWs in an unmagnetized collisionless quantum plasma. We have derived the KP equation using the standard reductive perturbation technique. It is seen that the quantum diffraction parameter H has a significant effect on the formation of the propagation of IASWs. It is found that with the increase of H, the width of the soliton increases, but the amplitude remains constant. It is found that an increase in the quantum Bohm potential increases the energy of solitons.