Misinformation influence minimization by entity protection on multi-social networks

Abstract

Massive amounts of information are generated in various social media and spread across multi-social networks through individual forwarding and sharing, which greatly enhance the speed and scope of transmission, but also bring great challenges to the control and governance of misinformation. The characteristics of the spread of misinformation across multi-social networks are considered, this article investigates the novel problem of misinformation influence minimization by entity protection on multi-social networks, and systematically tackling this problem. We analyse the hardness and the approximation property of the problem. We construct a multi-social networks coupled method and devise a pruning and filtering rule. We develop a two-stage discrete gradient descent (TD-D) algorithm to solve NP-Hard problems. We also construct a two-stage greedy (TG) algorithm with the approximate guarantee to verify the algorithm we developed. Finally, the effectiveness of our proposed methods is analysed in synthetic and real multi-network datasets (contains up to 202K nodes and 2.5M edges). The results show that the ability of the TD-D and TG algorithms to suppress the spread of misinformation is basically the same, but the running time of the TG algorithm is much higher than (far more than 10 times) that of the TD-D algorithm.

1 Introduction

As online social media has grown in diversity and disruption, large numbers of users are viewing, evaluating or forwarding information across multiple online social networks, greatly enhancing the scope and speed of information diffusion. Information dissemination presents magnanimity, dispersion, and uncontrollable characteristics. While online social media brings great convenience for people to obtain positive content (news, stories, knowledge, etc.), it is also a double-edged sword, urging a large amount of negative content (misinformation, violence, terrorist information, etc.) to form network public opinion, causing social unrest. For example, in 2017, online social media in India sparked panic across the country when false news surfaced that the perpetrators of two shootings in eastern Jharkhand were members of child trafficking gangs [1].

At present, the governance of negative content has attracted the attention of many researchers [2,3,4], but most of them study the control strategy of negative content in a single online social network, which ignores the ever-changing network environment in real life. Without considering fake accounts, the individual characteristics reflected by a single social network are obviously not comprehensive and objective compared to multi-social networks. For example, in the case of friend relationship recommendation content, the acceptance rate of the recommendation information will be higher when the recommendation information is integrated with the friend relationship of multi-social networks than the recommendation only on the single online social network. Hence, it is not comprehensive enough to study the control strategy of misinformation only in a single online social network. It is more reasonable and convincing to propose a misinformation governance strategy by comprehensively considering the attributes of multi-social networks.

Example 1

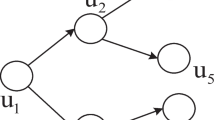
Given a multi-social networks G containing two online social networks G¹ and G², we call the nodes in G¹ or G² the accounts, and an individual who controls the accounts in multi-social networks is called an entity. In G¹ and G², a node represents the account controlled by the entity, and directed edges indicate the spread of content, as illustrated in Fig. 1. In the multi-social networks G(G¹,G²), entity a controls two accounts, a¹ and a². In G¹, account a¹ will send the information actively, and account a² will only passively receive information in G². It can be seen that different accounts controlled by the same entity may play completely distinct roles in information dissemination.

Fig. 1

A simple multi-social networks G(G¹,G²)

Different misinformation control and governance strategies have been proposed based on distinct actual backgrounds [5,6,7,8,9,10]. Some scholars [7, 8, 10, 11] considered the influence of nodes, and chose to block a set of nodes or links to reduce the final acceptance rate of misinformation. Although these strategies exhibit good performance in suppressing the spread of misinformation, they violate the ethical standards of censorship. Since the blocking nodes (links) measures mainly work on the accounts (posts published) that an entity owns on a social network platform, they seem to be ineffective or pay multiple times to achieve the desired results in multi-social networks. Therefore, this paper considers the characteristics of multi-social networks and designs a misinformation control strategy that acts on entities. Of course, some scholars [9, 12, 13] have proposed a misinformation control strategy that acts on entities: select some entities to spread positive information. Since whether entities spread positive information in real life is mainly based on their own wishes, this measure strongly assumes that selected individuals must spread positive information, which greatly violates the ethical standards of censorship. Hence, to compensate for the shortcomings of the existing research, this paper proposes an ‘entity protection’ strategy to combat the spread of misinformation.

Given a multi-social networks G(G¹, G², ⋯ , Gⁿ) = G(V,E) containing n online social networks, the initial influence entities $\mathfrak {R}\subseteq V$, and a positive integer K, we aim to centrally identify and protect the set Λ of K entities to minimize the number of entities ultimately influenced by $\mathfrak {R}$. The contributions of this work are as follows:

• We devise a model of information propagation across multi-social networks, and investigate a novel problem of Misinformation Influence minimization by Entity protection on multi-social networks (MIE-m).

• We prove the hardness of the MIE-m problem and discuss the properties of the objective function. We devise the procedure of coupled multi-social networks and the pruning rules, and construct a discrete gradient descent method to optimize the supermodular set function.

• We introduce the method of estimating the influence of information and define the supermodular curvature of the supermodular function. A two-stage discrete gradient descent algorithm is developed. We also construct a two-stage greedy algorithm with approximate guarantees as a baseline to evaluate our developed algorithm.

• We appraise our methods in synthetic and three real-world multi network datasets. The experimental results show that the comprehensive performance of our algorithm is superior to the existing heuristic methods, even the greedy algorithm.

The content of this article is arranged as follows. In Section 2, we review the related work. We give the preliminary knowledge in Section 3. Section 4 formulates the problem of MIE-m and discusses its valuable properties. In Section 5, we explore approximate methods to optimize the problem of influence minimization. We develop a two-stage discrete gradient descent algorithm to solve the problem in Section 6. Section 7 uses synthetic and real-world multi networks to verify the efficiency and effectiveness of our algorithm. Finally, the article is summarized and prospected in Section 8. Table 1 gives the characters required in the article.

Table 1 Frequency of Special Characters

2 Related works

Domingos and Richardson [14] first put forward the problem of maximizing the influence of information, and then Kempe et al. [15] turned the problem into a discrete optimization problem, and proposed two classic information diffusion models: the independent cascade (IC) model and the linear threshold (LT) model. Many researchers [10, 16, 17] have expanded or improved the IC (LT) model to propose strategies for suppressing negative contents.

Taking into account the topological structure of online social networks, the utility experience of users and the method of user interaction, many scholars [18,19,20] have proposed the active control strategy of blocking nodes or links to minimize the influence of negative contents. Zhang et al. [19] formulated a novel rumour containment problem based on the user’s browsing behaviour, namely, the rumour block based on user browsing, to actively limit the spread of rumours. Yan et al. [20] blocked a set of links from the perspective of diminishing margins to minimize the total probability of nodes being activated by rumours. As proactive measures to control misinformation may have a negative impact on the user experience, some researchers [9, 21, 22] have proposed a strategy of publishing positive information or strategies of reflexive rumours to counter the spread of misinformation. Wu et al. [9], based on the maximum influence arborescence structure, constructed two heuristic algorithms CMIA-H and CMIA-O to identify a set of seeds that initiate positive information against misinformation dissemination. Lv et al. [22] considered the locality of influence diffusion and proposed a new community-based algorithm to optimize the influence blocking maximization problem. Ghoshal et al. [21] leveraged a known community structure to propose probability strategies for beacon node placement to combat the spread of misinformation in online social networks. In addition, some scholars [6] have proposed suppressing the spread of misinformation by injecting influence messages related to multiple hot topics. Summarizing the existing research works, we know that most scholars investigated information dissemination in the context of virtual single social network and rarely considered the characteristics of information dissemination across multi-social networks in real life. Moreover, most of the existing misinformation control strategies do not consider the ethical standards of censorship, and the main body of the control strategy is mostly an account owned by the entity on a certain social network. Therefore, this paper devises a misinformation control strategy that acts on entities, called entity protection, for multi-social networks.

At present, some scholars [23, 24] have also carried out research on the dissemination of misinformation based on multi-social networks. Yang et al. [23], based on the study of dynamic behaviors related to multiple network topologies, constructed a competitive information model on multi-social networks. Hosni et al. [24] considered individuals and social behavior in multi-social networks and proposed an individual behavior statement that simulates damped harmonic motion in response to rumours. It can be seen from the above that they pay more attention to the aggregation of multi-social networks and do not make a detailed modelling of the details of misinformation dissemination among multi-social networks. Hence, it is necessary to carefully consider the details of misinformation dissemination between multi-social networks and propose a reasonable model of the dissemination of misinformation across multi-social networks.

Computational influence propagation has been proven to be #P-hard [15]. It has been proven that using a greedy strategy can obtain the solution of the (1 − 1/e) approximate guarantee of the set function with submodular [15]. Manouchehri et al. [25] developed a two-step algorithm of the (1 − 1/e − ε)-approximate guarantee based on the martingale to solve the influence blocking maximization. Unfortunately, the set function without submodules will no longer hold this property [26, 27]. Zhu et al. [26] proposed the disbanding strategy of groups in online social networks to curb the spread of misinformation and constructed a greedy algorithm without approximate guarantees to solve nonsubmodular objective functions.

Moreover, many scholars have constructed heuristic methods [28,29,30] to tackle nonsubmodular set functions. Wang et al. [28] constructed the upper and lower bounds of the submodular for the nonsubmodular function and used the sandwich method to maximize activity. Unfortunately, there is currently no universal and effective way to find the lower and upper bounds of the submodular of the nonsubmodular set function. Ghoshal et al. [30] leveraged the underlying community structure of an online social network to select influential nodes with true information for misinformation blockage. Hosseini-Pozveh et al. [29] applied random key representation technology to propose a continuous particle swarm optimization method to solve the nonsubmodular set function. Most of the current heuristic methods sacrifice the accuracy of the solution in exchange for the solution speed of the nonsubmodular function. Hence, the solving efficiency and accuracy of the equilibrium algorithm in this paper, develops a two-stage discrete gradient descent algorithm to solve the supermodular set function.

3 Preliminaries

3.1 Definitions

Since multi-social networks are disparate from a single social network in terms of network topology, nodes, and edges, we will define multi-social networks and their characteristics.

Definition 1

(Multi-social networks) A directed asymmetric multi-social networks G(V,E) = G(G¹,G²,⋯ ,Gⁿ) containing n online social networks, v ∈ V denotes the entity in G, and (v,w) ∈ E denotes the relationship between entities. For the online social network Gⁱ(Vⁱ,Eⁱ) (1 ≤ i ≤ n), Vⁱ and Eⁱ respectively represent the node set and edge set. The precondition for the existence of an edge (v,w) is that there is an edge (vⁱ,wⁱ) in at least one online social network Gⁱ. A simple multi-social networks is shown in Fig. 2.

Fig. 2

A simple multi-social networks G(G¹,G²,G³) with eight entities {v₁,v₂,⋯ ,v₈}. The solid lines represent information exchanges between accounts, and the dotted lines indicate the accounts controlled by the entity

Definition 2

(Entity and Account) Without causing ambiguity, we call the node in the online social network the account and an individual who controls the accounts in multi-social networks is called an entity. When an entity controls multiple accounts in G, w = {ξ(wⁱ)|wⁱ ∈ Vⁱ,1 ≤ i ≤ n} represents the account controlled by it, and ξ(wⁱ) means mapping wⁱ to w.

Definition 3

(Entity Preference) When an entity accepts information through account wⁱ in Gⁱ, he/she may forward the information to other online social networks G^o(o≠i). Considering the discrepancies in services provided by different online social networks, the propensity of entities to use distinct online social networks to spread information is also inconsistent. Hence we define the entity’s propensity to employ diverse online social networks as the entity’s preference for different online social networks, and the preference of entity w for Gⁱ is denoted as ${\rho _{w}^{i}}$.

Definition 4

(Account and Entity Status) In multi-social networks, when an entity accepts information through the account, we call that entity successfully activated. When an entity is activated, the accounts it controls are also activated simultaneously.

Definition 5

(Entity Protection). Entity protection refers to the use of personalized recommendation technology to let some entities know positive information in advance before receiving misinformation, so that they will not share it when they receive misinformation to achieve the purpose of actively ‘blocking’ misinformation dissemination.

In real life, once people are influenced by the correct information spread by verified sources, they will believe the correct information regardless of the misinformation [30, 31]. Since people are more inclined to share novel information with their friends [32, 33], entities that receive positive information may be willing to share it. Considering that forcing an entity to spread positive information violates the ethical standards of censorship, this paper assumes that an entity receives positive information and does not spread it. People with correct information will not be affected by misinformation [30, 34]. If entities already realize positive information before receiving misinformation, they are likely to ignore it when they receive misinformation and will not share it again to fulfil the intention of actively ‘blocking’ misinformation dissemination.

3.2 Dissemination model

This article studies governance strategies of misinformation based on the IC model. Next, we review the IC model. Consider a directed social network $\overline {G}(\overline {V},\overline {E})$, where $\overline {V}$ denotes the set of nodes, $(\overline {u}, \overline {v})\in \overline {E}$ denotes the relationship between node $\overline {u}$ and $\overline {v}$, and each edge $(\overline {u}, \overline {v})$ has an attribute $\overline {p}_{\overline {u}\overline {v}}$ that indicates the probability of node $\overline {u}$ successfully activating node $\overline {v}$.

Let R_t be the set of nodes that are activated in time steps t(t = 0,1,2,⋯ ), and when $\overline {u} \in R_{t}$, it has one and only one chance to activate its inactive neighbor child node $\overline {v}$ with $\overline {p}_{\overline {u}\overline {v}}$ in t + 1. In addition, in the process of information dissemination, the node can only switch from the inactive state to the active state, not reverse. The specific spreading process of information in discrete time is as follows: At time t = 0, information diffusion starts, and source nodes $\mathfrak {R}$ are triggered at the same time, that is, $R_{0}=\mathfrak {R}$. In t = q(q ≥ 1), $\overline {u}\in R_{q-1}$ activates the set of its inactive child neighbors with probability $\overline {p}_{\overline {u} \cdot }$. If the node is successfully activated, it will be added to R_q, and the information dissemination will stop when R_q is empty.

4 Problem formulation

In this part, we first devise a model of information propagation across multi-social networks, then give a formal statement of the problem of MIE-m, and discuss the properties of the objective function.

4.1 Misinformation dissemination across multi-social networks

In multi-social networks G(G¹,G²,⋯ ,Gⁿ), when entity w accepts misinformation in online social network Gⁱ, the entity w may choose i (1 ≤ i ≤ n) online social networks to disseminate misinformation in the next. Entities send misinformation to other online social networks by forwarding or sharing, and the entity’s preferences affect the probability of misinformation being forwarded and shared among its own accounts. Therefore, we define the probability that entity w forwards misinformation to account wⁱ in Gⁱ as

$$ P^{fwd}(w^{i})=\frac{\varphi \cdot(1+{\sum}_{o=1, o\neq i}^{n} \frac{{\rho_{w}^{i}}}{{\rho_{w}^{o}} + {\rho_{w}^{i}}}) }{\vert w \vert} $$

(1)

where φ is a constant parameter, ${\rho _{w}^{o}}$ represents entity w’s preference for online social network G^o, and |w| denotes the number of accounts controlled by entity w.

In an online social network Gⁱ, the higher the similarity between accounts, the more similar the types of topics they follow, and the greater the probability of sending misinformation to each other. Moreover, according to the ideology of the celebrity effect [15, 24], the higher the out-degree of account is, the greater the impact on other accounts and the less likely they are to be influenced by other accounts. Hence, we conclude that the probability that account wⁱ successfully activates account uⁱ ∈ N^out(wⁱ) is

$$ P^{inf}(w^{i}, u^{i}) = \frac{\varpi + \vert N^{out} (w^{i}) \bigcap N^{out} (u^{i}) \vert} { \vert N^{out} (w^{i}) \vert + \vert N^{out} (u^{i})\vert} $$

(2)

where ϖ is a constant parameter and N^out(wⁱ) represent the child neighbors of account wⁱ in online social network Gⁱ.

Based on the IC model, we construct a dynamic propagation model of misinformation across multi-social networks. In multi-social networks G(G¹,G²,⋯ ,Gⁿ), misinformation dissemination occurs in discrete steps t = 0,1,2,⋯. Once the entities (accounts) are activated, they will remain active until the end of misinformation dissemination. The specific process of dissemination of misinformation across multi-social networks is as follows:

• 1. When misinformation in multi-social networks begins to spread at step t = 0 and simultaneously triggers a set of initial activation entities $\mathfrak {R}\subset V$. Let $\mathfrak {R}_{t}$ be the entities that are influenced in steps t(t = 0,1,2,⋯ ) and $\mathfrak {R}_{0}=\mathfrak {R}$.

• 2. At step t (t ≥ 1), first, the $w\in \mathfrak {R}_{t-1}$ forwards the misinformation to each account wⁱ (1 ≤ i ≤ n) with the probability P^fwd(wⁱ). Then, account wⁱ tries to activate the inactivated child neighbor uⁱ ∈ N^out(wⁱ) with the probability P^inf(wⁱ,uⁱ). If account uⁱ is activated, its mapped entity u is converted into an activated entity and added to $\mathfrak {R}_{t}$.

• 3. Repeat Steps 2. until $\mathfrak {R}_{t}=\varnothing$, and the dissemination of misinformation across multi-social networks stops.

Algorithm 1 outlines the procedure of misinformation spread across multi-social networks.

Example 2

In Fig. 3, given $\mathfrak {R}=\{z\}$, the influence probability P^inf(⋅,⋅) = 1 for all edges in each online social network, and the probability P^fwd(⋅) = 1 for all entities. At t = 0, $\mathfrak {R}_{0}=\mathfrak {R}=\{z \}$. When t = 1, entity z activates v¹ with account z¹ in G¹ and activates w² with account z² in G². Then entities v and w are added to $\mathfrak {R}_{1}$. At t = 2, entity v successfully activates account u¹ in G¹, and all child neighbors of entity w have been activated; then, $\mathfrak {R}_{2}=\{v \}$. At t = 3, all entities in G have been activated, so $\mathfrak {R}_{3}=\varnothing$, and misinformation dissemination is terminated.

Fig. 3

A simple multi-social networks G(G¹,G²) with four entities {z,w,u,v}

4.2 Problem definition

Since misinformation spreads across multi-social networks, which increases the dissemination speed and expands the spread range of misinformation, it also brings great challenges to the control and governance of misinformation. For this reason, considering the characteristics of the dissemination of misinformation across multi-social networks, we propose the problem of Misinformation influence Minimization by Entity protection on multi-social networks (MIE-m). Next, we give the formal statement of this problem.

Definition 6

(MIE-m) Let G(V,E) = G(G¹,G², ⋯ ,Gⁿ) denote directed multi-social networks with n online social networks Gⁱ(Vⁱ,Eⁱ). Given an initial influence entities $\mathfrak {R}$, the positive integers K and a propagation model $\mathfrak {M}$. MIE-m tries to identify and protect the set Λ containing K entities from the $V \backslash \mathfrak {R}$ to minimize the number of entities ultimately activated by $\mathfrak {R}$,

$$ \begin{array}{@{}rcl@{}} {\varLambda}^{*}=\arg \min\limits_{{\varLambda} \subseteq V \backslash \mathfrak{R},\vert {\varLambda} \vert \leq K} \mathbb{E} \left[\sigma_{\mathfrak{R}}({\varLambda})\right] \end{array} $$

(3)

where $\mathbb {E}[\cdot ]$ is the expectation operator and $\sigma _{\mathfrak {R}}({\varLambda })$ is the number of entities successfully activated by $\mathfrak {R}$ when entity set Λ is protected.

Example 3

In Fig. 1, a multi-social networks G(G¹,G²) with entities {a,b,c,d,v,w}. We set $\mathfrak {R}=\{a \}$, the probability P^inf(⋅,⋅) = 1 for all edges in G¹ and G², and probability P^fwd(⋅) = 1 for all entities. When ${\varLambda } =\varnothing$, the spread value of misinformation $\sigma _{\mathfrak {R}}({\varLambda }) = 6$. Let K = 1, protect the entity $u\in V\backslash \mathfrak {R}$, and obtain $\sigma _{\mathfrak {R}}(\{b \}) = 2$, $\sigma _{\mathfrak {R}}(\{c \}) = 4$, $\sigma _{\mathfrak {R}}(\{v \}) = 3$, $\sigma _{\mathfrak {R}}(\{w \}) = 3$, $\sigma _{\mathfrak {R}}(\{d \}) = 4$. Obviously, choosing to protect entity a can better suppress the spread of misinformation, that is, Λ^∗ = {b}.

4.3 Hardness results

Definition 6 shows that the problem of MIE-m is a discrete optimization problem, then we evaluate the hardness of this problem.

Theorem 1

Influence minimization is NP-hard in multi-social networks.

Proof

See Appendix A. □

Theorem 2

Given initial influence entities $\mathfrak {R}\subseteq V$, computing $\sigma _{\mathfrak {R}}({\varLambda })$ is #P-hard in multi-social networks.

Proof

See Appendix A. □

4.4 Modularity of objective function

Next, we prove the monotonicity and modularity of the objective function. Let SG be the set of ‘live-edge’ graphs [15] generated from G based on the existence probability of the edges, where the existence probability of the edges means the influence probability or forwarding probability. Pr(sg) is the probability of generating graph sg ∈ SG. $\sigma _{\mathfrak {R}}^{sg}({\varLambda })$ is the number of entities influenced by $\mathfrak {R}$ in the network topology sg∖Λ. Therefore, the number of entities that are expected to accept the misinformation after protecting K entities until the end of the dissemination of misinformation is $\sigma _{\mathfrak {R}}({\varLambda })={\sum }_{sg\in SG}Pr(sg)\sigma _{\mathfrak {R}}^{sg}({\varLambda })$.

Theorem 3

$\sigma _{\mathfrak {R}}({\varLambda })$ is nonnegative and monotonically decreasing.

Proof

Since $\sigma _{\mathfrak {R}}^{sg}({\varLambda })$ is nonnegative, $\sigma _{\mathfrak {R}}({\varLambda })$ is also nonnegative. For a fixed sg ∈ SG, given $L_{1}\subseteq L_{2}\subseteq V$, there is $\sigma _{\mathfrak {R} }^{sg} (L_{1}) \geq \sigma _{\mathfrak {R} }^{sg} (L_{2})$. That is, $\sigma _{\mathfrak {R} }(L_{1}) = {\sum }_{sg \in SG} Pr(sg) \sigma _{\mathfrak {R} }^{sg} (L_{1}) \geq {\sum }_{sg \in SG } Pr(sg) \sigma _{\mathfrak {R}}^{sg} (L_{2})$ $=\sigma _{\mathfrak {R}} (L_{2})$. Therefore, $\sigma _{\mathfrak {R}} ({\varLambda })$ is monotonically decreasing. □

Theorem 4

$\sigma _{\mathfrak {R}}({\varLambda })$ is supermodular in multi-social networks

Proof

Because $\sigma _{\mathfrak {R}}({\varLambda })={\sum }_{sg\in SG}Pr(sg)\sigma _{\mathfrak {R}}^{sg}({\varLambda })$, we prove that $\sigma _{\mathfrak {R}}({\varLambda })$ is supermodular, and we only need to prove that ${\Xi }_{\mathfrak {R}}({\varLambda })=\sigma _{\mathfrak {R}}^{sg}({\varLambda })$ is supermodular for each ‘live edge’ graph sg. Let L₁, L₂ be two subsets of $V\backslash \mathfrak {R}$ and L₁ ⊂ L₂. We have v ∈ V ∖L₂, considering the difference between ${\Xi }_{\mathfrak {R}}(L_{1})$ and ${\Xi }_{\mathfrak {R}}(L_{1} \cup \{v\})$, which must come from node v that can be reached, but node set L₁ cannot be reached. Similarly, the difference between ${\Xi }_{\mathfrak {R}}(L_{2})$ and ${\Xi }_{\mathfrak {R}}(L_{2} \cup \{v\})$ must be reachable from v but cannot be reachable from the nodes L₂. Since L₁ ⊂ L₂, it follows that ${\Xi }_{\mathfrak {R}}(L_{2}) -{\Xi }_{\mathfrak {R}}(L_{2} \cup \{v\}) \leq {\Xi }_{\mathfrak {R}}(L_{1}) -{\Xi }_{\mathfrak {R}}(L_{1} \cup \{v\})$, that is, ${\Xi }_{\mathfrak {R}}(L_{2} \cup \{v\}) -{\Xi }_{\mathfrak {R}}(L_{2}) \geq {\Xi }_{\mathfrak {R}}(L_{1}\cup \{v\}) -{\Xi }_{\mathfrak {R}}(L_{1})$. Hence, ${\Xi }_{\mathfrak {R}}({\varLambda })$ is supermodular and the theorem is proven. □

5 Solutions methods

In this section, we explore approximate methods for solving MIE-m. First, we design the method of coupled multi-social networks. Then, a pruning and filtering rule is introduced. Finally, a discrete gradient descent method is developed for solving NP-Hard problems.

5.1 Multi-social networks coupled method

Considering that the account only serves as a carrier for spreading misinformation, the subject of sending and accepting misinformation is still an entity. In addition, if the problem of MIE-m is solved by using accounts as the object, the time complexity of solving the problem will be increased. Therefore, we hide accounts, map the relationships between accounts to entities, and devise methods for coupled multi-social networks.

In the coupled of multi-social networks, the accounts controlled by the entity cannot be simply regarded as the same entity for coupled. The characteristics and attributes of the account should be guaranteed first, and then how to add connections among multiple social factors should be considered. To more directly add relationships between entities, we give the relational network $G_{cou}(\hat {V},\hat {E})$, $\hat {V}$ is the entity set, and $\hat {E}$ is the edge set that maps from accounts connections to entities.

Based on the entity’s preference for diverse online social networks, we give the calculation formula for the probability $\hat {p}(\hat {w},\hat {v})$ that entity $\hat {w}$ successfully activates $\hat {v}$ as

$$ \hat{p}(\hat{w},\hat{v})=1-\prod\limits_{i=1}^{n}(1-P^{fwd}(w^{i})\cdot P^{inf} (w^{i},v^{i})). $$

(4)

In Algorithm 2, the procedure of multi-social networks coupled into a single social network is summarized.

Example 4

In Fig. 4a, multi-social networks G contain three online social networks (G¹, G², G³), and V = (v₁,v₂,v₅,v₈). P^inf(⋅,⋅) is calculated, which is shown on the edge between the accounts in Fig. 4a. The result of $P^{fwd}(v_{\cdot }^{i})$ for each account $v_{\cdot }^{i}\in \{{v_{1}^{2}},\ {v_{1}^{3}},\ {v_{5}^{1}},\ {v_{5}^{2}},\ {v_{2}^{2}},\ {v_{2}^{3}},\ {v_{8}^{1}},\ {v_{8}^{2}},\ {v_{8}^{3}}\}$ is {0.77, 0.61,0.61, 0.63, 0.88, 0.67, 0.83, 0.67, 0.67, 0.67}. Next, given the relationship network $G_{cou}(\hat {V}, \hat {E})$, $\hat {V} = \{ \hat {v}_{1},$ $\hat {v}_{2},\hat {v}_{5}, \hat {v}_{8} \}$, $\hat {E} = \{ (\hat {v}_{1},\ \hat {v}_{5})$, $(\hat {v}_{5}, \hat {v}_{8}), {\cdots } \}$, and $\hat {p}(\cdot , \cdot )$ is calculated according to (4), such as, $\hat {p}(\hat {v}_{1}, \hat {v}_{5})= 1-(1-0.77*0.6)(1-0.61*0.22)=0.54$. Finally, Fig. 4b provides the result of the coupled social network G_cou, and the number on the edges denotes the influence probability between entities.

Fig. 4

The example of coupled of multi-social networks G into a single social network G_cou

Proposition 1

Given a multi-social networks G(V,E) = G(G¹,⋯ ,Gⁿ), let $N_{e} = {\sum }_{i=1}^{n} \vert E^{i} \vert$ and $N_{a} = {\sum }_{i=1}^{n} \vert V^{i} \vert$, CMN(G) ends in O(N_e) time.

Proof

For every online social network Gⁱ that needs O(|Vⁱ|) (1 ≤ i ≤ n) to compute P^fwd(⋅), and O(|Eⁱ|) to compute P^inf(wⁱ,uⁱ),(uⁱ,wⁱ ∈ Vⁱ). It takes O(N_e) to compute the $\hat {p}(\hat {e})$ for each $\hat {e}\in \hat {E}$. Thus, the time complexity of algorithm 2 is 2 ∗ O(N_e) + O(N_a). Since N_e ≫ N_a in online social networks, the proposition has followed immediately. □

Based on the above analysis, this article couples multi-social networks G(V,E) into $G_{cou}(\hat {V},\hat {E})$. Then, the problem of MIE-m is transformed into the problem of Misinformation Influence minimization by Entity protection in a coupled social network (MIE-c), and the objective function (3) can be converted to

$$ \begin{array}{@{}rcl@{}} \hat{{\varLambda}}^{*}=\arg \min\limits_{\hat{{\varLambda}} \subseteq \hat{V} \backslash \mathfrak{R},\vert \hat{{\varLambda}} \vert \leq K} \mathbb{E} \left[\hat{\sigma}_{\mathfrak{R}}(\hat{{\varLambda}})\right] \end{array} $$

(5)

where $\hat {{\varLambda }}$ is the set of K entities identified and protected from $\hat {V} \backslash \mathfrak {R}$.

Next, we prove in proposition 2 that the MIE-m problem is equivalent to the MIE-c problem.

Proposition 2

Given a multi-social networks G(V,E), a coupled social network $G_{cou}(\hat {V},\hat {E})$ of G, and an initial influence entities $\mathfrak {R}$, $\sigma _{\mathfrak {R}}({\varLambda })= \hat {\sigma }_{\mathfrak {R}}(\hat {{\varLambda }})$ for any ${\varLambda } \subset V\backslash \mathfrak {R}$ and ${\varLambda }=\hat {{\varLambda }}$.

Proof

See Appendix A. □

Since the problem of MIE-c is equivalent to the problem of MIE-m, $F(\hat {{\varLambda }})$ is a nonnegative monotonically decreasing supermodular function, where $F(\hat {{\varLambda }}) = \hat {\sigma }_{\mathfrak {R}}(\hat {{\varLambda }})$.

5.2 Candidates prune

Since there are disparities in the influence of different entities in G_cou, we introduce the pruning rules to discard the relatively ‘unimportant’ entities. The following propositions prune and filter the candidate set of entities.

Proposition 3

If $N^{in}(\hat {w})=\varnothing ,\ \hat {w} \in \hat {V}\backslash \mathfrak {R}$, protecting $\hat {w}$ does not affect the spread value of misinformation.

Proof

When $N^{in}(\hat {w})=\varnothing$, $\hat {w}\in \hat {V}\backslash \mathfrak {R}$ exists, that is, the parent entity set of the existing entity $\hat {w}$ is empty. Therefore, protecting $\hat {w}$ will not affect the amount of misinformation finally accepted, and the entity $\hat {w}$ can be removed from $\hat {V}$. □

Proposition 4

If $\hat {w}\notin \mathfrak {R}$, $N^{out}(\hat {w})=\varnothing$ or $N^{out}(\hat {w})\subset \mathfrak {R}$ exists, protecting $\hat {w}$ does not affect the probability that $\hat {u}\in \hat {V}\backslash \{\mathfrak {R} \cup \{\hat {w}\} \}$ will be activated by $\mathfrak {R}$.

Proof

When $\hat {w}\notin \mathfrak {R}$, $N^{out}(\hat {w})=\varnothing$ or $N^{out}(\hat {w})\subset \mathfrak {R}$ exists, that is, $\hat {w}$ does not have a child neighbor or all child neighbors are activation entities. Thus, protecting $\hat {w}$ will not affect the probability of other entities being activated by $\mathfrak {R}$, and the entity $\hat {w}$ can be removed from $\hat {V}$. □

Proposition 5

If $\hat {w}\notin \mathfrak {R}$, $\vert N^{in}(\hat {w})\vert =1$, $N^{in}(\hat {w})\notin \mathfrak {R}$, entity $\hat {w}$ can be “discarded” from $\hat {V}$.

Proof

When $\hat {w}\in \hat {V}\backslash \mathfrak {R}$, $\vert N^{in}(\hat {w})\vert =1$, $N^{in}(\hat {w})\notin \mathfrak {R}$ exists, that is, the entity has and only one parent neighbor that is not the source. The effect of protecting the parent neighbor of entity $\hat {w}$ is better than that of protecting itself. Therefore, the entity $\hat {w}$ can be removed from $\hat {V}$. □

According to propositions 3–5, we obtain the candidate set of entities. Algorithm 3 provides the procedure to obtain candidate set $\hat {V}_{sa}$ from $\hat {V}$.

Example 5

In Fig. 4b, the coupled social network G_cou has four entities $\{\hat {v}_{1},\hat {v}_{2},\hat {v}_{5},\hat {v}_{8}\}$. Let $\mathfrak {R}=\{\hat {v}_{1} \}$. For the entity $\hat {v}_{2}$ that satisfies $\hat {v}_{2}\notin \mathfrak {R}$, $N^{out}(\hat {v}_{2}) = \varnothing$, the entity $\hat {v}_{2}$ can be pruned from the candidate set. Thus, the candidate set $\hat {V}_{sa}$ of G_cou is $\{\hat {v}_{5},\hat {v}_{8} \}$.

5.3 Discrete gradient descent method

In this part, combining the characteristics of the gradient descent method [35], we propose the discrete gradient descent method to solve the supermodular function. We set K protected entities as variables, denoted as X = {x₁, x₂, ⋯ , x_K}. Let d be the discrete step size, and B(x_q) be the set of entities d steps away from the entity x_q.

For the K-variable single-valued function h(X) = h(x₁,x₂,⋯ ,x_K), let ${\Delta } {h_{s}^{q}}(X)=h(x_{1},\ \cdots ,\ x_{q}$, x_q+ 1,⋯ ,x_K) − h(x₁,⋯, x_q− 1,s,x_q+ 1,⋯ ,x_K), where |x_q,s| = d,s ∈ B(x_q). ${\Delta } {h_{s}^{q}}(X)$ is the difference between the function value of X and the function value when x_q is substituted for s in X. The approximate discrete partial derivative of a single-valued function with a given d is

$$ \begin{array}{@{}rcl@{}} \frac{\partial_{s} h}{\partial_{s} x_{q}}(X)= \frac{{\Delta}_{max} {h_{s}^{q}}(X)}{d} \end{array} $$

(6)

where ${\Delta }_{max} {h_{s}^{q}} (X)=\max \limits _{s\in B(x_{q})} {\Delta } {h_{s}^{q}}(X)$.

From the properties of online social networks, it is concluded that the discrete step size d between entities is integers; then, d = 1 is given in this article, so (6) is equivalent to

$$ \begin{array}{@{}rcl@{}} \frac{\partial_{s} h}{\partial_{s} x_{q}}(X)= \max_{s \in B(x_{q})} {\Delta} {h_{s}^{q}} (X). \end{array} $$

(7)

We can derive the properties of (7) as follows: When $\frac {\partial _{s} h}{\partial _{s} x_{q}}(X)\leq 0$, x_q is at the local optimum. When $\frac {\partial _{s} h}{\partial _{s} x_{q}}(X) > 0$, x_q points s in the fastest descending direction; that is, when the variable s replaces the variable x_q, h(X) decreases the most. Then, we give

$$ \begin{array}{@{}rcl@{}} \gamma^{q}= \begin{cases} 1, &\frac{\partial_{s} h}{\partial_{s} x_{q}}(X)> 0 \\ 0, &\frac{\partial_{s} h}{\partial_{s} x_{q}}(X) \leq 0 \end{cases} \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} SV^{q}= \begin{cases} s, &\frac{\partial_{s} h}{\partial_{s} x_{q}}(X)> 0 \\ x_{q}, &\frac{\partial_{s} h}{\partial_{s} x_{q}}(X) \leq 0 \end{cases} \end{array} $$

(9)

Definition 7

(Discrete gradient) Given the discrete step size d, the discrete gradient of h(X) is

$$ \begin{array}{@{}rcl@{}} \nabla_{d} h(X) = (\frac{\partial_{s_{1}} h}{\partial_{s_{1}} x_{1}}(X^{1}), \cdots, \frac{\partial_{s_{K}} h}{\partial_{s_{K}} x_{K}}(X^{K}))^{T} \end{array} $$

(10)

where X¹ = X, X^q = X^q− 1 ∪{γ^q− 1 ⋅ SV^q− 1}∖{γ^q− 1 ⋅ x_q− 1}(1 < q ≤ K). Then, ∇_dh(X) can be rewritten as ∇_dh(X) = (γ¹,γ²,⋯ ,γ^K), and the corresponding set of substitution variables is SV = (SV¹, SV², ⋯ , SV^K).

In the discrete gradient ∇_dh(X) of h(X), $x_{q}\rightarrow s$ is one of the steepest descent directions. For the sequence X₁, X₂, ⋯, X_z, ⋯, there is X_z+ 1 = X_z ∪{∇_dh(X_z) ⋅ SV^z}∖{∇_dh(X_z) ⋅ X_z}. Because h(X₀) ≥ h(X₁) ≥ h(X₂) ≥⋯, the iteration terminates when ∇_dh(X_z) = 0 or h(X_z) − h(X_z+ 1) < ε. For the discrete case, in a certain precision ε, may appear along the fastest descent direction search objective function value decreases and convergence the speed slow, then think that has met the accuracy requirements, can stop the search.

Theorem 5

Given a nonnegative set function h(X) and sequence X₁, X₂, ⋯, X_z, ⋯, h(X_z) will converge to a local optimal solution after using the discrete gradient descent method.

Proof

The termination condition of the discrete gradient descent method is ∇_dh(X_z) = 0 or h(X_z) − h(X_z+ 1) < ε, then for the sequence X₁, X₂, ⋯, X_z, ⋯, we only need to prove h(X₀) ≥ h(X₁) ≥⋯ ≥ h(X_z) ≥⋯. ∇_dh(X_z) = (γ¹,γ²,⋯ ,γ^K) exists in variable set X_z, because ${X_{z}^{1}}=X_{z}$, ${X_{z}^{q}}=X_{z}^{q-1}\cup \{\gamma ^{q-1}\cdot SV^{q-1}\} \backslash \{\gamma ^{q-1} \cdot x_{q-1}\} (1< q\leq K)$, and $h({X_{z}^{1}})\geq h({X_{z}^{2}})\geq {\cdots } \geq h({X_{z}^{K}})$. For $X_{z}={X_{z}^{1}}$, $X_{z+1}={X_{z}^{K}} \cup \{\gamma ^{K}\cdot SV^{K}\}\backslash \{\gamma ^{K}\cdot x_{K}\}$, then, we have $h(X_{z})=h({X_{z}^{1}})\geq h({X_{z}^{K}})\geq h(X_{z+1})$. Therefore, we have h(X₀) ≥ h(X₁) ≥ h(X₂) ≥⋯, that is, h(X_z) will converge to the local optimal solution. □

6 Problem solutions

This section first presents methods for estimating the influence of misinformation. Then, a two-stage discrete gradient descent algorithm is constructed, a baseline algorithm is proposed, and the efficiency of the algorithm is analysed.

6.1 Influence estimation

Since computing $\sigma _{\mathfrak {R} ({\varLambda })}$ is #P-hard in multi-social networks, we estimate the influence of misinformation by utilizing the (𝜖,δ)-approximation method [36].

Definition 8

((𝜖,δ)-approximation). The mean and variance of samples Y₁, Y₂, Y₃, ⋯ are μ_Y and ${\delta _{Y}^{2}}$, which follows the independent identical distribution of Y in the interval [0,1]. The Monte Carlo estimator of μ_Y is $\bar {\mu }_{Y} = {\sum }_{j=1}^{N} Y_{j} /N$, if $Pr[(1-\epsilon )\mu _{Y} \leq \bar {\mu }_{Y} \leq (1+\epsilon )\mu _{Y}] \geq 1- \delta$, where δ ≥ 0 and 0 ≤ 𝜖 ≤ 1.

Lemma 1

The mean of samples Y₁, Y₂, Y₃, ⋯ is μ_Y, which follows the independent identical distribution of Y. Let $ZY={\sum }_{j=1}^{N} Y_{j}$, $\bar {\mu }_{Y} =ZY/N$, $\gamma =4(e-2)\cdot \ln (2/\delta )/\epsilon ^{2}$ and γ₁ = 1 + (1 + 𝜖)γ. When ZY ≥ γ₁, if N is the number of samples, then $Pr[(1-\epsilon )\mu _{Y} \leq \bar {\mu }_{Y} \leq (1 + \epsilon )\mu _{Y}] \geq 1-\delta$ and $\mathbb {E}[N]\leq \gamma _{1} /\mu _{Y}$.

From lemma 1, we know the stopping rule for obtaining misinformation propagation estimates. Given δ ≥ 0, 0 ≤ 𝜖 ≤ 1, $\gamma =4(e-2)\cdot \ln (2/\delta )/\epsilon ^{2}$ and γ₁ = 1 + (1 + 𝜖)γ. When the sum of N times $F(\hat {{\varLambda }})'/\vert \hat {V}\vert$ is greater than γ₁, then $Pr[(1-\epsilon ) F(\hat {{\varLambda }}) \leq F(\hat {{\varLambda }})' \leq (1 + \epsilon ) F(\hat {{\varLambda }})] \geq 1-\delta$. The procedure for obtaining the estimated value $F (\hat {{\varLambda }})'$ is given in Algorithm 4.

Proposition 6

The time complexity of the Influence Estimate Procedure is $O(N*\vert \hat {E}\vert )$.

Proof

Algorithm 4 takes O(1) to compute γ₁. It needs at most $O(\vert \hat {E}\vert )$ to try to activate the inactive entities. Satisfying ZY ≥ γ₁ takes at most $O(N*\vert \hat {E}\vert )$ time. Thus, algorithm 4 takes $O(N*\vert \hat {E}\vert )$ time to obtain $F(\hat {{\varLambda }})'$. □

6.2 Supermodular curvature

Since the optimization problem of the set function is NP-hard, minimizing the influence of misinformation is generally impossible to achieve. Fortunately, we can use the supermodular curvature to obtain the worst-case upper bound. The supermodular curvature mainly indicates how far the supermodular function is modular.

Given a nondecreasing set function $g:2^{I} \rightarrow \mathbb {R}_{+}$ with submodularity, and $g(\varnothing )=0$, the (total) curvature [37] of the function g is ${\varrho }_{g} = 1 -min_{v\in I} \frac {g(I)-g(I\backslash \{v\} )}{g(v)}$. Since $0\leq g(I)-g(I\backslash \{v\}) \leq g(v)-g(\varnothing )$, we can get 0 ≤ ϱ_g ≤ 1, and when ϱ_g = 0, g is modular. Let $f: 2^{U} \rightarrow \mathbb {R}_{+}$ be a monotonic nonincreasing supermodular function with f(U) = 0. Suppose $J(\cdot ) = f(\varnothing )- f(\cdot )$. Then, we can obtain that J(⋅) is a nondecreasing submodular function, and $J(\varnothing ) =0$. Hence, according to the (total) curvature of the submodular function, we give the definition of the supermodular curvature.

Definition 9

(Supermodular curvature) Given a monotonic nonincreasing supermodular function $f: 2^{U} \rightarrow \mathbb {R}_{+}$, and f(U) = 0. Then its supermodular curvature is defined as

$$ {\varrho}^{f} = 1 -min_{u\in U} \frac{f(U\backslash \{u\})}{f(\varnothing) - f(u)}. $$

Since the set function f is supermodular and f(U) = 0, then $0\leq f(U\backslash \{u\}) = f(U\backslash \{u\}) -f(U) \leq f(\varnothing ) - f(u)$, we have 0 ≤ ϱ^f ≤ 1. When ϱ^f = 0 (or ϱ^f = 1), we say that f is modular (fully curved). we know that F(⋅) is a nonincreasing supermodular function, then $F(\hat {U})=0$ for $\hat {U}=\hat {V}\backslash \mathfrak {R}$. Hence, we can derive the supermodular curvature ϱ^F of the set function F.

Given a monotonic nonincreasing supermodular objective function F(⋅) of the problem of MIE-c, computing the supermodular curvature ϱ^F of function F(⋅) is #P-hard. Given a coupled social network $G_{cou}(\hat {V}, \hat {E})$, a supermodular objective function F(⋅) and $\mathfrak {R}$, let N be the number of Monte Carlo simulations, it takes $O(N*\vert \hat {V}\vert \vert \hat {E}\vert )$ time to obtain the estimated value $\acute {{\varrho }}^{F}$ of ϱ^F.

6.3 Two-stage discrete gradient descent method

In this part, we develop a Two-stage Discrete gradient Descent (TD-D) algorithm to solve the problem of MIE-c. The main idea of the TD-D algorithm is to first obtain the candidate entity set $\hat {V}_{sa}$. Then, based on certain criteria (given in Section 7.3), select $\hat {W}$ as the initial solution $\hat {W}= \{ \hat {w}_{1}, \hat {w}_{2}, \cdots , \hat {w}_{K} \}$. Finally, $\hat {W}$ is iterated $F(\hat {w})$ to reach the local optimal solution. Algorithm 5 summarizes the specific steps of the TD-D procedure.

Proposition 7

The time complexity of the TD-D algorithm is $O(MI\cdot N\vert \hat {E}\vert \vert \hat {V}\vert )$.

Proof

Let MI be the number of iterations when the TD-D algorithm converges, and let D be the maximum degree of the entity in the coupled social network $G_{cou}(\hat {V},\hat {E})$. In the TD-D algorithm, O(N_e) time is required to obtain G_cou, where $N_{e} = {\sum }_{i=1}^{n} \vert E^{i} \vert$. It takes $O(\vert \hat {V}\vert )$ to obtain $\hat {V}_{sa}$. At most, $O(K\cdot D\cdot N\vert \hat {E}\vert )$ is required to update $\hat {W}$. Since $K\cdot D \ll \vert \hat {V}\vert$, the time complexity of the TD-D algorithm is $O(MI\cdot N\vert \hat {E}\vert \vert \hat {V}\vert )$. □

6.4 Two-stage greedy method

A Two-stage Greedy (TG) algorithm is constructed based on the hill climbing approach [38] and used as a baseline for evaluating the TD-D algorithm. The procedure of the TG algorithm is given in Algorithm 6. In Algorithm 6, first, $\hat {V}_{sa}$ is obtained according to Algorithm 3, and then the entity with the largest reduction in F(⋅) is selected to protect it until the K entities are selected.

Proposition 8

The time complexity of the TG algorithm is $O(KN\vert \hat {V}\vert \vert \hat {E}\vert )$.

Proof

In the TG algorithm, it takes O(N_e) to couple multi-social networks G into G_cou, and it needs to spend $O(\vert \hat {V}\vert )$ to obtain $\hat {V}_{sa}$. At most $O(KN\vert \hat {V}\vert \vert \hat {E}\vert )$ is required to select protected entity sets $\hat {{\varLambda }}$. The total time spent is $O(N_{e} + \vert \hat {V}\vert + KN\vert \hat {V}\vert \vert \hat {E}\vert )$, and the time complexity of the TG algorithm is $O(KN\vert \hat {V}\vert \vert \hat {E}\vert )$. □

Theorem 6

Let $\hat {{\varLambda }}^{*}$ be the optimal solution of the supermodular function F(⋅), and $\hat {{\varLambda }}$ is the solution obtained by the TG algorithm, which satisfies

$$ F(\hat{{\varLambda}}) \leq \frac{1-{\varrho}^F}{{\varrho}^F}[e^{\frac{{\varrho}^F}{1-{\varrho}^F}} -1] F(\hat{{\varLambda}}^{*}) $$

where ϱ^F is the supermodular curvature of function F.

Proof

See Appendix A. □

Remark 1

When the number of Monte Carlo simulations MC ≥ N in the TG algorithm, the $\hat {{\varLambda }}^{\prime }$ obtained by the TG algorithm is an $(\frac {1 - {\varrho }^{F} }{ {\varrho }^{F}} (e^{ \frac { {\varrho }^{F} }{ 1-{\varrho }^{F} }} -1) + \epsilon )$ approximation of $\hat {{\varLambda }}^{*}$ and satisfies

$$ Pr[F(\hat{{\varLambda}}^{\prime}) \leq (\frac{ 1- {\varrho}^F }{ {\varrho}^F} (e^{\frac{{\varrho}^F}{ 1- {\varrho}^F}} -1)+\epsilon) F(\hat{{\varLambda}}^{*}) ] \geq 1 - \delta. $$

7 Experiment

Experiments were performed on a synthetic multi-networks and three real-world multi-social networks to verify the effectiveness of our developed algorithm. We implemented our algorithms and other heuristic algorithms in Python. All experiments were performed on a PC with a 3.60GHz Intel Core i9-9900K processor and 32 GB Memory, running Microsoft Windows 8.

7.1 Datasets

The synthetic multi-networks contains five random networks generated by the forest fire model [39]. By article [39], we know that there are two parameters in the forest fire model: the forward burning probability f_p and the backwards burning ratio b_r. With the increase in f_p and b_r, the networks generated by the forest fire model gradually become denser, and the effective diameter decreases slowly. Therefore, to make the synthetic network conform to the realistic situation and form a complement to the real-world network, we set f_p = 0.33, b_r ∈ [0,0.2]. The properties of the synthetic network are as follows: the number of nodes from 1870 to 4846, the number of edges from 7122 to 21786, the forward burning probability is 0.33, and the edge probabilities (backwards burning ratio) were randomly selected from a uniform distribution between 0 and 0.2 for each synthetic network. Accounts owned by entities on distinct random networks are set to the same tag (ID), and the main procedure is: (1) A set of potential entities V q is given, and each entity is assigned a unique tag. (2) Obtain V c to satisfy $Vc\subseteq Vq$ as the node set of the random network. It is worth pointing out that a node in a random network indicates an account owned by an entity and has the same tag as its corresponding entity. (3) A random network is generated based on nodes set V c leveraging the forest fire model. Repeat steps (2) and (3) to ensure that accounts owned by an entity in different random networks have the same tag. The multi-networks detailed description is given in Table 2, where ND is the average degree of accounts, and MD denotes the maximum degree of accounts.

Table 2 The statistics of the Synthetic multi-networks

At present, the multiple accounts identification problem [40] has become an independent research branch, and various methods, such as FPM-CSNUIA [41] and ExpandUIL [42], have been proposed to identify the multiple accounts owned by an entity. Since the recognition of multiple accounts of entities is not the focus on this article, we do not present a method for multi-social networks account recognition in real life, but conduct experiments with the help of datasets with multiple accounts information. Next, we introduce three real-world multi-social networks datasets: Collaborator datasets, Social datasets, and multi-layer Twitter datasets. The Collaborator datasets [39] contain three collaborator networks in the fields of general relativity and quantum cosmology, high energy physics and phenomena, and high energy physics theory. In the collaborator network, nodes represent scientists and edges indicate collaborations (co-authoring a paper). Each scientist in the Collaborator datasets is characterized by a unique label. Table 3 gives details of the Collaborator datasets. The Social datasets contain three online social networks: Flixster [43], Epinions [43], and YouTube [44]. Considering the characteristics of multi-social networks, in the Social datasets, we define accounts with the same label as belonging to the identical entity. The specific information about the Social datasets is given in Table 4. The Twitter [45] datasets contain four sub-layer network: Mention, Reply, Retweet, and Social. Accounts of entities in the four sub-layer networks in the Twitter datasets have the same labels. Table 5 shows the attributes of specific layers in Twitter.

Table 3 The statistics of Collaborator datasets

Table 4 The statistics of Social datasets

Table 5 The statistics of Twitter datasets

Table 6 summarizes the information of entity control accounts in multi-social networks. Table 6 shows that entities with multiple accounts in multi-social networks account for a small proportion of all entities. Entities with two or more accounts accounted for the highest proportion of Social datasets, and the lowest was Collaborator datasets, accounting for only 10.45%. Thus, this is one of the reasons for constructing the synthetic multi-networks in this article.

Table 6 The statistics of accounts controlled by entities in multi-social networks

7.2 Experimental setting

7.2.1 Parameter setting

Since there is no common neighbor between the accounts in the online social network, it is possible for them to exchange information, so ϖ = 0.3 is given. We give the parameter φ = 0.9. We use the degree of the entity’s control of the account in the online social network to express the entity’s preference for it. We randomly and uniformly select 3% of the total number of entities from each dataset as $\mathfrak {R}$. Moreover, we give $K=0.03*\vert \hat {V} \vert$ in the social dataset and $K=0.05*\vert \hat {V}\vert$ in the other datasets and the iterative termination value of TD-D, ε = 0.01. To control the approximate quality of the misinformation spread value, we set 𝜖 = 0.05, δ = 0.01.

7.2.2 Coupled of multi-social networks

Use Algorithm 2 to couple multi-social networks G into a single social network G_cou. The details of the coupled social network are given in Table 7, where Max.Deg denotes the maximum degree of the entity, and D is the diameter of G_cou.

Table 7 The statistics of coupled social network datasets

7.3 Selection of initial feasible solution

The TD-D algorithm needs to be given an initial feasible solution $\hat {W}=\{\hat {w}_{1}, \hat {w}_{2}, \cdots , \hat {w}_{K} \}$. Since different initial solutions will affect the convergence speed of the TD-D algorithm, we study the selection method of the initial feasible solution based on entity characteristics such as Out-degree Centrality (abbreviated as Out-degree) [15], Closeness Centrality (Closeness) [46], and Betweenness Centrality (Betweenness) [47]. We use the Synthetic CN and Twitter CN datasets to evaluate the acquisition method of the initial feasible solution, and the experimental results are shown in Tables 8 and 9, where K is the number of protected entities and the numbers in the table indicate the spread value of misinformation.

Table 8 The performance of all methods on Synthetic CN

Table 9 The performance of all methods on Twitter CN

As seen from Tables 8 and 9, the initial feasible solution $\hat {W}$ selected by distinct methods on different datasets has little disparity in the local optimal solutions obtained after iteration. Then, we evaluate the efficiency of all initial feasible solution selection methods by comparing the time to obtain the local optimal solution, and the final result is shown in Fig. 5. In Fig. 5, the time consumed by diverse methods to obtain the optimal solution is discrepant, on the whole; the Betweenness method is better than other methods.

Fig. 5

The running time of all methods on Synthetic and Twitter CN

Next, we give the average number of iterations of the discrete gradient in the TD-D algorithm based on diverse initial solution selection methods on the Synthetic and Twitter CN in Table 10. From Table 10, the Betweenness method has the minimum number of iterations, and its running time is relatively short, which is shown in Fig. 5. Considering the performance and running time of distinct initial feasible solution selection methods, the Betweenness method is used to select the initial feasible solution $\hat {W}$ in the TD-D Algorithm.

Table 10 The number of iterations of the discrete gradient on Synthetic and Twitter CN by distinct methods

7.4 Comparison method

The TG algorithm is used as a baseline to evaluate the TD-D algorithm we developed, and the TD-D method is compared with heuristic methods such as Degree Centrality and PageRank. Next, we give the core ideas of these heuristic methods.

Two-stage PageRank (TPR). PageRank [48] is a technology that is calculated based on the hyperlinks between web pages to reflect the relevance and importance of web pages. The core of the TPR algorithm is to select the entity with the largest PR in the candidate set $\hat {V}_{sa}$ for protection.

Two-stage Degree Centrality (TDC). Degree Centrality [49] is an index that characterizes the centrality of a node based on its degree. The TDC algorithm selects the K entities with the largest degree of centrality in $\hat {V}_{sa}$ for protection.

Two-stage RanDom (TRD). The TRD algorithm randomly and uniformly selects K entities from the candidate set $\hat {V}_{sa}$ for protection.

7.5 Comparison of TD-D and heuristic methods

Next, we compare the TD-D algorithm with other existing heuristic methods in four datasets by observing the disparities of the misinformation spread value when protecting diverse numbers of entities. The experimental results are shown in Fig. 6.

Fig. 6

The misinformation spread on four datasets by diverse methods

We observe Fig. 6 and draw the following conclusions: 1) With the increase in the number of protected entities, the influence of misinformation declines in distinct datasets or diverse algorithms. 2) The performance of the TPR and TDC algorithms is inconsistent. The TPR algorithm in Collaboration CN is better than the TDC algorithm in its ability to limit the spread of misinformation, but vice versa in Twitter CN. 3) In the four datasets, we developed the TD-D algorithm, which has the best performance in misinformation control, while the TRD algorithm performed the worst. 4) We assume that the mean value of the reduction rate of the misinformation spread in the four datasets under the action of the TD-D algorithm is Ms(TDD). When $K=0.03*\vert \hat {V}\vert$, we can obtain Ms(TDD) = 34.43%, Ms(TDC) = 23.57%, Ms(TPR) = 24.23% and Ms(TRD) = 12.11%. It is obvious that the performance of the TD-D algorithm in suppressing the spread of misinformation is at least 10% higher than that of other heuristic algorithms. In summary, the performance of the existing heuristic methods on distinct datasets is inconsistent and unstable. The performance of the TD-D algorithm is stable under diverse datasets, and the results are better than those of the existing heuristic methods.

7.6 Comparison of TD-D and TG algorithms

Next, we utilize the TG algorithm as the baseline to evaluate the TD-D algorithm in four datasets. Figure 7 shows the difference between the TD-D and TG algorithms to suppress the spread of misinformation when protecting the same number of entities, where $gR = \frac {SVm(TD-D)-SVm(TG)}{SVo-SVm(TG)}$. SV m(TD-D) and SV m(TG) represent the spread value of misinformation under the TD-D and TG algorithms, respectively. SV o indicates the propagation value of misinformation when K = 0.

Fig. 7

The gap between the spreading value of misinformation under the TD-D and TG algorithms

From Fig. 7, we can observe that when the same number of entities is protected, the discrepancy between the spreading value of misinformation under the TD-D algorithm and TG algorithm is very small in different datasets; that is, the ability of the two algorithms to suppress the spread of misinformation is basically the same.

In Table 11, we show the running time of the TD-D and TG algorithms when protecting different numbers of entities in the three datasets. In each dataset through the comparison, we found that the running time of the TD-D algorithm is far less than that of the TG algorithm. Moreover, with the increase in the number of protected entities, the difference in running time between the two algorithms gradually shrinks, but the running efficiency of the TD-D algorithm is still much higher than that of the TG algorithm. According to Fig. 7 and Table 11, TD-D and TG have basically the same ability to suppress the spread of misinformation, but the running time of TD-D algorithm is much lower than that of TG algorithm. Therefore, the comprehensive performance of TD-D algorithm in controlling misinformation is better than that of the TG algorithm. In general, the TD-D algorithm outperforms other existing algorithms under distinct datasets and diverse evaluation indexes.

Table 11 TD-D and TG algorithms in running times

8 Conclusion

In this article, the characteristics of the spread of misinformation across multi-social networks are considered, and we propose an entity protection strategy to control misinformation in multi-social networks, and explore the problem of misinformation influence minimization by entity protection on multi-social networks. We prove that the computing information spread is #P-hard, and the objective function of the problem of MIE-m is supermodular. We utilize techniques such as multi-social networks coupled and pruning rules to develop approximate methods for solving MIE-m. We also construct a two-stage greedy algorithm with approximate guarantees as a baseline to evaluate our developed TD-D algorithm. Experimental results on a synthetic and three real-world multi-social networks, verify the feasibility and effectiveness of our methods. In the future, we will be interested in studying the control strategies and dissemination laws of misinformation in multi-social networks, including interpersonal networks.

Appendix A:: Proof

1.1 A. 1 Proof of theorem 1

Proof

The problem of MIE-m tries to minimize the number of entities ultimately activated by the misinformation,

which is equivalent to maximizing the number of entities that are not influenced by $\mathfrak {R}$ such that $g({\varLambda })=\vert V \vert - \mathbb {E} \left [\sigma _{\mathfrak {R}}({\varLambda })\right ]$. We prove this by reducing the problem from the NP-complete set cover problem [50]. We set |V | = m. Let a ground set V = {v₁,v₂,⋯ ,v_m} and a collection of sets Λ = {Λ₁,Λ₂,⋯ ,Λ_y}, where $\cup _{j=1}^{y}{\varLambda }_{j} = V$. The set cover problem is to determine whether the union of K sets in Λ is equal to V. Next, we will show that the set cover problem can be regarded as a special case of the MIE-m problem. Given an arbitrary instance of the set cover problem, we construct a directed graph with m(n + 1) + y nodes. For each subset Λ_j we construct a related node a_j, for each element v_z (1 ≤ z ≤ m), construct n + 1 nodes $u_{z},{u_{z}^{1}},\cdots ,{u_{z}^{n}}$, and create a directed edge $(u_{z},{u_{z}^{i}})$ for each node ${u_{z}^{i}} (1\leq i\leq n)$ with probability $p_{u_{z}{u_{z}^{i}}}=1$. When element v_z belongs to Λ_j, we create a directed edge (a_j,u_z) with probability $p_{a_{j} u_{z}}=1$. Since the influence probability between nodes is 1, the dissemination of information is a fixed process. Therefore, the set covering problem is equivalent to deciding whether there are K nodes of Λ. □

1.2 A.2 Proof of theorem 2

Proof

When the number of online social networks is one, that is, n = 1, the account in an online social network can be equivalent to the entity. At this time, the problem of MIE-m is equivalent to the problem of misinformation influence minimization in single online social networks. We already know that the influence spread computation problem in online social network under the IC model is #P-hard [15]. Since the problem of misinformation influence minimization in online social networks is a special case of the problem of MIE-m, the influence spread computation problem in multi-social networks is also #P-hard, that is, computing $\sigma _{\mathfrak {R}}({\varLambda })$ is #P-hard in multi-social networks. □

1.3 A.3 Proof of proposition 2

Proof

We use the formula [51] to calculate the probability $\vartheta (w, \mathfrak {R})$ of w being activated by $\mathfrak {R}$ to prove it. In multi-social networks G(G¹,G²,⋯ ,Gⁿ), given $\mathfrak {R}$, we can get $\vartheta (w, \mathfrak {R})= 1-{\prod }_{i=1}^{n} {\prod }_{v^{i}\in N^{in}(w^{i})} [1-P^{fwd}(v^{i}) P^{inf}(v^{i},w^{i})]$ for any w ∈ V, where Nⁱⁿ(wⁱ) is the set of parent neighbours of entity w in online social network Gⁱ. Then, we obtain that $\vartheta (w, \mathfrak {R}) =1- {\prod }_{v\in N^{in}(w)} {\prod }_{i=1}^{n} [1-P^{fwd}(v^{i}) P^{inf}(v^{i},w^{i})] = 1- {\prod }_{v\in N^{in}(w)} 1-\hat {p}(v,w) = 1- {\prod }_{\hat {v}\in N^{in}(\hat {w})} 1-\hat {p}(\hat {v},\hat {w}) = \vartheta (\hat {w}, \mathfrak {\hat {R}})$ for any $\hat {w}\in \hat {V}$, where Nⁱⁿ(w) is the set of parent neighbors of entity w. Since $V=\hat {V}$, we have $\sigma _{\mathfrak {R}}({\varLambda })={\sum }_{w\in V} \vartheta _{{\varLambda }}(w, \mathfrak {R})={\sum }_{\hat {w}\in \hat {V}} \vartheta _{{\varLambda }}(\hat {w}, \mathfrak {R})=\sigma _{\mathfrak {\hat {R}}}(\hat {{\varLambda }})$ for all $\hat {{\varLambda }}\subseteq \hat {V}$, and the proposition follows. □

1.4 A.4 Proof of theorem 6

The proof framework is based on [52], but the supermodular function that makes the proof applicable to the problem of MIE-c requires some changes in the following. Given a coupled social network $G_{cou}(\hat {V}, \hat {E})$, an initial influence entities $\mathfrak {R}$ and a nonnegative nonincreasing supermodular function F(⋅) with supermodular curvature ϱ^F. We set $U = \hat {V} \backslash \mathfrak {R}$, then F(U) = 0. Let $W,M \subseteq U$, W = {w₁,w₂,⋯,w_a} and M = {m₁,m₂,⋯ ,m_b}, where W_i = {w₁,w₂,⋯ ,w_i} (i = 1,⋯ ,a) and M_s = {m₁,m₂,⋯ ,m_s} (s = 1,⋯ ,b) are sequences. For any $W\subseteq U$, we set b_w(W) = F(W∖w) − F(W).

Lemma 2

For any $W\subseteq U$, $F(W)={\sum }_{w_{j} \in U\backslash W} b_{w_{j}} (W_{a+j})$.

Proof

By the definition of b_⋅(⋅), we can get $F(W)= F(W_{a})= F(W_{a+1} )+ b_{w_{a+1}}(W_{a+1}) =b_{w_{a+1}}(W_{a+1})+ F(W_{a+2} ) + b_{w_{a+2}}(W_{a+2}) ={\cdots } = F(U) + {\sum }_{w_{j} \in U\backslash W} b_{w_{j}} (W_{a+j})$. Since F(U) = 0, the lemma is proved immediately. □

Lemma 3

For any $W,M \subseteq U$, it holds

$$ \begin{array}{@{}rcl@{}} \begin{aligned} F(W\cap M)&=F(M) + \sum\nolimits_{w_{j} \in M\backslash W} b_{w_{j}}(M\cap W_{a+j})\\ &=F(W)+\sum\nolimits_{m_{z} \in W\backslash M} b_{m_{z}} (W\cap M_{b+z}). \end{aligned} \end{array} $$

Proof

F(M ∩ W) = F(M ∩ W_a) = F((M ∩ W_a+ 1)∖w_a+ 1). If w_a+ 1 ∈ M∖W, we obtain F((M ∩ W_a+ 1)∖w_a+ 1 $)=F(M\cap W_{a+1} )+ b_{w_{a+1}}(M \cap W_{a+1} )$. For any w_a+ 1∉M, we have F({M ∩ W_a+ 1}∖w_a+ 1) = F(M ∩ W_a+ 1),⋯. Finally, we can deduce that $F(M\cap W)=F(\{ M \cap W_{a} \} \cup \{ M\backslash W \}) + {\sum }_{w_{j}\in M\backslash W} b_{w_{a+j}} (M \cap$ $W_{a+j})= {\sum }_{w_{j} \in M\backslash W} b_{w_{a+j}} (M\cap W_{a+j}) + F(M)$. Then the first equation proof is complete. Using a similar method, we can get $F(W\cap M)=F(W)+\sum \nolimits _{m_{z} \in W\backslash M} b_{m_{z}} (W\cap M_{b+z})$.

Given that Opt is an optimal solution to the problem of MIE-c, the TG algorithm consecutively acquires the sequences $C_{0} = \varnothing$, C₁ = {c₁}, ⋯, C_i = {c₁,c₂,⋯ ,c_i}, ⋯, C_K = {c₁,c₂,⋯ ,c_K}. Suppose r = |U|−|C_i|, $\overline {W} =U \backslash W$, $\overline {W}_{i} =U \backslash W_{i}$, and $w_{j} \in \overline {W}_{i}$. Without causing ambiguity, we abbreviate $b_{c_{i}}(C_{i})$ as b_i. Then, we can derive Theorem 7. □

Theorem 7

For i = 1, 2,⋯ ,K, it holds

$$ \begin{array}{@{}rcl@{}} F(Opt) \geq (r-s_{i}) b_{i} + \sum\limits_{j: c_{j} \in \overline{C_{i}} \cap \overline{Opt} } b_{j} - \eta \sum\limits_{j: c_{j} \in \overline{C_{i}} \backslash \overline{Opt}} b_{j} \end{array} $$

where $s_{i} = \vert \overline {Opt} \cap \overline {C_{i}} \vert$ and $\eta = \frac {{\varrho }^{F} }{1- {\varrho }^{F}}$.

Proof

Given any $W,\ M \subseteq U$, from Lemma 3, we have $F(M) = F(W)+ {\sum }_{m_{z} \in W \backslash M} b_{m_{z}} (W \cap M_{b+z})$ $-{\sum }_{w_{j} \in M \backslash W} b_{w_{j}}(M \cap W_{a+j})$. By the definition of supermodular and ϱ^F, we have $b_{w_{j}} (M \cap W_{a+j}) \leq b_{w_{j}}(w_{j}) \leq \frac {1}{1 - {\varrho }^{F}} b_{w_{j}}(U) \leq \frac {1}{1 - {\varrho }^{F}} b_{w_{j}}(W_{a+j})$. Since $b_{m_{z}} (W \cap M_{b+z}) \geq b_{m_{z}} (W)$ for all m_z ∈ W∖M. Then, we can obtain $F(M) \geq {\sum }_{w_{j} \in \overline {W} } b_{w_{j}} (W_{a+j}) +{\sum }_{m_{z} \in \overline {M} \backslash \overline {W}} b_{m_{z}} (W)- \frac {1}{1-{\varrho }^{F}} {\sum }_{w_{j} \in \overline {W} \backslash \overline {M}} b_{w_{j}}(W_{a+j})$ $={\sum }_{w_{j} \in \overline {W} \cap \overline {M} } b_{w_{j}} (W_{a+j}) +{\sum }_{m_{z} \in \overline {M} \backslash \overline {W}} b_{m_{z}} (W)- \frac {{\varrho }^{F} }{1- {\varrho }^{F}} {\sum }_{w_{j} \in \overline {W} \backslash \overline {M}} b_{w_{j}}(W_{a+j})$.

Let M = Opt, W = C_i and $\eta = \frac {{\varrho }^{F} }{1- {\varrho }^{F}}$, we can get $F(Opt) \geq {\sum }_{m_{z} \in \overline {Opt} \backslash \overline {C_{i}}} b_{m_{z}} (C_{i}) + {\sum }_{c_{j} \in \overline {C_{i}} \cap \overline {Opt} } b_{c_{j}} (C_{i+j})$ $-\eta {\sum }_{c_{j} \in \overline {C_{i}} \backslash \overline {Opt}} b_{c_{j}}(C_{i+j})$. By definition of Opt and C_i, for any $m_{z} \in \overline {Opt} \backslash \overline {C_{i}}$, $b_{m_{z}} (C_{i}) \geq b_{c_{i}} (C_{i})$. Therefore, ${\sum }_{m_{z} \in \overline {Opt} \backslash \overline {C_{i}}} b_{m_{z}} (C_{i}) \geq \vert \overline {Opt} \backslash \overline {C_{i}} \vert \cdot b_{c_{i}} (C_{i}) = \vert \overline {Opt} \backslash \{ \overline {Opt} \cap \overline {C_{i}} \} \vert \cdot b_{i} = (r-s_{i}) b_{i}$, where $s_{i} = \vert \overline {Opt} \cap \overline {C_{i}} \vert$. Finally, we get $F(Opt) \geq (r-s_{i}) b_{i} + {\sum }_{j: c_{j} \in \overline {C_{i}} \cap \overline {Opt} } b_{j} - \eta {\sum }_{j: c_{j} \in \overline {C_{i}} \backslash \overline {Opt}} b_{j}$. □

Given C = C_K, $\overline {C}=\{c_{1},\cdots ,c_{j},\cdots , c_{r}\}$ and $\overline {C_{j}} =\{c_{1},c_{2},\cdots ,c_{j} \}$. Let $\overline {Opt} \cap \overline {C} = \{ u_{1}, u_{2}, \cdots , u_{s}\}$, where s ≤ r, that is {u₁,u₂,⋯ ,u_s} be the elements not contained in Opt or C. Suppose $b_{j}= F(C\cup \{\overline {C_{j}}\backslash c_{j}\})-F(C\cup \overline {C_{j}})$. By Lemma 2, we can obtain $F(C)={\sum }_{j: c_{j} \in \overline {C} } b_{j}$. Then, the approximation ratio is defined as $\frac {F(C)}{F(Opt)} = {\sum }_{j: c_{j} \in \overline {C} } \frac {b_{j}}{F(Opt)}$. Define $y_{j} := \frac {b_{j}}{F(Opt)}, j \in [r]$. Since b_j ≥ 0, then y_i ≥ 0. We define $L(\overline {Opt} \cap \overline {C}) = {\sum }_{j: c_{j} \in \overline {C} } \frac {b_{j}}{F(Opt)}$.

Considering 1 ≤ s ≤ r, for the variables y_j, there are r constraints. Hence, the worst-case approximate ratio of $\frac {F(C)}{F(Opt)}$ can be expressed as the following Linear Programming (LP).

$$ \begin{array}{@{}rcl@{}} &L(\{ u_{1}, \cdots, u_{s}\}) =\max \sum\nolimits_{j=1}^{r} y_{j}\\ &s.t.\ \ y_{j} \geq 0,\ j=1,\cdots,r \end{array} $$

(A1)

$$ \begin{array}{@{}rcl@{}} \begin{bmatrix} r & & & & & & & & \\ -\eta & r & & & & & & & \\ {\vdots} &\vdots&{\ddots} & & & & & & \\ -\eta &-\eta &{\cdots} & r & & & & & \\ -\eta &-\eta &{\cdots} & 1 & r-1 & & \multicolumn{2}{l}{\raisebox{1.2ex}[0pt]{\Huge0}} & \\ {\vdots} &\vdots& &\vdots&\vdots&\ddots& & & \\ -\eta &-\eta &{\cdots} & 1 & 1 &\cdots&r-s & & \\ {\vdots} &\vdots& &\vdots&\vdots& &{\vdots} &\ddots& \\ -\eta &-\eta &{\cdots} & 1 & 1 &\cdots& -\eta &\cdots&r-s \end{bmatrix} \begin{bmatrix} y_{1} \\ y_{2} \\ {\vdots} \\ y_{j} \\ y_{j+1} \\ {\vdots} \\ y_{s} \\ {\vdots} \\ y_{r} \end{bmatrix}\!\leq\! \begin{bmatrix} 1 \\ 1 \\ {\vdots} \\ 1 \\ 1 \\ {\vdots} \\ 1 \\ {\vdots} \\ 1 \end{bmatrix} \end{array} $$

Lemma 4

L({u₁,u₂,⋯ ,u_s− 1}) ≥ L({u₁,u₂,⋯ ,u_s}) for any s = 1, 2,⋯ ,r.

Proof

We abbreviate L({u₁,u₂,⋯ ,u_s}) as L_s for simplicity. Let c_j = u_s. When y_j > 0, an optimal solution for LP L_s has the following form $Y_{s}^{*} = \{y_{1},\cdots , y_{j-1}, y_{j}, y_{j}, y_{j}\frac {r-s+\eta }{r-s}, \cdots , y_{j} (\frac {r-s+\eta }{r-s})^{r-j-1} \}$. We construct a feasible solution Y_s− 1 of L_s− 1. Suppose the first j elements of Y_s− 1 are consistent with the first j elements of $Y_{s}^{*}$, then Y_s− 1 can be expressed as $\{ y_{1},\cdots , y_{j-1}, y_{j}, y_{j}\frac {r-s+\eta +1}{r-s+1}, \cdots , y_{j}(\frac {r-s+\eta +1}{r-s+1})^{r-j} \}$. We can obtain $L^{*}_{s}- L_{s-1}= y_{j}+ y_{j}\frac {r-s+\eta }{r-s}+ \cdots + y_{j} (\frac {r-s+\eta }{r-s})^{r-j-1} - y_{j}\frac {r-s+\eta +1}{r-s+1}- \cdots - y_{j}(\frac {r-s+\eta +1}{r-s+1})^{r-j} = y_{j}[1- \frac {r-s+\eta +1}{r-s+1}] +{\cdots } + y_{j}[(\frac {r-s+\eta }{r-s})^{r-j-1} -(\frac {r-s+\eta +1}{r-s+1})^{r-j}] \leq 0$. When y_j = 0, the form of the optimal solution of LP L_s can be written as $Y_{s}^{*} = \{y_{1},\cdots , y_{j-1}, 0, y_{j-1}\frac {r-s+\eta +1}{r-s},$ $y_{j-1}\frac {r-s+\eta +1}{r-s} \frac {r-s+\eta }{r-s}, \cdots , y_{j-1}\frac {r-s+\eta +1}{r-s} (\frac {r-s+\eta }{r-s})^{r-j-1} \}$. Similarly, let the first j − 1 items of Y_s− 1 be consistent with the first j − 1 items of $Y_{s}^{*}$, then Y_s− 1 can be expressed as $\{y_{1},\cdots , y_{j-1}, y_{j-1}\frac {r-s+\eta +1}{r-s+1}, \cdots , y_{j-1} (\frac {r-s+\eta +1}{r-s+1})^{r-j+1} \}$. Then $L^{*}_{s}- L_{s-1} \leq 0$. Hence, L({u₁,u₂,⋯ ,u_s− 1}) ≥ L({u₁,u₂,⋯ ,u_s}) for any s = 1, 2,⋯ ,r. □

Theorem 8

Given that C is the solution obtained by the greedy algorithm, Opt is the optimal solution of MIE-c, which satisfies

$$ F(C) \leq \frac{1-{\varrho}^F}{{\varrho}^F}[e^{\frac{{\varrho}^F}{1-{\varrho}^F}} -1] F(Opt). $$

where ϱ^F is the supermodular curvature of set function F.

Proof

From LP (A1), it can be inferred that F(C) ≤ F(Opt) ⋅ L({u₁,⋯ ,u_s}) for any s = 1,⋯ ,r. By lemma 4, we can obtain $L(\{ u_{1}, \cdots , u_{s}\}) \leq L(\{ u_{1}, \cdots , u_{s-1}\}) \leq {\cdots } \leq L(\varnothing )$. Hence, $F(C) \leq F(Opt)\cdot L(\varnothing )$. When $\overline {Opt} \bigcap \overline {C}= \varnothing$, based on LP (A1), we can derive $L(\varnothing )= \frac {1}{r} + \frac {r+\eta }{r \cdot r}+{\cdots } + \frac {(r+\eta )^{j}}{r \cdot r^{j}} +{\cdots } + \frac {(r+\eta )^{r-1}}{r \cdot r^{r-1}} = \frac {1}{\eta } [\frac {(r+\eta )^{r}}{r^{r}} -1] = \frac {1}{\eta } [(1+\frac {\eta }{r})^{r} -1] \leq \frac {1}{\eta } [e^{\eta } -1]$. Let $\eta = \frac {{\varrho }^{F}}{1-{\varrho }^{F}}$, and the theorem is proved immediately. □