1 Introduction

Alzheimer’s disease (AD) is the most frequent type of neurodegenerative dementia and a growing health problem. Approximately 5.8 million Americans age 65 and older had AD in 2020, and the figure is expected to grow to 13.8 million by 2050 [1]. Nearly $244 billion worth of care was provided by family members and caregivers in 2019 [2]. The latest statistics of 2018 indicate that 122,019 deaths have been attributed to AD, making it the sixth leading cause of death in the United States [3]. There is an urgent need to discover the abnormal changes in the patient’s brain as early as possible to implement a timely treatment and slow down the disease progression. Extensive studies have been conducted to develop diagnostic technology with reliable biomarkers. One example is diagnostic imaging, e.g., magnetic resonance imaging (MRI), a noninvasive examination of brain structure, function, and connectivity. The physiological changes in the brain caused by AD can be quantitatively analyzed with MRI to detect and monitor the progression of the disease.

The human brain is an extremely complex structure composed of neurons and connections. Therefore, researchers have studied brain functions from the perspective of brain networks, where nodes represent brain regions, and edges connect the regions. Graph analysis is often used to detect connectivity patterns among brain regions to diagnose AD [4,5,6,7,8]. Two data types represent the brain network in a graph: the graph signal and graph weight. A graph signal refers to the attribute of each node, which is typically the brain region of interest (ROI). The node attributes can be quantitative measures (e.g., volume, thickness, area) of the brain structures detected using segmentation techniques [9,10,11,12] or fused features. Magnin et al. [13] parcellated T1-weighted magnetic resonance (MR) images of the brain into 116 ROIs and used a histogram to determine the proportion of gray matter, white matter, and cerebrospinal fluid in the ROIs. The results were input into a support vector machine (SVM) for AD classification. The graph weight describes the connectivity between each pair of nodes. Khazaee et al. [14] parcellated the resting-state functional MR images of the brain into 90 ROIs. A representative signal of each region was acquired by averaging the time series of voxels in the ROI. Functional connectivity networks were constructed, and the edges were defined using Pearson’s correlation coefficients of the signals of all pairs of brain regions. An SVM model was developed using the features derived from the local and global graph measures (e.g., node degree) to differentiate AD individuals from healthy controls.

Using a graph model to describe brain networks is a straightforward approach. However, extracting the features from the graph in a meaningful way for AD diagnosis is challenging. Researchers have used some common graph features, including the node degree, clustering coefficient, and the small world. For example, Wee et al. [15] computed the clustering coefficients (common metrics used in brain networks to measure the connectivity among brain regions) as features for SVMs to differentiate mild cognitive impairment (MCI) individuals from cognitively normal (CN) individuals. Prasad et al. [16] developed two connectivity networks. One quantified the pairwise connectivity strength as the relative proportion of fibers connecting the two brain regions. The other quantified the maximum flow between brain regions by interpreting the diffusion image as a flow graph. An SVM classifier was used to differentiate CN, MCI, and AD individuals, and the performance was evaluated using global efficiency, transitivity, path length, modularity, and small world [16]. These methods are based on prior brain network information using domain knowledge (e.g., using a pre-defined brain atlas). In the analysis of mental disorders, domain knowledge improves the classification performance of small sample tasks and the interpretability of experimental results. Although this approach has been successful, studies have mainly focused on deriving features without considering the stochastic nature of the data. This approach may be problematic as data stochasticity prevails due to patient heterogeneity and variability.

Other studies used a data-driven approach for feature extractions that does not require a priori brain network topology. Principal component analysis (PCA) is a common technique for dimensionality reduction; it transforms the data into principal components with fewer dimensions [17,18,19]. Salvatore et al. [20] used PCA to reduce the dimensions of white matter and gray matter density maps. The results were fed into an SVM for classifying patients who were likely or unlikely to develop AD. Data-driven approaches have the advantages of computational efficiency, addressing the curse of dimensionality, and being less dependent on domain knowledge. However, we contend that ignoring the inherent topological properties may be problematic because the extracted features may be difficult to interpret. Here we argue that studies on the connectivity among brain ROIs should focus on improving clinical interpretation and using domain knowledge (e.g., brain atlas).

The challenge of AD diagnosis is efficient feature dimension reduction while retaining feature interpretability. High interpretability of features will promote the use of machine learning methods for clinical diagnosis. However, the latest research in brain network analysis has not addressed this issue adequately. In this paper, we propose a novel feature extraction method for graph-structured data based on maximum mutual information (MMI-GSD). The proposed MMI-GSD can efficiently reduce the dimensionality of GSD while retaining the interpretability of the extracted features. This method has promising application prospects in pathological interpretation. We develop a Gaussian graphical model (GGM) for neuroimaging data. We utilize the scale of attention (SOA) concept, describing the range of connection weights for a specific node in the network. Information entropy is employed to quantify the uncertainty of the variables, and mutual information is used as a decision criterion to reduce the degree of uncertainty with respect to (w.r.t.) the knowledge from other variables [21]. Specifically, an optimization problem on the mutual information is constructed to select the salient features with different SOAs. Since the features are derived from the ROIs defined by domain knowledge, they provide meaningful clinical interpretations, enabling biomarker studies to discover new biomarkers. A synthetic dataset and a real AD dataset are used to validate the proposed method. Our method outperforms traditional network metrics and existing feature extraction methods.

2 Related work

Mutual information is a measure of the statistical dependency between random variables. It has also been used as a key measure to evaluate the effectiveness of feature extraction in some recent studies. Marinoni and Gamba [22] proposed a method for identifying affinity patterns using mutual information maximization and validated the method using remote sensing images. Özdenizci and Erdoğmuş [23] presented an MMI linear transformation and a nonlinear transformation framework. The proposed method was applied to a brain–computer interface task and was assessed with electroencephalographic data. However, the above feature extraction methods based on the MMI were not specially designed for graph-structured data, which is the most common form of data in the task of brain network analysis.

In addition, neural networks have also been used for automatic feature extraction [24,25,26,27], and graph convolutional networks (GCNs) were recently designed for non-Euclidean data [28, 29]. However, there are two problems when applying GCNs to neuroimaging-related tasks [30,31,32]. First, the feature extraction processes in GCN are automatic, and spectral graph convolutional layers are typically used. Thus, the internal high-level features of the model are difficult to interpret. Second, the GCN inputs are graph signals (i.e., node features). However, we can only obtain graph weights (i.e., adjacency matrices) after preprocessing the diffusion tensor images (DTI). In previous studies, graph weights have represented the similarity between individuals. Graph signals were constructed from the vectorized adjacency matrices or measures of the brain regions without considering the topological properties of individual brain networks. Table 1 lists the characteristics of traditional methods and our proposed method for an intuitive comparison.

Table 1 Comparison of the Characteristics of Different Methods
Full size table

We propose the MMI-GSD, which is inspired by graph convolutional layers and considers mutual information. We extract the features from the adjacency matrices spatially, retaining the flexibility of the graph convolutional layer and enhancing the interpretability of the extracted features. The main contributions of this paper are as follows: (1) We develop a novel feature extraction method for GSD and discuss its interpretability. (2) We develop a framework to optimize the extracted features based on MMI. (3) We carry out experiments to verify the performance of the proposed method. We verify its applicability on a real AD dataset and analyze the interpretability of the features. The remainder of the paper is organized as follows. Section 2 presents the feature extraction method and the optimization framework. Section 3 describes experiments using synthetic and real data. In Section 4, we discuss the physiological meaning of the experimental results. Section 5 concludes the paper.

3 Methodology

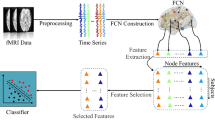
The aim of feature extraction is to reduce the dimensionality of the data. In this study, the data dimension is D × D, where D is the number of nodes in the individual brain network. The proposed MMI-GSD derives the M (M < D) feature vectors of dimension D. This section introduces the proposed MMI-GSD. As shown in Fig. 1, given a graph describing the brain network, the features are derived from the adjacency matrix and are fit to multivariate distributions. Next, a GGM is developed based on the observations. The entropy is calculated to consider the uncertainty of the variables. The mutual information obtained from the GGM is used as the criterion to evaluate the quality of the extracted features. An optimization problem is constructed to maximize the mutual information. The MMI-GSD identifies the salient network features, which are input into the classifiers.

Fig. 1
figure 1

The framework of the MMI-GSD. (A) A brain network with D nodes (Fig. 1A top), D × D adjacency matrix of the network (Fig. 1A bottom). (B) The adjacency matrix of different powers is multiplied by a direction vector bm to obtain several column vectors (Fig. 1B bottom). The greater the power, the more connection information is contained in the column vector. The adjusted brain network after the multiplication operation (Fig. 1B top). (C) Fitting the GGM; the mutual information is used to optimize \(\mathbf {b}_{m}^{\ast }\)

Full size image

3.1 Data acquisition and preprocessing

The data used in the experiments were obtained from the Alzheimer’s Disease Neuroimaging Initiative 3 (ADNI3) database (adni.loni.usc.edu) [33, 34]. The ADNI3 began in 2016 and includes scientists at 59 research centers in the United States and Canada. The primary goal of the ADNI is to measure the progression of MCI and early AD. In this study, the selected subjects included three cohorts: CN, MCI, and AD. We used T1-weighted MR images and DTI. We selected imaging scans from the same manufacturer (SIEMENS) to avoid data discrepancy. Images from baseline visit, initial visit, and screening visit of 260 subjects (119 CN, 105 MCI, and 36 AD) were used.

The DTI data processing and white matter network construction were performed using the PANDA toolbox [35]. Fiber Assignment by Continuous Tracking (FACT), a deterministic fiber-tracking algorithm, was used with an angle threshold of 45∘ and a fractional anisotropy (FA) range of 0.2-1. The brain was segmented into 90 ROIs using the automated anatomical labeling (AAL) atlas [36]. The nodes in the network were defined by the ROIs, and the edges were defined by the number of fibers connecting two ROIs. The construction of the white matter brain network is shown in Fig. 2.

Fig. 2
figure 2

Construction of the white matter brain network. (1) Registration of DTI image (B) to T1-weighted image (A) in the native space. (2) Deterministic fiber tracking (C). (3) Registration (T) of T1-weighted image in the native space to the ICBM152 T1 template in the Montreal Neurological Institute (MNI) space [37] (D). (4) Inverse transformation (T− 1) to the AAL atlas in the MNI space. (5) The brain connectivity matrix (F) is calculated by counting the fiber numbers between each pair of brain regions defined by the AAL atlas. (6) Data dimensionality reduction (R) is performed on the brain connectivity matrix, and the feature vectors are obtained as the input of the classifier

Full size image

3.2 Feature extraction from the graph using direction vectors

Given N weighted undirected graphs \(\mathcal {G}_{n}\left (n=1,\cdots ,N\right )\), let \(\mathcal {G}_{n}=\left (\mathcal {V}_{n},\mathcal {E}_{n},\mathbf {W}_{n}\right )\), where \(\mathcal {V}_{n}\) is a set of nodes (vertices), and \(\vert \mathcal {V}_{n}\vert =D\), \(\mathcal {E}_{n}\) is a set of edges. Wn is the adjacency matrix, and element Wn,kl is the connection weight between node k and node l (k≠l). Let \(\left (\mathbf {W}_{n}\right )^{m}\) be the mth power of Wn, indicating the connectivity between any two nodes within m hops. With a direction vector bm, we obtain:

$$ \mathbf{x}_{n,m}=\left( \mathbf{W}_{n}\right)^{m}\mathbf{b}_{m}. $$
(1)

The kth component in xn,m represents a linear combination of weights of the m-hop pathways connected to the kth node. According to the concept

of “hop” in a network, an increase in m indicates that a broader region of the network is being explored. Here we call m the SOA. For example, when m is 1, \(\mathbf {b}_{1} = \left [1\ \ 1\ \cdots \ 1\right ]^{T}\),

$$ \mathbf{x}_{n,1}=\left( \mathbf{W}_{n}\right)^{1}\mathbf{b}_{1}= \begin{bmatrix} {\sum}_{l=1}^{D}{W_{n,1l}}\\ {\vdots} \\ {\sum}_{l=1}^{D}{W_{n,kl}}\\ {\vdots} \\ {\sum}_{l=1}^{D}{W_{n,Dl}} \end{bmatrix}, $$
(2)

where xn,1 is a column vector. The features xn,m are extracted independently from different SOAs. Next, we create matrix \(\mathbf {X}_{n}=\left [\mathbf {x}_{n,1} \mathbf {x}_{n,2} {\cdots } \mathbf {x}_{n,M}\right ]\in \mathbb {R}^{D\times M}\) where M < D. The matrix Xn contains the extracted features with reduced dimensionality. Note that M is the number of direction vectors bm; it is related to the scale of the network and is determined empirically.

3.3 Gaussian graphical model fitting with direction vector as a prior

Without loss of generality, we remove subscript m for simplification. With respect to the direction vector b, we obtain the column feature vector xn. We use the GGM to fit the observations \(\left \{\mathbf {x}_{n}\right \}\). Specifically, the vector \(\mathbf {x}\in \mathbb {R}^{D}\) with a multivariate Gaussian (MVG) distribution \(\mathcal {N}_{D}(\boldsymbol {\mu },\mathbf {\Sigma })\) has the following density function:

$$ f \left( \mathbf{x};\boldsymbol{\mu},\mathbf{\Sigma}\right) = \frac{1}{\left( 2\pi\right)^{\frac{D}{2}} \vert\mathbf{\Sigma}\vert^{\frac{1}{2}}}\exp \left\{ -\frac{1}{2} \left( \mathbf{x} - \boldsymbol{\mu}\right)^{T} \mathbf{\Sigma}^{-1} \left( \mathbf{x} - \boldsymbol{\mu}\right) \right\}, $$
(3)

where μ is the mean, Σ is the covariance matrix, |Σ| is the determinant of Σ, and Θ, Θ = Σ− 1 is the precision matrix.

Let \(\mathcal {G}_{\mathcal {N}}=\left (\mathcal {V},\mathcal {E}\right )\) be an undirected graph where each node represents a component of the vector \(\mathbf {x}\in \mathbb {R}^{D}\) (\(\vert \mathcal {V}\vert =D\)). Vector x satisfies the (undirected) GGM with graph \(\mathcal {G}_{\mathcal {N}}\) if it has an MVG distribution \(\mathcal {N}_{D}(\boldsymbol {\mu },\mathbf {\Sigma })\) with the following constraint:

$$ \left( \mathbf{\Theta}\right)_{i,j}=\left( \mathbf{\Sigma}^{-1}\right)_{i,j}=0 \quad \mathrm{for\ all} \left( i,j\right)\notin\mathcal{E}. $$
(4)

The constraint means that the variables on nodes i and j are conditionally independent given the variables on the other nodes if there is no edge between nodes i and j. If the two variables are independent, the element in the precision matrix Θ is equal to 0.

With observations \(\left \{\mathbf {x}_{1},\mathbf {x}_{2},\cdots ,\mathbf {x}_{N}\right \}\), the likelihood function is defined as:

$$ \begin{array}{@{}rcl@{}} &&L\left( \boldsymbol{\mu},\mathbf{\Sigma};\mathbf{x}_{1},\mathbf{x}_{2},\cdots,\mathbf{x}_{N}\right)=\prod\limits_{n=1}^{N}f\left( \mathbf{x}_{n};\boldsymbol{\mu},\mathbf{\Sigma}\right) \\ &&=\!\frac{1}{\left( 2\pi\right)^{\frac{ND}{2}}\vert\mathbf{\Sigma}\vert^{\frac{N}{2}}}\exp\!\left\{ - \frac{1}{2}\!\sum\limits_{n=1}^{N}\left( \mathbf{x}_{n} - \boldsymbol{\mu}\right)^{T}\!\mathbf{\Sigma}^{- 1}\!\left( \mathbf{x}_{n} - \boldsymbol{\mu}\right)\right\}. \end{array} $$
(5)

The log-likelihood function of (5) is:

$$ \begin{array}{@{}rcl@{}} l\left( \boldsymbol{\mu},\mathbf{\Sigma}\right)&=&\log L\left( \boldsymbol{\mu},\mathbf{\Sigma};\mathbf{x}_{1},\mathbf{x}_{2},\cdots,\mathbf{x}_{N}\right) \\ &=&-\frac{ND}{2}\log\left( 2\pi\right)-\frac{N}{2}\log\vert\mathbf{\Sigma}\vert \\ && \quad -\frac{1}{2}\sum\limits_{n=1}^{N}\left( \mathbf{x}_{n}-\boldsymbol{\mu}\right)^{T}\mathbf{\Sigma}^{-1}\left( \mathbf{x}_{n}-\boldsymbol{\mu}\right). \end{array} $$
(6)

We remove the first term, which is a constant, and re-write the log-likelihood function as:

$$ \begin{array}{@{}rcl@{}} l\left( \boldsymbol{\mu},\mathbf{\Sigma}\right)\!& = &\!-\frac{N}{2}\log\vert\mathbf{\Sigma}\vert-\frac{1}{2}\sum\limits_{n=1}^{N}\left( \mathbf{x}_{n}-\boldsymbol{\mu}\right)^{T}\mathbf{\Sigma}^{-1}\left( \mathbf{x}_{n}-\boldsymbol{\mu}\right) \\ \!& = &\!\frac{N}{2}\!\left( -\log\vert\mathbf{\Sigma}\vert - \mathrm{T}\mathrm{r}\!\left( \mathbf{\Sigma}^{-1}\mathbf{S}\right) - \left( \boldsymbol{\mu} - \Bar{\mathbf{x}}\right)^{T}\!\mathbf{\Sigma}^{-1}\!\left( \boldsymbol{\mu} - \Bar{\mathbf{x}}\right)\right), \end{array} $$
(7)

where x̄ and S are the empirical mean and covariance, respectively [38].

The maximum likelihood estimation (MLE) of GGM is called the covariance selection [39]. It is expressed with constraints as:

$$ \begin{array}{@{}rcl@{}} && \text{maximize\quad} \log\vert\mathbf{\Theta}\vert-\mathrm{T}\mathrm{r}\left( \mathbf{\Theta S}\right)-\left( \boldsymbol{\mu} - \Bar{\mathbf{x}}\right)^{T}\!\mathbf{\Theta}\!\left( \boldsymbol{\mu} - \Bar{\mathbf{x}}\right) \\ && \text{subject\ to\quad} \mathbf{\Theta}_{ij}=0,\ \text{if} \left( i,j\right)\notin\mathcal{E}, \end{array} $$
(8)

with the domain \(\{\left (\boldsymbol {\mu },\mathbf {\Theta }\right )\in \mathbb {R}^{N}\times \mathbb {R}^{N\times N}\vert \mathbf {\Theta }\succ 0,\mathbf {\Theta }=\mathbf {\Theta }^{T}\}\) Since Θ is a positive definite matrix, the third term of the objective function \(\left (\boldsymbol {\mu } - \Bar {\mathbf {x}}\right )^{T}\!\mathbf {\Theta }\!\left (\boldsymbol {\mu } - \Bar {\mathbf {x}}\right )>0\) if and only if μ −x̄≠ 0. To maximize the log-likelihood function, we have

$$ \hat{\boldsymbol{\mu}}=\Bar{\mathbf{x}}=\frac{1}{N}\sum\limits_{n=1}^{N}\mathbf{x}_{n}. $$
(9)

The problem construct can be simplified as:

$$ \begin{array}{@{}rcl@{}} & &\text{maximize\quad} l\left( \mathbf{\Theta}\right)=\log\vert\mathbf{\Theta}\vert-\mathrm{T}\mathrm{r}\left( \mathbf{\Theta S}\right) \\ & &\text{subject\ to\quad} \mathbf{\Theta}_{ij}=0,\ \text{if} \left( i,j\right)\notin\mathcal{E}. \end{array} $$
(10)

This equality-constrained convex optimization problem can be solved using a modified regression algorithm due to its simplicity and computational efficiency [40]. The outcome of this process is a GGM with a given direction vector b. Next, we will discuss the use of the entropy and mutual information to assess the quality of the extracted features.

3.4 Mutual information maximization for director vector identification

The selection of the direction vector b affects the distribution of the observations \(\left \{\mathbf {x}_{n}\right \}\). In this research, we utilize information entropy to assess the impact of b quantitatively. Information entropy describes the uncertainty of a random variable, and mutual information measures the dependence between two random variables.

The entropy is defined as follows for a single discrete random variable:

$$ H(X)=-\sum\limits_{x}p(x)\log p(x), $$
(11)

where p(x) is the probability mass function. For continuous variables, the entropy is:

$$ H(X)=-{\int}_{x}f(x)\log f(x)dx. $$
(12)

For a vector of random variables with density f(x1,⋯ ,xD), the joint entropy is:

$$ H(X_{1},X_{2},\cdots,X_{D})=-\int f(x^{D})\log f(x^{D})dx^{D}. $$
(13)

The conditional entropy is denoted by H(X|Y ), which measures the entropy of a random variable X conditional on the knowledge of the random variable Y. Mutual information is defined as:

$$ \begin{array}{@{}rcl@{}} I(X;Y) & = &\sum\limits_{x,y} p(x,y)\log\frac{p(x,y)}{p(x)p(y)}\\ & =& H(X)-H(X\vert Y)\\ & = &H(Y)-H(Y\vert X). \end{array} $$
(14)

We consider a classification task where X are the observations and Y are the labels (responses) of the observations. Mutual information can be used to evaluate the features extracted from the observations. If H(Y ) is constant, H(Y |X) decreases as I(X;Y ) increases. We can extract a set of features to maximize I(X;Y ) and minimize the uncertainty Y.

When graph \(\mathcal {G}_{\mathcal {N}}\) is a complete graph, we first consider the MLE of GGM (in (10)) without constraints, which is similar to an MVG distribution:

$$ \text{maximize\quad} l\left( \mathbf{\Theta}\right)=\log\vert \mathbf{\Theta}\vert-\mathrm{T}\mathrm{r}\left( \mathbf{\Theta S}\right). $$
(15)

The gradient of the objective function is a log-likelihood function:

$$ \nabla l\left( \mathbf{\Theta}\right)=\mathbf{\Theta}^{-1}-\mathbf{S}. $$
(16)

For MLE, we have \(\nabla l\left (\mathbf {\Theta }\right )=0\):

$$ \hat{\mathbf{\Sigma}}={\hat{\mathbf{\Theta}}}^{-1}=\mathbf{S}. $$
(17)

Considering (12) and (13), the entropy of MVG [21] is:

$$ \begin{array}{@{}rcl@{}} H\left( X_{1},X_{2},\cdots,X_{D}\right) &=& H\left( \mathcal{N}_{D}\left( \boldsymbol{\mu},\mathbf{\Sigma}\right)\right)\\ &=& \frac{1}{2}\log\left[\left( 2\pi e\right)^{D}\vert\mathbf{\Sigma}\vert\right]\\ &=& \frac{1}{2}\log\left[\left( 2\pi e\right)^{D}\vert\mathbf{\Theta}\vert^{-1}\right]\\ &=& \frac{D}{2}\log\left( 2\pi e\right)-\frac{1}{2}\log\vert\mathbf{\Theta}\vert. \end{array} $$
(18)

The mutual information between \(X^{D}=\left (X_{1},\cdots ,X_{D}\right )\) and Y is:

$$ I\left( X^{D};Y\right)=H\left( X^{D}\right)-H\left( X^{D}\vert Y\right), $$
(19)

and it can be calculated by

$$ \begin{array}{@{}rcl@{}} H\left( X^{D}\vert Y\right) &=& \sum\limits_{c} P\left( Y=y_{c}\right)H\left( X^{D}\vert Y=y_{c}\right)\\ &=& \sum\limits_{c} \frac{N_{c}}{N}H\left( \mathcal{N}_{D}\left( \boldsymbol{\mu}_{c},\mathbf{\Sigma}_{c}\right)\right)\\ &=& \sum\limits_{c} \frac{N_{c}}{N}\left( \frac{D}{2}\log \left( 2\pi e\right)-\frac{1}{2}\log \vert\mathbf{\Theta}_{c}\vert\right)\\ &=& \frac{D}{2}\log\left( 2\pi e\right)-\frac{1}{2}\log\left( \prod\limits_{c} \vert\mathbf{\Theta}_{c}\vert^{\frac{N_{c}}{N}}\right), \end{array} $$
(20)

where

$$ \begin{array}{@{}rcl@{}} && N = \sum\limits_{c} N_{c}\\ && \mathbf{\Theta}_{c} = {\mathbf{\Sigma}_{c}}^{-1}. \end{array} $$
(21)

By substituting (18) and (20) into (19), we obtain:

$$ \begin{array}{@{}rcl@{}} I\left( X^{D};Y\right) &=& \frac{1}{2}\log\left( \prod\limits_{c} \vert\mathbf{\Theta}_{c}\vert^{\frac{N_{c}}{N}}\right)-\frac{1}{2}\log\vert\mathbf{\Theta}\vert\\ &=& \frac{1}{2}\log\frac{{\prod}_{c} \vert\mathbf{\Theta}_{c}\vert^{\frac{N_{c}}{N}}}{\vert\mathbf{\Theta}\vert}. \end{array} $$
(22)

When the graph structure of the GGM is complete,

$$ \begin{array}{@{}rcl@{}} I\left( X^{D};Y\right) &=& \frac{1}{2}\log\frac{{\prod}_{c} \vert{\hat{\mathbf{\Theta}}}_{c}\vert^{\frac{N_{c}}{N}}}{\vert\hat{\mathbf{\Theta}}\vert}\\ &=& \frac{1}{2}\log\frac{\vert\mathbf{S}\vert}{{\prod}_{c} \vert\mathbf{S}_{c}\vert^{\frac{N_{c}}{N}}}. \end{array} $$
(23)

Without loss of generality, let the power of Wn equal one; then

$$ \bar{\mathbf{x}}=\frac{1}{N}\sum\limits_{n=1}^{N}\mathbf{x}_{n}=\frac{1}{N}\sum\limits_{n=1}^{N}\mathbf{W}_{n}\mathbf{b}=\bar{\mathbf{W}}\mathbf{b}. $$
(24)

We substitute (24) into the empirical covariance matrix S and obtain:

$$ \begin{array}{@{}rcl@{}} \mathbf{S} &=& \frac{1}{N}\sum\limits_{n=1}^{N}\left( \mathbf{W}_{n}\mathbf{b}-\bar{\mathbf{W}}\mathbf{b}\right)\left( \mathbf{W}_{n}\mathbf{b}-\bar{\mathbf{W}}\mathbf{b}\right)^{T}\\ &=& \frac{1}{N}\sum\limits_{n=1}^{N}{\left( \mathbf{W}_{n}-\bar{\mathbf{W}}\right)\mathbf{b}\mathbf{b}^{T}}\left( \mathbf{W}_{n}-\bar{\mathbf{W}}\right)^{T}. \end{array} $$
(25)

Let b = λa, and λ be a scalar; we obtain:

$$ \begin{array}{@{}rcl@{}} \mathbf{S}^{(b)} &=& \frac{\lambda^{2}}{N}\sum\limits_{n=1}^{N}{\left( \mathbf{W}_{n}-\bar{\mathbf{W}}\right)\mathbf{a}\mathbf{a}^{T}}\left( \mathbf{W}_{n}-\bar{\mathbf{W}}\right)^{T}\\ &=& \lambda^{2}\mathbf{S}^{(a)}, \end{array} $$
(26)

and

$$ \begin{array}{@{}rcl@{}} I\left( X^{D};Y\right) &=& \frac{1}{2}\log\frac{\vert\mathbf{S}^{(b)}\vert}{{\prod}_{c} \vert\mathbf{S}^{(b)}\vert^{\frac{N_{c}}{N}}}\\ &=& \frac{1}{2}\log\frac{\vert\lambda^{2}\mathbf{S}^{(a)}\vert}{{\prod}_{c} \vert\lambda^{2}\mathbf{S}^{(a)}\vert^{\frac{N_{c}}{N}}}\\ &=& \frac{1}{2}\log\frac{\lambda^{2D}\vert\mathbf{S}^{(a)}\vert}{{\prod}_{c} \lambda^{2D}\vert\mathbf{S}^{(a)}\vert^{\frac{N_{c}}{N}}}\\ &=& \frac{1}{2}\log\frac{\vert\mathbf{S}^{(a)}\vert}{{\prod}_{c} \vert\mathbf{S}^{(a)}\vert^{\frac{N_{c}}{N}}}. \end{array} $$
(27)

Equation (27) indicates that the mutual information between XD and Y is not influenced by the scalar λ. Thus, we can regard the direction vector b as a unit vector. By restricting the space of b to a hypersphere, we can reduce the range of the search space. The mutual information is not affected when we scale the adjacency matrix to the range of 0 to 1.

Next, we revisit (10) with constraints. The optimization problem construct is:

$$ \begin{array}{@{}rcl@{}} && \text{maximize\quad} I\left( X^{D};Y\right) = \frac{1}{2}\log\frac{{\prod}_{c} \vert{\hat{\mathbf{\Theta}}}_{c}(\mathbf{b})\vert^{\frac{N_{c}}{N}}}{\vert\hat{\mathbf{\Theta}}(\mathbf{b})\vert}\\ && \text{subject\ to\quad} {\parallel\mathbf{b}\parallel}_{2}=1, \end{array} $$
(28)

where the estimation of the precision matrix (Θ) is a function of the direction vector b. This is a non-convex optimization problem. We choose a particle swarm optimization (PSO) solver due to its simplicity and high convergence rate [41]. Interested readers are referred to [41] for the technical details on PSO. Algorithm 1 describes the MMI-GSD.

figure d

4 Experiments

4.1 Experiment on synthetic networks

We first conducted an experiment on synthetic networks to analyze the properties of the MMI-GSD. They included two patterns of networks; a two-class classification was carried out. We evaluated multiple characteristics of the proposed method by adjusting the hyperparameter settings. We also compared the MMI-GSD with the traditional PCA method to evaluate the feature extraction ability of the MMI-GSD for graph data.

4.1.1 Synthetic network generation

We generated small networks with 6 nodes to evaluate the impacts of the parameter settings (see Fig. 3). We assumed that the two classes of networks share basic connection patterns with noise of the same distribution. In addition, the two classes of networks have different network-dependent connection patterns (Pattern 0 vs. Pattern 1). The shared basic patterns, network-dependent patterns, and noise result in two classes of synthetic networks. The network weights are constrained to non-negative integers to represent the number of fiber connections between two brain regions (note this research focuses on neuroimaging and AD). The noise added to the weights follows the Poisson distribution, and the weights have a Gaussian distribution. As a result, two groups of networks were generated: 2000 Class-0 samples and 2000 Class-1 samples. The synthetic network generation is described in Algorithm 2.

figure e
Fig. 3
figure 3

Generating the two patterns of the networks

Full size image

4.1.2 Gaussian graphical model

The GGM was derived based on the number of synthetic networks. Since the connection weights in the networks contain noise, we first focused on the precision matrix and used sparse constraints to identify zero elements. This approach reduces the number of GGM parameters to be estimated, which is crucial for studies with limited data. We performed a two-sample t-test on each connection weight in a set of network observations. A higher p-value cutoff indicates more connections and a higher sparsity rate (SR), which is the ratio of the number of existing edges to the number of all possible edges. The edge with a predetermined SR (see Section 4.1.3 describing the experiments on different SRs) was removed from the graph. Since the GGM estimation requires a connected graph structure, we ensured that each node had at least one edge connected to other nodes.

4.1.3 Feature extraction based on maximum mutual information

Among the 4000 synthetic networks, 3600 samples were used as the training set, and 400 samples were used as the testing set. First, we performed feature extraction on the training set. A PSO was employed as the solver for the non-convex optimization problem (Section 3.4.). We used different SRs (SR= 0.2, 0.4, 0.6, 0.8, 1) during preprocessing. The best performance was achieved for SR= 0.2. We report the results of SR= 0.2 in the following and summarize the overall performance at the end of the section.

As shown in Fig. 4, we used 20 particles for searching the extrema and tracked the mutual information convergence when m in Wm is equal to 1. The dotted red line represents the MMI value of the particle group. The MMI reaches 99% (the global optimum obtained from PSO) at the 27th iteration (black star). Although the focus of this research is not PSO, it is noteworthy that the mutual information trajectory of each particle fluctuates substantially at the beginning, and most particles converge after 700 iterations. Figure 5 shows the convergence of the mutual information for different numbers of particles (5, 10, 20, and 30). The four curves converge to the maximum after 25 iterations. The convergence for 5 and 10 particles occurs at a lower MMI value than for 20 and 30 particles, indicating that the number of particles is insufficient for this search space. In addition, the optimal solution is slightly better for 30 particles than for 20 particles, but a larger number of particles results in greater computation and learning time. The PSO algorithm balances the number of particles and the learning performance.

Fig. 4
figure 4

Mutual information convergence (SR= 0.2). The mutual information value of a group of 20 particles increases during the iterations of the particle swarm optimization algorithm. The dotted red line shows the mutual information corresponding to the globally optimal particle

Full size image
Fig. 5
figure 5

Mutual information convergence with different numbers of particles

Full size image

We performed feature extraction on the network weights using different SOA values, i.e., we changed the m in Wm from 1 to 6. The bigger the value of m, the higher the information level of the feature extraction is. Figure 6 illustrates the mutual information convergence for different values of m. The curves converge after about 50 iterations. The mutual information value is the highest value for an SOA of 6 (mutual information: 1.77), followed by 3 (mutual information: 1.49), 2 (mutual information: 1.39), 1 (mutual information: 1.32), 4 (mutual information: 1.27), and 5 (mutual information: 1.26). These results indicate that features with different SOAs describe the different characteristics of the network. For example, some features may describe the local graph features (the SOA m is small), whereas some features may describe the connectivity at a larger range (the SOA m is large). This result demonstrates the need for optimization to identify the salient features at different scales.

Fig. 6
figure 6

Mutual information convergence with different scale of attention (SOA) values (SR= 0.2)

Full size image

We visualized the extracted features for m= 1 to 6 using 400 samples from the testing set (Fig. 7). We used the t-distributed stochastic neighbor embedding (t-SNE) method to map the high-dimensional samples into a two-dimensional plane. Figure 7(A) – (F) are the visualization maps for the six SOAs. Figure 7(G) shows all extracted features from the six SOAs, and Fig. 7(H) depicts the sample after PCA transformation. It is observed that the features from different SOAs have different levels of discriminative power to differentiate the two groups of networks.

Fig. 7
figure 7

Visualizations of 400 samples in the testing set (SR= 0.2). (A)-(F) correspond to different SOAs from 1 to 6. (G) contains all extracted features of different SOAs. (H) contains the features transformed by PCA

Full size image

4.1.4 Classification of synthetic networks

We used the extracted features and transformed each original brain network Wn into a feature matrix Xn composed of multiple feature column vectors \(\left (\mathbf {W}_{n}\right )^{m}\mathbf {b}_{m}\). Each column vector corresponds to a different SOA. Fisher’s scoring, a widely used supervised feature selection method, was applied for feature selection. For a set of labeled scalar observations O = {O1,O2,⋯ ,ON}, the mean and variance of each class is μc and σc. The Fisher’s score of this set of observations is defined as:

$$ F\left( \mathbf{O}\right)=\frac{{\sum}_{c} N_{c}\left( \mu_{c}-\mu\right)^{2}}{{\sum}_{c} N_{c}\left( \sigma_{c}\right)^{2}}, $$
(29)

where μ is the mean of all observations.

We obtain 36 features from the 6-node synthetic networks with 6 SOAs. The Fisher’s scores were sorted from large to small (Fig. 8). We observe that the features with a larger Fisher’s score are distributed in different SOAs, confirming our hypothesis that the features from different SOAs contribute to the classification. We used Fisher’s score to select the top 10 features as inputs to a classifier.

Fig. 8
figure 8

P-value ranks of the extracted features (SR= 0.2)

Full size image

We adopted an SVM with a Gaussian radial basis function kernel for classification. The SVM is a nonlinear classifier that performs spatial partitioning of data with high-dimensional complex features. The classification accuracies for different SRs are listed in Table 2. The highest accuracy (95.0%) is obtained for an SR of 0.2. As the SR increases (the network becomes more connected), the classification accuracy decreases. The accuracy is 92.0% for a fully connected graph (SR= 1). For comparison, we implemented PCA. We chose to extract the same number of features as 10, the final classification accuracy rate is 92.8%.

Table 2 Classification accuracy for Different Sparsity Rates (SRs)
Full size table

4.2 Alzheimer’s disease classification experiments

4.2.1 Brain network preprocessing to reduce dimensionality

A brain network with 90 ROIs would be too computationally expensive and may result in overfitting for our small dataset. Similar to the experiment on the synthetic network, we extracted a smaller brain network. Specifically, we first performed a t-test for each edge weight in the network and retained the edges with significant connectivity. We divided the dataset into 10 parts to ensure the robustness of the derived network. In each run, 9 parts were chosen to identify which edges should be retained. 10 runs were conducted. The nodes connected by the retained edges in all 10 runs were used in the smaller brain network.

4.2.2 Feature extraction based on maximum mutual information and graph metrics

Three classification experiments were conducted: CN vs. AD, CN vs. MCI, and MCI vs. AD. After preprocessing the brain network, the original 90-node network was reduced to a network with fewer nodes (16 for all three comparisons). The MMI-GSD was implemented with different SOAs. Based on our preliminary experiments, we used SOAs ranging from 1 to 4. Four direction vectors were obtained in each classification task after mutual information optimization, as shown in Fig. 9. Each element in a direction vector has values ranging from -1 to 1, indicating the impact of the node on maximizing mutual information.

Fig. 9
figure 9

Visualization of the direction vectors. Four direction vectors are optimized in each classification task. The four pictures from left to right correspond to SOAs from 1 to 4. Red indicates a value of 1, and blue indicates a value of -1 of the direction vector

Full size image

Similar to the synthetic network experiment, we compared our method with the PCA and other state-of-the-art methods. In addition, we selected the most commonly used graph metrics to extract the network features: degree, average neighbor degree, and clustering coefficient. The metrics are indicators of nodal centrality, network resilience, and functional segregation [42]. The weighted degree of node k is the sum of the edge weights for edges adjacent to that node; it is defined as:

$$ Deg(v_{k})=\sum\limits_{v_{l}\in\mathcal{V}_{k}} W_{kl}, $$
(30)

where \(\mathcal {V}_{k}\) is the set of neighbors of node k.

The average neighbor degree of node k is the average degree of the neighbors of that node:

$$ AvgDeg(v_{k})=\frac{1}{\vert\mathcal{V}_{k}\vert} \sum\limits_{v_{l}\in\mathcal{V}_{k}} Deg(v_{l}). $$
(31)

For unweighted graphs, the clustering coefficient of node k is the fraction of the triangles passing through that node to all possible triangles; it is defined as:

$$ Cluster(v_{k})=\frac{2T(v_{k})}{Deg(v_{k})(Deg(v_{k})-1)}, $$
(32)

where T(vk) is the number of triangles passing through node k. After calculating the graph metrics, we conducted feature selection based on Fisher’s scoring to reduce the dimensions of the learning model inputs.

We implemented the t-SNE method to visualize the discriminative power from the features selected from the proposed MMI-GSD, commonly used graph metrics and PCA (see Fig. 10). The degree of separation indicates the difference between the two classes of the samples. The visualization results are not necessarily consistent with the classification results since the samples may be discriminated with higher dimensional features (see Section 4.2.3).

Fig. 10
figure 10

Visualization of the samples using three different feature extraction methods in three classification tasks

Full size image

4.2.3 Classification results

Fisher’s scoring was used for feature selection. The selected features were fed into classifiers for three tasks: CN vs. AD, CN vs. MCI, MCI vs. AD. Ten-fold cross-validation was implemented to prevent overfitting. Three performance metrics were calculated: accuracy, sensitivity, and specificity. We selected some samples from one group to match with the other group with fewer samples to avoid sample imbalance. Since the samples came from multiple clinical sites, we gave priority to the subjects from the same sites when matching samples, and we aimed for a similar male to female ratio. We obtained 38/36 (CN vs. AD), 119/105 (CN vs. MCI), and 39/36 (MCI vs. AD) samples in the three experiments.

We compared the performances of the MMI-GSD and other feature extraction methods. As the most commonly used methods in brain network analysis, PCA and graph metrics are selected for comparison; PCA and graph metrics with dimensionality reduction preprocessing (DRP) are selected to validate the effectiveness of the proposed DRP. A GCN [43] was selected to compare the classification performance of a deep learning network and the proposed MMI-GSD. The MMI-LinT and MMI-NonLinT proposed in [23], two mutual information-based methods, were selected for comparison. As shown in Table 3, the MMI-GSD achieved accuracies of 77.03%, 63.39%, and 76.00% for the three classification tasks. We believe that the MMI-GSD achieved the highest classification performance because the edge weights in the graph have an inherent connection pattern, which is not considered in other methods.

Table 3 Classification of CN vs. MCI vs. AD individuals
Full size table

In summary, our proposed MMI-GSD can be used to extract features from neuroimaging GSD and classify CN, MCI, and AD. The classification results show that the MMI-GSD considers the inherent network connections between the data, resulting in better classification performance than comparable methods.

5 Discussion

We focus on the discussion of distinguishing AD from MCI because early detection is crucial for AD. We conducted dimensionality reduction using a t-test to reduce the size of the brain network. We obtained the brain regions with the most significant differences between the MCI and AD groups, as shown in Table 4. These abnormal brain regions are consistent with the results of previous studies, including inferior and middle frontal gyri [44,45,46], Rolandic operculum [47], parieto-temporal cortex [48], caudate nucleus [49], putamen [50], and parts of the temporal lobe [51].

Table 4 Discriminative Brain Regions Between MCI and AD
Full size table

The MMI-GSD with the smaller network identified important connectivity-related features to distinguish different groups of AD patients (see Table 5). In a previous study [52], the local nodal attributes in the left temporal lobe were significantly different between amnestic MCI converters and amnestic MCI non-converters. Our results agree with these findings, i.e., discriminative connections exist for the direction vector with an SOA of 1 (Fig. 11). For an SOA of 2, we found that the connection weights between the left supramarginal gyrus and the left fusiform gyrus were significantly different (p = 0.0473 < 0.05) between the two groups. The connection weight between two nodes with a distance of two hops is defined as the sum of the weights of all possible two-hop pathways. The weight of a two-hop pathway is defined as the product of its two components. Within all possible two-hop pathways between the left supramarginal gyrus and the left fusiform gyrus, we found two white matter connection pathways with significant differences, as shown in Fig. 12. One pathway is “SMG.L-MTG.L-FFG.L”, and the other one is “SMG.L-ITG.L-FFG.L”. The p-value of pathway “SMG.L-MTG.L-FFG.L” is 0.0894, which has a certain trend toward significance, and the p-value of pathway “SMG.L-ITG.L-FFG.L” is 0.0535, which is close to being statistically significant. We found that the connectivity of these two pathways was substantially worse in the AD individuals than the MCI individuals. The left supra-marginal gyrus is crucial for writing [53], and the left fusiform gyrus is required for visual word recognition [54]. The middle temporal gyrus and inferior temporal gyrus are involved in semantic memory processing. The impairment of these two pathways may lead to dysfunction in reading and writing in AD patients. Changes in these pathways also have the potential for biomarkers to diagnose AD patients.

Table 5 Discriminative Connections Between MCI and AD
Full size table
Fig. 11
figure 11

Discriminative connections between MCI and AD. The blue balls represent discriminative brain regions selected by a two-sample t-test, and the orange lines represent discriminative connections detected by the MMI-GSD

Full size image
Fig. 12
figure 12

Two white matter connection pathways with significant changes in AD group

Full size image

6 Conclusion

The challenge in AD diagnosis is efficient feature extraction while preserving feature interpretability. We proposed a novel feature extraction method and an optimization framework based on mutual information to address this problem. The result of experiments with synthetic networks and AD classification showed that the proposed method achieved higher classification accuracy than comparable methods. The other advantage of our method is the high interpretability of the extracted features. The AD patients exhibited abnormal connections in the left hemisphere, especially in the left temporal lobe. Two white matter connection pathways had lower connectivity in the AD group, indicating reading and writing dysfunction in AD patients.

In future works, we intend to analyze whether the brain white matter changes found in this study can be used as a reliable biomarker for AD diagnosis. In addition, investigating the form of the proposed method in the nonlinear case is a way to improve performance.