1 Introduction

Zero-norm, defined as a total number of non-zero elements in a vector, is an important basic concept for modeling data sparsity. Resulting optimization problems are nonsmooth nonconvex programs with many application domains, which have attracted increasing attention from researchers in recent years.

Given a vector \(x \in \mathbb {R}^{n}\). The support of x, denoted s u p p(x) , is the set of the indices of the non-zero components of x, say

$$supp(x)=\left\{ i\in \left\{ 1,...,n\right\} :\;x_{i}\neq 0\right\} , $$

and the zero norm of x, denoted ℓ 0-norm, is defined as

$$\left\Vert .\right\Vert_{0}:=\text{cardinality of }supp(x). $$

Note that although one uses the term ”norm” to design ∥.∥0, ∥.∥0 is not a norm in the mathematical sense. Indeed, for all \(x\in \mathbb {R}^{n}\) and λ ≠ 0, one has ∥λ x∥0=∥x∥0, which is not true for a norm. Formally, a so called ℓ 0-regularized problem takes the form

$$ \min \left\{ \phi (x,y)+\rho \left\Vert x\right\Vert_{0}:(x,y)\in \mathbb{R}^{n}\mathbb{\times R}^{p}\ \right\} , $$
(1)

where the function ϕ corresponds to a given criterion and ρ is a positive number, called the regularization parameter, that makes the trade-off between the criterion ϕ and the sparsity of x.

In some applications, one wants to control the sparsity of solutions (for example, in order to limit the number of assets to be investigated in portfolio management), the ℓ 0-term is thus put in constraint, and the corresponding optimization problem is

$$ \left\{ \begin{array}{ll} \min_{x,y} & \phi (x,y) \\ s.t. & \left\Vert x\right\Vert_{0}\leq k, \:(x,y)\in \mathbb{R}^{n}\times \mathbb{R}^{p}. \end{array} \right. $$
(2)

These are challenging nonconvex programs in machine learning, image analysis and finance.

In this paper we consider a class of ℓ 0-regularized problems (1) where the function ϕ is defined by

$$ \phi (x,y):=f(x,y)+\lambda \Vert x{\Vert_{2}^{2}}. $$
(3)

Here λ>0, and f is a loss function which is assumed to be convex. The ℓ 0-regularized problem becomes the so called ℓ 2- ℓ 0-regularized problem

$$ \min_{(x,y)\in \mathbb{R}^{n}\mathbb{\times R}^{p}}\left\{ F^{\lambda ,\rho }(x,y):=f(x,y)+\lambda \Vert x{\Vert_{2}^{2}}+\rho \left\Vert x\right\Vert_{0}\right\} . $$
(4)

If the function ϕ is strongly convex in the variable x, i.e.,there is λ>0such that the function\(f(x,y):=\phi (x,y)-\lambda \Vert x{\Vert _{2}^{2}}\)is convex in the couple of variables (x,y),thenthe ℓ 0 -regularized problem (1) can be expressed as the ℓ 2- ℓ 0-regularized problem (4) and so the techniques developed in this paper can be used for the ℓ 0-regularized problem in this case.

Let us mention some important applications in machine learning related to the model (4).

Feature selection in support vector machine (SVM) learning

Feature selection is one of the fundamental problems in machine learning. In many applications such as text classification, web mining, gene expression, micro-array analysis, combinatorial chemistry, image analysis, etc, data sets contain a large number of features, many of which are irrelevant or redundant. Feature selection is often applied to high-dimensional data, prior to classification learning. The main goal is to select a subset of features of a given data set while preserving or improving the discriminative ability of a classifier. Research on feature-selection methods is very active in recent years, and an excellent review can be found in the book by [16]. We will show that the embedded (feature and classifier are simultaneously determined during the training process) feature selection method for linear classification in SVM learning is an instance of the problem (4).

Given a training data {a i ,b i } i=1,...,m where each \( x_{i}\in \mathbb {R}^{n}\) is labeled by its class b i ∈{+1,−1}, the goal of SVM learning is to construct a linear classifier function that discriminates the data points Λ:={a i } i=1,...,m with respect to their classes {b i } i=1,...,m . A classical way to obtain this classifier consists of minimizing the following loss function, [2, 8],

$$ f(w,\gamma ):=\frac{1}{m}{\sum}_{i=1}^{m}\max (0,1-b_{i}(\langle a_{i},w\rangle +\gamma )), $$
(5)

on \(w\in \mathbb {R}^{n}\) and \(\gamma \in \mathbb {R}\). If (w,γ) is a solution of this problem, then the classifier is given by F(x)=sign(〈a i ,w〉 + γ). Since in many practical applications the data set Λ is large, the model based directly on solving (5 ) leads to over-fit. [8] proposed to take into account the margin, between the separating hyperplane x↦w T x + γ and the data points {a i } i=1,...,m , and to make it maximal as possible. This results in the classical SVM problem, which is the ℓ 2 -regularized problem

$$(\ell_{2}-SVM)\ \ \min_{(w,\gamma )\in \mathbb{R}^{n}\mathbb{\times R} }\left\{ f(w,\gamma)+\lambda\Vert w\Vert_{2}^{2}\right\} . $$

The regularization parameter λ>0 makes the trade-off between the classifier criterion f and the amplitude of the margin.

The embedded feature selection in SVM involves determining the separating hyperplane x↦w T x + γ which uses as few features as possible, which leads to the following optimization problem like (4):

$$ (\ell_{2}-\ell_{0}-SVM)\text{\ \ }\min_{(w,\gamma )\in \mathbb{R}^{n} \mathbb{\times R}}\left\{ f(w,\gamma )+\lambda \left\Vert w\right\Vert_{2}^{2}+\rho \left\Vert w\right\Vert_{0}\right\} . $$
(6)

Sparse linear regression

Consider a training data set \(\left \{ b_{i},a_{i}\right \}_{i=1}^{m}\) of m independent and identically distributed samples, composed of explanatory variables \(a_{i}\in \mathbb {R}^{n}\) (inputs) and response variables \( b_{i}\in \mathbb {R}\) (outputs). Let b:=(b i ) i=1,...,m and \( A:=(a_{i,j})_{i=1,...,m}^{j=1,...,n}\) denote the vector of outputs and the matrix of inputs respectively. Linear regression aims to find a relation which can possibly exist between A and b, in other words, relating b to a function of A and a model parameter x. Such a model parameter x can be obtained by solving the optimization problem

$$ \min_{x}\;\;\;\frac{1}{m}\left\Vert Ax-b\right\Vert_{2}^{2}. $$
(7)

In many practical applications simple least squares regression leads to over-fit. This occurs when the fitted model has many feature variables with (relatively) large weights (i.e., x i is large). A classical way to remedy to these curses is provided by regularization methods, among them the ℓ 2 regularization technique, called ridge regression in the statistical literature [17, 18], is very useful. This technique leads to the convex quadratic program

$$ \min_{x\in \mathbb{R}^{n}}\left\{ \frac{1}{m}\Vert Ax-b\Vert_{2}^{2}+\lambda\Vert x\Vert_{2}^{2}\right\} . $$
(8)

The sparse linear ridge regression problem aims to find a sparse solution of the above linear ridge regression model, it takes the form of (4):

$$ \min_{x\in \mathbb{R}^{n}}\left\{ \frac{1}{m}\left\Vert Ax-b\right\Vert_{2}^{2}+\lambda \left\Vert x\right\Vert_{2}^{2}+\rho \left\Vert x\right\Vert_{0}\right\} . $$
(9)

This problem has many important applications, among them sparse signal/image recovery and feature selection in classification.

Sparse fisher linear discriminant analysis

Discriminant analysis captures the relationship between multiple independent variables and a categorical dependent variable in the usual multivariate way, by forming a composite of the independent variables. Given a set of m independent and identically distributed samples composed of explanatory variables \(a_{i}\in \mathbb {R}^{n}\) and binary response variables b i ∈{−1,1}. The idea of Fisher linear discriminant analysis is to determine a projection of variables onto a straight line that best separates the two classes. The line is determined so as to maximize the ratio of the variances of between and within classes in this projection, i.e., maximize the function \(f(\zeta )=\frac {\langle \zeta ,S_{B}\zeta \rangle }{\langle \zeta ,S_{W}\zeta \rangle },\) where S B and S W are, respectively, the between and within classes scatter matrix (which are symmetric positive semidefinite) given by

$$S_{B}:=(s_{+}-s_{-})(s_{+}-s_{-})^{T}\ ,S_{W}=S_{+}+S_{-}, $$
$$\begin{array}{l} S_{+}={\sum}_{i=1,b_{i}=+1}^{m}(a_{i}-s_{+})(a_{i}-s_{+})^{T}, \\ S_{-}={\sum}_{i=1,b_{i}=-1}^{m}(a_{i}-s_{-})(a_{i}-s_{-})^{T}. \end{array} $$

Here, for j∈{±}, s j is the mean vector of classj, l j is the number of labeled samples in class j. If ζ is an optimal solution of the problem, then the classifier is given by F(a) = ζ T a + c, c=−0.5ζ T(s + + s −). The sparse Fisher Discriminant model is defined by (ρ>0 )

$$ \left\{ \begin{array}{ll} \min_{(\zeta )} & \zeta^{T}S_{W}\zeta +\rho \left\Vert \zeta \right\Vert_{0} \\ s.t. & \zeta^{T}(s_{+}-s_{-})=b, \end{array} \right. $$
(10)

which takes the form of (4) (with the additional constraint ζ T(s +−s −) = b which is imposed to avoid multiplicity of solutions) when S W is a symmetric positive definite matrix. Indeed, let λ m i n (S W )>0 be the smallest eigenvalue of S W . For any 0<λ<λ m i n (S W ), the matrix S W −λ I is positive definite, and then the function \(\zeta ^{T}S_{W}\zeta -\lambda \left \Vert \zeta \right \Vert _{2}^{2}\) is convex. The problem (10) can be expressed as

$$ \left\{ \begin{array}{ll} \min_{(\zeta )} & \underbrace{\zeta^{T}S_{W}\zeta -\lambda \left\Vert \zeta \right\Vert_{2}^{2}}_{\text{convex}}+\lambda \left\Vert \zeta \right\Vert_{2}^{2}+\rho \left\Vert \zeta \right\Vert_{0} \\ s.t. & \zeta^{T}(s_{+}-s_{-})=1. \end{array} \right. $$
(11)

During the last two decades, research is very active in models and methods optimization involving the zero-norm. Works can be divided into three categories depending on how to treat the zero-norm: convex approximation, nonconvex approximation, and exact reformulation via Difference of Convex functions (DC) programming.

The best known convex approach is the ℓ 1 regularization approach proposed in [41] in the context of linear regression, called LASSO (Least Absolute Shrinkage and Selection Operator), which consists in replacing the ℓ 0 term ∥w∥0 by ∥w∥1, the ℓ 1-norm of the vector w. Since its introduction, several works have been developed to study the ℓ 1 -regularization technique, from the theoretical point of view to efficient computational methods (see [17], Chapter 18). The LASSO penalty has been shown to be, in certain cases, inconsistent for variable selection and biased [46]. Hence, the Adaptive LASSO is introduced in [46] in which adaptive weights are used for penalizing different coefficients in the ℓ 1 -penalty.

In parallel, nonconvex approximation approaches (the ℓ 0 term ∥w∥0 is approximated by a nonconvex function) were extensively developed

A variety of sparsity-inducing penalty functions have been proposed to approximate the ℓ 0 term: exponential concave function [3], ℓ p -norm with 0<p<1 [11] and p<0 [37], Smoothly Clipped Absolute Deviation (SCAD) [10], Logarithmic function [43], Capped- ℓ 1 [33]. The shared properties of these approaches are that the nonconvexregularization used for approximating the ℓ 0 norm are DC functions, and the resulting optimization problems are DC programs.

Using these approximations, several algorithms have been developed for resulting optimization problems, most of them are in the context of feature selection in classification, sparse regressions or more especially for sparse signal recovery: Successive Linear Approximation (SLA) algorithm [3], DCA (Difference of Convex functions Algorithm) based algorithms [6, 7, 12, 15, 19, 21, 22, 26, 30–32], Local Linear Approximation (LLA) [47], Two-stage ℓ 1 [45], Adaptive Lasso [46], reweighted- ℓ 1 algorithms [4]), reweighted- ℓ 2 algorithms such as Focal Underdetermined System Solver (FOCUSS) ([36, 37]), Iteratively reweighted least squares (IRLS) and Local Quadratic Approximation (LQA) algorithm [10, 47].

Very recently, in a more general framework, Le Thi et all [24] offered a unifying nonconvex approximation approach, with solid theoretical tools as well as efficient algorithms based on DC programming and DCA, to tackle the zero-norm and sparse optimization. A common DC approximation of the zero-norm including all standard sparse inducing penalty functions was proposed and four DCA schemes were developed that cover all standard algorithms in nonconvex sparse approximation approaches as special versions.

In the third category, called the exact reformulation nonconvex approach, the ℓ 0-regularized problem is reformulated as a continuous nonconvex program. The ℓ 0-regularized problem is first equivalently formulated as a combinatorial optimization problem by using the binary variables u i =0 if x i =0 and u i =1 if x i ≠0, and then the last problem is reformulated as a DC program via an exact penalty technique. Works in this direction were developed in [19, 21, 40].

Convex regularization approaches involve convex optimization problems for which several standards methods are available. Nonconvex approaches can produce good sparsity, but the resulting optimization problems are still difficult since they are nonconvex and a local minimum may not be a global one. The development of new models and algorithms for minimizing the zero-norm is always a challenge for researchers in optimization and machine learning.

Our contributions

Our main contributions are threefold. First, we investigate a new convex approach for solving the ℓ 2- ℓ 0-regularized problem (4). We propose a tight convex minorant function of F λ,ρ by convexifying the nonconvex term \(\lambda \left \Vert .\right \Vert _{2}^{2}+\rho \left \Vert .\right \Vert _{0}\) in F λ,ρ with the help of biconjugate function technique in nonconvex programming and explicitly computing the greatest convex minorant of this term. We show that the proposed convex relaxation is a special hard-thresholding operation. Secondly, to exploit simultaneously the advantage of convex and nonconvex approximation approaches, we propose a combined convex - nonconvex regularization approach. In the first phase, the convex relaxation is used and in the second phase an efficient DCA based algorithm is applied on DC approximate problems from the solution given by Phase 1. Third, as an application of our method, we implementit in the context of feature selection in Support Vector Machine learning. In the two-phase method, by the convex relaxation, the first phaseperforms better than ℓ 2−ℓ 1 regularization on classification while, with a ”good” approximation of the ℓ 0 -norm, the second phase can produce better sparsity. The proposed methods are compared with two standard approaches for (ℓ 2- ℓ 0-SVM): the convex regularization (ℓ 2- ℓ 1-SVM ) and the nonconvex approximation (ℓ 2- E x p-SVM ) studied in [31]. We also compare these methods with the classical ℓ 2-regularized SVM (ℓ 2-SVM ). Numerical results, on tested datasets, showthe efficiency of the proposed approaches and their superiority over the competitive methods.

Besides the main contributions concerning solution methods, we also study, in a natural way, the link between optimal solutions of both the resulting convex relaxation problem and the ℓ 2- ℓ 0 -regularized problem (4). More precisely we establish a sufficient condition so that an optimal solution of the convex relaxation problem solves the original problem (4). It turns out that this condition is quite strong and it does not hold when ρ, the coefficient parameter of ℓ 0, is quite large (however ρ should not be small when a sparse solution is desired !) This result motivates us to investigate a combined convex relaxation - nonconvex approximation approach. In fact, since the solution obtained from the convex problem is just an approximate solution to ℓ 2- ℓ 0 -regularized problem (4), further refinement for the solution via DCA is strongly recommended to produce good sparsity.

The paper is organized as follows. The convex relaxation technique is developed in Section 2. In the first two subsections of this section, we introduce a convex lower bound of the ℓ 2- ℓ 0 term and describe the resulting convex relaxation problem of (4). In the next two subsections, we state the link between this technique and hard-thresholding operation and sufficient global optimality conditions for the nonconvex problem (4) while in the last subsection we give a short discussion about numerical methods for the convex relaxation problem. The two phase algorithm is discussed in Section 3 which is started by a short presentation of DC programming and DCA. Section 4 deals with the application of the proposed approaches on feature selection in SVM and, finally, Section 5 concludes the paper.

Before beginning, let us introduce some notations that will be used in the paper.

Notations: For a vector \(x\in \mathbb {R}^{n}\), its components are x i , i=1,...,n. The vector e stands for the vector of ones and 〈x,y〉: = x T y is the standard Euclidean inner product with the corresponding norm ∥.∥2, while ∥.∥1 the ℓ 1 norm. For a scalar \(s\in \mathbb {R}\), |s| denotes the absolute value of s, s +:= max(0,s),s −:= max(0,−s). For a vector \(x\in \mathbb {R}^{n}\), |x|, x + and x − denote the previous operations componentwise. In the sequel |.|0 is ∥.∥0 in the one-dimensional case. In convex analysis, let \({\Gamma }_{0}(\mathbb {R}^{n})\) be the convex cone of all convex functions \(f:\mathbb {R}^{n}\rightarrow \mathbb {R}\cup \{+\infty \} \) semicontinuous and proper (i.e. dom \(f:=\{x\in \mathbb {R}^{n}:f(x)<+\infty \}\) is nonempty) on \(\mathbb {R}^{n}\). For a convex functionh, the subdifferential of h at x 0, denoted by ∂ h(x 0), is defined by

$$\partial h(x_{0}):=\{y\in \mathbb{R}^{n}:h(x)\geq h(x_{0})+\ \langle x-x_{0},y\rangle ,\forall x\in \mathbb{R}^{n}\}. $$

For a proper function g admitting an affine minorant on \(\mathbb {R}^{n}\), its conjugate function g ∗ is defined by

$$ g^{\ast }(y):=\sup \left\{ \langle y,x\rangle -g(x):\;x\in \mathbb{R} ^{n}\right\} , $$
(12)

and its biconjugate is the function g ∗∗:=(g ∗)∗. Recall that g ∗∗ is the greatest proper convex lower semicontinuous minorant of g on \(\mathbb {R}^{n}\) and \(f\in {\Gamma }_{0}(\mathbb {R}^{n})\) if and only if f = f ∗∗.

2 A Convex relaxation technique

Let \(\tau :=\sqrt {\frac {\rho }{\lambda }}\) and μ:= \(\frac {1}{\lambda } . \) To simplify the presentation, in what follows we consider the ℓ 2 - ℓ 0-regularized problem (4) in the form

$$\begin{array}{@{}rcl@{}} (P^{\mu ,\tau })\text{ \ }\ \nu &\!:=\!&\min_{(x,y)\in \mathbb{R}^{n}\mathbb{ \times R}^{p}}\left\{ F^{\mu ,\tau }(x,y):\,=\,\mu f(x,y)+\left\Vert x\right\Vert_{2}^{2}\right.\\&&\quad\qquad\qquad\left.+\tau^{2}\left\Vert x\right\Vert_{0}\right\} . \end{array} $$
(13)

The ℓ 0 term ∥.∥0 in (13) makes the problem nonconvex, discontinuous, NP-hard and intractable directly in general. To circumvent these difficulties, we propose to replace the nonconvex ℓ 2- ℓ 0 regularized term

$$ \left\Vert .\right\Vert_{2}^{2}+\tau^{2}\left\Vert .\right\Vert_{0} $$
(14)

by its convex biconjugate function (its greatest convex lower semicontinuous minorant on \(\mathbb {R}^{n}\))

$$ (\left\Vert .\right\Vert_{2}^{2}+\tau^{2}\left\Vert .\right\Vert_{0})^{\ast \ast }, $$
(15)

to build the following convex relaxation of (4)

$$ \text{(CR) }\left\{ \begin{array}{ll} \min & G^{\mu ,\tau }(x,y):\,=\,\mu f(x,y)\,+\,(\left\Vert .\right\Vert_{2}^{2}\,+\,\tau^{2}\left\Vert .\right\Vert_{0})^{\ast \ast }(x) \\ s.t. & x\in \mathbb{R}^{n},y\in \mathbb{R}^{m}. \end{array} \right. $$
(16)

As \((\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})^{\ast \ast }\leq (\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})\), we always have G μ,τ(x,y)≤F μ,τ(x,y) and the optimal value of (CR) is a lower bound of ν.

2.1 Computation of \((\left \Vert .\right \Vert _{2}^{2}+\protect \tau ^{2}\left \Vert .\right \Vert _{0})^{\ast \ast }\)

Proposition 1

The biconjugate of the ℓ 2 - ℓ 0 regularized function is computed by

$$ \ (\left\Vert .\right\Vert_{2}^{2}+\tau^{2}\left\Vert .\right\Vert_{0})^{\ast \ast }(x)=\left\Vert x\right\Vert_{2}^{2}-\left\Vert \left(\tau e-\left\vert x\right\vert \right)^{+}\right\Vert_{2}^{2}+\tau^{2}n. $$
(17)

Proof

Let \(\varphi :\mathbb {R}\rightarrow \mathbb {R}\) be the function defined by φ(r): = r 2 + τ 2|r|0. We have \(\left \Vert x\right \Vert _{2}^{2}+\tau ^{2}\left \Vert x\right \Vert _{0}={\sum }_{i=1}^{n}\varphi (x_{i})\) separable and φ is nonnegative, finite and lower semicontinuous on \(\mathbb {R}\). According to the well known result on the conjugate and biconjugate of a separable function [38] we have

$$ (\left\Vert .\right\Vert_{2}^{2}+\tau^{2}\left\Vert .\right\Vert_{0})^{\ast \ast }(x)={\sum}_{i=1}^{n}\varphi^{\ast \ast }(x_{i}). $$
(18)

φ ∗∗ is the upper envelope of all affine minorants of φ on \(\mathbb {R}\), i.e., for \(t\in \mathbb {R}\),

$$\begin{array}{@{}rcl@{}} \varphi^{\ast \ast }(t)&=&\sup \left\{ at+b:\;a\in \mathbb{R},b\in \mathbb{R} ,\;a z +b\right.\\&\leq&\left. \varphi (z ),\forall z \in \mathbb{R}\right\} \\&=&\sup \left\{ at+b:\;a\in \mathbb{R},b\in \mathbb{R},\;az +b\leq z^{2}\right.\\&&\left.+\tau^{2}\left\vert z \right\vert_{0},\forall z \in \mathbb{R }\right\} . \end{array} $$

The condition

$$az +b\leq z^{2}+\tau^{2}\left\vert z \right\vert_{0},\forall z\in \mathbb{R} $$

is equivalent to

$$(b\leq 0\text{ and }a z +b\leq z^{2}+\tau^{2},\forall z \in \mathbb{R},z \neq 0) $$

which is also equivalent to

$$(b\leq 0\text{ and }az +b\leq z^{2}+\tau^{2},\forall z \in \mathbb{R}). $$

Using the discriminant of the second degree polynomial z 2−a z−b + τ 2, the condition \(az +b\leq z^{2}+\tau ^{2},\forall z \in \mathbb {R}\) can be rewritten as Δ: = a 2−4(τ 2−b)≤0. Then we obtain

$$\begin{array}{l} \varphi^{\ast \ast }(r)\,=\,\sup \left\{ at\!+b:\;a\in \mathbb{R},b\leq 0,\;a^{2}\!-4(\tau^{2}-b)\leq 0\right\} \\ =\sup \left\{ at+b:\;a\in \mathbb{R},b\leq 0,b\leq \frac{4\tau^{2}-a^{2}}{4} \right\} \\ =\sup \left\{ at+\frac{1}{4}\min (4\tau^{2}-a^{2},0):\;a\in \mathbb{R} \right\} \\ =\sup \left\{ a\left\vert t\right\vert +\frac{1}{4}\min (4\tau^{2}-a^{2},0):\;a\geq 0\right\} \\ =\sup \left\{ a\left\vert t\right\vert +\frac{1}{4}(4\tau^{2}-a^{2}):\;a\geq 2\tau \right\} \\ =\sup \left\{ -\frac{1}{4}a^{2}+a\left\vert t\right\vert +\tau^{2}:\;a\geq 2\tau \right\} \\ =\left\{ \begin{array}{ll} t^{2}+\tau & \;\text{if}\;\left\vert r\right\vert \geq \tau \\ 2\tau \left\vert t\right\vert & \text{otherwise} \end{array} \right. \\ =t^{2}-\left[ \left(\tau -\left\vert t\right\vert \right)^{+}\right]^{2}+\tau^{2}. \end{array} $$

Combining this and (18) we get (17). □

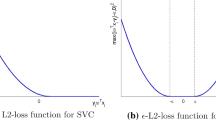
On Fig. 1, we illustrate the functions \(\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0}\), \((\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})^{\ast \ast }\) and the convex approach ℓ 2- ℓ 1, \(\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{1}\), in the one-dimensional case (n=1).

Fig. 1
figure 1

Graph of φ in green, φ ∗∗ in red and the ℓ 2- ℓ 1 approximation in blue

Full size image

We are now in a position to give the explicit formulation of the convex relaxation program (CR) of (13).

2.2 Convex relaxation formulation of (4)

From (17), the explicit formulation of (CR) can be written as

$$ \left\{ \begin{array}{ll} \min & \mu f(x,y)+\left\Vert x\right\Vert_{2}^{2}-\left\Vert \left(\tau e-\left\vert x\right\vert \right)^{+}\right\Vert_{2}^{2}+\tau^{2}n \\ s.t. & \;x\in \mathbb{R}^{n},y\in \mathbb{R}^{p}. \end{array} \right. $$
(19)

The formulation of (19) can be refined according to the definition of the function f in order to get an efficient solver for the resulting convex program. For example, we can express the term \(\left \Vert x\right \Vert _{2}^{2}-\left \Vert \left (\tau e-\left \vert x\right \vert \right )^{+}\right \Vert _{2}^{2}\) as a convex quadratic function and get another formulation of (19) as shown in (24) below. This formulation is interesting when the function f is quadratic or linear, because it becomes a convex quadratic program for which several efficient solvers are available.

Let K be the closed convex cone \(\mathbb {R}_{+}^{n}\), then its polar cone \( K^{o}:=\{y\in \mathbb {R}^{n}:\langle x,y\rangle \leq 0,\forall x\in K\}\) is \( \mathbb {R}_{-}^{n}\) and there hold the following well known properties:

i) For \(u\in \mathbb {R}^{n}\), u += max(0,u) is the projection of u on K, i.e. the solution of

$$\min \{\left\Vert u-x\right\Vert_{2}:x\in K\}$$

and −u −=−max(0,−u) is the projection of u on K o, i.e. the solution of

$$\min \{\left\Vert u-x\right\Vert_{2}:x\in K^{o}\}$$
$$\begin{array}{@{}rcl@{}} ii) u&=&u^{+}-u^{-},\: |u|=u^{+}+u^{-},\: \langle u^{+},u^{-}\rangle =0,\text{and }\\ \Vert u{\Vert_{2}^{2}}&=&\Vert u^{+}{\Vert_{2}^{2}}+\Vert u^{-}\Vert_{2}^{2}. \end{array} $$
(20)

Therefore, (19) can be rewritten as

$$\begin{array}{@{}rcl@{}} \min\!\! \!&&\mu f(x,y)+\!\Vert x{\Vert_{2}^{2}}-\!\left\Vert \tau e\,-\,|x|\right\Vert_{2}^{2}+\!\Vert (\tau e-\!|x|)^{+}\,-\,(\tau e\,-\,|x|){\Vert_{2}^{2}} \\ s.t. &&x\in \mathbb{R}^{n},\,y\in \mathbb{R}^{p}. \end{array} $$
(21)

It follows from (20) that the problem (21) is equivalent to

$$\begin{array}{@{}rcl@{}} \min &&\mu f(x,y)+\Vert x{\Vert_{2}^{2}}\!-\left\Vert \tau e-|x|\right\Vert_{2}^{2}+\Vert u\!-(\tau e-|x|){\Vert_{2}^{2}}\\ s.t. &&x\in \mathbb{R}^{n},\,y\in \mathbb{R}^{p},\,u\in \mathbb{R}_{+}^{n} \end{array} $$
(22)

in the sense that \((\bar {x},\bar {y})\) is an optimal solution of ( 21 ) iff \((\bar {x},\bar {y},\overline {u}=\left [ \tau e-\left \vert \bar {x}\right \vert \right ]^{+})\) is an optimal solution of ( 22 ).

The last problem can be written in a simpler form

$$\left\{ \begin{array}{ll} \min & \mu f(x,y)+\left\Vert x\right\Vert_{2}^{2}+\left\Vert u\right\Vert_{2}^{2}+2\left\vert x\right\vert^{T}u-2\tau e^{T}u \\ s.t. & (x,y,u)\in \mathbb{R}^{n}\times \mathbb{R}^{p}\times \mathbb{R}_{+}^{n} \end{array} \right. $$

which is equivalent to

$$ \left\{ \begin{array}{ll} \min & \mu f(x,y)+\left\Vert \sigma \right\Vert_{2}^{2}+\left\Vert u\right\Vert_{2}^{2}+2\sigma^{T}u-2\tau e^{T}u \\ s.t. & \left\vert x\right\vert \leq \sigma ,(x,\sigma ,y,u)\in \mathbb{ R}^{n}\times \mathbb{R}^{n}\times \mathbb{R}^{p}\times \mathbb{R}_{+}^{n} \end{array} \right. $$
(23)

or again

$$ \left\{ \begin{array}{ll} \min & G^{\mu ,\tau }(x,y,\sigma ,\vartheta ):=\mu f(x,y)+q(\sigma ,u) \\ s.t. & \left\vert x\right\vert \leq \sigma ,(x,\sigma ,y,u)\in C\times \mathbb{R}^{p}\times \mathbb{R}_{+}^{n}, \end{array} \right. $$
(24)

where

$$\begin{array}{@{}rcl@{}} q(\sigma ,u)&:=&\left\Vert \sigma \right\Vert_{2}^{2}+\left\Vert u\right\Vert_{2}^{2}+2\sigma^{T}u-2\tau e^{T}u;\\ C&:=&\left\{ (x,\sigma )\in \mathbb{R}^{n}\times \mathbb{R}^{n}:\left\vert x\right\vert \leq \sigma \right\} . \end{array} $$

2.3 Link with the hard-threshold operation

Let H T s (.) be defined by

$$ HT_{s}(\left\vert \theta \right\vert )=s^{2}-(\left\vert \theta \right\vert -s)^{2}I(\left\vert \theta \right\vert <s), $$
(25)

with I(|𝜃|<s):=1 if |𝜃|<s and 0 otherwise. One can see (19) as an approximated problem of (13) in which the term ∥x∥0 is replaced by

$$ \frac{1}{\tau^{2}}{\sum}_{i=1}^{n}HT_{\tau }(\left\vert x_{i}\right\vert ). $$
(26)

Hence, this convex relaxation is a special hard-threshold operation. In general, a hard-thresholding operation of ℓ 0-norm involves a nonconvex program for which only local solutions are guaranteed by iterative methods and there are some difficulties for setting the threshold parameter s. The nice effect of our approach (19) resides in the fact that the resulting program is convex with its explicit threshold parameter s = τ.

2.4 Optimality conditions: links between the convex relation (19), the ℓ 2-regularized and ℓ 2- ℓ 0-regularized problems

Consider the convex relaxation (19) of (P μ,τ), its optimality condition can be expressed as follows

$$ (0,0)\in \partial G^{\mu ,\tau }(x^{\ast },y^{\ast })\subset \mathbb{R} ^{n}\times \mathbb{R}^{p}. $$
(27)

This is equivalent to the following condition: there exists \(u\in \mathbb {R }^{n}\) such that

$$\begin{array}{@{}rcl@{}} &&(u,0)\!\in\! \mu \partial f(x^{\ast },y^{\ast })\;\text{and}\\ &&\quad\quad\!-u\in \mu \partial \left[ \left\Vert .\right\Vert_{2}^{2}\,-\,\left\Vert \left(\tau e\,-\,\left\vert .\right\vert \right)^{+}\right\Vert_{2}^{2}\right] (x^{\ast }). \end{array} $$
(28)

Let (x ∗,y ∗) be an optimal solution of the convex relaxation problem (19). It is interesting to study when (x ∗,y ∗) becomes an optimal solution to the original problem (P μ,τ). Since G μ,τ(x ∗,y ∗)≤ν≤F μ,τ(x,y)\(\forall (x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{p},\) it is clear that if G μ,τ(x ∗,y ∗) = F μ,τ(x ∗,y ∗), say \((\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})^{\ast \ast }(x^{\ast })=(\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})(x^{\ast }),\) then (x ∗,y ∗) is also an optimal solution to (P μ,τ). Hence the following useful results are immediate.

Proposition 2

1) Let (x ∗ ,y ∗ ) be an optimal solution of ( 19 ), i.e., (x ∗ ,y ∗ ) satisfying ( 28 ). If

$$ \min \{\left\vert x_{i}^{\ast }\right\vert :i\in \sup p(x^{\ast })\}\geq \mathit{\tau ,} $$
(29)

then (x ∗ ,y ∗ ) is an optimal solution of (P μ,τ ). 2) (0,y ∗ ) is an optimal solution of ( 19 ) if and only if there exists u∈[−2τ,2τ] n satisfying (u,0)∈∂f(0,y ∗ ). In this case, (0,y ∗ ) is also an optimal solution of (P μ,τ ).

Proof

1) is straightforward because the condition \( \left \vert x_{i}^{\ast }\right \vert \geq \mathit {\tau }\) for all i∈supp(x ∗) implies that \((\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})^{\ast \ast }(x^{\ast })=(\left \Vert .\right \Vert _{2}^{2}+\tau ^{2}\left \Vert .\right \Vert _{0})(x^{\ast })\) and then G μ,τ(x ∗,y ∗) = F μ,τ(x ∗,y ∗) = ν.

2. It is clear that with x ∗=0, the second condition in (28) becomes u∈[−2τ,2τ]n. The proof of the first part is then complete. The second part comes from the fact that when x ∗=0 one has G μ,τ(x ∗,y ∗) = F μ,τ(x ∗,y ∗). □

Now let (x μ,0,∗,y μ,0,∗) be an optimal solution of the ℓ 2-regularized problem (i.e. (13) without the ℓ 0 -term)

$$(P^{\mu ,0})\;\min \left\{ \mu f(x,y)+\left\Vert x\right\Vert_{2}^{2}:\;(x,y)\in \mathbb{R}^{n}\times \mathbb{R}^{p}\right\} . $$

The following proposition shows the link between the solutions of ℓ 2 -regularized and ℓ 2−ℓ 0-regularized problems and gives another sufficient optimality condition for the problem (P μ,τ).

Proposition 3

(x μ,0,∗ ,y μ,0,∗ ) is an optimal solution to (P μ,τ ) for all μ>0, τ>0 satisfying

$$ \mathit{\min \left\{ |x_{i}^{\mu ,0,\ast }|:\;i\in \text{supp}(x^{\mu ,0,\ast })\right\} \geq \tau \ .} $$
(30)

Proof

Let \(0<\tau \leq \min \left \{ |x_{i}^{\mu ,0,\ast }|:\;i\in \text {supp}(x^{\mu ,0,\ast })\right \} \). From 1) of Proposition 2, it suffices to show that (x μ,0,∗,y μ,0,∗) is an optimal solution of (19). Clearly, (x μ,0,∗,y μ,0,∗) is an optimal solution of the convex program (P μ,0) iff

$$(0,0)\in \partial f(x^{\mu ,0,\ast },y^{\mu ,0,\ast })+(2x^{\mu ,0,\ast },0). $$

It is clear that (x μ,0,∗,y μ,0,∗) and u ∗:=−2x μ,0,∗ satisfy the optimality condition (28) for (19). Thus (x μ,0,∗,y μ,0,∗) is an optimal solution of (19). □

Remark 1

  • i) Proposition 3 gives an interesting interpretation in the use of the ℓ 2-regularized problem in practice. It shows that, in some cases, the ridge regularization in learning methods affects not only on predictor but also on sparsity.

  • ii) Meanwhile, we observe that the conditions (29) and (30) are too strong, they hold only when \(\tau =\sqrt {\rho /\lambda }\) is quite small, i.e., when the ℓ 0-regularized term does not play an important role in the ℓ 2−ℓ 0 regularized problem. For example, in our first experiment we check the condition (29) on the same dataset when τ varies, (29) holds in 8/18 cases with τ 2 taking a value in the set {0.1,0.2,0.5,1,2,10}. In other words, to produce sparse solutions τ should not be small, in this case an optimal solution of the corresponding convex program (19) is only an approximate solution to the original problem (P μ,τ). Such a solution could be refined by considering a better approximation of the ℓ 2−ℓ 0 term. This shoul be donne by using a nonconvex approximation, since the biconjugate of the ℓ 2- ℓ 0 regularized function is its tighteness convex lower bound. Hence we are motivated to develop a two phase algorithm that combines convex relaxation - nonconvex approximation approaches.

2.5 On solution methods for the convex program (19)

Since (19) is a convex program, one can use several standard algorithms and software in convex programming for solving it. For machine learning applications where one is often faced with large scale setting problems, it is important to develop fast and scalable algorithms. Such approaches should exploit the structure and properties of the convex function f. Efficient specific numerical methods should be developed for each problem when the function f is given. Although convex programming has been studied for about a century, much effort has been put recently into developing fast and scalable algorithms to deal with large scale problems. While some convex regularizations involve convex quadratic programs (QP) for which standard QP solvers can be certainly used, many first-order methods have been developed in the last years for large scale convex problems, e.g. the coordinate gradient descent [42], the fast iterative shrinkage-thresholding algorithms [1], smoothing proximal gradient methods [5].

Since convex programs constitute a nice class of DC programs for which DCAs converge to optimal solutions, DCA can be used to solve the convex program (19). Assume that there exists a nonnegative number η such that the function \(\frac {1}{2}\eta \Vert (x,y)\Vert ^{2}-\mu f(x,y)\) is convex (in many practical problems such a η exists and can be easily computed; for example, when f is a smooth function with Lipschitz continuous gradient, we can take η: = μ L, where L is the Lipschitz constant of ∇f). Then we can derive a DCA scheme which is the first order method based on the projection onto C and onto \(\mathbb {R}_{+}^{n}\).

In this paper, as we focus on the tightness of the proposed convex regularization and its effect in the combined convex-nonconvex approaches, we simply use, in our experiment on feature selection in SVM, the CPLEX software to solve the convex program (24). It is in fact a quadratic program (note that this software uses efficient techniques for large scale setting such as interior points methods).

In the next section we will present DCA for solving a nonconvex approximate problem of (4).

3 Nonconvex approximation approaches

As nonconvex approximation approaches produce, in general, good sparsity, we can improve the convex regularization approach by solving, in the second step, a resulting nonconvex approximation problem from the solution given by the convex approach.

Nonconvex approximation approaches for sparse optimization involving a DC function and the ℓ 0 term have been intensively studied in [24] in the unified DC programming framework. Considering a class of DC approximation functions of the zero-norm including all usual sparse inducing approximation functions, the authors have proved several novel and elegant results concerning the consistency between global (resp. local) minimizers of the approximate problem and the original problem, the equivalence between these two problems in some cases, etc, and have developed various DCA schemes that cover all standard nonconvex approximation algorithms as special versions.

In this section, we adapt the first DCA scheme proposed in [24] for solving the problem (4) where the function f is convex (but not “real” DC as considered in [24]). For some practical problems this DCA scheme enjoys interesting convergence properties and it has been shown to be the most efficient among DCA based algorithms proposed in [24]) for feature selection in SVM.

Before presenting this DCA based algorithm, let us describe the philosophy of DCA.

3.1 Philosophy of DCA

DCA [20, 23, 34, 35] aims to solve a nonconvex program of the form

$$\inf \{F(x):=G(x)-H(x):x\in \mathrm{I\!R}^{n}\}\qquad \qquad (P_{dc}) $$

where G,H∈Γ0(I Rn) (the convex cone of all lower semicontinuous proper convex functions defined on I Rn and taking values in I R∪{+∞}. A convex constrained DC problem with the constraint x∈C can be rewritten in the form (P d c ) by adding the indicator function of C, denoted by χ C ,χ C (x)=0 if x∈C, and + ∞ otherwise) into G:

$$\begin{array}{@{}rcl@{}} \inf \{F(x)\!&:=&\!G(x)\!-H(x):x\in C\}\Leftrightarrow \inf \{(\chi_{C}(x)+G(x))\\&&-H(x):x\in \mathrm{I\!R}^{n}\} \end{array} $$

The main idea of DCA is simple: each iteration of DCA approximates the concave part −H by its affine majorization (that corresponds to taking y k∈∂ H(x k)) and solves the resulting convex program:

DCA - general scheme initializations

let x 0∈I Rn be a guess, set k:=0. repeat 1. calculate y k∈∂ H(x k). 2. calculate x k+1∈ argmin{G(x)−〈x,y k〉:x∈I Rn} (P k ). 3. k = k+1. untilconvergence of {x k}.

It has been proved in [23, 34, 35] that DCA is a descent method without linesearch, and either the sequence x k converges after a finitely number of iterations to a critical point of G−H, or if the infinite sequence {x k} is bounded and the optimal value of problem (P d c ) is finite then every limit point x ∗ of the sequence {x k} is a critical point of G−H.

The construction of DCA, and so its efficiency, depends on the choice of the functions G and H and the so called DC composition G−H. The flexibility of DCA according to the choice of DC decomposition is a crucial point to design efficient DCA based algorithms. It is worth noticing that with suitable DC decomposition DCA recovers most of standard methods in convex and nonconvex programming, in particular the three popular methods in machine learning, namely the EM (Expectation-Maximization) ([9] ), the SLA (Succesive Linear Approximation) ([3]) and the CCCP (Convex-Concave Procedure) ([44]).

DCA has been successfully applied to many (smooth or nonsmooth) large-scale nonconvex programs in various domains of applied sciences, in particular in Machine Learning (see e.g. [7, 12, 19, 21, 22, 25, 27–32, 48–52]) for which they provided quite often global solutions and proved to be more robust and efficient than standard methods.

3.2 A DCA based algorithm for nonconvex approximation problems

By the definition, the step function \(\ |.|_{0}:\mathbb {R}\rightarrow \mathbb {R}\) is given by |t|0=1 for t ≠ 0 and 0 otherwise. Then \( \Vert x\Vert _{0}={\sum }_{i=1}^{n}|x_{i}|_{0}\). The idea of approximation methods is to replace the discontinuous step function by a continuous approximation function, denoted r 𝜃 , where 𝜃>0 is a parameter controlling the tightness of approximation.

By the way, the original problem

$$\min_{(x,y)\in \mathbb{R}^{n}\mathbb{\times R}^{p}}\left\{ F^{\lambda ,\rho }(x,y):=f(x,y)+\lambda \Vert x{\Vert_{2}^{2}}+\rho \left\Vert x\right\Vert_{0}\ \right\} . $$

becomes

$$\begin{array}{@{}rcl@{}} \min\! \left\{ F_{\theta }(x,y)=\!f(x,y)\,+\,\lambda \Vert x{\Vert_{2}^{2}}\!+\rho {\sum}_{i=1}^{n}r_{\theta }(x_{i})\!:\!(x,y)\!\in\! \mathbb{R}^{n}\mathbb{\!\times\! R}^{p}\right\}.\\ \end{array} $$
(31)

With the following DC decomposition of r 𝜃 :

$$ r_{\theta}(t)=\eta |t|-(\eta |t|-r_{\theta}(t))\quad \forall t\in \mathbb{R}, $$
(32)

where η is a positive number such that ψ(t) = η|t|−r 𝜃 (t) is convex (the existence of such a η has been proved in [24] ), a DC formulation of the problem (31) is given by

$$ \min_{x,y}\{F_{\theta }(x,y):=G(x,y)-H(x,y)\}, $$
(33)

where

$$\begin{array}{@{}rcl@{}} G(x,y)&=&f(x,y)+\lambda \Vert x{\Vert_{2}^{2}}+\rho \eta \Vert x\Vert_{1},\\\\~H(x,y) &=&\rho {\sum}_{i=1}^{n}\left(\eta |x_{i}|-r_{\theta}(x_{i})\right) , \end{array} $$

Note that the use of the DC approximation r 𝜃 of the form (32) aims at introducing ρ η∥.∥1 in the DC program (33) . It has been stated in [24] a list of continuous such functions r 𝜃 , which contains all standard DC approximations and the explicit computation of their corresponding subdifferential ∂ ψ . Following the generic DCA scheme described above, DCA applied to (33) is given by Algorithm 1 below, for a given sparse inducing function r 𝜃 .

figure d

3.3 The two-phase algorithm

As mentioned in the introduction, convex regularization approaches involve convex optimization problems which are so far “easy” to solve. However, even if our convex relaxation is a special hard-threshold operation (hence it can promote sparsity), nonconvex approaches are still needed to produce better sparsity (see Remark 1). But the resulting optimization problems are very hard. Several sparse inducing nonconvex functions and corresponding algorithms are proposed in the literature, they are all special versions of DCA (see [24]). Due to its local character, finding a good starting point is important for DCA to reach global solutions. Using the solution of the convex relaxation problem seems to be a good fit for that purpose. It is therefore suggested to design a two-phase algorithm combining convex and nonconvex approaches. In the first phase the convex relaxation is performed and in the second phase an efficient DCA based algorithm is used for the nonconvex approximation problem, starting from the solution given by Phase 1. One can see that the solution given by the convex relaxation is refined (to be sparser) via the second phase via a closer (nonconvex) approximation of the ℓ 2- ℓ 0-term. So, this method can exploit simultaneously the advantage of both convex and nonconvex approximation approaches.

4 Application to feature selection in SVM

4.1 Convex relaxation formulation for feature selection in SVM model (6)

As mentioned in Section 1, the (ℓ 2- ℓ 0-SVM) problem takes the form (with the use of μ and τ instead to λ and ρ):

$$ \left\{ \begin{array}{ll} \min\! & \!\frac{\mu }{m}{\sum}_{i=1}^{m}\max (0,1\,-\,b_{i}(\langle a_{i},w\rangle \,+\,\gamma \!))\,+\,\left\Vert w\right\Vert_{2}^{2}\,+\,\tau^{2}\!\left\Vert w\right\Vert_{0} \\ s.t. & (w,\gamma )\in \mathbb{R}^{n}\times \mathbb{R} \end{array} \right. $$
(34)

or again

$$\begin{array}{@{}rcl@{}} &&(\ell_{2}\text{-}\ell_{0}\text{-SVM})\\ &&\text{ \ }\left\{ \begin{array}{ll} \min & F^{\mu ,\tau }(w,\gamma ,\xi ):=\frac{\mu }{m}e^{T}\xi +\left\Vert w\right\Vert_{2}^{2}+\tau^{2}\left\Vert w\right\Vert_{0} \\ s.t. & b_{i}({a_{i}^{T}}w+\gamma )\geq 1-\xi_{i},\;i=1,...,m, \\ & (w,\gamma ,\xi )\in \mathbb{R}^{n}\times \mathbb{R}\times \mathbb{R} _{+}^{m} \end{array} \right. \end{array} $$
(35)

Its convex relaxation formulation (24) becomes

$$\begin{array}{@{}rcl@{}} &&\text{(CR-SVM)}\\ &&\left\{ \begin{array}{ll} \min & G^{\mu ,\tau }(w,\gamma ,u ,\sigma ,\xi ):=\frac{\mu }{m}e^{T}\xi +\ q(\sigma ,u) \\ s.t. & b_{i}({a_{i}^{T}}w+\gamma )\geq 1-\xi_{i},\;i=1,...,m, \\ & \left\vert w\right\vert \!\leq\! \sigma ,(w,\gamma ,u,\sigma ,\xi )\!\in\! \mathbb{R}^{n}\!\times\! \mathbb{R}\!\times\! \mathbb{R}_{+}^{n}\!\times\! \mathbb{R} ^{n}\times \mathbb{R}_{+}^{m} \end{array} \right. \end{array} $$
(36)

which is a convex quadratic program.

4.2 A combined convex-nonconvex approximation approach: the two-phase algorithm

For feature selection in classification, convex regularization approaches perform better in classification while nonconvex approximation approaches, with a ”good” approximation of the ℓ 0-norm and based on an efficient algorithm for nonconvex resulting optimization problem, produce better sparsity. In order to get both quality and sparsity of the classifier, we use a two-phase algorithm.

A state-of-the-art algorithm for the problem (ℓ 2- ℓ 0-SVM ) is the DCA scheme developed in [31] with the concave exponential approximation proposed in [3]:

$$ r_{\alpha} (x)=\left\{ \begin{array}{ll} 1-\varepsilon^{-\alpha x} & \text{ if }x\geq 0, \\ 1-\varepsilon^{\alpha x} & \text{ if }x < 0, \\ & \end{array} \right. $$
(37)

In this approach, the resulting nonconvex problem takes the form

$$\begin{array}{@{}rcl@{}} &&(\ell_{2}\text{-}Exp\text{-SVM})\\ &&\;\left\{ \begin{array}{ll} \min & \frac{\mu }{m}e^{T}\xi +\left\Vert w\right\Vert_{2}^{2}+\tau^{2}e^{T}(e-exp(-\alpha \left\vert w\right\vert )) \\ s.t. & b_{i}({a_{i}^{T}}w+\gamma )\geq 1-\xi_{i},\;i=1,...,m, \\ & (w,\gamma ,\xi )\in \mathbb{R}^{n}\times \mathbb{R}\times \mathbb{R} _{+}^{m}, \end{array} \right. \end{array} $$

and the DCA based algorithm requires solving one quadratic program at each iteration (see [31] for more details).

It has been shown in [30] and [24] that, for the concave exponential approximation [3], the DC decomposition (32) is better than the one used in [31]. Therefore we employ this DC decomposition and Algorithm 1 for solving the approximate problem (ℓ 2-E x p-SVM). Algorithm 1 with the function r defined in (37) is described as follows.

figure e

Note that DCA has been successfully applied in several works on feature selection in classification [3, 4, 22, 30–32], and sparse signal recovery [12, 26], in particular it furnished a good sparse solution. Here, we hope that the two-phase algorithm performs classification like convex relaxation approach and produces sparsity like DCA applied on (ℓ 2- E x p-SVM ).

Two-phase algorithm(for solving (ℓ 2- ℓ 0 -SVM ))

Phase 1. Solve the convex program (CR-SVM) to get an optimal solution

(w CR,γ CR,𝜗 CR,σ CR,ξ CR).

Phase 2. Apply Algorithm (ℓ 2−ℓ 0)-DCA1 from the starting point (w CR,γ CR).

5 Numerical experiments

For evaluating the effectiveness of the proposed approaches (the convex relaxation approach named CR-SVM and the two-phase algorithm) we execute numerical experiments on several datasets and compare them with two state-of-the-art algorithms for the (ℓ 2- ℓ 0 regularized SVM: the convex approach (ℓ 2- ℓ 1-SVM)

$$(\ell_{2}\text{-}\ell_{1}\text{-SVM})\;\left\{ \begin{array}{ll} \min & \frac{\mu }{m}e^{T}\xi +\left\Vert w\right\Vert_{2}^{2}+\tau^{2}\left\Vert w\right\Vert_{1} \\ s.t. & b_{i}({a_{i}^{T}}w+\gamma )\geq 1-\xi_{i},\;i=1,...,m \\ & {(w,\gamma ,\xi )\in \mathbb{R}^{n}\times \mathbb{R}\times \mathbb{R} _{+}^{m}} \end{array} \right. $$

and the nonconvex approach developed in [31]. We also consider the (ℓ 2-SVM) approach which measures more or less the difficulty degree of classification task in test problems. All algorithms are coded in C++ and tested on an Intel Core TM I7 (2×2.2 Ghz) processor of 4 Gb RAM. The three convex approaches solve one convex quadratic problem while the nonconvex approach requires solving one convex quadratic program at each iteration. We use CPLEX solver library 13.2 for solving convex quadratic programs. The number of nonzero features in w are determined by c a r d{j:|w j |>10−5}.

5.1 Data

We consider 8 datasets which can be found at the web-site of UCI Machine Learning Repository, and 3 micro-array datasets - Leukemia cancer [13], prostate cancer [39] and Lung cancer [14]. They are described in detail in the Tables 1 and 2.

Table 1 UCI datasets
Full size table
Table 2 Micro-array datasets
Full size table

We consider also a synthetic data in which six features of 202 were relevant. The probability of y=1 or −1 was equal. The first (resp. second) three features x 1,x 2,x 3 (resp. x 4,x 5,x 6) were drawn as \(x_{i}=y\mathcal {N}(i,1)\) (resp. \(x_{i}=\mathcal {N}(0,1))\) with a probability of 0.7, otherwise the first (resp. second) three as \(x_{i}= \mathcal {N}(0,1)\) (resp. \(x_{i}=y\mathcal {N}(i-3,1))\). The remaining features are noise \(x_{i}=\mathcal {N}(0,20)\), i=1,...,202.

5.2 Experiment 1: the tightness of the convex minorant

In the first experiment, our aim is to evaluate the tightness of the proposed lower bound for solving the ℓ 2- ℓ 0-SVM problem (35). For this purpose, we measure the optimality gap (in %) which is defined by

$$ Gap:=\frac{Ub-Lb}{\left\vert Ub\right\vert }\times 100. $$
(38)

Here U b: = F μ,τ(w CR,γ CR) and L b: = G μ,τ(w CR,γ CR) are, respectively, an upper bound and a lower bound of the optimal value of (35) which are given by (w CR,γ CR), an optimal solution of the problem (CR-SVM).

We consider the Inosphere dataset and run CR-SVM on various problems with different values of λ and ρ (the coefficient of the ℓ 2 -term and ℓ 0-term). The results are reported in Table 3.

Table 3 CR-SVM: optimality gap (”Gap”), for solving ℓ 2- ℓ 0-SVM on inosphere data
Full size table

The columns ”Gap” in Table 3 show that the lower bound G μ,τ(w CR,γ CR) obtained from CR-SVM is very close to the upper bound F μ,τ(w CR,γ CR) (and then close to the optimal value): the mean of gap is only 0.24%. Moreover, in 8/18 cases this lower bound is exactly the optimal value of the corresponding ℓ 2- ℓ 0-SVM problem., i.e. the sufficient optimality condition (29) holds and CR-SVM gives an optimal solution to ℓ 2- ℓ 0-SVM problem. This shows that our convex approach CR-SVM is very promising for solving this type of problem.

5.3 Experiment 2: comparison between the two convex approaches on the synthetic data and the micro-array data

First, we evaluate the performance of the CR-SVM and the ℓ 2−ℓ 1 approaches in terms of feature selection and classification on the synthetic data. The results are reported in Table 4 for various training set sizes, taking the average test error on 500 samples over 30 runs of each training set size. The set of parameters

$${\Lambda} :=\left\{ 0.0001;0.0002;0.0003;0.0004;0.0005\right\} \;\text{and}\; $$
$${\Gamma} :=\left\{ 0.1;0.2;0.3;0.4;0.5\right\} $$

has been used.

Table 4 Synthetic data: number of selected feature (num) and classification error (ERR %)
Full size table

From Table 4, we observe that CR-SVM performs better, both in feature selection and classification, than ℓ 2- ℓ 1-SVM on this data set. Another important result is that CR-SVM selects a number of features around 6 which represents the number of relevant features on the synthetic data.

Second, we compare the two convex approaches on the three micro-array datasets. Here the training and test sets are explicitly given, and we perform the algorithms on the set of parameters.

Λ:={0.0001;0.0002;0.0003;0.0004;0.0005} and Γ:={0.01;0.02;0.03;0.04;0.05} to get the best parameters for each algorithm. More precisely, for each 𝜃∈Θ:=Λ×Γ, we apply the algorithm on the training set to get classifier and selected features, and then take the best parameter 𝜃 ∗=(λ ∗,ρ ∗) as the one corresponding to the best criterion on the test set. As we are interested on both accuracy of classification and sparsity of classifier, the best evaluated criterion used in our experiment is the smallest value of (ERRt+FS)/ACC, where ERRt, FS, ACC denote, respectively, the percentage of classification error on the test set, the percentage of selected features and the percentage of classification accuracy on the test set (i.e., ACC = 100-ERRt). The results are reported in Table 5.

Table 5 Comparative results on micro-array datasets
Full size table

On the three micro-array data sets, we observe that CR-SVM performs better feature selection than the the ℓ 2- ℓ 1-SVM on the data sets Leukemia (28 features versus 29 features) and Prostate (45 versus 260 ) and performs equally as well as ℓ 2- ℓ 1-SVM on the Lung Cancer. In term of generalization error on the test sets, CR-SVM, ℓ 2 - ℓ 1-SVM give equal generalization error on Leukemia (2.94%). On the Prostate data, CR-SVM is more competitive with 0% of generalization versus 2.94% for the ℓ 2- ℓ 1-SVM. And finally, CR-SVM ∗ performs better than the others with only 0.67% of generalization error. As for time consuming, ℓ 2- ℓ 1-SVM is slightly better than CR-SVM.

5.4 Experiment 3: comparison of all approaches on UCI datasets

In this experiment we compare the efficiency of the proposed convex approach (CR-SVM) and the two-phase algorithm with the convex approaches (ℓ 2−ℓ 1-SVM and ℓ 2-SVM), as well as the nonconvex approach [31] (denoted ℓ 2-Exp-SVM).

We fix a finite set of parameters Θ:={λ,ρ} and use the ten-fold cross-validation for the choice of the best parameters for each algorithm. More precisely, we divide the dataset into 10 equal parts. For each fold, we set 9 parts as the training set and one as the test set. By changing the test set we get ten folds.

For each 𝜃∈Θ, we apply the algorithm on each of 10 folds to determine,on each fold, the classifier and selected features on the train set and compute the classification error (ERR) on the test set as well as on the train set. Then the average result on 10 folds is used for determining the best parameters 𝜃 ∗∈Θ.

Here, we fix the parameter 𝜃 ∗=(λ ∗,ρ ∗)∈Θ that gives the best average evaluated criterion which is, as in the experiment on the micro-array datasets, (ERRt+FS)/ACC.

The set of parameters for the cross-validation procedure is

$$\begin{array}{@{}rcl@{}} {\Lambda} &:=&\{0.001;0.003;0.005;0.007;0.009\};\\ {\Gamma} &:=&\{0.01;0.03;0.05;0.07;0.09\}. \end{array} $$

For ℓ 2-Exp-SVM, the parameter α of concave approximation function is set to 5 as proposed in [3]. Since ℓ 2 -Exp-SVM is a local approach which depends on the choice of initial point, for each run, we perform it 10 times from random initial points and report the average results. The other algorithms are performed one time, because they do not depend on initial points.

In Tables 6, 7, 8, 9, 10, 11, 12 we report the best average results on 10 folds (ERR on the train set (Train) and on the test set (Test), the number (Number) and the corresponding percent (%) of selected features (Select. features)). We also indicate the values λ ∗ and ρ ∗ corresponding to these best results.

Table 6 Comparative results on PIM dataset
Full size table
Table 7 Comparative results on BCW dataset
Full size table
Table 8 Comparative results on CLE dataset
Full size table
Table 9 Comparative results on INO dataset
Full size table
Table 10 Comparative results on SPA dataset
Full size table
Table 11 Comparative results on SON dataset
Full size table
Table 12 Comparative results on ADV dataset
Full size table

We observe from the numerical results that

  1. i)

    Among the convex approaches, CR-SVM is better than ℓ 2−ℓ 1 -SVM on both classification and feature selection: in all datasets (except for ADV) CR-SVM suppresses more features than ℓ 2−ℓ 1-SVM while the ERRt are smaller on 4/7 datasets and very slightly (less than 1%) larger on 3/7 datasets. As for l 2, it deals more or less with sparsity on 2 out of 7 dataset (INO and ADV) where it selects 97% and 53.9% features.

  2. ii)

    Not surprisingly, nonconvex approach ℓ 2-Exp-SVM is better than convex approaches on feature selection while it is worse than convex approaches on classification.

  3. iii)

    The two-phase algorithm improves considerably the accuracy of classification of ℓ 2-Exp-SVM while the number of selected features of the former is slightly larger than the oneof the later. We observe that the two-phase algorithm performs classification like CR-SVM while it selects features like ℓ 2-Exp-SVM. Hence this algorithm realizes the trade-off between accuracy and sparsity and it is the best approach for simultaneously performing feature selection and classification.

6 Conclusion

We have proposed a new convex relaxation technique for minimizing a class of functions involving the zero norm that includes several important problems in machine learning. The approach is based on computing the biconjugate of the nonconvex ℓ 2- ℓ 0 regularization function which is its tightest convex minorant. It is worth to note the nice effect of our approach compared with hard-thresholding algorithms: with an appropriate choice of threshold parameter our resulting program is convex while, in general, the hard-threshold approximation of ℓ 0 involves a nonconvex program. This new and efficient way to deal with the ℓ 0 norm constitutes the most important contribution of the paper.

Secondly, the idea of combining the two convex - nonconvex approaches is interesting. The two-phase algorithm is a promising approach that we suggest to use for feature selection and classification as well as for other sparse optimization problems. The proposed approaches have been successfully applied to the feature selection in SVM via experiments on several datasets.

The new results developed in this paper open the door to several research issues. Firstly, the tightness of the proposed lower bound suggests us to develop global algorithms based on this lower bound for the nonconvex ℓ 2- ℓ 0 problem and/or for extension cases, say nonconvex programs involving ℓ 0 norm. Secondly, this convex relaxation can be useful for the combined convex relaxation - nonconvex approximation approaches. Thirdly, the global optimality condition should be exploited in the above mentioned approaches to check (and/or to get) the globality of solutions. Fourthly, numerical methods for efficiently solving large scale convex relaxation problems should be developed for practical applications, i.e. for various forms of the function f in the considered ℓ 2- ℓ 0 problem.

Works on these issues are under progress.