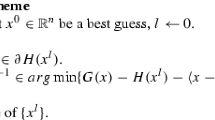Feature selection in SVM via polyhedral k-norm

Abstract

We treat the feature selection problem in the support vector machine (SVM) framework by adopting an optimization model based on use of the $\ell _0$ pseudo-norm. The objective is to control the number of non-zero components of the normal vector to the separating hyperplane, while maintaining satisfactory classification accuracy. In our model the polyhedral norm $\Vert .\Vert _{[k]}$, intermediate between $\Vert .\Vert _1$ and $\Vert .\Vert _{\infty }$, plays a significant role, allowing us to come out with a DC (difference of convex) optimization problem that is tackled by means of DCA algorithm. The results of several numerical experiments on benchmark classification datasets are reported.

1 Introduction

A relevant problem in binary classification is to design good quality classifiers by resorting to a minimal number of sample parameters. One of the main motivations is to gather a more clear interpretation of phenomena underlying the class membership distribution of the samples. In the more general setting of Machine Learning, such problem falls in the area of Feature Selection (FS), which has been the object of intensive research in recent decades (see, e.g., the survey [13]).

In this paper we focus on FS in binary classification (see [7, 28] for FS models in other areas of machine learning, such as unsupervised learning and regression, respectively). In particular, we consider the Support Vector Machine (SVM) framework [5, 29], where binary classification is pursued by finding an “optimal” two-class separating hyperplane, either in the original parameter (or “feature”) space or upon appropriate kernel transformation.

Numerical optimization algorithms play a relevant role in SVM area and, more specifically, in FS. The problem is to guarantee a reasonable trade-off between classification accuracy and the number of features actually used. Controlling the latter consists basically in minimizing the number of non-zero components of the normal vector to the separating hyperplane.

The literature offers several contributions. In [1] NP-hardness of the problem has been assessed.

In [3, 4] the model adopted is based on considering the step function for each component of the normal vector; discontinuity is handled by introducing two different approximations, the standard sigmoid and a concave exponential, respectively. In particular, by adopting the concave approximation, FS problem is tackled by solving a finite sequence of linear programs. Different approximations are given in [25, 32], where, in particular, the concave and separable objective functions, derived by the approximations, are handled via variants of Frank-Wolfe method.

It is interesting to note that in [20] an approximation scheme of the step function is cast into a DC (Difference of Convex) framework, providing thus the opportunity of resorting to the algorithmic machinery for dealing with such class of nonconvex problems. An early survey on properties and relevance of this class of functions is in [16] (see also [26]).

Parallel to treatment of FS via approximation methods, Mixed Integer Programming formulations have been successfully adopted. The idea is to introduce binary variables, one for each component of the normal vector to the supporting hyperplane, that are switched to “1” if and only if the corresponding component is non-zero. From among the proposed approaches, we recall here [2, 9, 21].

In this paper we tackle FS in the general setting of sparse optimization, where one is faced to the (regularized) problem:

$$\begin{aligned} \min _{x \in \mathbb {R}^n} f(x) + \Vert x\Vert _0 \end{aligned}$$

(1.1)

where $f:\mathbb {R}^n \rightarrow \mathbb {R}$ and $\Vert .\Vert _0$ is the $\ell _0$ pseudo-norm, which counts the number of non-zero component of any vector. Sometimes sparsity of the solution, instead of acting on the objective function, is enforced by introducing a constraint on the $\ell _0$ pseudo-norm of the solution, thus defining a cardinality-constraint problem [24].

In many applications, the $\ell _0$ pseudo-norm in (1.1) is replaced by the $\ell _1$-norm, which is definitely more tractable from the computational point of view, yet ensuring sparsity, to a certain extent (see [33] for a discussion on a general regularization scheme).

In the seminal paper [31], a class of polyhedral norms (the k-norms), intermediate between $\Vert .\Vert _1$ and $\Vert .\Vert _{\infty }$, is introduced to obtain sparse approximation solutions to systems of linear equations. The use of other norms to recover sparsity is described in [8]. In more recent years the use of k-norms has received much attention and has led to several proposals for dealing with $\ell _0$ pseudo-norm cardinality constrained problem [12, 15, 27, 34].

In this paper we cast the classic SVM approach into the sparse optimization framework (1.1). Our work is inspired by [12], the main difference being in the explicit (and not parametric) minimization of the $\ell _0$ pseudo-norm. We formulate our SVM-$\ell _0$ pseudo-norm problem ($SVM_0$, for short) and we tackle it by means of a penalization approach which allows us to put the problem in DC form. The algorithm adopted is of DCA type [19].

The paper is organized as follows. In Sect. 2 we recall first the standard SVM model and introduce the FS problem as a sparse optimization one. Then we discuss the use of the polyhedral k-norm in sparse optimization, coming out with a DC formulation. On such basis we formulate in Sect. 3 the $SVM_0$ problem. The results of several numerical experiments on benchmark datasets are in Sect. 4. Some conclusions are finally drawn in Sect. 5.

2 Feature selection and $\ell _0$ pseudo-norm minimization

The binary classification problem in the SVM setting is usually put in the following form. Given two point-sets $\mathcal{A} {\mathop {=}\limits ^{\triangle }}\{ a_1, \ldots , a_{m_1} \}$ and $\mathcal{B} {\mathop {=}\limits ^{\triangle }}\{b_1, \ldots , b_{m_2} \}$ in $\mathbb {R}^n$, we look for linear separation of the two sets, that is for a hyperplane $\{x| x \in \mathbb {R}^n,\, x^{\top }w'=\gamma '\}$, $(w' \in \mathbb {R}^n, \gamma ' \in \mathbb {R})$, strictly separating $\mathcal{A}$ and $\mathcal{B}$, thus ensuring

$$\begin{aligned} a_i^{\top }w' < \gamma ',\,\,\,\, i=1,\ldots ,m_1 \,\,\,\,\hbox {and} \,\,\,\, b_l^{\top }w' > \gamma ', \,\,\,\,l=1,\ldots ,m_2. \end{aligned}$$

It is easy to verify that such a hyperplane exists if and only if there exists a hyperplane $\{x| x \in \mathbb {R}^n,\, x^{\top }w=\gamma \}$, $(w \in \mathbb {R}^n, \gamma \in \mathbb {R})$, such that

$$\begin{aligned} a_i^{\top }w \le \gamma -1,\,\,\,\, i=1,\ldots ,m_1 \,\,\,\,\hbox {and} \,\,\,\, b_l^{\top }w \ge \gamma +1, \,\,\,\,l=1,\ldots ,m_2. \end{aligned}$$

Gordan’s theorem of the alternative [22] guarantees linear separation if and only if $\mathrm{conv}\mathcal A \cap \mathrm{conv}\mathcal B =\emptyset$, a property which is not usually known in advance to hold.

Consequently, an error function of $(w, \gamma )$, which is convex, piecewise linear and nonnegative, is introduced. It assumes zero value if and only if $(w, \gamma )$ actually defines a (strictly) separating hyperplane and it has the form:

$$\begin{aligned} e(w,\gamma )=\displaystyle \sum _{i=1}^{m_1} \max \{0, a_i^{\top }w- \gamma +1\} + \displaystyle \sum _{l=1}^{m_2} \max \{0, -b_l^{\top }w+ \gamma +1\} \end{aligned}$$

(2.1)

The SVM approach consists in solving the following convex problem:

$$\begin{aligned} \min _{w, \gamma } \Vert w\Vert + Ce(w, \gamma ) \end{aligned}$$

(2.2)

where the addition of the norm of w to the error function is aimed at obtaining a maximum-margin separation, C being a positive trade-off parameter [5].

Several variants of problem (2.2) are available in literature, according to possible choices of the norm. The $\ell _2$ norm is mostly adopted, while for feature selection purposes the $\ell _1$ norm is preferred. We observe that the latter plays also a relevant role in many areas of machine learning through the so called LASSO approach (see, e.g. [14, 28]). Weighted sums of the $\ell _1$ and $\ell _2$ norms have been considered within the elastic net [35] and the doubly regularized SVM [30] approaches.

In the following two sub-sections we address first problem (2.2), casting it into the sparse optimization paradigm (1.1), by means of the $\ell _0$ pseudo-norm. Then we discuss a DC formulation of the resulting problem.

2.1 Sparse minimization and k-norms

As previously mentioned, the $\ell _0$ pseudo-norm counts the number of non-zero components of any vector. We resume here its basic properties and highlight the relationship with polyhedral k-norm, which allows us to reformulate the sparse optimization problem (1.1).

The usual notation $\Vert .\Vert _0$ for indicating the $\ell _0$ pseudo-norm is motivated by the observation

$$\begin{aligned} (\Vert .\Vert _p)^p \rightarrow \Vert .\Vert _0 \quad \text{ when }\quad p \rightarrow 0. \end{aligned}$$

(2.3)

Relevant properties of function $x \mapsto \Vert x\Vert _0$ are:

• (i) it is lower-semicontinuous, that is to say

  $$\begin{aligned} \lim \inf _{k \rightarrow + \infty } \Vert x_k\Vert _0 \ge \Vert x\Vert _0 \quad \text{ whenever } \quad x_k \rightarrow x, \end{aligned}$$

  a property which is fundamental in view of using descent algorithms;

• (ii) it is homogeneous of degree 0, ($\Vert \lambda x\Vert _0=\Vert x\Vert _0$, for $\lambda \ne 0$); constancy along rays makes difficult the design of minimization algorithms;

• (iii) the convex hull of $\Vert .\Vert _0$ on the ball $\{x|\, \Vert x\Vert _{\infty } \le r \}$ is exactly the function $\frac{1}{r}\Vert \Vert _1$. This is a mathematical justification for frequent substitution of $\Vert .\Vert _0$ by $\Vert .\Vert _1$, which in fact ensures, in practical applications, attractive sparsity properties of the solution.

In our approach to FS we fix $\Vert w\Vert _0$ in formulation (2.2), thus we consider a sparse optimization problem of the type

$$\begin{aligned} f_0^*=\min _{x \in \mathbb {R}^n} f(x)+\Vert x\Vert _0, \end{aligned}$$

(2.4)

where $f:\mathbb {R}^n \rightarrow \mathbb {R}$, $n \ge 2$, is convex, not necessarily differentiable. We observe, in passing, the significant parallelism between sparse optimization and certain problems in matrix optimization [17, 23]. See, in particular, the recent approach to the rank function minimization described in [12].

In tackling problem (2.4) we resort to the vector k-norm of x, indicated by $\Vert x\Vert _{[k]}$, which is defined as the sum of k largest components (in modulus) of x, $k=1,\ldots ,n$. In fact $\Vert .\Vert _{[k]}$ is a polyhedral norm, intermediate between $\Vert .\Vert _1$ and $\Vert .\Vert _{\infty }$.

The following properties hold:

• (i) $\Vert x\Vert _{\infty } =\Vert x\Vert _{[1]}\le \cdots \le \Vert x\Vert _{[k]} \le \cdots \Vert x\Vert _{[n]}=\Vert x\Vert _1;$

• (ii) $\Vert x\Vert _0 \le k \,\,\, \Rightarrow \,\,\,\Vert x\Vert _1-\Vert x\Vert _{[s]}=0, \,\,\,k \le s \le n$.

Moreover, it is easy to prove the equivalence, valid for $1 \le k \le n$,

$$\begin{aligned} \Vert x\Vert _0 \le k \,\,\, \Leftrightarrow \,\,\,\Vert x\Vert _1-\Vert x\Vert _{[k]}=0, \end{aligned}$$

(2.5)

which allows to replace any constraint of the type $\Vert x\Vert _0 \le k$ with a difference of norms, that is a DC constraint.

Taking any point $\bar{x} \in \mathbb {R}^n$ and letting $I_{[k]} {\mathop {=}\limits ^{\triangle }}\{i_1,\ldots ,i_k\}$ be the index set of k largest in modulus components of $\bar{x}$, a subgradient $\bar{g}^{[k]}$ of the vector k-norm at $\bar{x}$ can be calculated by setting:

$$\begin{aligned} \bar{g}^{[k]}_i= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 1 &{} \text{ if } &{} i \in I_{[k]} \,\,\,\text{ and }\,\,\, \bar{x}_i \ge 0\\ -1 &{} \text{ if } &{} i \in I_{[k]} \,\,\, \text{ and } \,\,\, \bar{x}_i < 0\\ 0 &{} \hbox {otherwise}&{} \end{array} \right. \end{aligned}$$

To tackle problem (2.4), we start from the observation (see [23, 34]):

$$\begin{aligned} \Vert x\Vert _{[k]} = \max _{y \in \psi _k}y^{\top }x, \end{aligned}$$

where $\psi _k$ is the subdifferential of $\Vert .\Vert _{[k]}$ at point 0,

$$\begin{aligned} \psi _k = \{y \in \mathbb {R}^n \,|\, y= u-v, \,\, 0 \le u,\,v \le e, \,\,(u+v)^{\top }e=k \}, \end{aligned}$$

with e being the vector of n ones. Then we formulate the following problem:

$$\begin{aligned} f^*_c=&\displaystyle \min _{x,u,v,z } f(x)+z&~ \end{aligned}$$

(2.6)

$$\begin{aligned}&e^{\top }(u+v)=z&\end{aligned}$$

(2.7)

$$\begin{aligned}&(u-v)^{\top }x\ge \Vert x\Vert _1&\end{aligned}$$

(2.8)

$$\begin{aligned}&0 \le u,\,v \le e, \quad x \in \mathbb {R}^n.&\end{aligned}$$

(2.9)

Remark 2.1

From $\Vert x\Vert _1 \ge \Vert x\Vert _{[k]}$, $k=1,\ldots ,n$ it follows that at any feasible point constraint (2.8) is satisfied by equality.

The following proposition highlights the relationship, at the optimum, between variable x and variables u, v.

Proposition 2.2

At any optimal (local) solution $(x^*,u^*,v^*,z^*)$ of problem (2.6)–(2.9), the following relations hold for $j=1,\ldots , n$:

$$\begin{aligned} \left\{ \begin{array}{lll} x^*_j>0 &{}\Leftrightarrow &{}u^*_j=1\\ x^*_j<0 &{}\Leftrightarrow &{}v^*_j=1\\ x^*_j=0 &{}\Leftrightarrow &{}u^*_j=v^*_j=0\\ \end{array} \right. \end{aligned}$$

(2.10)

Proof

Note first that $u^*_j$ and $v^*_j$ cannot be both positive. In fact, in such case the solution obtained by replacing $u^*_j$ and $v^*_j$ by $u^*_j-\delta _j$ and $v^*_j-\delta _j$, with $\delta _j {\mathop {=}\limits ^{\triangle }}\min \{u^*_j,\, v^*_j\}>0$, would be still feasible and would reduce the objective function value.

Now observe that, while constraint (2.9) ensures

$$\begin{aligned} -|x_j| \le x_j(u_j-v_j) \le |x_j|, \,\,\,\,j=1,\ldots ,n, \end{aligned}$$

satisfaction of constraint (2.8) guarantees $x_j(u_j-v_j)=|x_j|$, $j=1,\ldots ,n$. Thus it is proved, in particular, $x^*_j>0 \Rightarrow u^*_j=1$ ($x^*_j<0 \Rightarrow v^*_j=1$).

The implication $x^*_j=0 \Rightarrow u^*_j=v^*_j=0$ can be proved by a simple contradiction argument, taking into account optimality of the solution. The same contradiction argument guarantees that the implications $x^*_j>0 \Leftarrow u^*_j=1$ ($x^*_j<0 \Leftarrow v^*_j=1$) hold true, while the last implication $x^*_j=0 \Leftarrow u^*_j=v^*_j=0$ can be proved by observing that $u^*_j=v^*_j=0$ and $x^*_j \ne 0$ would lead to violation of constraint (2.8).$\square$

Remark 2.3

Implications (2.10) ensure $z^*=\Vert x^*\Vert _0$. Moreover, letting $(x^*,u^*,v^*,z^*)$ be any local minimum of problem (2.6)–(2.9), then $x^*$ is a local minimum for problem (2.4).

By eliminating the scalar variable z in problem (2.6)–(2.9) we come out with the reformulation

$$\begin{aligned} f^*_c=&\displaystyle \min _{x,u,v} f(x)+e^{\top }(u+v)&~ \end{aligned}$$

(2.11)

$$\begin{aligned}&(u-v)^{\top }x\ge \Vert x\Vert _1&\end{aligned}$$

(2.12)

$$\begin{aligned}&0 \le u,\,v \le e, \quad x \in \mathbb {R}^n,&\end{aligned}$$

(2.13)

which we approach by penalizing the nonlinear nonconvex constraint (2.12) through the scalar penalty parameter $\sigma >0$. We obtain

$$\begin{aligned} f_c(\sigma )=\displaystyle \min _{x,u,v}&f(x)+e^{\top }(u+v)+ \sigma \big (\Vert x\Vert _1 - (u-v)^{\top }x\big )&~ \end{aligned}$$

(2.14)

$$\begin{aligned}&0 \le u,\,v \le e,\quad x \in \mathbb {R}^n.&\end{aligned}$$

(2.15)

Problem (2.14)–(2.15) is box-constrained and nonconvex, due to presence of a bilinear term in the objective function. We introduce next a possible DC decomposition.

2.2 DC decomposition

To obtain the required decomposition, we observe first that, letting $p^{\top }{\mathop {=}\limits ^{\triangle }}(x^{\top },u^{\top },v^{\top })$, the term

$$\begin{aligned} q(p) {\mathop {=}\limits ^{\triangle }}(v-u)^{\top }x, \end{aligned}$$

in (2.14) can be written in DC form as

$$\begin{aligned} q(p)= p^{\top }Q_1p -p^{\top }Q_2p, \end{aligned}$$

where the symmetric positive semidefinite matrices $Q_1$ and $Q_2$ of dimension (3n, 3n) are as follows:

$$\begin{aligned} Q_1=\frac{1}{4} \left( \begin{array}{lll} 2I&{}\quad -I &{}\quad I\\ -I &{}\quad I &{}\quad 0\\ I &{}\quad 0 &{}\quad I\\ \end{array} \right) \end{aligned}$$

(2.16)

and

$$\begin{aligned} Q_2=\frac{1}{4} \left( \begin{array}{lll} 2I&{}\quad I &{}\quad -I\\ I &{}\quad I &{}\quad 0\\ -I &{}\quad 0 &{}\quad I\\ \end{array} \right) , \end{aligned}$$

(2.17)

with I and 0 being, respectively, the identity matrix and the zero matrix of dimension (n, n).

Summing up, the objective function (2.14) is decomposed as follows:

$$\begin{aligned} f(x)+e^{\top }(u+v)+ \sigma \big (\Vert x\Vert _1 - (u-v)^{\top }x\big )= h_1(p)-h_2(p), \end{aligned}$$

with

$$\begin{aligned} h_1(p) {\mathop {=}\limits ^{\triangle }}f(x)+e^{\top }(u+v)+ \sigma \big (\Vert x\Vert _1+p^{\top }Q_1p \big ), \end{aligned}$$

and

$$\begin{aligned} h_2(p) {\mathop {=}\limits ^{\triangle }}\sigma p^{\top }Q_2p. \end{aligned}$$

Before concluding the section, we state a property related to parametric normalization of a convex function via the $\ell _1$ norm. It will be useful in explaining the role of parameter $\sigma$ in the numerical experiments of Sect. 4.

Proposition 2.4

Let $f:\mathbb {R}^n\rightarrow \mathbb {R}$ be convex and define, for $\sigma >0$, $f_{\sigma }(x)= f(x)+ \sigma \Vert x\Vert _1$. If

$$\begin{aligned} \sigma > \min _{g \in \partial f(0)} \Vert g\Vert _{\infty }, \end{aligned}$$

then $x^*=0$ is the unique minimum of $f_{\sigma }$.

Proof

Our aim is to prove

$$\begin{aligned} f(x)+ \sigma \Vert x\Vert _1 > f(0) \quad \forall x \in \mathbb {R}^n, \quad x \ne 0. \end{aligned}$$

(2.18)

According to the definition of $g \in \partial f(0)$,

$$\begin{aligned} f(x) \ge f(0)+ g^{\top }x, \quad \forall x \in \mathbb {R}^n, \end{aligned}$$

whence

$$\begin{aligned} f(x)+\sigma \Vert x\Vert _1 \ge f(0)+ \sigma \Vert x\Vert _1+g^{\top }x, \quad \forall x \in \mathbb {R}^n. \end{aligned}$$

Since $g^{\top }x \ge -\Vert g\Vert _{\infty }\Vert x\Vert _1$, we infer from the above

$$\begin{aligned} f(x)+\sigma \Vert x\Vert _1 \ge f(0)+ (\sigma -\Vert g\Vert _{\infty })\Vert x\Vert _1, \quad \forall x \in \mathbb {R}^n. \end{aligned}$$

To ensure (2.18) it suffices fo have $\sigma - \Vert g\Vert _{\infty } >0$ for one $g \in \partial f(0)$. This is secured with the assumption $\displaystyle \sigma > \min \nolimits _{g \in \partial f(0)}\Vert g\Vert _{\infty }$.$\square$

In next section, after recalling the standard $\ell _1$ norm formulation of the SVM model, we state the $\ell _0$ FS model and we adapt to it the previously defined DC decomposition.

3 The $\ell _0$-SVM problem $\mathbf {(SVM_0)}$

We rewrite first the SVM model (2.2), taking into account the definition (2.1) of the classification error and adopting the $\ell _1$ norm. We obtain problem $SVM_1$.

$$\begin{aligned}&z^*=\displaystyle \min _{w, \gamma , \xi , \zeta } \Vert w\Vert _1 + C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right)&~ \end{aligned}$$

(3.1)

$$\begin{aligned}&\text {subject to}&~ \nonumber \\&a_i^{\top }w- \gamma +1\le \xi _i,&i=1,\ldots , m_1&\end{aligned}$$

(3.2)

$$\begin{aligned}&-b_l^{\top }w+ \gamma +1\le \zeta _l,&l=1,\ldots , m_2&\end{aligned}$$

(3.3)

$$\begin{aligned}&\xi _i \ge 0,&i=1,\ldots ,m_1&\end{aligned}$$

(3.4)

$$\begin{aligned}&~ \zeta _l \ge 0,&l=1,\ldots ,m_2, \end{aligned}$$

(3.5)

where the nonnegative auxiliary variables $\xi _i$, $i=1,\ldots ,m_1$ and $\zeta _l$, $l=1,\ldots ,m_2$ have been introduced to eliminate nonsmoothness in the definition (2.1).

Moreover, by letting

$$\begin{aligned} w=w^+-w^-, \,\,\,w^+,\, w^- \ge 0, \end{aligned}$$

and indicating by e the vector of ones of dimension n, the above problem can be rewritten in a Linear Programming form as follows

$$\begin{aligned}&z^*=\displaystyle \min _{w^+, w^-, \gamma , \xi , \zeta } e^{\top }(w^++w^-) + C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right)&~ \end{aligned}$$

(3.6)

$$\begin{aligned}&\text {subject to}&~ \nonumber \\&a_i^{\top }(w^+-w^-)- \gamma +1\le \xi _i,&i=1,\ldots , m_1&\end{aligned}$$

(3.7)

$$\begin{aligned}&-b_l^{\top }(w^+-w^-)+ \gamma +1\le \zeta _l,&l=1,\ldots , m_2&\end{aligned}$$

(3.8)

$$\begin{aligned}&\xi _i \ge 0,&i=1,\ldots ,m_1&\end{aligned}$$

(3.9)

$$\begin{aligned}&~ \zeta _l \ge 0,&l=1,\ldots ,m_2, \end{aligned}$$

(3.10)

$$\begin{aligned}&~ w^+ \ge 0, \,\,\, w^- \ge 0&\end{aligned}$$

(3.11)

Of course (3.1)–(3.5) or (3.6)–(3.11) are equivalent formulations of $SVM_1$.

We remark that choice of $\Vert .\Vert _1$ in (2.2), instead of $\Vert .\Vert _2$, has a beneficial effect in terms of feature selection (see [3]).

To guarantee, however, a better control on the number of features actually entering the classification process, we replace $\Vert .\Vert _1$ with $\Vert .\Vert _0$ into the model (3.1)–(3.5).

In the sequel we tailor the sparse optimization approach via k-norm of previous section to Feature Selection in SVM model. We obtain the $SVM_0$ problem

$$\begin{aligned}&z^*=\displaystyle \min _{w^+, w^-, \gamma , \xi , \zeta ,u,v } C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right) + e^{\top }(u+v) ~&\end{aligned}$$

(3.12)

$$\begin{aligned}&\text {subject to}&~ \nonumber \\&(u-v)^{\top }(w^+-w^-)\ge e^{\top }(w^++w^-)&\end{aligned}$$

(3.13)

$$\begin{aligned}&a_i^{\top }(w^+-w^-)- \gamma +1\le \xi _i,&i=1,\ldots , m_1&\end{aligned}$$

(3.14)

$$\begin{aligned}&-b_l^{\top }(w^+-w^-)+ \gamma +1\le \zeta _l,&l=1,\ldots , m_2&\end{aligned}$$

(3.15)

$$\begin{aligned}&\xi _i \ge 0,&i=1,\ldots ,m_1&\end{aligned}$$

(3.16)

$$\begin{aligned}&~ \zeta _l \ge 0,&l=1,\ldots ,m_2&\end{aligned}$$

(3.17)

$$\begin{aligned}&~ w^+ \ge 0, \,\,\, w^- \ge 0&\end{aligned}$$

(3.18)

$$\begin{aligned}&0 \le u,\,v \le e&\end{aligned}$$

(3.19)

Penalizing, as in (2.14), the (nonlinear) constraint (3.13) we obtain

$$\begin{aligned}&z^*=\displaystyle \min _{w^+, w^-, \gamma , \xi , \zeta ,u,v } e^{\top }(u+v) + C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right) +\sigma \big (e^{\top }(w^++w^-)\nonumber \\&\quad -(u-v)^{\top }(w^+-w^-)\big ) ~&\end{aligned}$$

(3.20)

$$\begin{aligned}&\text {subject to}&~ \nonumber \\&a_i^{\top }(w^+-w^-)- \gamma +1\le \xi _i, \,\,\,\, i=1,\ldots , m_1&\end{aligned}$$

(3.21)

$$\begin{aligned}&-b_l^{\top }(w^+-w^-)+\gamma +1\le \zeta _l, \,\,\,\, l =1,\ldots , m_2&\end{aligned}$$

(3.22)

$$\begin{aligned}&\xi _i \ge 0, \,\,\,\, i=1,\ldots ,m_1&\end{aligned}$$

(3.23)

$$\begin{aligned}&~ \zeta _l \ge 0, \,\,\,\, l=1,\ldots ,m_2,&\end{aligned}$$

(3.24)

$$\begin{aligned}&~ w^+ \ge 0, \,\,\, w^- \ge 0&\end{aligned}$$

(3.25)

$$\begin{aligned}&0 \le u,\,v \le e&\end{aligned}$$

(3.26)

Remark 3.1

Definition of an exact nondifferentiable penalty function of the type described in [6] would require the introduction into the objective function of the term

$$\begin{aligned} \sigma \max \big (0, e^{\top }(w^++w^-)-(u-v)^{\top }(w^+-w^-)\big ), \end{aligned}$$

which in our case, according to Remark 2.1, is simply replaced by

$$\begin{aligned} \sigma \big (e^{\top }(w^++w^-)-(u-v)^{\top }(w^+-w^-)\big ), \end{aligned}$$

giving rise to a differentiable exact penalty function

In a way analogous to that followed in previous section, problem (3.20)–(3.26) can be put in DC form. In fact, letting $s^{\top }{\mathop {=}\limits ^{\triangle }}(w^{+T}, w^{-T},u^{\top },v^{\top })$, the function

$$\begin{aligned} r(s) {\mathop {=}\limits ^{\triangle }}(v-u)^{\top }(w^+-w^-) \end{aligned}$$

can be rewritten as

$$\begin{aligned} r(s)= s^{\top }\hat{Q}_1s -s^{\top }\hat{Q}_2s, \end{aligned}$$

where the symmetric positive semidefinite matrices $\hat{Q}_1$ and $\hat{Q}_1$ of dimension (4n, 4n) are defined as follows

$$\begin{aligned} \hat{Q}_1=\frac{1}{4} \left( \begin{array}{llll} 2I&{}\quad -2I&{}\quad -I &{}\quad I\\ -2I&{}\quad +2I&{}\quad I &{}\quad -I\\ -I&{}\quad I &{}\quad I &{}\quad 0\\ I&{}\quad -I &{}\quad 0 &{}\quad I\\ \end{array} \right) \end{aligned}$$

(3.27)

and

$$\begin{aligned} \hat{Q}_2=\frac{1}{4} \left( \begin{array}{llll} 2I&{}\quad -2I&{}\quad I &{}\quad -I\\ -2I&{}\quad +2I&{}\quad -I &{}\quad I\\ I&{}\quad -I &{}\quad I &{}\quad 0\\ -I&{}\quad I &{}\quad 0 &{}\quad I\\ \end{array} \right) , \end{aligned}$$

(3.28)

with I and 0 being, respectively, the identity and the zero matrix of dimension (n, n).

The objective function is then decomposed in DC form $f_1(w^{+}, w^{-},\gamma , \xi , \zeta , u, v)-f_2(w^{+}, w^{-},u,v)$ with

$$\begin{aligned} f_1(w^{+}, w^{-},\gamma , \xi , \zeta , u, v)=e^{\top }(u+v) + C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right) +\sigma \big (e^{\top }(w^++w^-)+s^{\top }\hat{Q}_1s\big ), \end{aligned}$$

and

$$\begin{aligned} f_2(w^{+}, w^{-},u,v) = \sigma s^{\top }\hat{Q}_1s \end{aligned}$$

We apply to problem above the DCA method [19], which tackles the unconstrained minimization of a function $q: \mathbb {R}^n \rightarrow \mathbb {R}$

$$\begin{aligned} q(x)=q_1(x)-q_2(x), \end{aligned}$$

with $q_1$ and $q_2$ convex, by solving a sequence of linearized convex problems. In particular, letting $x^{(k)}$ be the estimate of a (local) minimum of g at iteration k, the next iterate $x^{(k+1)}$ is calculated as

$$\begin{aligned} x^{(k+1)}= \arg \min _{x \in \mathbb {R}^n} \left\{ q_1(x)-[q_2(x^{(k)})+ g^{(k)\top }(x-x^{(k)})]\right\} , \end{aligned}$$

with $g^{(k)} \in \partial q_2(x^{(k)})$. For other methods to solve DC problems see [10, 11, 18] and the references therein.

We remark that, in applying the successive linearization method to our case, a convex quadratic minimization problem is solved at each iteration.

3.1 Mixed binary programming formulation $\mathbf {MBP_0}$

Before reporting in next section the results of the implementation of our algorithm to solve $SVM_0$, we provide the following mixed binary programming formulation $MBP_0$ [9] of the $\ell _0$ pseudo norm FS, which is based on the introduction of the set of binary variables $y_j$, $j=1,\ldots ,n$.

$$\begin{aligned}&z^*=\displaystyle \min _{w, \gamma , \xi , \zeta , y } \Vert w\Vert _1 + C \left( \displaystyle \sum _{i=1}^{m_1} \xi _i + \displaystyle \sum _{l=1}^{m_2} \zeta _l\right) + D \displaystyle \sum _{j=1}^{n} y_j&~\\&\text {subject to}&~ \\&a_i^{\top }w+ \gamma + 1\le \xi _i,&\, i=1,\ldots , m_1&\\&-b_l^{\top }w- \gamma +1\le \zeta _l,&\,l=1,\ldots , m_2&\\&-u_jy_j \le w_j \le u_jy_j,&j=1,\ldots ,n&\\&\xi _i \ge 0,&\,i=1,\ldots ,m_1&\\&~ \zeta _l \ge 0,&\,l=1,\ldots ,m_2 \\&y_j \in \{0,1\},&j=1,\ldots ,n, \end{aligned}$$

where $u_j >0$, $j=1,\ldots ,n$, is a given bound on the modulus of the j-th component of w (see [9] for a discussion on setting the $u_j$’s) . The binary variable $y_j$, $j=1,\ldots ,n$ is equal to 1 at the optimum if and only if $w_j \ne 0$, $j=1,\ldots ,n$. Consequently the term $\displaystyle \sum \nolimits _{j=1}^n y_j$ in the objective function represents the $\ell _0$ pseudo-norm of w. The positive parameter D provides the trade-off between the $\ell _0$ pseudo-norm objective and that of the $SVM_1$ problem (3.6)–(3.11).

4 Numerical experiments

The core of our numerical experiments has been the comparison of the results provided by $SVM_0$ with those of $MBP_0$. We have also implemented, as a useful reference, the standard $SVM_1$ model. For better explanation of the results of $SVM_0$ we have introduced a discussion on tuning of the penalty parameter $\sigma$.

We have also provided some additional results comparing our approach with the smoothing methods described in [4, 25].

4.1 $\mathbf {SVM_0}$ versus $\mathbf {MBP_0}$

We have performed our experiments on two groups of five datasets each. They are the same datasets adopted as benchmark for the feature selection method described in [9]. In particular in datasets 1–5 (Group 1), available at http://www.tech.plym.ac.uk/spmc/, the number of samples is small with respect to the number of features. The opposite happens for Datasets 6–10 (Group 2), which are available at https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/. Thus for the latter ones a certain class-overlap is expected.

The datasets are listed in Table 1, where $m=m_1+m_2$ is the total number of samples.

Table 1 Description of the datasets

As a possible reference, we report first the results of the $SVM_1$ problem provided by CPLEX solver. A standard tenfold cross validation has been performed. The results are in Table 2, where the columns “Test” and “Train” indicate the average testing and training correctness, respectively, expressed as percentage of samples correctly classified. Columns “$\Vert w\Vert _1$” and “Time” report the average $\ell _1$ norm of w and the average execution time (in seconds). Finally columns “%ft(0)”–“%ft(−9)” report the average percentage of components of w whose modulus is greater than or equal to $10^0$–$10^{-9}$, respectively. Note that, assuming, conventionally, to be equal to “zero” any component $w_j$ of w such that $|w_j| < 10^{-9}$, the percentage of zero-components is $(100-\%ft(-9))$.

Two different values of parameter C have been adopted for the two dataset groups. In fact we have taken the “best” values obtained through the so called “Model selection” phase performed in [9], where a grid of values ranging in the interval $[10^{-1}, 10^2]$ has been considered.

Table 2 $SVM_1$—Cplex implementation—tenfold cross validation

Before reporting the results of the implementation of our algorithm to solve $SVM_0$, we illustrate in Tables 3 and 4 the results provided by CPLEX implementation of model $MBP_0$, described in Sect. 3.1, with maximum running time of 1000 s. Note that on some test problems, the maximum running time has been achieved with no optimality certification. The results we provide in such cases are related to the best solution found.

Table 3 $MBP_0$—Cplex implementation—tenfold cross validation—Group 1

Table 4 $MBP_0$—Cplex implementation—tenfold cross validation—Group 2

Some comments are in order. We observe first that the average computation time for solving the Linear Program $SVM_1$ is negligible.

As for classification performance, comparison of Table 2 with Tables 3 and 4 highlights that the use of an explicit feature selection mechanism results in a mild downgrading of the classification correctness. Such phenomenon is compensated by the reduction in the percentage of the numerically significant features (columns“ft(0)”–“ft(−9)”).

Coming now to our method (referred to, in the sequel, as the “$SVM_0$ Algorithm”), we report in Table 5 the results on the two groups of datasets.

We have added the two columns “%Viol.” and “$e^{\top }(u+v)$”. In particular, column “%Viol.” reports the percentage ratio between the average violation of the relaxed constraint (3.13) and the average norm $\Vert w\Vert _1$. Column “$e^{\top }(u+v)$” reports the average value of the scalar product $e^{\top }(u+v)$, which, for small values of the companion parameter “%Viol.”, reasonably approximates $\Vert w\Vert _0$.¹

Table 5 $SVM_0$ algorithm—tenfold cross validation

We have run the algorithm on each dataset for different values of the penalty parameter $\sigma$, and we indicate in Table 5 the specific value of $\sigma$ the results refer to.

Some comments follow.

• In terms of classification correctness, the results of the $SVM_0$ Algorithm are comparable with those of $MBP_0$.

• The $SVM_0$ Algorithm provides better results in terms of number of zero-components of w. In fact, the percentage of components conventionally assumed equal to zero, that is $(100-\%ft(-9))$, is significantly bigger, except that in two cases, in $SVM_0$ Algorithm than in $MBP_0$.

• The computation time is, for both algorithms, negligible on the datasets of Group 2 while it is remarkably smaller for $SVM_0$ Algorithm as far as datasets of Group 1 are concerned.

4.2 Tuning of the penalty parameter

In running the $SVM_0$ Algorithm, the most relevant issue is the appropriate tuning of the penalty parameter $\sigma >0$, which is, of course, dataset-specific. Two aspects are to be taken into account.

• “Small” values of $\sigma$ may lead to significant violation of the penalized constraint at the optimum of problem (3.20)–(3.23). Note that in such case, variables u and v may loose their “marker” role highlighted in Proposition (2.2).

• “Large” values of $\sigma$ may result in trivial solutions ($w=0$) to the penalized problem (see Proposition 2.4).

To illustrate in details the impact on the solution of parameter $\sigma$, we analyze the results for increasing values of $\sigma$. In particular we focus on the datasets CARC and IONO, from the first and second group, respectively. The results are reported in Tables 6 and 7.

Table 6 Results on dataset CARC for different values of $\sigma$

Table 7 Results on dataset IONO for different values of $\sigma$

We observe that on both datasets increasing values of $\sigma$ results, as expected, in deterioration of the classification correctness (under such point of view, significant data are those obtained in the training phase). On the other hand, the violation of the relaxed constraint gets smaller and smaller, until, for too large values of $\sigma$, the results become meaningless, as w gets close to zero.

4.3 $\mathbf {SVM_0}$ versus smoothing methods

To provide a better assessment of the proposed method we present some comparisons with results taken from [4, 25], where a number of smoothing approaches to $\ell _0$ pseudo-norm minimization in SVM framework are described.

As for comparison with [4] we take in consideration the datasets of Group 2, which have been in fact adopted as test problems in [4]. We do not consider here the Breast Cancer (BC) dataset, since two different variants of such dataset have been used in this paper and in [4]. In Table 8 we compare training correctness and percentage of zero-value features provided by FSV algorithm from [4] and by our $SVM_0$. In reporting the results of $SVM_0$, we have assumed equal to zero any component of w smaller than $10^{-9}$.

Table 8 Comparison with FSV algorithm [4]

The results are comparable in terms of correctness, while $SVM_0$ seems to produce a stronger feature reduction effect. Comparison in terms of computing time does not appear particularly significant, as for FSV the available data provided in [4] refer only to IONO dataset.

As for comparison with [25], we have considered the datasets of Table 9, which are both linearly separable.

Table 9 Description of the datasets

In Table 10 we report the detailed results obtained by $SVM_0$.

Table 10 $SVM_0$ algorithm

In [25] two different formulations of the sparse minimization problem are discussed; they are based on two smooth concave approximations of the zero pseudo-norm inspired by property (2.3) and are referred to, respectively, as Formulation 1 and 2. The approach adopted is a multi-start one, with 100 runs for randomly selected starting point. The comparison is in Table 11, where for Formulation 1 and 2 are reported both the average and the best value of number of nonzero features. As for $SVM_0$, the average number of nonzero components in the tenfold cross validation procedure is, as usual, reported.

We note, however, that the approach in [25] is a global optimization one, while ours is local. This fact makes comparison difficult, mainly from point of view of computation time.

Table 11 Comparison with [25]

5 Conclusions

We have tackled the Feature Selection problem within SVM binary classification by using the polyhedral k-norm, in the sparse optimization context. The numerical experiments show that the approach is a promising alternative to continuous approximations of the $\ell _0$ pseudo-norm and to integer programming-based methods.

As Feature Selection is an important subject also in other areas of Machine Learning (see, e.g., [7, 28]), we believe that a possible future development of our work would be the extension of the k-norm approach to regression and clustering problems. Yet another possible research direction would be the use of kernel transformations within our model.