Altruistic coordination for multi-robot cooperative pathfinding

Abstract

When multiple robots perform tasks in a shared workspace, they might be confronted with the risk of blocking each other’s ways, which will lead to conflicts or interference among them. Planning collision-free paths for all the robots is a challenge for a multi-robot system, which is also known as the multi-robot cooperative pathfinding problem in which each robot has to navigate from its starting location to the destination while keeping avoiding stationary obstacles as well as the other robots. In this paper, we present a novel fully decentralized approach to this problem. Our approach allows robots to make real-time responses to dynamic environments and can resolve a set of benchmark deadlock situations subject to complex spatial constraints in a shared workspace by means of altruistic coordination. Specifically, when confronted with congested situations, each robot can employ waiting, moving-forwards, dodging, retreating and turning-head strategies to make local adjustments. Most importantly, each robot only needs to coordinate and communicate with the others that are located within its coordinated network in our approach, which can reduce communication overhead in fully decentralized multi-robot systems. In addition, experimental results also show that our proposed approach provides an efficient and competitive solution to this problem.

1 Introduction

Autonomous multi-robot systems are now expected to perform complicated tasks consisting of multiple subtasks that need to be completed concurrently or sequentially [7]. In order to accomplish a specific subtask, a robot usually needs to navigate to the right location first where the subtask can be performed. When multiple robots are engaged in performing tasks in a shared workspace, there is an inherent risk that they may frequently block each other’s ways. As a result, the use of multiple robots may lead to conflicts or interference, which might decrease the performance of an individual robot. In particular, deadlock situations have to be taken into consideration in highly congested settings especially for distributed or decentralized robots to plan their individual paths. This work is motivated by many practical applications such as unmanned underwater/ground vehicles, autonomous forklifts in warehouses, and deep-sea mining robots.

Interference in the Multi-Robot Cooperative Pathfinding (MRCP), or called Multi-Robot Path Planning (MRPP), problem stems from conflicting paths, along which multiple robots attempt to occupy the same places at the same time, or to pass each other. The issue of how to plan collision-free paths for multiple robots has been extensively studied in [3, 8, 13–15, 19], where the robots are supposed to navigate to distinct destinations from their starting locations. Finding an optimal solution to such a problem, however, is NP-hard and intractable [14]. Centralized solutions are usually based on global search and therefore could guarantee completeness, but they do not scale well with large robot teams [3] and cannot be solved in real-time [10]. However, in many practical applications, the robots are expected to be fully autonomous and can make their own decisions, rather than being managed by a central controller [9], and they are supposed to make real-time responses to dynamic environments. Decoupled (or called distributed) solutions are fast enough for real-time applications, but they usually cannot guarantee completeness [8], and the robots may easily get stuck in common deadlock situations. Recent decoupled advances [12, 13, 17] have considered highly congested scenarios. In comparison with our proposed approach, the essential feature of decoupled approaches is that the robots are still connected by a common database, e.g., the reservation table in [12] and the conflict avoidance table in [13]. In this work, we are interested in a fully decentralized solution, where the robots explicitly communicate with one another to keep track of each other’s states and intentions, instead of accessing a common database to be aware of the plans of the others in decoupled solutions.

The advantage of decentralized solutions for multi-robot systems is that, as the robots do not use any shared database, they can be fully autonomous and each robot can be a stand-alone system. On the other hand, such a solution often suffers from high communication overhead in large-scale robot teams because the robots need to directly communicate with each other. To deal with this problem, each robot in our approach only needs to communicate with the ones locating within its coordinated network. For a team of k robots, the communication overhead will be reduced to 12k times in each time step, rather than k(k−1) times in traditional decentralized systems. We analyze various deadlock situations using graph-based models, and propose an altruistic coordination algorithm to identify which situation a robot is confronted with and which strategy it should adopt. Specifically, following the estimated shortest path to its destination, a robot can employ waiting, moving-forwards, dodging, retreating, and turning-head strategies to make local adjustments to avoid potential collisions.

We begin this work by discussing the state-of-the-art approaches to the MRCP problem in Section 2. We analyze the models of our decentralized approach in Section 3, and then discuss the altruistic coordination framework in Section 4. The simulated experiments and results are discussed in Section 5. Finally, Section 6 concludes this work.

2 Related Work

The problem of how to plan collision-free paths has also been studied in the context of exploration (e.g., in [2, 11]). The difference is that the robots in [11] do not have long-term destinations to move towards; instead, they are continually attempting to choose one of the unexplored neighboring vertices to cover. A decision-theoretic approach to multi-robot exploration is presented in [2], where the robots have long-term destinations but do not consider congested configurations. Our work focuses on a general MRCP problem, in which multiple robots are supposed to navigate to distinct long-term destinations from their respective starting locations in a shared workspace that may have highly congested environmental configurations.

Earlier work [1, 15, 20] presented their decoupled solutions based on prioritized planning, where the robots need to plan respective paths in order of their priorities. In other words, the robot with the highest priority first plans its path without considering the locations and plans of the other robots, and then this robot is treated as a moving obstacle so that subsequent robots have to avoid it when planning their individual paths later. In such an approach, each robot is expected to find a path without colliding with the paths of higher priority robots, but the overall path planning algorithm will fail if there is a robot unable to find a collision-free path for itself. In particular, such an approach does not respond well in highly congested scenarios such as intersections. The work in [4] introduced an approach to solving the two-way intersection traffic problem, which is not considered as a congested configuration in our work. Traffic problems usually have two-way roads and thus can be solved by introducing traffic lights, whereas one-way intersections cannot be simply solved by using the traffic light theory.

Recent decoupled advances considering highly congested environments include FAR [16], WHCA* [12], MAPP [17], and ID [13]. FAR and WHCA* are fast and can scale well with large robot teams, but they are still incomplete and offer no guarantee with regard to the running time and the solution length. MAPP has an assumption that for every three consecutive vertices in a robot’s path to its destination, an alternative path that does not go through the middle vertex should exist, which apparently does not suit a narrow corridor setting. As the ID [13] approach claims that it provides a complete and efficient algorithm by breaking a large MRCP problem into smaller problems that can be solved independently, we use it to compare with our proposed approach in the experimental study.

Our work takes the advantage of push and swap ideas proposed in [8], which presents a centralized approach that allows one robot to push the other one away from its path, or makes two robots switch their positions at a vertex with degree ≥3. This approach only allows one robot (or paired robots) to move in each time step. In contrast, we propose a fully decentralized approach in which the robots are assumed to be altruistic, i.e., each robot has the willingness to make concessions in congested situations, even a concession may result in disadvantage for itself. In our approach, each robot follows a heuristic estimated shortest path towards its destination, but it needs to make local adjustments to deal with potential collisions with other robots. When facing congested situations, the robots can apply waiting, moving-forwards, dodging, retreating, and turning-head strategies to coordinate with the other robots that are located within its coordinated network to make further progress. This work focuses on a general MRCP problem that is analyzed based on graph-based models, so the motion planning problems with regards to low-level control parameters, such as speed, acceleration, deceleration and turning angle, are beyond the scope of this paper.

3 Models of Decentralized Cooperative Pathfinding

In this section, we first formulate the problem that we study here and then discuss the coordinated network that is used for the robots to make local adjustments.

3.1 Problem Formulation

A shared workspace can be divided into a finite set of n discrete cells $\mathcal {V}$ with k robots $\mathcal {R}$, k<n, and we use an undirected graph $\mathcal {G}(\mathcal {V}, \mathcal {E})$ to represent the entire environment of the workspace. The edges $\mathcal {E}$ indicate whether two vertices are connected or not in $\mathcal {G}$. We assume that $\mathcal {G}$ is divided uniformly, so edges have unit length l, i.e., it costs l for a robot to move to a neighboring vertex from its current vertex. In order to model realistic robots that are usually equipped with physical actuators and effectors, we define a spatial constraint in the graph: robots must be present at distinct vertices at any time t:

$$ \forall i, j \in [1,k], i \neq j: \mathcal{A}_{t}[i] \neq \mathcal{A}_{t}[j], $$

(1)

where ${A}_{t}[i] \in \mathcal {V}$ indicates the vertex in which the i-th robot locates at time t. The sets of starting locations and destinations are denoted as $\mathcal {S}\subset \mathcal {V}$ and $\mathcal {T} \subset \mathcal {V}$, respectively. We use $\mathcal {S}[i]$ and $\mathcal {T}[i]$ to denote the starting location and destination of the i-th robot. The robots are supposed to navigate from their own starting locations to destinations without blocking each others ways.

We assume that each robot can only move one unit length per time step. In our work, in order to move to its destination, a robot should have a next-step plan $\mathcal {P}_{t+1}$ at any time t, either staying at its current vertex $\mathcal {A}_{t}$ or moving to one of its neighboring vertices $\mathcal {A}_{t+1}$:

$$ \mathcal{P}_{t+1}[i] \Rightarrow \left\{ \begin{array}{ll} \mathcal{A}_{t}[i] = \mathcal{A}_{t+1}[i] & \text{(stay at its current vertex)}\\ (\mathcal{A}_{t}[i], \mathcal{A}_{t+1}[i]) \in \mathcal{E} & \text{(move to a neighbouring vertex)} \end{array}\right. ,i \in [1,k]. $$

(2)

Give the starting location $\mathcal {S}[i]$ and the destination $\mathcal {T}[i]$ of the i-th robot, when beginning to carry out the task, the robot needs to plan an initial path π₀[i]:

$$ {\Pi}_{0}[i]=\{ \mathcal{S}[i], \ldots, \mathcal{T}[i]\}. $$

(3)

At any time t, the robot may need to adjust its initial planned path π₀[i] because of the existence of the other robots, so we use π _t [i] to represent its real-time planned path of the i-th robot:

$$ {\Pi}_{t}[i]=\{ \mathcal{A}_{t}[i], \mathcal{A}_{t+1}[i], \ldots, \mathcal{T}[i]\}. $$

(4)

If the robot has arrived at its destination at time e, then we can know $\mathcal {A}_{e}[i]=\mathcal {T}[i]$ and ${\Pi }_{e}[i]=\{\mathcal {T}[i]\}$, which means that the robot does not need to move anymore and its next-step plan is staying at the current location. Therefore, the objective of the robots working in such a shared environment is to minimize e, while avoiding collisions with stationary obstacles as well as the other robots.

3.2 Heuristic Estimated Shortest Paths

Figure 1a shows an example of the initial configuration of an environment for multi-robot path planning, where four robots need to start from S1,S2,S3 and S4 to go to their destinations T1,T2,T3 and T4. When planning their respective paths to the destinations, if each robot disregards the presence of the others, they can easily find the shortest paths, as shown in Fig. 1b. Such a path, only considering avoiding stationary obstacles, provides a heuristic optimal estimate with the shortest travel distance that can be calculated by performing a graph search, for example, using Dijkstra’s algorithm.

Fig. 1

Heuristic estimated shortest paths

Although these estimated paths do not guarantee that a robot can successfully arrive at its destination without any collisions with the other robots, it indeed provides an idealized estimate, and at least indicates which direction the robot can move towards. We use $\mathcal {H}_{t}[i]$ to denote the heuristic estimated shortest path of the i-th robot at time t:

$$ \mathcal{H}_{t}[i] = \{\mathcal{U}_{1}[i], \mathcal{U}_{2}[i], \ldots, \mathcal{T}[i]\}, $$

(5)

where $\mathcal {U}_{1}[i]$ and $\mathcal {U}_{2}[i]$ are the first and second successor vertices in $\mathcal {H}_{t}[i]$, representing which vertices the robot is planning to move in the next two steps. Thus, (4) can be written as:

$$ {\Pi}_{t}[i]=\mathcal{A}_{t}[i] \bigcup \mathcal{H}_{t}[i] = \{ \mathcal{A}_{t}[i], \mathcal{U}_{1}[i], \mathcal{U}_{2}[i],, \ldots, \mathcal{T}[i]\}, $$

(6)

and we can know that $(\mathcal {A}_{t}[i],\mathcal {U}_{1}[i])\in \mathcal {E}$, $(\mathcal {U}_{1}[i], \mathcal {U}_{2}[i])\in \mathcal {E}$. If at time t the i-th robot can move to its destination after one step, then $\mathcal {H}_{t}[i]=\{\mathcal {T}[i]\}$, ${\Pi }_{t}[i] = \{ \mathcal {A}_{t}[i], \mathcal {T}[i]\}$ and $\mathcal {U}_{1}[i] = \mathcal {T}[i]$, $\mathcal {U}_{2}[i]=0$. When the robot has arrived at its destination, we can have $\mathcal {U}_{1}[i] = \mathcal {U}_{2}[i]=0$, which means that the robot does not have any plans of moving.

3.3 Coordinated Network

As mentioned above, a robot takes unit length l to move to a neighboring vertex in $\mathcal {G}$. For any robot $r \in \mathcal {R}$ at time t, it has the first and second successor vertices, $\mathcal {U}_{1}[r]$ and $\mathcal {U}_{2}[r]$, along its estimated shortest path $\mathcal {H}_{t}[r]$ (see (5)). At the moment, $\mathcal {U}_{1}[r]$ might be occupied by one of its teammates, or be free but its teammate(s) is going to occupy it. For example, Fig. 2a shows that the vertex that robot r wants to move into is occupied by robot s, whereas Fig. 2b shows that although that vertex is not occupied by any teammates right now, but robot s and w also want to move into it. Thus, if robot r executes its next-step plan, according to its estimated shortest path, it might collide with another one, which can be regarded as a conflicting plan.

Fig. 2

Coordinated network with the communication range of 2l

From Figs. 2a and b, we can know that if the next-step plan of robot r conflicts with the plan of robot s, s must be locating within the distance of 2l. This means that in order to avoid potential collisions, robot r only needs to care about the presence of the others that are locating within the range of 2l. The robot thus needs to coordinate with those robots so that they can make local adjustments to avoid collisions. To this end, the robot only need to communicate with a few local robots, instead of all the other robots in the workspace.

For k decentralized robots, normally, each of them needs to communicate with all the other k−1 robots. Thus, the robots need to communicate at least k(k−1) times in each time step. Excessive communication is then required when a large number of robots is working in a shared environment. In this work, each robot will construct a coordinated network with the communication range of 2l, and it only needs to communicate and coordinate with the others locating within its coordinated network. As shown in Fig. 2c, within that communication range, at most there are 12 other robots, so the communication overhead can be reduced to no more than 12k times for each time step.

In addition, each robot, e.g., robot r, does not need to communicate all the information about its heuristic estimated shortest paths $\mathcal {H}_{t}[r]$; instead, it only needs to broadcast its first and second successor vertices, i.e., $\mathcal {U}_{1}[r]$ and $\mathcal {U}_{2}[r]$, in our approach. We will detail how the robots use such information to make local adjustments to avoid collisions in the next section.

4 Decentralized Multi-Robot Altruistic Coordination

In this section, we first discuss how a robot plans its next-step towards its destination, and then discuss how it makes local adjustments in order to avoid potential collisions with the others.

4.1 Decision Making for Planning Next-Step

As robots can make their own decisions in decentralized systems, we will discuss our proposed approach from the point of view of an individual robot. Algorithm 1 shows the main decision making process for an individual robot r to make its next-step plan.

According to Algorithm 1, robot r needs to continuously make its next-step plan until arriving at its destination (line 2). It either chooses the successor vertices along the estimated shortest path (see line 6), or needs to turn its head to a new coordinated robot (line 4) if it took a turning-head strategy in the last cycle of the decision process, which will be discussed in detail in Algorithm 2. If the first successor vertex of robot r is occupied by another robot s, then r needs to coordinate with s (line 8). Sometimes the successor vertex might not be occupied, but one of its teammates has planned to move into it (line 9). In this case, the robot needs to wait at its current location for the next cycle of decision making. Otherwise, it can make the plan to move to the free successor vertex (line 11). In Algorithm 2, the robot can also adjust its planned successor vertices, according to the situation that it is facing at the moment. For communication, the robot only needs to broadcast its adjusted successor vertices and next-step plan to the others that are locating within its coordinated network (line 13). It happens that several robots may make decisions to go to the same vertex synchronously. In our approach, while executing a plan to move to a vertex, if a robot finds that there is another one moving to the same vertex as well, the robot will immediately stop moving, give up its original plan and inform the other robot about its decisions.

4.2 Altruistic Coordination in Deadlock Situations

When moving towards its destination along the estimated shortest path, if a robot realizes that its first successor vertex is occupied by another robot, it needs to make local adjustments. The principle of our approach is that all the robots are assumed to be altruistic, which means that each of them has the willingness to make concessions in a congested situation in order to avoid collisions, even if a concession may result in disadvantage for itself. In some situations such as a narrow corridor, if two robots intend to pass each other, one of them has to move backwards. Otherwise, they will be blocked by each other. Thus, the robots need a method to reach an agreement on which robot should make a concession and what kind of concessions is needed to make further progress.

When the first successor vertex of a robot is occupied by the other robot, they might be facing various environmental configurations. We list the instances that may lead to a set of benchmark deadlock situations in Fig. 3. In order to show the completeness of the set of possible deadlock situations, the listed instances will be analysed in different groups. Basically, we need to check whether they are heading the same direction, or they intend to swap their locations. For the former case, we need to further check when their paths will deviate from each other because they have different destinations. Such a configuration is called trail following in this work. For the later case, we need to consider whether, and if so, how many neighboring vertices each of the robots has. In the graph models, apart from the neighboring vertex that a robot has planned to move in (i.e., the first successor vertex), it may have no, one, two or three other vertices. According to the current and intended locations of both of the robots, the possible configuration might be a T-junction, an intersection, a narrow corridor, or a dead-end corridor. In the following subsections, we will discuss how to identify a possible situation, and which kind of strategies should be used in each situation.

Fig. 3

Various environmental configurations that may result in a deadlock situation

4.2.1 Trail Following

Figure 3a and b depict that robot r is following the trail of robot s, $(\mathcal {U}_{1}[r] == \mathcal {A}_{t}[s])\bigcap (\mathcal {A}_{t}[r] \neq \mathcal {U}_{1}[s]).$ This means that robot r wants to move into the vertex where robot s is staying, but robot s wants to go to another vertex that differs from the location where robot r is staying. Still, the choices of robot s can be classified into two categories, as shown in Figs. 3a and b, respectively. More specifically, after the first successor vertex, robot r may diverge from s (see Fig. 3a), $\mathcal {U}_{2}[r] \neq \mathcal {U}_{1}[s]$, or still follow the trail of s (see Fig. 3b), $\mathcal {U}_{2}[r] == \mathcal {U}_{1}[s]$.

In both instances, robot r would believe that s is trying to move away from the occupied vertex at the moment, so it can move forwards to the location of robot s. Sometimes they may come to a situation, as shown in Fig. 3c, where robot s cannot move away right now just because it is blocked by another robot v and does not have any other free neighboring vertex. It should be noted that in such a case it is not robot r who should try to find a solution for robot s because s must be coordinating with v in its own decision process at the same time. Robot r still believes that robot s can successfully move away from that occupied vertex, so it can wait at this time step for robot s to succeed.

4.2.2 Intersections

In the remaining instances, i.e., from Figs. 3d to c, robot r and s want to swap their positions, $(\mathcal {U}_{1}[r] == \mathcal {A}_{t}[s])\bigcap (\mathcal {A}_{t}[r] == \mathcal {U}_{1}[s])$, but they still can be further categorized into different congested situations. Figures 3a, b and c shows T-junction or intersection configurations, where at least one robot has the other free neighboring vertex that differs from the second successor vertex of the other one. This means that in order to avoid collisions and pass each other, one of them can move to a temporal vertex that is not a planned vertex of any robots along their estimated shortest paths.

Such a temporal vertex can be available for both robot r and s, as in Figure 3d, and only for one of them, as in Figs. 3e and f. In our approach, as all the robots are assumed to be altruistic, when robot r realizes that it has a free vertex in Figs. 3d and e, it will actively dodge itself to this vertex. For the instance in Fig. 3f, robot r believes that robot s would apply the same strategy as what it will do in Fig. 3e because they are all altruistic. Thus, robot r can confidently move forwards to its first successor vertex in this case because it believes that robot s will make a concession.

4.2.3 Corridors

Figures 3g, h and i show that both robot r and s do not have the other free neighboring vertex, except for each other’s second successor vertex. Such a configuration corresponds to usual narrow or dead-end corridors, where one of them has to go backwards in order to make further progress and avoid collisions.

The difference between these instances is that in Fig. 3g each robot can go backwards, whereas only one of them can do so in Figs. 3h and i. In our altruistic coordination framework, as robot r believes that it can go backwards in Fig. 3g and h, it will actively retreat itself and move backwards at this time step. However, when confronted with the situation, as shown in Fig. 3i, robot r will take it for granted that robot s can retreat as what it will do in the case of Fig. 3h, so it can confidently move forwards to the location where robot s is staying at the moment.

4.2.4 Clusters

Figures 3j, k and l show that robots are clustering together, i.e., robot r and s do not have any free neighboring vertex. In Figs. 3j and k, robot r has a neighboring vertex but occupied by another robot w, whereas in Fig. 3l, apart from the vertex occupied by robot s, r does not have any other neighboring vertex, but s has the one but occupied by robot v.

At the moment, we can see that the coordination relationship is constructed between robot r and s, and they cannot make any further progress to deal with such a deadlock situation. But in Figs. 3j and k, robot r can turn its head and reconstruct a relationship to coordinate with robot w, instead of keeping coordinating with s. Similarly, robot s can reconstruct a relationship with robot v in its own decision process when confronted with the case of Fig. 3l. Applying the turning-head strategy, a robot can turn its head towards a different direction, but it still needs to wait at this time step because it cannot make any movements.

It should be noted that in the instances as shown in Figs. 3d, g and j, one may worry that both robot r and s will apply the same strategy (i.e., dogging, retreating or turning-head) to make a concession at the same time step. In our work, as the robots are fully decentralized, their decision making processes are asynchronous. This means that once robot r makes a decision and informs robot s, the environmental configuration for s will be changed. Therefore, robot s does not need to face the same situation.

4.3 Transformation of Deadlock Situations

As discussed above, the robots can employ waiting, moving-forwards, dodging, retreating and turning-head strategies to cope with a set of benchmark congested situations that have trail following, intersection, corridor, or cluster configurations. In the trail following situation, robot r needs to either move forwards or just wait, so it still can keep the first and second successor vertices, i.e., $\mathcal {U}_{1}[r]$ and $\mathcal {U}_{2}[r]$, along its estimated shortest path. But in the other situations, the robot may need to make local adjustments, i.e., move to a vertex that differs from the planned $\mathcal {U}_{1}[r]$, or head towards a direction that differs from $\mathcal {U}_{1}[r]$, even if it cannot move. We will discuss how these congested situations will be transformed after applying corresponding strategies discussed above and how robot r and s can successfully swap their locations.

4.3.1 Transforming Intersections

Figure 4 shows how robot r and s swap their locations in an intersection situation shown in Fig. 3d, which is also applied to the instance in Fig. 3e. According to the estimated shortest path, if robot r does not make local adjustments at time t, it should move to its first successor vertex $\mathcal {U}_{1}[r]$, which is, however, impossible because robot s occupies that vertex at the moment. If robot r applies the dodging strategy, it will go to a free neighboring vertex. This means that the robot needs to change its original next-step plan because of such an adjustment (see Fig. 4b), and it will also inform the others including robot s about the change of its next-step plan. Here we replace $\mathcal {U}_{1}[r]$ by this free vertex and set $\mathcal {U}_{2}[r]=0$. Then, from the point of view of robot s, it does not need to swap its location with robot r at the moment; instead, it will face a new situation in which it is following the trail of robot r, and, therefore, it can move forwards to its first successor vertex.

Fig. 4

Transforming the intersection situation in Fig. 3d

After one step moving (i.e., at time t+1 as shown in Fig. 4c), robot r and s need to calculate their respective estimated shortest paths again. As a result, robot r needs to go backwards¹ to the location where robot s is staying. Since robot s has passed r, it can continue moving forwards along its estimated path. For robot r, we can see that it will be following the trail of robot s at time t+1, so it can move into its current first successor vertex, i.e., the current location of robot s. Finally, they can swap their locations after robot r applying the dogging strategy. We can notice that intersection situations can be transformed into trail following situations if one of robots applies the dogging strategy.

4.3.2 Transforming Corridors

Figure 5 shows how robot r and s attempt to swap their locations in a narrow corridor depicted in Fig. 3g, which is also applied to the instance in Fig. 3g. Figure 5b shows that robot r applies the retreating strategy, so it will change its original next-step plan $\mathcal {U}_{1}[r]$ and move backwards. At the same time, robot s can confidently move forwards if it knows that robot r has changed its heading direction. After one time step, both of them need to make further progress by re-calculating their respective shortest paths to their destinations, as shown in Fig. 5c. It should be noted that if robot s applies the retreating strategy at time t+1, Fig. 5c will become Fig. 5a again. This means that they may still get stuck in a very long narrow corridor because of such stochastic back and forth movements.

Fig. 5

Transforming the corridor situation in Fig. 3g

We can imagine that the only solution to breaking deadlocks in a long narrow corridor is that one of the robots must go backwards until they leave the corridor. To this end, it requires that one robot must always go backwards, while the other can continue moving forwards. In our work, once a robot applies (or believes that the other robot will apply) the retreating strategy, it needs to remember its choice. After this time step, if they are still facing the corridor situation, they need to apply the same strategy so that they can stick to their choices. As shown in Fig. 5d, robot r should continue retreating, whereas robot s can move forwards. The corridor situation can be transformed into an intersection situation if robot r can finally find a free neighbouring vertex to dodge.

4.3.3 Transforming Clusters

In the cluster situations in Figs. 3j, k and l, both robot r and s cannot make further progress, but one of them can turn its heading direction to coordinate with the other robot. If robot r turns its head to robot w at time t, it needs to change its next-step plans $\mathcal {U}_{1}[r]$ (also set $\mathcal {U}_{2}[r]=0$) and inform the other robots about its change. Since the environment configurations might be highly congested, we do not expect that robot r will turn its head again to robot s at time t+1 just because it will be facing a new cluster situation with robot w. Our solution is that once a robot applies a turning-head strategy, it should remember its choice so that it will not turn back again to robot s at time t+1.

In cluster situations, even though applying the turning-head strategy does not allow robot r or s to move one step, the attempt to break up a cluster can be transmitted to the other peripheral robots that have free neighboring vertex to make room. Fig. 6 shows the basic idea of how a cluster situation can be gradually transformed into a trail following situation. An effective step for the robots to make further progress in cluster situations is that they can finally find a free neighboring vertex, which can be a narrow corridor situation, or even an intersection situation. As mentioned above, a narrow corridor situation can be transformed into an intersection situation, which can then be broken up by a trail following situation.

Fig. 6

Gradually transforming clusters into trail following

4.4 Algorithm of Altruistic Coordination

Algorithm 2 gives the details on identifying which situation a robot is confronted with and which strategy it should use. A robot can employ waiting, moving-forwards, dodging, retreating and turning-head strategies to make local adjustments in the altruistic coordination framework. In Algorithm 2, we still we use robot r as an example to explain how it copes with congested situations.

As mentioned in Algorithm 1, robot r needs to coordinate with robot s if its first successor vertex $\mathcal {U}_{1}[r]$ is occupied by robot s at the moment. In general, robot r could be following the trail of s (line 4-8), or attempts to swap its location with s (line 9-26), which can be further grouped into intersection situations (line 10-14), corridor situations (line 15-19), or cluster situations (line 20-25). It should be noted in Algorithm 2 that if the robot only chooses waiting or moving-forwards strategy, its original planned $\mathcal {U}_{1}[r]$ and $\mathcal {U}_{2}[r]$ do not need to be changed, and its next step plan $\mathcal {P}_{t+1}[r]$ will be either staying at current location (line 7, 13, 18 and 24), or moving to the first successor vertex $\mathcal {U}_{1}[r]$. However, if the robot chooses both turning-head and waiting strategies in the cluster situations, its should also adjust its $\mathcal {U}_{1}[r]$ and $\mathcal {U}_{2}[r]$ (line 22). For the dogging and retreating strategies, the robot always needs to accordingly adjust its first and second successor vertices (line 11, 16).

4.5 Cooperative Teams

We have discussed how an individual robot makes its next-step plan towards its destination in Algorithm 1, and how it makes local adjustments in order to avoid collisions or swap positions with another robot. Here we need to consider an important issue in which, for example, robot r has arrived at its destination, but robot s, according to its estimated shortest path, has to pass the location of robot r. In this case, for robot r, in principle it does not need to move anymore because of $\mathcal {U}_{1}[r] = \mathcal {U}_{1}[r] = 0$, but if robot s is considered as its teammate, it should has the willingness to help robot s. In our approach, if robot r has arrived at its destination but realizes that s needs to pass its current location, it can actively apply dogging, retreating, or turning-head strategy to temporally move away from its current location. Once robot r deviates from its destination, it can again use Algorithm 1 to replan a path to its destination, which can be achieved by the same procedures discussed above.

5 Experiments and Results

5.1 Experimental Setup

For the sake of repeatability and accessibility, our experimental study is performed in a simulator, called the Blocks World for Teams (BW4T).² Robots in the BW4T are GOAL[5], the agent programming language that we have used for implementing our proposed approach. We also use GOAL agents to control real robots in the work [18], but the simulator is much easier for collecting data and repeat experiments. GOAL, is a rule-based language that supports explicit communication among agents that make decisions based on mental states consisting of knowledge, beliefs, and goals. Here beliefs keep track of the current state of the world, while goals keep track of the desired state of the world. Fig. 7 gives an example of how to use the GOAL agent programming language to implement the altruistic coordination module, i.e., Algorithm 2. Of course, the agents in our approach also need other modules to work in the BW4T, such as the modules to obtain environmental percepts and to handle messages. Detailed information about the GOAL, agent programming language and the development of GOAL, agents can be found in [5].

Fig. 7

Implementing Algorithm 2 using GOAL, agent programming language: bel(Fact) means the agent believes that Fact is true. When the agent adopt(Goal), it will insert Goal into its goal base and execute an corresponding action to achieve the goal. When the agent insert(Fact), it will insert Fact into its belief base. Agents can also use send( Message) to explicitly send messages to other robots

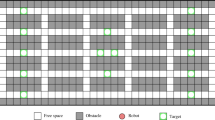
The environment of the BW4T simulator can be constructed using grid maps (see Fig. 8), and each cell in a map only allows one robot to be present at a time in this work. In our experiments, as shown in Fig. 8, the robots start from the bottom of the map, and randomly choose distinct destinations locating at the top of the map to navigate towards in each simulation. The other gray cells represent the stationary obstacles. In the experiments, we investigate scalable robot teams ranging from 1 to 8, and each simulation has been run for 100 times to reduce variance and filter out random effects. We consider the performance metrics, time-cost and energy-cost, in which time-cost is concerned with the average time that each robot spends on navigating to its destination, and energy-cost is used to measure the average steps that each robot has moved when arriving at its destination. Our experiments run on an Intel i7-3720 QM at 2.6 GHz with 8 GB of RAM.

Fig. 8

The map used for the experiments in the BW4T simulator

5.2 Results

Figure 9 shows the results of the experimental study in which we have tested our proposed decentralized approach, called DMRCP, and the ID approach proposed in [13]. The horizontal axis in Fig. 9 indicates the number of robots working in the environment.

Fig. 9

Experimental results of the DMRCP and ID approaches

5.2.1 Time-Cost

As the program of each approach implemented by the GOAL, agent programming language has different complexities, we can get a general impression that for each cycle of decision processes, the DMRCP agents run slower than the ID agents. For instance, using the DMRCP approach, a single robot takes 5.13 seconds to arrive at its destination on average, whereas it only takes 3.92 seconds for the ID approach (see Fig. 9a). We can see that for a small number of robots, i.e., 1 to 4 robots, the DMRCP approach always spends more time than the ID approach, but when the number of the robots increases, i.e., 5 to 8 robots, the DMRCP approach takes less time than the ID approach. Therefore, we can conclude that even though the running time of the DMRCP’s program is more expensive than the ID’s program implemented by GOAL, agents, the DMRCP approach can provide a competitive solution to the multi-robot cooperative pathfinding problem.

In addition, we can see in Fig. 9a that from 1 robot to 8 robots, the time-cost of the ID approach almost linearly goes up from 3.96 to 10.45 seconds. The increasing rate is around $\frac {10.45-3.96}{8-1} \approx 0.92$. Comparatively, the time-cost of the DMRCP approach grows from 5.13 to 9.24 seconds, and its increasing rate is only about 0.59. The results thus can reveal that with the increase of the robots working in a shared space, the time-cost of the DMRCP approach goes up slower than the ID approach. It is because the main strategy of the ID approach is that if two robots have conflicting paths, one of them needs to find an alternative path, the length of which might be much longer than the previous one. It will become much more severe when the number of robots increases because more robots may need to frequently find alternative paths. In contrast, the robots in the DMRCP approach always take the shortest paths to their destinations and only need to make local adjustments to avoid conflicting plans. Most importantly, the robots can employ waiting strategy in our approach, which cannot be easily modelled in other approaches to the MRCP problem. We can see that waiting can be an effective strategy to avoid potential collisions, but it does not significantly increase the time-cost because the robots can still keep the shortest paths towards their destinations. Thus, we believe that our solution can scale well to a large number of robots.

5.2.2 Energy-Cost

More robots will bring in more conflicts in a shared workspace. From Fig. 9b, we can see the fact that if there are more robots, each of them takes more moving steps on average in order to arrive at their destinations. Theoretically, for the single robot case, the DMRCP approach and the ID approach take the same moving steps as there is no other robot interfering it, which can also be seen in Fig. 9b.

With the increase of the number of the robots, the energy-cost of the DMRCP approach goes up slowly, whereas it rises quickly in the ID approach. For instance, in the case of 8 robots, the DMRCP approach needs 15.69 moving steps on average; comparatively, the ID approach takes 25.25 moving steps. We can also see that the increasing rate of energy-cost using the ID approach is $\frac {25.25-10.94}{8-1} \approx 2.04$ , while it is only $\frac {15.69-11.24}{8-1} \approx 0.64$ if the robots use the DMRCP approach. This is because the DMRCP approach can benefit greatly from the waiting strategy as well as the other local small adjustments. Waiting does not increase energy-cost at all, and local adjustments allow the robots to take as few additional moving steps as possible but still keep the shortest paths towards their respective destinations.

6 Conclusion

In this paper, we analyzed the decentralized multi-robot cooperative pathfinding problem using graph-based models, and then proposed a novel fully decentralized solution to this problem. When confronted with congested situations, a robot only needs to coordinate with the ones locating within its coordinated network, which can also reduce the communication overhead in decentralized systems. Our solution allows the robots to make local adjustments by employing waiting, moving-forwards, dodging, retreating and turning-head strategies, and the experimental results have shown that our approach can provide a competitive solution to this problem and, in particular, scale well with the increase of the robots.